Abstract
In recent years, there is an emerging direction that leverages information theory to solve many challenging problems in scientific data analysis and visualization. In this article, we review the key concepts in information theory, discuss how the principles of information theory can be useful for visualization, and provide specific examples to draw connections between data communication and data visualization in terms of how information can be measured quantitatively. As the amount of digital data available to us increases at an astounding speed, the goal of this article is to introduce the interested readers to this new direction of data analysis research, and to inspire them to identify new applications and seek solutions using information theory.
1. Introduction
The field of visualization is concerned with the creation of images from data to enhance the user’s ability to reason and understand properties related to the underlying problem. Over the past twenty years, visualization has become a standard means to perform data analysis for a variety of data intensive applications. Numerical simulations for fluid flow modeling, high resolution biomedical imaging, and analysis of genome and protein sequences are some examples that can benefit from effective visual data analysis. For these applications, visualization as a fast maturing discipline offers many standard techniques such as isosurfaces, direct volume rendering, and particle tracing to analyze scalar and vector data defined in the spatial domain. For non-spatial data which is more common for business applications, methods such as parallel coordinates, treemaps, and node-link diagrams are widely used.
Currently, the visual analysis process is mostly operated by the user through trial and error in an ad hoc manner. Important parameters for visualization algorithms, such as transfer functions, values of isocontours, levels of detail, and camera positions and directions, often need to be frequently updated and refined before satisfactory visualization results are obtained. As the size of data continues to grow, however, it becomes increasingly difficult to generate useful visualization using this ad hoc approach. Even after many visualizations have been produced, it may be still difficult to determine whether the data have been completely analyzed, or if some important features are left undiscovered. One major cause of the difficulties in visual analysis of large datasets is the lack of quantitative metrics to measure the visualization quality relative to the amount of information contained in the data. As the size of data grows even larger, these problems will become even worse since the user’s ability to move and process the data will be severely limited. Without a systematic and quantitative way to guide the user through the visual analysis process, visualization could soon lose its value to be a viable approach for large-scale scientific data analysis.
In recent years, there is an emerging trend where the principles of information theory are used to solve the aforementioned problems. Introduced by Shannon and Wiener in the late 1940s, information theory was originally used to study the fundamental limit of reliably transmitting messages through a noisy communication channel. To date, information theory has made a profound impact on many fields including electrical engineering, computer science, mathematics, physics, philosophy, art, and economics [1]. Purchase et al. [2] discussed the role of information theory in the context of information visualization. In this article, we interpret information theory principles in the context of scientific visualization. For data analysis and visualization, one may naturally wonder whether information theory can be applied to improve our understanding of the data and furthermore, to assist us to extract hidden salient data features. To better help interested visualization researchers and practitioners answer the questions, we present the key concepts of information theory that are related to the problem of data analysis and visualization. We draw connections between data communication and data visualization, and explain how information theory can be used to quantify the amount of information in scientific datasets and to measure the quality of visualization. We present several representative problems in visualization research and illuminate them with successful applications of information theory. As the amount of data available to us increases at an astounding speed, the goal of this article is to introduce the interested readers to this new direction of research, and to inspire them to identify a broader range of applications and seek solutions using information theory.
Recently, Chen and Jänicke [3] presented an information-theoretic framework for visualization. Their work concentrates on the theoretical aspect of information theory and its relation to data communication. They also interpret different stages of the visualization pipeline using the taxonomy of information theory. Our article complements their work by taking a retrospective look at related work and presenting our view of how information theory principles can be applied to scientific visualization.
2. Visualization and Information Channel
Figure 1 illustrates the analogy between data communication and data visualization. In data communication, one attempts to transmit a message X through a noisy communication channel to the destination, the receiver. Due to the noisy nature of the channel, information loss could be inevitable, resulting in a different version of the message, which we denote as . One familiar example of data communication is transmitting voice over the telephone line. Such a channel often fails to exactly reproduce the original voice signal. Noise, periods of silence, and other forms of signal corruption often degrade the quality. One obvious goal of data communication is therefore to understand the uncertainty of the symbols embedded in a message so that the message can be encoded properly to reduce the possibility of being contaminated in the noisy channel.
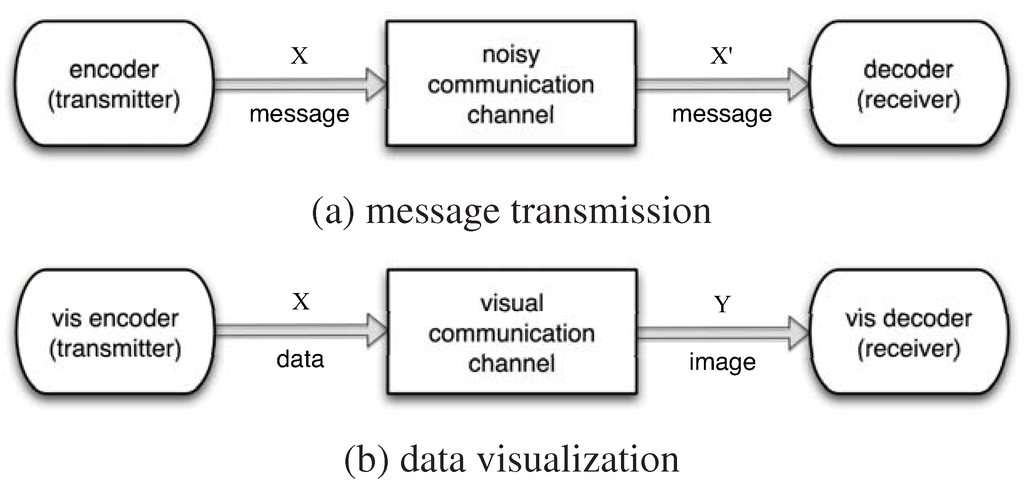
Figure 1.
The analogy between message transmission and data visualization. Here we only sketch a simple model in one stage transmission. In reality, either message transmission or data visualization consists of multiple stages. Refer to the work by Chen and Jänicke [3] for more detailed illustration.
Similarly, the visualization process can be treated as an information channel, i.e., a visual communication channel that attempts to communicate the information in the source data to the destination, the viewer. In a typical visualization pipeline, the data need to be transformed by a sequence of steps such as denoising, filtering, visual mapping, and projection. Each of the transformation steps in the visualization pipeline can be thought of as an encoding process where the goal is to preserve the maximum amount of information from the input and generate the output for the next stage of the pipeline. When information loss is inevitable, such as in the case of projecting 3D data to 2D images, special care is needed so that appropriate parameters are chosen to preserve as much information as possible. Only in doing so, are we able to faithfully reveal the information embedded in the data through visualization.
3. Concepts of Information Theory
3.1. Entropy
Information theory provides a theoretical foundation to quantify the information content, or the uncertainty, of a random variable represented as a distribution. Formally, let X be a discrete random variable with alphabet and probability mass function , . The Shannon entropy of X is defined as
where , , and represents the information associated with a single occurrence of x. The unit of information is called a bit. Normally, the logarithm is taken in base 2 or e. For continuity, zero probability does not contribute to the entropy, i.e., . As a measure of the average uncertainty in X, the entropy is always nonnegative, and indicates the number of bits on average required to describe the random variable. The higher the entropy, the more information the variable contains. An important property of the entropy is that is a concave function and reaches its maximum of if and only if is equal for all x, i.e., when the probability distribution is uniform. As we shall see in Section 4, the notion of “equal probability, maximum entropy" is at the heart of probability function design in many of the visualization examples we will review. The key of applying the concept of entropy to visualization problems lies in how to properly specify the random variable X and define the probability function . In most cases, these probability functions can be defined heuristically to meet the need of individual applications.
To apply the Shannon entropy, we can model a scientific dataset as a discrete random variable where each data point in the domain carries a value as the outcome. The probability mass function of the random variable X can be estimated using histogram. That is, we can use the normalized frequency of each histogram bin as the probability . In a simple example, given a 3D volume dataset, we can model the entire dataset as a discrete random variable X where each voxel carries a scalar value. The entropy indicates how much information the dataset contains. If the distribution in the histogram is uniform across all bins, then it is difficult to predict the value of a voxel. Thus the entropy of the dataset is high. On the contrary, if the histogram distribution is highly skewed into a few bins, then it is easy to guess the value of a voxel. Thus the entropy of the dataset is low.
In Figure 2, we show an example 2D hurricane dataset and its derived entropy fields. For Figure 2(b) and (c), a constant-size 2D local window centered at each pixel is used to compute the entropy in the pixel’s neighborhood. We discretize the velocity magnitude or direction into a certain number of bins and compute a 1D histogram for each local window accordingly. The derivation of entropy follows Equation (1). As we can see in (b) and (c), around the center of the hurricane, the entropy is high in both evaluations. Unlike the velocity magnitude, the velocity direction also varies greatly around local regions on the right side of the hurricane’s center (as we can see that those regions have high entropies as well). We can also trace streamlines from the 2D flow field and evaluate the entropy associated with each control point along the streamlines. For Figure 2(d), a constant-size 1D local window centered at each control point along each streamline is used to evaluate the entropy at the control point. We create a 2D histogram in this case for each local window with one dimension for velocity magnitude and the other dimension for velocity direction. We can see that the streamlines close to the hurricane’s center have high entropies, mainly due to the changes of velocity direction (as evident by the circular flow pattern). Intuitively, the entropy images highlight which regions in the data are important or interesting in terms of exhibiting more variation or change in their local neighborhood compared with other regions.
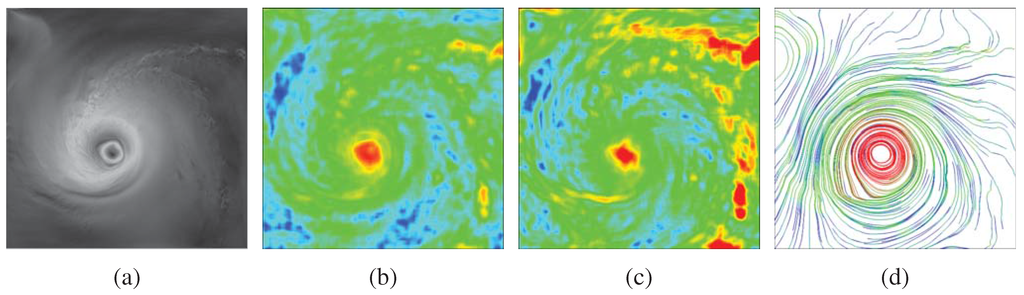
Figure 2.
(a) a 2D hurricane field of velocity magnitude. (b) the entropy field derived from velocity magnitude. (c) the entropy field derived from velocity direction. (d) uniformly placed streamlines with color coded entropy derived from velocity direction and magnitude. The entropy value increases from blue to green to red in (b), (c), and (d).
Wang et al. [4] demonstrated that in practice, the evaluation of data entropy can be more flexible. For instance, depending on the need, we can partition a large volume dataset into individual blocks and evaluate the entropy on a per-block basis. We can also consider more than just a single scalar field when building a histogram. This means that the histogram can be multidimensional, including not only the raw data, but also other derived quantities such as local features (e.g., gradient magnitude or direction) and/or domain-specific derivatives. Furthermore, each bin in such a multidimensional histogram can carry a weight indicating its relative importance in the entropy calculation. This is the place where domain knowledge about the data or visualization-specific quantities can be leveraged. For example, in volume visualization, the user needs to specify a transfer function so that scalar data values can be mapped to optical quantities such as colors and opacities. The opacity value can be used to set the weight for its corresponding histogram bin. A bin with a higher opacity value is likely to have more contribution to the resulting image per voxel, and therefore, should be assigned with a higher weight.
3.2. Joint Entropy and Relative Entropy
The concept of entropy can be extended to two or more variables. For instance, the joint entropy for a pair of random variables with a joint distribution of is defined as
Note that is always at least equal to the entropies of X and Y alone, as adding a new variable can never reduce the available uncertainty, i.e.,
Furthermore, two variables X and Y, considered together, can never have more entropy than the sum of the entropy in each of them
To measure the distance between two distributions, we can use the Kullback-Leibler divergence, or relative entropy. Given two random variables P and Q, the Kullback-Leibler divergence between them is defined as
where and are the probability mass functions of P and Q, respectively. Typically, P represents the true distribution of data or observations and Q represents a model or approximation of P. is used to describe the deficiency of using one distribution q to represent the true distribution p, which is useful for comparing two related distributions, e.g., two different resolutions of the same dataset. For instance, Wang and Ma [5] utilized the Kullback-Leibler divergence to quantify the difference between wavelet coefficient distributions of the original and distorted data. The Kullback-Leibler divergence is always nonnegative and equals zero if and only if .
There are some issues with the Kullback-Leibler divergence measure that make it less than ideal. First, it is not a true metric, i.e., . Second, if and for any x, then is undefined. Third, the Kullback-Leibler divergence does not offer any nice upper bounds. To overcome these problems, we may consider the symmetric Jensen-Shannon divergence measure [6]
The Jensen-Shannon divergence can be expressed in terms of entropy, i.e.,
In general, the Jensen-Shannon divergence has the following form
where and . Bordoloi and Shen [7] utilized the Jensen-Shannon divergence to evaluate the similarity of two viewpoints, The similarity values were used to generate a view space partitioning and select representative views.
3.3. Mutual Information and Conditional Entropy
We can measure how much information of a random variable X is conveyed by another random variable Y using the concept of mutual information. Mutual information can be treated as a special case of relative entropy: it is the relative entropy between the joint distribution and the product distribution , i.e.,
Mutual information measures the amount of information that X and Y share. It is the reduction in the uncertainty of one random variable due to the knowledge of the other [1]. For example, if X and Y are independent, i.e., , then knowing X does not give any information about Y and vice versa. Therefore, . At the other extreme, if X and Y are identical, then all information conveyed by X is shared with Y: knowing X determines the value of Y and vice versa. As a result, is the same as the uncertainty contained in X (or Y) alone, namely the entropy of X (or Y).
is bounded above by the smaller of and . Jänicke et al. [8] used the normalized mutual information, i.e., , to compute the distance between two power spectra transformed from climate data. Bruckner and Möller [9] used another version of normalized mutual information, i.e., , to evaluate the similarity between two isosurfaces.
Mutual information is related to the concept of conditional entropy, , which models the remaining entropy of variable X given that variable Y is known. Written in equation,
where is the entropy of the variable X conditional on the variable Y taking a certain value y. is the result of averaging over all possible values y that Y may take. In other words, variables X and Y combined contain bits of information. If we know the value of Y, we have gained bits of information, and the uncertainty remaining is bits. if and only if the value of X is completely determined by the value of Y. Conversely, if and only if X and Y are independent random variables.
3.4. Relationships among Information Theory Concepts
Mutual information, entropy, joint entropy, and conditional entropy have the following relationships
In practice, we can treat X and Y as two relevant random variables, such as two scalar volumes drawn from different timesteps of the same dataset. Mutual information indicates the amount of information X and Y share in common, conditional entropy tells how much information about X is still unknown after observing Y, and joint entropy indicates the total information the two volumes have.
Another important property for entropy is the chain rule [1], which states that the entropy of a collection of random variables is the sum of the conditional entropies. Let be drawn according to respectively, then
Assuming a Markov sequence model for the random variables, i.e., any variable is dependent on variable , but independent of other variables, we have
The chain rule in conjunction with the Markov sequence model described above was utilized by Bordoloi and Shen [7] to define a viewpoint goodness measure for time-varying volume data and by Wang et al. [4] to select representative timesteps from time-varying data.
Figure 3 summarizes the relationships among the various measures in information theory between two random variables X and Y. It also highlights the goal of data visualization on the right. Assuming the input dataset is denoted as a random variable X, we can model the visualization as another random variable Y, the output from the visual communication channel. To produce insightful visualization, the amount of mutual information needs to be as high as possible (or equivalently, the conditional entropy should be as low as possible). When reaches zero, the visualization fully conveys the information contained in the dataset. By optimization, we mean adjusting visualization parameters, such as the view or transfer function, so that the mutual information between the input data X and the output visualization Y can be maximized.
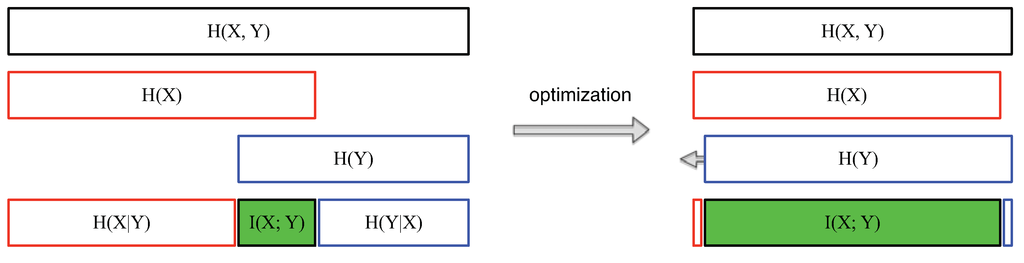
Figure 3.
Left: Relationships among different entropy measures between two random variables X and Y. Right: The goal of data visualization is to maximize the mutual information between the input data X and the output visualization Y.
4. Applications of Information Theory in Scientific Visualization
4.1. View Selection for Volumetric Data
The goal of view selection is to automatically suggest interesting or optimal viewpoints that maximize the amount of information received in the 2D projection of a given 3D dataset. Good viewpoints reveal essential information about the underlying data. Therefore, presenting them sooner to the viewers can improve both the speed and efficiency of data understanding. For example, in Figure 4, we show three representative views of a cube with different amounts of information revealed. Clearly, the rightmost one corresponds to the best view which reveals the maximum amount of information about the data by displaying the object in the least uncertain way. View selection has its practical value in large-scale data visualization when interactive rendering cannot be achieved. Bordoloi and Shen [7] introduced a solution for view selection for direct volume rendering. They treated the entire volume dataset as a random variable and defined the visual probability for a voxel j as follows
where is the visibility of voxel j at the view V, is the noteworthiness of voxel j which indicates the significance of its value, and N is the total number of voxels in the volume. The summation is taken over all voxels in the data. The division by σ is required to make all probabilities add up to unity. The noteworthiness is defined as
where is the opacity of voxel j looked up from the transfer function, is the information carried by voxel j, which can be derived from the frequency of its histogram bin . represents the amount of information associated with voxel j.
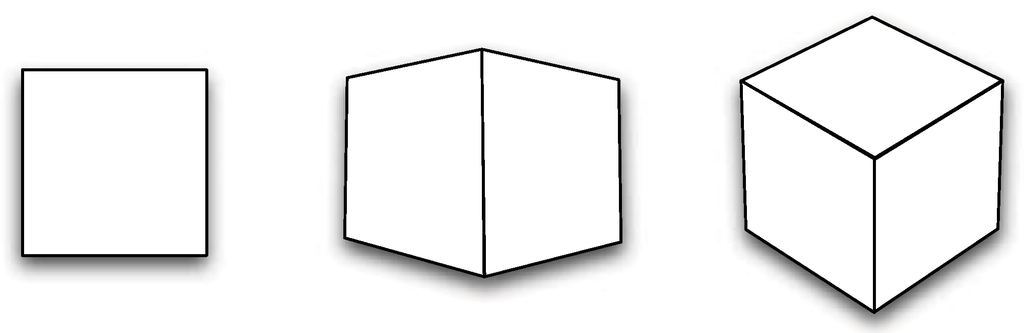
Figure 4.
Three representative views of a cube showing the increasing amount of information revealed about the object.
The intuition of their visual probability design can be explained as follows. In volume rendering, different voxels contribute differently to the final rendered image. The user assigns high opacity to voxels that are deemed more important. A voxel that is more important, or noteworthy, should be more visible in the rendering. Conversely, a voxel that is less noteworthy should be less visible. Consequently, the ratio between visibility and noteworthiness should be somewhat even for all voxels to maximize the view entropy. In other words, a good viewpoint should strive for a good balance among the visual probabilities of all voxels in the volume so that the information received by the viewer is maximized.
Takahashi et al. [10] considered surface rendering for volumetric data and presented a viewpoint entropy measure for isosurfaces. In this scenario, each isosurface was treated as a random variable. Given an isosurface , they defined the probability function of a face of the isosurface as
where is the visible area of the j-th face of on the screen and S is the total area of the 2D screen. Note that they also included the background area so that the summation of all equals S. The viewpoint entropy of the isosurface thus follows Equation (1). The intuition in their probability function design is that a good viewpoint should allow each face of the surface to be equally visible. In this case, the maximum amount of information about the surface can be received. The entropy of the entire volume takes the average of viewpoint entropies of the extracted isosurfaces. Each contributing isosurface may carry a weight indicating its importance on average. Such a weight can be derived from the opacity transfer function (i.e., higher opacity, higher weight). They also extended the same idea to define the viewpoint entropy for interval volumes.
Ji and Shen [11] took an image-space approach for view selection. Unlike [7], they treated the rendered image rather than the volume data as the random variable. They considered three aspects of the rendered image, namely, opacity, color, and curvature, to evaluate the information content of the image associated with a given viewpoint. A good view should maximize the projection size and maintain an even distribution of opacity values. It should also maximize the area of the salient colors while maintaining an even distribution of these colors in the image. Finally, it should allow the viewer to view the surface curvatures more easily. Based on this static view selection method, they proposed a solution to select dynamic views for time-varying volume data visualization. Their goal was to maximize the information perceived from the time-varying dataset under the constraints of smooth view change and near-constant speed.
4.2. Streamline Seeding and Selection
The concept of entropy can be applied to detect salient regions and generate streamlines for flow visualization. In this case, the direction of flow in a vector field can be considered as a random variable, and the distribution of vector directions indicates the amount of information in the vector field. Xu et al. [12] computed the entropy for every point in the vector field by considering its local neighborhood. They discretized vector directions into a finite number of bins to construct the histogram. In the resulting entropy field, high entropy regions correspond to a larger degree of variation in the vector directions. These regions are usually near the critical points or other important flow features such as separation lines. Streamline seeds can be placed accordingly to enhance these important features. After a set of streamlines are placed near high entropy regions, to evaluate how well these streamlines represent the underlying flow field, they proposed to reconstruct an intermediate flow field and use the conditional entropy as the measure. In their computation of , X is the original field and Y is the reconstructed field. The rationale behind it is that if is low, then most of the information in the original field has been revealed by the reconstructed field; otherwise, more streamlines need to be seeded. The principle for selecting new seed locations is that the higher the conditional entropy around a spatial point, the more likely the point to be selected as the next seed. A probability distribution function (PDF) can be constructed to record the expected probability of dropping a seed for each point in the domain. They distributed the seeds according to the probability distribution function using importance sampling.
Another direction of applying information theory to flow visualization is to place the focus on traced streamlines instead of seed placement. We can apply the entropy measure to evaluate the information content of each individual streamline by treating each line as a random variable. The goal is to prioritize the set of 3D streamlines according to their entropies for selective rendering so that a less cluttered visualization is presented. Furuya and Itoh [13] defined the probability function as follows
where is the length of the i-th streamline segment’s projection on the 2D screen, and L is the total length of the streamline in the 3D space. The intuition is to favor streamlines that have a nearly equal projected length for all segments. This idea was later adopted by Marchesin et al. [14] in their definition of the linear and angular entropies for streamlines.
4.3. Transfer Function for Multimodal Data
Haidacher et al. [15] proposed an information-based transfer function specification for multimodal data visualization. Multimodal visualization complicates the transfer function design because multiple values at every data point need to be considered. The challenge for multimodal visualization is how to fuse multiple parameters in the high-dimensional transfer function space to enable easy and intuitive transfer function design in the 2D screen space. In this work, the authors considered the joint occurrence of multiple features from one or multiple variables by utilizing the concept of point-wise mutual information (PMI). The PMI of a pair of outcomes and from two random variables describes the discrepancy between the probability of their coincidence given their joint distribution versus the probability of their coincidence given only their individual distributions and , assuming independence. That is,
It is clear that when . This corresponds to the case that the two values are statistically independent from each other. If the pair of values occurs more frequently as one would expect, then . Conversely, if the pair of values occurs less frequently as expected, then . The authors leveraged this information as one additional dimension to specify the transfer function where high opacity is assigned to regions with low PMI. Thus, statistical features that only occur in a single variable can be separated from those that are present in both.
4.4. Selection of Representative Isosurfaces
Isosurface rendering is one of the most popular techniques to visualize volumetric datasets. Similar to isocontours in 2D, isosurfaces in 3D reveal important object and/or material boundaries. The key issue is how to select salient isovalues such that the surfaces extracted are informative and representative. Conventional solutions made use of histograms to depict the frequency of isovalues and derived quantities (such as gradient magnitude) to suggest interesting isovalues in the plots. Bruckner and Möller [9] proposed to evaluate the similarity between isosurfaces using mutual information. They produced an isosurface similarity map to guide representative isovalue selection. Instead of explicit extraction of each individual isosurface for similarity evaluation, they opted to represent individual isosurface implicitly using a distance transform. Therefore, in their mutual information computation, X and Y are actually the distances from any point in the volume to a pair of isosurfaces and , respectively. The minimum distance of a point to the surface was used. The intuition is that two isosurfaces are similar if their distance distributions are similar and vice versa. To select representative isovalues, they presented an algorithm that automatically detects coherent structures (i.e., distinct squares) from the isosurface similarity map and selects the most representative isovalues.
4.5. LOD Selection for Multiresolution Volume Visualization
Building a multiresolution data hierarchy from a large-scale dataset allows us to visualize the data at different scales and balance image quality and computation speed. To construct such a hierarchy, a given volume dataset is first partitioned into blocks following either the bottom-up or top-down strategy. A level-of-detail (LOD) in the hierarchy consists of a sequence of data blocks at various resolutions. The key to multiresolution volume visualization is to select appropriate LODs that highlight important features in the data for rendering. The goal is to maximize the amount of information contained in the image under a certain constraint about the computation cost.
Wang and Shen [16] proposed to quantitatively evaluate the LOD quality using the concept of entropy. They analyzed the LOD quality by investigating the quality of each individual block as well as the relationships among them. Different blocks may have different distortions with respect to the original data. They may convey different optical contents when the color and opacity transfer function is applied. Furthermore, the sequence of data blocks in the LOD are rendered to the screen. Different blocks have different contributions to the final image depending on their projections and occlusion relationships. Therefore, the probability of a multiresolution data block was defined as
where and are the contribution and distortion of block i respectively, M is the total number of blocks in the data hierarchy. The entropy of a LOD then follows the definition in Equation (1). The multiplication of contribution and distortion in Equation (19) should be somewhat even for all blocks in order to maximize the LOD entropy. This means that if a data block has high contribution, we should reduce its distortion by replacing it with its descendant blocks. Conversely, if neighboring data blocks have low contribution, we should increase their distortion by replacing them with their ancestor blocks.
Note that for any LOD, it is impossible for all the data blocks in the hierarchy to have the equal probability. This is because a LOD constitutes a cut in the data hierarchy and thus not all of the data blocks can be selected. Any block which is not included in the LOD receives zero probability and does not contribute to the entropy. Ideally, since a higher entropy indicates a better LOD quality, the best LOD (with the highest information content) could be achieved when we select all the leaf nodes in the data hierarchy. However, this requires rendering the volume data at the original resolution, and defeats the purpose of multiresolution rendering. In practice, a meaningful goal is to find the best LOD under some constraint, such as a certain block budget, which is usually much smaller than M. Accordingly, the quality of a LOD could be improved by splitting data blocks with large distortion and high contribution, and joining those blocks with small distortion and low contribution. The split operation aims at increasing the entropy with a more balanced probability distribution. The join operation is to offset the increase in block number and keep it under the budget.
4.6. Time-varying and Multivariate Data Analysis
Time-varying and multivariate data analysis and visualization has received increasing attention in recent years. Identifying important regions in the data enables effective data reduction, viewing, and understanding, which provides a scalable solution to handle large-scale data. Jänicke et al. [17] introduced an approach to detect importance regions for multifield data by extending the concept of local statistical complexity (LSC) from finite state cellular automata to discretized multifields. They defined past and future light-cones (i.e., influence regions) for all grid points, which are used to estimate conditional distributions and calculate the LSC. Specifically, the LSC at a grid point p was defined as
where and are the configurations of the field in the past and future cones respectively, ε is the minimum sufficient statistic which maps past configurations to their equivalence classes (i.e., classes with the same conditional distribution ), are the causal states of the system which predict the same possible futures with the same possibilities. Intuitively, mutual information indicates the minimum amount of information of a past light-cone needed to determine its causal state. Thus, the LSC tells how complex it is around the past configuration centered at point p. The higher the , the more complex the local region around p.
Wang et al. [4] presented a block-wise technique to analyze the important aspect of time-varying data. They partitioned the volume data at each timestep into spatial blocks and investigated the importance of each individual data block by examining the amount of relative information between them. Such a block-wise approach is more suitable than a voxel-wise approach when the size of data becomes too large to be handled efficiently. Specifically, they considered the importance of a data block from two perspectives. First, a data block itself contains a different amount of information. For example, a data block evenly covering a wide range of values contains more information than another block with uniform values everywhere. Second, a data block conveys a different amount of information with respect to other blocks in the time sequence. For instance, a data block conveys more information if it has less common information with other blocks at different timesteps. Therefore, intuitively, a data block is important if it contains more information by itself and its information is more unique with respect to other blocks. By defining the importance as the amount of data change over time, they employed the conditional entropy to measure the importance of data blocks quantitatively. The importance value of each block varies over time, indicating its temporal behavior. Clustering all these importance curves for the volume allows classification of data blocks and importance-driven visualization of time-varying datasets.
4.7. Information Channel between Objects and Viewpoints
Compared to previously described visualization examples, the work by Viola et al. [18] on importance-driven focus of attention is unique in the sense that they built an information channel in terms of visibility between objects and viewpoints. Previously Sbert et al. [19] showed that for polygonal data, the viewpoint entropy [20] is very sensitive to the discretization of the objects. Viola et al. built the information channel between two random variables (the input, i.e., viewpoints, and the output, i.e., objects) by computing a probability matrix which determines the output distribution given the input. They defined a new measure, called the viewpoint mutual information (VMI), which is better than the viewpoint entropy due to its robustness to deal with any type of discretization or resolution of the volumetric dataset.
The mutual information between a set of viewpoints V and a set of objects O is defined as
where
In Equation (21), , i.e., each viewpoint has an equal probability. is the normalized visibility of object o from viewpoint v and . is the average visibility of object o obtained from the set of viewpoints V, i.e.,
is the VMI, which indicates the degree of dependence or correlation between the dataset O and viewpoint v. We sketch two examples to illustrate the intuition of this VMI measure. In the left image of Figure 5, the viewpoint and the set of objects O are highly coupled, i.e., the average visibility of and is low due to the occlusion of by . This implies that has a high value which corresponds to a low quality viewpoint. In the right image of Figure 5, the viewpoint and the set of objects O are more independent, i.e., the two objects and are equally visible from without occluding each other. This implies that has a low value which corresponds to a high quality viewpoint. The best viewpoint is achieved when is minimized.
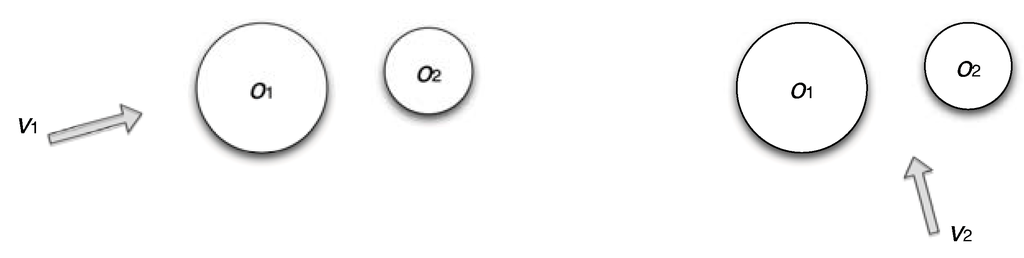
Figure 5.
Illustration of the viewpoint mutual information. Left: a low quality viewpoint indicating a highly dependent view between the viewpoint and the set of objects . Right: a high quality viewpoint indicating a more independent view between the viewpoint and the set of objects O.
Leveraging Bayes’ theorem, i.e., , Ruiz et al. [21] reversed the information channel proposed by Viola et al. [18].
where
In their context, o represents each individual voxel in the volume. Therefore, they defined as the voxel mutual information, which was utilized in various visualization applications such as volume illustration and viewpoint selection.
5. Information Theory in Imaging and Graphics
Prior to its utilization in data visualization, information theory has found a wide variety of applications in imaging and graphics. These applications were believed to inspire many of the visualization examples we discuss in Section 4. In this section, we review related work in imaging and graphics. The review is by no means exhaustive. Rather, it provides a bird’s-eye view on some of the selective topics.
Information theory has been applied to solve many tasks in imaging such as image enhancement, registration, and segmentation. For example, Cheng et al. [22] proposed to perform image enhancement by transforming an image into a fuzzy domain with maximum fuzzy entropy. Their method selects the fuzzy region according to the nature of the input image and determines the membership function automatically for image enhancement. Mutual information has been widely used in medical image registration since the early 1990s [23,24]. Registration is assumed to correspond to maximizing mutual information between the reference and target images. It has also been shown that maximizing the mutual information gives an effective solution in terms of both accuracy and robustness for registering multimodal [25] and multiresolution [26] images. For image segmentation, Kim et al. [27] presented an information-theoretic approach that maximizes the mutual information between the region labels and the image pixel intensities, subject to a constraint on the total length of the region boundaries. Wang and Vemuri [28] proposed to use the square root of the J-divergence (i.e., symmetrized Kullback-Leibler divergence) between two Gaussian distributions corresponding to the diffusion tensor images (DTIs) being compared. This dissimilarity measure leads to a novel closed form expression for the distance, which is incorporated into a region-based active contour model for DTI segmentation.
In computer graphics, information theory has been utilized to effectively solve a number of problems including scene complexity analysis, pixel supersampling, viewpoint selection, light source placement, ambient occlusion, mesh simplification, and image aesthetics measure. We refer interested readers to the book written by Sbert et al. [29] for an excellent overview of basic concepts of information theory and their applications in computer graphics. Feixas et al. [30] presented an information-theoretic approach for the analysis of scene visibility and radiosity complexity. Using continuous and discrete mutual information, their measures indicate the degree of correlation or dependence between all the points or patches of a scene. Such a measure is useful for analyzing the difficulty of performing illumination computations using Monte Carlo radiosity algorithms. Rigau et al. [31] proposed new contrast measures to guide pixel supersampling in stochastic raytracing which take into account both pixel color entropy and pixel geometry entropy. This solution leads to a better representation (i.e., with more supersampling) of critical areas such as shadow contours and edges in the scene.
Solutions to viewpoint selection have been proposed for the problem of modeling a 3D object from range data [32] and from images [33], for object recognition [34], and also for cinematography [35]. In computer graphics, Vázquez et al. [20,36] introduced the viewpoint entropy as a measure to automatically compute good viewing positions for polygonal scenes. The viewpoint entropy for any given view is derived from the projected areas of the faces of the geometric models in the scene. The motivation is to achieve a balance between the number of faces visible and the size of projection areas. They also used the viewpoint entropy together with a greedy algorithm to choose the minimal set of views that captures the maximum amount of information about the scene. Along the same spirit, visualization researchers later on came up with similar entropy measures for isosurface rendering [10], volume rendering images [11], and streamline visualization [13,14]. Gumhold [37] presented an entropy-based solution for placing light sources for given camera parameters in a scene. The goal was to maximize the information added to the image through illumination. The solution includes a fast global optimization process and an extension to multiple light sources.
Recently, González et al. [38] presented a new ambient occlusion technique that builds a channel between various viewpoints and an object’s polygons using mutual information. Their viewpoint-based ambient occlusion maps have multiple application possibilities including viewpoint selection, viewpoint importance, and relighting for nonphotorealistic rendering. Castelló et al. [39] proposed to use viewpoint mutual information for polygonal mesh simplification. Their algorithm applies the best half-edge collapse as a decimation criterion and uses the variation in mutual information to measure the errors introduced by collapsing edges. Feixas et al. [40] presented a global framework to deal with viewpoint selection and mesh saliency using a communication channel between viewpoints and polygons. Rigau et al. [41] studied informational aesthetics for paintings from an information-theoretic perspective. They defined a set of ratios based on information theory and Kolmogorov complexity to quantify the aesthetic experience. They also investigated macroaesthetic and microaesthetic descriptions through image composition. This was achieved through an adaptive algorithm that partitions the image using a binary space partitioning (BSP) structure driven by the maximum information gain at each partition.
6. Outlook for Future Research
A significant difference between data visualization and data communication is that visualization transforms raw data into another representation, the visual images. Therefore, the fundamental challenge for scientific visualization is to design an appropriate transfer function that maps data values to colors and opacities that can preserve the saliency of the data. From the information theory point of view, a good set of transfer functions is the one that can convey the most amount of information or insight into the data. Although there exist several guidelines in transfer function design for medical datasets, there is a lack of more generic criteria for visualizing scientific datasets. In general, a transfer function may consist of multiple dimensions and thus the parameter search space becomes immense. This makes transfer function specification a very difficult issue since there are essentially no constraints. An information-aware solution or user interface could be very helpful for either automatic or semiautomatic transfer function specification. Feedback on what information in the data has been explored and what remains to be explored can provide criteria as to when the visualization process can be stopped. The initial work by Haidacher et al. [15] was encouraging, yet we need further research to establish a complete framework for information-aware transfer function design.
Scientific applications are now producing extreme-scale data on a regular basis. Although the amount of data produced doubles every year, the amount of information pertinent to scientific discovery does not necessarily scale proportionally. This suggests an information-aware solution for data simplification or reduction. Similar to the ideas of information theory based streamline seeding [12] and mesh simplification [39], a promising solution is to simplify the volume data through partitioning or clustering and in the meanwhile, preserving the feature information as much as possible. That is, the data is reduced while we achieve minimal loss of mutual information with respect to the features. This idea can be extended to time-varying multivariate datasets where multivariate temporal features should be considered. Another unsolved issue for multivariate data is to derive the connection or influence among multiple variables. Understanding this would help us solve important questions such as: which variables dominate other variables; how their causal relationships vary over time; and could we select important or representative variables from a large number of input variables?
While information theory based methods have demonstrated a great potential in scientific visualization, they do have their own limitations. For example, information theory considers the dataset as a collection of distributions, which may not be suitable to extract specific spatial structures embedded in the underlying features. Even though datasets with the same histogram certainly have the same entropy, the distributions of their data values in space could be totally different. In addition, when using histogram, the result can be sensitive to the level of discretization, i.e., the number of bins. This problem can be remedied by using various probability density estimation techniques [42,43]. Another limitation of information theory is that although it works well with frequency probability (in terms of frequencies of occurrence of events, or by relative proportions in populations or collectives), its application with Bayesian probability (in terms of degree of rational belief) is not clear. Bayesian probability is more difficult to apply practically since human observers’ input needs to be incorporated. Frequency probability allows us to access the information content of a dataset, but Bayesian probability allows scientists to update their belief when the new evidence is presented or the new result is generated. We believe that further research is necessary in order to develop a more robust information-theoretic framework that incorporates Bayesian probability as well.
Acknowledgements
This work was supported by the U.S. National Science Foundation through grants IIS-1017635 and IIS-1017935. The hurricane dataset, courtesy of the U.S. National Center for Atmospheric Research and the U.S. National Science Foundation, was made available through IEEE Visualization 2004 Contest. We wish to thank the reviewers for their helpful comments.
References
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Purchase, H.C.; Andrienko, N.; Jankun-Kelly, T.J.; Ward, M. Theoretical foundations of information visualization. In Information Visualization: Human-centered Issues and Perspectives; Kerren, A., Stasko, J.T., Fekete, J.D., North, C., Eds.; Springer-Verlag: Berlin/ Heidelberg, Germany, 2008; pp. 46–64. [Google Scholar]
- Chen, M.; Jänicke, H. An Information-theoretic framework for visualization. IEEE Trans. Vis. Comput. Graph. 2010, 16, 1206–1215. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Yu, H.; Ma, K.L. Importance-driven time-varying data visualization. IEEE Trans. Vis. Comput. Graph. 2008, 14, 1547–1554. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Ma, K.L. A statistical approach to volume data quality assessment. IEEE Trans. Vis. Comput. Graph. 2008, 14, 590–602. [Google Scholar] [CrossRef] [PubMed]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Bordoloi, U.D.; Shen, H.W. View selection for volume rendering. In Proceedings of IEEE Visualization Conference, Minneapolis, MN, USA, October 2005; pp. 487–494.
- Jänicke, H.; Böttinger, M.; Mikolajewicz, U.; Scheuermann, G. Visual exploration of climate variability changes using wavelet Analysis. IEEE Trans. Vis. Comput. Graph. 2009, 15, 1375–1382. [Google Scholar] [CrossRef] [PubMed]
- Bruckner, S.; Möller, T. Isosurface similarity maps. Comput. Graph. Forum 2010, 29, 773–782. [Google Scholar] [CrossRef]
- Takahashi, S.; Fujishiro, I.; Takeshima, Y.; Nishita, T. A feature-driven approach to locating optimal viewpoints for volume visualization. In Proceedings of IEEE Visualization Conference, Minneapolis, MN, USA, October 2005; pp. 495–502.
- Ji, G.; Shen, H.W. Dynamic view selection for time-varying volumes. IEEE Trans. Vis. Comput. Graph. 2006, 12, 1109–1116. [Google Scholar] [PubMed]
- Xu, L.; Lee, T.Y.; Shen, H.W. An information-theoretic framework for flow visualization. IEEE Trans. Vis. Comput. Graph. 2010, 16, 1216–1224. [Google Scholar] [PubMed]
- Furuya, S.; Itoh, T. A streamline selection technique for integrated scalar and vector visualization. In Proceedings of the IEEE Visualization Conference Poster Compendium, Columbus, OH, USA, October 2008.
- Marchesin, S.; Chen, C.K.; Ho, C.; Ma, K.L. View-dependent streamlines for 3D vector fields. IEEE Trans. Vis. Comput. Graph. 2010, 16, 1578–1586. [Google Scholar] [CrossRef] [PubMed]
- Haidacher, M.; Bruckner, S.; Kanitsar, A.; Gröller, M.E. Information-based transfer functions for multimodal visualization. In Proceedings of Eurographics Workshop on Visual Computing for Biomedicine, Delft, The Netherlands, October 2008; pp. 101–108.
- Wang, C.; Shen, H.W. LOD map—A visual interface for navigating multiresolution volume visualization. IEEE Trans. Vis. Comput. Graph. 2006, 12, 1029–1036. [Google Scholar] [CrossRef] [PubMed]
- Jänicke, H.; Wiebel, A.; Scheuermann, G.; Kollmann, W. Multifield visualization using local statistical complexity. IEEE Trans. Vis. Comput. Graph. 2007, 13, 1384–1391. [Google Scholar]
- Viola, I.; Feixas, M.; Sbert, M.; Gröller, M.E. Importance-driven focus of attention. IEEE Trans. Vis. Comput. Graph. 2006, 12, 933–940. [Google Scholar] [CrossRef] [PubMed]
- Sbert, M.; Plemenos, D.; Feixas, M.; González, F. Viewpoint quality: Measures and applications. In Proceedings of Eurographics Workshop on Computational Aesthetics in Graphics, Visualization and Imaging, Girona, Spain, May 2005; 2005; pp. 185–192. [Google Scholar]
- Vázquez, P.P.; Feixas, M.; Sbert, M.; Heidrich, W. Viewpoint selection using viewpoint entropy. In Proceedings of Vision, Modeling, and Visualization Conference, Stuttgart, Germany, November 2001; pp. 273–280.
- Ruiz, M.; Boada, I.; Feixas, M.; Sbert, M. Viewpoint information channel for illustrative volume rendering. Comput. Graph. 2010, 34, 351–360. [Google Scholar] [CrossRef]
- Cheng, H.D.; Chen, Y.H.; Sun, Y. A novel fuzzy entropy approach to image enhancement and thresholding. Signal Process. 1999, 75, 277–301. [Google Scholar] [CrossRef]
- Viola, P.A.; Wells, W.M., III. Alignment by maximization of mutual information. Int. J. Comput. Vision 1997, 24, 137–154. [Google Scholar] [CrossRef]
- Pluim, J.P.W.; Maintz, J.B.A.; Viergever, M.A. Mutual-information-based registration of medical images. IEEE Trans. Med. Imag. 2003, 22, 986–1004. [Google Scholar] [CrossRef] [PubMed]
- Maes, F.; Collignon, A.; Vandermeulen, D.; Marchal, G.; Suetens, P. Multimodality image registration by maximization of mutual information. IEEE Trans. Med. Imag. 1997, 16, 187–198. [Google Scholar] [CrossRef] [PubMed]
- Thévenaz, P.; Unser, M. Optimization of mutual information for multiresolution image registration. IEEE Trans. Image Process. 2000, 9, 2083–2099. [Google Scholar] [PubMed]
- Kim, J.; Fisher, J.W., III; Yezzi, A.; Cetin, M.; Willsky, A.S. A nonparametric statistical method for image segmentation using information theory and curve evolution. IEEE Trans. Image Process. 2005, 14, 1486–1502. [Google Scholar] [PubMed]
- Wang, Z.; Vemuri, B.C. DTI Segmentation using an information theoretic tensor dissimilarity measure. IEEE Trans. Med. Imag. 2005, 24, 1267–1277. [Google Scholar] [CrossRef] [PubMed]
- Sbert, M.; Feixas, M.; Rigau, J.; Chover, M.; Viola, I. Information Theory Tools for Computer Graphics; Morgan & Claypool Publishers: San Rafael, CA, USA, 2009. [Google Scholar]
- Feixas, M.; del Acebo, E.; Bekaert, P.; Sbert, M. An information theory framework for the analysis of scene complexity. Comput. Graph. Forum 1999, 18, 95–106. [Google Scholar] [CrossRef]
- Rigau, J.; Feixas, M.; Sbert, M. New contrast measures for pixel supersampling. In Proceedings of Computer Graphics International, Bradford, UK, July 2002; pp. 439–451.
- Wong, L.; Dumont, C.; Abidi, M. Next best view system in a 3-D modeling task. In Proceedings of International Symposium on Computational Intelligence in Robotics and Automation, Monterey, CA, USA, November 1999; pp. 306–311.
- Fleishman, S.; Cohen-Or, D.; Lischinski, D. Automatic camera placement for image-based modeling. Comput. Graph. Forum 2000, 19, 101–110. [Google Scholar] [CrossRef]
- Arbel, A.; Ferrie, F.P. Viewpoint selection by navigation through entropy maps. In Proceedings of International Conference on Computer Vision, Kerkyra, Corfu, Greece, September 1999; pp. 248–254.
- He, L.W.; Cohen, M.F.; Salesin, D.H. The virtual cinematographer: A paradigm for automatic real-time camera control and directing. In Proceedings of ACM SIGGRAPH Conference, New Orleans, LA, USA, August 1996; pp. 217–224.
- Vázquez, P.P.; Feixas, M.; Sbert, M.; Heidrich, W. Automatic view selection using viewpoint entropy and its applications to image-based modelling. Comput. Graph. Forum 2003, 22, 689–700. [Google Scholar] [CrossRef]
- Gumhold, S. Maximum entropy light source placement. In Proceedings of IEEE Visualization Conference, Boston, MA, USA, October 2002; pp. 275–282.
- González, F.; Sbert, M.; Feixas, M. Viewpoint-based ambient occlusion. IEEE Comput. Graph. Appl. 2008, 28, 44–51. [Google Scholar] [CrossRef] [PubMed]
- Castelló, P.; Sbert, M.; Chover, M.; Feixas, M. Viewpoint-driven simplification using mutual information. Comput. Graph. 2008, 32, 451–463. [Google Scholar] [CrossRef]
- Feixas, M.; Sbert, M.; González, F. A unified information-theoretic framework for viewpoint selection and mesh saliency. ACM Trans. Graph. 2009, 6, 1–23. [Google Scholar] [CrossRef]
- Rigau, J.; Feixas, M.; Sbert, M. Informational aesthetics measures. IEEE Comput. Graph. Appl. 2008, 28, 24–34. [Google Scholar] [CrossRef] [PubMed]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman & Hall/CRC: London, UK, 1986. [Google Scholar]
- Scott, D.W. Multivariate Density Estimation: Theory, Practice, and Visualization; Wiley-Interscience: New York, NY, USA, 1992. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).