Understanding Atmospheric Behaviour in Terms of Entropy: A Review of Applications of the Second Law of Thermodynamics to Meteorology
Abstract
:1. Introduction
2. Major Concepts of Entropy Used Frequently in Meteorology
2.1. Thermodynamic Entropy
2.2. The Entropy of Statistical Mechanics
2.3. Information Entropy
3. On Entropy Balance
4. Entropy Production
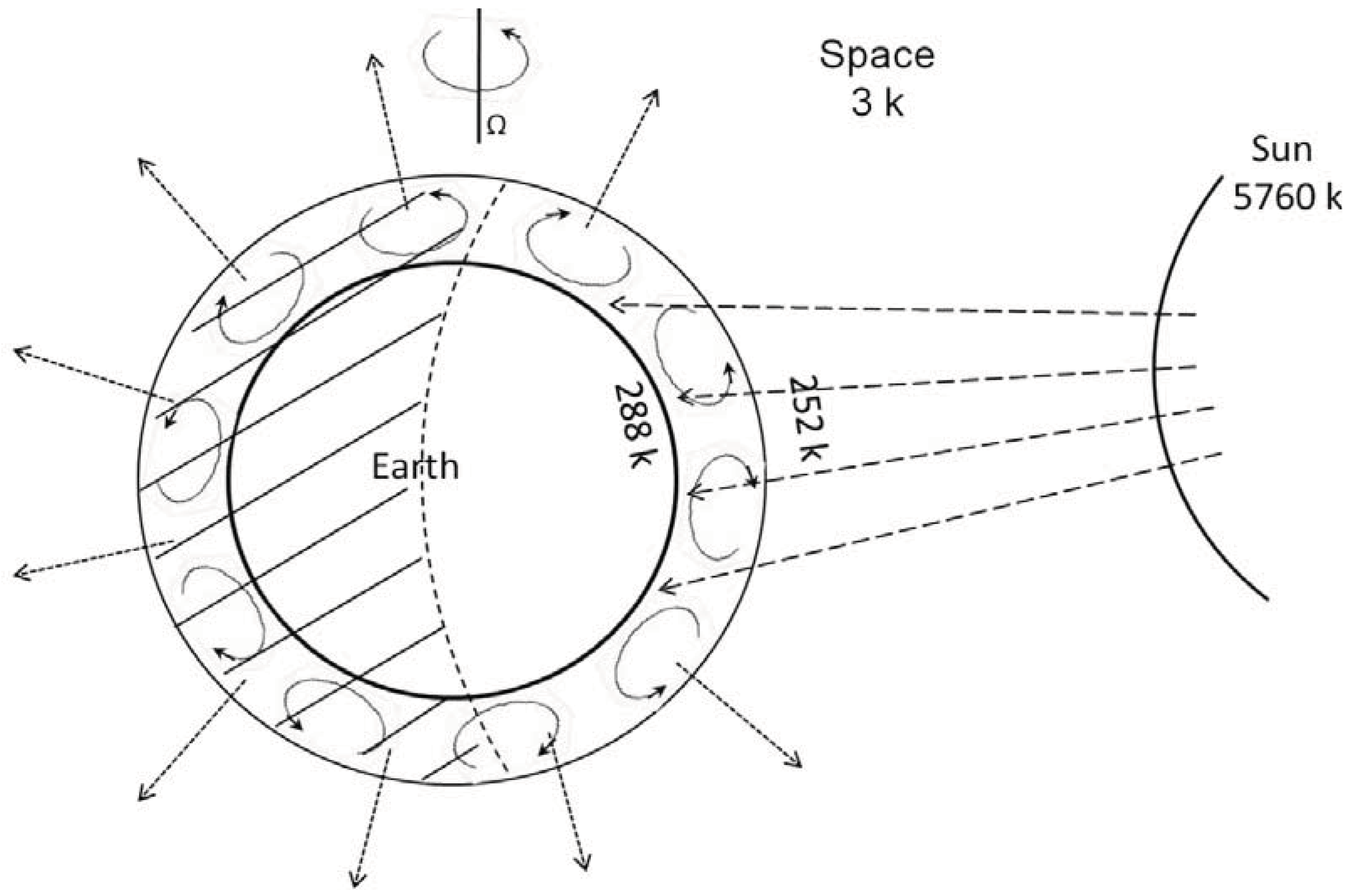
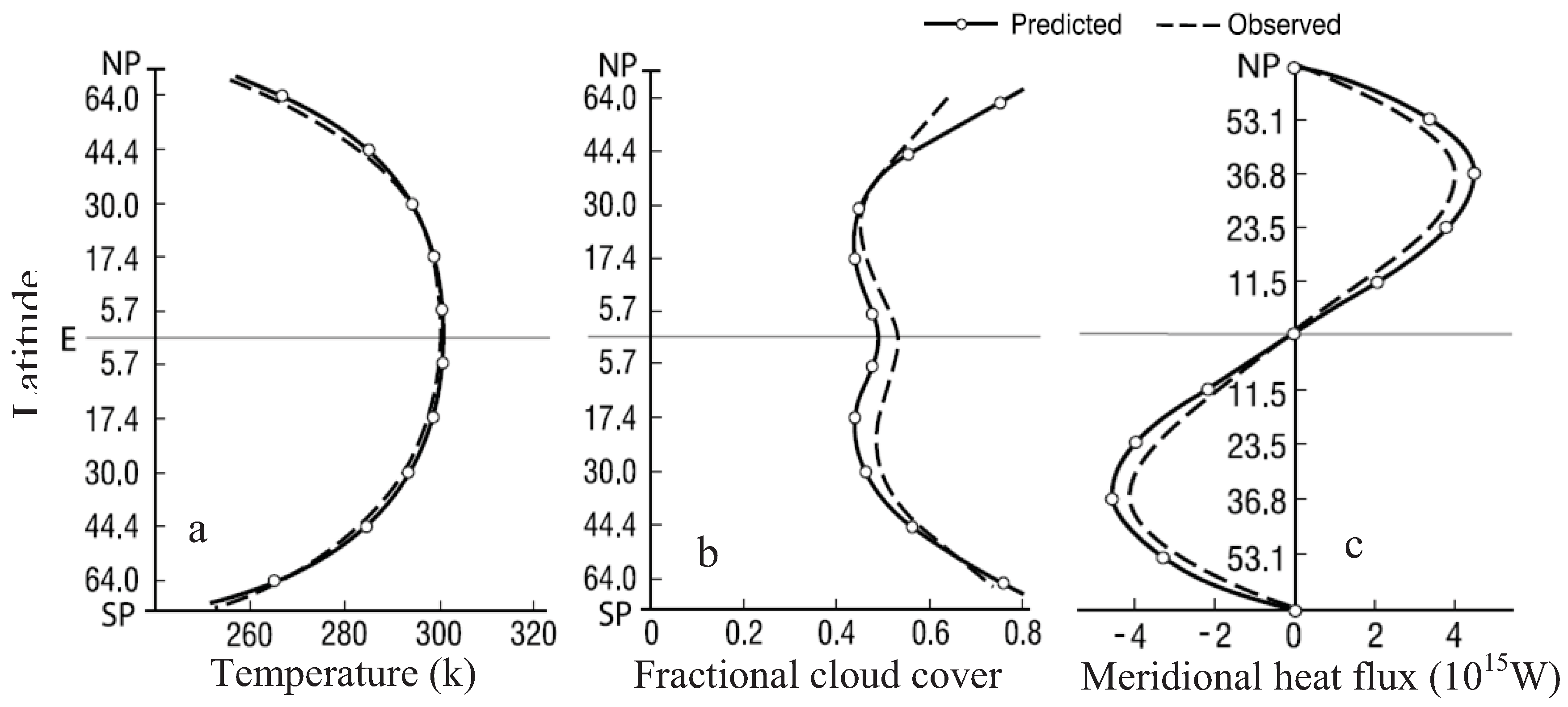
5. Entropy Flow
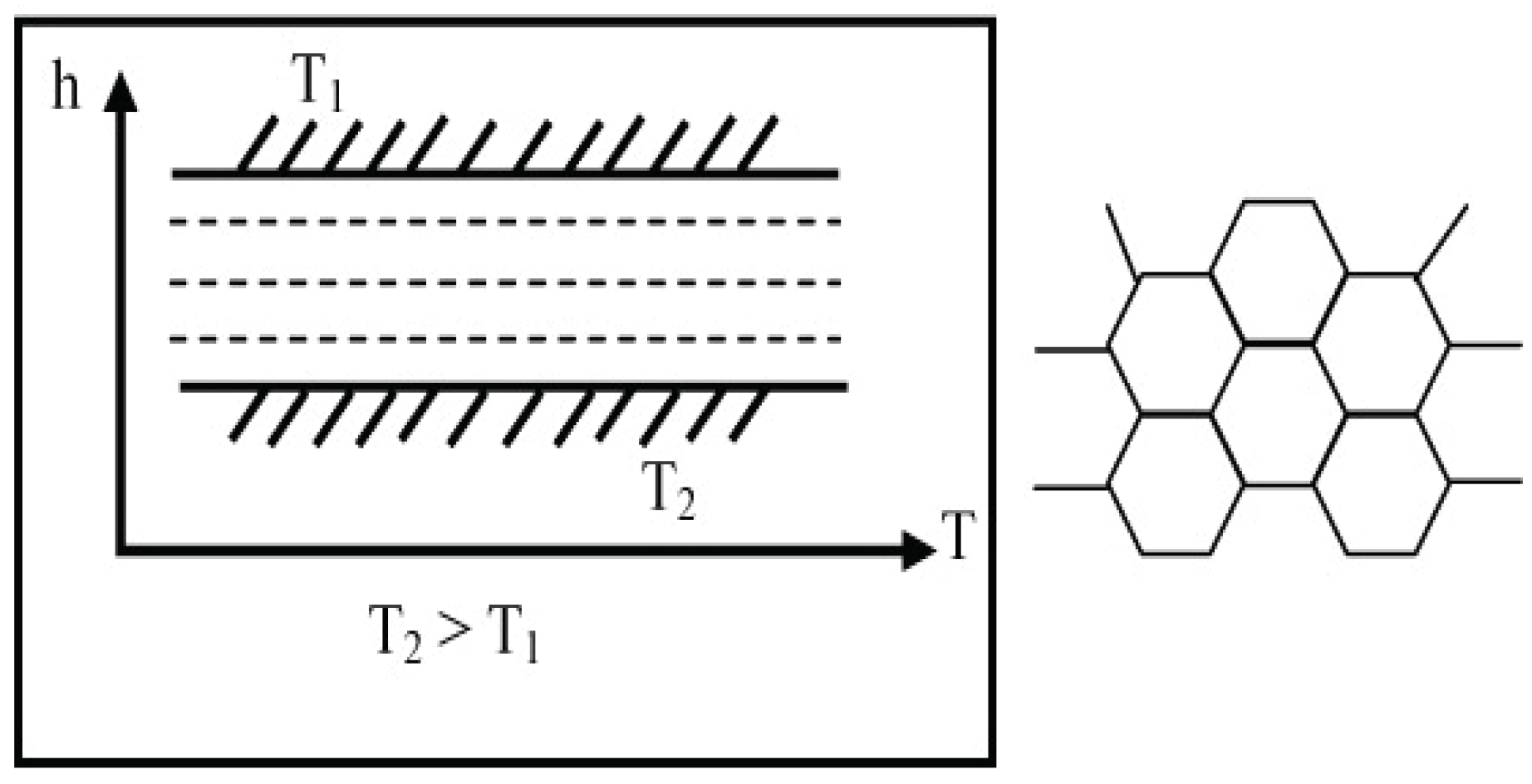
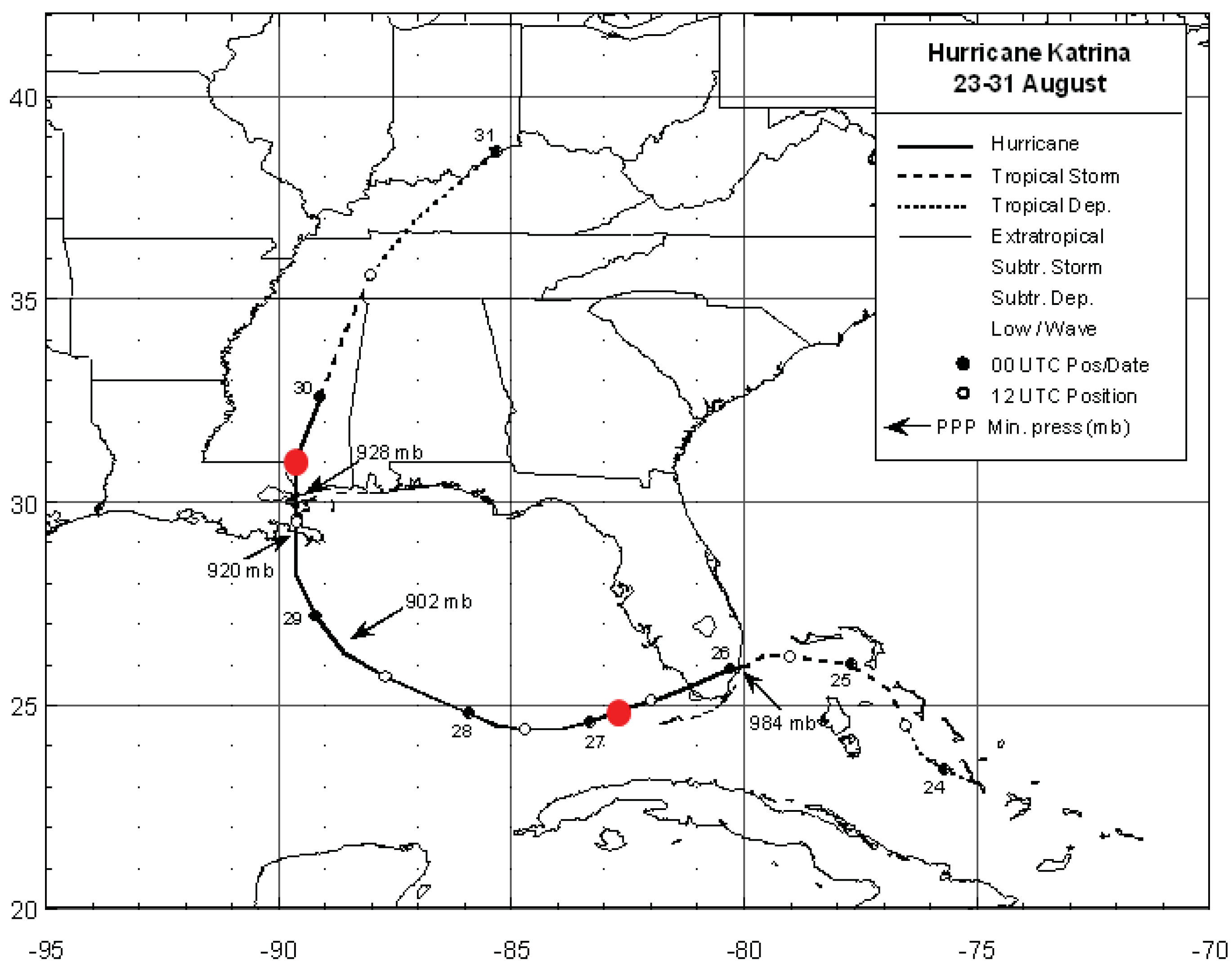
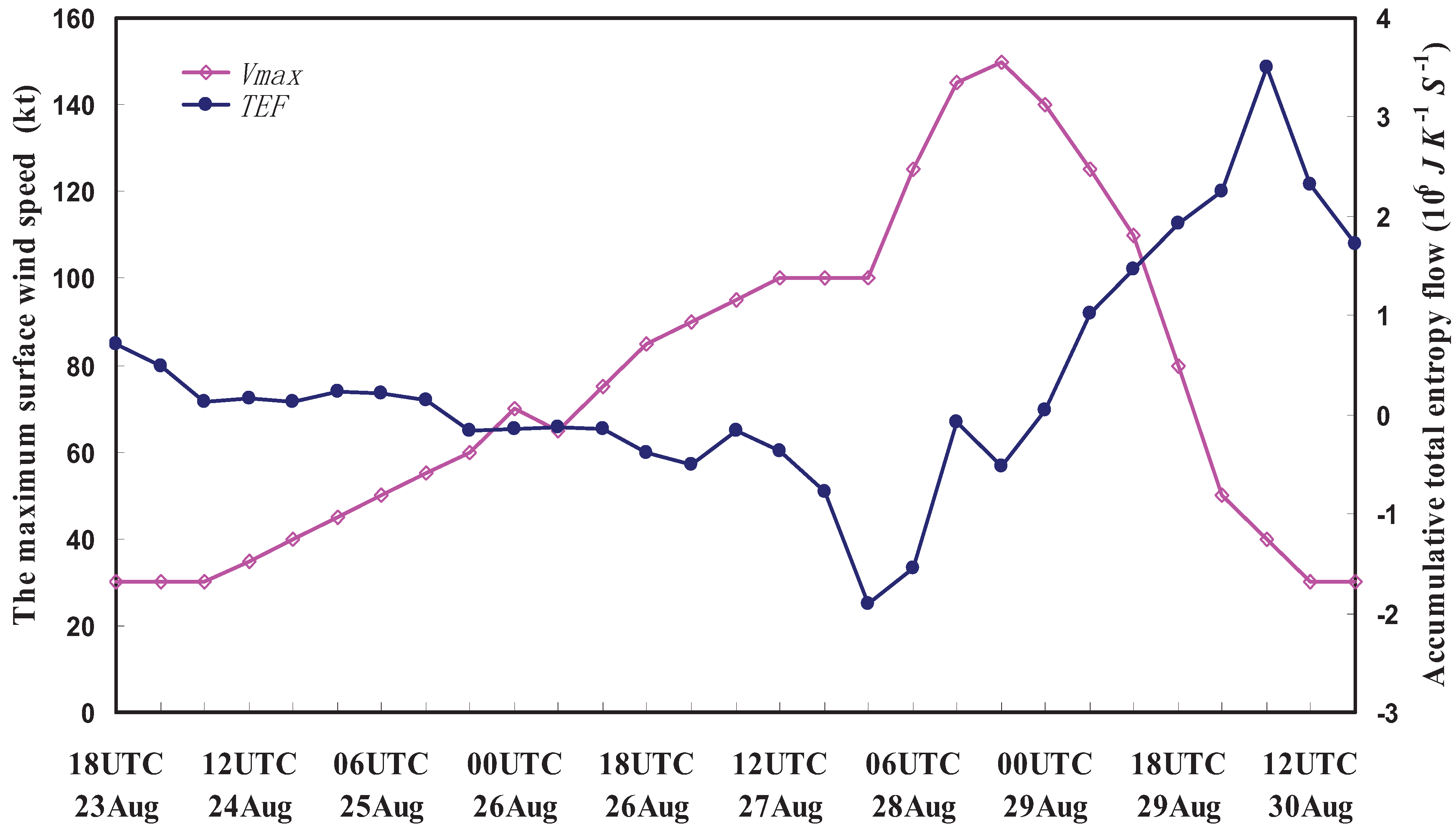
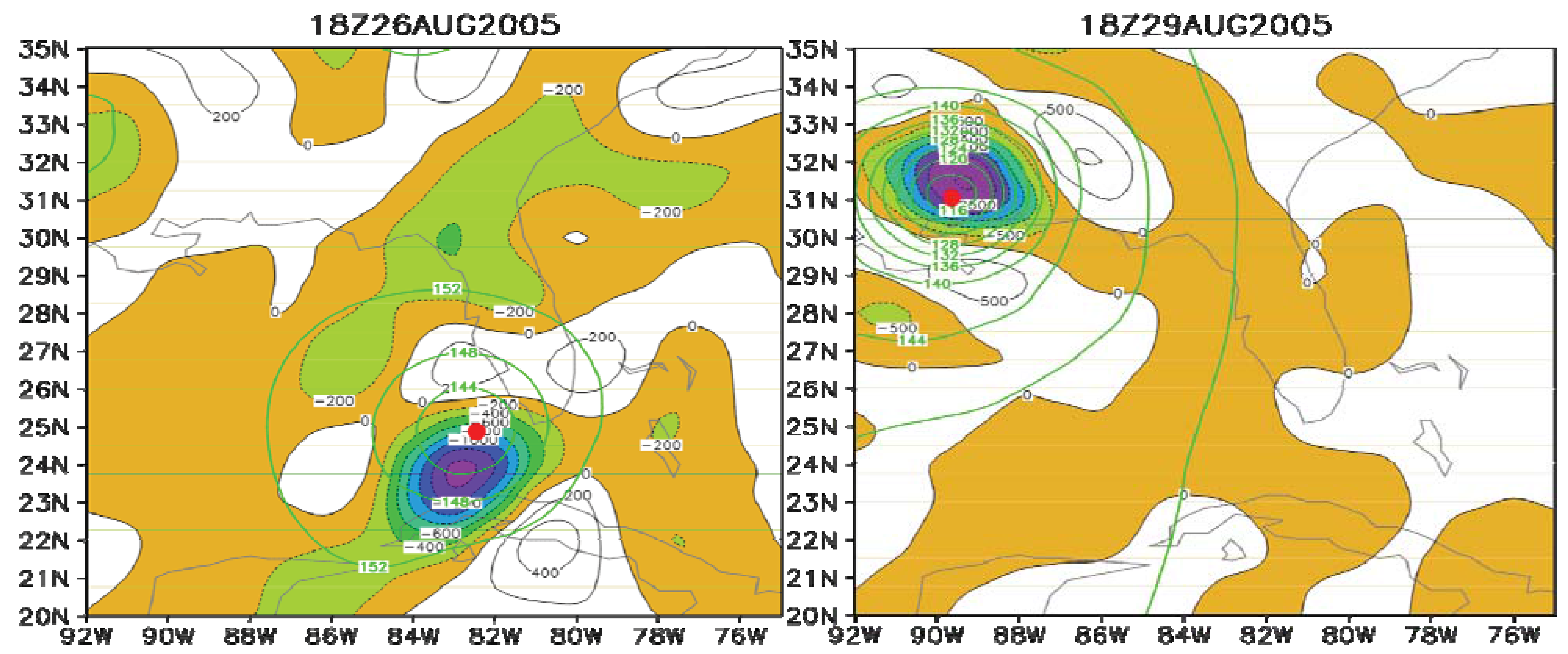
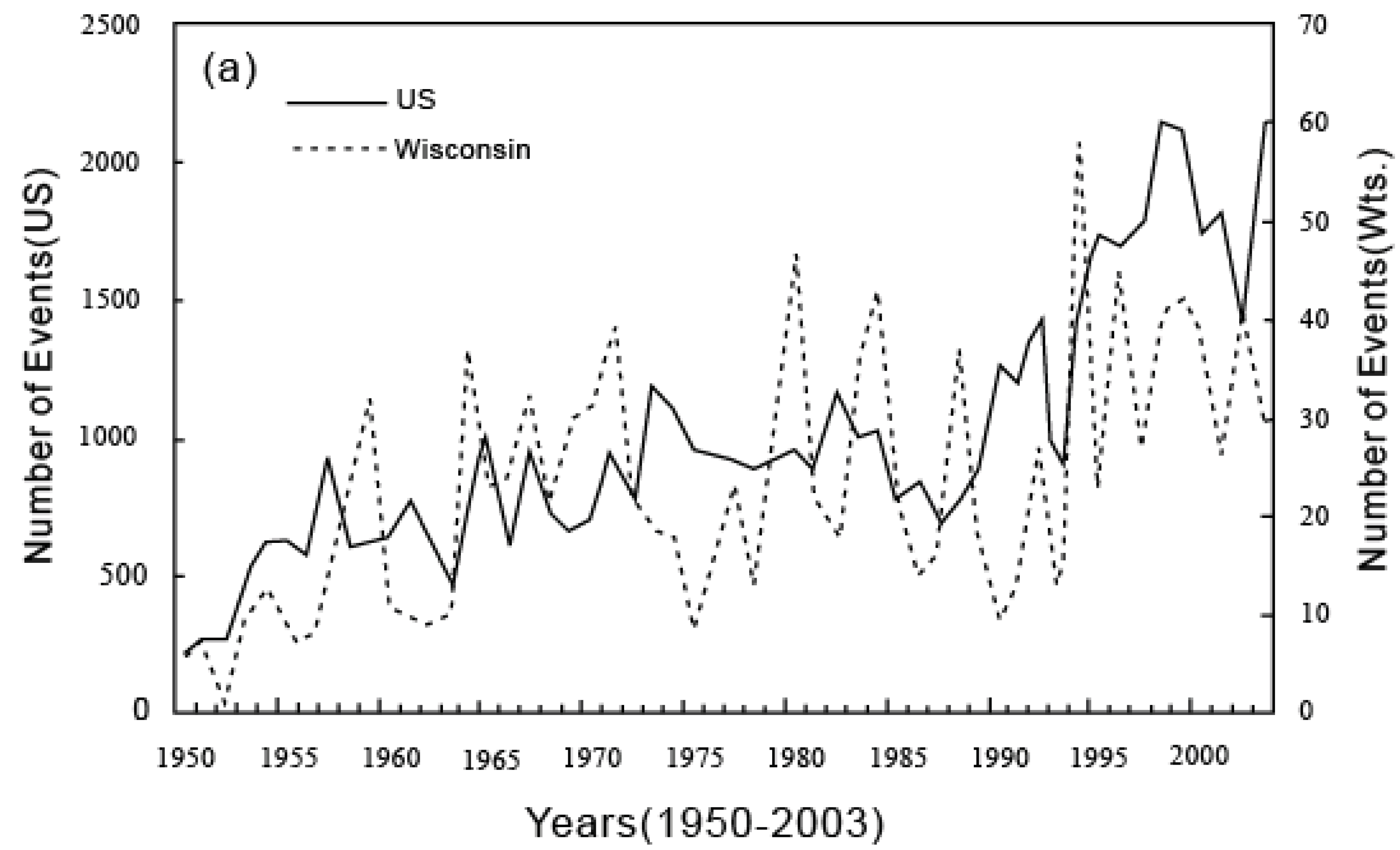
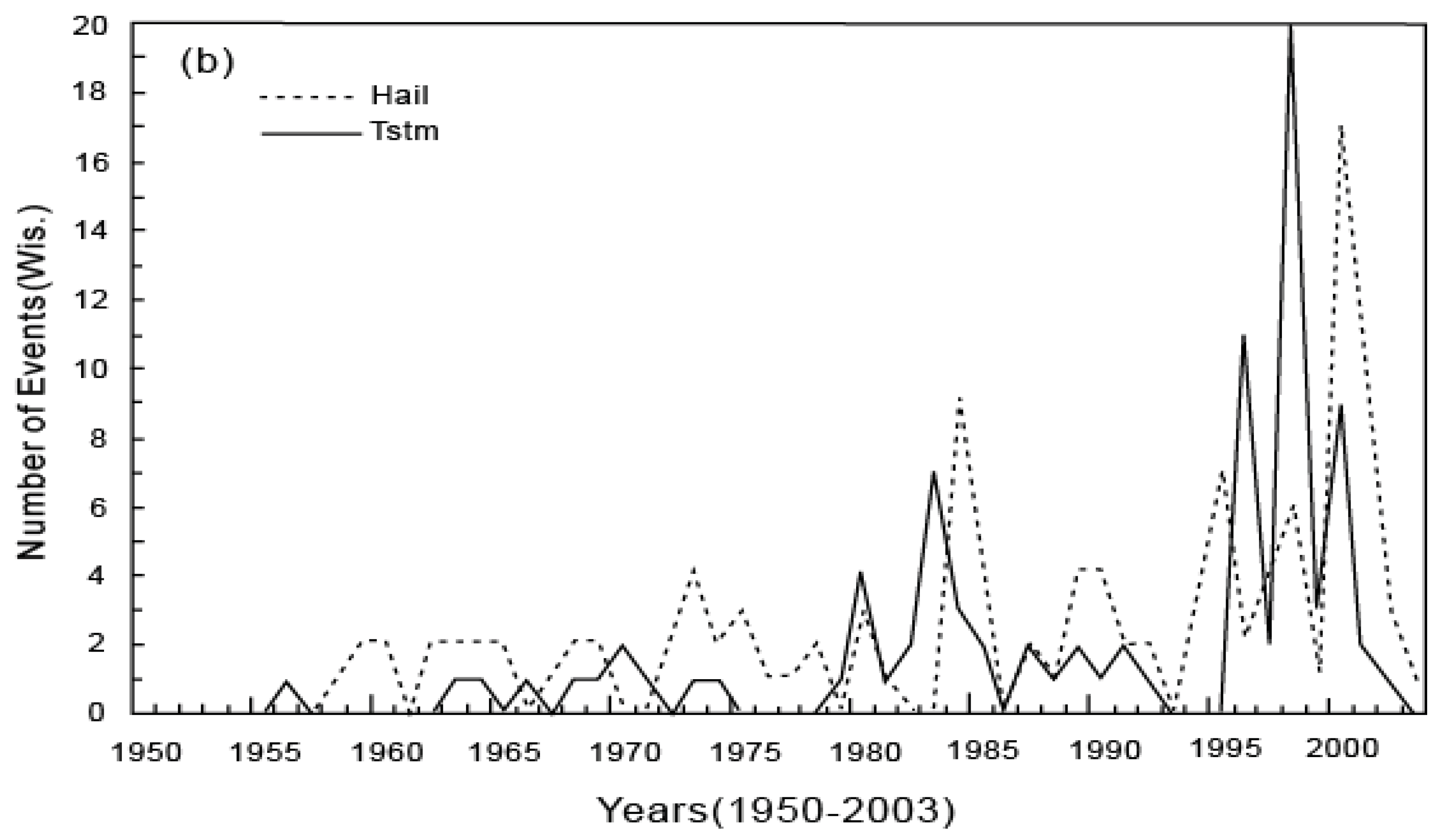
6. Applications of the Principle of the Second Law
7. Discussion and Conclusions
Acknowledgements
References
- Liu, C.; Xu, H.; Liu, Y. Linking entropy flow with typhoon evolution: a case-study. J. Phys. D Appl. Phys. 2007, 40, 6694–6704. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, C. On the entropy flow properties of a severe tropical storm. Appl. Phys. Lett. 2007, 91(1). [Google Scholar] [CrossRef]
- Romps, D.M. The dry-entropy budget of a moist atmosphere. J. Atmos. Sci. 2008, 65, 3779–3799. [Google Scholar] [CrossRef]
- Ozawa, H.; Ohmura, A.; Lorenz, R.D.; Pujol, T. The second law of thermodynamics and the global climate system: A review of the maximum entropy production principle. Rev. Geophys. 2003, 41, 1018. [Google Scholar] [CrossRef]
- Carnot, S. Reflexions on the Motive Power of Fire; Manchester Univ. Press: Manchester, UK, 1986; p. 230. [Google Scholar]
- Verkley, W.T.M.; Lynch, P. Energy and enstrophy spectra of geostrophic turbulent flows derived from a maximum entropy principle. J. Atmos. Sci. 2009, 66(8), 2216–2236. [Google Scholar] [CrossRef]
- Martyushev, L.M.; Seleznevb, V.D. Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 2006, 426, 1–45. [Google Scholar] [CrossRef]
- Ozawa, H.; Ohmura, A. Thermodynamics of a global-mean state of the atmosphere—A state of maximum entropy increase. J. Climate 1997, 10, 441–445. [Google Scholar] [CrossRef]
- Duane, G.S.; Curry, J.A. Entropy of a connecting water-air system and the interpretation of cloud morphogenesis. Quart. J. Roy. Meteorol. Soc. 1997, 123, 605–629. [Google Scholar] [CrossRef]
- Barsugli, J.J.; Battisti, D.S. The basic effects of atmosphere-ocean thermal coupling on midlatitude variability. J. Atmos. Sci. 1998, 55, 477–493. [Google Scholar] [CrossRef]
- Egger, J. Numerical generation of entropies. Mon. Wea. Rev. 1999, 127, 2211–2216. [Google Scholar] [CrossRef]
- Nicolis, C. Irreversible thermodynamics of a simple atmospheric model. Int. J. Bifurcation Chaos 2002, 12, 2557–2566. [Google Scholar] [CrossRef]
- Fraedrich, K.; Blender, R. Scaling of atmosphere and ocean temperature correlations in observations and climate models. Phys. Rev. Lett. 2003, 90, 108501. [Google Scholar] [CrossRef] [PubMed]
- Gade, H.G.; Gustafson, K. Application of classical thermodynamics principle to study of oceanic overturning circulation. Tellus 2004, 56, 371–387. [Google Scholar] [CrossRef]
- Curry, J.A. Thermodynamics of Atmospheres and Oceans; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Bohren, C.F.; Albrecht, B.A. Atmospheric Thermodynamics; Oxford University Press: London, UK, 1999. [Google Scholar]
- Tsonis, A.A. An Introduction to Atmospheric Thermodynamics; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Zdunkowski, W.; Bott, A. Thermodynamics of the Atmosphere; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Downarowicz, T. Entropy. Scholarpedia 2007, 2(11), 3901. Available online: http://www.scholarpedia.org/article/Entropy (accessed on 30 September 2010). [Google Scholar] [CrossRef]
- Balasis, G.; Daglis, I.A.; Papadimitriou, C.; Kalimeri, M.; Anastasiadis, A.; Eftaxias, K. Investigating dynamical complexity in the magnetosphere using various entropy measures. J. Geophys. Res. 2009, 114, A00D06. [Google Scholar] [CrossRef]
- Clausius, R. Ueber verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der mechanischen Wärmetheorie. Ann. Phys. Chem. 1865, 125, 353–400. [Google Scholar] [CrossRef]
- Anderson, G. Thermodynamics of Natural Systems; Cambridge University Press: Cambridge, UK, 2005; p. 105. [Google Scholar]
- Wikipedia. Entropy (order and disorder). Available online: http://en.wikipedia.org/wiki/Entropy_(order_and_disorder) (accessed on 2 December 2010).
- Landsberg, P.T. Is equilibrium always an entropy maximum? J. Stat. Physics. 1984, 35, 159–69. [Google Scholar] [CrossRef]
- Greven, A.; Keller, G.; Warnercke, G. Entropy—Princeton Series in Applied Mathematics; Princeton University Press: Princeton, NJ, USA, 2003; ISBN 0-691-11338-6. 2003. [Google Scholar]
- Wikipedia. Entropy in thermodynamics and information theory. Available online: http://en.wikipedia.org/wiki/Entropy_in_thermodynamics_and_information_theory (accessed on 2 December 2010).
- Weiss, V.; Weiss, H. The golden mean as clock cycle of brain waves. Chaos Soliton. Fractal. 2003, 18, 643–652. [Google Scholar] [CrossRef]
- Roopun, A.K.; Kramer, M.A.; Carracedo, L.M.; Kaiser, M.; Davies, C.H.; Traub, R.D.; Kopell, N.J.; Whittington, M.A. Temporal interactions between cortical rhythms. Front. Neurosci. 2008, 2, 145–154. [Google Scholar] [CrossRef] [PubMed]
- Mahulikar, S.P.; Herwig, H. Exact thermodynamic principles for dynamic order existence and evolution in chaos. Chaos Soliton. Fractal. 2009, 41(4), 1939–1948. [Google Scholar] [CrossRef]
- Glansdorff, P.; Prigogine, I. Thermodynamic Theory of Structure, Stability and Fluctuations; Wiley Interscience: New York, NY, USA, 1971. [Google Scholar]
- Strutt, J.W.; Rayleigh, L. Some general theorems relating to vibrations. Proc. London Math. Soc. 1873, 4, 357–368. [Google Scholar]
- Onsager, L. Reciprocal relations in irreversible processes. I. Phys. Rev. 1931, 37, 405–426. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal relations in irreversible processes. II. Phys. Rev. 1931, 38, 2265–2279. [Google Scholar] [CrossRef]
- Sawada, Y. A thermodynamic variational principle in nonlinear non-equilibrium phenomena. Prog. Theor. Phys. 1981, 66, 68–76. [Google Scholar] [CrossRef]
- Malkus, W.V.R.; Veronis, G. Finite amplitude cellular convection. J. Fluid Mech. 1958, 4(3), 225–260. [Google Scholar] [CrossRef]
- Dewar, R. Information theory explanation of the fluctuation theorem, maximum entropy production and self-organized criticality in non-equilibrium stationary states. J. Phys. A: Math. Gen. 2003, 36, 63. [Google Scholar] [CrossRef]
- Dewar, R.C. Maximum entropy production and the fluctuation theorem. J. Phys. A: Math. Gen. 2005, 38, L371. [Google Scholar] [CrossRef]
- Kleidon, A.; Lorenz, R.D. Nonequilibrium thermodynamics and the production of entropy. In Life, Earth, and Beyond; Springer-Verlag: Berlin, Germany, 2005. [Google Scholar]
- Beretta, G.P. Steepest entropy ascent in quantum thermodynamics. Lect. Notes Phys. 1986, 278, 441. [Google Scholar]
- Beretta, G.P. Nonlinear quantum evolution equations to model irreversible adiabatic relaxation with maximal entropy production and other nonunitary processes. Rep. Math. Phys. 2009, 64, 139–168. [Google Scholar] [CrossRef]
- Maddox, J. Uniting mechanics and statistics. Nature 1985, 316, 11. [Google Scholar]
- Beretta, G.P. Modeling non-equilibrium dynamics of a discrete probability distribution: General rate equation for maximal entropy generation in a maximum-entropy landscape with time-dependent constraints. Entropy 2008, 10, 160–182. [Google Scholar] [CrossRef]
- Prigogine, I. Thermodynamics of irreversible processes. Bull. Class. Sci. Acad. Roy. Belg. 1945, 31, 600–621. [Google Scholar]
- Prigogine, I. Introduction to Thermodynamics of Irreversible Processes; Charles C Thomas Publisher: Springfield, IL, USA, 1955. [Google Scholar]
- De Groot, S.R.; Mazur, P. Non-equilibrium Thermodynamics; North-Holland: Amsterdam, The Netherlands, 1962. [Google Scholar]
- Katchalsky, A.; Curran, P.F. Non-equilibrium Thermodynamics in Biophysics; Harvard University Press: Cambridge, MA, USA, 1965. [Google Scholar]
- Schrödinger, E. What Is Life? Cambridge University Press: Cambridge, UK, 1992; pp. 19–25. [Google Scholar]
- Clausius, R. Ueber verschiedene für die Anwendung bequeme formen der Hauptgleichungen der mechanischen Wärmetheorie. Ann. Phys. Chem. 1865, 125, 53–400. [Google Scholar] [CrossRef]
- Gibbs, J.W. Elementary Principles in Statistical Mechanics: Developed with Especial Reference to the Rational Foundation of Thermodynamics; Kessinger Publishing’s Photocopy Edition; Kessinger Publishing: Whitefish, MT, USA, 1902. [Google Scholar]
- Boltzmann, L. Further studies on the thermal equilibrium of gas molecules. In Wisssenschaftliche Abhandlungen; Hasenohrl, F., Ed.; J.A. Barth: Leipzig, Germany, 1909; Volume 1, pp. 316–402. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27(7), 379–423. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27(10), 623–656. [Google Scholar] [CrossRef]
- Gibbs, W.J. On the equilibrium of heterogeneous substances. Transactions of the Connecticut Academy 1876. III, October 1875–May 1876, 108–248, May 1877–July 1878, 343–524. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106(4), 620–630. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics II. Phys. Rev. 1957, 108(2), 171–190. [Google Scholar] [CrossRef]
- Dewar, R. Information theory explanation of the fluctuation theorem, maximum entropy production and self-organized criticality in non-equilibrium stationary states. J. Phys. A Math. Gen. 2003, 36(3), 634–641. [Google Scholar] [CrossRef]
- Ruelle, D.P. Extending the definition of entropy to nonequilibrium steady states. Proc. Natl. Acad. Sci. U. S. A. 2003, 100(6), 3054–3058. [Google Scholar] [CrossRef] [PubMed]
- Peixoto, J.P.; Oort, A.H.; de Almeida, M.; Tome, A. Entropy budget of the atmosphere. J. Geophys. Res. 1991, 96, 10981–10988. [Google Scholar] [CrossRef]
- Carlstead, E.M. A study of constant absolute vorticity trajectories on isentropic surfaces. J. Meteorol. 1953, 10(5), 356–361. [Google Scholar] [CrossRef]
- Uccellini, L.W.; Johnson, D.R.; Schlesinger, R.E. An isentropic and sigma coordinate hybrid numerical model: Model development and some initial tests. J. Atmos. Sci. 1979, 36(3), 390–414. [Google Scholar] [CrossRef]
- Shapiro, M.A. Simulation of Upper-level frontogenesis with a 20-level isentropic coordinate primitive equation model. Mon. Weather Rev. 1975, 103(7), 591–604. [Google Scholar] [CrossRef]
- Bleck, R. Short-range prediction in isentropic coordinates with filtered and unfiltered numerical models. Mon. Weather Rev. 1974, 102(12), 813–829. [Google Scholar] [CrossRef]
- Anthens, R.A. A numerical model of the slowly varying tropical cyclone in isentropic coordinates. Mon. Weather Rev. 1971, 99(8), 617–635. [Google Scholar] [CrossRef]
- Yang, H.; Olaguer, E.; Tung, K.K. Simulation of the present-day atmospheric ozone, odd nitrogen, chlorine and other species using a coupled 2-D model in isentropic coordinates. J. Atmos. Sci. 1991, 48(3), 442–471. [Google Scholar] [CrossRef]
- Yueh-Jiuan, G.; Hsu, A.A. Numerical modeling of the atmosphere with an isentropic vertical coordinate. Mon. Weather Rev. 1990, 118(10), 1933–1959. [Google Scholar]
- Trevisan, A.; Ferranti, L.; Malguzzi, P. Further developments of normal mode theory of lee cyclogenesis: Isentropic coordinate model. J. Atmos. Sci. 1988, 45(24), 3880–3888. [Google Scholar] [CrossRef]
- Black, T.L. A Comparison of Key Forecast variables derived from isentropic and sigma coordinate regional models. Mon. Weather Rev. 1987, 115(12), 3097–3114. [Google Scholar] [CrossRef]
- Merrill, J.T.; Bleck, R.; Boudra, D. Techniques of lagrangian trajectory analysis in isentropic coordinates. Mon. Weather Rev. 1986, 114(3), 571–581. [Google Scholar] [CrossRef]
- Andrews, D.G. A Finite-amplitude eliassen-palm theorem in isentropic coordinates. J. Atmos. Sci. 1983, 40(8), 1877–1883. [Google Scholar] [CrossRef]
- Ka, K.T. On the two-dimensional transport of stratospheric trace gases in isentropic coordinates. J. Atmos. Sci. 1982, 39(10), 2330–2355. [Google Scholar]
- Brankovic, C. A transformed isentropic coordinate and its use in an atmospheric model. Mon. Weather Rev. 1981, 109(9), 2029–2039. [Google Scholar] [CrossRef]
- Reames, F.M.; Zapotocny, T.H. Inert trace constituent transport in sigma and hybrid isentropic-sigma models. Part II: Twelve Semi-Lagrangian Algorithms. Mon. Weather Rev. 1999, 127(2), 188–200. [Google Scholar] [CrossRef]
- Reames, F.M.; Zapotocny, T.H. Inert trace constituent transport in sigma and hybrid isentropic-sigma models. Part I: Nine advection algorithms. Mon. Weather Rev. 1999, 127(2), 173–187. [Google Scholar] [CrossRef]
- Zapotocny, T.H.; Johnson, D.R.; Reames, F.M. A comparison of regional isentropic-sigma and sigma model simulations of the January 1979 Chicago blizzard. Mon. Weather Rev. 1993, 121(7), 2115–2136. [Google Scholar] [CrossRef]
- Johnson, D.R.; Zapotocny, T.H.; Reames, F.M.; Wolf, B.J.; Bradley, P.R. A comparison of simulated precipitation by hybrid isentropic-sigma and sigma models. Mon. Weather Rev. 1993, 121(7), 2088–2114. [Google Scholar] [CrossRef]
- Pierce, R.B.; Reames, F.M.; Zapotocny, T.H.; Johnson, D.R.; Wolf, B.J. Numerical investigations with a hybrid isentropic-sigma model. Part I: Normal-mode characteristics. J. Atmos. Sci. 1991, 48(18), 2005–2024. [Google Scholar] [CrossRef]
- Bleck, R.; Benjamin, S.G. Regional weather prediction with a model combining terrain-following and isentropic coordinates. Part I: Model description. Mon. Weather Rev. 1993, 121(6), 1770–1785. [Google Scholar] [CrossRef]
- Buzzi, A.; Trevisan, A.; Salustri, G. Internal frontogenesis: A two-dimensional model in isentropic, Semi-Geostrophic coordinates. Mon. Weather Rev. 1981, 109(5), 1053–1060. [Google Scholar] [CrossRef]
- Benjamin, S.G.; Grell, G.A.; Brown, J.M.; Smirnova, T.G.; Bleck, R. Mesoscale weather prediction with the RUC hybrid isentropic-terrain-following coordinate model. Mon. Weather Rev. 2004, 132(2), 473–494. [Google Scholar] [CrossRef]
- Bleck, R; Benjamin, S.; Lee, J.; MacDonald, A.E. On the use of an adaptive, hybrid-isentropic vertical coordinate in global atmospheric modeling. Mon. Weather Rev. 2010, 138(6), 2188–2210. [Google Scholar]
- Pauluis, O.; Czaja, A.; Korty, R. The global atmospheric circulation in moist isentropic coordinates. J. Climate 2010, 23(11), 3077–3093. [Google Scholar] [CrossRef]
- Arakawa, A.; Lamb, V.R. Computational Design of the Basic Dynamical Process of the UCLA General Circulation Model. Methods in Computational Physics; Academic Press: New York, NY, USA, 1977; pp. 173–265. [Google Scholar]
- Sommerfeld, A. Mechanics of Deformable Bodies—Lectures on Theoretical Physics Volume II; Academic Press: New York, NY, USA, 1964; Kuerti, G., Translator. [Google Scholar]
- Johnson, D.R.; Lenzen, A.J.; Zapotocny, T.H.; Schaack, T.K. Numerical uncertainties in the simulation of reversible isentropic processes and entropy conservation. J. Climate 2000, 13(21), 3860–3884. [Google Scholar] [CrossRef]
- Johnson, D.R.; Lenzen, A.J.; Zapotocny, T.H.; Schaack, T.K. Numerical uncertainties in simulation of reversible isentropic processes and entropy conservation: Part II. J. Climate 2002, 15(14), 1777–1804. [Google Scholar] [CrossRef]
- Paltridge, G.W. Global dynamics and climate—A system of minimum entropy exchange. Quart. J. Roy. Meteorol. Soc. 1975, 101, 475–484. [Google Scholar] [CrossRef]
- Wikipedia. Non-equilibrium_thermodynamics. Available online: http://en.wikipedia.org/wiki/Non-equilibrium_thermodynamics (accessed on 2 December 2010).
- Tuck, A.F. Atmospheric Turbulence: A Molecular Dynamics Perspective; Oxford University Press: London, UK, 2008; p. 33. [Google Scholar]
- Paltridge, G.W. A physical basis for a maximum of thermodynamic dissipation of the climate system. Quart. J. Roy. Meteorol. Soc. 2001, 127, 305–313. [Google Scholar] [CrossRef]
- Platridge, G.W. The steady-state format of global climate. Quart. J. Roy. Meteorol. Soc. 1978, 104, 927–945. [Google Scholar] [CrossRef]
- Paltridge, G.W. Climate and thermodynamic systems of maximum dissipation. Nature 1979, 279, 630–631. [Google Scholar] [CrossRef]
- Ozawa, H.; Shimokawa, S.; Sakuma, H. Thermodynamics of fluid turbulence: A unified approach to the maximum transport properties. Phys. Rev. E 2001, 64, 026303. [Google Scholar] [CrossRef]
- Goody, R.M. Sources and sinks of climate entropy. Quart. J. Roy. Meteorol. Soc. 2000, 126, 1953–1970. [Google Scholar] [CrossRef]
- Lorenz, E.N. The Nature and Theory of the General Circulation of the Atmosphere; World Meteorological Organization: Geneva, Switzerland, 1967; p. 161. [Google Scholar]
- Lorenz, E.N. Generation of available potential energy and the intensity of the general circulation. In Dynamics of Climate; Pfeffer, R.L., Ed.; Pergamon: Tarrytown, NY, USA, 1960; pp. 86–92. [Google Scholar]
- Grassl, H. The climate at maximum entropy production by meridional atmospheric and oceanic heat fluxes. Quart. J. Roy. Meteorol. Soc. 1981, 107, 153–166. [Google Scholar] [CrossRef]
- Shutts, G.J. Maximum entropy production states in quasigeostrophic dynamical models. Quart. J. Roy. Meteorol. Soc. 1981, 107, 503–520. [Google Scholar] [CrossRef]
- Mobbs, S.D. Extremal principles for global climate models. Quart. J. Roy. Meteorol. Soc. 1982, 108, 535–550. [Google Scholar] [CrossRef]
- Noda, A.; Tokioka, T. Climates at minima of the entropy exchange rate. J. Meteorol. Soc. Jpn. 1983, 61, 894–908. [Google Scholar]
- Sohn, B.J.; Smith, E.A. Energy transports by ocean and atmosphere based on an entropy extremum principle, part I, Zonal averaged transports. J. Climate 1993, 6, 886–899. [Google Scholar] [CrossRef]
- Sohn, B.J.; Smith, E.A. Energy transports by ocean and atmosphere based on an entropy extremum principle, part II, Two-dimensional transports. Meteorol. Atmos. Phys. 1994, 53, 61–75. [Google Scholar] [CrossRef]
- Ozawa, H.; Ohmura, A. Thermodynamics of a global mean state of the atmosphere––A state of maximum entropy increase. J. Climate 1997, 10, 441–445. [Google Scholar] [CrossRef]
- Pujol, T.; Llebot, J.E. Extremal principle of entropy production in the climate system. Quart. J. Roy. Meteorol. Soc. 1999, 125, 79–90. [Google Scholar] [CrossRef]
- Dewar, R. Information theory explanation of the fluctuation theorem, maximum entropy production and self-organized criticality in non-equilibrium stationary states. J. Phys. A Math. Gen. 2003, 36, 631–641. [Google Scholar] [CrossRef]
- Dewar, R.C. Maximum entropy production and the fluctuation theorem. J. Phys. A Math. Gen. 2005, 38, L371–L381. [Google Scholar] [CrossRef]
- Grinstein, G.; Linsker, R. Comments on a derivation and application of the ‘maximum entropy production’ principle. J. Phys. A Math. Gen. 2007, 40, 9717–9720. [Google Scholar] [CrossRef]
- Dewar, R. Information theory explanation of the fluctuation theorem, maximum entropy production and self-organized criticality in non-equilibrium stationary states. J. Phys. A Math. Gen. 2003, 36, 63. [Google Scholar] [CrossRef]
- Dewar, R.C. Maximum entropy production and the fluctuation theorem. J. Phys. A Math. Gen. 2005, 38, L371. [Google Scholar] [CrossRef]
- Center for Molecular Modeling (CMM). Available online: http://cmm.cit.nih.gov/maxent/letsgo.html (accessed on 30 September 2010).
- Cornwell, T. J.; Evans, K.F. A simple maximum entropy deconvolution algorithm. Astron. Astrophys. 1985, 143, 77–83. [Google Scholar]
- Wernecke, S.J.; D’Addario, L.R. Maximum entropy image reconstruction. IEEE Trans. Comput. 1976, C-26, 351–364. [Google Scholar] [CrossRef]
- Gull, S.F.; Daniell, G. Image reconstruction from noisy and incomplete data. Nature 1978, 272, 686–690. [Google Scholar] [CrossRef]
- Jaynes, E.T. The ratinable of maximum entropy methods. Proc. IEEE 1982, 70, 939–952. [Google Scholar] [CrossRef]
- Frieden, B.R. Restoring with maximum likelihood and maximum entropy. J. Opt. Soc. Am. 1972, 62, 511–518. [Google Scholar] [CrossRef] [PubMed]
- Narayan, R.; Nityananda, R. Maximum Entropy—Flexibility versus Fundamentalism, in Indirect Imaging; Roberts, J.A., Ed.; Cambridge University Press: Cambridge, UK, 1984; pp. 281–290. [Google Scholar]
- Narayan, R.; Nityananda, R. Maximum entropy image restoration in astronomy. Ann. Rev. Astron. Astrophys. 1986, 24, 127–170. [Google Scholar] [CrossRef]
- Ou, H.-W. Possible Bounds on the earth’s surface temperature: From the perspective of a conceptual Global-Mean model. J. Climate 2001, 14(13), 2976–2988. [Google Scholar] [CrossRef]
- Nye, T.; Yamamoto, T.; Trevorrow, M. Measurements of the directional spectra of shallow water waves using the maximum entropy principle and a single ocean bottom seismometer. J. Atmos. Ocean. Technol. 1990, 7(5), 781–791. [Google Scholar] [CrossRef]
- Steinwagner, J.; Schwarz, G.; Hilgers, S. Use of a maximum entropy method as a regularization technique during the retrieval of trace gas profiles from limb sounding measurements. J. Atmos. Ocean. Technol. 2006, 23(12), 1657–1667. [Google Scholar] [CrossRef]
- Kivman, G.A.; Kurapov, A.L.; Guessen, A.V. An entropy approach to tuning weights and smoothing in the generalized inversion. J. Atmos. Ocean. Technol. 2001, 18(2), 266–276. [Google Scholar] [CrossRef]
- Bernard, Urban. Humidity profile retrieval using a maximum entropy principle. Mon. Weather Rev. 1995, 123(4), 1185–1196. [Google Scholar] [CrossRef]
- Verkley, W.T.M.; Lynch, P. Energy and enstrophy spectra of geostrophic turbulent flows derived from a maximum entropy principle. J. Atmos. Sci. 2009, 66(8), 2216–2236. [Google Scholar] [CrossRef]
- Elsner, J.B.; Kara, A.B.; Owens, M.A. Fluctuations in North Atlantic hurricane frequency. J. Climate 1999, 12(2), 427–437. [Google Scholar] [CrossRef]
- Sultan, B.; Janicot, S.; Correia, C. Medium lead-time predictability of intraseasonal variability of rainfall in West Africa. Weather Forecast. 2009, 24(3), 767–784. [Google Scholar] [CrossRef]
- Kane, R.P. Quasi-biennial and quasi-triennial oscillations in the summer monsoon rainfall of the meteorological subdivisions of India. Mon. Weather Rev. 1995, 123(4), 1178–1184. [Google Scholar] [CrossRef]
- Christensen, R.A.; Eilbert, R.F. Seasonal precipitation forecasting with a 6–7 month lead time in the Pacific Northwest using an information theoretic model. Mon. Weather Rev. 1985, 113(4), 502–519. [Google Scholar] [CrossRef]
- Simpson, J. Use of the gamma distribution in single-cloud rainfall analysis. Mon. Weather Rev. 1972, 100(4), 309–312. [Google Scholar] [CrossRef]
- Mo, K.C. Adaptive filtering and prediction of intraseasonal oscillations. Mon. Weather Rev. 2001, 129(4), 802–817. [Google Scholar] [CrossRef]
- Bocquet, M.; Pires, C.A.; Wu, L. Beyond Gaussian statistical modeling in geophysical data assimilation. Mon. Weather Rev. 2010, 138(8), 2997–3023. [Google Scholar] [CrossRef]
- Prieto, R.; Schubert, W.H. Analytical predictions for zonally symmetric equilibrium states of the stratospheric polar vortex. J. Atmos. Sci. 2001, 58(18), 2709–2728. [Google Scholar] [CrossRef]
- Schubert, W.H.; Montgomery, M.T.; Taft, R.K.; Guinn, T.A.; Fulton, S.R.; Kossin, J.P.; Edwards, J.P. Polygonal eyewalls, asymmetric eye contraction, and potential vorticity mixing in hurricanes. J. Atmos. Sci. 1999, 56(9), 1197–1223. [Google Scholar] [CrossRef]
- Liu, Y.G.; Hallett, J. On size distributions of cloud droplets growing by condensation: A new conceptual model. J. Atmos. Sci. 1998, 55(4), 527–536. [Google Scholar] [CrossRef]
- Frederiksen, J.S.; Dix, M.R.; Kepert, S.M. Systematic energy errors and the tendency toward canonical equilibrium in atmospheric circulation models. J. Atmos. Sci. 1996, 53(6), 887–904. [Google Scholar] [CrossRef]
- Tai, K.-S.; Ogura, Y. An observational study of easterly waves over the eastern pacific in the northern summer using FGGE data. J. Atmos. Sci. 1987, 44(2), 339–361. [Google Scholar] [CrossRef]
- Hayashi, Y.; Golder, D.G. The seasonal variation of tropical transient planetary waves appearing in a GFDL general circulation model. J. Atmos. Sci. 1980, 37(4), 705–716. [Google Scholar]
- Cadet, D.; Teitelbaum, H. Observational evidence of internal inertia-gravity waves in the tropical stratosphere. J. Atmos. Sci. 1979, 36(5), 892–907. [Google Scholar] [CrossRef]
- Hayashi, Y.; Golder, D.G. The generation of equatorial transient planetary waves: control experiments with a GFDL general circulation model. J. Atmos. Sci. 1978, 35(11), 2068–2082. [Google Scholar] [CrossRef]
- Schönwiese, C-D. Moving spectral variance and coherence analysis and some applications on long air temperature series. J. Clim. Appl. Meteorol. 1987, 26(12), 1723–1730. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Kidd, C.; Levizzani, V.; Marzano, F.S. A neural networks-based fusion technique to estimate half-hourly rainfall estimates at 0.1° resolution from satellite passive microwave and infrared data. J. Appl. Meteorol. 2004, 43(4), 576–594. [Google Scholar] [CrossRef]
- Johnson, D.R. “General coldness of climate models” and the second law: Implications for modeling the earth system. J. Climate 1997, 10(11), 2826–2846. [Google Scholar] [CrossRef]
- Adams, D.K.; Rennó, N.O. Thermodynamic efficiencies of an idealized global climate model. Clim. Dynam. 2005, 25, 801–813. [Google Scholar] [CrossRef] [Green Version]
- Johnson, D.R. General coldness of climate models and the second law: Implications for modeling the earth system. J. Climate 1997, 10, 2826–2846. [Google Scholar] [CrossRef]
- Paltridge, G.W. Thermodynamic dissipation and the global climate system. Quart. J. Roy. Meteorol. Soc. 1981, 107, 531–547. [Google Scholar] [CrossRef]
- Nicolis, G.; Prigogine, I. Self-organization in Non-equilibrium Systems; John Wiley & Sons Inc.: New York, NY, USA, 1977. [Google Scholar]
- Liu, C. The generalized Liapunovian stability for the atmospheric systems. Acta Meteorologica Sinica 1988, 2(1), 30–40. [Google Scholar]
- Pujol, T.; Llebot, J.E. Second differential of the entropy as a criterion for the stability in low-dimensional climate models. Quart. J. Roy. Meteorol. Soc. 1999, 125, 91–106. [Google Scholar] [CrossRef]
- Stephens, G.L.; O’Brien, D.M. Entropy and climate. I: ERBE observations of the entropy production. Quart. J. Roy. Meteorol. Soc. 1993, 119, 121–152. [Google Scholar] [CrossRef]
- Wu, W.; Liu, Y. Radiation entropy flux and entropy production of the Earth system. Rev. Geophys. 2010, 48, RG2003. [Google Scholar] [CrossRef]
- Eckert, K.; Bestehorn, M.; Thess, A. Square cells in surface-tension-driven Bénard convection: experiment and theory. J. Fluid Mech. 1998, 356, 155–197. [Google Scholar] [CrossRef]
- Olby, R. Schrodinger’s problem: What is life? J. Hist. Biol. 1971, 4, 119–148. [Google Scholar] [CrossRef] [PubMed]
- Katchalsky, A.; Curran, P.F. Non-Equilibrium Thermodynamics in Biophysics; Harvard University Press: Cambridge, MA, USA, 1965. [Google Scholar]
- Liu, C.; Liu, Y. Negative entropy flow and its effect on the organization of synoptic-scale severe atmospheric systems. Geophys. Res. Lett. 2004, 31, L01108. [Google Scholar] [CrossRef]
- Xu, H.; Liu, C. Entropy flow properties of a typhoon as simulated by a meso-scale model. EPL. 2008, 83, 18001. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, C. Entropy flow and the evolution if a storm. Entropy 2008, 10, 430–440. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, C. Negative entropy flow and the life-cycle of a severe tropical storm. Atmos. Res. 2009, 9, 39–43. [Google Scholar] [CrossRef]
- Liu, C.; Luo, Z.; Liu, Y.; Yu, H.; Zhou, X.; Wang, D.; Ma, L.; Xu, H. Implication of entropy flow for the development of a system as suggested by the life cycle of a hurricane. Mod. Phys. Lett. B 2010, 24(16), 1747–1757. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, D.L.; Yau, M.K. A multiscale numerical study of Hurricane Andrew (1992), Part I: Explicit simulation and verification. Mon. Wea. Rev. 1997, 125, 3073–3093. [Google Scholar] [CrossRef]
- Knabb, R.D.; Rhome, J.R.; Brown, D.P. Tropical cyclone 1 report: Hurricane Katrina (23–30 August 2005). Available online: http://www.nhc.noaa.gov/pdf/TCR-AL122005_Katrina.pdf (accessed on 30 September 2010).
- McTaggart-Cowan, R.; Bosart, L.F.; Gyakum, J. R.; Atallah, E. H. Hurricane Katrina (2005). Part I: Complex lifecycle of an intense tropical cyclone. Mon. Wea. Rev. 2007, 135, 3905–3926. [Google Scholar] [CrossRef]
- E. Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Amer. Meteor. Soc. 1996, 77(3), 437–471. [Google Scholar] [CrossRef]
- Nitschke, K.; Bestehorn, M.; Thess, A. Square cells in surface-tension-driven Bénard convection. J. Fluid Mech. 1998, 356, 155–197. [Google Scholar]
- Peixoto, J.P.; Oort, A.H.; Almeida, M.D.; Tomé, A. Entropy budget of the atmosphere. J. Geophys. Res. 1991, 96, 10,981–10,988. [Google Scholar] [CrossRef]
- Easterling, D.R.; Evana, J.L.; Grosman, P.Ya.; Karl, T.R.; Kunkel, K.E.; Ambenje, P. Observed variability and trends in extreme climate. Bull. Am. Metor. Soc. 2000, 81, 417–425. [Google Scholar] [CrossRef]
- Karl, T.R.; Kukla, G.; Razuvayev, V.N.; Changery, M.J.; Quayle, R.G.; Heim, R.R., Jr.; Easterling, D.R.; Fu, C.B. Global warming: Evidence for asymmetric diurnal temperature change. Geophys. Res. Lett. 1991, 18, 2253–2256. [Google Scholar] [CrossRef]
- Manton, M.J.; Eral, J. Trend in extreme daily rainfall and temperature in southeast Asia and the South Pacific: 1961–1998. Int. J. Climatol. 2001, 21, 269–284. [Google Scholar] [CrossRef]
- Wang, S.W.; Gong, D.Y. Enhancement of the warming trend in China. Geophys. Res. Lett. 2000, 27(16), 2581–2584. [Google Scholar] [CrossRef]
- Goody, R. Maximum entropy production in climate theory. J. Atmos. Sci. 2007, 64(7), 2735–2739. [Google Scholar] [CrossRef]
- Dryden, W.A. On the flux of eddy energy in small-scall turbulent motion. J. Meteorol. 1956, 13(5), 433–447. [Google Scholar] [CrossRef]
- Blackadar, A. Extension of the laws of thermodynamics to turbulent systems. J. Meteorol. 1955, 12(2), 165–175. [Google Scholar] [CrossRef]
- Pauluis, O. Thermodynamic consistency of the anelastic approximation for a moist atmosphere. J. Atmos. Sci. 2008, 65(8), 2719–2729. [Google Scholar] [CrossRef]
- Weaver, A. J.; Eby, M. On the numerical implementation of advection schemes for use in conjunction with various mixing parameterizations in the GFDL ocean model. J. Phys. Oceanogr. 1997, 27(2), 369–377. [Google Scholar] [CrossRef]
- Wulf, O.R.; Davis, L., Jr. On the efficiency of the engine driving the atmosphere circulation. J. Meteorol. 1952, 9(2), 80–82. [Google Scholar] [CrossRef]
- Burkhardt, U.; Becker, E. A consistent diffusion-dissipation parameterization in the ECHAM climate model. Mon. Weather Rev. 2006, 134(4), 1194–1204. [Google Scholar] [CrossRef]
- Kleeman, R. Measuring dynamical prediction utility using relative entropy. J. Atmos. Sci. 2002, 59(13), 2057–2072. [Google Scholar] [CrossRef]
- Romps, D.M. The dry-entropy budget of a moist atmosphere. J. Atmos. Sci. 2008, 65(12), 3779–3799. [Google Scholar] [CrossRef]
- Liu, C.; Liu, Y.; Kang, H.W. A new technique of physical dissipation and its application to a mesoscale numerical weather prediction model. Sci. China Ser. D 2002, 45(9), 769–780. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, C.; Kang, H.W. The modeling improvement of hurricane Andrew by the technique of irreversible thermodynamic operators. Acta Meteorologica Sinica 2002, 16(4), 441–450. [Google Scholar]
- Liu, Y.; Liu, C.; Xu, H.; Zhao, Y.M. A numerical study of sensitivity of the physical dissipative technique to precipitation parameterization in a mesoscale model. Acta Meteorologica Sinica 2005, 19(1), 67–75. [Google Scholar]
- Liu, C.; Zhao, L.N.; Liu, Y. Physical dissipative technique and its application to the MM4. Acta Meteorologica Sinica 2002, 59(5), 516–524. [Google Scholar]
- Liu, C.; Liu, Y.; Xu, H. A physics-based diffusion scheme for numerical models. Geophys. Res. Lett. 2006, 33, L12805. [Google Scholar] [CrossRef]
- Liu, C.; Liu, Y.; Xu, H. A new diffusion scheme for numerical models based on full irreversibility. Weather Forecast. 2009, 24, 595–600. [Google Scholar] [CrossRef]
- Liu, C.; Liu, Y.; Luo, Z. Improving numerical simulation of a hurricane by irreversible thermodynamic operators. Atmos. Res. 2009, 93, 44–49. [Google Scholar] [CrossRef]
- Shutts, G.J. Maximum entropy production states in quasi-geostrophic dynamical models. Quart. J. Roy. Meteorol. Soc. 1981, 107, 503–520. [Google Scholar] [CrossRef]
- Pielke, R.A. Mesoscale Meteorological Modeling; Academic Press: New York, NY, USA, 1984; p. 599. [Google Scholar]
- Grell, G.A.; Dudhia, J.; Stauffer, D.R. A Description of the Fifth-generation Penn State/NCAR Mesoscale Model (MM5); National Center for Atmospheric Research: Boulder, CO, USA, 1995; p. 138. [Google Scholar]
- Liu, C.; Liu, Y. An attempt at improving a global spectral model by incorporating the second law of thermodynamics. Geophys. Res. Lett. 2005, 32, L03806. [Google Scholar] [CrossRef]
- Liu, C.; Ma, L.; Liu, Y.; Luo, Z.; Lei, X.; Zhou, X.; Wang, D.; Xu, H. Linking tropical cyclone frequency over the western north pacific with sea surface temperatures. In Hurricanes and Climate Change; Elsner, J.B., Hodges, R.E., Malmstadt, J.C., Scheitlin, K.N., Eds.; Springer: New York, NY, USA, 2010; Volume 2. [Google Scholar] [CrossRef]
- Nicolis, G.; Nicolis, C. On the entropy balance of the earth-atmosphere system. Quart. J. Roy. Meteorol. Soc. 1980, 125, 1859–1878. [Google Scholar] [CrossRef]
- Lucia, U. Irreversible entropy variation and the problem of the trend to equilibrium. Physica A 2007, 376, 289–292. [Google Scholar] [CrossRef]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Liu, Y.; Liu, C.; Wang, D. Understanding Atmospheric Behaviour in Terms of Entropy: A Review of Applications of the Second Law of Thermodynamics to Meteorology. Entropy 2011, 13, 211-240. https://doi.org/10.3390/e13010211
Liu Y, Liu C, Wang D. Understanding Atmospheric Behaviour in Terms of Entropy: A Review of Applications of the Second Law of Thermodynamics to Meteorology. Entropy. 2011; 13(1):211-240. https://doi.org/10.3390/e13010211
Chicago/Turabian StyleLiu, Ying, Chongjian Liu, and Donghai Wang. 2011. "Understanding Atmospheric Behaviour in Terms of Entropy: A Review of Applications of the Second Law of Thermodynamics to Meteorology" Entropy 13, no. 1: 211-240. https://doi.org/10.3390/e13010211
APA StyleLiu, Y., Liu, C., & Wang, D. (2011). Understanding Atmospheric Behaviour in Terms of Entropy: A Review of Applications of the Second Law of Thermodynamics to Meteorology. Entropy, 13(1), 211-240. https://doi.org/10.3390/e13010211



