Combined Effects of Pipe Diameter, Reynolds Number and Wall Heat Flux and on Flow, Heat Transfer and Second-Law Characteristics of Laminar-Transitional Micro-Pipe Flows
Abstract
:1. Introduction
2. Theoretical Background
2.1. Micro-Pipe and Roughness
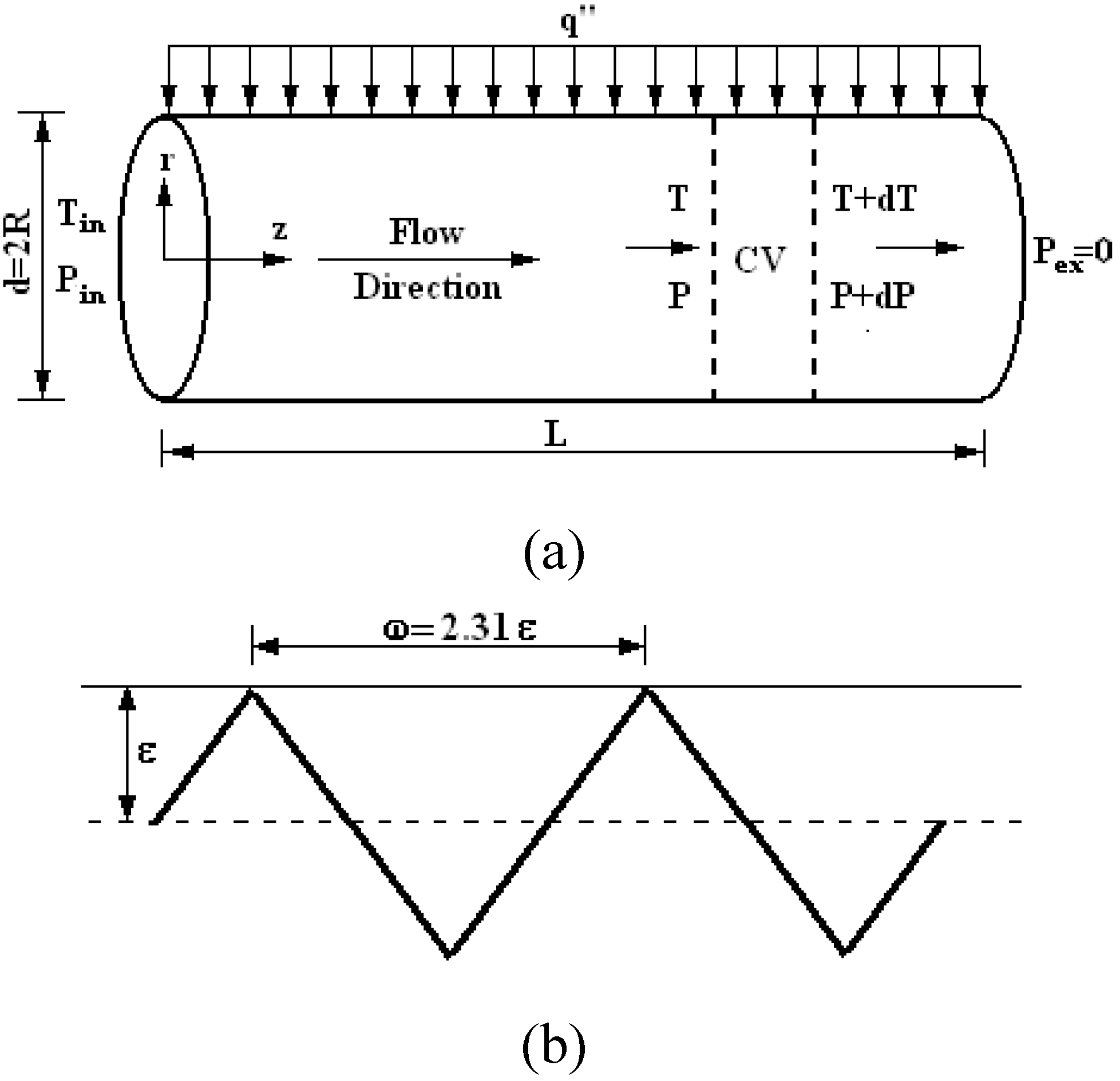
2.2. Governing Equations
2.3. Computational Method
3. Results and Discussion
3.1. Analyses of Flow and Heat Transfer Characteristics
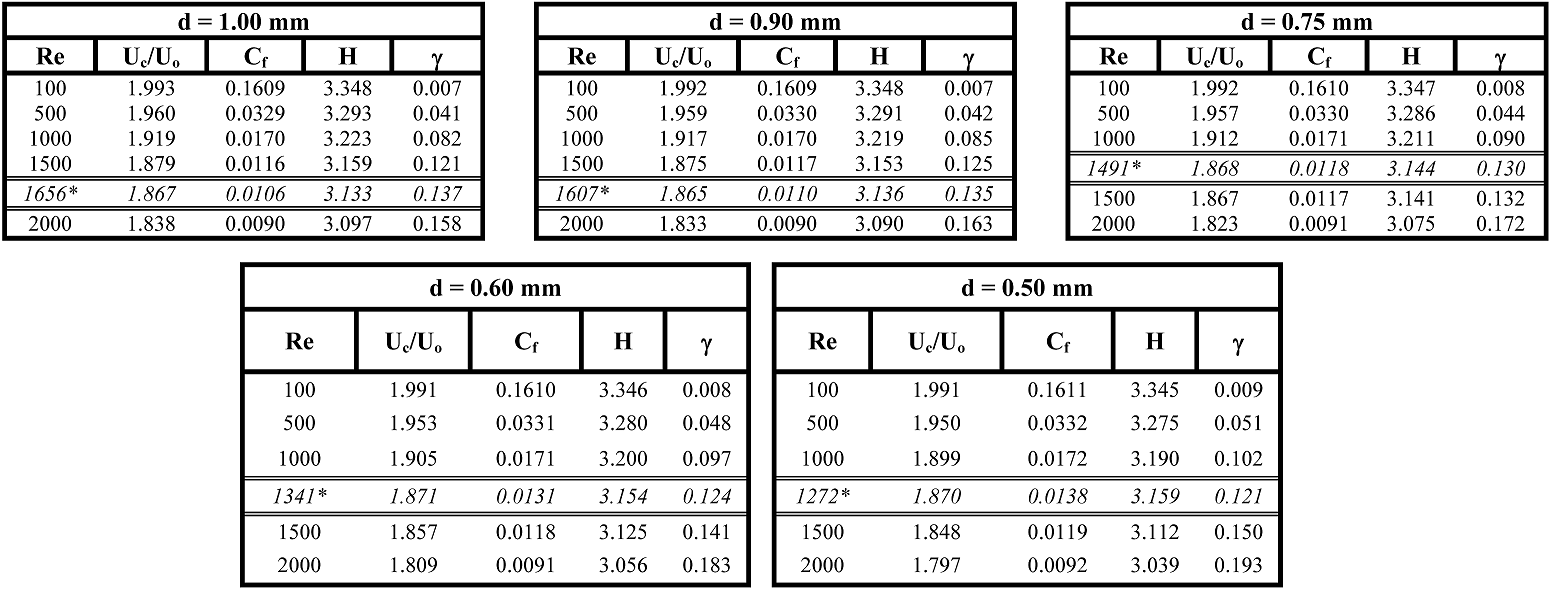
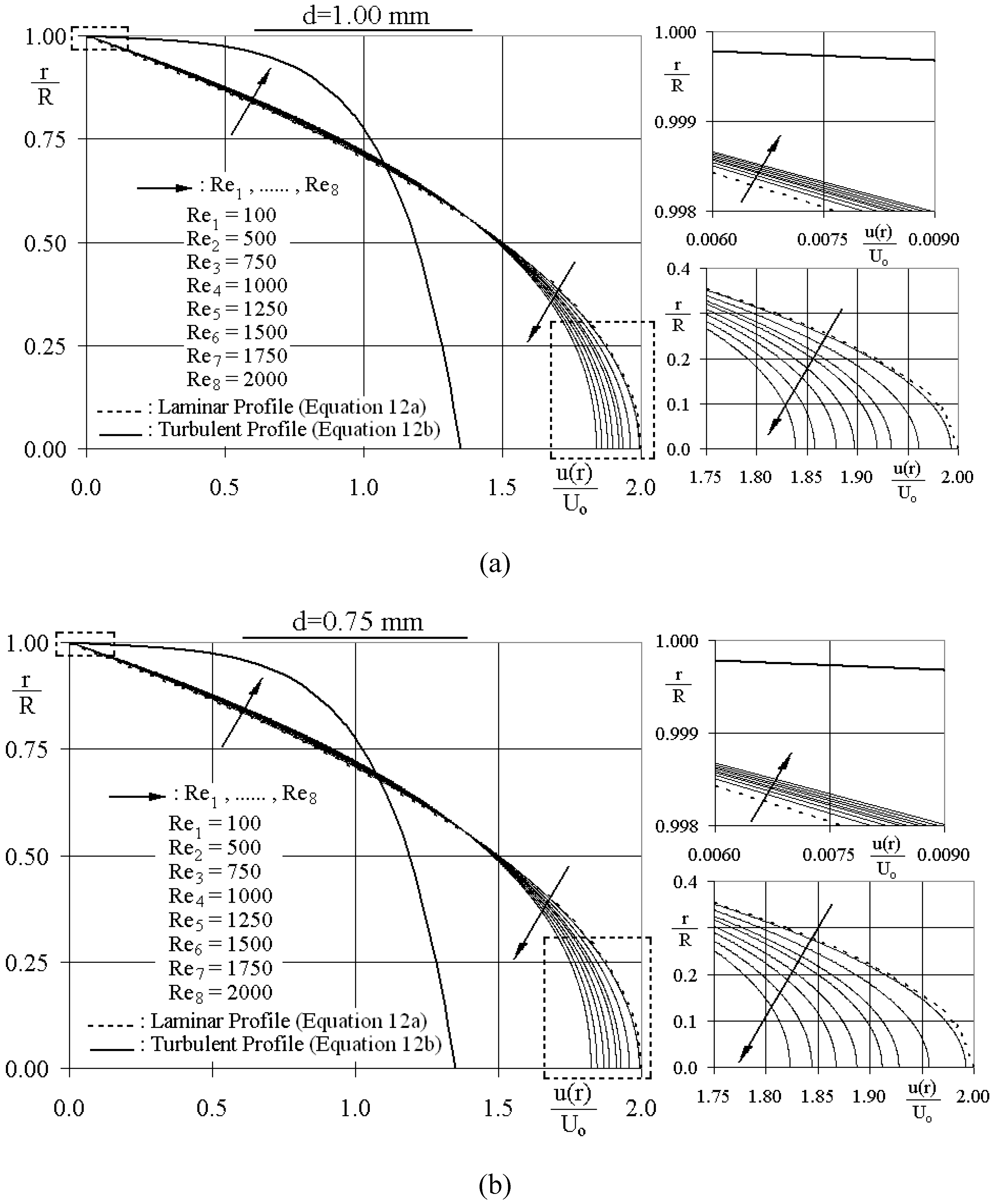
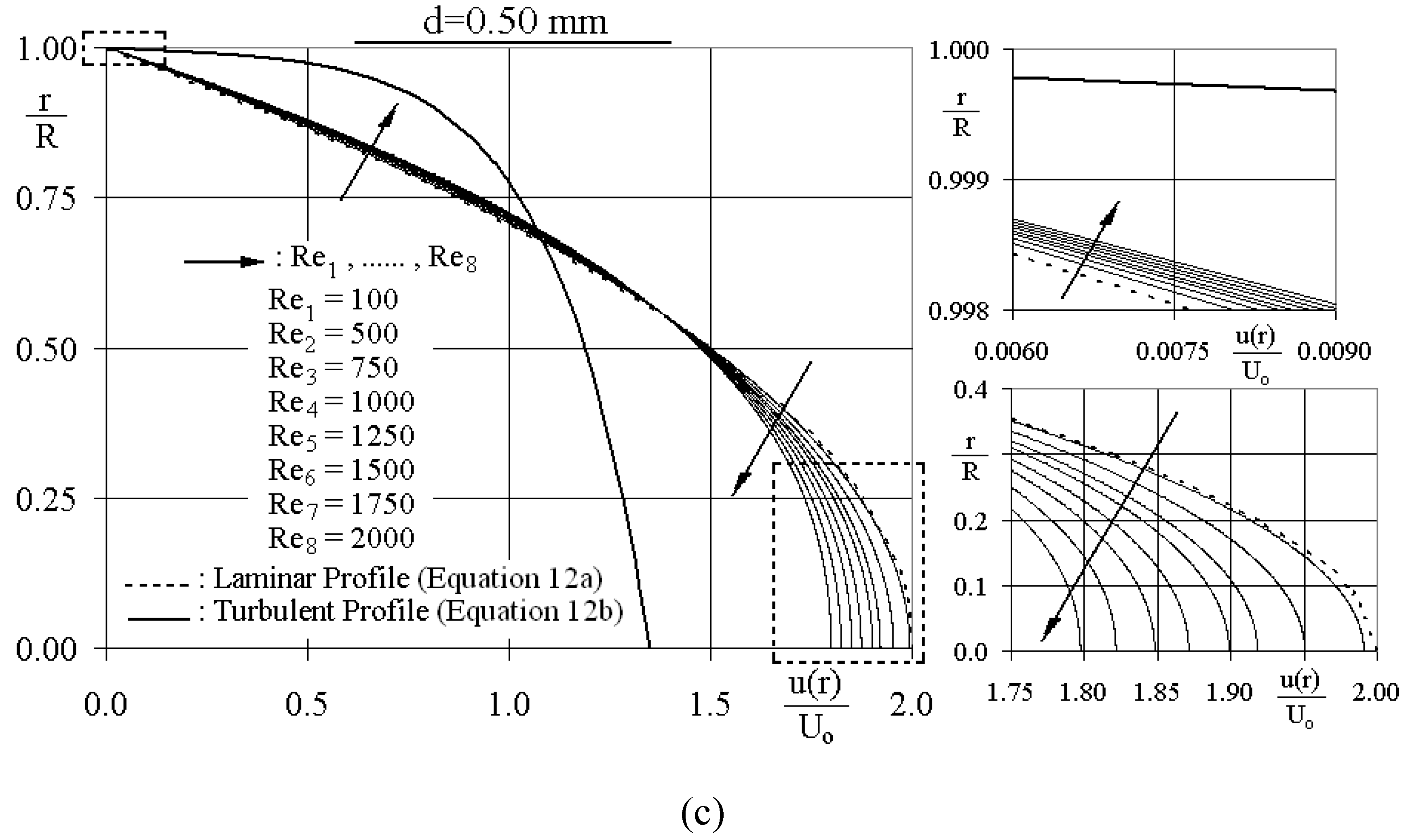
3.1.1. Radial schemes
| d (mm) | q'' (W/m2) | Qs (W) | Re = 100 | Re = 500 | Re = 1000 | Re = 1500 | Re = 2000 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ΔT (K) | Ψloss (W) | ΔT (K) | Ψloss (W) | ΔT (K) | Ψloss (W) | ΔT (K) | Ψloss (W) | ΔT (K) | Ψloss (W) | |||
| 1.00 | 1000 | 1.571 | 4.690 | 1.333E-04 | 0.936 | 3.336E-03 | 0.465 | 1.337E-02 | 0.307 | 3.017E-02 | 0.227 | 5.386E-02 |
| 0.75 | 1000 | 1.178 | 4.690 | 2.371E-04 | 0.933 | 5.931E-03 | 0.460 | 2.378E-02 | 0.298 | 5.369E-02 | 0.215 | 9.594E-02 |
| 0.50 | 1000 | 0.785 | 4.688 | 5.334E-04 | 0.922 | 1.335E-02 | 0.437 | 5.354E-02 | 0.265 | 1.211E-01 | 0.170 | 2.166E-01 |
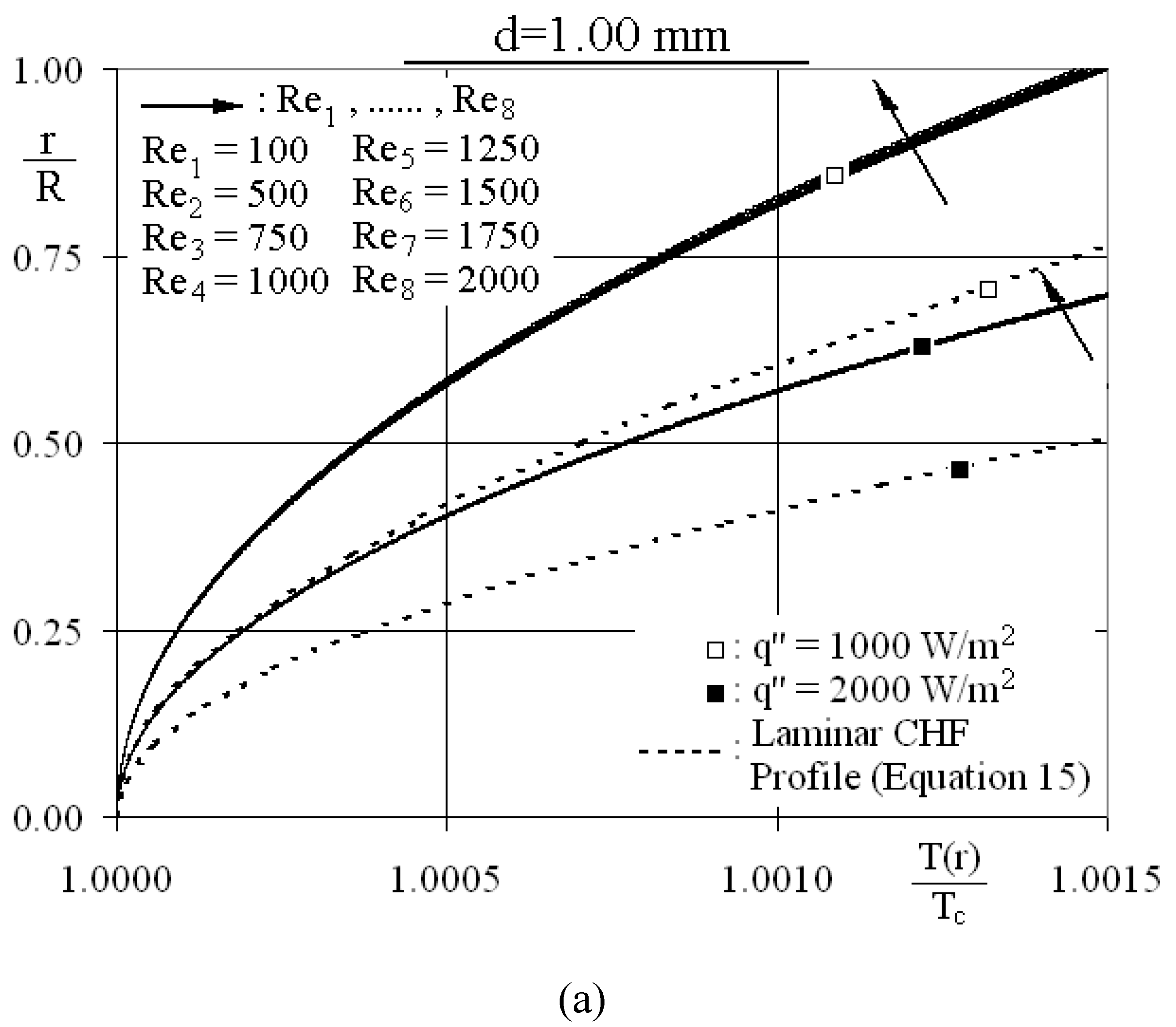
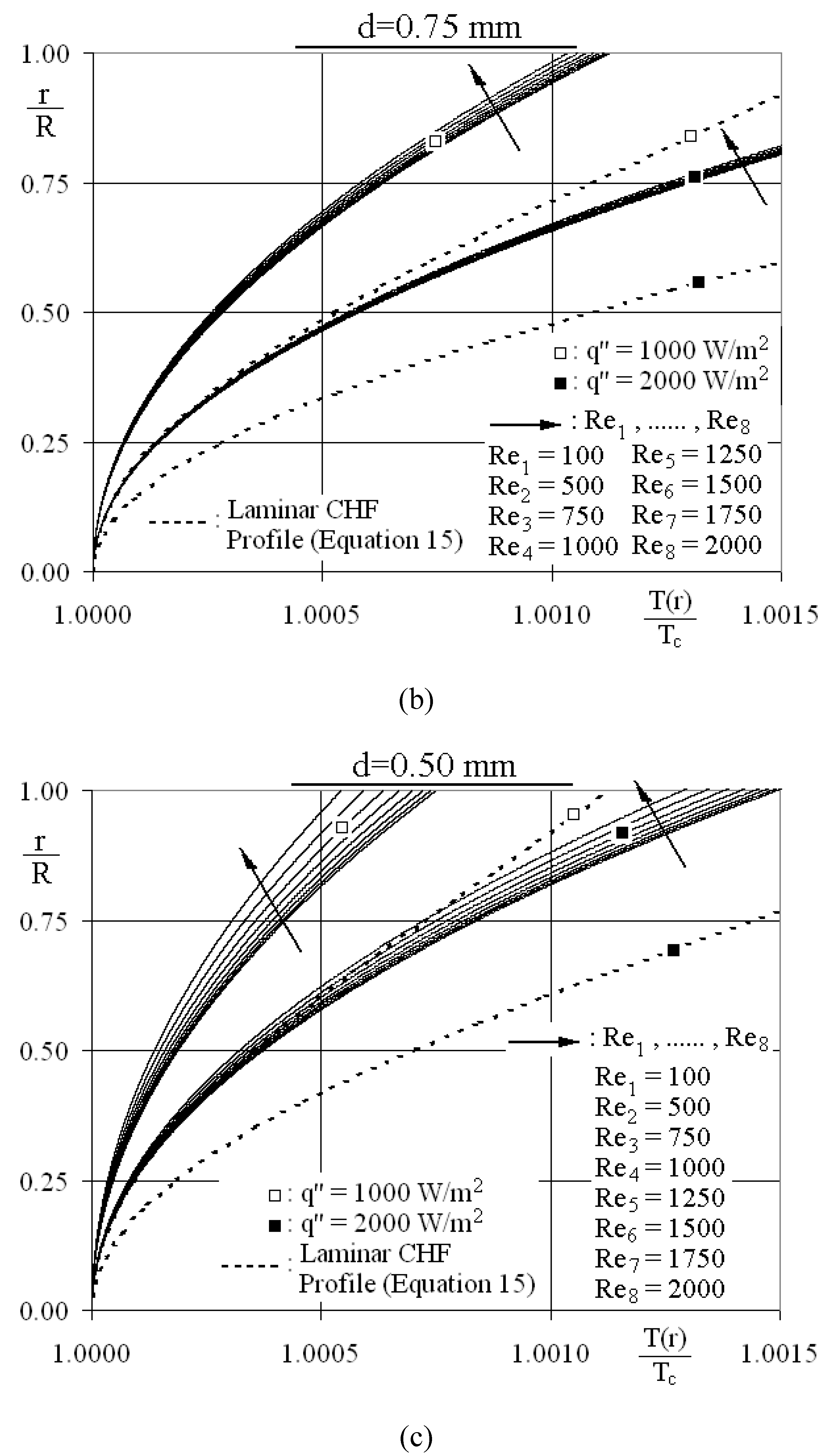
3.1.2. Characteristic parameters
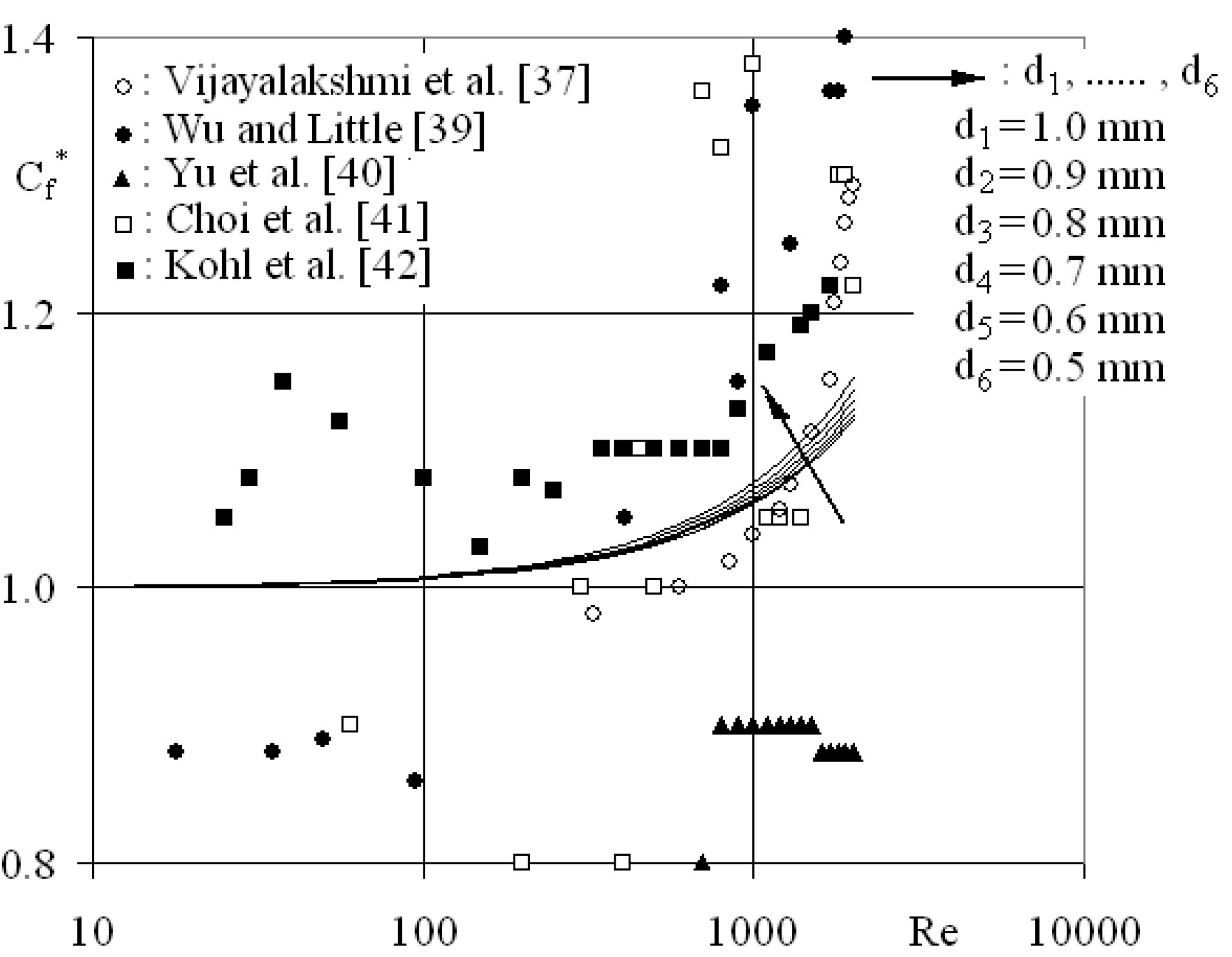
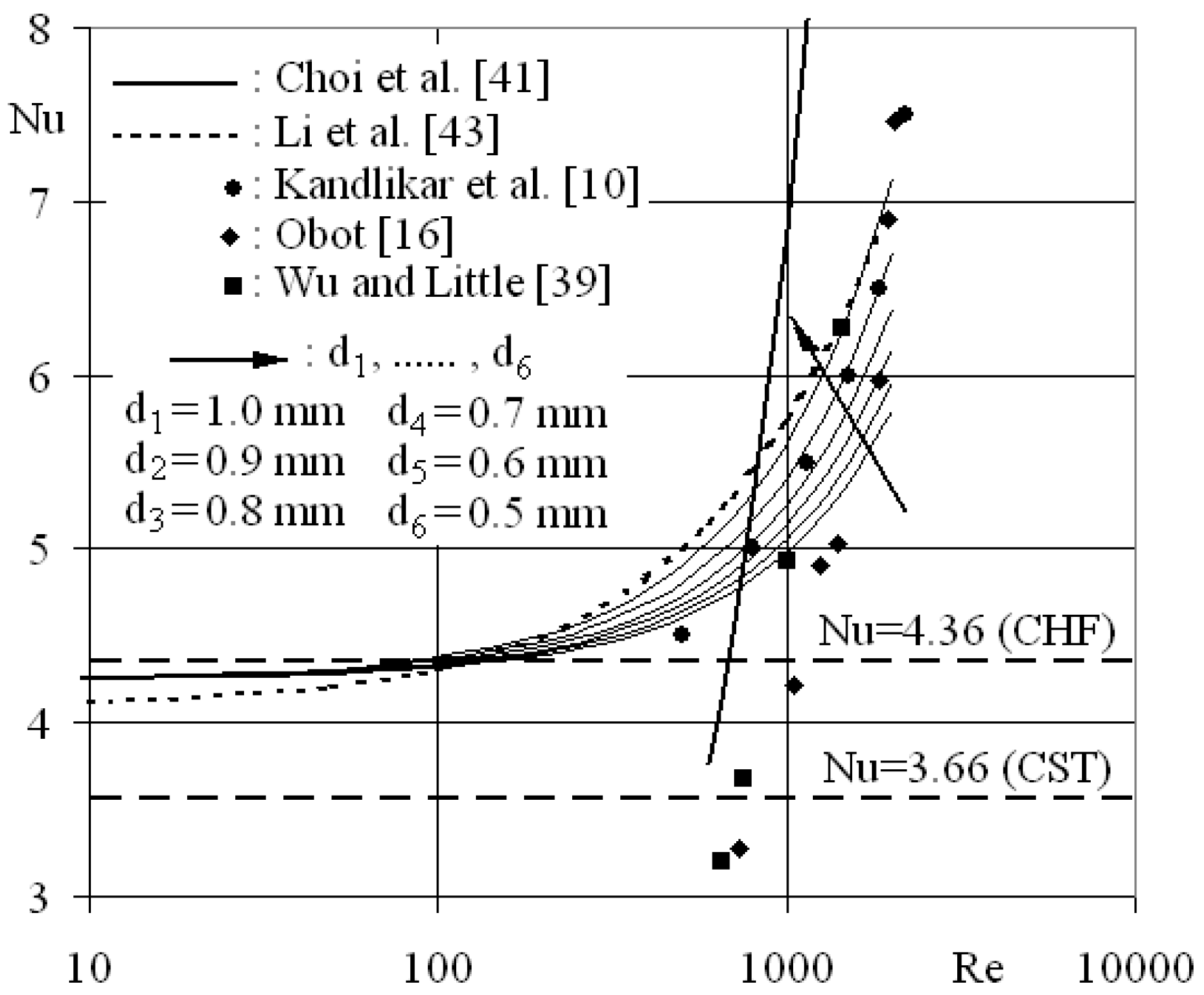
3.2. Analyses on Second-Law Characteristics
3.2.1. Radial schemes
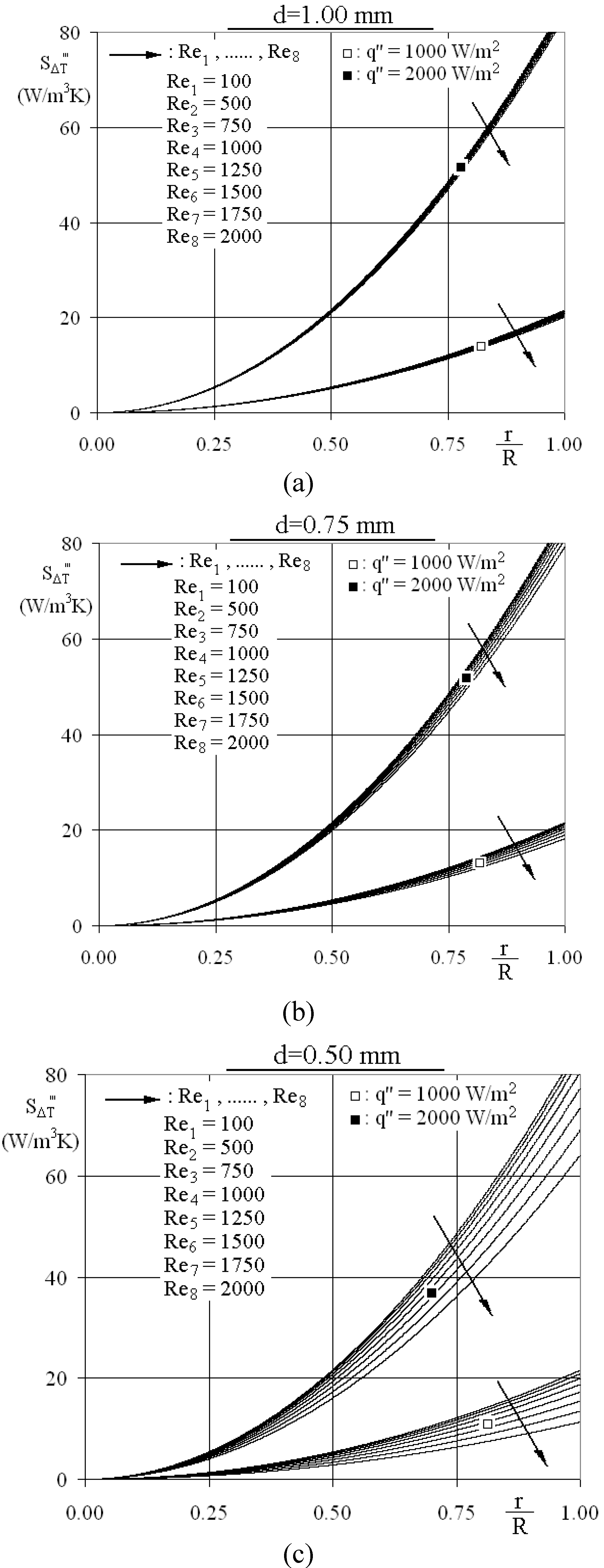
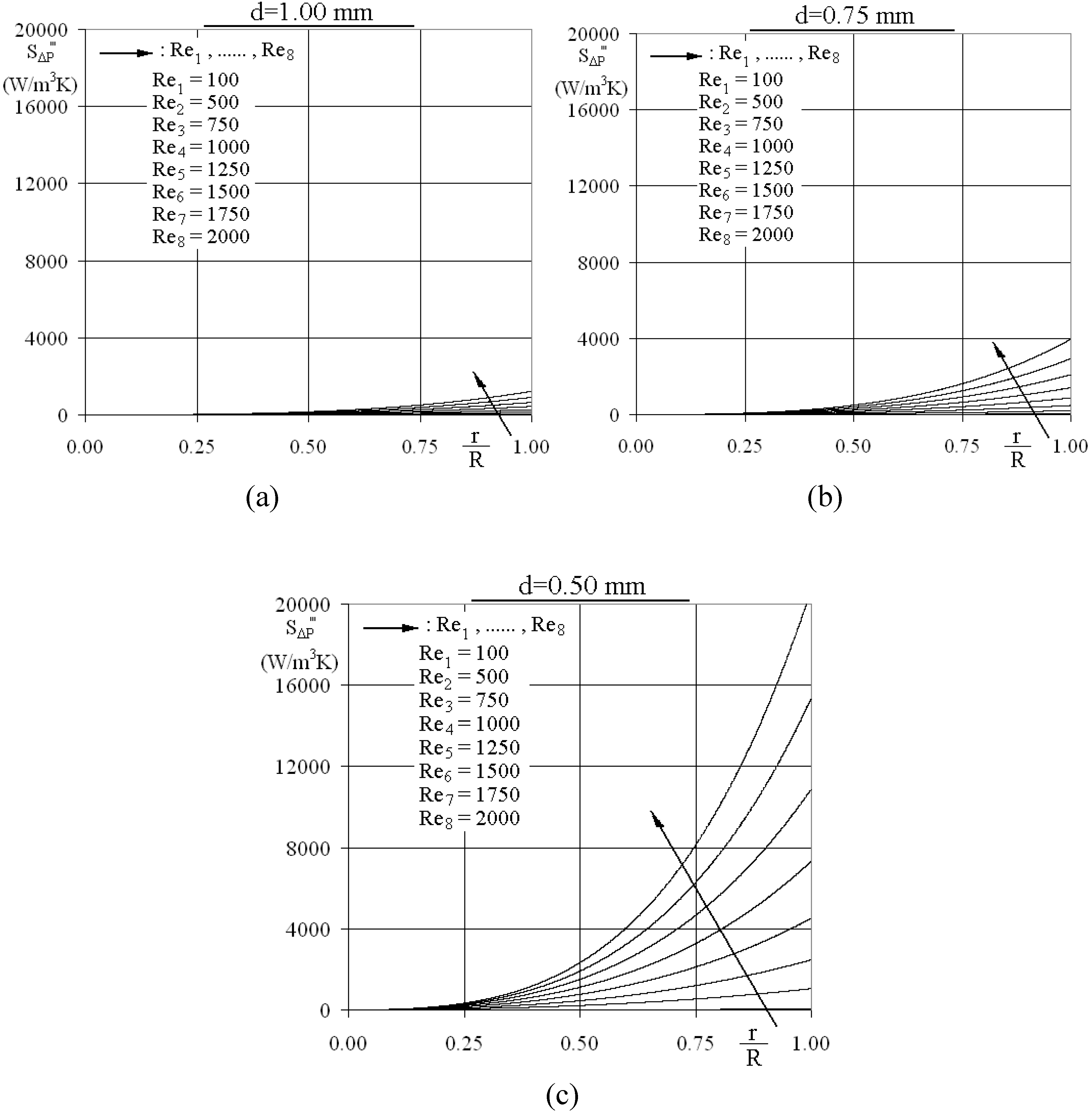
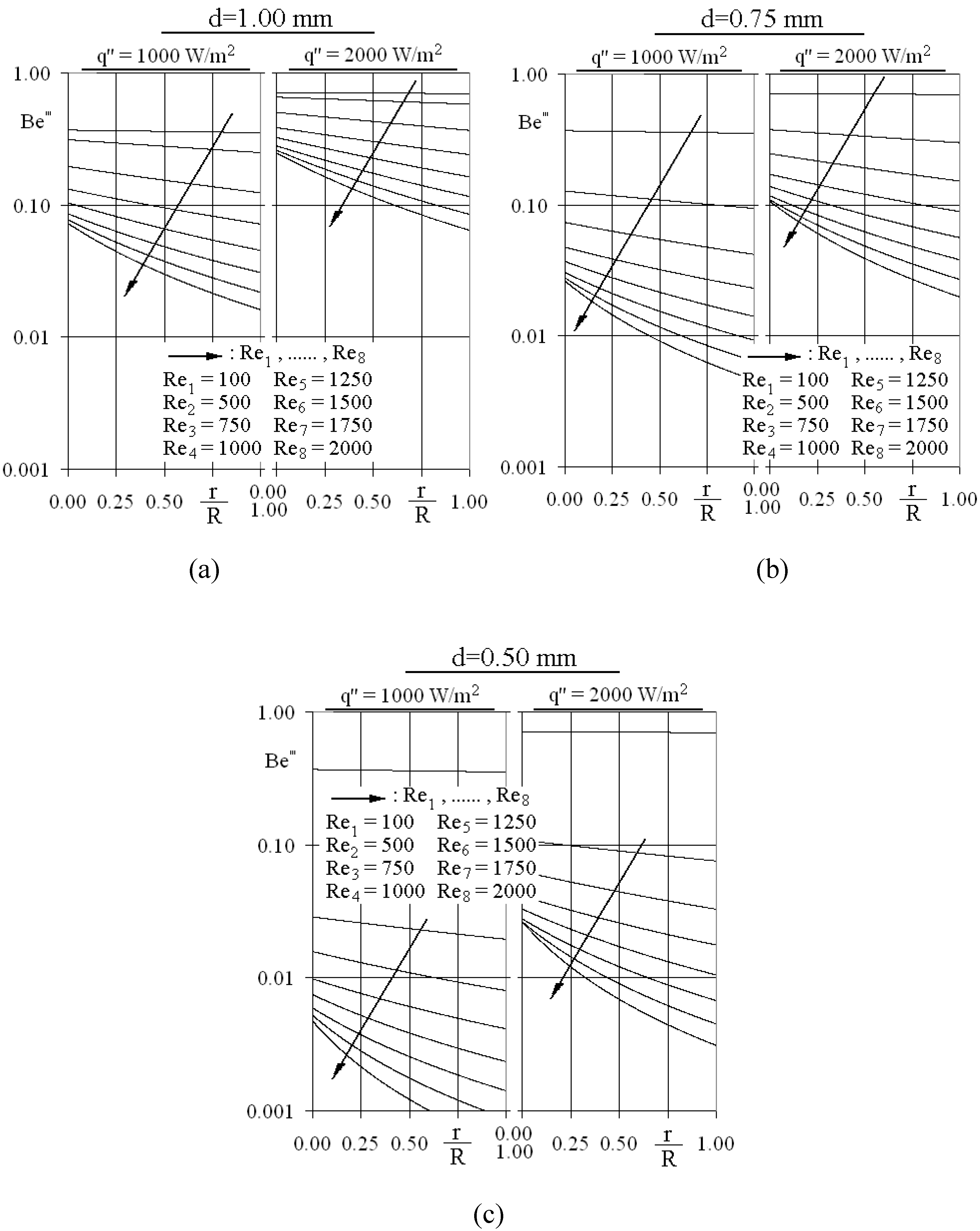
3.2.2. Characteristic parameters
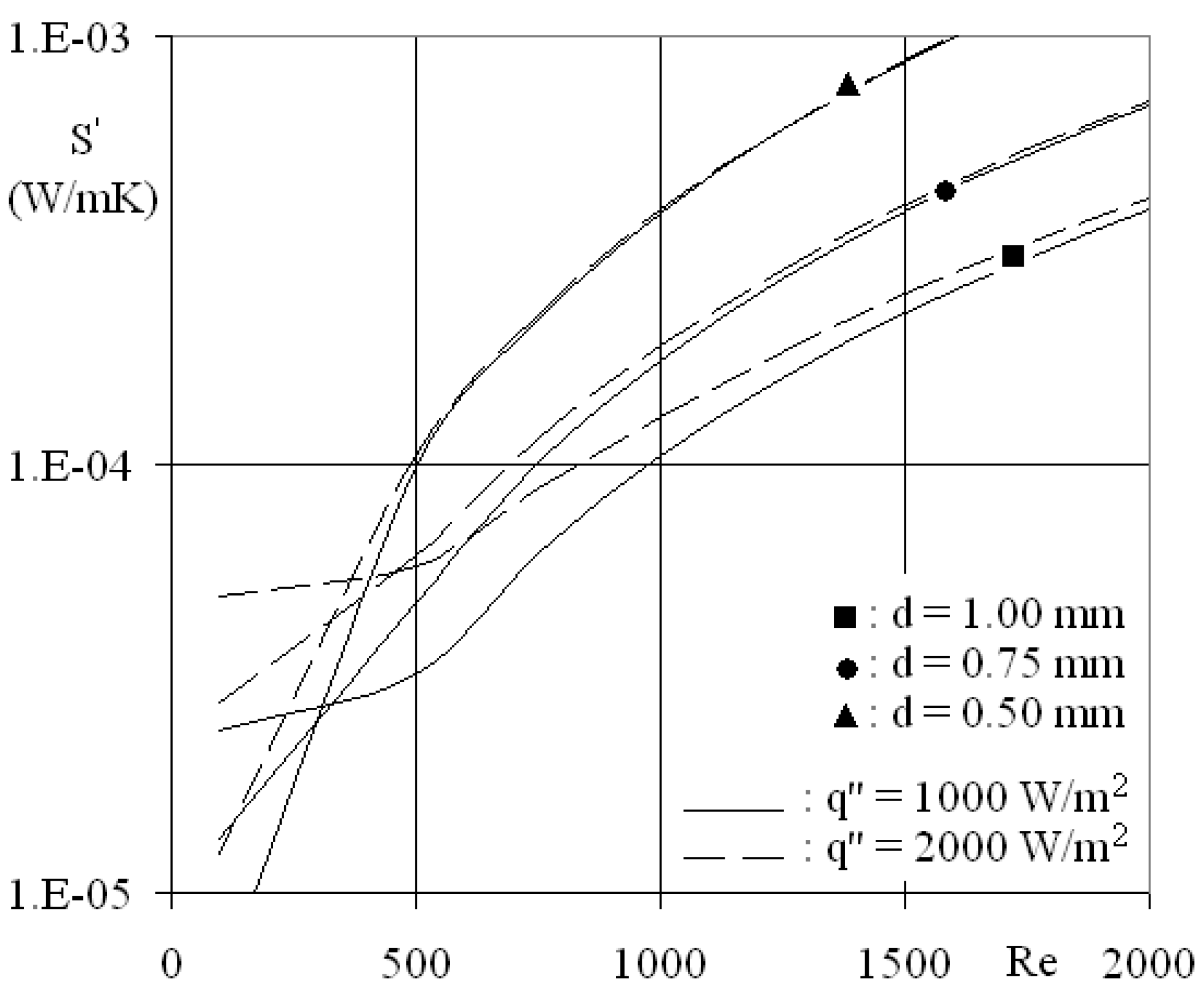
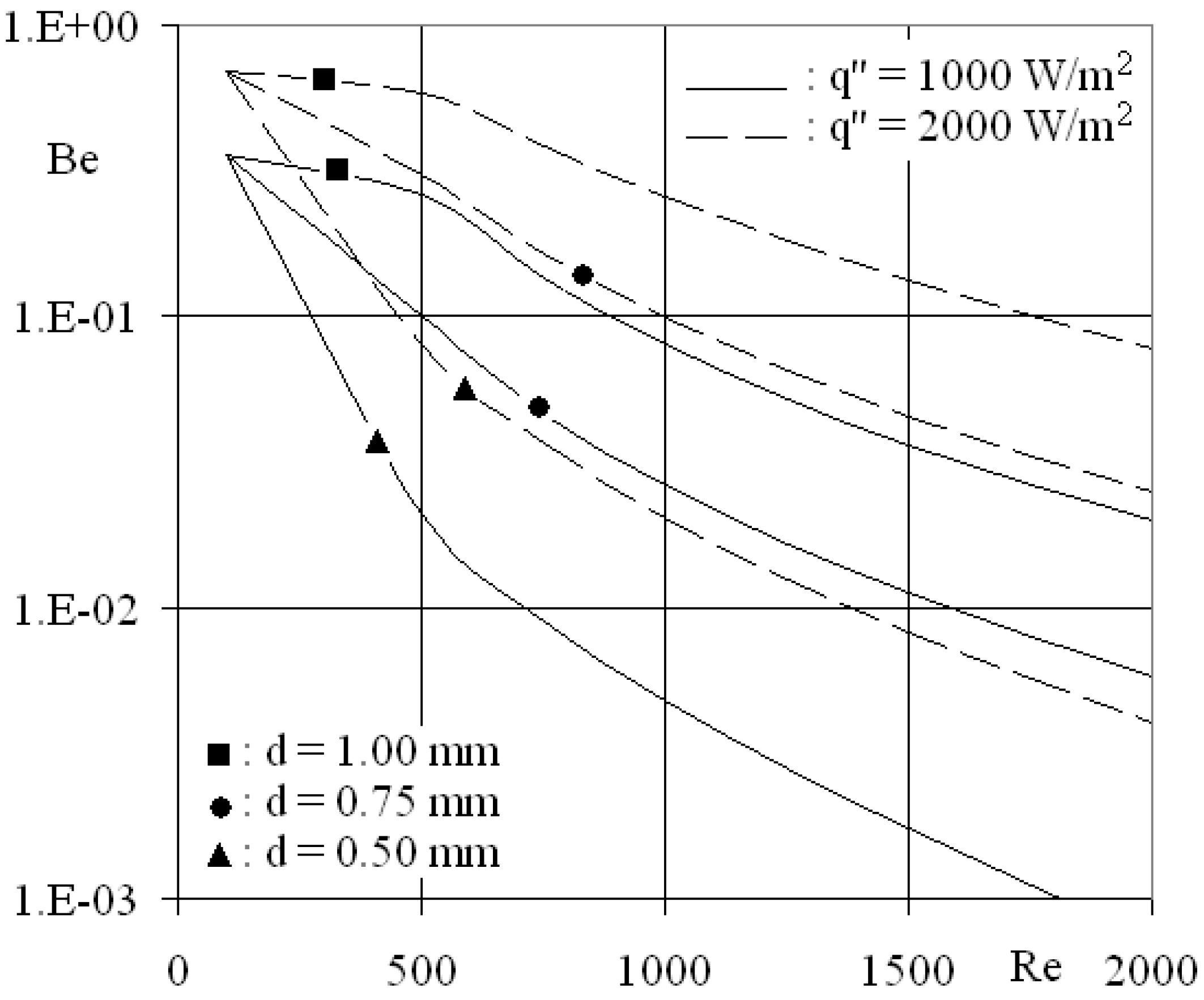
4. Conclusions
| Nomenclature | Greek Symbols | ||
| a | curve fit constants | ε | roughness amplitude (mm) |
| A | cross sectional area (m2) | ε∗ | non-dimensional surface roughness (=ε/d) |
| Cf | friction coefficient | δi | Kronecker unit tensor |
| Cf* | normalized friction coefficient | κf | thermal conductivity of fluid (W/mK) |
| Cp | specific heat (J/kgK) | γ | intermittency |
| d | diameter (m) | μ | dynamic viscosity (Pa.s) |
| ΔT | temperature rise of flow (K) | ν | kinematic viscosity (m2/s) |
| e | internal energy per unit mass (J/kg) | θ | peripheral direction |
| fε(z) | surface roughness model function | ρ | density (kg/m3) |
| h | convective heat transfer coefficient (W/m2K) | τ | shear stress (Pa) |
| H | shape factor | ξ | water properties |
| k | kinetic energy per unit mass (J/kg) | Ψloss | energy loss (W) |
| L | pipe length (m) | ω | roughness period (mm) |
| mass flow rate (kg/s) | ω’ | roughness periodicity parameter (=ω/ε) | |
| Nu | Nusselt number | Subscripts | |
| P | static pressure (Pa) | ||
| surface heat flux (W/m2) | c | center | |
| radial heat flux (W/m2) | cr | critical | |
| axial heat flux (W/m2) | ΔP | frictional | |
| Qs | total surface heat transfer (W) | ΔT | thermal |
| r | radial direction | h | hydraulic |
| R | radius (m) | in, ex | inlet, exit |
| Re | Reynolds number | lam | laminar |
| cross-sectional total entropy generation (W/mK) | o | mean | |
| t | time (s) | r, θ, z | radial, peripheral, axial |
| T | temperature (K) | ||
| Uz | axial velocity (m/s) | s, w | surface, wall |
| velocity vector (m/s) | th | thermal | |
| z | axial direction | tra | transitional |
| turb | turbulent | ||
| Superscripts | |||
| local rate | |||
| T | temperature dependency |
Acknowledgments
References
- Kolb, G.; Schurer, J.; Tiemann, D. Fuel processing in integrated micro-structured heat-exchanger reactors. J. Power Source. 2007, 171, 198–204. [Google Scholar]
- Fan, M.Q.; Sun, L.X.; Xu, F. Feasibility study of hydrogen generation from the milled al-based materials for micro fuel cell applications. Energy Fuels 2009, 23, 4562–4566. [Google Scholar]
- Dau, V.T.; Dinh, T.X.; Tanaka, K. Design and simulation of a valveless micro pump. J. Adv. Mech. Des. Syst. Manuf. 2009, 3, 69–75. [Google Scholar]
- Riccio, G.; Chiaramonti, D. Design and simulation of a small polygeneration plant cofiring biomass and natural gas in a dual combustion micro gas turbine (BIO_MGT). Biomass Bioenerg. 2009, 33, 1520–1531. [Google Scholar] [CrossRef]
- Guo, Z.Y.; Li, Z.X. Size effect on microscale single-phase flow and heat transfer. Int. J. Heat Mass Transfer 2003, 46, 149–159. [Google Scholar] [CrossRef]
- Celata, G.P.; Lorenzini, M.; Morini, G.L.; Zummo, G. Friction factor in micropipe gas flow under laminar, transition and turbulent flow regime. Int. J. Heat Fluid Flow 2009, 30, 814–822. [Google Scholar] [CrossRef]
- Ogedengbe, E.O.B.; Naterer, G.F.; Rosen, M.A. Slip flow irreversibility of dissipative kinetic and internal energy exchange in microchannels. J. Micromech. Microeng. 2006, 16, 2167–2176. [Google Scholar] [CrossRef]
- Engin, T.; Dogruer, U.; Evrensel, C.; Heavin, S.; Gordaninejad, F. Effect of wall roughness on laminar flow of bingham plastic fluids through microtubes. ASME J. Fluids Eng. 2004, 126, 880–883. [Google Scholar] [CrossRef]
- Vicente, P.G.; Garcia, A.; Viedma, A. Experimental study of mixed convection and pressure drop in helically dimpled tubes for laminar and transition flow. Int. J. Heat Mass Transfer 2002, 45, 5091–5105. [Google Scholar] [CrossRef]
- Kandlikar, S.G.; Joshi, S.; Tian, S. Effect of surface roughness on heat transfer and fluid flow characteristics at low reynolds numbers in small diameter tubes. Heat Transfer Eng. 2003, 24, 4–16. [Google Scholar] [CrossRef]
- Wen, M.Y.; Jang, K.J.; Yang, C.C. Augmented Heat transfer and pressure drop of strip-type inserts in the small tubes. Heat Mass Transfer 2003, 40, 133–141. [Google Scholar] [CrossRef]
- Koo, J.; Kleinstreuer, C. Viscous dissipation effects in microtubes and microchannels. Int. J. Heat Mass Transfer 2004, 47, 3159–3169. [Google Scholar] [CrossRef]
- Celata, G.P.; Cumo, M.; McPhail, S.; Zummo, G. Characterization of fluid dynamic behaviour and channel wall effects in microtube. Int. J. Heat Fluid Flow 2006, 27, 135–143. [Google Scholar] [CrossRef]
- Celata, G.P.; Morini, G.L.; Marconi, V.; McPhail, S.J.; Zummo, G. Using viscous heating to determine the friction factor in microchannels – an experimental validation. Exp. Therm. Fluid Sci. 2006, 30, 725–731. [Google Scholar] [CrossRef]
- Morini, G.L. Viscous heating in liquid flows in micro-channels. Int. J. Heat Mass Transfer 2005, 48, 3637–3647. [Google Scholar] [CrossRef]
- Obot, N.T. Toward a better understanding of friction and heat/mass transfer in microchannels – a literature review. Microscale Thermophys. Eng. 2002, 6, 155–173. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Y.; Zhang, J. Influence of ribbon structure rough wall on the microscale poiseuille flow. ASME J. Fluids Eng. 2005, 127, 1140–1145. [Google Scholar] [CrossRef]
- Sheikh, A.K.; Zubair, S.M.; Younas, M.; Budair, M. O. Statistical aspects of fouling processes. Proc. Inst. Mech. Eng. E 2001, 215, 331–354. [Google Scholar] [CrossRef]
- Sahin, A.Z.; Zubair, S.M.; Al-Garni, A.Z.; Kahraman, R. Effect of fouling on operational cost in pipe flow due to entropy generation. Energy Convers. Manag. 2000, 41, 1485–1496. [Google Scholar] [CrossRef]
- Cao, B.Y.; Chen, M.; Guo, Z. Y. Effect of surface roughness on gas flow in microchannels by molecular dynamics simulation. Int. J. Eng. Sci. 2006, 44, 927–937. [Google Scholar] [CrossRef]
- Ozalp, A.A. A Computational study to predict the combined effects of surface roughness and heat flux conditions on converging-nozzle flows. Trans. Can. Soc. Mech. Eng. 2006, 29, 67–80. [Google Scholar]
- Ozalp, A.A. Numerical analysis of choked converging nozzle flows with surface roughness and heat flux conditions. Sadhana-Acad. Proc. Eng. 2006, 31, 31–46. [Google Scholar] [CrossRef]
- Kotas, T.J.; Mayhew, Y.R.; Raichura, R.C. Nomenclature for exergy analysis. Proc. Inst. Mech. Eng. A 1995, 209, 275–280. [Google Scholar] [CrossRef]
- Zimparov, V. Energy conservation through heat transfer enhancement techniques. Int. J. Energy Res. 2002, 26, 675–696. [Google Scholar] [CrossRef]
- Lin, W.W.; Lee, D.J. Second-law analysis on wavy plate fin-and-tube heat exchangers. ASME J. Heat Transfer 1998, 120, 797–801. [Google Scholar] [CrossRef]
- Ratts, E.B.; Raut, A.G. Entropy generation minimization of fully developed internal flow with constant heat flux. ASME J. Heat Transfer 2004, 126, 656–659. [Google Scholar] [CrossRef]
- Sahin, A.Z. Second-law analysis of laminar viscous flow through a duct subjected to constant wall temperature. ASME J. Heat Transfer 1998, 120, 77–83. [Google Scholar] [CrossRef]
- Rakshit, D.; Balaji, C. Thermodynamic optimization of conjugate convection from a finned channel using genetic algorithms. Heat Mass Transfer 2005, 41, 535–544. [Google Scholar] [CrossRef]
- Zimparov, V. Extended performance evaluation criteria for enhanced heat transfer surfaces: heat transfer through ducts with constant wall temperature. Int. J. Heat Mass Transfer 2000, 43, 3137–3155. [Google Scholar] [CrossRef]
- Richardson, D.H.; Sekulic, D.P.; Campo, A. Low reynolds number flow inside straight micro channels with irregular cross sections. Heat Mass Transfer 2000, 36, 187–193. [Google Scholar] [CrossRef]
- Ko, T.H. Numerical analysis of entropy generation and optimal reynolds number for developing laminar forced convection in double-sine ducts with various aspect ratios. Int. J. Heat Mass Transfer 2006, 49, 718–726. [Google Scholar] [CrossRef]
- Ko, T.H. Numerical investigation of laminar forced convection and entropy generation in a helical coil with constant wall heat flux. Numer. Heat Transfer PT A 2006, 49, 257–278. [Google Scholar] [CrossRef]
- Ozalp, A.A. Roughness induced forced convective laminar-transitional micropipe flow: energy and exergy analysis. Heat Mass Transfer 2008, 45, 31–46. [Google Scholar] [CrossRef]
- Ozalp, A.A. Entropy analysis of laminar-forced convection in a pipe with wall roughness. Int. J. Exergy 2009, 6, 249–275. [Google Scholar] [CrossRef]
- Ozalp, A.A. 1st and 2nd Law characteristics in a micropipe: integrated effects of surface roughness, heat flux and reynolds number. Heat Transfer Eng. 2009, 30, 973–987. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Vijayalakshmi, K.; Anoop, K.B.; Patel, H.E. Effects of compressibility and transition to turbulence on flow through microchannels. Int. J. Heat Mass Transfer 2009, 52, 2196–2204. [Google Scholar] [CrossRef]
- White, F.M. Fluid Mechanics; McGraw-Hill: Singapore, 1988. [Google Scholar]
- Wu, P.; Little, W.A. Measurement of friction factors for the flow of gases in very fine channels used for microminiature joule–thompson refrigerators. Cryogenics 1983, 23, 273–277. [Google Scholar]
- Yu, D.; Warrington, R.; Baron, R.; Ameel, T. An experimental and theoretical investigation of fluid flow and heat transfer in microtubes. In Proceedings of the 4th ASME/JSME Thermal Engineering Conference, Maui, HI, USA, 19th–24th March 1995; ASME: New York, NY, USA; Volume 1, pp. 523–530.
- Choi, S.B.; Barron, R.F.; Warrington, R.O. Fluid flow and heat transfer in microtubes. Micromech. Sensor. Actuator. Syst. 1991, 32, 123–134. [Google Scholar]
- Kohl, M.J.; Abdel-Khalik, S.I.; Jeter, S.M.; Sadowski, D.L. An experimental investigation of microchannel flow with internal pressure measurements. Int. J. Heat Mass Transfer 2005, 48, 1518–1533. [Google Scholar] [CrossRef]
- Li, J.; Peterson, G. P.; Cheng, P. Three-dimensional analysis of heat transfer in a micro-heat sink with single phase flow. Int. J. Heat Mass Transfer 2004, 47, 4215–4231. [Google Scholar] [CrossRef]
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ozalp, A.A. Combined Effects of Pipe Diameter, Reynolds Number and Wall Heat Flux and on Flow, Heat Transfer and Second-Law Characteristics of Laminar-Transitional Micro-Pipe Flows. Entropy 2010, 12, 445-472. https://doi.org/10.3390/e12030445
Ozalp AA. Combined Effects of Pipe Diameter, Reynolds Number and Wall Heat Flux and on Flow, Heat Transfer and Second-Law Characteristics of Laminar-Transitional Micro-Pipe Flows. Entropy. 2010; 12(3):445-472. https://doi.org/10.3390/e12030445
Chicago/Turabian StyleOzalp, A. Alper. 2010. "Combined Effects of Pipe Diameter, Reynolds Number and Wall Heat Flux and on Flow, Heat Transfer and Second-Law Characteristics of Laminar-Transitional Micro-Pipe Flows" Entropy 12, no. 3: 445-472. https://doi.org/10.3390/e12030445
APA StyleOzalp, A. A. (2010). Combined Effects of Pipe Diameter, Reynolds Number and Wall Heat Flux and on Flow, Heat Transfer and Second-Law Characteristics of Laminar-Transitional Micro-Pipe Flows. Entropy, 12(3), 445-472. https://doi.org/10.3390/e12030445