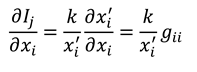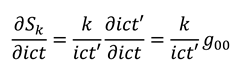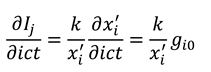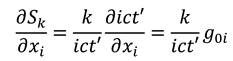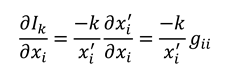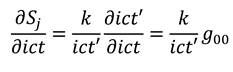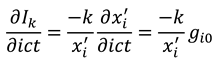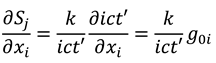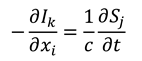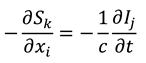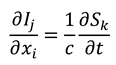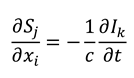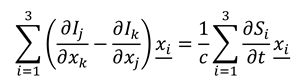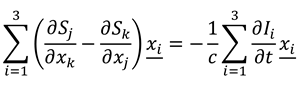1. Introduction
The close relationship between information and entropy is well recognised [
1,
2], e.g., Brillouin considered a negative change in entropy to be equivalent to a change in information (negentropy [
3]), and Landauer considered the erasure of information
to be associated with an increase in entropy
, via the relationship
[
1,
4]. In previous work, we qualitatively indicated the dynamic relationship between information and entropy, stating that the movement of information is accompanied by the increase of entropy in time [
5,
6], and suggesting that information propagates at the speed of light in vacuum
c [
5,
6,
7,
8,
9]. Opinions on the physical nature of information have tended to be contradictory. One view is that information is inherent to points of non-analyticity (discontinuities) [
5,
7,
9] that do not allow “prediction”, whereas other researchers consider the information to be more distributed (delocalised) in nature [
10,
11,
12]. Such considerations are akin to the paradoxes arising from a wave-particle duality, with the question of which of the two complements best characterises information. In the following analysis, by initially adopting the localised, point of non-analyticity definition of information, we ultimately find that information and entropy may indeed also exhibit wavelike properties, and may be described by a pair of coupled wave equations, analogous to the Maxwell equations for electromagnetic (EM) radiation, and a distant echo of the simple difference relationship above.
2. Analysis
We start our analysis by consideration of a meromorphic [
13] function
in a reduced 1+1 (
i.e., one space dimension and one time dimension) complex space-time
, with a simple, isolated pole at
, as indicated in
Figure 1:
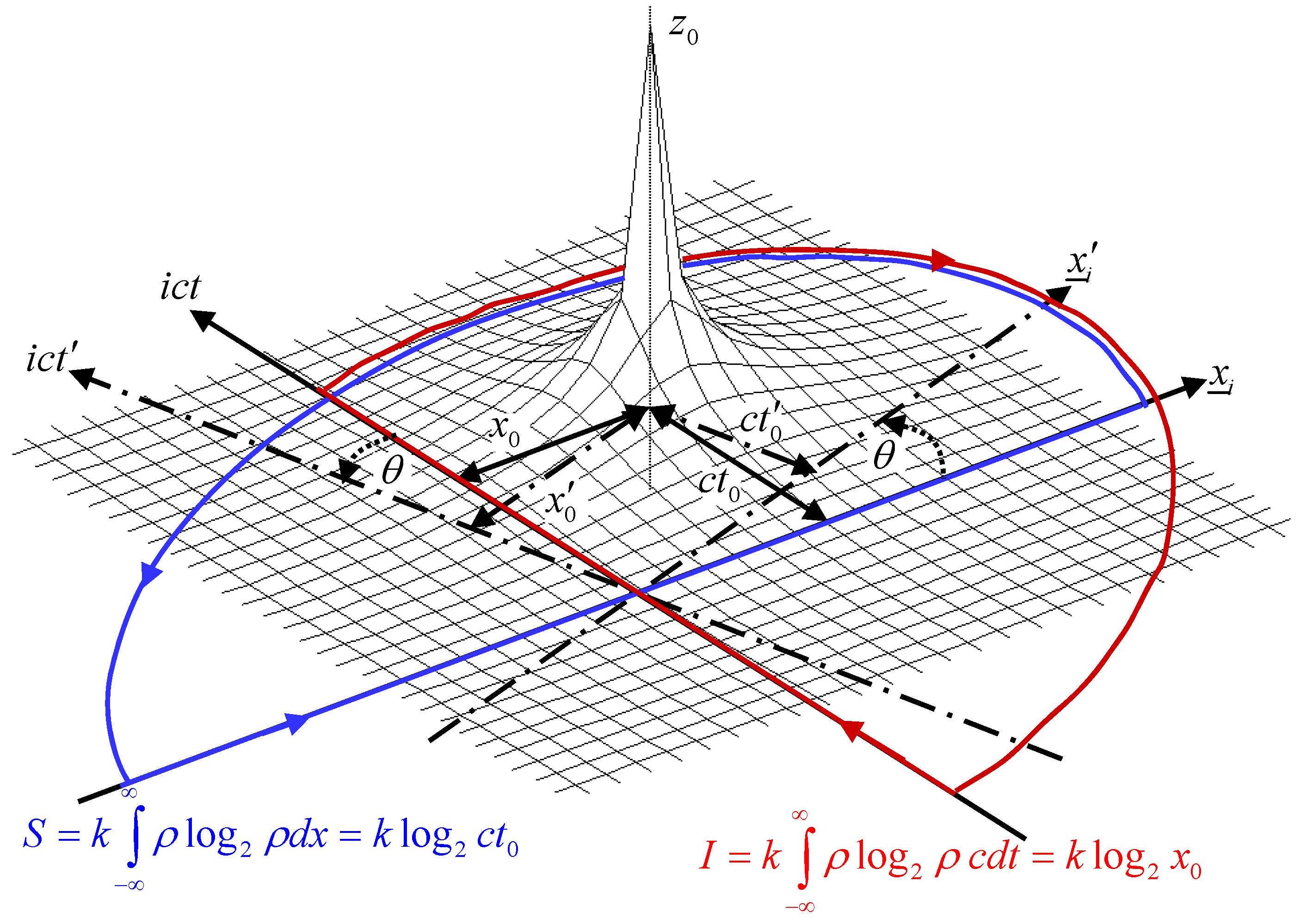
Figure 1.
Information I (integration over imaginary ct-axis) and entropy S (integration over real x-axis) due to a point of non-analyticity (pole) at the space-time position z0.
Figure 1.
Information I (integration over imaginary ct-axis) and entropy S (integration over real x-axis) due to a point of non-analyticity (pole) at the space-time position z0.
The point of non-analyticity
travels at the speed of light in vacuum
c [
5,
6,
7,
8,
9]. We note that
acts as an inverse-square law function, e.g., as proportional to the field around an isolated charge, or the gravitational field around a point mass. It is also square-integrable, such that
, and
, where
, and obeys the Paley-Wiener criterion for causality [
14]. We now calculate the differential information [
5,
15] (entropy) of the function
. By convention, in this paper, we define the logarithmic integration along the spatial
x-axis to yield the entropy
S of the function; whereas the same integration along the imaginary
t-axis yields the information
I of the function. This can be qualitatively understood to arise from the entropy of a system being related to its spatial permutations (e.g., the spatial fluxions of a volume of gas), whereas the information of a system is related to its temporal distribution (e.g., the arrival of a data train of light pulses down an optical fibre.) Considering the differential entropy first, substituting Equation (1) with
and calculating the sum of the residues of the appropriate closed contour integral in the
z-plane,
S is given by:
where
k is the Boltzmann constant. We have defined
S using a positive sign in front of the integral, as opposed to the conventional negative sign [
15], so that both the entropy and information of a space-time function are calculated in a unified fashion. In addition, this has the effect of aligning equation (2) with the 2nd Law of Thermodynamics, since
S increases monotonically with increasing time
. Performing the appropriate closed contour integral in the
z-plane with
we find that the differential information is given by:
Note that in (2) and (3) some constant background values of integration have been ignored, since they disappear in the following differential analyses. We see that the entropy and information are given by surprisingly simple expressions. The information is the logarithm of the space-time distance
of the point of non-analyticity from the temporal
t-axis; whilst the entropy content is simply the logarithm of the distance (
i.e., time
) of the pole from the spatial
x-axis. The overall info-entropy
of the function
is given by the summation of the two orthogonal logarithmic integrals,
, where the entropy
S is in quadrature to the information
I, since
I depends on the real axis quantity
, whereas
S depends on the imaginary axis quantity
. Since the choice of reference axes is arbitrary, we could have chosen an alternative set of co-ordinate axes to calculate the information and entropy. For example, consider a co-ordinate set of axes
, rotated an angle
about the origin with respect to the original
axes. In this case, the unitary transformation describing the position of the pole
in the new co-ordinate framework is:
Using (2) and (3), the resulting values of the information and entropy for the new frame of reference are given by:
with overall info-entropy
of the function again given by the summation of the two quadrature logarithmic integrals,
. We next perform a dynamic calculus on the equations (5), with respect to the original
axes, using (4) to calculate:
and:
where we have ignored the common factor
, and we have assumed the equality of the calculus operators
and
, since the trajectory of the pole in the
z-plane is a straight line with
, and
. Since the point of non-analyticity is moving at the speed of light in vacuum
c [
5,
7,
9], such that
, we must also have
, as
c is the same constant in any frame of reference [
16]. We can now see that equations (6) and (7) can be equated to yield a pair of Cauchy-Riemann equations [
17]:
where we have dropped the primes, since equations (8) are true for all frames of reference. Hence, the info-entropy function
is analytic (
i.e., holographic in nature [
13]), and the Cauchy-Riemann equations (8) indicate that information and entropy (as we have defined them) may propagate as waves travelling at the speed
c. In the
Appendix we extend the analysis from 1+1 complex space-time to the full 3+1 (three-space and one-time dimensions) case, so that it can be straightforwardly shown that Equations (8) generalise to:
where
and
are in 3D vector form. Further basic calculus manipulations reveal that the scalar gradient (divergence) of our information and entropy fields are both equal to zero:
Together, Equations (9) and (10) form a set of equations analogous to the Maxwell equations [
16] (with no sources or isolated charges, and in an isotropic medium). Equations (9) can be combined to yield wave equations for the information and entropy fields:
3. Discussion
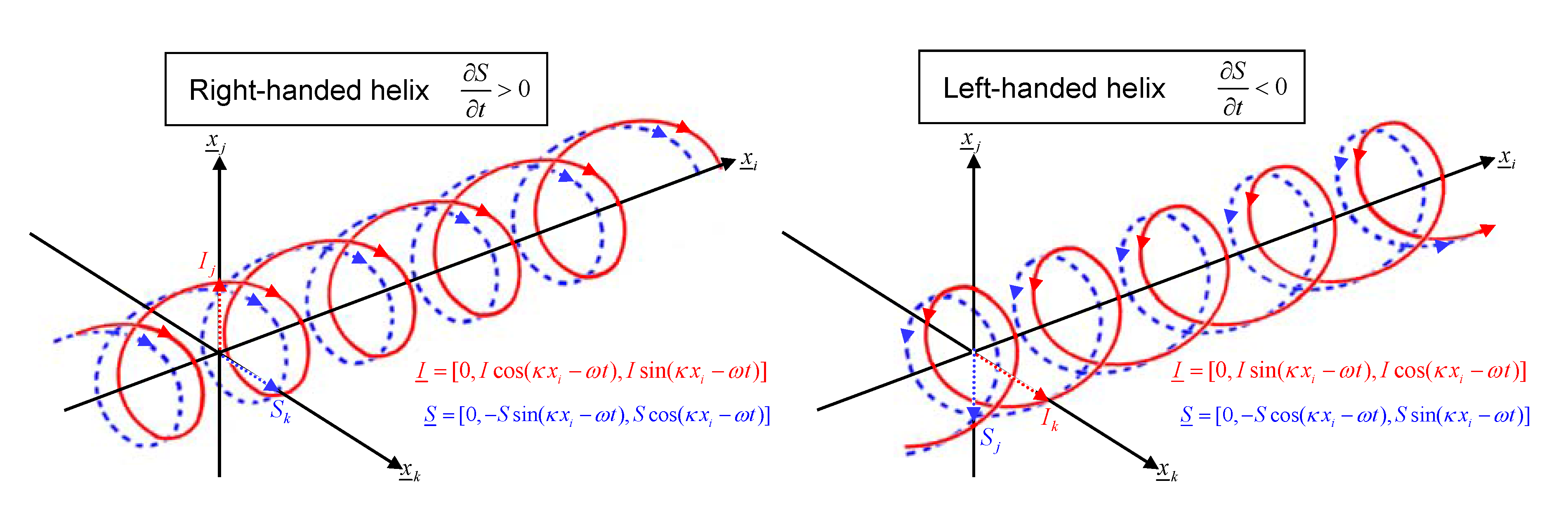
As defined previously, the information and entropy fields are mutually orthogonal, since
. Analogous to the Poynting vector describing energy flow of an EM wave, the direction of propagation of the wave is given by
, e.g., see
Figure 2. The dynamic relationship between
I and
S implies that information flow tends to be accompanied by entropy flux [
5,
6], such that the movement of data is dissipative in order to satisfy the 2nd Law of Thermodynamics. Analytic functions such as
I and
S only have points of inflection, so that, again, the 2nd Law with respect to the
S-field is a natural consequence of its monotonicity. However, in analogy to an EM-wave, Equations (9) and (10) in combination imply that the sum of information and entropy
may be a conserved quantity. Hence, the 2nd Law of Thermodynamics should perhaps be viewed as a conservation law for info-entropy, similar to the 1st Law for energy. This has implications for the treatment of information falling into a black hole.
Figure 2.
(a) Right-handed polarisation helical info-entropy wave, propagating in positive -direction given by . (b) Left-handed polarisation helical info-entropy wave travelling in same direction.
Figure 2.
(a) Right-handed polarisation helical info-entropy wave, propagating in positive -direction given by . (b) Left-handed polarisation helical info-entropy wave travelling in same direction.
The reason that the differential Equations (6) and (7) obey the laws of relativity is that they are simple spatial reciprocal quantities, with their ratios equivalent to velocities, such that the relativistic laws are applicable. This reciprocal space aspect implies that calculation of Fourier-space info-entropy quantities result in quantities proportional to real space, which are therefore also relativistically-invariant and holographic.
Equation (9a) shows that a right-handed helical spatial information distribution may be associated with an increase of entropy with time (
Figure 2a); in contrast to a left-handed chirality where entropy may decrease with time (
Figure 2b). A link is therefore possibly revealed between the high information density of right-handed DNA [
18] and the overall increase of entropy with time in our universe [
19]. A molecule such as DNA is an efficient system for information storage. However, our dynamic model suggests that information would radiate away, unless a localisation mechanism were present, e.g., the existence of a standing wave. Such waves require forward and backward wave propagation of the same polarisation. We see that the complementary anti-parallel (C2 spacegroup) symmetry of DNA’s double helix means that information waves of the same polarisation (chirality) would travel in both directions along the helix axis to form a standing wave, thus localising the information. Small left-handed molecules (e.g., amino acids, enzymes and proteins, as well as short sections of Z-DNA [
20]) are known to exist alongside DNA within the cell nucleus. Their chirality may be thus associated with a decrease of entropy with time. In conjunction with right-handed molecules they can be understood to possibly regulate the thermodynamic function of the DNA molecule. As is well known, highly dynamic systems require negative feedback to direct and control their output, without which they become unstable. We can draw parallels to the high entropic potential of DNA, with left-handed molecules (as well as right-handed molecules) potentially acting as damping agents to control its thermodynamic action.
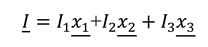
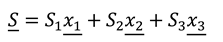
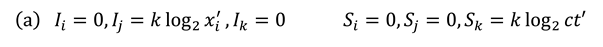
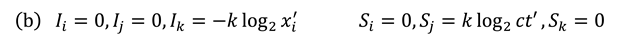
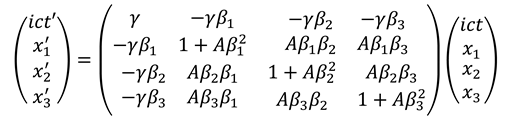
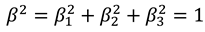 in this case, since the overall wave velocity is equal to c. In addition the parameters and A are related by
in this case, since the overall wave velocity is equal to c. In addition the parameters and A are related by 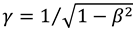 , and also
, and also 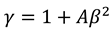 . We note that equation (A3) is made equivalent to (4), by substituting
. We note that equation (A3) is made equivalent to (4), by substituting 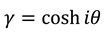 , and
, and 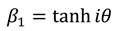 , with . Performing a dynamic calculus on equations (A2a), we derive the following expressions:
, with . Performing a dynamic calculus on equations (A2a), we derive the following expressions: