Using Exergy to Understand and Improve the Efficiency of Electrical Power Technologies

Abstract

The benefits are demonstrated of using exergy to understand the efficiencies of electrical power technologies and to assist improvements. Although exergy applications in power systems and electrical technology are uncommon, exergy nevertheless identifies clearly potential reductions in thermodynamic losses and efficiency improvements. Various devices are considered, ranging from simple electrical devices to generation systems for electrical power and for multiple products including electricity, and on to electrically driven. The insights provided by exergy are shown to be more useful than those provided by energy, which are sometimes misleading. Exergy is concluded to have a significant role in assessing and improving the efficiencies of electrical power technologies and systems, and provides a useful tool for engineers and scientists as well as decision and policy makers.

1. Introduction

The use of energy as a measure for understanding and improving the efficiencies of energy systems can be misleading and confusing. The quantity exergy can be used to assess and improve the efficiencies energy systems, and can help better understand the losses in energy systems by providing more useful and meaningful information than energy provides. Exergy is the maximum work (or electricity) producible from a system or a flow of matter or energy relative to a reference environment. Exergy is a measure of the potential of the usefulness or value of a system or flow. Exergy is also a measure of the potential to cause change, as a consequence of not being in equilibrium relative to the reference environment.

Exergy can clearly identify efficiency improvements and reductions in thermodynamic losses. Exergy can also identify better than energy the environmental benefits and economics of energy technologies. Thus, exergy has an important role to play in increasing efficiencies of energy systems and technologies.

Many feel that exergy is applicable only to systems or studies involving extensive thermodynamics, in areas like mechanical and chemical engineering. Thus the full value of exergy is not achieved because it is neglected or underutilized in other fields. One such area is electrical engineering, where exergy applications are uncommon.

One reason that exergy is not used extensively in electrical engineering studies is that general thermodynamic assessments often deal with many energy forms, e.g., electricity, work, heat, chemical, kinetic, potential, etc., while electrical engineering assessments often focus on electricity, and sometimes work. In such situations, energy and exergy flows are identical (since exergy is the work or electrical equivalent of energy), so efficiencies tend to be the same and the benefits of using exergy methods are less obvious. Nevertheless, there are benefits. First, losses are identified in terms of cause and located more accurately with exergy. Second, in systems where non-electrical quantities are involved, efficiencies on energy and exergy bases differ, sometimes markedly.

This paper goes on to describe exergy and exergy methods and their applicability to electrical systems. Examples are used to illustrate the use of exergy as a tool to understand and improve efficiency. The objective is to improve how efficiencies and losses are understood for electrical systems, thereby assisting efforts to improve them.

2. Exergy and Exergy Analysis

Exergy is defined as the maximum amount of work which can be produced by a system or a flow of matter or energy as it comes to equilibrium with a reference environment. Exergy is a measure of the potential of the system or flow to cause change, as a consequence of not being completely in stable equilibrium relative to the reference environment. Unlike energy, exergy is not subject to a conservation law (except for ideal, or reversible, processes). Rather exergy is consumed or destroyed, due to irreversibilities in any real process. The exergy consumption during a process is proportional to the entropy created due to irreversibilities associated with the process.

Exergy analysis [1,2,3,4,5,6,7,8,9] is a methodology that uses the conservation of energy principle (embodied in the first law of thermodynamics) together with non-conservation of entropy principle (embodied in the second law) for the analysis, design and improvement of energy and other systems. The exergy method is useful for improving the efficiency energy-resource use, for it quantifies the locations, types and magnitudes of wastes and losses. In general, more meaningful efficiencies are evaluated with exergy rather than energy analysis, since exergy efficiencies are always a measure of the approach to the ideal. Therefore, exergy analysis identifies the margin available to design more efficient energy systems by reducing inefficiencies.

In exergy analysis, the characteristics of the reference environment must be specified completely. This is commonly done by specifying the temperature, pressure and chemical composition of the reference environment. The results of exergy analyses, consequently, are relative to the specified reference environment, which in most applications is modelled after the actual local environment. The exergy of a system is zero when it is in equilibrium with the reference environment. This tie between exergy and the environment leads to some of the implications regarding environmental impact that are discussed subsequently.

Exergy also can be applied beyond assessing efficiencies and losses, in areas such as economics [10,11,12] and environmental impact assessment [13,14,15]. The relationship between exergy and economics, particularly the trade-offs that normally occur between efficiency and costs, has been an important concern for decades and continues to be so. Economic methods based on exergy, e.g., exergoeconomics, have evolved and are applied in some areas. The environmental impacts and non-sustainability of energy use have become of significant concerns recently, and exergy methods can assist improvement efforts by (1) reducing environmental emissions and lengthening the lives of resources through increasing efficiencies, and (2) assessing the potential impacts of emissions. The linkages between exergy and economics and environmental impact are beyond the scope of this article and thus not considered further here.

Many engineers and scientists suggest that energy systems are best evaluated using exergy analysis because it provides more insights, especially for efficiency improvement, than energy analysis. Exergy analysis and its application to many processes and systems are discussed further elsewhere [1,2,3,4,5,6,7,8,9]. As energy policies increasingly play an important role in addressing development and sustainability issues, decision and policy makers would also benefit from an appreciation the exergy concept and its applications.

3. Applications of Exergy to Electrical Systems

Exergy can be applied to electrical systems in much the same way as it is to general thermodynamic systems. Usually, since there are fewer energy forms involved, the analyses are less involved and complex for electrical systems.

The range of devices that can be considered is extensive, ranging from generators and transformers to power plants. Here, we consider four categories of electrical systems:

• Simple electrical conversion devices.
• Electrical generation systems.
• Generation systems for multiple products including electricity.
• Electrical storage systems.
• Devices and systems that use or are driven by electricity.

Many examples can be used to demonstrate how exergy methods improve understanding of efficiencies and help increase them. Several examples in each of the above categories are presented in subsequent sections for illustrative purposes.

4. Illustrations for Various Electrical Systems

4.1. Simple Electrical Conversion Devices

Simple electrical conversion devices include transformers, alternators, generators, motors and static converters, and these are considered here. In such devices, electrical energy is being converted to other type of electrical energy, or work and electricity quantities are being interchanged.

Since electricity and work are the same on energy and exergy bases, the overall energy and exergy efficiencies for such devices are the same. The losses differ greatly on energy and exergy bases, however, as all energy losses are typically associated with waste heat. Most exergy losses are associated with internal consumptions of exergy due to irreversibilities and little with waste thermal exergy emissions.

Electrical losses often involve resistive losses, which appear as waste heat. Electric generator losses usually include losses in the winding and magnetizing losses in the core, plus rotational losses. Power transformer losses are usually of the same kind as electric generator losses. Transformer losses have two main components: (1) Core loss (or no-load loss), due to magnetizing and de-magnetizing the core during normal operation; this loss occurs whenever the transformer is energized and does not vary with load. (2) Coil loss (or load loss), which occurs in the primary and secondary coils of the transformer. This loss is a function of the resistance of the winding materials and which varies with the transformer load. Losses in these devices are also caused friction.

4.2. Electrical Generation

Idealized and actual electrical power plants are considered here, including thermal power plants, hydroelectric plants and fuel cells.

Ideal Thermal Power Plant

A Carnot heat engine represents an ideal power plant. Energy efficiencies for this device are counter-intuitive. For a Carnot power plant operating between a heat source at a temperature of 600 K and a heat sink at 300 K, for example, the energy efficiency is 50% (i.e., 1 – 300/600 = 0.5). Yet a Carnot engine is ideal. Clearly, the energy efficiency is misleading as it indicates that a significant margin for improvement exists when in fact there is none. Although a significant amount of waste heat is emitted, it is rejected at the temperature of the reference environment, where heat is freely available in abundance. Thus the waste heat is useless for processes. The exergy efficiency of an ideal device is 100%, properly indicating its ideal nature in a straightforward and clear manner. Zero exergy is associated with the waste heat, reflecting its value or usefulness.

Coal and Nuclear Power Plants

Actual coal-fired and nuclear electricity generation plants are considered.

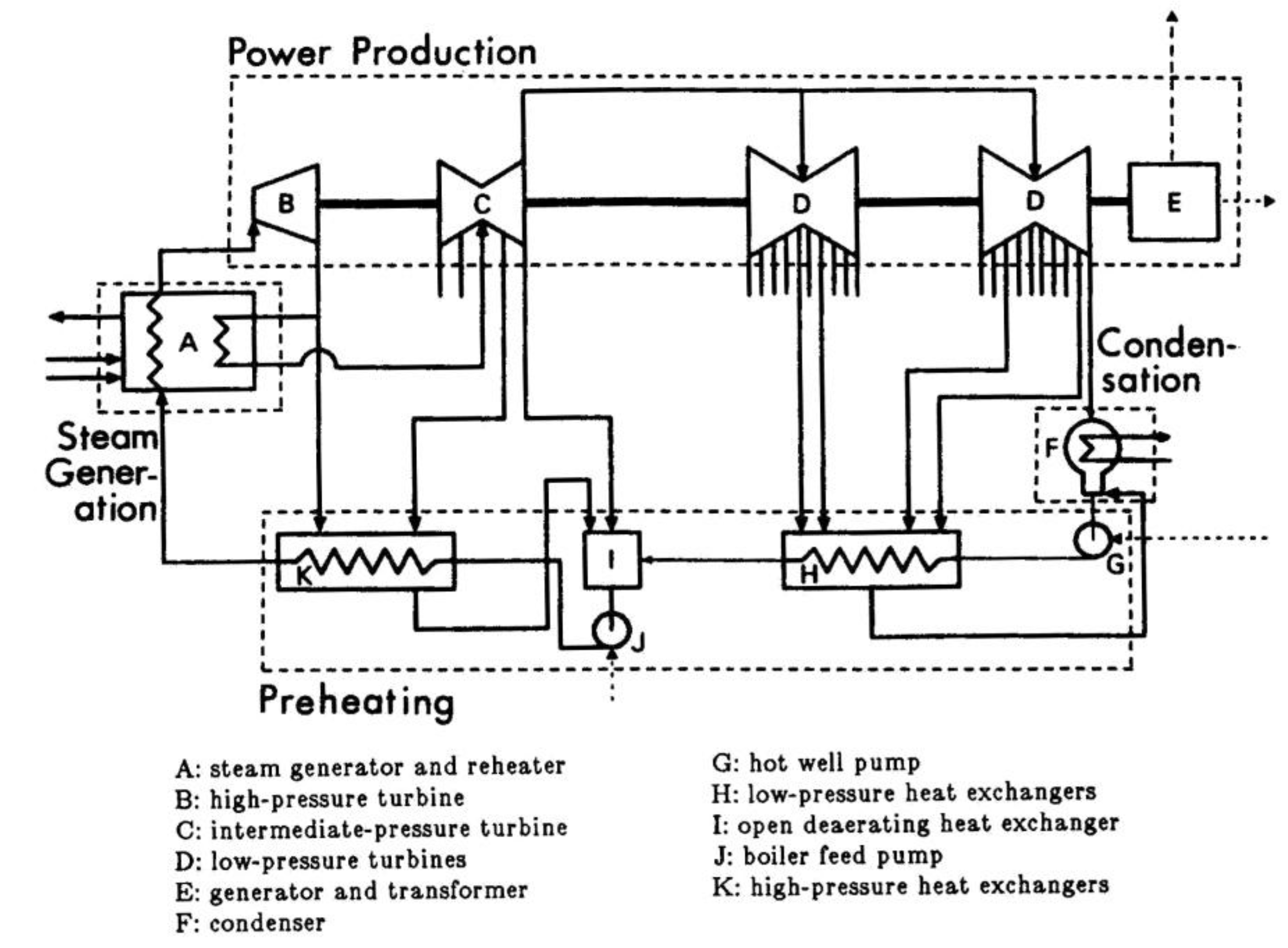
First, we consider the coal-fired Nanticoke generating station, which has been operating since 1981 in in community of Nanticoke, Ontario (Canada). Each of the eight station units has net outputs of 505 MW of electricity. A single station unit (see Figure 1) can be divided into four main sections [15,16]:

• Steam Generators: Natural circulation steam generators combust pulverized coal to produce primary and reheat steam, and flue gas exits via chimneys.
• Turbine Generators and Transformers: Electricity is generated as steam passes through a turbine generator connected to a transformer. Each turbine generator has one single-flow high-pressure cylinder, one double-flow intermediate-pressure cylinder and two double-flow low-pressure cylinders. Steam exhausted from the high-pressure cylinder is reheated in the steam generator.
• Condensers: Steam exhausted from the low-pressure turbines enters the condenser, where cooling water condenses the steam.
• Preheating Heat Exchangers and Pumps: The pressure of the condensed steam is increased in a series of electrical pumps, while the temperature of the condensate is increased in a series of heat exchangers, with heat supplied from steam extractions from the turbines.

Figure 1. Breakdown of the electrical generating station unit considered into four main sections. The external inputs are coal and air, and the output is stack gas and solid waste for unit A. The external outputs for unit E are electricity and waste heat. Electricity is input to units G and J, and cooling water enters and exits unit F.

Figure 1. Breakdown of the electrical generating station unit considered into four main sections. The external inputs are coal and air, and the output is stack gas and solid waste for unit A. The external outputs for unit E are electricity and waste heat. Electricity is input to units G and J, and cooling water enters and exits unit F.

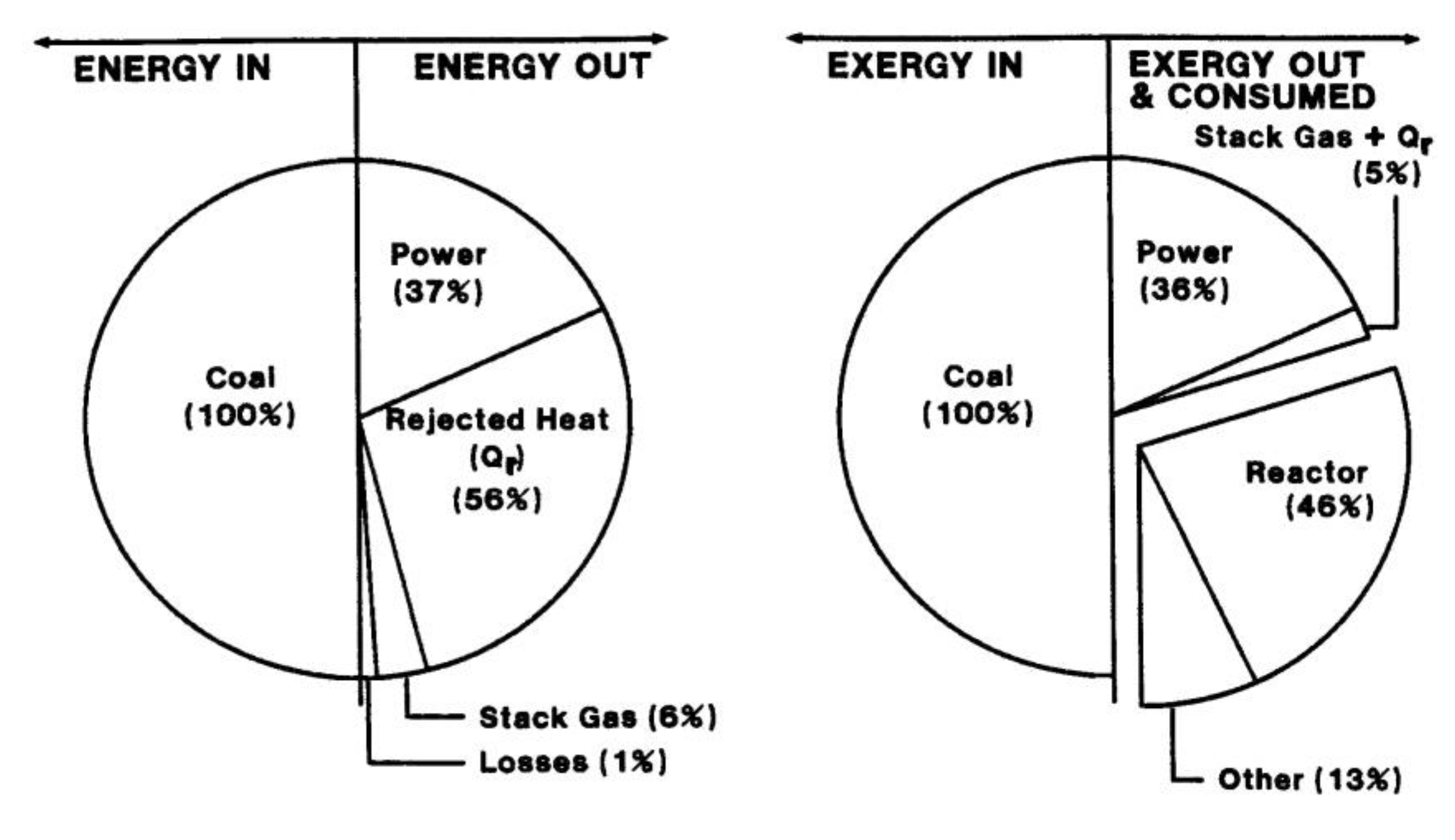
Overall balances of exergy and energy for the station are illustrated in Figure 2. The main findings, which improve understanding of the thermodynamic behaviour of the plant and help identify areas having significant efficiency-improvement potential, follow:

• The overall energy efficiency (ratio of net electrical energy output to coal energy input), is 37%, and the corresponding exergy efficiency 36%.
• The steam generators appear significantly more efficient on an energy basis (95%) than on an exergy basis (50%). Physically, this discrepancy implies that, although most of the input energy is transferred to preheated water, the energy is degraded as it is transferred. Most of the exergy losses in the steam generators are associated with internal consumptions, mainly due to combustion and heat transfer.
• Large quantities of energy enter the condensers (about 775 MW per unit), of which close to 100% is rejected. A small quantity of exergy enters (about 54 MW per unit), of which about 25% is rejected and 75% internally consumed.
• Energy losses in other plant devices are very small (about 10 MW). The exergy losses are moderately small (about 150 MW), and are mainly associated with internal consumptions.

Similar results are observed for a nuclear power plant, the main difference being that the large exergy consumptions occur in a nuclear reactor instead of a coal combustor. In the nuclear plant, the main losses are associated with the fission reactor, the turbines, the heat exchangers, the pumps and the electrical generator and transformer.

Figure 2. Overall energy and exergy balances for the station. Energy balance inputs and outputs of energy (left). Exergy balance showing inputs and outputs and consumptions of exergy (right).

Figure 2. Overall energy and exergy balances for the station. Energy balance inputs and outputs of energy (left). Exergy balance showing inputs and outputs and consumptions of exergy (right).

Hydroelectric Plant

For a hydroelectric generating station, the potential energy of elevated water is converted into electricity. As potential energy and potential exergy are identical, the overall energy and exergy efficiencies are the same. However, the energy losses exit mainly with the water leaving the system, while the main exergy losses are associated with internal consumptions. In these analyses, the reference environment elevation is taken to be that at the bottom of the system.

Fuel Cell

For a fuel cell system, electricity is generated electrochemically as the inputs, hydrogen and oxygen, react to form water. As the energy and exergy values of hydrogen differ somewhat, the energy and exergy efficiencies differ slightly for these systems. But the energy and exergy losses differ, the main exergy losses being due to internal consumptions and the main exergy losses associated with waste heat. The main losses are associated with the fuel cell stack, the expanders, the heat exchangers and the pumps.

Wind Turbine System

For a wind generating station, the kinetic energy of moving air is converted to electricity. As potential energy and kinetic exergy are identical, the overall energy and exergy efficiencies are the same. However, the energy losses exit mainly with the air leaving the device, while the main exergy losses are associated with internal consumptions. In these analyses, the reference environment for velocity is taken to be a non-moving point on the earth.

Solar Photovoltaic System

For a solar photovoltaic generating station, the energy of sunlight is converted directly to electricity. As the energy and exergy of sunlight are very close, they are assumed identical here. Thus, the overall energy and exergy efficiencies are the same. However, the energy losses exit mainly with the waste heat leaving the system, while the main exergy losses are associated with internal consumptions.

Solar Thermal Power Generation

For a solar thermal power generation, the energy of sunlight is converted indirectly to electricity, using a thermal power cycle that often is similar to a Rankine cycle. Again, the overall energy and exergy efficiencies are the same since the energy and exergy of sunlight are assumed identical, and energy losses exit mainly with the waste heat emissions while internal consumptions are responsible for the main exergy losses.

4.3. Cogeneration and Trigeneration

Cogeneration and trigeneration systems are considered. These systems generate multiple products including electricity.

Cogeneration Systems

Cogeneration, or combined heat and power (CHP), systems generate co-products: electricity and useful heat. The energy and exergy efficiencies for such systems vary due to the thermal product, for which energy and exergy differ. The energy and exergy efficiencies are nearer when the temperature of the product heat is higher, and deviate more as the temperature of the product heat decreases toward the reference environment temperature. The energy and exergy losses for such systems are identified to be in different locations and due to different causes. The main losses are associated with the furnace and boiler, the turbines, the heat exchangers, the electrical generator and transformer, the stack gas and the pumps.

Trigeneration Systems

Trigeneration systems are extended cogeneration systems which generate a cold product in addition to electricity and useful heat. The energy and exergy efficiencies for such systems vary due to the hot and cold thermal products. For each of these commodities, energy and exergy differ. The energy and exergy efficiencies are deviate more when the temperatures of the product thermal quantities are further removed from the reference-environment temperature (i.e., the hot product is hotter and the cold product colder). The energy and exergy efficiencies are nearer as the temperatures of the thermal quantities approach the reference-environment temperature. There are particular difficulties in evaluating the energy efficiencies of such systems due to the cold product, and the difficulty in assessing its energy. The exergy of cold are hot thermal products are straightforwardly evaluated, so meaningful exergy efficiencies are readily determined.

As for cogeneration systems, the energy and exergy losses for such systems are identified to be in different locations and due to different causes. The main losses are associated with the furnace and steam generator, the turbines, the heat exchangers, the stack gas, the electrical generator and transformer, and the chiller.

4.4. Electrical Storage Systems

Electrical storage systems are considered here, the most common of which are batteries. The energy efficiency on a fractional basis of an electrical storage device is usually determined as the ratio of the quantity of electricity obtained from the storage while discharging divided by the electrical energy supplied to the storage while charging. For a battery, the energy loss is observed as heat, which warms the battery and the surroundings. Low charging and discharging rates help keep a battery cool and improve the battery life. Given that the inputs and outputs are both electricity for electrical storage systems, the energy and exergy efficiencies are equal.

4.5. Electrically Driven Devices and Systems

Space and Hot Water Heaters

Space and hot water heating can be accomplished in many ways. Two competing technologies are considered here:

• Electrical Resistance Space Heater: In an electrical resistance space heater, almost all of the electricity that enters the unit is dissipated to heat within the space. Thus the energy efficiency is nearly 100% and there are almost no energy losses. Yet the exergy efficiency of such a device is typically less than 10%, indicating that the same space heating can in theory be achieved using one-tenth of the electricity.
• Heat Pump: Some of the savings in electricity use identified in the previous point can be attained using a heat pump. The use of even a relatively inefficient heat pump can reduce the electricity used to achieve the same space heating by one-third. A high-efficiency heat pump can achieve even greater reductions electricity usage. The main losses occur in the motor and compressor, the condenser, the heat exchangers and the throttle valve.

Efficiencies for hot water heating are also markedly different for different technologies and losses differ in characteristics and amount. For electrical hot water heaters, the efficiencies are low and wastes are mainly attributable to waste heat (on an energy basis) and to internal consumptions (on an exergy basis). For natural gas-fired, as an alternative, the results are similar, although the technologies differ.

Clearly the use of energy efficiencies and losses is quite misleading for heating.

Industrial Furnaces and Heaters

Energy efficiencies for industrial process heating vary slightly depending on the heat retention characteristics of the heater. Exergy efficiencies for industrial process heating vary significantly, depending primarily on the temperature of the product heat. Typically, the exergy efficiency is high when a high-quality input such as electricity is used for a high-quality task (like producing high-temperature heat). Thus, the use of energy efficiencies and losses is quite misleading for industrial heating.

A breakdown of the exergy losses for such systems often reveals that the exergy losses are divided among those due to irreversibilities associated with the combustion reaction (even if done adiabatically) and those due to heat transfer from the peak theoretical combustion temperature to the actual temperature of the working fluid.

Refrigeration Systems

Refrigeration systems operate like heat pumps, but with the heat removal from the cold space, rather than the warmer heat rejected, being the product. As for trigeneration systems which involve a cold product, the energy and exergy efficiencies for such systems vary due to the dependence of the exergy of the cold thermal product on temperature. The energy of the cold product is also difficult to determine, so the energy-based figure of merit used for refrigeration systems is the coefficient of performance (COP), which is simply the energy efficiency divided by 100. The energy and exergy efficiencies differ markedly for refrigeration systems, but the exergy efficiencies are more intuitively meaningful.

The energy and exergy losses for such systems are identified to be in different locations and due to different causes. The main losses occur in the motor and compressor, the condenser, the heat exchangers and the throttle valve.

Pumps and Fans

Electric pumps and fans convert electricity to mechanical energy in the form of pressure rise and kinetic energy. The energy and exergy of the products are usually similar, leading to similar device efficiencies.

Lights

Not only does lighting consume a significant amount of energy in society, it is also extremely inefficient. Light bulbs convert electricity to visible light. As the product electromagnetic radiation can be taken to have similar energy and exergy contents, the energy and exergy efficiencies of lighting are similar. Lighting efficiencies differ markedly from the efficiencies of many home appliances. The potential for energy and exergy savings from lighting is large, due to its inefficiency and large contribution to societal energy use.

Home Electric Appliances for Heating-Based Services

Electric household appliances for heating services (e.g., ovens, toasters, clothes dryers) have characteristics of the heating devices discussed earlier in this section, with the main differences dependent on the temperature of the product heat. The exergy efficiencies also depend on the temperatures of the waste heat emissions.

Electric Transportation Systems

Electric railways trains supplied by AC or DC contact lines are equipped with three-phase induction motors and variable voltage and frequency inverters [26,27]. Using structural diagrams and high-performances converters, appropriate vehicle control can be achieved so the optimum traction and minimum electrical energy use are ensured. In such devices, the energy and exergy efficiencies are equal, as the product kinetic energy and kinetic exergy are equivalent. With the same induction machines and use of appropriate controls, these drive systems can realize both traction and electric braking as part of the operation of the electric traction vehicle.

5. Numerical Examples

Typical values of energy and exergy efficiencies for the electrical devices and systems considered in the previous section are given in Table 1. In addition, exergy losses are broken down in that table into internal exergy consumptions and waste exergy emissions.

An examination of the efficiencies in Table 1 shows that in some instances the energy and exergy efficiencies are the same, while in other cases they differ significantly. Where they differ, the exergy efficiencies provide a measure of how nearly the process approaches ideality and the energy efficiencies can cause confusion. Where the efficiencies are similar, the energy efficiencies can be treated as good approximations of the more meaningful exergy efficiencies. The efficiencies tend to be similar where the energy input and product energy outputs are of the same quality. The efficiencies differ when energy inputs and outputs are of significantly different quality (e.g., electricity as opposed to heat at high temperature as opposed to cold thermal energy).

Of the electrical resistance heaters, the industrial has the higher exergy efficiency because it delivers heat of a higher quality, as reflected by its temperature. Space and hot water heaters deliver lower quality heat.

The refrigeration and heat pump systems are difficult to assess using energy efficiencies as the values exceed 100%. The energy efficiency for trigeneration is not a true efficiency as it includes the cold product energy, which is normally evaluated with a coefficient of performance (COP) as a figure of merit. In both these cases, exergy efficiencies are rational and meaningful.

Table 1. Energy and exergy efficiencies and breakdown of exergy losses for selected electrical devices.

Device	Efficiency (%)		Breakdown of exergy loss (%)*
	Energy	Exergy	Consumption	Emission
Simple electrical conversion devices
Transformer (high power)	93–98	93–98	73	27
Transformer (low power)	75–90	75–90	73	27
Alternator (low power)	70–73	70–73	73	27
Generator (high power)	90–95	90–95	73	27
Motor	80–87	80–87	73	27
Static converter	97–99	97–99	73	27
Electrical generation systems
Ideal thermal power plant	64	100	–	–
Coal–fired power plant	37	36	92	8
Nuclear power plant	30	30	98	2
Hydroelectric power plant	90	90	88	12
Fuel cell system	33	33	89	11
Wind turbine system	80–97	80–97	97	3
Solar photovoltaic system	6–25	6–25	88	12
Solar thermal power generation	10–30	10–30	70	30
Cogeneration and trigeneration systems
Cogeneration system	74	31	99	1
Trigeneration system	94	28	92	8
Electrical storage systems
Battery (lead–acid)	75–85	75–85	92	8
Battery (lead–acid) with charging circuit**	45–68	45–68	92	8
Electrically driven devices and systems
Resistance space heater	99	6	97	3
Heat pump	380***	19	94	6
Hot water heater	90	10	92	8
Industrial heater	70	51	70	30
Refrigeration system	310***	24	95	5
Pump	70	70	97	3
Fan	90	90	97	3
Lighting (incandescent)	5	5	92	8
Lighting (fluorescent)	20	20	97	3
Electric oven (home)	70–85	50–55	92	8
Toaster	70	40	92	8
Clothes dryer	60	30	92	8
Electric transportation system (traction)	80	80	92	8
Urban electric transportation system (electric rheostatic braking)	80	30	70	30
Urban electric transportation system (electric braking with recovery)	80	73****	99	1

* Breakdown values indicate percentage of overall exergy loss for the device, and thus sum for each device to 100%.

** Assumes charging circuit has an energy efficiency between 60 and 80%.

*** Conventionally expressed as coefficient of performance (COP) by dividing by 100.

**** Actual electric transportation systems use static converters and induction machines to facilitate electric regenerative braking, with recovered energy provided to other operating trains and increasing energy and exergy efficiencies.

Table 1. Energy and exergy efficiencies and breakdown of exergy losses for selected electrical devices.

Device	Efficiency (%)		Breakdown of exergy loss (%)*
	Energy	Exergy	Consumption	Emission
Simple electrical conversion devices
Transformer (high power)	93–98	93–98	73	27
Transformer (low power)	75–90	75–90	73	27
Alternator (low power)	70–73	70–73	73	27
Generator (high power)	90–95	90–95	73	27
Motor	80–87	80–87	73	27
Static converter	97–99	97–99	73	27
Electrical generation systems
Ideal thermal power plant	64	100	–	–
Coal–fired power plant	37	36	92	8
Nuclear power plant	30	30	98	2
Hydroelectric power plant	90	90	88	12
Fuel cell system	33	33	89	11
Wind turbine system	80–97	80–97	97	3
Solar photovoltaic system	6–25	6–25	88	12
Solar thermal power generation	10–30	10–30	70	30
Cogeneration and trigeneration systems
Cogeneration system	74	31	99	1
Trigeneration system	94	28	92	8
Electrical storage systems
Battery (lead–acid)	75–85	75–85	92	8
Battery (lead–acid) with charging circuit**	45–68	45–68	92	8
Electrically driven devices and systems
Resistance space heater	99	6	97	3
Heat pump	380***	19	94	6
Hot water heater	90	10	92	8
Industrial heater	70	51	70	30
Refrigeration system	310***	24	95	5
Pump	70	70	97	3
Fan	90	90	97	3
Lighting (incandescent)	5	5	92	8
Lighting (fluorescent)	20	20	97	3
Electric oven (home)	70–85	50–55	92	8
Toaster	70	40	92	8
Clothes dryer	60	30	92	8
Electric transportation system (traction)	80	80	92	8
Urban electric transportation system (electric rheostatic braking)	80	30	70	30
Urban electric transportation system (electric braking with recovery)	80	73****	99	1

* Breakdown values indicate percentage of overall exergy loss for the device, and thus sum for each device to 100%.

** Assumes charging circuit has an energy efficiency between 60 and 80%.

*** Conventionally expressed as coefficient of performance (COP) by dividing by 100.

**** Actual electric transportation systems use static converters and induction machines to facilitate electric regenerative braking, with recovered energy provided to other operating trains and increasing energy and exergy efficiencies.

The energy loss can be found using the corresponding energy efficiency as 100% minus the energy efficiency. The exergy loss can be found similarly. The overall energy loss is made up entirely of waste energy emissions from the system. The overall exergy loss differs significantly, as it consists of both waste exergy emissions from the system and internal exergy consumptions (or destructions) due to irreversibilities.

An examination of the breakdown of exergy losses in Table 1 shows that in most instances, the exergy losses are mainly associated with internal exergy consumptions. The waste exergy emissions tend to be smaller, usually less than 30% of the total exergy loss.

Table 1 is a compilation of data from different sources, which has been modified to be comparable and illustrative. Some details on the values presented in Table 1 are as follows:

• The reference-environment temperature is taken to be 20 °C.
• Energy efficiency values are presented for the transformer, generator, alternator motor and static converter which are typical of some types. Heat losses from the transformer, generator, alternator and motor are taken to occur at 130 °C. These values can also vary markedly among devices.
• Data for the coal-fired plant is based on the Nanticoke generating station [15,16].
• Data for the nuclear plant is based on the Pickering nuclear generating station [16], located in Pickering, Ontario (Canada). The input is taken to be the net heat of fission delivered to the reactor (rather than the uranium).
• The ideal thermal power plant is taken to be operating using a heat source at a temperature of 550 °C, which roughly corresponds to the temperature of the high-pressure superheated steam exiting the steam generator of the coal-fired Nanticoke generating station [15,16].
• For the hydroelectric power plant, water is assumed to exit at the elevation of the reference environment with negligible kinetic energy, thus having zero exergy and energy. It is also assumed that waste heat is released at an average temperature of 60 °C.
• The fuel cell system is based on an automotive fuel cell system assessed previously by Cownden et al. [18]. The system includes the fuel cell stack and the balance of plant, which includes pumps, compressors, heat exchangers, etc.
• Wind turbine system energy efficiencies vary significantly with wind speed, and are usually designed for highest efficiency operation at a given wind speed. Values are reported here for typical operating energy efficiencies for wind turbine systems at wind speeds that are reasonable in terms of systems operation. The main component of the system is the wind turbine itself, which has energy efficiencies typically ranging from 75% to 94% [20,21]. The device is assumed to emit waste heat at 30 °C, a temperature near the ambient condition.
• Energy efficiencies values for photovoltaic electricity generation are based on confirmed efficiencies for terrestrial solar cells and modules, measured under the global AM1-5 spectrum (1,000 W/m²) at 25 °C [22,23]. These devices are assumed to emit waste heat at 60 °C, a temperature between ambient conditions and waste heat flows for industrial heating.
• Solar thermal energy conversion devices use the energy in sunlight to heat a working fluid to a temperature sufficiently high to drive a thermal power cycle. Such systems usually utilize concentrating solar collectors so that reasonably high temperatures can be attained. The mean annual efficiencies reported are about 10%–20% for systems built over the past two decades and 30% for more recent systems [23]. The devices are taken to emit waste heat at a temperature of 145 °C, which is typical for industrial heating systems and some solar thermal systems.
• The cogeneration plant is based on the steam cycle-based plant analyzed in Section 6.3 of Kotas [2]. The plant has an electrical power output of 6 MW and a useful thermal output of 25 MW delivered at a mean temperature of 133 °C. The high-pressure steam temperature and pressure are 400 °C and 40 bar, respectively.
• The trigeneration system is based on a design for a cogeneration-based heating and cooling project in downtown Edmonton, Alberta (Canada) [17]. The system design has an initial supply capacity of 230 MW (thermal) for heating and 100 MW (thermal) for cooling and used electric centrifugal chillers. The efficiency data are based on a previous analysis by Rosen et al. [17]. The exergy loss breakdown is assumed the same as for the coal power generation example.
• The electrical storage systems considered are common lead-acid batteries, without and with a charging circuit. The energy efficiency represents the percentage of electricity supplied to the battery system that is recovered on discharging. Energy efficiency values for typical lead-acid batteries and charging circuit are obtained from a company [19]. For the battery, the charging circuit and the combination of the two, the exergy efficiency is identical to the energy efficiency. The heat loss from the battery is assumed released at 45 °C.
• The electrical resistance space heater is assumed to deliver product heat at 40 °C, and to emit waste heat at 30 °C.
• The electrical hot water heater is assumed to deliver product heat at a temperature of 55 °C, and to emit waste heat at 45 °C.
• The electrical industrial heater is assumed to deliver product heat at a temperature 800 °C, and to emit waste heat at 145 °C.
• The refrigeration system is based on the vapour-compression plant analyzed in Section 5.4 of Kotas [2]. The plant, which uses ammonia as the working fluid, has a refrigerating duty of 93 kW and maintains the cold space at –1 °C. The waste from the refrigeration system is taken to be the heat released from evaporator, which is assumed to occur at 35 °C. The plant efficiency is relatively low compared to systems available presently.
• The heat pump taken to be same as refrigeration system, except that the heat delivered is the product. Waste from the heat pump system includes miscellaneous heat releases from all devices and assumed to be small (10% of the exergy loss), which are assumed to occur at 40 °C. The plant efficiency is relatively low compared to available systems.
• Pump and fan efficiencies vary greatly, depending on capacity and other characteristics of the device. Values are taken for pumps used in variable air volume systems for an office building [25], while typical values are used for fans [24]. Waste heat emissions for both devices are assumed to occur at 30 °C.
• Lighting efficiencies vary significantly. Incandescent light bulbs and compact fluorescent lamps (a phosphor-coated gas discharge tube) convert about 5% and 20%, respectively, of the electricity they use to visible light [24]. Waste heat emissions from incandescent bulbs are assumed to occur at 45 °C and from compact fluorescent lamps at 30 °C.
• The home electric appliances for heating-based services considered here are electric ovens, clothes dryers and toasters. All convert electricity to useful heat with a typical energy efficiency of at least 60% [24]. The product heat and waste heat emission temperatures vary, depending on the device. The device temperatures are taken to be between the temperatures for industrial and hot water heating, while waste heat emissions are all assumed to occur 45 °C, for simplicity.
• The electric transportation systems on the basis of variable voltage and frequency static converters and induction machines facilitate improved electric braking, with energy recovery. In that operating regime, the vehicle provides energy to the DC network through an inverter. The recovered energy is used by other running trains, increasing energy and exergy efficiencies. For the traction-based electric transportation system, the energy and exergy efficiencies are calculated on basis of the efficiencies of static converters, electric transformers and induction motors. For the urban electric transportation system with electric braking, braking regimes with and without energy recovery are shown. The exergy efficiency is low for the system with rheostatic braking and high for the case of braking with energy recovery. The braking regime is only of significance for urban vehicles, when it is performed often.

6. Discussion

The efficiencies and losses for the electrical technologies and systems considered in this article can be compared. Clearly the energy efficiencies of such systems are inconsistent, in that some use a simple efficiency, others a coefficient of performance and others a different figure of merit. Also, the energy losses are misleading, in that they focus attention on areas where the main deviations from ideality are not occurring.

The exergy efficiencies and losses describe the efficiencies of the electrical technologies and systems better and provide more meaningful information. With these insights, a better understanding is attained of the factors affecting efficiency, and efforts to improve performance can be better allocated and directed.

In particular, low values of exergy efficiencies, or high exergy losses, indicate that a significant margin for efficiency improvement exists in theory. Realizing this efficiency improvement requires ingenuity and creativity, and involves trade offs with other factors such as economics and environmental impact. The breakdown in exergy losses allows the causes, locations and magnitudes of the exergy losses to be understood better, so that efficiency-improvement efforts can focus more directly on those factors likely to be causing efficiency losses.

7. Conclusions

The benefits of using exergy to understand the efficiencies of electrical technologies systems and to guide improvement efforts have been demonstrated. It is concluded that the concepts encompassing exergy have a significant role to play in evaluating and increasing the efficiencies of such technologies. Exergy should prove useful in such activities to engineers and scientists, as well as decision and policy makers.