1. Introduction
In this paper we are interested in differential entropy and mutual information as it applies to wireless communication systems employing antenna arrays at both the transmission and receiving sites. Systems of this type are more commonly known as Multiple-Input Multiple-Output (MIMO) communication systems. MIMO communication techniques are known to provide increased information capacity over that
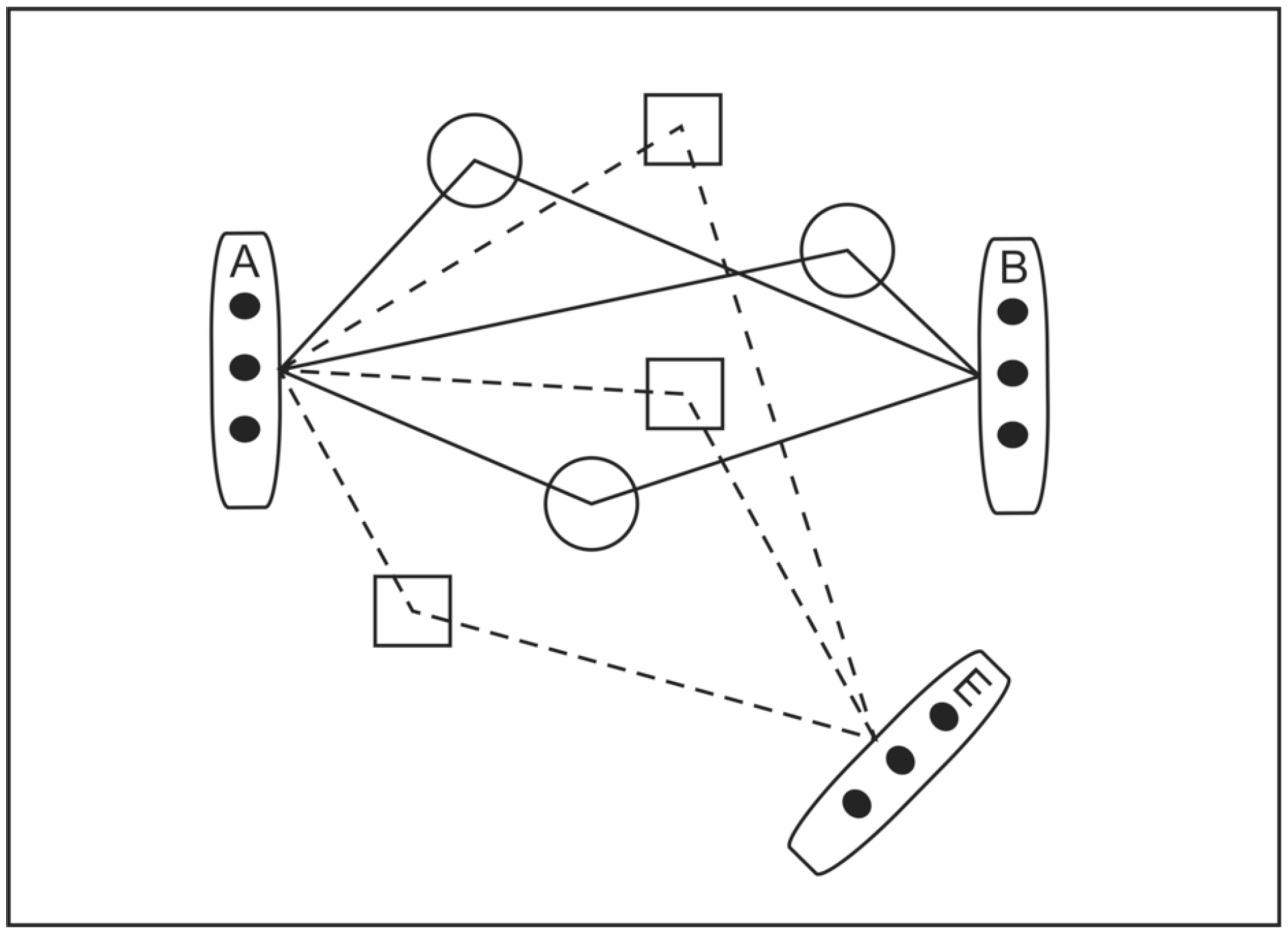
Figure 1.
MIMO Wireless Intercept Model.
Figure 1.
MIMO Wireless Intercept Model.
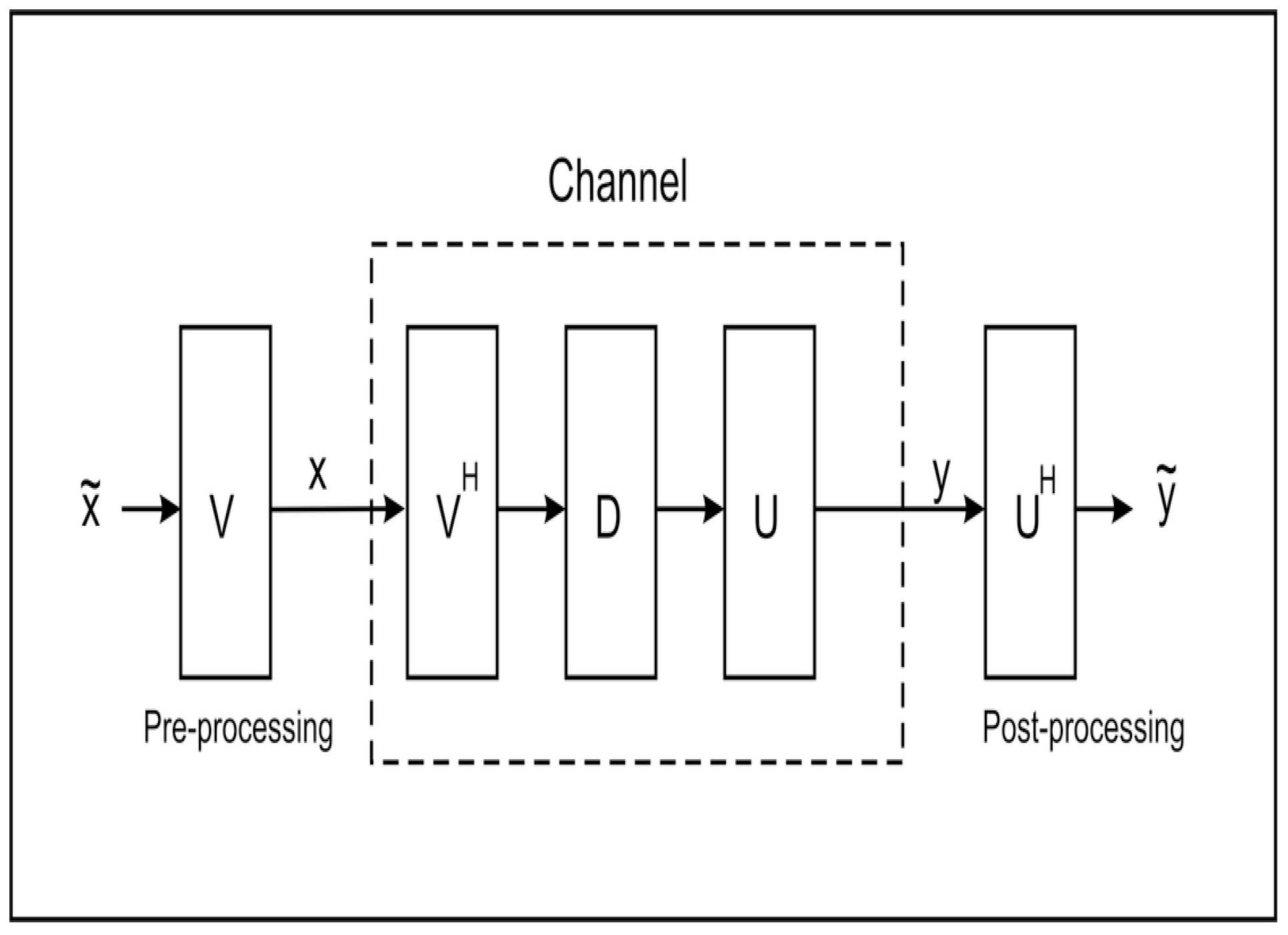
Figure 2.
Converting MIMO channel to parallel channel via SVD.
Figure 2.
Converting MIMO channel to parallel channel via SVD.
obtainable via a single transmit antenna to single receive antenna system [
1,
2]; however this extra capacity comes at the expense of increased system complexity and additional processing. To correctly receive and detect the transmitted message, the receive system must know the channel, or mixing, matrix as well as the message symbol set being used. The channel matrix may be estimated when a predetermined, known message sequence is incorporated into the transmitted message and the receiver knows where in the message this sequence occurs. However this training sequence may not always be available and this presents a blind source estimation problem where neither the message nor the channel matrix are known to the receiver. One possible solution to this problem is to employ a Blind Source Separation (BSS) technique such as Independent Component Analysis (ICA) [
3] which can go some way to extracting the signals from individual transmission antennae with the caveat that all but one of the transmitted signals must have a non-gaussian probability distribution. In some cases the transmitted signals may have been preprocessed in a manner unknown to the receiver. In this paper we consider the situation where a communications receiving system has prior knowledge of the message symbol set, the channel matrix between the transmission system and the receiving system, is able to resolve the transmissions from the, assumed independent, transmitter antennae but does not know the unitary transformation that has been applied at the transmitter. The question then becomes: what is the mutual information available to the receiver when an unknown unitary transformation matrix is employed by the transmitter?
In the following sections we derive expressions for differential entropy, mutual information and hence capacity for a two-element transmit array to two-element receive array system which we shall refer to as a 2-Dimensional (2D) system. The 3D case is studied in the
appendix giving a basis for a high snr approximation for the general N-Dimensional (ND) case. The general snr, ND case is derived and the resulting intended-receiver and intercept receiver mutual informations are compared.
2. Problem and Assumptions
The model that we shall employ for a MIMO system is the simple linear transformation
where
is the received signal vector,
is the transmitted vector,
is additive receiver noise and
is the channel gain or mixing matrix between the transmitter and receiver. The standard MIMO channel model [
11] assumes independent identically distributed (i.i.d.), frequency-flat Rayleigh fading between the transmit and receive antennae. Consequently the components
of
are typically modelled with a complex Normal density i.e.
. Here we shall assume
to be constant for both the intended and eavesdropper channels. In [
11] the authors show that, for the case where the channel is unknown and with block coding over a coherence time
T, the signal structure that achieves capacity is formed by the product of an isotropically distributed unitary matrix and a independent real, nonnegative diagonal matrix. For the purpose of this study we shall treat all of
,
, and
as real random variables. The benefit of this approach will be to simplify the derivations whilst recognising that, if the real and imaginary parts of the variables are independent, the results may be readily extended to the complex case by increasing the dimensionality of the vectors.
Figure 1 illustrates the scenario that we are studying. Employing a well-known cryptographic convention [
4], the transmission source array is labelled Alice (A), the intended cooperative receiver array is labelled Bob (B) and the unintended, passive intercept receiver is labelled Eve (E). The lines represent the paths that signals take from transmitter antennae to receiver antennae. Shapes in the signal paths represent objects that cause signal scattering. An important point to realise here is that the paths (channel
) between A and B are different to those between A and E (channel
).
The channel matrix can be factorized using Singular Value Decomposition (SVD) as :
and we can then use:
This allows us to view the MIMO system as if it were composed of a set of parallel channels and the input data vector can be designed with this in mind.
Figure 2 shows how this channel, with pre and post-processing, may be configured. For such an approach to work the transmitter requires precise knowledge of the channel matrix and it is a simple matter for the intended receiver to obtain the (scaled) message, since
is a real diagonal matrix. However for an unintended receiver, with a different (known) channel matrix, an unknown unitary transformation has been applied. In this case we desire to know how the mutual information, is affected. We make the following assumptions:
is a real observation vector.
is a real unitary (orthogonal) matrix.
is a real random Gaussian signal vector, .
is a real random Gaussian noise vector, .
.
the intended channel () is known to both Alice and Bob.
Eve knows the intercept channel () but not the intended channel.
the channels and vary slowly with time (or over many symbol periods) and may be assumed constant for the present study.
Based on the last assumption, Eve attempts to estimate the signal vector by applying the channel inverse as
Eve is therefore unable to directly obtain
due to the unknown unitary matrix
. In applying the channel inverse, the noise vector has also been scaled and the modified noise covariance term
shows that the intercept receiver may be operating with a different signal to noise ratio to that of the intended receiver. This also indicates that Eve could obtain better mutual information with a better channel.
Optimal power allocation to the parallel channels between Alice and Bob would typically be implemented via a technique called waterfilling, see [
5] chapter 5, and hence lead to optimal system capacity. We have not taken waterfilling into account in this study and simply assume that equal power is assigned to each of the parallel channels.
We could proceed to derive the eavesdropper mutual information in a cartesian or a polar coordinate system. Of course it doesn’t matter which coordinate system we choose - we should get the same answer. It is well known that differential entropy involves a Jacobian (J) in the transformation of coordinates [
6] , leading to a
term but this will cancel in the mutual information calculations because mutual information is a relative entropy i.e. the difference between two entropies. For the purpose of this study our derivations will be based on a cartesian coordinate system. We shall derive differential entropies according to the definitions given by Cover and Thomas in [
7], i.e. the differential entropy
of a continuous random variable
Y with a probability density
is defined as
where
is the support set of the random variable. When we have two random variables
with joint probability density
, the conditional differential entropy is defined as
where
is the support set of the random variable
X. The Mutual Information (MI) between the two random variables
Y and
X is defined as
The capacity
C is then obtained by maximizing the mutual information over all probability distributions for the source i.e. over
:
It is well known [
7] that a Gaussian source distribution is an entropy maximizer (for a given variance) so that, by treating
as a vector with i.i.d Gaussian components, the resulting differential entropy expressions will determine the capacity. Since the channels are assumed known we may consider
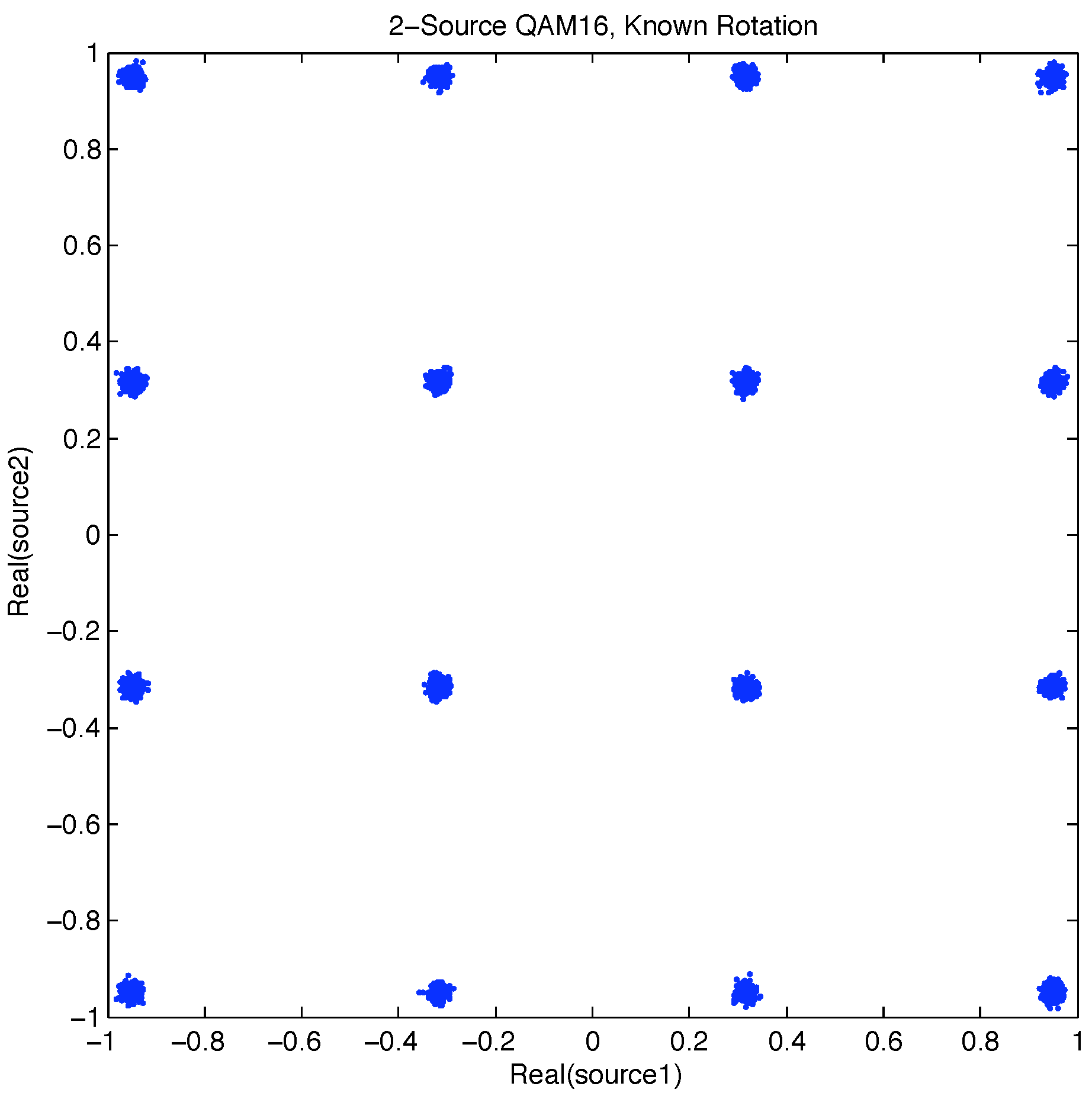
Figure 3.
2D Transmitter message symbol set.
Figure 3.
2D Transmitter message symbol set.
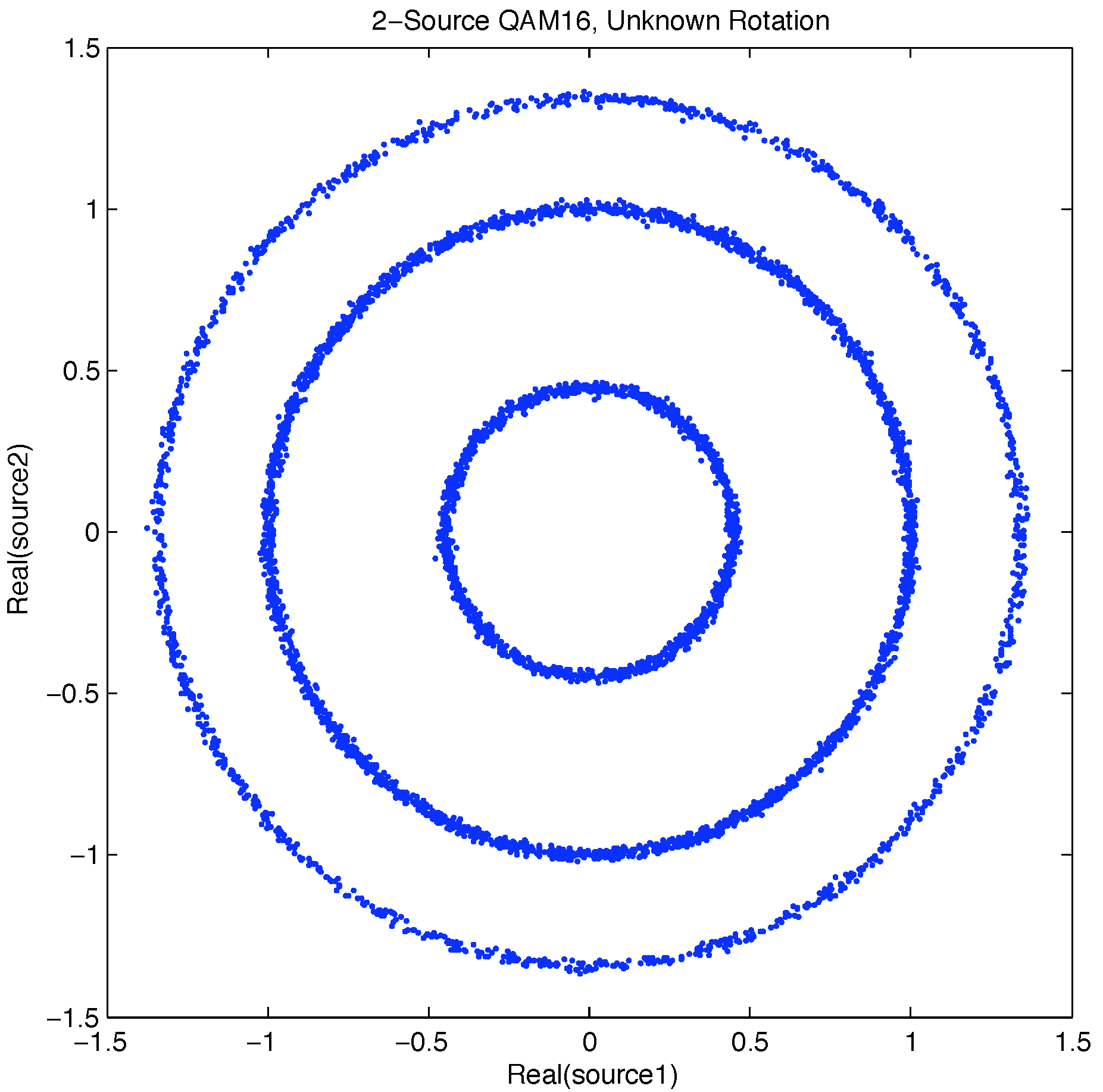
Figure 4.
Received ring distribution caused by unknown rotation on message symbol set.
Figure 4.
Received ring distribution caused by unknown rotation on message symbol set.
to represent the fully informed (unitary transformation known) case and
to represent the partially informed (unitary transformation unknown) case. We can write
to obtain
where
and
is a unit vector for which we may or may not know the rotations. For the random vectors
and
the mutual information for the fully informed model is given by:
and for the partially informed model the mutual information is obtained from:
where the message amplitude
A is known but not the rotation angles.
5. Summary
The problem of determining the information intercept capacity, available to a receiving system which knows its channel matrix but has no prior knowledge of a unitary transformation that has been applied at the transmitter, has been analysed. Entropy derivations were carried out for two dimensions and three dimensions giving some insight to the general dimensional, high snr case. The exact capacity for the N-Dimensional case has been obtained but requires numerical integration to derive the differential entropy for the partially informed case.
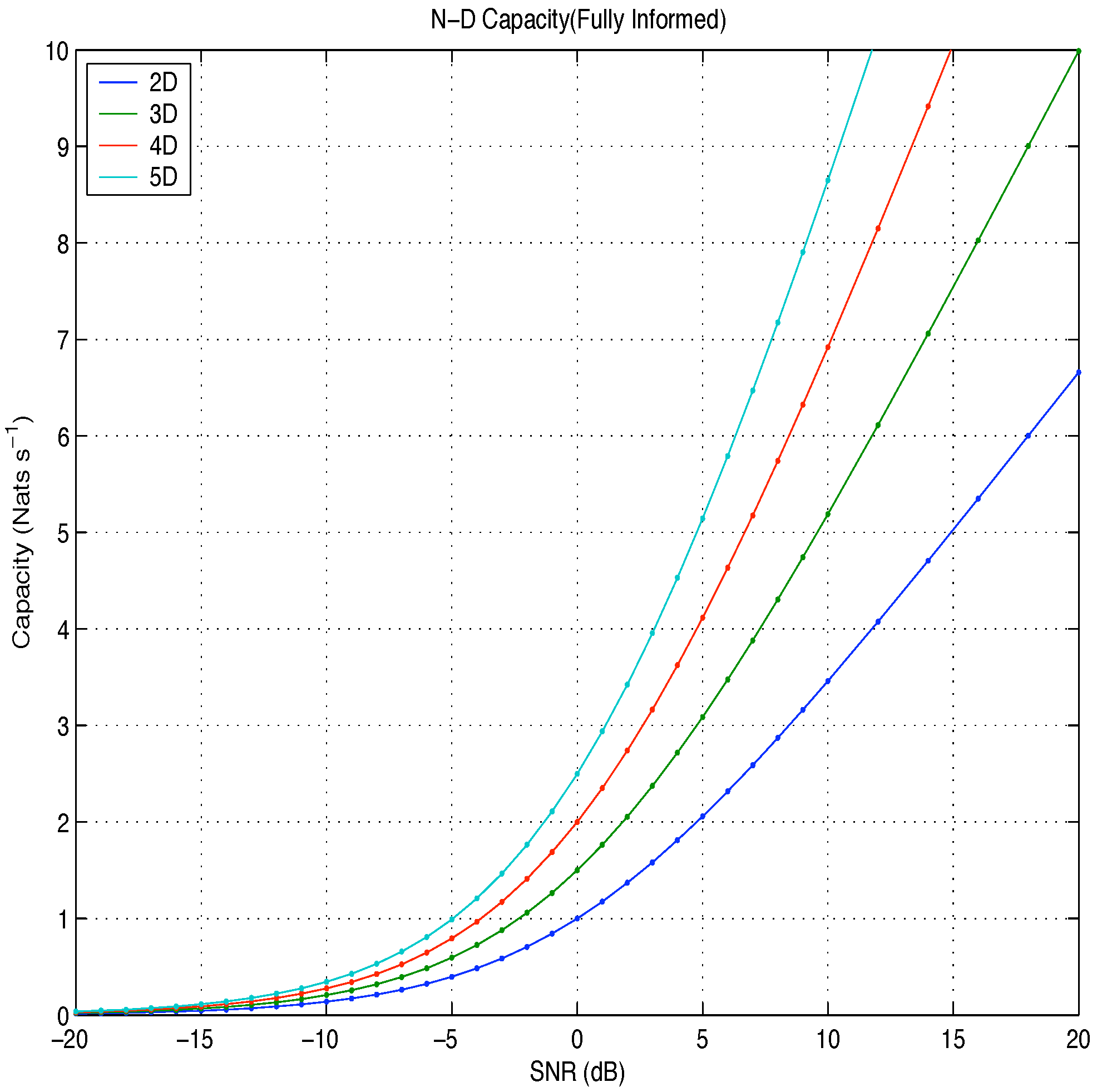
Figure 5.
Capacity: fully informed Vs SNR.
Figure 5.
Capacity: fully informed Vs SNR.
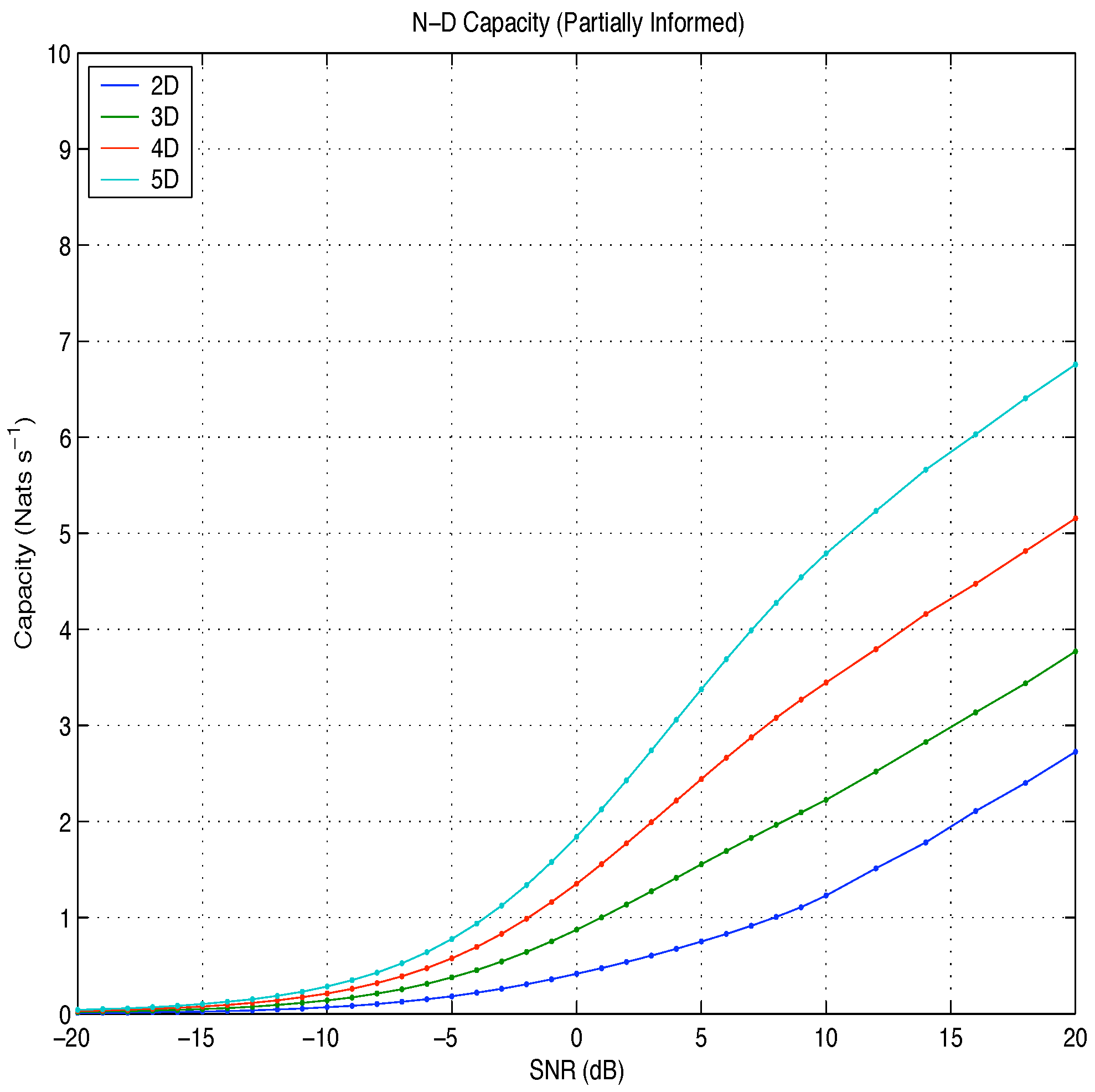
Figure 6.
Capacity: partially informed Vs SNR.
Figure 6.
Capacity: partially informed Vs SNR.
The fully informed capacity has been likened to the difference in entropy between two N-dimensional probability spheres: the larger sphere, representing the distribution of the signal plus noise vector, and the smaller sphere, representing the distribution of the noise vector. At high snr, the partially informed capacity was found to be equal to the difference in entropy between an N-dimensional probability sphere, representing the distribution of the signal plus noise vector, and an N-dimensional probability shell, representing the distribution of the amplitude plus noise vector.