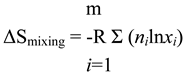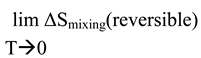1. Introduction
Residual entropy present in certain crystals comprised of non-symmetric molecules, e.g., CO, is detected only by the difference between spectroscopic calculations of the absolute entropy of gaseous CO and calorimetric measurements of heat capacity and phase change from 0 K to the temperature of the gas [
1]. This phenomenon results in the occurrence of a non-zero entropy at absolute zero [
2]. Residual entropy can be calculated by using the Boltzmann-Planck equation:
where W is the number of molecular arrangements [
1,
2,
3,
4].
Thus, textbooks have often shown that the way to calculate (and by implication, to understand) residual entropy is by counting molecular arrangements, i.e., “head-to-head,” CO-OC vs. “head-to-tail”, CO-CO, and call the process configurational entropy [
5,
6,
7,
8,
9,
10]. Such simple calculations result in correct answers for the value of residual entropy in joules/K because the number of configurations/arrangements at thermal equilibrium is equal to the number of different equiprobable varieties of dipole-dipole bonds (W) that could be formed from them [
11], in combination with eq. (1).
However, understanding the fundamental reason for the existence of residual entropy and its particular values – namely, the distribution over energy states of some of the potential energy of fusion that is “frozen-in” certain solids – is not aided by simple combinatorics divorced from energy distribution. For more than a decade, a modern interpretation of thermodynamic entropy as a
measure of energy dispersal/spreading has become increasingly accepted [
12,
13,
14,
15,
16,
17,
18]. This, of course, is in accord with the thermodynamic definition of entropy by Clausius as the following temperature-dependent state function wherein q (heat) is a form of energy:
Consistent with the view of entropy in terms of energy dispersal, this paper will show that residual entropy is no less energy-involved and no less “thermal” than "thermal entropy”
per se. Further, since residual entropy may also be considered as the entropy of mixing of differently aligned types of molecular pairs, this paper will also clarify the question of latent potential energy retained in the system when a liquid composed of unsymmetrical molecules freezes to form a nearly-ideal mixture at the freezing point [
19]. The scope of this paper is limited to crystals (as opposed to glasses) to make possible the accurate application of reversible thermodynamics.
2. Background: the molecular partition function
Molecular partition functions can be used to reveal the connection between “thermal” and “configurational” entropy. Intermolecular vibrations/interactions within the condensed phases may be separated from the other modes of molecular motion by means of a configurational partition function,
Z, obtained by integration of the potential energy over the entire system [
20,
21]. Then, similar to other partition functions for translational, rotational, and vibrational modes of molecular motion, the corresponding molecular partition function (the value per average molecule or other representative unit),
z, can be calculated:
where N is the number of particles (N=N
A for 1 mole). The single-molecule partition function (
z) shows the average number of accessible configurations (having different values of potential energies) per average molecule at a given temperature.
On the other hand, molecular partition functions are obtained within the micro-canonical ensemble for non-interacting particles (we will be using the “spinless” Boltzmann distribution because it adequately describes large amounts of molecules (molar quantities) at not-too-low temperatures). The relative population of the energy levels can be calculated using the following equations [
10,
20]:
where N
i, ε
i, and g
i are the population, energy, and degeneracy of a certain
i-th energy level, respectively,
j refers to a different energy level than
i-th, separated from it by the energy gap, Δε), N = ΣN
i is the total number of particles in the system, and
z =
is the molecular partition function.
Note that the presence of temperature in the Boltzmann distribution provides the link between the microcanonical ensemble (i.e., constant energy) and stochastically achieved canonical ensemble (i.e., constant temperature). The number of microstates (W) in eqs. (1) and (3) can also be calculated as a function of temperature (rather than energy) using the well-known combinatorial formula for a system containing
m energy levels:
In the important case when N
i=N/
m (i.e., equipopulation of the energy levels at “infinitely high” T), eq. (5a) may be shown to convert to a simpler combinatorial formula [
11]:
Under these conditions, as can be seen from the comparison of eqs (3) and (5b), the pertinent molecular partition function (
z) is numerically equal to the number of energy levels (if this number is finite) [
11].
3. The use of configurational partition functions to describe residual entropy
In order to connect the “thermal” and “configurational” approaches to residual entropy, let us consider freezing of a heteroatomic pure chemical substance, e.g., CO, using the partition function as a measure of entropy. When a liquid crystallizes at a thermodynamic melting point, resulting in the release of energy (or enthalpy if the process is conducted under constant pressure),
where ΔH
fusion reflects the release of energy due to the formation of stronger intermolecular interactions in the solid than the liquid. The corresponding entropy change, based on the derivations from the previous section, may be described as follows:
S
fusion accounts, at the same time, for this particle’s “immobilization” (loss of free rotation) due to the formation of stronger bonds and decrease in volume common during freezing of most liquids (stronger intermolecular bonds bring the molecules closer to each other due to the asymmetry of molecular potential energy surfaces).
However, both the entropy of fusion and corresponding configurational partition function [eq (3)], besides these averaged-out intermolecular interactions, may or may not include the additional intermolecular vibrational component arising from the preferential formation of certain configurations. For strong dipoles, e.g., HCl, the molecular configurations are uniform in solids as well as in the liquids at the freezing point [
zsolid(T
fusion)=
zliquid(T
fusion)=
zaligned(T
fusion)] because the strong dipole-dipole interactions result in a preferred aligned structure with an alternating, ‘ordered’ pattern of positive and negative charges. This “aligned” partition function yields the corresponding entropy, ΔS
aligned(T
fusion), via eqs (1) and (3). By contrast, weak dipoles, e.g. CO, freeze with random orientation of molecules resulting in
two statistically different configurations exhibiting different corresponding vibrational energies. Thus,
zsolid(T
fusion) in eq (7) may be adjusted as follows:
Single-molecule partition functions for different degrees of freedom contributing to the system’s partition function are multiplied as inverse probabilities for independent events [
10,
20]. Since
zliquid(T
fusion) may also be broken down to two similar terms, the corresponding separation of entropy terms can be achieved upon considering the
zsolid(T
fusion)/
zliquid(T
fusion) ratio in eq. (7):
The second entropy term in eq. (8b) is zero under thermodynamic equilibrium at T
fusion [
zsolid(T
fusion)/
zliquid (T
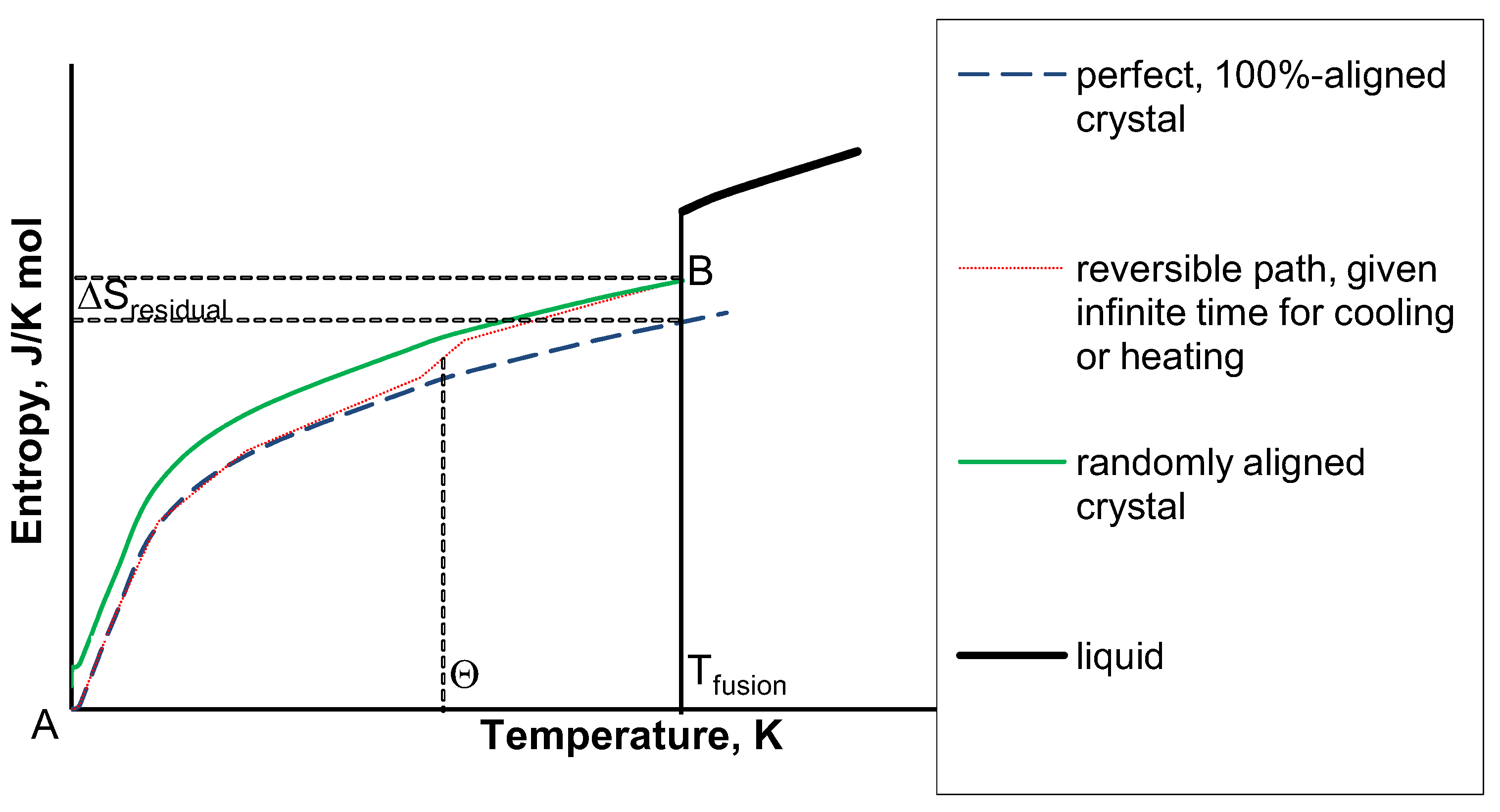
fusion)=1]. This is shown as point B in
Figure 1. However, it is this term that is the source of residual entropy. Since the liquid does not exist below the freezing point under thermal equilibrium, the temperature dependence of ΔS
alignment(T) shown as a red dotted line in
Figure 1 is fully determined by the change of
zsolid upon cooling below T
fusion.
Figure 1.
Entropy of condensed phases (sketch).
Figure 1.
Entropy of condensed phases (sketch).
In turn, zalignment at Tfusion (i.e., at thermodynamic equilibrium) may be calculated for CO using the Boltzmann distribution among the two energy levels reflecting different configurations. The “head-to-tail” alignment has a lower energy due to the interactions of oppositely charged dipoles, whereas two equivalent “head-to-head” alignments (only one being independent in the organized crystal structure) comprise a higher energy level.
As shown earlier, this treatment may be expanded to
m energy levels representing
m possible spatial configurations [
11]. These energy levels/configurations are equi-accessible because the energy gaps (Δε) between these levels are overcome, at the melting point, by the heat bath, kT: Δε/kT
fusion<<1 or Θ<<T
fusion, where Θ = Δε/k is the characteristic temperature for the given energy gap. If this condition is met, the pertinent entropy may be calculated using eq. (5b). By contrast, if this condition is
not met (so, Δε>kT
freezing or Θ>>T
fusion, e.g., strong dipoles), the upper energy levels are scarcely populated, the corresponding spatial configurations are poorly accessible, and
zalignment(T
fusion)=
m(accessible) ≈1. Hence, at the corresponding freezing points, for HCl (strong dipoles),
m=1; for CO (weak dipoles),
m=2 (higher energy “head-to-head” and lower energy “head-to tail”);
m=4 for weak dipoles like FClO
3, etc. [
11]. Note that these values pertain only to well-defined temperature ranges set by the value of Θ; for example, in sub- or supercritical fluids, even strong dipoles, e.g., HCl, become randomized (
m=2) when T> Θ whereas in supercooled liquids, if T<Θ, ordering would occur even for weak dipoles, CO or FClO
3 (
m=1).
Thus, weak dipoles retain, upon freezing, the following latent entropy:
which is equal to Rln
m for the molar amounts of the above-considered substances. The observed molar residual entropy values for CO, RbCN,
p-chloronitrobenzene,
p-bromochlorobenzene, and NNO are 4.6, 5.43, 2.96, 5.7, and 6 J/K/mole, respectively [
1,
22,
23,
24,
25]. The last two values are similar to the predicted value (Rln2 = 5.76 J/K/mole). The fact that the first three values are lower than predicted may be explained as 1<
zalignment(T
melting)<2, i.e.,
partial alignment at the melting point for these dipoles of an intermediate strength.
For ice crystals (which may also freeze in
three randomly accessible configurations [
11], all of them being “head-to-head” [
26]), the expected residual entropy (Rln3) has to be adjusted/reduced due to the impossibility of the “head-to-tail” alignment, Rln2. According to eq. (9), ΔS
alignment (T
fusion) = Rln3 - Rln2= Rln(3/2) [
11].
Thus, the configurational partition function yields configurational entropy
which is temperature-dependent, as any partition function, under the conditions of thermodynamic equilibrium
. However, since the systems possessing residual entropy are inherently not at thermal equilibrium [
1], conventional methods of determining residual entropy do not consider this temperature dependence between the absolute zero and T
fusion, instead proceeding directly to its limiting value.
This traditional approach appears to be well-justified, first, because it is based on the established concept of configurational entropy and, second, because the “frozen-in” ΔSresidual corresponds to a totally irreversible process and, it seems, can only be calculated as a limiting value using combinatoric methods.
4. Transition to the use of reversible thermodynamics involving energy transfer
However, classical reversible thermodynamics still can be applied to cases of residual entropy using eq. (3) (with the important qualification that the temperature of interest is below the melting point). The entropy of interest is the second term in eq. (8b):
Let us consider the further cooling of a non-aligned crystal. As any partition function,
zalignment decreases with temperature due to the increase of the population of lower energy level for the expense of higher energy levels. If the substance, e.g. CO or H
2O et al., were liquid instead of solid, a realignment process would occur reversibly as the system progresses toward the structure of a perfect crystal. Just as HCl is a strong enough dipole to freeze in the “ordered” form at its melting point, which is below the characteristic temperature of its “ordering,” CO would become a strong enough dipole (Δε>>kT) below
its corresponding characteristic temperature (which is below the melting point). Thus, during the cooling process, the crystal would disperse to its surroundings the infinitesimal increments of heat as a result of re-alignment, and its corresponding entropy would decrease accordingly. This is shown as a dotted line in
Figure 1 [along with the corresponding decrease of S
alignment (T)] as the distance between the dotted and lower dashed line when T<T
fusion. At T=0, as a limiting value, regardless of N, all of the particles would have become realigned as in the “perfect” crystal.
Note that in
Figure 1 for the perfect and real crystals only two points [A and B, respectively reflecting the entropy values for the perfect and random crystals in eq. (10)] correspond to thermal equilibrium with the surroundings. The reversible path, S
alignment(T), between these two points would correspond to reversible cooling described above. Since entropy is a state function, this reversible path can be chosen. Then, the value of residual entropy can be calculated using the Boltzmann-Planck formula:
Such a reversible path has been proposed recently [
27]. Eq. (12) and the rest of our treatment provided above complement this fundamental thermodynamic concept, thus linking it to both configurational entropy/statistical thermodynamics and the heat inherently coupled to it as shown below. Note that this treatment is applicable only to the systems in which the alignment kinetics is of an “all-or-none” kind: the kinetic barrier is totally insurmountable for any
finite time but is surmounted given infinite time. Thus, only crystals rather than glasses are considered henceforth. This lifts potential objections to the treatment suggested in reference [
27] and discussed [
28,
29].
Considering heat in this process, it is fanciful to believe that a ‘magic trick’ could be discovered that would – without increasing the temperature of the solid – allow the non-aligned molecules of CO or H
2O to rotate, become aligned, release their “frozen-in” potential energy, and eliminate the residual entropy. Surprising as it may seem, such a process (following the reversible path in
Figure 1, shown by the dotted line) was experimentally observed for crystalline KOH-doped ice [
26,
30,
31] as well as for some clathrate hydrates [
32]. It is exhibited as a spike on the plot of C
p vs. temperature at T=72 ± 2 K in H
2O (76 K in D
2O) followed by elevated values of C
p at higher temperatures up to the melting point [
26,
30]. Thus, unlike the case of any other crystal possessing residual entropy, the corresponding potential energy of ice can be released to the surroundings. There is a good physico-chemical reason for this effect: This transition in ice does not occur within a reasonable amount of time without the addition of small amounts of KOH [
26]. Therefore, KOH may be viewed as a
catalyst of this thermodynamically-favored process that lowers its activation energy (apparently via providing a proton relay in water that is well-known). Ice XI rather than common ice Ih is the true thermodynamically stable low-temperature form of solid water at equilibrium;
i.e., it has no residual entropy.
This reveals a way to consider the molecular realignment of the randomized crystalline solid as a
phase transition, similar to eq. (6):
with a transition temperature equal to the characteristic temperature (Θ) for
zalignment(T) [
33]. Since the bulk of the rise of the exponential function in the Boltzmann distribution occurs within a narrow temperature range, ΔS
”phase transition” can then be roughly approximated by ΔS
residual; although the former is smaller than the latter because the entropy of this phase transition follows the reversible curve in
Figure 1 thus lying between the curves for the perfect and non-aligned crystals.
Illustrating this, only 82% of the expected energy (while substituting the ΔS
residual value of for ice in eq. (8) can be recovered for such a phase transition of ice, despite having collected all the latent heat released between T
fusion and Θ [
26,
31]. A possible reason for this is that in ice XI, which is at thermal equilibrium with the surroundings, energy transfer from the warmer surroundings not only is dispersed to molecular motion (lattice energy) but some also to the transformation of intermolecular interactions according to eq 4b while being warmed. Heating ice XI from 0 to Θ=72 K follows the dotted rather than the dashed line in
Figure 1. Note that this difference, accounting for the difference between ΔS
”phase transition” and ΔS
residual, cannot be revealed by calorimetric measurements because stable ice XI, without a KOH “catalyst,” cannot be obtained [
34].
Thus, residual entropy does not violate the Third Law; the achievement of zero entropy at T=0 is just delayed (although, for infinite time) due to kinetic reasons (high activation energy barriers) which can be surmounted if a catalyst is available to restore the process to its thermodynamically reversible path.
5. Other Cases of Residual Entropy
Residual entropy may be observed in systems other than crystals of heteroatomic molecules. The case of
para-/
ortho- H
2 shows that intermolecular interactions (yielding the configurational partition function) are not unique for causing the phenomenon of residual entropy as long as some other latent energy can be “frozen-in.” In this system, the equilibrium of nuclear spins is established extremely slowly; thus, samples prepared at room temperature retain the random 1:3
para-/
ortho- ratio (resulting from the triple spin degeneracy of rotational energy levels in
ortho-H
2 with odd values of J) upon cooling to significantly low temperatures to “freeze” the rotational motion [
10,
20]. This latent energy can be released with the addition of a catalyst, e.g., activated carbon, to form the low-energy
para-H
2 with J=0. Without a catalyst, this mixture possesses residual entropy whereas with the catalyst it does not, because the reversible path is followed as shown in
Figure 1 (dotted line). Spin degeneracy contributes the Rln3 term for
ortho-H
2 [
20] thus yielding the Rln4 value for the residual entropy of the mixture. Among other cases of spin relaxation, Dy
2Ti
2O
7 should be mentioned because its residual entropy of Rln2 can be relaxed by anisotropic application of a strong magnetic field resulting in the release of heat according to eq. (6) [
35].
In yet another example, Levine [
20] pointed out that the isotopes of the same nuclear spin are usually miscible at the melting point but become immiscible at low T; therefore, residual entropy equal to Rln
m is also “frozen in” solid mixtures of
m different isotopes mixed at equimolar ratios. If they are mixed at other ratios, the residual entropy may be calculated by eq. (14) discussed in the next section. This example, similar to other ideal solutions/mixtures, necessitates the consideration of entropy of mixing; even though this topic has been considered before [
19], we shall offer a simple yet technically correct way of assuring the connection of energy and entropy of mixing.
6. The Relation of Residual Entropy to the Entropy of Mixing
The established formula for the entropy of mixing arises from configurational considerations:
(
ni is the number of moles of each component; for 1 mole of the mixture it is numerically equal to
xi, the corresponding molar fraction).
Note that eqs. (3-5) are applicable for distinguishable particles, and in crystals all particles are distinguished by their specific location in the network of intermolecular forces. However, eq. (14) not only applies to miscible liquids such as a benzene/toluene mixture, but also may be used for ideal gases,
i.e., for indistinguishable molecules with no intermolecular interactions (Δε =0). This is because eq. (14) does not require the
lack of intermolecular interactions but rather assumes no preference in them [
10], i.e., an
ideal solution. This condition is applicable to crystals only at the melting point (when they are at thermal equilibrium with the ideal solution) and only when the molecular orientations are absolutely random – exactly the case of our interest, when N
1 = N
2 = … = N
m,
i.e., when an “infinitely high” temperature for this particular Boltzmann distribution is achieved. Then, there is no preference for any molecular orientation; one can say that the
effective energy gap is zero because it is totally overpowered by kT
mixing. This explains why no detectable heat release is observed upon mixing of liquids and gases that form near-ideal solutions.
Yet, according to the Third Law,
Thus, no matter how small the Δε values are between different miscible chemicals at any finite temperature (e.g., standard room temperature), they are not equal to zero, and, thus, a finite quantity of enthalpy would be released at characteristic temperatures according to eq. (13) if the reversible path is attainable (i.e., if Θ lies within the temperature limits of the existence of the liquid phase or if a catalyst is available to dissipate this latent energy to the surroundings). This enthalpy, ΔH
mixing, reflects the difference between the energies of homo- and heteromolecular interactions (i.e., that in the separated components and in the mixture). When this energy is overcome by the kT (RT on the molar scale) heat bath at higher temperatures, the chemicals are miscible (for example, even hydrocarbons dissolve in hot subcritical water; however, upon cooling they separate with a concomitant release of the corresponding energy [
36]).
The numerical values of both characteristic temperature (Θ) and ΔH
mixing may become smaller when the solutions are very close to being “ideal,” (i.e., isotopes or the benzene/toluene mixture); yet, they are never equal to zero. This condition is essential for the connection of configurational and thermal entropy. However, since for near-ideal solutions the very low characteristic temperature of this process corresponds to the solid state, the reversible path of
Figure 1 is not attainable. Thus, the heat remains latent in the solid except for the specific cases of “catalysis” considered above.