Background
A number of approaches have been proposed for estimating the glass transition temperature of mixtures from knowledge of the properties of the pure components. Although different in detail, the proposed relationships are based on the additivity of basic properties.
Gordon and Taylor [
1] based their theory on two basic assumptions: volume additivity,
i.e., ideal volume of mixing, and a linear change in volume with temperature. Their proposed expression is arguably the most widely used equation for predicting the glass transition temperature of amorphous mixtures:
where the subscripts 1, 2 and
m denote component
1 component
2, and the mixture, respectively and
w is the weight fraction concentration in the mixture. The term
k in Equation 2 is a parameter whose value depends on the change in thermal expansion coefficient (
α) of the components as they change from the glassy (amorphous) to the liquid (rubbery) form, during the glass transition. Accordingly,
, where
V denotes the specific volume at the corresponding
Tg. In most practical applications however, the Gordon-Taylor equation is simplified in one of two ways in order to remove the
α terms from the expression. By invoking the Simha-Boyer rule [
10] (Δ
α ·
Tg = constant) we get
. Another common simplification is to let
k as a curve fitting parameter [
11].
Couchman and Karasz [
4] proposed a thermodynamic approach for predicting the glass transition temperature of mixtures. Their treatment is based on considering that even though it is not a second order transition, the
Tg has the façade of such, in the sense that the entropy of mixing is continuous during the glass transition to give:
where
x is the mole fraction concentration, Δ
Cpi is the difference in the heat capacity of the liquid (
) and the heat capacity of the glass (
) forms of component
i, and the subscripts 1, 2 and
m are the same as above. By defining
in the above expression, the Couchman-Karasz equation can be expressed in the general form of Equation 1:
Another expression for predicting the
Tg of mixtures is the Fox equation [
3]:
which can be obtained directly from the general Equation 1 if in addition to the Simha-Boyer rule used in the Gordon-Taylor treatment, we assume similar specific volume for the two components, such that
in the Gordon-Taylor expression.
In the limiting case where
k = 1, Equation 1 reduces to the expression for the linear combination:
which has been used as the simplest estimate used for the glass transition of mixtures [
12].
Equations 2 through 6 can all be directly obtained from the general Equation 1. Being mathematically equivalent, these expressions give similar predictions. There are however, experimentally observed
Tg–composition profiles that differ from the type of predictions obtainable from the general expression set [
13]. Jenkel and Heusch [
2] proposed an expression that accounts for monotonic (all positive or all negative) deviations from the linear combination (Equation 6):
where
k takes the role of an empirical fitting parameter.
Kwei investigated polymer mixtures including systems where the
Tg showed S-shaped profiles,
i.e., showing both negative and positive deviations from the linear combination profile. Kwei proposed the following expression [
5]:
where
k and
q are both fitted parameters. The origins of the Kwei expression are empirical, the physical meaning of the parameters
k and
q has been the subject of subsequent interpretations based on the intermolecular interactions between the components in the mixture [
13,
14].
The
Tg values of amorphous mixtures are generally interpreted in terms of intermolecular interactions [
5,
12,
14,
15,
16,
17]. Strongly interacting compounds tend to give mixtures whose glass transition is higher than would be expected from predictions from the different variants of (the general) Equation 1 [
12]. It is interesting to note that mixing effects on the glass transition are typically studied from an enthalpy perspective, even though it is entropy the quantity that plays a central role in glass formation [
6]. An entropy-based analysis on the effect of mixing on the glass transition temperature is presented here.
The role of entropy on glass formation and the glass transition
From a thermodynamic point of view, entropy is the defining parameter for glass formation. More specifically, vanishing of the accessible configurational entropy (
Sc) is the thermodynamic criterion for a liquid turning into a glass [
7,
18]. The glass transition is thus a manifestation of the smallness of configurational entropy,
i.e., of a “dearth of configurations” [
19]. We should clarify from the onset that the glass transition is a kinetically controlled phenomenon, such that any thermodynamic definition is in effect constrained by the timescale of the experiment. We will look into the thermodynamic argument before discussing the constraints imposed by kinetic considerations.
Consider a system of two glass forming components,
1 and
2, with glass transition temperatures
Tg1 and
Tg2, respectively, such that
Tg2 >
Tg1. The two components form a nearly athermal mixture, such that their mixing is entropically controlled. In addition, the system is such that the heat capacities of mixtures of the two components are given by:
where
Cp is the isobaric heat capacity and the superscripts
g and
L denote the glass and liquid forms, respectively,
x is the (mole fraction) concentration in the mixture, and the subscripts 1, 2 and
m denote component
1, component
2 and the mixture, respectively. We will make use of a thermodynamic cycle in order to establish the effect that the entropy of mixing ought to have on the glass transition temperature.
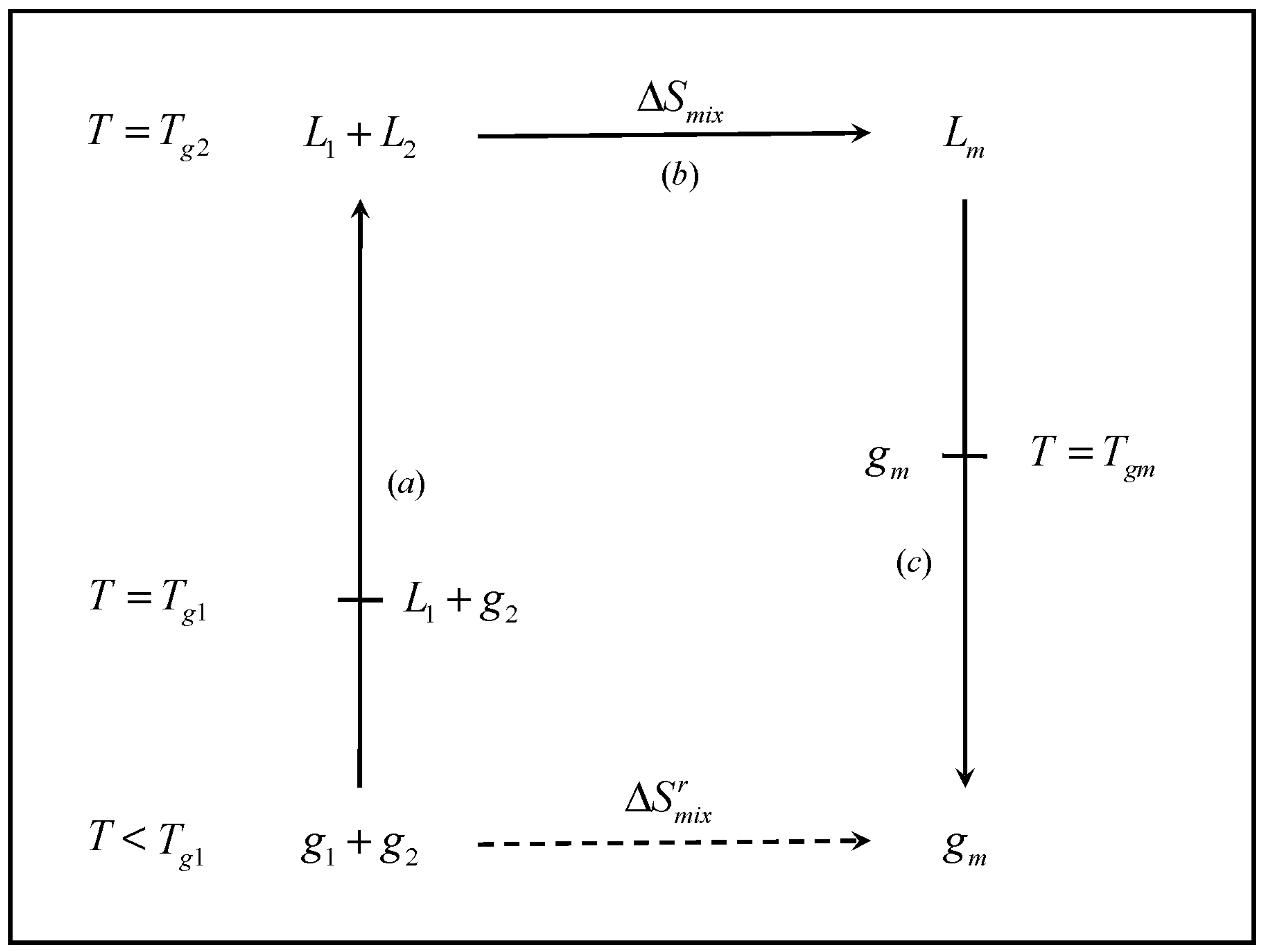
The cycle, shown in
Figure 1 involves the formation of mixture of glass former components
1 and
2, at concentrations
x1 and
x2, respectively. The cycle starts at an arbitrarily low temperature
T, such that each individual component is in the glassy state (
i.e.,
). The temperature is raised such that each individual component turns to the liquid state (
i.e.,
). The two liquids are mixed and the resulting liquid mixture is subsequently cooled back to the initial temperature, where the mixture exists as a glass. Namely,
| Step a | The separate components are heated from the initial temperature T to Tg2, the higher pure-component Tg, where the two materials exist as liquids. In the process, the temperature of the system passes through Tg1, where the pure component 1 turns into a liquid |
| Step b | The two components, are mixed in the liquid state at Tg2 |
| Step c | The liquid mixture is cooled from Tg2 to the initial temperature T. In the process, the mixture undergoes the transition to the glass at Tgm |
Figure 1.
Schematic representation of the thermodynamic cycle used to obtain the entropy of mixing of the glassy mixture (). L and g denote liquid and glass, respectively, and the subscripts 1, 2 and m denote component 1, component 2 and the mixture, respectively.
Figure 1.
Schematic representation of the thermodynamic cycle used to obtain the entropy of mixing of the glassy mixture (). L and g denote liquid and glass, respectively, and the subscripts 1, 2 and m denote component 1, component 2 and the mixture, respectively.
The entropy of mixing of such process,
, is necessarily the same as that from the thermodynamic cycle involving steps
a through
c. The entropy change contributions for the cycle are
The entropy change for the entire cycle (
Figure 1) can be expressed as follows:
In order to establish the effect of the entropy of mixing on the glass transition temperature, it is necessary to establish the link between the entropy of mixing in the liquid () and the entropy of mixing in the glass (). The key question resides on what portion of the entropy of mixing i) is configurational in nature and ii) is accessible to the liquid within the timescale of the experiment. To address this question, it is necessary to take into consideration the kinetic character of the glass transition.
Any thermodynamically obtained quantity is independent of time. Therefore, the entropy change in the above expression represents the value obtained at infinitely slow cooling rate,
i.e.,
where the superscript
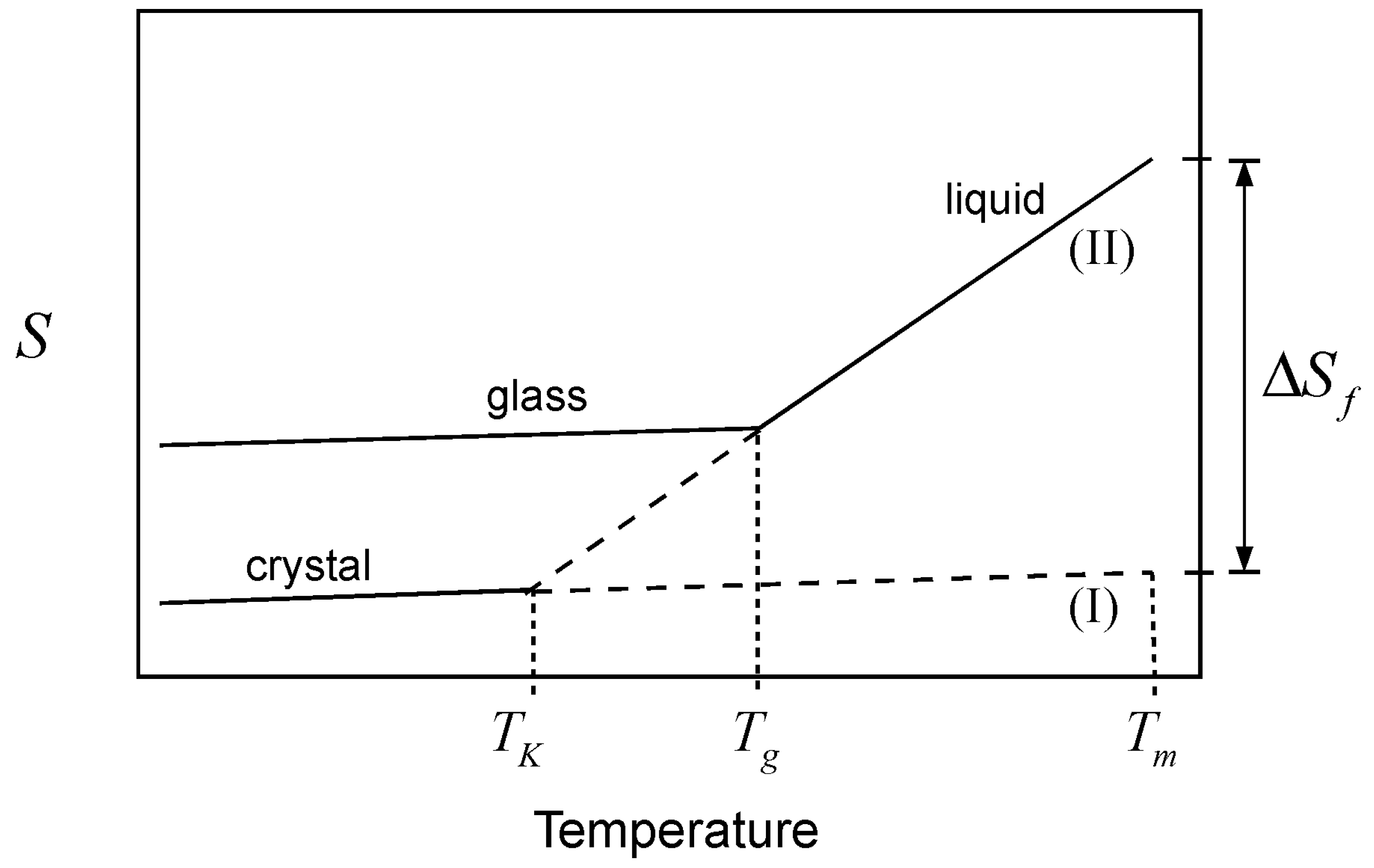
indicates an infinitely slow (thermodynamic) measurement. We start by considering the similarity between the entropy of mixing of liquids and the entropy of melting of a crystal, in the sense that the two quantities are predominantly configurational [
20]. Cooling the melt of a pure crystalline material has the effect of “consuming” the entropy of melting (
) [
7]:
where
Tm and
are the melting and Kauzmann temperatures, respectively, and
is the heat capacity difference between the liquid and the crystalline forms of the material. This depletion, which occurs because the heat capacity of the liquid is greater than that of the crystal, is graphically depicted in
Figure 2. The Kauzmann temperature is the temperature where the configurational entropy accessible to the liquid vanishes; the liquid and crystal lines (II and I, respectively) cross, so that both crystal and liquid have the same entropy at the same temperature, or crystallization takes place without an entropy change. Besides the potential entropy crisis in the former case, such a state is unattainable since it requires an infinitely slow cooling rate. Hence, a common thermodynamic view of the glass transition is that
is the temperature of an underlying but experimentally unattainable second order transition. The transition is kinetically masked by finite cooling rates such that the glass transition is observed at some higher temperature,
Tg. Because of the kinetic nature of the glass transition, there is no single
Tg value; the observed value varies with the kinetics of the experiment [
21]. In other words, the observed
Tg for a given glass forming liquid will vary, depending on how fast or slow the liquid is cooled. This is an important point; different cooling rates will “consume” different amounts of configurational entropy up to the point where a
Tg is observed. In each case, a different amount of residual entropy will remain trapped in the glass as part of its thermal history. This trapped configurational component includes the entropy that is subsequently lost upon aging of the glass, as it undergoes structural relaxation.
Figure 2.
Schematic representation of the glass transition. Cooling of the liquid melt (line II) below the melting temperature (Tm) consumes the entropy of melting, . In an infinitely slow experiment, the entire quantity would vanish at the Kauzmann temperature (TK), where curves for the crystal (line I) and the liquid (line II) cross, but the glass transition (observed at Tg) intervenes when the configurational entropy is no longer accessible to the liquid within the experimental timescale.
Figure 2.
Schematic representation of the glass transition. Cooling of the liquid melt (line II) below the melting temperature (Tm) consumes the entropy of melting, . In an infinitely slow experiment, the entire quantity would vanish at the Kauzmann temperature (TK), where curves for the crystal (line I) and the liquid (line II) cross, but the glass transition (observed at Tg) intervenes when the configurational entropy is no longer accessible to the liquid within the experimental timescale.
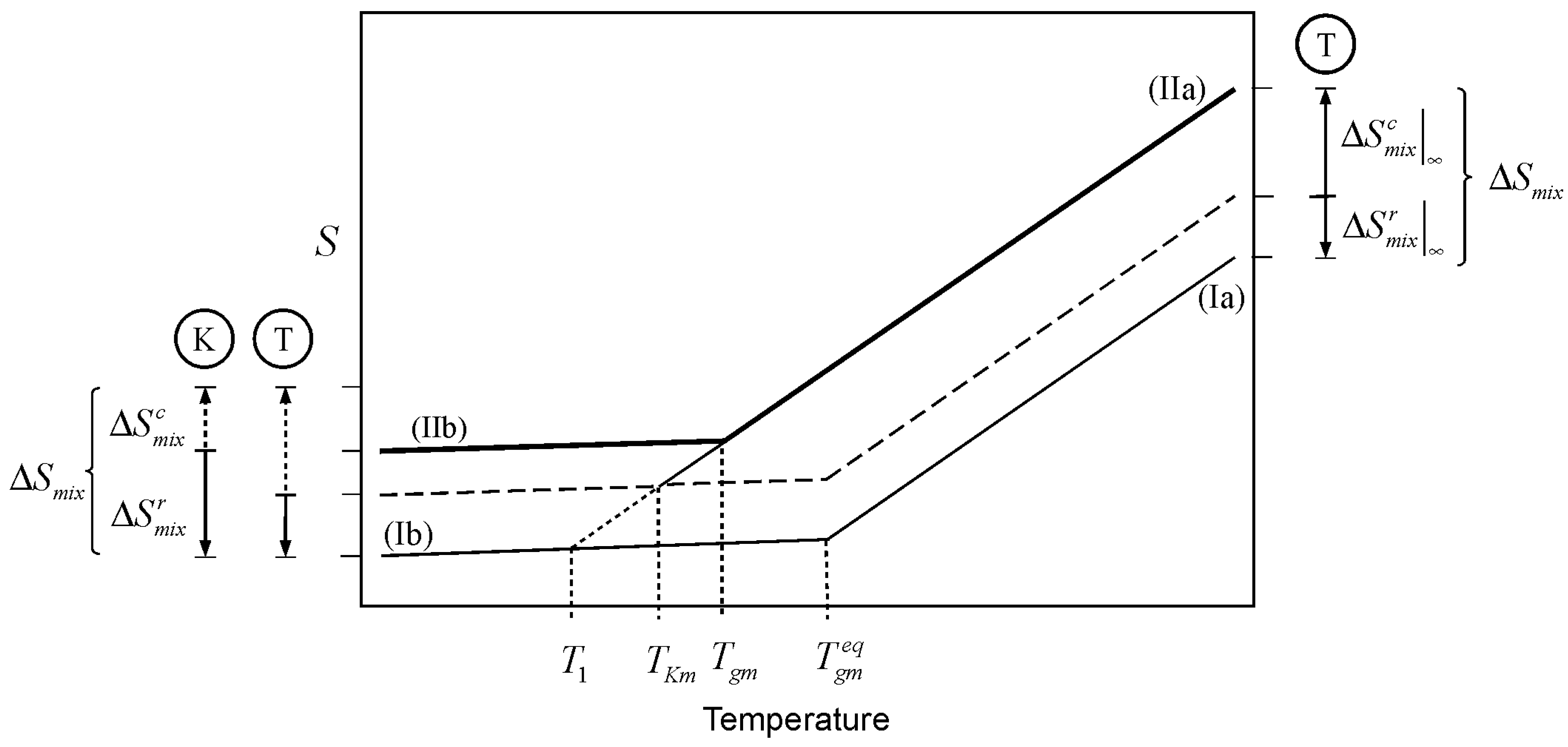
A similar argument can be made for the entropy resulting from the mixing of two liquids. This case is illustrated in
Figure 3, where lines Ia and IIb depict the glass transition of a mixture where the entropy of mixing plays no role at all (
as per Equation 1). The entropy of mixing adds to the entropy of the liquid mixture, shifting the liquid line Ia, by the amount
, to line IIa. The shift is upward for positive entropy of mixing, as in the case for athermal solutions. Cooling the liquid mixture consumes the configurational entropy (of which the entropy of mixing has an important component) in the same way as cooling consumes the entropy of melting discussed above. However, the analysis presented here is based on the notion that the entropy of mixing in a glass forming mixture is not all accessible for “thermal consumption” to the liquid. The reason being, without getting into molecular interpretations, that any real glass mixture will have some entropy of mixing in it. The entropy of mixing consists of two parts, a configurational portion (
), and a residual part (
). The former is the entropy of mixing accessible to the liquid, the latter is the mixing entropy in the vitrified mixture.
is expected to be vibrational to a large extent, but not entirely so. The simplest view is that the difference in entropy between a liquid and its glass is all configurational. However, real liquids exhibit important vibrational differences in relation to their glasses. Such differences are in turn the result of different configurational states between liquid and glass [
22,
23]. It is therefore important to point out that the main characteristic of the quantity
discussed here is not that it is (largely) of vibrational nature; the important attribute of
is that it is inaccessible to the liquid when the mixture vitrifies. This unavoidable residual entropy of mixing in the glass removes the physically problematic situation of having a glassy mixture with the exact same entropy as the sum of the entropies of its pure components. At an infinitely slow cooling rate, the Kauzmann temperature is the point where the configurational entropy accessible to the liquid, including the contribution from mixing (
), is depleted. The balance toward the whole quantity is the residual entropy of mixing remaining in the glass,
. The latter is arguably the minimum amount of entropy necessary to create stable glassy mixture. Accordingly, the partitioning of the entropy of mixing is represented as
A partition marker for the entropy of mixing is shown on the top right of
Figure 3. The marker (T-marker) is labeled by an encircled T, to indicate that it corresponds to the thermodynamic (infinitely slow) partitioning of the entropy of mixing. The dashed line traces
above the zero-entropy of mixing line (segments Ia and Ib). The Kauzmann temperature of the mixture (
) is the point where line IIa meets the dashed line; this is the point where the amount of thermally consumed entropy equals
. This decrease in entropy is “gauged” by the T-marker on the lower left of the figure. The point marked
in
Figure 3 corresponds to the Kauzmann temperature for a system where the separate glass components have the same entropy as the glass mixture; an unrealistic situation, and one impossible for an athermal mixture.
Let us now consider the kinetic effect,
i.e., the effect of the timescale of the experiment. Cooling a glass forming liquid at a finite rate will eventually lead to a situation where the drop in configurational entropy cannot keep up with the pace of change in temperature. At this point, the system falls out of structural equilibrium and the glass transition is observed. The
Tgm is the point (above
) where line IIa changes to IIb in
Figure 3. At finite cooling rates, the configurational entropy of mixing accessible to the liquid within the timescale of the experiment (
) is different from the value of an infinitely slow experiment, the same is necessarily true for the residual entropy of mixing trapped in the glass (
).
A partition marker for the entropy of mixing under finite cooling rates is shown on the bottom left corner of
Figure 3. The marker is labeled by an encircled K, indicating that it reflects the kinetics of the experiment. The K-marker serves as gauge for the drop in entropy at finite cooling rates. Kinetics has the effect of changing the partition of the entropy of mixing between the (configurational) portion that is accessible to the liquid during cooling, and the portion that remains in the glass. The residual entropy of mixing in the glass comprises
plus any kinetically trapped configurational entropy that became inaccessible to the liquid as a result of the experimental timescale. However, the entropy of mixing has a thermodynamic origin so that its magnitude as a whole remains invariant, regardless its kinetic breakup:
Figure 3.
Effect of the entropy of mixing on the glass transition temperature of a mixture. is the glass transition temperature of the mixture where the entropy of mixing plays no role, as per Equation 1. 1) Thermodynamic scenario: Mixing changes the entropy of the liquid mixture by
, shifting the liquid line from Ia to IIa. Cooling of the liquid mixture “consumes” the configurational entropy up to the amount
, which corresponds to infinitely slow cooling. The dashed line traces
, the portion of the entropy of mixing that remains in the glass when produced with infinitely slow cooling. The thermodynamic marker, labeled with and encircled T, depicts the split of the entropy of mixing between the liquid and glass at an infinitely slow cooling rate. The Kauzmann temperature is the point where line IIa and the dashed line meet. 2) Kinetic scenario: At finite cooling rates, the glass transition takes place at Tgm (above TKm) leaving some configurational entropy kinetically trapped in the glass. The kinetic split of
is depicted with the marker labeled with an encircled K. The T and K markers on the bottom left serve as gauges for the consumption of configurational entropy of mixing at finite (kinetic) and infinitely slow (thermodynamic) cooling rates.
Figure 3.
Effect of the entropy of mixing on the glass transition temperature of a mixture. is the glass transition temperature of the mixture where the entropy of mixing plays no role, as per Equation 1. 1) Thermodynamic scenario: Mixing changes the entropy of the liquid mixture by
, shifting the liquid line from Ia to IIa. Cooling of the liquid mixture “consumes” the configurational entropy up to the amount
, which corresponds to infinitely slow cooling. The dashed line traces
, the portion of the entropy of mixing that remains in the glass when produced with infinitely slow cooling. The thermodynamic marker, labeled with and encircled T, depicts the split of the entropy of mixing between the liquid and glass at an infinitely slow cooling rate. The Kauzmann temperature is the point where line IIa and the dashed line meet. 2) Kinetic scenario: At finite cooling rates, the glass transition takes place at Tgm (above TKm) leaving some configurational entropy kinetically trapped in the glass. The kinetic split of
is depicted with the marker labeled with an encircled K. The T and K markers on the bottom left serve as gauges for the consumption of configurational entropy of mixing at finite (kinetic) and infinitely slow (thermodynamic) cooling rates.
![Entropy 10 00207 g003]()
Equations 13 and 14, represented by the T and K marker bars in
Figure 3, are the thermodynamic and kinetic scenarios, respectively, for partitioning the same quantity: the total entropy of mixing,
, between the liquid and the glass. The equality between Equations 13 and 14 frames the thermodynamic constraint of a kinetically controlled process such as the glass transition. A signature property of glasses is that the configurational entropy kinetically trapped in the glass is lost over time via structural relaxation following glass formation. From the above considerations, the entropy of mixing contributes toward the entropy available for loss upon structural relaxation of the glass by an amount equal to the difference between the kinetic and thermodynamic values:
Substituting Equations 10 and 14 into Equation 11 we obtain
It follows that for an infinitely slow experiment, as
and
where
is the Kauzmann temperature of the mixture. Equation 16 in turn leads to the following result
The first term on the right hand side of equation 18 corresponds, exactly, to the Couchman-Karasz equation [
4]. Therefore, the result can be expressed in the following form:
where
is the glass transition temperature of the mixture predicted by the Couchman-Karasz model (Equation 4). Equation 18 describes deviations in the glass transition from the
TCK value as a result of the liquid-accessible configurational entropy of mixing, and reduces to Equation 4 when the value approaches zero. In the case of polymer mixtures, the entropy of mixing is small [
17], so that the exponential term in equation 18 may not represent a large correction. However, even if small, spontaneous mixing is almost invariably (and always so if the mixture is athermal) accompanied by a non zero entropy of mixing. In the case of mixtures of low molecular weight compounds, the contribution of the entropy of mixing toward the observed
Tg can be expected to be of greater significance. The original derivation of the Couchman-Karasz equation in effect equates the entropy of mixing in the liquid and glass [
4]. Such an assumption has generated significant debate [
9,
15], as has the meaning of the entropy of mixing in the glassy state. The analysis presented here is based on the partitioning of the entropy of mixing into two parts: one portion that
i) is configurational and
ii) is accessible to the liquid within the timescale of the experiment, and a residual portion, which
i) can have both vibrational and configurational components, but most importantly,
ii) remains in the glass upon vitrification.
Different experimental timescales (heating/cooling rates and thermal histories) affect the amount of configurational entropy trapped in pure glasses. With that, the position of the observed glass transition shifts accordingly [
24]. The same is true for mixtures, where part of the trapped configurational entropy necessarily originates from the mixing process. Therefore, the kinetic character of the glass transition should result in observed
Tgm and
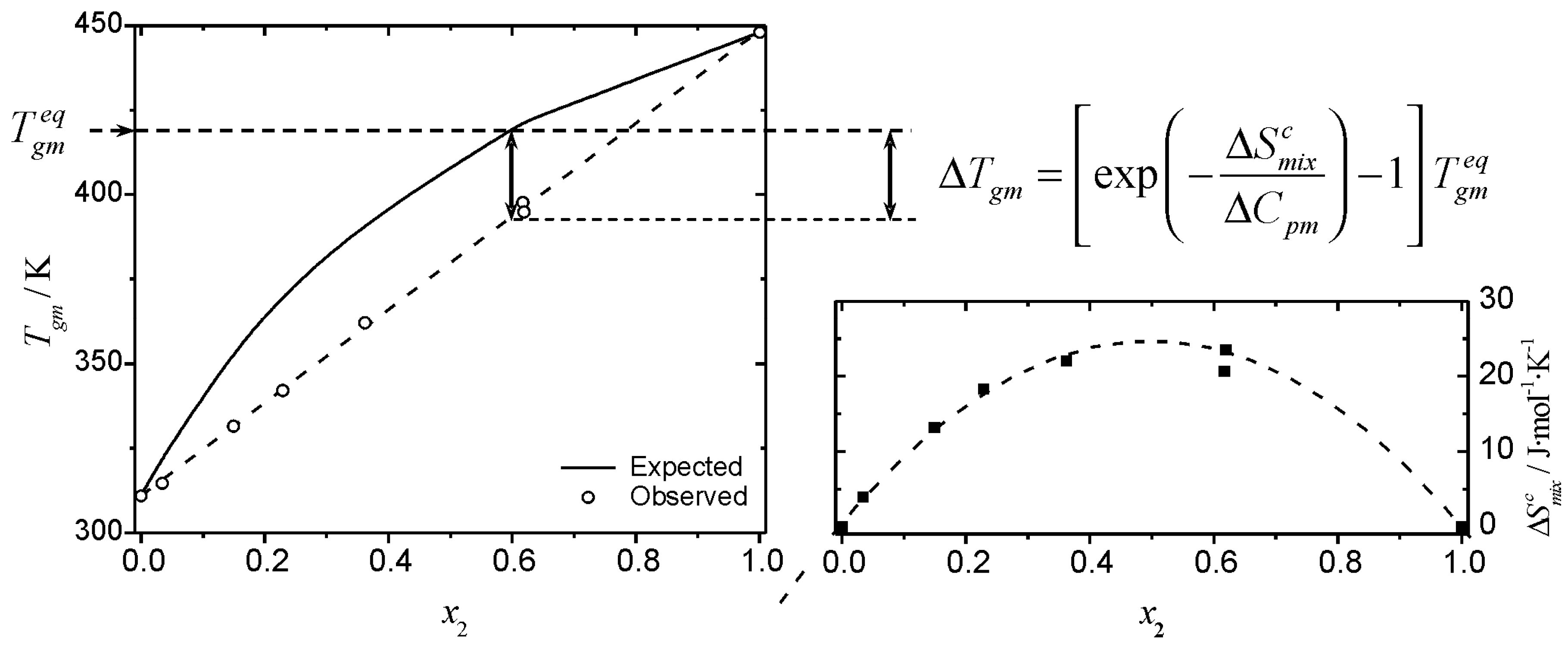
values that vary with the timescale of the experiment. A graphical synopsis of the effect of the entropy of mixing (Equation 18) on the
Tg of a mixture is shown in
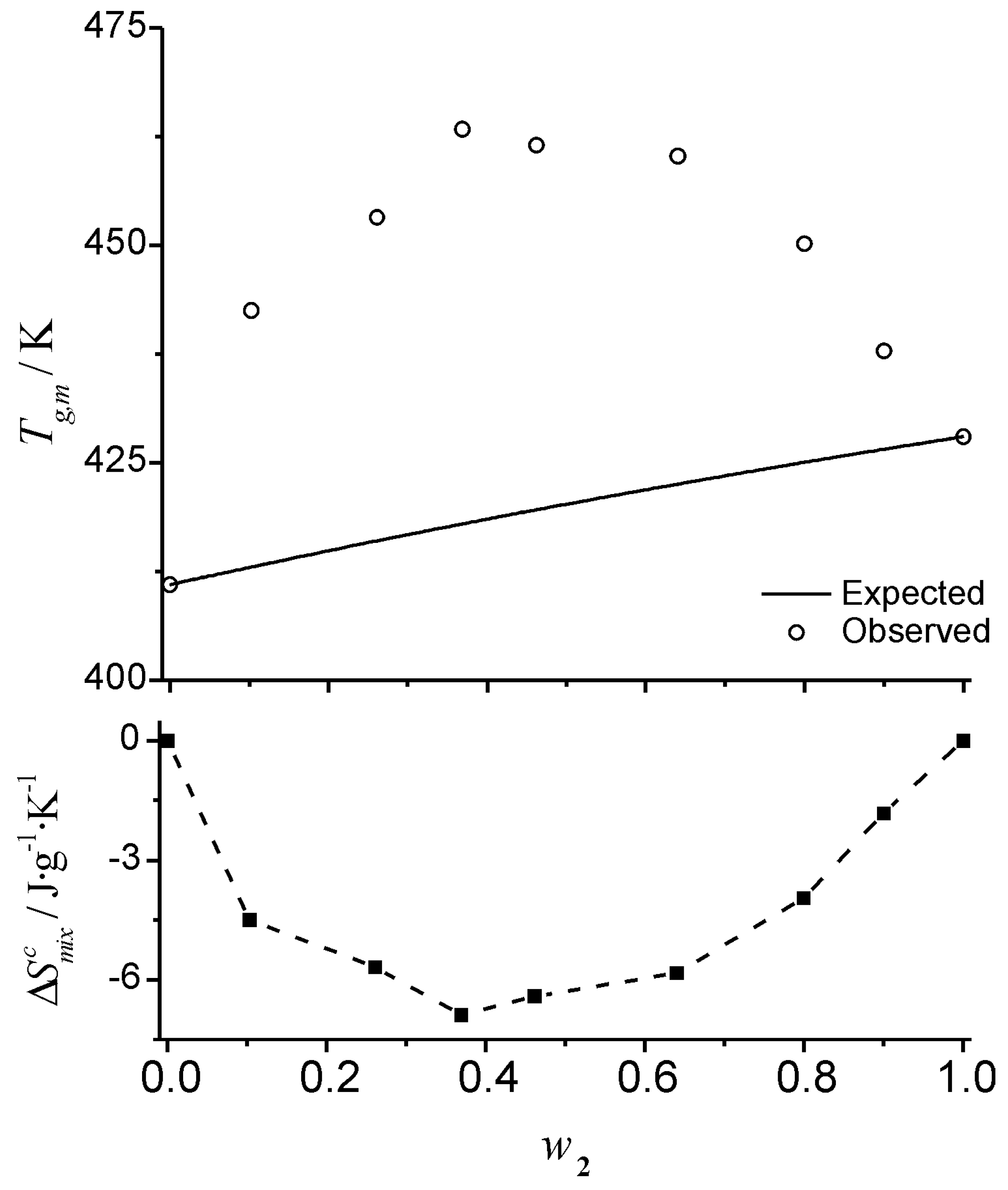
Figure 4, where the observed and expected glass transition data for mixtures of glucose-maltohexaose reported by Orford
et al. [
25] are shown. The experimental profile shows a clear linear relationship between
Tgm and the composition of the mixture. The linear relationship makes this a deceptively simple system; even though it is a straight line of the form of Equation 6, the profile corresponds to negative deviations from the profile predicted by the Couchman-Karasz equation. The corresponding
values, obtained from Equation 18 for this system are also shown in
Figure 4. The configurational entropy of mixing accessible to the liquid during cooling (
) has the effect of “shifting” the
Tg from the “expected” (
) values. The
values are obtained from the deviation from the predictions of Equation 1:
Figure 4.
Graphic representation of the effect of the entropy of mixing on the glass transition temperature of a mixture. The combinatorial entropy of mixing has the effect of shifting the glass transition temperature from the expected value,
(Eq. 1), shown by the solid line in the left inset. The magnitude of the shift is given by an exponential term that depends on the timescale of the experiment (see text). Filled squares (bottom right inset) are the values of
obtained from Eq. 18. The data plotted correspond to the glass transition temperature of glucose (1) – maltohexaose (2) mixtures published by Orford
et al. [
25]. Dashed lines are visual guides.
Figure 4.
Graphic representation of the effect of the entropy of mixing on the glass transition temperature of a mixture. The combinatorial entropy of mixing has the effect of shifting the glass transition temperature from the expected value,
(Eq. 1), shown by the solid line in the left inset. The magnitude of the shift is given by an exponential term that depends on the timescale of the experiment (see text). Filled squares (bottom right inset) are the values of
obtained from Eq. 18. The data plotted correspond to the glass transition temperature of glucose (1) – maltohexaose (2) mixtures published by Orford
et al. [
25]. Dashed lines are visual guides.
The magnitude of the observed shift on
Tg is kinetically controlled and is maximum for an infinitely slow experiment, when
. An example of a mixture with strong intermolecular interactions reported by Painter
et al. [
15] is shown in
Figure 5. This mixture involves a strong hydrogen bond donor and a strong hydrogen bond acceptor (polyvinylphenol and polyvinylpyridine, respectively). The strong interaction between components results in strong positive deviations from the predicted
TCK values. Strongly interacting mixtures give place to structured mixtures [
12,
26] and a negative entropy of mixing can be expected. The contribution of the entropy of mixing obtained from Equation 18 reflects such a character for this mixture.
Figure 5.
Positive deviations in a strongly interacting mixture. Glass transition temperature of mixtures of polyvinylphenol (1) and polyvinylpyridine (2). Top: symbols correspond to data adapted from Painter
et al. [
15]. The solid line is the profile predicted by the Couchman-Karasz equation. Bottom: filled squares represent the entropy of mixing contribution obtained from Eq. 18.
Figure 5.
Positive deviations in a strongly interacting mixture. Glass transition temperature of mixtures of polyvinylphenol (1) and polyvinylpyridine (2). Top: symbols correspond to data adapted from Painter
et al. [
15]. The solid line is the profile predicted by the Couchman-Karasz equation. Bottom: filled squares represent the entropy of mixing contribution obtained from Eq. 18.
An approximation for the plasticizer effect
The plasticizer effect is an interesting mixing condition because it encompasses two limiting cases: 1) it comprises extremes in composition where one component is present in trace quantities while the main component is present in nearly pure form; 2) it also comprises systems where components have vastly different glass transition temperatures; plasticizers are liquid diluents, used not only well above their
Tg, but well above their melting temperature. It is common practice to apply predictive equations of the type of Equation 1 for estimating the effect of plasticizers on the glass transition of amorphous materials. The process involves plugging in the
Tg values of the pure components and the corresponding weighing parameters (toward the value of
k in the expression) into the chosen rendition of Equation 1. This straightforward practice bears nonetheless rather bold assumptions regarding items 1) and 2) above, thus raising an intriguing question: how does a plasticizer “know” its
Tg? The glass transition is a supramolecular process; it involves cooperative rearranging regions acting through the concerted participation of increasingly large groups of molecules as the
Tg is approached [
27]. If the plasticizer is present at very small concentrations and we plug in its
Tg and corresponding
k-related parameters into Equation 1, it is hard to say that we are not implicitly assuming that a highly dilute solvent operates through cooperative regions of the same size and character as when pure. Moreover, consider the common situation where the plasticizer used is well above its melting temperature. By plugging in pure-component parameters into Equation 1, we are implicitly assuming that supramolecular information pertaining to the vitrification of the pure liquid diluent, somehow extrapolates intact, across wide temperature ranges, including the melting transition, and high dilution factors. The same type of question can be posed in practical terms by comparing the predicted effect of two plasticizers, one that is a glass former and one that is not. From predictive schemes based on Equation 1, it is not possible to tell what would be the plasticizing effect of a liquid diluent if it is not a glass former.
The analysis presented in the previous section can be applied to the effect of liquid diluent on the glass transition of an amorphous material. Consider a system where small concentrations of a liquid diluent are mixed with an amorphous material. We will assume that
i) the liquid of interest and the plasticizer give place to an athermal mixture and
ii) that the amount of plasticizer is small enough not to produce any appreciable change in the heat capacity of the major component. This situation is depicted in
Fig. 6, where addition of a small amount plasticizer increases the configurational entropy the accessible to the liquid by
. It should be pointed out that the drawing in
Figure 6 has been simplified, showing only
, which determines the magnitude of the change in
Tg. However, the exact same arguments regarding the partitioning of the entropy of mixing presented in
Figure 3, apply without change to the case illustrated in
Figure 6. The effect of
is illustrated with the shift of the liquid line from the original dashed line (line I) to line II in
Figure 6. The liquid lines are drawn parallel to each other, depicting no appreciable change in heat capacity. The glass transition temperature of the plasticized material is the point where the liquid and glass lines (II and III) meet. When a plasticizer is present, the configurational entropy of mixing has the effect of shifting the
Tg to a new value denoted as
, such that the configurational entropy accessible to the plasticized liquid mixture is
where the subscript
M denotes mixture (as opposed to mixing). The configurational entropy accessible to the liquid
mixture has two sources. One is the thermal component represented by the first term on the right hand side of Equation 20. The other is (
), which originates from the mixing process. It is readily seen that the effect of shifting the liquid line upwards by the quantity
, has the effect of lowering the position of the glass transition. The glass transition of the plasticized material will occur when the kinetically accessible configurational entropy is consumed by cooling it to a temperature
,
i.e., when
the above expression relates the glass transition temperatures of the plasticized (
) and unplasticized (
Tg) material. Form Equation 21, the following relationship is obtained
Figure 6.
The plasticizer effect. Addition of a plasticizer increases the configurational entropy accessible to the liquid by the amount . Line I represents the pure liquid, line II the liquid-plasticizer mixture, line III represents the glass. Upon cooling, the glass transition is shifted to the temperature
, the point where lines II and III meet.
Figure 6.
The plasticizer effect. Addition of a plasticizer increases the configurational entropy accessible to the liquid by the amount . Line I represents the pure liquid, line II the liquid-plasticizer mixture, line III represents the glass. Upon cooling, the glass transition is shifted to the temperature
, the point where lines II and III meet.
Equations 18 and 22 are mathematically equivalent. The difference is that the former reflects the glass transition temperature expected as two glass formers contribute on equal basis toward the glass forming properties of the mixture. In contrast, Equation 22 corresponds to the limiting case where the observed glass transition reflects the Tg of the major component in the mixture while the minor component simply acts as a modifier. According to Equation 22, a plasticizing liquid present at very low concentrations acts as a modifier of the major component, whether the plasticizing liquid is itself a glass former or not.