Calculation of Differential Entropy for a Mixed Gaussian Distribution

Abstract

In this work, an analytical expression is developed for the differential entropy of a mixed Gaussian distribution. One of the terms is given by a tabulated function of the ratio of the distribution parameters.

1. Introduction

The concept of entropy for a random process was introduced by Shannon [1] to characterize the irreducible complexity in a particular process beyond which no compression is possible. Entropy was first formulated for discrete random variables, and was then generalized to continuous random variables in which case it is called differential entropy. By definition, for a continuous random variable X with probability density function p(x), the differential entropy is given by

$$h(X)=-{{\displaystyle \int }}_{S}p(x)\log \left(p(x)\right)dx$$

(1)

where S = {x|p(x) > 0} is the support set of X. The log function may be taken to be log₂, and then the entropy is expressed in bits; or as ln, in which case the entropy is in nats. We shall use the latter convention for the computations in this paper.

Textbooks (e.g. Cover & Thomas [2]) which discuss the concept of entropy often do not provide analytic calculations of differential entropy for many probability distributions; specific cases are usually limited to the uniform and Gaussian distributions. Cover & Thomas [2], (pg. 486-487) does provide a table of entropies for a large number of the probability density functions usually listed in a table of statistical distributions. This table was extracted from a paper by Lazo & Rathie [3]. In addition, a very detailed computation of these entropies may be found in Michalowicz et al. [4]. (Note: There are two typographical errors in the Cover & Thomas list; please double check by using the other two references, both of which have the correct formulas).

In this paper we calculate the differential entropy for a case not appearing in the lists cited above; namely, for a mixed Gaussian distribution with the probability density function

$$p(x)=\frac{1}{2\sqrt{2\pi }\sigma }\left[e^{-(x-\mu {)}^2/2{\sigma }^2}+e^{-(x+\mu {)}^2/2{\sigma }^2}\right]-\infty <x<\infty$$

(2)

Clearly this distribution is obtained by just splitting a Gaussian distribution N (0, σ²) into two parts, centering one half about +µ and the other about −µ and summing the resultants. Such a density function is depicted in Figure 1. This distribution has a mean of zero and a variance given by ${\sigma }_{mg}^2$ = σ² + µ². This is because the second moment of the mixed Gaussian is 1/2 the sum of the second moments for the Gaussian components, each of which is σ² + µ². It can also be written in the more compact form

$$p(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-(x+\mu {)}^2/2{\sigma }^2}\cosh (\mu x/{\sigma }^2).$$

(3)

The mixed Gaussian distribution is often considered as a noise model in a number of signal processing applications. This particular noise model is used in describing co-channel interference, for example, where thermal, Gaussian distributed noise is combined with man-made “clutter” e.g., signals from communication systems [5]. Wang and Wu [6] considered a mixed-Gaussian noise model in a nonlinear signal detection application. Mixed Gaussian noise was also used for modeling purposes in Tan et al. [7]. Additional works on mixed Gaussian noise include that of Bhatia and Mulgrew [5], who looked at a non-parametric channel estimator for this type of noise, and Lu [8], who looked at entropy regularized likelihood learning on Gaussian mixture models. It has also been demonstrated that entropy-based parameter estimation techniques (e.g. mutual information maximization) are of great utility in estimating signals corrupted by non-Gaussian noise [9, 10], particularly when the noise is mixed-Gaussian [11]. However, these works relied on non-parametric estimation of signal entropy due to the absence of a closed-form expression. Our work is therefore aimed at providing an analytical expression for signal entropy in situations where the corrupting noise source is mixed-Gaussian.

The calculation of the differential entropy, in terms of nats, proceeds as follows

If we let y = µx/σ² in this integral, the above expression becomes

$$h_e(X)=\ln (\sqrt{2\pi }\sigma )+\frac{{\mu }^2}{{\sigma }^2}+\frac{1}{2}-\frac{1}{\sqrt{2\pi }\sigma }{e}^{-{\mu }^2/2{\sigma }^2}({\sigma }^2/\mu )\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{e}^{-{\sigma }^2{y}^2/2{\mu }^2}\cosh (y)\ln (\cosh (y))dy.$$

(5)

Noting that the integrand is an even function, we obtain

$$h_e(X)=\frac{1}{2}\ln (2\pi e{\sigma }^2)+\frac{{\mu }^2}{{\sigma }^2}-\frac{2}{\sqrt{2\pi }}{e}^{-{\mu }^2/2{\sigma }^2}(\sigma /\mu )\underset{0}{\overset{\infty }{{\displaystyle \int }}}{e}^{-{\sigma }^2{y}^2/2{\mu }^2}\cosh (y)\ln (\cosh (y))dy.$$

(6)

Let α = µ/σ. Then

$$h_e(X)=\frac{1}{2}\ln (2\pi e{\sigma }^2)+{\alpha }^2-\frac{2}{\sqrt{2\pi }\alpha }{e}^{-{\alpha }^2/2}\underset{0}{\overset{\infty }{{\displaystyle \int }}}{e}^{-y/2{\alpha }^2}\cosh (y)\ln (\cosh (y))dy.$$

(7)

The first term is recognized as the entropy in nats of a Gaussian distribution. When µ = 0 (and so α = 0), our distribution reduces to a Gaussian distribution and the entropy reduces to just this first term.

An analytic expression for the integral in Eqn. (7) could not be found. However, there are analytic bounds for the integral term which are derived by noting that

y − ln 2 ≤ ln(cosh(y)) ≤ y ∀ y ≥ 0.

Thus, for the upper bound to the integral term we have

(8)

by means of formula 3.562 (4) in [12], where erf denotes the error function, defined as

$$\mathrm{erf}(z)=\frac{2}{\sqrt{\pi }}\underset{0}{\overset{z}{{\displaystyle \int }}}{e}^{-u^2}du.$$

(9)

Likewise, for the lower bound we have

(10)

by means of formula 3.546 (2) in [12].

Since the integrand in I is always greater than or equal to 0, we know that I ≥ 0, so we can write

$$h_e(X)=\frac{1}{2}\ln (2\pi e{\sigma }^2)+{\alpha }^2-I$$

(11)

where

$$\max (0;{\alpha }^2\mathrm{erf}(\alpha /\sqrt{2})+\sqrt{2/\pi }\alpha e^{-{\sigma }^2/2}-\ln 2)\le I\le {\alpha }^2\mathrm{erf}(\alpha /\sqrt{2})+\sqrt{2/\pi }\alpha e^{-{\sigma }^2/2}$$

for all α = µ/σ ≥ 0.

The graph of I as a function of α is shown in Figure 2, along with the analytic upper and lower bounds. Clearly I converges rapidly to the lower bound as α increases. A tabulation of numerically computed values of I is presented in

Table 1. Tabulated values for I(α) and α² − I

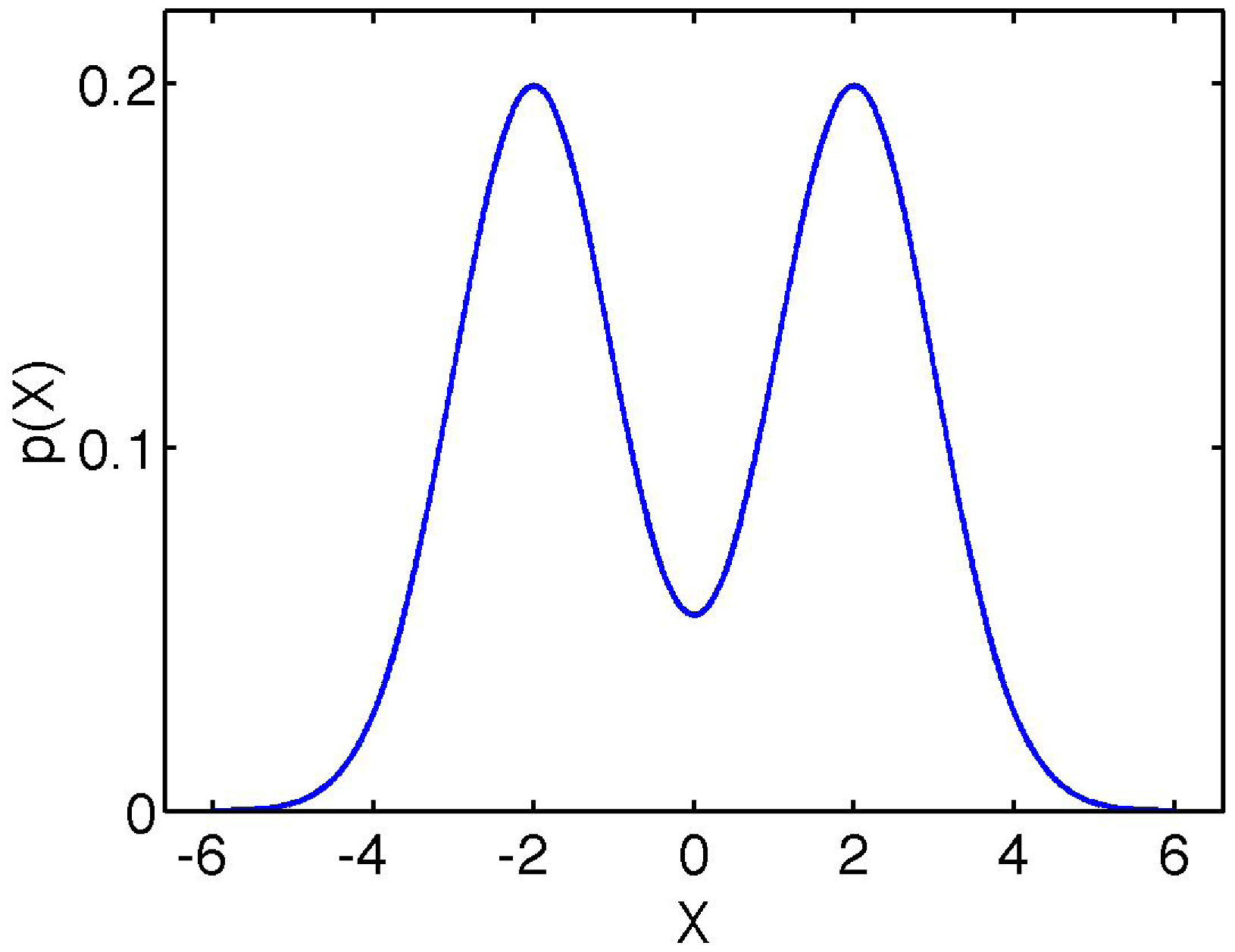
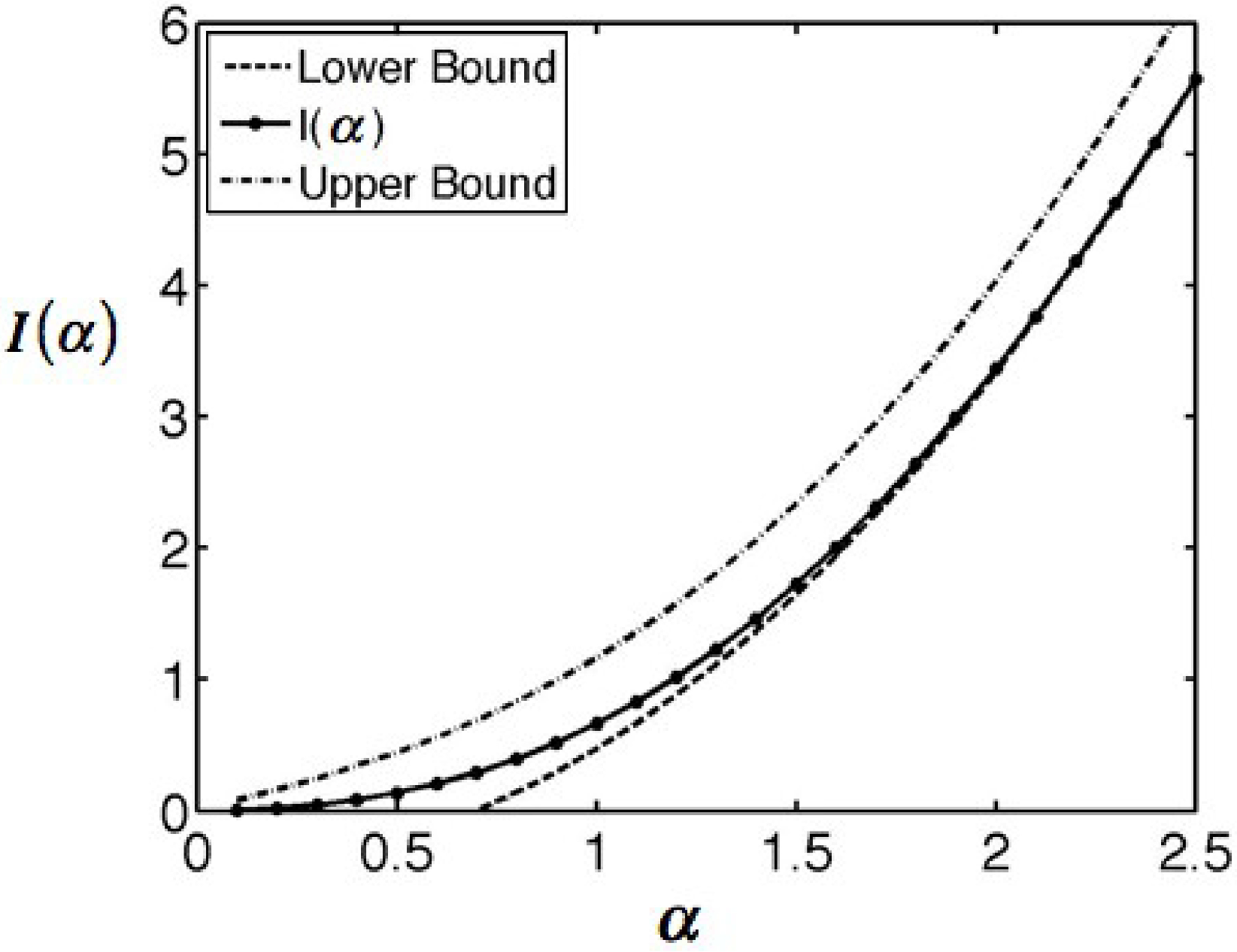
α	I(α)	α2 − I		α	I(α)	α2 − I
0.0	0.000	0.000		(continued)
0.1	0.005	0.005		2.1	3.765	0.645
0.2	0.020	0.020		2.2	4.185	0.656
0.3	0.047	0.043		2.3	4.626	0.664
0.4	0.086	0.074		2.4	5.089	0.671
0.5	0.139	0.111		2.5	5.574	0.676
0.6	0.207	0.153		2.6	6.080	0.680
0.7	0.292	0.198		2.7	6.607	0.683
0.8	0.396	0.244		2.8	7.154	0.686
0.9	0.519	0.291		2.9	7.722	0.688
1.0	0.663	0.337		3.0	8.311	0.689
1.1	0.829	0.381		3.1	8.920	0.690
1.2	1.018	0.422		3.2	9.549	0.691
1.3	1.230	0.460		3.3	10.198	0.692
1.4	1.465	0.495		3.4	10.868	0.692
1.5	1.723	0.527		3.5	11.558	0.692
1.6	2.005	0.555		3.6	12.267	0.693
1.7	2.311	0.579		3.7	12.997	0.693
1.8	2.640	0.600		3.8	13.747	0.693
1.9	2.992	0.618		3.9	14.517	0.693
2.0	3.367	0.633		4.0	15.307	0.693

, together with corresponding values of α² − I. As is clear in the Table, (α² − I) monotonically increases from 0 to ln 2 = 0.6931. Hence the differential entropy, in nats, of a mixed Gaussian distribution, as depicted in Figure 1, can be expressed as

$$h_e(X)=\frac{1}{2}\ln (2\pi e{\sigma }^2)+({\alpha }^2-I)$$

(12)

where (α² − I) is a function of α = µ/σ (tabulated in Table 1) which is equal to zero at α = 0 (in which case the distribution is Gaussian) and monotonically increases to ln 2 as α increases to α > 3.5 (in which case the distribution is effectively split into two separate Gaussians). In particular, if σ = 1, h_e(X) is a monotonically increasing function of µ which has the value 1.419 for µ = 0 and converges to the value 2.112 as µ is increased and the two parts of the mixed Gaussian distribution are split apart.

To express the differential entropy in bits, Eqn. (12) needs to be divided by ln 2, which gives

$$h(X)=\frac{1}{2}{\log }_2(2\pi e{\sigma }^2)+(\frac{{\alpha }^2-I}{\ln 2})$$

(13)

where the second term is a monotonically increasing function of α = µ/σ which goes from 0 at α = 0 to 1 for α > 3.5. In particular, for σ = 1, the differential entropy in bits goes from 2.05 to 3.05 depending on the value of µ; that is, depending on how far apart the two halves of the mixed Gaussian distribution are.

2. Conclusions

This paper calculates the differential entropy for a mixed Gaussian distribution governed by the pa- rameters µ and σ. A closed form solution was not available for one of the terms, however, this term was calculated numerically and tabulated, as well as estimated by analytic upper and lower bounds. For µ = 0 the entropy corresponds to the entropy for a pure Gaussian distribution; it monotonically increases to a well-defined limit for two well-separated Gaussian distribution halves (µ >> 0). Parameter estimation techniques based on information theory are one area where such calculations are likely to be useful.