Entropic Behavior of Binary Carbonaceous Mesophases
Abstract
:1. Introduction
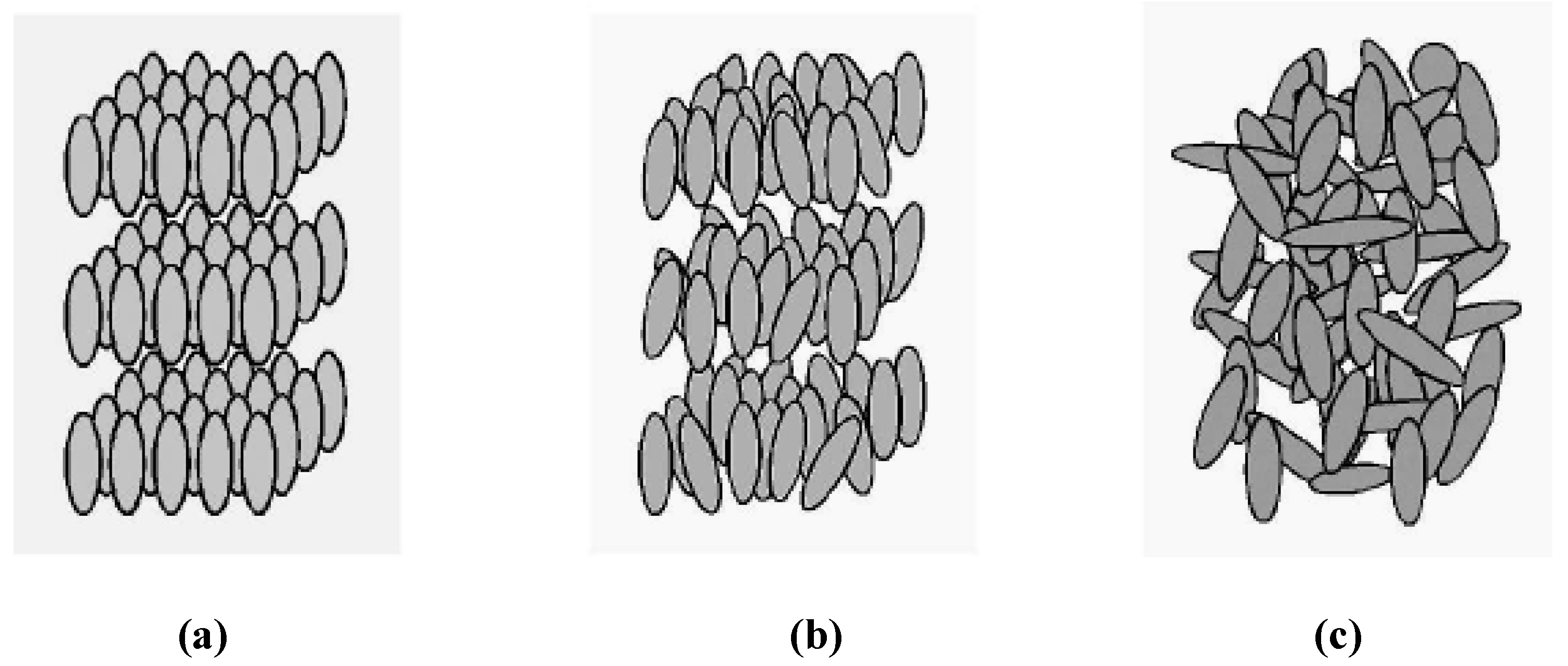
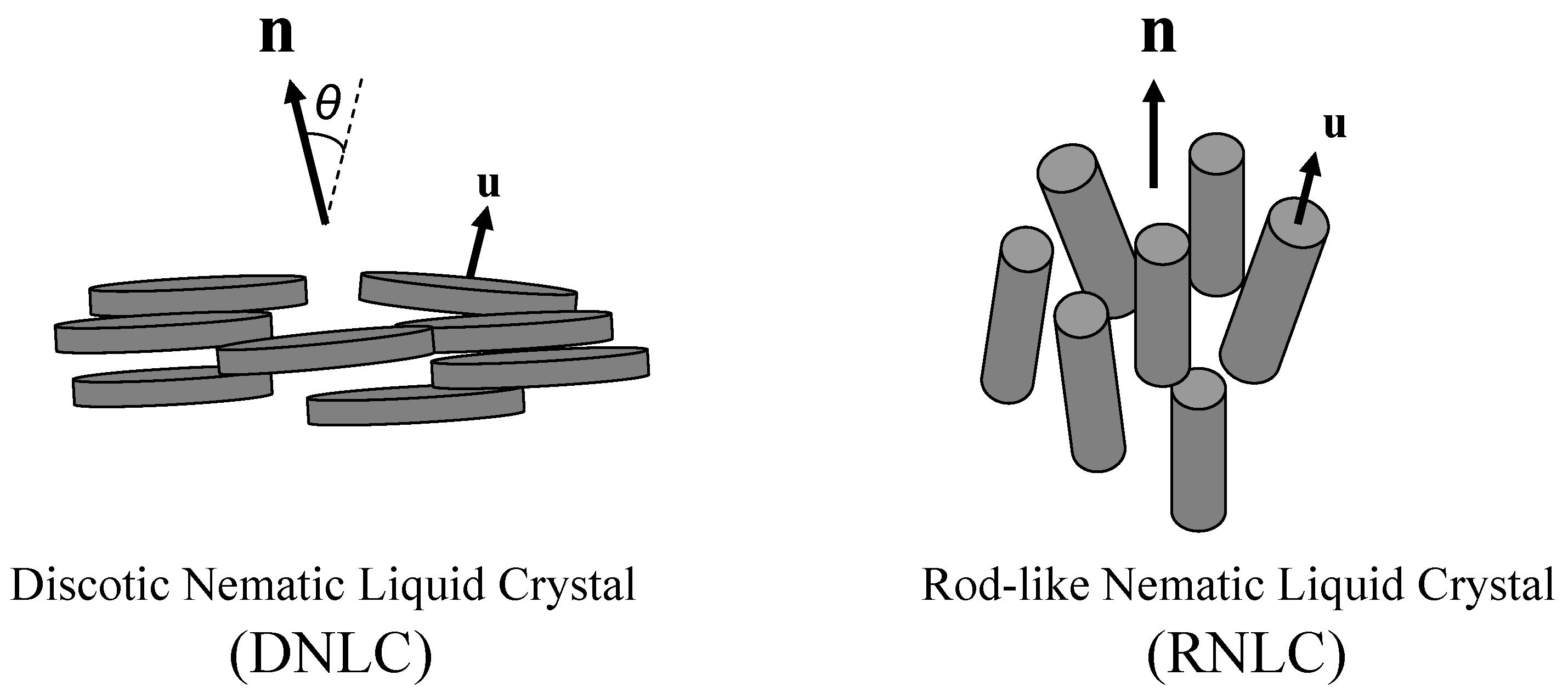
- (i)
- isotropic (I) : s1 = 0, s2 = 0.
- (ii)
- nematic (N12) with s1 ≥ s2.
- (iii)
- nematic (N21) with s1 ≤ s2.
- (i)
- To determine the entropic behavior of ideal and non-ideal mixtures.
- (ii)
- To calculate heat capacities of the two types of mixtures.
- (iii)
- To determine their entropic variation at transition.
2. Maier-Saupe Binary Mixture Model
3. Specific Heat
4. Results and Discussion
- (i)
- NI transition temperature:
- (ii)
- scalar order parameter in the N phase at transition: sNI = 0.4289
- (iii)
- Latent heat at the NI transition:
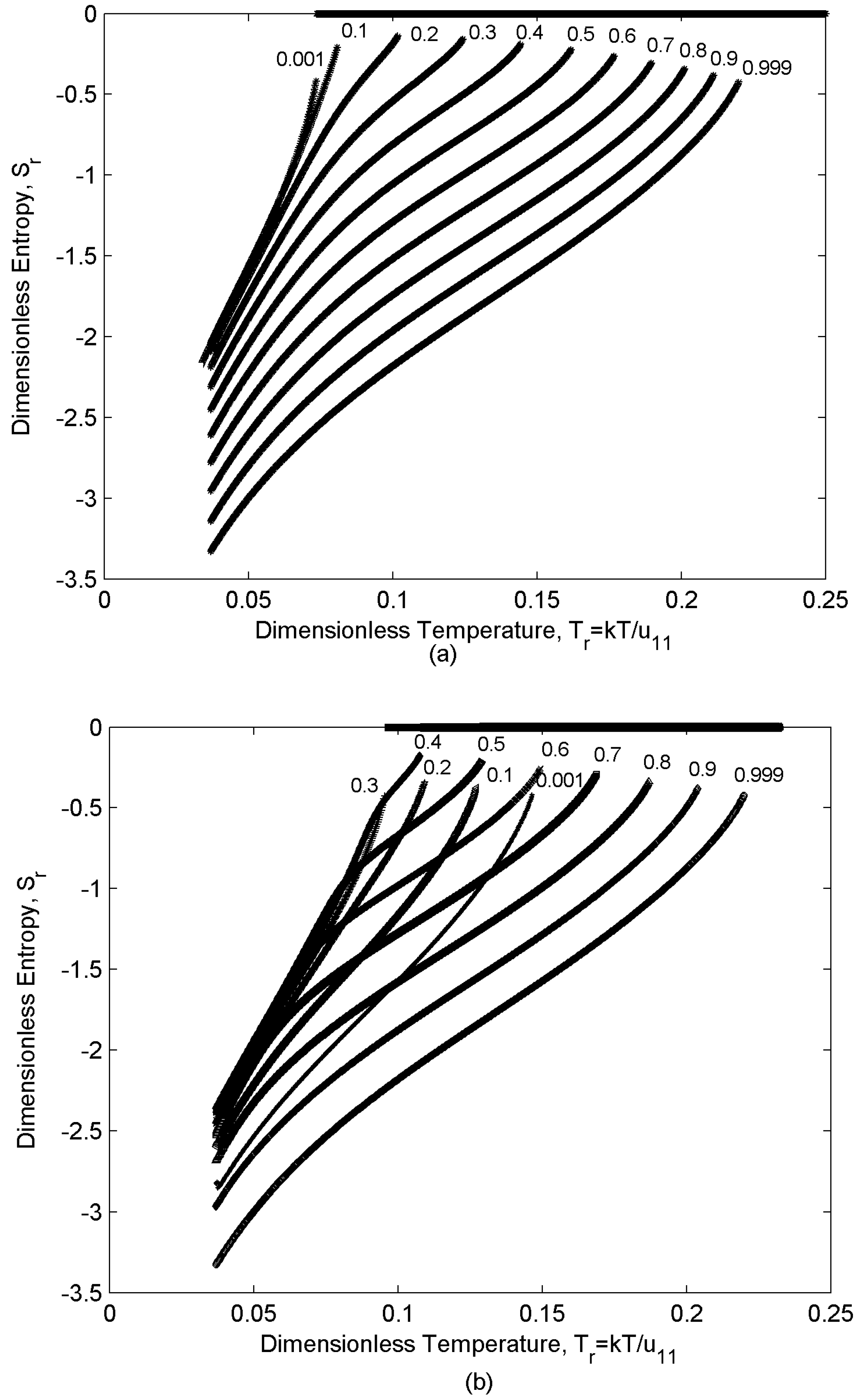
4.1. Entropic Behavior
- (i)
- For any given concentration, entropy increases monotonically with increasing temperature (Figure 5).
- (ii)
- For any given temperature, entropy increases with decreasing concentration: component “1” has higher Mw, so it is more ordered in the nematic range. Therefore, as the concentration m1 increases the mixture ordering increases and entropy decreases.
- (iii)
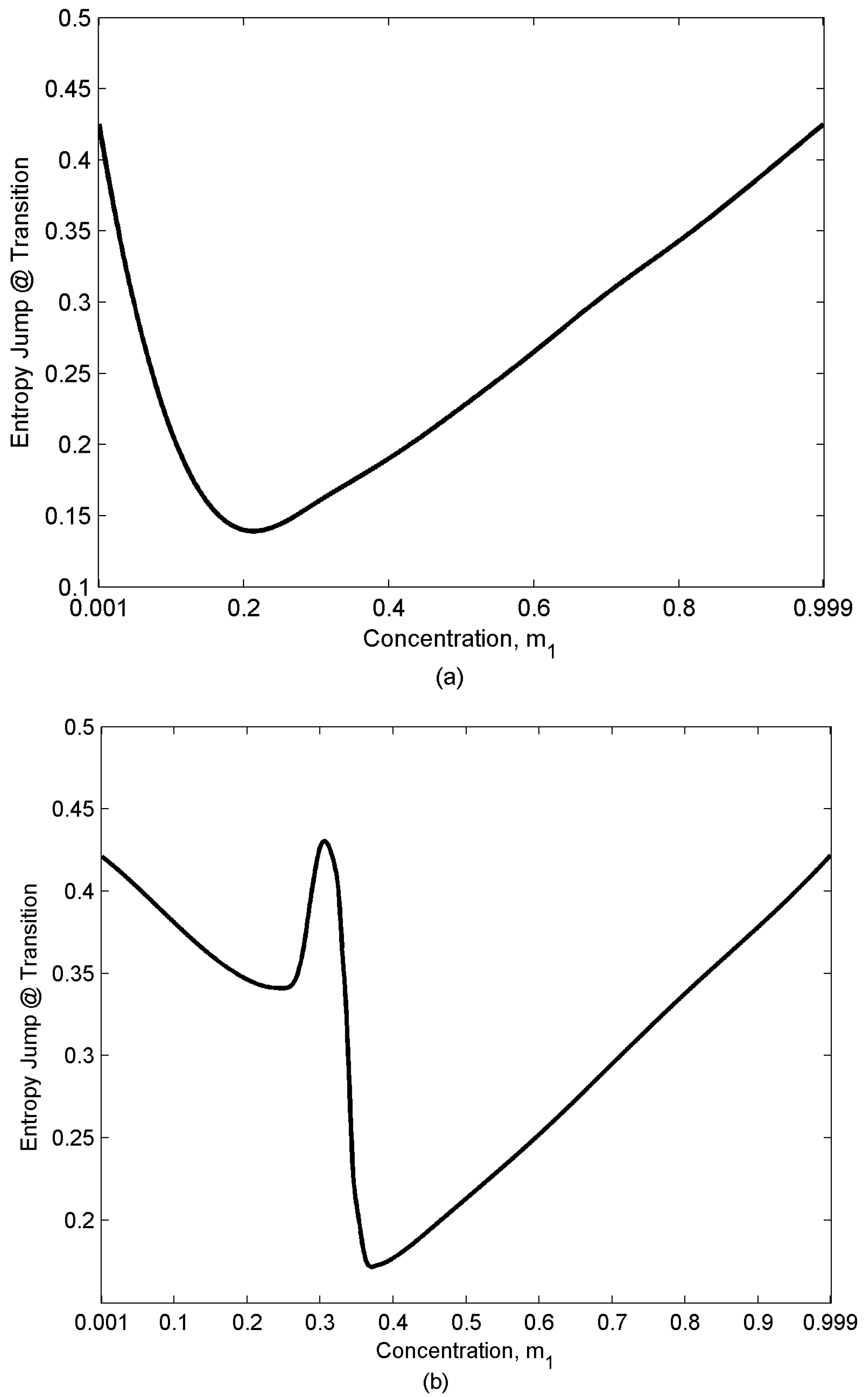
- Entropy jumps at the nematic-isotropic first order phase transition that sets in at temperature TNI (the entropy of the isotropic phase is assumed to be zero; as a result, this entropy represents the orientational entropy); the entropy jump value which is defined as (entropy of the isotropic phase) – (entropy of the nematic phase) at NI transition temperature for the almost pure mixtures (m1 = 0.001,0.999) are essentially the universal value , and mixing just decreases the magnitude of jump.
- (iv)
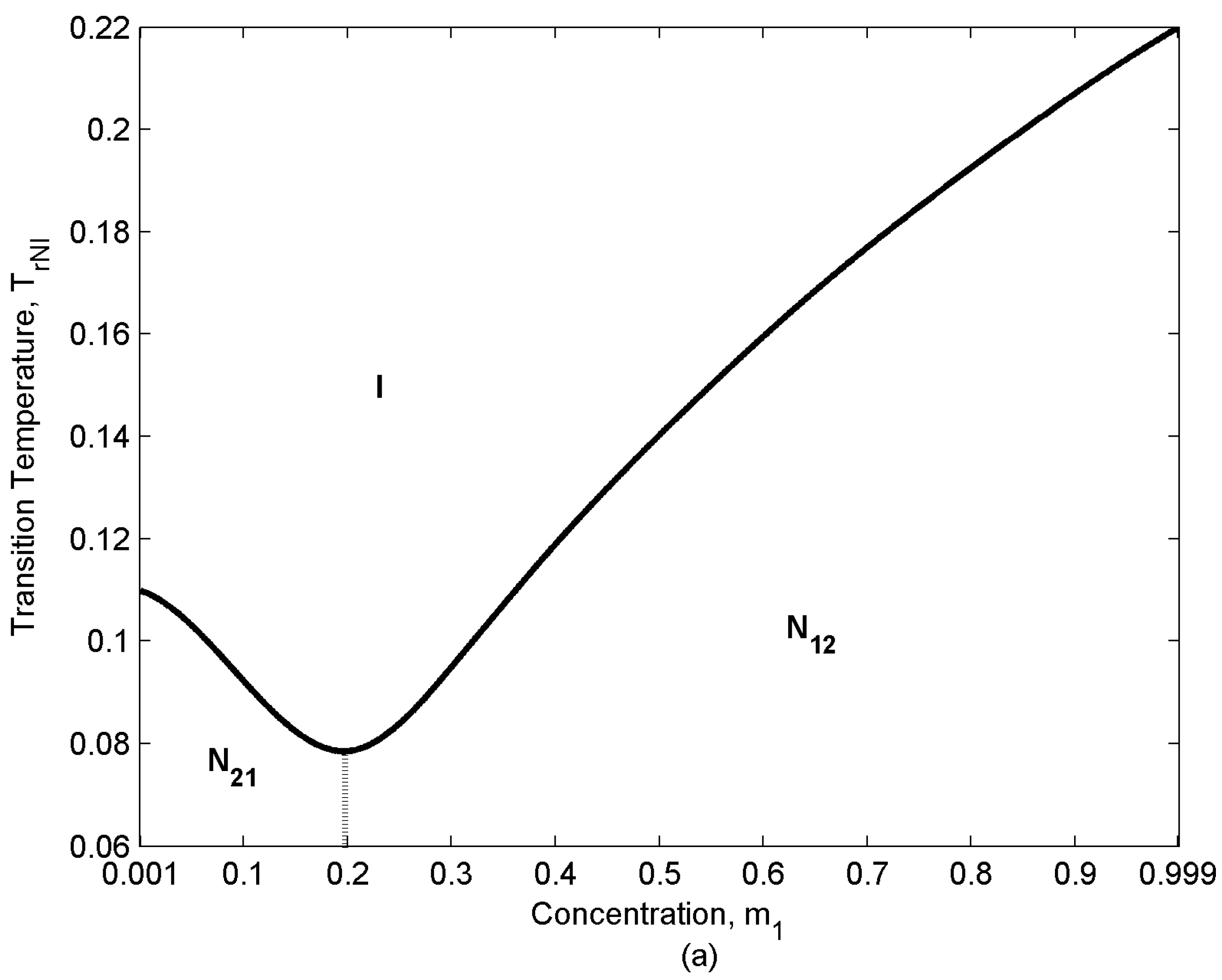
- Depending on the relative population of two components there are three distinct concentration regions: (i) m1 [0-0.1], (ii) m1 [0.2-0.3], (iii) m1 [0.4-1]. The rate of entropy change (δSr/δTr) which corresponds to the rate of ordering change in the mixture shows a rapid decrease in region (ii). Component “2” has lower Mw; as a result, it has a lower TNI (eqn.10). Therefore, while component “1” tends to remain nematic (N12 state), component “2” tends to transform to the isotropic (I) state and lose the ordering, though due to the interaction between the components it retains a low nematic ordering. As a result, when approaching the NI transition temperature of “2” the rate of ordering change in this component decreases and because of eqn.(2) the overall rate of change in the mixture decreases. The appearance of the inflection point in the graphs corresponds to this change in the rate of entropy trend. This phenomenon becomes enhanced when the relative concentrations of both components are significant (region (ii) m1 [0.2-0.3]).
- (i)
- Like the ideal case increasing the temperature decreases the ordering and increases the entropy (Figure 3) of all the mixtures.
- (ii)
- Unlike the ideal case, the effect of concentration on the ordering and entropy is different at different temperatures, increasing concentration does not necessarily decreases the entropy. The following three distinctive dilution regions arise: (i) m1 [0-0.3], (ii) m1 [0.4-0.6], (iii) m1 [0.7-1]. Region (i) is located in N21 state (s2 > s1) of the phase diagram (lower left region in Figure 3); in this region the lower molecular weight species “2” is the majority component. Therefore, increasing m1, dilutes the mixture, decreases the ordering and increases the entropy (Figure 5). The second and the third regions, both are located in N12 state (s1 > s2); therefore, the trend is opposite. As component “1” is dominant in this region, increasing its concentration makes the mixture more ordered and decreases the entropy.
- (iii)
- there is a difference between region (ii) and region (iii). Like the ideal case, the rate of entropy change (δSr/δTr) in the mixture shows a rapid decrease in region (ii). When approaching the NI transition temperature of “2” the rate of ordering change in this component decreases; as a result, the overall rate of change in the mixture decreases [eqn. (2)]. This phenomenon becomes enhanced in the region (ii), where m1 = [0.4-0.6] and the concentration of both components is significant.
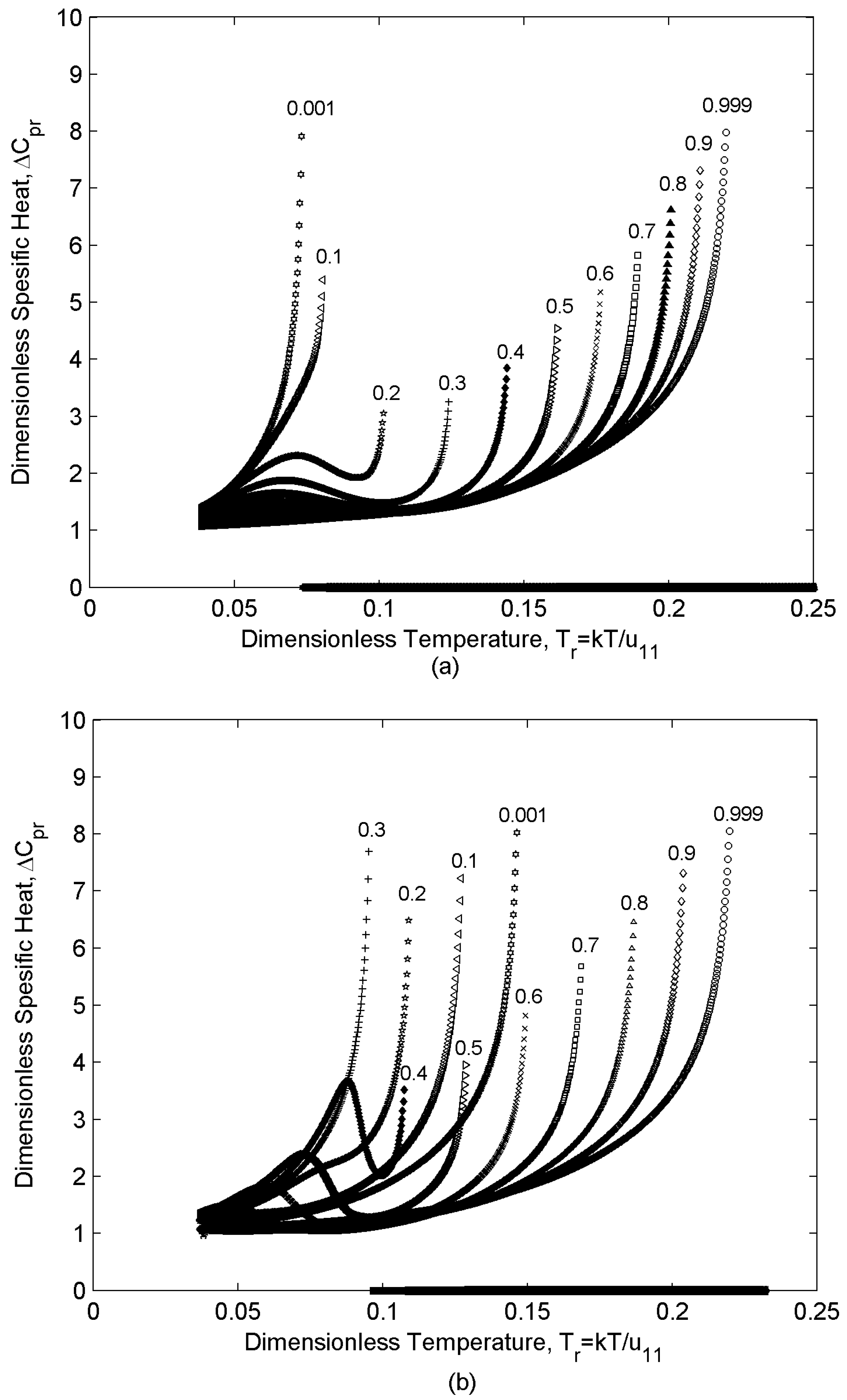
4.2. Specific Heat
- (i)
- At any given temperature, increasing the concentration decreases the ordering and increases the specific heat.
- (ii)
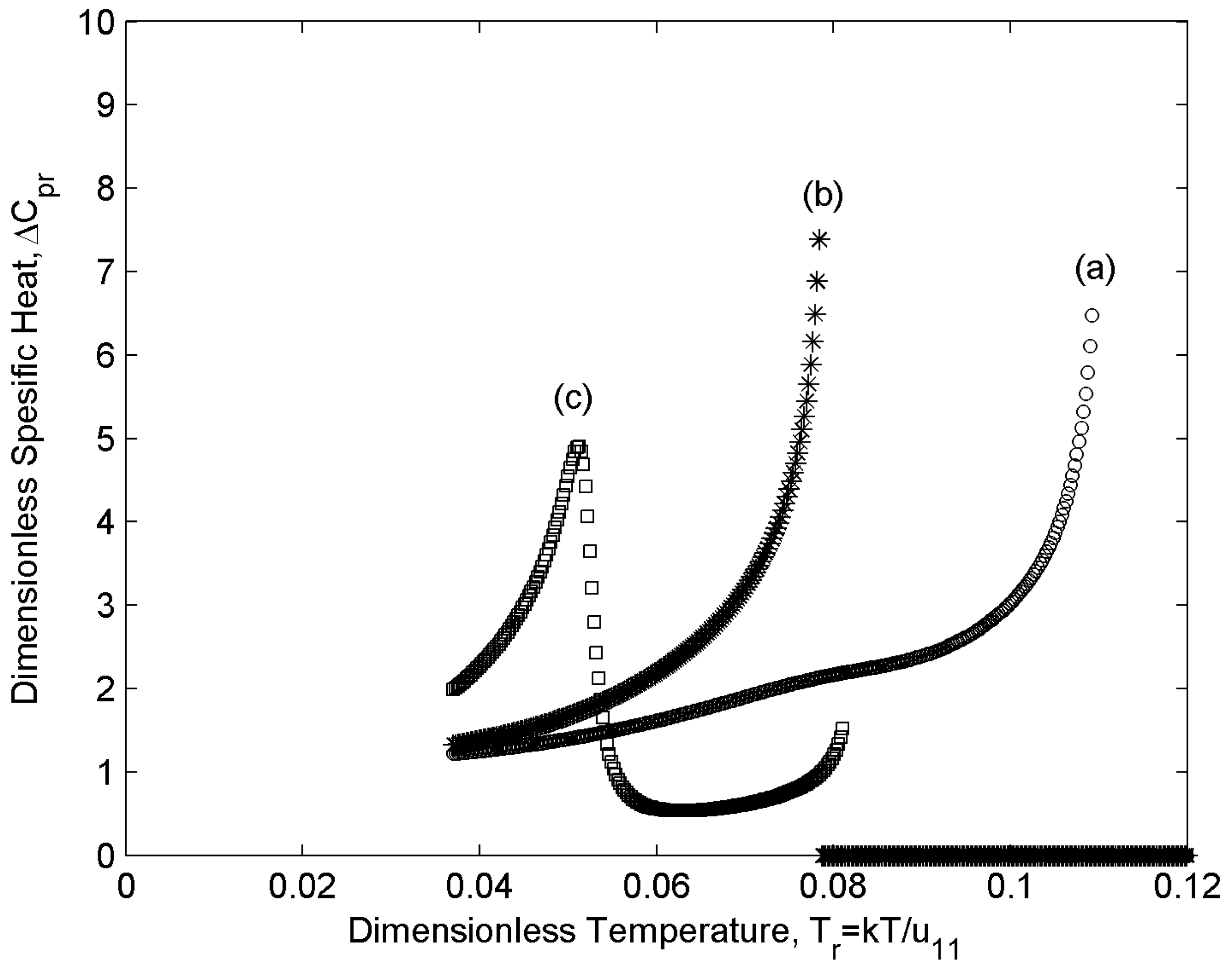
- By sweeping over temperature, specific heat behaves differently for different concentrations. Depending on the concentration region ((i) m1 [0-0.1], (ii) m1 [0.2-0.3], (iii) m1 [0.4-1] , (see Section 4.1) two different trends are observed in the specific heat values versus temperature: in region (i) and (iii), when the population of one of the components is insignificant, and (δSr/δTr) changes monotonically, specific heat increases monotonically with temperature; however, in region (ii), where m1 = [0.2-0.3], specific heat increases by increasing temperature and then it shows a decrease which is followed by another increase. As mentioned in section 3, the non-monotonicity of the specific heat is due to the direct contributions of the Tr and (δSr/δTr) to its value. According to section 4.1 (δSr/δTr) in region (ii) shows a rapid decrease in the vicinity of TNI of component “2”; as a result, ΔCpr decreases in this range. On the other hand, increasing temperature increases ΔCpr; as a result, a minimum appears in the ΔCpr as a function of temperature.
- (i)
- A transition is observed in ΔCpr trend vs. concentration. This transition takes place at the critical concentration where N21→ N12. Region (i) is located in N21 where increasing m1 decreases the ordering and increases ΔCpr; however, regions (ii) and (iii) are both located in N12 where increasing m1 increases the ordering and decreases ΔCpr.
- (iii)
- Depending on the concentration region ((i) m1 [0-0.3], (ii) m1 [0.4-0.6], (iii) m1 [0.7-1], (see Section 4.1) two different trends are observed in the specific heat values versus temperature: in region (i) and (iii), when the effect of one of the components is weak, (δSr/δTr) changes monotonically and specific heat increases monotonically with temperature; however, in region (ii), where m1 = [0.4-0.6] and hence essentially no majority component, (δSr/δTr) changes non-monotonically (section 4.2). As (δSr/δTr) has a contribution to the specific heat values, ΔCpr exhibits a minimum vs. temperature in this region (see section 3).
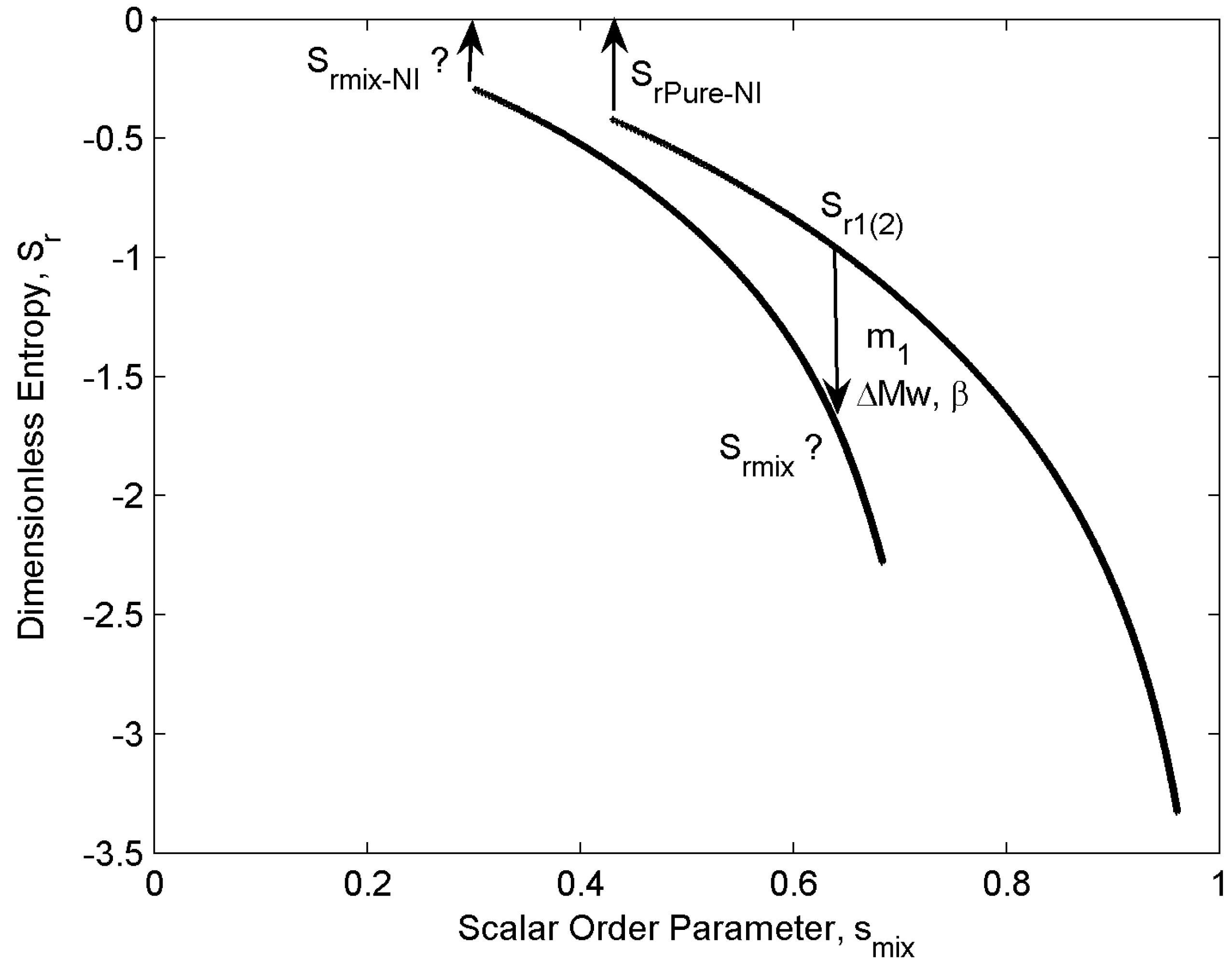
4.3. Entropy Jump at Transitions
5. Conclusions
Acknowledgements
References
- Golmohammadi, M.; Rey, A.D. A thermodynamic model for binary carbonaceous mesophases. J. Chem. Phys. 2008. (submitted). [Google Scholar]
- van der Veen, J.; de Jeu, W.H.; Wannlnkhof, M.W.M.; Tlenhoven, C.A.M. Transition entropies and mesomorphic behavior of para-distributed azoxy benzenes. J. Phys. Chem. 1973, 77, 2153–2155. [Google Scholar] [CrossRef]
- Hwang, D.K. Computational optical science of textured liquid crystals for biosensors, rheooptics, and carbon composites. PhD Thesis, McGill University, Montreal, Canada, 2006; p. 7. [Google Scholar]
- Rey, A.D. Capillary models for liquid crystal fibers, membranes, films, and drops. Soft Matter 2007, 3, 1349–1368. [Google Scholar] [CrossRef]
- Singer, L.S. The mesophase in carbonaceous pitches. Faraday Discuss. 1985, 79, 265–272. [Google Scholar] [CrossRef]
- Dubois, J.; Agache, C.; White, J.L. The carbonaceous mesophase formed in the pyrolysis of graphitizable organic materials. Mater. Charact. 1997, 39, 105–137. [Google Scholar] [CrossRef]
- Marsh, H. Carbonization and liquid-crystal (mesophase) development: Part 1. The significance of the mesophase during carbonization of coking coals. Fuel 1973, 52, 205–212. [Google Scholar] [CrossRef]
- Gupta, G.; Rey, A.D. Texture rules for concentrated filled nematics. Phys. Rev. Lett. 2005, 95, 127802:1–127802:4. [Google Scholar] [CrossRef]
- Edie, D.D.; Robinson, K.E.; Fleurot, O.; Jones, S.P.; Fain, C.C. High thermal conductivity ribbon fibers from naphthalene-based mesophase. Carbon 1994, 32, 1045–1054. [Google Scholar] [CrossRef]
- Hurt, R.H.; Hu, Y. Thermodynamics of carbonaceous mesophase. Carbon 1999, 37, 281–292. [Google Scholar] [CrossRef]
- Yoon, S.H.; Korai, Y.; Mochida, I. Spinning characteristics of mesophase pitches derived from naphthalene and methylnaphthalene with HF/BF3. Carbon 1993, 31, 849–856. [Google Scholar] [CrossRef]
- Naggapa, S.; Nataraju, S.K.; Marthandappa, M. Order parameter of mixtures of nematic compounds. Mol. Cryst. Liq. Cryst. 1991, 197, 15–20. [Google Scholar] [CrossRef]
- Rey, A.D.; Denn, M.M. Dynamical phenomena in liquid crystalline materials. Annu. Rev. Fluid Mech. 2002, 34, 233–266. [Google Scholar] [CrossRef]
- Yan, J.; Rey, A.D. Texture formation in carbonaceous mesophase fibers. Phys. Rev. E. 2002, 65, 031713:1–031713:14. [Google Scholar] [CrossRef]
- Yan, J.; Rey, A.D. Theory and simulation of texture formation in mesophase carbon fibers. Carbon 2002, 40, 2647–2660. [Google Scholar] [CrossRef]
- Hong, S.; Chan, P.K. Computational study of the texture formation in mesophase pitch-based carbon fibers. Liq. Cryst. 2006, 33, 295–306. [Google Scholar] [CrossRef]
- Hong, S.; Chan, P.K. Structure development and texture formation in carbonaceous mesophase fibers. Comput. Mater. Sci. 2006, 36, 310–318. [Google Scholar] [CrossRef]
- Sori, M. Calorimetric measurments in nematics. In Physical properties of liquid crystals: nematics; Dunmur, D.A., Fukuda, A., Luckhurst, G.R., Eds.; INSPEC: London, UK, 2001; pp. 14–50. [Google Scholar]
- Alapati, P.R.; Saran, D. An investigation of smectic a-nematic and nematic-isotropic phase transitions. Phys. Stat. Sol. B 1991, 168, 39–47. [Google Scholar] [CrossRef]
- Naggapa, S.; Mahadeva, J.; Somashekarappa, H.; Somashekar, R. Variation of the entropy of the transition in nemtaic mixtures. Indian J. Phys. A Proc. Indian. Assoc. Cultiv. Sci. 2000, 74A, 45–48. [Google Scholar]
- Grasso, D.; Gandolfo, C.; Fasone, S. Calorimetry of homologous p-n-alkoxybenzyliden-p′-n-pentyloxyanilines. Thermo. Acta. 1984, 77, 413–420. [Google Scholar] [CrossRef]
- Nagappa, S.; Jagadish, K.N.; Mahadeva, J.; Naveenkumar, S.K.; Somashekar, R. Variation of the entropy of the transition in nematic mixtures. Mol. Cryst. Liq. Cryst. 2001, 366, 239–246. [Google Scholar] [CrossRef]
- Stephen, M.J.; Straley, J.P. Physics of liquid crystals. Rev. Mod. Phys. 1974, 46, 617–702. [Google Scholar] [CrossRef]
- L'huillier, d.; Rey, A.D. Liquid crystalline nematic polymers revisited. J. Non-Newtonian Fluid Mech. 2004, 120, 85–92. [Google Scholar] [CrossRef]
- Chhandrasekhar, S. Liquid crystals, 2nd ed.; Cambridge University Press: New York, NY, USA, 1992; pp. 40–45. [Google Scholar]
- Humphrieps, R.L.; James, G.; Luckhurst, G.R. A molecular field treatment of liquid crystalline mixtures. Symp. Faraday Soc. 1971, 5, 107–118. [Google Scholar] [CrossRef]
- Bates, G.S.; Beckmann, P.A.; Burnell, E.E. Deuteron nuclear magnetic resonance and orientational order in binary mixtures of liquid crystals. Mol. Phys. 1986, 57, 351–357. [Google Scholar] [CrossRef]
- Muhoray, P.P.; Dunmur, D.A.; Miller, W.H. Orientational order in binary mixtures of nematic liquid crystals. Liq. Cryst. Ord. Fluids 1984, 4, 615–641. [Google Scholar]
- Muhoray, P.P.; de Bruyn, J.J. Mean field theory of binary mixtures of nematic liquid crystals. Mol. Cryst. Liq. Cryst. 1985, 127, 301–319. [Google Scholar] [CrossRef]
- Hu, Y.; Hurt, R.H. Thermodynamics of carbonaceous mesophase II. General theory for non ideal solutions. Carbon 2001, 39, 887–896. [Google Scholar] [CrossRef]
- Bates, G.S.; Burnell, E.E.; Hoatson, G.L.; Muhoray, P.P.; Weaver, A. Orientational order of rod-and disk-like solutes in the nematic liquid crystal 5CB. Chem. Phys. Lett. 1986, 134, 161–165. [Google Scholar] [CrossRef]
- Cervo, E.G.; Thies, M.C. Control of the molecular weight distribution of petroleum pitches via dense-gas extraction. Chem. Eng. Technol. 2007, 30, 742–748. [Google Scholar] [CrossRef]
- Huebner, K.H.; Dewhirst, D.L.; Smith, D.E.; Byrom, T.G. The finite element methods for engineers, 4th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2001; pp. 61–62. [Google Scholar]
- Prausnitz, J.M.; Lichtenthaler, R.N.; Azevedo, E.G. Molecular thermodynamics of fluid-phase equilibrium; Prentice Hall Inc.: Englewood Cliffs, NJ, USA, 1986; p. 13. [Google Scholar]
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Golmohammadi, M.; Rey, A.D. Entropic Behavior of Binary Carbonaceous Mesophases. Entropy 2008, 10, 183-199. https://doi.org/10.3390/entropy-e10030183
Golmohammadi M, Rey AD. Entropic Behavior of Binary Carbonaceous Mesophases. Entropy. 2008; 10(3):183-199. https://doi.org/10.3390/entropy-e10030183
Chicago/Turabian StyleGolmohammadi, Mojdeh, and Alejandro D. Rey. 2008. "Entropic Behavior of Binary Carbonaceous Mesophases" Entropy 10, no. 3: 183-199. https://doi.org/10.3390/entropy-e10030183
APA StyleGolmohammadi, M., & Rey, A. D. (2008). Entropic Behavior of Binary Carbonaceous Mesophases. Entropy, 10(3), 183-199. https://doi.org/10.3390/entropy-e10030183





