1. Introduction
The objective of this paper is to provide a coherent Bayesian measure of evidence for precise null hypotheses. Significance tests [
1] are regarded as procedures for measuring the consistency of data with a null hypothesis by the calculation of a
p-value (tail area under the null hypothesis). [
2] and [
3] consider the
p-value as a measure of evidence of the null hypothesis and present alternative Bayesian measures of evidence, the Bayes Factor and the posterior probability of the null hypothesis. As pointed out in [
1], the first difficult to define the
p-value is the way the sample space is ordered under the null hypothesis. [
4] suggested a
p-value that always regards the alternative hypothesis. To each of these measures of evidence one could find a great number of counter arguments. The most important argument against Bayesian test for precise hypothesis is presented by [
5]. Arguments against the classical
p-value are full in the literature. The book by [
6] and its review by [
7] present interesting and relevant arguments to the statisticians start to thing about new methods of measuring evidence. In a more philosophical terms, [
8] discuss, in a great detail, the concept of evidence. The method we suggest in the present paper has simple arguments and a geometric interpretation. It can be easily implemented using modern numerical optimization and integration techniques. To illustrate the method we apply it to standard statistical problems with multinomial distributions. Also, to show its broad spectrum, we consider the case of comparing two gamma distributions, which has no simple solution with standard procedures. It is not a situation that appears in regular textbooks. These examples will make clear how the method should be used in most situations. The method is “Full” Bayesian and consists in the analysis of credible sets. By Full we mean that one needs only to use the posterior distribution without the need for any adhockery, a term used by [
8].
2. The Evidence Calculus
Consider the random variable D that, when observed, produces the data d. The statistical space is represented by the triplet
where
is the sample space, the set of possible values of d,
is the family of measurable subsets of
and
is the parameter space. We define now a prior model
, which is a probability space defined over
. Note that this model has to be consistent, so that
turns out to be well defined. As usual after observing data d, we obtain the posterior probability model
, where
is the conditional probability measure on
given the observed sample point,
. In this paper we restrict ourselves to the case where the function
has a probability density function.
To define our procedure we should concentrate only on the posterior probability space
. First we will define
as the subset of the parameter space where the posterior density is greater than
.
The credibility of
is its posterior probability,
where
if
and zero otherwise.
Now, we define
f* as the maximum of the posterior density over the null hypothesis, attained at the argument
,
and define
as the set “tangent” to the null hypothesis,
H, whose credibility is
.
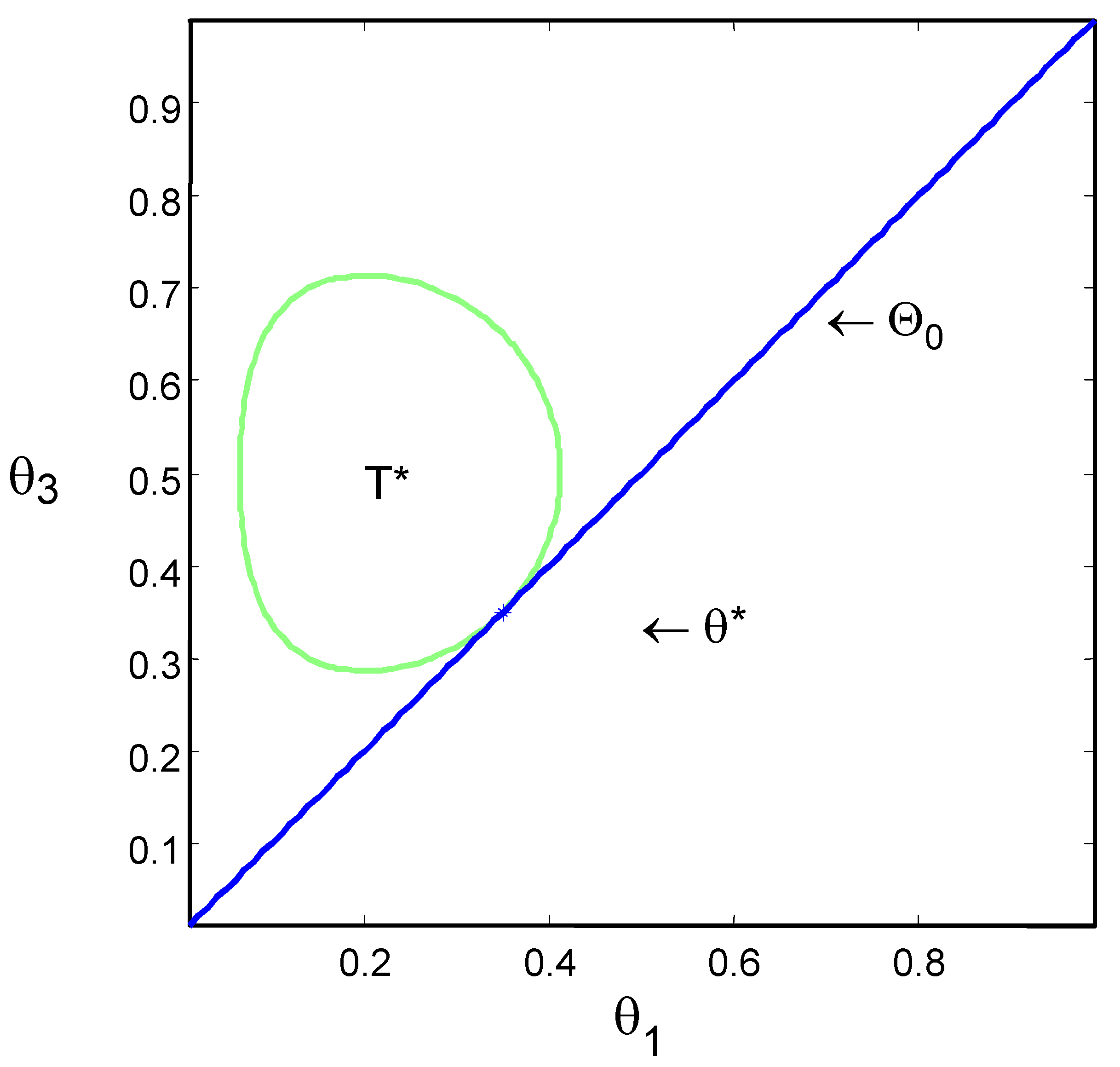
Figure 1 and
Figure 2 show the null hypothesis and the contour of set
T* for Examples 2 and 3 of
Section 4.
The measure of evidence we propose in this article is the complement of the probability of the set
T*. That is, the evidence of the null hypothesis is
If the probability of the set T* is “large”, it means that the null set is in a region of low probability and the evidence in the data is against the null hypothesis. On the other hand, if the probability of T* is “small”, then the null set is in a region of high probability and the evidence in the data is in favor of the null hypothesis.
Although the definition of evidence above is quite general, it was created with the objective of testing precise hypotheses. That is, a null hypothesis for which the dimension is smaller than that of the parameter space, i.e.
.
3. Numerical Computation
In this paper the parameter space,
, is always a subset of
Rn, and the hypothesis is defined as a further restricted subset
. Usually,
is defined by vector valued inequality and equality constraints:
Since we are working with precise hypotheses, we have at least one equality constraint, hence
. Let
be the probability density function for the measure
, i.e.,
The computation of the evidence measure defined in the last section is performed in two steps, a numerical optimization step, and a numerical integration step. The numerical optimization step consists of finding an argument
that maximizes the posterior density
under the null hypothesis. The numerical integration step consists of integrating the posterior density over the region where it is greater than
. That is,
where
if
and zero otherwise.
Efficient computational algorithms are available for local and global optimization as well as for numerical integration in [
9], [
10], [
11], [
12], [
13], and [
14]. Computer codes for several such algorithms can be found at software libraries as NAG and ACM, or at internet sites as
www.ornl.org.We notice that the method used to obtain T* and to calculate
can be used under general conditions. Our purpose, however, is to discuss precise hypothesis testing, under absolute continuity of the posterior probability model, the case for which most solutions presented in the literature are controversial.
4. Examples
In the sequel we will discuss five examples with increasing computational difficulty. The first four are about the Multinomial model. The first example presents the test for a specific success rate in the standard binomial model, and the second is about the equality of two such rates. For these two examples the null hypotheses are linear restrictions of the original parameter spaces. The third example introduces the Hardy-Weinberg equilibrium hypothesis in a trinomial distribution. In this case the hypothesis is quadratic.
Forth example considers the test of independence of two events in a
contingency table. In this case the parameter space has dimension three, and the null hypothesis, which is not linear, defines a set of dimension two.
Finally, the last example presents two parametric comparisons for two gamma distributions. Although straightforward in our paradigm, it is not presented by standard statistical textbooks. We believe that, the reason for this gap in the literature is the non-existence of closed analytical forms for the test. In order to be able to fairly compare our evidence measure with standard tests, like Chi-square tail (pV), Bayes Factor (BF), and Posterior-Probability (PP), we always assume a uniform prior distribution. In these examples the likelihood has finite integral over the parameter space. Hence we have posterior density functions that are proportional to the respective likelihood functions. In order to achieve better numerical stability we optimize a function proportional to the log-likelihood,
, and make explicit use of its first and second derivatives (gradient and Jacobian).
For the 4 examples concerning multinomial distributions we present the following figures (
Table 1,
Table 2, and
Table 3):
Our measure of evidence, Ev, for each d;
the p-value, pV obtained by the
test; that is, the tail area;
the posterior probability of
H,
For the definition of the Bayes Factor and properties we refer to [
8] and [
15].
4.1. Success rate in standard binomial model
This is a standard example about testing that a proportion,
, is equal to a specific value,
p. Consider the random variable,
D being binomial with parameter
and sample size
n. Here we consider
trials,
and
d is the observed success number. The parameter space is the unit interval
. The null hypothesis is defined as
. For all possible values of
d,
Table 1 presents the figures to compare our measure with the standard ones. To compute the Bayes Factor, we consider a priori
and a uniform density for
under the “alternative” hypothesis,
. That is,
Table 1.
Standard binomial model.
Table 1.
Standard binomial model.
| d | Ev | PV | BF | PP |
|---|
| 0 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.00 | 0.00 | 0.00 | 0.00 |
| 3 | 0.00 | 0.00 | 0.02 | 0.02 |
| 4 | 0.01 | 0.01 | 0.10 | 0.09 |
| 5 | 0.02 | 0.03 | 0.31 | 0.24 |
| 6 | 0.06 | 0.07 | 0.78 | 0.44 |
| 7 | 0.16 | 0.18 | 1.55 | 0.61 |
| 8 | 0.35 | 0.37 | 2.52 | 0.72 |
| 9 | 0.64 | 0.65 | 3.36 | 0.77 |
| 10 | 1.00 | 1.00 | 3.70 | 0.79 |
4.2. Homogeneity test in 2× 2 contingency table
This model is useful in many applications, like comparison of two communities with relation to a disease incidence, consumer behavior, electoral preference, etc. Two samples are taken from two binomial populations, and the objective is to test whether the success ratios are equal. Let
x and
y be the number of successes of two independent binomial experiments of sample sizes
m and
n, respectively. The posterior density for this multinomial model is
The parameter space and the null hypothesis set are:
The Bayes Factor considering a priori
and uniform densities over
and
is given in the equation below. See [
16] and [
17] for details and discussion about properties.
Left side of
Table 2 presents figures to compare
Ev(
d) with the other standard measures for
.
Figure 1 presents
H and
T* for
and
with
.
Table 2.
Tests of homogeneity and Hardy-Weinberg equilibrium.
Table 2.
Tests of homogeneity and Hardy-Weinberg equilibrium.
| Homogeneity | Hardy-Weinberg |
|---|
| x | y | Ev | pV | BF | PP | x1 | x3 | Ev | pV | BF | PP |
|---|
| 5 | 0 | 0.05 | 0.02 | 0.25 | 0.20 | 1 | 2 | 0.01 | 0.00 | 0.01 | 0.01 |
| 5 | 1 | 0.18 | 0.08 | 0.87 | 0.46 | 1 | 3 | 0.01 | 0.01 | 0.04 | 0.04 |
| 5 | 2 | 0.43 | 0.21 | 1.70 | 0.63 | 1 | 4 | 0.04 | 0.02 | 0.11 | 0.10 |
| 5 | 3 | 0.71 | 0.43 | 2.47 | 0.71 | 1 | 5 | 0.09 | 0.04 | 0.25 | 0.20 |
| 5 | 4 | 0.93 | 0.71 | 2.95 | 0.75 | 1 | 6 | 0.18 | 0.08 | 0.46 | 0.32 |
| 5 | 5 | 1.00 | 1.00 | 3.05 | 0.75 | 1 | 7 | 0.31 | 0.15 | 0.77 | 0.44 |
| 5 | 6 | 0.94 | 0.72 | 2.80 | 0.74 | 1 | 8 | 0.48 | 0.26 | 1.16 | 0.54 |
| 5 | 7 | 0.77 | 0.49 | 2.31 | 0.70 | 1 | 9 | 0.66 | 0.39 | 1.59 | 0.61 |
| 5 | 8 | 0.58 | 0.31 | 1.75 | 0.64 | 1 | 10 | 0.83 | 0.57 | 2.00 | 0.67 |
| 5 | 9 | 0.39 | 0.18 | 1.21 | 0.55 | 1 | 11 | 0.95 | 0.77 | 2.34 | 0.70 |
| 5 | 10 | 0.24 | 0.10 | 0.77 | 0.43 | 1 | 12 | 1.00 | 0.99 | 2.55 | 0.72 |
| 10 | 0 | 0.00 | 0.00 | 0.00 | 0.00 | 1 | 13 | 0.96 | 0.78 | 2.57 | 0.72 |
| 10 | 1 | 0.00 | 0.00 | 0.02 | 0.02 | 1 | 14 | 0.84 | 0.55 | 2.39 | 0.71 |
| 10 | 2 | 0.01 | 0.01 | 0.07 | 0.06 | 1 | 15 | 0.66 | 0.33 | 2.05 | 0.67 |
| 10 | 3 | 0.05 | 0.02 | 0.19 | 0.16 | 1 | 16 | 0.47 | 0.16 | 1.58 | 0.61 |
| 10 | 4 | 0.12 | 0.05 | 0.41 | 0.29 | 1 | 17 | 0.27 | 0.05 | 1.06 | 0.51 |
| 10 | 5 | 0.24 | 0.10 | 0.77 | 0.43 | 1 | 18 | 0.12 | 0.00 | 0.58 | 0.37 |
| 10 | 6 | 0.41 | 0.20 | 1.23 | 0.55 | 5 | 0 | 0.02 | 0.01 | 0.05 | 0.05 |
| 10 | 7 | 0.61 | 0.34 | 1.74 | 0.63 | 5 | 1 | 0.09 | 0.04 | 0.25 | 0.20 |
| 10 | 8 | 0.81 | 0.53 | 2.21 | 0.69 | 5 | 2 | 0.29 | 0.14 | 0.60 | 0.38 |
| 10 | 9 | 0.95 | 0.75 | 2.54 | 0.72 | 5 | 3 | 0.61 | 0.34 | 1.00 | 0.50 |
| 10 | 10 | 1.00 | 1.00 | 2.66 | 0.73 | 5 | 4 | 0.89 | 0.65 | 1.29 | 0.56 |
| 12 | 0 | 0.00 | 0.00 | 0.00 | 0.00 | 5 | 5 | 1.00 | 1.00 | 1.34 | 0.57 |
| 12 | 1 | 0.00 | 0.00 | 0.00 | 0.00 | 5 | 6 | 0.90 | 0.66 | 1.18 | 0.54 |
| 12 | 2 | 0.00 | 0.00 | 0.01 | 0.01 | 5 | 7 | 0.66 | 0.39 | 0.89 | 0.47 |
| 12 | 3 | 0.01 | 0.00 | 0.04 | 0.04 | 5 | 8 | 0.40 | 0.20 | 0.58 | 0.37 |
| 12 | 4 | 0.03 | 0.01 | 0.10 | 0.09 | 5 | 9 | 0.21 | 0.09 | 0.32 | 0.24 |
| 12 | 5 | 0.07 | 0.03 | 0.24 | 0.19 | 5 | 10 | 0.09 | 0.04 | 0.16 | 0.13 |
| 12 | 6 | 0.14 | 0.06 | 0.46 | 0.32 | 9 | 0 | 0.21 | 0.09 | 0.73 | 0.42 |
| 12 | 7 | 0.26 | 0.11 | 0.80 | 0.44 | 9 | 1 | 0.66 | 0.39 | 1.59 | 0.61 |
| 12 | 8 | 0.42 | 0.21 | 1.24 | 0.55 | 9 | 2 | 0.99 | 0.91 | 1.77 | 0.64 |
| 12 | 9 | 0.62 | 0.34 | 1.73 | 0.63 | 9 | 3 | 0.86 | 0.59 | 1.33 | 0.57 |
| 12 | 10 | 0.81 | 0.53 | 2.21 | 0.69 | 9 | 4 | 0.49 | 0.26 | 0.74 | 0.43 |
| | | | | | | 9 | 5 | 0.21 | 0.09 | 0.32 | 0.24 |
| | | | | | | 9 | 6 | 0.06 | 0.03 | 0.11 | 0.10 |
| | | | | | | 9 | 7 | 0.01 | 0.01 | 0.03 | 0.03 |
Figure 1.
Homogeneity test with ,
and
.
Figure 1.
Homogeneity test with ,
and
.
4.3. Hardy-Weinberg equilibrium law
In this biological application there is a sample of
n individuals, where
x1 and
x3 are the two homozigote sample counts and
is hetherozigote sample count.
is the parameter vector. The posterior density for this trinomial model is
The parameter space and the null hypothesis set are:
The problem of testing the Hardy-Weinberg equilibrium law using the Bayes Factor is discussed in detail by [
18] and [
19].
The Bayes Factor considering uniform priors over
and
is given by the following expression:
Here
is a sufficient statistic under H. This means that the likelihood under H depends on data d only through t.
Right side of
Table 2 presents figures to compare
Ev(
d) with the other standard measures for
.
Figure 2 presents
H and
T* for
,
and
.
4.4. Independence test in a 2× 2 contingency table
Suppose that laboratory test is used to help in the diagnostic of a disease. It should be interesting to check if the test results are really related to the health conditions of a patient. A patient chosen from a clinic is classified as one of the four states of the set
in such a way that
h is the indicator of the occurrence or not of the disease and
t is the indicator for the laboratory test being positive or negative. For a sample of size
n we record
, the vector whose components are the sample frequency of each the possibilities of (
t,
h). The parameter space is the simplex
and the null hypothesis, h and t are independent, is defined by
Figure 2.
Hardy-Weinberg test with ,
and
.
Figure 2.
Hardy-Weinberg test with ,
and
.
The Bayes Factor for this case is discussed by [
17] and has the following expression:
where
,
,
and
.
Table 3.
Test of independence.
Table 3.
Test of independence.
| x00 | x01 | x10 | x11 | Ev | pV | BF | PP |
|---|
| 12 | 6 | 95 | 35 | 0.96 | 0.57 | 4.73 | 0.83 |
| 48 | 25 | 9 | 10 | 0.54 | 0.14 | 1.04 | 0.51 |
| 96 | 50 | 18 | 20 | 0.24 | 0.04 | 0.50 | 0.33 |
| 18 | 5 | 39 | 30 | 0.29 | 0.06 | 0.50 | 0.33 |
| 36 | 10 | 78 | 60 | 0.06 | 0.01 | 0.11 | 0.10 |
4.5. Comparison of two gamma distributions
This model may be used when comparing two survival distributions, for example, medical procedures and pharmacological efficiency, component reliability, financial market assets, etc. Let
and
be samples of two gamma distributed survival times. The sufficient statistic for the gamma distribution is the vector [
n,
s,
p], i.e. the sample size, the observations sum and product. Let
and
, all positive, be these gamma parameters. The likelihood function is:
This likelihood function is integrable on the parameter space. In order to allow comparisons with classical procedures, we will not consider any informative prior, i.e., the likelihood function will define by itself the posterior density.
Table 4 presents time to failure of coin comparators, a component of gaming machines, of two different brands. An entrepreneur was offered to replace brand 1 by the less expensive brand 2. The entrepreneur tested 10 coin comparators of each brand, and computed the sample means and standard deviations. The gamma distribution fits nicely this type of failure time, and was used to model the process. Denoting the gamma mean and standard deviation by
and
, the first hypothesis to be considered is
. The high evidence of
H',
, corroborates the entrepreneur decision of changing its supplier. Note that the naive comparison of the sample means could be misleading. In the same direction, the low evidence of
,
, indicates that the new brand should have smaller variation on the time to failure. The low evidence of H suggests that costs could be further diminished by na improved maintenance policy [
20].
Table 4.
Comparing two gamma distributions.
Table 4.
Comparing two gamma distributions.
| Brand 1 sample |
| 39.27 | 31.72 | 12.33 | 27.67 | 56.66 |
| 28.32 | 53.72 | 29.71 | 23.76 | 33.55 |
| mean1=33.67 | | std1=13.33 |
| Brand 2 sample |
| 28.32 | 53.72 | 29.71 | 23.76 | 33.55 |
| 24.07 | 33.79 | 33.10 | 26.93 | 27.23 |
| mean2=29.25 | | std2=3.62 |
| Evidence |
| | |