Abstract
This paper, the first in a series of four, will expose the lack of inner consistency of the analysis through which Clausius re-expressed the second law of thermodynamics: "Heat cannot, of itself, pass from a colder to a hotter body", as the law of increasing entropy: "The entropy of the universe tends to a maximum". In the two following papers the flaw in Clausius analysis producing the said lack of consistency will be located, corrected and some of its consequences, discussed. Among them the one stating that the identification of the two above written statements of the second law is valid only under certain circumstances. In the fourth and final paper, Clausius arguments of proof will be refuted.
Introduction
Once Clausius enunciated the second main principle of thermodynamics as: "Heat cannot, of itself, pass from a colder to a hotter body" [1], he set himself, with the aid of his results on the study of reversible cyclical processes to… "bring out the second main principle anew in an altered form" [2]. On his way to this objective he summarized the result of a simple reversible cyclical process in the following terms: "Two transformations are produced, a transformation from heat into work (or vice versa) and a transformation from heat of a higher temperature to heat of a lower (or vice versa)" [3], and he further expressed that…"the relation between these two transformations is therefore that which is to be expressed by the Second Main Principle" [2]. The result of this endeavor was by him expressed in terms of what he called The Principle of the Equivalence of Transformations [4]:
Hence, the second main principle of the mechanical Theory of Heat, which in this form may perhaps be called the principle of the Equivalence of Transformations, can be expressed in the following terms: if we call two transformations which may cancel each other without requiring any other permanent change to take place, Equivalent Transformations, then the generation out of work of the quantity of heat Q of temperature τ has the equivalence value Q/τ and the transference of the quantity of heat Q from temperature T1 to temperature T2 has the equivalence valuein which τ is a function of temperature independent of the kind of process by which the transformation is accomplished.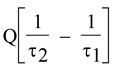
Subsequently and after showing that the combined value of all the transformations occurring in a however complex reversible cyclical process could be reduced to a summation of Q/τ terms [5], and after identifying τ with T, the absolute temperature [6], he arrived, as the final result of his analysis concerning reversible cyclical processes, to the following equation [7]:
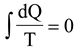 in which the integral is to be taken for all the quantities of heat given off by the different bodies. In words, the above equation can be expressed by saying that in a reversible cyclical process the total value of all the transformations must be equal to nothing .
in which the integral is to be taken for all the quantities of heat given off by the different bodies. In words, the above equation can be expressed by saying that in a reversible cyclical process the total value of all the transformations must be equal to nothing .
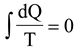
In further likening any decrease in such a quantity to the spontaneous passage of heat from a colder to a hotter body [7], he was able to forward his heralded new form of the second main principle for both reversible and irreversible processes as... "The algebraic sum of all the transformations which occur in a cyclical process must always be positive, or in the limit equal to zero" [7], or more briefly as... "Uncompensated transformations must always be positive" [7]. In terms of the entropy function, S, introduced later on by Clausius and by him defined, for an infinitesimal reversible change as dS = dQ/T [8], the above expression took final form in what is now known as the law of increasing entropy: The entropy of the universe tends to a maximum. Clausius accomplishment however was not so. As it will be in these papers demonstrated the law of increasing entropy can only under certain circumstances be taken as an alternate expression of the second law of thermodynamics. The starting point of the endeavor herein undertaken will be the exposure of the lack of agreement between Clausius principle of the Equivalence of Transformations and current second law thermodynamics, whose structure has the said principle as foundation.
The Nature of the Inconsistency
If Clausius principle of the Equivalence of Transformations is indeed correct then, if in a reversible cyclical process we were able to identify the two transformations therein occurring and also to calculate their values, i.e. the entropy changes to they associated, we would have to find that the transformation into work of an amount of heat Q of temperature Th would have associated an entropy change equal to −Q/Th; while the entropy change associated to the transformation of an amount of heat Q' from temperature Th to temperature Tc would be equal to Q'(Th − Tc)/ ThTc complying these values with the condition that..."in every reversible process of the kind given above the two transformations that take place must be equal in magnitude but of opposite sign, so that their algebraical sum is zero" [9]. We will demonstrate however, through a simple analysis on a reversible cyclical process, that none of the two transformations occurring in the said reversible cyclical process comply with the values required by Clausius principle of the Equivalence of Transformations. This analysis is shown next, and in going through it, it has to be understood that a transformation encompass all the bodies in any way involved in its occurrence. For example, the transformation of heat from high to low temperature, as it occurs in a reversible cyclical process, could not be possible if either the hot reservoir, the cold reservoir or the proper sequence of changes of the variable body were missing. It is the concerted concatenation of changes of each of these bodies what makes possible the occurrence of the said transformation. The value or entropy change of a particular transformation will thus be determined by the contributions associated to the changes each and every body in it participating has to sustain in order to accomplish it. Now, if by the universe of a process we understand the collection of bodies in any way participating in the said process it then follows that a given transformation is a universe in itself, and on this perspective the universe of a simple reversible cyclical process can be thought of as formed by the conjunction of the universes of the two transformations constituting it or vice versa.
Analysis
In what follows, [Q(Th)→ w]rev and [Q'(Th)→ Q'(Th)]rev will represent the two transformations taking part in a simple reversible cyclical process, such as the one depicted in Figure 1 and commonly known as Carnot's ideal gas reversible engine. Thus, [Q(Th)→ w]rev indicates the fact that an amount of heat Q of temperature Th has been reversibly converted into an equivalent amount of work (w), while [Q'(Th)→ Q'(Tc)]rev indicates that an amount of heat Q' has been reversibly transformed from temperature Th to temperature Tc. The entropy changes associated to these transformations will be represented as ΔS[Q(Th)→ w]rev and ΔS[Q'(Th)→ Q'(Tc)]rev , respectively [10].
The analysis to be performed and which will allow the splitting of Carnot's reversible engine universe into its two constitutive transformations will start in the state represented by point A in Figure 1, being this state chosen in such a way that the amount of heat Q' absorbed by the engine's working substance in its isothermal expansion at Th from A to B, be equal to the amount by it released to the cold reservoir during its isothermal compression at Tc from C to D. The first part of the said analysis will concern itself with the entropy change calculations for the processes taking place as the variable body evolves from state A to E.
Process 1. Reversible and isothermal (Th) expansion of the working substance from state A to state B
(a). Entropy change of the working substance: Q'/Th.
(b). Entropy change of the hot reservoir: −Q'/Th.
Net entropy change of process 1: zero.
Process 2. Reversible and adiabatic expansion of the working substance from state B to state C
(a). Entropy change of the working substance: zero.
Net entropy change of process 2: zero.
Process 3. Reversible and isothermal (Tc) compression of the working substance from state C to D
(a). Entropy change of the working substance: Q'/Tc
(b). Entropy change of the cold reservoir: Q'/Tc
Net entropy change of process 3: zero
Process 4. Adiabatic and reversible compression of the working substance from state D to state E
(a). Entropy change of the working substance: zero.
Net entropy change of process 4: zero.
Since at the end of this sequence no other change has taken place but that through which the variable body transfers to the cold reservoir at TC the heat Q’ previously absorbed from the hot reservoir at Th, it thus follows that the said sequence has brought about transformation [Q'(Th)→ Q'(TC)]rev with an entropy change equal to the sum of the entropy changes of processes 1 through 4 which are the ones defining the referred sequence, i.e.
ΔS[Q'(Th)→ Q'(Tc)]rev = 0 (1)
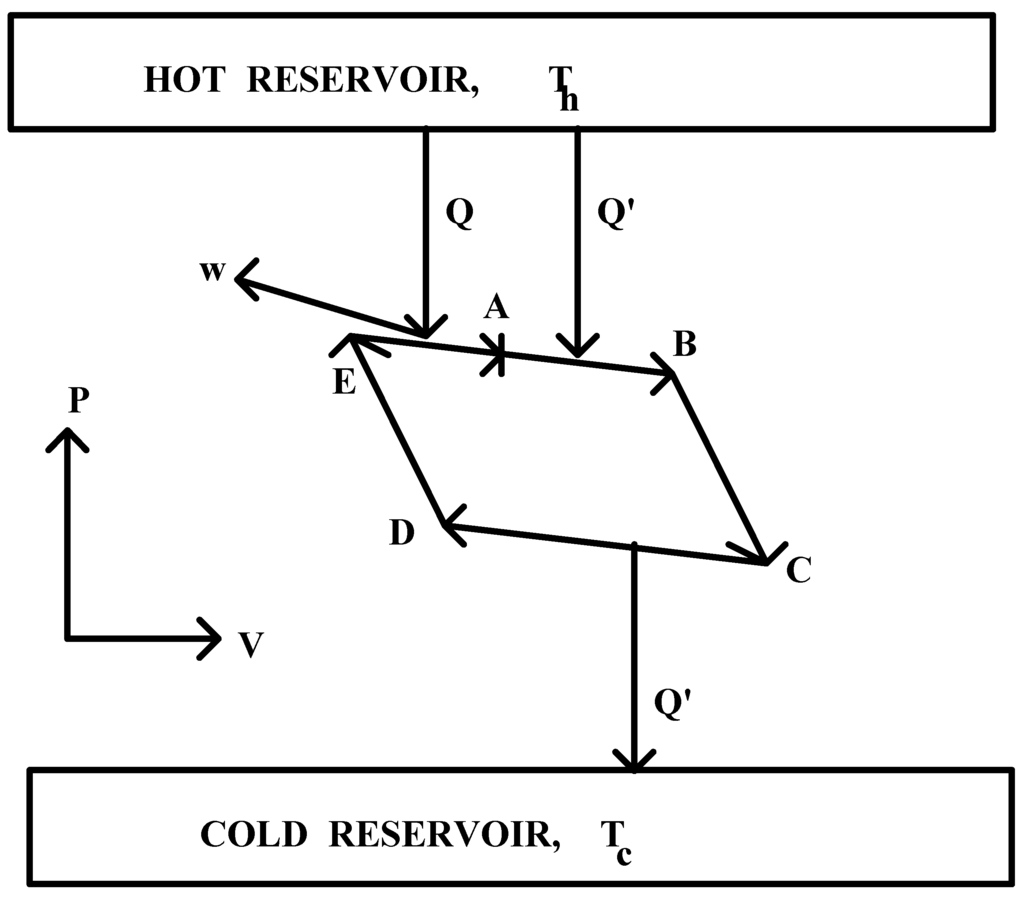
Figure 1.
Splitting of the reversible operation of Carnot's engine into its two constitutive transformations: [Q'(Th)→Q'(TC)]rev and [Q(Th)→w]rev.
It can now be easily seen from Figure 1 that the process required to complete the cycle in the operation of Carnot's reversible engine, i.e. the isothermal and reversible expansion of the working substance from state E to state A, corresponds to transformation [Q(Th)→ w]rev. Through it, an amount of heat Q of temperature Th is quantitatively transformed into work. The entropy change associated to this transformation will be given in the following calculation:
Process 5. Isothermal and reversible expansion of the working substance from state E to state A
(a). Entropy change of the working substance: Q/Th.
(b). Entropy change of the hot reservoir: −Q/Th.
Net entropy change of process 5: zero.
Thus:
ΔS[Q(Th)→ w]rev = 0 (2)
So, the values of the transformations occurring in a reversible cyclical process instead of being:
and
as Clausius principle of the equivalence of transformations demands, they both turn out to be, as eqs. 1 and 2 show, equal to zero.
ΔS[Q'(Th)→ Q'(Tc)]rev = Q'(Th − Tc)/ThTc
ΔS[Q(Th)→ w]rev = −Q/Th
Discussion
Current second law thermodynamics and the methods of analysis to it associated are essentially a product of Clausius work leading to the principle of the equivalence of transformations. However, when the former is used in order to reproduce the basic tenets of the latter, i.e. the values of the transformations associated to a reversible cyclical process, it is found that the values of the transformations obtained are not the ones expected.
A similar situation arises when, at the light of what was above stated regarding a transformation being a universe in itself, a contrast is made between the principle of the equivalence of transformations and the zero entropy change principle. These expressions, as should be recalled, are supposedly equivalent statements of Clausius second main principle of the mechanical theory of heat, as applied to reversible processes. Thus, while the former tells us that the entropy change for the universe of the reversible processes [Q(Th)→w]rev and [Q'(Th)→Q'(Tc)]rev are the non zero quantities respectively represented as −Q/Th and Q'(Th − Tc)/ThTc , the latter affirms that the entropy change for the universe of any reversible process is equal to zero. As can be clearly seen from this contrast, the problem here arising is that the veracity of any of these statements imply the falsity of the other. These statements are thus not equivalent. They are contradictory.
Finally, from current second law thermodynamics it is learned that while the entropy change for the universe of the reversible transfer of an amount of heat Q' from Th to Tc is equal to zero, that of the irreversible transfer is equal to Q'(Th −Tc)/ThTc. Looking back now at the principle of the equivalence of transformations one can only qualify as peculiar the fact that the entropy change in it associated to the reversible transfer of heat taking place in the reversible cyclical process to which such a principle refers, instead of being zero, as should correspond to a reversible process, be Q'(Th −Tc)/ThTc which is the one associated to an irreversible heat transfer.
The inconsistencies just exposed are indicative of a flaw in Clausius work. Since all the disagreements involve the values of the above referred transformations, a new way of ascertaining the said values, different to that of Clausius, will be developed. Through them the identification and further correction of Clausius analysis flaw will be undertaken. This is the matter of the following papers.
References and Notes
- Clausius, R. The Mechanical Theory of Heat; MacMillan: London, 1879; p. 78. [Google Scholar]
- Clausius, R. The Mechanical Theory of Heat; MacMillan: London, 1879; p. 92. [Google Scholar]
- Clausius, R. The Mechanical Theory of Heat; MacMillan: London, 1879; p. 91. [Google Scholar]
- Clausius, R. The Mechanical Theory of Heat; MacMillan: London, 1879; p. 100. [Google Scholar]
- Clausius, R. The Mechanical Theory of Heat; MacMillan: London, 1879; p. 102. [Google Scholar]
- Clausius, R. The Mechanical Theory of Heat; MacMillan: London, 1879; p. 108. [Google Scholar]
- Clausius, R. The Mechanical Theory of Heat; MacMillan: London, 1879; p. 213. [Google Scholar]
- Clausius, R. The Mechanical Theory of Heat; MacMillan: London, 1879; p. 109. [Google Scholar]
- Clausius, R. The Mechanical Theory of Heat; MacMillan: London, 1879; p. 98. [Google Scholar]
- The square brackets, it should be recognized, enclose the representation of a physical process. When preceded by the ∆S function (or any other thermodynamic function, for that matter) they become the argument of such a function and the whole expression “∆S[ ]” is ultimately given by a number called the entropy change of such a process. An arbitrary concatenation of those “∆S[ ]” numbers does not necessarily imply the existence i.e. the physical possibility of the process defined by the concatenation of their arguments.
© 1999 by MDPI (http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.