1. Introduction
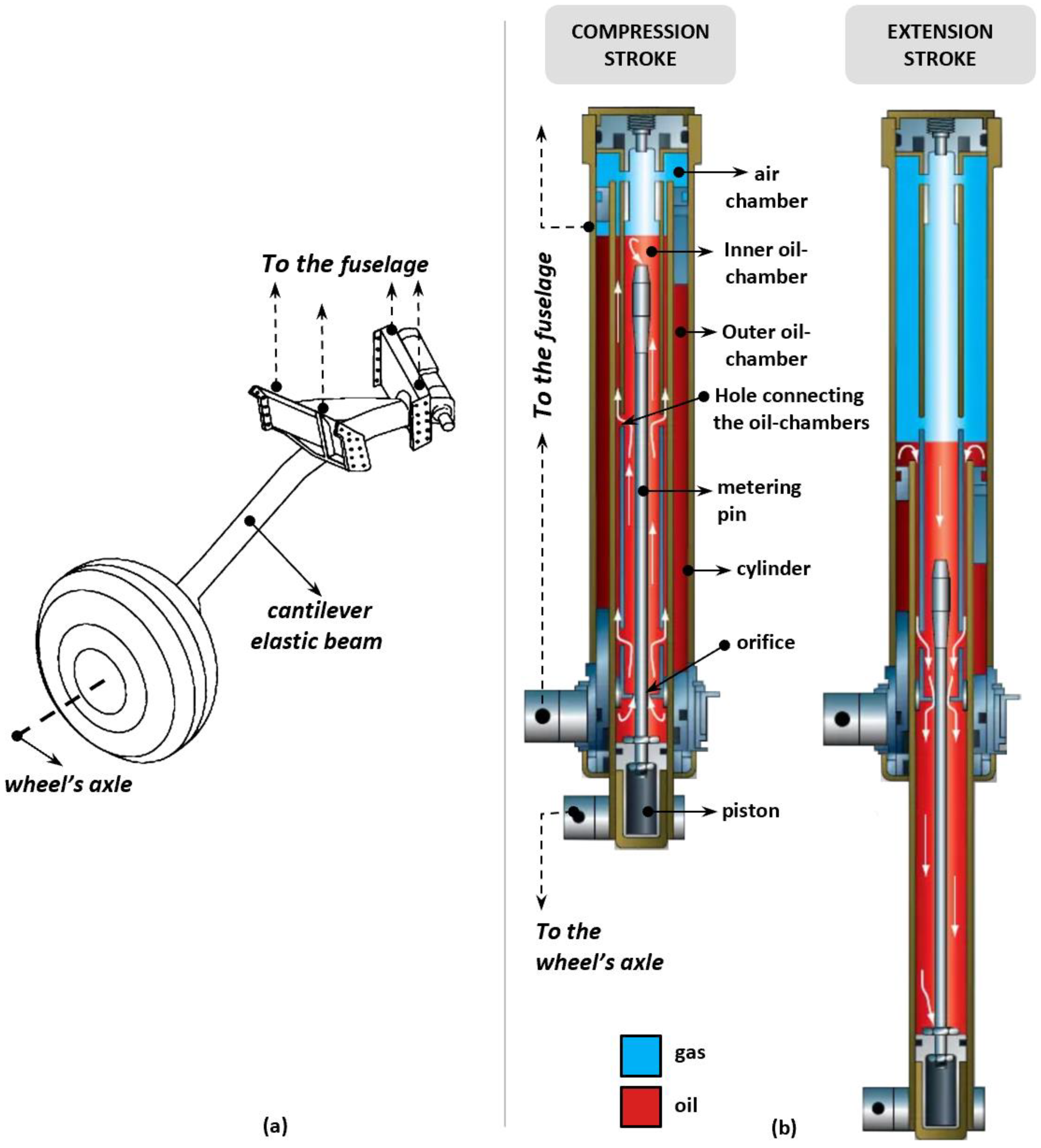
Oleo-pneumatic landing gear represents a key technology in modern aviation due to its remarkable efficiency in smoothly absorbing large amounts of energy in a short period of time. The rapid growth of airplane dimensions, weight, and flight speed has been made possible by the development of ever more sophisticated systems enabling safe landing throughout the entire operative life of the vehicle. Owing to its compact dimensions, relatively competitive weight, and fatigue life, the oleo-pneumatic strut has quickly replaced the classical cantilever solution (
Figure 1a), which is nowadays only considered for the main landing units of very light aircraft or small general aviation aircraft [
1].
Apart from the general layout, the main difference between cantilever and oleo-pneumatic struts is in the way the landing energy is dissipated. In the first case, the dissipation occurs through the deformation of an elastic beam connecting the wheels’ axles to the fuselage; in the second case, it occurs through the motion of a piston inside a cylinder filled with a mixture of gas and oil (
Figure 1b).
The piston-cylinder assembly is generally referred to as a
shock absorber, and the dissipative force generated during the landing is mainly due to the flow of viscous oil into an orifice with a cross-section that varies with the piston stroke. In more detail, the oil flows between two coaxial chambers, depending on the direction of motion of a tapered metering pin mounted on the piston (
Figure 1b). During the compression stroke, the metering pin enters the inner chamber through an orifice with net section area
As; to compensate for the reduction in the amount of available volume, part of the oil contained in the inner chamber moves into the outer chamber, flowing into the same orifice crossed by the metering pin and into some holes connecting the two chambers. At the same time, the gas contained in a compensation air chamber (placed at the top of the oil chamber) is compressed, thus contributing to the balance of fluid volume in the different compartments of the cylinder.
Unlike the communication holes between oil chambers, the portion of the orifice hosting the oil flow has a variable section area, Atr, given by the difference AS–Amp, where Amp is the metering pin’s net section area, which varies with the pin length. During the extension stroke, the pin comes out the inner oil chamber, the air chamber volume expands, and the oil flows from the outer chamber into the inner chamber. The damping force produced by the oleo-pneumatic system can be then modulated by working on the shock absorber’s main characteristics, with the ultimate goal of adequately limiting the aircraft’s vertical acceleration to the maximum value the aircraft structure can absorb after impacting the ground.
A reliable simulation tool for landing gear impact dynamics can therefore provide tremendous support for the design of new airplanes, as it facilitates the integrated definition of coherent layouts for both the landing unit and the airframe. In full awareness of this consideration, several approaches have been proposed to efficiently model the dynamic behavior of oleo-pneumatic landing gear, each with its own level of complexity, pros and cons.
The first attempt at shock absorber analysis was made by Hadekel [
4], who focused on evaluating the system’s overall damping efficiency rather than proposing effective models for simulating the impact dynamics. Milwitzky and Cook [
5] presented an integral model for the entire shock absorber, which was considered as a dynamic system with a single degree of freedom. The model was successfully validated by experiments but did not accurately account for the influence of many parameters involved in the drop dynamics. Currey [
6] investigated the relationship between the dissipated energy and the air chamber’s physical characteristics and described effective thermodynamic models to predict the behavior of the gas during the compression and extension stroke of the piston. Relying on these studies, Daniels [
7] built a sophisticated model allowing for precise simulation of hydraulic dissipative forces; unfortunately, its validity was limited to telescopic landing gears only.
Working on a six degree-of-freedom system, Sivakumar and Haran [
8,
9] were able to fairly represent shock absorber dynamics during taxiing. Their approach adopted linear differential equations of motion, which were very useful in predicting the vibration levels induced by the ground asperities on the fuselage structure and passengers. On the other hand, the equations could not realistically capture the energy dissipation mechanism at touchdown due to their linear formulation. To overcome this limitation, Sivakumar and Syedhaleem [
10] used a series of two mass-spring-damper models to simulate the impact dynamics of the shock absorber and wheel assembly. The model was validated against the numerical results of finite element analysis carried out in ABAQUS [
11] and proved to be reliable in predicting the time history of vertical displacement, acceleration, and reaction force. Unfortunately, no equations were considered for obtaining the wheel axle’s vibrations along the horizontal direction consequent to the aircraft flight speed at the moment of impact, and the friction between the tire and the ground. This made it impossible to estimate spin-up and spring-back loads, which are among the most severe loads in landing gear design [
12].
Recent studies offer comprehensive simulation strategies for landing gear impact dynamics, relying upon ever more advanced finite element solvers; some relevant examples can be found in a good review article by Kruger and Morandini [
13].
An interesting finite element analysis accounting for the nonlinear problems in landing dynamics was proposed by Lyle [
14], while Khapane et al. used multibody dynamics software (Simpack) combined with the FE solver NASTRAN to investigate the load instability produced by the interaction of the brake mechanism with the landing gear’s wheels [
15]. Lernbeiss introduced a multi-body system-based landing gear model for numerical simulation of simple static and dynamic load conditions and successfully correlated the simulation results with the outcomes of a more accurate finite element simulation [
16]. The Lernbeiss model was then revised and improved by Kong, based on drop-impact analysis and experiments conducted on a smart UAV landing system [
17]. LMS
® analysis software for multi-body dynamics was used by Xue and Yu to build a coupled rigid-flexible simulation model of light aircraft main landing gear, showing very good capability in terms of drop-test load estimation [
18].
Finite element models represent effective tools to support the design of landing gear, enabling accurate investigation of the mechanical behavior of each subcomponent under the action of static and dynamic loads. The development of new software for parametric FEA and the introduction of elastic models in simplified multi-body dynamics packages have recently led to the possibility of accounting for some enhanced levels of detail in simulations of drop dynamics even in the preliminary design stage of the landing gear, while also allowing for trade-off studies on the effects induced by configuration changes on the overall landing performance. On the other hand, FE-based approaches become somewhat impractical at the beginning of the preliminary design phase of an aircraft, when there are too many undefined design variables to consider the generation of the landing gear’s 3D CAD or structural mesh convenient for estimating its influence on ground loads.
Referring to modern aircraft, characterized by ever more light and flexible structures, the possibility of predicting ground loads and vertical acceleration levels at landing is crucial from the early stages of the project, as it enables proper design choices to be made.
According to airworthiness regulations, determining ground loads and acceleration follows a general process that is independent of the aircraft certification category and can be summarized in four consecutive steps:
Estimate the design load factor at landing by means of conservative assumptions or rational analysis. (The design load factor at landing, or ground load factor, is defined as the ratio between the maximum vertical acceleration arising at the aircraft’s center of gravity during landing and the acceleration of gravity.)
Apply standard criteria to evaluate landing loads and vertical acceleration referring to the assumed load factor and design-relevant landing conditions defined in terms of the aircraft’s inertial configurations and attitudes.
Determine the most critical load/acceleration and landing conditions among those of the previous step.
After landing system design and manufacture, conduct drop tests on landing gear and experimentally evaluate the maximum ground load factor.
The reference aircraft certification category has an influence only on the specific approaches and formulations that must be followed to accomplish the tasks at each step, while the general logic of the process is essentially common to all certification standards.
If the experimental load factor obtained by drop tests is lower than that assumed at the beginning of the process, then the landing gear design is approved, provided that it is also shown (by test) that the landing gear is also able to withstand the most critical static/dynamic load conditions among those evaluated.
Landing gear design approval is-therefore-based on demonstrating compliance with two concomitant criteria:
The structure must be able to withstand the most severe loads expected in service without damage or failure (as for all components of the aircraft primary structure).
The maximum ground load factor developed during prescribed drop tests must be lower than that assumed for the evaluation of ground loads in the first place.
If the landing gear fails to meet the first criterion, then recovery actions can be taken to strengthen the structural layout of the item and new tests can be performed to prove the adequacy of the implemented corrections. If it fails to meet the second criterion, then the entire set of ground loads is compromised and needs to be evaluated again, in correspondence of a new assumption on the load factor value; this severely impacts the design process of the landing gear and the structural components whose layout is influenced by ground loads magnitude.
The initial estimation of ground load factor therefore plays an important role in the correct assessment of ground loads and the subsequent design of the airframe and landing system; the accuracy of this estimation is ultimately related to good prediction of the landing gear’s shock absorption performance in standardized drop tests, and at the phase of the project when the design of the landing gear has just started and no detailed simulation models are available.
In line with this evidence, the author developed a numerical method for simulating landing gear dynamics in a typical certification drop test, which rationally balances the low level of sophistication of the adopted model with the need for accurate results. A nonlinear dynamic model is adopted, which properly accounts for all the energy-dissipation mechanisms occurring at the impact; in this regard, the shock absorber’s vertical reaction force is combined with the horizontal solicitation induced by the tire friction with the ground. A general description of the proposed model is outlined in this work, together with the adopted formulation and software tools to simulate the impact dynamics.
Relying upon these tools, the drop test of a reference landing gear was numerically replicated, and the implemented approaches were successfully validated against already available experimental data.
2. Formulation of Landing Gear Impact Dynamics
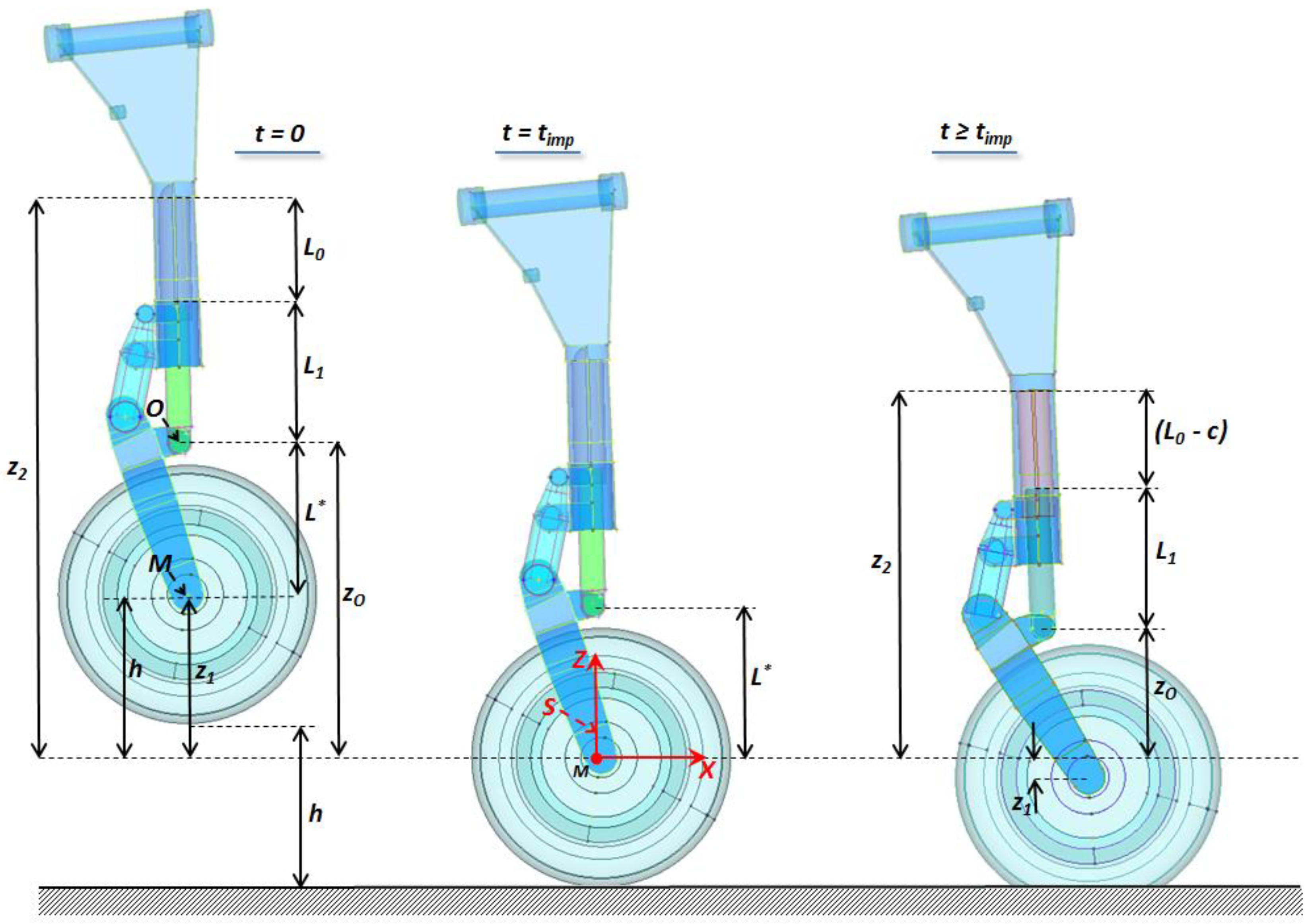
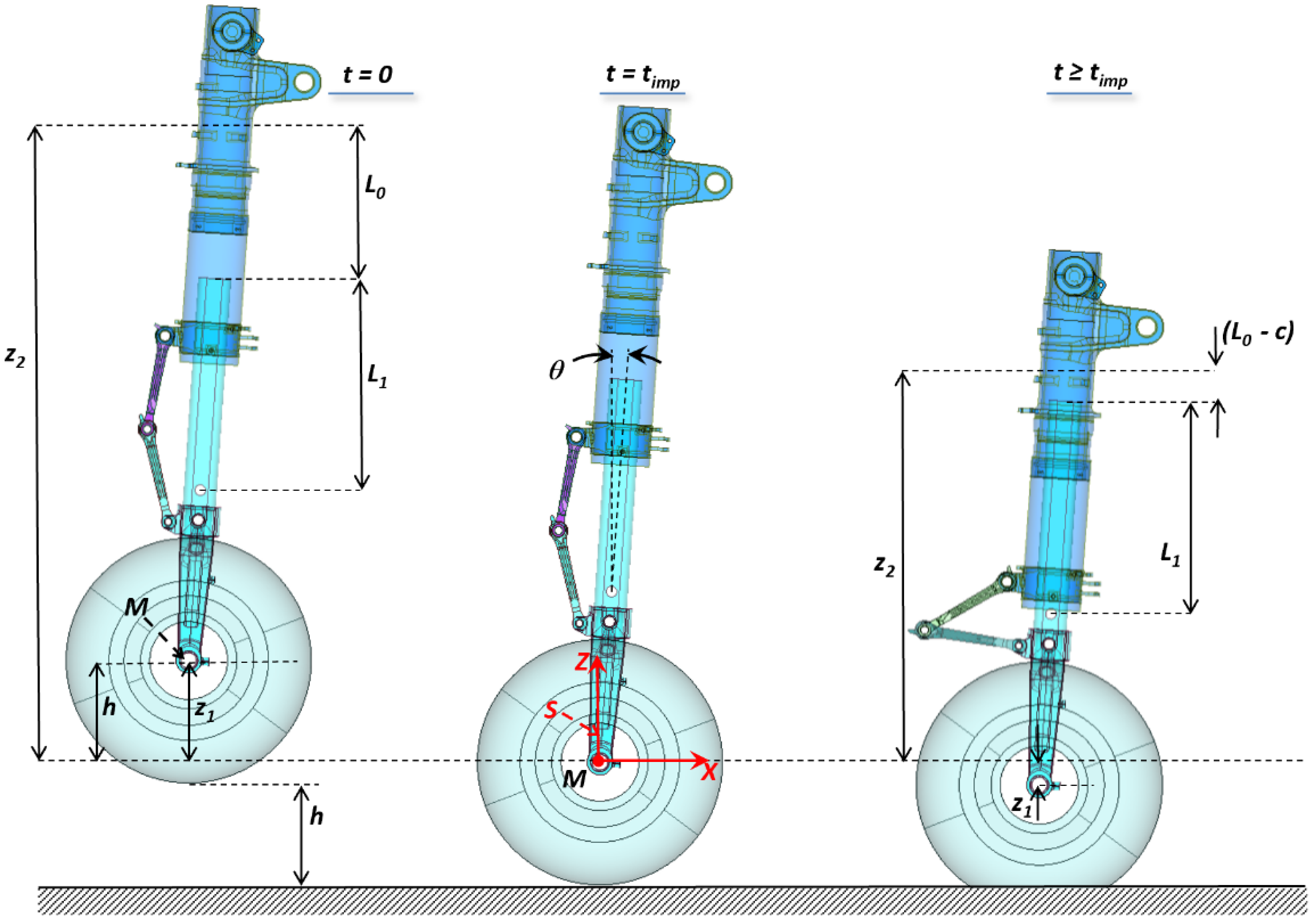
The landing gear was modeled as an elastic system with four degrees of freedom, adequately selected to effectively capture the impact dynamics.
The following Lagrangian coordinates were defined with reference to the Cartesian system
S depicted in
Figure 2:
x1, z1: x- and z-coordinates of point M located at the center of the wheel hub;
z2: z-coordinate of the cylinder head; and
φ: wheel rotation angle.
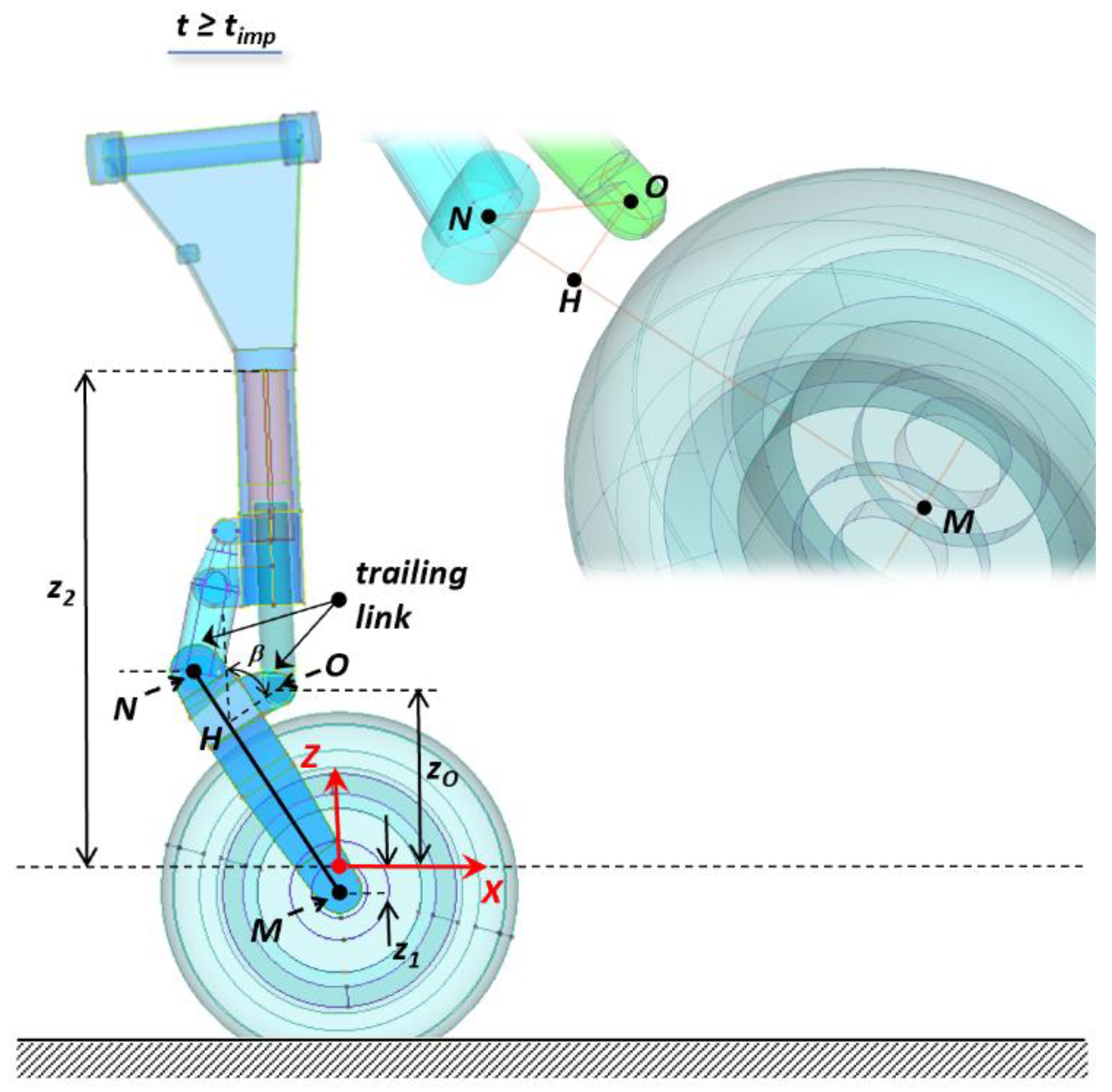
According to the scheme of
Figure 2, the impact dynamics was roughly divided into three subsequent time phases:
Free fall, on the left side of the figure, during which the landing gear is approaching the ground;
Impact, at the center of the figure, occurring at the single instant timp, when the wheel touches the ground; and
Shock absorption, on the right side of the figure, during which the landing gear works to dampen the impact-induced acceleration.
If
c indicates the stroke of the piston and
z0 the z-coordinate of point
O located at the base of the piston corresponding to the piston–fork joint, at any instant of time
t, the result is:
where
L0 and
L1 indicate the longitudinal dimension of the air chamber and piston, respectively.
Equation (1) can be easily rearranged to express the stroke as a function of variables
z0 and
z2:
Although not evident in Equation (2), the stroke is dependent only on Lagrangian coordinates
z1 and
z2 (
.
z0 is a dummy variable used only to express the stroke in a more intuitive and compact manner; this variable is linked to
z1 and
z2 by a nonlinear equation, which is derived in
Appendix A by means of simple geometric and kinematic considerations.
During free fall, the stroke is identically equal to zero.
At the origin of the investigation time frame (
t = 0), we have:
and, according to Equation (2):
If
, then:
and, again,
The stroke is also identically null at the instant of impact; when
, the following occurs:
and, finally,
When
, the piston’s stroke is no longer equal to zero; the motion of the piston into the cylinder generates vertical reaction forces
Fa and
Fd due to the compression of gas and the flow of oil into the oleo-pneumatic chamber, respectively. In addition, a further reaction force,
FPN, arises along the vertical direction due to the compression of gas in the tire.
Fa and
Fd depend on the geometric characteristics of the oleo-pneumatic chamber and can be expressed as functions of the piston’s stroke and its time derivative, according to the following equations [
7]:
where
A0 and
P0 are the air chamber section area and pre-load pressure in the air chamber, respectively;
L0 is the initial length of the air chamber (i.e., its longitudinal length at
t <
tinp);
γ is the polytropic index of gas in the air chamber;
ρoil and
cvisc are the density and viscosity of oil in the hydraulic chamber, respectively;
As is the section area of the piston; and
Atr is the net section of the orifice of the hydraulic chamber traversed by the oil flow, generally variable with the piston stroke.
FPN basically depends on the tire’s mechanical properties and is generally provided by tire manufacturers in the form of experimental curves relating the reaction force to the tire crushing and inflation pressure. For a given tire and inflation pressure, FPN is therefore considered as a function of the variable z1 only. The tire’s overall reaction force is more precisely given by the sum of FPN and Fd0, where Fd0 stands for the reaction force due to the deformation of the tire’s material (at zero inflating pressure). Fd0 is dependent on the rate of deformation of the tire (dz1/dt) since the tire’s material is characterized by viscoelastic behavior. Within the limits of the proposed formulation, Fd0 was considered negligible compared to FPN.
By imposing the equilibrium of all forces acting along the
z-axis of the reference S (
Figure 2), the following equations for the impact dynamics of the system can be written:
where
Me is the effective mass, supposed to be lumped at the head of the cylinder and accounting for the amount of aircraft weight acting on the landing gear element at the moment of impact, and
m is the swinging mass, supposed to be lumped at the middle point of the wheel hub and equal to the sum of the wheel and tire masses, plus one-third of the landing gear leg’s mass.
Equation (5) are valid also when t < timp, and basically describe the free fall of masses Me and m as two separate bodies;in this case Fa, Fd and FPN are all equal to zero.
After the impact, the elastic oscillation of the wheel hub along the
x-axis is governed by the equation:
where
σ and
K are the structural (viscous) damping and stiffness exhibited by the landing gear leg along the
x-axis;
Fx is the module of the friction force due to the tire contact with the ground, which can be reasonably assumed equal to
μ·FPN(
z1), where
μ is the tire sliding coefficient of friction, and
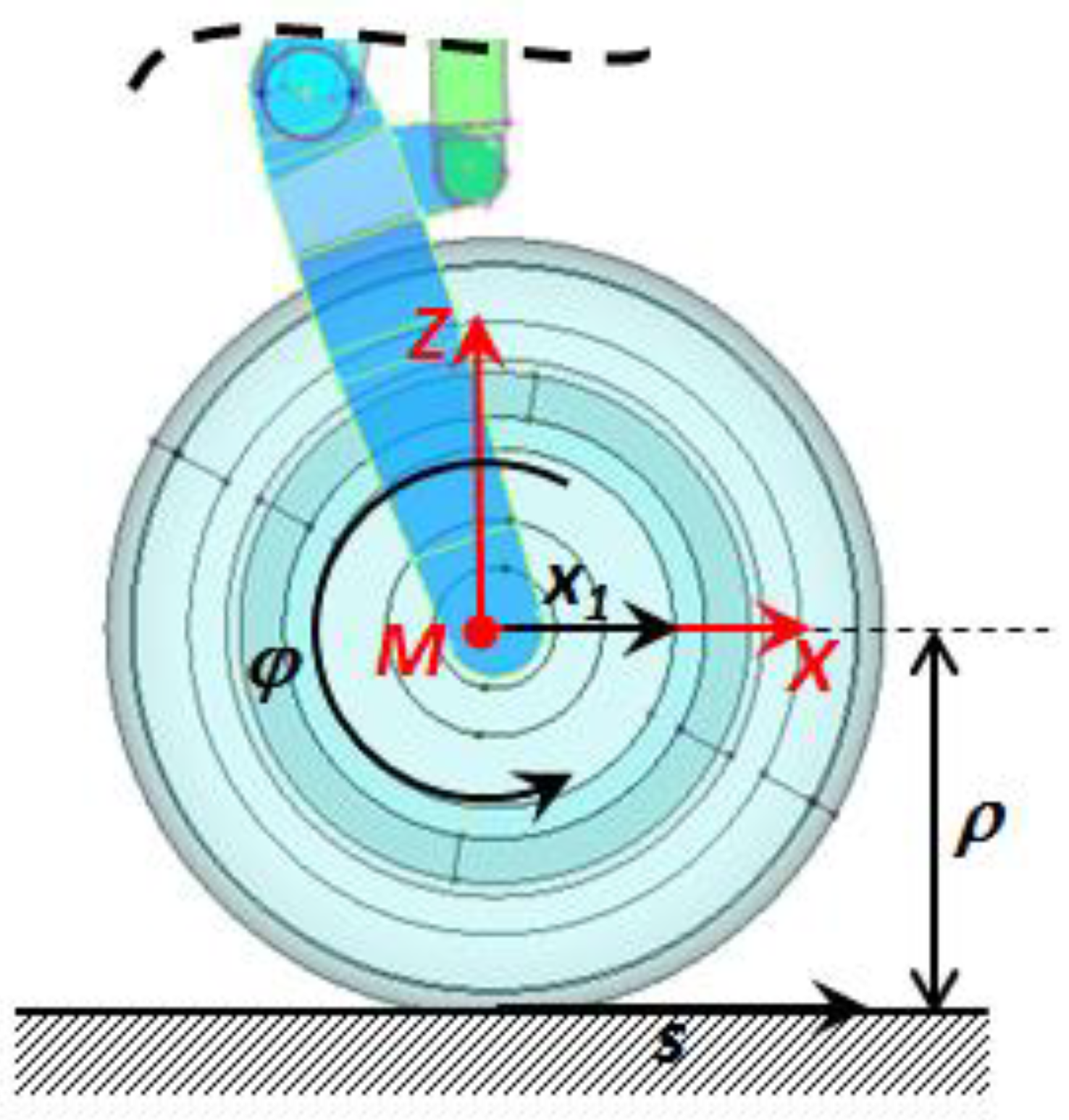
s is the x-displacement of the point of contact between the tire and the ground (tire slip,
Figure 3), given by
, where
ρ is the distance of the wheel hub axis to the ground, or the difference between the radius of the wheel and the tire crushing.
The friction force
Fx and displacement
s do not represent two independent variables, provided that they are both called to satisfy the rotational equilibrium equation of the wheel about the hub axis. Under the assumption of negligible bearing friction, the wheel rotational equilibrium may be formulated in the following way:
with
I equal to the wheel’s polar moment of inertia. Well-performing, and well-lubricated, bearings are commonly used in aeronautics; consequently, and within the limits of approximation of the proposed formulation, the torque due to bearing friction can be reasonably considered negligible compared to that induced by the friction force between the tire and the ground.
As a whole, Equations (5)–(7) define the system of nonlinear and coupled differential equations whose solution describes the impact dynamics of the landing gear in terms of the time-dependent state variables x1, z1, z2, and φ.
It is worth noting that the expressions of the stroke given by (2) and the vertical equilibrium given by (5) are valid for the specific landing gear arrangement depicted in
Figure 2.
This arrangement is typical of main landing gear and is characterized by a hinged connection between the fork, the piston, and the cylinder, usually referred to as a
trailing link. The cylinder’s inclination angle with respect to the vertical axis
z is null or negligible. In some other arrangements generally adopted for nose landing gear, the fork and piston move together with no relative rotation between them, and the movement occurs along a direction that is inclined with respect to the normal to the ground (
Figure 4). In such cases, Equations (2) and (5) can be easily rewritten following the same approach that has been used so far.
Referring to the typical nose landing gear arrangement in
Figure 4 (telescopic landing gear), we can immediately observe that:
and then,
By imposing the equilibrium along the vertical axis
z, we can finally obtain:
Equations (6) and (7) have general validity and can therefore be used together with (8) and (9) to complete the set of equations governing the impact dynamics of the landing gear arrangement of
Figure 4.
In conclusion, the proposed simulation approach leads to two different formulations for the equations of drop impact dynamics, depending on the type of landing gear under investigation. Equations (5)–(7), and the expression of the stroke given by (2) apply to landing gear with a trailing link arrangement and vertical leg (typical configuration of main landing systems), while Equations (6), (7), and (9) combined with Equation (8) for the stroke apply to nose landing gear, generally characterized by the configuration depicted in
Figure 4.
During the preliminary landing gear design stage, a geometric layout of the item is assumed in combination with a wheel type. Based on these assumptions and the drop-test prescriptions of the reference airworthiness regulations, all the input data required to run the simulation are available at the preliminary design stage, with the exception of σ and K (used in Equation (6)).
Nevertheless, first trial values may be assigned to σ and K by using the structural similitude of landing gear belonging to the same category (i.e., suitable for installation on aircraft in the same category of MTOW). It can be observed that the natural frequency of the (main or nose) landing gear’s fore and aft bending mode does not significantly change over different landing gear models in the same category.
If the natural frequency f of the fore-and-aft bending mode is reasonably assumed according to the landing gear category, then K can be approximately obtained as m*4π*f2, with m equal to the mass of the wheel; similarly, σ can be expressed as ζ*σcr, where σcr is the critical damping given by 2 m*(K/m)0.5 = 4 mπf and ζ is the damping ratio, which is generally in the range of 0.03–0.05 for metallic structures with joints.
The design of the landing gear is clearly an iterative process; after the preliminary assumptions of σ, K (and on all other input data needed for the simulation), the first loop of dynamic impact loads can be evaluated and a preliminary structural model can be generated for the landing gear. New simulations can then be carried out to produce the second loop of loads, this time using input values directly derived from the preliminary structural model. The second loop of loads is used to update the structural model, and the process goes on until the executive design of the item is reached. In all of these stages, the proposed simulation approach provides an efficient tool to evaluate the drop dynamics of the landing gear (and associated loads), relying upon input data that are continuously updated to follow the progress of the design.
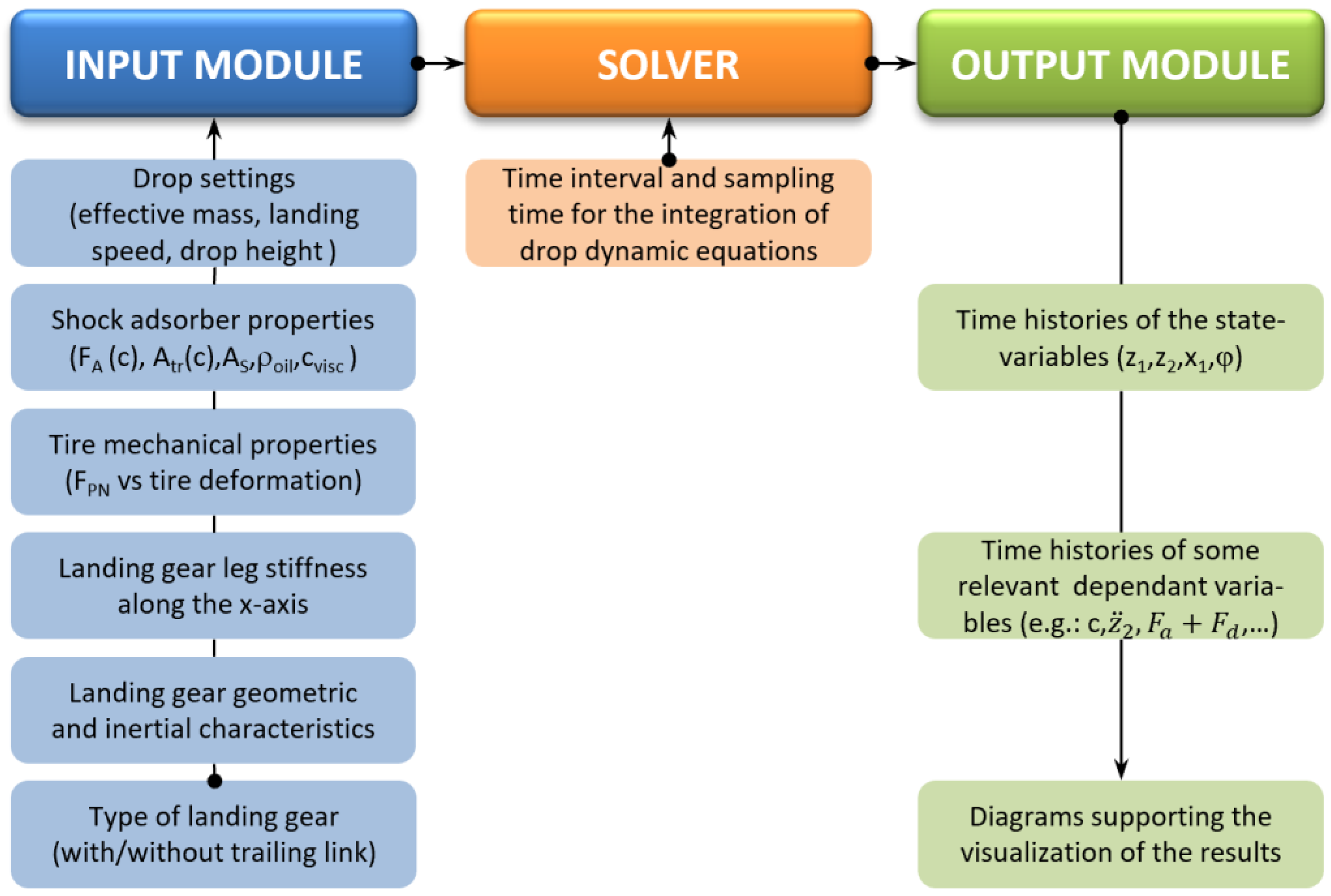
3. Drop Test Simulation and Results
A set of intercommunicating MATLAB
® [
19] routines was implemented and arranged in a compact software environment to automatically solve the differential equations governing the drop dynamics of the landing gear according to the approaches described in
Section 2.
The tool consists of three main modules (
Figure 5):
An input module, which reads and processes the input data of the problem, in terms of both the landing gear type (main or nose) and characteristics.
A solver module, which implements the Runge-Kutta method [
20] to integrate the system of differential equations numerically.
An output module, which prints the time histories of the most relevant physical parameters and plots practical diagrams to visually support the result analysis.
To check the reliability of the proposed numerical approach and its implementation in the software tool, a drop test of a reference landing gear was simulated, and the results were compared with already available experimental data.
The main landing gear of a large UAV was selected as a reference; the name and pictures of the aircraft are here omitted for confidentiality reasons. To properly frame the application scenario, it is sufficient only to mention that the UAV had a maximum landing weight (
MLW) of 3040 kg and a wing surface area (
S) of 21 m
2, and was designed in compliance with NATO-STANAG 4671 airworthiness requirements [
21].
Among the tests performed to qualify the main landing gear, the limit drop (paragraph 725 of [
21]) was selected as a benchmark case for the drop simulation code.
According to the limit drop test requirements, the drop height must be equal to:
and not lower than 0.234 m or greater than 0.475 m.
The landing gear must be dropped while carrying an effective mass equal to:
where
Me is the effective mass to be used in the drop test;
h is the specified drop height;
d is the deflection under the impact of the tire, plus the vertical component of the wheel hub travel relative to the drop mass at the instant of time when the piston stroke reaches its maximum value;
M is equal to the static weight on the main landing gear with the UAV in level attitude with the nose wheel clear; and
L is the ratio of assumed wing lift to UAV weight (not greater than 2/3).
Replacing MLW = 3040 kg and S = 21 m2 in Equation (10), the reference landing gear’s drop height was equal to 0.497 m and therefore was limited to 0.475 m per regulatory requirements.
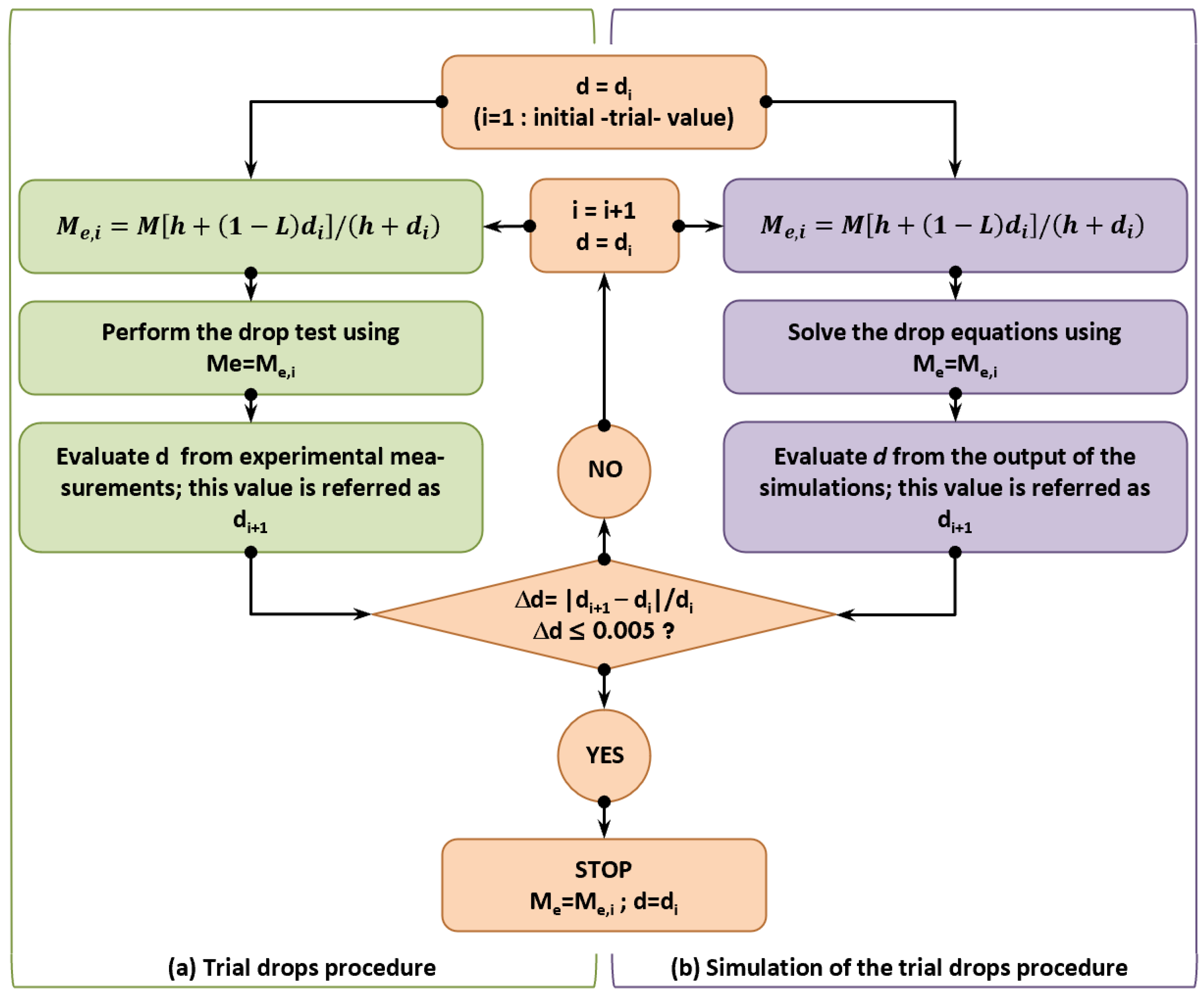
The effective mass to be used in the drop test depends on the parameter
d, which is an output of the drop itself; for this reason, an iterative process, based on trial drops, is usually carried out to determine the couple (
Me,
d) satisfying Equation (11) with a given level of approximation (
Figure 6a).
Although the
Me and
d values used during the limit drop tests were already available from the landing gear’s test reports, they were calculated by simulating the trial drop procedure usually carried out before the limit drop test (
Figure 6b); this was clearly done to get a first proof of validation for the proposed numerical formulations.
An initial (trial) value, d1, was imposed on d, and then, the corresponding effective mass Me,1 was obtained by Equation (11); L was imposed as equal to 2/3, and M, as equal to half of the MLW (M = 1520 kg). Drop dynamics equations were solved, thus giving in output the effective value d2 of parameter d. A new value of effective mass Me,2 was then recalculated by Equation (11), this time corresponding to d = d2; the input parameters Me,2, d2, were used for a new drop simulation, leading to a new output value d3.
The process was repeated until the difference, Δd, between the values of d obtained in two consecutive iterations were lower than 0.005 m.
After three iterations, the convergence of the process was reached, resulting in Δd = 0.003 m, d = 0.360 m, and Me = 1083 kg. Obtained values for d and Me were in full agreement with those reported in the drop test documentation of the reference landing gear (d = 0.45 m, Me = 1090 kg).
At each iteration, the drop dynamics equations were integrated starting from the initial conditions (listed in
Table 1), considering a time step of 5 × 10
−4 s over an interval of 1 s.
The complete set of data related to the reference landing gear and used to run the simulations is reported in
Appendix B.
The output related to the last iteration was considered relevant for the drop test under investigation, as it led to coherent values of Me and d.
The time histories obtained for the variables
z1,
z2, and
z0 are reported in
Figure 7.
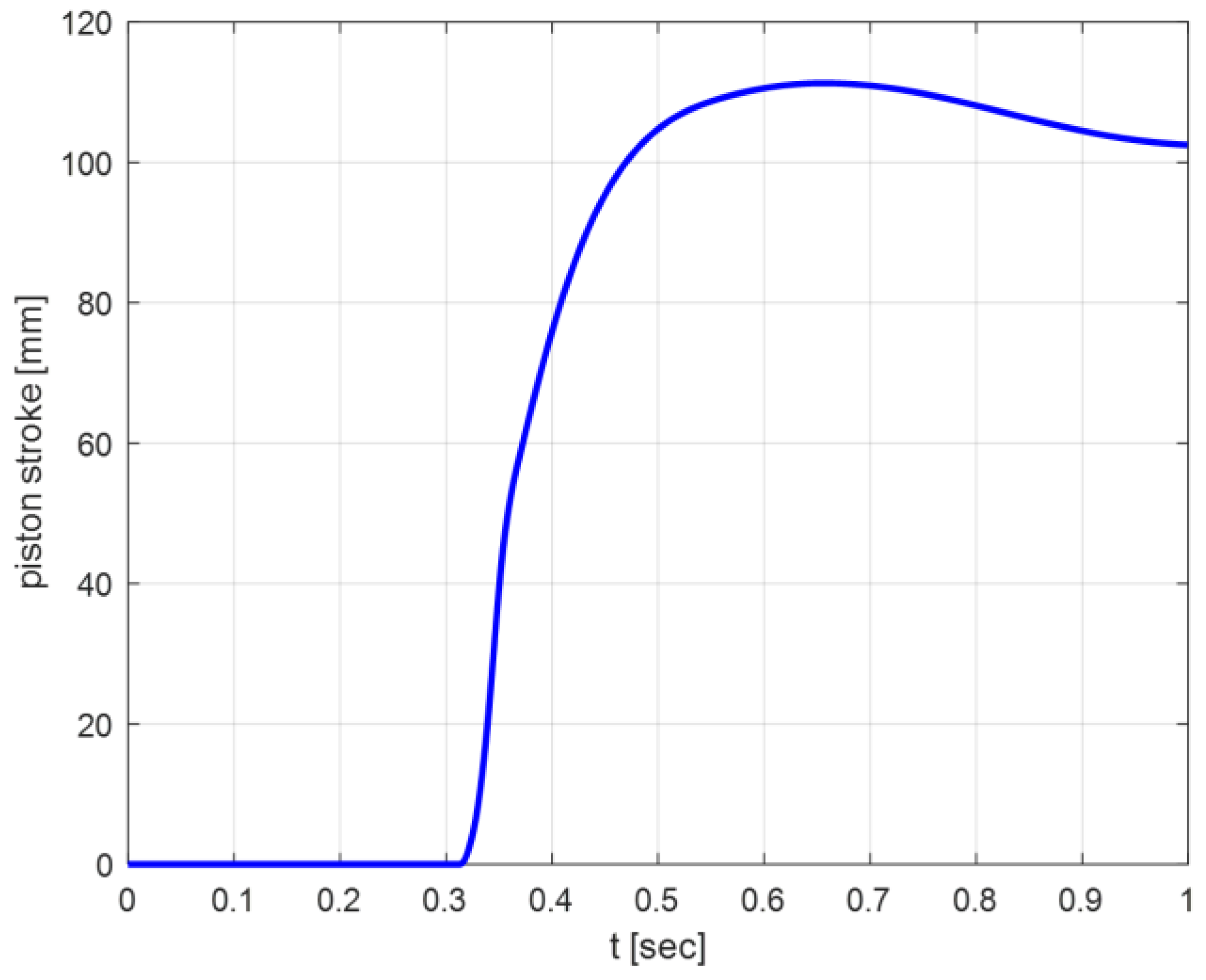
Before the impact (
t <
timp), the landing gear and drop mass are in free fall and all the variables show the same parabolic trend versus time. Therefore, the piston stroke is identically null (
Figure 8) and no work is done by the shock absorber.
After the impact, the piston stroke increases up to its maximum value; in this time interval, z1, z0, and z2 continue to decrease coherently to what is expected during the shock absorber’s compression. Their trends are now different and no longer parabolic, as they are influenced by the shock absorber dynamics and the crushing of the tire. The tire’s crushing effect is more evident in the wheel hub vertical displacement (z1) and becomes less dominant for z0 and z2 due to the shock absorber’s damping action.
When the piston stroke decreases, the shock absorber starts its extension phase and the displacements z1, z0, and z2 consequently increase.
During this phase, the vertical displacement trends are practically affected only by the shock absorber’s dissipation force.
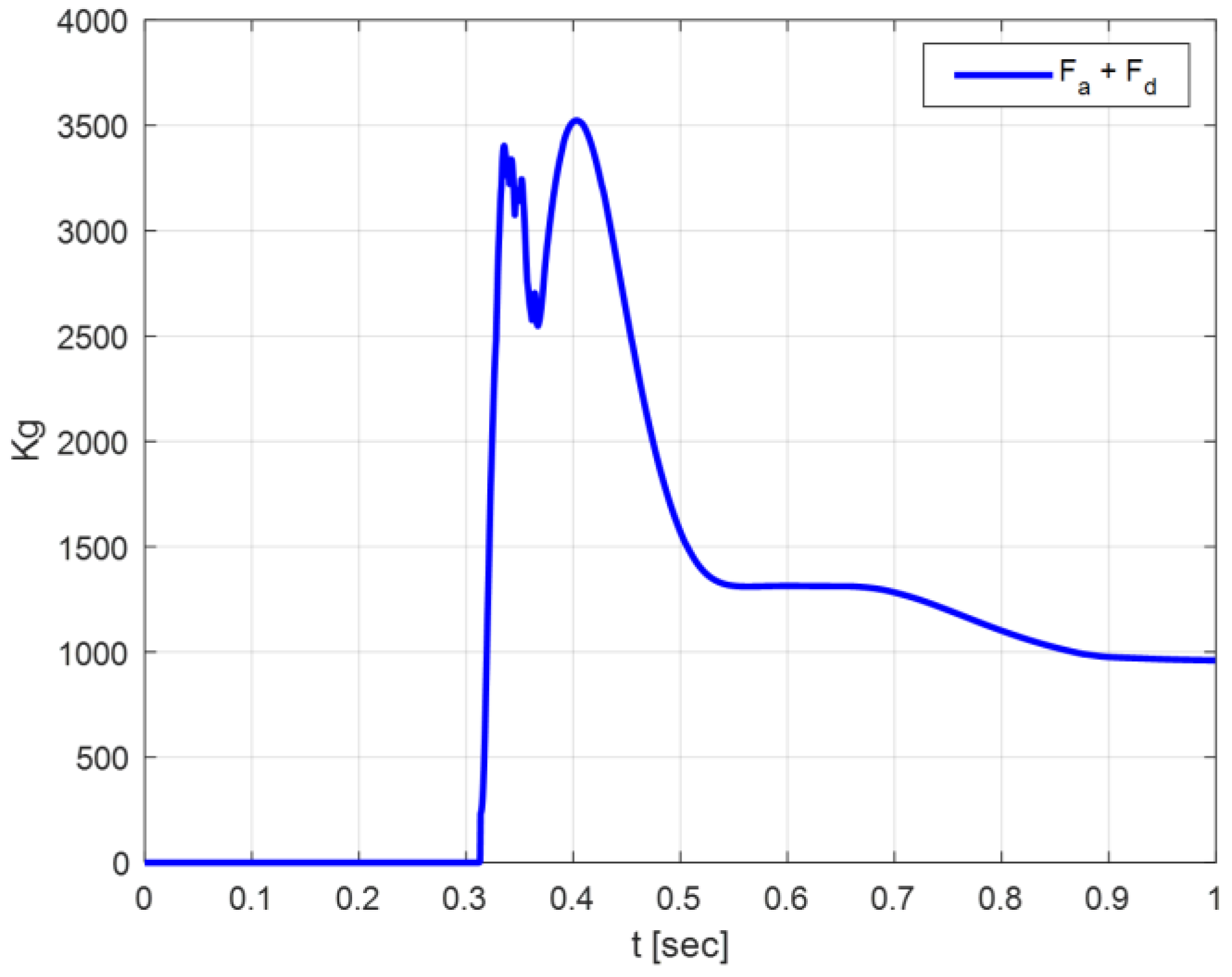
This is even more evident if we consider the time histories of the effective mass acceleration (
) (
Figure 9) and the overall shock absorber force
Fsa(
t) = (
Fa(
t) +
Fd(
t)) (
Figure 10).
Since the effect of
FPN on
is negligible along the entire piston stroke, the effective mass experiences an enforced motion that is practically driven only by the effective mass weight and overall shock absorber force. Thus, as shown by the results plotted in
Figure 9 and
Figure 10, the time histories of
and
Fsa(
t) have similar trends, represented by the linear relation
.
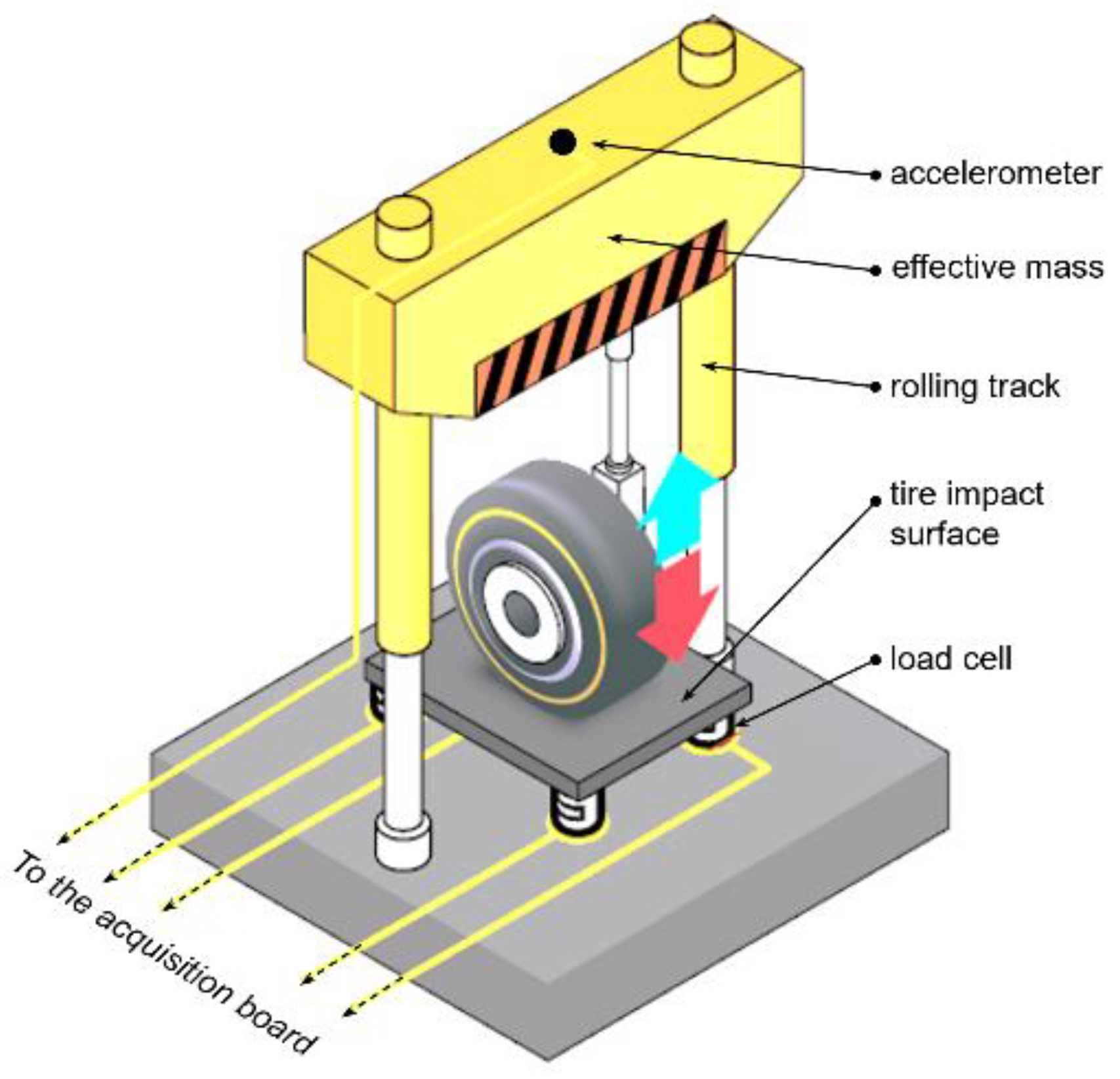
The acceleration of the effective mass was one of the two parameters measured during the drop test, using a monoaxial accelerometer placed at the top of the effective mass (
Figure 11).
The nominal acquisition range of the accelerometer was equal to 3 Hz to 5 KHz; during the test, the vertical acceleration was acquired with a sampling frequency of 100 Hz. The most significant measurement points are reported in
Figure 9, and they show excellent agreement between numerical expectations and experimental findings (to enhance the quality of the figure, the experimental data were plotted with a marker every 0.05 s).
The ground reaction force (
Fz) was the other parameter measured during the drop test; experimental data were obtained by placing four load cells under the tire’s impact area (
Figure 11). Each load cell measured along the normal to the plane of impact (
z-axis) and was characterized by a nominal acquisition range of 0.08 Hz to 25 KHz and an allowable compressive load of 5000 lb; for the acquisition of vertical load, a sampling frequency of 100 Hz was set. The four outputs of the cells were summed to get the experimental trend of
FZ; with the experimental error of each measurement equal to ±10 lb, the overall experimental uncertainty of
FZ values was equal to ±40 lb (±18.14 kg).
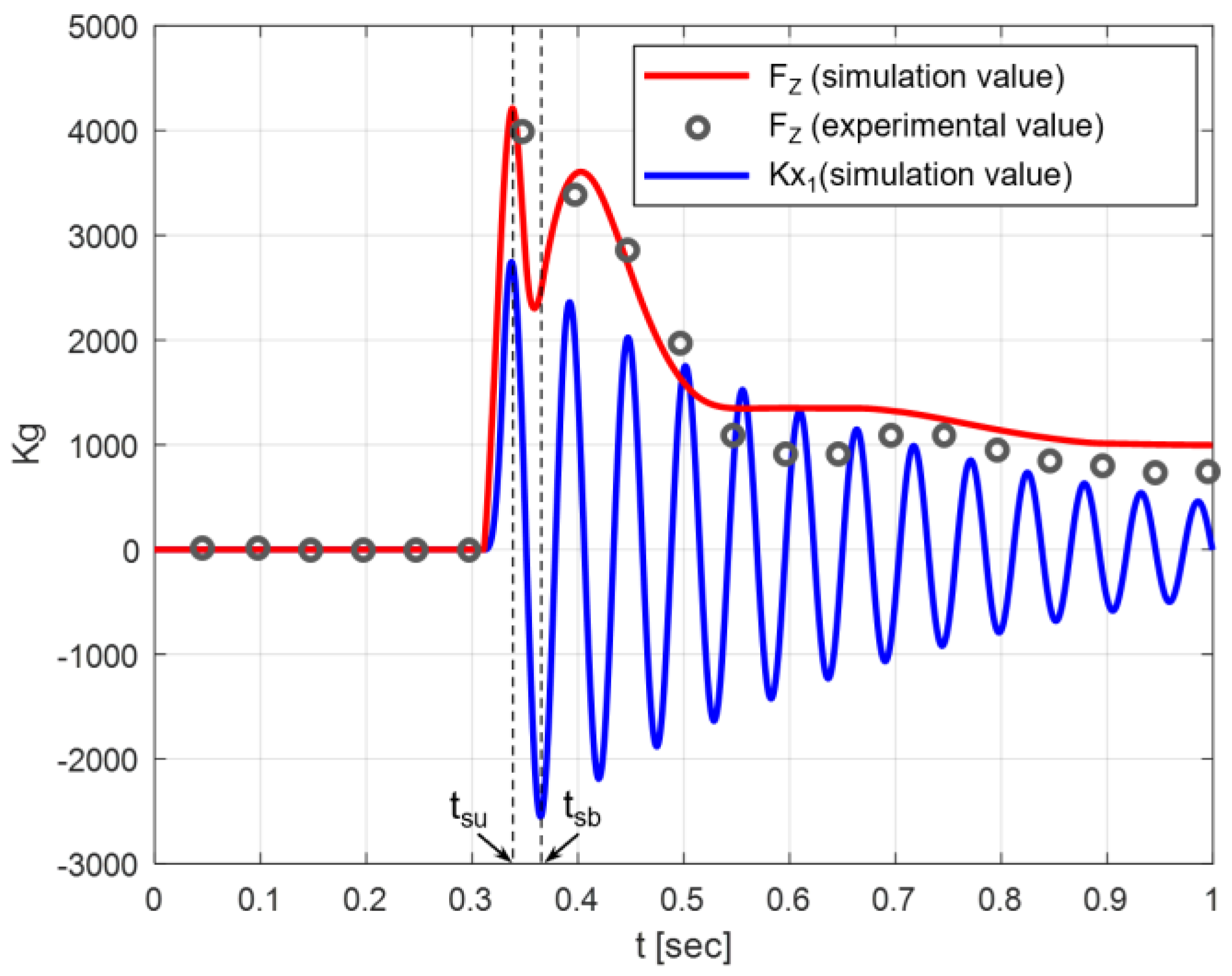
By working on simulation output,
Fz was numerically evaluated as −
FPN(
t), and its trend satisfactorily followed the experimental measurements (
Figure 12); to enhance the quality of the graph, the experimental data were plotted with a marker every 0.05 s.
The theoretical time history of the horizontal force acting on the wheel hub is reported in
Figure 12 to facilitate a discussion on its consistency with
Fz(
t).
Before the impact, the tire has relative horizontal speed with respect to the ground, which is equal to the aircraft’s landing speed.
At touchdown, the horizontal friction force between the tire and the ground induces elastic displacement of the wheel hub along the x-axis (x1). A recovery force due to the elasticity of the landing gear leg then arises (Kx1), and the damped oscillatory motion of the wheel hub begins.
The maximum and minimum values of the elastic recovery force are referred to as spin-up and spring back, respectively; as shown in
Figure 12, they occur at
tsu = 0.33 s and
tsb = 0.37 s.
When tsu < t < tsb, vertical force Fz abruptly decreases; this is in full agreement with the physics of the phenomenon, as the ground impact force is alleviated by the forward bending of the landing gear leg. As also confirmed by the experimental data, after tsb Fz increases because of the amplification induced by the rearward bending of the landing gear leg, and then its trend becomes prevalently influenced by the shock absorber dynamics rather than by the horizontal (elastic) deflections of the leg.
The initial oscillation of Fz vs. time is essentially due to the elastic response of the landing gear along the x-axis; a first peak arises when the horizontal force reaches the spin-up value (t = tsu), then the vertical load decreases up to a local minimum occurring at t = tsb, that is, when the horizontal load reaches the spring-back value. Since the numerical trend of Fz follows the same initial oscillation resulting from the experiment, it is indirectly proven that the landing gear motion along the x-axis is coherently reproduced in terms of instants of time when spin-up and spring-back occur.
Moreover, during this oscillation, the amplitude of Fz(t) is deeply influenced by the elastic bending of the landing gear leg, which is in turn driven by the horizontal load at the wheel; since, at tsu and tsb, the amplitude of Fz is well predicted by the model, it is reasonable to deduce that the same applies to the amplitude of the spin-up and spring-back loads (even if no direct measurement was made for these entities during the experiment).
In light of all of these considerations, it can be concluded that the proposed numerical method coherently captured the physics of the drop dynamics along both the vertical and horizontal axis of motion while producing results that are fully consistent with experimental outcomes.