Abstract
In the operational management of e-commerce platforms, online reviews and user feedback render the issue of anticipated product failure more transparent. The anticipated product failures are often negatively correlated with product quality, while related service guarantees can help customers avoid utility losses caused by such failures. Additionally, the network effect characteristics of products significantly influence customer purchasing behavior and firms’ pricing strategies. This paper employs the multinomial logit (MNL) model to establish an optimization framework for product line and value-added services pricing that accounts for the anticipated failure and associated services. It analyses three scenarios: developing a single product, homogeneous products, and heterogeneous products, deriving optimal price, market share, and maximum profit. Theoretical analysis focuses on how the optimal solutions for single and homogeneous products vary with changes in anticipated failure-induced utility losses, negative network effects, product quality, and service quality. In the numerical experiment, the study explores the effects of variations in utility losses from anticipated failure, network effects, and product and service quality on optimal solutions for heterogeneous products. Finally, the importance of incorporating anticipated failure-induced utility losses into product line and service pricing decisions is emphasized.
1. Introduction
The rapid development of e-commerce platforms is fundamentally reshaping the global retail landscape, emerging as a pivotal driver of digital economic growth. An increasing number of manufacturers now distribute their products through platforms such as Tmall, JD, eBay, and Amazon. However, rising competition has led to major challenges: severe product homogenization, declining profits, and higher consumer expectations. Manufacturers’ existing product differentiation strategies are struggling to effectively meet consumers’ increasingly diverse and high-quality demands, which further exacerbates market competition [1]. This is particularly evident in the durable consumer goods sector, such as 3C electronics. Consumers consider not only price and initial quality but also after-sales support. Consequently, value-added services targeting after-sales quality problems have been developed as new sources of profit growth. Given the unique nature of e-commerce, where consumers cannot physically inspect products, the anticipated failure rate becomes a critical factor influencing purchasing decisions. Platforms now use extended warranties and return policies as crucial tools to build trust and gain competitive advantage. For instance, JD offers a series of value-added services, including JD Appliance Extended Warranty and JD Worry-Free Returns, which provide comprehensive protection throughout the entire purchase and usage cycle. By reshaping the consumer experience through enhanced assurance, JD has established a strong competitive edge and secured a leading position in the industry. Therefore, it is of great practical significance to investigate how firms can effectively coordinate product quality with value-added services design and how to strategically price both products and services.
In e-commerce, the failure caused by product quality issues exerts multiple impacts on platform operations. A high failure rate leads to increased negative reviews and returns, damaging merchant credibility and platform reputation. However, enterprises can effectively mitigate the risk of sales losses by formulating optimal upgrade strategies for durable products [2], meaning product failures strongly influence both manufacturing decisions and profitability. Furthermore, improving product quality not only reduces malfunctions but also boosts consumer surplus [3]. However, due to market competition and cost constraints, it is often impractical for companies to offer completely fault-free products. Therefore, providing service guarantees, such as after-sales warranties, becomes essential to protect customers from product failures and signal quality reliability [4,5], especially under information asymmetry [6]. As manufacturing industries pivot from traditional pure manufacturing models towards the servitization trend, post-sales services revolving around the value conferred by products to customers have assumed paramount importance for manufacturing firms [7]. For example, in the industry of automobiles, the quality of services provided in maintenance events closely correlates with customer brand loyalty and repurchase intentions. In electronics, Dell has built its reputation through high-quality after-sales support, and Apple’s “Apple Care+” program has garnered strong customer support. According to industry research reports, the global market size for extended warranty services in the consumer electronics sector was approximately USD 50.6 billion in 2023 and is projected to reach USD 87.9 billion by 2033. Meanwhile, the rapid expansion of online shopping platforms has significantly enhanced both the accessibility and convenience of related value-added services, such as extended warranties, thereby accelerating their adoption and shaping new competitive dynamics within the digital retail ecosystem [8]. Thus, service serves as a key carrier for realizing product value [9]. In the development and design of value-added services, it is critical to consider the interaction between product quality and expected failure, which is of great significance in guiding the production practice of firms.
Furthermore, product network effects significantly influence consumer choices and firm pricing strategies. Network effects refer to the increase in a product’s value as its user base grows [10]. However, durable consumer products typically do not rely on the number of users to provide value. Instead, they depend more on factors such as product quality, performance, and brand reputation. In the realm of general durable consumer products, increasing the number of users usually does not directly result in a decrease in the overall value of the product or brand. People purchasing more durable consumer products generally do not directly compromise the quality or performance of the product. For example, in e-commerce platform transactions, a larger user base (buyers) generates a greater volume of user-generated content, including reviews, photos, Q&A discussions, and shopping guides. Such content substantially facilitates new users’ purchasing decisions by reducing information asymmetry, thereby exhibiting a positive network effect within the platform ecosystem. However, for some luxury items such as high-end watches and automobiles, their brands are often built upon uniqueness, scarcity, and quality. If a brand’s product begins mass production or sales expansion, it may compromise the brand’s scarcity. This could decrease the product’s uniqueness and attractiveness, thus affecting customers’ perception and purchase decisions, manifesting as negative network effects [11]. For example, certain e-commerce platforms strategically establish dedicated luxury channels, such as JD Luxury and Tmall Luxury Pavilion, to implement supply-side constraint mechanisms and limited-sale strategies. By controlling the supply volume, these platforms enable a more effective realization of brand premium management. While there is a substantial body of literature examining the application of positive network effects [12,13], there is a paucity of research investigating negative network effects within the context of the consumer durables industry. Consequently, there is a need for a comprehensive examination of the influence of negative network effects on consumer purchasing utility and firm pricing decisions.
Durable consumer products are relatively expensive, prompting consumers to meticulously evaluate various factors such as product quality, pricing, anticipated failure rates, utility loss in case of malfunctions, quality of accompanying value-added services, pricing of such services, and brand effects when making purchasing decisions. Consequently, it is imperative for firms to incorporate considerations of consumer choice behavior into the product design and pricing processes [14]. Existing research typically employs probability choice models to describe consumer behavior [15,16], with the multinomial logit (MNL) model being the most widely applied. For example, Du et al. [17] used the MNL model to simulate consumer purchasing decision behavior, considering the impact of network effects on the seller’s optimal pricing decisions. Li et al. [18] applied MNL to simulate customer choice behavior when faced with multiple products, investigating how the firm determines and optimizes the quality and pricing of new products within a continuously evolving product line. Wang et al. [19] explored dynamic pricing strategies for retailers, focusing on inventory management and reference pricing, specifically tailored for loss-averse customers within a defined range. Wang et al. [16] investigated the joint optimization of product quality, pricing, and service duration within a customer choice modeling framework. While existing research based on the MNL model has incorporated factors such as network effects, service time, and inventory into their analyses of consumer choice behavior, less attention has been paid to the role of product failure and customer service preferences.
Therefore, this paper utilizes the multinomial logit (MNL) model to simulate customer purchasing decisions, incorporating factors such as product quality, expected failure rates, and value-added services into the product pricing model and explores the optimization of product and service provision decisions. This study addresses the following key questions:
- How should firms collaboratively determine their product quality decisions and value-added service pricing strategies across different sales contexts?
- How do anticipated product failures and network effects collectively influence customer demand, and thereby affect firms’ pricing decisions and overall profitability?
- How can the impact of utility loss caused by anticipated failures be quantified, and what managerial implications does this factor offer for optimizing marketing strategies and service design?
The main contributions of this paper are as follows:
- This work incorporates consumers’ preferences for service purchases into the consumer choice model. This extends the analytical scope of traditional product line design theory and offers a new theoretical modeling framework for joint pricing in service-embedded product systems.
- Pricing models are developed for single-product, homogeneous, and heterogeneous product lines, incorporating failure-induced utility loss to maximize profit. Closed-form solutions for price, market share, and profit are derived, thereby filling a research gap in the interaction between failure risk perception and product line pricing.
- The analysis highlights the necessity of considering the utility loss to consumers caused by anticipated product failures and investigates how such losses impact the pricing decisions for product lines and value-added services. The findings provide valuable insights for firms to develop optimized pricing strategies based on product attributes, thereby enhancing profitability.
The organization of this paper is outlined as follows: Section 2 provides a review of the relevant literature. Section 3 introduces model construction and theoretical analysis. Section 4 presents numerical analyses under different influencing factors in the heterogeneous product scenario. Section 5 provides the conclusion of this study and managerial insights.
2. Literature Review
2.1. Pricing of Durable Consumer Products
Durable consumer products refer to products that can be used multiple times and have a longer lifespan, such as automobiles, mobile phones, household appliances, etc. Consumers exercise careful consideration when purchasing such commodities, with quality and price being significant factors influencing consumer decisions [20,21,22]. Regarding internal factors such as product quality, researchers improve the performance of product fault detection through algorithm optimization to ensure a healthy production line [23]. Concurrently, scholars have conducted extensive and in-depth research on the pricing issues pertaining to durable consumer products. In earlier studies, Dhebar [24] analyzed firms’ game-perfect equilibrium pricing and quality strategies under different product improvement rates, considering heterogeneity in customers’ assessment of product quality. The study also posited that if technological changes occur too rapidly, producers cannot reliably commit to future prices and quality, thus leading to the absence of equilibrium strategies. Building upon this, Kornish [25] extended the research and found that in situations where products undergo rapid improvements, if a firm offers upgraded products without adjusting prices accordingly and provides different pricing for consumers who have purchased earlier versions, then equilibrium pricing strategies can indeed exist. With the advancement of research perspectives, studies on the pricing of durable goods have begun to shift from a strategic direction. Zhang and Chiang [26] considered the reference price effect and their findings indicate that while skimming pricing is the optimal choice for those with a short-term perspective, forward-thinking sellers may find that skimming price strategies or penetration strategies are more beneficial in the long term. Krishnamoorthy et al. [27] employed differential game theory to analyze dynamic advertising and pricing policies in the duopoly of durable products. Kogan [28] considered inventory dynamics and discussed Bertrand pricing competition between two firms that produce partially differentiated durable products within a limited schedule. Majumder et al. [29] investigated the optimal pricing and rebate promotion strategies for quality-differentiated products (i.e., regular and upgraded versions) in a manufacturer–retailer supply chain. From the perspective of product circulation, Vafaeinejad and Sajadieh [30] studied trade-in prices and basic warranty periods for durable products based on heuristic algorithms for strategic customers.
Furthermore, related research has expanded into the joint optimization of firms’ operational decisions and product–service strategies. For instance, Mukherjee et al. [31] examined optimal decisions in pricing, advertising, and product quality, while simultaneously incorporating product recall and recovery strategies. Liu and Wang [32] analyzed pricing and warranty decisions following failures within the initial warranty period and their impact on subsequent maintenance services. While these studies have deepened our understanding of integrated decision-making in durable goods markets across multiple dimensions, they largely overlook the impact of customer choice behavior, such as service preferences, on operational management. Our work specifically notices this gap.
2.2. Pricing of Value-Added Services
Under the highly competitive market environment and continuous differentiation of customer needs, value-added services have transitioned from serving as mere value-realization instruments to becoming pivotal strategic differentiators for competitive advantage. This shift reflects the move from product-focused to service-driven business models, pushing companies to adopt customer-centered operations [33]. Consequently, the impact of services on customer choice behavior, as well as the pricing strategies for these services, has emerged as a prominent area of research. Luo et al. [34] systematically investigate the attribute interdependencies and systemic complementarity between products and services. By incorporating manufacturers’ operational capacities and consumers’ heterogeneous preferences into a yield management paradigm, they establish an optimal product–service bundling configuration through a dual-aspect matching protocol. Taking factors like competition intensity, service cost, and product reliability into account, Huang et al. [35] investigated the warranty service improvement strategies of two competing manufacturers. Bian et al. [36] investigated whether trade-in services are for the same product or an upgraded version of the old product, examining optimal warranty strategies and related pricing decisions under two scenarios: providing traditional extended warranties (EWR) and providing new extended warranties with trade-in services (EWT). Hong et al. [37] addressed the novel research question of integrating value-added services into the remanufacturing model, studying the role of value-added services in closed-loop supply chains (CLSCs) and their impact on optimal profits and related decision variables. Tan et al. [38] developed a novel analytical model for e-commerce, incorporating value-added services and order cancellation behavior to explore optimal pricing strategies and value-added service approaches in both centralized and decentralized channels. Liu et al. [39] investigated online product pricing in a dual-channel context, accounting for quality differences, potential defects, and offline services of dual-channel products from the perspective of product after-sale.
Although the existing literature emphasizes the importance of value-added services in mitigating product quality issues, our study extends this discourse by analyzing how product failure and customer service preferences influence product line design and development.
2.3. Negative Network Effects
A product exhibits network effects when the utility that a customer derives from purchasing it is affected by the sales volume of the same or similar products. This means that the perceived value or satisfaction a consumer gains from the product increases with the number of other users or the adoption rate of similar products in the market [40]. Network effects can be positive [10] or negative; if a consumer’s demand for a product decreases as the quantity purchased by other consumers increases, the product experiences negative network effects [41]. There are numerous scenarios in daily life where products demonstrate negative network effects, such as transportation mode choices and customization of high-end products. For instance, if there is an increasing number of customers purchasing cars in a city, it leads to traffic congestion and insufficient parking spaces, resulting in a decrease in utility for customers; similarly, if a firm produces a series of products and the number of customers buying these products increases, consumers with personalized demands become less willing to purchase these products. Such products exhibit diminishing attractiveness as more customers purchase them, resulting in reduced utility for customers. Agarwal and Kickhöfer [42] considered emission and congestion as two negative network effects and proposed a simulation-based approach to compute correct dynamic price levels for transportation systems, providing average charge levels per kilometer during both peak and off-peak hours. Additionally, Wang and Wang [40] pointed out that ignoring network effects could result in significant revenue losses if they exist. Meanwhile, Qi et al. [43] found that considering negative network effects in the pricing optimization problem can significantly improve a firm’s anticipated profits. As a result, integrating negative network effects into the design and optimization of both products and services plays a crucial role in maximizing revenue.
In summary, the existing research in revenue management and marketing has extensively explored consumer pricing, value added service design, and network effects. However, the integration of customer choice behavior, especially under product failure and network effects, remains understudied. With the rise of digital commerce, diverse sales contexts, such as single, homogeneous, and heterogeneous product sales, have also become operationally significant. This paper uses a multinomial logit (MNL) model to examine how value-added services influence customer choices. The model incorporates product failure rates, utility loss from malfunctions, negative network effects, and service preferences into a unified pricing framework. We derive optimal pricing strategies for products and services, accounting for quality and consumer behavior. Table 1 summarizes our contributions relative to prior work.

Table 1.
An overview of considering product quality and network effects.
3. Problem Description and Model Construction
Consider a monopolistic firm aiming to develop n distinct products, denoted as , where each product is mutually independent. Given the importance of product quality assurance, firms not only ensure that their products are designed and manufactured to high standards but also provide complementary value-added services to build consumer trust and enhance satisfaction. Consumers can choose to purchase the product alone or, depending on their specific needs, opt for additional value-added services alongside the product. To simplify, assume that the market size is normalized to 1, and the utility that a customer derives from purchasing product i is represented by the following expression:
where stands for the deterministic component of utility acquired by customers upon selecting product i, whereas represents the random disturbance term resulting from unpredictable variables, which is assumed to be independently and identically distributed (i.i.d.) and follow a Gumbel distribution, adhering to the IIA assumption [16,17].
Considering the simultaneous influence of product characteristics and value-added services on consumer satisfaction, it can be further derived that the anticipated utility a customer derives from purchasing the product is:
where represents the perceived quality of the product purchased by the customer, denotes the level of value-added services accompanying the product, and signifies the price of the product. Building on the findings of Zhang et al. [46], which suggest that optimal service pricing may exhibit a proportional relationship with optimal product pricing, we assume the ratio of the service price to the product price is given as m (), such that . Considering that the anticipated failure rate of the product, is inversely correlated with product quality, where higher quality leads to a lower anticipated failure rate and it follows that . Moreover, the anticipated product failure exerts a significant influence on customers’ decisions to purchase value-added services. Within a specific timeframe, if a product experiences a failure, customers who opted not to purchase value-added services incur direct utility losses, which may substantially degrade their user experience. Conversely, customers who acquired value-added services can avoid such utility losses through timely repair services, ensuring the continuity of their consumption experience and enhancing overall satisfaction. This disparity underscores the pivotal role of value-added services in shaping customer decisions and bolstering product competitiveness. We define as the utility loss incurred by customers due to product failure.
Additionally, recognizing that certain product attributes or market conditions may generate negative impacts as the user base grows, we incorporate negative network effects, denoted as (), into the model. This integration highlights the dual impact of network effects and product quality on consumer behavior. Customer preferences for value-added services are captured by , where . indicates no preference for value-added services. At this point, the purchase utility is , while reflects a strong preference, resulting in a definitive purchase of the product’s services. In this case, the customer’s purchase utility is .
It is assumed that consumers entering the market will purchase no more than a single unit of the product or its corresponding value-added service. We can utilize the multinomial logit (MNL) probability choice model to describe customers’ choice behavior. This model allows us to derive the probability of purchasing product i as follows:
The probability of a consumer choosing not to purchase any product is represented by , where . Define . Assuming the development cost of the product is denoted as , Zhang et al. [47] found that service costs are ultimately allocated to product costs and prices, effectively bundled into the initial cost structure and pricing as a composite expense. Therefore, for modeling simplicity and clarity, we disregard the cost investment in value-added services. The maximum achievable profit for the enterprise can be expressed as follows:
For the firms offering products and services, they typically set differentiated prices based on the quality levels of their offerings to achieve market segmentation. Generally, firms determine which options to provide based on a menu of “product + service” combinations—that is, they consider a feasible set of product and service options , along with the optimal pricing strategy for the offered options.
Under the objective of profit maximization, the pricing problem for product line and value-added services can be expressed as:
Theorem 1.
- (a)
- The optimal offer set is to offer all available product and service options, i.e., .
- (b)
- For all , , the firm’s optimal profit margins are identical,
- (c)
- The total purchase probability is
Proof.
See Appendix A.1. □
Theorem 1 explains the optimal decision-making for companies when developing product lines. First, a firm continuously produces and introduces new products; the new addition will cannibalize market share from existing products proportionally. However, adding a new product option will always attract some specific customers, helping to increase total market share. It can also be interpreted as follows: the firm will extend its product line if the new product generates positive marginal profit after accounting for the demand loss due to proportional substitution. Second, companies should set prices based on the “Equalization of Effective Margins” rule. This prevents new products from stealing sales from existing ones, which could hurt overall profits. Finally, the probability of customers buying a product can be directly calculated as a function of expected profit. This means that with the right product selection and pricing strategy, companies can predict customer purchasing behavior more accurately.
To derive explicit expressions for prices, we refer to existing research that has demonstrated that the profit function is not concave with respect to price [48]; the variables are transformed into functions of market share for ease of solution. Given the one-to-one mapping between price and market share, the price of product i is determined through this transformation as follows:
Thus, the pricing problem for the firm’s product line is:
The following section will explore the optimal decisions under various development scenarios and analyse the impacts of factors such as product quality, anticipated failure rate, and service quality on the optimal solution.
3.1. Single Product
First, we examine the pricing issue when a firm only develops a single product. The product quality is denoted as b, development cost as c, and the anticipated failure rate of the product is inversely correlated with its quality, denoted as .
If a product failure results in a utility loss of for the consumer, the level of service associated with the product is s, and the degree of consumer preference for complementary services can be quantified as . The service price is expressed as , (where p is the product price, with ). The product’s negative network effect is denoted by the parameter (), and the purchase probability is represented by q.
The profit function is given by:
The optimal product pricing problem can be represented as:
Proposition 1.
When the firm focuses on developing a single product, the profit function exhibits a concave relationship with market share q. The optimal theoretical solutions for market share, product price, service price, and profit can be derived as follows:
where ,
Proof.
See Appendix A.2. □
Proposition 1 demonstrates that when the firm develops a single product and provides value-added services for it, the profit function exhibits concavity in relation to the probability of purchase. This allows for the optimal theoretical derivation of the market share, product price, service price, and profit. Therefore, when developing a single product, the firm should comprehensively consider factors such as the price ratio between the service and the product, product quality, negative network effects, product development cost, service level, the utility reduction resulting from product failures, and consumer preferences for value-added services before making pricing decisions.
3.2. Homogeneous Products
Homogeneous products refer to items that offer identical quality and price, with any variations limited to non-core attributes such as color. Such products provide consumers with equivalent systematic utility. For example, if an e-commerce platform sells both black and white versions of a smartphone that are identical in all key aspects including performance, price, and model specifications, these variants should be modeled as homogeneous products in consumer choice theory. In this context, the consumer’s choice of color depends solely on random and unobservable preferences, captured by the random utility term , rather than on any discernible difference in observable utility.
When the firm develops n homogeneous products, the quality of each product is denoted by , the unit production cost by , and the utility reduction resulting from product failures by . Assuming that the service provided for each product are also homogeneous, with the service level denoted as and consumer preference for the value-added service as . The product’s price is , and the proportion between the product price and the service price is denoted by m. So the purchase probability for each product is given by:
According to Equation (6), the product price can be formulated as:
where ; the profit can be expressed as:
Proposition 2.
For the firm developing n homogeneous products, the profit function exhibits a concave relationship with market share . The optimal theoretical solutions for market share, product price, service price, and profit can be expressed as follows:
where ,
Proof.
See Appendix A.3. □
Proposition 2 demonstrates that when a firm develops a product line consisting of homogeneous products and offers uniform services, the profit function exhibits a concave relationship with purchase probability. The optimal prices for both products and services, market share, and the maximum profit achievable by the firm are all influenced by a combination of factors, including product quality, service levels, consumer preferences for services, network effects, and utility losses incurred by customers due to product failures. Furthermore, these optimal solutions differ significantly from those obtained when the firm develops only a single product, highlighting the complexity of product line expansion and the selection of value-added services, as well as their profound impact on strategic decision-making within the firm.
3.3. Heterogeneous Products
Heterogeneous products refer to items that differ in quality, price, or other key attributes within the consumer’s utility function, thereby providing distinct levels of systematic utility. For instance, if an e-commerce platform offers both high-end and low-end smartphones with significant and observable differences in performance, price, or model specifications, these products should be classified as heterogeneous. In this case, consumers would exhibit different choice probabilities for each variant based on their perceived utility.
This section further delves into the scenario where the firm develops n heterogeneous products. Assuming represents the quality of product i, with a development cost of . The anticipated failure rate is inversely proportional to quality, indicated by . The utility loss to customers due to product failure is denoted as . The level of value-added services provided for product i is represented by , and the degree of customer preference for the services is . Similarly, customer purchase utility is also influenced by the negative network effects . The firm shapes customers’ perceived utility of its offerings by modifying product quality and service standards. Subsequently, it determines the optimal product pricing and service pricing to achieve maximum profitability.
When the firm develops n products with distinct characteristics, the firm’s profit function and the issue of optimal pricing of value-added services are described by Equations (7) and (8). The following demonstrates that when customers exhibit a uniform preference for services across different products, the firm’s profit function remains concave with respect to product sales .
Proposition 3.
The profit function exhibits a concave relationship with market share , and the optimal theoretical solutions for market share, product price, service price, and profit can be expressed as follows:
where ,
Proof.
See Appendix A.4. □
Proposition 3 affirms that when a firm develops distinct products, each accompanied by corresponding value-added services, it can achieve optimal profitability under the condition that customers exhibit consistent yet differentiated preferences for the services across the product line. To attain this goal, the firm must adopt an optimal decision-making approach that accounts for multiple factors, including product quality, development costs, negative network effects, service levels, and customer preferences for value-added services. Additionally, the firm should strategically determine the ratio between product prices and service prices to maximize overall profits.
3.4. Theoretical Analysis
Corollary 1.
When the firm develops either a single product or n products with identical attributes, and customers exhibit no absolute preference for value-added services (), the optimal product price, purchase probability, and the firm’s maximum profit are all negatively correlated with the utility loss experienced by customers due to product failures, i.e., , , , , , .
Proof.
See Appendix A.5. □
Corollary 1 indicates that an increase in utility loss resulting from product failures leads to a reduction in the firm’s optimal pricing strategy, a contraction in market share, and a decline in the maximum achievable profit. When the utility loss caused by product failure rises, the perceived total utility of the product decreases, leading to lower willingness to pay and reduced purchase probability. In response, the firm must adopt a price reduction strategy. However, contracting demand and lower prices also undermines the firm’s optimal profit. Take the example of Romoss power banks: due to potential overheating, combustion, and explosion risks during usage, flagship stores on major e-commerce platforms such as Tmall and JD have delisted the relevant product series, resulting in significant losses for the company. For firms, product quality issues not only represent an operational crisis at the product level but also a trust crisis at the brand level.
From a practical perspective, this finding underscores the critical importance for firms to prioritize product reliability and quality control. In a market where consumer awareness of rights is growing and information spreads rapidly, product failures not only impact short-term sales but also cause long-term damage to brand reputation and customer loyalty. Firms should increase investment in quality management and after-sales services to reduce failure rates and improve response efficiency, thereby mitigating consumers’ perceived negative utility. Additionally, value-added measures such as extended warranties and hassle-free return policies can help rebuild trust, partially offset utility losses, stabilize pricing, and protect profit margins. Ultimately, building a reliability-driven product differentiation strategy will be key to sustaining competitiveness in quality-sensitive markets.
Corollary 2.
Regardless of whether the firm develops a single product or a homogeneous product line, both the optimal product sales volume and the maximum achievable profit for the firm are positively correlated with the increase in the network effect parameters, i.e., , , , . However, when or , the optimal product price decreases with the increase of the network effect parameters, i.e., , .
Proof.
See Appendix A.6. □
The market share and the optimal profit of the product increase with the increase of the network effect parameter of the product. However, when market share falls below a certain threshold, the product’s price decreases as the network effect intensifies. This contrasts with conventional findings on the positive influence of network effects on pricing [17]. In the presence of negative network effects, a larger market share requires the firm to offer greater price compensation, necessitating lower pricing. Thus, price reduction becomes a key strategy for mitigating negative network effects and improving profitability.
Furthermore, the firm’s market share and profit reach their maximum, and the price is minimal when is 0. This indicates that negative network effects significantly influence firm decisions and cannot be overlooked. Therefore, firms should take measures to mitigate the adverse effects of negative network effects by introducing personalized and customized products. By segmenting user needs and offering differentiated functionalities, firms can mitigate potential experience degradation or congestion effects resulting from user base expansion. For instance, through algorithmic recommendations, modular design, or user tagging systems to achieve more precise matching. From a long-term strategic perspective, companies should closely monitor the critical point where network effects may shift from positive to negative while scaling their user base. This requires ongoing data surveillance and user feedback to promptly detect adverse signals. Only by balancing market expansion with experience preservation can firms avoid the erosion of profits and market position due to negative network effects.
Corollary 3.
In the scenario where firms develop single products and homogeneous products, as long as consumers’ preference for services is not zero, the influence trends of changes in product quality and service level on the optimal solution are the same, exhibiting a monotonically increasing trend. Additionally, the rate at which the optimal solution increases with the increment of product quality is greater than or equal to the rate of increase with the increment of service quality, i.e., , , , , , .
Proof.
See Appendix A.7. □
Corollary 3 confirms that an increase in both product quality and service quality leads to an increase in optimal market share, optimal price, and profit. This suggests that an increase in product quality and service level attracts more consumers to the market, in which case firms can increase their prices accordingly to realize an increase in profits. Furthermore, the optimal pricing, market share, and profitability exhibit greater sensitivity to variations in product quality than to changes in service quality. High product quality not only meets customer expectations and reduces the burden of after-sales services but also often generates positive word-of-mouth and brand loyalty, attracting more potential customers. After establishing a solid foundation in product quality, enhancing service quality can further improve customer experience and satisfaction. Premium services not only compensate for any potential product deficiencies but also provide personalized, efficient support and solutions to customers, thereby strengthening the competitive advantage of the firm in the market. Therefore, under similar market conditions, firms should prioritize improving product quality while also considering service quality. Only when consumers’ preference for services is at its maximum should firms give equal weight to the quality of services and product quality.
Corollary 4.
The optimal market share of the firm developing single products and homogeneous products is seen to increase in line with an increase in consumer preference for value-added services, i.e., , .
Proof.
See Appendix A.8. □
From Corollary 4, it can be observed that as consumer preferences for services increase, product sales gradually increase. This indicates that an increase in consumer preferences for services stimulates new market demand, prompting firms to provide services and continuously improve service quality. Consequently, firms gain advantages in product and service sales and enhance the potential for profit growth. To effectively address this trend, firms can take measures to enhance consumer preferences for services, such as offering experiential services and increasing consumer awareness and emotional trust in services.
4. Numerical Experiments
The theoretical section analyses the optimal solutions for a firm developing a single product and multiple homogeneous products. To explore the effects of parameter variations on the optimal solution when the firm develops two heterogeneous products, this section presents the numerical experiment.
4.1. Variations in Utility Loss
Firstly, the analysis is conducted on the influence of changes in utility loss resulting from expected product failure on the optimal solution. Referring to Wang and Ye [49], suppose that the utility loss incurred by consumers due to the anticipated failure of two products is represented by . Let , , , , , , , . Figure 1 depicts the trend of the optimal solution with variations in consumer utility loss.
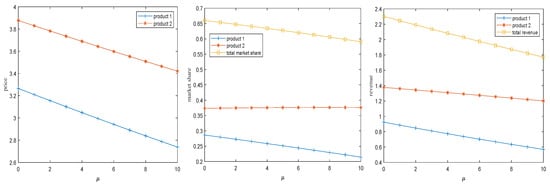
Figure 1.
The impact of the utility loss from the anticipated failure on the optimal solution.
As shown in Figure 1, an increase in the utility loss caused by expected failures leads to a decline in optimal prices regardless of product quality, along with a corresponding reduction in total market share and industry profit. It is noteworthy, however, that the market share of high-quality products slightly rises despite the overall market contraction. This phenomenon stems from the negative correlation between expected failure and product quality: as consumers become more sensitive to the risk and consequences of failures, they tend to prefer more reliable products, thereby shifting demand toward higher-quality alternatives.
This finding aligns closely with consumer behavior. In the case of high-end durable goods such as computers and automobiles, where high prices and long lifecycles amplify both economic and psychological costs of failure, consumers place greater emphasis on reliability and durability. Consequently, by consistently improving product quality firms can not only enhance brand credibility but also capture a larger market share in environments characterized by high perceived failure risk. Conversely, for daily necessities, consumer tolerance for failure is relatively higher, and the perceived utility loss from expected malfunction is low. As a result, price often becomes the dominant decision factor. In such contexts, firms may adopt a cost-oriented low-quality strategy to gain market share through competitive pricing without overinvesting in extreme reliability.
4.2. Variations in Network Effects
The subsequent section examines the impact of the product’s network effect parameter on the optimal solution, assuming that the network effect parameter, denoted as , varies within the range of [45], with other parameters set as , , , , . The trend of the optimal solution as the network effect varies is illustrated in Figure 2 and Figure 3.
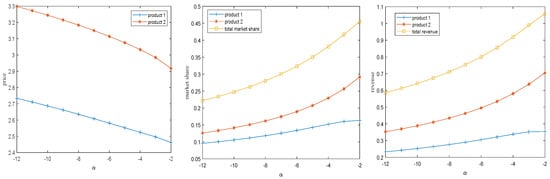
Figure 2.
The impact of network effects on the optimal solution when , .
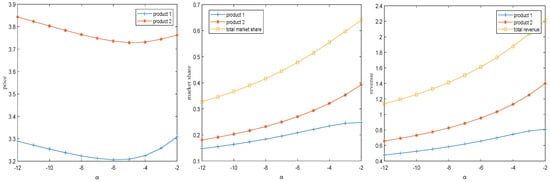
Figure 3.
The impact of network effects on the optimal solution when , .
Figure 2 provides a detailed illustration of how the network effect parameter influences the optimal pricing, market share, and profit, under the condition that no value-added services are offered. The analysis reveals that as the network effect parameter increases, both optimal market share and profit experience a gradual rise, while the optimal price decreases. This indicates that network effects are a critical factor that firms must account for in their product line strategies. Specifically, when the impact of network effects on consumer choice behavior is minimal, i.e., when the network effect parameter approaches zero, firms are able to set a lower product price to attract a larger market share, thereby increasing their profit. However, the scenario shifts as the influence of network effects intensifies. With the strengthening of network effects, or as the magnitude of the network effect parameter increases, the firm faces a trade-off. While the firm may be inclined to raise the product price due to the increasing interdependence among consumers, the optimal market share and profit experience a decline. This phenomenon occurs because, as network effects strengthen, consumers’ utility is increasingly affected by the choices of others in the market, which can lead to a reduction in demand and, ultimately, a reduction in the firm’s profitability. In essence, while network effects can initially enhance a firm’s market share and profits by leveraging consumer interdependence, excessive network effects may have detrimental consequences. These include higher prices, which can discourage potential customers and reduce overall market penetration. Therefore, understanding the balance between product pricing and network effects is essential for firms when developing their product lines, as it directly impacts both the profitability and competitive dynamics in the market.
From Figure 3, when value-added services are provided, it can be observed that both the optimal market share and optimal profit increase with the network effect parameter, while the price initially decreases and then increases. When there are no value-added services, enterprises counteract negative network effects by continuously reducing prices, thereby achieving growth in market share and profits. Relatively speaking, the presence of value-added services indicates that the strategy has become completely different, and enterprises no longer need to blindly lower prices. When the negative network effect parameters increase to a certain extent, enterprises can even start to raise prices while still continuing to expand their market share and profits. Therefore, through the strategic innovation of providing services, the traditional single pricing model can be transformed into value-oriented differentiated pricing, and the impact brought by negative network effects can be reduced, achieving comprehensive growth in pricing power, market share, and profits.
Thus, it can be seen that, unlike in the cases of developing a single product or homogeneous products, the impact of negative network effects is more complex when developing heterogeneous products. The presence and enhancement of negative network effects are generally unfavorable for the firm, but offering personalized value-added services can help reduce the impact of negative network effects to some extent.
4.3. Quality Variations
Subsequently, we analyze the influence of both product quality and service quality on the optimal solution under conditions of product failures and network effects. Assuming product quality b ranges from [18], with the network effect parameter for product 1 set as and for product 2 set as , while other parameters are set as , , , , , , the trend of the optimal solution in relation to variations in product quality is illustrated in Figure 4.
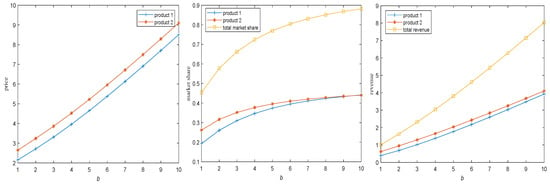
Figure 4.
The impact of product quality on the optimal solution.
Additionally, assuming the service quality s for both products ranges from , with product 1 quality , and product 2 quality . With all other parameters held constant, the trend of the optimal solution with respect to changes in service quality is shown in Figure 5.
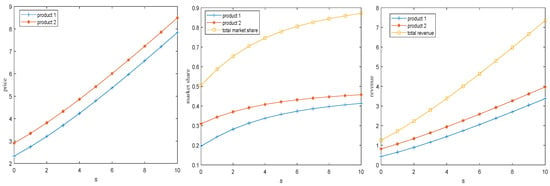
Figure 5.
The impact of service quality on the optimal solution.
As shown in Figure 4 and Figure 5, as the product quality and service quality improve, the optimal price and the market share of each product, as well as the total market share and maximum profit of the firm, all increase. For the firm, even in the presence of negative network effects, increasing product or service quality—without considering product development costs—can help the firm capture a larger market share, set higher prices for its products or services, and ultimately increase its profit. Therefore, if a firm aims to expand its profit margin and enhance the core competitiveness of its products or services, it must continuously optimize the quality of both the products and the services offered. To translate this insight into actionable strategies, firms should adopt several practical measures. For instance, service quality can be integrated into differentiation strategy by offering exclusive customer service for premium product lines, providing 24 h technical support or on-site maintenance, thereby supporting a high-price positioning through enhanced service value. Additionally, marketing campaigns such as “quality certification” or “user experience enhancement” programs can be implemented. Utilizing third-party certifications and user-generated review videos will help strengthen consumers’ perception of quality improvements, thereby increasing their willingness to pay a premium.
From the perspective of e-commerce platforms, a “warranty tiering” strategy can be introduced, offering extended warranty periods or comprehensive coverage including accidental damage to high-rated and reputable brands. Differentiated warranty services will also help attract more high-quality brands to the platform. Furthermore, to promote overall service quality, platforms may establish service performance incentive mechanisms, for example, by dynamically adjusting traffic allocation or search rankings based on sellers’ service quality scores, such as response speed and return handling satisfaction. This approach encourages sellers to proactively improve their service levels.
4.4. Analysis of Necessity
In the presence of anticipated failures, the influence of utility loss incurred by consumers due to such failures on product line and value-added service pricing decisions cannot be overlooked. Failure to consider this aspect may result in a certain degree of loss for the firm. Subsequently, numerical experiments are conducted under three scenarios: a firm developing a single product, a line of homogeneous products, and a line of heterogeneous products. When developing a single product, let , , , , , . When developing homogeneous products, assume the development of only two homogeneous products with parameters set the same as those for developing a single product. When developing heterogeneous products, similarly assume the development of two heterogeneous products with parameters set as , , , , , , , , , . Assuming the utility loss caused by anticipated failures is .
In Table 2, the values of optimal profits , , and are obtained through Propositions 1, 2, and 3, respectively, where , , and represent the profits corresponding to scenarios where the utility loss from anticipated failures is not considered. The price is determined from propositions 1, 2, and 3 under the condition of , with the corresponding market share obtained from Equation (6) incorporating the actual utility loss . In general, unless the actual utility loss is zero. The profits without considering the utility loss from anticipated failures are computed using . , , and l represent the profit losses incurred when the utility loss from anticipated failures is not considered.

Table 2.
Comparison of optimal profits considering utility loss from anticipated failure.
The data from the table demonstrates a clear pattern: regardless of whether the firm is developing a single product, a homogeneous product line, or heterogeneous products, the optimal profit, when accounting for utility loss from anticipated product failures, consistently exceeds the profit obtained in the absence of such considerations. Specifically, when the profit loss reaches as high as 5.51%. This trend indicates that the omission of anticipated utility losses could significantly undermine the firm’s profitability. Moreover, as the magnitude of the utility loss resulting from product failures increases, the potential for profit erosion escalates substantially, further reinforcing the importance of factoring in these losses when determining pricing strategies. In light of this, firms must recognize that product failures, particularly those that result in consumer dissatisfaction and utility loss, can have a long-term impact on their financial outcomes. By neglecting to incorporate these losses into the pricing model, companies risk not only immediate profit reductions but also the potential for a deteriorating customer base. Consumers who experience utility loss due to product failures may become less loyal and more likely to turn to competitors offering more reliable products or enhanced service levels.
This analysis also underscores the significance of value-added services in mitigating the effects of product failures. By offering value-added services that reduce or eliminate the negative consequences of product failures, companies can cushion the impact of utility loss, protect their profit margins, and maintain a competitive edge in the market. Additionally, incorporating utility loss into pricing decisions allows firms to more accurately align their pricing strategies with the perceived value of the product or service, ensuring that consumers’ expectations are met while optimizing the firm’s profitability.
In conclusion, the integration of utility loss from anticipated product failures into pricing decisions is not merely a theoretical consideration but also a practical necessity. Firms that overlook this aspect may face severe profitability challenges. Therefore, businesses must carefully analyze and incorporate all relevant factors, including the potential utility loss resulting from product failures, to develop pricing strategies that maximize both short-term profits and long-term customer loyalty.
4.5. Robust Analysis
This section investigates the robustness of the model when there are estimation errors in the utility-loss parameters caused by anticipated failures. Without loss of generality, only the scenario of developing two heterogeneous products is considered. Assume the firm has an estimate of the utility-loss parameters, denoted as . The pricing decision based on is , where and . However, the true utility-loss parameters are , and the resulting market shares under the pricing strategy are , . If , then ; otherwise, . The actual profit is calculated as . All other parameters remain consistent with those in Section 4.4. The profit loss is defined as , where represents the optimal profit achieved when no estimation error exists in the utility-loss parameters attributable to anticipated failures. The results of the profit and loss analysis are presented in Table 3.

Table 3.
Robustness of profit.
As shown in Table 3, the model exhibits strong robustness in terms of profit performance when there are certain estimation errors in the utility-loss parameters attributable to anticipated failures. Under reasonable error conditions, the maximum absolute profit loss is 1.95%, with most cases not exceeding 1%. Therefore, when estimation errors in these parameters remain within an acceptable range, near-optimal robust profit can be achieved. Consequently, the product line design and pricing model incorporating product quality and value-added services, as proposed in this study, demonstrates significant robustness in the presence of parameter estimation errors. This finding holds important implications for developing and implementing effective service design and pricing strategies, particularly in market environments characterized by high uncertainty.
5. Conclusions
As product diversification expands and market competition intensifies, the provision of value-added services has become an essential strategy for manufacturing firms navigating transformation. This study investigates the utility loss faced by consumers due to the anticipated failure of products, under the assumption that value-added services provided by the firm can effectively mitigate and repair such failures. Consumer preferences for these services significantly influence the firm’s product–service design and pricing strategies. To model consumer choice behavior, the multinomial logit (MNL) model is applied, and the study examines optimal pricing strategies for three scenarios: a single product, a homogeneous product line, and a heterogeneous product line. Theoretical analyses investigate how optimal solutions for single and homogeneous products are impacted by factors such as negative network effects, product quality, service levels, and utility loss due to expected product failures. In the Section 4, the focus shifts to heterogeneous products, exploring how variations in negative network effects, product and service quality, and the utility loss from anticipated failures affect the optimal decisions. Finally, the study highlights the critical role of incorporating anticipated failure-related utility loss into pricing strategies for product lines and associated services.
The specific findings of this paper are as follows:
(1) Utility loss induced by anticipated failures leads to a decline in overall market price, profit, and total market share. In contrast, the market share of high-quality products exhibits an upward trend, indicating that consumers shift toward more reliable high-quality alternatives to mitigate risks when perceiving high failure potential.
(2) In the presence of negative network effects, both the optimal market share and maximum profit increase with the network intensity parameter, irrespective of value-added service provision. However, optimal price decreases with the parameter when no service is offered, whereas it decreases first and then increases when service is incorporated. Providing value-added services enhances both market share and profit.
(3) Both product quality and service quality show positive correlations with the firm’s optimal pricing, market share, and profit. They function as core drivers in establishing brand differentiation, improving customer satisfaction, and ultimately promoting sustained business growth.
(4) The study underscores the necessity of incorporating utility loss from anticipated failures into decision-making. Ignoring this influence in product line and service pricing may result in non-trivial profit loss for the firm. Moreover, the model demonstrates strong profitability robustness even under parameter estimation errors.
Based on the above conclusions, the corresponding management implications are as follows:
(1) Firms should establish a product-category-differentiated strategy centered on consumer risk perception. For high-end durable goods (e.g., automobiles, premium electronics), where anticipated failures lead to substantial consumer utility loss, a quality-oriented product strategy is recommended. This includes enhancing reliability design and offering extended warranty service bundles. For low-value consumables (e.g., daily necessities), a cost-priority strategy helps maintain focus on essential functionality and price competitiveness, avoiding profit erosion from excessive quality investment.
(2) When developing a product line, firms should not only emphasize product heterogeneity and offer personalized and customized products but also account for the adverse impact of negative network effects. Enhancing service quality in this context can mitigate the detrimental effects of negative network effects to some extent.
(3) Continuous improvement in product quality serves as the driving force behind a firm’s rapid growth, while a customer-centric approach to enhancing service quality represents the primary productive power of development. In the context of increasing product homogenization and intensified industry competition, firms are shifting their strategic focus toward enhancing the customer service experience. Service quality has become a critical metric for achieving rapid growth. By creating “distinctiveness” and “differentiation” in product quality and service from the perspective of customers, firms can exceed customer expectations, attract more buyers, and ultimately enhance business performance.
This study has several limitations. In terms of the market environment, it does not account for competitive interactions among firms. Regarding customer behavior, the model assumes homogeneous customer choice and does not analyze product line and service pricing under heterogeneous preferences. Furthermore, the cost bundling assumption may not hold in contexts where service and product cost structures are highly independent, services operate as standalone profit centers, or highly customized services are offered. These limitations also help identify directions for future research.
Author Contributions
Conceptualization, W.Q. and N.L.; methodology, X.L. and B.Z.; formal analysis, J.P.; writing—original draft preparation, N.L. and J.P.; writing—review and editing, W.Q. and N.L.; visualization, B.Z.; supervision, X.L.; funding acquisition, W.Q. and X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China, grant number 72001071, in part by the National Social Science Foundation of China, grant number 24FGLB001, in part by the Philosophy and Social Sciences Planning Project of Henan Province in China, grant number 2022BJJ031, in part by the Program of Higher Education Philosophy and Social Sciences Innovative Talents of Henan Province in China, grant number 2024-CXRC-02, in part by the Postdoctoral Science Foundation of China, grant number 2024M750784, in part by the Planning Fund Project of Humanities and Social Sciences Research of the Ministry of Education of China, grant number 24YJA630069, in part by the Key Research and Promotion Project of Henan Province (Soft Science Research), grant number 252400411228, in part by the Humanities and Social Sciences in Henan Provincial Colleges and Universities (General Category), grant number 2026-ZZJH-015, and in part by Philosophy and Social Sciences in Henan Provincial Colleges and Universities (Major Project), grant number 2026-JCZD-02.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MNL | Multinomial Logit model |
| VAS | Value-added services |
Appendix A
Appendix A.1. Proof of Theorem 1
For any given assortment S and price , let . After rearranging terms and performing algebraic operations, we obtain:
where Here, the left-hand side can be interpreted as a 45° line, while the right-hand side is a strictly decreasing function of r for any fixed S and . Thus, the optimization problem reduces to finding the unique intersection point between this decreasing function and the 45° line.
Consequently, the problem is equivalent to:
where is defined as:
By taking the first-order partial derivative of with respect to , we derive:
The above equation reveals that when , increases with , whereas when , decreases with . Therefore, reaches the maximum at . At this point:
Since is always positive, the optimal strategy is to offer all products, i.e., . Moreover, there exists a unique solution satisfying:
For each product , , the optimal profit margin is identical:
The total purchase probability is given by:
Appendix A.2. Proof of Proposition 1
Because
where , , so . Thus, the function regarding q is concave, and has a maximum value.
Let , , we obtain
Let , then , , .
Based on the Lambert W function,
Appendix A.3. Proof of Proposition 2
Because
Let , , and in this case, the Hessian matrix of takes the form:
For any nonzero vector , . Hence, is a concave function with respect to . In this case, let to find the optimal market share of the product, i.e.,
Appendix A.4. Proof of Proposition 3
The first derivative of the profit function with respect to market share is:
The second derivative of the profit function with respect to market share is:
For the Hessian matrix of , the proof process is similar to Proposition 2; hence, is concave with respect to .
Let to find the optimal market share of the product, i.e.,
Let ; the optimal market share is:
where
Appendix A.5. Proof of Corollary 1
For the case of developing a single product:
Therefore, we can have
For the scenario of developing n homogeneous products:
So we can have
Appendix A.6. Proof of Corollary 2
For the case of developing a single product:
For the scenario of developing n homogeneous products, given , differentiating both sides of the equation with respect to yields:
Since the n products are homogeneous, we have:
Then,
From Equation (A5), it can be derived that:
When , ; otherwise .
The profit function is:
Its derivative with respect to is:
Appendix A.7. Proof of Corollary 3
For the case of developing a single product:
When , due to , it follows that , , .
For the scenario of developing n homogeneous products:
Similarly, when , due to , it follows that , , .
Appendix A.8. Proof of Corollary 4
For the case of developing a single product:
For the scenario of developing n homogeneous products:
References
- Zhu, T.; Nie, C.; Jiang, Z.R.; Hu, X.P. When do consumers buy during online promotions? A theoretical and empirical investigation. Decis. Support Syst. 2024, 182, 114233. [Google Scholar] [CrossRef]
- Mollenkopf, D.A.; Peinkofer, S.T.; Chu, Y. Supply chain transparency: Consumer reactions to incongruent signals. J. Oper. Manag. 2022, 68, 306–327. [Google Scholar] [CrossRef]
- Shen, B.; Cao, Y.; Xu, X. Product line design and quality differentiation for green and non-green products in a supply chain. Int. J. Prod. Res. 2020, 58, 148–164. [Google Scholar] [CrossRef]
- Liu, C.; Chen, T.; Pu, Q.; Jin, Y. Text mining for consumers’ sentiment tendency and strategies for promoting cross-border e-commerce marketing using consumers’ online review data. J. Theor. Appl. Electron. Commer. Res. 2025, 20, 125. [Google Scholar] [CrossRef]
- Bakshi, N.; Kim, S.-H.; Savva, N. Signaling new product reliability with after-sales service contracts. Manag. Sci. 2015, 61, 1812–1829. [Google Scholar] [CrossRef]
- Mitra, A. Warranty parameters for extended two-dimensional warranties incorporating consumer preferences. Eur. J. Oper. Res. 2021, 291, 525–535. [Google Scholar] [CrossRef]
- Golara, S.; Dooley, K.J.; Mousavi, N. Are dealers still relevant? How dealer service quality impacts manufacturer success. Prod. Oper. Manag. 2021, 30, 3560–3578. [Google Scholar] [CrossRef]
- Market Research Future. Consumer Electronics Extended Warranty Market Research Report by Warranty Type, Product Category, Duration, Sales Channel, Customer Segment, and Region (2025–2034). Available online: https://www.marketresearchfuture.com/reports/consumer-electronics-extended-warranty-market-29593 (accessed on 25 August 2025).
- Dai, A.; Yang, X.; Yang, D.; Li, T.; Wang, X.; He, S. Optimizing extended warranty options with preventive maintenance service under multinomial logit model. Eur. J. Oper. Res. 2025, 321, 600–613. [Google Scholar] [CrossRef]
- Hajihashemi, B.; Sayedi, A.; Shulman, J.D. The perils of personalized pricing with network effects. Mark. Sci. 2022, 41, 477–500. [Google Scholar] [CrossRef]
- Belloni, A.; Deng, C.; Pekeč, S. Mechanism and network design with private negative externalities. Oper. Res. 2017, 65, 577–594. [Google Scholar] [CrossRef]
- Xu, B.; Li, H.; Zhang, X.; Alejandro, T.B. Equilibrium blockchain adoption strategies for duopolistic competitive platforms with network effects. J. Bus. Res. 2023, 164, 113953. [Google Scholar] [CrossRef]
- Yi, Z.; Li, F.; Ma, L. The impact of distribution channels on trial-version provision with a positive network effect. Omega-Int. J. Manag. S. 2019, 85, 115–133. [Google Scholar] [CrossRef]
- Zhu, S.; Du, S.; Nie, T.; Zhu, Y. Pricing strategy for co-created products in platform-based consumer innovation. Electron. Commer. Res. Appl. 2024, 67, 101431. [Google Scholar] [CrossRef]
- Gallego, G.; Wang, R. Multiproduct price optimization and competition under the nested logit model with product-differentiated price sensitivities. Oper. Res. 2014, 62, 450–461. [Google Scholar] [CrossRef]
- Wang, R.; Ke, C.; Cui, S. Product price, quality, and service decisions under consumer choice models. Manuf. Serv. Oper. Manag. 2022, 24, 430–447. [Google Scholar] [CrossRef]
- Du, C.; Cooper, W.L.; Wang, Z. Optimal pricing for a multinomial logit choice model with network effects. Oper. Res. 2016, 64, 441–455. [Google Scholar] [CrossRef]
- Li, H.; Webster, S.; Yu, G. Product design under multinomial logit choices: Optimization of quality and prices in an evolving product line. Manuf. Serv. Oper. Manag. 2020, 22, 1011–1025. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, N.; Wu, J.; Zhu, Q. Optimal pricing and inventory policies with reference price effect and loss-averse customers. Omega-Int. J. Manag. S. 2021, 99, 102174. [Google Scholar] [CrossRef]
- Shen, Y. Price and advertising competition in an online marketplace: The tradeoff between quality and cost. Electron. Commer. Res. Appl. 2023, 60, 101276. [Google Scholar] [CrossRef]
- Sun, F.; Yang, H.; Chen, J.; Chen, B.; Yu, B. Information service and quality strategies in a supply chain. Transp. Res. Pt. E-Logist. Transp. Rev. 2025, 199, 104169. [Google Scholar] [CrossRef]
- Dong, H.; Park, K.K.C.; Kim, J.M. The role of product type in online review generation and perception: Implications for consumer decision-making. J. Theor. Appl. Electron. Commer. Res. 2025, 20, 135. [Google Scholar] [CrossRef]
- Kang, Z.Q.; Catal, C.; Tekinerdogan, B. Product failure detection for production lines using a data-driven model. Expert Syst. Appl. 2022, 202, 117398. [Google Scholar] [CrossRef]
- Dhebar, A. Durable-goods monopolists, rational consumers, and improving products. Mark. Sci. 1994, 13, 100–120. [Google Scholar] [CrossRef]
- Kornish, L.J. Pricing for a durable-goods monopolist under rapid sequential innovation. Manag. Sci. 2001, 47, 1552–1561. [Google Scholar] [CrossRef]
- Zhang, J.; Chiang, W.Y.K. Durable goods pricing with reference price effects. Omega-Int. J. Manag. S. 2020, 91, 102018. [Google Scholar] [CrossRef]
- Krishnamoorthy, A.; Prasad, A.; Sethi, S.P. Optimal pricing and advertising in a durable-good duopoly. Eur. J. Oper. Res. 2010, 200, 486–497. [Google Scholar] [CrossRef]
- Kogan, K. Pricing competition with inventory considerations in a hazard rate-prone market of durables. J. Econ. Dyn. Control 2016, 73, 298–313. [Google Scholar] [CrossRef]
- Majumder, S.; Nielsen, I.; Maity, S.; Saha, S. Consumer rebate strategy for a manufacturer selling price-quality differentiated products. Int. Trans. Oper. Res. 2025, 32, 3008–3049. [Google Scholar] [CrossRef]
- Vafaeinejad, K.; Sajadieh, M.S. Trade-in price and base warranty length: A heuristic algorithm for concurrent optimization. Comput. Ind. Eng. 2022, 171, 108504. [Google Scholar] [CrossRef]
- Mukherjee, A.; Carvalho, M.; Zaccour, G. Managing quality and pricing during a product recall: An analysis of pre-crisis, crisis and post-crisis regimes. Eur. J. Oper. Res. 2023, 307, 406–420. [Google Scholar] [CrossRef]
- Liu, P.; Wang, G.J. Two-dimensional warranty policy design with the consideration of protection term. Int. J. Prod. Econ. 2024, 276, 109350. [Google Scholar] [CrossRef]
- Li, Y.; Tsang, Y.P.; Lee, C.K.M.; Chen, Z.-S. Strategic service supplier selection in servitized manufacturing: A linguistic preference-based decision support system. Int. J. Prod. Econ. 2025, 283, 109566. [Google Scholar] [CrossRef]
- Luo, J.; Jiang, Q.; Song, W. Hybrid offering configuration in servitization of manufacturing. Expert Syst. Appl. 2023, 224, 120028. [Google Scholar] [CrossRef]
- Huang, H.; Liu, F.; Zhang, P. To outsource or not to outsource? Warranty service provision strategies considering competition, costs and reliability. Int. J. Prod. Econ. 2021, 242, 108298. [Google Scholar] [CrossRef]
- Bian, Y.W.; Xie, J.Z.; Archibald, T.W.; Sun, Y.H. Optimal extended warranty strategy: Offering trade-in service or not? Eur. J. Oper. Res. 2019, 278, 240–254. [Google Scholar] [CrossRef]
- Hong, X.P.; Wang, L.; Gong, Y.M.; Chen, W.Y. What is the role of value-added service in a remanufacturing closed-loop supply chain? Int. J. Prod. Res. 2020, 58, 3342–3361. [Google Scholar] [CrossRef]
- Tan, Y.Y.; Guo, C.X.; Cai, D. Value-added service decision and coordination under fresh produce e-commerce considering order cancelation. Manag. Decis. Econ. 2023, 44, 2199–2210. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Qi, W.; Luo, X. Online product pricing considering product quality and return policy. J. Intell. Fuzzy Syst. 2023, 45, 659–673. [Google Scholar] [CrossRef]
- Wang, R.; Wang, Z. Consumer choice models with endogenous network effects. Manag. Sci. 2017, 63, 3944–3960. [Google Scholar] [CrossRef]
- Dupor, B.; Liu, W.-F. Jealousy and equilibrium overconsumption. Am. Econ. Rev. 2003, 93, 423–428. [Google Scholar] [CrossRef]
- Agarwal, A.; Kickhöfer, B. The correlation of externalities in marginal cost pricing: Lessons learned from a real-world case study. Transportation 2016, 45, 849–873. [Google Scholar] [CrossRef]
- Qi, W.; Liu, X.; Luo, X.; Zhang, Z.L. Product line optimization considering network effects. IEEE Syst. J. 2020, 16, 543–553. [Google Scholar] [CrossRef]
- Feng, Y.; Hu, M. Market entry and competition under network effects. Oper. Res. 2024, 72, 2467–2487. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, C.; Qi, W.; Wang, J. Product line and service pricing considering negative network effects. Comput. Ind. Eng. 2022, 170, 108328. [Google Scholar] [CrossRef]
- Zhang, X.; Han, X.; Liu, X.; Liu, R.; Leng, J. The pricing of product and value-added service under information asymmetry: A product life cycle perspective. Int. J. Prod. Res. 2015, 53, 25–40. [Google Scholar] [CrossRef]
- Zhang, Y.; Han, M.S.; Wang, K. Symmetric or asymmetric? Value-added service design for new and remanufactured products under competition. Int. J. Prod. Econ. 2025, 45, 659–673. [Google Scholar] [CrossRef]
- Li, H.; Huh, W.T. Pricing multiple products with the multinomial logit and nested logit models: Concavity and implications. Manuf. Serv. Oper. Manag. 2011, 13, 549–563. [Google Scholar] [CrossRef]
- Wang, X.; Ye, Z.S. Design of customized two-dimensional extended warranties considering use rate and heterogeneity. IISE Trans. 2020, 53, 341–351. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).