Dynamic Pricing for Internet Service Platforms with Initial Demand Constraints: Unified or Differentiated Pricing?

Abstract

Internet service platforms dynamically charge service prices to satisfy the time-varying service demand by leveraging both full- and part-time service providers. This study developed a dynamic pricing model for a monopolistic service platform under two pricing strategies: unified pricing and differentiated pricing. The model incorporates key factors such as demand fluctuations, initial demand constraints, and service quality. It proved the optimal dynamic pricing scheme aimed at maximizing the platform’s expected revenue and analyzed the equilibrium gap between the two strategies based on the optimal control theory. The results reveal the following: (a) The service quality elasticity coefficient, potential market, and demand fluctuation factor all positively affect the optimal service price under the two types of pricing strategies, whereas service quality has the opposite effect. (b) Regardless of pricing strategy, the initial service demand restriction negatively affects the optimal price of the platform. The gap between the optimal service prices under the two types of pricing strategies narrows as the potential service demand rises when customers are less sensitive to service price. (c) With initial demand restriction, the optimal service price rises over time as long as the service market satisfies specific conditions, but the expected revenue under the two types of pricing strategies evolves in significantly different trajectories. (d) The differentiated pricing strategy can help the platform improve revenue by setting a lower revenue-sharing ratio.

1. Introduction

Internet service platforms (abbreviated as service platforms) have emerged as critical infrastructure in the digital economy. Service platformization fundamentally reshapes service delivery across industries ranging from transportation (e.g., ride-hailing, takeout) and healthcare to cloud computing [1,2]. It has been propelled by a confluence of factors, including robust policy support, intense market stimulation, and the booming of the digital economy, especially the catalysis of the COVID-19 pandemic [3]. Service platforms spanning common industries leverage service diversity and demand dynamism to mediate real-time interactions between providers and customers, and generate service value through operational efficiency [4]. Pricing, undoubtedly, is one of the most direct and crucial management tools for service platforms [5]. A reasonable service pricing strategy not only balances supply and demand but also ensures the platform’s sustainable operation. Conversely, an unreasonable pricing strategy can severely undermine the platform’s operational profits. Meanwhile, dynamic pricing has been recognized as a pivotal tool for balancing supply–demand mismatches and maximizing platform profitability [6]. Critical challenges persist within the realm of research concentrated on dynamic pricing issues associated with the multifaceted operational characteristics of service platforms, which motivate our research. This study pays attention to three prevalent characteristics inherent in the real-world operation of service platforms: the selection of pricing strategies, the response to service demand fluctuations, and the simultaneous involvement of full-time and part-time service providers.

Unified vs. Differentiated Pricing: In practice, service platforms commonly adopt two main pricing strategies, unified pricing and differentiated pricing, to effectively manage customer markets. Notably, many platforms opt for a differentiated service pricing strategy to better serve segmented markets. For example, ride-sharing platforms offer limousine and express services at different price points to attract distinct passenger segments [7]. Crowdsourcing platforms provide merchant and third-party delivery services with varying prices to target different customer groups. Cloud platforms offer primary and professional cloud services at different prices to segmented client markets, and healthcare platforms provide telephone and graphic consultations at different prices to segmented patient markets. Figure 1a illustrates that the WeDoctor Healthcare Platform simultaneously offers telephone consultation and graphic doctor consultation services to patients at different prices. Telephone (graphic) consultation refers to the healthcare service in which doctors provide consultation services to patients through telephone (graphic)-based communication. This digital consultation not only transcends geographical barriers but also offers patients convenient access to professional medical advice. These platforms tailor their services to satisfy customer needs and differentiate themselves through pricing, defined as a differentiated pricing strategy. However, due to limited customer resources, price and quality competition often exists among the diversified services offered by a single platform. To achieve efficient operation, a small number of service platforms, such as Baidu Map ride-hailing, Hua Xiaozhu Taxi, Indriver, Gett, and Via, have integrated the limousine car drivers and the express car drivers into a flat-rate riding service [8]. As depicted in Figure 1b, T3 Trip offers passengers a flat-rate ride-hailing service at a uniform price. Healthcare platforms like Jingdong Healthcare Platform consolidate all available doctors (high and low professional levels) as a quick consultation service to treat patients with varying symptoms [9]. These platforms charge a uniform price for a unified service by pooling different service providers, defined as a unified pricing strategy. Service platforms with a unified pricing strategy randomly match service providers and customers to attract two-sided users. Each pricing strategy has distinct advantages [9]. Understanding the optimal usage scenarios of these pricing strategies can empower service platforms to make more scientific decisions, enhance their competitiveness, and drive sustainable growth. Despite the prevalence of these two strategies, the specific conditions under which each strategy is most applicable in a service platform remain largely unexplored. This significant knowledge gap forms a core motivation for our research.

Initial Demand Constraints: Customer demand on service platforms is inherently dynamic and fluctuating over time, which is influenced by a multitude of internal and external factors. For example, during peak commute hours, the demand for taxi services skyrockets [10], and during the COVID-19 epidemic, the demand for healthcare services surged due to limited physical medical resources. In response to such demand fluctuations, service platforms typically rely on dynamic pricing as a key mechanism for demand management. Additionally, initial sales volume restrictions and initial inventory limitations [11] play a critical role in the dynamic operation of a retailer. The results of research related to initial demand constraints exert a substantial influence across multiple operational dimensions, including—but not limited to—strategic pricing, platform design, and revenue management. This practice, often regarded as “Hunger Marketing,” aims to stimulate greater demand and increase service prices in the long run by limiting customer access and service scale at the beginning [12]. Many service platforms impose restrictions on customer service demand during their initial operational phase due to the influence of environmental factors such as performance limitations and policy regulations. Cloud computing platforms limit the number of concurrent users and resource requests during working hours to maintain service quality, and healthcare platforms restrict the number of patient appointments and consultations per day to enhance the patient experience. In real-world scenarios, the initial operation phase of service platforms is unique. Whether platforms actively or passively control customer demand during the initial phase, they can guarantee a smooth and stable service commencement while stimulating the potential customer market. Incorporating these initial demand constraints into the dynamic pricing model is essential for accurately reflecting service platform operations, thus further motivating our research to develop a more comprehensive and realistic pricing framework.

Most service platforms host both full-time and part-time service providers to engage in service activities. The employment model, characterized by the coexistence of two distinct types of service providers, has found widespread application in ride-hailing platforms [13,14]. On these platforms, full-time drivers typically engage in daily work exceeding 7 h, whereas part-time drivers commit less than 3 h per day. Ride-hailing companies recognize the unique contributions of each driver category and thus implement diverse incentive mechanisms tailored to the two types of drivers [14]. The model extends beyond the ride-hailing industry. For instance, both full-time and part-time nurses play crucial roles in the realm of homecare services [15]. When formulating work schedules for homecare, it is of paramount importance to accommodate the flexibility inherent in part-time nurses’ participation [16]. As a flexible employment relationship, part-time workers can buffer the human resource demands of enterprises [16]. It also has a significant impact on individual health [17] and income [18], public management, and social welfare [19,20]. Specifically, part-time employment enables female workers to better balance professional responsibilities with family obligations [21]. On the Didi ride-hailing platform, nearly 90 percent of affiliated drivers engage in part-time driving activities. Similarly, as of September 2024, approximately 73 percent of active physicians affiliated with tertiary hospitals participate in part-time work through the haodf.com Health platform. The part-time pattern illustrates the increasing flexibility of employment models in the digital era, which reflects a broader transformation in labor market dynamics. Thus, pricing decisions on service platforms are significantly influenced by the composition of registered service providers. Full-time service providers are engaged by service platforms through fixed wages to ensure a stable service supply [22], while part-time providers are attracted by splitting revenue to capture fragmented service value [23]. In this study, we use fixed wages and sharing ratios to represent the participation of both types of service providers, respectively, as their participation profoundly impacts the platform’s cost structure and its pricing decisions. This aspect has received comparatively limited attention in the existing literature. It thereby reinforces the motivation for this study to address the gap and contribute to a more comprehensive understanding of service platform pricing.

For service platform operation, the wage of service providers and the investment in service construction constitute the operation costs, while fulfilled service orders generate revenue. Service platforms must make dynamic pricing decisions to strike a balance between revenue and costs under time-varying customer demand, formulated as an optimal control issue. Despite the importance of this issue, research on the optimal dynamic pricing of diversified services remains scarce. Solving the optimal control issue designed to mirror real-world operation is fraught with challenges. To bridge this gap and contribute to the field, we focus on the dynamic pricing problem of a general service platform, adapting a differentiated or unified pricing strategy. Our research aims to answer several key questions: Which pricing strategy should the service platform adopt to maximize expected revenue? How can the service platform dynamically set the service price to adjust supply and demand under initial service demand restrictions? What are the differences in the optimal service prices and the expected revenues under the two types of pricing strategies?

To address these questions, we develop a dynamic pricing model for service platforms under unified and differential pricing strategies, taking into account initial service demand restriction, time-varying customer demand, service quality, and two types of service providers’ participation. We then utilize optimal control theory to analyze the characteristics of the optimal dynamic price and revenue from mathematical and numerical perspectives. By regarding service quality as an endogenous variable, the basic dynamic pricing model is further extended to verify the robustness of some key findings. The main contributions of this study are three-fold.

Firstly, this study comprehensively examines the impact of customer demand fluctuation, service competition, initial demand constraints, and pricing strategies. Our findings offer valuable guidance for all kinds of service platforms to optimize their operational revenue through making dynamic pricing decisions. Specifically, we find that, regardless of initial service demand restriction, service quality elasticity coefficient, potential market, and demand fluctuation factor all positively affect the optimal service price, while service quality has a negative impact. Moreover, regardless of the pricing strategy, the initial service demand restriction negatively affects the platform’s optimal price. These insights can help service platforms anticipate how changes in crucial factors will influence pricing and make proactive adjustments to their operational strategies.

Secondly, this paper determines the optimal dynamic pricing and revenue for a general service platform. By comparing the differences under the two pricing strategies and investigating the impact of crucial factors, we provide a theoretical foundation and decision support for all kinds of service platforms. For example, we derive that with initial demand restriction, both the optimal unified price and the optimal differentiated price increase over the operation time when there is a higher price elasticity coefficient and the potential customers’ scale is below a certain threshold. Moreover, as the potential service demand grows and customers are less price sensitive, the gap between the optimal service prices under the two pricing strategies narrows. However, when the platform limits initial demand, the expected revenue evolution trajectories under the two pricing strategies differ significantly. These detailed findings not only enrich the theoretical understanding of service platform pricing but also offer practical tools for platforms to make more reasonable pricing decisions, ultimately improving their operational efficiency and profitability.

Thirdly, we enhance the basic dynamic pricing model by regarding service quality as an endogenous variable. Through these enhancements, we further verify the robustness of some key findings. Our analysis reveals that when the synergistic effect of two types of service sharing ratios exceeds a specific threshold, service platforms under both pricing strategies can carry out the optimal pricing schedule to maximize the discount revenue. Moreover, we find that when the service quality elasticity coefficient exceeds a certain threshold, service quality exerts positive and negative effects on the optimal unified service price and the optimal differentiated service price, respectively. These research findings not only strengthen the theoretical foundation of service platform pricing research but also provide a more comprehensive understanding of pricing decisions in dynamic market environments.

The remainder of this paper is laid out as follows. Section 2 reviews the related literature. Section 3 describes the general dynamic pricing problem with associated assumptions. Section 4 analyses the optimal dynamic pricing and revenue of a service platform without or with initial service demand restriction under two types of pricing strategies, respectively. Section 5 carries out a comparative analysis. Section 6 numerically analyzes the combined effect of the operation time and some crucial parameters on the platform’s pricing and revenue. Some extensions under endogenous service quality are provided in Section 7. Finally, Section 8 highlights some of the findings and discusses future research.

2. Literature Review

This study investigates the optimal dynamic pricing decisions for a general service platform with diversified service providers under a unified or differentiated pricing strategy. Thus, this section concentrates on three streams of the literature: dynamic pricing for service platforms, pricing strategies of service systems, and pricing for a gig economy service platform.

2.1. Dynamic Pricing for Service Platforms

The dynamic pricing strategy, in contrast to the fixed pricing strategy, empowers service providers to adapt prices with flexibility in response to the continuation of operations, alterations in service status, or fluctuations in market conditions.

Recently, a significant number of scholars and practitioners have continuously demonstrated their interest in the dynamic pricing issue faced by service platforms, but the majority of their research focuses on the pricing of a single ride-hailing service. Cachon et al. (2017) and Lin & Zhou (2019) compared and analyzed the operational impacts of three different pricing strategies—static pricing, dynamic pricing, and surge pricing—on ride-hailing services, which implied that the surge pricing strategy shows more advantages [24,25]. Similarly, many scholars have studied the effectiveness and superiority of surge pricing extensively in the operation of ride-hailing platforms from a theoretical model perspective [26,27]. Nourinejad & Ramezani (2020) developed a dynamic pricing model for a ride-hailing platform and solved it using an optimal controller [10]. Characterizing fluctuations in ridesharing service supply and demand, Chen et al. (2020) proposed a dynamic transaction model for drivers and passengers and presented the optimal dynamic decision-making of a ride-hailing platform [28]. In the research on the optimal pricing of ride-hailing services, Mejjaouli and Tadj (2023) found that the growth rate of the passenger market actively contributes to an increase in ride-hailing prices [29]. The aforementioned research, however, ignores competition between services, service demand restrictions, and different types of service providers in service platforms.

2.2. Pricing Strategies of Service Systems

Differentiated pricing and unified pricing are the pricing strategies commonly adopted in service systems. Although numerous scholars have conducted studies on the differentiated pricing of service systems (companies), there is a dearth of research on the topic of service platforms’ differentiated pricing. Using queuing theory, Maglaras et al. (2018) analyzed the characteristics of optimal pricing and service quality for differentiated services in a single large-scale service system. The results showed that the service system should implement differentiated pricing when segmented markets with low delay sensitivity have sufficient elasticity [6]. Yu et al. (2019) pointed out in their empirical investigation that two competing shipping companies can generate more profits under differentiated pricing than a uniform pricing strategy [30]. Miao et al. (2020) in their research demonstrated that differentiated pricing can not only increase the revenue of electric vehicle rental service companies but also enhance customer satisfaction levels [31]. Ma and Guo (2020) studied the optimal arrival rate and service rate control problems of two types of queues and indicated that, when customers have a relatively low waiting-time cost, the optimal price monotonically increases with the growth of the potential customer scale [32]. Considering the competition between taxis and ride-hailing on the passenger side, Zhao et al. (2022) applied bilateral market theory to study the optimal differentiated pricing of a ride-hailing platform [33]. The above literature concentrated on static differentiated pricing decisions for the service systems; however, it ignores the fluctuation and time-varying features of service demand.

Moreover, uniform pricing has been shown to positively influence customers’ purchasing propensity by shaping their value perceptions, while also mitigating the adverse effects commonly associated with differential pricing [34]. For instance, Suning and Gome have adopted unified pricing across both online and offline channels as part of their omnichannel transformation strategies [35]. Empirical evidence from Fan et al. (2023) further supports the efficacy of uniform pricing and demonstrates that unified carbon pricing can reduce regional economic costs [36]. In the context of live-streaming commerce, Wang et al. (2025) conducted a comparative analysis of brand owners’ optimal decisions and equilibrium outcomes under uniform and differential pricing strategies from the cannibalization effect [37]. The dual-channel services strategy in the service system is essentially a differential services strategy. Taking two types of services as dual-channel to reach the customer market, our work is also closely related to dual-channel pricing operated by a company. However, the existing research on dual-channel pricing mainly covered fields such as pure dual-channel pricing [35], coordinating [38], and profit mode decision [39]. Considering customers’ free-riding effect, Guo et al. (2022) and Li et al. (2019) investigated the dual-channel optimal pricing of a retailer who sells products through both offline and online channels [40,41]. To the best of our knowledge, most dual-channel pricing studies were conducted in the tangible commodity market, rarely involving the service market, especially dynamic service pricing.

2.3. Pricing for a Gig Economy Service Platform

Gig economy service platforms represented by ride-hailing platforms commonly draw in both full-time and part-time service providers. Most existing research on the pricing of ride-hailing platforms has been conducted based on the assumption that only part-time service providers are involved. Some scholars recently have also extended pricing analysis to ride-hailing platforms by incorporating privacy policies [42], car rental services [43], and autonomous vehicles [44] from the perspective of driver and passenger behavioral utility. For instance, Lin et al. (2024) performed a comparative analysis of optimal service pricing determined by a ride-hailing platform under asset-light and asset-heavy modes [45]. For a gig economy service platform, Chen et al. (2025) analyzed the impact of bounded rationality among customers and service providers on the platform’s equilibrium status [46]. Additionally, a growing number of studies have examined how gig economy platforms determine users’ access fees [47,48,49].

For gig economy service platforms, the decentralized (separating/dedicated) mode is associated with differential pricing, whereas the centralized (pooling) mode is linked to unified pricing. As far as we know, fewer research works have explored the pricing of a gig economy service platform through theoretical analysis. Zhong et al. (2020) developed pricing models for an on-demand service platform with two service modes: delivering services to low-sensitivity customers only and to two types of customers simultaneously. They highlighted that the service platform aimed at operational revenue should adopt corresponding service modes according to market status, rather than cover large-scale customers blindly [50]. Considering the safety care of female riders, Tang et al. (2021) studied the optimal service price decision-making problem of a ride-hailing platform under a traditional service mode where all users are pooled together, and a mixed service mode in which female drivers can be chosen, respectively. The results showed that the ride-hailing platform pursuing a win–win status should switch from traditional service mode to a mixed one when the mismatch cost of female riders with safety needs exceeds a certain threshold [51]. Wang and Huang (2022) studied the optimal pricing of a ride-sharing platform simultaneously operating two types of services: express and limousine, where there are entry barriers for limousine [7]. Based on the assumption that a ride-hailing platform can operate low- and high-quality services, Zhong et al. (2023) analyzed the differences in the optimal service price and revenue of the ride-hailing platform under dedicated and pooling service modes and revealed that the ride-hailing platform with pooling service mode can achieve a win–win situation when the opportunity cost of drivers is not very high and the difference in opportunity costs between the two types of drivers is small [8]. Similarly, Li et al. (2025) solved and analyzed the bilateral pricing model for a monopolistic healthcare platform by separating or pooling high and low professional-level doctors [9].

Regarding dynamic pricing for service platforms, although both the literature [10] and our study leverage optimal control theory to construct a dynamic pricing model and analyze the characteristics of an optimal pricing scheme, our study further takes into account the competitive effects between services and the simultaneous participation of two types of service providers. Regarding the pricing of a gig economy service platform, while both the existing literature [8,43] and our study consider the simultaneous engagement of diverse service providers and compare unified pricing with differentiated pricing, they all employ static equilibrium analysis to explore the optimal pricing of ride-hailing platforms, overlooking the dynamic nature of service demands in the real world. These differences precisely highlight the theoretical significance and application value of this study.

Table 1. The differences between our study and some of the more relevant research.

References	Platform	Supply	Demand	Service Competition	Pricing Strategy	Method Adopted	Theory
Zhong et al. [50]	On-demand service platform	Only part-time service providers	Static deterministic	NO	Unified pricing	Equilibrium analysis	Two-sided market theory
Nourinejad & Ramezani [10]	Ride-hailing platform	Only part-time drivers	Dynamic deterministic	NO	Unified pricing	Optimal control	Optimal control theory
Tang et al. [51]	Ride-hailing platform	Male and female drivers	Static deterministic	NO	Unified vs. differentiated pricing	Equilibrium analysis	Two-sided market theory
Zhong et al. [8]	Ride-hailing platform	High-quality and low-quality drivers	Static deterministic	NO	Unified vs. differentiated pricing	Equilibrium analysis	Two-sided market theory
Li et al. [9]	Healthcare platform	Low- and high-level professional doctors	Static deterministic	NO	Unified vs. differentiated pricing	Equilibrium analysis	Two-sided market theory
Our study	Service platform	Full-time and part-time service providers	Dynamic volatility	YES	Unified vs. differentiated pricing	Optimal control	Optimal control theory

summarizes some of the more relevant research and shows the differences between our study and the others.

Overall, despite the significant research achievements of numerous scholars in the pricing of a gig economy platform, the majority of these studies rely on static equilibrium analysis. They overlook the time-varying and fluctuating nature of service demand and the competitive interactions among services. Our study fills a gap not covered by previous work in two key aspects. Firstly, we abstracted the common characteristics of the real-world operations of service platforms across various fields. These characteristics encompass time-varying demand, competition among services, and the involvement of diversified service providers. Leveraging these abstractions, we constructed a dynamic pricing model for a general service platform. This model is more closely aligned with the actual operations of the platform, and the conclusions drawn from it are more universal.

Secondly, to maximize expected revenue, the optimal pricing scheme of a general service platform was derived by leveraging optimal control theory. Our study comprehensively compares scenarios of no initial demand constraints vs. with initial demand constraints, exogenous vs. endogenous service quality, as well as unified pricing vs. differentiated pricing strategy, contributing to the theoretical framework of dynamic pricing on service platforms. This comprehensive research allows for a more in-depth understanding of how crucial factors like initial demand restriction and service quality influence dynamic pricing decisions under a unified or differentiated pricing strategy.

3. Problem Formulation

This section outlines the foundational assumptions and the research problem that inform the construction of the model framework. For convenience, the notations used in this paper are summarized in

Table 2. The notations used throughout this paper.

Parameters
$a$	The number of potential customers	$b$	The evolution trend of customer demand	$T$	Service operation duration	${\alpha }_i$	Price elasticity coefficient of service type $i, i=1,2$
$\alpha$	Price elasticity coefficient	${\beta }_i$	Quality elasticity coefficient of service type $i, i=1,2$	$\beta$	Quality elasticity coefficient	$\eta$	The competitive effect of service quality
$\gamma$	The competitive effect of service price	${\theta }_i$	Revenue-sharing ratio of service type $i, i=1,2$	${\rho }_i$	Cost coefficient of service type i’s quality	$f_i$	Initial demand limit of service type $i, i=1,2$
$f$	Initial demand limit of the service platform	$w$	The cost of hiring full-time service providers	$\phi$	Participation coefficient of full-time service providers	$\delta$	Service quality decay coefficient
Control variables
$p^{DU}\left(t\right)$	Service price at time t under DU strategy, $p^{DU}\left(t\right)\in [\underset{\_}{p},\overline{p}]$	$p_i^{DD}\left(t\right)$	Price of service type i at time t under DD strategy, $p_i^{DD}(t)\in [\underset{\_}{p},\overline{p}]$	$S_i\left(t\right)$	The participation degree of full-time service providers for service type i, $S_i\left(t\right)\in \left[\mathrm{0,1}\right]$
Status variables
$\dot{\dot{D}}$(t)	Demand rate of unified service at time t	${\dot{D}}_i$(t)	Demand rate of service type $i$ at time t, $i=1,2$	$Q\left(t\right)$	Demand for unified service at time t	$Q_i\left(t\right)$	Demand of service type $i$ at time t, $i=1,2$
$q_i\left(t\right)$	Quality of service type i at time t, $i=1,2$	${\pi }^{DU}\left(t\right)$	The profit of the service platform at time t under the DU strategy	${\pi }^{DD}\left(t\right)$	The profit of the service platform at time t under the DD strategy

. We utilize the superscript DU, DD to represent dynamic unified pricing and differentiated pricing strategies, respectively.

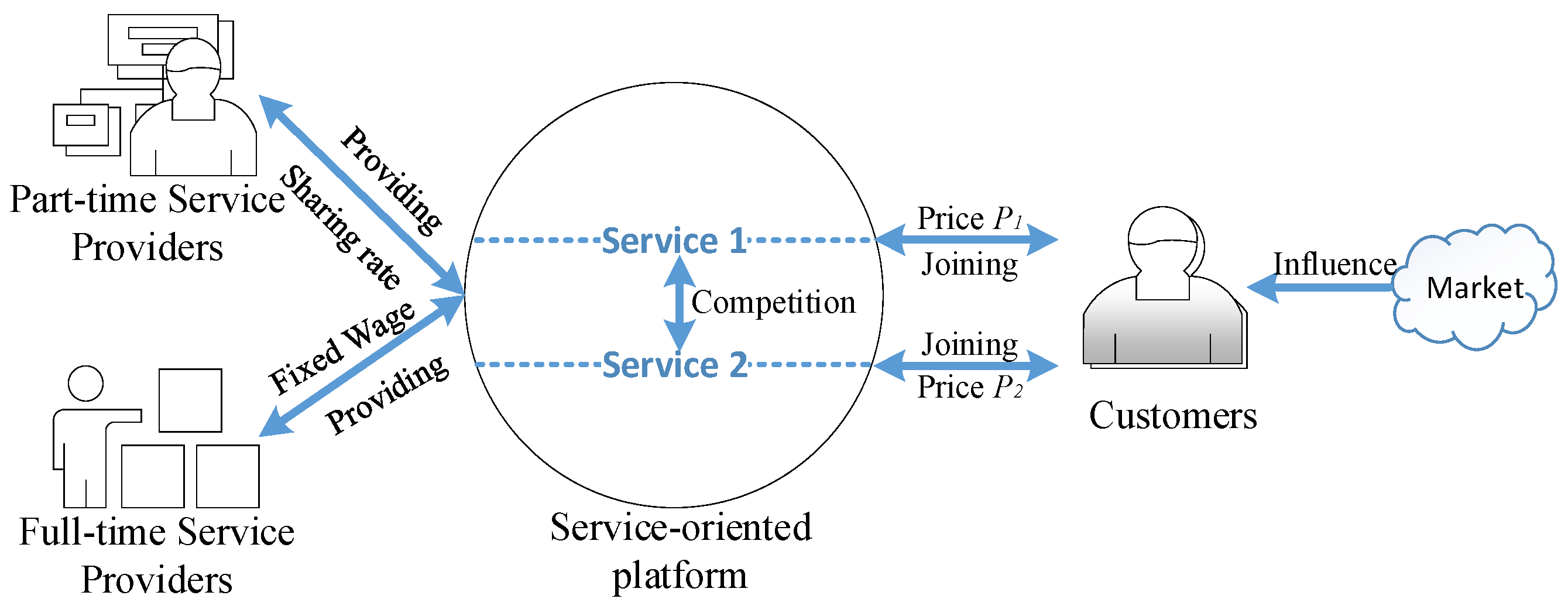
In a particular service market, a general service platform (e.g., cloud computing platform, ride-hailing platform, and healthcare platform) operates two types of services and dynamically charges service prices by connecting service providers and customers throughout a finite continuous-time horizon, $T\in Q^{+}$. The operational duration of the service could be as short as a few months (for example, six months or $T=1/2$) or as long as a few years (for example, two years or $T=2$). Thus, the operational duration of the service can be a fraction. This assumption is frequently adopted in research related to dynamic pricing [52] (the assumption of the continuity of operation duration).

Both full-time and part-time service providers are attracted to the service platform as human resources. They are competent in tasks to meet customers’ service needs on the service platform, since both full-time and part-time service providers possess professional capabilities. For instance, on the Haodf.com platform, both full-time and part-time doctors are required to acquire medical practice qualifications before providing medical consultation services. It is reasonable to assume that there is no difference in the effectiveness of customers enjoying services provided by part-time or full-time service providers. The service platform provides a fixed salary $w(w>0)$ for full-time service providers [53]. Meanwhile, the platform shares revenue with part-time service providers involving type i service at a sharing ratio ${\theta }_i({\theta }_i>0)$ and ${\theta }_1\ne {\theta }_2$ [54], which is determined and announced in advance by the platform in the form of operating rules and remains unchanged during the operation time. The revenue-sharing mechanism for part-time service providers on the service platform is essentially one kind of gig economy (the assumption concerning the resemblance in professional competencies and remuneration forms between the two types of service providers).

The service platform simultaneously operates two types of services $i=1,2$ at a price $p_1\left(t\right),p_2\left(t\right)>0$ during $t+dt$ a period where $t\in [0,T]$, and the corresponding service quality is $q_1,q_2$ with $q_1\ne q_2>0$. Service quality represents the extent to which the service platform streamlines its end-to-end service delivery, which is exemplified by measures such as integrating AI-powered assistance systems and refining two-sided matching algorithms. Following the definitions of previous related works [38,39,41], the cost of platform operating service i is a quadratic function of service quality $q_i$, defined as ${\rho }_i{q}_i^2/2$, where ${\rho }_i({\rho }_i>0)$ is the operation cost coefficient of service i. For customers, the two types of services are similar in terms of function and have a substitution effect to some extent (the assumption of service operation costs based on service quality).

We further assume that the service demand per customer is 1 unit. As demonstrated in previous research [1,23,54], the effective transaction volume on the service platform equals the number of customers who paid for the service because one customer can directly communicate with any service provider assigned by the platform or the service provider chosen by herself/himself after payment during the $t+dt$ period (the assumption of effective transaction volume on service platforms).

The service platform dynamically adjusts service price(s) to cope with customer market fluctuations. If a service platform implements a differential pricing strategy, it will charge distinct prices to two types of services to satisfy the specific demands of segmented markets, which is indeed the pricing strategy employed by the majority of service platforms. Conversely, when a service platform decides to set an identical price for two types of services, it typically combines them into a unified service. For instance, ride-hailing platforms such as Hua Xiaozhu Taxi and Didi enable both luxury car drivers and express car drivers to jointly provide a flat-rate service. Similarly, on the healthcare 160 service platform, doctors from top-tier hospitals and non-top-tier hospitals are grouped together to offer quick medical consultation services. The operation mode of the monopoly service platform is shown in Figure 2.

Service Demand Rate: Based on the linear demand function [11], the service demand rate function is constructed in this study. Under the influence of the market environment, the service demand evolution of potential customers with size $a(a>0)$ may exhibit a growth ($b>0$), decline ($b<0$), or stability ($b=0$) trend during the $t+dt$ period. According to the Malthus model, the population growth rate is expressed in an exponential form; thus, the growth rate of potential customers in this study is also expressed in the form of an exponential function, $a{e}^{bt}$, which contributes to fluctuations in service demand. According to the customer utility theory, when customers are confronted with a relatively high service price, they will shift away from or withdraw from the current service, thus leading to a decrease in the demand for the service. The negative impact of the service price on the service demand is characterized by the service price elasticity coefficient ${\alpha }_i$. When customers perceive a relatively high service quality, they will flock to the service, thereby causing an increase in the service demand. The positive impact of the service quality on the service demand is described by the service quality elasticity coefficient ${\beta }_i$. Simultaneously, grounded in the customer reference theory, when other services with similar functions are priced lower, customers tend to opt for the alternative service with a lower price, which in turn leads to a decline in the demand for the current service. The impact of service price competition on the service demand is characterized by the service price competition coefficient $\gamma$. When other services with similar functions have a higher quality, customers tend to choose the alternative service with a higher quality. The impact of service quality competition on the service demand is described by the service quality competition coefficient $\eta$. At time t, the customer demand rate of service i operated by the service platform is linearly determined by the potential customer size a, service demand fluctuation factor b, service price $p_i\left(t\right)$, service quality $q_i$, and competition effect between two types of services [40,53], which is defined as follows:

$${\dot{D}}_i(t,p_i(t),p_{3-i}(t))=a{e}^{bt}-{\alpha }_i{p}_i(t)+{\beta }_i{q}_i+\gamma (p_{3-i}(t)-p_i(t))+\eta (q_i-q_{3-i}), i=1,2$$

(1)

where ${\alpha }_i,{\beta }_i$ represent the elasticity coefficients of price and quality of service i, respectively. They are, respectively, employed to measure the sensitivity of service demand rate to changes in service price and service quality. $\gamma ,\eta$ are the competition coefficients of price and quality between the two types of services, respectively, and $0<{\alpha }_i,{\beta }_i,\gamma ,\eta <1$. The service price elasticity coefficient, the service quality elasticity coefficient, and the competitive effect among services are all grounded in factual logic and the practical operation of the service platform.

The service demand evolution is not only affected by current market conditions but also has a carry-over effect to subsequent periods, which reflects the intertemporal characteristics. Let $Q_i\left(t\right)$ denote the cumulative demand of service i up to time t, determined by the following:

$$d{Q}_i\left(t\right)={\dot{D}}_i\left(t,p_i\left(t\right),p_{3-i}\left(t\right)\right)dt$$

(2)

Profit Function: Without loss of generality, the other operating costs of the service platform are assumed to be 0 [39,53]. The income of the service platform is closely related to effective service volume, which is defined as ${\sum }_{i=1}^2(1-{\theta }_i)p_i(t)Q_i(t)$ at time t. The profit function of the service platform at time t is specified as follows:

$$\pi (t,p_i(t),p_{3-i}(t))={\displaystyle \sum _{i=1}^2(1-{\theta }_i)Q_i(t)}-{\rho }_i{q}_i^2/2-w, i=1,2$$

(3)

where $w$ is considered the fixed operating cost of the service platform, which is utilized to cover the salary expenses for hiring full-time service providers. The total profit of the platform equals revenue minus service operation costs ${\rho }_i{q}_i^2/2+w$.

The service platform initiates its operation at $t=0$, which is regarded as the initial stage. After operating for a duration of T, the total profit of the service platform can be expressed as follows:

$$\pi (p_i(t),p_{3-i}(t))={\displaystyle \underset{0}{\overset{T}{\int }}[{\displaystyle \sum _{i=1}^2((1-{\theta }_i)d{Q}_i(t)}-{\rho }_i{q}_i^2/2)-w]dt}, i=1,2$$

(4)

Dynamic Pricing Model: Dynamic pricing is a strategy that actively adjusts service prices according to real-time market demand. Based on the above description, we formulate a continuous-time dynamic pricing problem for the service platform with diversified services. Let $\mathit{A}=\left\{\right(p_1\left(t\right),p_2\left(t\right)\left)\right|(p_1\left(t\right),p_2\left(t\right))\in [\underset{\_}{p},\overline{p}]\times [\underset{\_}{p},\overline{p}]\}$ denote the platform’s admissible control set and $\underset{\_}{p},\overline{p}$ represent the lower and upper bounds of the service price, respectively. The service platform dynamically adjusts the prices of two types of services $(p_1^{\ast }\left(t\right),p_2^{\ast }\left(t\right)\in \mathit{A}$ to achieve the maximum profit within the operation time T, defined as

$$\underset{(p_i\left(t\right),p_{3-i}\left(t\right))\in \mathit{A}}{\max }\pi (p_i\left(t\right),p_{3-i}\left(t\right)), i=1,2$$

(5)

and subject to Equation (2).

Specifically, the dynamic pricing model (5) directs the service platform to adopt a unified pricing strategy if $p_1\left(t\right)=p_2\left(t\right)=p\left(t\right)$; otherwise, $p_1\left(t\right)\ne p_2\left(t\right)$, it adopts a differentiated pricing strategy. Moreover, due to the performance limitations of the service platform in the initial stage, the initial demand should be restricted, $Q_i\left(0\right)=f_i>0$ and $f=f_1+f_2$, to the model (5), which can have a cascading effect on subsequent service pricing and demand dynamics. Similarly, initial demand or capacity constraints have been incorporated into relevant dynamic pricing research [55]. The dynamic pricing problem, subject to initial demand constraints, constitutes a special instance of the problem without demand constraints. In reality, when an excessive number of customers initiate service requests concurrently, upon surpassing the capacity threshold defined by the maximum concurrent restriction, a service system will generate notifications like “The maximum concurrent capacity has been reached” or “The connection count exceeds the maximum restriction.”

4. Dynamic Pricing for a Service Platform Under Exogenous Service Quality

When the service platform defines service quality in advance, the service quality can be regarded as an exogenous variable. Under exogenous service quality, the section considers the initial service demand without and with restriction, respectively, and proves the optimal dynamic pricing and total profit for a service platform adapting the unified or differentiated pricing strategies.

4.1. Dynamic Unified Pricing (DU) Under Exogenous Service Quality

(1)

Without Initial Service Demand Restriction

Under the DU strategy, the service platform organizes both full-time and part-time service providers, coordinating their efforts to present a unified service that is clearly observable within the market landscape. At this point, it is important to note that customer demand does not cease to exist. On the contrary, it undergoes a shift and converges specifically into this unified service offering. The reason is that rejecting the unified service means leaving the service platform, resulting in a perceived utility of 0. This convergence indicates a redirection of customer preferences and needs towards the unified service presented by the platform. The service platform sets a uniform price $p\left(t\right)$ for the unified service. Meanwhile, the service platform takes the unified service price as the control variable and the cumulative service demand of customers as the status equation. Based on Equation (1), the customer demand rate for the unified service is as follows:

$$\dot{D}\left(t,p\left(t\right)\right)={\dot{D}}_1\left(t,p\left(t\right)\right)+{\dot{D}}_2\left(t,p\left(t\right)\right)$$

(6)

where

$$\dot{D_1}\left(t,p\left(t\right)\right)=a{e}^{bt}-{\alpha }_{1}p\left(t\right)+{\beta }_1{q}_1+\eta (q_1-q_2)$$

$$\dot{D_2}\left(t,p\left(t\right)\right)=a{e}^{bt}-{\alpha }_{2}p\left(t\right)+{\beta }_2{q}_2+\eta (q_2-q_1)$$

The competitive effect no longer exists in the demand rate, represented by Equation (6).

The cumulative demand on the service platform up to time t is determined by the following:

$$dQ\left(t\right)=\dot{D}\left(t,p\left(t\right)\right)dt$$

(7)

The total profit of the service platform can be determined as follows:

$${\pi }^{DU}(p(t))={\displaystyle \underset{0}{\overset{T}{\int }}\{[(1-{\theta }_1)d{Q}_1(t)+(1-{\theta }_2)d{Q}_2(t)]p(t)-{\rho }_1{q}_1^2/2}-{\rho }_2{q}_2^2/2-w\}dt$$

(8)

Let ${\mathit{A}}_{\mathbf{1}}=\left\{p\right(t\left)\right|p\left(t\right)\in [\underset{\_}{p},\overline{p}]\}$ denote the platform’s admissible control set under a unified pricing strategy. The service platform dynamically adjusts the unified service price $p^{\ast }\left(t\right)\in {\mathit{A}}_{\mathbf{1}}$ covering the operation time $T$ to maximize total profit. Therefore, the dynamic pricing problem (5) can be transformed into

$$\underset{p\left(t\right)\in {\mathit{A}}_{\mathbf{1}}}{\max }{\pi }^{DU}\left(p\right(t\left)\right)$$

(9)

subject to Equation (7).

For the dynamic pricing problem (9), the Lagrange multiplier $\lambda$ is introduced to construct the Hamiltonian function as follows:

$$H^{DU}=[(1-{\theta }_1)(dQ(t)-d{Q}_2(t))+(1-{\theta }_2)d{Q}_2(t)]p(t)-{\rho }_1{q}_1^2/2-{\rho }_2{q}_2^2/2-w+\lambda \dot{D}(t)$$

Lemma 1

(The existence of a unified optimal pricing). The total profit of the service platform is a concave function of the service price under the unified pricing strategy, and there is an optimal dynamic service price $p^{\ast }\left(t\right)$.

Please see Appendix A.1 for the proof of Lemma 1.

Proposition 1

(The expressions of the optimal price and the expected revenue). Under the unified pricing strategy, the optimal pricing decision and total profit for the service platform are as follows:

$$p^{DU}(t)={\displaystyle \frac{C{e}^{-t}({\alpha }_1+{\alpha }_2)+a{e}^{bt}(k_1+k_2)+K}{{\alpha }_1{k}_1-{\alpha }_2(k-k_2)}}$$

(10)

$$\begin{array}{l}{\pi }^{DU}={\displaystyle \frac{1}{2}}\{-2Tw-{\rho }_{1}T{q}_2^2+{\displaystyle \frac{1}{{\alpha }_1{k}_1-{\alpha }_2{(k-k_2)}^2}}[{\displaystyle \frac{k{\alpha }_2{a}^2(e^{2bT}-1){(k_1+k_2)}^2}{b}}+{\displaystyle \frac{4akK{\alpha }_2(k_1+k_2)(1-e^{bT})}{b(b-1)}}\\ +Cb{k}_1(e^{(b-1)T}-1){({\alpha }_1+{\alpha }_2)}^2+2bkK{\alpha }_2(e^{bT}-1)]+2k_{1}CK{e}^{-T}(e^T-1)\\ {({\alpha }_1+{\alpha }_2)}^2+2k{\alpha }_{2}T{K}^2+2e^{-T}\sinh (T)({\alpha }_1{k}_1+{\alpha }_2{k}_2)C^2{({\alpha }_1+{\alpha }_2)}^2)\}\end{array}$$

(11)

where let $k={\theta }_1-{\theta }_2$, $k_1={\theta }_1-1<0$, $k_2={\theta }_2-1<0$, $K={\beta }_1{k}_1{q}_1+\eta k{q}_1-q_2\left({\beta }_2+\eta {\theta }_1\right)+q_2{\theta }_2({\beta }_2+\eta )$. k indicates the difference in revenue-sharing ratios. $k_1,k_2$ represent the opposite of the revenue ratio on the original two types of services, respectively. C is the freedom coefficient, which is determined by an indefinite integral. K can be regarded as the relative value to the platform. Furthermore, $C{e}^{-t}({\alpha }_1+{\alpha }_2)$ represents the basic revenue evolution of the platform determined by its structure. $a{e}^{bt}(k_1+k_2)$ indicates the operational revenue evolution from serving the customer market. The optimal price under the unified pricing strategy can be simply understood as the ratio of revenue from operating a unified service to the economic capacity, as shown below.

$$p^{DU}(t)={\displaystyle \frac{\stackrel{\mathrm{Revenue} \mathrm{from} \mathrm{operating} \mathrm{a} \mathrm{unified} \mathrm{service}}{\overbrace{C{e}^{-t}({\alpha }_1+{\alpha }_2)+a{e}^{bt}(k_1+k_2)+K}}}{\underset{\mathrm{Economic} \mathrm{capacity}}{\underbrace{{\alpha }_1{k}_1-{\alpha }_2(k-k_2)}}}}$$

Please see Appendix A.2 for the proof of Proposition 1.

Theorem 1

(The evolutionary trend of the optimal unified price). When $C,b>0$ and $\mathit{max}\left\{0,{\displaystyle \frac{{\alpha }_2\left(k-k_2\right)}{k_1}}\right\}<{\alpha }_1<1$, noted as Condition 1, the optimal unified price for the service platform increases over time; otherwise, the optimal unified price for the service platform decreases over time. Condition 1 means that customers are sensitive to service price and have a growing service demand.

Please see Appendix A.3 for the proof of Theorem 1.

Theorem 1 indicates that even if customers are sensitive to service price, the service platform still raises its unified service price over time to maximize total profit in the context that there is a surging trend in customer demand without initial service demand restriction.

Corollary 1

(The impacts of platform performance parameters). When $0<{\theta }_2<{\theta }_1$, the elasticity coefficients of service quality $({\beta }_1,{\beta }_2)$, alternative service quality $\left(q_2\right)$, potential demand $\left(a\right)$, and demand fluctuation factor $\left(b\right)$ all contribute to an increase in the optimal unified pricing. The optimal unified pricing reduces with an increase in service quality $\left(q_1\right)$ when the elasticity coefficient of service quality $\left({\beta }_1\right)$ is less than a certain threshold. Under the unified pricing strategy, a negative relationship exists between the total profit of the platform and the cost coefficients of the two types of services $({\rho }_1,{\rho }_2)$ and the fixed salary $\left(w\right)$.

Please see Appendix A.4 for the proof of Corollary 1.

Corollary 1 shows that the quality of alternative services, the elasticity coefficient of service quality, and potential demand positively stimulate customer service demand when the service platform adopts the unified pricing strategy. Driven by huge service demand, the service platform tends to set a higher unified service price (consistent with intuition). However, service quality negatively affects the unified service price when the elasticity coefficient of service quality is smaller. This is because the impact of service quality on service demand is relatively small. Hence, improving service quality does not significantly promote service demand but increases the platform operation costs.

(2)

With Initial Service Demand Restriction

Proposition 2

(The expressions of the optimal price and the expected revenue). When the service platform restricts the initial service demand, $Q\left(0\right)=f$, the optimal unified price and total profit of the platform are as follows:

$$p^{DU}(t)={\displaystyle \frac{C{e}^{-t}({\alpha }_1+{\alpha }_2)+a{e}^{bt}(k_1+k_2)+K}{{\alpha }_1{k}_1-{\alpha }_2(k-k_2)}}$$

$${\pi }^{DU}={\displaystyle \underset{0}{\overset{T}{\int }}[((1-{\theta }_1)(dQ(t)-d{Q}_2(t))+(1-{\theta }_2)d{Q}_2(t))p^{DU}(t)-\frac{{\rho }_1{q}_1^2}{2}-\frac{{\rho }_2{q}_2^2}{2}-w]dt}$$

where $C={\displaystyle \frac{k[a({\alpha }_1-3{\alpha }_2)+{\alpha }_1{\beta }_2{q}_2+\eta (q_2-q_1)({\alpha }_1+{\alpha }_2)]+f[{\alpha }_1-{\alpha }_1{\theta }_1+{\alpha }_2(k-k_2)]-k(2{\beta }_1{q}_1{\alpha }_2+{\beta }_2{q}_2{\alpha }_2)}{{({\alpha }_1+{\alpha }_2)}^2}}$.

The expression of the unified price with initial service demand restriction is the same as that of the unified price without initial service demand restriction, but the freedom coefficient is determined.

Please see Appendix A.5 for the proof of Proposition 2.

Theorem 2

(The evolutionary trend of the optimal unified price). Considering the initial service demand constraint, the optimal unified price and its evolution intensity steadily rise over time when $3{\alpha }_2<{\alpha }_1<min\{{\displaystyle \frac{{\alpha }_2\left(k-k_2\right)}{k_1}},1\}$ and $0<a<{\displaystyle \frac{f\left[{\alpha }_1{k}_1-{\alpha }_2\left(k-k_2\right)\right]+A}{\left({\alpha }_1-3{\alpha }_2\right)k+b^{2}B}}$, noted as Condition 2, and under the unified pricing strategy; otherwise, the optimal unified price and its evolution intensity decline over time. Additionally, the initial service demand restriction hurts the optimal unified price of the service platform. Condition 2 means that the customers’ sensitivity to service price and the number of potential customers are, respectively, less than a certain threshold.

Please see Appendix A.6 for the proof of Theorem 2.

Theorem 2 reveals that in the case of an initial service demand constraint, the service platform gradually raises the unified service price as the operation continues when customers exhibit relatively low sensitivity to service price and the potential customer demand is less than a certain threshold (consistent with intuition). At the same time, the increase in the unified service price is more significant in the later stages of operation due to the cumulative effect of service demand. With the initial service demand restriction, service demand and service price rise as the platform continues to operate. This section explains a common market phenomenon that most service companies prefer “hunger marketing” regardless of the market demand trend, such as crowd-sourcing platforms, cloud computing platforms, and healthcare platforms.

Corollary 2

(The evolutionary trend of the expected revenue). Considering the initial service demand constraint, the total profit of the service platform rises with the increase in operating times when $0<f<max\left\{\right|F_1|,|F_2\left|\right\}$, noted as Condition 3, where $F_1,F_2$ are the real roots of ${\displaystyle \frac{\partial {\pi }^{DU}\left(T\right)}{\partial T}}=0$ on f. Otherwise, the total profit of the service platform declines over operation time. Condition 3 means that the platform limits the initial service demand to less than a certain threshold.

Please see Appendix A.7 for the proof of Corollary 2.

Corollary 2 suggests that if the service platform adopts the unified pricing strategy, it is better to keep the initial service demand below a certain level to achieve sustained profit, which provides theoretical support for the unified pricing decision-making of service platforms.

In conclusion, regardless of whether or not the initial service demand is constrained, the optimal unified price of a service platform increases over time when certain conditions hold.

4.2. Dynamic Differentiated Pricing (DD) Under Exogenous Service Quality

(1)

Without Initial Service Demand Restriction

Under the DD strategy, the service platform simultaneously organizes full-time and part-time service providers to offer two types of services that can be observed by the market, each catering to different market segments. The service platform sets different prices, $p_1\left(t\right)\ne p_2\left(t\right)$, for two types of services. Meanwhile, the platform takes different service prices as the control variables, ${\mathit{p}}^{DD}\left(t\right)=\{p_1\left(t\right),p_2\left(t\right)\}$, and the cumulative demand on two types of services as the status equations, $\mathit{Q}\left(t\right)=\{Q_1\left(t\right),Q_2(t\left)\right\}$, where the customer demand rates for service type 1 and 2 are expressed as Equation (1).

The service platform adjusts different service prices covering the operation time T to maximize total profit, which is defined as follows:

$${\pi }^{DD}(p_1(t),p_2(t))={\displaystyle \underset{0}{\overset{T}{\int }}[(1-{\theta }_1)d{Q}_1(t)p_1(t)+(1-{\theta }_2)d{Q}_2(t)p_2(t)-\frac{{\rho }_1{q}_1^2+{\rho }_2{q}_2^2}{2}-w]dt}$$

(12)

Let ${\mathit{A}}_{\mathbf{2}}=\left\{\right(p_1\left(t\right),p_2\left(t\right)\left)\right|{(p}_1\left(t\right),p_2\left(t\right))\in [\underset{\_}{p},\overline{p}]\times [\underset{\_}{p},\overline{p}\left]\right\}$ denote the platform’s admissible control set under a unified pricing strategy. The service platform dynamically adjusts the differentiated service prices $(p_1^{\ast },p_2^{\ast })\in {\mathit{A}}_{\mathbf{2}}$ covering the operation time T to maximize total profit. Therefore, the dynamic pricing problem (5) can be transformed into

$$\underset{(p_1\left(t\right),p_2\left(t\right))\in {\mathit{A}}_{\mathbf{2}}}{\max }{\pi }^{DD}(p_1\left(t\right),p_2\left(t\right))$$

(13)

subject to Equation (2).

For the dynamic pricing problem (9), Lagrange multipliers $\mathit{\lambda }=\{{\lambda }_1,{\lambda }_2\}$ are introduced to construct the Hamiltonian function as follows:

$$H^{DD}=(1-{\theta }_1)d{Q}_1(t)p_1(t)+(1-{\theta }_2)d{Q}_2(t)p_2(t)+{\lambda }_1{\dot{D}}_1(t)+{\lambda }_2{\dot{D}}_2(t)-{\displaystyle \frac{{\rho }_1{q}_1^2+{\rho }_2{q}_2^2}{2}}-w$$

Lemma 2

(The existence of a differentiated optimal pricing). The total profit of the service platform is a concave function of service price under the differentiated pricing strategy, and there is an optimal dynamic service price $(p_1^{\ast },p_2^{\ast })$ when ${\alpha }_1>{\displaystyle \frac{\gamma [\gamma k^2+4{\alpha }_2({\theta }_1+{\theta }_2-{\theta }_1{\theta }_2-1\left)\right]}{4k_1{k}_2({\alpha }_2+\gamma )}}$, noted as Condition 4, which means that customers are more sensitive to service price; otherwise, there is no optimal dynamic service price.

Please see Appendix B.1 for the proof of Lemma 2.

Lemma 2 indicates that the service platform can charge the optimal differentiated price to optimize total profit when the service price elasticity coefficient exceeds a certain threshold. The threshold is determined by the sharing ratio of two types of services, the intensity of price competition, and the elasticity coefficient of the alternative service’s price.

Proposition 3

(The expressions of the optimal price and the expected revenue). Under the differentiated pricing strategy, the optimal pricing decisions and total profit for the service platform are determined as follows:

$$\begin{array}{l}{p}_1^{DD}(t)={\displaystyle \frac{e^{-t}}{({\alpha }_2\gamma +{\alpha }_1{R}_2)Z}}\{-C_1[{\alpha }_1{R}_2+\gamma ({\alpha }_2+\gamma {\theta }_1)]+\gamma k{C}_2{R}_2+\\ aZ{e}^{t+bt}({\alpha }_2+2\gamma )+e^{t}Z[{\beta }_1{q}_1{R}_2+\eta {\alpha }_2{q}_1+q_2(\gamma {\beta }_2-\eta {\alpha }_2)]\}+C_1{\theta }_2{R}_1{R}_2\end{array}$$

(14)

$$\begin{array}{l}{p}_2^{DD}(t)={\displaystyle \frac{e^{-t}}{({\alpha }_2\gamma +{\alpha }_1{R}_2)Z}}\{C_2[{\alpha }_1{k}_1{R}_2+\gamma ({\alpha }_2{k}_1+\gamma k)]-\gamma k{C}_1{R}_1+\\ aZ{e}^{t+bt}({\alpha }_1+2\gamma )+e^{t}Z[\gamma {\beta }_1{q}_1+{\beta }_2{q}_2{R}_1+\eta {\alpha }_1(q_2-q_1)]\}\end{array}$$

(15)

$$\begin{array}{l}{\pi }^{DD}(T)={\displaystyle \frac{a(C_1+C_2)[e^{(b-1)T}-1]}{b-1}}+{\displaystyle \frac{e^{-T}\sinh (T)[k_1{R}_2{C}_2^2+k_2{R}_1{C}_1^2-\gamma C_1{C}_2(k_1+k_2)]}{Z}}-{\displaystyle \frac{{\rho }_{1}T{q}_1^2+{\rho }_{2}T{q}_2^2}{2}}\\ +[C_1{q}_1({\beta }_1+\eta )+C_2{q}_2({\beta }_2+\eta )-\eta C_2{q}_1-\eta C_1{q}_2][1-\cosh (T)-\sinh (T)]-Tw\end{array}$$

(16)

where $z=k_1{k}_2>0$, $R_1={\alpha }_1+\gamma$, $R_2={\alpha }_2+\gamma$, and $0<R_1,R_2<2$. $C_1,C_2$ Nare the freedom coefficients, which are determined by an indefinite integral. z represents the synergy effect of services operated by the platform on the revenue rate. $R_1,R_2$, respectively, indicate the elasticity of service demand to prices of service 1 and 2 under the service substitution effect. Interestingly, although there is a similar structure to the optimal unified price, the expression of the optimal service price under the differentiated pricing strategy is more complex as a result of competition and the synergy of alternative services.

Please see Appendix B.2 for the proof of Proposition 3.

Theorem 3

(The evolutionary trend of the optimal differentiated price). The optimal differentiated prices of the service platform decrease over time when $b>0$ and $0<a<min\{{\displaystyle \frac{e^{-(b+1)t}[\gamma k{C}_2{R}_2+C_1{\theta }_2{R}_1{R}_2-C_1({\alpha }_1{R}_2+\gamma {\alpha }_2+{\theta }_1{\gamma }^2\left)\right]}{bZ({\alpha }_2+2\gamma )}},1\}$, noted as Condition 5, which means the potential service demand from customers is smaller but has an increasing trend; otherwise, the optimal differentiated prices of the service platform rise over time.

Please see Appendix B.3 for the proof of Theorem 3.

Theorem 3 shows that even though the demand market has a surging trend, the optimal service price of the service platform adopting the differentiated pricing strategy gradually declines when potential customer demand is below a certain threshold, which means the pricing decision of the service platform is significantly influenced by the potential demand market.

Corollary 3

(The impacts of platform performance parameters). The optimal service price (taking type 1 service as an example) rises with its service quality $\left(q_1\right)$, the elasticity coefficients of service quality $({\beta }_1,{\beta }_2)$, potential demand $\left(a\right)$, and demand fluctuation factor $\left(b\right)$ when the platform adopts a differentiated pricing strategy. When the elasticity coefficient of alternative service quality $\left({\beta }_2\right)$ is less than a certain threshold, the optimal service price decreases with the improvement of alternative service quality $\left(q_2\right)$. When there is a quality difference between two types of services $(q_1<q_2)$, the intensity of service quality competition $\left(\eta \right)$ positively affects the optimal service price. The cost coefficients of the two types of services $({\rho }_1,{\rho }_2)$ and fixed salaries $\left(w\right)$ harm the total profit of the platform.

Please see Appendix B.4 for the proof of Corollary 3.

From Corollary 3, it can be seen that, similar to the case of a unified pricing strategy, service quality, elasticity coefficient of service quality, and potential demand market all positively affect the optimal differentiated price. The difference is that alternative service quality positively affects the optimal differentiated price when the elasticity coefficient of alternative service quality is lower. The substitutability between services positively affects the optimal differentiated price when the service quality is smaller. The main reason is that the positive effect of alternative service synergy outweighs the negative effect of competition.

(2)

With Initial Service Demand Restriction

Proposition 4

(The expressions of the optimal price and the expected revenue). When the service platform restricts the initial service demand, $\mathit{Q}\left(\mathbf{0}\right)=\left\{f_1,f_2\right\}>\mathbf{0}$, the optimal differentiated price and total profit of the platform are derived as follows:

$$p_1^{DD}(t)={\displaystyle \frac{e^{-t}[a{e}^{(1+b)t}({\alpha }_2+2\gamma )+\gamma {\beta }_2{q}_2+{\beta }_1{q}_1{R}_2+{\alpha }_2\eta (q_1-q_2)-\gamma f_2-f_1{R}_2]}{\gamma {\alpha }_2+{\alpha }_1{R}_2}}$$

$$p_2^{DD}(t)={\displaystyle \frac{e^{-t}[a{e}^{(1+b)t}({\alpha }_1+2\gamma )+\gamma {\beta }_1{q}_1+{\beta }_2{q}_2{R}_1+{\alpha }_1\eta (q_2-q_1)-\gamma f_1-f_2{R}_1]}{\gamma {\alpha }_2+{\alpha }_1{R}_2}}$$

$$\begin{array}{l}{\pi }^{DD}={\displaystyle \frac{1}{2(\gamma {\alpha }_2+{\alpha }_1{\beta }_2)}}\{{\displaystyle \frac{2a[e^{(b-1)T}-1][f_1{k}_1({\alpha }_2+2\gamma )+f_2{k}_2({\alpha }_1+2\gamma )]}{1-b}}+e^{-2T}[k_1(e^{2T}-1)f_1^2-2e^T{f}_1(e^T-1)(q_1{\beta }_1{R}_2+\eta q_1{\alpha }_2+\\ q_2(\gamma {\beta }_2-\eta {\alpha }_2)]k_1+k_2{R}_1{f}_2^2(e^{2T}-1)+f_1(2e^T(\gamma {\beta }_1{q}_1+{\beta }_2{q}_2{R}_1+\eta {\alpha }_1(q_2-q_1))k_2-\gamma f_1(k_1+k_2)+e^{2T}(2q_1{k}_2(\eta {\alpha }_1-\gamma {\beta }_1)\\ -2q_2(\gamma {\beta }_2+{\alpha }_1{k}_2({\beta }_2+\eta )+\gamma f_1(k_1+k_2)))-e^{2T}T(\gamma {\alpha }_2+{\alpha }_1{R}_2)(2w+{\rho }_1{q}_1^2+{\rho }_2{q}_2^2))\}\end{array}$$

The form of the optimal differentiated price with service demand restriction is similar to that of the optimal unified price with service demand restriction, but all service quality, initial service demand, and service competition factors play an important role.

Please see Appendix B.5 for the proof of Proposition 4.

Theorem 4

(The evolutionary trend of the optimal differentiated price). Considering the initial service demand constraints, the optimal differentiated price rises over time when the service demand market surges under the differentiated pricing strategy. Additionally, the initial service demand has a negative impact on the optimal differentiated price of the service platform.

Please see Appendix B.6 for the proof of Theorem 4.

Theorem 4 reveals that if there is a surging trend in customer service demand, implementing “hunger marketing” and adopting the differentiated pricing strategy is beneficial for gradually increasing the optimal differentiated service prices set by the service platform (consistent with intuition), which is consistent with common sense for service platforms operating with a differentiated pricing strategy in fact.

Corollary 4

(The optimal operation duration). Considering the initial service demand constraints, there is $T^{\ast }\in [0,T]$ that makes the service platform achieve the maximum total profit when $b<1$ and

$$0<a<{\displaystyle \frac{e^{-(1+b)T}{f}_1\{2f_1{R}_2-e^T[{\alpha }_2{\beta }_1{q}_1+\gamma ({\beta }_1{q}_1+{\beta }_2{q}_2)+\eta {\alpha }_2(q_1-q_2)]+2k_2{R}_1{f}_2^2+2\gamma f_1{f}_2(k_1+k_2)\}+e^{-bT}{f}_2{k}_2[\gamma {\beta }_1{q}_1+{\beta }_2{q}_2{R}_2+{\alpha }_1\eta (q_2-q_1)]}{(b-1)[f_1{k}_1({\alpha }_2+2\gamma )+f_2{k}_2({\alpha }_1+2\gamma )]}},$$

noted as Condition 6, under the differentiated pricing strategy. Condition 6 means that the service demand of customers with a smaller potential scale has a slowly increasing trend.

Please see Appendix B.7 for the proof of Corollary 4.

Corollary 4 shows that the service platform adopting “hunger marketing” can maximize its total profit within the constrained operational period $T^{*}$ when the potential service demand and fluctuation factor are lower under the differentiated pricing strategy. Under such circumstances, it is best for the service platform to make a suitable plan for the operation cycle according to the service demand and market characteristics.

In conclusion, under the differentiated pricing strategy, the optimal differentiated price of the service platform decreases over time if the initial service demand is unlimited and the service demand of customers with smaller potential market rises. On the contrary, the optimal differentiated price increases over time if the initial service demand is constrained and shows a surging trend.

5. Comparison Analysis Under Exogenous Service Quality

We theoretically compare the differences in service prices and the differences in operational profit between the two pricing strategies: unified pricing and differential pricing.

Corollary 5

(Service price comparison). Taking the optimal differentiated price of service 1 as an example, the gap between the optimal unified price and the optimal differentiated price of the service platform narrows as the potential service demand or demand fluctuation factor increases when $0<{\alpha }_1<min\{{\displaystyle \frac{{\alpha }_2\left(k-k_2\right)}{k_1}},1\}$, noted as Condition 7, which means that the elasticity coefficient of service 1 price is lower; otherwise, the gap between the optimal unified price and the optimal differentiated price of the service platform expands as the potential service demand or demand fluctuation factor increases.

Please see Appendix C.1 for the proof of Corollary 5.

Corollary 5 indicates that when customers’ price sensitivity is less than a certain threshold, the gap between the optimal unified price and the optimal differentiated price of the service platform narrows as potential customer demand grows. The partial reason is that service prices adjusted by the service platform primarily follow the market-pulling effect in response to demand situations, but weaken the pricing strategies’ role.

Corollary 6

(Profit comparison). The total profit gap of the service platform between the unified pricing strategy and the differentiated pricing strategy widens with the increasing intensity of service price competition when $C_1>{\displaystyle \frac{k_1{C}_2}{k_2}}$, $0<{\theta }_1,{\theta }_2<1$, noted as Condition 8, which means that the revenue ratio of service 2 is greater than that of service 1; otherwise, the total profit gap of the service platform between the unified pricing strategy and the differentiated pricing strategy narrows with the increasing intensity of service price competition.

Please see Appendix C.2 for the proof of Corollary 6.

Corollary 6 suggests that strengthening competition among service prices can highlight the differences and advantages of pricing strategies on operational profit when the revenue ratio of one service to part-time service providers is relatively smaller.

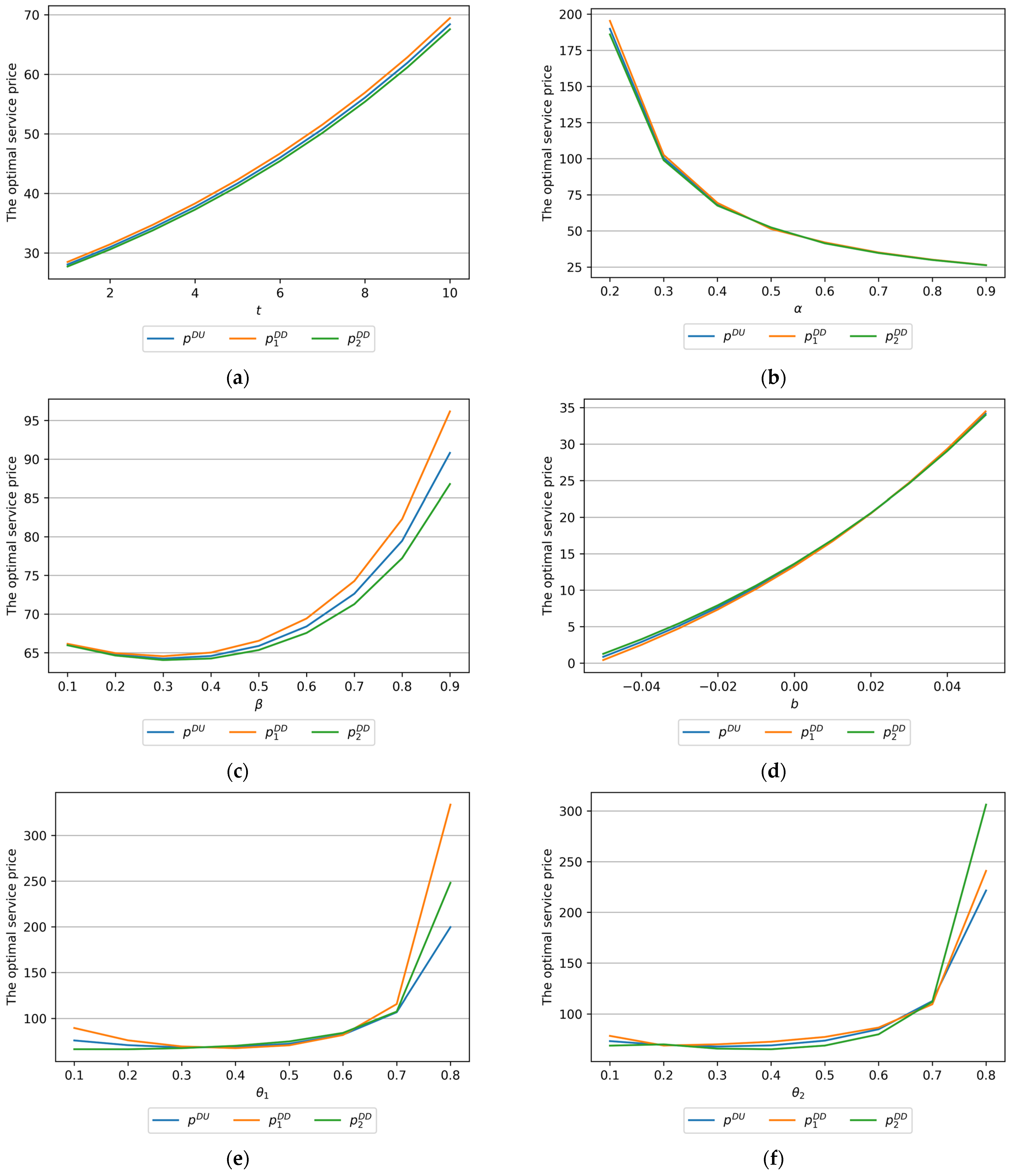
6. Numerical Analysis

In this section, we utilize numerical calculations to analyze the sensitivity of the service platform’s optimal service price and total profit to important factors under two types of pricing strategies. Crucial parameters in this study can be quantified utilizing questionnaires, interviews, and empirical analysis. Taking Jingdong Health as an example, the number of potential patients accessed is greater in reality. The critical parameter values are standardized and displayed in

Table 3. Parameter value settings.

Parameter	Value	Parameter	Value	Parameter	Value	Parameter	Value
$a$	20	$b$	0.1	$T$	10	${\alpha }_1$	0.4
${\alpha }_2$	0.5	${\beta }_1$	0.7	${\beta }_2$	0.65	$\eta$	0.8
$\gamma$	0.75	$q_1$	7.8	$q_2$	8.1	${\theta }_1$	0.3
${\theta }_2$	0.25	${\rho }_1$	1.0	${\rho }_2$	1.2	$w$	38
$f$	10	$f_1$	5	$f_2$	5	\	\

according to the actual situation of this healthcare platform.

(1)

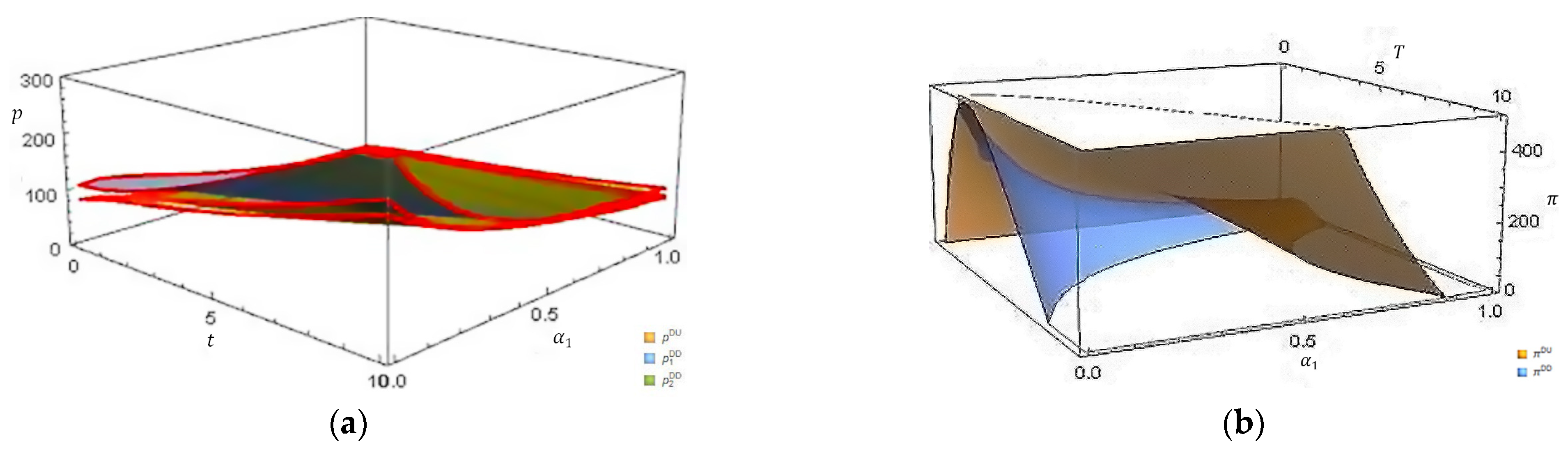
Service price elasticity

Taking the price elasticity of service 1 as an example, Figure 3a,b, respectively, show the joint impact of the service price elasticity and operation time on the optimal service price and total profit of the service platform under the two types of pricing strategies. From Figure 3a, the service platform prefers to set higher service prices over time due to the cumulative effect of service demand, which balances excess service demand for increasing profitability. It further validates Theorems 1, 2, 3, and 4. As customers become more sensitive to service prices, the optimal service price decreases regardless of the pricing strategy adopted by the service platform. When the elasticity of the service price is small, the evolution trend in the service price is particularly evident under the differentiated pricing strategy; conversely, when the elasticity of the service price is larger, the evolution trend in the alternative service price is particularly apparent under the differentiated pricing strategy. The simulation further validates Corollaries 2 and 4; in this parameter setting, whether the service platform chooses the differentiated pricing strategy or the unified pricing strategy, its profit exhibits, respectively, an approximate inverted “U” shape and a positive relationship with operational time. Additionally, the profit of the service platform decreases as customer sensitivity to service price increases, as Figure 3b shows.

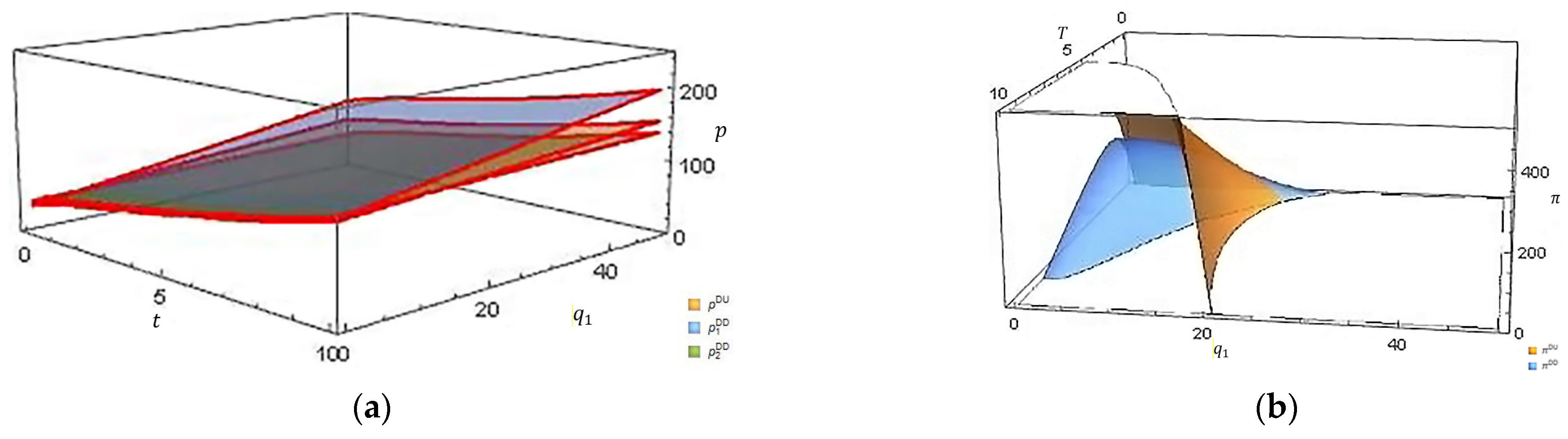
(2)

Revenue-sharing ratio

Taking the revenue-sharing ratio of service 1 as an example, Figure 4a,b, respectively, depict the joint impact of the revenue-sharing ratio and operation time on the optimal service price and total profit under the unified and differentiated pricing strategies. Figure 4a shows that, in our parameter setting, the evolution trend in optimal service price under two types of pricing strategies remains unchanged when the revenue-sharing ratio is smaller, similar to Figure 3a. In contrast, the growth trend in the optimal service price under the unified pricing strategy is vital. However, the service platform with the unified pricing strategy tends to set a lower service price when the revenue-sharing ratio is larger. As the revenue-sharing ratio rises, the optimal service price under the differentiated pricing strategy gradually grows, while the optimal service price under the unified pricing strategy slowly drops. As Figure 4b shows, the revenue-sharing ratio has the opposite effect on the service platform’s profit under two types of pricing strategies. There is an approximate inverted “U” shape relationship between the revenue-sharing ratio and the service platform’s profit. Compared to the unified pricing strategy, the higher revenue-sharing ratio under the differentiated pricing strategy means that higher compensation is paid to part-time service providers, which results in the platform bearing higher operating costs. Thus, the service platform should charge a lower sharing ratio when using a differentiated pricing strategy to maximize profit.

(3)

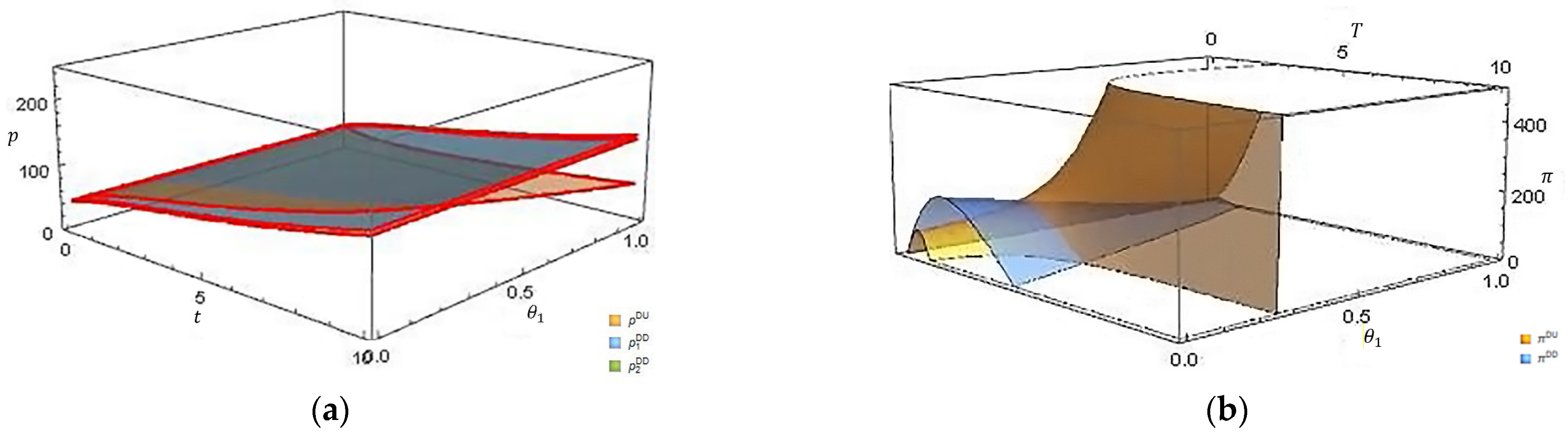
Service quality

Taking quality of service 1 as an example, Figure 5a,b, respectively, display the joint impact of service quality and operation time on the optimal service price and total profit under the unified and differentiated pricing strategies. Figure 5a reveals that, similar to Figure 3a, the evolution trend in the optimal service price under the two types of pricing strategies remains unchanged, whereas the growth trend in the optimal service price is greater under the differentiated pricing strategy. Simultaneously, there is a positive relationship between the service quality and the optimal service price under two types of pricing strategies. This is because the service platform provides customers with higher quality service at the cost of higher service investment and operating costs. The optimal revenue of the service platform under two types of pricing strategies decreases accordingly with an improvement of service quality and also has an approximate inverted “U” shape with operational time, as Figure 5b shows.

7. Extension: Under Endogenous Service Quality

To incorporate the complex relationship between service quality and the engagement of full-time service providers into this model framework, service quality is treated as an endogenous variable. This modelling makes an extension of the basic dynamic pricing structure. In the section, the engagement of full-time service providers, service quality, and revenue discount rate are introduced to improve the original dynamic pricing model and further verify the robustness of the conclusions.

Since the available service time of full-time service providers is relatively stable and can be controlled by the service platform, a reasonable assumption is made: the service quality of type-i service is influenced by the engagement of full-time service providers $s_i\left(t\right)$. According to the extended model of Nerlove–Arrow [56], the evolution of service quality for type-i service at the period $t+∆t$ is defined as follows:

$$q_i(t+∆t)=\phi s_i\left(t\right)-\delta q_i\left(t\right), q_i\left(T\right)=m_i>0, i=1,2$$

(17)

where the engagement of full-time service providers is positively correlated with the salary provided by the service platform. $\phi$ represents the coefficient of full-time service providers’ engagement. $\delta$ is the decay rate. And $\phi , \delta >0$.

7.1. Dynamic Unified Pricing (DU) Under Endogenous Service Quality

From the basic model in Section 3, the functional form of the service demand evolution remains unchanged. The variable branches are further integrated, ${\alpha }_1={\alpha }_2=\alpha$, ${\beta }_1={\beta }_2=\beta$, and $0<\alpha ,\beta <1$. The change rate of service demand under the dynamic unified pricing strategy is modified as follows:

$${\dot{D}}_i\left(t,p\left(t\right),q_i\left(t\right),q_{3-i}\left(t\right)\right)=a{e}^{bt}-\alpha p\left(t\right)+\beta q_i\left(t\right)+\eta \left[q_i\left(t\right)-q_{3-i}\left(t\right)\right], i=1,2$$

(18)

The cumulative demand on the service platform up to time t is determined by the following:

$$dQ\left(t\right)=[{\dot{D}}_1\left(t,p\left(t\right),q_1\left(t\right),q_2\left(t\right)\right)+{\dot{D}}_2\left(t,p\left(t\right),q_1\left(t\right),q_2\left(t\right)\right)]dt$$

(19)

$$Q\left(0\right)=f>0$$

Let ${\mathit{B}}_{\mathbf{1}}=\left\{\right(p\left(t\right),s_1\left(t\right),s_2\left(t\right)\left)\right|(p\left(t\right),s_1\left(t\right),s_2\left(t\right))\in [\underset{\_}{p},\overline{p}]\times \left[\mathrm{0,1}\right]\times \left[\mathrm{0,1}\right]\}$ denote the platform’s admissible control set. The platform should make decisions on both the unified price and the participation level of full-time service providers simultaneously $(p^{\ast }\left(t\right),s_1^{\ast }\left(t\right),s_2^{\ast }\left(t\right))\in {\mathit{B}}_{\mathbf{1}}$ to maximize expected revenue covering the operation time $T$,

$${\pi }^{DU}(p(t),s_1(t),s_2(t))=\underset{(p(t),s_1(t),s_2(t))\in B_1}{\max }{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\sigma t}[(1-{\theta }_1)p(t)d{Q}_1(t)+(1-{\theta }_1)p(t)d{Q}_2(t)-{\rho }_i{s}_i^2(t)/2}]dt$$

(20)

subject to Equations (17) and (19). $e^{-\sigma t}$ and $\sigma$ are the discount factor and discount rate, respectively.

For the dynamic pricing problem (20), Lagrange multipliers ${\lambda }_1,{\lambda }_2,{\lambda }_3$ are introduced to construct the Hamiltonian function as follows:

$$\begin{gathered} H^{DU}=\left(1-{\theta }_1\right)p(t)d{Q}_1(t)+\left(1-{\theta }_1\right)p(t)d{Q}_2(t)+{\lambda }_1[\phi s_1\left(t\right)-\delta q_1\left(t\right)]+{\lambda }_2[\phi s_2\left(t\right)-\delta q_2\left(t\right)]+{\lambda }_3({\dot{D}}_1 \\ +{\dot{D}}_2)-{\displaystyle \frac{{\rho }_1{s}_1^2(t)+{\rho }_2{s}_2^2(t)}{2}} \end{gathered}$$

Proposition 5

(The existence of a unified optimal pricing). Under the unified pricing strategy, there is an optimal decision-making scheme for the service platform.

$$p^{DU}\left(t\right)={\displaystyle \frac{\beta k_1{q}_1\left(t\right)-q_2\left(t\right)(\beta +\eta {\theta }_1)+\eta k{q}_1\left(t\right)+R_3{\theta }_2{q}_2\left(t\right)+a{e}^{bt}({\theta }_1+{\theta }_2-2)}{2\alpha ({\theta }_1+{\theta }_2-2)}}$$

$$s_1^{DU}\left(t\right)={\displaystyle \frac{\phi {\lambda }_1}{{\rho }_1}}, s_2^{DU}\left(t\right)={\displaystyle \frac{\phi {\lambda }_2}{{\rho }_2}}$$

where

$$q_1\left(t\right)={\displaystyle \frac{e^{-t\delta -t{R}_4}p(1-e^{t\delta +t{R}_4})(\beta k_1+\eta k){\phi }^2}{{\rho }_1{R}_4(2\delta +\sigma )}}-{\displaystyle \frac{e^{-t\delta }p(\beta k_1+\eta k)(R_4{e}^{t\delta }+\delta e^{-t{R}_2}){\phi }^2}{\delta {\rho }_2{R}_4(2\delta +\sigma )}}+e^{-t\delta }{C}_1$$

$$+{\displaystyle \frac{e^{-t\delta }(e^{t\delta +t{R}_2}-1){\phi }^2{C}_2}{{\rho }_1(2\delta +\sigma )}}$$

$$+q_2\left(t\right)={\displaystyle \frac{e^{-t\delta -t{R}_4}p(1-e^{t\delta +t{R}_4})(\beta k_2-\eta k){\phi }^2}{{\rho }_2{R}_4(2\delta +\sigma )}}-{\displaystyle \frac{e^{-t\delta }p(\beta k_2-\eta k)({R_{2}e}^{t\delta }+{\delta e}^{-t{R}_4}){\phi }^2}{\delta {\rho }_2{R}_4(2\delta +\sigma )}}+e^{-t\delta }{C}_3$$

$$+{\displaystyle \frac{e^{-t\delta }(e^{t\delta +t{R}_2}-1){\phi }^2{C}_4}{{\rho }_2(2\delta +\sigma )}}$$

$${\lambda }_1=-{\displaystyle \frac{p\left(t\right)(\beta k_1+\eta k)}{R_4}}+e^{t{R}_4}{C}_2, {\lambda }_2=-{\displaystyle \frac{p\left(t\right)(\beta k_2-\eta k)}{R_4}}+e^{t{R}_4}{C}_4, {\lambda }_3={\displaystyle \frac{p{k}_1}{1-\sigma }}+e^{t(\sigma -1)}{C}_5$$

$$R_3=\beta +\eta , R_4=\delta +\sigma$$

Based on all boundary conditions, the coefficients $C_1~C_5$ can be determined, and the final form of the optimal decisions and expected revenue can be derived.

Please see Appendix D.1 for the proof of Proposition 5.

Corollary 7.

Under the unified pricing strategy, the optimal unified service price increases with the expansion of operating duration $\left(t\right)$, service quality elasticity coefficient $\left(\beta \right)$, the number of potential customers $\left(a\right)$, and demand volatility factor $\left(b\right)$, but decreases with the service price elasticity coefficient $\left(\alpha \right)$ rising. When the service quality elasticity coefficient exceeds a certain threshold $(\beta >\{{\displaystyle \frac{-\eta k}{k_1}},{\displaystyle \frac{\eta k}{k_2}}\})$, the improvement of service quality $(q_1,q_2)$ can promote the optimal unified price. When the current service quality is lower than the alternative service quality, the revenue-sharing ratios of current service $\left({\theta }_1\right)$ and alternative service $\left({\theta }_2\right)$ have opposite effects on the optimal unified price, which are positive and negative, respectively.

Corollary 7 reveals that, in service platform operations under the unified pricing strategy, the optimal unified service price is intricately shaped by multiple factors. Longer operating durations, higher service quality elasticity coefficients, larger numbers of potential customers, and increased demand volatility all contribute to price increases. Conversely, a rise in the service price elasticity coefficient, as in ride-hailing platforms where customers are highly price sensitive, leads to price decreases. Moreover, when the service quality elasticity coefficient crosses a certain threshold, such as in a software-as-a-service platform, service quality enhancements can drive up the optimal price (consistent with intuition). These are also similar to some of the findings in Theorems 1 and 2, Corollary 1. Please see Appendix D.2 for the proof of Corollary 7.

7.2. Dynamic Differentiated Pricing (DD) Under Endogenous Service Quality

Similarly, the customer demand rate under the dynamic differentiated pricing strategy is modified as follows:

$${\dot{D}}_i\left(t,p_i\left(t\right),p_{3-i}\left(t\right),q_i\left(t\right),q_{3-i}\left(t\right)\right)=a{e}^{bt}-\alpha p\left(t\right)+\beta q_i\left(t\right)+\gamma \left[p_{3-i}\left(t\right)-p_i\left(t\right)\right]+\eta [q_i\left(t\right)-q_{3-i}\left(t\right)], i=1, 2$$

(21)

The cumulative demand on the service i up to time t determined by the following:

$$d{Q}_i\left(t\right)={\dot{D}}_i\left(t,p_i\left(t\right),p_{3-i}\left(t\right),q_i\left(t\right),q_{3-i}\left(t\right)\right)dt$$

(22)

$$Q_i\left(0\right)=f_i>0$$

Let ${\mathit{B}}_{\mathbf{2}}=\left\{\right(p_i\left(t\right),p_{3-i}\left(t\right),q_i\left(t\right),q_{3-i}\left(t\right)\left)\right|(p_i\left(t\right),p_{3-i}\left(t\right),q_i\left(t\right),q_{3-i}\left(t\right))\in [\underset{\_}{p},\overline{p}]\times [\underset{\_}{p},\overline{p}]\times \left[\mathrm{0,1}\right]\times \left[\mathrm{0,1}\right]\}$ denote the platform’s admissible control set. The platform should make decisions on both the differentiated price and the participation level of full-time service providers simultaneously $(p_1^{\ast }\left(t\right),p_2^{\ast }\left(t\right),s_1^{\ast }\left(t\right),s_2^{\ast }\left(t\right))\in {\mathit{B}}_{\mathbf{2}}$ to maximize expected revenue covering the operation time $T$,

$${\pi }^{DD}(p_1(t),p_2(t),s_1(t),s_2(t))=\underset{(p_1(t),p_2(t),s_1(t),s_2(t))\in B_2}{\max }{\displaystyle \underset{0}{\overset{T}{\int }}{e}^{-\sigma t}[{\displaystyle \sum _{i=1}^2(1-{\theta }_i)p_i(t)d{Q}_i(t)-{\rho }_i{s}_i^2(t)/2}}]dt$$

(23)

subject to Equation (22).

For the dynamic pricing problem (23), Lagrange multipliers ${\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4$ are introduced to construct the Hamiltonian function as follows:

$$\begin{gathered} H^{DD}=(1-{\theta }_1)p_1\left(t\right)d{Q}_1\left(t\right)+(1-{\theta }_2)p_2\left(t\right)d{Q}_2\left(t\right)+{\lambda }_1[\phi s_1\left(t\right)-\delta q_1\left(t\right)]+{\lambda }_2[\phi s_2\left(t\right) \\ -\delta q_2\left(t\right)]+{\lambda }_3{\dot{D}}_1\left(t\right)+{\lambda }_4{\dot{D}}_2\left(t\right)-{\displaystyle \frac{{\rho }_1{s}_1^2\left(t\right)+{\rho }_2{s}_2^2\left(t\right)}{2}} \end{gathered}$$

Proposition 6

(The existence of a differentiated optimal pricing). Under the differentiated pricing strategy, there is an optimal decision-making scheme for the service platform when $z>max\{{\displaystyle \frac{{\gamma }^2{k}^2}{4{\alpha }^2+8\alpha \gamma }},{\displaystyle \frac{{\gamma }^2{\left({\theta }_1+{\theta }_2-2\right)}^2}{4R^2}}\}$.

$$p_1^{DD}\left(t\right)={\displaystyle \frac{k_2[q_1\left(t\right)\left(2\beta \gamma k_1+2\alpha k_1{R}_3+\gamma \eta k\right)+q_2\left(t\right)\left(2\alpha \eta -2\alpha \eta {\theta }_1-\gamma \eta {\theta }_1+\gamma \eta {\theta }_2+\beta \gamma {\theta }_1+\beta \gamma {\theta }_2-2\beta \gamma \right)+a{e}^{bt}\left(2\alpha k_1+3\gamma {\theta }_1+\gamma {\theta }_2-4\gamma \right)]}{4z{\alpha }^2+8\alpha \gamma z-{\gamma }^2{k}^2}}$$

$$p_2^{DD}\left(t\right)={\displaystyle \frac{k_1[q_2\left(t\right)\left(2\beta \gamma k_2+2\alpha k_2{R}_3-\gamma \eta k\right)+q_1\left(t\right)\left(\beta \gamma {\theta }_1+\beta \gamma {\theta }_2-2\beta \gamma +2\alpha \eta +\gamma \eta {\theta }_1-2\alpha \eta {\theta }_2-\gamma \eta {\theta }_2\right)+a{e}^{bt}\left(2\alpha k_2+\gamma {\theta }_1+3\gamma {\theta }_2-4\gamma \right)]}{4z{\alpha }^2+8\alpha \gamma z-{\gamma }^2{k}^2}}$$

$$s_1^{DD}\left(t\right)={\displaystyle \frac{\phi {\lambda }_1}{{\rho }_1}}, s_2^{DD}\left(t\right)={\displaystyle \frac{\phi {\lambda }_2}{{\rho }_2}}$$

where

$$\begin{gathered} q_1\left(t\right)={\displaystyle \frac{e^{-t\delta -t{R}_4}\left(1-e^{t\delta +t{R}_4}\right)[k_1{R}_3{p}_1\left(t\right)-\eta k_2{p}_2\left(t\right)]{\phi }^2}{{\rho }_1{R}_4(2\delta +\sigma )}}-{\displaystyle \frac{e^{-t\delta }[k_1{R}_3{p}_1\left(t\right)-\eta k_2{p}_2\left(t\right)](R_4{e}^{t\delta }+\delta e^{-t{R}_2}){\phi }^2}{\delta {\rho }_1{R}_4(2\delta +\sigma )}} \\ +e^{-t\delta }{C}_1+{\displaystyle \frac{e^{-t\delta }(e^{t\delta +t{R}_4}-1){\phi }^2{C}_2}{{\rho }_1(2\delta +\sigma )}} \end{gathered}$$

$$\begin{gathered} q_2\left(t\right)={\displaystyle \frac{e^{-t\delta -t{R}_4}\left(1-e^{t\delta +t{R}_4}\right)[k_2{R}_3{p}_2\left(t\right)-\eta k_1{p}_1\left(t\right)]{\phi }^2}{{\rho }_2{R}_4(2\delta +\sigma )}}+{\displaystyle \frac{e^{-t\delta }(\eta k_1{p}_1\left(t\right)-k_2{R}_3{p}_2\left(t\right))(R_4{e}^{t\delta }+\delta e^{-t{R}_2}){\phi }^2}{\delta {\rho }_2{R}_4(2\delta +\sigma )}} \\ +e^{-t\delta }{C}_3+{\displaystyle \frac{e^{-t\delta }(e^{t\delta +t{R}_4}-1){\phi }^2{C}_4}{{\rho }_2(2\delta +\sigma )}} \end{gathered}$$

$${\lambda }_1={\displaystyle \frac{\eta k_2{p}_2\left(t\right)-R_3{k}_1{p}_1\left(t\right)}{R_2}}+e^{t{R}_2}{C}_2, {\lambda }_2={\displaystyle \frac{\eta k_1{p}_1\left(t\right)-R_3{k}_2{p}_2\left(t\right)}{R_2}}+e^{t{R}_2}{C}_4, {\lambda }_3={\displaystyle \frac{p_1\left(t\right)k_1}{1-\sigma }}+e^{t(\sigma -1)}{C}_5, {\lambda }_4={\displaystyle \frac{p_2\left(t\right)k_2}{1-\sigma }}+e^{t(\sigma -1)}{C}_6$$

$$R=\alpha +\gamma$$

It derives the final forms of the optimal decisions and expected revenue based on all boundary conditions.

Please see Appendix D.3 for the proof of Proposition 6.

Corollary 8.

As the operating duration $\left(t\right)$, potential customer scale $\left(a\right)$, and demand volatility factor increase $\left(b\right)$, the optimal service price rises accordingly. When the service quality elasticity coefficient exceeds a certain threshold $(\beta >max\{{\displaystyle \frac{\eta (-2\alpha k_1-\gamma k)}{2k_{1}R}},{\displaystyle \frac{\eta (2\alpha k_1+\gamma K)}{\gamma ({\theta }_1+{\theta }_2-2)}}\})$, both the current service quality $\left(q_1\right)$ and the alternative service quality $\left(q_2\right)$ have a negative impact on the optimal service price. When the synergistic effect of two types of service sharing ratio exceeds a specific threshold (${\displaystyle \frac{{\gamma }^2{k}^2+4{\alpha }^2\left({\theta }_1+{\theta }_2-{\theta }_1{\theta }_2-1\right)}{8\alpha \gamma }}<z$), the optimal service price increases with the growth of the service quality elasticity coefficient $\left(\beta \right)$.

Corollary 8 suggests that, under a differential pricing strategy, the effect of service quality on the optimal price is opposite to that under a unified pricing strategy. At this time, the negative effect of competition among services becomes apparent (consistent with intuition). The service price elasticity coefficient exhibits a non-linear effect on the optimal price. Additionally, some of the properties of the findings in Corollary 8 are consistent with those in Corollary 3 and Theorem 4. Please see Appendix D.4 for the proof of Corollary 8.

7.3. Comparison Analysis Under Endogenous Service Quality

Since it is not possible to directly derive the explicit expression for the platform’s optimal service price and expected revenue, we use numerical analysis to compare the optimal service prices and the expected revenues between the two pricing strategies, respectively. Let $\alpha =0.4$, $\beta =0.6$, $\phi =1, \delta =0.8, \sigma =0.7, m_1=m_2=0.6$. Other parameter values remain the same.

(1)

Service price comparison

As shown in Figure 6, the optimal differential price and the optimal unified price exhibit similar changing trends under the impact of crucial parameters. With the continuous operation of the platform (Figure 6a) or a gradual increase in the demand fluctuation factor (Figure 6d), the optimal service price increases nearly linearly. However, the elasticity coefficient of price (Figure 6b) has a negative effect on the optimal service price. The optimal service price demonstrates an approximately U-shaped relationship with the elasticity coefficient of quality (Figure 6c) or the sharing ratio (Figure 6e,f). Interestingly, when the sharing ratio exceeds a certain threshold, the service platform sharply raises the service price to balance the revenue-sharing cost. In most cases, the price of type 1 service is the highest, and that of type 2 service is the lowest under the differentiated pricing strategy.

(2)

Revenue comparison

Under the parameter setting, the effects of these crucial parameters on the platform’s expected revenue are generally similar to their effects on the optimal service price, as shown in

Table 4. Revenue comparison between the two service pricing strategies.

$T$	${\pi }^{DU}$	${\pi }^{DD}$	${\pi }^{DU}-{\pi }^{DD}$	$\alpha$	${\pi }^{DU}$	${\pi }^{DD}$	${\pi }^{DU}-{\pi }^{DD}$	$\beta$	${\pi }^{DU}$	${\pi }^{DD}$	${\pi }^{DU}-{\pi }^{DD}$
1	123.00	123.09	−0.09	0.1	43394.70	46865.80	−3471.10	0.1	478.28	478.23	0.05
2	260.50	260.70	−0.20	0.2	1478.20	1486.10	−7.90	0.2	448.63	448.42	0.22
3	338.91	339.14	−0.24	0.3	675.98	677.09	−1.10	0.3	428.62	428.64	−0.02
4	384.65	384.94	−0.29	0.4	433.53	433.87	−0.34	0.4	418.57	418.49	0.08
5	409.09	409.41	−0.32	0.5	318.22	318.19	0.03	0.5	419.08	419.24	−0.16
6	421.61	421.94	−0.33	0.6	251.12	251.14	−0.02	0.6	433.53	433.87	−0.34
7	427.90	428.24	−0.34	0.7	207.29	207.28	0.01	0.7	467.58	468.78	−1.20
8	431.05	431.39	−0.34	0.8	176.45	176.43	0.03	0.8	534.30	538.20	−3.90
9	432.61	432.98	−0.37	0.9	153.58	153.55	0.03	0.9	665.27	678.32	−13.05
10	433.53	433.87	−0.34
b	${\pi }^{DU}$	${\pi }^{DD}$	${\pi }^{DU}-{\pi }^{DD}$	${\theta }_1$	${\pi }^{DU}$	${\pi }^{DD}$	${\pi }^{DU}-{\pi }^{DD}$	${\theta }_2$	${\pi }^{DU}$	${\pi }^{DD}$	${\pi }^{DU}-{\pi }^{DD}$
−0.05	240.74	240.76	−0.01	0.1	580.45	692.52	−112.07	0.1	536.80	556.55	−19.75
−0.04	249.47	249.50	−0.02	0.2	488.41	508.69	−20.27	0.2	459.89	459.95	−0.05
−0.03	258.63	258.66	−0.03	0.3	433.53	433.73	−0.20	0.3	413.68	417.42	−3.74
−0.02	268.24	268.28	−0.04	0.4	407.37	409.18	−1.81	0.4	392.78	406.60	−13.82
−0.01	278.34	278.39	−0.05	0.5	412.52	418.96	−6.44	0.5	401.42	422.94	−21.52
0	288.95	289.16	−0.20	0.6	468.32	472.76	−4.44	0.6	460.63	480.73	−20.10
0.01	300.12	300.34	−0.21	0.7	665.94	649.14	16.81	0.7	667.07	659.38	7.70
0.02	311.89	312.11	−0.22	0.8	1821.15	2273.98	−452.83	0.8	1959.63	2190.83	−231.20
0.03	324.15	324.53	−0.38

. In most cases, the differentiated pricing strategy yields a higher expected revenue, which also highlights the advantages of differentiated pricing. However, when the elasticity coefficient of service is greater than a certain threshold, the platform can achieve a higher expected revenue by adopting a unified pricing strategy.

(3)

The impacts of initial demand restriction

The impacts of initial demand constraints on the optimal service price and expected revenue are shown in Figure 7a,b, respectively. In Figure 7a, taking the price of service type 1 as an example, the initial demand constraints are sequentially set as $f_1=f_2=0, f_1=4 \mathrm{and} f_2=5, f_1=10 \mathrm{and} f_2=9$. In Figure 7b, the initial demand constraints are sequentially set as $f_1=f_2=\mathrm{0,1},2,\cdots ,11$. Under this parameter setting, the initial demand constraint has a negative impact on the service price and expected revenue, which further validates Theorems 2 and 4. It represents one of the crucial driving forces behind the restriction of initial service demand on service platforms like the Huawei Cloud Computing Platform and the Xinhua Internet Hospital. Interestingly, when the service platform increases the restrictions on initial demand, the service price gradually converges as the operation continues, while the gap in expected revenue under the two pricing strategies remains stable within a certain range. It indicates that the long-term effect of initial demand restriction on the service price gradually weakens, while the long-term effect on the expected revenue is relatively stable.

In conclusion, some core findings still hold in the extension section, which further demonstrate the robustness of the research conclusion.

8. Conclusions

Service platforms represent a critical pathway for the transformation and upgrading of service industries in the digital economy. The simultaneous involvement of full- and part-time service providers, the time-varying service demands of customers, and the initial demand constraints exacerbate the complexity of the operational management of service platforms. In reality, service platforms commonly employ unified pricing or differential pricing strategies to directly regulate the platform’s status and thereby achieve operational goals. However, the majority of existing research on service platform pricing has been conducted from a static equilibrium perspective and overlooks the profound influence exerted by the time-varying nature of service demand on optimal pricing.

By distilling the common features inherent in the actual operations of service platforms across various industries, this study constructs a general dynamic pricing model for a revenue-maximizing service platform using optimal control theory. Specifically, this study determines and analyzes the optimal pricing scheme and expected revenues under scenarios with and without initial demand constraints, as well as for the two distinct pricing strategies. Moreover, it conducts both theoretical and numerical comparisons of the disparities in optimal pricing schemes and expected revenues between these two pricing strategies. Finally, by incorporating service quality as an endogenous variable, the fundamental dynamic pricing model is extended. This extension serves to further validate the robustness of some key research findings. Overall, this study makes significant theoretical contributions and holds substantial practical value for the operational management of service platforms.

8.1. Theoretical Contributions

This study can enrich the theoretical knowledge in the field of scientific pricing of service platforms and make several important contributions to the literature on dynamic pricing of service systems, unified pricing vs. differential pricing, and the pricing for a gig economy service platform.

Regarding the dynamic pricing of service systems, this study extends the single service situation without initial demand constraints to a two-service competition situation with initial demand constraints, and solves for and analyzes the optimal dynamic pricing. This study reveals that initial demand constraints exert a negative impact on the optimal service price and a positive impact on the expected revenues, yet their long-term effects are both limited. When the service quality elasticity coefficient exceeds a certain threshold, the service quality has a positive and a negative effect on the optimal unified price and the optimal differential price, respectively. Blind investment in service quality does not necessarily increase service price and expected revenue.

Regarding the unified pricing vs. differential pricing in service systems, this study extends the static pricing scenario of tangible goods to the dynamic pricing scenario of intangible services. It compares the differences in optimal service prices and expected revenues of the service platform under the two pricing strategies, and presents the applicable conditions for the two pricing strategies. This study determines that, during periods of surging service demand, when the revenue-sharing ratio is smaller or the difference in service quality is greater, the service platform should adopt the differential pricing strategy to achieve higher operational revenue. Otherwise, it should adopt the unified pricing strategy. Meanwhile, an over-sensitivity of customers to service prices proves detrimental to promoting the expected revenue.

Regarding the pricing for a gig economy service platform, this study formulates a dynamic pricing model for the service platform based on optimal control theory. To a certain extent, it transcends the limitations inherent in the equilibrium pricing model. This study shows that the optimal dynamic price rises as the potential customers’ demand expands. When the service price elasticity coefficient falls below a certain threshold, the gap between the optimal service prices under unified and differentiated pricing strategies narrows as potential demand and the demand fluctuation factor increase, while the gap in expected revenues between the two pricing strategies widens with the intensification of price competition.

8.2. Practical Implications

The research conclusions can serve platform managers and policymakers with actionable insights as follows.

The conclusions revealed by this study can assist service platform managers in understanding how initial demand restriction and service competition affect optimal dynamic pricing and expected revenue, which provides support for service pricing decision-making. Under the circumstances of initial demand constraints and two service types in competition, there exists an optimal pricing scheme for service platforms. In actual operations, service platform managers should exercise caution when implementing the “hunger marketing” strategy, that is, restricting initial demand. Specifically, to increase service prices, managers should impose stringent limitations on initial demand. To achieve higher operational revenue, managers are advised to relax the initial demand constraints. Service platform managers can also adjust the optimal service price by modifying service quality, and the specific adjustment approach depends on the pricing strategy adopted. When investing in service quality improvements, managers must conduct rigorous cost–benefit analyses to ensure that the gains from enhanced customer satisfaction outweigh the associated increases in operational expenditure.

The conclusions derived from this study can provide a theoretical foundation for service platform managers to select appropriate pricing strategies. Service platform managers should fully leverage the advantages of AI technology to accurately capture customer market trends and their own operational status, and then choose suitable pricing strategies to effectively achieve operational revenue goals. To capitalize on surging demand, for example, medical service platforms that simultaneously operate multiple types of services with significant differences in service quality should adopt a differential pricing strategy. Similarly, takeout service platforms, which usually set a relatively low revenue-sharing ratio, should also adopt a differential pricing strategy. In contrast, ride-hailing platforms, which typically offer similar ride-hailing services with a relatively high revenue-sharing ratio, may be better off adopting a unified pricing strategy. Meanwhile, service platforms can exert influence on and even mitigate customers’ sensitivity to service prices through measures such as targeted marketing (issuing coupons), improving after-sales service, and furnishing complimentary additional services.

The conclusions drawn from this study can offer theoretical insights for policymakers to regulate the service market. Policymakers are empowered to implement macroscopic regulatory measures on the service market via scientific and efficient policy instruments. Specifically, these efforts can be directed towards cultivating potential customers, offering policy-based support, steering the trends of the customer market, and standardizing service competition. By leveraging advanced data-mining tools, policymakers can closely monitor customers’ sensitivity to service prices and comprehensively analyze the developmental status of the service market. Subsequently, through modulating the potential service demand and the intensity of service competition, they can mitigate the disparities in service prices and operational revenues that arise from diverse pricing strategies adopted by service platforms. It, in turn, contributes to fostering the sound development of the service market.

8.3. Limitations and Future Directions

This study has certain limitations in theoretical modelling and numerical analysis. The formulation of the service platform dynamic pricing model in this study heavily relies on fundamental assumptions. Some of these assumptions overly simplify the real-world operational scenarios of service platforms. In the theoretical modelling, this study assumes that all customers are homogeneous and perceive no difference in the effectiveness of services provided by full-time and part-time service providers, that service providers can respond to customers in a timely manner, and the revenue-sharing ratio remains constant throughout the entire operational cycle. In the numerical analysis, the determination of key parameter values does not comprehensively draw on the real-world operational data of service platforms. Consequently, there is a lack of empirical validation for the crucial findings and conclusions of this research.

Future research could incorporate the heterogeneity in the customer market, the stochastic nature of supply and demand, and the endogeneity of the revenue-sharing ratio to further enhance the theoretical model developed in this study. The theoretical model established herein could also be further extended to accommodate complex real-world situations, such as continuous service quality management, the operation of more than two service types, and competition among service platforms. Moreover, real-world platform data could be collected to verify the accuracy of the constructed model’s predictions and the robustness of the research conclusions.