Inventory Allocation: Omnichannel Demand Fulfillment with Admission Control
Abstract
:1. Introduction
- (1)
- What is the nature of the joint policy?
- (2)
- Does the proposed policy offer advantages over the traditional policy?
- (3)
- How does considering carry-over inventory affect the policy?
2. Literature Review
3. The Model and Notation
4. Optimal Strategy Analysis
4.1. Optimal Strategy Structure
4.2. Property Study
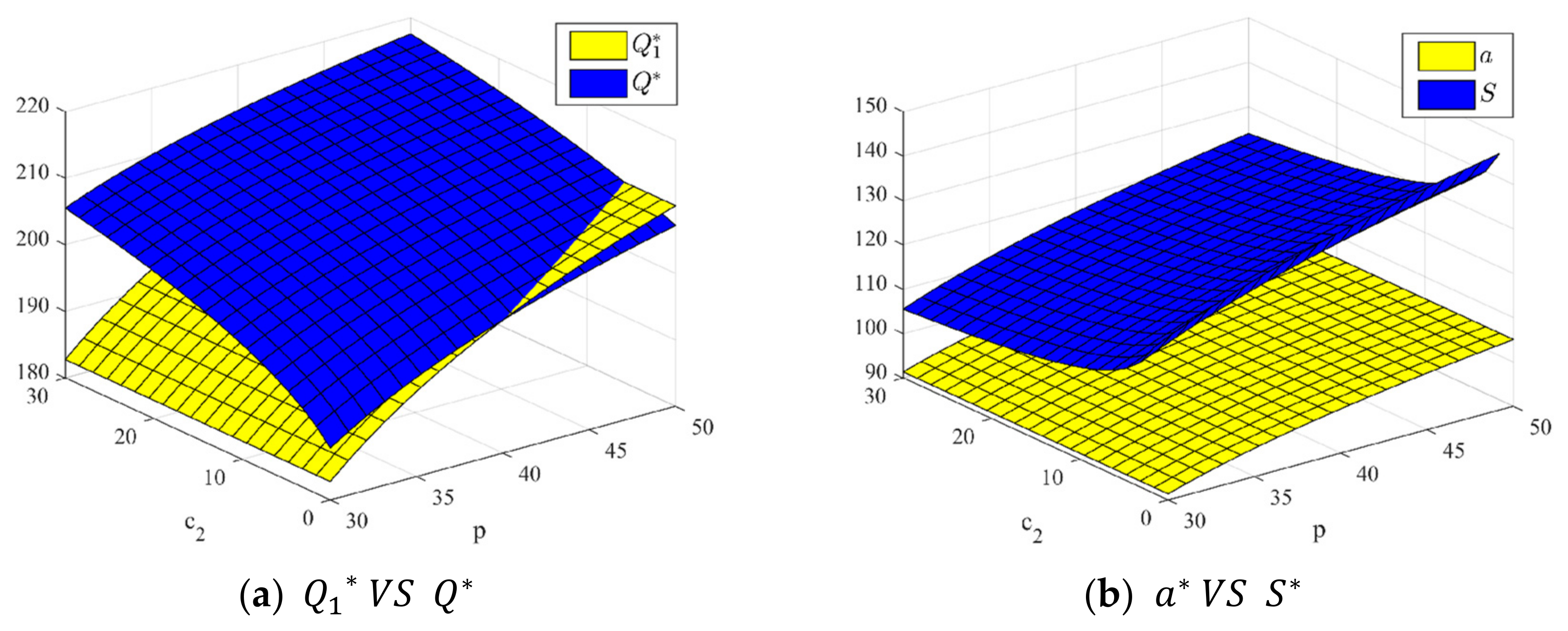
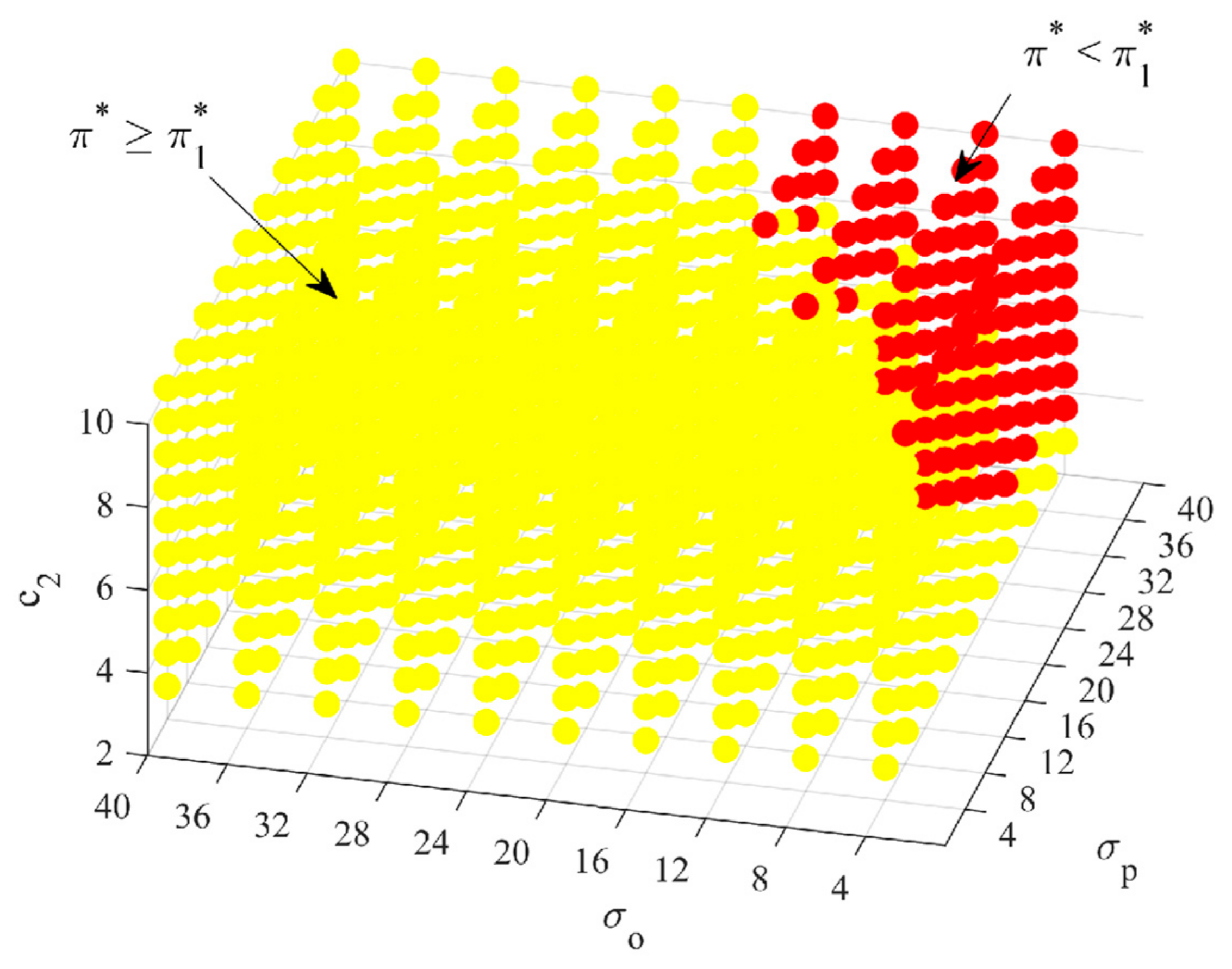
4.3. Strategy Comparison
5. Impact of Inventory Roll-Over
5.1. Model Description
5.2. Optimal Strategy
- (1)
- When , the optimal strategy satisfies the following equation:
- (2)
- When , the optimal strategy satisfies the following equation:
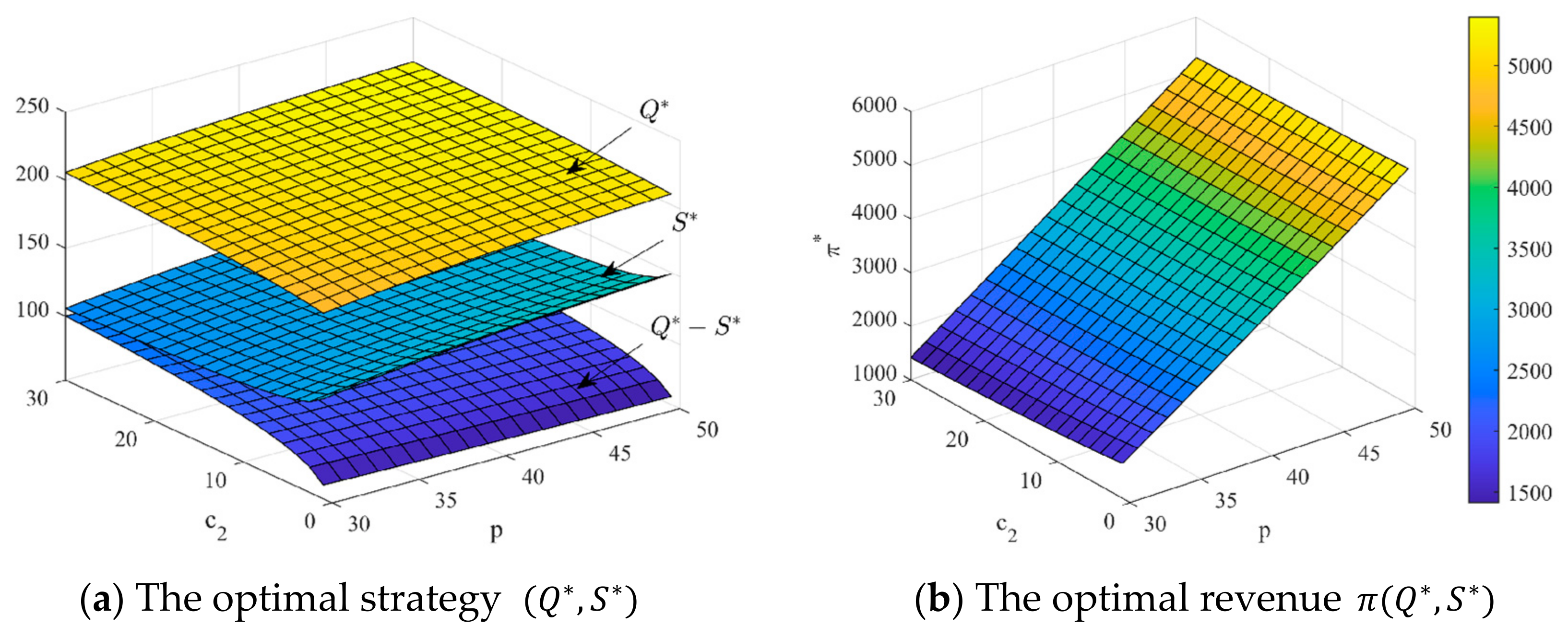
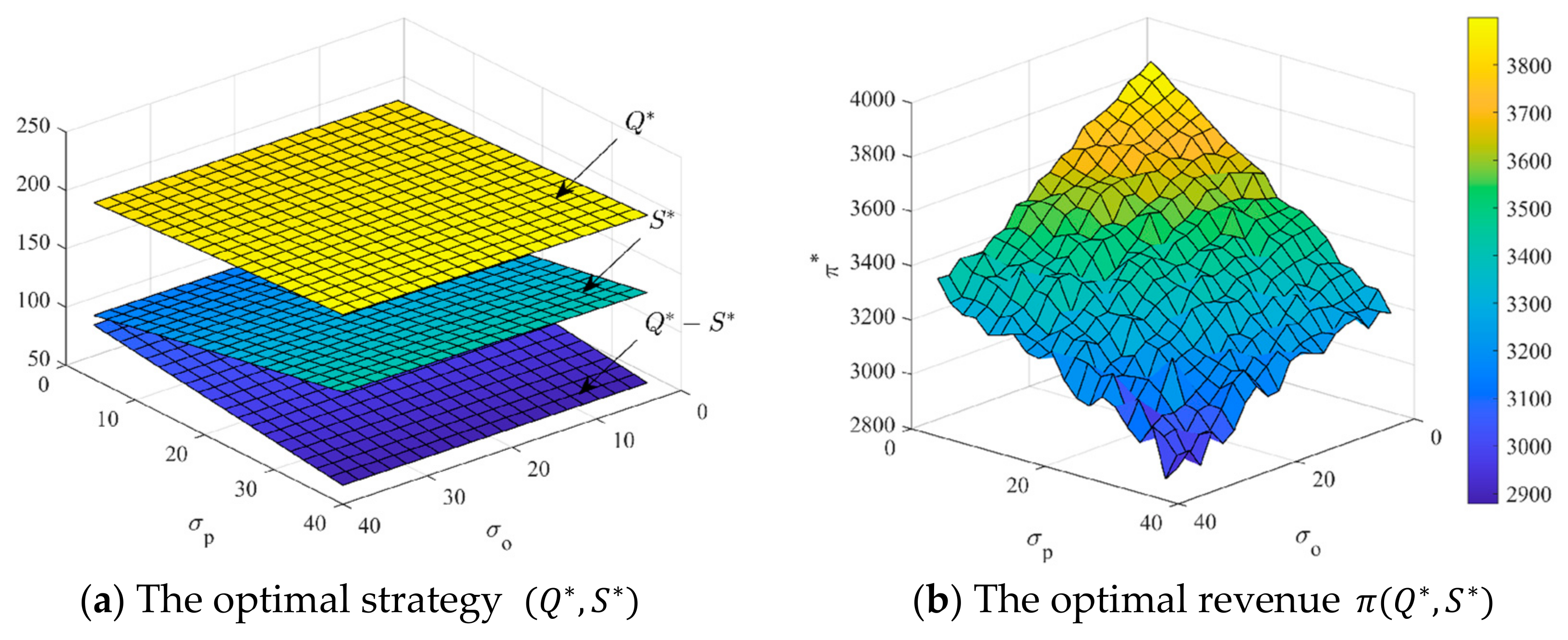
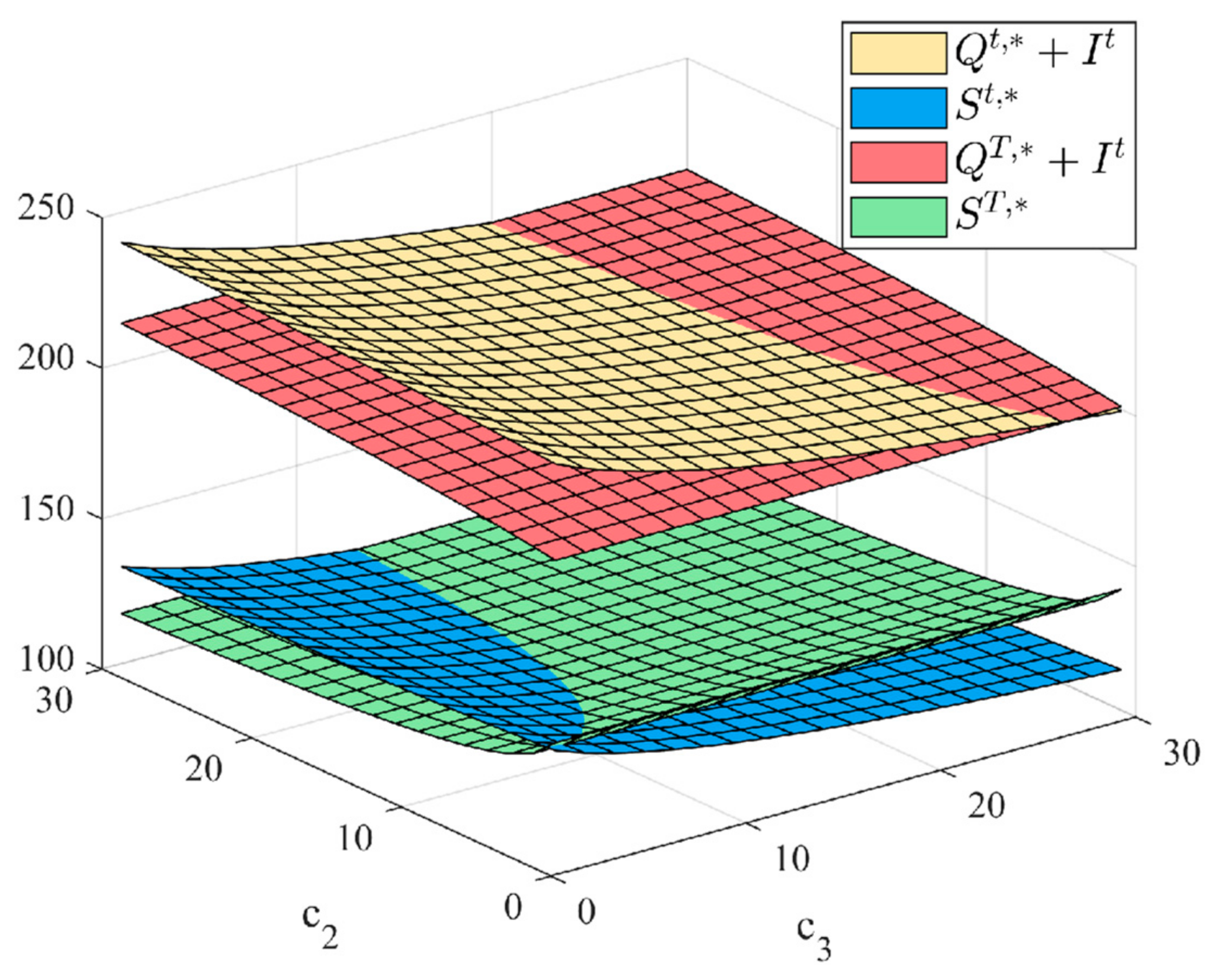
5.3. Numerical Study
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Proof of Proposition 1
Appendix A.2. Proof of Proposition 2
Appendix A.3. Proof of Proposition 4
- (1)
- First, it is verified that the revenue function of the store in the Period is a concave function of the order decision and the threshold .
- (2)
- Similarly, verify that is a concave function of .
- (3)
- Assume that the revenue function of the store in period is a concave function of the inventory level and the threshold . Below, we will prove that is a concave function of and .
References
- Hübner, A.; Hense, J.; Dethlefs, C. The revival of retail stores via omnichannel operations: A literature review and research framework. Eur. J. Oper. Res. 2022, 302, 799–818. [Google Scholar] [CrossRef]
- Rooderkerk, R.; de Leeuw, S.; Hübner, A. Advancing the marketing-operations interface in omnichannel retail. J. Oper. Manag. 2023, 69, 188–196. [Google Scholar] [CrossRef]
- Cai, Y.; Lo, C.K.Y. Omni-channel management in the new retailing era: A systematic review and future research agenda. Int. J. Prod. Econ. 2020, 229, 107729. [Google Scholar] [CrossRef]
- Verhoef, P.C.; Kannan, P.K.; Inman, J.J. From Multi-Channel Retailing to Omni-Channel Retailing. J. Retail. 2015, 91, 174–181. [Google Scholar] [CrossRef]
- Mou, S.; Robb, D.J.; DeHoratius, N. Retail store operations: Literature review and research directions. Eur. J. Oper. Res. 2018, 265, 399–422. [Google Scholar] [CrossRef]
- Goedhart, J.; Haijema, R.; Akkerman, R.; de Leeuw, S. Replenishment and fulfilment decisions for stores in an omni-channel retail network. Eur. J. Oper. Res. 2023, 311, 1009–1022. [Google Scholar] [CrossRef]
- Goedhart, J.; Haijema, R.; Akkerman, R. Inventory rationing and replenishment for an omni-channel retailer. Comput. Oper. Res. 2022, 140, 105647. [Google Scholar] [CrossRef]
- Jia, S.; Karp, J.; Ravi, R.; Tayur, S. Effective Online Order Acceptance Policies for Omnichannel Fulfillment. Manuf. Serv. Oper. Manag. 2022, 24, 1650–1663. [Google Scholar] [CrossRef]
- Bendoly, E. Integrated inventory pooling for firms servicing both on-line and store demand. Comput. Oper. Res. 2004, 31, 1465–1480. [Google Scholar] [CrossRef]
- Bendoly, E.; Blocher, D.; Bretthauer, K.M.; Venkataramanan, M.A. Service and cost benefits through clicks-and-mortar integration: Implications for the centralization/decentralization debate. Eur. J. Oper. Res. 2007, 180, 426–442. [Google Scholar] [CrossRef]
- Ishfaq, R.; Raja, U. Evaluation of Order Fulfillment Options in Retail Supply Chains. Decis. Sci. 2018, 49, 487–521. [Google Scholar] [CrossRef]
- Gao, F.; Su, X. Omnichannel Retail Operations with Buy-Online-and-Pick-up-in-Store. Manag. Sci. 2016, 63, 2478–2492. [Google Scholar] [CrossRef]
- Lin, X.; Zhou, Y.; Hou, R. Impact of a “Buy-online-and-pickup-in-store” Channel on Price and Quality Decisions in a Supply Chain. Eur. J. Oper. Res. 2021, 294, 922–935. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, X. Omnichannel operations with ship-from-store. Oper. Res. Lett. 2020, 48, 257–261. [Google Scholar] [CrossRef]
- Akturk, M.S.; Ketzenberg, M.; Heim, G.R. Assessing impacts of introducing ship-to-store service on sales and returns in omnichannel retailing: A data analytics study. J. Oper. Manag. 2018, 61, 15–45. [Google Scholar] [CrossRef]
- Sun, K.; Liu, Y.; Li, X. Mail back or in-store dropoff? Optimal design of product-exchange policies in omnichannel retailing systems. Omega 2024, 125, 103024. [Google Scholar] [CrossRef]
- Topkis, D.M. Optimal Ordering and Rationing Policies in a Nonstationary Dynamic Inventory Model with n Demand Classes. Manag. Sci. 1968, 15, 160–176. [Google Scholar] [CrossRef]
- Paul, J.; Agatz, N.; Spliet, R.; Koster, R.D. Shared Capacity Routing Problem − An omni-channel retail study. Eur. J. Oper. Res. 2019, 273, 731–739. [Google Scholar] [CrossRef]
- Bayram, A.; Cesaret, B. Order fulfillment policies for ship-from-store implementation in omni-channel retailing. Eur. J. Oper. Res. 2021, 294, 987–1002. [Google Scholar] [CrossRef]
- Abouelrous, A.; Gabor, A.F.; Zhang, Y. Optimizing the inventory and fulfillment of an omnichannel retailer: A stochastic approach with scenario clustering. Comput. Ind. Eng. 2022, 173, 108723. [Google Scholar] [CrossRef]
- Jiu, S. Robust omnichannel retail operations with the implementation of ship-from-store. Transp. Res. Part E Logist. Transp. Rev. 2022, 157, 102550. [Google Scholar] [CrossRef]
- Baron, O.; Cire, A.A.; Savaser, S.K. Decentralized Online Order Fulfillment in Omni-Channel Retailers. Prod. Oper. Manag. 2024, 33, 1719–1738. [Google Scholar] [CrossRef]
- Boran, M.; Cavdar, B.; Isik, T. Queueing Systems with Preferred Service Delivery Times and Multiple Customer Classes. arXiv 2022, arXiv:2203.01433. [Google Scholar] [CrossRef]
- Gao, Z.; Ling, Z.; Gupta, V.; Xin, L. Real-Time Omnichannel Fulfillment Optimization. SSRN. 2023. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4314250 (accessed on 10 April 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, F.; Fu, S.; Zhang, Y.; Miao, B. Inventory Allocation: Omnichannel Demand Fulfillment with Admission Control. J. Theor. Appl. Electron. Commer. Res. 2025, 20, 72. https://doi.org/10.3390/jtaer20020072
Ma F, Fu S, Zhang Y, Miao B. Inventory Allocation: Omnichannel Demand Fulfillment with Admission Control. Journal of Theoretical and Applied Electronic Commerce Research. 2025; 20(2):72. https://doi.org/10.3390/jtaer20020072
Chicago/Turabian StyleMa, Fangfang, Shaochuan Fu, Yuanyuan Zhang, and Benxuan Miao. 2025. "Inventory Allocation: Omnichannel Demand Fulfillment with Admission Control" Journal of Theoretical and Applied Electronic Commerce Research 20, no. 2: 72. https://doi.org/10.3390/jtaer20020072
APA StyleMa, F., Fu, S., Zhang, Y., & Miao, B. (2025). Inventory Allocation: Omnichannel Demand Fulfillment with Admission Control. Journal of Theoretical and Applied Electronic Commerce Research, 20(2), 72. https://doi.org/10.3390/jtaer20020072





