Reward in Cash or Coupon? Joint Optimization of Referral Reward and Pricing

Abstract

The popularity of social media has provided great convenience for firms to conduct online referral marketing by using referral reward programs. We contribute to the existing works by examining the profitability of the two referral reward programs, namely reward in cash and reward in discount coupons, and measuring the instant product sales and the informative utility output from consumer referrals. We established two-period optimization models and found that referral reward programs are effective only if the unit referral cost of customers is low and if the repurchase rate of consumers is high enough. To redeem the reward instantly or not (in cash or discount coupon) interacts with the pricing strategy: the cash reward is fixed in combination with a high price followed by a low price strategy, and the coupon reward is fixed in combination with a low price followed by a high price strategy. With the increase in the unit referral cost, a firm will be more inclined to use the joint strategy of coupon reward and a low price followed by a high price strategy. Under the conditions that the referral reward program is ineffective, the pricing strategy with a high price followed by a low price is optimal.

1. Introduction

In online referral marketing, new consumers are acquired through referral reward programs (RRPs) that exploit existing consumers’ social networks and encourage existing consumers to make social referrals [1,2]. The referral rewards come in different forms such as cash, shopping vouchers, prizes, discount coupons, redeemable points, etc. [3]. In general, the forms of referral rewards can be divided into monetary rewards and in-kind rewards [4]. Focusing on monetary rewards, cash and discount coupons are most commonly used in RRPs. For example, Taobao merchants send cards with referral reward information to the consumers who have purchased products and explain that he/she can receive monetary rebates if he/she makes a successful referral. The monetary rebates could be in cash, where the consumers can obtain the value instantly, or in a discount coupon, where the consumers can only redeem it in their future purchases.

Although both cash and coupon rewards could motivate consumers to make referrals [5], there are significant differences in the incentive effects of the two forms of rewards. Intuitively, due to the uncertainty of coupon rewards for the consumers, they are not as effective as cash rewards in motivating consumers to make referrals when the face values of the two forms of rewards are equal. Meanwhile, the uncertainty may also affect the actual redemption rate, which means the firm will not necessarily redeem all of the coupons issued to consumers, but cash rewards are 100% paid out. It is difficult to determine the efficiency of these two RRPs intuitively, and it is necessary to further explore it by constructing mathematical models. However, few of the existing analytical works on RRPs focus on delayed redemption rewards like coupon rewards. As far as we know, the early studies discussed the conditions under which firms should use RRPs by comparing the profitability of RRPs with traditional marketing methods, such as pricing [6,7] and advertising [8]. As social media has driven the popularity of RRPs, scholars have focused on how to design more effective RRPs, such as how to set the reward payment rules [9], select or combine the various RRPs [10], and design the optimal reward allocation scheme [11]. The above studies did not discuss the immediacy of reward redemption in RRPs, although whether the reward is redeemed instantly may greatly impact consumers’ referral behavior and firms’ profits. In this study, we investigated a firm’s two-period sales to evaluate and compare the effectiveness of cash and coupon rewards.

To obtain the rewards, the consumers acting as the referrers always recommend to more than one potential consumer in practice because of the difficulty of making a successful referral. Before a successful referral occurs, the “failed” referrals of referrers still make the recipients who are not instantly converted into buyers aware of the product. It means the “failed” referrals produce informative utility outputs for firms. In the long run, the informative utility outputs may continue to be transformed into product sales in the future stage. However, most existing studies on optimizing RRPs have often ignored the value of the “failed” referrals and have only measured the instant product sales from consumer referrals. One of the prior studies that paid attention to the “failed” referrals is that of Ref. [10]. They considered two RRPs with different rules: the RRP that does not care whether it is successful (RRWS) and the RRP that must be successful (RRMS). In their study, the value of RRPs is not only instant sales but also product awareness and future sales, and the strategy selection between the RRWS, the RRMS, and a dual strategy was studied. Similar to the work of Ref. [10], in the present study, we considered both the instant sales output and the informative utility outputs of RRPs to discuss the profitability of the RRP with cash rewards and the RRP with coupon rewards.

Continuing the setting of some prior studies [6,7,9], we conducted our study on the combination of RRPs and pricing because the price of the referred product is one of the factors affecting the difficulty of a successful referral. The difficulty for a successful referral not only determines the referral cost of consumers, which influences the firm’s reward cost in turn, but it also has an impact on the informative utility output generated in the whole referral process. The difficulties come from the following two aspects: the operational difficulty of consumer referral itself and the difficulty of prompting the recipients to purchase the referred product, which depends on the recipients’ perceived value of the referred product and the price. For firms, adjusting the product price is an efficient way to regulate the difficulty of a successful referral and control the incentive efficiency of RRPs. We also explored the interaction between the two-period prices and RRPs.

In summary, we explored the following questions in this paper:

1.

Which reward program is more effective: cash reward or coupon reward?

2.

How does the two-period price affect the optimal choice between the two kinds of RRPs?

3.

What is the optimal joint strategy of RRPs and pricing strategy?

The remainder of the paper is organized as follows: In Section 2, we present a brief literature review. In Section 3, we adopt analysis to examine the three referral reward strategies (no reward, cash reward, and coupon reward) of operation mode and consumer behavior. In Section 4 and Section 5, we conduct two-period mathematical analysis models under two different pricing strategies, respectively, and use optimization methods to solve the optimal pricing and rewards. In Section 6, we compare the optimal results in Section 4 and Section 5 and discuss the joint optimization of referral reward and pricing. In Section 7, we present our conclusions.

2. Literature Review

2.1. RRP Effectiveness

At the outset, scholars have paid more attention to the effectiveness of RRPs on the referral likelihood of consumers [12,13,14] and come to a common conclusion that RRPs are effective in increasing the referral likelihood. Schmitt et al. [15] further provided evidence that customers acquired through RRPs are more loyal and valuable than customers acquired through other marketing programs. Armelini et al. [16] replicated Schmitt et al.’s work and confirmed that RRPs positively affect the loyalty of referred customers. Nevertheless, some works have proven that monetary rewards may increase the perceived social cost of referrers to a greater extent, which weakens the effectiveness of RRPs. Tuk et al. [17] pointed out that monetary rewards will lead to the recipients’ skepticism of the rewarded referrers. The subsequent studies showed that the skepticism from recipients further increases the referrers’ perceived social risk, thereby reducing the referrers’ likelihood to make referrals in turn [18,19]. Wirtz et al. [5] also showed that the impression management concerns of referrers may weaken the positive effects of monetary rewards on referral likelihood. Orsingher and Wirtz [20] found that two opposing psychological mechanisms influence the effectiveness of RRPs: a positive effect via the perceived attractiveness of the financial incentives and a negative effect via meta-perception of the referral. Vilnai and Levina [21] also pointed out that a crowding-out effect exists in the impact of RRPs and referrers’ social needs on referral likelihood.

Recent works have explored the effectiveness of RRPs by regarding referrals as prosocial behavior. Gershon et al. [22], Jung et al. [23], and Jung et al. [24] emphasized that customer referral is prosocial and revealed that an intrinsically prosocial element in framing the RRPs to initiate the referral process is a necessary condition for success. Scholars have paid more attention to social factors such as referral scarcity, social contagion, and social distance between referrers and recipients to investigate the impact on the effectiveness of RRPs [25,26,27,28]. Furthermore, some research on mitigating the crowding-out effect between RRPs and intrinsic incentives has been performed. Dose et al. [29] and Zhan et al. [30] pointed out that RRPs with a private reward attenuate the negative effect of monetary rewards on intrinsic incentives. In addition to the visibility of the reward, different forms of rewards and reward allocation schemes exert unique impacts. Jin and Huang [19] found that monetary rewards lead to less referral generation and acceptance than in-kind rewards. Peng et al. [31] also emphasized that nonmonetary rewards are more effective at referral generation than monetary rewards. Chen and Hao [32] discussed the difference in the effectiveness of the two reward presentations (dollar and percentage). In terms of reward allocation schemes, the existing works found a common conclusion that prosocial referral incentives (recipient-benefiting or both-benefiting) recruit more new customers than selfish incentives (sender-benefiting) [19,22,23,24].

The above works have shown that RRPs are effective in acquiring new consumers, while the effectiveness varies depending on the visibility of the reward, reward allocation schemes, and forms of rewards. In terms of reward forms, the existing works have paid more attention to the differential effects of monetary rewards versus nonmonetary rewards, but few have focused on the different forms of monetary rewards. In this paper, we focus on the two forms of monetary rewards (cash and coupon), which are different in the immediacy of reward redemption, and discuss the different effectiveness of these two RRPs.

2.2. RRP Optimization

The existing studies on the optimal decision of RRPs have mostly been conducted on the combination of RRPs and pricing. Biyalogorsky et al. [6] were the first to investigate the optimal decision concerning RRPs and study the scenarios of low pricing strategy and reward programs as well as the dual hybrid strategy. Kornish and Li [7] discussed the problem of optimizing the combination of referral rewards and pricing based on the assumption that the driving forces of customers for making referrals include firm-offered rewards and placing a value on a friend’s outcome. Jing and Xie [4] established an analytical model to depict the information-sharing effect between informed customers and less-informed customers and further examined the conditions under which group buying or RRPs is more profitable and the combination optimization of pricing and RRPs. Lobel et al. [9] studied the optimal design of different payment policies (linear payment or threshold payment) and the joint strategy with pricing. Arbatskaya et al. [8] developed an analytical model to examine the effect of using RRPs on pricing and the intensity of a firm’s advertising investment. In addition, RRPs have also been discussed as an auxiliary promotion tool for other marketing strategies. Geng [33] focused on the situation in which RRPs act as a means of promoting freemium mode, while Cao and Li [34] focused on the marketing practices with which firms use RRPs as an incentive method to encourage consumers to participate in group buying.

Some scholars have combined the characteristics of social media-based RRPs in online referral marketing practices and discussed the optimal design of referral rules (make referral privately or publicly) in an RRP [35] or explored the optimal selection among different reward strategies: the RRP that does not care whether it is successful, the RRP that must be successful, and the dual strategy [10]. Furthermore, some works have explored the optimal reward allocation scheme when using RRPs. Xiao et al. [36] took the referrer’s concerns about creating a negative impression when making a rewarded referral into account to discuss the optimal reward allocation scheme. Zhang and Zhang [11] explored the effect of the referrer’s altruism on the optimal reward allocation scheme. A common result that emerged from these works is that the optimal reward scheme shifts from rewarding the referrer to rewarding the recipient.

The above works mainly focused on the instant new sales output from consumers’ successful referrals but ignored the information diffusion effect from consumers’ failed referrals, which may be translated into new sales in future stages. In the present study, we developed a two-period model to capture the two kinds of outputs from consumer referrals.

2.3. Delayed Redemption Rewards

The existing research on decisions about delayed redemption rewards has mostly focused on loyalty reward programs based on the context that a firm is selling a product through two periods, and the firm issues delayed redemption rewards to the consumers who have already purchased the product in the first period, but only those loyal consumers who purchase the product again in the second period can redeem the rewards. Singh et al. [37] studied the optimization decision on pricing and loyalty reward programs in a duopoly market. Gandomi and Zolfaghrari [38] examined the impact of consumers’ structure and their post-purchase satisfaction level on the profitability of a loyalty reward program with a delayed redemption reward. Su et al. [39] studied the retailers’ combination optimization decision of the tradable coupon reward and pricing in a supply chain consisting of two suppliers and one retailer. Shen et al. [40] investigated the impact of delayed redemption rewards on consumers’ repeat-purchase decisions. The purpose of using delayed redemption rewards is to encourage consumers to make repeat purchases rather than to motivate them to make referrals. In this paper, we attempt to analyze the incentive effect of delayed redemption rewards on consumers’ referral behavior and repeat-purchase behavior and further discuss how the firms make optimal choices between the instant redemption reward (cash) and delayed redemption reward (coupon).

3. Problem Description and Consumer Behavior

3.1. Problem Description

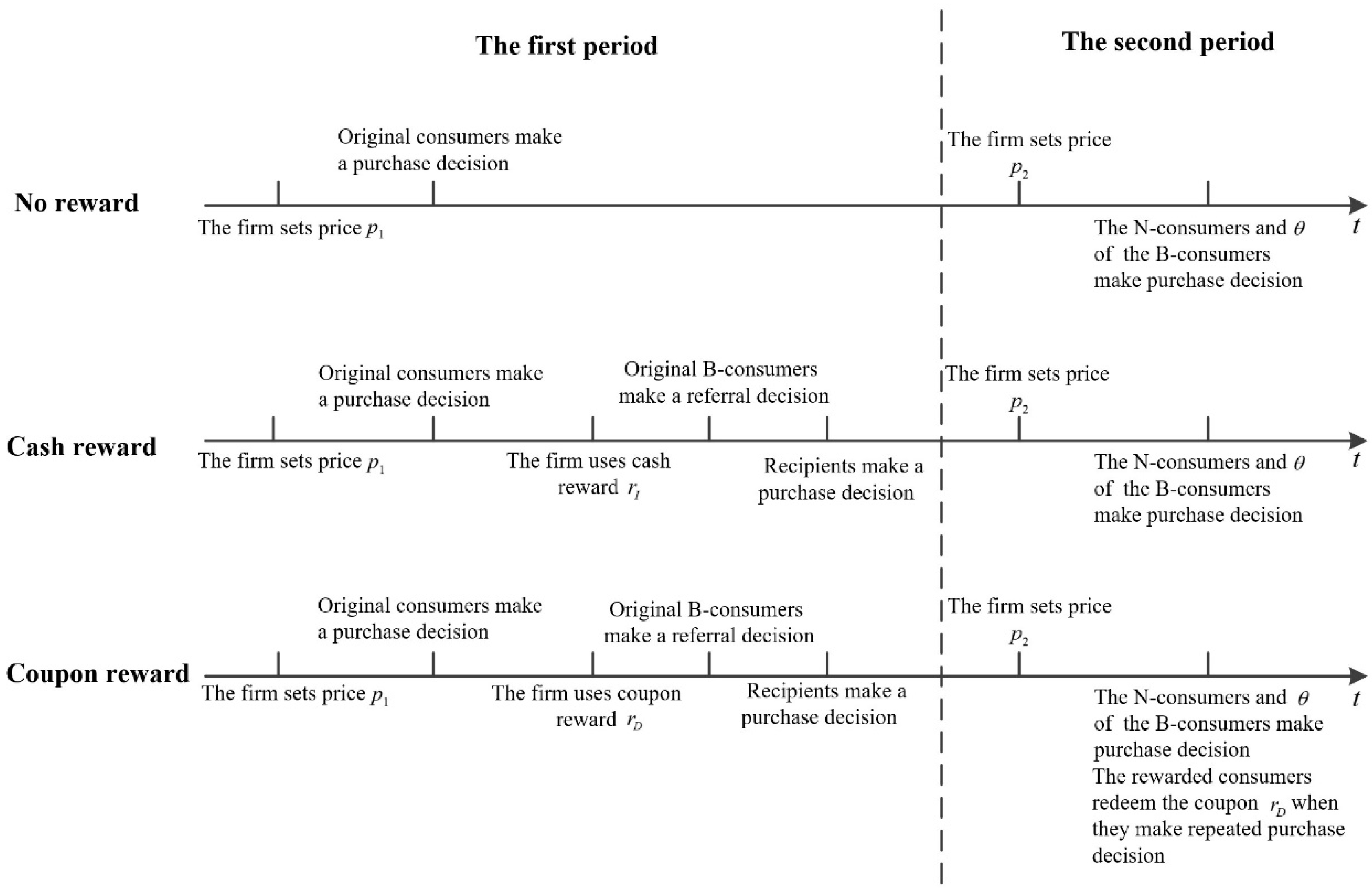
Consider a firm selling products through two periods based on the effect of pre-marketing efforts that have made a certain number $m$ of consumers (original consumers) aware of the existence of the product. The firm considers using an RRP in the first period to motivate the original consumers who have bought the product to make recommendations. If the reward is in cash, the referrer instantly gets the value of the reward in the first period. Reversely, if the reward is in coupon, it will be deferred cash until the referrers make repeat purchases in the second period. Therefore, the following three cases are possible:

(1) Not using RRP. In the first period, the original consumers make purchase decisions based on the first-period price $p_1$. Then, the consumers are divided into two types: the consumers who buy the product (B-consumers) and the consumers who do not buy the product (N-consumers). In the second period, only a proportion of the B-consumers make repeat-purchase decisions [37], and the N-consumers make purchase decisions based on second-period price $p_2$.

(2) Reward in cash. For an original B-consumer in the first period, if he successfully recommends the product to one of his friends, he gets the cash rewards $r_I$, and his friend becomes a referred B-consumer. In the second period, a proportion of the B-consumers make repeat-purchase decisions, and the N-consumers make purchase decisions based on second-period price $p_2$.

(3) Reward in coupon. The original B-consumers who successfully recommend the product get the coupon rewards $r_D$ in the first period, and a proportion of them make repeat-purchase decisions based on $p_2-r_D$ in the second period. A proportion of the referred B-consumers and the N-consumers make purchase decisions based on the second-period price $p_2$ in the second period.

The decision-making orders under different cases are shown in Figure 1.

Our study has the following objectives: (1) establish a model that does not use RRP and optimizes the two-period prices by solving the model; (2) establish models that use RRPs with cash and coupon rewards, respectively, and solve them for optimal reward amount and prices; (3) determine the optimal joint strategy of referral reward and pricing according to the solution results of the above models.

3.2. Consumer Behavior

Assume that the potential consumer capacity of the product is $M$, where $M\gg m$. This indicates that the consumer market is large enough so that the recipients are all new consumers and do not intersect with the original consumers $m$. For any consumer $i$ who is aware of the product, his perceived value of the product $v_i$ obeys a uniform distribution on $\left[0,1\right]$, i.e., $v_i\sim U\left[0,1\right]$. The consumer buys one unit of the product when $v_i-p\ge 0$. Based on the opinions of Sing and Gandomi that only a certain percentage of consumers who have already purchased the product in the first period will move to the second period to make a repeat-purchase decision [36,37], we assume that the repeat-purchase rate of the first-period B-consumers is $\theta$, where $0<\theta <1$.

3.2.1. Consumer Behavior in the First Period

When no reward is available, no referrals happen, and only the original consumers $m$ are aware of the product. Any original consumer $i$ will buy the product when his utility $u_i=v_i-p_1$ satisfies $u_i\ge 0$; then, the probability of purchasing the product is $\mathrm{Pr}\left(u_i\ge 0\right)=1-p_1$. Therefore, the number of B-consumers in the first period is as follows:

$$Q_{1S}^B=m\left(1-p_1\right).$$

(1)

And the number of the N-consumers in the first period is as follows:

$$Q_{1S}^N=m-Q_{1S}^B=m{p}_1.$$

(2)

If an RRP works on the original B-consumers, referrals happen when the B-consumers’ expected surplus obtained from a successful referral is nonnegative. We assume that the unit referral cost is $c$, which relates to the communication efficiency of the consumers themselves and the technical support of social media. The total expected referral cost for a B-consumer to achieve a successful referral is $C$, determined by both the unit referral cost and the expected total number of referrals $q$ when the successful referral happens, i.e., $C=cq$. If the reward is in cash, the original B-consumer will obtain the reward $r_I$ only if he makes a successful referral; then, he makes referrals when $r_I-C\ge 0$. If the reward is in coupon, the original B-consumer will obtain the coupon with face value $r_D$, which can only be redeemed upon repeated purchases in the second period; then, he makes referrals when $\theta r_D-C\ge 0$. Each original B-consumer achieves $q$ new consumers, and only one of them buys the product. After the first period, $Q_1=m+Q_{1S}^{B}q$ consumers know the presence of the product, including $Q_1^B=2Q_{1S}^B$ B-consumers and $Q_1^N=Q_1-Q_1^B$ N-consumers, and $Q_{1S}^B$ original B-consumers are rewarded with cash rewards $r_I$ or coupon reward $r_D$. By substituting Equations (1) and (2) into $Q_1^B$ and $Q_1^N$, we obtain the following:

$$Q_1^B=2Q_{1S}^B=2m\left(1-p_1\right).$$

(3)

$$Q_1^N=Q_1-Q_1^B=m+m\left(1-p_1\right)q-2m\left(1-p_1\right).$$

(4)

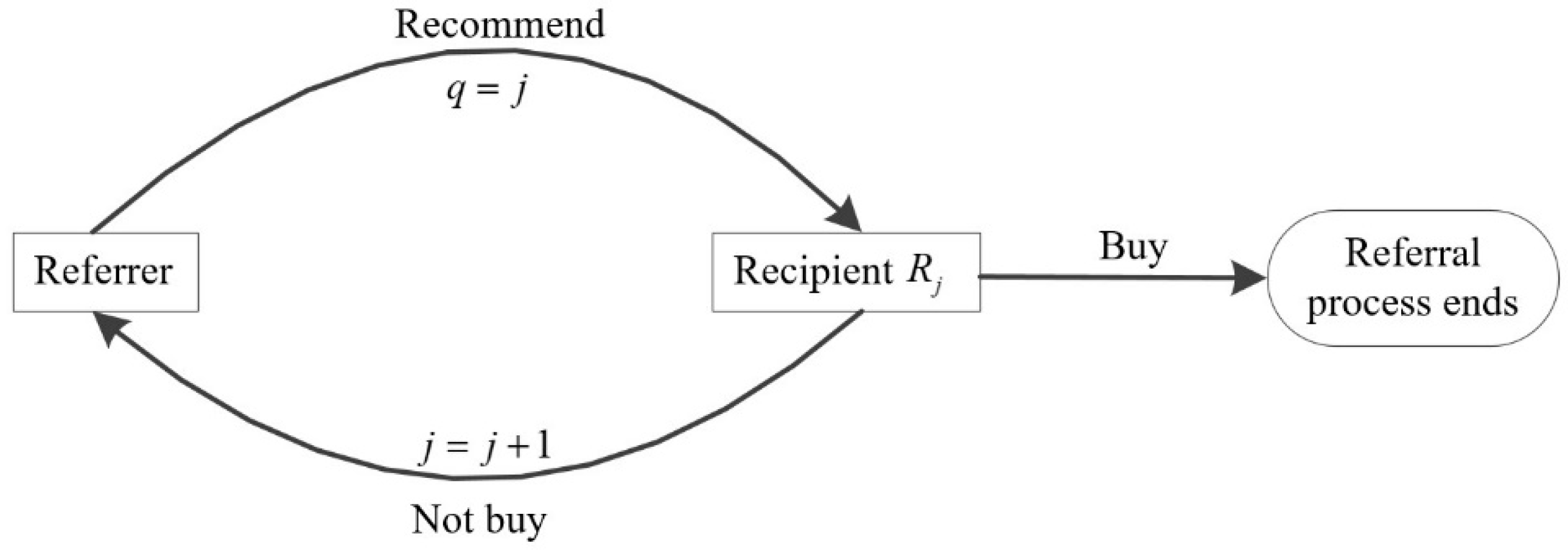
It is obvious that $q$ represents the number of new consumers aware of the product as a result of each successful referrer. For any referrer, when he recommends the product to a recipient who is new to the product, the probability of the recipient purchasing the product is $\mathrm{Pr}\left(v_i-p_1\ge 0\right)=1-p_1$. The referrer recommends the product to the first recipient with a unit referral cost. If the first recipient buys the product, the referral process ends, i.e., $q=1$,$C=c$. Otherwise, the referral process continues, and the referrer recommends the product to the second recipient with one additional unit cost. If the second recipient buys the product, the referral process ends, i.e., $q=2$, $C=2c$. Otherwise, the referral process continues, and the referrer recommends to the third recipient. The referral process continues until a new recipient buys the referred product. The referral process is shown in Figure 2.

Analysis of the referral process above determined that it satisfies the Bernoulli test characteristics. Each referral is regarded as a trial, and there are two trial results, namely success and failure. The probability of success equals the probability of any recipient purchasing the product, i.e., $1-p_1$. Thus, the expected number of trials until a successful referral occurs for the first time equals $q$,

$$q={\displaystyle \frac{1}{1-p_1}}.$$

(5)

3.2.2. Consumer Behavior in the Second Period

A certain percentage ($\theta$) of the B-consumers and all of the N-consumers decide whether to buy at price $p_2$. As we know, the B-consumers’ perceived value from the product $v_i^B\ge p_1$ obeys a uniform distribution on $\left[p_1,1\right]$, and the N-consumers’ perceived value from the product $v_i^N<p_1$ obeys a uniform distribution on $\left[0,p_1\right)$. If $p_2<p_1$, the N-consumers who meet $v_i^N-p_2>0$ buy the product in the second period, and all of the B-consumers repurchase the product. If $p_2\ge p_1$, none of the N-consumers buys the product, and the B-consumers who meet $v_i^B-p_2\ge 0$ buy the product when no reward or cash reward is available in the first period, and the B-consumers rewarded by the coupon in the first period repurchase the product only when they meet $v_i^B-p_2+r_D\ge 0$.

Obviously, the price strategies of the two periods directly affect the structure of consumers who move to the second period to make purchase decisions, which affects the composition of the firm’s profits in turn. Therefore, we built profit optimization models under two price strategies with $p_1>p_2$ and $p_1\le p_2$, respectively, and detail them in the following two sections.

Main notation descriptions of the three strategies are shown in

Table 1. Description of Key Notations.

Notations	Description
$m$	Original consumer base
$p_1$	The first-period price
$p_2$	The second-period price
$r_I$	The amount of cash reward
$r_D$	The denomination of discount coupon reward
$Q_1$	The number of consumers making purchase decisions in the first period
$Q_2$	The number of consumers making purchase decisions in the second period
$\theta$	The repurchase rate
$v_i$	The perceived value of the consumer $i$
$u_i$	The utility of consumer $i$
$c$	Per referral cost
$C$	The expected total referral cost for a successful referral
$q$	The expected total times of referrals for a successful referral
${\pi }_0$	The firm’s profit from no reward program
${\pi }_I$	The firm’s profit from the cash reward program
${\pi }_D$	The firm’s profit from the coupon reward program

. To clearly distinguish the composition of the consumers involved in the two stages of the decision, the relevant notations in Table 1 are labeled with subscript $S$ for the original consumers, a superscript $B$ for the B-consumers, and a superscript $N$ for the N-consumers.

4. Model and Analysis Under $H-L$ Pricing Strategy ($p_1>p_2$)

4.1. Model of No Reward Under $p_1>p_2$

The profit in the first period is ${\pi }_{01}^{H-L}=Q_{1S}^B{p}_1$. In the second period, $\theta Q_{1S}^B$ B-consumers and $Q_{1S}^N\mathrm{Pr}(v_i^N-p_2>0)=Q_{1S}^N{\displaystyle \frac{p_1-p_2}{p_1}}$ N-consumers buy the product, and the profit is ${\pi }_{02}^{H-L}=\left(Q_{1S}^N{\displaystyle \frac{p_1-p_2}{p_1}}+\theta Q_{1S}^B\right)p_2$. The total profit is ${\pi }_0^{H-L}={\pi }_{01}^{H-L}+{\pi }_{02}^{H-L}$. By substituting Equations (1) and (2), we obtain the profit optimization model:

$$\begin{array}{l}\max {\pi }_0^{H-L}=m\left(1-p_1\right)p_1+\left(m\left(p_1-p_2\right)+\theta m\left(1-p_1\right)\right)p_2\\ s.t. p_1>0, p_2>0, p_1>p_2\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}.\end{array}$$

(6)

Solve (3) to obtain Lemma 1.

Lemma 1.

Under the pricing strategy with a high price followed by a low price ($p_1>p_2$), when no reward is available, the optimal prices and the maximum profit of the firm are as follows:

$$\left\{\begin{array}{l}\left(p_1^{*},p_2^{*}\right)=\left({\displaystyle \frac{2-\theta }{3-\theta }},{\displaystyle \frac{1}{3-\theta }}\right)\hfill \\ {\pi }_0^{*H-L}={\displaystyle \frac{m}{3-\theta }}\hfill \end{array}.\right.$$

4.2. Model of Cash Rewards Under $p_1>p_2$

The $Q_{1S}^B$ original consumers buy the product at price $p_1$. Then, the firm announces the RRP with cash rewards $r_I$ to the original B-consumers, and $Q_{1S}^B$ B-consumers decide whether to recommend the product. For any B-consumer, only if $r_I-C\ge 0$, he recommends the product. According to the analysis of the expected accumulated referral cost for a successful referral mentioned above, we obtain the following:

$$C=qc={\displaystyle \frac{c}{1-p_1}}.$$

(7)

Under the RRP with cash reward $r_I$, which satisfies $r_I-C>0$, the original B-consumers make referrals, and each of them makes $q$ new consumers aware of the product but only achieves one new sale. After the first period, there are $Q_1^B=2Q_{1S}^B$ B-consumers, and half of them are rewarded with $r_I$. Thus, the profit of the firm in the first period is ${\pi }_{I1}^{H-L}=Q_1^B{p}_1-Q_{1S}^B{r}_I$. In the second period, $\theta Q_1^B$ B-consumers and $Q_1^N\mathrm{Pr}(v_i^N-p_2>0)=Q_1^N{\displaystyle \frac{p_1-p_2}{p_1}}$ N-consumers buy the product, and the profit of the firm is ${\pi }_{I2}^{H-L}=\left(Q_1^N{\displaystyle \frac{p_1-p_2}{p_1}}+\theta Q_1^B\right)p_2$. The total profit of the two periods is ${\pi }_I^{H-L}={\pi }_{I1}^{H-L}+{\pi }_{I2}^{H-L}$. By substituting Equations (3) and (4), we obtain the profit optimization model:

$$\begin{array}{l}\max {\pi }_I^{H-L}=2m\left(1-p_1\right)p_1-m\left(1-p_1\right)r_I+\left(2m\left(p_1-p_2\right)+\theta *2m\left(1-p_1\right)\right)p_2\\ s.t. p_1>0, p_2>0, p_1>p_2>r_I>0,r_I-{\displaystyle \frac{c}{1-p_1}}\ge 0\end{array}.$$

(8)

Solve (8) to obtain the optimal prices $\left(p_1^{*},p_2^{*}\right)$, the optimal cash rewards ${r_I}^{*}$, and the maximum profit ${\pi }_I^{*H-L}$. The optimal solution is shown in Lemma 2.

Lemma 2.

Under the pricing strategy with a high price followed by a low price ($p_1>p_2$), the optimal solution of the optimization problem (8) exists only when the unit referral cost $c$ and the consumer repeat-purchase rate $\theta$ satisfy $c<{\displaystyle \frac{1}{4}}$ and ${\displaystyle \frac{12c-1}{4c+1}}<\theta <1$, and the optimal prices, cash reward, and the maximum profit of the firm are as follows:

$$\left\{\begin{array}{l}\left(p_1^{*},p_2^{*}\right)=\left({\displaystyle \frac{1}{2\left(3-\theta \right)}}\left(5-2\theta -\sqrt{{\displaystyle \frac{K}{\left(1+\theta \right)}}}\right),{\displaystyle \frac{1}{4\left(3-\theta \right)}}\left(5-\theta -\left(1-\theta \right)\sqrt{{\displaystyle \frac{K}{\left(1+\theta \right)}}}\right)\right)\hfill \\ r_I^{*}={\displaystyle \frac{2c\left(3-\theta \right)\left(1+\theta \right)}{1+\theta +\sqrt{\left(1+\theta \right)K}}}\hfill \\ {\pi }_I^{*H-L}={\displaystyle \frac{m}{8{\left(3-\theta \right)}^2}}\left(\begin{array}{l}\left(5-3\theta -\sqrt{\left(1+\theta \right)K}\right)\left(5-\theta -\left(1-\theta \right)\sqrt{{\displaystyle \frac{K}{\left(1+\theta \right)}}}\right)+\\ 2\left(1+\sqrt{K}\right)\left(\left(10+\theta -{\theta }^2\right)-\left(2-\theta \right)\sqrt{\left(1+\theta \right)K}\right)\end{array}\right)-mc\hfill \end{array}\right.$$

where $K=1+\theta +4\theta c-12c$.

4.3. Model of Coupon Rewards Under $p_1>p_2$

As in the cash reward model, there are $Q_{1S}^B$ original consumers who buy the product at price $p_1$. Under the RRP with coupon reward $r_D$, which satisfies $\theta r_D-C\ge 0$, the original B-consumers make referrals and obtain the coupon rewards $r_D$. Unlike the cash reward, the coupon reward can only be redeemed in the second period when the rewarded B-consumers make repeat purchases.

In the first period, $Q_1^B$ B-consumers and $Q_{1S}^B$ of the B-consumers are rewarded with coupon rewards $r_D$. Thus, the firm’s profit in the first period is ${\pi }_{D1}^{H-L}=Q_1^B{p}_1$. In the second period, all of the $\theta Q_1^B$ B-consumers and $Q_1^N\mathrm{Pr}(v_i^N-p_2>0)=Q_1^N{\displaystyle \frac{p_1-p_2}{p_1}}$ N-consumers buy the product. Among them, $\theta Q_{1S}^B={\displaystyle \frac{1}{2}}\theta Q_1^B$ B-consumers redeem the coupons when they buy the product. Therefore, the firm’s profit in the second period is ${\pi }_{D2}^{H-L}=\left(Q_1^N{\displaystyle \frac{p_1-p_2}{p_1}}+{\displaystyle \frac{1}{2}}\theta Q_1^B\right)p_2+{\displaystyle \frac{1}{2}}\theta Q_1^B\left(p_2-r_D\right)$. The total profit is ${\pi }_D^{H-L}={\pi }_{D1}^{H-L}+{\pi }_{D2}^{H-L}$. By substituting Equations (3) and (4), we obtain the profit optimization model:

$$\begin{array}{l}\max {\pi }_D^{H-L}=2m\left(1-p_1\right)p_1+\left(2m\left(p_1-p_2\right)+\theta m\left(1-p_1\right)\right)p_2+\theta m\left(1-p_1\right)\left(p_2-r_D\right)\\ s.t. p_1>0, p_2>0, p_1>p_2>r_D, \theta r_D-{\displaystyle \frac{c}{1-p_1}}\ge 0\end{array}$$

(9)

Solve (9) to obtain the optimal prices $\left(p_1^{*},p_2^{*}\right)$, the optimal coupon rewards ${r_D}^{*}$, and the maximum profit ${\pi }_D^{*H-L}$. The optimal solution is shown in Lemma 3.

Lemma 3.

Under the pricing strategy with a high price followed by a low price ($p_1>p_2$), the optimal solution of the optimization problem (9) exists only when the unit referral cost $c$ and the consumer repeat-purchase rate $\theta$ satisfy $c<{\displaystyle \frac{1}{4}}$ and ${\displaystyle \frac{12c-1}{4c+1}}<\overline{\theta }<\theta <1$, and the optimal prices, coupon reward, and the maximum profit of the firm are as follows:

$$\left\{\begin{array}{l}\left(p_1^{*},p_2^{*}\right)=\left({\displaystyle \frac{1}{2\left(3-\theta \right)}}\left(5-2\theta -\sqrt{{\displaystyle \frac{K}{\left(1+\theta \right)}}}\right),{\displaystyle \frac{1}{4\left(3-\theta \right)}}\left(5-\theta -\left(1-\theta \right)\sqrt{{\displaystyle \frac{K}{\left(1+\theta \right)}}}\right)\right)\hfill \\ r_D^{*}={\displaystyle \frac{2c\left(3-\theta \right)\left(1+\theta \right)}{\theta \left(1+\theta +\sqrt{\left(1+\theta \right)K}\right)}}\hfill \\ {\pi }_D^{*H-L}={\displaystyle \frac{m}{8{\left(3-\theta \right)}^2}}\left(\begin{array}{l}\left(5-3\theta -\sqrt{\left(1+\theta \right)K}\right)\left(5-\theta -\left(1-\theta \right)\sqrt{{\displaystyle \frac{K}{\left(1+\theta \right)}}}\right)+\\ 2\left(1+\sqrt{{\displaystyle \frac{K}{\left(1+\theta \right)}}}\right)\left(\left(10+\theta -{\theta }^2\right)-\left(2-\theta \right)\sqrt{\left(1+\theta \right)K}\right)\end{array}\right)-mc\hfill \end{array}\right.$$

where $K=1+\theta +4\theta c-12c$.

4.4. The Optimal Reward Program Under $H-L$ Pricing Strategy ($p_1>p_2$)

Firstly, we need to distinguish clearly the conditions under which the firm should use RRPs by comparing and analyzing the firm’s profits under the above three strategies. Comparing the firm’s profit in Lemma 1 with those in Lemma 2 and Lemma 3, we find that, under the overlapping conditions, the firm’s profit with no reward is always lower than those with reward strategies, i.e., when $c<{\displaystyle \frac{1}{4}}$ and ${\displaystyle \frac{12c-1}{4c+1}}<\theta <1$, ${\pi }_0^{*H-L}<{\pi }_I^{*H-L}$; when $c<{\displaystyle \frac{1}{4}}$ and ${\displaystyle \frac{12c-1}{4c+1}}<\overline{\theta }<\theta <1$, ${\pi }_0^{*H-L}<{\pi }_D^{*H-L}$. Under other conditions, only no reward strategy is feasible. Proposition 1 presents the conditions for using RRPs.

Proposition 1.

Under the $H-L$ pricing strategy, using RRPs is effective when the unit referral cost is low enough, i.e., $c<{\displaystyle \frac{1}{4}}$, and the consumer repeat-purchase rate $\theta$ satisfies ${\displaystyle \frac{12c-1}{4c+1}}<\theta <1$.

This result shows that, under the $H-L$ pricing strategy, using RRP is effective for the firm only when the unit referral cost is low enough and when the repeat-purchase rate is high enough. That is because, at a given first-period price, the low unit referral cost puts the total cost for a successful referral on a low level. Accordingly, the reward offered by the firm that needs to cover the total cost is also low. In other words, the low unit referral cost also reduces the reward cost of the firm and gives the firm enough ability to pay the rewards. The high repeat-purchase rate of consumers makes the firm more interested in generating more B-consumers in the first period. Given the first-period price, the firm is more willing to use RRPs to motivate the original B-consumers to make successful referrals for more B-consumers in the first period. Therefore, the firm has sufficient driving force and payment capacity to use RRPs only if the unit referral cost and the repeat-purchase rate meet certain conditions.

We further analyzed Lemma 2 and Lemma 3 and find that the effective conditions of cash rewards for the firm are broader than those of coupon rewards. While under the jointly effective conditions of the two reward forms, the firm’s profits corresponding to the use of the two reward forms are equal. It can be seen that, under the $H-L$ pricing strategy, the firm should use cash rewards rather than coupon rewards. Proposition 2 summarizes this finding.

Proposition 2.

Under the $H-L$ pricing strategy, if the firm uses an RRP in the first period, cash rewards are always not inferior to coupon rewards.

The result indicates that cash rewards are optimal for the firm when using RRP is more effective under the $H-L$ pricing strategy. From a realistic perspective, under the $H-L$ pricing strategy, the B-consumers who move to the second period are bound to buy again at the lower second-period price. This suggests that if the firm uses coupon rewards in the first period, the B-consumers who receive the coupon rewards will redeem the coupon as soon as they enter the second period. Using the coupon rewards takes advantage of its delayed redemption feature. Based on the delayed redemption of coupon rewards and the uncertainty of the original B-consumers’ repeat purchase in the second period, the firm designs coupon rewards with higher value to achieve the same incentive effect as the cash reward. Meanwhile, the $H-L$ pricing strategy completely squeezes the advantage of the delayed redemption of coupon rewards, and the firm cannot manipulate the redemption rate to control the reward in a cost-effective manner. The result of using coupon rewards is not more effective than using cash rewards.

5. Models and Analysis Under $\mathit{L}-\mathit{H}$ Pricing Strategy ( ${\mathit{p}}_{\mathbf{1}}\le {\mathit{p}}_{\mathbf{2}}$)

Under the $L-H$ ($p_1\le p_2$) pricing strategy with a low price followed by a high price, all N-consumers in the first period will not buy the product at the second-period price $p_2$. Therefore, it is not necessary to consider the purchase behavior of the first-period N-consumers in the second period.

5.1. Model of No Reward Under $p_1\le p_2$

The firm’s profit in the first period is the same as under the $H-L$ pricing strategy,${\pi }_{01}^{L-H}=Q_{1S}^B{p}_1$. In the second period, $\theta Q_{1S}^B$ B-consumers enter this period and make purchase decisions at price $p_2$. Because of $p_1\le p_2$, $\theta Q_{1S}^B\mathrm{Pr}\left(v_i^B-p_2\ge 0\right)=\theta Q_{1S}^B{\displaystyle \frac{1-p_2}{1-p_1}}$ B-consumers buy the product in the second period. The profit of the firm in the second period is ${\pi }_{02}^{L-H}=\theta Q_{1S}^B{\displaystyle \frac{1-p_2}{1-p_1}}{p}_2$. The total profit is ${\pi }_0^{L-H}={\pi }_{01}^{L-H}+{\pi }_{02}^{L-H}$. By substituting Equations (1) and (2), we obtain the profit optimization model:

$$\begin{array}{l}\max {\pi }_0^{L-H}=m\left(1-p_1\right)p_1+\theta m\left(1-p_2\right)p_2\\ s.t. p_1>0, p_2>0, p_1\le p_2\end{array}.$$

(10)

Solve (10) to obtain Lemma 4.

Lemma 4.

Under the $L-H$ pricing strategy, when no reward is available, the optimal prices and the maximum profit of the firm are as follows:

$$\left\{\begin{array}{l}\left(p_1^{*},p_2^{*}\right)=\left({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}}\right)\hfill \\ {\pi }_0^{*L-H}={\displaystyle \frac{\left(1+\theta \right)m}{4}}\hfill \end{array}\right..$$

5.2. Model of Cash Reward Under $p_1\le p_2$

The first-period product sales are the same as under the $H-L$ pricing strategy, with cash rewards $r_I$ that satisfy $r_I-C\ge 0$, $Q_1^B$ consumers buy the product at price $p_1$, and $Q_{1S}^B={\displaystyle \frac{1}{2}}{Q}_1^B$ original B-consumers receive the cash rewards $r_I$. The profit of the firm in the first period is ${\pi }_{I1}^{L-H}=Q_1^B{p}_1-{\displaystyle \frac{1}{2}}{Q}_1^B{r}_I$. The N-consumers and $\theta Q_1^B$ B-consumers enter the second period, and only $\theta Q_1^B\mathrm{Pr}\left(v_i^B-p_2\ge 0\right)=\theta Q_1^B{\displaystyle \frac{1-p_2}{1-p_1}}$ B-consumers will repurchase the product because of $p_1\le p_2$. The profit of the firm in the second period is ${\pi }_{I2}^{L-H}=\theta Q_1^B{\displaystyle \frac{1-p_2}{1-p_1}}{p}_2$. The total profit is ${\pi }_I^{L-H}={\pi }_{I1}^{L-H}+{\pi }_{I2}^{L-H}$. By substituting Equations (3) and (4), we obtain the profit optimization model:

$$\begin{array}{l}\max {\pi }_I^{L-H}=2m\left(1-p_1\right)p_1-m\left(1-p_1\right)r_I+\theta \ast 2m\left(1-p_2\right)p_2\\ s.t. p_1>0, p_2>0, p_2\ge p_1>r_I, r_I-{\displaystyle \frac{c}{1-p_1}}\ge 0\end{array}.$$

(11)

We solve (11) and find no solution under the corresponding constraint conditions. Then, Lemma 5 is obtained.

Lemma 5.

Under the $L-H$ pricing strategy, RRP with cash reward is not effective.

5.3. Model of Coupon Reward Under $p_1\le p_2$

Under the RRP with coupon rewards $r_D$, which satisfies $\theta r_D-C\ge 0$, $Q_1^B$ B-consumers and $Q_{1S}^B={\displaystyle \frac{1}{2}}{Q}_1^B$ original B-consumers are rewarded with coupon rewards $r_D$ in the first period. The profit of the firm in the first period is ${\pi }_{D1}^{L-H}=Q_1^B{p}_1$. The N-consumers and $\theta Q_1^B$ B-consumers enter the second period. Since $p_1\le p_2$, ${\displaystyle \frac{1}{2}}\theta Q_1^B\mathrm{Pr}\left(v_i^B-p_2\ge 0\right)={\displaystyle \frac{1}{2}}\theta Q_1^B{\displaystyle \frac{1-p_2}{1-p_1}}$ B-consumers repurchase the product at price $p_2$, and ${\displaystyle \frac{1}{2}}\theta Q_1^B\mathrm{Pr}\left(v_i^B-p_2+r_D\ge 0\right)={\displaystyle \frac{1}{2}}\theta Q_1^B{\displaystyle \frac{1-p_2+r_D}{1-p_1}}$ rewarded consumers repurchase the product at price $p_2-r_D$. The firm’s profit in the second period is ${\pi }_{D2}^{L-H}={\displaystyle \frac{1}{2}}\theta Q_1^B{\displaystyle \frac{1-p_2}{1-p_1}}{p}_2+{\displaystyle \frac{1}{2}}\theta Q_1^B{\displaystyle \frac{1-p_2+r_D}{1-p_1}}\left(p_2-r_D\right)$. The total profit is ${\pi }_D^{L-H}={\pi }_{D1}^{L-H}+{\pi }_{D2}^{L-H}$. By substituting Equations (3) and (4), we obtain the profit optimization model:

$$\begin{array}{l}\max {\pi }_D^{L-H}=2m\left(1-p_1\right)p_1+\theta m\left(1-p_2\right)p_2+\theta m\left(1-p_1+r_D\right)\left(p_2-r_D\right)\\ s.t. p_1>0, p_2>0, p_2\ge p_1>r_D, \theta r_D-{\displaystyle \frac{c}{1-p_1}}\ge 0\end{array}.$$

(12)

Solve (12) and obtain Lemma 6.

Lemma 6.

Under the $L-H$ pricing strategy, the optimal solution to the optimization problem (12) exists only when the unit referral cost $c$ and the repeat-purchase rate $\theta$ satisfy $c<{\displaystyle \frac{1}{4}}$ and $\theta >4c$, and the optimal prices, coupon reward amount, and maximum profit of the firm are as follows:

$$\left\{\begin{array}{l}\left(p_1^{*},p_2^{*}\right)=\left({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}}+{\displaystyle \frac{c}{\theta }}\right)\hfill \\ r_D^{*}={\displaystyle \frac{2c}{\theta }}\hfill \\ {\pi }_D^{*L-H}={\displaystyle \frac{m\left(1+\theta \right)}{2}}-{\displaystyle \frac{4m{c}^2}{\theta }}\hfill \end{array}.\right.$$

5.4. The Optimal Reward Program Under the $L-H$ Pricing Strategy ($p_1\le p_2$)

As Lemma 5 shows that the cash reward program is not effective under the $L-H$ pricing strategy, we distinguished the conditions under which the firm should use RRPs by comparing and analyzing the firm’s profits under the no reward and coupon reward strategies. Comparing Lemma 4 and Lemma 6, we found that the firm’s profit with no reward is always lower than that with coupon reward strategy under the overlapping conditions, i.e., when $c<{\displaystyle \frac{1}{4}}$ and $4c<\theta <1$, ${\pi }_0^{*L-H}<{\pi }_D^{*L-H}$. Under other conditions, only the no reward strategy is feasible. Proposition 3 presents the conditions for using RRPs and the optimal reward program under the $L-H$ pricing strategy.

Proposition 3.

Under the $L-H$ pricing strategy, only when the unit referral cost is low enough, i.e., $c<{\displaystyle \frac{1}{4}}$, and the repeat-purchase rate $\theta$ satisfies $4c<\theta <1$ should the firm use RRPs, and it is optimal to use coupon rewards rather than cash rewards. Otherwise, the firm should not use any reward program.

As with the $H-L$ pricing strategy, this result also shows that the firm has sufficient driving force and payment capacity to use RRPs only if the unit referral cost and the repeat-purchase rate meet certain conditions. Different from the $H-L$ pricing strategy, this result indicates that under the $L-H$ pricing strategy, coupon reward is optimal for the firm when using RRP is effective. Under this pricing strategy, the first-period lower price increases the number of original B-consumers and reduces the difficulty of making a successful referral, which increases the number of first-period B-consumers. Meanwhile, the second-period higher price combined with the repeat-purchase rate further reduces the actual redemption rate of the coupons in the second period. The delayed redemption feature of coupon rewards is fully exploited by the firm through the $L-H$ pricing strategy. In this way, even if the firm designs coupons with higher face value to achieve the same incentive effect of cash rewards in the first period, the final reward cost will be well controlled at a lower level by adjusting the actual redemption rate of the coupons through this pricing strategy. Therefore, coupon rewards are more effective than cash rewards under the $L-H$ pricing strategy.

6. Joint Optimization of Referral Reward and Pricing

In this section, we use numerical analysis to explore the joint optimization of RRPs with different reward forms and price strategies by comparing and analyzing the firm’s profits of the above cases.

6.1. The Optimal Price Strategy When RRP Is Not Available

According to Proposition 1 and Proposition 3, when the unit referral cost is high and satisfies $c\ge {\displaystyle \frac{1}{4}}$ or when the unit referral cost and the repeat-purchase rate satisfy $c<{\displaystyle \frac{1}{4}}$ and $0<\theta \le \max \left\{0,{\displaystyle \frac{12c-1}{4c+1}}\right\}$, RRPs are not feasible. We investigate the optimal price strategy by comparing the maximum profits under the two price strategies:

$${\pi }_0^{*H-L}-{\pi }_0^{*L-H}={\displaystyle \frac{m{\left(1-\theta \right)}^2}{4\left(3-\theta \right)}}.$$

(13)

Obviously, ${\pi }_0^{*H-L}-{\pi }_0^{*L-H}>0$. Therefore, the $H-L$ price strategy is optimal under the corresponding conditions.

We further analyze the firm’s profits under the conditions of $c<{\displaystyle \frac{1}{4}}$ and $\max \left\{0,{\displaystyle \frac{12c-1}{4c+1}}\right\}<\theta \le 4c$ to determine whether RRPs are more effective. According to Proposition 1 and Proposition 3, we need to determine the size of ${\pi }_0^{*H-L}$, ${\pi }_I^{*H-L}$, and ${\pi }_0^{*L-H}$ under these conditions. 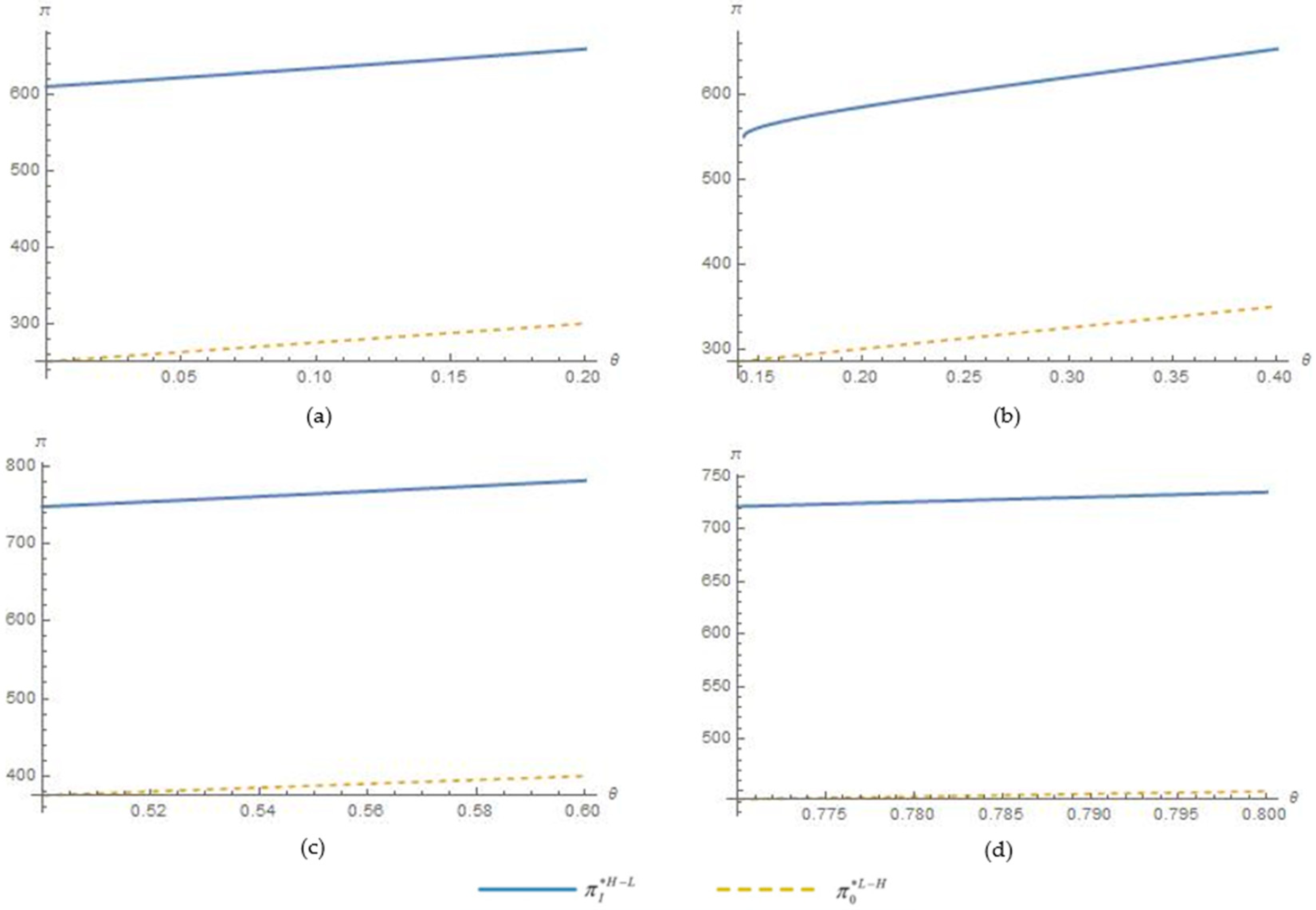Proposition 1 shows ${\pi }_0^{*H-L}<{\pi }_I^{*H-L}$, and we further compare ${\pi }_I^{*H-L}$ and ${\pi }_0^{*L-H}$ by numerical analysis. We assume $m=1000$ and set four sets of values for the unit referral cost $c$, which are $c=0.05$, $c=0.1$, $c=0.15$, and $c=0.2$. Given the unit referral cost, the value ranges of the corresponding repeat-purchase rate are $\theta \in \left(0,0.2\right]$, $\theta \in \left(0.14,0.4\right]$, $\theta \in \left(0.5,0.6\right]$, and $\theta \in \left(0.77,0.8\right]$. Figure 3 shows the sizes of ${\pi }_I^{*H-L}$ and ${\pi }_0^{*L-H}$.

Figure 3 indicates that when $c<{\displaystyle \frac{1}{4}}$ and $\max \left\{0,{\displaystyle \frac{12c-1}{4c+1}}\right\}<\theta \le 4c$, ${\pi }_I^{*H-L}>{\pi }_0^{*L-H}$. That is, the cash reward joined with the $H-L$ price strategy is more effective than having no reward program.

Based on the above analysis, we obtain Proposition 4.

Proposition 4.

When the unit referral cost is high or both the unit referral cost and repeat-purchase rate are low enough, the firm should not use any RRP, and the $H-L$ price strategy is optimal.

As with Proposition 1 and Proposition 3, if the unit referral cost is not low enough, the firm has to pay the original B-consumers a high reward but obtains lower incentive efficiency and lower profit. Even if the unit referral cost is low enough, the RRPs cannot effectively promote profit growth when the repeat-purchase rate is very low. This is because the low repeat-purchase rate greatly weakens the motivation for the firm to rely on the existing consumers’ referrals to reach potential consumers in the first period. At these points, the firm increases the profits to a greater extent by adjusting the prices instead of using RRPs.

This result also indicates that the firm should use the price strategy with a high price followed by a low price when the firm does not use RRP. Under this price strategy, only the high-value consumers will buy the product in the first period, and some of them who move to the second period will be bound to repurchase the product because of the lower price in the second period. Although the low-value consumers will not buy in the first period, a lower price in the second period can attract these consumers. In this way, the firm obtains the surplus of the high-value consumers to the maximum extent in the first period and captures the surplus of the low-value consumers in the second period. Therefore, the price strategy with a high price followed by a low price enables the firm to capture full consumer surplus to a greater extent when a referral reward is not feasible. This finding can also explain the phenomenon that the newest product is always priced high, and then, the price is lowered gradually.

6.2. The Optimal Joint Strategy When the RRPs Are Effective

Proposition 1 and Proposition 3 indicate that the firm uses RRPs only when the unit referral cost and the repeat-purchase rate satisfy $c>{\displaystyle \frac{1}{4}}$ and $\theta >{\displaystyle \frac{12c-1}{4c+1}}$. According to the numerical analysis of Section 6.1, the use cash rewards joined with the $H-L$ price strategy is optimal when ${\displaystyle \frac{12c-1}{4c+1}}<\theta \le 4c$. Thus, we further compare the size of ${\pi }_I^{*H-L}$ and ${\pi }_D^{*L-H}$ when $\theta >4c$. 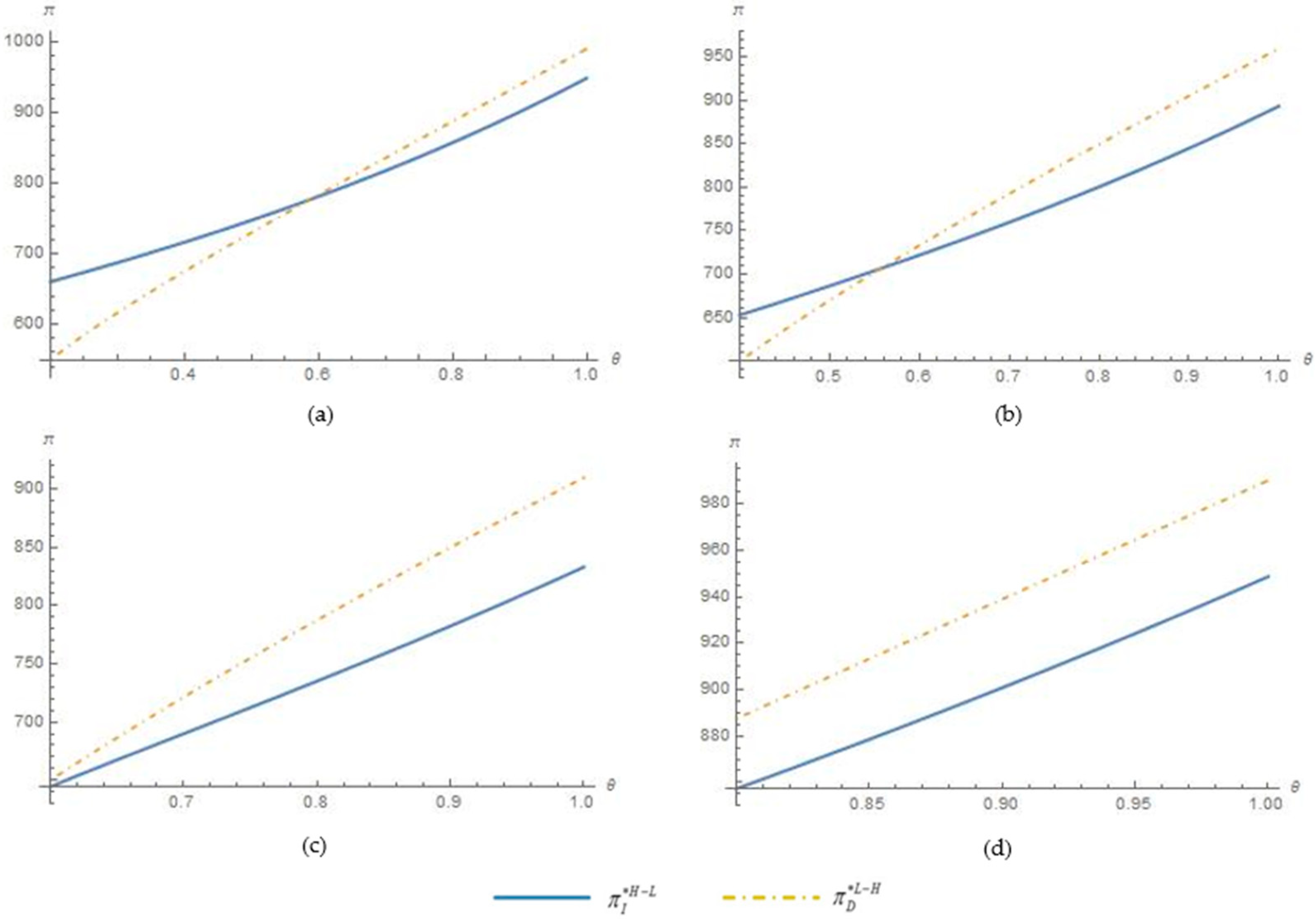We assume $m=1000$ and set four sets of values for the unit referral cost $c$, which are $c=0.05$, $c=0.1$, $c=0.15$, and $c=0.2$. Give, the unit referral cost, the value ranges of the corresponding repeat-purchase rate are $\theta \in \left(0.2,1\right)$, $\theta \in \left(0.4,1\right)$, $\theta \in \left(0.6,1\right)$, and $\theta \in \left(0.8,1\right)$. Figure 4 shows the sizes of ${\pi }_I^{*H-L}$ and ${\pi }_D^{*L-H}$.

Figure 4 indicates that when the unit referral cost $c$ is small, there exists $\overline{\theta }\in \left(4c,1\right)$, which is satisfied by ${\pi }_I^{*H-L}$ and ${\pi }_D^{*L-H}$:

$$\left\{\begin{array}{l}{\pi }_I^{*H-L}\ge {\pi }_D^{*L-H}, if 4c<\theta \le \overline{\theta }\hfill \\ {\pi }_I^{*H-L}<{\pi }_D^{*L-H}, if \overline{\theta }<\theta <1\hfill \end{array}.\right.$$

When the unit referral cost $c$ is higher but still satisfies $c<{\displaystyle \frac{1}{4}}$, the sizes of ${\pi }_I^{*H-L}$ and ${\pi }_D^{*L-H}$ meet ${\pi }_I^{*H-L}<{\pi }_D^{*L-H}$.

Based on the above analysis, we obtain Proposition 5.

Proposition 5.

When RRPs are effective, the use of cash rewards joined with the $H-L$ price strategy is optimal under the condition that both the unit referral cost and the repeat-purchase rate are low. Meanwhile, the firm tends to use coupon rewards joined with the $L-H$ price strategy as the unit referral cost increases.

We have explained the two fixed joint strategies, namely that the cash reward needs to be combined with the price strategy in which a low price is followed by a high price and the coupon reward needs to be combined with the pricing strategy in which a high price is followed by low price, in detail in Proposition 2 and Proposition 3. Under the condition that the RRPs are more effective for the firm if the unit referral cost is small, the firm can pay the reward cost whether the firm uses a cash reward or coupon reward. At this point, the higher the repeat-purchase rate, the greater the incentive for the firm to strive for more product sales by setting lower prices in the first period. However, the first-period lower price together with the referral reward cost also weakens the profitability of the firm to a great extent. If the repeat-purchase rate is not high enough, the product sales revenue in the second period may have difficulty in making up for the profit loss caused by the lower first-period price. Therefore, when the unit referral cost is small, the optimal pricing strategy should be determined according to the repeat-purchase rate. Specifically, the price strategy in which a low price is followed by a high price is optimal when the repeat-purchase rate is high enough; otherwise, the price strategy in which a high price is followed by a low price is optimal.

7. Conclusions

In this study, we developed analytical models to evaluate the difference in profitability between the two RRPs differing in the immediacy of cashing out rewards, namely cash rewards and coupon rewards, and we discussed the joint optimization of the two-period price strategy and the two RRPs. By solving the two-period optimization models, we obtained two fixed joint strategies. It can be seen that the cash rewards should be fixed in combination with the pricing strategy in which a high price is followed by a low price, and the coupon rewards should be fixed in combination with the price strategy in which a low price is followed by a high price. Moreover, if a referral reward is not available, the firm should use the pricing strategy in which a high price is followed by a low price to capture the surplus of both high-value and low-value consumers. We further established the effect of the consumer unit referral cost and repeat-purchase rate on the profitability of the RRPs. This shows the firm could earn higher profits using the RRPs only if the unit referral cost is small and if the repeat-purchase rate is high enough. In these cases, coupon rewards used jointly with the price strategy in which a low price is followed by a high price are more profitable as the unit referral cost increases. In the case where the consumer unit cost is small, the optimal joint strategy of referral reward and pricing can be determined depending on the level of the repeat-purchase rate.

We contribute to the literature on RRPs in two ways. First, we contribute to comparative studies on the effectiveness of cash and coupon rewards through mathematical analysis models. Although empirical work has already covered such a topic, few analytical works have done this, especially highlighting the difference in the immediacy of cashing out the rewards. Second, the informative utility output generated by the consumer referrals is fully considered in our models. Existing researchers have given little attention to the informative utility output and focused exclusively on the new product sales output of consumer referrals when measuring the output of RRPs. Consumer referrals first make the referred consumers aware of the product’s existence, that is, the informative utility output, and then generate new product sales only if one of the referred consumers buys the product. Our findings also provide guidelines for firms to design efficient RRPs, especially considering the joint strategy with pricing. The impact of the repeat-purchase rate on the optimal decision shows that RRPs are more feasible for FMCG than durable goods. In addition, the two-period price strategies directly affect the firms’ selection between cash rewards and coupon rewards when using RRPs.

Despite the theoretical contributions and practical implications, there are several limitations. This study ignores the discount factor of the delayed redemption rewards (the coupon rewards). In common sense, instant access is always more satisfying than delayed access, and consumers may consider the discount factor of the coupon rewards in practice. Would the boundary conditions of the RRPs with different reward forms change? It appears interesting to investigate. Another interesting direction would be exploring the impact of consumers’ organic referrals on the optimal decision. Organic referrals are referrals that occur in the absence of external rewards, and they are stimulated by internal motives such as satisfaction, social motives, etc. Consumers’ organic referrals influence firms’ RRP decisions in two ways. First, when a firm uses RRPs, the rewards can sometimes be given to consumers who make organic referrals, causing a waste of rewards. Second, some empirical works have proven that firm-offered rewards crowd out the internal motives of consumers, and the crowding-out effect can be moderated by reward forms. In further research, we can fully consider consumers’ organic referrals to explore the boundary conditions of using RRPs and the impact on firms’ reward costs.