Strategic Interactions in Omnichannel Retailing: Analyzing Brand Competition and Optimal Strategy Selection

Abstract

The rapid advancement of digital technology has blurred the line between online and brick-and-mortar stores, leading to the proliferation of omnichannel retailing. Two widely adopted strategies are Buy Online and Pick Up in Store (BOPS) and Ship from Store (SFS). This study examines a supply chain where a manufacturer sells national brand products through an e-commerce platform (e-platform) that also offers its own brand products. We analyze the optimal omnichannel strategies for both the e-platform and the manufacturer, considering scenarios of cooperation and brand competition, across four strategy combinations. Our findings highlight that the profits of both the e-platform and manufacturer are primarily influenced by the commission rate, product category valuation and competition intensity. The commission rate plays a pivotal role in shaping the e-platform’s strategy: a low rate leads to direct competition with the manufacturer, while a high rate prioritizes the manufacturer’s products. When the spillover profit is less than the net difference between the customer’s additional benefits and the firm’s additional costs for SFS compared to BOPS, and the commission rate is high, an equilibrium is achieved. Sensitivity analyses reveal that as the product differentiation decrease, the manufacturer’s profits decline, while the e-platform’s profits rise with an increasing commission rate.

1. Introduction

The rapid advancement of digital technology, particularly artificial intelligence (AI), has significantly transformed the retail landscape, blurring the lines between online and brick-and-mortar stores and leading to the proliferation of omnichannel retailing. Traditional brick-and-mortar retailers like Walmart and Target have expanded their online sales platforms, while digital native e-commerce platform (e-platform) such as Amazon, Tmall and JD have ventured into physical stores to offer customers a tangible shopping experience, particularly for products that require display and experience [1].

Omnichannel retailing has emerged as a response to this evolving landscape, enabling retailers to engage customers through various digital and physical touchpoints, including in-store digital signage, kiosks and mobile device interactions. This approach ensures a consistent and seamless shopping experience for consumers. Many retailers are incorporating omnichannel strategies as part of their overall media strategy within physical stores, aiming to enhance their reach, visibility and impact on consumer audiences [2]. Moreover, customers now expect omnichannel retailers to provide flexible product delivery options, such as Buy Online and Pick Up in Store (BOPS) and Ship from Store (SFS). AI technologies play a crucial role in optimizing these omnichannel strategies. AI-driven analytics enable retailers to better understand consumer behavior, predict purchasing patterns and personalize marketing efforts, thereby enhancing customer engagement and satisfaction. These innovations ensure that products are available when and where customers want them, further improving the efficiency of BOPS and SFS strategies.

BOPS allows customers to make online purchases and retrieve them from nearby physical stores instead of opting for home delivery. Retailers like BestBuy, Nordstrom and Gap have embraced this approach, offering the convenience of BOPS to their customers [3,4]. In contrast, SFS leverages retail stores as distribution centers, enabling orders to be fulfilled and shipped directly from the nearest store with available inventory. Retailers such as Macy’s and Zilla employ this strategy, leveraging their physical store networks to expedite delivery and enhance customer satisfaction. BOPS eliminates shipping costs and reduces wait times, while SFS optimizes fulfillment and shipping processes by utilizing physical stores as hubs.

Alongside the competition among delivery channels, brand competition has intensified, particularly between national brands and private-label brands. National brand products, offered by manufacturers and resold through multiple retail stores, enjoy widespread recognition, extensive marketing efforts and higher levels of consumer trust and loyalty. Manufacturers invest in product development, quality control and branding to maintain a competitive advantage. For example, Walmart offers well-known brands like Unilever and Procter & Gamble. On the other hand, private-label brand products, often referred to as generic products, are developed by retailers to provide more affordable alternatives with comparable quality to national brands. Retailers like Sephora and Watsons have introduced extensive ranges of private-label brand products in the cosmetics and personal care markets. By investing in private-label brand development, retailers seek to differentiate themselves and capture more market share. With growing emphasis on quality and value, private-label brands have gained popularity among cost-conscious consumers who prioritize price savings without sacrificing product satisfaction. In recent years, private-label brands have been strategically increasing their presence on retailer shelves as they actively pursue customer loyalty. According to the 2022 private-label Yearbook of the private-label Manufacturers Association, private-label brand products experienced sales growth of 11.3% in 2022, nearly double the growth rate of national brand products at 6.1%. In terms of dollar share, private-label brands reached 18.9% in 2022, a 0.7% increase from 18.2% in 2021. This indicates the rising prominence and market share of private-label brands in the retail landscape.

Driven by the emerging trend of omnichannel retailing and brand competition, we examine an online co-opetitive supply chain consisting of a national brand manufacturer and an e-platform that sells both its own brand and national brand products. The manufacturer sells its renowned products on the e-platform’s marketplace and pays commissions, benefiting from access to an established customer base and reduced risk of fraudulent transactions. Additionally, the e-platform develops its own private-label brand products to expand its market share, selling them on its marketplace alongside the national brand. Both brands are available online and through physical stores. The manufacturer and e-platform also employ omnichannel strategies to deliver a seamless shopping experience. Specifically, they have the option to adopt either BOPS or SFS. The strategic choices of each party impact retail prices and profits. In this context, the selection of BOPS or SFS by the manufacturer and the e-platform leads to four combination cases of omnichannel strategy selection (cases BB, BS, SB and SS), for instance, in case BS, the manufacturer chooses the BOPS strategy, while the e-platform opts for the SFS strategy.

Our study addresses the following research questions: How should the manufacturer and e-platform select their omnichannel strategies while considering each other’s decisions? How does the coexistence of brand competition and supply chain cooperation influence the dynamics of the firms’ omnichannel strategy choices? What are the main factors affecting these decisions and in what manner?

Through our investigation, we have made several significant findings. Firstly, we observe that national brand products, which have higher customer values compared to private-label brand products, are priced higher under most circumstances. The e-platform, benefiting from profits earned through selling both private-label brand products and commissions from national brand products, achieves higher profitability than the manufacturer under certain conditions. Secondly, our analysis shows that the e-platform’s best response strategies are influenced by spillover profits, operating cost differences and the commission rate. Thirdly, an equilibrium can be achieved where the manufacturer prefers the SFS strategy while the e-platform opts for the BOPS strategy. This condition occurs when the following occurs: the spillover profit is positive but less than the difference between the customer’s additional benefits from the SFS strategy compared to the BOPS strategy and the firm’s additional costs for implementing the SFS strategy over the BOPS strategy; and the commission rate is high.

This study contributes to the literature in several key ways. Firstly, it introduces a strategic game framework, which examines the simultaneous competition and cooperation between a national brand manufacturer and an e-platform, offering insights into their omnichannel strategy selections. Second, our research reveals that, under certain market conditions, either the manufacturer or the e-platform is willing to adopt a more costly omnichannel strategy, even if it results in voluntary market share relinquishment. This strategic behavior, previously underexplored, provides new understanding into the complex decision-making processes in omnichannel retailing. Third, unlike existing studies, which primarily focus on pricing or channel mode trade-offs (such as reselling versus agency models), our research uniquely explores the mode selection between two specific omnichannel strategies.

The structure of this research paper is as follows: Section 2 provides a comprehensive review of the relevant literature. The model is presented in Section 3. Section 4 outlines the four different combinations of omnichannel strategies and evaluates the optimal outcomes for each case. In Section 5, a comparison is made between equilibrium prices and profits across the different cases, along with an analysis of the manufacturer and e-platform’s optimal strategy choices. The influence of key factors on the equilibrium results is examined in Section 6. Finally, Section 7 summarizes the key findings and suggests directions for future research. All proofs are provided in Appendix A.

2. Literature Review

This paper explores the strategic interactions between a national brand manufacturer and an e-platform across four combinations of omnichannel strategies. This study is grounded in three streams of research: omnichannel strategy, brand competition, and mode selection.

(1) Omnichannel Strategy.

The literature on omnichannel strategies primarily focuses on the implementation of BOPS and SFS. Yan et al. (2018) [5] developed a theoretical model that explores optimal channel strategies for dual-channel and physical retailers, considering scenarios where no retailer or both retailers serve the BOPS channel. Zhang et al. (2019) [6] examined the effectiveness of the “preorder-online, pickup-in-store” strategy in enhancing profitability and market share for dual-channel retailers through investigations of monopoly and competition cases. Wang et al. (2020) [7] analyzed pricing strategies employed by competitive dual-channel retailers and utilized a Stackelberg game model to determine optimal strategies based on sequential decision-making processes. Several retailers have recently adopted BOPS by integrating online and offline channels. Kong et al. (2020) [8] investigated the effects of implementing BOPS on retailer decisions, considering consistent and inconsistent pricing strategies in a store selling products through online and physical stores. Lin et al. (2021) [9] employed a Stackelberg game-theoretic model to study the implications of BOPS on pricing and profitability for a retailer selling products through physical stores, online channels or BOPS channels. Guo et al. (2022) [10] developed a game theory model to investigate how the order-online-and-dine-in-store strategy affects a restaurant’s optimal decisions, expected profits and the environment. Wang et al. (2023) [11] examined pricing and channel strategies for two retailers using a game-theoretic model, considering the choices between when operating online and physical channels separately or when integrating them into a BOPS channel, as well as accounting for shipping cost differences among online channels and the impact of consumer-covered shipping costs through the online channel on the utilization of the BOPS channel.

In recent years, scholars have also devoted considerable attention to the SFS strategy. He et al. (2021) [12] modeled the effects of the SFS option on retailer and platform price decisions, incorporating the competition from the platform’s self-run store and the retailer’s offline operations. Bayram and Cesaret (2021) [13] analyzed the dynamic order fulfillment strategy of a retailer with an inventory of online and store operations, identifying optimal profit function properties and developing an optimal threshold strategy for guiding fulfillment decisions. Additionally, Jiu (2022) [14] developed an omnichannel retail operations model for a retailer selling multiple products through a multi-cycle and capacitated retail network.

This paper contributes in two key ways. First, while existing research has largely focused on competition between retailers, our study delves into the co-opetition between a manufacturer and an e-platform. The manufacturer focuses on producing and selling national brand products, whereas the e-platform provides retail services to the manufacturer while also selling its own private-label products. Second, while much of the prior literature on omnichannel strategy has concentrated on pricing and channel strategies for retailers implementing BOPS or SFS, our research uniquely examines the strategic selection between these two omnichannel strategies for both the manufacturer and the e-platform, with a focus on four distinct strategy combinations.

(2) Brand Competition.

The related existing literature primarily focuses on the competition between two products with horizontal differentiation in the market, notably the competition between private-label brands and national brands.

Tyagi et al. (2018) [15] explained how national brands limit losses due to the entry of two types of entrants by positioning their brands. Assarzadegan and Hejazi (2021) [16] explored a game model between a national brand manufacturer and a retailer, presenting a Stackelberg game-theoretic model with two leader cases across three scenarios. Al-Monawer et al. (2021) [17] investigated the willingness of retailers to cooperate with manufacturers when introducing private-label brand products using game theory. Chakraborty et al. (2022) [18] analyzed quality competition between national brand manufacturers and private-label brand retailers, describing equilibrium price and quality levels under different channel power structures. Hsieh et al. (2023) [19] employed Hotelling’s model to examine the competition between physical and online retailers in an experience products marketplace where a national brand product is available to both retailers, exploring how brick-and-mortar retailers counter showrooming through the introduction of private-label brands and customized product offerings.

Many existing studies on brand competition also consider the competition between manufacturers and retailers upon the introduction of private-label brands. The introduction of private-label brand products not only puts additional pressure on upstream manufacturers, but also leads consumers to increasingly consider transactional fairness when choosing between different brands. Yu et al. (2022) [20] employed the Stackelberg game model to investigate how national brand manufacturers use direct consumer incentives to delay the entrance of private-label brand products by retailers in response to consumer fairness concerns. Karray and Martín-Herrá (2019) [21] developed a sequential game theory model for dual channels, considering the decisions of retailers to introduce private-label brands. Li et al. (2022) [22] examined the interaction between an existing national brand manufacturer and a retailer determining private-label brand product encroachment strategies, analyzing the optimal decisions based on the cost–quality trade-off between low and high-quality private-label brand products. Zheng et al. (2022) [23] employed noncooperative game theory to investigate the impact of private-label brand introduction on multilateral contracts in a vertical supply relationship, considering different information structures.

Our study adds to the existing body of literature in two main ways. First, whereas prior research has predominantly examined competition in terms of market share between manufacturers and retailers—often with retailers introducing their own brand products—our work focuses on the dynamic interplay between a national brand manufacturer and an e-platform that sells its own private-label products. Second, we contribute by merging the analysis of brand competition with omnichannel strategy, exploring how consumer preferences are shaped by the selection of different omnichannel strategies and brand preferences across two types of brand products.

(3) Mode Selection.

In recent years, there has been considerable research interest in the mode selection of e-platforms, specifically focusing on channel and sales mode choices.

Tian et al. (2018) [24] studied the optimal mode choice for an intermediary in a game between two competing suppliers selling substitutable products through a common online e-platform. Shen et al. (2019) [25] examined manufacturers’ channel decisions between platform retailers and conventional distributors using a three-stage Stackelberg game. Chen et al. (2022) [26] investigated the effective utilization of reselling and agency selling business modes for promotion. Liu et al. (2021) [27] explored the sales model selection for e-platforms selling fresh food and competing with traditional retailers, considering blockchain technology. Li et al. (2021) [28] analyzed vertical integration strategies for retailers in a supply chain with manufacturers and service providers, considering different business models. Qin et al. (2021) [29] developed a model to study the interaction between a logistical service strategy and sales model decision for online platforms. Xu et al. (2021) [30] examined collaboration models for manufacturers selling through offline channels and online platforms under cap-and-trade regulation. Wang et al. (2022) [31] considered a platform-oriented supply chain with online retailers reselling products on a platform and manufacturers choosing a sales model with dual channels. Ha et al. (2022) [32] investigated a channel selection problem for online platforms aiming to increase sales channel demand through service efforts. Zhong and Shen (2022) [33] constructed a game-theoretic model to examine a manufacturer’s optimal selling mode choice for a new-version product between reselling and agency selling, given that the old-version product was already sold in different selling modes ex ante.

Previous studies have largely examined the e-platform’s selection between sales and channel modes, such as reselling or agency models. In contrast, our research investigates the strategic selection between two omnichannel strategies: the BOPS strategy and the SFS strategy. We analyze the strategic interactions between a manufacturer and an e-platform under four potential strategic combinations (BB, BS, SB, and SS), providing a comprehensive framework for understanding these interactions.

3. Model Description

We examine an online supply chain consisting of a national brand manufacturer and an e-platform selling two products which are homogeneous. The manufacturer sells its renowned national brand products through the e-platform at a retail price $p_n$ and pays a commission rate $r(0<r<1)$ to the e-platform. Additionally, the e-platform introduces private-label brand products at a retail price $p_s$ to compete with the national brand products for market share. Examples of well-known private-label brands are Amazon Basics and Great Value, provided by Amazon and Walmart, respectively. Since we assume that there is no quality difference between the two brands, we simplify the model by assuming zero marginal production costs for both products. The availability of the two brand products is through both online channels and physical stores. Retailers have the option to adopt omnichannel strategies individually or jointly [34]. We assume that the e-platform can choose between two different omnichannel strategies: BOPS and SFS, aiming to provide consumers with a seamless shopping experience. The manufacturer also has the choice to participate in either strategy at its own cost.

Our focus is on the strategic decisions of the manufacturer and e-platform regarding the implementation of BOPS and SFS. Under the BOPS strategy, consumers purchase products online and retrieve them from the nearest physical stores, incurring a pickup cost t. Alternatively, under the SFS strategy, consumers make online purchases and have the products shipped to their homes, resulting in waiting costs represented by w. We assume that $w<t$, indicating that the cost of waiting is lower for consumers compared to the inconvenience cost of picking up from physical stores [35]. Implementing BOPS typically involves staff updating online information, tracking pickup orders, and preparing them for customer pickup. In contrast, executing the SFS strategy not only requires the same tasks performed by the BOPS staff but also additional efforts to pack, label, and ship products directly to customers’ homes. Consequently, we posit that the operating costs associated with SFS exceed those of BOPS. To streamline our model, we assume that the cost of implementing the BOPS strategy is zero, while the cost of implementing the SFS strategy is c, which represents the incremental operating costs between SFS and BOPS, essentially reflecting the costs associated with packing and shipping products to consumers [12]. Furthermore, when the BOPS strategy is employed, consumers need to visit physical stores for product pickup, which can drive up in-store traffic and potentially lead to additional sales. Getting customers into the store not only reduces the likelihood that they will choose a competitor but also increases the chances of impulse purchases [36]. Thus, when adopting a BOPS strategy, both the manufacturer and e-platform may earn incremental profits from consumers who enter physical stores due to the spillover effect. This effect refers to additional purchases made by consumers when they visit a store to pick up online orders, which leads to higher overall sales. For instance, according to the statistical data (See https://www.digizuite.com/blog/omnichannel-statistics, accessed on 15 May 2024), omnichannel strategies can increase store visits by 80% and boost overall sales by 20%. A typical example could be a customer who orders a product from Zara’s online store and chooses to pick it up at a physical Zara location. Upon arriving at the store, the customer may be exposed to additional products through in-store displays or promotions, potentially leading to impulse purchases. The extra sales generated from these purchases constitute spillover profits. For simplicity, we assume that the spillover profits, denoted by $en$ for the manufacturer and $es$ for the e-platform, are equal, i.e., $en=es=e$. This assumption is made for simplicity in our model and allows us to focus on other key dynamics of the system.

When the manufacturer and e-platform select different omnichannel strategies, consumers’ preferences are primarily influenced by the differences between these two channels. However, when the firms choose the same omnichannel strategy, consumers’ choices are more influenced by brand differences. Therefore, both the manufacturer and e-platform face the challenge that strategic selections impact each other’s pricing decisions and profits. To analyze this, we consider four combination cases of omnichannel strategy selection: case BS represents the scenario when manufacturer chooses BOPS and e-platform chooses SFS, while cases BB, SB, and SS denoting other possible strategy combinations.

The consumer’s valuation of a product category also influences firms’ omnichannel strategies [37,38]. We denote the consumer’s valuation of this product category as v, which ranges between 0 and 1. The range from 0 to 1 allows us to capture the full spectrum of consumer preferences within this particular product category. A value of 0 indicates that the consumer has no interest or preference for products in this category, while a value of 1 signifies that they highly value and prioritize these products. Generally, national brand products enjoy higher consumer recognition and awareness compared to private-label brand products. To capture consumers’ discounted valuation of private-label brand products, we introduce the discount factor $\theta \in (0,1)$. Consequently, the utility from consuming the national brand product is v, while the utility from consuming the private-label product is $\theta v$. Following Hotelling’s model, consumers’ preferences for the two brand products are uniformly distributed along a unit line, with national brand products located at 0 and private-label brand products located at 1. The distance of a consumer located at x from national brand products is denoted as x, while the distance from private-label brand products is represented as $1-x$. The x also indicates the degree of the mismatch with national brand products, whereby the larger the x, the less the national brand products satisfy the consumer’s demand and the higher the consumer’s mismatch cost. We set the unit mismatch cost to 1 to maintain generality.

Since the manufacturer utilizes the e-platform’s channels, it is reasonable to assume that the e-platform possesses certain advantages in terms of collecting information. Based on this assumption, we formulate a three-stage game that determines the pricing and channel options for both the manufacturer and e-platform. In the first stage, the manufacturer decides on the omnichannel strategy to adopt and sets price $p_n$ for national brand products. In the second stage, the e-platform, having learned the manufacturer’s decision, selects its omnichannel strategy and sets price $p_p$ for its own products. Finally, in the third stage, consumers make their purchasing decisions by choosing between two brand products.

4. Model Analysis

4.1. Case BB

In this scenario, we consider that both the manufacturer and the e-platform adopt the BOPS strategy. As a result, consumers’ purchasing decisions are influenced by the differences between the two brand products and their individual preferences. Based on this assumption, we can define the utility functions for consumers who purchase national brand products $\left(U_n^{BB}\right)$ and private-label brand products $\left(U_s^{BB}\right)$ as follows:

$$\begin{array}{c}{U}_n^{BB}=v-p_n^{BB}-x-t,\hfill \end{array}$$

(1)

$$\begin{array}{c}{U}_s^{BB}=\theta v-p_p^{BB}-(1-x)-t.\hfill \end{array}$$

(2)

Setting $U_n^{BB}$ equal to $U_s^{BB}$, we can identify the point of indifference $x^{BB}={\displaystyle \frac{(1-\theta )v-p_n^{BB}+p_p^{BB}+1}{2}}$, where consumers are equally satisfied with both brand products. Here, the demand for national brand products is denoted as $D_n^{BB}={\displaystyle \frac{(1-\theta )v-p_n^{BB}+p_p^{BB}+1}{2}}$, and the demand for private-label brand products is denoted as $D_s^{BB}={\displaystyle \frac{1-(1-\theta )v+p_n^{BB}-p_p^{BB}}{2}}$. The profit functions of the manufacturer and e-platform can be expressed as follows:

$$\begin{array}{c}{\pi }_n^{BB}=(1-r)p_n^{BB}{D}_n^{BB}+e{D}_n^{BB},\hfill \end{array}$$

(3)

$$\begin{array}{c}{\pi }_e^{BB}=\left(p_p^{BB}+e\right)D_s^{BB}+r{p}_n^{BB}{D}_n^{BB}.\hfill \end{array}$$

(4)

By employing backward induction and substituting the demand functions into the previously mentioned profit functions, we derive the optimal prices and profits as follows:

$$\begin{array}{c}{p}_n^{BB\ast }={\displaystyle \frac{3-2e+v(1-\theta )}{2(1-r)}},\hfill \end{array}$$

(5)

$$\begin{array}{c}{p}_p^{BB\ast }={\displaystyle \frac{5-4e+3(1-\theta )rv+r-(1-\theta )v}{4(1-r)}},\hfill \end{array}$$

(6)

$$\begin{array}{c}{\pi }_n^{BB\ast }={\displaystyle \frac{1}{16}}{(3-\theta v+v)}^2,\hfill \end{array}$$

(7)

$$\begin{array}{c}{\pi }_e^{BB\ast }={\displaystyle \frac{r(32e+(\theta -1)v((\theta -1)v+26)-23)-{((\theta -1)v+5)}^2}{32(r-1)}}.\hfill \end{array}$$

(8)

Proposition 1. 

(i) 

In case BB, $p_n^{BB\ast }>p_p^{BB\ast }$.

(ii) 

${\pi }_n^{BB\ast }<{\pi }_e^{BB\ast }$ when $0<v\le 8\sqrt{2}-11$; or $8\sqrt{2}-11<v<1$, $0<r<r_1$, ${\theta }_1<\theta <1$; or $8\sqrt{2}-11<v<1$, $r_1<r<1$.

${\pi }_n^{BB\ast }>{\pi }_e^{BB\ast }$ When $8\sqrt{2}-11<v<1$, $0<r<r_1$ and $0<\theta <{\theta }_1$.

The proposition above demonstrates that when both the manufacturer and e-platform adopt a BOPS strategy, the price of national brand products consistently exceeds that of private-label brand products. With both firms using the same omnichannel strategy, there are no differences in operating costs or potential sales from impulse purchases. Consequently, national brand products, being widely recognized by consumers, command higher market prices than private-label brands. However, higher market prices do not necessarily translate to higher profits. When the valuation of the product category is low (i.e., low-value products), consumers are not sensitive to brand competition, allowing the e-platform to achieve higher profitability than the manufacturer as it can generate profits from selling both national and private-label products. For moderate or high-value products, the profitability of both firms depends on competition intensity and commission rates. Specifically, at low commission rates, the manufacturer can achieve higher profits than the e-platform if competition intensity is low, meaning that there is a significant difference between consumers’ valuations of national and private-label products. Conversely, if the difference is relatively small, the e-platform will achieve higher profits than the manufacturer. However, at higher commission rates, the e-platform consistently earns higher profits than the manufacturer by taking a larger share of the manufacturer’s profits as commission fees.

4.2. Case BS

In this section, we consider the scenario where the manufacturer adopts the BOPS strategy and the e-platform adopts the SFS strategy. We assume that consumers who use the BOPS strategy can only go to the physical store that offers BOPS, but cannot purchase products from the store owned by the e-platform. In this case, consumers’ selection is generally influenced by their preference for different omnichannel strategies. Consequently, the utility derived by consumers from purchasing national brand products and private-label brand products can be expressed as $U_n^{BS}$ and $U_s^{BS}$, respectively:

$$\begin{array}{c}{U}_n^{BS}=v-p_n^{BS}-x-t,\hfill \end{array}$$

(9)

$$\begin{array}{c}{U}_s^{BS}=\theta v-p_p^{BS}-(1-x)-w.\hfill \end{array}$$

(10)

By equating $U_n^{BS}$ and $U_s^{BS}$, we can determine the point of indifference, denoted as $x^{BS}={\displaystyle \frac{(1-\theta )v-p_n^{BS}+p_p^{BS}-t+w+1}{2}}$, at which consumers are indifferent between the two brand products. Based on this, we can formulate the demand for the national brand product as $D_n^{BS}={\displaystyle \frac{(1-\theta )v-p_n^{BS}+p_p^{BS}-t+w+1}{2}}$ and the demand for the private-label brand product as $D_s^{BS}={\displaystyle \frac{1-(1-\theta )v+p_n^{BS}-p_p^{BS}+t-w}{2}}$. Consequently, the profit functions of the manufacturer and e-platform can be expressed as follows:

$$\begin{array}{c}{\pi }_n^{BS}=(1-r)p_n^{BS}{D}_n^{BS}+e{D}_n^{BS},\hfill \end{array}$$

(11)

$$\begin{array}{c}{\pi }_e^{BS}=(p_p^{BS}-c)D_s^{BS}+r{p}_n^{BS}{D}_n^{BS}.\hfill \end{array}$$

(12)

By utilizing backward induction to solve the model, we determine the optimal prices and the corresponding profits as follows:

$$\begin{array}{c}{p}_n^{BS\ast }={\displaystyle \frac{-c+e+t+\theta v-v-w-3}{2(r-1)}},\hfill \end{array}$$

(13)

$$\begin{array}{c}{p}_p^{BS\ast }={\displaystyle \frac{c(r-3)+r(e+3t-3v-3w)+e+\theta (3r-1)v-r-t+v+w-5}{4(r-1)}},\hfill \end{array}$$

(14)

$$\begin{array}{c}{\pi }_n^{BS\ast }={\displaystyle \frac{1}{16}}{(c+e-t-\theta v+v+w+3)}^2,\hfill \end{array}$$

(15)

$$\begin{gathered} \begin{array}{c}{\pi }_e^{BS\ast }={\displaystyle \frac{c^2(r-1)+e^2(r-1)+2\theta v(r(t-v-w+13)-t+v+w-5)+(t-v-w)(r(t-v-w+26)-t+v+w)-23r-5(2t-2v-2w+5)}{32(r-1)}}\\ \\ +{\displaystyle \frac{2c(e(r-1)+r(-t-\theta v+v+w-13)+t+(\theta -1)v-w+5)+2e(r(-t-\theta v+v+w+3)+t+(\theta -1)v-w+5)+{\theta }^2(r-1)v^2}{32(r-1)}}.\end{array} \end{gathered}$$

(16)

Proposition 2. 

(i) 

In case BS, when ${\displaystyle \frac{3(t-w)+c+e-1}{3(1-\theta )}}<v<1$, $p_n^{BS\ast }>p_p^{BS\ast }$; when $0<v<{\displaystyle \frac{3(t-w)+c+e-1}{3(1-\theta )}}$, $p_n^{BS\ast }<p_p^{BS\ast }$.

(ii) 

When $0<r<max\{0,r_2\}$, ${\pi }_n^{BS\ast }>{\pi }_e^{BS\ast }$; when $max\{0,r_2\}<r<1$, ${\pi }_n^{BS\ast }<{\pi }_e^{BS\ast }$.

In the BS scenario, the manufacturer adopts an omnichannel strategy with lower operating costs but introduces additional inconvenience for consumers by implementing the BOPS strategy, as opposed to the SFS strategy used by the e-platform. When purchasing high-value products such as computers and home appliances, consumers are more sensitive to brand competition. Consequently, even though the manufacturer’s omnichannel approach imposes extra costs on consumers, the prices of national brand products can still be higher than those of private-label brand products. However, for low-value products, the difference in omnichannel strategies plays a more significant role. Thus, the prices of national brand products need to be lower than those of private-label brands, as consumers have to pay extra costs to pick up products from the store. In terms of profit levels, the determining factor is the commission rate, which indicates the share of the manufacturer’s profits taken by the e-platform. When the commission rate is low, the manufacturer earns higher profits compared to the e-platform. Conversely, when the commission rate is high, a larger proportion of the manufacturer’s profits is taken by the e-platform, resulting in higher profits for the e-platform.

4.3. Case SB

In this scenario, the manufacturer adopts the SFS strategy, while the e-platform adopts the BOPS strategy. Similar to previous cases, consumer choices are influenced by both brand differentiation and their preference for different omnichannel strategies. Hence, the utility functions for consumers purchasing the two brand products are as follows:

$$\begin{array}{c}{U}_n^{SB}=v-p_n^{SB}-x-w,\hfill \end{array}$$

(17)

$$\begin{array}{c}{U}_s^{SB}=\theta v-p_p^{SB}-(1-x)-t.\hfill \end{array}$$

(18)

By setting $U_n^{SB}=U_s^{SB}$, we can determine the point of indifference $x^{SB}={\displaystyle \frac{(1-\theta )v-p_n^{SB}+p_p^{SB}+t-w+1}{2}}$, at which consumers are indifferent between the two brand products. Consequently, the demand for the national brand product and the private-label brand product can be expressed as $D_n^{SB}={\displaystyle \frac{(1-\theta )v-p_n^{SB}+p_p^{SB}+t-w+1}{2}}$ and $D_s^{SB}={\displaystyle \frac{1-(1-\theta )v+p_n^{SB}-p_p^{SB}-t+w}{2}}$, respectively. The profit functions of the manufacturer and e-platform are as follows:

$$\begin{array}{c}{\pi }_n^{SB}=(1-r)p_n^{SB}{D}_n^{SB}-c{D}_n^{SB},\hfill \end{array}$$

(19)

$$\begin{array}{c}{\pi }_e^{SB}=\left(p_p^{SB}+e\right)D_s^{SB}+r{p}_n^{SB}{D}_n^{SB}.\hfill \end{array}$$

(20)

By applying backward induction, we obtain the optimal prices and profits:

$$\begin{array}{c}{p}_n^{SB\ast }={\displaystyle \frac{-c+e-t+\theta v-v+w-3}{2(r-1)}},\hfill \end{array}$$

(21)

$$\begin{array}{c}{p}_p^{SB\ast }={\displaystyle \frac{c(r+1)+e(r-3)+3r(t+v-w)+\theta (1-3r)v+r-t-v+w+5}{4(1-r)}},\hfill \end{array}$$

(22)

$$\begin{array}{c}{\pi }_n^{SB\ast }={\displaystyle \frac{1}{16}}{(c+e-t+(\theta -1)v+w-3)}^2,\hfill \end{array}$$

(23)

$$\begin{array}{c}{\pi }_e^{SB\ast }={\displaystyle \frac{c^2(r-1)+(e-t-v+w)(e(r-1)-r(t+v-w-26)+t+v-w)-10e-23r+5(2t+2v-2w-5)}{32(r-1)}}\hfill \end{array}$$

$$\begin{array}{c}+{\displaystyle \frac{2c(e(r-1)-r(t+v-w+3)+\theta (r-1)v+t+v-w-5)+2\theta v(e(r-1)-r(t+v-w-13)+t+v-w-5)+{\theta }^2(r-1)v^2}{32(r-1)}}.\hfill \end{array}$$

(24)

Proposition 3. 

(i) 

In case SB, $p_n^{SB\ast }>p_p^{SB\ast }$.

(ii) 

When $0<r<max\{0,r_3\}$, ${\pi }_n^{SB\ast }>{\pi }_e^{SB\ast }$; when $max\{0,r_3\}<r<1$, ${\pi }_n^{SB\ast }<{\pi }_e^{SB\ast }$.

Under case SB, the manufacturer adopts the SFS strategy, which reduces consumer costs, while the e-platform adopts the BOPS strategy. As discussed in Proposition 1, when both firms adopt the same omnichannel strategy, the manufacturer’s products are consistently priced higher than private-label products. In case SB, the manufacturer’s choice of omnichannel strategy further enhances its advantage by providing a higher value to consumers. Consequently, as Proposition 3(i) states, national brand products are always priced higher than private-label brand products in case SB. Regarding profit levels, similar to the findings in Proposition 2, when the two firms adopt different omnichannel strategies, their relative profitability is primarily determined by the commission rate. At low commission rates, the manufacturer is more profitable; however, when the rate is high, the e-platform is more profitable.

4.4. Case SS

Under the SS strategy combination, where both the manufacturer and e-platform adopt the SFS strategy to offer consumers cost-friendly shopping services, the utility functions for consumers to choose between the two brand products are as follows:

$$\begin{array}{c}{U}_n^{SS}=v-p_n^{SS}-x-w,\hfill \end{array}$$

(25)

$$\begin{array}{c}{U}_s^{SS}=\theta v-p_p^{SS}-(1-x)-w,\hfill \end{array}$$

(26)

By setting $U_n^{SS}=U_s^{SS}$, we determine the point of indifference $x^{SS}={\displaystyle \frac{(1-\theta )v-p_n^{SS}+p_p^{SS}+1}{2}}$. The demand functions for the two brand products are $D_n^{SS}={\displaystyle \frac{(1-\theta )v-p_n^{SS}+p_p^{SS}+1}{2}}$ and $D_s^{SS}={\displaystyle \frac{1-(1-\theta )v+p_n^{SS}-p_p^{SS}}{2}}$, and the profit functions of the manufacturer and e-platform are as follows:

$$\begin{array}{c}{\pi }_n^{SS}=(1-r)p_n^{SS}{D}_n^{SS}-c{D}_n^{SS},\hfill \end{array}$$

(27)

$$\begin{array}{c}{\pi }_e^{SS}=(p_p^{SS}-c)D_s^{SS}+r{p}_n^{SS}{D}_n^{SS},\hfill \end{array}$$

(28)

And the optimal prices and profits are as follows:

$$\begin{array}{c}{p}_n^{SS\ast }={\displaystyle \frac{-2c+\theta v-v-3}{2(r-1)}},\hfill \end{array}$$

(29)

$$\begin{array}{c}{p}_p^{SS\ast }={\displaystyle \frac{4c-3(\theta -1)rv+r+(\theta -1)v+5}{4(1-r)}},\hfill \end{array}$$

(30)

$$\begin{array}{c}{\pi }_n^{SS\ast }={\displaystyle \frac{1}{16}}{(3-\theta v+v)}^2,\hfill \end{array}$$

(31)

$$\begin{array}{c}{\pi }_e^{SS\ast }={\displaystyle \frac{r(-32c+(\theta -1)v((\theta -1)v+26)-23)-{((\theta -1)v+5)}^2}{32(r-1)}}.\hfill \end{array}$$

(32)

Proposition 4. 

(i) 

In case SS, $p_n^{SS\ast }>p_p^{SS\ast }$.

(ii) 

${\pi }_n^{SS\ast }<{\pi }_e^{SS\ast }$ when $0<v\le 8\sqrt{2}-11$ or $8\sqrt{2}-11<v<1$, $0<r<r_4$, ${\theta }_2<\theta <1$ or $8\sqrt{2}-11<v<1$, $r_4<r<1$.

${\pi }_n^{SS\ast }>{\pi }_e^{SS\ast }$ When $8\sqrt{2}-11<v<1$, $0<r<r_4$, $0<\theta <{\theta }_2$.

Proposition 4(i) mirrors the findings in Proposition 1(i) that when both the manufacturer and the e-platform employ the same omnichannel strategy, the national brand products are priced higher than the private-label brand products due to their higher perceived value. The reasoning in Proposition 4(ii) also aligns with that in Proposition 1(ii). For low-value products, the manufacturer’s profit is less than that of the e-platform. For moderate or high-value products, at low commission rates, the manufacturer can earn higher profits than the e-platform if competition intensity is low; otherwise, it earns lower profits than the e-platform. At high commission rates, the e-platform’s profit consistently exceeds that of the manufacturer.

Comparing Proposition 1 and 4 reveals that when both entities adopt the same omnichannel strategies, their profits are influenced by the product valuation, commission rate, and competition intensity.

5. Strategy Selection

In the preceding section, we examined the equilibrium outcomes resulting from different omnichannel strategy combinations. These findings shed light on the interactions between the manufacturer and the e-commerce platform, laying the groundwork for analyzing their strategy selection decisions.

5.1. Comparison of Cases

In the subsection, we concentrate on comparing the cases where both the manufacturer and the e-commerce platform adopt the same omnichannel strategy.

Proposition 5. 

(i) 

In case SS, both the prices of national brand products and private-label brand products are higher compared to case BB, that is, $p_n^{BB\ast }<p_n^{SS\ast }$, $p_p^{BB\ast }<p_p^{SS\ast }$; the manufacturer’s profit in case BB is the same as that in case SS, that is, ${\pi }_n^{BB\ast }={\pi }_n^{SS\ast }$.

(ii) 

The e-platform is consistently more profitable in case SS than in case BB, that is, ${\pi }_e^{BB\ast }<{\pi }_e^{SS\ast }$.

As per Proposition 5(i), it is observed that under case SS, the retail prices of both national brand products and private-label brand products are higher compared to case BB. This suggests that the firms have partially transferred the additional handling and shipping costs to the customers by increasing the retail prices under case SS. Interestingly, the manufacturer achieves the same profits in cases BB and SS. When both brands adopt the same omnichannel strategy, consumers who are willing to buy national brand products are more concerned about the products’ prices than the format of the omnichannel strategy.

Even though the manufacturer’s profits are independent of the selection of the omnichannel strategy, the e-platform earns more profit in case SS than in case BB. This indicates that customers who prefer to buy private-label brand products are less sensitive to price increases, as they value the convenience of home delivery over picking up products from physical stores.

5.2. Optimal Strategy Selection

In the three-stage game, the e-platform determines its omnichannel strategy after observing the strategic decisions of the national brand manufacturer. Thus, in this subsection, our focus is on analyzing the e-platform’s best responses to the manufacturer’s decisions.

Proposition 6. 

(i) 

When the manufacturer adopts the BOPS strategy, the e-platform’s strategy is determined by the size of the spillover profit e and the commission rate r, as shown in

Table 1. The e-platform’s strategy when the manufacturer adopts the BOPS strategy.

e	r	e-Platform’s Strategy
$t-w-c<e<1$	$0<r<r_5$	BOPS
	$r_5<r<1$	SFS
$0<e<t-w-c$	$0<r<r_5$	SFS
	$r_5<r<1$	BOPS

.

(ii) 

When the manufacturer adopts the SFS strategy, the e-platform’s strategy is determined by the size of the spillover profit e and the commission rate r, as shown in

Table 2. The e-platform’s strategy when the manufacturer adopts the SFS strategy.

e	r	e-Platform’s Strategy
$t-w-c<e<1$	$0<r<r_6$	BOPS
	$r_6<r<1$	SFS
$0<e<t-w-c$	$0<r<r_6$	SFS
	$r_6<r<1$	BOPS

.

Proposition 6 highlights the e-platform’s optimal strategies in response to the manufacturer’s chosen omnichannel strategy. As shown in Table 1 and Table 2, the e-platform’s responses follow a consistent pattern when reacting to the manufacturer’s strategy choices. In most cases, the e-platform adopts the BOPS strategy when the commission rate is relatively low and switches to the SFS strategy when the commission rate is higher.

Since the e-platform’s private-label products initially face a disadvantage due to their lower customer valuation, the platform should set a lower market price to differentiate its products from the national brand and capture market share. When the commission rate is low, the e-platform’s revenue from the manufacturer’s sales is limited, meaning its profitability depends heavily on the success of its private-label products. Consequently, the e-platform’s omnichannel strategy focuses on enhancing the competitiveness of its own products. In this scenario, the e-platform opts for the BOPS strategy, which has lower operational costs but offers less value to customers. Under these conditions, the relationship between the e-platform and the manufacturer is primarily characterized by brand competition, as the two firms directly compete by offering differentiated products and services.

However, when the commission rate is high, the e-platform’s profit from the commission might outweigh its profit from selling its private-label brand products. In this condition, the e-platform’s omnichannel strategy selection focuses more on maximizing the joint profits from selling both products. Therefore, it can strategically adopt the omnichannel strategy that brings more value to customers but also requires higher operational costs. As shown in Proposition 2, this might even result in the price of private-label brand products being higher than national brand products. By doing so, it can strategically give up its private-label brand’s sales and incentivize customers to purchase the national brand products. The extra commission earned from the increased sales of national brand products compensates for the loss of profits from private-label brands. By choosing its omnichannel strategy, the e-platform and the manufacturer reach a condition where cooperation dominates their relationship.

Even though this pattern covers most cases, when $0<e<t-w-c$, the e-platform’s best responses show another pattern. When the size of the spillover demand is small, i.e., e is small, adopting the BOPS strategy is not as attractive compared to adopting the SFS strategy. Thus, when the commission rate is low and the e-platform’s profits mainly come from selling its private-label brand products, the e-platform would adopt the SFS strategy, as the benefits from adopting the BOPS strategy are too low. When the commission rate is high, as previously discussed, the e-platform would strategically give up the sales of private-label brand products, making adopting a weaker strategy, i.e., BOPS in this case, more profitable.

Another way to look at this case is that $t-w$ indicates the customer’s additional benefits when the firms adopt the SFS strategy. c is the additional cost the firm needs to pay by adopting the SFS strategy. Thus, $t-w-c$ can be treated as the “net” benefits of adopting the SFS strategy. On the other hand, the spillover profit, e, indicates the additional benefit that the BOPS strategy can bring to the firm. Therefore, when the commission rate is low, and the e-platform’s profits are mainly from selling its private-label brand products, the e-platform would like to directly compete against the manufacturer. Under this circumstance, the e-platform will adopt the SFS strategy since the net benefits from the SFS strategy are larger than the net benefits from the BOPS strategy. As the commission rate becomes high enough, the e-platform would strategically give up the sales of private-label brand products; thus, adopting a weaker strategy, i.e., BOPS in this case, becomes more profitable.

Furthermore, it is noteworthy that although the patterns in Table 1 and Table 2 are similar, the thresholds, $r_5$ and $r_6$, are different. Specifically, if $t-w-c<e<1$, then $r_5<r_6$; if $0<e<t-w-c$, then $r_5>r_6$. This finding suggests that when the manufacturer adopts the BOPS strategy, the e-platform is less inclined to adopt the same BOPS strategy compared to the scenario where the manufacturer adopts the SFS strategy. Conversely, when the manufacturer adopts the SFS strategy, the e-platform is less likely to adopt the SFS strategy, compared to when the manufacturer adopts the BOPS strategy. This pattern is consistent across all parameter combinations. The e-platform recognizes that the manufacturer’s national brand products have inherent advantages over its own private-label products. Therefore, the e-platform seeks to enhance its competitive position by offering differentiated services. Consequently, if market conditions allow, the e-platform is more likely to choose an omnichannel strategy different from the one adopted by the manufacturer. This is a naturally optimal response as the second mover, emphasizing that brand competition is the primary factor influencing the dynamic relationship between the e-platform and the manufacturer.

In the next step of our analysis, we seek to determine the conditions under which both the manufacturer and the e-platform would choose their respective omnichannel strategies, resulting in an equilibrium state.

Proposition 7. 

The optimal omnichannel strategy selections for the manufacturer and e-platform are influenced by the size of the spillover profit and the commission rate. An equilibrium exists where the manufacturer adopts the SFS strategy and the e-platform adopts the BOPS strategy if $0<e<t-w-c$ and $r_5<r<1$.

Proposition 7 suggests that the decision-making process for selecting omnichannel strategies by both the manufacturer and the e-platform is influenced by several key factors, including spillover profits and the commission rate. Specifically, the proposition indicates that an equilibrium can be reached when the following criteria are met: the spillover profit is positive but less than the difference between the customer’s additional benefits from the SFS strategy compared to the BOPS strategy and the firm’s additional costs for implementing the SFS strategy over the BOPS strategy (represented by $t-w-c$); and when the commission rate is high. In this scenario, the manufacturer prefers the SFS strategy, while the e-platform opts for the BOPS strategy. This demonstrates that the relative appeal of each strategy to the respective firm depends on how these factors balance in terms of cost and potential revenue generation.

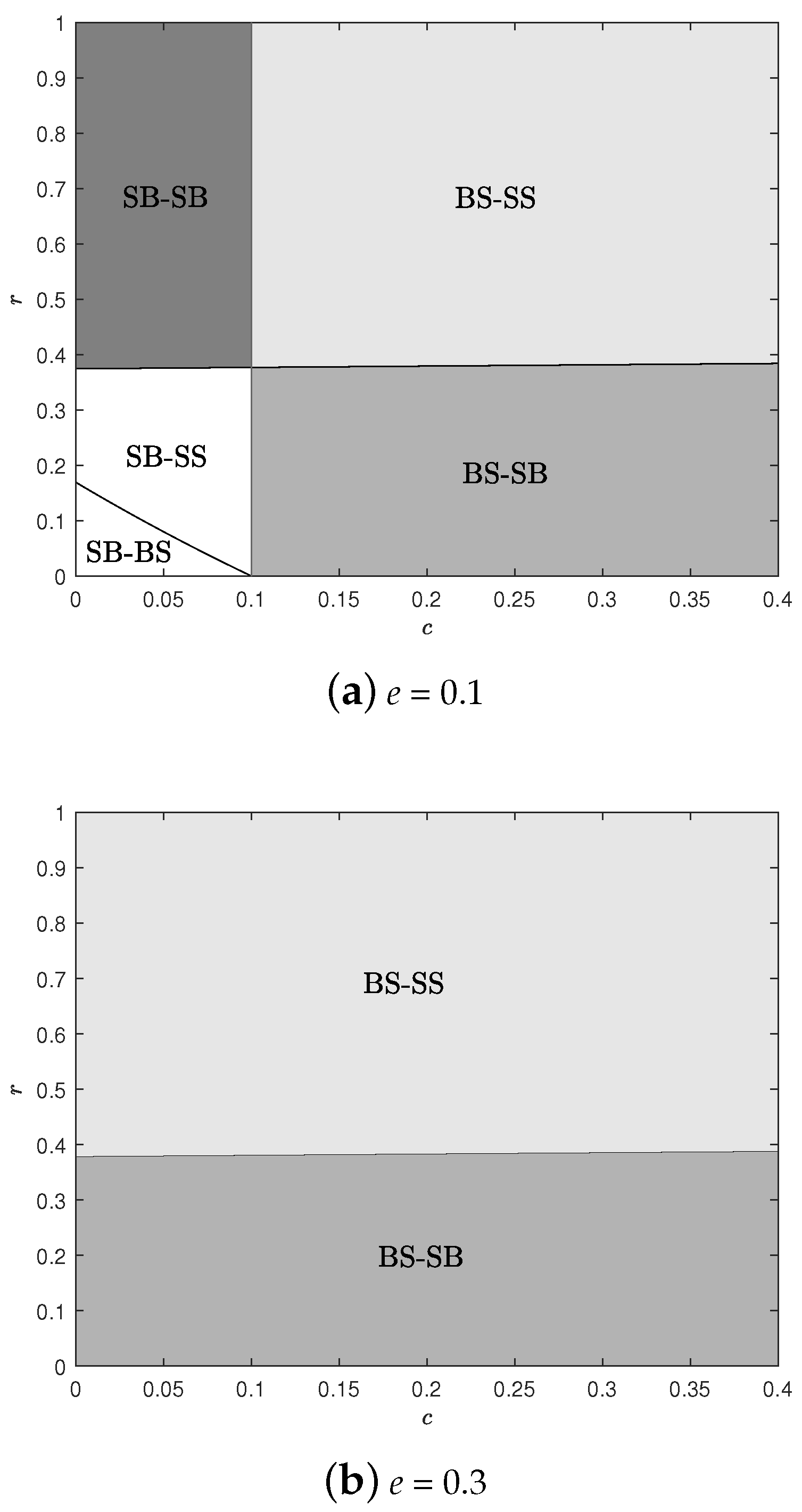
To provide a deeper understanding of how the two firms’ optimal omnichannel strategy decisions are affected by these three factors, we conducted a numerical analysis and present the results in Figure 1. We use notations like “BS-SS” and “SB-SB” to represent optimal strategy selection combinations for both the manufacturer and the e-platform. For example, “BS-SS” means that the manufacturer is better off in case BS, while the e-platform is also better off in case SS.

As shown in panel (b), when the spillover effect is large, there is no case in which the platform and the manufacturer can reach an equilibrium. The manufacturer always obtains the highest profits in the BS scenario. For the e-platform, when the commission rate is low, it achieves the highest profits in the SB scenario, and when the commission rate is high, it prefers the SS scenario. A similar pattern can be found when the spillover effect is relatively small, but the additional cost of operating the SFS strategy is large, as shown on the right side of panel (a). When the spillover effect is small, the commission rate is high, and it is not very costly to adopt the SFS strategy compared to the BOPS strategy. Both firms’ best scenario is the SB case.

6. Sensitivity Analysis

In previous sections, we focused on how firms make their optimal omnichannel strategies and how these decisions are influenced by factors such as spillover profits, operating cost differences, and the commission rate. In this section, we shift our focus to examine how these factors can affect optimal prices and profits.

6.1. The Impact of Competition Intensity $\theta$

Corollary 1. 

(1) 

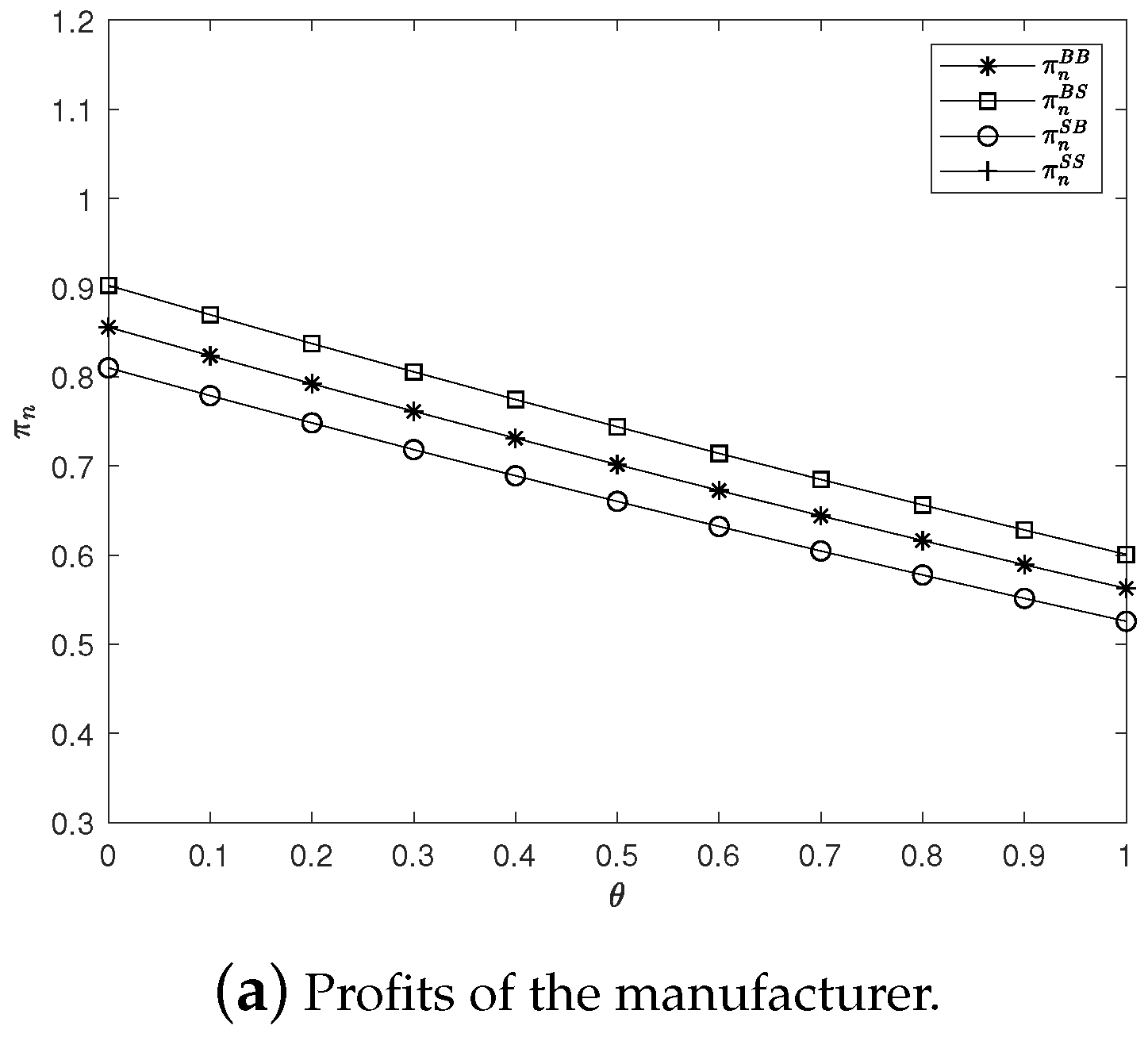
In all four cases, the national brand products’ retail prices always decrease as θ increases.

(2) 

In all four cases, if $0<r<{\displaystyle \frac{1}{3}}$, the private-label brand products’ retail prices increase as θ increases; otherwise, the private-label brand product’s retail prices decrease as θ increases.

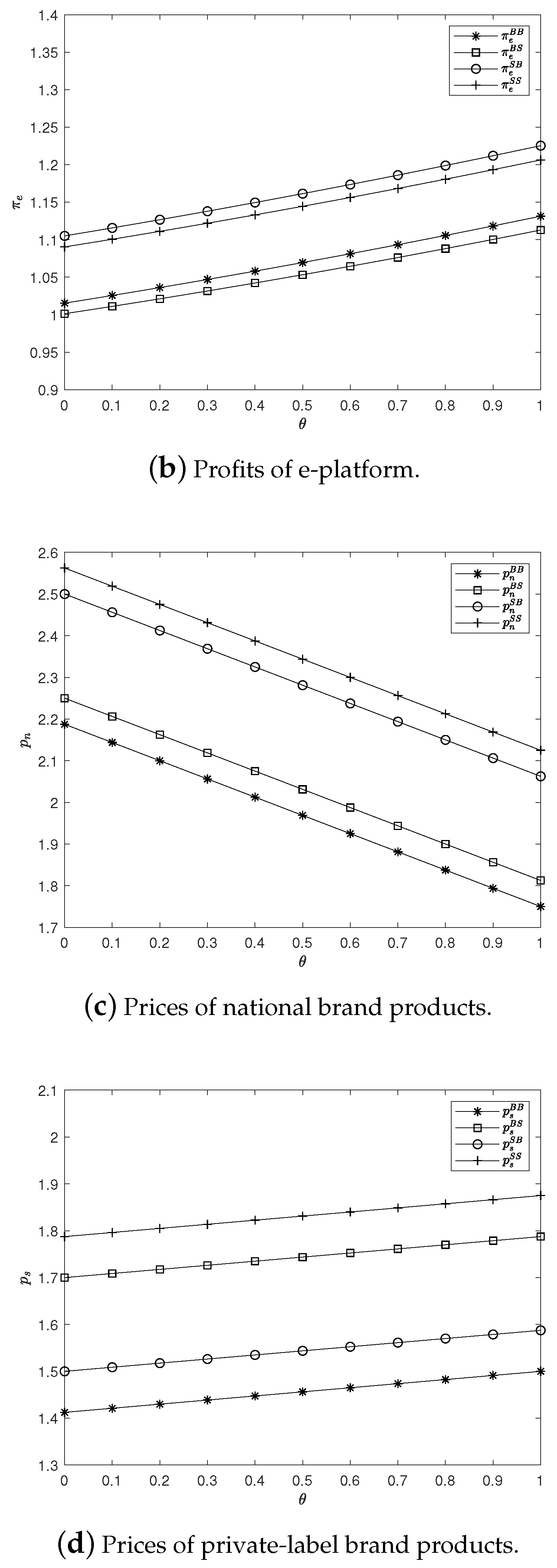
The difference in consumer valuation between national and private-label brand products is represented by $1-\theta$. When $\theta$ becomes smaller, the national brand products are perceived as more superior. Consequently, the manufacturer can charge higher prices for its products. The effect of $\theta$ on the e-platform’s pricing depends on the commission rate, r. If r is low, the e-platform’s profit margin from selling its own brand products is higher than the commission received from selling the manufacturer’s products. As a result, as $\theta$ decreases, indicating a decrease in consumer valuation of the private-label brand, the e-platform lowers the retail price of its private-label brand products. However, when the rate of commission is high, the commission earned from selling the manufacturer’s products could exceed the profit margin of private-label brands. Therefore, the e-platform may prefer consumers to purchase national brand products rather than private-label brand products. As a result, the e-platform increases the retail price of private-label brand products as $\theta$ decreases, influencing consumer perception.

Corollary 2. 

In all four cases, the manufacturer’s profits always decrease as θ increases.

The intuition behind Corollary 2 is similar to that of Corollary 1. As $\theta$ increases, indicating an increase in consumer acceptance of private-label brand products, the demand for these products also increases. This poses a stronger competition for the manufacturer, whose national brand products may face reduced demand. As a result, the profit of the manufacturer decreases in the presence of a competitor with stronger customer valuation for private-label brand products.

Corollary 3. 

(1) 

(In case BB and case SS, if $0<r<{\displaystyle \frac{\theta v-v+5}{\theta v-v+13}}$, ${\pi }_e^{BB\ast }$ and ${\pi }_e^{SS\ast }$ increase with θ; otherwise, ${\pi }_e^{BB\ast }$ and ${\pi }_e^{SS\ast }$ decrease with θ.

(2) 

In case BS, if $0<r<{\displaystyle \frac{c+e-t-\theta v+v+w-5}{c+e-t-\theta v+v+w-13}}$, ${\pi }_e^{BS\ast }$ increases with θ; otherwise, ${\pi }_e^{BS\ast }$ decreases with θ.

(3) 

In case SB, if $0<r<{\displaystyle \frac{c+e-t+\theta v-v+w+5}{c+e-t+\theta v-v+w+13}}$, ${\pi }_e^{SB\ast }$ increases with θ; otherwise, ${\pi }_e^{SB\ast }$ decreases with θ.

Corollary 3 demonstrates that the impact of $\theta$ on the e-platform’s profit is not monotonic and is sensitive to the commission rate, which aligns with the observations in Propositions 6 and 7, and Corollary 1. When the rate of commission is low, the profit margin of private-label brand products is higher than the commission earned from selling national brand products. Consequently, as the customer valuation of private-label brand products increases (as $\theta$ increases), the e-platform’s profit also increases. Furthermore, when the rate of commission is high, the e-platform’s profits primarily come from commissions. As shown in Corollary 1, the price of private-label brand products decreases with increasing $\theta$, leading to a decrease in profit for the e-platform.

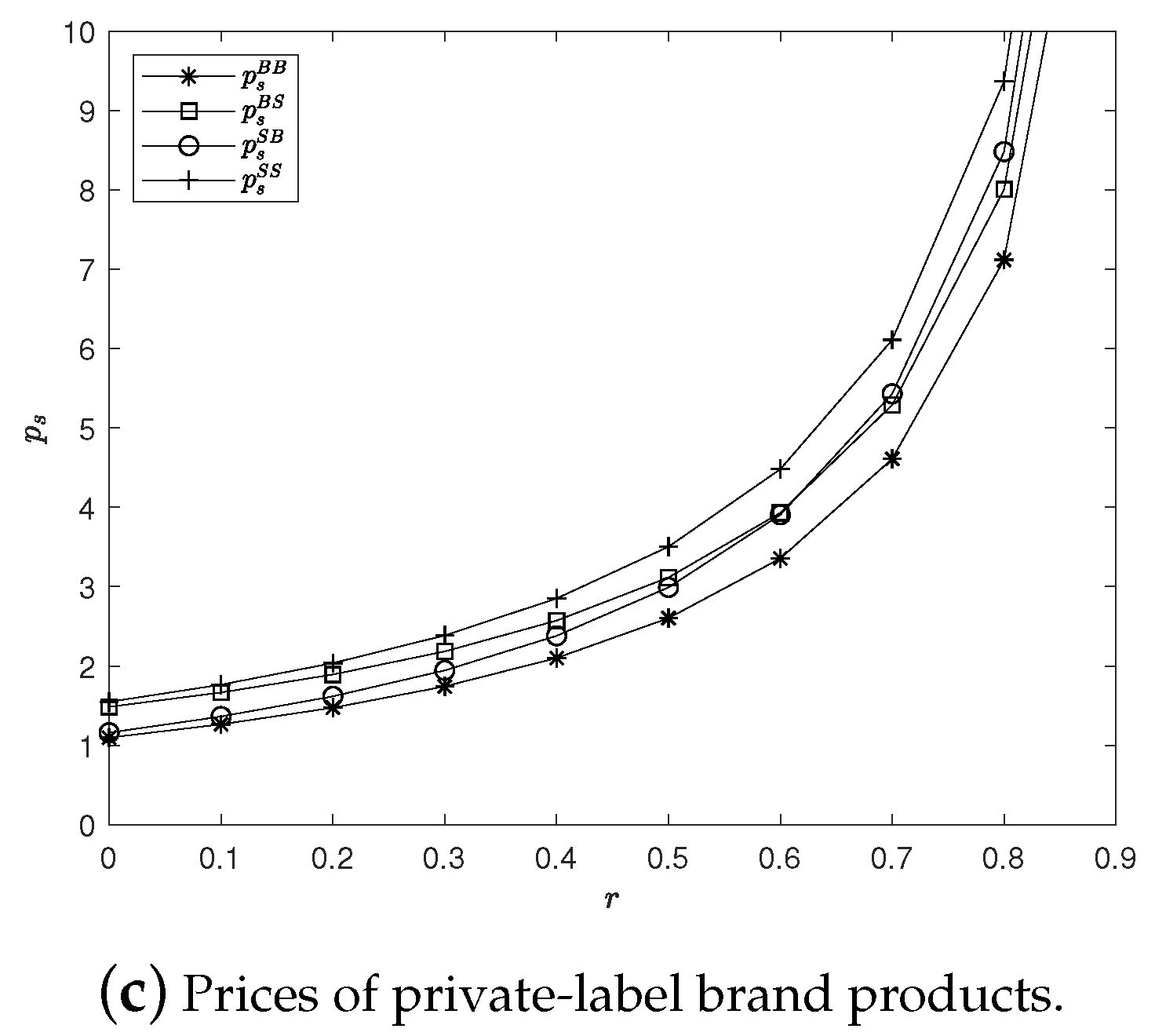
To provide more intuitive insights, we present a numerical example with specific parameter values $t=0.3,v=0.7,w=0.1,e=0.1,c=0.2,$ ans $r=0.2$. The impacts of $\theta$ on both firms’ optimal prices and profits are depicted in Figure 2. In this subsection, we show the impacts of $\theta$ on both firms’ optimal prices and profits.

6.2. The Impact of Commission Rate r

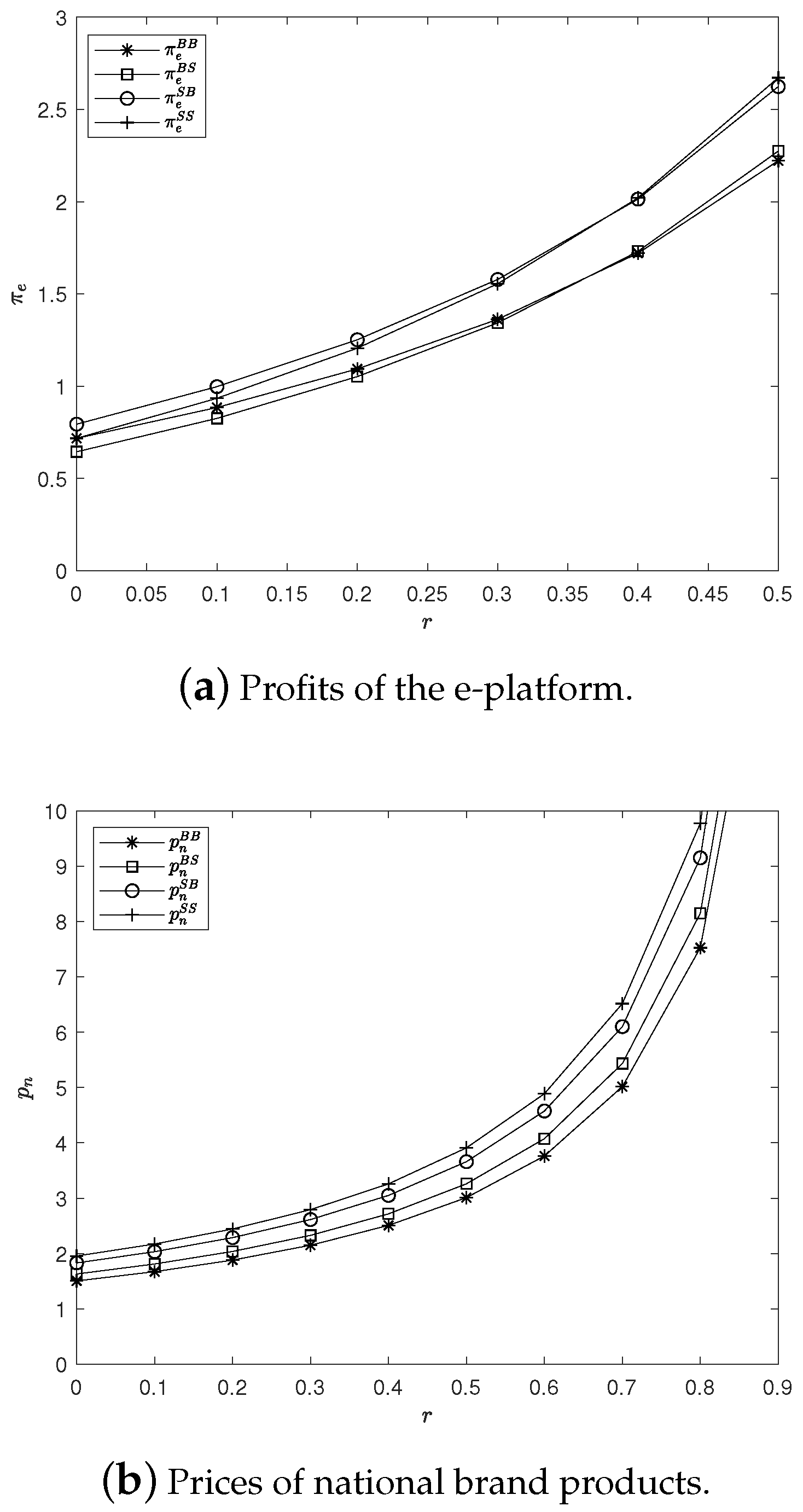
Corollary 4. 

In all four cases, the national brand products’ retail prices always increase with the rate of commission r.

Clearly, as the rate of commission r increases, the manufacturer needs to raise the retail prices of national brand products in order to offset the loss in profit margin caused by the higher commission rate.

Corollary 5. 

In all four cases, the private-label brand products’ prices always increase with the commission rate r.

Corollary 5 suggests that as the rate of commission r increases, the retail prices of private-label brand products also increase. This is because when the commission rate rises, the manufacturer raises the retail prices of national brand products to compensate for increased costs. In response, the e-platform increases the retail prices of private-label brand products to maximize its profits, as consumers have to make a choice between the two brands.

Corollary 6. 

In all four cases, the e-platform’s profits always increase with the rate of commission r.

The results in Corollary 6 can be attributed to two factors. Firstly, a higher commission rate increases the e-platform’s profits from commissions earned on the sales of both national and private-label brand products. Secondly, the private-label brand product prices also increase with a higher commission rate, resulting in higher profits from the sales of private-label brands.

To provide further insight, we plot the impacts of commission rate on prices and profits using a numerical example with the following parameters: $t=0.3,v=0.7,w=0.1,e=0.1,$$c=0.35,$ and $\theta =0.7$. The corresponding results are presented in Figure 3.

6.3. The Impact of Waiting Cost w and Pickup Cost t

This subsection focuses on the impact of waiting and pickup costs on the optimal profit levels for both firms. Generally, a higher waiting cost increases the expense associated with choosing the SFS strategy, while a higher pickup cost disadvantages the firm adopting the BOPS strategy. This intuition aligns with the findings in Corollary 7.

Corollary 7. 

(1) 

In case BS, ${\pi }_n^{BS\ast }$ increases with w and decreases with t.

(2) 

In case SB, ${\pi }_n^{SB\ast }$ decreases with w and increases with t.

In the BS case, where the manufacturer adopts the BOPS strategy and the e-platform adopts the SFS strategy, a higher pickup cost increases the consumer’s cost of purchasing national brand products, thereby reducing the manufacturer’s profit. Conversely, a higher waiting cost raises the consumer’s cost of purchasing private-label products, making national brand products more competitive and ultimately increasing the manufacturer’s profit. A similar logic applies to the SB case, where the manufacturer adopts the SFS strategy and the e-platform adopts the BOPS strategy. In summary, when the two firms adopt different omnichannel strategies, the manufacturer’s profit shows a monotonic relationship with both its own operational costs and those of the opposing firm.

Corollary 8. 

(1) 

In case BS, if $0<r<{\displaystyle \frac{c+e-t-\theta v+v+w-5}{c+e-t-\theta v+v+w-13}}$, ${\pi }_e^{BS\ast }$ decreases with w and increases with t; otherwise, ${\pi }_e^{BS\ast }$ increases with w and decreases with t.

(2) 

In case SB, if $0<r<{\displaystyle \frac{c+e-t+\theta v-v+w+5}{c+e-t+\theta v-v+w+13}}$, ${\pi }_e^{SB\ast }$ increases with w and decreases with t; otherwise, ${\pi }_e^{SB\ast }$ decreases with w and increases with t.

However, Corollary 8 reveals that the impact of waiting and pickup costs on the e-platform’s profits is less straightforward than it is for the manufacturer. In both the BS and SB cases, when the commission rate is low, the effects of waiting and pickup costs on the e-platform’s profits mirror their effects on the manufacturer’s profits. Specifically, when the e-platform adopts the BOPS strategy (as in the SB case), a higher pickup cost raises the consumer’s cost of purchasing private-label products, while a higher waiting cost makes consumers more inclined to purchase national brand products.

When the commission rate is high, however, the effects of waiting and pickup costs on the e-platform’s profits reverse. As previous results show, a high commission rate enables the e-platform to earn a larger share of profit from selling national brand products. Consequently, the e-platform is incentivized to strategically reduce its private-label sales, allowing the national brand to capture more market share. The extra commission earned from selling national brand products compensates for the loss in private-label sales. For example, while a higher pickup cost does reduce the e-platform’s profits in the SB case, it simultaneously boosts national brand product sales. This positive effect is strong enough to outweigh the negative impact, especially when the commission rate is high.

In conclusion, the analysis of consumer costs reveals that the commission rate determines whether the e-platform primarily competes against or cooperates with the manufacturer. A lower commission rate fosters competition, whereas a higher commission rate encourages cooperation between the e-platform and the manufacturer. These findings echo our results regarding firms’ omnichannel strategy selections. We extend our thanks to the anonymous reviewer for their excellent suggestion.

7. Conclusions

The utilization of information technology has significantly contributed to the growth and popularity of omnichannel retailing. This approach enhances the flexibility of order fulfillment and meets the diverse shopping preferences of consumers, thereby improving the profitability of firms. Moreover, as the merchandise market becomes more diverse, intense competition arises among various brands. This competition often involves conflicts between national brands and private-label brands. Academic research has consistently focused on studying this competition and its implications. This study provides valuable insights into decision-making regarding brand competition and omnichannel strategy selection, with a particular focus on the role of information technology, specifically AI, in enhancing these strategies. AI-driven analytics enable firms to make data-informed decisions that optimize pricing, customer personalization, and omnichannel strategies. Furthermore, AI helps firms better understand consumers’ product valuations, which is crucial for setting competitive prices and optimizing product assortment. Building upon this, this study combines omnichannel strategies and brand competition by examining a co-opetitive supply chain consisting of a manufacturer producing national brand products and an e-platform selling both national brands and private-label brands. Both firms have the option to choose between two omnichannel strategies, BOPS and SFS. We explore the strategic interactions between these firms across four different combinations of omnichannel strategies.

In the first step, we analyze the optimal prices and profits of both the manufacturer and the e-platform across the four different cases. We find that when both firms choose the same omnichannel strategies, i.e., in cases BB and SS, which firm can earn a higher profit is jointly determined by the valuation of the product category, the commission rate, and competition intensity. Specifically, for low-value products, the manufacturer’s profit is less than that of the e-platform. For moderate or high-value products, at low commission rates, the manufacturer can earn higher profits than the e-platform if competition intensity is low; otherwise, it earns lower profits than the e-platform. At high commission rates, the e-platform’s profit consistently exceeds that of the manufacturer. When firms choose different omnichannel strategies, i.e., in cases BS and SB, which firm earns a higher profit is determined solely by the commission rate. Generally, when the commission rate is low, the manufacturer can earn a higher profit than the e-platform, and vice versa.

In the second step, we analyze the e-platform’s best response strategies after observing the manufacturer’s decisions, considering factors such as spillover profits, operating cost differences, and the commission rate. The e-platform’s strategy choice aims to balance its competitive advantage and the joint profits with the manufacturer. When the spillover effect is large and the commission rate is low, the e-platform adopts the BOPS strategy to differentiate its products and services from the national brand products and split the market. Conversely, as the commission rate increases, the e-platform can strategically adopt the omnichannel strategy that brings more value to customers but also requires higher operational costs, i.e., the SFS strategy. In this scenario, it strategically gives up its private-label brand’s sales and incentivizes customers to purchase national brand products, which can generate higher profit through high commission fees. However, when the spillover effect is small, especially when it is smaller than the net difference between the customer’s additional benefits and the firm’s additional costs for SFS compared to BOPS, the strategy that enhances the e-platform’s competitive advantage shifts from the BOPS to the SFS strategy. Thus, the e-platform’s optimal strategy choice flips under different commission rates.

Furthermore, an equilibrium can be achieved where the manufacturer prefers the SFS strategy while the e-platform opts for the BOPS strategy. This condition occurs when the spillover profit is positive but less than the net benefit difference between the SFS and BOPS strategies, and the commission rate is high.

Lastly, we conduct a sensitivity analysis to examine the impact of competition intensity and the commission rate. The manufacturer’s profits consistently decrease as the difference between the two brands’ products diminishes. Meanwhile, the e-platform’s profits always increase with a higher commission rate.

This study offers valuable insights for decision-making regarding brand competition and omnichannel strategy selection, elucidating important factors that influence a firm’s profitability under various omnichannel strategy combinations. When both firms adopt the same strategy, profitability is influenced by the product category value, competition intensity, and commission rate. However, when firms adopt different omnichannel strategies, profitability is primarily affected by the commission rate.

The commission rate plays a critical role in shaping the e-platform’s response to the manufacturer’s omnichannel strategy. Specifically, a low commission rate encourages the e-platform to compete directly with the national brand manufacturer, focusing on promoting its private-label brand to maximize profits. Conversely, a high commission rate incentivizes the e-platform to prioritize the sales of the manufacturer’s products over its private-label brand. This is because higher profits can be earned through commissions by enhancing the sales of the competitor’s products.

Furthermore, under conditions where the commission rate is high and the spillover effect is less than the net benefits of choosing the SFS strategy, an equilibrium is established where the manufacturer opts for the BOPS strategy, and the e-platform adopts the SFS strategy. This equilibrium allows both firms to optimize their profits based on the current market dynamics.

For products of moderate or high value, the profitability of both firms depends significantly on the competition intensity and commission rates. At low commission rates, the manufacturer can achieve higher profits than the e-platform, especially if competition intensity is low. Consequently, manufacturers should focus on differentiating their national products from private-label products to capitalize on this advantage.

While this research makes valuable contributions to the existing literature, there are certain limitations that provide opportunities for future investigation. For instance, the study focuses on horizontal differences between the two brand products but does not account for variations in production costs. Future research could explore vertical differences and incorporate production costs into the model. Additionally, our analysis is grounded in a theoretical framework, which is consistent with much of the existing literature (e.g., [39,40,41]). While testing the model’s predictions using empirical data or experiments is beyond the scope of this study, it represents a promising direction for future research. Another potential extension of this study would be to incorporate more players into the model, allowing for a more comprehensive exploration of competitive dynamics in a broader omnichannel retail environment. Furthermore, while we assume equal spillover profits between the manufacturer and the e-platform in this study, future research could investigate scenarios where the spillover effect is differentiated. Varying the distribution of spillover profits between stakeholders could offer deeper insights into profitability and strategic decision-making in omnichannel settings. We are grateful to one anonymous reviewer for suggesting this excellent recommendation.