Abstract
This research investigates the effects of “choose-one-over-another” monopolistic strategies on two-sided platforms, analyzing the implications of such practices on network effects and platform economics through the Hotelling model. Our key findings include the following: (1) “Choose-one-over-another” policies enhance positive network effects, increasing multi-homing on the demand side but reducing overall platform revenue. These policies also intensify negative network effects, leading to higher prices for supply-side users and thereby undermining the welfare of demand-side users. (2) After antitrust interventions, platforms adjust pricing dynamically, increasing for one side and decreasing for the other in response to changes in same-side network effects, which in turn influences multi-homing behaviors and revenue impacts differently before and after the enforcement of such policies. (3) Without exclusive selection mandates, platform pricing strategies tend to lower prices for supply-side users, especially under competitive pressures or weaker positive network effects, potentially increasing platform revenue and overall supply chain welfare under certain conditions. This study highlights the critical role of regulatory oversight in curbing monopolistic platform behaviors to protect user rights and ensure market health, offering strategic guidance for platform management amidst competitive and operational challenges.
1. Introduction
As the platform economy garners increasing attention with societal advancement, leading corporations such as Tencent (a social platform) and Alibaba (an e-commerce platform), both listed in Hong Kong and U.S. stock markets, have emerged as the entities with the highest market values in mainland China. Other platform companies like Meituan, Pinduoduo, Kuaishou, JD.com, and ByteDance have valuations exceeding USD one hundred billion, underscoring the dominance of internet platform businesses, which constitute seven of the top ten global corporations by market value. Internet platforms have become integral to daily life, facilitating services ranging from e-commerce (e.g., Taobao and JD.com) to food delivery (e.g., Meituan and Ele.me), acting as intermediaries that connect demand and supply sides to offer value-added services related to transactions and goods exchange, thus forming the backbone of platform supply chains [1].
The essence of platforms is underpinned by the internet, with network effects showcasing the degree of mutual influence among user groups, a fundamental characteristic of platforms [2]. Network effects encourage diverse users to participate in platforms; for instance, an increase in buyers on an e-commerce platform attracts more sellers, and vice versa, illustrating the positive cross-side network effects. However, network effects also manifest among like users, both positively and negatively [3]. The utility for users on the same side increases with platform scale due to scale effects, but it can diminish with an increase in the number of suppliers due to crowding and competition. The existence of same-side and cross-side network effects plays a crucial role in the growth of platform supply chains, with leveraging these effects being key to success [4].
The Digital Markets Act targets entities surpassing a EUR 75 billion market value and a EUR 7.5 billion annual turnover and maintaining at least 45 million monthly active and 10,000 yearly commercial users within the EU as “gatekeepers”. Notably, in September 2023, major firms such as Alphabet, Amazon, Apple, ByteDance, Meta, and Microsoft were classified under this designation. This act emphasizes the urgent need to mitigate monopolistic tendencies in the rapidly growing platform economy, particularly against the backdrop of the “choose-one-of-two” policy that demands exclusive partnerships from merchants on e-commerce platforms. In response to similar concerns, the Chinese government introduced the “Platform Anti-Monopoly Guidelines” in February 2021, underscoring a global recognition of the issue. Following these guidelines, Alibaba was fined CNY 18.228 billion in April 2021 for its adherence to the “choose-one-of-two” policy, with Meituan also coming under scrutiny for alleged monopolistic practices [5].
The growing concern over “choose-one-of-two” practices among public media and governmental regulators, especially after antitrust actions that led platforms to cease such practices, raises pertinent questions about the resultant shifts in pricing, market share, revenue, and the broader implications for the platform supply chain ecosystem [6]. In this study, we utilize the Hotelling competition model to delve into the effects of implementing or abstaining from “choose-one-of-two” practices on the pricing strategies and revenue outcomes for platforms and other stakeholders within the supply chain, enriched by a comparative numerical simulation.
This research delves into the nuanced dynamics of “choose-one-of-two” strategies within two-sided platforms and their profound effects on the interplay between positive and negative network effects, revealing complex implications for platform economics and supply chain welfare. Existing studies primarily focus on cross-group network effects and the complete multi-homing of platform users while neglecting intra-group negative network effects, the partial multi-homing of platform users, and monopolistic behaviors during the mature phases of platforms. These aspects are crucial for a comprehensive understanding of platform dynamics. This study aims to fill these gaps by exploring the transitions in platform behaviors before and after antitrust interventions, uncovering strategic adjustments in pricing and their consequential impacts on user multi-homing tendencies alongside variations in platform and stakeholder revenues.
This investigation highlights that exclusive selection practices, while aiming to leverage positive network effects by encouraging demand-side multi-homing, inadvertently reduce overall platform revenue due to intensified negative network effects. This not only leads to an increase in supply-side pricing to counterbalance revenue losses but also compromises the welfare of demand-side users. In contrast, the cessation of such practices, mandated by antitrust regulations, prompts platforms to recalibrate their pricing strategies. This recalibration aims to balance the intricate dynamics of same-side network strengths, fostering an environment where multi-homing becomes more prevalent among supply-side users and, subsequently, attracts a broader demand-side user base.
The absence of “choose-one-of-two” policies unveils a scenario where platforms, no longer constrained by the need to enforce exclusivity, can adopt more flexible pricing strategies. This flexibility is particularly beneficial for supply-side users, who face reduced prices in a more competitive landscape. Interestingly, this study indicates that platform revenue does not inevitably decline without exclusive selection policies; it may, in fact, rise when positive network effects are significant enough. Moreover, the overall welfare of the platform supply chain, including both supply-side revenue and aggregate revenue, demonstrates potential for growth in the absence of such monopolistic practices, especially under conditions of fierce competition or diminished positive network effects.
From a managerial perspective, these findings underscore the critical importance of regulatory oversight in curbing monopolistic practices within platform economies. This research advocates for a balanced approach to platform governance that safeguards user rights while promoting healthy market competition and stability. It suggests that platforms can navigate post-antitrust landscapes by innovating in competitive strategies and operational behaviors that enhance user engagement and loyalty without resorting to exclusionary practices. Furthermore, the study sheds light on the strategic importance of fostering a competitive yet cooperative ecosystem for all stakeholders within the platform supply chain. It suggests that platforms can leverage insights from antitrust interventions to offer better services and incentives to merchants, aiming to reduce their operational costs and spur sustainable growth. Such strategies not only align with regulatory expectations but also enhance the platform’s value proposition to both sides of the market, ultimately contributing to a more vibrant, equitable, and thriving digital economy. This approach, exemplified by Alibaba’s response to regulatory penalties, points towards a future where platforms can achieve growth by prioritizing the collective welfare of their ecosystems over short-term monopolistic gains.
The structure of this paper is organized as follows: Section 2 reviews the relevant literature, providing a foundation for our study. In Section 3, we develop and analyze our model. Section 4 presents a comparative analysis through numerical simulations to elucidate the implications of our findings. Finally, Section 5 concludes the paper.
2. Literature Review
Our work is primarily connected with two domains in the existing literature: one is the impact of network effects on pricing strategies under platform competition, and the other is about the participation decisions of users on the platform.
Network effects are a fundamental characteristic of the platform economy, encapsulating how a user’s utility from a product or service changes with the number of users consuming the same product or service. Katz and Shapiro [7] were pioneers in defining network effects, laying the groundwork for understanding the intricate dynamics within platform economies. However, platforms face a classic “chicken-and-egg” problem requiring a critical mass of suppliers to attract buyers and vice versa, highlighting the paradoxical nature of platform growth [8]. Addressing this conundrum, Eisenmann et al. [3] suggested that platforms initially adopt low pricing or even provide subsidies to one side to ensure participation, subsequently charging the other side higher prices to compensate for losses and secure profits. This strategy, employed by many platforms during their initial stages, has been instrumental in rapid market penetration and early user base accumulation. They further differentiated network effects into same-side and cross-side effects, with the former describing how a user’s utility increases with the expansion of their group and the latter indicating an increase in utility with the growth of the opposite market side. These interactions, also referred to as indirect network effects [9], generally posit positive cross-side network effects and potentially positive or negative same-side network effects. Empirical research by Zhu and Iansiti [10] on market entry factors for platforms found that the success of entrants depends on the strength of cross-side network effects. Anderson et al. [11] questioned the conventional wisdom of “winner-takes-all” by examining how investments in the presence of strong cross-side network effects impact platform performance, suggesting that substantial investments do not always translate into competitive advantages. Recent work by Sui et al. [12] indicates that network effects can influence the value of investments in value-added services by platforms, affecting the pricing strategies for both sides of the market. Reisinger [13] developed a model incorporating negative cross-network externalities, uncovering that an increase in users on one side could lead to a decrease on the other, highlighting the impact of negative cross-side network effects. However, this body of research often overlooks the implications of negative same-side network effects and primarily focuses on the early stages of platform development, neglecting the mature phase where network effects could manifest differently. This oversight underscores a gap in the literature, pointing to the need for a more nuanced understanding of network effects throughout the lifecycle of platforms, especially considering the strategic implications for platform growth and sustainability.
The “choose-one-of-two” policy fundamentally aims to limit user participation on platforms, which significantly influences platform dynamics based on whether users join a single platform or multiple platforms. This variation in user behavior impacts platforms differently [14]. The discourse typically centers around three scenarios: scenarios where both market sides are single homing, scenarios where one side is multi-homing while the other remains single homing, and scenarios where both sides engage in multi-homing [6]. Rochet and Tirole [15] were pioneers in developing a dual-platform competition model that highlighted the phenomenon of multi-homing in the marketplace. Their subsequent research illustrated that multi-homing arises from users’ desires to benefit from network externalities in a non-exclusive platform environment [14]. They further explored the implications of cardholders’ multi-homing behavior on competition in the credit card industry, finding that product bundling could enhance social welfare [16]. Armstrong [17] innovatively proposed the competitive bottleneck model, and Belleflamme and Peitz [18] analyzed the optimal pricing strategies within the competitive bottleneck model for pure single-homing users. While their research did not specifically address dual-side multi-homing, they underscored its significance in studying platform competition. Additionally, scholars have begun to focus on scenarios involving user multi-homing. Bryan and Gans [19] simulated competition between two ridesharing platforms, examining the change in platform idleness as consumers shift from single to full multi-homing. Bernstein et al. [20] investigated optimal pricing strategies for ride-hailing platforms under single- and multi-homing scenarios amidst congestion effects. Bakos and Hanna [21] delved into the subsidy strategies of platforms under multi-homing conditions. Liu et al. [22] explored pricing strategies and model selection between third-party aggregator platforms and ridesharing platforms under single and multiple affiliations, considering the impact of network effects and user participation. However, these studies often assume complete multi-homing, overlooking the more nuanced scenario of partial multi-homing. In reality, user affiliation behavior is not uniform; within the same user group, some may choose single homing, while others opt for multi-homing. Thus, the phenomenon of partial multi-homing among platform users is prevalent and offers significant research value, highlighting the complexity of user behavior in platform economies and underscoring the need for a deeper understanding of its implications for platform strategy and market dynamics.
In Table 1, we provide a summary and comparative analysis of existing studies that are pertinent to our research yet differ in certain key aspects. This research highlights a gap in the existing literature that primarily focuses on cross-group network effects while neglecting intra-group negative network effects, crucial for understanding platform dynamics. It emphasizes the significant yet varied impact of same-side network effects, such as positive effects driving gamer aggregation on gaming platforms and negative effects due to excessive competition among merchants on e-commerce platforms. Moreover, this study points out the oversight of mature platform phases and partial multi-homing scenarios, which are vital for depicting realistic platform–user interactions. Existing research, often from a platform-centric viewpoint, largely ignores the broader implications on the platform supply chain’s overall revenue distribution [23,24,25,26,27,28,29,30,31,32,33,34]. Addressing these gaps, our analysis explores the influence of both same-side and cross-side network effects on platform supply chains, comparing the competitive strategies and revenue implications for stakeholders under different platform policies. This approach offers a comprehensive insight into platform economics, focusing on the nuanced effects of network dynamics across platform lifecycle stages.

Table 1.
Literature comparison on network effects and multi-homing decisions.
3. Model Construction and Analysis
This section introduces a model involving a two-sided platform supply chain, characterized by users engaging with two oligopolistic platforms. It contrasts scenarios of monopolistic enforcement versus non-enforcement of a “choose-one-of-two” policy for suppliers, labeled with the superscripts MS (multi-homing and single homing) and MM (multi-homing and multi-homing), respectively, with an asterisk (*) indicating equilibrium states.
The framework posits two monopolistic platforms, , situated at the extremities of a Hotelling line, providing identical products or services to a diverse user base. The market consists of two user groups, : demand-side () and supply-side (), uniformly distributed along a Hotelling line with a length of one. The symbol represents the scale or market share of each side’s users on the platforms, with the overall market size for both groups fixed at 1. The segment of single-homing users on side j of platform i is notated as , whereas multi-homing users are denoted as . The term indicates the distance of side users to platform 0, serving as a measure of their preference for platform 1 over platform 0, beyond network effects. Higher values imply a greater inclination towards platform 1. The location where side j users on platform i achieve zero utility is marked as . Under the assumption that both platforms monopolistically span the entire market, the intensity of cross-side network effects between demand and supply sides is expressed as , and the strength of same-side network effects within each user group is expressed as . Positive network effects are assumed for both cross-side interactions and same-side effects among demand-side users, while supply-side users experience negative same-side network effects. Given the presence of scale economies, it is presumed that the marginal costs for both platforms are null. Inspired by the setup in Xie et al. [6], platform profits stem from service fees levied on users from both sides, , where signifies no charge to users on side j by platform i, and indicates that users are receiving subsidies.
3.1. Enforced “Choose-One-of-Two” Scenario (MS)
In this scenario, platforms adopt a “choose-one-of-two” policy, exhibiting monopolistic behavior characteristic of a duopolistic market. Following the accumulation of an initial user base, platforms frequently enforce stringent management practices. Among these, exclusivity agreements that compel merchants to select only one of the two platforms for their sales are particularly prevalent. This strategy is most common in the e-commerce industry during promotional periods, wherein platforms may mandate merchants to conduct sales activities solely on their platform, culminating in the execution of “exclusive cooperation agreements”.
When platforms enforce a “choose-one-of-two” policy, demand-side users are free to choose which platform to use based on utility, resulting in a mix of multi-homing (users engaging with multiple platforms) and single-homing (users engaging with only one platform) behaviors. On the other hand, supply-side users are constrained by the “choose-one-of-two” policy to engage with only one platform, leading to exclusive single homing. This structure is depicted in Figure 1, where the number of demand-side users on a platform is divided into single-homing users, denoted as , and multi-homing users, denoted as . In contrast, the number of supply-side users on platform i consists solely of single-homing users, represented as .
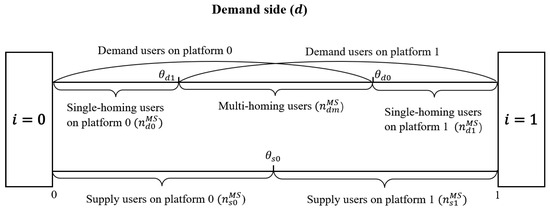
Figure 1.
Structure of the platform supply chain with “choose-one-of-two” enforcement.
Demand-side utility: As depicted in Figure 1, the points and represent the positions where the utility of demand-side users on platforms 0 and 1 is zero, respectively. If the position of a demand-side user in the market lies within the range , the user is single homed to platform 0. The utility of a single-homing demand-side user on platform 0 is given by
Equation (1) indicates that the utility of a demand-side user single homed to platform 0 is equal to the user’s preference for platform 0, plus the same-side and cross-side network effects gained from joining platform 0, minus the price paid. The same-side network effect is calculated as the same-side network strength multiplied by the scale of same-side users on the platform. The cross-side network effect is the cross-side network strength multiplied by the scale of opposite-side users on the platform.
Similarly, if falls within the range , the user is multi-homed to both platforms. The utility for a multi-homing user is given by
If is within the range , the user is single homed to platform 1. The utility of a single-homing demand-side user on platform 1 is
Supply-side utility: As illustrated in Figure 1, the utility of supply-side users is equal at the point , where a user’s location within the interval implies single homing to platform 0, and within to platform 1. Their utilities are as follows:
Unlike the utility expressions for demand-side users, supply-side users are negatively impacted by same-side network effects due to competition and congestion.
Pricing and profit analysis: Given that and are points where the utility of demand-side users on platforms 0 and 1 is zero, by setting in the utility functions (1) and (3), we obtain
From consumer utility theory, users only join a platform if their utility is positive, hence , , .
At the point , the utility of suppliers on both platforms is equal, so
with and . By combining Equations (6)–(8), the market share expressions for two-sided users on both platforms are
where .
The platform’s revenue is
The total utility for the demand-side user group in the market is
The total utility for the supply-side user group in the market is
The total revenue for the platform supply chain is
Proposition 1.
Under the condition where platforms enforce a “choose-one-of-two” policy, an equilibrium exists if the following condition is met: and . The equilibrium pricing for demand-side users by the competing platforms is , and for supply-side businesses, . At equilibrium, the number of multi-homed demand-side users is , and the single-homed supply-side is . The platform’s profit is . The derivation of these results is detailed in Appendix A.
According to Proposition 1, in equilibrium, the market shares of the two platforms are symmetrically distributed. This means that the supply-side market is equally split between them, and each platform retains an equal number of exclusively affiliated demand-side users, along with a shared segment of multi-homing demand-side users. The number of multi-homing demand-side users on the platforms is directly proportional to the strength of cross-side network effects and demand-side same-side network strength, but it is independent of the supply-side same-side network strength. The pricing for demand-side users by the platforms is influenced only by cross-side network effects, leading to the platforms charging fees to these users. In contrast, pricing for supply-side users is affected by both same-side and cross-side network effects. When , indicating intense competition among supply-side users, the platforms charge fees to supply-side users. Conversely, when , suggesting strong positive network effects between users on both sides of the platform, the platforms provide subsidies to supply-side users. Inserting the results from Proposition 1 into Equations (11)–(13) yields Proposition 2. The derivation process for this is not repeated here for brevity.
Proposition 2.
With the implementation of a “choose-one-of-two” policy and given the condition that an equilibrium solution exists, the total revenues for the demand side, supply side, and the entire platform supply chain in the market are
Proposition 2 indicates that the total revenue for the demand side in the market is independent of the same-side network strength among supply-side users on the platform. This suggests that the intensity of competition among supply-side users does not impact the pricing for demand-side users and the overall revenue for the demand side. According to supply and demand theory, demand-side participants benefit from intense competition among supply-side users. However, when platforms enforce a “choose-one-of-two” policy, the more intense the competition among supply-side users, the higher the fees platforms charge supply-side users, while pricing for demand-side users remains unchanged. Consequently, the monopolistic actions of the platform encroach upon the welfare that should belong to demand-side users and adversely affect the utility of supply-side users.
In scenarios where platforms enforce a “choose-one-of-two” policy, the equilibrium pricing, market share, and revenue of the platforms are influenced by network effects from both sides. By analyzing the partial derivatives with respect to these network effects, the following insights emerge:
- (1)
- , , , , ;
- (2)
- , , , , , ;
- (3)
- , , ; .
Enforcing a “choose-one-of-two” policy means that platforms’ pricing is directly influenced by cross-side network effects. Increased cross-side strength on the demand side leads to more multi-homing and a higher total user count, while supply-side numbers stay constant. To balance this, platforms raise prices for demand-side users and lower them for supply-side users to encourage better service provision. As supply-side cross-side strength grows, so does the tendency for supply-side multi-homing, prompting platforms to reduce prices for all users to maintain or grow their user base. Demand-side pricing is not influenced by same-side network effects, whereas supply-side pricing negatively correlates with demand-side same-side strength and positively with its cross-side strength. This dynamic ensures that platforms adjust supply-side prices downward to balance increased demand-side users. Increased same-side strength among supply-side users, indicating heightened competition, allows platforms to charge more, potentially raising their revenue. However, as the number of multi-homing demand-side users increases with cross-side strength, platforms moderate their pricing, which might slightly decrease revenue.
Similarly, the impact of two-side network strength on the revenues of both user groups and the total revenue of the platform supply chain is derived from analyzing the partial derivatives with respect to these network effects:
- (1)
- , , , ;
- (2)
The signs of the results derived from partial derivatives regarding the two-sided network strengths are uncertain and will be explored in the numerical simulation section. The analysis indicates that positive network effects on the platform benefit the total revenue of suppliers, while negative network effects adversely impact it. Given the assumption that both platforms cover the entire market, implying a fixed total market capacity, stronger positive network effects enhance user utility and, consequently, increase total supplier revenue. Competition among supply-side users fosters platform growth but negatively affects the revenue of supply-side users and the overall platform supply chain. Monopolistic actions by platforms disrupt market competition, harming overall social welfare. Hence, regulatory oversight on platform monopolistic practices is essential.
3.2. Without “Choose-One-of-Two” Enforcement Scenario (MS)
In this scenario, platforms are restricted from enforcing the “choose-one-of-two” policy following antitrust regulations that aim to maintain market stability and protect consumer interests. Regulatory bodies emphasize the need for lawful platform operations. With the regulation in place, supply-side users are no longer obligated to choose exclusively between platforms, leading to a situation where both demand and supply sides engage in partial multi-homing. As depicted in Figure 2, while the demand-side user affiliation remains akin to that seen in Figure 1, a notable difference is that the supply side on platforms now includes both single-homing users and multi-homing users , unlike in Figure 1, where all supply-side users were single homed.
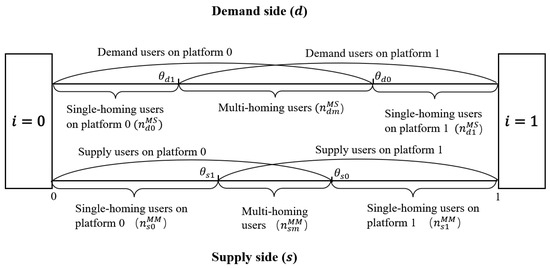
Figure 2.
Structure of the platform supply chain without “choose-one-of-two” enforcement.
Demand-side utility: As shown in Figure 2, the setup for demand-side users is akin to Figure 1, with users either exclusive to platform 0 or platform 1 or multi-homing across both. The points and indicate where the utility for demand-side users on platforms 0 and 1, respectively, drops to zero. Consequently, users within the intervals , , and are singly affiliated with platform 0, multi-homed across both platforms, and singly affiliated with platform 1, with their utilities calculated as follows:
The distinction in Equation (14) from Equation (1) lies in the cross-side network effect being the product of cross-side network strength and the sum of both single-homed and multi-homing users on the opposing side .
Supply-side utility: In contrast to Figure 1, Figure 2 includes both single-homed () and multi-homing () supply-side users. The points and mark where the utility of supply-side users on platforms 0 and 1, respectively, falls to zero. Within the intervals , , and , supply-side users are singly affiliated with platform 0, multi-homing across both platforms, and singly affiliated with platform 1, with their utilities expressed as
where: , .
Setting , , , and in Equations (14), (16), (17) and (19), we obtain:
Here, and .
Pricing and revenue analysis: By solving Equations (20)–(23) together, we derive the market shares for both single-homed and multi-homing users on the two platforms as follows:
The profits for platforms are
The total utility for demand-side users in the market is
The total utility for supply-side users in the market is
The overall revenue for the platform supply chain is
Proposition 3.
After platforms stop enforcing a “choose-one-of-two” policy, the existence of an equilibrium in the platform supply chain depends on several conditions: (1); (2); (3). The equilibrium pricing for demand-side users is , and for supply-side users, it is . At equilibrium, the number of multi-homing demand-side users is , and for multi-homing supply-side users, it is , with the platform’s revenue given by,.
Proposition 3 suggests that when platforms do not mandate a “choose-one-of-two” policy for supply-side users, in a competitive equilibrium, the platforms are symmetrical in terms of both pricing for users on both sides and their respective market shares. Differing from the previous scenario, here, the equilibrium pricing is influenced by a combination of cross-side and same-side network strengths. Platforms charge fees to demand-side users when , indicating lower same-side network strengths among users; otherwise, platforms offer subsidies. Similarly, platforms charge fees to supply-side users when , a condition reflecting lesser same-side and greater cross-side network strengths; otherwise, subsidies are provided. Proposition 4 is derived by applying the results from Proposition 3 into equations for total utility and profit, the details of which are not reiterated here.
Proposition 4.
Without the “choose-one-of-two” policy enforcement, the total revenues for both sides of the market and the entire platform supply chain are
where;; and .
When platforms do not enforce a “choose-one-of-two” policy, their pricing strategies, market shares, and revenues are impacted by the network effects from both sides. The results from analyzing the partial derivatives of these elements with respect to the network strengths are as follows:
- (1)
- When , We can obtain: , , , , ;
- (2)
- , , , ;
- (3)
- , , , , ;
The impact of two-sided network strengths on certain variables remains uncertain and will not be discussed here. From the analysis, it is clear that as the same-side network effects change for users on both sides, platforms invariably raise prices for one group while reducing them for the other. The strength of same-side network effects on the demand side is directly proportional to the number of multi-homing users on both sides, whereas it is inversely proportional on the supply side. Platform revenue is positively correlated with positive network strength and negatively with negative network strength. This outcome contrasts with the scenario where platforms enforce or do not enforce a “choose-one-of-two” policy, indicating differing impacts of network effects on platform revenue under various enforcement conditions. Hence, a further comparative analysis of these dynamics is essential.
4. Numerical Analysis
The preceding discussion provided insights into the equilibrium outcomes for platform pricing and the equilibrium responses of participants within the platform supply chain, both before and after the enforcement of a “choose-one-of-two” policy. Next, we will compare the equilibrium solutions under both scenarios to further explore the impact of the “choose-one-of-two” policy and two-sided network effects on the platform supply chain.
Table 2 illustrates changes in market share for users on both sides when platforms enforce or do not enforce the “choose-one-of-two” policy. Without this enforcement, multi-homing users on both the supply and demand sides increase, while single-homing users decrease. The rise in supply-side multi-homing users attracts more demand-side users to multi-home, adversely affecting platform revenue. Thus, platforms enforce the “choose-one-of-two” policy to secure more single-homing sellers and buyers, thereby maximizing revenue from exclusive users and gaining a competitive edge. Section 3.2 reveals that when the “choose-one-of-two” policy is banned, the demand-side same-side network strength is proportional to the number of multi-homing users, while the supply-side same-side network strength is inversely proportional. Consequently, enhancing the supply-side same-side network strength after the ban can reduce multi-homing users and increase single-homing users. Hence, even after antitrust interventions, intense competition among sellers can strategically benefit the platform.

Table 2.
Changes in equilibrium market shares of users with and without the “choose-one-of-two” policy.
Next, we examine the relationship between changes in dual-side pricing and network strengths, setting parameters following the methodology of Xie et al. [6]. For analyzing the impact of same-side network effects, we set , ; for cross-side effects, we set , . Based on the conditions for the existence of an equilibrium solution, the results of the numerical simulations are as follows.
Figure 3a,b showcase the relationship between demand-side pricing adjustments and both same-side and cross-side network strengths after the “choose-one-of-two” policy is prohibited. Once platforms permit multi-homing for supply-side users, the adjustments in demand-side pricing largely hinge on the comparative cross-side network strengths of users on both sides. This means that platforms adjust demand-side pricing based on the supply-side user dynamics. If the demand-side’s cross-side network strength exceeds that of the supply side (), the absence of a “choose-one-of-two” policy results in higher equilibrium pricing for demand-side users; otherwise, it results in lower pricing. Figure 3b illustrates that without the “choose-one-of-two” policy, greater cross-side network strength on the supply side leads to lower demand-side pricing, indicating that platforms reduce charges for demand-side users when they have a stronger attraction to the supply side. Conversely, Figure 3a indicates that the same-side network effects of both sides influence demand-side pricing. Without the “choose-one-of-two” policy, stronger same-side network effects among demand-side users lead to lower pricing, whereas increased same-side network effects among supply-side users result in higher demand-side pricing adjustments.
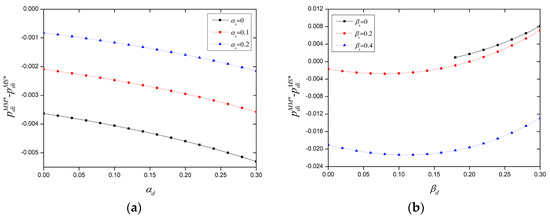
Figure 3.
Impact of same-side network strength (a) and cross-side network strength (b) on demand-side pricing.
Figure 4a,b illustrate how platform pricing for supply-side users (such as merchants, gig drivers, etc.) changes in relation to same-side and cross-side network strengths in the absence of a “choose-one-of-two” policy. The impact on pricing changes for supply-side users is significantly more pronounced than for demand-side users following antitrust actions. Allowing multi-homing for supply-side users leads platforms to reduce prices to prevent them from switching allegiance. Figure 4a shows that as the attractiveness among demand-side users increases, or the same-side network strength on the demand side grows, the extent of price reduction for the supply side decreases. Conversely, more intense competition among supply-side users, indicated by greater same-side network strength, leads to lower pricing for these users. This outcome contrasts with the scenario before antitrust enforcement, as intense competition among supply-side users after antitrust interventions encourages multi-homing behaviors, prompting platforms to lower their fees to retain them. Figure 4b suggests that larger cross-side network strengths lead to smaller price reductions for supply-side users. This indicates that the presence of cross-side network effects plays a crucial role in maintaining pricing stability for users on both sides of the platform.
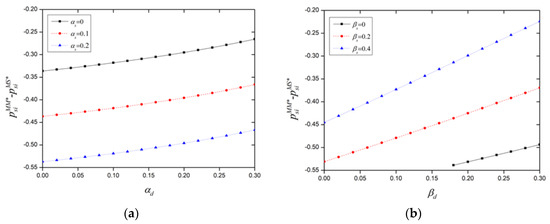
Figure 4.
Impact of same-side network strength (a) and cross-side network strength (b) on supply-side pricing.
Figure 5a,b demonstrate the relationship between platform revenue changes and both same-side and cross-side network strengths after the abolition of the “choose-one-of-two” policy. A pronounced same-side network effect on the supply side leads to a preference for multi-homing among supply-side users, causing a decrease in platform revenue. Figure 5a illustrates that platform revenue declines more significantly when the same-side network strength of demand-side users decreases or the same-side network strength of supply-side users increases in the absence of a “choose-one-of-two” policy. Figure 5b indicates that after allowing multi-homing for supply-side users, smaller cross-side network strengths lead to greater declines in platform revenue, whereas greater cross-side network strengths result in increased platform revenue. Hence, after antitrust interventions, platforms should enhance cross-side network effects and offer discounts or subsidies to supply-side users to boost their utility and, in turn, protect the platform’s interests.
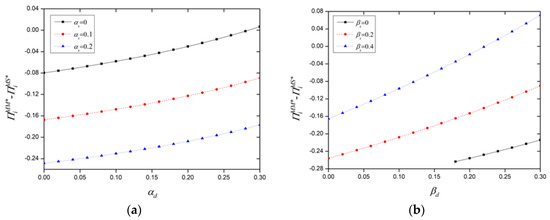
Figure 5.
Impact of same-side network strength (a) and cross-side network strength (b) on platform revenue.
Figure 6a,b explore how demand-side total revenue changes with variations in same-side and cross-side network strengths after platforms discontinue enforcing a “choose-one-of-two” policy. From Figure 6a, it is observed that with multi-homing allowed for supply-side users, demand-side total revenue shows a negative correlation with the same-side network strength of supply-side users when demand-side network strength is low. As the demand-side same-side network strength reaches a threshold, a decrease in supply-side same-side network strength leads to reduced demand-side total revenue. Figure 6b reveals that after the removal of the “choose-one-of-two” mandate for supply-side users, if the cross-side network strength of supply-side users increases while the demand-side cross-side network strength is low, the total revenue for demand-side users increases; this trend reverses when the demand-side cross-side network strength crosses a certain threshold. These findings suggest that after abandoning the “choose-one-of-two” policy, the interplay between same-side and cross-side network strengths critically influences the total revenue of demand-side users, highlighting the nuanced dynamics of platform economies in a multi-homing context.
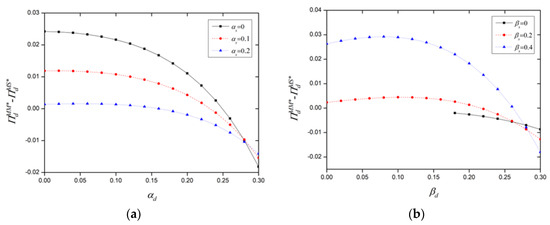
Figure 6.
Impact of same-side network strength (a) and cross-side network strength (b) on demand-side revenue.
Figure 7a,b depict the relationship between the total revenue of supply-side users and both same-side and cross-side network strengths. Following the government’s prohibition of platforms’ “choose-one-of-two” policies, there is a significant increase in the total revenue for supply-side users. Furthermore, as the same-side network strength of supply-side users increases, and the other three network effect parameters decrease, the total revenue for supply-side users experiences greater growth.
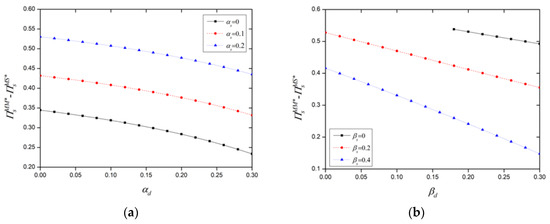
Figure 7.
Impact of same-side network strength (a) and cross-side network strength (b) on supply-side Revenue.
Figure 8a,b show the total revenue changes for all participants in the platform supply chain in relation to same-side and cross-side network strengths. These figures illustrate an increase in total revenue across the platform supply chain following antitrust measures. Figure 8a reveals that, in the absence of a “choose-one-of-two” policy, the total revenue for the platform supply chain is negatively correlated with the same-side network strength of supply-side users. Stronger same-side network effects among demand-side users increase total revenue when the demand-side’s same-side network strength is low. However, as this strength surpasses a certain threshold, further increases in the demand-side’s same-side network strength actually decrease total supply chain revenue. Conversely, Figure 8b shows that without the “choose-one-of-two” policy, the total revenue for the platform supply chain positively correlates with the cross-side network strengths of users on both sides. Therefore, enhancing the cross-side network effects of both user sides and reducing the same-side network strength of supply-side users can benefit the overall revenue of the platform supply chain.
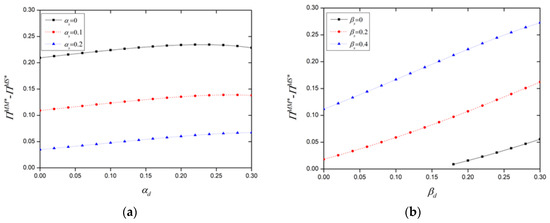
Figure 8.
Impact of same-side network strength (a) and cross-side network strength (b) on total revenue of platform supply chain.
5. Conclusions
This paper develops a horizontal differentiation model that delves into the nuanced dynamics of “choose-one-of-two” strategies within two-sided platforms. It reveals the complex interplay between positive and negative network effects, with significant implications for platform economics and supply chain welfare. By analyzing platform behaviors before and after antitrust interventions, the study uncovers strategic adjustments in pricing and their impacts on user multi-homing tendencies, as well as variations in platform and stakeholder revenues. The proposed model offers several advantages over existing models. It comprehensively considers both same-side and cross-side network effects and is applicable to dual-oligopoly contexts. Unlike traditional models, our approach captures the dynamic interactions between different user groups, providing a more realistic depiction of platform economics.
The main conclusions of this study are as follows:
- Impact of “choose-one-of-two” strategy: When platforms enforce the “choose-one-of-two” strategy, positive network effects between users lead to more multi-homing on the demand side, reducing platform revenue. This aligns with Armstrong’s [17] competitive bottleneck model and the findings of Xie et al. [6]. However, our study emphasizes that intensified negative network effects compel platforms to raise prices for supply-side users to increase revenue, which reduces welfare for demand-side users—an aspect not covered in other literature.
- Post-antitrust scenario: In the absence of the “choose-one-of-two” strategy, similar to the MH-MH scenario in Xie et al. [6], we compared the changes for platform supply chain participants before and after antitrust interventions. We found that when the same-side network strength varies for both user sides, the platform typically increases prices for one side while decreasing prices for the other. More multi-homing supply-side users attract more multi-homing demand-side users. The impact of bilateral network effects on platform revenue differs before and after enforcing the “choose-one-of-two” policy.
- Equilibrium pricing without “choose-one-of-two”: Without the “choose-one-of-two” requirement, the platform’s equilibrium pricing for demand-side users remains largely unaffected, while prices for supply-side users decrease. The smaller the positive network strength between user sides, the more intense the competition among supply-side users, leading to greater price reductions for them. Platform revenue does not necessarily decrease without the “choose-one-of-two” strategy. When positive network effects between users are strong enough, platform revenue may increase. Additionally, without “choose-one-of-two”, both supply-side user and platform supply chain total revenues increase. The weaker the positive network effects or the more intense the competition among supply-side users, the greater the revenue increase for supply-side users and the smaller the increase in total supply chain revenue.
Our strategic recommendations align with real-world examples such as Alibaba’s adjustments and findings by Sui et al. [12] and Zhu and Iansiti [10], highlighting the importance of strategic innovations in response to regulatory changes.
This study provides insights into the impact of network effects on dual-oligopoly platform markets. However, several limitations warrant further investigation. First, it simplifies real-world pricing strategies to fee-only models. Future research should explore competitive and cooperative dynamics under various pricing models across multiple oligopolies. Second, our analysis assumes symmetric platforms, while real-world platforms often differ in technological capabilities [29] or initial user base advantages [30]. Investigating “choose one from two” behaviors in asymmetric platforms and related antitrust implications is a valuable future direction. Finally, we assume that supply-side sellers are interchangeable, with negative same-side network effects. However, according to Carroni et al. [31], high cross-network externalities from a super seller can benefit other sellers, creating ripple effects that attract high-cost sellers to the platform. Future research should classify supply-side sellers based on their impact on consumers and examine the effects of such heterogeneity, as well as the associated regulatory policies. By addressing these limitations, future research can provide a more comprehensive understanding of the dynamics in platform markets and inform more effective regulatory strategies.
Author Contributions
Conceptualization, H.C. and Q.X.; methodology, H.C. and Q.X.; software, H.C.; validation, H.C. and Q.X.; formal analysis, H.C.; investigation, H.C.; writing—original draft preparation, H.C.; writing—review and editing, H.C.; project administration, Q.X.; funding acquisition, Q.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Social Science Fund of China (Grant No. 21BGL014).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Proof of Proposition 1.
Given , deriving with respect to platform pricing yields the following partial derivatives and conditions for a profit-maximizing equilibrium:
The conditions derived from the Hessian matrix are as follows:
To ensure a feasible market share of multi-homing on the demand side within (0,1), we require . Thus, the existence conditions for an equilibrium solution are and .
By setting the first-order derivatives of platform profit with respect to pricing to zero, the equilibrium prices are determined as follows: , .
Incorporating these equilibrium prices into the model reveals the following: the proportion of demand-side users who multi-home, ; each platform secures half of the single-homing supply-side market, with . This leads to a calculated platform profit of □
Proof of Proposition 3.
Given , deriving with respect to platform pricing yields the following partial derivatives and conditions for a profit-maximizing equilibrium:
From the constraints of the Hessian matrix and the multi-user ownership on the demand and supply sides greater than 0, it can be concluded that
The existence conditions can be obtained by solving the above equation system as follows:
The first-order partial derivative of platform profit to price is 0, and the equilibrium price can be obtained by combining the equations as follows:
By substituting the equilibrium pricing of the two platforms for bilateral users into Equations (24) and (25), it can be obtained that under the equilibrium situation, the number of multiple users belonging to the demand side is
The number of multiple users on the supply side is
The platform’s revenue is
References
- Hagiu, A.; Wright, J. Marketplace or reseller? Manag. Sci. 2015, 61, 184–203. [Google Scholar] [CrossRef]
- Evans, D.S. Some empirical aspects of multi-sided platform industries. Rev. Netw. Econ. 2003, 2, 191–209. [Google Scholar] [CrossRef]
- Eisenmann, T.R.; Parker, G.A.; Van Alstyne, M. Strategies for Two-Sided Markets. Harv. Bus. Rev. 2006, 84, 92–101+149. [Google Scholar]
- Thies, F.; Wessel, M.; Benlian, A. Network effects on crowdfunding platforms: Exploring the implications of relaxing input control. ISJ Inf. Syst. J. 2018, 28, 1239–1262. [Google Scholar] [CrossRef]
- Takigawa, T. What Should We Do about E-Commerce Platform Giants?—The Antitrust and Regulatory Approaches in the US, EU, China, and Japan. Social Science Research Network, 1 January 2022. [Google Scholar] [CrossRef]
- Xie, J.; Zhu, W.; Wei, L.; Liang, L. Platform competition with partial multi-homing: When both same-side and cross-side network effects exist. Int. J. Prod. Econ. 2021, 233, 108016. [Google Scholar] [CrossRef]
- Katz, M.L. Network externalities, competition, and compatibility. Am. Econ. Rev. 1985, 75, 424–440. [Google Scholar]
- Caillaud, B.; Jullien, B. Chicken & Egg: Competition among Intermediation Service Providers. RAND J. Econ. 2003, 34, 309. [Google Scholar] [CrossRef]
- Parker, G.; Van Alstyne, M.W. Two-Sided Network Effects: A Theory of Information Product design. Manag. Sci. 2005, 51, 1494–1504. [Google Scholar] [CrossRef]
- Zhu, F.; Iansiti, M. Entry into platform-based markets. Strateg. Manag. J. 2011, 33, 88–106. [Google Scholar] [CrossRef]
- Anderson, E.G.; Parker, G.; Tan, B. Platform performance investment in the presence of network externalities. Inf. Syst. Res. 2014, 25, 152–172. [Google Scholar] [CrossRef]
- Sui, R.; Zhang, X.; Dan, B.; Zhang, H.; Liu, Y. Bilateral value-added service investment in platform competition with cross-side network effects under multihoming. Eur. J. Oper. Res. 2023, 304, 952–963. [Google Scholar] [CrossRef]
- Reisinger, M.; Ressner, L.; Schmidtke, R. Two-Sided markets with pecuniary and participation externalities. J. Ind. Econ. 2009, 57, 32–57. [Google Scholar] [CrossRef]
- Rochet, J.C.; Tirole, J. Two-sided markets: A progress report. RAND J. Econ. 2006, 37, 645–667. [Google Scholar] [CrossRef]
- Rochet, J.C.; Tirole, J. Platform competition in Two-Sided markets. J. Eur. Econ. Assoc. 2003, 1, 990–1029. [Google Scholar] [CrossRef]
- Rochet, J.C.; Tirole, J. Tying in two-sided markets and the honor all cards rule. Int. J. Ind. Organ. 2008, 26, 1333–1347. [Google Scholar] [CrossRef]
- Armstrong, M. Competition in two-sided markets. RAND J. Econ. 2006, 37, 668–691. [Google Scholar] [CrossRef]
- Belleflamme, P.; Peitz, M. Platform competition: Who benefits from multihoming? Int. J. Ind. Organ. 2019, 64, 1–26. [Google Scholar] [CrossRef]
- Bryan, K.; Gans, J.S. A theory of multihoming in rideshare competition. J. Econ. Manag. Strategy 2019, 28, 89–96. [Google Scholar] [CrossRef]
- Bernstein, F.; DeCroix, G.A.; Keskin, N.B. Competition between Two-Sided platforms under demand and supply congestion effects. Manuf. Serv. Oper. Manag. 2021, 23, 1043–1061. [Google Scholar] [CrossRef]
- Bakos, Y.; Hałaburda, H. Platform Competition with Multihoming on Both Sides: Subsidize or Not? Manag. Sci. 2020, 66, 5599–5607. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, X.; Gu, Q. Pricing strategy and platform competition with partial multi-homing agents: When the aggregation platform exists in ride-sharing market. Transp. Res. Part E Logist. Transp. Rev. 2024, 184, 103483. [Google Scholar] [CrossRef]
- Armstrong, M.; Wright, J. Two-sided markets, competitive bottlenecks and exclusive contracts. Econ. Theory 2006, 32, 353–380. [Google Scholar] [CrossRef]
- Chellappa, R.K.; Mukherjee, R. Platform Preannouncement Strategies: The Strategic Role of Information in Two-Sided Markets Competition. Manag. Sci. 2021, 67, 1527–1545. [Google Scholar] [CrossRef]
- Ji, H.; Wang, X. Competition model of two-sided markets with platform differentiation and users partially multihoming. Syst. Eng.–Theory Pract. 2014, 34, 1398–1406. [Google Scholar]
- Jung, D.; Kim, B.C.; Park, M.; Straub, D.W. Innovation and Policy Support for Two-Sided Market Platforms: Can Government Policy Makers and Executives Optimize Both Societal Value and Profits? Inf. Syst. Res. 2019, 30, 1037–1050. [Google Scholar] [CrossRef]
- Dou, G.; Lin, X.; Xu, X. Value-added service investment strategy of a two-sided platform with the negative intra-group network externality. Kybernetes 2018, 47, 937–956. [Google Scholar] [CrossRef]
- Kurucu, G. Negative intra group network externalities in a monopolistic Two-Sided market. Rev. Netw. Econ. 2018, 17, 51–73. [Google Scholar] [CrossRef]
- Bedre-Defolie, Ö.; Biglaiser, G. Competition for exclusivity of a superior input and quality implications. Social Science Research Network, 1 January 2022. [Google Scholar] [CrossRef]
- Hagiu, A.; Lee, R.S. Exclusivity and control. J. Econ. Manag. Strategy 2011, 20, 679–708. [Google Scholar] [CrossRef]
- Carroni, E.; Madio, L.; Shekhar, S. Superstar Exclusivity in Two-Sided Markets. Manag. Sci. 2024, 70, 991–1011. [Google Scholar] [CrossRef]
- Shah, N.H.; Chaudhari, U.; Jani, M.Y. Optimal policies for time-varying deteriorating item with preservation technology under selling price and trade credit dependent quadratic demand in a supply chain. Int. J. Appl. Comput. Math. 2017, 3, 363–379. [Google Scholar] [CrossRef]
- Shah, N.H.; Chaudhari, U.; Jani, M.Y. Optimal down–stream credit period and replenishment time for deteriorating inventory in a supply chain. J. Basic Appl. Res. Int. 2015, 14, 101–115. [Google Scholar]
- Shah, N.H.; Chaudhari, U.; Jani, M.Y. Inventory control policies for substitutable deteriorating items under quadratic demand. Oper. Supply Chain. Manag. Int. J. 2019, 12, 42–48. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).