Abstract
Patient-generated health data (PGHD) have great potential to improve clinical outcomes. As providers consider whether and how to incorporate PGHD into their clinical workflows, platforms by Apple and Amazon stand to fundamentally alter the landscape. With the aim to examine the conditions under which providers would adopt PGHD and possibly sign on with a platform, we analyzed the incentives and optimal strategies of two healthcare providers, a monopoly platform, and consumers using stylized game-theoretic models and solve for potential equilibria. We found that consumer surplus always increased with PGHD adoption, but social welfare may drop. The larger provider had more incentive to adopt PGHD than the smaller provider, but these incentives were reversed in the case of platform adoption. Accordingly, the platform enrolled the smaller provider first and possibly both providers. The emergence of the platform raised provider surplus, potentially at the expense of the consumers, despite offering its service to them for free. These results illustrate the importance of economic incentives regarding whether and how PGHD could be incorporated into our current healthcare system.
1. Introduction
Wearable devices with continuous data collection, real-time analytics, and presentation of actionable health insights provide unprecedented opportunities for revolutionizing care in clinical and hospital settings. A typical fitness band monitors activity data, including the number of steps taken, floors climbed, calories burnt, heart rate, and sleeping patterns. Some of the measurable parameters also include blood pressure, pulse rate, muscle activity, perspiration level, glucose level, ECG, core temperature, oxygen saturation, stress levels, and eating habits. These patient-generated health data (PGHD) can serve to supplement clinical records to develop a longitudinal profile of patient health, as well as promote care coordination. Moreover, the COVID-19 pandemic demonstrated the importance of collecting and tracking PGHD via telemetry-enhanced smart technologies [1,2], especially for the older generation [3]. Clinical use of the data collected by wearable devices would present a more compelling value proposition for consumers, which is needed to ensure their sustained usage [4].
Empirical evidence shows that at least for some conditions, such as diabetes and high blood pressure, collecting and acting on PGHD improve clinical outcomes in cost-effective ways [5]. For example, health professionals at Cedars-Sinai Hospital use wearable technologies to track and improve recovery times for post-operative patients. The program includes patients who receive a fitness tracker after undergoing major surgery in order to track their physical activity. The tracker not only helps physicians measure the patient’s steps, but it also motivates users while improving the recovery process [6].
Surveys report substantial interest by both healthcare providers and consumers in incorporating PGHD into clinical care. According to the 2022 HIMMS Future of Healthcare Report, the majority of consumers, in the USA and globally, are willing to share their smartwatch and fitness tracker app data with their healthcare providers. In addition, health app usage to manage specific conditions is estimated to grow by 33% or more in the next three to five years [7]. HIMMS further noted that 79 percent of physicians would like to have more data about patients in between encounters, 72 percent agree that they need PGHD to make good decisions on chronic disease management, and 90 percent of the physicians incorporating wearable devices into the clinical workflow say that the technology can positively impact chronic care [8]. This would be a welcome change for consumers who increasingly demand a better digital experience, given that as high as 78 percent of tech-savvy consumers say the healthcare digital customer experience needs improvement, and half of them say they would leave their current physician for a better digital customer experience [9].
Federal and industry initiatives emphasize the seamless sharing of patient data for clinical care. The 21st Century Cures Act, which was signed into law in 2016, includes provisions on data sharing and interoperability to encourage the access, exchange, or use of electronic health data [10]. A proposed rule from the Centers for Medicare and Medicaid Services requires healthcare facilities to implement technologies that support open application programming interfaces that allow for real-time bidirectional data exchange between patients and providers [11]. These regulations are designed to accelerate the development of mobile health technologies that are compliant with PGHD interoperability standards [12]. Unfortunately, the electronic integration of PGHD into existing systems is still widely considered an important but largely unmet need [13] and simply an “aspiration” [14].
Big tech companies see the opportunity and have ramped up their efforts to fill the void. Apple embraced healthcare as the next big battleground in the tech world and has been aggressive with its Health initiative, as well as its very successful Apple Watch, which has increasingly become a health-oriented product. Google acquired Fitbit for $2.1 billion in 2019. Amazon recently entered the space with a new fitness band and health service known as Halo, which is designed to seamlessly integrate with Cerner’s electronic health record (EHR) software. Such integration enables users to feed health data, like body fat percentage, activity, and sleep data, directly to the EHR systems of their physicians. Sharp HealthCare, which is a San Diego-based provider and Cerner client, was the first health system to implement Halo in a clinical setting [15]. Accordingly, PGHD may be the perfect “Trojan horse” for the big platforms (i.e., Google, Apple, and Amazon) to expand their power to the healthcare sector at the expense of health care providers and possibly the consumers at large [16].
Against this backdrop, we took an analytical approach and asked the following research questions: Does a larger healthcare provider have more incentive to adopt PGHD than a smaller provider? What is the impact of the adoption of PGHD on consumer surplus and social welfare? What type of provider, large or small, would have more incentive to join a PGHD platform? What is the impact of the platform on provider profits and consumer surplus?
We took a game-theoretic approach to investigating these research questions. The analysis of our stylized models revealed that the consumer surplus always increases with PGHD adoption, but social welfare may drop. While the larger provider has more incentive to adopt PGHD than the smaller provider, these incentives are reversed in the case of platform adoption. Accordingly, the platform either enrolls just the smaller provider or both providers. The emergence of the platform raises the provider surplus, potentially at the expense of consumers, despite offering its service to them for free. Therefore, unless regulated and carefully monitored, platforms may expand their reach to the healthcare sector, further strengthening their already established monopolistic powers across many other industries [16].
Section 2 presents a brief review of the related literature. Section 3 presents game-theoretic models and their solutions with no PGHD, with PGHD, and with a PGHD platform, in that order. Section 4 provides a discussion of our findings and contributions to the literature. Section 5 presents the concluding remarks and limitations of this study.
2. Literature Review
The importance of the integration of healthcare data across providers was recognized by past information systems research [17,18]. What distinguishes this study is that we considered the integration of health data collected by consumers with healthcare data collected by providers. In this light, several research streams are relevant to this study. We believe the research on the adoption of wearable devices is the most relevant because PGHD are created and potentially streamed by such devices. Research on the privacy impacts of PGHD is also important because the sharing of such data, especially with a platform, has the potential to seriously elevate privacy concerns. Additionally, providers’ adoption of health information exchanges (HIEs) is a decision similar to the adoption of PGHD in that in both cases, healthcare providers consider sharing their patient data with a third party. In what follows, we briefly discuss some of the representative work in these domains and their relevance to the current study.
The information systems literature on the adoption of wearable devices is nascent but quickly growing. Healthcare is the predominant context for the studies in this research stream. From a methodological perspective, the most commonly used theories and frameworks in this domain are the technology acceptance model, diffusion of innovation theory, unified theory of acceptance and use of technology, and privacy calculus theory [19]. Using the technology acceptance model, Huarng et al. [20] found that the key factors that influence the intention to use wearable medical devices include economic cost, data privacy, perceived ease of use, and perceived usefulness. Pancar and Yildirim [21] used the unified theory of acceptance and use of technology to show that goal clarity and technology compatibility are determinants of behavioral intention to use wearable devices for health-tracking purposes. Using the same theory, Wang et al. [22] demonstrated that performance expectancy, effort expectancy, facilitating conditions, social influence, and task–technology fit positively affect consumers’ behavioral intention to use healthcare wearable devices. Binyamin and Hoque [23] used a similar methodology and found that performance expectancy, social influence, facilitating conditions, hedonic motivation, and habit significantly impact users’ behavioral intention to adopt wearable health monitoring technology. Zhang et al. [24] reported that the intention to adopt healthcare wearable technology is influenced by technical attributes, health attributes, and consumer attributes simultaneously. Li et al. [25] found that individuals adopt healthcare wearable devices if the perceived benefits are greater than the perceived costs—the perceived privacy risk in particular. Studies in this line of research use empirical methods and aim mainly to understand the factors that drive adoption among patients. In contrast, in this study, we used analytical methods to examine not just patients’ but also providers’ incentives to adopt PGHD.
Among analytical work, Wu et al. [26] investigated whether wearable device firms should employ a big data and analytics strategy and how much they should invest in such an initiative. They characterized the conditions under which firms would employ a conservative strategy versus an expansive strategy depending on the prevailing consumer density in the market. Wu et al. [27] examined the role of network externality on competition in the wearable device market and found a negative impact on firm profits, which is similar to our result that provider profits may drop as a result of PGHD adoption. Tarakci et al. [28] investigated the role of wearable devices in managing chronic conditions and found that their use in a clinical setting may increase the overall health conditions of patients, even when healthcare providers do not always utilize the most advanced technology. Wu et al. [29] examined the adoption of big data and analytics in the mobile healthcare market using a stylized two-dimensional product differentiation framework and they found that it is not optimal for all firms in the market to adopt these technologies, even though doing so improves social welfare. Similar to these studies, we confirmed that the incentive to adopt PGHD can vary, and not all firms (providers) may adopt it in equilibrium. On the flip side, this may not be all that bad because the adoption of PGHD by all parties may in fact reduce social welfare (see Proposition 2). In addition, we also found conditions under which all providers adopt PGHD and find themselves in a Prisoner’s dilemma (i.e., they are all worse off with PGHD and yet adopt it anyway given that others adopt). Furthermore, we also investigated the effect of a PGHD platform on provider profits, as well as consumer surplus, and found that the overall impact was positive, whereas the impact on consumer surplus was mixed.
Privacy risks and costs are an important theme among studies on the adoption of wearable devices for healthcare [30]. For example, Fox and Connoly [31] highlighted that the mobile health digital divide is deepening due to older adults’ perceived inability to adopt the technology and their unwillingness to adopt stemming from mistrust, high risk perceptions, and a strong desire for privacy. Becker et al. [32] developed a taxonomy that reveals that the most relevant dimensions of privacy risks regarding consumer health wearables are perceived data sensitivity, perceived data variety, and perceived tracking activity. Marakhimov and Joo [33] also found that consumers’ health and privacy concerns significantly impact the challenge and threat appraisals in the infusion of wearable devices for healthcare. Finally, Gabel et al. [34] showed, through a randomized controlled field experiment, that privacy concerns mediate individuals’ decisions to adopt personal electronic health records (one would expect this result to hold for PGHD as well).
The commonality of the studies on the adoption of wearable devices is that there are cost and benefit implications for consumers. Privacy costs loom large, especially in the healthcare context. Similarly, this study took into account a utility increase for consumers due to the improved monitoring of their condition by their providers, as well as a potential privacy cost. In addition, we considered the adoption cost that healthcare providers incur. All of these factors enter the consumers’ and providers’ decision mechanisms.
One notable aspect of this study was that it focused on the adoption decision of providers, whereas the extant research almost exclusively focused on the adoption of wearables by individuals, despite the fact that the providers’ perspectives are just as important, if not more. For wearable devices to make a true impact in the healthcare space, providers have to get on board. And for this to happen, it is essential that their economic incentives are accounted for. In this study, providers decide whether to integrate the PGHD being streamed from their patients’ devices into their EHR systems for monitoring purposes.
A few studies on the adoption of health information exchanges (HIEs) considered healthcare providers’ economic incentives. In this context, the HIE is the external party that providers decide whether to share their patients’ data with. Since HIEs are established mainly for medical purposes, sharing patient data with them does not trigger consumers’ privacy concerns in the same manner as it does with a third party, such as Google, which is purely driven by profit. Using a game-theoretic approach, Demirezen et al. [35] developed models to study the sustainability of HIEs and participation levels in these networks. They examined how heterogeneity among healthcare providers affects their participation in HIEs and found that the benefit the providers can get from the HIE might decrease the number of providers that want to join the HIE in a competitive equilibrium. Martinez et al. [36] noted that competition between hospitals, coupled with volume-based payment systems, creates no incentives for smaller hospitals to exchange data with competitors. They developed game-theoretic models to estimate the willingness of healthcare organizations to join an HIE network, and they found that a proposed federal penalty of up to USD 2,000,000 has a higher impact on increasing HIE adoption than current federal monetary incentives. Similar to these studies, this research emphasizes the importance of getting the provider incentives aligned with what improves social welfare (i.e., sharing patient data to improve health outcomes). Whereas these studies were concerned with the sharing of clinical data with a (typically) nonprofit HIE, this study focused on the sharing of patient-generated health data with a for-profit online platform. Furthermore, while these studies assumed the existence of digitized patient data on healthcare providers’ premises, we started from a baseline where PGHD are not shared with the providers at all and investigated whether the providers would be interested in storing this data on their premises. The question of whether such data should then be shared with a PGHD platform was examined after this initial analysis, assuming that the providers would adopt PGHD in the absence of a platform.
3. Models and Analyses
In this section, we present and then analyze a stylized game-theoretic model of a market with heterogeneous healthcare providers that allowed us to examine the optimal PGHD- and platform-adoption strategies in a competitive equilibrium. As is customary in game-theoretic analyses, each player maximized either a utility function (in the case of consumers) or a profit function (in the case of providers), while taking into account the best response of other players to the decisions that they make. An outcome that arises from a specific set of decisions made by the participating players is said to be an “equilibrium” when no player has an incentive to deviate from their decision. As we analyzed the potential equilibria, we also checked the impact of PGHD adoption on social welfare, which was the total aggregate surplus (utility and profit) in the market.
For comparison purposes, we first started with the case with no PGHD.
3.1. Benchmark Case: No PGHD
The market is composed of three types of players: providers, consumers, and a monopolist platform. There are two profit-maximizing providers (denoted with and ) who are differentiated with respect to their effectiveness in delivering healthcare. Factors such as past experience and available technology and resources may allow a provider to outperform others. Consequently, consumers derive different gross utilities when they receive care from the providers. We denote the gross utilities of receiving care from and by and , respectively, where without loss of generality.
In addition to effectiveness, the providers are also distinguished by the number of consumers for whom they have medical and health records on file. In what follows, we refer to the totality of medical and health records about a consumer as “digital records.” Each consumer starts the game as having been assigned to one of the providers. Hence, each consumer’s complete digital history is held by one of the two providers. We denote the proportion of digital consumer health records that has on file by .
Furthermore, the start of the game is characterized by a random “disturbance” to the consumers’ provider preferences. Such disturbances can arise because of changes in preferences, attitudes, situational conditions, etc. Healthcare is a service that can be considered as an experience good, and experiences affect and refine preferences. There can be a host of reasons as to why a consumer may want to end an established medical relationship with a provider. For example, preferences may change when a consumer relocates to a new area. The possibility of switching providers arising from the exogenous change in preferences at the outset of the game reflects the common phenomenon of patients who, for various reasons, consider obtaining healthcare from a different provider.
To characterize the change in consumer preferences at the beginning of the game, we assumed a randomly assigned and uniformly distributed disutility associated with each consumer. In other words, each consumer is randomly placed on a Hotelling-style linear city [0,1], regardless of their previously established provider relationship, while the providers were located at the two ends of the city (it is conceivable that in reality, a provider will have fewer patients who do not particularly favor them than those who do. The conceptualization could be generalized by assuming that the density of patients whose records reside with uniformly drop from at point 0 to at point 1, where . Although such a conceptualization is arguably closer to reality, it significantly complicates the analysis without adding any new insights). Accordingly, when a consumer receives care from a provider, they incur a utility loss equivalent to the distance on the linear city between her location and that of the provider due to this change in consumer preferences. We further assumed for simplicity and ease of exposition that the two segments of consumers (those who have their records with and ) are also uniformly distributed in the linear city. In doing so, we took the view that the disturbance to the consumer utility is independent of the likelihood of having digital records with a certain healthcare provider.
The process of seeking care from a new provider entails providing authorizations; establishing a medical and health history through transferring records from the previous provider to the new provider; filling out online forms at the new provider’s website; and repeating certain tests in case the previous test results are missing, incomplete, or simply deemed uninformative or unacceptable by the new provider. These tasks involve both pecuniary and non-pecuniary costs to the consumer. Especially in the case of emergencies during travel, these tasks may not be easily performed, in which case the patient may incur certain utility losses due to not getting the best treatment in the absence of pertinent information. We denote the expected cost of these tasks and situations to the consumer by and henceforth call it the “switching cost.” As we will see later, the switching cost can drop when providers can electronically share documents. In the analyses that follow, the consumers who consider receiving care from a new provider weigh the utility gain from switching to the new provider on the one hand and the associated cost of the process on the other. The sequence of events is illustrated in Figure 1.
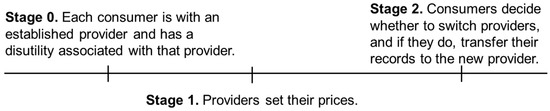
Figure 1.
The sequence of events in the benchmark case (no PGHD).
It is worth noting that taking as exogenous (1) the pre-existing provider–patient relationships and (2) the subsequent changes in consumer preferences allow for the characterization of a market with consumer switching behavior in equilibrium in a static model. An alternative approach would have been to set up a dynamic model where each period would be characterized by a new disturbance to consumer preferences. The static model presented here captures the essence of all the strategic elements that are needed to answer the research questions presented in Section 1 while maintaining simplicity and analytical tractability. When we introduce the availability of PGHD in Section 3, we compare the consumers’ switching behavior in that case versus the benchmark case presented here. That comparison is based solely on the impact of the adoption of PGHD on the equilibrium outcomes.
Solution and analysis: In order to find the market shares of each provider, we needed to determine the precise utility change (i.e., locations) of consumers who are indifferent between working with their established provider and switching to a new one.
For consumers whose health records are initially maintained by , the utility of obtaining care from the same provider is , where is the patient’s distance from the provider. Alternatively, these consumers can incur the cost to switch to and obtain the utility . Taking into account the prices charged by these providers, the location of the indifferent consumer who has an established relationship with satisfies
Similarly, for consumers whose records are initially maintained by , the location of the indifferent consumer (denoted with ) satisfies
Recall that the size of the first segment of consumers is . In the first segment, proportion of consumers continue to work with , while the rest switch to . In the second segment, proportion of consumers switch to , while the rest continue to work with . We assumed that there exists at least one consumer who switches from to and from to in equilibrium: . Thus, the providers’ profits are given as
Solving for and and the profit-maximizing prices, we found the optimal profits to be the following, where the superscript represents the benchmark case. Here, as well as later, all second-order conditions hold.
Note that the switching cost has opposite effects on the profits of the two providers. The provider that maintains fewer medical records at the beginning of the game benefits from a drop in the switching cost, while the other provider is harmed by it. This is because and for , and vice versa, assuming a positive market share for both providers in equilibrium. We also found that the number of patients that switch to and are and , respectively. The rate of switching increases with the difference in utility that one provider offers with respect to the other and decreases with the cost of switching. The consumer surplus is calculated as follows:
3.2. The Availability and Providers’ Adoption of Patient-Generated Health Data
Much like the emergence of the genome, the proteome, and the microbiome, telemedicine and electronic health records are leading the emergence of the digitome—how patients’ digital records are used for diagnostic predictions and how patients respond to their therapies [37]. In our context, the providers have the option to integrate and aggregate their patients’ PGHD on their EHR systems and monitor them at a cost denoted with . We call this option the “adoption of PGHD on-premise.” This service benefits the patients of the adopting provider and increases their gross utility of receiving care there. The service is costly to the provider because, in addition to any necessary investment needed for the existing EHR infrastructure to handle the new data, there is also a need to develop stringent quality, supervision, and training programs to manage patient- and provider-specific risks associated with the storage and usage of PGHD. In particular, patients may pose a barrier to healthcare providers’ participation in PGHD due to various concerns, including issues related to trust, privacy, security, and identity (we thank an anonymous referee for this insightful comment) [38].
The increase in utility depends on the nature of the provider–patient relationship. The utility increases more if the service is obtained from the established provider than when it is obtained from a new provider , where , unless the patient transfers any existing PGHD from the previous provider to the new provider. If both providers offer the PGHD service and the patient switches providers, then they may transfer any existing PGHD from the previous provider to the new provider at a cost denoted with (this is in addition to the cost associated with switching providers). In other words, the adoption of PGHD increases the switching cost for patients since additional data need to be transferred to the EHR system of the new provider for the patient to receive a similar service there. Subject to such a transfer, which we assumed to increase the utility , the patient obtains the full utility increase with the new provider’s PGHD service.
Solution and analysis: Each provider decides whether to adopt PGHD, resulting in a total of four potential outcome combinations. Thus, there are three new scenarios to consider. The solution methodologies for these scenarios are similar to the one provided above. For example, when only adopts PGHD, equations (1) and (2) above become
In Equation (7), the left-hand side of the equation has the additional utility because the established patients of benefit more from PGHD adoption compared with the patients who recently switched from and get the additional utility shown on the left-hand side of Equation (8).
The case where only adopts PGHD is symmetric to the above, and in the case where both providers adopt PGHD, these equations become
The optimal outcomes for the providers in all these cases are presented in Table 1, where . denotes the advantage has over due to offering a more valuable service and having a larger established clientele by . The upper and lower expressions in each cell are the profits of and , respectively. As can be seen, the adopting provider potentially increases its profit subject to the implementation cost being low enough.

Table 1.
Provider profits for various PGHD adoption scenarios.
We now investigate the providers’ incentives to aggregate their patients’ PGHD, which, as we will see, may indeed occur in equilibrium. However, we would like to first introduce a lemma that suggests that a provider’s decision to adopt PGHD may be negatively impacted by its competitor’s adoption. In other words, if a provider has the incentive to adopt PGHD when its competitor also adopts them, the provider will continue to have the incentive to adopt PGHD when its competitor does not adopt them.
Lemma 1.
The incentive to aggregate and monitor PGHD is smaller when the competing provider adopts PGHD than when it does not.
Lemma 2 outlines which of the two providers is likely to have a larger incentive to adopt PGHD. The larger the market share, the easier it is for a provider to recoup the cost of aggregating and monitoring their patients’ PGHD. Since the provider that offers more utility to its patients is guaranteed to command a larger share of the market if it starts the game with a larger base of patients, it will also have a larger incentive to adopt PGHD than its competitor.
Lemma 2.
The better/larger provider has a larger incentive to aggregate and monitor PGHD.
For ease of exposition, we henceforth consider the more realistic case where (since the services of a better provider will be utilized more). Let , which is always positive. is a measure of the advantage has over due to offering a more valuable service and having a larger established clientele . Also, let , where and . is a measure of the weighted average utility gain for ’s patients when it adopts PGHD. The larger the established clientele for , the larger the weighted average utility gain.
Proposition 1.
If , then neither provider adopts PGHD. If , then only adopts PGHD. If , then both providers adopt PGHD.
As expected, the adoption of PGHD is more likely with a small implementation cost and a large incremental surplus for consumers due to adoption. We also observed that adoption by both providers is facilitated by a lower cost of transferring PGHD and a lower level of differentiation between providers in terms of taste, quality, and market share.
Note also that the providers make the same profit when they both adopt PGHD and when neither adopts them, but in the former case, providers incur the additional implementation cost. In other words, the adoption of PGHD puts the providers in a worse situation than the benchmark case. Using economic terminology, this represents a Prisoner’s dilemma for the providers—either would be better off not adopting PGHD, but competitive pressures force them to do so regardless. The benefits of PGHD adoption are completely absorbed by the consumers.
Proposition 2.
The adoption of PGHD always raises the consumer surplus. However, when the PGHD adoption cost is high, the utility of the new service to the patients is low, and when the cost to transfer PGHD between providers is low, social welfare may drop with the adoption of PGHD.
The consumer surplus increases with the utility coming from the improved service , while provider surplus decreases with the cost of PGHD implementation . Comparing the benchmark case and the case where both providers adopt PGHD, all consumers get the additional utility after adoption. ’s patients pay extra, while ’s patients pay less in equilibrium with PGHD compared with the benchmark case. Also, consumers who switch providers incur the extra switching cost . Given that , the net benefit to consumers ( less a fraction of ) is positive. The optimal prices are provided in Appendix A in Equations (A5) through (A10).
We also found that the provider surplus increases with the cost of transferring PGHD . This is because ’s profit decreases with , while ’s profit increases with it. Comparing the profits in Table 1 when neither provider adopts PGHD and when they both adopt, ’s profit increases more than that of with respect to their profits in the benchmark case. The difference in differences of profits compared with the case with no PGHD adoption equals , suggesting that higher values of benefits more than it sets back from a competitive perspective.
Social welfare is the sum of consumer surplus and provider profits, and it may drop for high values of and low values of and . We calculated the consumer surplus using Equation (6) for the benchmark case and similarly for other cases.
3.3. The PGHD Platform
We introduce the emergence of a platform in this section while keeping the possibility of providers integrating PGHD into their EHR systems themselves. Similar to Amazon Halo, a PGHD platform (henceforth referred to as “the platform”) offers an online data aggregation service to patients and providers. The data is encrypted and stored in the cloud in a format that readily integrates with the providers’ EHR systems. The main benefit of this service is that it provides patients with up-to-date online and secure access to their complete PGHD collected from various devices, wearable or otherwise. However, the online storage of health records, especially by a platform, may exacerbate consumers’ privacy concerns [39], and we denote the associated cost with . Granted, consumers may also experience a privacy loss when they share their PGHD with only their provider. However, because a platform can easily develop and offer value-added services using consumer health data, with or without the use of third parties, the privacy loss is typically greater than that in the case of sharing PGHD with a healthcare provider. When it comes to consumer psychology, it does not always matter what the platform can or cannot do legally; what really matters is what the platform can do with consumer health data in the presence of perceived ineffective or incomplete governmental regulation and/or potential noncompliance. Accordingly, we assumed that the utility loss in the latter case is zero.
To offer patients this value-added service, each provider should first sign up with the platform by paying the fee . A fixed fee implies that the platform does not price discriminate between providers. We later relaxed this assumption and allowed for price discrimination, which is equivalent to charging a price as a function of provider characteristics, including the number of patients being cared for.
After paying the platform fee, consumers can then establish an account with the platform and start aggregating their data in the cloud, knowing that their provider will have access to their data. Because this is a value-added service, we assumed that individuals derive a net utility benefit from the PGHD adoption and, therefore, always accept the service whenever their provider makes it available, despite the privacy loss (i.e., is sufficiently small). By strategically positioning itself between patients and providers, the platform can act as the intermediary as far as PGHD are concerned.
The platform takes on the responsibility of developing the technological infrastructure that enables the automatic transfer of patients’ PGHD from the cloud to the providers’ EHR systems. Having a platform account eliminates the cost a patient incurs when transferring their PGHD to a new provider () when both providers are on the platform. All the patient needs to do in this case is to grant appropriate access rights to the new provider. If the new provider has not joined the platform, they can download the records and email them to the provider or bring physical copies in person. We assume that the cost of transferring records in this fashion is still .
Assuming that the providers handle PGHD integrations themselves in the absence of a platform, the sequence of events is as follows. In the first stage, consumers are assigned to their providers with an associated disutility. In the second stage, the platform announces the price that it charges to providers for its service (). In the third stage, providers simultaneously decide whether to aggregate their patients’ PGHD themselves or whether to join the platform. They then announce their prices ( and ) for delivering healthcare. Finally, given the switching costs and PGHD strategies of the providers, consumers decide which provider to work with and transfer their records if necessary. These stages are illustrated in Figure 2.
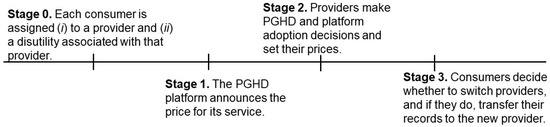
Figure 2.
The sequence of events with PGHD and a PGHD platform.
Solution and analysis: A provider would either join the platform or handle the integration itself; it would not do both. The benchmark case in this section is the one where both providers handle PGHD integrations themselves, for which we have established provider profits (see Table 1):
where the arguments of the profit expressions indicate the platform adoption decisions of providers (J for “join” and NJ for “do not join”; the first argument is for and the second one is for ). Since both providers adopt and monitor PGHD, all consumers receive the full associated utility increase . As we have seen in Proposition 1, the providers find themselves in this equilibrium when is sufficiently small. Even if PGHD integration costs are not sufficiently small to lead to such an equilibrium today, we expect that Moore’s law will all but guarantee it in the not-too-distant future. We later compare the platform’s impact with the case when the providers’ benchmark decision is not to adopt PGHD at all.
The platform knows that it should structure its service in an attractive way to the providers. When a provider joins the platform, it gains access to the PGHD of its patients stored in the cloud and can then monitor patients remotely, thereby improving clinical outcomes and the value of its service as perceived by the patients. When both providers join the platform, then the sharing of PGHD between providers becomes seamless (). Since providers will join the platform as long as doing so will improve their bottom line, and because they still have the option to integrate PGHD into their EHR systems, the platform has to make sure that providers are better off with the platform than without it in pricing its service. The platform charges to providers and offers its service to consumers free of charge. This is in line with the freely available services, such as Apple’s Health app. The alternative would require the platform to charge both the providers and consumers, which would limit the providers’ ability to raise their prices in return for their platform adoption.
There are three possibilities regarding who joins the platform: (i) only , (ii) only , and (iii) both and . Recall that has more incentive to monitor PGHD than according to Lemma 2. The ability to offer the value-added service of monitoring PGHD to a larger group of patients means a larger economic incentive to make such an investment. We have seen that this is due to offering a more valuable service to a larger patient segment. It may be tempting to think that should have more incentive to join the platform than as well since the same incentive structure should be in play regardless of whether PGHD integration is executed on-premise or acquired through a platform. This was also our initial expectation. However, we will see that this is not necessarily true.
Suppose that only and its patients join the platform. Recall that these patients incur the privacy cost . Among the consumers whose records are initially maintained by , the location of the one (denoted with ) who is indifferent between continuing with and switching to satisfies
For consumers whose records are initially maintained by , the location of the consumer (denoted with ) who is indifferent between continuing with and switching to satisfies
The profit expressions are the same as in Equations (3) and (4). Solving for and and the profit-maximizing prices, we found the optimal profits to be the following:
where is the price the platform charges for its service.
The case when only and its patients join the platform is symmetric and leads to the following profit expressions:
The platform’s optimal prices in these outcomes is derived in the proof of Lemma 3 in Appendix A.
Suppose now that both providers and all patients join the platform. This time, patients who switch their providers no longer incur the cost in transferring their PGHD. They simply log in to their PGHD account and give the new provider access to their data. This allows any switching patient to obtain the full additional utility of with the new provider. Among the consumers whose records are initially maintained by , the location of the one (denoted by ) who is indifferent between continuing with and switching to satisfies
The location of the indifferent consumer (denoted by ) among those whose records are initially maintained by satisfies
Once again, the profit expressions are the same as in Equations (3) and (4). Solving for and and the profit-maximizing prices, we found the optimal profits to be the following:
The platform’s optimal price in this outcome is derived in the proof of Lemma 3, which is available in Appendix A.
Lemma 3.
Given the option to integrate PGHD into EHR systems when not joining the platform, the smaller provider has a larger incentive to join the platform than the larger provider
The intuition is that since the platform does not accrue any additional benefit to the consumers because their PGHD will be monitored anyway, the provider with the larger patient base stands to lose more from the privacy concerns originating from the aggregation of PGHD by the platform. While both providers benefit from any cost advantages of joining the platform versus implementing the PGHD themselves, such benefits are mitigated by privacy costs, which are cumulatively higher for the larger provider.
Note that this result is predicated on our choice of benchmark. The larger provider would have a higher incentive to join the platform if we were to take the “No PGHD” as our comparison benchmark (see the top-left cell in Table 1) due to the cost of PGHD integration being too high or this option being unavailable altogether. The larger provider would then have a larger incentive to join the platform because it would benefit more from an increase in its service value due to having a larger customer base. Note that since the platform does not raise switching costs for patients, the larger provider does not benefit from a higher switching cost regime, unlike the case when both providers integrate PGHD into their EHR systems (which is our benchmark in this section). Accordingly, while the larger provider would have a larger incentive to join the platform in the absence of the in-house PGHD integration option, such an incentive would not be as strong as what we characterized in Lemma 2.
Now that we have established that would be the first to join the platform in the absence of price discrimination, we can state the possible equilibrium outcomes.
Proposition 3.
In the absence of price discrimination, the following occurs:
- If , the platform charges and works with and its patients only.
- Otherwise, the platform charges and works with both providers and all patients.
The platform’s price is set in reference to the providers’ cost savings , as well as their incentives associated with improving their service with respect to their competition. Since has a larger incentive to join the platform (see Lemma 3), the platform can charge a relatively high price to enroll only. Alternatively, it can lower its price and work with both providers. Since higher cost savings mean a higher revenue from each provider, the platform is more likely to work with both providers when the cost of adopting PGHD is high. A lower privacy cost and a lower switching cost () allows the platform to charge a higher price and increases the likelihood of working with both providers and all patients (see the proof of Lemma 3 and Proposition 3 in Appendix A). Accordingly, publicly emphasizing and promoting strong data and privacy protection policies is essential for today’s platforms. Early indications suggest that this is indeed taking place. For example, Amazon’s Halo service encrypts any health data it collects in transit and in the cloud. It deletes body scan images and voice snippets automatically after processing. Consumers are able to delete all other data. Amazon also pledged to never sell consumers’ PGHD to any third party or to correlate them with any other data for product recommendation purposes or otherwise [15].
Another implication of Proposition 3 is that a low PGHD transfer cost makes more likely to join the platform. Since is the second to join and has inherent incentives to keep switching costs high due to its larger established clientele, a drop in transfer costs makes more likely to join the platform. Accordingly, platforms have the economic incentive to invest in the interoperability of PGHD across various EHR systems. The ability to seamlessly transfer PGHD from the platform to the EHR system of a new provider who is not yet on the platform would increase that provider’s incentive to also join.
Proposition 4.
The larger provider is always better off with the emergence of the platform. The smaller provider is indifferent when it is the only provider on the platform and better off when the competing provider also joins. Accordingly, the platform raises provider surplus. Consumers are worse off when only the smaller provider joins the platform; they may or may not be better off when both providers join. These comparisons are all with respect to the benchmark case where both providers integrate PGHD into their EHR systems when they do not join the platform.
Comparing in Equation (15) with the one in the benchmark case , we found that the larger provider benefits from the partnership between the platform and its competitor, mainly due to the elevated privacy concerns of ’s patients. In the equilibrium when only joins the platform, all of ’s patients incur the privacy cost . ’s patients pay less than the amount they pay in the benchmark case, and thus, ’s patients are cumulatively worse off by 2 with the platform. ’s patients pay more in this equilibrium than the amount they pay in the benchmark case, and thus, ’s patients are also worse off with the emergence of the platform.
In the equilibrium when both providers join the platform, all patients incur the privacy cost . ’s patients pay more than the amount they pay in the benchmark case, while ’s patients pay less. Also, patients who switch providers no longer incur . Therefore, the overall impact of both providers’ joining the platform on consumer surplus is not clear cut.
We found that the larger provider benefits from its competitor having more interest in joining the platform. The platform gives an advantage when it enrolls only since ’s patients now incur the privacy cost. The optimal price that is attractive enough for to join the platform makes both providers better off. As a result, benefits from ’s muted interest when the platform’s optimal strategy is to enroll both of them. Interestingly, every consumer is worse off when only joins the platform. ’s patients are worse off because they incur the privacy cost, and the improvement in the provider’s price does not make up for the privacy loss. ’s patients are worse off as well, as this provider finds it optimal to raise its price given the privacy loss of the competing provider’s patients, although the negative impact of ’s higher price for them is less than the privacy-related utility loss that ’s patients experience.
So far, we have assumed that the providers would integrate PGHD into their EHR systems when they do not join the platform and referred to this outcome as the “benchmark case” of this section. We previously established that this outcome represented a Prisoner’s dilemma for the providers since their profits drop after adopting PGHD (see Proposition 1), and we took this outcome as given when analyzing the optimal strategies in the presence of the platform. It is in the context of this “new” benchmark case that producer surplus rises with the emergence of the platform. Since the platform does not face the PGHD implementation cost structure that providers do, it can reduce its price as necessary in order to make its service attractive to the providers. Similar to Lemma 2 and contrary to Lemma 3, when the on-premise implementation of PGHD is not a viable option for the providers for whatever reason, has a larger incentive to join the platform than , and the platform would price its service accordingly. Since providers are more likely to join the platform than to implement PGHD themselves due to the platform’s cost advantage, a Prisoner’s dilemma (i.e., a drop in equilibrium profits) is now more likely. However, given what we found in Proposition 4 regarding the provider surplus, such a dilemma is less unfavorable for the providers than the one in which they implement PGHD themselves.
Propositions 3 and 4 assume that the platform charges the same price to both providers. We noted earlier that we would relax this assumption and allow for price discrimination. Charging a price as a function of provider characteristics, including the number of patients being cared for, can be possible. Our last proposition outlines the impact of the platform’s ability to price discriminate on providers’ profits. Please note that when we allow for price discrimination, the platform charges a separate price to each provider by taking into account each provider’s characteristics, such as perceived quality and the number of patients.
Proposition 5.
The larger provider is indifferent to price discrimination. The smaller provider benefits from price discrimination when the platform’s optimal strategy is to work with the smaller provider only in the absence of price discrimination, and it is worse off otherwise.
The platform is strictly better off as it either enrolls the larger provider that it would not otherwise or by charging a higher price to the smaller provider (when working with both providers). Due to having a smaller incentive to join the platform than , is always indifferent to joining the platform—with or without price discrimination. The potentially interesting finding is that can be better off with price discrimination when the platform’s optimal strategy is to work with only in the absence of price discrimination, in which case is indifferent to joining the platform (it makes the same profit as in the benchmark case). This is because the platform works with both providers when it can price discriminate, and the highest price it can charge is what makes indifferent to joining when is on the platform. Since makes more profit when only joins (in which case ’s patients incur the privacy cost while ’s patients do not) compared with its profit in the benchmark case where neither provider joins the platform, is better off with price discrimination under these conditions.
We established earlier that a low PGHD implementation cost , a high privacy cost , and a high PGHD transfer cost are associated with the optimal platform strategy of working with the smaller provider only in the absence of price discrimination. Therefore, these are also the same conditions that render the platform’s price discrimination a Pareto-optimal scenario for the market participants.
4. Discussion
Past research on the adoption of PGHD has predominantly focused on the consumers’ perspective rather than that of providers. Accordingly, our main contribution to this research stream was a focus on the PGHD adoption of providers, as well as their incentive to join a PGHD platform. In doing so, we took a game-theoretic perspective with the intention to characterize the optimal conditions for providers’ adoption in competitive equilibria, both in the absence and presence of a PGHD platform. We found that providers with a larger patient base are less likely to join a platform than smaller providers after having adopted PGHD themselves. Accordingly, we expect large providers to possibly show an interest in joining a platform when they would not adopt PGHD on their own and when the platform reduces the technical and process-related costs of monitoring PGHD. On the flip side, small providers are more likely to join a platform, even after having adopted PGHD themselves.
The main implication for a PGHD platform is that their entry point to this space is likely to be via small healthcare providers. While high-profile partnerships with large healthcare systems can provide visibility to a platform, they should seek initial growth in the small business segment. Given that the concentration of PGHD within a single platform would make it easier for patients to switch providers and that large providers have more to lose from such a prospect, these providers would likely be especially wary of signing on with the largest platform. Conversely, the platform that can entice the largest providers should be able to attract smaller providers with greater ease, potentially leading to a winner-take-all dynamic.
Our results should be of particular interest to major EHR software vendors. A recent review of the literature on the integration of PGHD into EHRs found that more than half of the articles reported existing integrations being with Epic’s EHR [40], which has the largest U.S. hospital market share, while Cerner comes second [41], although it has been losing ground to Epic [42]. The latest PGHD encroachment by the tech giants, which collectively invested USD 3.6 billion in health-related deals in 2021 alone [43], raises an eyebrow and must be worrisome to large EHR vendors, such as Epic and Cerner. Numerous reports highlight the fact that if they are not properly regulated, we risk perpetuating a power imbalance that will need to be recalibrated in the interests of the individuals and smaller players [44]. In our analysis, we assumed an exogenous fixed cost for the adoption of PGHD by the providers. In reality, vendors like Epic and Cerner control this cost. Therefore, rather than leaving the field to big tech, they can work together to mitigate or eliminate the technological and financial barriers before the providers’ PGHD adoption by collaborating on new interoperability standards and standardized APIs to simplify integration, as well as developing their own apps and platforms that store PGHD that readily integrate with doctors’ EHRs. If big tech’s threat is too great to ignore, which we believe it is, then these traditional competitors of EHR software may want to collaborate in coming up with a consortium and a PGHD platform of their own. While our model does not speak to any of these issues, it does present the possibility of a platform to become the source of all PGHD in the future. Whatever its final form, such a platform will also need to handle the many data quality issues that may arise as healthcare providers integrate PGHD into their workflow. Cho et al. [45] identified several such intrinsic data quality challenges that may compromise the reliability and utility of these data. Such challenges are best dealt with by a PGHD platform.
From a public policy standpoint, our results contribute to the debate on the sharing of patients’ records between providers. Introducing PGHD into the clinical setting so that clinicians can make use of these data is an essential issue. However, PGHD currently appear to be seldomly incorporated into clinical care, and practices on how to incorporate PGHD into clinical workflows are not yet available [40]. An important concern regarding the incorporation of PGHD into clinical workflows is that there is little clinical guidance on how mobile apps should be utilized to add value to patient care. As aptly pointed out by Rowland et al. [46], patients are often not involved in the development of mobile health guidelines, and professionals’ views regarding high-quality health apps may not reflect patients’ views. Furthermore, data security and privacy is a major concern for patients when using mobile health apps [20]. These challenges will need to be addressed for PGHD to impact clinical outcomes in a meaningful way.
Interestingly, our results show that platforms may extend their already established monopolistic powers into the healthcare sector, potentially at the expense of consumer welfare. These findings provide further support for the need for regulations [47] and safeguarding the platforms’ control over consumers’ health data [48]. At the federal level, the Federal Trade Commission should take enforcement action against any entity that falsely claims that they would not share health data with third parties without users’ consent. The Office for Civil Rights at the Department of Health and Human Services should inform HIPAA-covered healthcare organizations regarding the security and privacy risks associated with third-party tracking technologies given the inherent risks of sharing identifiable health information with big tech firms, after which all control of that information is lost [49]. At the state level, legislatures can regulate what health data is collected, how it is used without patient consent, and how it should be protected. They can also add or supplant consent requirements to any existing data privacy legislation.
Last but not least, there are important ethical considerations regarding the entrance of big tech companies into the healthcare field. While technological prowess can help the medical field in developing new drugs, devices, and algorithms, protecting patient privacy and confidentiality may be impossible given all the other data that they have accumulated on the vast majority of people. Indeed, researchers have found that it is possible to correctly identify 99.98% of Americans in de-identified data sets using 15 demographic attributes [50]. One has to wonder how the big tech companies will monetize the billions of dollars that they pour into their healthcare initiatives. A healthcare provider has to be HIPAA-compliant to serve patients and has no incentive to make money off of their medical records other than making their services sticky for their patients, but a platform such as Amazon Comprehend Medical can remain HIPAA-eligible, thereby relieving itself from the responsibility of complying with patient privacy regulations to [51]. In the absence of clear incentives and regulatory oversight, the platforms that belong to big tech will have a hard time gaining consumers’ trust, which is equivalent to the high privacy cost we have in our models in this paper. Technical competence is never enough by itself to make things happen at the practical level, since there is also a need to build and develop trust into a shared and enduring state of systemic trustworthiness [52].
5. Conclusions and Limitations
In this research, we showed that providers with a larger patient base stand to gain more from adopting PGHD, as this raises the value of their services for a larger clientele. We also found that PGHD adoption always raises consumer surplus, but social welfare may drop depending on the cost of monitoring such data for the providers. Furthermore, given that larger providers are more likely to adopt PGHD in the absence of a platform, they would not have as much of an incentive as a smaller provider to join the platform when that option becomes available. This is because platform adoption raises privacy concerns that cumulatively put a larger provider at a disadvantage with respect to a smaller provider. On the flip side, large providers benefit more from the emergence of a platform relative to smaller providers, and consumers can be worse off if their providers adopt PGHD anyway in the absence of a platform.
As is customary in any analytical modeling exercise, we have made several simplifying assumptions for the purpose of tractability. No model can do complete justice to a healthcare system as complex as the one in the USA, and it is instructive to mention some of the important issues that our analysis does not address. For example, we have not explicitly considered the possibility of a patient working with multiple providers simultaneously who may or may not collaborate for the benefit of the patient, potentially using PGHD. Also, we assumed that the platform was a monopoly when in reality multiple platforms are currently competing for market share. We chose to do this simplification on the basis that we are still in the very early days of PGHD adoption and that any preliminary or existing collaboration between major platforms and providers has so far been completely disjointed events. Obviously, this does not preclude the possibility of serious competition between the major PGHD platforms of the future. It is just that platform competition has not materialized yet in this context.
Another implicit assumption was that the two providers could not exchange digital records with one another via an HIE. Relatedly, PGHD is only one type of patient-oriented digital investment by providers. The presence/absence of a patient-oriented technology, such as a patient portal, may have a complementary effect and be a differentiator for providers. There may be other technologies that are relevant. We ignored any such technology in order to focus on the impact of the adoption of PGHD on the equilibrium outcomes.
An extension of this research could consider the competition between for-profit and possibly not-for-profit platforms and more advanced uses of telemedicine. For example, it may be possible to virtually visit physicians and perform medical tests at home with the help of new applications and technological infrastructure, such as 5G. Already, recent advances in augmented reality headgear, delivery drones, visual imaging devices, and operation-performing robots have the potential to turn our homes into advanced healthcare facilities [53]. These new applications, along with the aggregation of PGHD in the cloud in a sharable format, have the potential to benefit medical research immensely. Anonymous and confidential use of PGHD may contribute greatly to our defense against future pandemics as well.
Future research may also investigate the best form of government regulation from a social welfare standpoint. As we have shown in this paper, the consumer surplus may drop with the emergence of the platform, with a potentially negative impact on social welfare as well. Given the socially important nature of the healthcare sector, outlining the optimal policy that the government should pursue is likely to be a valuable research avenue.
Author Contributions
Conceptualization, M.T.A.; Methodology, Z.D.O.; Formal analysis, Z.D.O.; Writing—original draft, Z.D.O.; Writing—review & editing, M.T.A. and H.T.; Supervision, H.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
No data were created as part of this research.
Conflicts of Interest
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors. The authors report there are no competing interests to declare.
Appendix A
Sketch of Solutions for the Profit Expressions in Table 1
First, we solved for the indifferent consumer between 0 and 1. Recall that there are two segments of consumers based on pre-established provider–patient relationships. The pre-established patient of who is indifferent to switching to is located at , where
Similarly, the pre-established patient of who is indifferent to switching to is located at , where
Solving for the indifferent consumer locations, we have and . The providers’ profits are
Solving for and , the first derivatives are
and .
The second derivatives are all negative. Thus, solving them simultaneously, we obtain the profit expressions for the benchmark case with no PGHD:
and .
The optimal prices are
The indifferent consumers are located at and .
Let . The prices can then be expressed as
Denote the case when both firms adopt PGHD with the superscript bb (this case is considered the benchmark case after the emergence of the platform). Using the same solution methodology as in the previous case, we found the optimal prices to be
The indifferent customers are located at and . The optimal prices are
The respective profits are provided in Table 1.
Proof of Lemma 1.
Comparing the profits of the providers in Table 1, we found that prefers to adopt PGHD when does not adopt if
Similarly, prefers to adopt PGHD when does adopt if
Comparing the first terms in both inequalities, we have since the difference equals , , and . A comparison of the second terms shows that since the difference equals . Thus, the latter condition is stricter than the former one given and , indicating that the incentive to adopt PGHD is smaller for when adopts them as well. prefers to adopt PGHD when does not adopt if
prefers to adopt PGHD when does adopt if
Comparing the first terms, we have since the difference equals . Comparing the second terms, Again, the incentive to adopt PGHD is smaller when the other provider also adopts them given and . □
Proof of Lemma 2.
The incentives of and to adopt PGHD when the other does or does not adopt are provided in the proof of Lemma 1. Using a similar approach that compares the terms in the respective Equations (A13) with (A15) and (A14) with (A16), the proof follows from the observation that ’s incentives are higher than ’s incentives provided that , and . □
Proof of Proposition 1.
Following the arguments in the proof of Lemma 1, neither provider adopts PGHD if the condition in Equation (A13) does not hold and . prefers adopting PGHD if given that does not adopt, and does not adopt PGHD if given that does adopt; see Equation (A16). Thus, and do not have an incentive to deviate from these adoption strategies when these two conditions hold. □
In contrast, if the condition in equation (A16) holds, and , then prefers to adopt PGHD. Given Lemma 2, has a larger incentive to adopt PGHD than , and thus, also does not have an incentive to deviate in an equilibrium where both adopt PGHD since the condition in Equation (A14) should also hold.
Proof of Proposition 2.
Comparing the benchmark case and the case where both providers adopt PGHD, all consumers get an additional utility with PGHD. ’s patients pay extra, while ’s patients pay less in equilibrium with PGHD compared with the benchmark; see Equations (A7) and (A8) in comparison with Equations (A11) and (A12). Also, consumers who switch providers (only) incur the extra switching cost . Given , the net benefit to consumers ( less a fraction of ) is positive.
The social welfare is the total surplus, which is the sum of consumer surplus and provider profits. We calculated the consumer surplus using Equation (6) for the benchmark case and similarly for other cases. We found that social welfare drops when both providers adopt PGHD compared with the benchmark case if
Clearly, consumer surplus increases with the utility coming from the improved service improvement , and the provider surplus decreases with the cost of PGHD implementation . Also, the provider surplus increases with the cost of transferring PGHD between patients . While ’s profit decreases with , ’s profit increases more with it. Accordingly, the social surplus may drop for high values of and low values of and . □
Sketch of the Solution with the Platform: We take the adoption of PGHD by both providers as the benchmark case, where Equations (A9) and (A10) provide the respective prices. We refer to this case as .
When only joins the platform, the solutions of Equations (11) and (12) yield and . Utilizing these in the respective profit expressions, we found the profit-maximizing prices to be
and the corresponding optimal profits to be
where is the price the platform charges for its service and, as before, .
When joins while does not join the platform, we have the following profit-maximizing prices:
and profits:
When both providers join the platform, we have the following profit-maximizing prices:
and profits:
□
Proof of Lemma 3.
We needed to compare the incentive to join the platform while taking into account whether the competing provider also joins. We first made the comparison when the competing provider does not join the platform.
Comparing the profits of with and without platform adoption (see Equation (A19)), joins the platform if
With the platform being a monopoly, it can therefore charge a price as high as
in this outcome and still guarantee ’s participation. At such a price, makes the same profit with and without joining the platform:
Following a similar procedure and using the profit expressions derived in the preceding sketch, we can show that the platform can charge as high as
when only joins the platform.
Since , has more incentive to join the platform than when the competing provider is not on the platform. Note that does not have an incentive to deviate from this equilibrium by joining the platform at this price since doing so makes worse off:
Next, we look at the incentives when the competing provider also joins the platform. Comparing the profit expressions in Equations (15) and (19), prefers to join the platform given that is on the platform if
Thus, the highest price the platform can charge while ensuring its participation is
Comparing the profit expressions in Equations (16) and (20), prefers to stay with the platform when also joins if
The highest price the platform can charge while ensuring its participation is , which is higher than the corresponding price for (see above). This means that has more incentive to join the platform than when the competing provider is also on the platform. is more likely to deviate from this equilibrium. Accordingly, the platform has to satisfy the price condition for and can, therefore, charge as high as the price given in Equation (A34). □
Proof of Proposition 3.
Given Lemma 3, is the first provider to join the platform and is the only one when the platform charges . This price is also the platform’s total revenue.
Lemma 3 also shows that both providers join the platform when it charges the price in Equation (A34). The platform’s revenue is twice this amount. Comparing the two revenues, working with only is preferable for the platform when :
This condition is more likely to be satisfied for lower values of , higher values of , and higher values of given the following:
□
Proof of Proposition 4.
Provider surplus:
is indifferent between the benchmark case and joining the platform (when the platform charges :
However, is better off as its profit rises compared with the benchmark case (see Equations (15) and (A23)):
When both providers join the platform, they have no incentive to deviate from that equilibrium since comparing Equations (A23) and (A20) with the benchmark profits produces the following:
The platform reduces the price to the point that makes indifferent to joining the platform. This price is lower than the point that makes indifferent to joining given its larger incentive to join than that of (see Lemma 3). Therefore, . Accordingly, both providers are better off when they both join the platform compared with the benchmark case.
Consumer surplus:
In the equilibrium when only joins the platform, all of ’s patients incur the privacy cost . Comparing Equations (A11) and (A12) with (A21) and (A22), ’s patients pay less than the amount they pay in the benchmark case, and thus, ’s patients are cumulatively worse off by 2 with the platform. ’s patients pay more in this equilibrium than the amount they pay in the benchmark case, and thus, ’s patients are also worse off with the platform.
In the equilibrium when both providers join the platform, all patients incur the privacy cost . ’s patients pay more than the amount they pay in the benchmark case, while ’s patients pay less. Also, patients who switch providers no longer incur . The overall impact of both providers’ joining the platform on consumer surplus is, therefore, not clear cut. □
Proof of Proposition 5.
When the platform cannot price discriminate, there can be an equilibrium outcome where only one provider joins the platform. In contrast, this does not happen when the platform can price discriminate. Both providers join the platform in equilibrium while paying the following maximum prices (based on the incentives derived in Lemma 3):
At these prices, the providers’ profits are
where the superscript represents “discrimination.” Both of these expressions are greater than their counterparts for the benchmark case.
First, consider the case when the platform’s optimal strategy is to work with only (no price discrimination). We see in the Proof of Proposition 4 that , which is less than . We also know from Equation (15) that , which is the same as . Accordingly, is better off with price discrimination, while is indifferent to it, when the platform’s optimal strategy is to work with only in the absence of price discrimination.
Next, consider the case when the platform’s optimal strategy is to work with (no price discrimination). We see in the Proof of Proposition 4 that , which is the same as , and thus, is indifferent to price discrimination. We see in Proof of Proposition 4 that Accordingly, is worse off with price discrimination. □
References
- Lin, L. China’s Plan to Make Permanent Health Tracking on Smartphones Stirs Concern. Wall Street Journal, 25 May 2020. [Google Scholar]
- Copeland, R. Google’s ‘Project Nightingale’ Gathers Personal Health Data on Millions of Americans. EMBO Mol. Med. 2020, 12, e12053. [Google Scholar]
- Farivar, S.; Abouzahra, M.; Ghasemaghaei, M. Wearable device adoption among older adults: A mixed-methods study. Int. J. Inf. Manag. 2020, 55, 102209. [Google Scholar] [CrossRef] [PubMed]
- Windasari, N.A.; Lin, F.; Kato-Lin, Y. Continued use of wearable fitness technology: A value co-creation perspective. Int. J. Inf. Manag. 2021, 57, 102292. [Google Scholar] [CrossRef]
- Wild, S.H.; Hanley, J.; Lewis, S.C.; McKnight, J.A.; McCloughan, L.B.; Padfield, P.L.; Parker, R.A.; Paterson, M.; Pinnock, H.; Sheikh, A.; et al. Supported Telemonitoring and Glycemic Control in People with Type 2 Diabetes: The Telescot Diabetes Pragmatic Multicenter Randomized Controlled Trial. PLoS Med. 2016, 13, e1002098. [Google Scholar] [CrossRef]
- Wicklund, E. An mHealth Wearable Helps Cedars-Sinai Doctors Manage Patient Care. mHealth Intelligence, 18 January 2018. [Google Scholar]
- HIMMS. 2022 Future of Healthcare Report. Available online: https://www.himss.org/resources/intelligence-and-new-trends-revealed-2022-future-healthcare-report (accessed on 31 July 2023).
- HIMMS-Media. The Role of Wearables and PGHD in the Care Delivery Continuum. Available online: https://healthsolutions.fitbit.com/wp-content/uploads/FINAL_HIMSS_FitBit_WP_10.01.20181.pdf (accessed on 31 July 2023).
- NTT-DATA. NTT DATA Study Finds Nearly Two-Thirds of Consumers Expect Their Healthcare Digital Experience to Be More Like Retail; NTT DATA Services: Plano, TX, USA, 2018. [Google Scholar]
- Black, J.R.; Hulkower, R.L.; Ramanathan, T. Health information blocking: Responses under the 21st Century Cures Act. Public Health Rep. 2018, 133, 610–613. [Google Scholar] [CrossRef] [PubMed]
- Pronovost, P.J.; Samitt, C.; Wang, Y.C.; Washington, V. Promoting Interoperability: Roles for Commercial Payers. NEJM Catal. 2019, 5. Available online: https://catalyst.nejm.org/doi/full/10.1056/CAT.19.0664 (accessed on 1 February 2024).
- Barlas, S. HHS Proposes Steps Toward Health Data Interoperability CMS and ONC Proposals Would Implement Cures Act. Pharm. Ther. 2019, 44, 347–349. [Google Scholar]
- Reading, M.J.; Merrill, J.A. Converging and diverging needs between patients and providers who are collecting and using patient-generated health data: An integrative review. J. Am. Med. Inform. Assoc. 2018, 25, 759–771. [Google Scholar] [CrossRef]
- Cresswell, K.; McKinstry, B.; Wolters, M.; Shah, A.; Sheikh, A. Five key strategic priorities of integrating patient generated health data into United Kingdom electronic health records. J. Health Inform. 2019, 25, 254–259. [Google Scholar] [CrossRef]
- Pifer, R. Amazon Launches Wellness Wearable, to Compete with Fitbit and Apple Watch. 27 August 2020. Available online: https://www.healthcaredive.com/news/amazon-launches-wellness-wearable-to-compete-with-fitbit-and-apple-watch/584262/ (accessed on 1 February 2024).
- Zuboff, S. The Age of Surveillance Capitalism: The Fight for a Human Future at the New Frontier of Power; Profile Books: London, UK, 2019. [Google Scholar]
- Pinsonneault, A.; Addas, S.; Qian, C.; Dakshinamoorthy, V.; Tamblyn, R. Integrated Health Information Technology and the Quality of Patient Care: A Natural Experiment. J. Manag. Inf. Syst. 2017, 34, 457–486. [Google Scholar] [CrossRef]
- Eze, B.; Kuziemsky, C.; Peyton, L.; Middleton, G.; Mouttham, A. Policy-based Data Integration for e-Health Monitoring Processes in a B2B Environment: Experiences from Canada. J. Theor. Appl. Electron. Commer. Res. 2010, 5, 56–70. [Google Scholar] [CrossRef]
- Niknejad; Ismail, W.B.; Mardani, A.; Liao, H.; Ghani, I. A comprehensive overview of smart wearables: The state of the art literature, recent advances, and future challenges. Eng. Appl. Artif. Intell. 2020, 90, 103529. [Google Scholar] [CrossRef]
- Huarng, K.H.; Yu, T.H.K.; Fang Lee, C. Adoption model of healthcare wearable devices. Technol. Forecast. Soc. Chang. 2022, 174, 121286. [Google Scholar] [CrossRef]
- Pancar, T.; Yildirim, S.O. Exploring factors affecting consumers’ adoption of wearable devices to track health data. Univers. Access Inf. Soc. 2023, 22, 331–349. [Google Scholar] [CrossRef]
- Wang, H.; Tao, D.; Yu, N.; Qu, X. Understanding consumer acceptance of healthcare wearable devices: An integrated model of UTAUT and TTF. Int. J. Med. Inform. 2020, 139, 104156. [Google Scholar] [CrossRef] [PubMed]
- Binyamin, S.S.; Hoque, M.R. Understanding the Drivers of Wearable Health Monitoring Technology: An Extension of the Unified Theory of Acceptance and Use of Technology. Sustainability 2020, 12, 9605. [Google Scholar] [CrossRef]
- Zhang, M.; Luo, M.; Nie, R.; Zhang, Y. Technical attributes, health attribute, consumer attributes and their roles in adoption intention of healthcare wearable technology. Int. J. Med. Inform. 2017, 108, 97–109. [Google Scholar] [CrossRef]
- Li, H.; Wu, J.; Gao, Y.; Shi, Y. Examining individuals’ adoption of healthcare wearable devices: An empirical study from privacy calculus perspective. Int. J. Med. Inform. 2016, 88, 8–17. [Google Scholar] [CrossRef]
- Wu, J.; Lia, H.; Lin, Z.; Goh, K.-H. How big data and analytics reshape the wearable device market—The context of e-health. Int. J. Prod. Res. 2017, 55, 5168–5182. [Google Scholar] [CrossRef]
- Wu, J.; Li, H.; Lin, Z.; Zheng, H. Competition in wearable device market: The effect of network externality and product compatibility. Electron. Commer. Res. 2017, 17, 335–359. [Google Scholar] [CrossRef]
- Tarakci, H.; Kulkarni, S.; Ozdemir, Z.D. The impact of wearable devices and performance payments on health outcomes. Int. J. Prod. Econ. 2018, 200, 291–301. [Google Scholar] [CrossRef]
- Wu, J.; Li, H.; Liu, L.; Zheng, H. Adoption of big data and analytics in mobile healthcare market: An economic perspective. Electron. Commer. Res. Appl. 2017, 22, 24–41. [Google Scholar] [CrossRef]
- Anderson, C.; Baskerville, R.; Kaul, M. Information Security Control Theory: Achieving a Sustainable Reconciliation Between Sharing and Protecting the Privacy of Information. J. Manag. Inf. Syst. 2017, 34, 1082–1112. [Google Scholar] [CrossRef]
- Fox, G.; Connolly, R. Mobile health technology adoption across generations: Narrowing the digital divide. Inf. Syst. J. 2018, 28, 995–1019. [Google Scholar] [CrossRef]
- Becker, M.; Matt, C.; Widjaja, T.; Hess, T. Understanding privacy risk perceptions of consumer health wearables–an empirical taxonomy. In Proceedings of the International Conference on Information Systems, Seoul, Republic of Korea, 10–13 December 2017. [Google Scholar]
- Marakhimov, A.; Joo, J. Consumer adaptation and infusion of wearable devices for healthcare. Comput. Hum. Behav. 2017, 76, 135–148. [Google Scholar] [CrossRef]
- Gabel, M.; Foege, J.N.; Nüesch, S. The (In)Effectiveness of Incentives—A Field Experiment on the Adoption of Personal Electronic Health Records. In Proceedings of the International Conference on Information Systems, Munich, Germany, 15–18 December 2019. [Google Scholar]
- Demirezen, E.M.; Kumar, S.; Sen, A. Sustainability of Healthcare Information Exchanges: A Game-Theoretic Approach. Inf. Syst. Res. 2016, 27, 240–258. [Google Scholar] [CrossRef]
- Martinez, D.A.; Feijoo, F.; Zayas-Castro, J.L.; Levin, S.; Das, T.K. A strategic gaming model for health information exchange markets. Health Care Manag. Sci. 2018, 21, 119–130. [Google Scholar] [CrossRef] [PubMed]
- Jack, A. Medical technology gives healthcare a shot in the arm. Financial Times, 20 November 2020. [Google Scholar]
- Simpson, E.; Brown, R.; Sillence, E.; Coventry, L.; Lloyd, K.; Gibbs, J.; Tariq, S.; Durrant, A.C. Understanding the barriers and facilitators to sharing patient-generated health data using digital technology for people living with long-term health conditions: A narrative review. Front. Public Health 2021, 9, 641424. [Google Scholar] [CrossRef]
- Stucke, M.E. Should We Be Concerned About Dataopolies? Georget. Law Technol. Rev. 2018, 2, 275–324. [Google Scholar]
- Tiase, V.L.; Hull, W.; McFarland, M.M.; Sward, K.A.; Del Fiol, G.; Staes, C.; Weir, C.; Cummins, M.R. Patient-generated health data and electronic health record integration: A scoping review. J. Am. Med. Inform. Assoc. Open 2020, 3, 619–627. [Google Scholar] [CrossRef]
- Landi, H. Epic, Meditech gain US hospital market share as other EHR vendors lose ground. Fierce Healthcare, 1 May 2020. [Google Scholar]
- Rodriquez, S. Epic, MEDITECH Top EHR Vendors by 2021 Hospital Market Share. EHR Intelligence, 2 May 2021. [Google Scholar]
- How health care is turning into a consumer product; Move fast and heal things. The Economist, 9 January 2022.
- Couldry, N.; Mejias, U.A. Big Tech’s latest moves raise health privacy fears. Financial Times, 6 December 2020. [Google Scholar]
- Cho, S.; Ensari, I.; Weng, C.; Kahn, M.G.; Natarajan, K. Factors Affecting the Quality of Person-Generated Wearable Device Data and Associated Challenges: Rapid Systematic Review. JMIR mHealth uHealth 2021, 9, e20738. [Google Scholar] [CrossRef] [PubMed]
- Rowland, S.P.; Fitzgerald, J.E.; Holme, T.; Powell, J.; McGregor, A. What is the clinical value of mHealth for patients? NPJ Digit. Med. 2020, 3, 4. [Google Scholar] [CrossRef] [PubMed]
- Montgomery, K.; Chester, J.; Kopp, K. Health Wearables: Ensuring Fairness, Preventing Discrimination, and Promoting Equity in an Emerging Internet-of-Things Environment. J. Inf. Policy 2018, 8, 34–77. [Google Scholar] [CrossRef]
- Singer, N. New Data Rules Empower Patients, But Risk Privacy. New York Times, 9 March 2020. [Google Scholar]
- Adler, S. Editorial: Big Tech and Health Data: How the Landscape Is Changing. Available online: https://www.hipaajournal.com/big-tech-and-health-data-how-the-landscape-is-changing/ (accessed on 19 December 2023).
- Rocher, L.; Hendrickx, J.M.; de Montjoye, Y.-A. Estimating the success of re-identifications in incomplete datasets using generative models. Nat. Commun. 2019, 10, 3069. [Google Scholar] [CrossRef]
- Chiruvella, V.; Guddati, A.C. Ethical Issues in Patient Data Ownership. Interact. J. Med. Res. 2021, 10, e22269. [Google Scholar] [CrossRef]
- Maeckelberghe, E.; Zdunek, K.; Marceglia, S.; Farsides, B.; Rigby, M. The ethical challenges of personalized digital health. Front. Med. 2023, 10, 1123863. [Google Scholar] [CrossRef]
- Tibken, S. Why 5G for smartphones is just the start. CNET, 30 July 2019. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).