Abstract
Credit rationing hindered the development of MSEs. Big data credit technology creates a great opportunity to address this issue. Then, how does big data credit technology affect and to what extent can it alleviate the credit rationing of MSEs? Based on the bounded rationality economic man hypothesis, the evolutionary game model of banks and MSEs under the traditional mode and big data credit technology are constructed, respectively, in this paper, and the evolutionary trajectory of bank-enterprise credit strategies under the two modes are comparatively analyzed. The results show that it is hard to alleviate the credit rationing of MSEs under the traditional mode. However, under big data credit technology, when the overall credit level of MSEs is high, the credit rationing of MSEs will be effectively alleviated. When the overall credit level of MSEs is too low, it is difficult to determine whether big data credit technology can alleviate the credit rationing of MSEs. In order to verify the feasibility of big data credit technology in alleviating the credit rationing of MSEs, a simulation experiment is conducted to compare the differences in the credit rationing of MSEs with different credit levels under the two credit modes. We found that the credit rationing of MSEs is always lower under big data credit technology than under the traditional mode. Therefore, big data credit technology can effectively alleviate the credit rationing of MSEs under any circumstances. The research provides theoretical support for banks to apply big data credit technology to achieve a win-win situation for both parties.
1. Introduction
According to the credit rationing theory developed by Stiglitz and Weiss (1981), due to adverse selection and moral hazard caused by information asymmetry in the credit market, there is no monotonic linear relationship between the expected return on bank loans and the interest rate. When borrowers’ demand for loans is greater than banks’ supply of loans, banks will implement restrictions on borrowers through non-price instruments rather than raising interest rates to clear the market; as a result, for undifferentiated borrowers, some can obtain loans while others cannot, and borrowers who could not obtain loans still have no access to loans even if they are willing to pay higher interest rates or provide more collaterals []. Enterprise size is considered to be one of the most important indicators in determining the financing barriers of borrowers. Macmillan (1931) [] suggested that enterprise size affects the financing accessibility of enterprises: the smaller the enterprise, the higher the probability of suffering from credit rationing []. Even if MSEs have growth potential, it is difficult for them to obtain credit support. “Financing is difficult and expensive” has been a major problem faced by MSEs [,].
As the main force in boosting national economic development, MSEs play an irreplaceable role in stabilizing economic growth, narrowing the income gap, improving labor productivity, and promoting market competition. Compared with large and medium-sized enterprises, MSEs are numerous and widely distributed, which creates a broad job market for the labor force in both developing and developed countries. However, credit rationing hindered the effective use of credit resources and weakened MSEs’ incentive to engage in technological innovation and alleviate employment pressure. Therefore, alleviating the credit rationing of MSEs is an important issue that needs to be addressed urgently.
The key to effectively alleviating the credit rationing of MSEs is to reduce the information asymmetry between MSEs and banks, so as to overcome the size disadvantage of MSEs, promote bank lending, and discourage MSEs from defaulting; therefore, banks need tools to obtain the risk information of MSEs. The emergence of big data brings an opportunity to address this issue and make enterprise size no longer a constraint restricting the credit acquisition of MSEs []. Using big-data-based credit technology, banks can efficiently analyze more than trillions of bytes of relevant information, thus improving loan approval efficiency and reducing information asymmetry. Therefore, banks could implement credit technology innovation based on big data to predict risks and identify MSEs according to the quantitative information residing in their information management system, rather than making credit decisions based on the qualitative characteristics of MSEs.
As shown in Figure 1, without considering enterprise size, the credit rationing situation is as follows: at the interest rate charged by banks , the demand for credit exceeds the supply , but when the interest rate exceeds , banks’ expected return will decrease. At the market clearing rate , the demand for credit is equal to the supply, but profit-maximizing banks will not issue loans at ; instead, they will make profits at the credit rationing rate , resulting in higher demand for credit than supply. Credit rationing then occurs, and there is a credit gap of size , which represents the unmet credit demand of MSEs.
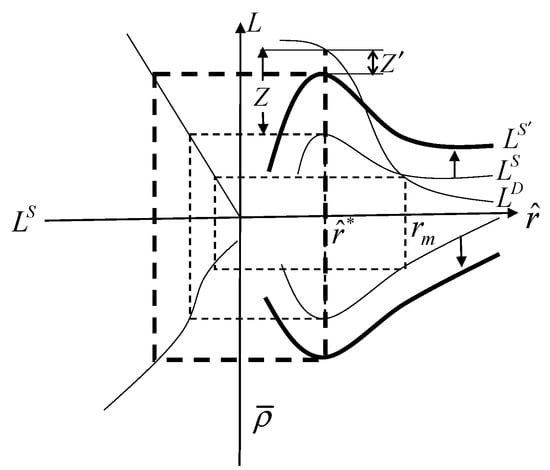
Figure 1.
Traditional credit rationing equilibrium and new equilibrium under big data technology without considering enterprise size, where * indicates when credit rationing exists.
The role of big data in reducing information asymmetry between banks and enterprises offers the possibility of generating new equilibrium solution sets []. Under the condition of banks implementing big data credit technology, the loan supply curve will shift from to ; correspondingly, the credit gap is reduced from to , so that MSEs that have credit demand but have not applied for loans or have applied for loans but cannot obtain loans have the opportunity to obtain loans, and MSEs whose credit demand has not been fully met have access to additional credit funds.
Figure 2 illustrates how credit rationing occurs when banks differentiate between enterprise size: suppose that the borrowing enterprises can be divided into three categories according to their size—MSEs, medium-sized enterprises, and large enterprises, denoted by 1, 2, and 3, respectively. For borrowers belonging to category , the interest rate at which banks obtain the maximum profit is . represents the total profit of banks when the interest rate charged to borrower is . When the opportunity cost of banks’ loanable funds is , since the total profit that banks can obtain from MSEs is less than the opportunity cost, MSEs cannot obtain loans; large enterprises will be able to obtain loans, while some medium-sized enterprises could obtain loans at . If the opportunity cost drops to , all large and medium-sized enterprises could obtain loans, while some MSEs could not obtain loans.
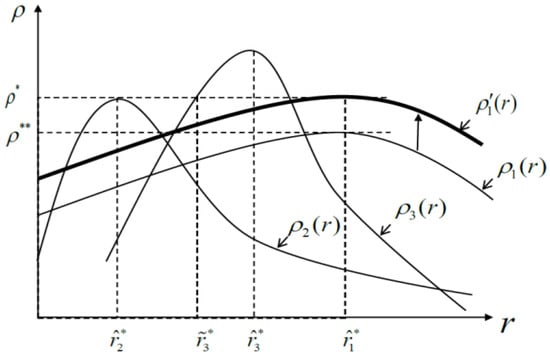
Figure 2.
Traditional credit rationing equilibrium and new equilibrium under big data credit technology when distinguishing between enterprise size, where * and ** refer to the situation before and after the reduction in the opportunity cost of banks’ loanable funds, respectively.
Big data can significantly improve banks’ efficiency in applying credit technology and prompt banks to make much more scientific and rational credit decisions [], so as to reduce the credit risks and transaction costs when lending to MSEs []. In addition, big data also promotes banks to expand their credit offerings to MSEs and obtain informatization benefits from “long-tail customers” []. Therefore, under big data credit technology, the total profit obtained by banks from MSEs will increase from to , so that MSEs can obtain loans at a lower opportunity cost of banks, thereby narrowing the credit gap of borrowers and alleviating the credit rationing of MSEs.
Existing research has demonstrated the prospects for the widespread use of big data in the credit market, but has not considered the impact of banks’ application of big data credit technology on MSEs’ credit rationing in depth; this paper attempts to explore the general mechanism of banks applying big data credit technology in alleviating the credit rationing of MSEs through evolutionary game models and simulation experiments. It is expected that this research can provide theoretical support for banks in implementing big data credit technology to alleviate the credit rationing of MSEs and create new profit growth points.
The rest of the article is structured as follows: in Section 2, research on the causes of the credit rationing of MSEs, countermeasures to alleviate the credit rationing of MSEs, and the role of big data in the credit market is reviewed; in Section 3, the evolutionary game model of banks and MSEs under the traditional mode and big data credit technology is constructed, respectively, and the evolutionary trajectory of bank–enterprise credit strategies under the two credit modes is obtained; in Section 4, a comparative analysis of the differences in the credit rationing of MSEs with different credit levels under the two credit modes is carried out to systematically verify the feasibility of big data credit technology in alleviating the credit rationing of MSEs; in Section 5, the challenges of applying big data credit technology, future prospects of big data credit technology, and the contribution and implications of this work are presented; and in Section 6, conclusions are drawn.
2. Literature Review
2.1. The Causes of the Credit Rationing of MSEs
Regarding the causes of the credit rationing of MSEs, scholars generally conclude that specific characteristics of the credit demand side and credit supply side, as well as the economic policy regime, affect credit transaction costs and credit risks, making it more difficult for MSEs to obtain loans than large and medium-sized enterprises. Demand-side factors mainly include entrepreneur characteristics [], enterprise size or age [,], ownership type and legal form [], geographic location [], industry affiliation [], and asset structure []. The literature shows that a deterioration in an enterprise’s own view of its credit history, economic outlook, and capital should reduce its access to finance [,,]. In addition, Beyhaghi et al. (2020) suggest that decreased profits increase the probability of an enterprise being rationed [].
The mechanism that leads to the credit rationing of MSEs from the credit supply side lies in that, owing to information asymmetry, evaluating the credit risk of small enterprises is difficult for lenders []. To maximize profitability, lenders may apply stricter selection criteria and credit discrimination on MSEs []. Masiak et al. (2019) and De Jonghe et al. (2020) revealed that, due to increased screening costs, smaller enterprises find it more difficult to access finance from banks [,]. The research of Sun et al. (2013) affirmed the existence of “the discrimination of scale” in the process of SME financing, and showed that the bank lending policies using fixed assets as collateral exacerbate the plight of small business financing [].
Economic policy regimes contribute to the credit rationing of MSEs as evidenced by the fact that financial institutions may restrict credit or charge risk premiums for enterprises that operate opaquely in economies where legal regimes do not adequately protect property rights, institutions operate inefficiently, and the regulatory system is imperfect [,,]. European evidence suggests that unique structural features combined with strict governance rules make MSEs less attractive to external financiers, and, as a result, this results in difficulties in accessing credit for them []. Based on the African context, Simba et al. (2023) suggest that, due to vast institutional voids, unco-ordinated domestic policies and the widespread application of derivative accounting practices in financial markets, the availability of financial resources for small enterprises can be dangerously low [].
Although scholars have explained the causes of the credit rationing of MSEs based on different perspectives and contexts, however, most studies did not make a clear distinction between MSEs and small and medium-sized enterprises (SMEs); the research on the credit rationing of MSEs is not systematic and in-depth. The concept of MSEs is derived from SMEs, and the explicit definition of MSEs is relevant to the understanding of the country’s economic structure and development, as well as to the allocation of resources and the identification of targets for government support. This work is different from the previous study. Focusing on the specificities of MSEs, we explain the persistence of credit rationing for MSEs under the traditional credit mode through an evolutionary game model. And we found that the credit strategies evolutionary trajectory of banks and MSEs under the traditional mode is extremely unstable and cannot reach equilibrium.
2.2. Countermeasures to Alleviate the Credit Rationing of MSEs
In order to alleviate the credit rationing of MSEs, scholars have put forward numerous countermeasures mainly for banks, governments, and MSEs. Policy recommendations for banks mainly include innovating credit technologies and providing loans to MSEs by large banks. Ferri et al. (2019) showed that transactional lending technologies increased enterprises’ credit rationing, whereas soft information mitigated asymmetric information problems and improved enterprises’ access to credit; when soft information was incorporated into transactional lending technologies, small enterprises’ credit rationing significantly reduced []. Vera and Onji (2010) argued that large banks can provide differentiated financial services and credit support to MSEs at different stages of development, and they have information technology advantages, network advantages, and the advantage of sharing information costs across time, which is more conducive to establishing long-term and stable co-operative relationships with MSEs and providing them with services []. However, large banks may face Williamson-type organizational diseconomies.
Government intervention can reduce the investigation cost of banks to MSEs, make banks’ deposit liquidity management more flexible, and improve the allocation efficiency of credit resources []. Government interventions for MSEs are categorized into indirect and direct interventions. Indirect interventions include taking measures to reduce transaction costs or increase the supply of funds, while direct interventions mainly include credit subsidies and loan guarantees []. Dai et al. (2020) showed that tax incentives from the government motivate enterprises to invest in short-term development opportunities with high returns rather than in long-term projects with high returns and high risks; tax incentives save capital expenditures for MSEs, and indirectly reduce the financing costs of MSEs []. Beck and Demirgü-Kunt (2010) point out that, as a form of risk sharing, government subsidies can help to increase the cash flow of MSEs and mitigate the negative impacts of co-ordination failures among guarantee agencies or the over-concentration of credit resources provided by collaborating banks []. Arping et al. (2010) examined the functioning mechanism of government credit guarantees on enterprise financing, noting that government subsidies for credit guarantees are more effective than other interventions [].
Credit rationing has restricted the development of MSEs, and MSEs need to enhance their capabilities and utilize the environment to create appropriate financing opportunities to solve the problem []. Policy recommendations for MSEs mainly include borrowing from small and medium-sized financial institutions, utilizing informal finance, and engaging in relationship lending. For example, Lehmann et al. (2003) point out that it is easy to form long-term relationships between small and medium-sized financial institutions and MSEs, which can help to reduce collateral requirements for MSEs and information asymmetry, thus alleviating the credit rationing of MSEs []. Isaksson’s (2002) study showed that, although the amount of each loan received by small enterprises from informal finance is small, they lend more often to informal finance and have a higher utilization of credit funds []. Cucculelli et al. (2019) argue that, by establishing soft-information-based and durable lending relationships with banks, the likelihood of small enterprises experiencing credit rationing is significantly reduced []. In addition, Olufunso and Francis (2011) advised the owners of MSEs to improve their management capacity by attending seminars and training programs to prepare them for access to finance []. Ogawa et al. (2013) showed that trade credit is an important source of finance for young and small enterprises that have difficulty in obtaining bank loans [].
Overall, although scholars have provided many policy recommendations based on different perspectives to alleviate the credit rationing of MSEs, and these policy recommendations have also played a certain role, however, on the whole, the credit rationing of MSEs has not been thoroughly reduced in many countries, especially in developing countries. Therefore, further research is needed on countermeasures against the credit rationing of MSEs. This work is different from existing research, since we believe that the credit rationing of MSEs is a kind of market mechanism defect. As a major player in the market, banks are the main external financing channels for MSEs; to alleviate the credit rationing of MSEs, banks desperately need tools to obtain the risk information of MSEs, and big data credit technology provides an opportunity for achieving this.
2.3. The Role of Big Data in the Credit Market
Improvements in socialization and the emergence of social networking platforms such as Facebook, Twitter, and Pinterest, as well as the tendency for data and programs to be accessed and stored over the Internet rather than on computer hard drives, have contributed to the era of big data []. “Big data” refers to massive data sets that are difficult to extract, store, search, share, analyze, and process with existing software tools, which require greater storage space and time, as well as sophisticated methods and technologies for managing and analyzing the []. Volume, Variety, and Velocity (“3V”) is a common framework for describing big data []. In addition to the “3V” characteristics of big data, in recent years, Veracity, Variability, and Value have become new dimensions of big data characteristics, and are even more challenging []. Reduced storage costs and the widespread availability of cloud solutions from well-known providers such as Amazon, Google, and Microsoft have had a positive impact on the adoption of big data technologies and methodologies []. Cloud computing solutions can be used for big data management, and provide opportunities for enterprises, especially small enterprises, which are often constrained by a lack of financial and organizational resources [].
Financial sectors can highly benefit from big data. They can access massive amounts of transaction data which can be processed to gain competitive advantages over their peers, enhancing the customer banking experience, risk analysis and mitigation, and operation and optimization []. The use of big data technology can break through the traditional mode of banks in dealing with information asymmetry. When big data technology is applied to the credit business, there is no human or subjective judgment factor; instead, through the analysis of the historical data that actually occurred, it can improve the amount of information and accuracy of the credit of borrowers to a certain extent. Jin et al. (2022) pointed out that the application of big data technology in credit evaluation facilitates the provision of unsecured credit based on industrial chain credit [].
For the financing of MSEs, the value of big data lies in their ability to alleviate the information asymmetry between banks and enterprises, enabling banks to discover more high-quality MSEs with low risks instead of making credit decisions based on the qualitative characteristics of loan applicants, thereby expanding banks’ credit allocation for the MSE group, effectively alleviating the problem of credit rationing for MSEs, and, at the same time, maximizing the banks’ own profits. The research of Kshetri (2016) shows that the main reason why low-income households or microenterprises in emerging economies lack access to financial services is not because they lack creditworthiness but merely because banks lack data, information, and capabilities to access the creditworthiness of and effectively provide financial services to this financially disadvantaged group []. Tencent’s Weizhong Bank has launched the “Microparticle Loan” product for its target customer groups, which is a microcredit product based on big data credit technology, and the speed of issuance of the product can be as fast as 45 s, and the slowest speed can be 90 s, which enables customers to enjoy a safer, faster, and more convenient service.
In summary, the existing literature provides many useful insights into the role of big data technology in the credit market, and the existing literature demonstrates that big data credit technology can reduce the information asymmetry between borrowers and lenders, thereby lowering the transaction costs of banks, and making the size of the enterprise no longer a constraint on the access to credit for MSEs. However, existing studies did not intensively consider the mechanisms by which banks’ use of big data credit technology affects the credit rationing of MSEs. By comparing the evolutionary trajectories of bank–enterprise credit strategies under big data credit technology and the traditional mode through an evolutionary game model, and comparing the extent to which big data credit technology alleviates the credit rationing of MSEs with different credit levels through simulation experiments, we demonstrate that big data credit technology can effectively alleviate the credit rationing of MSEs.
3. Evolutionary Game Analysis of Bank–Enterprise Credit Strategies
3.1. Evolutionary Game Analysis under the Traditional Mode
In order to verify the feasibility of big data credit technology in alleviating the credit rationing of MSEs, we began by analyzing the credit rationing of MSEs under the traditional mode as a benchmark. Considering that banks’ credit decisions are affected by information asymmetry and the dynamics of bank–enterprise behavior, the evolutionary game process is divided into two stages, as shown in Figure 3. In stage 1—the loan application stage, banks take the “lend” or “reject” decisions on the premise of profit maximizing; in stage 2—the loan repayment stage, the strategy set of MSEs includes “repay” and “default”. For the stability criterion of the evolutionary game, refer to the relatively weak evolutionary stability criterion of Swinkels (1992) [], assuming that in the bank–enterprise interactive process, the proportion of each mutation strategy combination is not too large; after the mutation strategy combination enters the bank–enterprise group, if a certain strategy combination always dominates the mutation strategy combination, then the strategy combination is evolutionarily stable.

Figure 3.
Bank–enterprise evolutionary game process.
3.1.1. Game Hypothesis
- (1)
- All players are bounded rational individuals who pursue profit maximization.
- (2)
- The information asymmetry degree between the banks and MSEs is , , where represents complete information asymmetry and represents complete information symmetry. MSEs know their own operating conditions, profitability, repayment ability and repayment willingness, etc., thus having an absolute information advantage. However, banks only know the average success probability of the projects invested by MSEs, and they need to pay high costs to obtain additional information.
- (3)
- The decision vectors of banks and MSEs are (lend, reject) and (repay, default), respectively; in the initial state, the probabilities of banks and MSEs choosing the two strategies are (, ) and (, ), respectively, where , and ; i.e., both and are functions of time . Banks do not know whether MSEs will repay or not before deciding whether to lend.
- (4)
- The fixed capital amount that MSEs need to invest in the project is , where is MSE’s private wealth, is the loan amount MSEs need to borrow from banks, and the interest rate is .
- (5)
- The collateral requirement is , ; when the MSE defaults, the bank confiscates the collateral. Since the use of collateral usually involves various costs, such as the assets’ regulatory cost of maintaining the collateral’s value at the agreed level or implicit costs for the borrower in being forced to relinquish discretionary use of the asset [], which is assumed to be and is undertaken by MSEs; the asset realization rate of the collateral is .
- (6)
- MSEs’ project success probability is ), the rate of return on capital when the project is successful is , the failure probability of the project is , and the return is when the project fails; the expected return of the MSE is .
- (7)
- If the bank chooses to decline the loan, and the MSE plans to continue operating the project and turn to non-bank financing channels, the amount to be repaid and the additional costs incurred during the loan application process are . Generally speaking, it is more expensive for borrowers to finance from non-bank institutions, which is manifested by higher interest rates and negotiation costs []; thus, assume that .
- (8)
- The risk-free rate of return on the bank loan is , . Since MSEs’ operating risks and the information asymmetry degree are higher than those of large-scale enterprises [], assume that the transaction cost for the bank to lend to MSEs is , ; the expected return of the bank is .
3.1.2. Basic Model
In the credit market with incomplete information, the payoff matrix of the evolutionary game is shown in Table 1. If the bank chooses to reject the loan and the MSE chooses to default, the bank’s return is the deposit interest , and the MSE’s return is ; if the MSE chooses to repay and borrow from non-bank financing channels, the bank’s return is the deposit interest , and the MSE’s return is the expected return of the project minus the cost of borrowing from non-bank financing channels . If the bank chooses to lend and the MSE chooses to repay, the bank’s return is the interest minus the transaction cost and the opportunity cost , the MSE’s return is the expected return of the project minus the principal and the loan interest, and the collateral cost ; if the MSE chooses to default, the bank’s return is the confiscated collateral value minus the loan transaction cost, the principal, and the deposit interest , and the MSE’s return is the expected return of the project minus the collateral value and the collateral cost .

Table 1.
The payoff matrix of the evolutionary game.
From Table 1, the expected return (i.e., fitness) of the MSE choosing the repay strategy and the default strategy, and the average return are:
Similarly, the expected return of the bank choosing the lend strategy and the reject strategy, and the average return are:
Due to information asymmetry, loan transactions involve high costs []. If MSEs choose to default, banks will lose the principal and interest, thus suffering great loss in lending; if MSEs repay the loan, banks will be more profitable if they choose to lend. To make the theoretical model consistent with reality, assume that, if the MSE chooses to repay, the return of the bank that chooses to lend is higher than the return of choosing to reject the loan. If the MSE chooses to default, the bank’s return from rejecting the loan is higher than the return from choosing to lend: mathematically, , , i.e.,
To ensure profitability, banks providing loans should meet the condition that the average return is not less than 0: , then the interest rate . Under information asymmetry, banks cannot predict whether MSEs will perform their contracts; moreover, investigating MSEs will incur huge costs. Therefore, banks can only ensure profitability by raising the interest rate ; if the interest rate is too high, low-risk borrowers will automatically exit from the credit market, and adverse selection occurs, resulting in more high-risk borrowers remaining in the market []. To control the credit risk, banks’ loan review conditions will be further strengthened, and credit rationing for MSEs will deteriorate.
3.1.3. Model Analysis
- (1)
- The evolution path and evolutionarily stable strategy of MSEs and banks
(1) Game evolutionary trend of MSEs
According to the Malthusian dynamic equation, the growth rate of a strategy is equal to its relative fitness []. As long as the return of an individual adopting this strategy is higher than the average return of the group, i.e., , this strategy will be imitated by more MSEs. The probability of MSEs choosing to repay () will, therefore, increase over time; conversely, decreases. And the change rate of is positively related to its value. Assume the relative adjustment speed of the strategy adoption frequency is proportional to the magnitude by which its payoff exceeds the average payoff; then, the replicated dynamic equation for MSEs to choose to repay is:
where represents the change rate of the probability that MSEs choose to repay over time. If , the probability of MSEs choosing to repay increases, and vice versa. The stable state of MSEs’ replication dynamics refers to the state in which the number of MSEs that choose the repay strategy and the default strategy reach equilibrium, where the probability of MSEs choosing to repay () no longer changes with time and remains at the stable state value, denoted as , which describes the probability that MSEs will eventually choose to repay through the dynamic evolutionary game. Differentiating with respect to yields
Obviously, must satisfy . From Equation (9), and are two possible stable state values. According to the stability theorem of differential equations and the properties of evolutionarily stable strategies, if , the value corresponding to is an evolutionarily stable strategy; if , the value corresponding to is an evolutionarily stable strategy [].
I. When , always hold; i.e., all values of are stable state values. The probability of banks adopting the lending strategy is ; there is no difference in the return of MSEs choosing the two strategies; i.e., all values of are evolutionarily stable strategies for MSEs. According to Equation (9), the replication dynamics of MSEs are shown in Figure 4a.
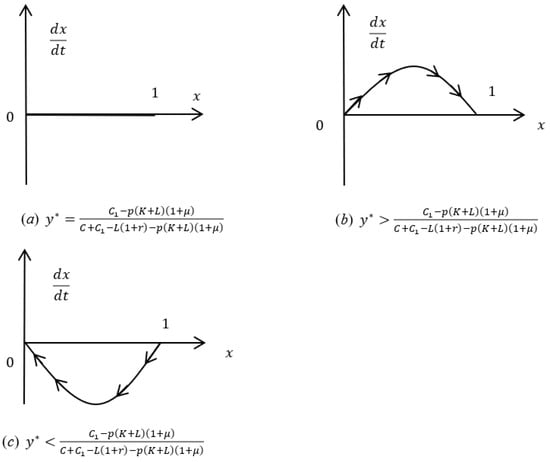
Figure 4.
The replication dynamic phase diagrams of MSEs under the traditional mode, where * means the stable state. (a–c) denote the cases when banks choose to lend with a probability equal to, greater than, and less than , respectively.
II. When , and are two possible stable strategies of . According to the assumptions and , it follows that .
- (a)
- If , for and , we have and , respectively; then, is the evolutionarily stable strategy; i.e., when banks choose to lend with a probability higher than , “repay” is the evolutionarily stable strategy for MSEs. The replication dynamics of MSEs are shown in Figure 4b.
- (b)
- If , for and , we have and , respectively; then, is the evolutionarily stable strategy; i.e., when banks choose to lend with a probability less than , “default” is the evolutionarily stable strategy for MSEs. The replication dynamics of MSEs are shown in Figure 4c. The replication dynamic phase diagrams of MSEs under different circumstances are shown in Figure 4:
(2) Game evolutionary trend of banks
According to Equations (4) and (6), the replication dynamic equation for banks to choose to lend is:
Differentiating with respect to yields
Denote the probability of banks choosing to lend in the replication dynamic stable state as . Let ; then, are two possible stable state values.
I. When , , always hold; then, all values of are stable states. The probability of MSEs choosing the repayment strategy is ; there is no difference in the return of banks choosing the two strategies; i.e., all values of are evolutionarily stable strategies for banks. The replication dynamics of banks are shown in Figure 5a.
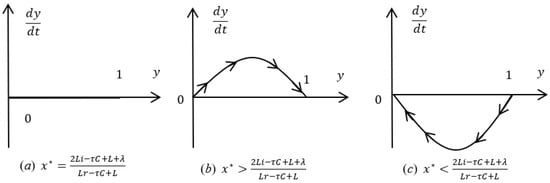
Figure 5.
The replication dynamic phase diagrams of banks under the traditional mode, where * means the stable state. (a–c) denote the cases when MSEs choose to repay with a probability equal to, greater than, and less than , respectively.
II. When , according to the assumptions (7), (8), and , it follows that .
- (a)
- When , is an evolutionarily stable strategy, the replication dynamics of banks are shown in Figure 5b. When MSEs choose to repay with a probability higher than , banks will gradually shift from rejecting loans to lending.
- (b)
- When , is an evolutionarily stable strategy, the replication dynamics of banks are shown in Figure 5c. When MSEs choose to repay with a probability less than , rejecting the loan is an evolutionarily stable strategy for banks. The replication dynamic phase diagrams of banks under different circumstances are shown in Figure 5:
- (2)
- Evolutionary stability analysis of the system
The stable state of the system refers to the replication behavior of MSEs, and banks are in an equilibrium state when the probability of MSEs choosing to repay () and the probability of banks choosing to lend () remain unchanged []. Denote the stable state values as and , respectively. According to Friedman (1991), by constructing the Jacobian matrix of the evolutionary game system, the stability of the local equilibrium point of the system can be obtained [].
According to the definition of the stable state values and , the local equilibrium point of the dynamic replication equation set should make the determinant of the Jacobian matrix equal to . By solving the replication dynamic equation set consisting of Equations (9) and (11), it follows that, in the planar region , there are five replication dynamic equilibrium points, which are (0, 0), (0, 1), (1, 0), (1, 1), and (, ), where , . The stability of these five equilibrium points can be determined by analyzing the local stability of its Jacobian matrix; i.e., the stability of the equilibrium point is determined by the characteristic root symbol of its Jacobian determinant. When the matrix determinant that corresponds to the equilibrium point is higher than and the trace is less than , the equilibrium point is an evolutionarily stable strategy (ESS); if the determinant is higher than and the trace is equal to , the equilibrium point is a center point. The Jacobian matrix, determinant, and trace of the differential dynamical system are:
where . According to the research hypothesis, it follows that ; substituting each equilibrium point into the determinant and trace yields their stability analysis result. The equilibrium point is a saddle point when and is uncertain; the equilibrium point is unstable when and ; the equilibrium point is stable when and . The analysis results are shown in Table 2.

Table 2.
Stability analysis results of each equilibrium point under the traditional mode.
According to the replication dynamic equation of banks and MSEs, the corresponding group dynamic evolution phase diagrams are shown in Figure 6.
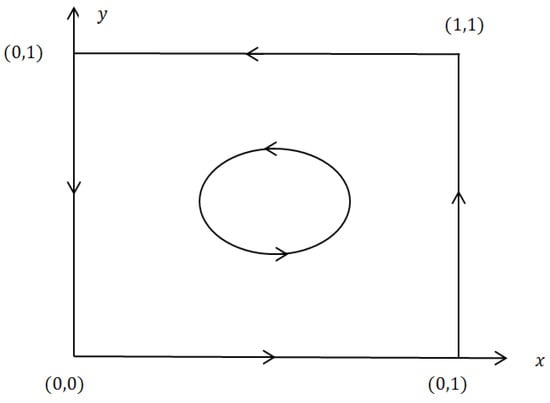
Figure 6.
Replication dynamics between MSEs and banks under the traditional mode.
Figure 6 shows that the evolutionary trajectory of banks and MSEs under the traditional mode is extremely unstable. This is because information asymmetry always exists between banks and enterprises, and MSEs are usually the party with the dominant information. Although banks can obtain the risk information and the credit level of MSEs in certain ways, it requires huge costs; at the same time, there is also the risk that MSEs may default, which will lead banks to choose to reject loans. For MSEs, if the default cost is low, after obtaining the loan, there may also be defaults, which will eventually lead to the long-term credit rationing phenomenon for MSEs. The causes of the credit rationing of MSEs are thus explained.
3.2. Evolutionary Game Analysis under Big Data Credit Technology
3.2.1. Game Hypothesis
Compared with the traditional case, banks can efficiently screen out high-quality MSEs by applying big data credit technology to make much more scientific credit decisions, and provide financing support to borrowers pertinently []. Because of the lower information asymmetry between high-quality MSEs and banks, the credit discrimination from banks can be alleviated or even eliminated; MSEs have more opportunities to obtain loans and obtain better credit conditions, such as lower interest rates, fewer collateral requirements, higher loan amounts, etc., thereby effectively improving their project returns []. The willingness of MSEs to repay the loan also increases, and the non-performing loan ratio of banks decreases; in addition, banks can mine potential “long-tail customers” through big data to gain higher returns []. Therefore, under big data credit technology, the following additional assumptions are proposed:
The cost of implementing big data credit technology is . In the case of banks implementing big data credit technology, the information asymmetry degree is reduced, and banks’ loan transactions will be more efficient and time-saving; then, assume that the transaction cost . In addition, big data also reduce the incomplete information degree in the credit market, so banks have more channels through which they can acquire customers []. Use to represent the informatization benefits that banks obtain from the “long-tail customers” when the bank chooses to lend and the enterprise chooses to repay, where .
Since banks can analyze and predict the credit status of MSEs based on their credit history, MSEs will pay more attention to their credit status and reputation, thus reducing the default probability to maintain a good credit record. Assuming that the credit level of MSEs is in the initial state, where , MSEs’ credit will increase when they choose to repay, and the credit growth rate is ; when they choose to default, their credit level will decrease, and the credit loss rate is . The credit level of honest MSEs will, therefore, increase. Finally, since the credit transactions under big data credit technology can generally be completed online, assume MSEs’ collateral cost rate .
3.2.2. Model Construct
Similar to the principles and methods under the traditional mode, the payoff matrix of the evolutionary game is shown in Table 3.

Table 3.
The payoff matrix of the evolutionary game under big data credit technology.
From Table 3, the expected return of MSEs choosing the repay strategy and the default strategy, and the average return are:
The expected return of banks choosing the lend strategy and the reject strategy, and the average return are:
Likewise, assume that, when MSEs choose to repay, the return of banks choosing to lend is higher than the return of banks choosing to reject the loan; when MSEs choose to default, banks’ return from rejecting the loan is higher than their return from choosing to lend: , , which are simplified as:
3.2.3. Model Analysis
- (1)
- The evolution path and evolutionarily stable strategy of MSEs and banks
(1) Game evolutionary trend of MSEs
The replication dynamic equation for MSEs to choose to repay is:
Substituting Equation (18) into Equation (24) yields
Substituting Equations (16) and (17) into Equation (25) yields
Differentiating with respect to yields
must satisfy . From Equation (26), and are two possible stable state values.
I When , always hold; i.e., all values of are stable states. The probability of banks adopting the lending strategy is ; all the values of are evolutionarily stable strategies for MSEs. According to Equation (26), the replication dynamics of MSEs are shown in Figure 7a.
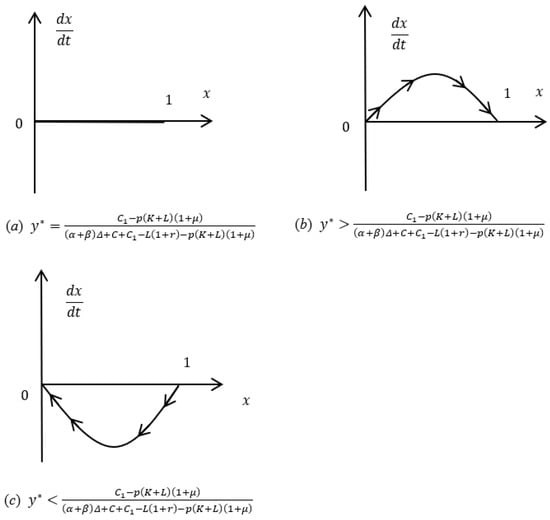
Figure 7.
The replication dynamic phase diagrams of MSEs under big data credit technology, where * means the stable state. (a–c) denote the cases when banks choose to lend with a probability equal to, greater than, and less than , respectively.
II When , and are two possible stable strategies of .
- (a)
- If , always hold; for and , there are and , respectively; therefore, is an evolutionarily stable strategy. The replication dynamics of MSEs are shown in Figure 7b; repaying is an evolutionarily stable strategy for MSEs;
- (b)
- If , always hold; for and , there are and , respectively; therefore, is an evolutionarily stable strategy. The replication dynamics of MSEs are shown in Figure 7c; defaulting is an evolutionarily stable strategy for MSEs;
- (c)
- If ,
① If , for and , we have and , respectively; then, is the evolutionarily stable strategy; i.e., when banks choose to lend with a probability higher than , repaying is the evolutionarily stable strategy for MSEs. The replication dynamics of MSEs are shown in Figure 7b.
② If , for and , there are and , respectively; then, is the evolutionarily stable strategy; i.e., when banks choose to lend with a probability less than , defaulting is the evolutionarily stable strategy for MSEs. The replication dynamics of MSEs are shown in Figure 7c. The replication dynamic phase diagrams of MSEs under different conditions are shown in Figure 7.
(2) Game evolutionary trend of banks
The replication dynamic equation for banks to choose to lend is:
Differentiating with respect to yields
Denote the probability of banks choosing to lend in the replication dynamic stable state as . Let ; then, are two possible stable state values.
I When , , always hold; then, all values of are stable states. The probability of MSEs choosing the repayment strategy is ; all values of are evolutionarily stable strategies for banks. The replication dynamics of banks are shown in Figure 8a.
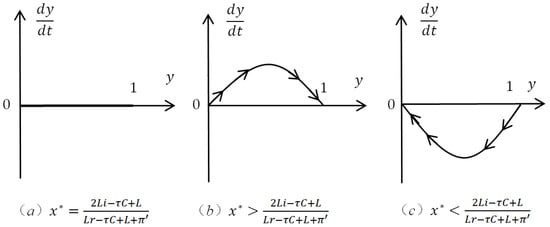
Figure 8.
The replication dynamic phase diagrams of banks under big data credit technology, where * means the stable state. (a–c) denote the cases when MSEs choose to repay with a probability equal to, greater than, and less than , respectively.
II when , according to the assumptions (22), (23), and , we have .
- (a)
- When , is an evolutionarily stable strategy; the replication dynamics of banks are shown in Figure 8b. When MSEs choose to repay with a probability higher than , banks will gradually shift from rejecting loans to lending.
- (b)
- When , is an evolutionarily stable strategy; the replication dynamics of banks are shown in Figure 8c. When MSEs choose to repay with a probability less than , rejecting the loan is an evolutionarily stable strategy for banks. The replication dynamic phase diagrams of banks under different circumstances are shown in Figure 8:
- (2)
- Evolutionary stability analysis of the system
By solving the replication dynamic equation set consisting of Equations (26) and (28), it follows that, in the region , there are five replication dynamic equilibrium points, which are , where . The Jacobian matrix , determinant , and trace of the differential dynamical system are:
where . According to the research hypothesis, it follows that . By substituting each equilibrium point into the determinant and trace , the stability analysis results of each equilibrium point are shown in Table 4.

Table 4.
Stability analysis results of each equilibrium point under big data credit technology.
From Table 4, there are four equilibrium points when and . The equilibrium point () is a stable local equilibrium point in the dynamic system. (), (0,), and () are unstable points or saddle points. When , there are five equilibrium points, and the equilibrium point () is the center point. The dynamic evolution phase diagrams of the corresponding group under the three circumstances are shown in Figure 9.
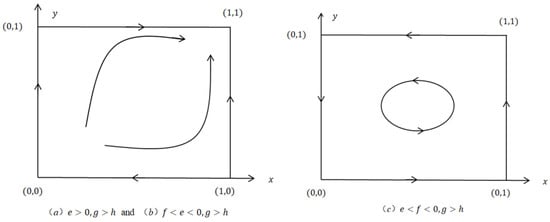
Figure 9.
The stability of the replication dynamics of the two groups under big data credit technology.
- (3)
- Model discussion
According to the value range of , the evolutionary game system of banks and MSEs can be divided into three cases.
Case 1. (): means the credit level of MSEs is high enough: when banks choose to lend, the return of MSEs choosing to repay is higher than the return of choosing to default, and the difference between the return on repayment and the return on default is higher than the return when they borrow from non-bank financing channels; when MSEs choose to repay the loan, the return of banks choosing to lend is higher than the return of choosing to reject the loan. Therefore, the strategy of MSEs and banks is: (repay, lend). In this case, although the replication dynamic equation has four equilibrium points: (), (), (), (), the stable point is (). As shown in Figure 9a, among the four strategy combinations of the game matrix, () corresponds to a win-win situation for both parties; accordingly, big data credit technology can significantly alleviate the credit rationing of MSEs.
Case 2. (): means, when banks choose to lend, the return of MSEs choosing to repay minus the return of choosing to default is less than the return of borrowing from non-bank financing channels; however, the return created by the credit level of MSEs is high enough to cover related costs, and MSEs tend to obtain loans from banks, which is their preferred financing channel. When banks choose to lend, the return of MSEs choosing to repay is higher than the return of choosing to default, and MSEs will choose to repay; when MSEs choose to repay, the return of banks choosing to lend is higher than that of choosing to reject the loan, and banks will choose to lend. Although there are four equilibrium points in the replication dynamic equation: (), (), (), (), the stable point is (). As shown in Figure 9b, banks will obtain higher returns and the credit rationing of MSEs will be alleviated.
Case 3. (): means the credit level of MSEs is too low: when banks choose to lend, the return of MSEs choosing to default is higher than that of choosing to repay, and MSEs will choose to default; when MSEs choose to default, banks will obtain higher returns if they choose to reject the loan. The replication dynamic equation has five equilibrium points: (), (), (), (), (), where () is the center point and the remaining four equilibrium points are unstable. As shown in Figure 9c, the group strategy state will dynamically fluctuate around the center point () and make periodic adjustments. The center point of the evolutionary game equilibrium is a stable equilibrium point, but it is not asymptotically stable and there is no limit cycle in this dynamic replication system []. In this case, it is difficult to determine whether big data credit technologies can alleviate the credit rationing of MSEs.
4. Comparison of MSEs’ Credit Rationing Degree
4.1. Simulation Experiment under the Traditional Mode
Under the traditional mode, the influencing variables of the evolutionary game path between banks and MSEs are . The initial states of and are set to and the evolution process ends at . The parameter values for the simulation experiments are set mainly based on the sensitivity of the factors to the choice of actions of the nodes in the credit system. In reality, it is necessary to analyze the situation on a case-by-case basis. The values of each variable are set as shown in Table 5; the initial values of the following parameters are brought into the replication dynamic equation of the bank-enterprise evolutionary game, and MATLAB is used for numerical simulation analysis.

Table 5.
Initial values of numerical simulation parameters.
According to Table 5, , , . Through the ode45 function of MATLAB, the strategy evolution path of banks, MSEs, and the game system are shown in Figure 10a–d, respectively, where Figure 10c represents the overall evolution path of the game system, and Figure 10d represents the local evolution situation around the center point of the game system.
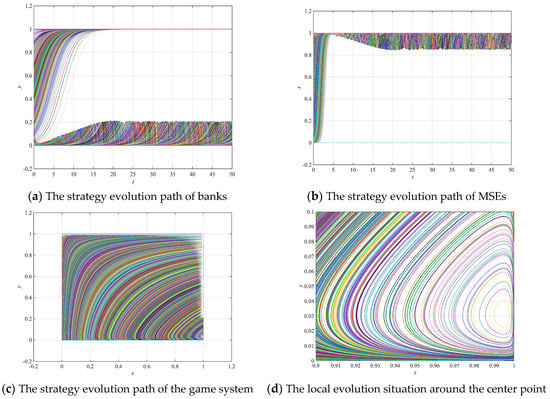
Figure 10.
Simulation results of the dynamic evolution path under the traditional mode, where (a,b) represent the strategy evolution path of banks and MSEs, (c) represents the overall evolution path of the game system, (d) represents the local evolution situation around the center point of the game system.
From Figure 10a, the evolution path of banks is related to the initial value. When the initial value is small, the evolution path of banks gradually evolves into periodic oscillation around the center point. As the initial value increases, the evolution path of banks gradually evolves to ; i.e., banks choose to lend, and the larger the initial value, the faster the speed of evolving to . Figure 10b shows that the evolution path of MSEs gradually evolves into periodic oscillations around the center point. As can be seen from Figure 10c, in the process of the evolutionary game, fluctuates greatly, also fluctuates up and down with the change of , and the evolution path of bank-enterprise strategy is unstable; i.e., banks’ decision changes with the decision of MSEs, and the strategy trajectory oscillates infinitely around the center point and cannot reach equilibrium. In the long run, since the strategy choice has an impact on the payoff matrix of both parties, there is great uncertainty in the co-operation between banks and MSEs, and it is difficult to form a stable co-operative relationship; as a result, the lend strategy and the repay strategy fluctuate constantly, and the credit rationing of MSEs will persist.
4.2. Simulation Experiment under Big Data Credit Technology
Under big data credit technology, in addition to variables , variables also affect the evolutionary game path between banks and MSEs. According to the model discussion results, by assigning values to each variable, a simulation analysis of the three cases can be obtained.
Case 1. (): set ; therefore, . The strategy evolution path of banks, MSEs, and the game system are shown in Figure 11a–c, respectively.
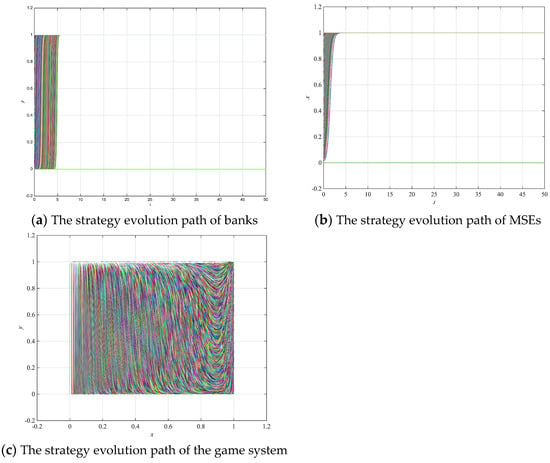
Figure 11.
Dynamic evolution path simulation results under big data credit technology (Case 1), where (a–c) represent the strategy evolution path of banks, MSEs and the game system respectively.
From Figure 11, when , the evolution path of banks and MSEs evolves to over time; i.e., banks choose to lend, and MSEs choose to repay, which shows that the application of big data credit technology can effectively reduce the information asymmetry and MSEs’ willingness to default, so that banks can provide targeted loans, thereby reducing credit risk and, ultimately, obtain a higher return. The credit rationing level of MSEs will be reduced as a result.
Case 2. (): set ; therefore, . The strategy evolution path of banks, MSEs, and the game system are shown in Figure 12a–c, respectively.
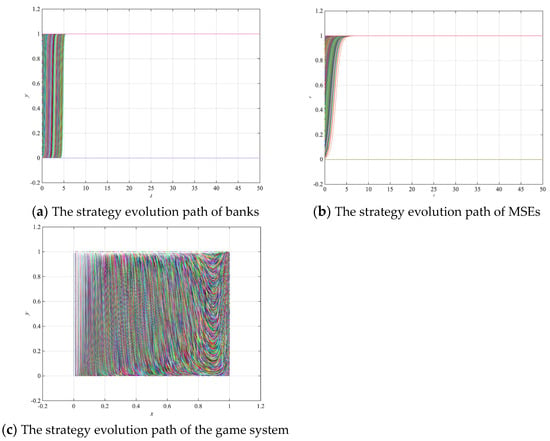
Figure 12.
Dynamic evolution path simulation results under big data credit technology (Case 2), where (a–c) represent the strategy evolution path of banks, MSEs and the game system respectively.
From Figure 12, when , the system evolution path of banks and MSEs gradually evolves into over time; i.e., banks choose to lend and MSEs choose to repay. It shows that, under this circumstance, the credit rationing of MSEs becomes significantly alleviated.
Case 3. (): set ; therefore, , , and . The strategy evolution path of the banks, MSEs, and the game system are shown in Figure 13a–c, respectively.
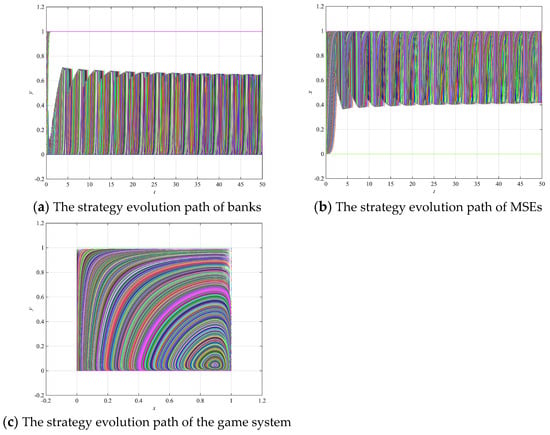
Figure 13.
Dynamic evolution path simulation results under big data credit technology (Case 3), where (a–c) represent the strategy evolution path of banks, MSEs and the game system respectively.
From Figure 13a,b, when , the evolution paths of banks and MSEs gradually evolve into periodic oscillations around the center point, which is similar to the evolution trajectory under the traditional mode. From Figure 13c, the evolution path of banks and MSEs is extremely unstable over time, and the strategy trajectory oscillates infinitely around the center point, which cannot reach equilibrium. This is because, in this case, the average credit level of MSEs is too low, which will affect the strategy choices of MSEs in the imitation learning process; the decision of MSEs to choose to default will affect the decision of banks to choose to lend. Since the strategy choice has an impact on the payoff matrix of both parties, there will be continuous fluctuations in lending strategy and repayment decisions. Therefore, in this case, the role of big data credit technology in the credit rationing of MSEs is uncertain.
4.3. Comparison of Credit Rationing Degree of MSEs
According to the results of the above analysis, since there are differences in the evolution results of the credit strategy trajectories of banks and MSEs under the three cases, in order to verify whether big data credit technology can alleviate the credit rationing of MSEs, we compare and analyze the differences in the credit rationing of MSEs under the traditional mode and big data credit technology for the three cases through simulation experiments. The probability of banks choosing to reject loans reflects the probability that the MSEs are subject to credit rationing; therefore, the credit rationing level of MSEs is measured by the probability of banks choosing to reject the loan. Take the initial values of and to perform the numerical simulation analysis.
Under the traditional mode, set ; correspondingly, , .
Under big data credit technology, for case 1, set ; then, , .
For case 2, set ; then, , ;
For case 3, set ; then, and .
The comparison results of the evolution path of credit rationing for MSEs under the two credit modes for the three cases are shown in Figure 14.
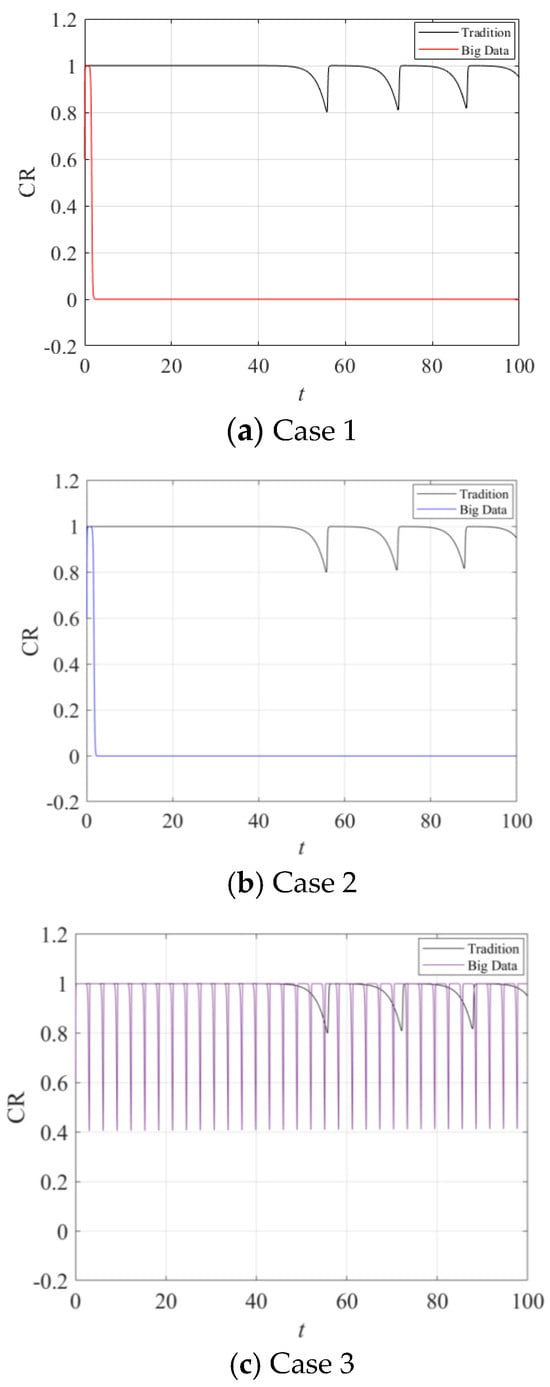
Figure 14.
Evolution paths of credit rationing for MSEs under different credit modes.
From Figure 14a,b, for cases 1 and 2, under the traditional mode, the credit rationing degree of MSEs evolves from to periodic fluctuations around over time. However, under big data credit technology, the credit rationing degree of MSEs evolves to around the initial point, but rapidly evolves to , indicating that big data credit technology has a significant effect on alleviating the credit rationing of MSEs when the overall credit level of MSEs is high. According to Figure 14c, for case 3, since the overall credit level of MSEs is too low, instead of evolving to , the credit rationing of MSEs will fluctuate periodically above the initial point, but, on the whole, the credit rationing level of SMEs under big data credit technology is still lower than that of the traditional mode, which means that, in any case, big data credit technology is effective in alleviating the credit rationing of MSEs.
5. Discussion
5.1. Challenges of Applying Big Data Credit Technology
The potential of big data technologies is undeniable, but data scientists face different challenges when dealing with large datasets to mine knowledge from these information sources. Oussous et al. (2017) indicated that the application of big data faces challenges in data acquisition, storage, search, sharing, analysis, management, and visualization; in addition, there are security and privacy issues for distributed-data-driven apps []. With regard to banks, on the one hand, big data puts forward higher requirements for the bank’s hardware equipment; big data, because they include a large amount of unstructured data, not only require the bank’s hardware equipment to have a higher performance, but also demand the bank’s practitioners to be highly competent. The employees in different departments of the bank need to be competent in applying and analyzing big data to ensure that the role of big data for the bank will be put into practice. On the other hand, big data put forward higher requirements for banks’ data security technology; in the context of big data, banks’ internal databases have stored huge amounts of user data, and the leakage of user data may lead to serious consequences. The occurrence of a large number of undesirable events has illustrated the importance of banks’ data security; in order to avoid the security risks of user information, banks need to improve the security of their information systems. Therefore, it will take time for banks to effectively implement big data credit technology, and they may lack experience at the beginning of the implementation of big data credit technology; moreover, they need to invest, which has huge costs. In the case where the overall credit level of MSEs is too low, the effect of banks’ implementation of big data credit technology may not be perfect; therefore, to better solve the problem of credit rationing for MSEs, it is also necessary to rely on the government’s macro-policy regulation at the same time.
5.2. Future Prospects
With the increasing availability of data, higher levels of data governance, and the integration of big data and artificial intelligence technologies, financial services will integrate deeper with the real economy and create more value. For banks and MSEs, there will be the following trends in the future: Firstly, demand for data security and privacy protection is increasing, and awareness of security and privacy protection is growing. Sensitive information constraints and data security inspection will be the difficult point of user data control on the Internet and mobile. Secondly, the single big data platform will develop into an integrated platform that integrates big data, artificial intelligence, and cloud computing. The traditional single big data platform no longer meets users’ application needs, and the big data analytics platform that integrates big data, artificial intelligence, and cloud computing will become a core system that links the IT system with employees, customers, partners, and the community to the equipment. Thirdly, banks and enterprises will gradually promote digital transformation. More and more banks and enterprises regard “data” as their core resources, assets, and wealth, and have formulated digital transformation strategies to realize the value of data, so as to occupy the new peaks of the digital economy and achieve the development goals of business innovation and intelligence.
From the perspective of the bank–enterprise relationship, traditionally, various financial services of banks to enterprises are mainly completed within the banking system; that is to say, the financial services of banks to enterprises are basically completed independently by banks internally. With the arrival of the big data era, various business segments of traditional banks have been continuously subdivided and outsourced to third-party institutions outside the banking system through a certain degree of standardization, which improves efficiency and realizes the social division of labor. As the degree of digitization continues to increase, external third parties are beginning to have easier and easier access to soft information that was previously available only through close bank–enterprise relationships, and this soft information is no longer exclusively possessed by the bank that maintains a close relationship with the enterprise, but is beginning to be progressively externalized and publicized, and, as a result, the bank–enterprise relationship is expected to undergo significant changes. On the one hand, banks can strengthen the established bank–enterprise relationship by building their own fintech platforms. On the other hand, if banks strengthen their co-operation with third-party technology platforms by sticking to financial segments such as payment, financing, and lending, the bank–enterprise relationship will gradually loosen up. With further development, the phenomenon of financial disintermediation may occur, with platform companies becoming the infrastructure for matching the supply and demand of financial services, and realizing their financial functions exclusively through direct financing and intermediary organizations.
5.3. Contributions
Our study makes three significant contributions to existing research: (1) We explain the persistence of credit rationing for MSEs under the traditional credit mode through an evolutionary game model. And we found that the credit strategies evolutionary trajectory of banks and MSEs under the traditional mode is extremely unstable and cannot reach equilibrium, which is a theoretical interpretation from a new perspective. (2) Different from the previous research on coping strategies for the credit rationing of MSEs, we consider the credit rationing of MSEs as a market mechanism defect; therefore, to alleviate the credit rationing of MSEs, banks need tools to obtain the risk information of MSEs, and big data credit technology provides an opportunity to realize this, and we demonstrated the theoretical feasibility of this strategy. (3) This study also fills the research gap on the impact of big data credit technology on the credit rationing of MSEs. By comparing the evolutionary trajectories of bank–enterprise credit strategies under big data credit technology and the traditional mode through an evolutionary game model, and comparing the extent to which big data credit technology alleviates the credit rationing of MSEs with different credit levels under the two credit modes through simulation experiments, we demonstrate that big data credit technology can effectively alleviate the credit rationing of MSEs, which complements research on the role of big data in the credit market.
5.4. Implications
Our study has some implications for MSEs and banks according to the findings. For MSEs, since the average credit level of MSEs will influence the strategy choices of MSEs in the imitation and learning process, and the strategy choices will have an impact on the payoff matrices of both parties, therefore, when the overall credit level of MSEs is too low, the default decision of MSEs will influence the lending decision of the bank, and, even in the case of the bank’s application of the big data credit technology, the evolution path of the bank and enterprise’s credit strategy is also not stable, and there will be a situation in which the bank’s lending strategy and the repayment decision of the MSEs are constantly fluctuating. When banks investigate the risk of MSEs, they mainly investigate the operational risk of the enterprise and the credibility risk of the owner, while the credibility risk of the owner is more important. According to the financing experience of MSEs around the world, more than half of the risk of MSEs’ loans depends on the honesty of the owner, followed by the operational status of the enterprise. Therefore, MSEs should strive to improve their credit level and optimize the construction of credit systems.
For banks, in the context of big data, the key to the success of banks in the competition lies in the acquisition of data value, and the core of the acquisition of data value lies in the analysis and processing of data; therefore, it is necessary for banks to promote the innovation of big data credit technology by constructing big data analysis platforms to improve the data analysis and processing capabilities. In addition, as an interdisciplinary field, “big data” involves different industries, which not only requires the bank’s big data analysts to have the ability to qualitatively analyze the credit risk, but also requires the big data analysts to have the ability to quantitatively analyze the risk model as well. The future competition of banks is the competition of talents; only by strengthening the cultivation of big data analysis talents can the bank realize better development with the help of big data. Therefore, banks should also pay attention to the cultivation of big data talents and strengthen the construction of a big data talent team.
Additionally, at present, banks tend to use big data technology more frequently in risk control, which is the most desired in the banking industry. However, the essence of risk control cannot create profits, only minimize losses. Therefore, as a tool to improve accuracy, even if the big data risk control technology is highly developed, there will be a limit; the reason is that the profitability of the credit business essentially relies on the net interest margin, and once the risk control technology reaches the limit, the net interest margin cannot be improved. Therefore, banks should turn to precision marketing as the future development direction by using big data technology as a vehicle.
6. Concluding Remarks
In light of the credit rationing phenomenon of MSEs and the opportunities that big data credit technologies provide to address this issue, based on the bounded rationality economic man hypothesis, the evolutionary game model of banks and MSEs under the traditional mode and big data credit technology is constructed, respectively, in this paper. By establishing the replication dynamic equation of the payoff matrix of banks and MSEs, the equilibrium points of the model under the two credit modes are solved, and the Jacobian matrix is constructed to analyze the stability of each equilibrium point; the evolutionary trajectory of bank–enterprise credit strategies under the two credit modes is obtained. In order to further verify the feasibility of big data credit technology in alleviating the credit rationing of MSEs, a simulation experiment is conducted to compare the differences in the credit rationing of MSEs with different credit levels under the traditional mode and big data credit technology.
The results show that the credit strategies evolutionary trajectory of banks and MSEs under the traditional mode is extremely unstable and cannot reach equilibrium; therefore, it is difficult to alleviate the credit rationing of MSEs. However, under big data credit technology, when the overall credit level of MSEs is high, the credit strategies’ evolutionary trajectory of banks and MSEs will eventually evolve into “lend” and “repay”, respectively; as a result, the credit rationing of MSEs will be effectively alleviated. When the overall credit level of MSEs is too low, the credit strategies evolutionary trajectory of banks and MSEs is relatively unstable; accordingly, it is difficult to determine whether big data credit technology can alleviate the credit rationing of MSEs. Nevertheless, the comparison results of the credit rationing of MSEs with different credit levels under the two credit modes show that the credit rationing of MSEs is always lower under big data credit technology than under the traditional mode. Consequently, we come to the conclusion that big data credit technology has a significant effect on alleviating the credit rationing of MSEs. This conclusion enriches the theoretical research on the role of big data credit technology and the credit rationing mechanism of MSEs, which provides a theoretical basis for banks to apply big data credit technology to achieve a win-win situation for both parties.
This study still has the following limitations: This paper demonstrates the feasibility of big data credit technology in alleviating the credit rationing of MSEs only by constructing evolutionary game models and implementing simulation experiments. However, due to data availability, we did not empirically test the theoretical model and conclusions of this paper by collecting real-world data related to the situation of credit rationing for MSEs before and after the implementation of big data credit technologies by banks.
Future research will consider quantifying the impact of banks’ application of big data credit technology on the credit rationing of MSEs by collecting real-world data to validate the theoretical model and conclusions of this paper. Furthermore, how external factors such as government policies, financial market competition, and economic trends affect the effectiveness of the implementation of big data credit technologies is also an important aspect for future research to consider.
Author Contributions
Conceptualization, Y.J.; methodology, Y.J.; software, S.Z.; validation, Y.J., S.Z. and X.L.; formal analysis, Y.J.; resources, S.Z.; writing—original draft preparation, Y.J.; writing—review and editing, Y.J. and S.Z.; visualization, X.L.; supervision, S.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Stiglitz, J.E.; Weiss, A. Credit Rationing in Markets with Imperfect Information. Am. Econ. Rev. 1981, 71, 393–410. [Google Scholar]
- Macmillan, H. Report of the Committee on Finance and Industry; CMD 3897; HMSO: London, UK, 1931. [Google Scholar]
- Lu, Z.; Wu, J.; Li, H.; Nguyen, D.K. Local Bank, Digital Financial Inclusion and SME Financing Constraints: Empirical Evidence from China. Emerg. Mark. Financ. Trade 2021, 58, 1712–1725. [Google Scholar] [CrossRef]
- Huber, K. Disentangling the Effects of a Banking Crisis: Evidence from German Firms and Counties. Am. Econ. Rev. 2018, 108, 868–898. [Google Scholar] [CrossRef]
- Moscalu, M.; Girardone, C.; Calabrese, R. SMEs’ Growth under Financing Constraints and Banking Markets Integration in the Euro Area. J. Small Bus. Manag. 2020, 58, 707–746. [Google Scholar] [CrossRef]
- Sen, D.; Ozturk, M.; Vayvay, O. An Overview of Big Data for Growth in SMEs. Procedia-Soc. Behav. Sci. 2016, 235, 159–167. [Google Scholar] [CrossRef]
- Kshetri, N. Big Data’s Role in Expanding Access to Financial Services in China. Int. J. Inf. Manag. 2016, 36, 297–308. [Google Scholar] [CrossRef]
- Wagdi, O.; Tarek, Y. The Integration of Big Data and Artificial Neural Networks for Enhancing Credit Risk Scoring in Emerging Markets: Evidence from Egypt. Int. J. Econ. Financ. 2022, 14, 32–43. [Google Scholar] [CrossRef]
- Vajjhala, N.R.; Ramollari, E. Big Data using Cloud Computing-Opportunities for Small and Medium-sized Enterprises. Eur. J. Econ. Bus. Stud. 2016, 4, 129–137. [Google Scholar] [CrossRef]
- Serena Garralda, J.M.; Tissot, B.; Doerr, S.; Gambacorta, L. Use of Big Data Sources and Applications at Central Banks; IFC Reports 13; Bank for International Settlements: Basel, Switzerland, 2021. [Google Scholar]
- Tsuruta, D. Japan’s Elderly Small Business Managers: Performance and Succession. J. Asian Econ. 2019, 66, 101147. [Google Scholar] [CrossRef]
- Brancati, E. Innovation Financing and the Role of Relationship Lending for SMEs. Small Bus. Econ. 2015, 44, 449–473. [Google Scholar] [CrossRef]
- Thuku, A.G. Factors Affecting Access to Credit by Small and Medium Enterprises in Kenya: A Case Study of Agriculture Sector in Nyeri County. Ph.D. Thesis, United States International University, Kenya, Africa, 2017. [Google Scholar]
- Bai, M.; Cai, J.; Qin, Y. Ownership Discrimination and Private Firms Financing in China. Res. Int. Bus. Financ. 2021, 57, 101406. [Google Scholar] [CrossRef]
- Kofarmata, Y.I.; Danlami, A.H. Determinants of Credit Rationing among Rural Farmers in Developing Areas. Agric. Financ. Rev. 2019, 79, 158–173. [Google Scholar] [CrossRef]
- Kira, A.; He, Z. The Impact of Firm Characteristics in Access of Financing by Small and Medium-sized Enterprises in Tanzania. Int. J. Bus. Manag. 2012, 7, 108–119. [Google Scholar] [CrossRef]
- Nguyen, H.; Qian, R. The Cross-Country Magnitude and Determinants of Collateral Borrowing; Policy Research Working Paper, No. 6001; World Bank: Washington, DC, USA, 2012; Available online: http://hdl.handle.net/10986/19878 (accessed on 20 May 2023).
- Moro, A.; Maresch, D.; Fink, M.; Ferrando, A.; Piga, C. Spillover Effects of Government Initiatives Fostering Entrepreneurship on the Access to Bank Credit for Entrepreneurial Firms in Europe. J. Corp. Financ. 2020, 62, 101603. [Google Scholar] [CrossRef]
- Calabrese, R.; Girardone, C.; Sclip, A. Financial Fragmentation and SMEs’ Access to Finance. Small Bus. Econ. 2021, 57, 2041–2065. [Google Scholar] [CrossRef]
- Aristei, D.; Gallo, M. Are Female-led Firms Disadvantaged in Accessing Bank Credit? Evidence from Transition Economies. Int. J. Emerg. Mark. 2022, 17, 1484–1521. [Google Scholar] [CrossRef]
- Beyhaghi, M.; Firoozi, F.; Jalilvand, A.; Samarbakhsh, L. Components of Credit Rationing. J. Financ. Stab. 2020, 50, 100762. [Google Scholar] [CrossRef]
- Long, J.; Jiang, C.; Dimitrov, S.; Wang, Z. Clues from Networks: Quantifying Relational Risk for Credit Risk Evaluation of SMEs. Financ. Innov. 2022, 8, 91. [Google Scholar] [CrossRef]
- Blanchflower, D.G.; Levine, P.B.; Zimmerman, D.J. Discrimination in the Small-Business Credit Market. Rev. Econ. Stat. 2003, 85, 930–943. [Google Scholar] [CrossRef]
- Masiak, C.; Block, J.; Moritz, A.; Lang, F.; Kraemer-Eis, H. How do Micro Firms Differ in Their Financing Patterns from Larger SMEs? Ventur. Cap. 2019, 21, 301–325. [Google Scholar] [CrossRef]
- De Jonghe, O.; Dewachter, H.; Mulier, K.; Ongena, S.; Schepens, G. Some Borrowers are More Equal than Others: Bank Funding Shocks and Credit Reallocation. Rev. Financ. 2020, 24, 1–43. [Google Scholar]
- Sun, H.; Cen, L.; Jiang, N. Our Empirical Study of Bank Loans Accessibility Influence Factors for SMEs. In Proceedings of the 2013 International Conference on Advanced ICT and Education, Hainan, China, 20–22 September 2013. [Google Scholar]
- Kariya, A. Earnings-Based Borrowing Constraints & Corporate Investments in 2007–09 Financial Crisis. J. Corp. Financ. 2022, 75, 102227. [Google Scholar]
- Shi, Y.; Li, J.; Liu, R. Financing Constraints and Share Pledges: Evidence from the Share Pledge Reform in China. J. Corp. Financ. 2023, 78, 102337. [Google Scholar] [CrossRef]
- Guo, J.; Fang, H.; Liu, X.; Wang, C.; Wang, Y. FinTech and Financing Constraints of Enterprises: Evidence from China. J. Int. Financ. Mark. Inst. Money 2023, 82, 101713. [Google Scholar] [CrossRef]
- Cooperatives Europe. A New SME Strategy: For an Inclusive SME Strategy at EU Level; Cooperatives Europe: Brussels, Belgium, 2020. [Google Scholar]
- Simba, A.; Tajeddin, M.; Dana, L.P.; Ribeiro Soriano, D.E. Deconstructing Involuntary Financial Exclusion: A Focus on African SMEs. Small Bus. Econ. 2023, 76, 1–21. [Google Scholar] [CrossRef]
- Ferri, G.; Murro, P.; Peruzzi, V.; Rotondi, Z. Bank Lending Technologies and Credit Availability in Europe: What Can We Learn from the Crisis? J. Int. Money Financ. 2019, 95, 128–148. [Google Scholar] [CrossRef]
- Vera, D.; Onji, K. Changes in the Banking System and Small Business Lending. Small Bus. Econ. 2010, 34, 293–308. [Google Scholar] [CrossRef]
- Gupta, P.; Tressel, T.; Detragiache, E. Finance in Lower Income Countries: An Empirical Exploration. IMF Work. Pap. 2005, 5, 1–49. [Google Scholar] [CrossRef]
- Swinnen, J.; Gow, H. The Role of Trade Credit and Foreign Investment in Improving the Agricultural Finance Situation in Transition Countries; Agricultural Finance and Credit Infrastructure in Transition Economies; OECD: Paris, France, 1999; pp. 54–66.
- Dai, X.; Verreynne, M.; Wang, J.; He, Y. The Behavioral Additionality Effects of a Tax Incentive Program on Firms’ Composition of R&D Investment. RD Manag. 2020, 50, 510–521. [Google Scholar]
- Beck, T.; Demirgü-Kunt, A. Financial Institutions and Markets across Countries and over Time. Soc. Sci. Electron. Publ. 2010, 24, 77–92. [Google Scholar]
- Arping, S.G.L.; Morrison, A.D. Public Initiatives to Support Entrepreneurs: Credit Guarantees versus Co-funding. J. Financ. Stab. 2010, 6, 26–35. [Google Scholar] [CrossRef]
- Ayadi, R.; Fanelli, A. A New Framework for Euro-Med Cooperation on MSME Support (No. 239); CEPS Policy, Centre for European Policy Studies: Brussels, Belgium, 2011. [Google Scholar]
- Lehmann, A.; Tamirisa, N.T.; Wieczorek, J. International Trade in Services: Implications for the IMF. IMF Policy Discuss. Pap. 2003, 6, 1–25. Available online: https://www.imf.org/external/pubs/ft/pdp/2003/pdp06.pdf (accessed on 15 May 2023).
- Isaksson, A. Access to Formal Finance in Kenyan Manufacturing. Afr. Dev. Perspect. Yearb. 2002, 9, 377–399. [Google Scholar]
- Cucculelli, M.; Peruzzi, V.; Zazzaro, A. Relational Capital in Lending Relationships: Evidence from European Family Firms. Small Bus. Econ. 2019, 52, 277–301. [Google Scholar] [CrossRef]
- Olufunso, F.O.; Francis, A. The Impact of Firm and Entrepreneurial Characteristics on Access to Debt Finance by SMEs in King Williams’ Town, South Africa. Int. J. Bus. Manag. 2011, 6, 170–179. [Google Scholar]
- Ogawa, K.; Sterken, E.; Tokutsu, I. The Trade Credit Channel Revisited: Evidence from Micro Data of Japanese Small Firms. Small Bus. Econ. 2013, 40, 101–118. [Google Scholar] [CrossRef]
- Lohr, S. The Age of Big Data; The New York Times: New York, NY, USA, 2012. [Google Scholar]
- Kaisler, S.; Armour, F.; Espinosa, J.A.; Money, W. Big Data: Issues and Challenges Moving Forward. In Proceedings of the 2013 46th Hawaii International Conference on System Sciences, Maui, HI, USA, 7–10 January 2013; pp. 995–1004. [Google Scholar]
- Kwon, O.; Lee, N.; Shin, B. Data Quality Management, Data Usage Experience and Acquisition Intention of Big Data Analytics. Int. J. Inf. Manag. 2014, 34, 387–394. [Google Scholar] [CrossRef]
- Gandomi, A.; Haider, M. Beyond the Hype: Big Data Concepts, Methods, and Analytics. Int. J. Inf. Manag. 2015, 35, 137–144. [Google Scholar] [CrossRef]
- Vance, A. The Data Knows. Bloom. Bus. Week. 2011, 70–74. [Google Scholar]
- Jaiswal, A.; Bagale, P. A Survey on Big Data in Financial Sector. In Proceedings of the 2017 International Conference on Networking and Network Applications (NaNA), Kathmandu, Nepal, 16–19 October 2017; pp. 337–340. [Google Scholar]
- Jin, B.; Cui, D.; Yang, R. Research on Industrial Chain Credit Reporting Based on Blockchain Technology. Credit. Ref. 2022, 40, 60–65. [Google Scholar]
- Swinkels, J.M. Evolution and Strategic Stability: From Maynard Smith to Kohlberg and Mertens. J. Econ. Theory 1992, 57, 333–342. [Google Scholar] [CrossRef]
- Chan, Y.S.; Kanatas, G. Asymmetric Valuations and the Role of Collateral in Loan Agreements. J. Money Credit. Bank. 1985, 17, 84–95. [Google Scholar] [CrossRef]
- Reilly, A. Non-bank Lending Growth under Threat. Int. Financ. Rev. 2019, 73. [Google Scholar]
- Mushtaq, R.; Gull, A.A.; Usman, M. ICT Adoption, Innovation, and SMEs’ Access to Finance. Telecommun. Policy 2022, 46, 102275. [Google Scholar] [CrossRef]
- Nguyen, C.; Pacheco, A. Confidentiality in Loan Credit Agreements. Int. J. Manag. Financ. 2021, 18, 336–364. [Google Scholar] [CrossRef]
- Saakian, D.B.; Fontanari, J.F. Evolutionary Dynamics on Rugged Fitness Landscapes: Exact Dynamics and Information Theoretical Aspects. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2009, 80, 593–598. [Google Scholar] [CrossRef]
- Xie, S. Economic Game Theory, 2nd ed.; Fudan University Press: Shanghai, China, 2002. [Google Scholar]
- Khan, A. Evolutionary Stability of Behavioural Rules in Bargaining. J. Econ. Behav. Organ. 2021, 187, 399–414. [Google Scholar] [CrossRef]
- Friedman, M.F. Decision Analysis and Optimality in Air Traffic Control Conflict Resolution: II. Optimal Heading (Vectoring) Control in a Linear Planar Configuration. Transp. Res. Part B Methodol. 1991, 25, 39–53. [Google Scholar] [CrossRef]
- Zhang, B. Application of Innovative Risk Early Warning Model Based on Big Data Technology in Internet Credit Financial Risk. J. Inf. Technol. Res. 2022, 15, 1–12. [Google Scholar] [CrossRef]
- Wessels, T.; Jokonya, O. Factors Affecting the Adoption of Big Data as a Service in SMEs. Procedia Comput. Sci. 2022, 196, 332–339. [Google Scholar] [CrossRef]
- Cornelli, G.; Doerr, S.; Gambacorta, L.; Tissot, B. Big Data in Asian Central Banks. Asian Econ. Policy Rev. 2021, 17, 255–269. [Google Scholar] [CrossRef]
- Albarrak, N.; Alsanousi, H.; Moulitsas, I.; Filippone, S. Using Big Data to Compare Classification Models for Household Credit Rating in Kuwait. In Proceedings of Sixth International Congress on Information and Communication Technology; Lecture Notes in Networks and Systems; Yang, X.S., Sherratt, S., Dey, N., Joshi, A., Eds.; Springer: Singapore, 2022; p. 216. [Google Scholar]
- Oussous, A.; Benjelloun, F.Z.; Lahcen, A.A.; Belfkih, S. NoSQL Databases for Big Data. Int. J. Big Data Intell. 2017, 4, 171–185. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).