The Impact of Return Shipping Insurance on a Retailer Based on Restricting Rights
Abstract
1. Introduction
2. Literature Review
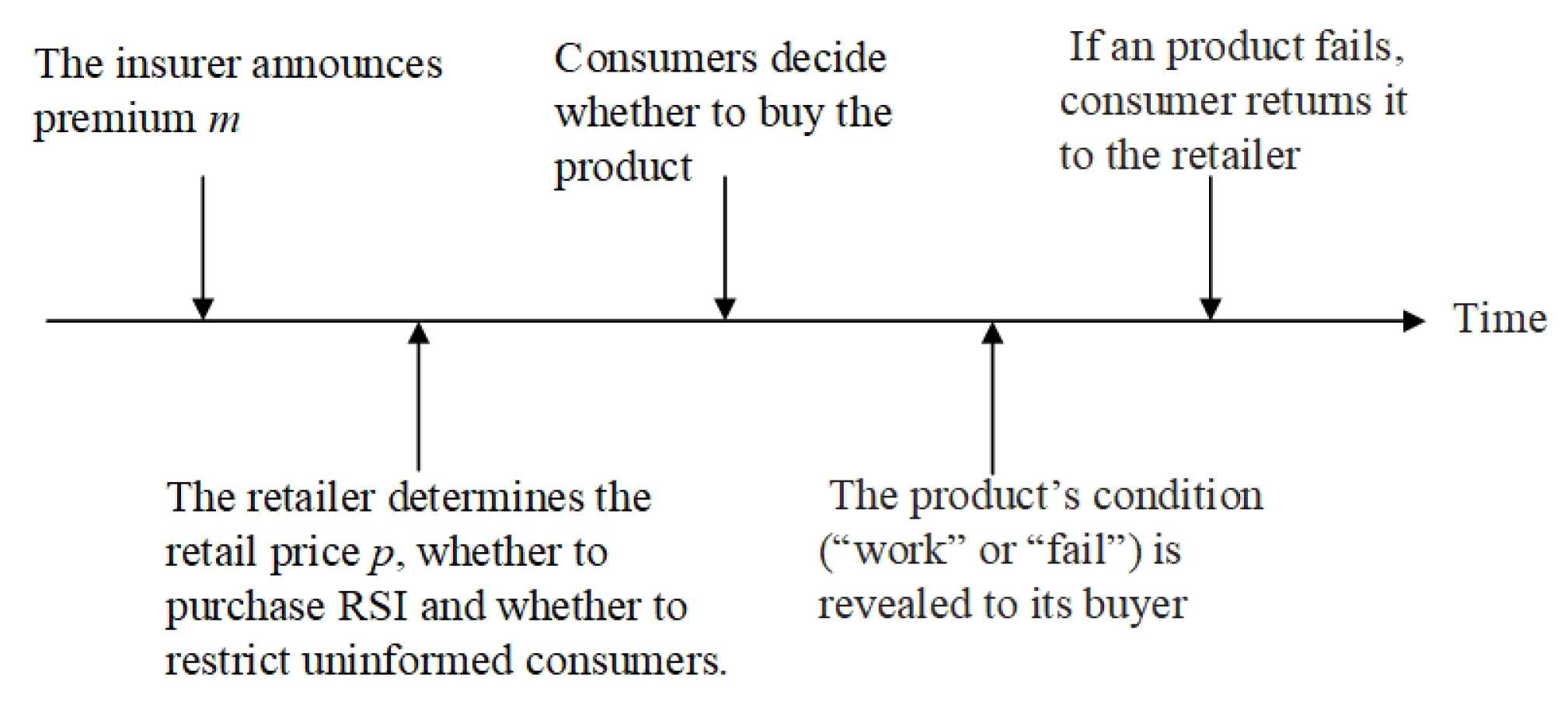
3. Problem Description
- (1)
- Scenario NN: Both the insurer and the retailer do not have the restricting right. In this case, the insurer decides the premium m. Then, the retailer decides the retail price p and whether to purchase RSI. Finally, consumers make their purchase and return decisions.
- (2)
- Scenario NR: The insurer does not have the restricting right, whereas the retailer has the restricting right. In this case, the insurer decides the premium m. Then, the retailer decides the retail price p, and whether to purchase RSI and restrict uninformed consumers from buying the product. Finally, consumers make their purchase and return decisions.
- (3)
- Scenario RN: The insurer has the restricting right, whereas the retailer does not have the restricting right. In this case, the insurer restricts uninformed consumers from obtaining RSI and decides the premium m. Then, the retailer decides the retail price p and whether to purchase RSI. Finally, consumers make their purchase and return decisions.
- (4)
- Scenario RR: Both the insurer and the retailer have the restricting right. In this case, the insurer restricts uninformed consumers from obtaining RSI and decides the premium m. Then, the retailer decides the retail price p and whether to purchase RSI and restrict uninformed consumers from buying the product. Finally, consumers make their purchase and return decisions.
4. Equilibrium Analysis
4.1. No Insurance–Benchmark Case (Scenario N)
4.2. Both the Insurer and the Retailer Do Not Have the Restricted Right (Scenario NN)
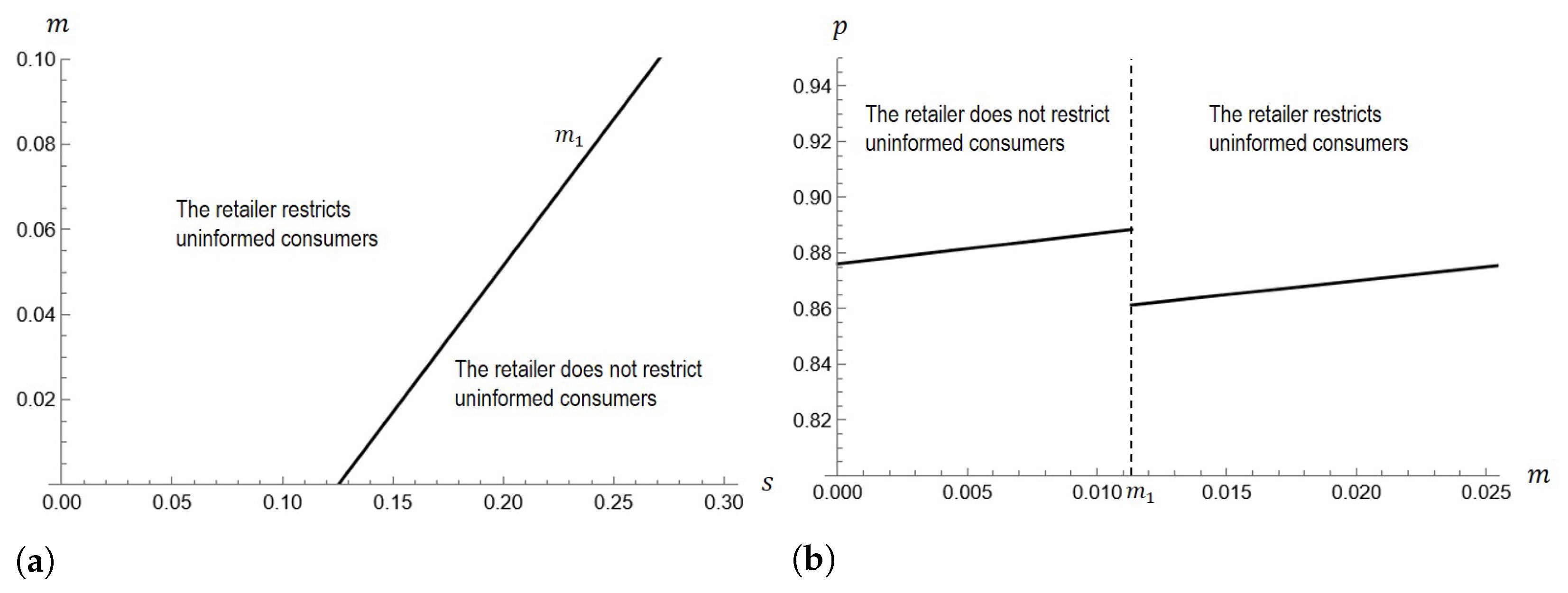
4.3. Only the Retailer Has the Restricted Right (Scenario NR)
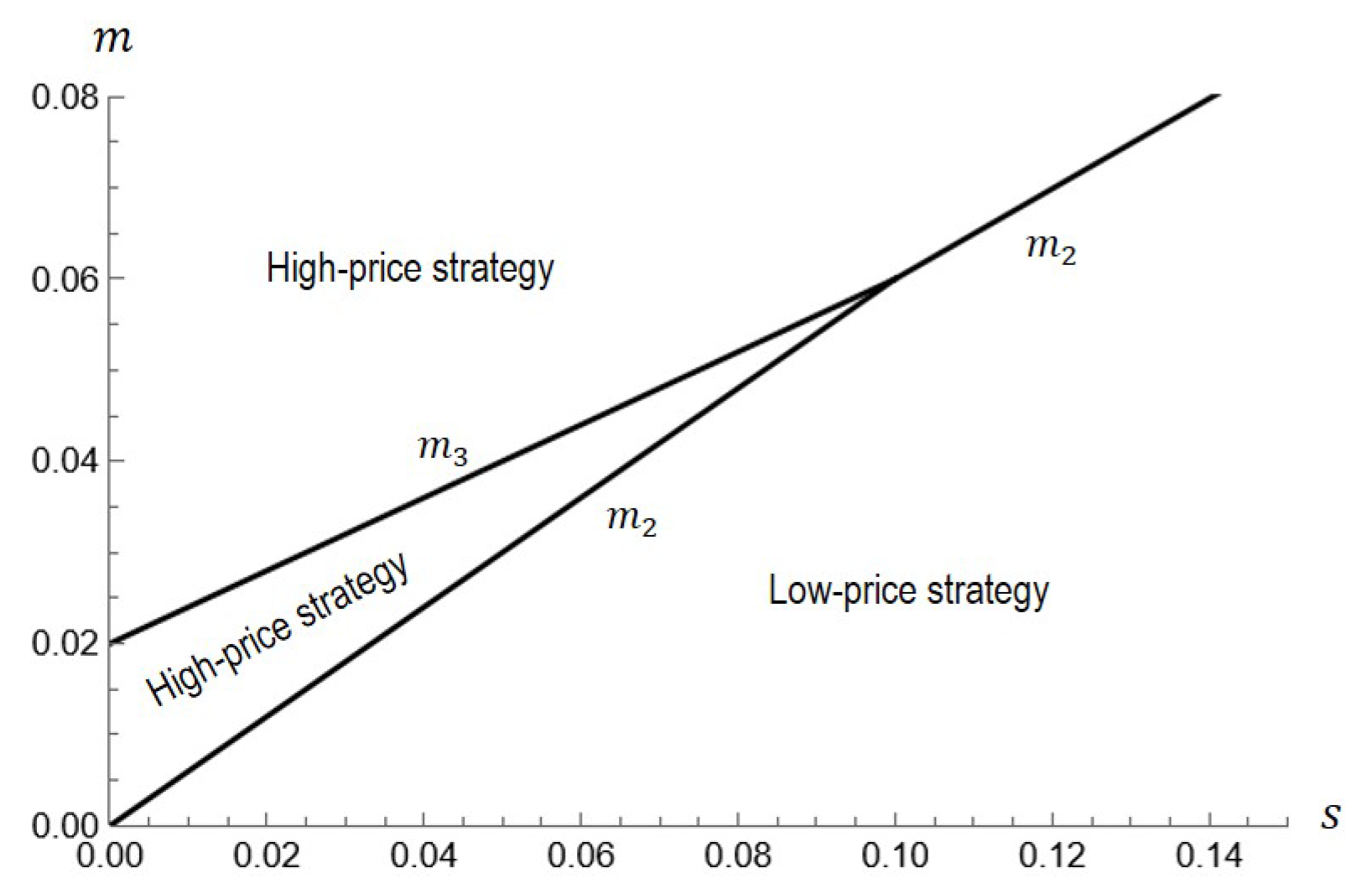
4.4. Only the Insurer Has the Restricted Right (Scenario RN)
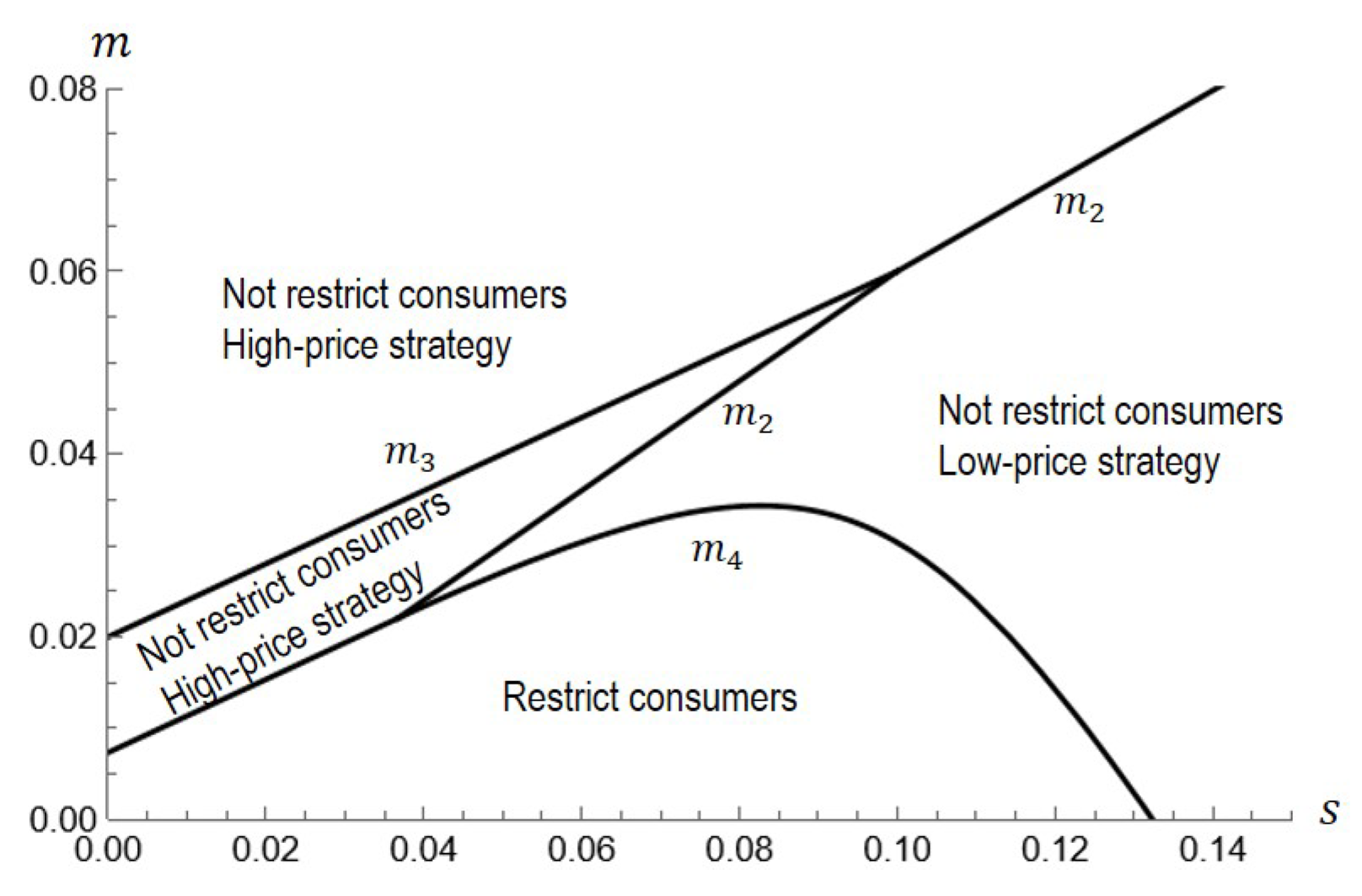
4.5. Both the Insurer and the Retailer Do Not Have the Restricted Right (Scenario RR)
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- CNNIC. The 49st Statistical Report on Internet Development in China. 2022. Available online: http://www.cnnic.net.cn/NMediaFile/old_attach/P020220721404263787858.pdf (accessed on 15 March 2022).
- Goldberg, J. E-Commerce Sales Grew 50% to $870 Billion during the Pandemic. 2022. Available online: https://www.forbes.com/sites/jasongoldberg/2022/02/18/e-commerce-sales-grew-50-to-870-billion-during-the-pandemic/?sh=4f681d294e83 (accessed on 15 March 2022).
- Saleh, K. E-Commerce Product Return Rate—Statistics and Trends. 2022. Available online: https://www.invespcro.com/blog/ecommerce-product-return-rate-statistics/ (accessed on 15 March 2022).
- ParcelLab. 5 Operations Experience Issues e-Commerce Brands Must Fix. 2021. Available online: https://parcellab.com/blog/5-post-purchase-tips (accessed on 15 March 2022).
- Marcia, K. The Growing Problem of Customer Returns. 2019. Available online: https://www.practicalecommerce.com/the-growing-problem-of-customer-returns (accessed on 15 March 2022).
- IAC. China Insurance Association Released the 2014–2019 Internet Property Insurance Market Analysis Report. 2020. Available online: http://www.iachina.cn/art/2020/3/16/art_22_104412.html (accessed on 15 March 2022).
- Davis, S.; Gerstner, E.; Hagerty, M. Money back guarantees in retailing: Matching products to consumer tastes. J. Retail. 1995, 71, 7–22. [Google Scholar] [CrossRef]
- Moorthy, S.; Srinivasan, K. Signaling quality with a money-back guarantee: The role of transaction costs. Mark. Sci. 1995, 14, 442–466. [Google Scholar] [CrossRef]
- Su, X. Consumer returns policies and supply chain performance. Manuf. Serv. Oper. Manag. 2009, 11, 595–612. [Google Scholar] [CrossRef]
- Hsiao, L.; Chen, Y.J. Returns policy and quality risk in e-business. Prod. Oper. Manag. 2012, 21, 489–503. [Google Scholar] [CrossRef]
- Xu, L.; Li, Y.; Govindan, K.; Xu, X. Consumer returns policies with endogenous deadline and supply chain coordination. Eur. J. Oper. Res. 2015, 242, 88–99. [Google Scholar] [CrossRef]
- Altug, M.S.; Aydinliyim, T. Counteracting strategic purchase deferrals: The impact of online retailers’ return policy decisions. Manuf. Serv. Oper. Manag. 2016, 18, 376–392. [Google Scholar] [CrossRef]
- Ofek, E.; Katona, Z.; Sarvary, M. “Bricks and clicks”: The impact of product returns on the strategies of multichannel retailers. Mark. Sci. 2011, 30, 42–60. [Google Scholar] [CrossRef]
- Chen, B.; Chen, J. When to introduce an online channel, and offer money back guarantees and personalized pricing? Eur. J. Oper. Res. 2017, 257, 614–624. [Google Scholar] [CrossRef]
- Ertekin, N.; Agrawal, A. How does a return period policy change affect multichannel retailer profitability? Manuf. Serv. Oper. Manag. 2021, 23, 210–229. [Google Scholar] [CrossRef]
- Hwang, E.H.; Nageswaran, L.; Cho, S.H. Value of Online–Off-line Return Partnership to Off-line Retailers. Manuf. Serv. Oper. Manag. 2022, 24, 1630–1649. [Google Scholar] [CrossRef]
- Geng, S.; Li, W.; Qu, X.; Chen, L. Design for the pricing strategy of return-freight insurance based on online product reviews. Electron. Commer. Res. Appl. 2017, 25, 16–28. [Google Scholar] [CrossRef]
- Chen, Z.; Fan, Z.P.; Zhao, X. Offering return-freight insurance or not: Strategic analysis of an e-seller’s decisions. Omega 2021, 103, 102447. [Google Scholar] [CrossRef]
- Li, Y.; Li, G.; Tayi, G.K.; Cheng, T. Return shipping insurance: Free versus for-a-fee? Int. J. Prod. Econ. 2021, 235, 108110. [Google Scholar] [CrossRef]
- Zhang, C.; Yu, M.; Chen, J. Signaling Quality with Return Insurance: Theory and Empirical Evidence. Manag. Sci. 2022, 68, 5847–5867. [Google Scholar] [CrossRef]
- Yang, G.; Ji, G. The impact of cross-selling on managing consumer returns in omnichannel operations. Omega 2022, 111, 102665. [Google Scholar] [CrossRef]
- Fan, Z.P.; Chen, Z. When should the e-tailer offer complimentary return-freight insurance? Int. J. Prod. Econ. 2020, 230, 107890. [Google Scholar] [CrossRef]
- He, J.; Liu, J.; Yang, F.; Zhao, X. Returns Freight Insurance Policy and the Impact from a BOPS Retailer. Oper. Res. Forum 2022, 3, 1–36. [Google Scholar] [CrossRef]
- Chen, Z.; Fan, Z.P.; Zhu, S.X. Extracting values from consumer returns: The role of return-freight insurance for competing e-sellers. Eur. J. Oper. Res. 2023, 306, 141–155. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, J.; Cheng, T.C.E. Optimal pricing and return policy and the value of freight insurance for a retailer facing heterogeneous consumers with uncertain product values. Int. J. Prod. Econ. 2020, 229, 107767. [Google Scholar] [CrossRef]
- Branco, F.; Sun, M.; Villas-Boas, J.M. Optimal search for product information. Manag. Sci. 2012, 58, 2037–2056. [Google Scholar] [CrossRef]
- Ke, T.T.; Shen, Z.J.M.; Villas-Boas, J.M. Search for information on multiple products. Manag. Sci. 2016, 62, 3576–3603. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, T. Price-directed consumer search. Int. J. Ind. Org. 2018, 58, 106–135. [Google Scholar] [CrossRef]
- Kuksov, D. Buyer search costs and endogenous product design. Mark. Sci. 2004, 23, 490–499. [Google Scholar] [CrossRef]
- Rhodes, A.; Zhou, J. Consumer search and retail market structure. Manag. Sci. 2019, 65, 2607–2623. [Google Scholar] [CrossRef]
- Jing, B. Showrooming and webrooming: Information externalities between online and offline sellers. Mark. Sci. 2018, 37, 469–483. [Google Scholar] [CrossRef]
- Ma, B.; Di, C.; Hsiao, L. Return window decision in a distribution channel. Prod. Oper. Manag. 2020, 29, 2121–2137. [Google Scholar] [CrossRef]
- Fruchter, G.E.; Gerstner, E. Selling with “satisfaction guaranteed”. J. Serv. Res-Us 1999, 1, 313–323. [Google Scholar] [CrossRef]
- Wu, D.; Ray, G.; Geng, X.; Whinston, A. Implications of reduced search cost and free riding in e-commerce. Mark. Sci. 2004, 23, 255–262. [Google Scholar] [CrossRef]
- Nageswaran, L.; Cho, S.H.; Scheller-Wolf, A. Consumer return policies in omnichannel operations. Manag. Sci. 2020, 66, 5558–5575. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, K.; Zhang, Y.; Duan, Y. Operation strategies with respect to insurance subsidy optimization for online retailers dealing with large items. Int. J. Prod. Econ. 2021, 232, 107944. [Google Scholar] [CrossRef]
- McCollough, M.A.; Gremler, D.D. A conceptual model and empirical examination of the effect of service guarantees on post-purchase consumption evaluations. Manag. Serv. Qual. 2004, 14, 58–74. [Google Scholar] [CrossRef]
- Lei, J.; de Ruyter, K.; Wetzels, M. Consumer responses to vertical service line extensions. J. Retail. 2008, 84, 268–280. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Dai, X.; Liu, Z. The Impact of Return Shipping Insurance on a Retailer Based on Restricting Rights. J. Theor. Appl. Electron. Commer. Res. 2023, 18, 706-724. https://doi.org/10.3390/jtaer18010036
Yang X, Dai X, Liu Z. The Impact of Return Shipping Insurance on a Retailer Based on Restricting Rights. Journal of Theoretical and Applied Electronic Commerce Research. 2023; 18(1):706-724. https://doi.org/10.3390/jtaer18010036
Chicago/Turabian StyleYang, Xingyi, Xiaopei Dai, and Zhenyu Liu. 2023. "The Impact of Return Shipping Insurance on a Retailer Based on Restricting Rights" Journal of Theoretical and Applied Electronic Commerce Research 18, no. 1: 706-724. https://doi.org/10.3390/jtaer18010036
APA StyleYang, X., Dai, X., & Liu, Z. (2023). The Impact of Return Shipping Insurance on a Retailer Based on Restricting Rights. Journal of Theoretical and Applied Electronic Commerce Research, 18(1), 706-724. https://doi.org/10.3390/jtaer18010036







