Abstract
The behavior-based discrimination price model (BBPD) needs to collect a large amount of user information, which would spark user privacy concerns. However, the literature on BBPD typically overlooks consumer privacy concerns. Additionally, most of the existing research provides some insights from the perspective of traditional privacy protection measures, but seldom discusses the role of quality discrimination in alleviating users’ privacy concerns. By establishing a Hotelling duopoly model of two-period price-quality competition, this paper explores the impact of quality discrimination on industry profits, user surplus, and social welfare under user privacy concerns. The results show that, with the increase of user privacy cost, given weak market competition intensity, quality discrimination can increase users’ surplus and social welfare, thereby alleviating users’ privacy concerns. We then discuss the managerial implications for alleviating consumer privacy concerns. In addition, we take Airbnb as an example to provide practical implications.
1. Introduction
E-commerce, search engines, and social media have promoted the rapid development of online platforms, making users enjoy a convenient life and leave a lot of private information on these platforms. After logging in, searching, or trading on online platforms, users will disclose multiple types of data, which, to a certain extent, reveal their personal characteristics, such as product preferences. Platforms can provide personalized services once they obtain users’ information, such as targeted advertising [1] and product recommendations [2,3]. Furthermore, platforms are able to charge different prices for different users, which is called personalized pricing [4]. One form of personalized pricing in reality is differentiated mobile coupons. For example, Lee and Choeh [5] find that the instantaneity of mobile phones has made mobile coupons one of the fastest growing promotional channels used by retailers and other companies. Mobile coupons are economic discounts that consumers receive electronically via their mobile devices.
Advances in information technologies have made it easier for platforms to collect, store, and analyze users’ personal data. The development of digital technology promotes platforms to learn about users’ willingness to pay, effectively improving platform firms’ abilities to personalize prices for users and enhances profits [6]. Shiller [7] shows that, compared with traditional demographic data, firms increase their profits by about 12.2% through analyzing users’ browsing data. According to the browsing records and purchasing history of users, platforms can easily distinguish old users from the new and provide differentiated strategies for different segments. A typical example of platform setting lower prices for new users occurred in 2000, when a user found that the price of a DVD on Amazon was lower after clearing the “Cookies” on the computer [8]. When the users clear the “Cookies”, the platform will no longer have their information, so these users can only be identified as new users, thus being charged a lower price. In addition, Dish, a TV service provider, assures new users that it can save them $250, while offering new product functions to old users, such as voice remote control, steam application, high-dimensional channels and advanced search, and providing them with personalized suggestions [9]. These examples show that platforms can not only offer price discounts to new users, but also offer higher product quality to old users. Furthermore, higher product quality is not only manifested in measurable product attributes, but also in perceived service quality. For example, Airbnb, a housing rental platform, can learn about the preferences of old users after analyzing their information. When the user makes a second purchase, Airbnb will give priority to presenting those houses that are well-aligned with users’ needs, thus bringing users a high-quality experience.
Although platforms can offer certain benefits to users through accessing their specific information, users are concerned about their privacy. As platforms collect more and more user information, users are increasingly aware that they are being monitored, which leads to their privacy concerns [10,11]. Additionally, one of the largest information providers, Acxiom, possesses more than 200 million pieces of information about Americans. Facebook, Google, and Amazon will collect more than 1 billion discrete units of information from users every month [9]. Data collection and usage as shown above directly exacerbate users’ privacy concerns. Some scholars who study the personalized services of firms also admit that such practices may raise users’ privacy concerns [12,13]. However, digital services need users’ data to improve service quality and generate revenues. In an era when users are paying more and more attention to privacy, how to balance the advantages of information technology and users’ privacy concerns is a question worth considering.
The previous studies primarily focus on two aspects to alleviate users’ privacy. Firstly, different privacy regulations or methods are proposed to protect users’ privacy [14,15,16]. In addition, some firms try to provide monetary benefits for users in exchange for their information. Information-collecting companies often offer a monetary reward to users to alleviate privacy concerns and ease the collection of personal information [17]. Despite users paying great attention to their privacy, their economic behaviors present otherwise. This phenomenon of contradictory privacy-related decisions is referred to as the privacy paradox [9,18]. If users realize the benefits of providing privacy, their concerns about privacy may be alleviated [19]. Quite a few papers have acknowledged the existence of the privacy paradox [18,20,21,22]. Since existing works have proved that monetary reward is an effective means to mitigate users’ privacy concerns, this paper tries to evaluate the impact of other benefits on this issue. We consider another feature of the product, i.e., this paper provides a new solution on how to ease the privacy concerns of users from the perspective of product quality.
To summarize, we consider users’ privacy concerns, examining the influence of the platforms’ behavior-based pricing model and quality discrimination on market participants. We focus on how the industry profits, user surplus, and social welfare will be affected after platforms implement quality discrimination, and discuss the impacts of market competition intensity and user privacy concerns on the results. Specifically, we address the following research questions: (1) With quality discrimination, how will the decision-making of platforms change? (2) Considering user privacy concerns, how should platforms provide product quality and charge for new and old users? (3) What influence does the market competition intensity have on the platforms’ quality strategy? (4) What changes will occur regarding industry profits, user surplus, and social welfare when considering quality discrimination? To solve these problems, we construct a two-period price-quality duopoly Hotelling competition game model, and analyze the equilibrium results with quality discrimination. Our contribution to the various strands of literature described above is as follows. Firstly, our study extends the study on BBPD by focusing not only on behavior-based pricing discrimination, but also on quality discrimination. Secondly, our study also focuses on consumers’ privacy concerns and introduces privacy cost into the model so as to study the impact of consumers’ privacy concerns on BBPD. Lastly, our study also provides a new idea for how to alleviate consumers’ privacy concerns, that is, how to alleviate consumers’ privacy concerns from the perspective of product quality. Our results not only provide new ideas for scholars to explore how to effectively mitigate the users’ privacy concerns, but also present some enlightenment for general platforms to make more effective strategies in the era when users pay more attention to privacy.
The paper is structured into seven sections. In Section 2, we review the related literature. In Section 3, we describe the problem, explain the symbols, and present the model. In Section 4, we show the equilibrium results of the benchmark model and main model. In Section 5, we analyze the social welfare impact of quality discrimination. In Section 6, we provide our conclusions and implications and the Appendix A contains proofs not provided in the main text.
2. Literature Review
This study is primarily related to the economic literature on behavior-based price discrimination (BBPD), which specifically means that platforms offer different prices to different users according to their purchase history. Zhang and Wang [23] consider online and offline e-commerce practices, while our study focuses on online platform practices. With the development of information technology, this pricing method is more and more widely used in data-driven industries. Most papers on BBPD mainly explore how platforms create price discrimination for new and old users. The conclusion of Fudenberg and Tirole [19] is that firms will reward new users with low prices. Shaffer and Zhang [24] extend BBPD and have challenged this view. They think that, when users face lower switching cost, firms may reward old users on price, i.e., the price offered to old users is lower. Belleflamme et al. [6] demonstrate that, if firms do not practice personalized pricing, they will eventually set the price at the marginal level, which will lead to the Bertrand paradox. Most scholars pay attention to how this pricing method is implemented but ignore its impact on consumers’ purchasing intention. In the empirical model, Akram et al. [25] assume that consumers’ trust in network providers would affect their purchasing behavior, and regard whether users’ privacy was protected as an item to measure their sense of trust. The hypothesis is proved to be valid. Since BBPD will spark privacy concerns among users, our study contributes to these studies through considering users’ privacy concerns.
There is also extensive literature about BBPD which involves quality discrimination. Pazgal and Soberman [26], based on the research of Fudenberg and Tirole [19], assume that firms provide high-quality products for old users, and present that, when firms adopt BBPD, they will charge lower prices to new users. They presuppose that old users will get a product with higher quality, while Li [27] regards the decision-making on quality as an endogenous process. The author uses a two-period dynamic game theory model to reveal the unique role of quality discrimination. It is found that there is an essential difference between quality discrimination and BBPD. BBPD intensifies the competition in the second period but weakens it in the first period. On the contrary, quality discrimination reduces competition in the second period and intensifies competition in the first period. Laussel and Resende [28] explore the influence of firms’ personalized practices concerning products and prices for old customers on firms’ profits, and focus on the effect of the size of firms’ old turfs and firms’ initial products on the results. Li [27] investigates the impact of quality discrimination on market competition. By contrast, this study focuses on how firms make price-quality decisions under different market competition intensity. Li [27] points out that firms should reward the new users in the price dimension and reward the old users in the quality dimension, which is consistent with our work.
Finally, our research is also related to the literature on how to alleviate users’ privacy concerns. A vast amount of literature considers the establishment of privacy protection regulations to alleviate users’ privacy concerns [14,15,16]. However, there is a huge gap between the views on the effectiveness of privacy regulation. Tayor [14] examines the impact of two regimes, i.e., confidential regime and disclosure regime on social welfare. He shows that, under the disclosure when users do not anticipate the sale of their information, users will be worse off while firms will fare well. Stigler [29] thinks that privacy protection causes low efficiency, i.e., the policies to protect user privacy have not improved social welfare. Lee et al. [16] report that whether privacy regulation increases social welfare is contingent on the specific circumstances, suggesting that regulation should be tailored to the circumstances. Loertscher and Marx [30] explore the two sides of interventions concerning an environment in which a digital monopoly can use data to either only improve matching or to improve matching as well as to adjust pricing. They report that privacy protection should protect users’ information rent, not their privacy. In addition, many privacy advocates believe that privacy regulations can have a positive impact on the tech giants’ data practices, while some critics worry that such restrictions could reduce firms’ investment in quality [31]. Since there are a number of open questions about the effectiveness of privacy regulation, this study examines how to make users better off from another perspective. Our finding is that, under certain conditions of market competition intensity and user privacy cost, platforms’ quality discrimination may benefit users.
Kummer and Schulte [32] reveal the transaction of exchanging money for privacy in the smartphone app market. Developers offer their apps at lower prices in exchange for more access to personal information, and users balance between lower prices and more privacy. Xu et al. [33] examined the usage of location-based services and found that monetary incentives made users more willing to be located by the operator, since product price, i.e., monetary dimension, has been proven to be beneficial to easing user privacy. This study puts forward a new idea, i.e., platforms can use higher product quality in exchange for users’ privacy. In other words, if platforms provide users with higher quality products, users’ privacy concerns may be alleviated to a certain extent.
In conclusion, we can find that the research on pricing decisions between platforms is relatively common, and some scholars consider other strategies based on product pricing [26,34], but there are still some limitations. First of all, the research on BBPD is relatively mature, but the consideration of privacy concerns is overlooked. BBPD will bring their privacy concerns for using specific information of users, but many models do not recognize users’ privacy concerns. This study extends the literature of BBPD and focuses on the impact of user privacy cost on BBPD. Secondly, research on price-quality decision-making between competitive platforms is still relatively rare. Based on BBPD, what impact will the quality discrimination have on the results of competitive equilibrium? In addition, the interactive effect between price and quality needs further study. Finally, the literature on alleviating users’ privacy concerns either focuses on how to implement privacy protection measures or provides monetary rewards; few scholars have studied another feature of products, i.e., product quality to alleviate user privacy concerns. This paper extends this issue.
Therefore, based on the research of Li [27], we construct a two-period duopoly competition game model considering the privacy cost and switching cost of users, obtain the equilibrium solutions under two scenarios i.e., with quality discrimination and non-quality discrimination, and explore the influence of quality discrimination on industry profits, user surplus and social welfare. Furthermore, this study also discusses the impact of quality discrimination on users’ privacy concerns. Our finding can help platforms to make better decisions in an environment where users are increasingly concerned about privacy, and have significant meaning for relevant government personnel to put forward appropriate initiatives to guide the effective operation of the market. For users, it can enable them to learn about the formulation process of platforms’ strategies, so as to make more informed consumption decisions.
3. The Two-Period Model
3.1. Problem Description
There are two competitive platforms providing homogeneous products or services in the market, which are located at both ends of the linear city. Users are evenly distributed in linear cities. Platforms have the ability to collect and analyze users’ specific information, distinguish between new and old users, and set different prices for them. If quality discrimination is available, platforms can also formulate different product or service quality for new and old users. This paper studies the effects of quality discrimination under different market competition intensity and the cost of user privacy concerns.
3.2. Notations Description
The variables involved in this study and their meanings are shown in Table 1.

Table 1.
Summary of notations.
3.3. Model Setups
Assume that there are two competing platforms, i.e., A and B, that offer the same products or services in the market, but the products or services provided by these two platforms have different characteristics. This paper uses the Hotelling model to describe the differences in products or services offered by the two platforms, i.e., these two platforms are located at the two ends of the interval [0, 1]. Without loss of generality, the number of users in the market is normalized to one, and they are evenly distributed in the horizontal market. Users’ locations stand for their preference for the service, which is aligned best with the products or services provided by the nearest platforms. Therefore, users will enter the nearest platform to consume. Every user’s retention utility of products is large enough to make sure the market is fully covered in each period. We also assume that each user only buys one unit of the product in each period. Users need to pay a transportation cost to purchase from platforms, which represents the degree of product differentiation between the two platforms [29] and is interpreted as the competition intensity.
To be mentioned, the price-quality game model of competitive platforms in this paper is divided into two periods. In the first period, since all users are anonymous users to platforms, only basic prices can be provided, i.e., . According to the standard Hotelling model [35], the quality provided by platforms in this case is symmetrical, so the quality of the first period is standardized to zero. After the end of the first period, platforms can collect the purchase history of users, and distinguish between new and old users. In the second period, when there is no quality discrimination, the platforms set the same level of product quality for the new and old users. Therefore, platforms decide and . When there is quality discrimination, platforms set different levels of product quality for new and old users, so platforms decide and . It is assumed that users all know that platforms can collect user information after first-period purchasing. Therefore, when users repeatedly purchase products or services from the same platform, they will have privacy concerns, such as the risk of identity theft, the shame of exposing personal information, the potential risk of price discrimination, and being troubled by too many advertisements [36]. This paper uses an average privacy cost to represent this negative utility.
In this paper, the model without quality discrimination is regarded as the benchmark model, while the model with quality discrimination is as our main model. The timing of the main model is as shown in Figure 1.
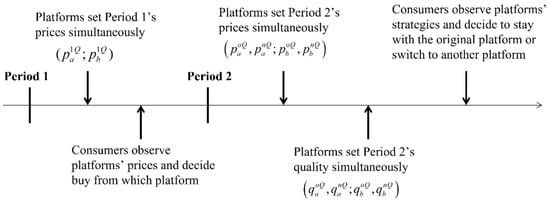
Figure 1.
The timing of the main model.
Using backward induction, the sub-game Nash equilibrium of the model is solved. Now, we will sort out the model assumptions in this paper:
1: The product quality of both platforms in the first period is standardized to zero [27].
2: When there is quality discrimination, both platforms will practice quality discrimination.
3: Users will face a privacy cost when they stay with the original platform to buy in the second period, while they incur a switching cost when they switch to another platform.
4: The marginal production cost of each platform is standardized as zero.
4. Analysis
4.1. Benchmark Model: Without Quality Discrimination
4.1.1. Competition in Period 2
Users’ decisions. Figure 2 depicts the consumption pattern without quality discrimination. For the users who purchase from platform A in the first period, i.e., (as shown in Figure 2), the utility they obtain from staying with the original firm is , and the utility they gain from switching to platform B is . Making the two utilities be equal, we obtain the marginal users’ location, i.e., . Similarly, for those users who buy from platform B in the first period, i.e., (as shown in Figure 2), the utility they gain from staying with the original platform is , and the utility they receive from switching to platform A is . Letting these two utilities be equal, the marginal users are obtained, i.e., .
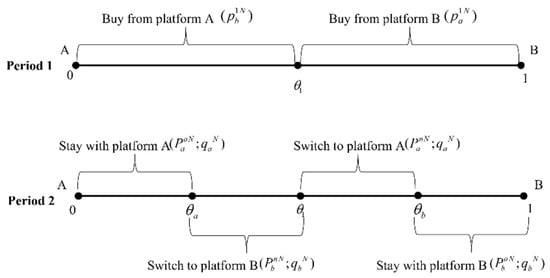
Figure 2.
The benchmark model.
Combining the two marginal users, it can be seen that the market shares for platform A are and , while the market shares for platform B are and .
Duopoly’ price decisions. The profit functions of the two platforms in the second period are:
The first-order optimization conditions are:
By solving the equations in (3), we can obtain the platforms’ prices for the new and old users as follows:
Duopoly’ quality decisions. Combine equations in (4) into platforms’ profit functions, and we obtain the first-order optimization conditions as follows:
By solving the equations in (5), we can obtain platforms’ quality decisions for users in each period as follows:
4.1.2. Competition in Period 1
Users’ decisions. For users (), the utility they have through purchasing from platform A in the first period and switching to platform B in the second period is . Similarly, the utility they have through purchasing from platform B in the first period and switching to platform A in the second period is . Letting these two utilities be equal, and combining equations in (4), (6), and (7), we obtain the marginal users in the first period, i.e., . Consequently, in the first period, platform A owns the turf in while platform B gains the market share in .
Duopoly’ price decisions. The platforms’ total profit functions are:
According to the first-order optimization conditions:
We solve the equations in (10), and obtain the prices platforms make in the first period as follows:
4.2. Main Model: With Quality Discrimination
4.2.1. Competition in Period 2
Users’ decisions. Figure 3 depicts the consumption pattern with quality discrimination. For the users who purchase from platform A in the first period, i.e., (as shown in Figure 3), the utility they obtain from staying with platform A is , and the utility they gain from switching to platform B is . Letting the two utilities be equal, we can get the marginal users’ location, i.e., . Similarly, for those users who buy from platform B in the first period, i.e., (as shown in Figure 3), the utility they get from continuing to choose platform B is , and the utility they receive from switching to platform A is . Letting these two utilities be equal, the marginal users are obtained, i.e., .
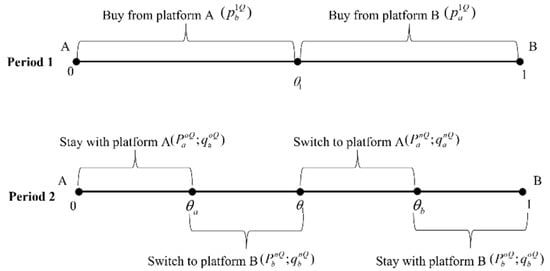
Figure 3.
The main model.
Combining the two marginal users, it can be seen that the turfs for platform A are and , while the turfs for platform B are and .
Duopoly’ price decisions. The profit functions of the two platforms in the second period are:
The first-order optimization conditions are:
By solving the equations in (14), we can obtain the platforms’ prices for the new and old users as follows:
Duopoly’ quality decisions. Combining equations in (15) into platforms’ profit functions, thus we obtain the first-order optimization conditions as follows:
By solving the equations in (16), we can obtain platforms’ quality decisions for the new and old users in the second period as follows:
4.2.2. Competition in Period 1
Users’ decisions. For users (), the utility they have for purchasing from platform A in the first period and switching to platform B in the second period is . Similarly, the utility they obtain from platform B in the first period and switching to platform A in the second period is . Letting these two utilities be equal, and then combining equations in (15), and (17) to (18), we get the marginal users in the first period, i.e., . Consequently, those who located in will buy from platform A while the users who located in will purchase from platform B in the first period.
Duopoly’ price decisions. The platforms’ total profit functions are:
The first-order optimization conditions are:
By solving the equations in (23), we obtain the platforms’ prices for users in the first period as follows:
To sum up, the equilibrium results of the competition game are shown in Table 2.

Table 2.
Equilibrium results with or without quality discrimination.
Proposition 1.
With quality discrimination, when and, or and, we can know. Without quality discrimination,can always be satisfied.
Figure 4 presents our numerical result of proposition 1 and shows how the product quality is affected by the privacy cost, i.e., and competition intensity, i.e., . Figure 4a shows that, when the privacy cost is low and there is quality discrimination, with the increase of competition intensity, platforms first set a higher quality for new customers than the old, and then set the opposite pricing strategy. Figure 4b demonstrates that, when the privacy cost is high and there is quality discrimination, with the increase of competition intensity, platforms first set a lower quality for new customers than the old, and then set the opposite pricing strategy. Proposition 1 indicates that, when there is quality discrimination, if the privacy cost of users is high, and when the competition intensity is relatively weak, the quality set by platforms for old users is relatively high, while the quality set for new users is lower. This is because, when users’ privacy cost is high, they are more likely to switch to another platform in the second period. The platform anticipates that users will choose to leave because they are worried about privacy in the second period, so the platform decides to reward the old users on product quality, and tries to compensate them with high quality. In addition, when the intensity of competition is weak, the products produced by platforms are more differentiated. The selection in the first period shows that the products produced by the original platforms are more in line with users’ preferences. If platforms innovate the original products, higher product quality or service quality can be provided, which makes it possible to improve users’ experience, thereby retainng old users.
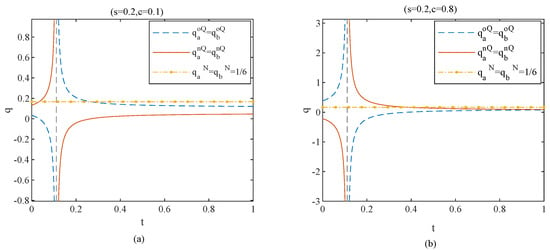
Figure 4.
Quality set by platforms in period 2 in equilibrium (c = 0.1 vs. c = 0.8).
On the other hand, if the privacy cost of users is low, when the competition intensity is strong, the platform will also set higher quality for old users and lower quality for new users. This is because, when the competition intensity is relatively strong, the degree of product differentiation between the two platforms is small. For users, the utilities from these two products will hardly be different, so it is more likely that users will switch to another platform in the second period. In anticipation of this, platforms try to defend their turf with higher quality. In the absence of quality discrimination, both firms provide a uniform quality for all users in equilibrium.
The Proposition 2 discusses how platforms charge new and old users in the second period as follows.
Proposition 2.
Without quality discrimination, when , we can obtain . However, with quality discrimination, only when and or and is there .
Proposition 2 reveals that, without quality discrimination, when users’ privacy cost is low, platforms will reward new users in the price dimension and poach competitors’ users through lower prices. This is because, when users’ privacy cost is low, they are more likely to stay with the original platform in the second period, so platforms can attract competitor’s turf through lower prices.
For the existence of quality discrimination, Proposition 2 indicates that, if the privacy cost of users is high, when the competition intensity is weak, platforms will choose to attract new users at a lower price. This is because, in this scenario, users are unlikely to stay in the original platform as the privacy issues plague them in the second period. At this time, if the firm lowers the price, it can easily poach competitors’ users. In addition, Proposition 1 indicates that platforms will reward old users with higher quality in this case.
On the other hand, if the privacy cost of users is low, when the competition intensity is relatively strong, platforms will also set lower prices for new users. This is because, when the competition intensity is relatively strong, the degree of product differentiation between the two competing platforms is relatively small. For users, there is not much difference between the two products, so it is more likely that users will choose to change platforms to buy in the second period. In anticipation of this situation, platforms will choose to attract new users at a lower price. In addition, Proposition 1 also shows that, in this case, platforms will retain old users with higher quality.
Propositions 1 and 2 show that, in equilibrium, platforms will formulate two different dimensions of strategies for two kinds of users, i.e., platforms will reward old users in the quality dimension and new users in the price dimension. The result is consistent with the conclusions of Li [27].
5. Social Welfare Impact of Quality Discrimination
From the equilibrium results in Section 4, we can further get the total profits, user surplus and social welfare of the two platforms with quality discrimination and non-quality discrimination, as shown in Table 3.

Table 3.
Total platforms’ profit, user surplus, and social welfare in equilibrium.
Proposition 3 can be obtained from Table 3:
Proposition 3.
When and , or , we can know and , while, when , we can get .
Figure 5 presents our numerical results of Proposition 3 and shows how the platform’s total profit is affected by the privacy cost, i.e., and competition intensity, i.e., . Figure 5a demonstrates that, when the competition intensity is weak, the total platform profit decreases first and then increases with the privacy cost under quality discrimination. In addition, compared with the scenario without quality discrimination, the platform profit is higher under quality discrimination. Figure 5b demonstrates that, when the competition intensity is strong, the total platform revenue will increase with the privacy cost, and the total platform revenue will be greater without quality discrimination. Proposition 5 shows that, when the market competition intensity is relatively weak, with users’ privacy cost, quality discrimination can bring more considerable profits. Propositions 3 and 4 have shown that platforms will choose to reward old users with higher quality and attract new users with lower price when the competition intensity is weak and the privacy cost of users is high. These two strategies enable platforms to expand their turf and achieve higher profits.
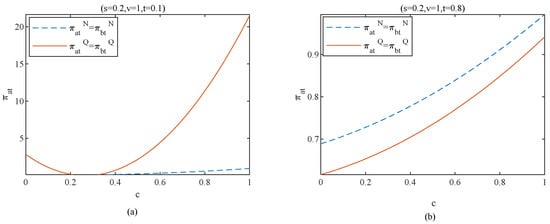
Figure 5.
Platform’s total profit in equilibrium (t = 0.1 vs. t = 0.8).
Proposition 5 also shows that, when the market competition is strong, with the increase of users’ privacy cost, the revenue from quality discrimination is always lower than that without quality discrimination. This is because, as shown in Figure 4, the uniform quality set by platforms for all users without quality discrimination is slightly higher than that set by firms for new and old users with quality discrimination. With the increase of users’ privacy cost, higher quality product can attract more users. Therefore, compared with adopting quality discrimination, platforms can obtain more profits without quality discrimination.
Proposition 4.
When and , we can know , while, when , there is always .
Figure 6 presents our numerical results of Proposition 4 and shows how the user surplus is affected by the privacy cost, i.e., and competition intensity, i.e., . Figure 6a depicts that, when competition intensity is weak, user surplus decreases first and then increases with the privacy cost under quality discrimination, while the user surplus continues to decrease without quality discrimination. Figure 6b depicts that, when competition intensity is strong, user surplus decreases with the privacy cost under both two scenarios. In addition, the user surplus under quality discrimination is always higher. Proposition 4 shows that, when competition intensity is weak and privacy cost is high, user surplus increases as users’ privacy cost grows under quality discrimination. In addition, compared with the scenario of without quality discrimination, user surplus is higher under quality discrimination. In addition, when the competition intensity is strong, users will always be better off with quality discrimination.
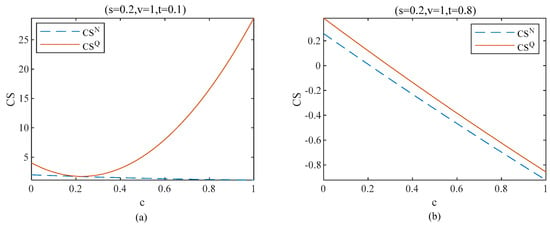
Figure 6.
User surplus in equilibrium (t = 0.1 vs. t = 0.8).
This is because, when the competition intensity is weak, as the privacy cost of users increases, platforms will reward old users with higher quality and attract new users with lower price. This benefits users more, so the user surplus increases with users’ privacy cost.
On the other hand, when the competition intensity is strong, the products produced by platforms are highly differentiated, and the first-period choice of users indicates that the products produced by the original platforms can better meet their preferences. Therefore, users are reluctant to switch to a new platform for purchase in the second period, but as users’ privacy cost increases, users become worse off if staying with the original platform. Therefore, user surplus decreases as users’ privacy cost declines. Furthermore, with quality discrimination, platforms also set lower prices for new users and set higher quality for old users. Therefore, in this case, users will always be in a better position if there is quality discrimination.
Proposition 5.
When and , we can obtain and , while when , we can know and .
Figure 7 presents our numerical results of Proposition 5 and how the social welfare is affected by the privacy cost, i.e., and competition intensity, i.e., . Figure 7a demonstrates that, when the competition intensity is weak, with the privacy cost, the social welfare under quality discrimination declines first and then increases, while the social welfare without quality discrimination shows a slightly upward trend. However, there is always the higher social welfare under quality discrimination. Figure 7b depicts that, when competition intensity is strong, social welfare decreases with the privacy cost. In addition, the social welfare is greater without quality discrimination. Proposition 5 shows that, when competition intensity is weak and there is quality discrimination, social welfare goes up as users’ privacy cost increases. However, when the competition intensity is strong, whether there is quality discrimination or not, with the increase of users’ privacy cost, the user surplus always declines.
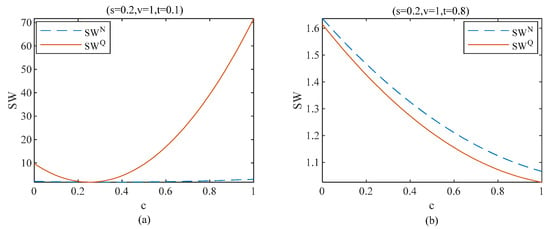
Figure 7.
Social welfare in equilibrium (t = 0.1 vs. t = 0.8).
This is because, when the competition intensity is weak as users’ privacy cost grows, the platforms’ total profit and the user surplus are increasing, so the social welfare is also on the rise. However, when the competition intensity is strong, the total profits obtained by platforms are higher without quality discrimination. Although the user’s surplus is small at this time, it can be found from the comparison of whether there is quality discrimination or not that the total platforms’ profit gap is larger than the user’s surplus gap. Therefore, when the competition intensity is weak, the social welfare without quality discrimination is higher than that with quality discrimination.
6. Conclusions
This paper establishes a two-period dynamic competition game model. In the first period, the platform sets the same price for all users, while, in the second period, it sets differentiated prices for new and old users and sets different levels of product quality. Firstly, the user’s privacy cost is considered to define the user’s utility function, and the different demand functions of platforms in the two periods are derived based on the Hotelling model. The optimal strategies regarding the price and quality of product or service by competing platforms are studied under the conditions of quality discrimination and non-quality discrimination. In addition, the impact of market competition intensity and user privacy cost on industry profits, user surplus, and social welfare are also investigated.
The research shows that, if there is no quality discrimination, when the privacy cost of users is low, platforms will reward new users with low price. However, with quality discrimination, there are two situations in which platforms will set lower prices for new users and higher quality for old users: when users’ privacy cost is high and competition intensity is weak, or when users’ privacy cost is low and competition intensity is strong. In these two scenarios, platforms will reward new and old users from price and quality dimensions in equilibrium. Furthermore, when the market competition intensity is weak, with the increase of users’ privacy cost, compared with not conducting quality discrimination, platforms implementing quality discrimination can achieve more profits.
When it comes to user surplus and social welfare, with weak competition intensity and quality discrimination, both user surplus and social welfare will increase with users’ privacy cost rising. When the competition intensity is strong, whether there is quality discrimination or not, with the increase of users’ privacy cost, user surplus and social welfare are always decreasing.
Our analysis provides deep theoretical implications of the effect of quality discrimination on platforms’ profits, user surplus, and social welfare. Extant research on BBPD acknowledges that BBPD can raise consumer privacy concerns, but offers few solutions, and our analysis makes a theoretical contribution to this aspect. We show that, when the market competition intensity is weak, with the increase of users’ privacy cost, quality discrimination can bring more considerable profits for platforms. As for user surplus and social welfare, when the competition intensity is weak and with quality discrimination, both user surplus and social welfare will increase with users’ privacy cost. However, when the competition intensity is strong, whether there is quality discrimination or not, with the increase of users’ privacy cost, the user surplus and social welfare are always decreasing. Part of our conclusion is similar to Li [24]’s study to some extent. For example, we agree that platforms should reward new customers on the price dimension and old customers on the quality dimension in some situations. However, different from Li [24]’s, in which the impact of quality discrimination on BBPD is focused, we focus on how quality discrimination alleviates consumer privacy concerns, so we consider the privacy cost, and explore the conditions where the quality discrimination can ease consumer privacy concerns.
The above conclusions also have important managerial implications for platforms seeking to enhance profits. With the development of modern technology, incidents concerning the leakage of users’ privacy emerge one after another, and users’ privacy concerns are growing. Therefore, how to effectively use big data while reducing users’ privacy concerns becomes extremely significant. Currently, privacy regulation is mainly relied on to alleviate consumers’ privacy concerns, but its effectiveness is controversial. The conclusion of this study provides a new way to solve this problem, i.e., platforms can provide higher product quality for old users in exchange for their privacy. For example, platforms can endeavor to innovate their products, designing products that are more in line with the preferences of old users. Platforms can also provide users with a higher level of service quality, including providing users with more diversified and accurate content push or product recommendation, so as to alleviate their privacy concerns to a certain extent.
Additionally, the conclusions of this paper provide some practical implications and explain Airbnb’s strategy in the Chinese market to a certain extent. Airbnb is an online platform on which registered users and third-party service providers can communicate and trade directly with each other. Airbnb is mainly targeted at Chinese users who want to go to foreign countries, while Tujia and Xiaozhu, as Airbnb’s competitors, are targeted at domestic users. Therefore, the products of Airbnb and the other two platforms are quite different. These platforms collect a large amount of users’ data on the platform, and release coupons to new users. According to Airbnb’s platform policy, the display position or ranking of products in search results may depend on many factors, including but not limited to the preferences of guests and homeowners, ratings, and convenience of booking. However, for the old users, Airbnb shows users more diversified characteristic houses based on “embedded technology”. Furthermore, Airbnb not only provides accommodation but also provides users with a “home” experience. In order to satisfy the users’ pursuit of authenticity and interactive accommodation experience, Airbnb builds a virtual community of platform for old users. In this community, old users can speak freely and share their housing demands and experiences. Additionally, Airbnb also launched the “Story” function in 2017, allowing old users to share their stories on their travel. These services provided by Airbnb to old users have greatly improved their perceived product quality, thus alleviating privacy concerns to a certain extent.
This study still has some limitations, such as only considering the average privacy cost of users, and not exploring the more complex market competition situation of platforms, etc. These are aspects that can be considered in future research work. In addition, further deep research in the future can also verify the conclusions of this study from an empirical perspective.
Author Contributions
X.L., Supervision, Conceptualization, Funding acquisition, Methodology, Model-setting, Writing—review and editing; X.H., Conceptualization, Methodology, Model—setting, Writing—original draft; S.L., Investigation, Resources, Writing—original draft; Y.L., Software, Validation, Investigation; H.L., Formal analysis, Methodology, Validation; S.Y., Methodology, Validation. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (No. 71991461), the Guangdong Province Soft Science Research Project (No. 2019A101002074), the Discipline Co-construction Project for Philosophy and Social Science in Guangdong Province (No. GD20XGL03), and the Project for Philosophy and Social Sciences Research of Shenzhen City (No. SZ2021B014).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors sincerely thank the editor-in-chief and anonymous reviews for the constructive comments, which have improved the paper significantly.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Proof of Proposition 1.
With quality discrimination, when
and ,
When and ,
Therefore, there are two situations, that is, either the competition intensity is small and the privacy cost is large, or the competition intensity is large and the privacy cost is small, and the product quality offered by the platform for old customers is higher than that of new customers. □
Proof of Proposition 2.
Without quality discrimination, when ,
with quality discrimination, when
and ,
When and ,
Therefore, when there is no quality discrimination and the cost of privacy is small, the platform sets a higher price for regular customers in the second period. Similarly, there are two situations, that is, either the competition intensity is small and the privacy cost is large, or the competition intensity is large and the privacy cost is small, and the product price for the old customers is higher than that of the new customers. □
Based on Propositions 1 and 2, it can be seen that, in some cases, the platform will reward new customers on the price dimension and old customers on the quality dimension.
Proof of Proposition 3.
When and ,
When ,
When ,
Therefore, in the scenario of quality discrimination, there are two situations, either the competition intensity is low and the privacy cost is high, or the competition degree is high, and the platform income increases with privacy cost. However, in the absence of quality discrimination, when the privacy cost is high, the platform revenue increases with privacy cost. □
Proof of Proposition 4.
When and ,
When ,
Therefore, when competition intensity is low and privacy cost is high, consumer surplus increases with privacy cost. In addition, when competition intensity is high, consumer surplus is better under quality discrimination. □
Proof of Proposition 5.
When and ,
When ,
Therefore, on the one hand, when competition intensity is low and privacy cost is high, social welfare increases with privacy cost in the scenario of quality discrimination. On the other hand, when competition intensity is high, social welfare decreases with the privacy cost regardless of quality discrimination. □
References
- Omid, R.; Hema, Y. Targeting and Privacy in Mobile Advertising. Mark. Sci. 2020, 40, 193–218. [Google Scholar]
- Chen, X.; Owen, Z.; Pixton, C.; Simchi-Levi, D. A Statistical Learning Approach to Personalization in Revenue Management. Manag. Sci. 2022, 68, 1923–1937. [Google Scholar] [CrossRef]
- Ettl, M.; Harsha, P.; Papush, A.; Perakis, G. A Data-Driven Approach to Personalized Bundle Pricing and Recommendation. Manuf. Serv. Oper. Manag. 2020, 22, 429–643. [Google Scholar] [CrossRef]
- Elmachtoub, A.N.; Gupta, V.; Hamilton, M. The Value of Personalized Pricing. Manag. Sci. 2021, 67, 6055–6070. [Google Scholar] [CrossRef]
- Lee, H.J.; Choeh, J.Y. Motivations for Obtaining and Redeeming Coupons from a Coupon App: Customer Value Perspective. J. Theor. Appl. Electron. Commer. Res. 2021, 16, 22–33. [Google Scholar]
- Belleflamme, P.; Lam, W.; Vergote, W. Competitive Imperfect Price Discrimination and Market Power. Mark. Sci. 2020, 39, 996–1015. [Google Scholar] [CrossRef]
- Shiller, B. First Degree Price Discrimination Using Big Data. Soc. Sci. Electron. Publ. 2013, 64, 419–438. [Google Scholar]
- Choudhary, V.; Ghose, A.; Mukhopadhyay, T.; Rajan, U. Personalized Pricing and Quality Differentiation. Manag. Sci. 2005, 51, 1015–1164. [Google Scholar] [CrossRef] [Green Version]
- Buckman, J.R.; Bockstedt, J.C.; Hashim, M.J. Relative Privacy Valuations Under Varying Disclosure Characteristics. Inf. Syst. Res. 2019, 30, 375–388. [Google Scholar] [CrossRef]
- Chen, Z.; Choe, C.; Matsushima, N. Competitive Personalized Pricing. Manag. Sci. 2020, 66, 4003–4023. [Google Scholar] [CrossRef] [Green Version]
- Bleier, A.; Goldfarb, A.; Tucker, C. Consumer privacy and the future of data-based innovation and marketing. Int. J. Res. Mark. 2020, 37, 466–480. [Google Scholar] [CrossRef]
- Xu, Z.; Dukes, A. Product Line Design under Preference Uncertainty Using Aggregate Consumer Data. Mark. Sci. 2019, 38, 669–689. [Google Scholar] [CrossRef]
- Yoganarasimhan, H. Search Personalization Using Machine Learning. Manag. Sci. 2020, 66, 1045–1070. [Google Scholar] [CrossRef]
- Taylor, C.R. Consumer Privacy and the Market for Customer Information. RAND J. Econ. 2004, 35, 631–650. [Google Scholar] [CrossRef]
- Conitzer, V.; Taylor, C.R.; Wagman, L. Hide and Seek: Costly Consumer Privacy in a Market with Repeat Purchases. Mark. Sci. 2012, 31, 277–292. [Google Scholar] [CrossRef]
- Lee, D.J.; Ahn, J.H.; Bang, Y. Managing Consumer Privacy Concerns in Personalization: A Strategic Analysis of Privacy Protection. Mis Q. 2011, 35, 423–444. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.; Lim, D.; Kim, H.; Zo, H.; Ciganek, A.P. Compensation paradox: The influence of monetary rewards on user behaviour. Behav. Inf. Technol. 2015, 34, 45–56. [Google Scholar] [CrossRef]
- Mohammed, Z.A.; Tejay, G.P. Examining the privacy paradox through individuals’ neural disposition in e-commerce: An exploratory neuroimaging study. Comput. Secur. 2021, 104, 102201. [Google Scholar] [CrossRef]
- Fudenberg, D.; Tirole, J. Customer Poaching and Brand Switching. RAND J. Econ. 2000, 31, 634–657. [Google Scholar] [CrossRef]
- Adjerid, I.; Peer, E.; Acquisti, A. Beyond the Privacy Paradox: Objective Versus Relative Risk in Privacy Decision Making. Mis Q. 2018, 42, 465. [Google Scholar] [CrossRef]
- Karwatzki, S.; Dytynko, O.; Trenz, M.; Veit, D. Beyond the Personalization-Privacy Paradox: Privacy Valuation, Transparency Features, and Service Personalization. J. Manag. Inf. Syst. 2017, 34, 369–400. [Google Scholar] [CrossRef]
- Zhu, H.; Ou, C.X.J.; van den Heuvel, W.; Liu, H.W. Privacy calculus and its utility for personalization services in e-commerce: An analysis of consumer decision-making. Inf. Manag. 2017, 54, 427–437. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, T. Understanding Purchase Intention in O2O E-Commerce: The Effects of Trust Transfer and Online Contents. J. Theor. Appl. Electron. Commer. Res. 2021, 16, 101–115. [Google Scholar] [CrossRef]
- Shaffer, G.; Zhang, Z.J. Preference-based price discrimination in markets with switching costs. J. Econ. Manag. Strategy 2000, 93, 397–442. [Google Scholar] [CrossRef]
- Akram, U.; Fülöp, M.; Tiron Tudor, A.; Topor, D.; Capusneanu, S. Impact of Digitalization on Customers’ Well-Being in the Pandemic Period: Challenges and Opportunities for the Retail Industry. Int. J. Environ. Res. Public Health 2021, 18, 7533. [Google Scholar] [CrossRef] [PubMed]
- Amit Pazgal, D.S. Behavior-Based Discrimination: Is It a Winning Play, and If So, When? Mark. Sci. 2008, 27, 977–994. [Google Scholar] [CrossRef]
- Li, K.J. Behavior-Based Quality Discrimination. Manuf. Serv. Oper. Manag. 2020, 23, 425–436. [Google Scholar] [CrossRef]
- Laussel, D.; Resende, J. When Is Product Personalization Profit-Enhancing? A Behavior-Based Discrimination Model. Manag. Sci. 2022. [Google Scholar] [CrossRef]
- Stigler, G.J. An Introduction to Privacy in Economics and Politics. Georg. J. Stigler 1980, 9, 623–644. [Google Scholar] [CrossRef]
- Loertscher, S.; Marx, L.M. Digital monopolies: Privacy protection or price regulation? Int. J. Ind. Organ. 2020, 71, 102623. [Google Scholar] [CrossRef]
- Lefouili, Y.; Ying Lei, T. Privacy Regulation and Quality Investment. Work. Pap. Ser. 2019, 19, 1–45. [Google Scholar] [CrossRef]
- Kummer, M.; Schulte, P. When Private Information Settles the Bill: Money and Privacy in Google’s Market for Smartphone Applications. Manag. Sci. 2019, 65, 3470–3494. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Teo, H.-H.; Tan, B.C.Y.; Agarwal, R. The Role of Push-Pull Technology in Privacy Calculus: The Case of Location-Based Services. J. Manag. Inf. Syst. 2009, 26, 135–174. [Google Scholar] [CrossRef]
- Dubé, J.-P.; Fang, Z.; Fong, N.; Luo, X. Competitive Price Targeting with Smartphone Coupons. Mark. Sci. 2017, 36, 944–975. [Google Scholar] [CrossRef]
- Thisse, J.-F.; Vives, X. On The Strategic Choice of Spatial Price Policy. Am. Econ. Rev. 1988, 78, 122–137. [Google Scholar]
- Marreiros, H.; Tonin, M.; Vlassopoulos, M.; Schraefel, M.C. ‘Now that you mention it’: A survey experiment on information, inattention and online privacy—ScienceDirect. J. Econ. Behav. Organ. 2017, 140, 1–17. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).