Improving E-Commerce Distribution through Last-Mile Logistics with Multiple Possibilities of Deliveries Based on Time and Location
Abstract
1. Introduction
2. Related Literature
3. Problem Formulation
4. Solution Procedures
4.1. Ad Hoc Heuristics
4.2. Ad Hoc Metaheuristics
4.3. Standard Metaheuristics
5. Results and Discussion
- SH: the weights of the distance to the depot, distance to the next customer location, and waiting time were taken as 0.34, 0.14, and 0.52, respectively.
- IH: in this case, the above weights were taken as 0.21, 0.49, and 0.30, respectively.
- PI: the weights were chosen as 0.26, 0.49, and 0.25, respectively.
- EP: maximum number of iterations equal to 50 times the total number of customer locations; population size equal to 150 for 10 and 25 customers, and to 200 for 50 and 100 customers; probability of mutation equal to 15%.
- TS: maximum number of iterations equal to 20 times the total number of customer locations; residence time in the tabu list approximated by the total number of customer locations divided by 7.
- SA: initial temperature equal to 1000; final temperature equal to 1; number of neighbor tests before cooling approximated by the total number of customer locations divided by 7.
5.1. Delivery Options vs. Only One Option
5.2. Comparison of Solution Procedures
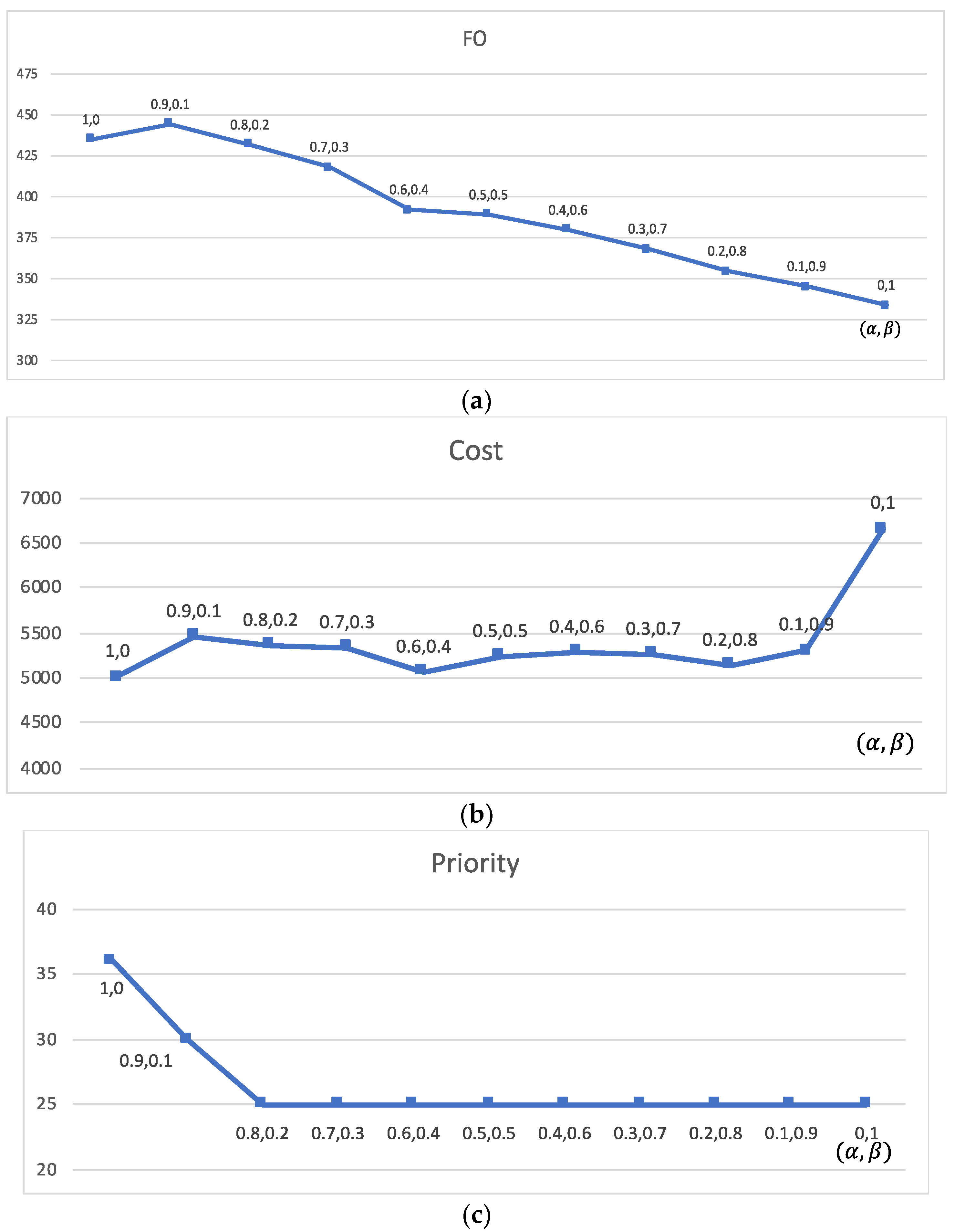
5.3. Priority Considerations
5.4. Discussion of Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rodríguez-Ardura, I.; Meseguer, A.; Vilaseca, J. Factors influencing the evolution of e-commerce: An empirical analysis in a developed market economy. J. Theor. Appl. Electron. Commer. Res. 2008, 3, 18–29. [Google Scholar] [CrossRef]
- Wang, J.Y.; Chang, C.U. How online ties and product-related risks influence purchase intentions: A facebook experiment. Electron. Commer. Res. Appl. 2013, 12, 337–346. [Google Scholar] [CrossRef]
- Pham, T.S.H.; Ahammad, M.F. Antecedents and consequences of online customer satisfaction: A holistic process perspective. Technol. Forecast. Soc. Chang. 2017, 124, 332–342. [Google Scholar] [CrossRef]
- Iglesias-Pradas, S.; Pascual-Miguel, F.; Hernández-García, A.; Chaparro-Pelaez, J. Barriers and drivers for non-shoppers in B2C e-commerce: A latent class exploratory analysis. Comput. Hum. Behav. 2013, 29, 314–322. [Google Scholar] [CrossRef]
- INE. Estadísticas de Comercio Electrónico. Available online: https://www.ine.es (accessed on 1 February 2022).
- Urueña, A.; Ballestero, M.P.; Castro, R.; Cadenas, S.; Maira, M.; Prieto, E. El Comercio Electrónico B2C en España en 2019; ONTSI: Madrid, España, 2020. [Google Scholar] [CrossRef]
- Tokar, T.; Jensen, R.; Williams, B.D. A guide to the seen costs and unseen benefits of e-commerce. Bus. Horiz. 2021, 64, 323–332. [Google Scholar] [CrossRef]
- Park, C.H.; Kim, Y.G. Identifying key factors affecting consumer purchase behavior in an online shopping context. Int. J. Retail Distrib. Manag. 2003, 31, 16–29. [Google Scholar] [CrossRef]
- Alam, S.S.; Yasin, N.M. An Investigation into the Antecedents of Customer Satisfaction of Online Shopping. J. Mark. Dev. Compet. 2010, 5, 71–78. [Google Scholar]
- Rodríguez-García, M.; Domínguez-Caamaño, P.; Prado-Prado, J.C. La nueva cadena de suministro en la era de los e-retailers: Una revisión bibliográfica actualizada. Dir. Y Organ. 2016, 59, 18–31. [Google Scholar] [CrossRef]
- Uzir, U.H.; Al Halbusi, H.; Thurasamy, R.; Thiam Hock, R.L.; Aljaberi, M.A.; Hasan, N.; Hamid, M. The effects of service quality, perceived value and trust in home delivery service personnel on customer satisfaction: Evidence from a developing country. J. Retail. Consum. Serv. 2021, 63, 102721. [Google Scholar] [CrossRef]
- Ramanathan, R. The moderating roles of risk and efficiency on the relationship between logistics performance and customer loyalty in e-commerce. Transp. Res. E 2010, 46, 950–962. [Google Scholar] [CrossRef]
- Ghezzi, A.; Mangiaracina, R.; Perego, A. Shaping the E-Commerce Logistics Strategy: A Decision Framework. Int. J. Eng. Bus. Manag. 2012, 4, 1–13. [Google Scholar] [CrossRef]
- Örazik, S.S.; Veelenturf, L.P.; van Woensel, T.; Laporte, G. Optimizing e-commerce last-mile vehicle routing and scheduling under uncertain customer presence. Transp. Res. Part E Logist. Transp. Rev 2021, 148, 102263. [Google Scholar] [CrossRef]
- Pan, S.; Giannikas, V.; Han, Y.; Grover-Silva, E.; Qiao, B. Using customer-related data to enhance e-grocery home delivery. Ind. Manag. Data Syst. 2017, 117, 1917–1933. [Google Scholar] [CrossRef]
- Buldeo Rai, H.; Verlinde, S.; Macharis, C.; Schoutteet, P.; Vanhaverbeke, L. Logistics outsourcing in omnichannel retail: State of practice and service recommendations. Int. J. Phys. Distrib. Logist. Manag. 2019, 49, 267–286. [Google Scholar] [CrossRef]
- Yrjola, H. Supply Chain Considerations for Electronic Grocery Shopping. Ph.D. Thesis, Helsinki University of Technology, Espoo, Finland, 2003. [Google Scholar]
- Yee, S.T. Impact analysis of customized demand information sharing on supply chain performance. Int. J. Prod. Res. 2005, 43, 3353–3373. [Google Scholar] [CrossRef]
- Xiao, D.; Kuang, X.; Chen, K. E-commerce supply chain decisions under platform digital empowerment-induced demand. Comput. Ind. Eng. 2020, 150, 106876. [Google Scholar] [CrossRef]
- Savelsbergh, M.; van Woensel, T. 50th anniversary invited article–city logistics: Challenges and opportunities. Transp. Sci. 2016, 50, 579–590. [Google Scholar] [CrossRef]
- Mahar, S.; Salzarulo, P.A.; Wright, P.D. Using online pickup site inclusion policies to manage demand in retail/E-tail organizations. Comput. Oper. Res. 2012, 39, 991–999. [Google Scholar] [CrossRef]
- Zhang, S.Z.; Lee, C.K.M. Flexible vehicle scheduling for urban last mile logistics: The emerging technology of shared reception box. In Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bali, Indonesia, 4–7 December 2016; IEEE, 2016. [Google Scholar]
- DPD Group. E-Shoppers in Europe. 2019 Barometer. 2020. Available online: https://www.dpd.com/group/wp-content/uploads/sites/77/2020/02/E-shoppers-in-Europe_2019-Barometer_EN.pdf (accessed on 1 February 2022).
- Buldeo Rai, H.; Cetinkaya, A.; Verlinde, S.; Macharis, C. How are consumers using collection points? Evidence from Brussels. Transp. Res. Procedia 2020, 46, 53–60. [Google Scholar] [CrossRef]
- Cullinane, S. From Bricks to Clicks: The Impact of Online Retailing on Transport and the Environment. Transp. Rev. 2009, 29, 759–776. [Google Scholar] [CrossRef]
- Rotem-Mindali, O.; Weltevreden, J.W.J. Transport effects of e-commerce: What can be learned after years of research? Transportation 2013, 40, 867–885. [Google Scholar] [CrossRef]
- Mommens, K.; Buldeo Rai, H.; van Lier, T.; Macharis, C. Delivery to homes or collections points? A sustainability analysis for urban, urbanized and rural areas in Belgium. J. Transp. Geogr. 2021, 94, 103095. [Google Scholar] [CrossRef]
- Wang, C.; Mao, Z.; O’kane, J.; Wang, J. An exploration on e-retailers’ home delivery–strategic elements and their prioritisation. Bus. Process Manag. J. 2016, 22, 614–633. [Google Scholar] [CrossRef]
- Rao, S.; Goldsby, T.J.; Griffis, S.E.; Iyengar, D. Electronic Logistics Service Quality (e-LSQ): Its Impact on the Customer’s Purchase Satisfaction and Retention. J. Bus. Logist. 2011, 32, 167–179. [Google Scholar] [CrossRef]
- Xing, Y.; Grant, D.B.; McKinnon, A.C.; Fernie, J. Physical distribution service quality in online retailing. Int. J. Phys. Distrib. Logist. Manag. 2010, 40, 415–432. [Google Scholar] [CrossRef]
- Goebel, P.; Moeller, S.; Pibernik, R. Paying for convenience. Int. J. Phys. Distrib. Logist. Manag. 2012, 42, 584–606. [Google Scholar] [CrossRef]
- Moccia, L.; Cordeau, J.F.; Laporte, G. An incremental tabu search heuristic for the generalized vehicle routing problem with time windows. J. Oper. Res. Soc. 2012, 63, 232–244. [Google Scholar] [CrossRef]
- Anbuudayasankar, S.P.; Ganesh, K.; Mohapatra, S. Models for Practical Routing Problems in Logistics; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Lin, C.; Choy, K.L.; Ho, G.T.S.; Chung, S.H.; Lam, H.Y. Survey of Green Vehicle Routing Problem: Past and future trends. Expert Syst. Appl. 2014, 41, 1118–1138. [Google Scholar] [CrossRef]
- Cáceres-Cruz, J.; Arias, P.; Guimarans, D.; Riera, D.; Juan, A.A. Rich Vehicle Routing Problem: Survey. ACM Comput. Surv. 2014, 47, 32. [Google Scholar] [CrossRef]
- Eksioglu, B.; Vural, A.V.; Reisman, A. The vehicle routing problem: A taxonomic review. Comput. Ind. Eng. 2009, 57, 1472–1483. [Google Scholar] [CrossRef]
- De Jaegere, N.; Defraeye, M.; Van Nieuwenhuyse, I. The Vehicle Routing Problem: State of the Art Classification and Review; Research Report KBI_1415; KU Leuven: Leuven, Belgium, 2014. [Google Scholar]
- Zhou, L.; Baldacci, R.; Vigo, D.; Wang, X. A multi-depot two-echelon vehicle routing problem with delivery options arising in the last mile distribution. Eur. J. Oper. Res. 2018, 265, 765–778. [Google Scholar] [CrossRef]
- He, Y.; Wang, X.; Zhou, F.; Lin, Y. Dynamic vehicle routing problem considering simultaneous dual services in the last mile delivery. Kybernetes 2019, 49, 1267–1284. [Google Scholar] [CrossRef]
- Janjevic, M.; Winkenbach, M.; Merchán, D. Integrating collection-and-delivery points in the strategic design of urban last-mile e-commerce distribution networks. Transp. Res. Part E Logist. Transp. Rev. 2019, 131, 37–67. [Google Scholar] [CrossRef]
- Orenstein, I.; Raviv, T.; Sadan, E. Flexible parcel delivery to automated parcel lockers: Models, solution methods and analysis. EURO J. Transp. Logist. 2019, 8, 683–711. [Google Scholar] [CrossRef]
- Sitek, P.; Wikarek, J. Capacitated vehicle routing problem with pick-up and alternative delivery (CVRPPAD): Model and implementation using hybrid approach. Ann. Oper. Res. 2019, 273, 257–277. [Google Scholar] [CrossRef]
- Tilk, C.; Olkis, K.; Irnich, S. The last-mile vehicle routing problem with delivery options. OR Spectr. 2021, 43, 877–904. [Google Scholar] [CrossRef]
- Ozbaygin, G.; Ekin Karasan, O.; Savelsbergh, M.; Yaman, H. A branch-and-price algorithm for the vehicle routing problem with roaming delivery locations. Transp. Res. Part B Methodol. 2017, 100, 115–137. [Google Scholar] [CrossRef]
- Reyes, D.; Savelsbergh, M.; Toriello, A. Vehicle routing with roaming delivery locations. Transp. Res. Part C Emerg. Technol. 2017, 80, 71–91. [Google Scholar] [CrossRef]
- Lombard, A.; Tamayo-Giraldo, S.; Fontane, F. Vehicle routing problem with roaming delivery locations and stochastic travel times (VRPRDL-S). Transp. Res. Procedia 2018, 30, 167–177. [Google Scholar] [CrossRef]
- Sampaio Oliveira, A.; Kinable, J.; Veelenturf, L.; van Woensel, T. A Scenario-Based Approach for the Vehicle Routing Problem with Roaming Delivery Locations under Stochastic Travel Times; Working Paper; Eindhoven University of Technology: Eindhoven, The Netherlands, 2019. [Google Scholar]
- He, Y.; Qi, M.; Zhou, F.; Su, J. An effective metaheuristic for the last mile delivery with roaming delivery locations and stochastic travel times. Comput. Ind. Eng. 2020, 145, 106513. [Google Scholar] [CrossRef]
- Felch, V.; Karl, D.; Asdecker, B.; Niedermaier, A.; Sucky, E. Reconfiguration of the last mile: Consumer acceptance of alternative delivery concepts. In Logistics Management; Lecture Notes in Logistics; Bierwirth, C., Kirschstein, T., Sackmann, D., Eds.; Springer International Publishing: Cham, Switzerland, 2019; Volume 13. [Google Scholar] [CrossRef]
- Schwerdfeger, S.; Boysen, N. Optimizing the changing locations of mobile parcel lockers in last-mile distribution. Eur. J. Oper. Res. 2020, 285, 1077–1094. [Google Scholar] [CrossRef]
- Los, J.; Spaan, M.T.J.; Negenborn, R.R. Fleet management for pickup and delivery problems with multiple locations and preferences. In Dynamics in Logistics; Lecture Notes in Logistics; Freitag, M., Kotzab, H., Pannek, J., Eds.; Springer: Cham, Switzerland, 2018; Volume 61. [Google Scholar] [CrossRef]
- Mancini, S.; Gansterer, M. Vehicle routing with private and shared delivery locations. Comput. Oper. Res. 2021, 133, 105361. [Google Scholar] [CrossRef]
- Grabenschweiger, J.; Doerner, K.F.; Hartl, R.F.; Savelsbergh, M.W.P. The vehicle routing problem with heterogeneous locker boxes. Cent. Eur. J. Oper. Res. 2021, 29, 113–142. [Google Scholar] [CrossRef]
- Cepolina, E.M.; Farina, A. A new urban freight distribution scheme and an optimization methodology for reducing its overall cost. Eur. Transp. Res. Rev. 2015, 7, 1–14. [Google Scholar] [CrossRef]
- Braysy, O.; Gendreau, M. Vehicle Routing Problem with Time Windows, Part II: Metaheuristics. Transp. Sci. 2005, 39, 119–139. [Google Scholar] [CrossRef]
- Laporte, G. Fifty Years of Vehicle Routing. Transp. Sci. 2009, 43, 408–416. [Google Scholar] [CrossRef]
- Sandhya, V.K. Relative Performance of Certain Meta Heuristics on Vehicle Routing Problem with Time Windows. Int. J. Inf. Technol. Comput. Sci. 2015, 12, 40–49. [Google Scholar]
- Archetti, C.; Speranza, M.G. A survey on matheuristics for routing problems. EURO J. Comput. Optim. 2014, 2, 223–246. [Google Scholar] [CrossRef]
| Instance | VRPTWDO | VRPTW | VRP |
|---|---|---|---|
| r25_3_1 | 349.26 | 567.58 | 317.26 |
| r25_3_2 | 294.40 | 523.99 | 342.69 |
| r25_3_3 | 267.77 | 436.43 | 340.07 |
| r25_3_4 | 232.36 | 393.20 | 304.87 |
| r25_3_5 | 310.91 | 493.10 | 347.42 |
| r25_3_6 | 271.09 | 460.06 | 326.25 |
| r25_3_7 | 260.37 | 404.27 | 348.73 |
| r25_3_8 | 231.49 | 374.97 | 367.14 |
| r25_3_9 | 272.37 | 428.79 | 358.40 |
| r25_3_10 | 243.74 | 412.46 | 336.69 |
| r25_3_11 | 241.77 | 397.84 | 318.76 |
| r25_3_12 | 230.82 | 392.83 | 324.04 |
| mean | 267.19 | 440.46 | 336.03 |
| Customers | Instance | Gurobi | SH | IH | PI | TS | SA | EP |
|---|---|---|---|---|---|---|---|---|
| 10 | r10_3_1 | 156.77 | 218.55 | 182.54 | 182.54 | 158.20 | 156.77 | 156.77 |
| r10_3_2 | 129.01 | 170.72 | 193.66 | 241.75 | 129.01 | 129.01 | 129.01 | |
| r10_3_3 | 122.46 | 206.31 | 197.14 | 208.26 | 129.01 | 129.01 | 122.46 | |
| r10_3_4 | 113.72 | 151.51 | 181.42 | 175.79 | 133.47 | 113.72 | 113.72 | |
| r10_3_5 | 154.15 | 184.45 | 191.13 | 191.13 | 154.76 | 154.15 | 154.15 | |
| r10_3_6 | 129.01 | 155.48 | 230.56 | 201.63 | 129.01 | 129.01 | 129.01 | |
| r10_3_7 | 99.90 | 187.06 | 169.36 | 179.07 | 129.01 | 122.46 | 122.46 | |
| r10_3_8 | 113.72 | 151.51 | 148.29 | 175.79 | 128.34 | 113.72 | 113.72 | |
| r10_3_9 | 141.67 | 172.37 | 178.49 | 178.49 | 141.67 | 141.67 | 141.67 | |
| r10_3_10 | 121.87 | 206.18 | 199.99 | 199.99 | 129.56 | 123.32 | 121.87 | |
| r10_3_11 | 129.01 | 163.29 | 152.73 | 221.45 | 129.01 | 129.01 | 129.01 | |
| r10_3_12 | 114.28 | 151.51 | 188.42 | 170.23 | 114.28 | 114.28 | 114.28 | |
| 25 | r25_3_1 | 466.34 | 627.87 | 576.40 | 401.59 | 395.89 | 349.26 | |
| r25_3_2 | 494.06 | 550.33 | 453.79 | 336.32 | 342.97 | 294.40 | ||
| r25_3_3 | 451.88 | 372.21 | 431.85 | 296.95 | 308.38 | 267.77 | ||
| r25_3_4 | 409.21 | 349.75 | 357.18 | 253.32 | 255.09 | 232.36 | ||
| r25_3_5 | 438.77 | 522.69 | 494.48 | 317.50 | 326.46 | 310.91 | ||
| r25_3_6 | 390.57 | 380.89 | 366.43 | 306.73 | 319.54 | 271.09 | ||
| r25_3_7 | 400.16 | 373.07 | 343.99 | 290.91 | 305.26 | 260.37 | ||
| r25_3_8 | 382.33 | 382.65 | 351.15 | 233.86 | 251.57 | 231.49 | ||
| r25_3_9 | 409.52 | 461.67 | 441.79 | 303.11 | 310.18 | 272.37 | ||
| r25_3_10 | 399.46 | 421.96 | 448.25 | 268.57 | 276.74 | 243.74 | ||
| r25_3_11 | 374.57 | 454.23 | 401.71 | 285.02 | 280.77 | 241.77 | ||
| r25_3_12 | 400.73 | 420.28 | 375.77 | 227.98 | 229.34 | 230.82 | ||
| 50 | r50_3_1 | 1297.38 | 1548.89 | 1707.91 | 1118.22 | 1141.15 | 987.70 | |
| r50_3_2 | 1216.53 | 1586.59 | 1405.93 | 1093.75 | 965.66 | 890.44 | ||
| r50_3_3 | 1084.07 | 1088.47 | 1136.47 | 936.67 | 861.56 | 803.45 | ||
| r50_3_4 | 955.23 | 981.75 | 958.16 | 870.22 | 722.52 | 749.97 | ||
| r50_3_5 | 1290.79 | 1537.16 | 1544.38 | 1137.34 | 1039.29 | 944.77 | ||
| r50_3_6 | 1063.07 | 1547.61 | 1311.73 | 1022.85 | 922.67 | 868.44 | ||
| r50_3_7 | 1057.04 | 1238.69 | 1054.89 | 878.92 | 832.91 | 833.60 | ||
| r50_3_8 | 901.20 | 987.49 | 1043.09 | 814.85 | 711.16 | 781.93 | ||
| r50_3_9 | 1068.03 | 1538.13 | 1478.49 | 1036.22 | 974.39 | 838.68 | ||
| r50_3_10 | 1174.49 | 1264.31 | 1272.67 | 949.90 | 905.58 | 837.46 | ||
| 100 | r100_3_1 | 2849.88 | 4163.91 | 4116.51 | 2915.56 | 2705.07 | 2464.56 | |
| r100_3_2 | 3033.32 | 3850.26 | 3441.89 | 2611.55 | 2322.26 | 2288.27 | ||
| r100_3_3 | 2488.50 | 2804.90 | 2381.78 | 2266.40 | 2026.82 | 2096.77 | ||
| r100_3_4 | 2222.10 | 2051.82 | 2128.04 | 2010.68 | 1798.69 | 2048.31 | ||
| r100_3_5 | 3018.96 | 4146.17 | 4014.05 | 2989.49 | 2611.47 | 2513.44 | ||
| r100_3_6 | 2894.37 | 3449.80 | 3166.35 | 2536.25 | 2152.14 | 2208.82 | ||
| r100_3_7 | 2376.72 | 2467.02 | 2445.43 | 2326.58 | 1987.55 | 2050.95 | ||
| r100_3_8 | 2096.30 | 2051.91 | 1863.85 | 1967.73 | 1769.55 | 2017.25 | ||
| r100_3_9 | 2931.43 | 3816.00 | 3572.80 | 2766.03 | 2483.00 | 2437.38 | ||
| r100_3_10 | 2672.54 | 3323.05 | 3400.73 | 2541.36 | 2230.80 | 2210.17 |
| Customers | Instance | TS | SA | EP | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Avg. | Std. Dev | Time | Avg. | Std. Dev | Time | Avg. | Std. Dev | Time | ||
| 10 | r10_3_1 | 177.33 | 13.10 | 11.14 | 162.85 | 5.33 | 6.00 | 157.31 | 1.57 | 5.28 |
| r10_3_2 | 153.43 | 21.17 | 14.92 | 137.06 | 4.94 | 6.00 | 129.15 | 1.02 | 5.28 | |
| r10_3_3 | 147.76 | 11.47 | 18.76 | 133.26 | 4.15 | 8.00 | 123.55 | 4.05 | 5.99 | |
| r10_3_4 | 144.85 | 6.05 | 19.54 | 128.08 | 4.10 | 10.24 | 115.79 | 3.68 | 6.22 | |
| r10_3_5 | 161.52 | 6.64 | 12.98 | 156.35 | 1.82 | 6.00 | 154.95 | 0.93 | 5.18 | |
| r10_3_6 | 140.76 | 12.79 | 14.72 | 134.22 | 4.91 | 7.00 | 132.97 | 9.24 | 5.27 | |
| r10_3_7 | 144.76 | 17.91 | 21.66 | 130.18 | 3.50 | 8.26 | 125.52 | 6.03 | 6.01 | |
| r10_3_8 | 141.08 | 12.27 | 18.56 | 123.22 | 5.68 | 10.90 | 114.22 | 1.82 | 6.29 | |
| r10_3_9 | 154.72 | 13.20 | 14.74 | 146.36 | 3.39 | 7.00 | 147.62 | 7.54 | 5.29 | |
| r10_3_10 | 140.73 | 20.06 | 20.10 | 129.46 | 0.89 | 8.52 | 127.00 | 8.44 | 5.24 | |
| r10_3_11 | 145.33 | 18.81 | 19.56 | 131.51 | 3.40 | 8.02 | 132.53 | 4.20 | 5.50 | |
| r10_3_12 | 135.75 | 21.04 | 19.40 | 122.71 | 5.68 | 11.98 | 114.68 | 1.78 | 5.93 | |
| 25 | r25_3_1 | 452.10 | 27.14 | 47.98 | 430.42 | 12.09 | 66.48 | 365.24 | 11.21 | 27.49 |
| r25_3_2 | 396.71 | 28.75 | 60.58 | 370.88 | 9.71 | 83.08 | 301.42 | 4.69 | 29.95 | |
| r25_3_3 | 357.17 | 36.60 | 73.22 | 331.61 | 7.35 | 95.56 | 280.13 | 7.67 | 30.86 | |
| r25_3_4 | 284.37 | 29.41 | 112.34 | 274.89 | 8.34 | 121.42 | 254.11 | 11.21 | 31.50 | |
| r25_3_5 | 395.15 | 41.95 | 49.10 | 381.09 | 17.92 | 67.04 | 318.74 | 5.97 | 30.52 | |
| r25_3_6 | 375.00 | 28.24 | 57.72 | 344.08 | 10.19 | 86.40 | 286.24 | 9.07 | 30.61 | |
| r25_3_7 | 343.67 | 30.72 | 77.94 | 319.36 | 7.60 | 103.86 | 272.19 | 7.03 | 32.43 | |
| r25_3_8 | 263.91 | 17.77 | 124.92 | 272.38 | 7.44 | 134.60 | 250.67 | 9.36 | 32.49 | |
| r25_3_9 | 352.53 | 26.28 | 56.82 | 341.33 | 10.76 | 79.62 | 285.86 | 11.79 | 30.54 | |
| r25_3_10 | 325.70 | 29.20 | 74.58 | 300.20 | 7.84 | 94.56 | 266.81 | 14.89 | 30.65 | |
| r25_3_11 | 326.09 | 29.99 | 80.66 | 305.31 | 10.51 | 101.04 | 255.35 | 11.23 | 31.49 | |
| r25_3_12 | 279.84 | 39.48 | 100.98 | 248.15 | 8.66 | 130.84 | 242.88 | 10.27 | 32.59 | |
| 50 | r50_3_1 | 1238.11 | 66.62 | 284.66 | 1234.20 | 44.99 | 171.02 | 1043.90 | 27.07 | 122.55 |
| r50_3_2 | 1257.79 | 101.16 | 305.68 | 1082.78 | 48.46 | 240.32 | 928.96 | 12.49 | 119.01 | |
| r50_3_3 | 1158.92 | 155.55 | 446.30 | 916.23 | 33.29 | 310.52 | 846.11 | 21.47 | 118.38 | |
| r50_3_4 | 1067.64 | 111.08 | 584.86 | 804.39 | 40.51 | 480.58 | 822.05 | 30.86 | 115.30 | |
| r50_3_5 | 1251.80 | 81.35 | 200.58 | 1144.72 | 55.01 | 168.32 | 988.17 | 25.11 | 116.37 | |
| r50_3_6 | 1204.22 | 115.91 | 297.08 | 1030.90 | 44.72 | 232.74 | 920.01 | 24.38 | 111.20 | |
| r50_3_7 | 1134.73 | 126.78 | 436.32 | 899.99 | 39.85 | 331.82 | 870.59 | 28.57 | 113.61 | |
| r50_3_8 | 1085.62 | 122.97 | 544.00 | 788.34 | 32.37 | 512.06 | 841.80 | 33.18 | 117.75 | |
| r50_3_9 | 1245.75 | 103.36 | 200.68 | 1056.64 | 35.44 | 181.00 | 898.47 | 29.47 | 110.75 | |
| r50_3_10 | 1156.13 | 95.65 | 267.60 | 998.06 | 45.67 | 212.82 | 917.38 | 39.96 | 112.82 | |
| 100 | r100_3_1 | 3217.75 | 163.13 | 988.88 | 2959.41 | 98.62 | 707.82 | 2634.96 | 58.72 | 397.32 |
| r100_3_2 | 3010.34 | 243.96 | 1207.06 | 2496.54 | 91.85 | 1241.44 | 2457.43 | 59.51 | 393.39 | |
| r100_3_3 | 2627.79 | 173.99 | 1727.04 | 2200.64 | 99.99 | 1546.28 | 2246.53 | 98.21 | 399.38 | |
| r100_3_4 | 2240.21 | 115.45 | 3799.78 | 1932.28 | 64.63 | 2171.92 | 2159.23 | 66.61 | 410.37 | |
| r100_3_5 | 3197.04 | 157.74 | 767.36 | 2833.05 | 101.60 | 730.58 | 2607.26 | 56.85 | 392.36 | |
| r100_3_6 | 2953.05 | 217.49 | 1335.36 | 2423.52 | 91.42 | 1219.56 | 2337.40 | 80.01 | 384.46 | |
| r100_3_7 | 2603.03 | 177.52 | 1800.94 | 2162.49 | 88.99 | 1576.56 | 2180.11 | 75.83 | 391.04 | |
| r100_3_8 | 2191.85 | 130.92 | 4149.24 | 1886.96 | 59.33 | 2230.52 | 2110.78 | 58.49 | 393.81 | |
| r100_3_9 | 3056.98 | 176.51 | 956.02 | 2706.84 | 90.47 | 793.64 | 2530.86 | 37.09 | 390.98 | |
| r100_3_10 | 2852.15 | 206.34 | 1171.50 | 2452.96 | 93.26 | 966.90 | 2308.79 | 48.83 | 378.20 |
| Customers | Instance | OF | Cost | Priority | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Avg. | Min | Gap | Avg. | Min | Gap | Avg. | Min | Gap | ||
| 25 | r25_3p_1 | 424 | 413 | 2.66% | 5223.09 | 5014.87 | 4.15% | 1.036 | 1 | 3.60% |
| r25_3p_2 | 413 | 388 | 6.44% | 5195.87 | 4505.05 | 15.33% | 1.064 | 1 | 6.40% | |
| r25_3p_3 | 428 | 419 | 2.15% | 5245.62 | 5115.03 | 2.55% | 1.028 | 1 | 2.80% | |
| r25_3p_4 | 408 | 393 | 3.82% | 5530.29 | 5304.27 | 4.26% | 1.008 | 1 | 0.80% | |
| r25_3p_5 | 411 | 402 | 2.24% | 5197.58 | 4998 | 3.99% | 1.004 | 1 | 0.40% | |
| r25_3p_6 | 411 | 405 | 1.48% | 5251.48 | 5160.81 | 1.76% | 1 | 1 | 0.00% | |
| r25_3p_7 | 407 | 394 | 3.30% | 5223.87 | 4967.22 | 5.17% | 1.032 | 1 | 3.20% | |
| r25_3p_8 | 431 | 418 | 3.11% | 5614.3 | 5066.46 | 10.81% | 1.108 | 1 | 10.80% | |
| r25_3p_9 | 385 | 370 | 4.05% | 4574.93 | 4363.56 | 4.84% | 1 | 1 | 0.00% | |
| r25_3p_10 | 398 | 387 | 2.84% | 4815.47 | 4533.15 | 6.23% | 1.02 | 1 | 2.00% | |
| 50 | r50_3p_1 | 356 | 346 | 2.89% | 8533.94 | 8260.79 | 1.80% | 1.006 | 1 | 0.60% |
| r50_3p_2 | 364 | 355 | 2.54% | 8607.28 | 8347.22 | 1.89% | 1.03 | 1 | 3.00% | |
| r50_3p_3 | 365 | 351 | 3.99% | 9037.99 | 8165.41 | 3.94% | 1.022 | 1 | 2.20% | |
| r50_3p_4 | 363 | 347 | 4.61% | 9190.26 | 8131.28 | 5.58% | 1.022 | 1 | 2.20% | |
| r50_3p_5 | 345 | 329 | 4.86% | 8228.71 | 7767.57 | 3.43% | 1 | 1 | 0.00% | |
| r50_3p_6 | 357 | 348 | 2.59% | 8941.46 | 8528.38 | 2.42% | 1.012 | 1 | 1.20% | |
| r50_3p_7 | 349 | 337 | 3.56% | 8553.5 | 8177.82 | 3.42% | 1.014 | 1 | 1.40% | |
| r50_3p_8 | 365 | 355 | 2.82% | 9369.44 | 8771.76 | 3.26% | 1.012 | 1 | 1.20% | |
| r50_3p_9 | 367 | 346 | 6.07% | 8577.33 | 8020.42 | 4.00% | 1.054 | 1 | 5.40% | |
| r50_3p_10 | 357 | 348 | 2.59% | 8821 | 8526.94 | 2.03% | 1 | 1 | 0.00% | |
| 100 | r100_3p_1 | 353 | 341 | 3.52% | 16,851.63 | 16,159.34 | 3.55% | 1.028 | 1 | 2.80% |
| r100_3p_2 | 353 | 334 | 5.69% | 16806.4 | 15,673.85 | 4.45% | 1.007 | 1 | 0.70% | |
| r100_3p_3 | 353 | 343 | 2.92% | 17,144.93 | 16,683.24 | 2.15% | 1.036 | 1 | 3.60% | |
| r100_3p_4 | 351 | 336 | 4.46% | 17,229.21 | 16,397.92 | 2.82% | 1.014 | 1 | 1.40% | |
| r100_3p_5 | 343 | 331 | 3.63% | 16,270.05 | 15,392.24 | 4.25% | 1.028 | 1 | 2.80% | |
| r100_3p_6 | 354 | 327 | 8.26% | 16,716.27 | 15,018.89 | 5.36% | 1.042 | 1 | 4.20% | |
| r100_3p_7 | 362 | 341 | 6.16% | 17,520.29 | 15,962.86 | 5.97% | 1.069 | 1 | 6.90% | |
| r100_3p_8 | 355 | 349 | 1.72% | 17,191.82 | 16,492.24 | 2.90% | 1.048 | 1 | 4.80% | |
| r100_3p_9 | 365 | 343 | 6.41% | 17,151.35 | 15,961.33 | 3.02% | 1.028 | 1 | 2.80% | |
| r100_3p_10 | 348 | 335 | 3.88% | 16,610.44 | 15,859.48 | 3.70% | 1.025 | 1 | 2.50% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Escudero-Santana, A.; Muñuzuri, J.; Lorenzo-Espejo, A.; Muñoz-Díaz, M.-L. Improving E-Commerce Distribution through Last-Mile Logistics with Multiple Possibilities of Deliveries Based on Time and Location. J. Theor. Appl. Electron. Commer. Res. 2022, 17, 507-521. https://doi.org/10.3390/jtaer17020027
Escudero-Santana A, Muñuzuri J, Lorenzo-Espejo A, Muñoz-Díaz M-L. Improving E-Commerce Distribution through Last-Mile Logistics with Multiple Possibilities of Deliveries Based on Time and Location. Journal of Theoretical and Applied Electronic Commerce Research. 2022; 17(2):507-521. https://doi.org/10.3390/jtaer17020027
Chicago/Turabian StyleEscudero-Santana, Alejandro, Jesús Muñuzuri, Antonio Lorenzo-Espejo, and María-Luisa Muñoz-Díaz. 2022. "Improving E-Commerce Distribution through Last-Mile Logistics with Multiple Possibilities of Deliveries Based on Time and Location" Journal of Theoretical and Applied Electronic Commerce Research 17, no. 2: 507-521. https://doi.org/10.3390/jtaer17020027
APA StyleEscudero-Santana, A., Muñuzuri, J., Lorenzo-Espejo, A., & Muñoz-Díaz, M.-L. (2022). Improving E-Commerce Distribution through Last-Mile Logistics with Multiple Possibilities of Deliveries Based on Time and Location. Journal of Theoretical and Applied Electronic Commerce Research, 17(2), 507-521. https://doi.org/10.3390/jtaer17020027






