The Impact of Guarantees on Peer-to-Peer Lending Platform: Evolutionary Game Analysis and Empirical Evidence from China
Abstract
1. Introduction
1.1. Related Literature
1.2. Contributions
2. Evolutionary Game Analysis
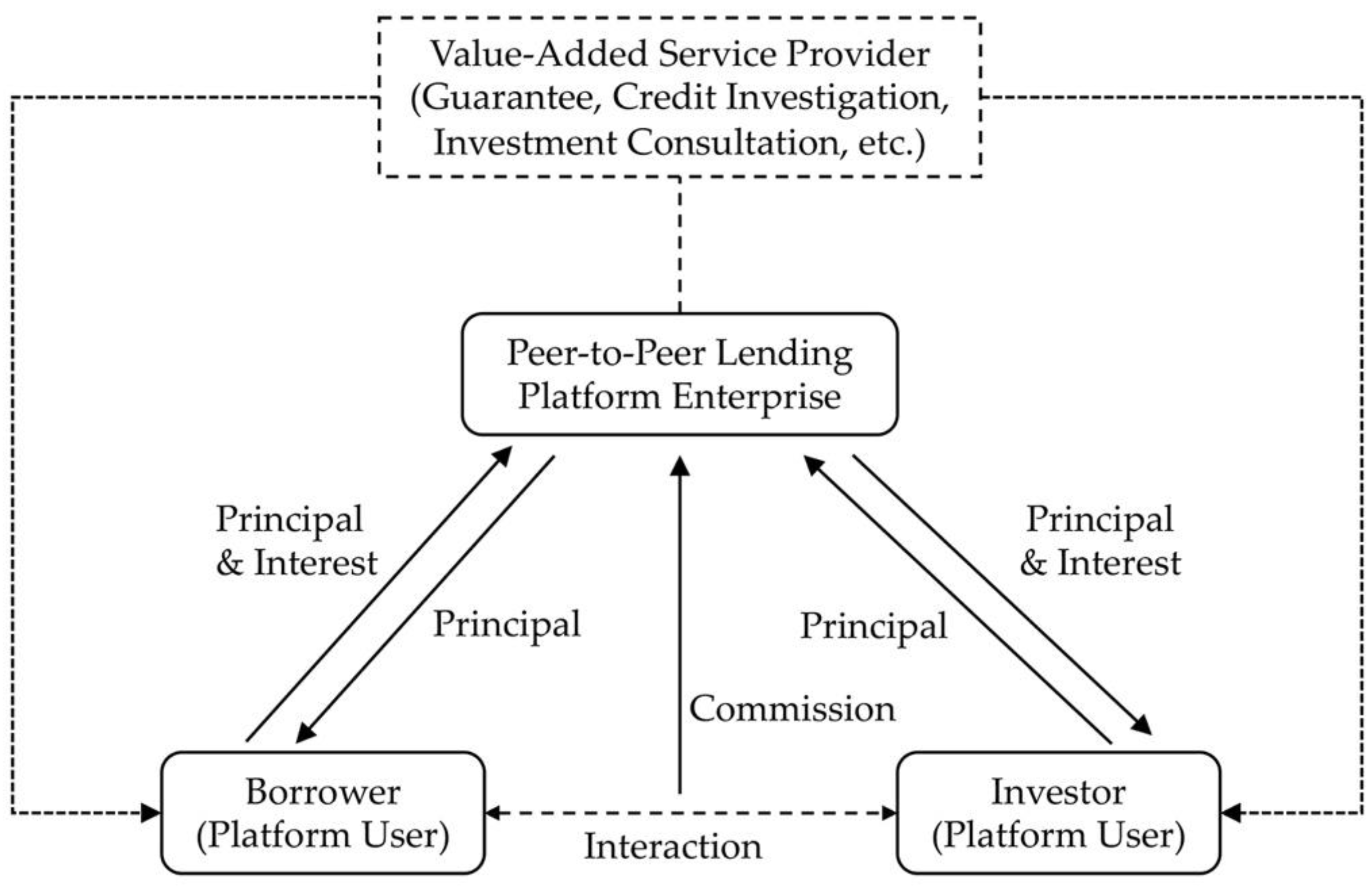
2.1. Model Framework and Assumption
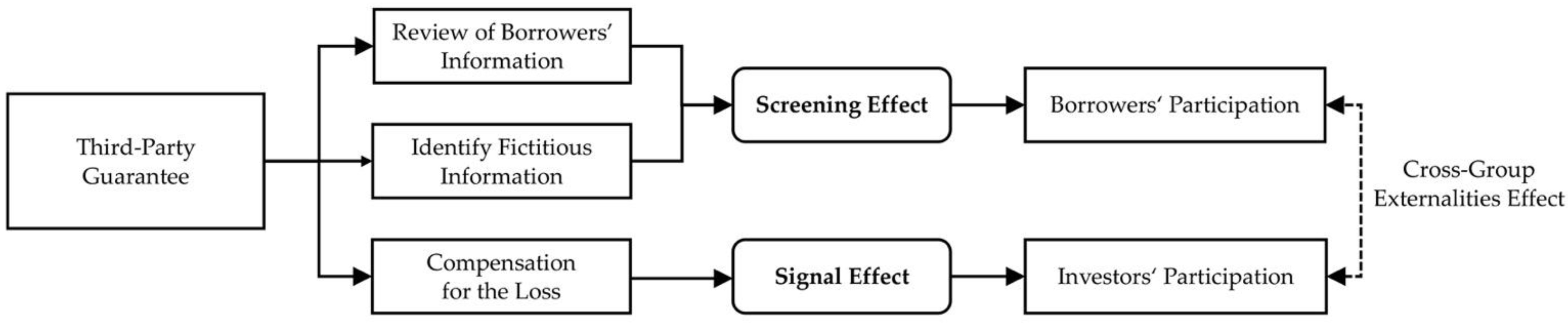
2.1.1. Model Framework
2.1.2. Model Assumption
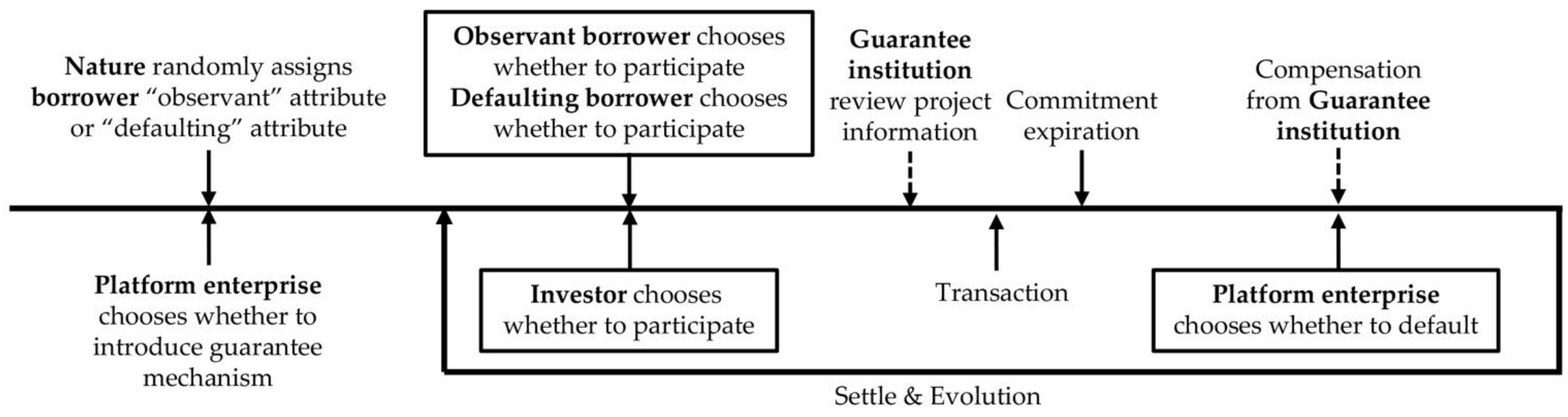
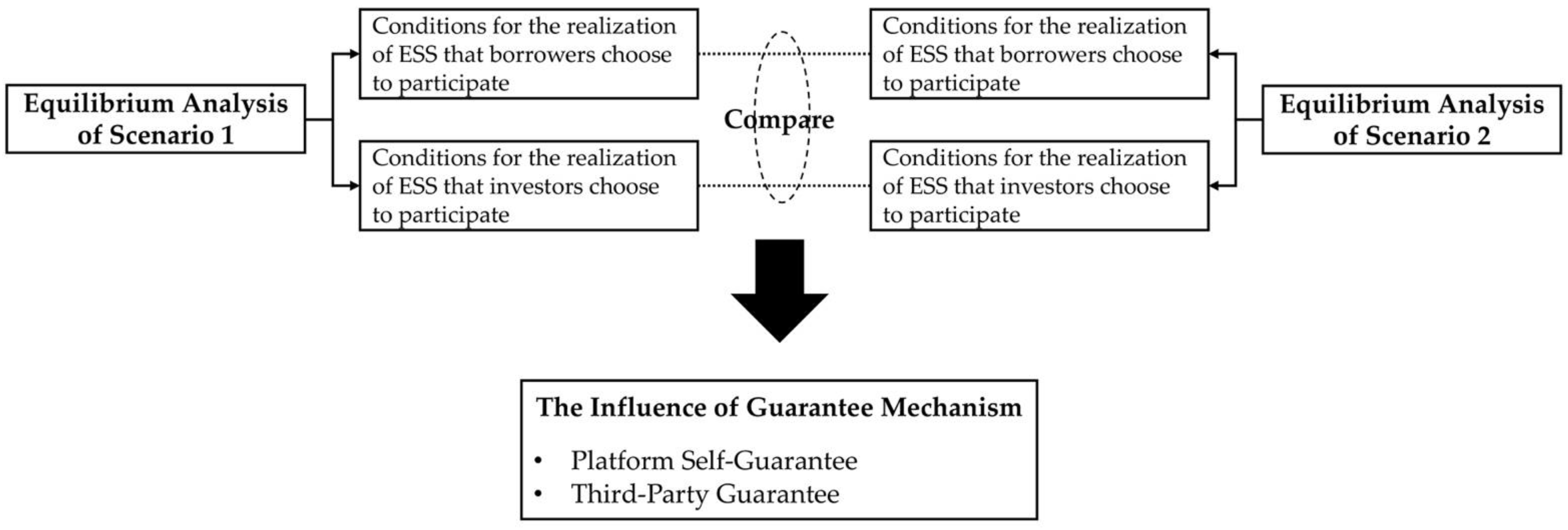
2.2. Equilibrium Analysis of the Evolutionary Game
2.2.1. Scenario 1: No Guarantee
2.2.2. Scenario 2: Guarantee Mechanism
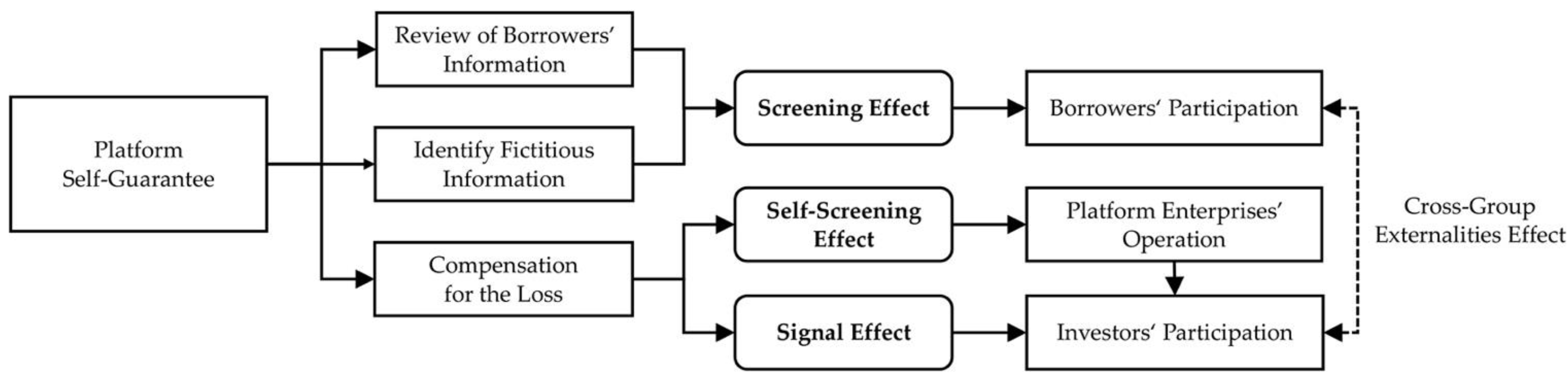
Analysis of Platform Self-Guarantee Mechanism
Analysis of Third-Party Guarantee Mechanism
3. Empirical Analysis of China’s Peer-to-Peer Platform
3.1. Materials and Methods
3.1.1. Model Setting
3.1.2. Data Collection
3.2. Result
3.2.1. Testing of the Fitness of the Model Setting
3.2.2. The Impact of Guarantee Mechanism
The Impact of the Guarantee Mechanism on the Scale of Borrowers
The Impact of the Guarantee Mechanism on the Scale of Investors
The Impact of the Guarantee Mechanism on Transaction Volume
4. Conclusions and Implications
4.1. Conclusions
4.2. Implications and Limitations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
| Model 6 | Model 7 | Model 8 | |
|---|---|---|---|
| . | Fixed Effect | Random Effect (FGLS) | Random Effect (MLE) |
| Constant | −2.8033 * | −3.0686 *** | −3.0686 *** |
| (1.6362) | (1.1796) | (0.9312) | |
| NOB | 0.1214 *** | 0.1191 *** | 0.1191 *** |
| (0.0355) | (0.0185) | (0.0185) | |
| NOI | 3.0319 *** | 3.0462 *** | 3.0462 *** |
| (0.2521) | (0.2343) | (0.0727) | |
| Rate | −0.1104 | −0.1088 * | −0.1088 |
| (0.0763) | (0.0557) | (0.0670) | |
| SG | 0.7911 *** | 0.8229 *** | 0.8229 ** |
| (0.2869) | (0.1381) | (0.4032) | |
| TG | 0.4608 | 0.4503 | 0.4503 |
| (0.4130) | (0.2873) | (0.3322) | |
| Control variable | Controlled | Controlled | Controlled |
| R2 | 0.7945 | - | - |
| N | 1260 | 1260 | 1260 |
| Item | Statistic | p-Value |
|---|---|---|
| F Test | 0.65 | 0.6630 |
| BP Test | 0.00 | 1.0000 |
| LR Test | 0.00 | 1.0000 |
References
- Greiner, M.E.; Wang, H. Building Consumer-to-Consumer Trust in E-Finance Marketplaces: An Empirical Analysis. Int. J. Electron. Commer. 2010, 15, 105–136. [Google Scholar] [CrossRef]
- Baghdadi, Y. From e-commerce to social commerce: A framework to guide enabling cloud computing. J. Theor. Appl. Electron. Commer. Res. 2013, 8, 12–38. [Google Scholar] [CrossRef][Green Version]
- Chen, X.; Hu, X.; Ben, S. How individual investors react to negative events in the FinTech era? Evidence from China’s Peer-to-Peer lending. J. Theor. Appl. Electron. Commer. Res. 2021, 16, 52–70. [Google Scholar] [CrossRef]
- Wei, Z.; Lin, M. Market mechanisms in online peer-to-peer lending. Manag. Sci. 2017, 63, 4236–4257. [Google Scholar] [CrossRef]
- Gu, D.; Lu, T.; Luo, P.; Zhang, C. The Impact of Venture Capital Investment on the Performance of Peer-to-Peer Lending Platforms: Evidence from China. Asia-Pac. J. Financ. Stud. 2019, 48, 640–665. [Google Scholar] [CrossRef]
- Cui, Y.; Mou, J.; Cohen, J.; Liu, Y.; Kurcz, K. Understanding consumer intentions toward cross-border m-commerce usage: A psychological distance and commitment-trust perspective. Electron. Commer. Res. Appl. 2020, 39, 100920. [Google Scholar] [CrossRef]
- Armstrong, M. Competition in two-sided markets. RAND J. Econ. 2006, 37, 668–691. [Google Scholar] [CrossRef]
- Rochet, J.C.; Tirole, J. Two-sided markets: A progress report. RAND J. Econ. 2006, 37, 645–667. [Google Scholar] [CrossRef]
- Hagiu, A.; Wright, J. Multi-sided platforms. Int. J. Ind. Organ. 2015, 43, 162–174. [Google Scholar] [CrossRef]
- Guo, J.; Luo, P. Does the Internet make contribution to TFP of China? Manag. World 2016, 10, 34–49. [Google Scholar]
- Serrano-Cinca, C.; Gutiérrez-Nieto, B.; López-Palacios, L. Determinants of default in P2P lending. PLoS ONE 2015, 10, e0139427. [Google Scholar] [CrossRef] [PubMed]
- Tao, Q.; Dong, Y.; Lin, Z. Who can get money? Evidence from the Chinese peer-to-peer lending platform. Inf. Syst. Front. 2017, 19, 425–441. [Google Scholar] [CrossRef]
- Guo, W.; Li, Y. Research on the P2P Network Lending Platform Model. China Bus. Mark. 2014, 28, 114–121. [Google Scholar]
- Li, J.; Hsu, S.; Chen, Z.; Chen, Y. Risks of p2p lending platforms in china: Modeling failure using a cox hazard model. Chin. Econ. 2016, 49, 161–172. [Google Scholar] [CrossRef]
- Hagiu, A. Merchant or Two-Sided Platform? Rev. Netw. Econ. 2007, 6, 115–133. [Google Scholar] [CrossRef]
- Weng, Z.; Luo, P. Supervision of the Default Risk of Online Car-Hailing Platform from an Evolutionary Game Perspective. Sustainability 2021, 13, 555. [Google Scholar] [CrossRef]
- Luo, P.; Gu, D. Transmission Path of VCs to Platform’s Transaction Volume: A Mediating Effect Model. Mod. Manag. 2018, 38, 1–4. [Google Scholar]
- Zhang, L.; Jing, Z.; Liu, Q. A meta-analysis of mobile commerce adoption and the moderating effect of culture. Comput. Hum. Behav. 2012, 28, 1902–1911. [Google Scholar] [CrossRef]
- Liao, L.; Li, M.; Wang, Z. The Intelligent Investor: Not-Fully-Marketized Interest Rate and Risk Identify——Evidence from P2P Lending. Econ. Res. J. 2014, 49, 125–137. [Google Scholar]
- Holmström, B. Moral hazard and observability. Bell J. Econ. 1979, 10, 74–91. [Google Scholar] [CrossRef]
- Yum, H.; Lee, B.; Chae, M. From the wisdom of crowds to my own judgment in microfinance through online peer-to-peer lending platforms. Electron. Commer. Res. Appl. 2012, 11, 469–483. [Google Scholar] [CrossRef]
- Weng, Z. Research on the Platformization and Default Risk Governance of Sharing Economy. Ph.D. Thesis, Fudan University, Shanghai, China, 16 October 2019. [Google Scholar]
- Rong, L. Research on Competition Strategy and Industry Regulation of Third-Party Payment Platform. Ph.D. Thesis, Fudan University, Shanghai, China, 5 June 2012. [Google Scholar]
- Evans, D.S. The Antitrust Economics of Two-Sided Markets. Yale J. Regul. 2003, 20, 325–381. [Google Scholar] [CrossRef]
- Régibeau, P. A comment on Evans, Hagiu and Schmalensee. CESifo Econ. Stud. 2005, 51, 225–232. [Google Scholar] [CrossRef]
- Zhou, B. Review of research on lemon market governance mechanism. Econ. Perspect. 2010, 3, 131–135. [Google Scholar]
- Ross, S.A. The Determination of Financial Structure: The Incentive Signaling Approach. Bell J. Econ. 1977, 8, 23–40. [Google Scholar] [CrossRef]
- Gu, D.; Zhao, X.; Luo, P. The signaling behavior of three-player games on P2P platforms. Syst. Eng.-Theory Pract. 2020, 40, 1210–1220. [Google Scholar]
- Bester, H. The role of collateral in credit markets with imperfect information. Eur. Econ. Rev. 1987, 31, 887–899. [Google Scholar] [CrossRef]
- Coco, G. On the use of collateral. J. Econ. Surv. 2000, 14, 191–214. [Google Scholar] [CrossRef]
- Biglaiser, G.; Li, F. Middlemen: The good, the bad, and the ugly. RAND J. Econ. 2018, 49, 3–22. [Google Scholar] [CrossRef]
- Jiang, Q. Research on the Efficiency Difference and the Influencing Factors of the Volume of P2P Loan Platform in China. J. Quant. Tech. Econ. 2018, 35, 60–77. [Google Scholar]
- Duarte, J.; Siegel, S.; Young, L. Trust and credit: The role of appearance in peer-to-peer lending. Rev. Financ. Stud. 2012, 25, 2455–2484. [Google Scholar] [CrossRef]
- Lin, M.; Prabhala, N.R.; Viswanathan, S. Judging borrowers by the company they keep: Friendship networks and information asymmetry in online peer-to-peer lending. Manag. Sci. 2013, 59, 17–35. [Google Scholar] [CrossRef]
- Lee, E.; Lee, B. Herding behavior in online P2P lending: An empirical investigation. Electron. Commer. Res. Appl. 2012, 11, 495–503. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, P. Rational herding in microloan markets. Manag. Sci. 2012, 58, 892–912. [Google Scholar] [CrossRef]
- Liu, D.; Brass, D.J.; Lu, Y.; Chen, D. Friendships in online peer-to-peer lending: Pipes, Prisms, and Relational Herding. Mis Q. 2015, 39, 729–742. [Google Scholar] [CrossRef]
- Pope, D.G.; Sydnor, J.R. What’s in a Picture? Evidence of Discrimination from Prosper. com. J. Hum. Resour. 2011, 46, 53–92. [Google Scholar]
- Liao, L.; Li, M.; Wang, Z. Regional Discrimination in Chinese Internet Finance. J. Quant. Tech. Econ. 2014, 31, 54–70. [Google Scholar]
- Zhao, L.; Qi, R. Can improving the quality of information disclosure weaken the professional identity discrimination in the P2P lending market? Transform. Bus. Econ. 2019, 18, 214–233. [Google Scholar]
- Zhang, B.; Zhan, H.; He, F. Guarantee Mechanisms and Intermediary Nature of P2P Lending Market in China—Model Construction and Quantitative Analysis Based on Investor Behavior. Nanjing Bus. Rev. 2018, 4, 73–103. [Google Scholar]
- Li, R. Research on network financing guarantee system construction. South China Financ. 2014, 4, 72–76. [Google Scholar]
- Chen, Z. Legal risk and prevention suggestions of the guarantee in P2P lending. Leg. Syst. Soc. 2015, 11, 95–96. [Google Scholar]
- Zhang, C.; Chen, F. Research on the model dissimilation and de-guarantee of P2P lending platform. South China Financ. 2018, 1, 68–74. [Google Scholar]
- Peng, B. Peer-to-Peer Lending and Illegal Financing. Financ. Regul. Res. 2014, 6, 13–25. [Google Scholar]
- Xiong, J.; Ma, C.; Yao, Z. The influence of guarantee certification service of P2P lending on borrowing -- Taking Renrendai as an example. Mod. Manag. 2015, 35, 1–3. [Google Scholar]
- Ye, X. The Risks of China’s P2P Lending Models and Related Regulations. Financ. Regul. Res. 2014, 3, 71–82. [Google Scholar]
- Zhang, H. Regulation of Information Disclosure and the Patterns of P2P Lending in China. China Econ. Q. 2017, 16, 371–392. [Google Scholar]
- Gu, D.; Ding, L.; Luo, P. Evolutionary Game Analysis on Credit Risk Control in P2P Online Lending Platforms. R D Manag. 2018, 30, 12–21. [Google Scholar]
- Smith, J.M.; Price, G.R. The logic of animal conflict. Nature 1973, 246, 15–18. [Google Scholar] [CrossRef]
- Taylor, P.D.; Jonker, L.B. Evolutionary stable strategies and game dynamics. Math. Biosci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
- Smith, J.M. Evolution and the Theory of Games; Cambridge University Press: Cambridge, UK, 1982; pp. 40–67. [Google Scholar]
- Weibull, J.W. Evolutionary Game Theory; MIT Press: Cambridge, UK, 1995; pp. 35–109. [Google Scholar]
- Liu, Y.; Chen, L.; Jin, S. Research on the application value of credit report in social governance. South China Financ. 2020, 8, 81–91. [Google Scholar]
- Baron, R.M.; Kenny, D.A. The moderator–mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. J. Personal. Soc. Psychol. 1986, 51, 1173–1182. [Google Scholar] [CrossRef]
- Wen, Z.; Ye, B. Analyses of Mediating Effects: The Development of Methods and Models. Adv. Psychol. Sci. 2014, 22, 731–745. [Google Scholar] [CrossRef]
- Xue, W.; Zuo, L. An Empirical Study on the Transmission Mechanism between the Cross Network Effect and Non-neutrality Price in Duopoly P2P Market. Mod. Financ. Econ.-J. Tianjin Univ. Financ. Econ. 2017, 37, 59–72. [Google Scholar]
- Rong360. 22 Peer-to-Peer Lending Platforms Hold the Small-Loan License: The Transformation Is Not Easy. Available online: https://www.rong360.com/news/2019/02/01/176528.html (accessed on 20 July 2021).
- Lu, S.; Lan, H. VC, The Third-Party Escrow and the Trading Volume of the P2P Lending Platforms in China—Analysis from the Perspective of the P2P Investors. Rev. Invest. Stud. 2015, 34, 23–37. [Google Scholar]
- Wang, Y.; Fu, K. Analysis of the Features of P2P Network Lending Platforms and Lending Effect in China. Mod. Manag. 2018, 38, 18–22. [Google Scholar]
- Wooldridge, J.M. Econometric Analysis of Cross Section and Panel Data. MIT Press: Cambridge, MA, USA, 2010; pp. 126–134, 241–256. [Google Scholar]

| Parameter | Definition |
|---|---|
| The possibility of the observant borrower taking the OB1 strategy | |
| The possibility of the defaulting borrower taking the DB1 strategy | |
| The possibility of the platform enterprises taking the PE1 strategy | |
| The possibility of the investor taking the IN1 strategy | |
| The investment amount of the project; the compensation amount from the guarantee institution | |
| The promised interest | |
| The commission charged by the platform enterprises to the investor for the normal transaction | |
| The profit of the observant borrower from participating in the transaction | |
| The post-event penalty imposed by the regulator on irregular platform enterprises | |
| The post-event penalty imposed by the regulator on defaulting borrowers | |
| The extra cost for borrowers to provide information for review | |
| The cost of platform enterprises for carrying out the project information review by themselves or hiring a third-party institution | |
| The probability of identifying the fictitious project | |
| Exogenous proportion of the observant borrowers in the whole borrower group |
| Observant Borrower | Defaulting Borrower | Platform Enterprise | |
|---|---|---|---|
| Regular Operation | Irregular Operation | ||
| Participation | Participation | ||
| Non-Participation | |||
| Non-Participation | Participation | ||
| Non-Participation | |||
| Observant Borrower | Defaulting Borrower | Platform Enterprise | |
|---|---|---|---|
| Regular Operation | Irregular Operation | ||
| Participation | Participation | ||
| Non-Participation | |||
| Non-Participation | Participation | ||
| Non-Participation | |||
| Type | Name | Unit | Definition and Interpretation |
|---|---|---|---|
| Experimental Variable | VOT | CNY 100 million | Volume of transactions on the platform (Monthly) |
| NOB | 10 thousand | Scale of borrowers (Monthly) | |
| NOI | 10 thousand | Scale of investors (Monthly) | |
| Rate | % | The average interest rate of the project (loan) on the platform (monthly, weighted by the amount) | |
| SG | / | Whether the platform applied a platform self-guarantee mechanism, including the risk reserve fund mode and platform enterprise compensation mode | |
| TG | / | Whether the platform applied a third-party guarantee mechanism, including financing guarantee mode, non-financing guarantee mode and other guarantees | |
| Control Variable | Capital | CNY 100 million | Registered capital |
| Duration | N | The duration of the platform (Month) | |
| Finance | / | Whether the platform experienced a history of financing | |
| Association | / | Whether the platform had joined the Chinese Internet Finance Association | |
| Flexible | / | Whether the project (loan) can be transferred before maturity | |
| Auto | / | Whether the investment amount could be automatically bid after the expiration of the project | |
| VC | / | Whether the platform had introduced venture capital | |
| Period | N | Average maturity of the project (Month) | |
| Amount | CNY 10 thousand | Per capita loan amount | |
| Mode | / | Whether the platform had the small-loan license [58] |
| Time | VOT of Sample Platforms | VOT of the Industry | Proportion |
|---|---|---|---|
| August 2018 | 70.96 | 119.33 | 59.46% |
| September 2018 | 63.63 | 110.74 | 57.46% |
| October 2018 | 58.69 | 102.27 | 57.39% |
| November 2018 | 60.79 | 111.45 | 54.54% |
| December 2018 | 62.20 | 106.02 | 58.67% |
| January 2019 | 57.61 | 103.71 | 55.55% |
| Variable | Mean | Standard Deviation | Median | Minimum | Maximum |
|---|---|---|---|---|---|
| VOT | 2.9672 | 9.8403 | 0.2720 | 0.0001 | 135.7133 |
| NOB | 2.1049 | 8.7726 | 0.0121 | 0.0001 | 88.4951 |
| NOI | 0.7738 | 2.5606 | 0.0523 | 0.0001 | 21.6800 |
| Rate | 10.0112 | 1.9983 | 9.8500 | 1.0700 | 18.5200 |
| SG | 0.1286 | 0.3349 | 0.0000 | 0.0000 | 1.0000 |
| TG | 0.8048 | 0.3965 | 1.0000 | 0.0000 | 1.0000 |
| Capital | 0.7937 | 1.8427 | 0.5000 | 0.0500 | 25.0000 |
| Duration | 46.9429 | 13.1060 | 46.0000 | 10.0000 | 119.0000 |
| Finance | 0.2381 | 0.4261 | 0.0000 | 0.0000 | 1.0000 |
| Association | 0.4857 | 0.5000 | 0.0000 | 0.0000 | 1.0000 |
| Flexible | 0.7000 | 0.4584 | 1.0000 | 0.0000 | 1.0000 |
| Auto | 0.6333 | 0.4821 | 1.0000 | 0.0000 | 1.0000 |
| VC | 0.1190 | 0.3240 | 0.0000 | 0.0000 | 1.0000 |
| Period | 7.8601 | 7.4080 | 5.4650 | 0.3200 | 46.5700 |
| Amount | 34.0343 | 78.4520 | 14.7550 | 0.1100 | 1239.3500 |
| Mode | 0.0333 | 0.1796 | 0.0000 | 0.0000 | 1.0000 |
| VOT | NOB | NOI | Rate | SG | TG | Capital | Duration | |
|---|---|---|---|---|---|---|---|---|
| VOT | 1.0000 | |||||||
| NOB | 0.5480 *** | 1.0000 | ||||||
| NOI | 0.8720 *** | 0.5647 *** | 1.0000 | |||||
| Rate | −0.0495 * | −0.0015 | −0.0045 | 1.0000 | ||||
| SG | 0.0225 | −0.0672 ** | −0.0325 | 0.1338 *** | 1.0000 | |||
| TG | −0.0640 ** | −0.1206 *** | −0.0818 *** | −0.0558 ** | −0.0261 | 1.0000 | ||
| Capital | 0.1710 *** | 0.0306 | 0.0896 *** | −0.0966 *** | −0.0292 | 0.0503 * | 1.0000 | |
| Duration | 0.4392 *** | 0.0729 *** | 0.4186 *** | −0.0093 | 0.2161 *** | −0.1136 *** | 0.0213 | 1.0000 |
| Finance | 0.1736 *** | 0.1701 *** | 0.2267 *** | 0.0330 | −0.0477 * | −0.1477 *** | −0.0177 | 0.2866 *** |
| Association | 0.1547 *** | 0.0486 * | 0.1859 *** | 0.0458 | −0.0033 | −0.0501 * | 0.1057 *** | 0.2799 *** |
| Flexible | 0.1174 *** | 0.0921 *** | 0.1308 *** | 0.1457 *** | 0.0962 *** | 0.1494 *** | 0.0443 | 0.1768 *** |
| Auto | 0.0501 * | 0.0004 | 0.0477 * | 0.0739 *** | 0.0856 *** | −0.0258 | 0.0402 | 0.1615 *** |
| VC | 0.0631 ** | −0.0245 | 0.1296 *** | 0.1566 *** | −0.0094 | −0.1157 *** | −0.0674 ** | 0.2536 *** |
| Period | 0.2159 *** | 0.1423 *** | 0.3131 *** | 0.1662 *** | −0.1276 *** | 0.0486 * | 0.0008 | 0.1114 *** |
| Amount | −0.0265 | −0.0999 *** | −0.0641 ** | −0.0431 | −0.0091 | 0.0415 | −0.0254 | 0.0883 *** |
| Mode | 0.2602 *** | 0.0765 *** | 0.3343 *** | 0.0125 | 0.0079 | 0.0245 | 0.0848 *** | 0.2630 *** |
| Finance | Association | Flexible | Auto | VC | Period | Amount | Mode | |
| Finance | 1.0000 | |||||||
| Association | 0.1502 *** | 1.0000 | ||||||
| Flexible | 0.0488 * | 0.1580 *** | 1.0000 | |||||
| Auto | 0.1701 *** | 0.1068 *** | 0.2135 *** | 1.0000 | ||||
| VC | 0.5885 *** | 0.0546 * | 0.0160 | 0.1577 *** | 1.0000 | |||
| Period | 0.0538 * | 0.2433 *** | 0.2163 *** | −0.0674 ** | 0.0801 *** | 1.0000 | ||
| Amount | −0.0732 *** | −0.1162 *** | −0.0006 | 0.0075 | −0.0532 * | −0.1716 *** | 1.0000 | |
| Mode | 0.0830 *** | 0.1911 *** | 0.1216 *** | 0.0862 *** | 0.0137 | 0.1317 *** | −0.0482 * | 1.0000 |
| Item | F-Statistic | p-Value |
|---|---|---|
| Endogeneity of NOI and Rate in NOB Equation | 11.99 | 0.0000 |
| Endogeneity of NOB and Rate in NOI Equation | 53.79 | 0.0000 |
| Endogeneity of NOB and NOI in Rate Equation | 3.56 | 0.0596 |
| Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | |
|---|---|---|---|---|---|
| Dependent Variables | NOB | NOI | VOT | VOT | VOT |
| Constant | −33.4737 *** | −23.1898 *** | −10.7336 *** | −2.9666 * | −3.0686 * |
| (9.6679) | (3.9772) | (2.5950) | (1.6909) | (1.7691) | |
| NOB | 0.2878 *** | 0.1157 *** | 0.1191 *** | ||
| (0.0946) | (0.0375) | (0.0359) | |||
| NOI | 1.0389 ** | 3.0397 *** | 3.0462 *** | ||
| (0.4822) | (0.2575) | (0.2579) | |||
| Rate | 3.7821 *** | 1.9710 *** | −0.2388 * | −0.0940 | −0.1088 |
| (0.8858) | (0.3882) | (0.1326) | (0.0778) | (0.0768) | |
| SG | −2.9825 ** | −1.0756 ** | 0.8229 *** | ||
| (1.2487) | (0.5251) | (0.2961) | |||
| TG | −1.6589 *** | 0.7888 *** | 0.4503 | ||
| (0.6435) | (0.2362) | (0.4099) | |||
| Control variable | Controlled | Controlled | Controlled | Controlled | Controlled |
| Chi2 | 153.56 *** | 359.79 *** | - | - | - |
| R2 | - | - | 0.2757 | 0.7928 | 0.7938 |
| N | 1260 | 1260 | 1260 | 1260 | 1260 |
| Mediating Pathway | The Inspection Process | Coefficient | Standard Error | Z-Statistics | p-Value | Mediating Effect |
|---|---|---|---|---|---|---|
| SG→NOB→VOT | SG→NOB | −2.9825 | 1.2487 | −1.9384 | 0.0526 | Exist |
| NOB→VOT | 0.1191 | 0.0359 | ||||
| SG→NOI→VOT | SG→NOI | −1.0756 | 0.5251 | −2.0182 | 0.0436 | Exist |
| NOI→VOT | 3.0462 | 0.2579 | ||||
| TG→NOB→VOT | TG→NOB | −1.6589 | 0.6435 | −2.0356 | 0.0418 | Exist |
| NOB→VOT | 0.1191 | 0.0359 | ||||
| TG→NOI→VOT | TG→NOI | 0.7888 | 0.2362 | 3.2136 | 0.0013 | Exist |
| NOI→VOT | 3.0462 | 0.2579 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weng, Z.; Luo, P. The Impact of Guarantees on Peer-to-Peer Lending Platform: Evolutionary Game Analysis and Empirical Evidence from China. J. Theor. Appl. Electron. Commer. Res. 2021, 16, 2708-2731. https://doi.org/10.3390/jtaer16070149
Weng Z, Luo P. The Impact of Guarantees on Peer-to-Peer Lending Platform: Evolutionary Game Analysis and Empirical Evidence from China. Journal of Theoretical and Applied Electronic Commerce Research. 2021; 16(7):2708-2731. https://doi.org/10.3390/jtaer16070149
Chicago/Turabian StyleWeng, Zhicheng, and Pinliang Luo. 2021. "The Impact of Guarantees on Peer-to-Peer Lending Platform: Evolutionary Game Analysis and Empirical Evidence from China" Journal of Theoretical and Applied Electronic Commerce Research 16, no. 7: 2708-2731. https://doi.org/10.3390/jtaer16070149
APA StyleWeng, Z., & Luo, P. (2021). The Impact of Guarantees on Peer-to-Peer Lending Platform: Evolutionary Game Analysis and Empirical Evidence from China. Journal of Theoretical and Applied Electronic Commerce Research, 16(7), 2708-2731. https://doi.org/10.3390/jtaer16070149






