Or-Based Intelligent Decision Support System for E-Commerce
Abstract
1. Significance of the Study
- Designing the OR-IDSS model for E-commerce utilizing the fuzzy logic theory and machine learning methods.
- Evaluating the mathematical model for decision making in E-commerce.
- The experimental results have been executed, and the proposed model enhances the performance, accuracy, precision and reduces the error rate compared to other existing models.
2. Literature Review
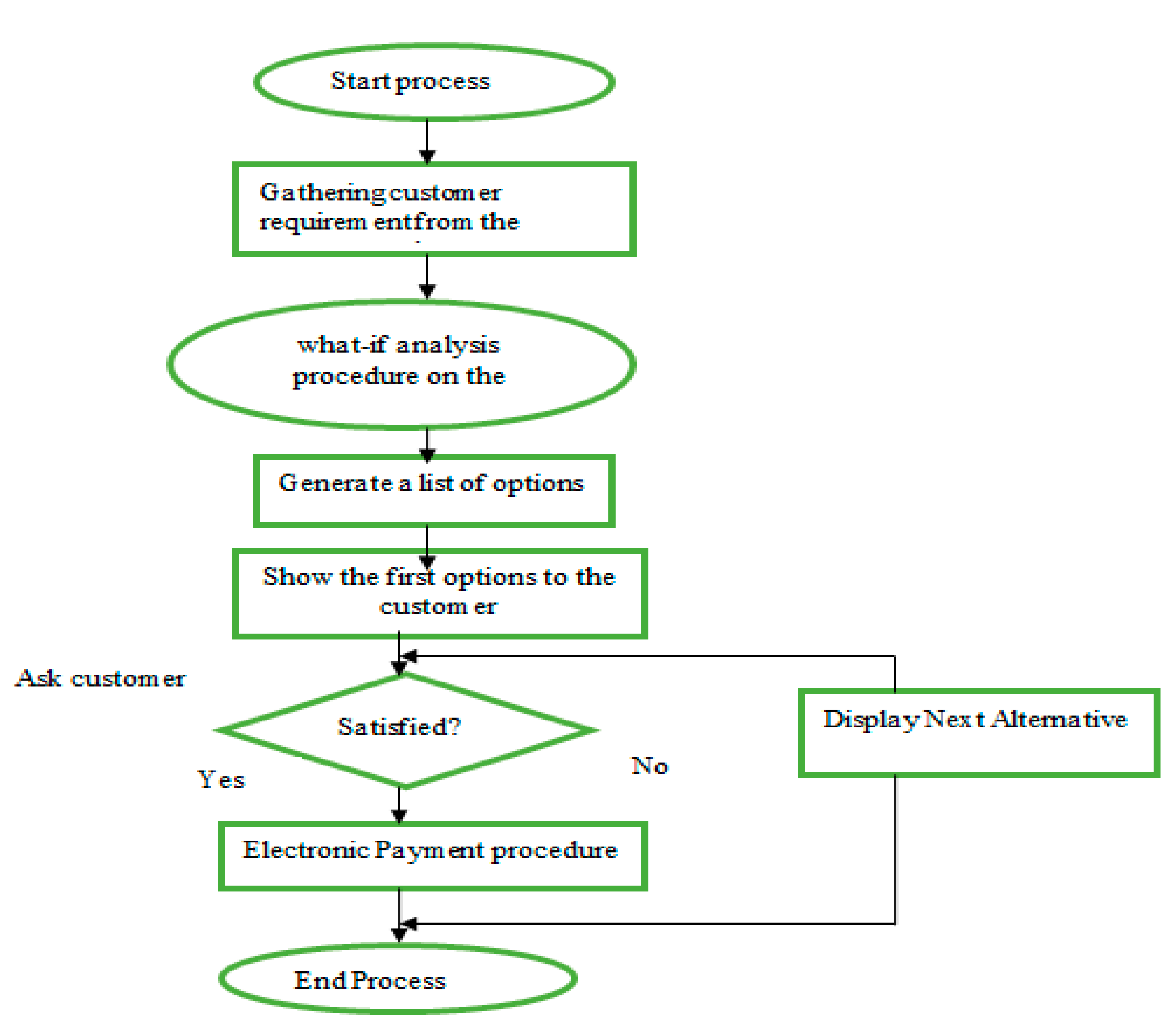
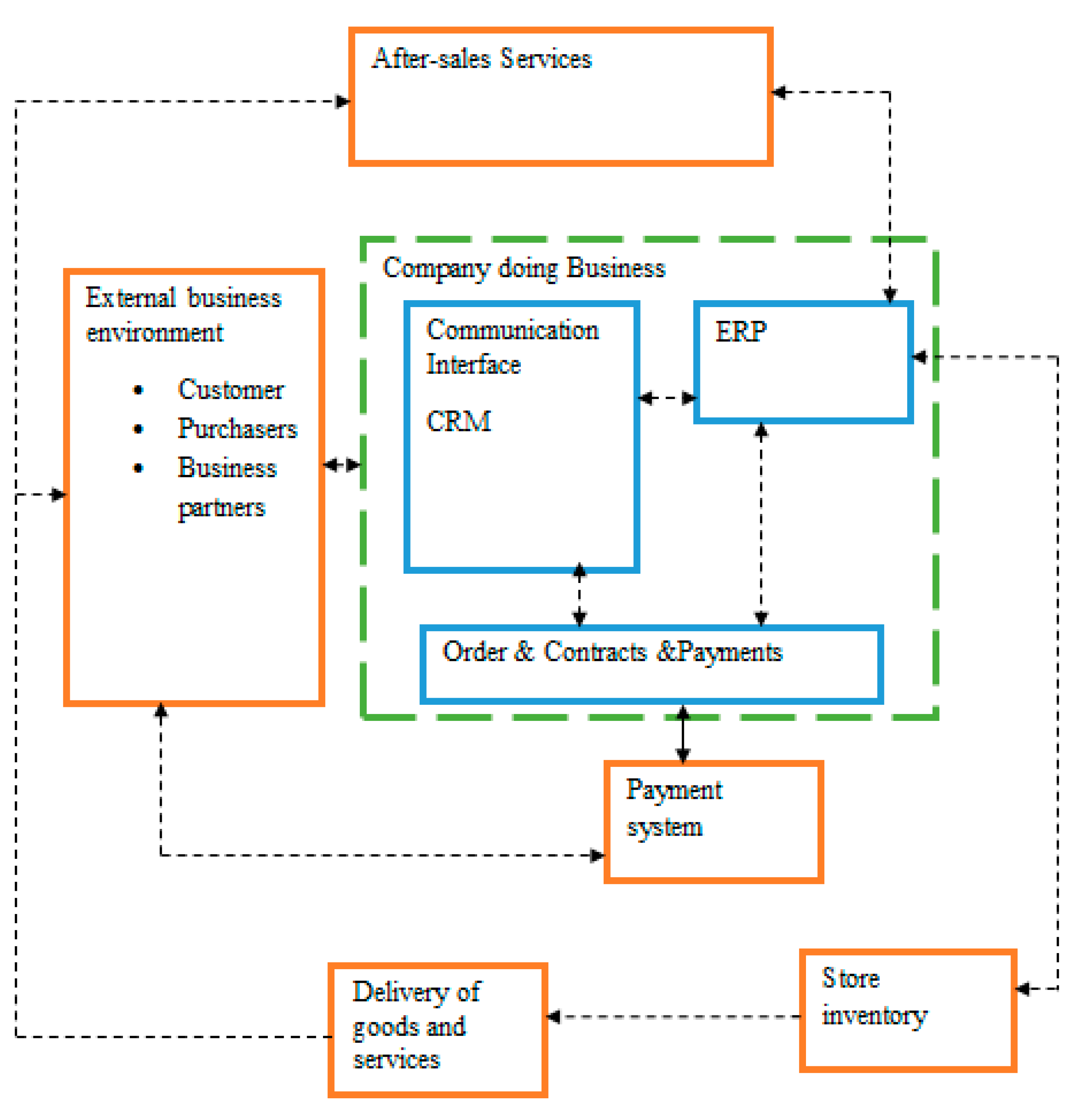
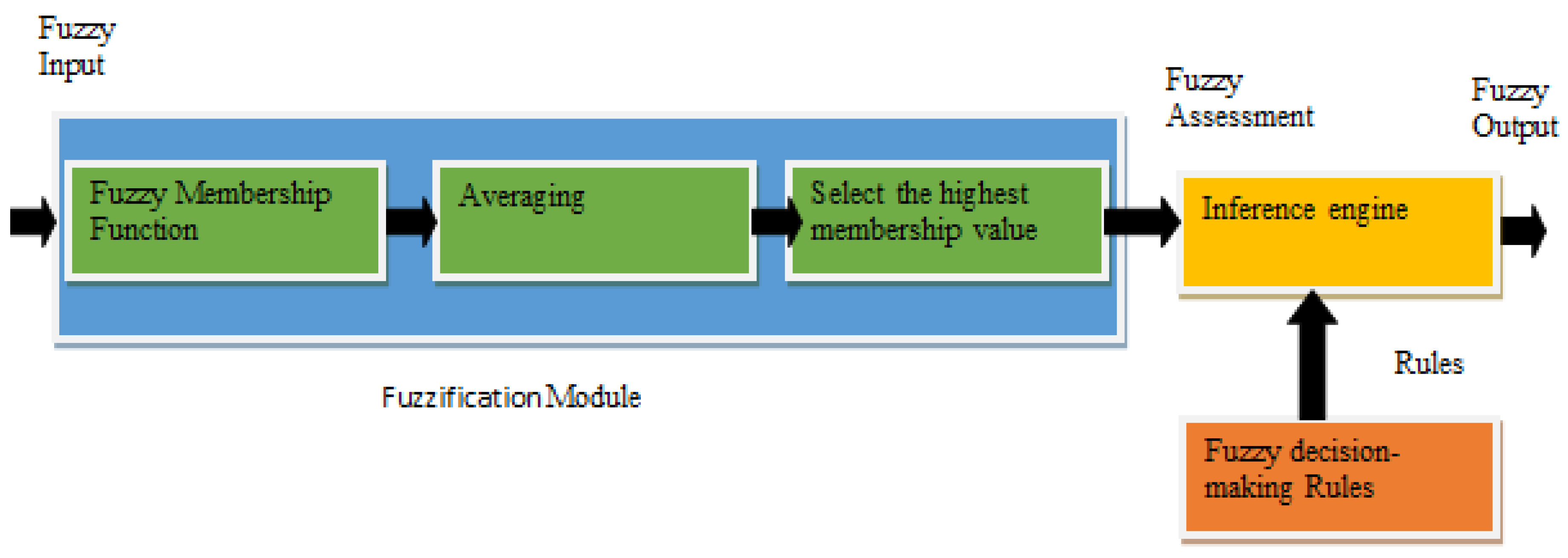
3. Proposed System (Operational Research-Based Intelligent Decision Support System)
| Algorithm 1: Gradient Descent Learning Algorithm |
| Input: i,j, l,k, h |
| Output: , |
| For (i = 0) |
| For (j = 0) |
| For (l = 0) |
| If (h = 0) |
| Else |
| End for |
| End for |
| End for |
| End if |
| End |
| Return |
4. Experimental Results
4.1. Performance Ratio
4.2. Accuracy
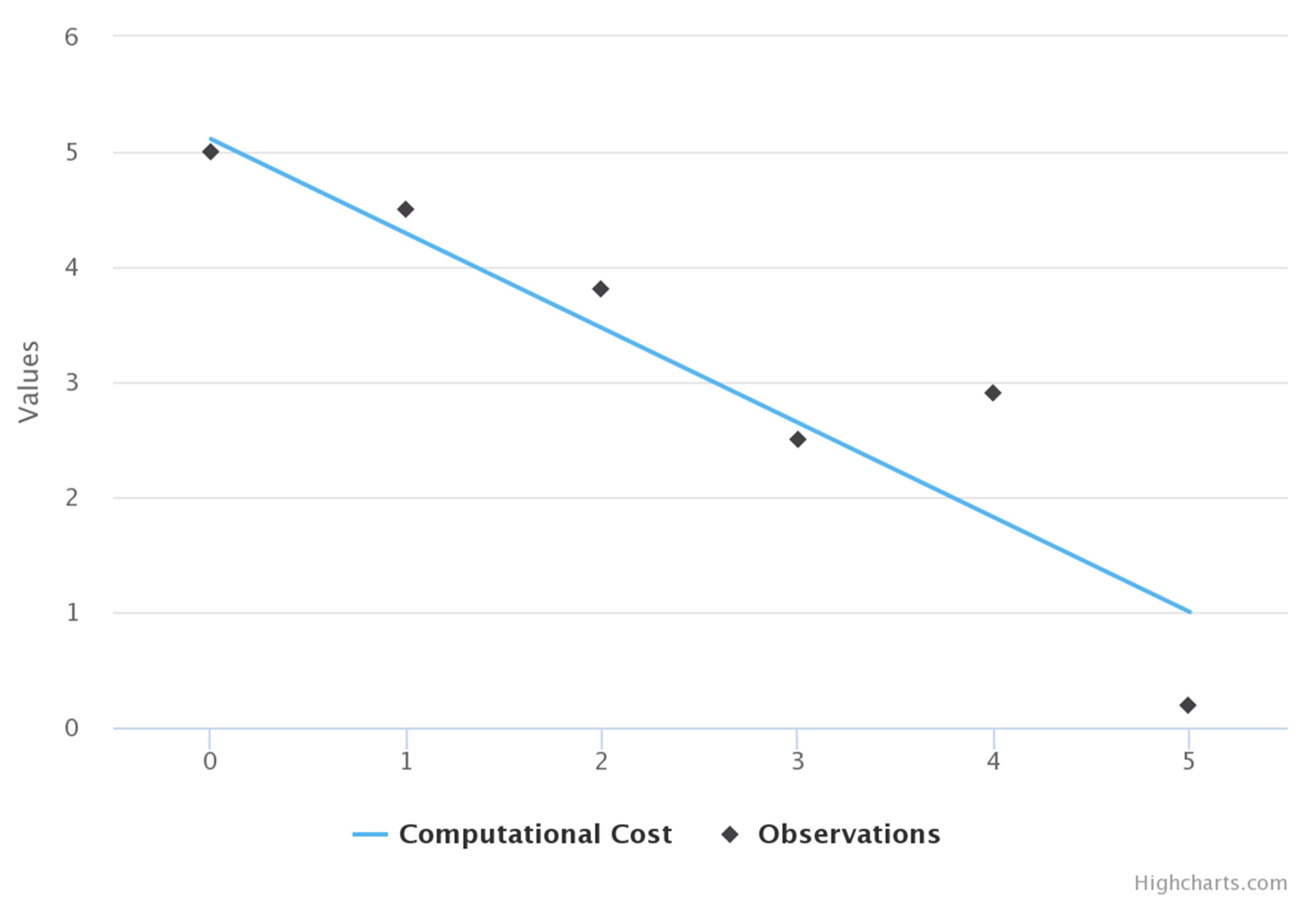
4.3. Computational Cost
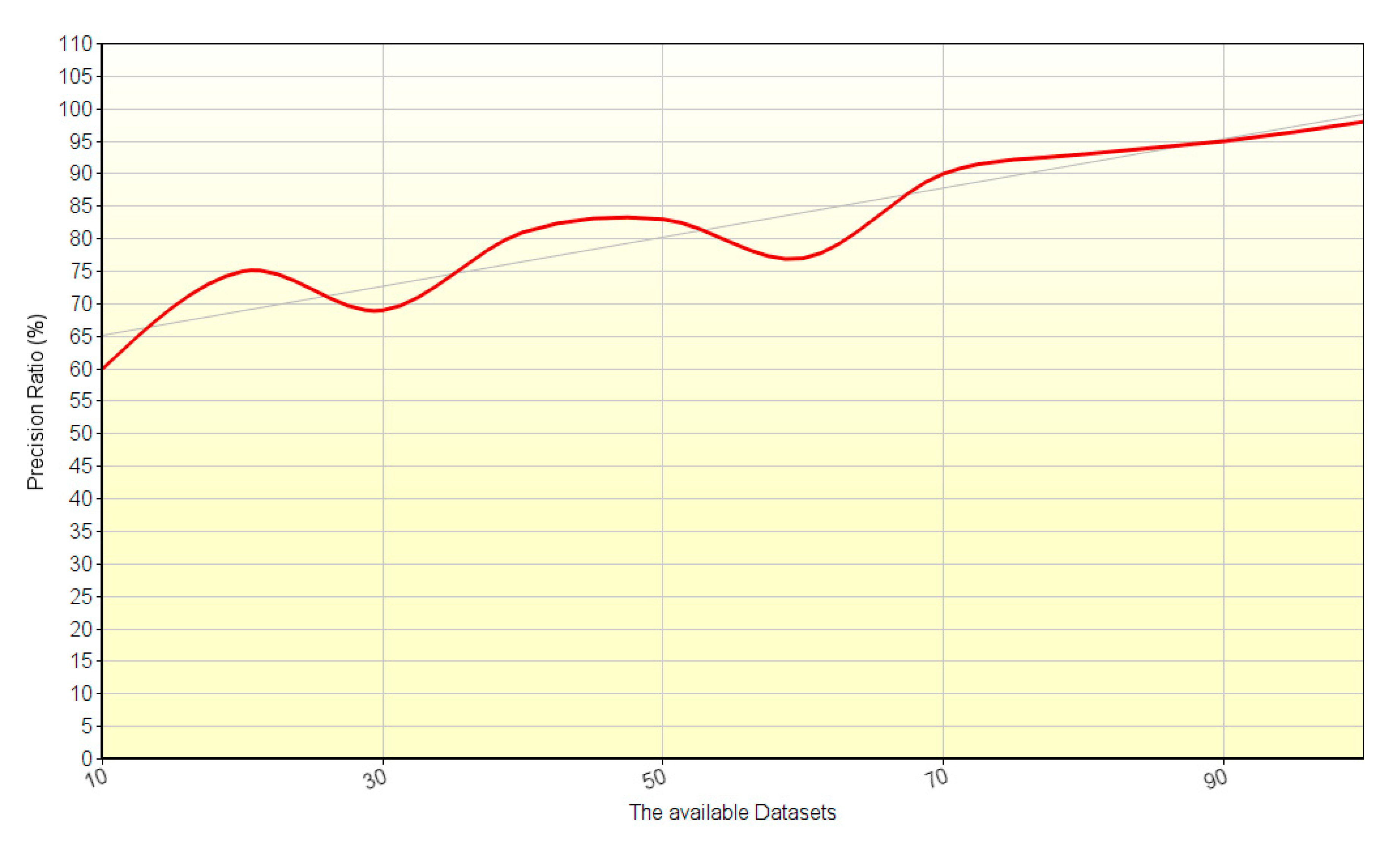
4.4. Precision Ratio
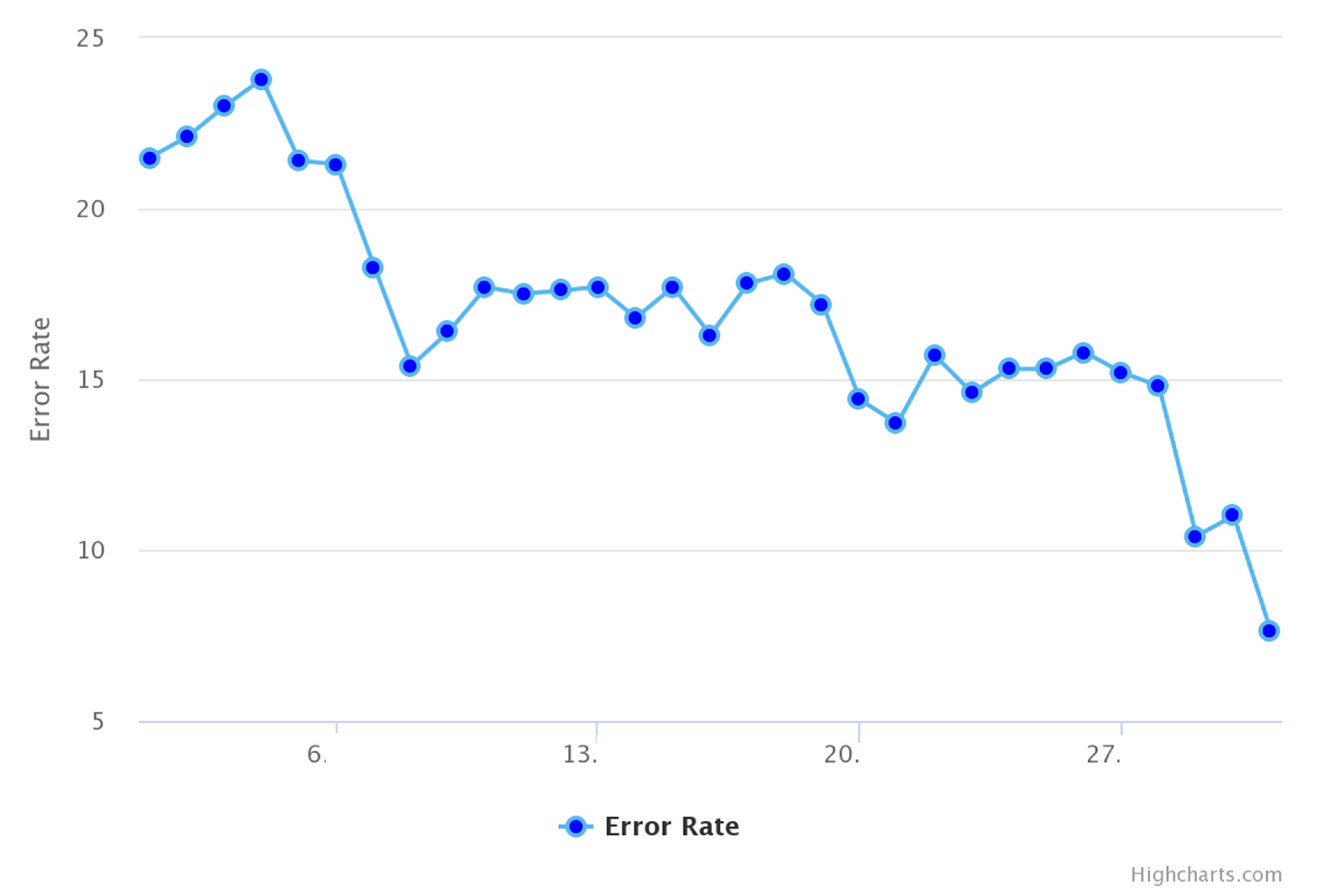
4.5. Error Rate
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DSS | Decision Support System |
| IT | Information Technology |
| Or | Operational Research |
| E-commerce | Electronic Commerce |
| EFT | Electronic Funds Transfers |
| EDI | Electronic Data Exchange |
| OR-IDSS | Operational research-based Intelligent Decision Support System |
| ICT | Information and Communication Technology |
| B-IDSS | Big data-based Intelligent Decision Support System |
| CIDSS | Consumer-oriented Intelligent Decision Support System |
| MCGDM | Multi-Criteria Group Decision Making |
| IFA | Intelligent Fuzzy Agent |
| GLA | Genetical Learner Agent |
| FARM | Fuzzy Association rule mining approach |
| B2B | Business-to-Business |
References
- Ngai, E.W.; Wat, F.K.T. Fuzzy decision support system for risk analysis in e-commerce development. Decis. Support Syst. 2005, 40, 235–255. [Google Scholar] [CrossRef]
- Stremousova, E.; Buchinskaia, O. Some approaches to evaluation macroeconomic efficiency of digitalization. Bus. Manag. Educ. 2019, 17, 232–247. [Google Scholar] [CrossRef]
- Oláh, J.; Kitukutha, N.; Haddad, H.; Pakurár, M.; Máté, D.; Popp, J. Achieving Sustainable E-Commerce in Environmental, Social and Economic Dimensions by Taking Possible Trade-Offs. Sustainability 2018, 11, 89. [Google Scholar] [CrossRef]
- Velmurugan, M.S.; Narayanasamy, K. Application of decision support system in e-commerce. Commun. IBIMA 2008, 5, 156–169. [Google Scholar]
- Bharati, P.; Chaudhury, A. An empirical investigation of decision-making satisfaction in web-based decision support sys-tems. Decis. Support Syst. 2004, 37, 187–197. [Google Scholar] [CrossRef]
- Al-nawayseh, M.K.; Alnabhan, M.M.; Al-Debei, M.M.; Balachandran, W. An adaptive decision support system for last-mile logistics in E-commerce: A study on online grocery shopping. Int. J. Decis. Support System Technol. (IJDSST) 2013, 5, 40–65. [Google Scholar] [CrossRef]
- Stolze, M.; Ströbel, M. Dealing with learning in e-commerce product navigation and decision support: The teaching salesman problem. In Proceedings of the Second Interdisciplinary World Congress on Mass Customization and Personalization, Munich, Germany, 6 October 2003. [Google Scholar]
- Leung, K.; Choy, K.; Siu, P.K.; Ho, G.; Lam, H.; Lee, C.K. A B2C e-commerce intelligent system for re-engineering the e-order fulfilment process. Expert Syst. Appl. 2018, 91, 386–401. [Google Scholar] [CrossRef]
- Silverman, B.G.; Bachann, M.; Al-Akharas, K. Implications of buyer decision theory for design of e-commerce websites. Int. J. Hum. Comput. Stud. 2001, 55, 815–844. [Google Scholar] [CrossRef]
- Gelmez, B.; Sancar, M.; Yilmaz, G.; Akbulut, A. An Autonomous Decision Support System Prototype ForSuply Management in e-Commerce Systems. In Proceedings of the IADIS e-Commerce 2008 Conference, Amsterdam, The Netherlands, 25–27 July 2008; pp. 25–27. [Google Scholar]
- Ji, P.; Zhang, H.-Y.; Wang, J.-Q. A Fuzzy Decision Support Model with Sentiment Analysis for Items Comparison in e-Commerce: The Case Study of http://PConline.com. IEEE Trans. Syst. ManCybern. Syst. 2018, 49, 1993–2004. [Google Scholar] [CrossRef]
- Olson, D.; Elbaum, S.; Goddard, S.; Choobineh, F. An e-commerce decision support system design for web customer re-tention. AMCIS 2002 Proc. 2002, 32. [Google Scholar]
- Anderson, G.; Anupam, V.; Hull, R.B.; Kumar, B. Methods and Apparatus for Automated Monitoring and Action Taking based on Decision Support Mechanism. U.S. Patent No. 7,170,993, 2007. [Google Scholar]
- Andreopoulou, Z.; Koliouska, C.; Tsekouropoulos, G. Strategic planning and decision support in small-medium wood enterprises using database technology. J. Agric. Inform. 2012, 3, 36–45. [Google Scholar] [CrossRef][Green Version]
- Wang, W.; Benbasat, I. Attributions of trust in decision support technologies: A study of recommendation agents for e-commerce. J. Manag. Inf. Syst. 2008, 24, 249–273. [Google Scholar] [CrossRef]
- Skulimowski, A.M. Future trends of intelligent decision support systems and models. In Future Information Technology; Springer: Berlin/Heidelberg, Germany, 2011; Volume 184, pp. 11–20. [Google Scholar]
- Phillips-Wren, G.E. AI Tools in Decision Making Support Systems: A Review. Int. J. Artif. Intell. Tools 2012, 21, 1240005. [Google Scholar] [CrossRef]
- Zhou, H.; Noble, C.; Cotter, J. A Big Data Based Intelligent Decision Support System for Sustainable Regional Development. In Proceedings of the 2015 IEEE International Conference on Smart City/SocialCom/SustainCom (SmartCity), Chengdu, China, 19–21 December 2015; pp. 822–826. [Google Scholar]
- Yu, C.-C. A web-based consumer-oriented intelligent decision support system for personalized e-services. In Proceedings of the 6th International Conference on Informatics, Environment, Energy and Applications, Jeju, Korea, 29–31 March 2017; pp. 429–437. [Google Scholar]
- Sohaib, O.; Naderpour, M.; Hussain, W.; Martinez, L. Cloud computing model selection for e-commerce enterprises using a new 2-tuple fuzzy linguistic decision-making method. Comput. Ind. Eng. 2019, 132, 47–58. [Google Scholar] [CrossRef]
- Lee, C.-S.; Pan, C.-Y. An intelligent fuzzy agent for meeting scheduling decision support system. Fuzzy Sets Syst. 2004, 142, 467–488. [Google Scholar] [CrossRef]
- Leung, K.; Luk, C.; Choy, K.; Lam, H.; Lee, C.K. A B2B flexible pricing decision support system for managing the request for quotation process under e-commerce business environment. Int. J. Prod. Res. 2019, 57, 6528–6551. [Google Scholar] [CrossRef]
- Pinter, G.; Mosavi, A.; Felde, I. Artificial Intelligence for Modeling Real Estate Price Using Call Detail Records and Hybrid Machine Learning Approach. Entropy 2020, 22, 1421. [Google Scholar] [CrossRef] [PubMed]
- Skulimowski, A.M.J. A Foresight Support System to Manage Knowledge on Information Society Evolution. In Proceedings of the Computer Vision, Florence, Italy, 7–13 October 2012; Volume 7710, pp. 246–259. [Google Scholar]
- Chichernea, V. The Use of Decision Support Systems (Dss) In Smart City Planning and Management. J. Inf. Syst. Oper. Manag. 2014, 8. [Google Scholar]
- Nabipour, M.; Nayyeri, P.; Jabani, H.; Shahab, S.; Mosavi, A. Predicting Stock Market Trends Using Machine Learning and Deep Learning Algorithms Via Continuous and Binary Data; A Comparative Analysis. IEEE Access 2020, 8, 150199–150212. [Google Scholar] [CrossRef]
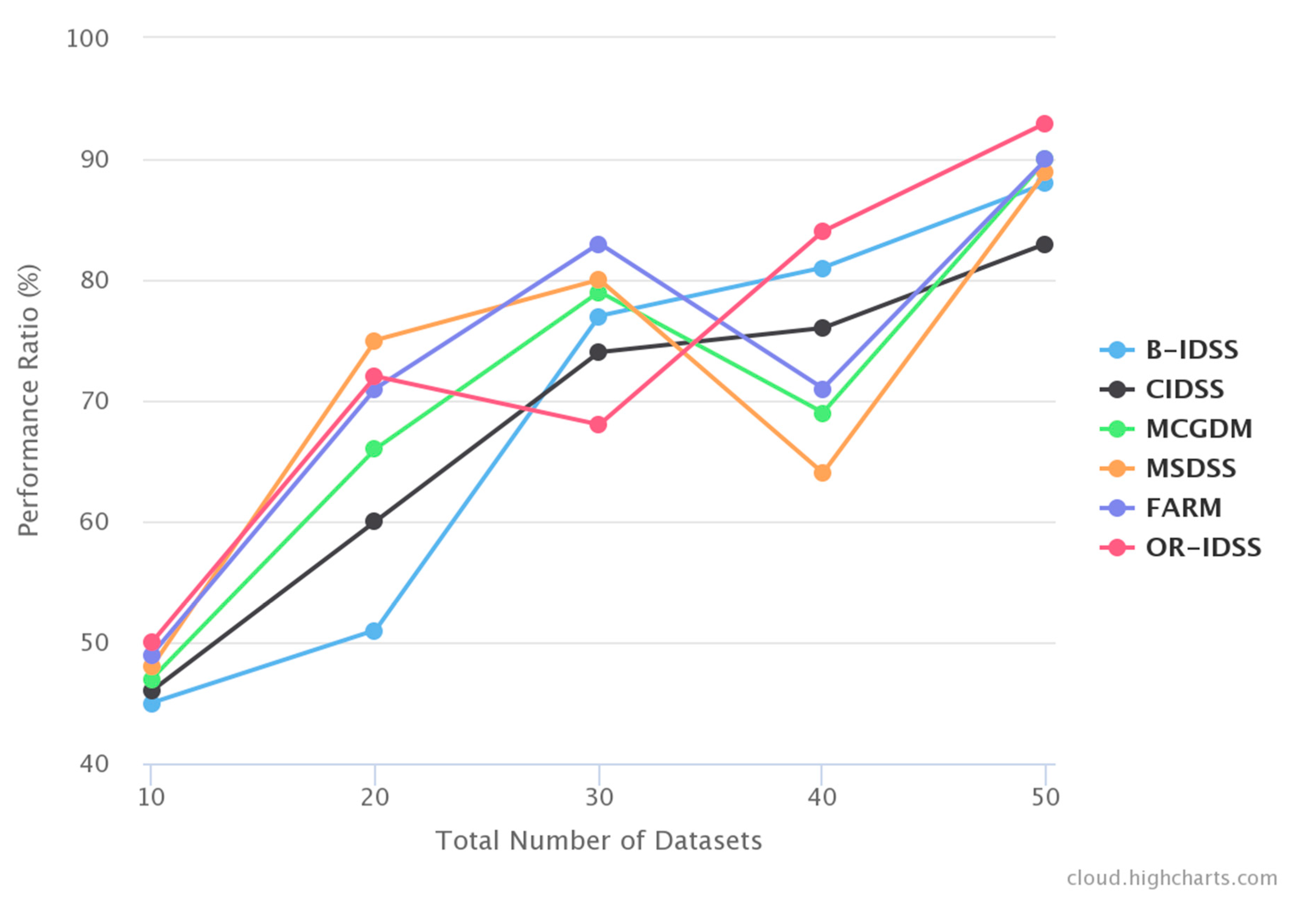
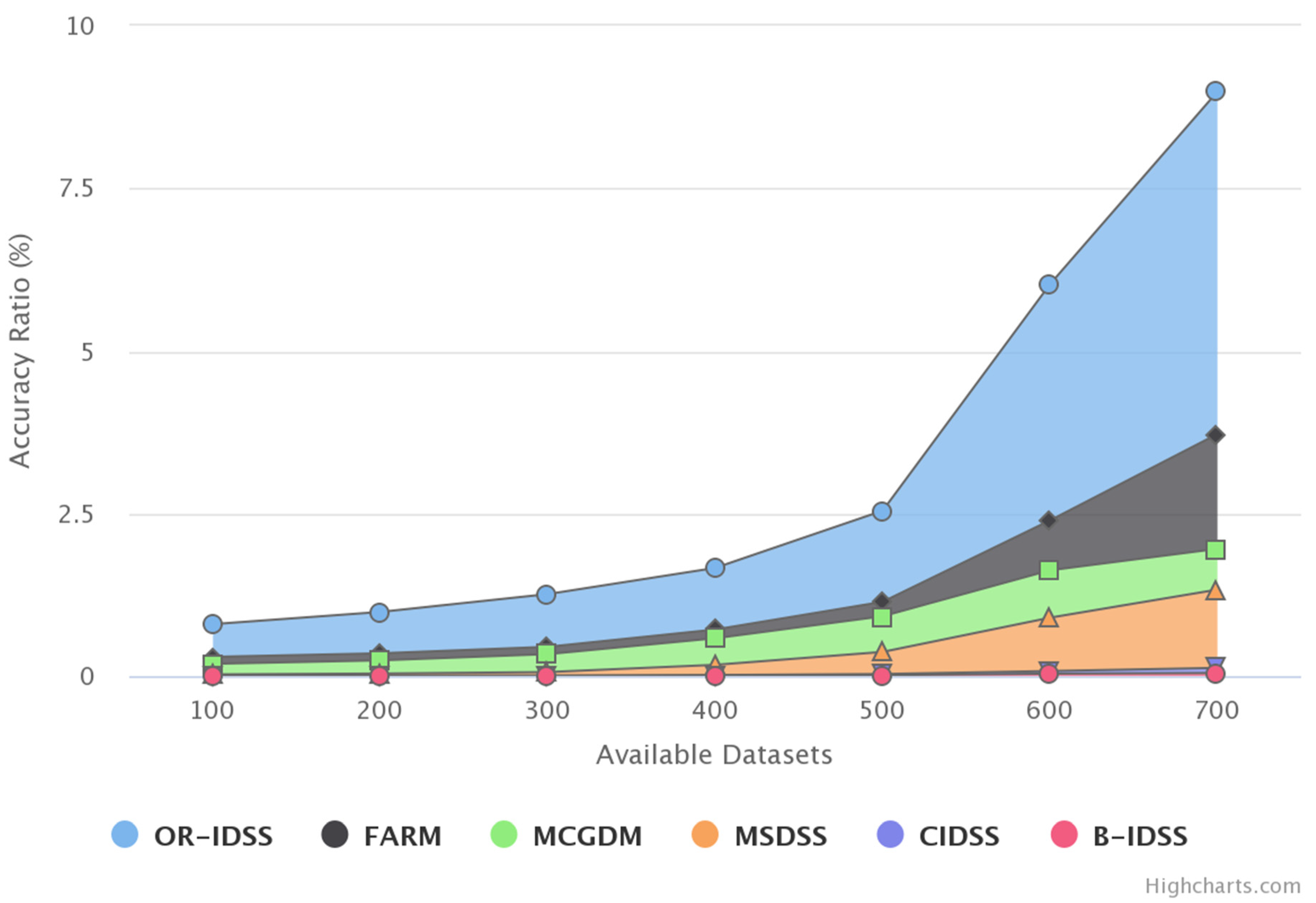
| Total Number of Datasets | B-IDSS | CIDSS | MCGDM | MSDSS | FARM | OR-IDSS |
|---|---|---|---|---|---|---|
| 10 | 45 | 46 | 47 | 48 | 49 | 50 |
| 20 | 51 | 60 | 66 | 75 | 71 | 72 |
| 30 | 77 | 74 | 79 | 80 | 83 | 68 |
| 40 | 81 | 76 | 69 | 64 | 71 | 84 |
| 50 | 88 | 83 | 90 | 89 | 90 | 95 |
| Available Datasets | B-IDSS | CIDSS | MCGDM | MSDSS | FARM | OR-IDSS |
|---|---|---|---|---|---|---|
| 100 | 4.5 | 4.6 | 4.7 | 4.8 | 4.9 | 5.0 |
| 200 | 5.1 | 6.0 | 6.6 | 7.5 | 7.1 | 7.2 |
| 300 | 7.7 | 7.4 | 7.9 | 8.0 | 8.3 | 6.8 |
| 400 | 8.1 | 7.6 | 6.9 | 6.4 | 7.1 | 8.4 |
| 500 | 8.8 | 8.3 | 9.0 | 8.9 | 9.0 | 9.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zong, K.; Yuan, Y.; Montenegro-Marin, C.E.; Kadry, S.N. Or-Based Intelligent Decision Support System for E-Commerce. J. Theor. Appl. Electron. Commer. Res. 2021, 16, 1150-1164. https://doi.org/10.3390/jtaer16040065
Zong K, Yuan Y, Montenegro-Marin CE, Kadry SN. Or-Based Intelligent Decision Support System for E-Commerce. Journal of Theoretical and Applied Electronic Commerce Research. 2021; 16(4):1150-1164. https://doi.org/10.3390/jtaer16040065
Chicago/Turabian StyleZong, Ke, Yuan Yuan, Carlos Enrique Montenegro-Marin, and Seifedine Nimer Kadry. 2021. "Or-Based Intelligent Decision Support System for E-Commerce" Journal of Theoretical and Applied Electronic Commerce Research 16, no. 4: 1150-1164. https://doi.org/10.3390/jtaer16040065
APA StyleZong, K., Yuan, Y., Montenegro-Marin, C. E., & Kadry, S. N. (2021). Or-Based Intelligent Decision Support System for E-Commerce. Journal of Theoretical and Applied Electronic Commerce Research, 16(4), 1150-1164. https://doi.org/10.3390/jtaer16040065







