Graphene-Based Absorber: Tunable, Highly Sensitive, Six-Frequency
Abstract
:1. Introduction
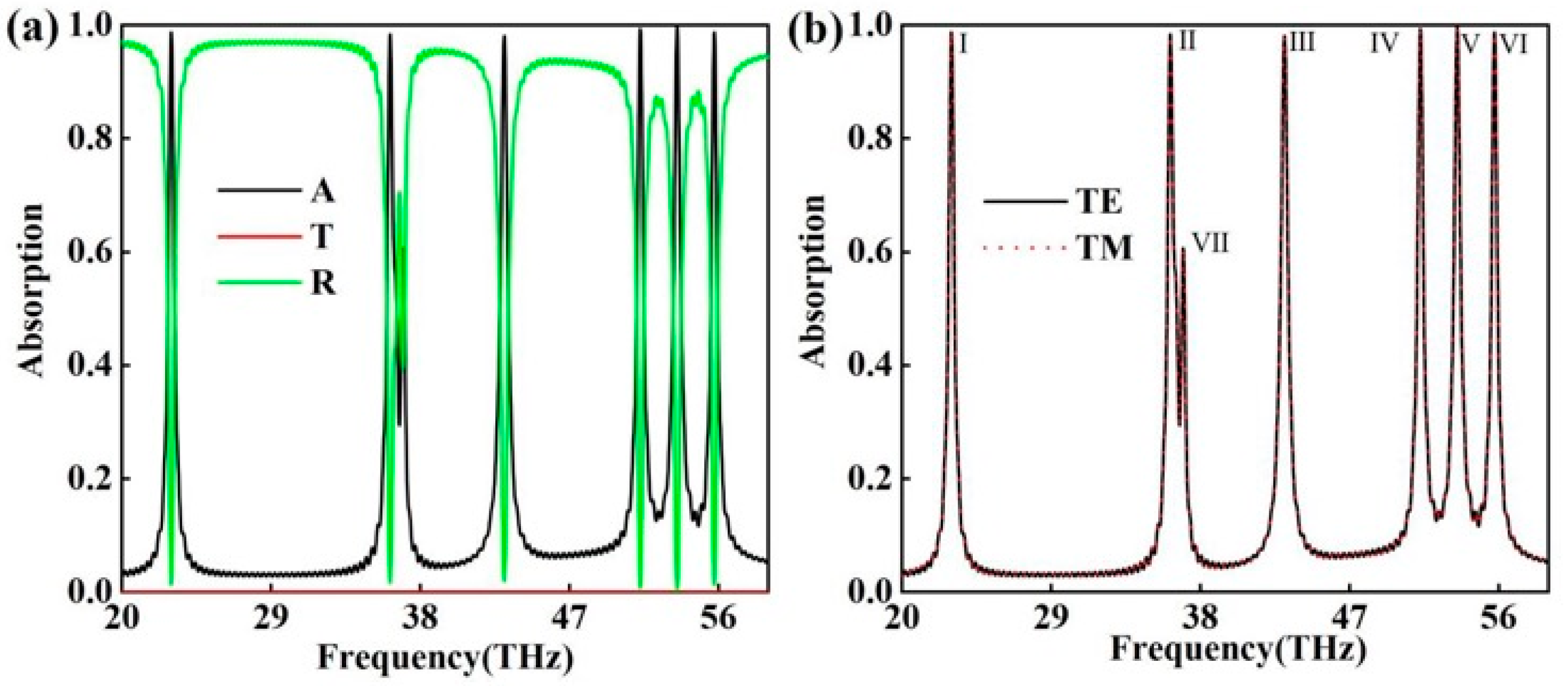
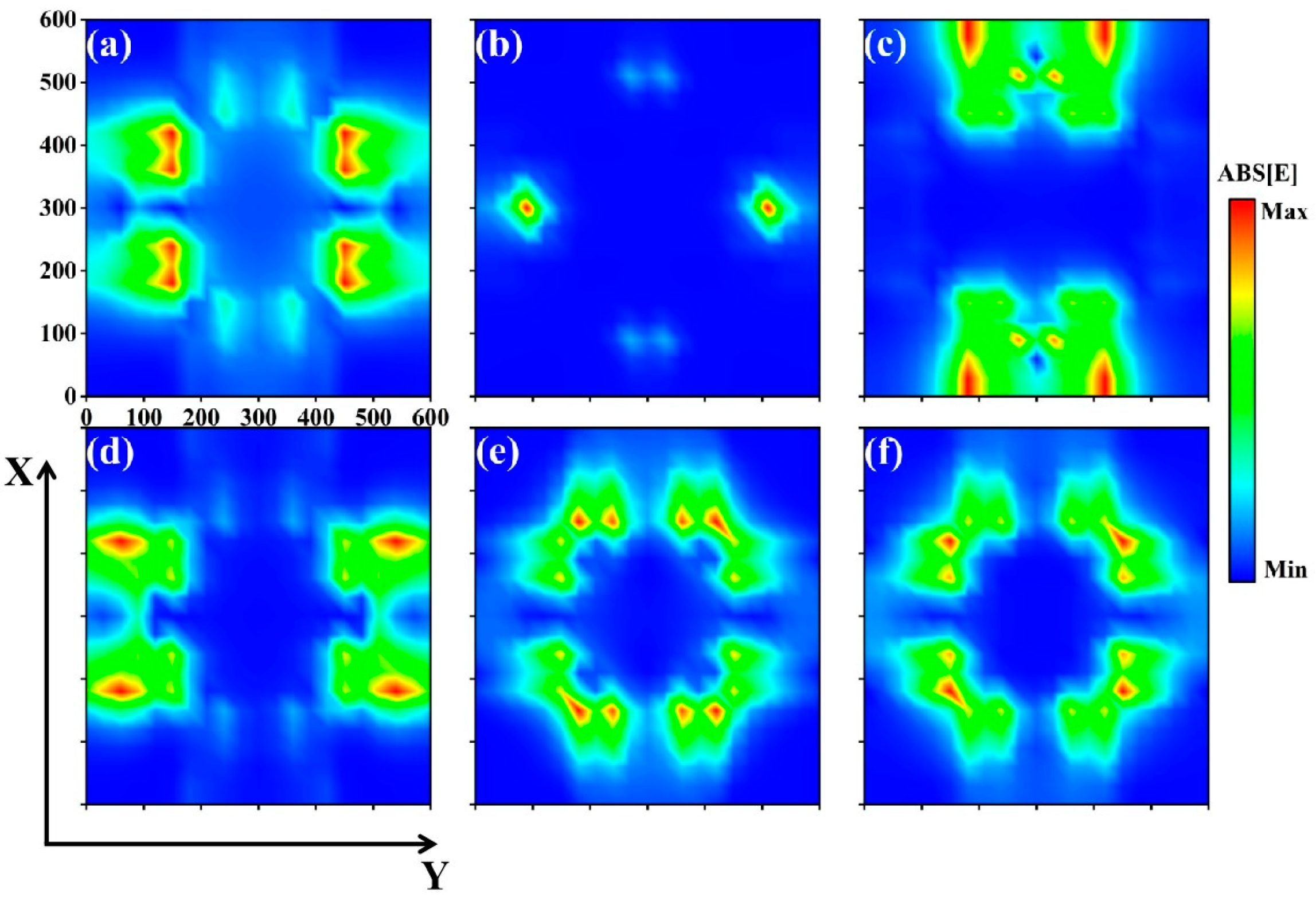
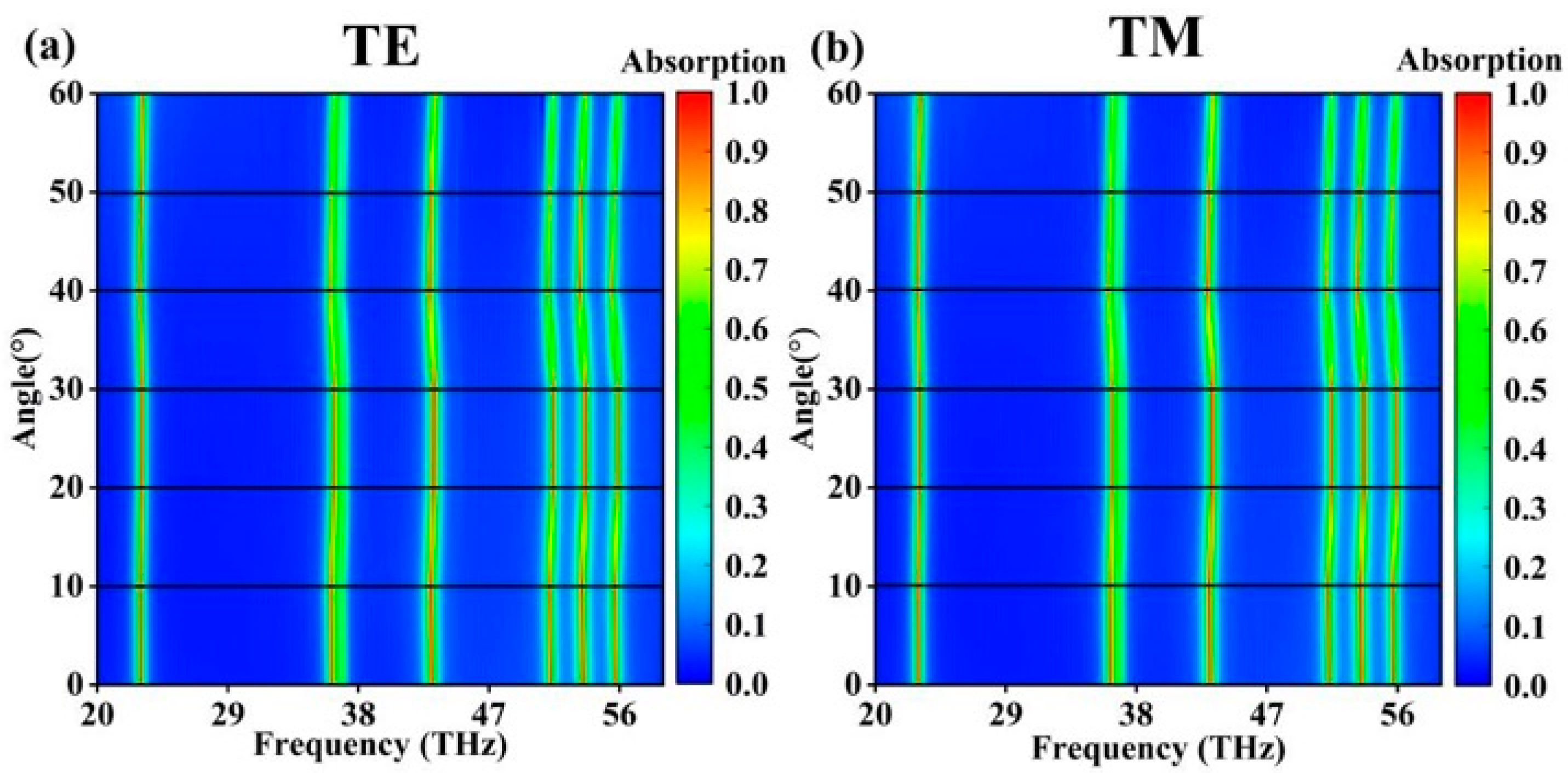
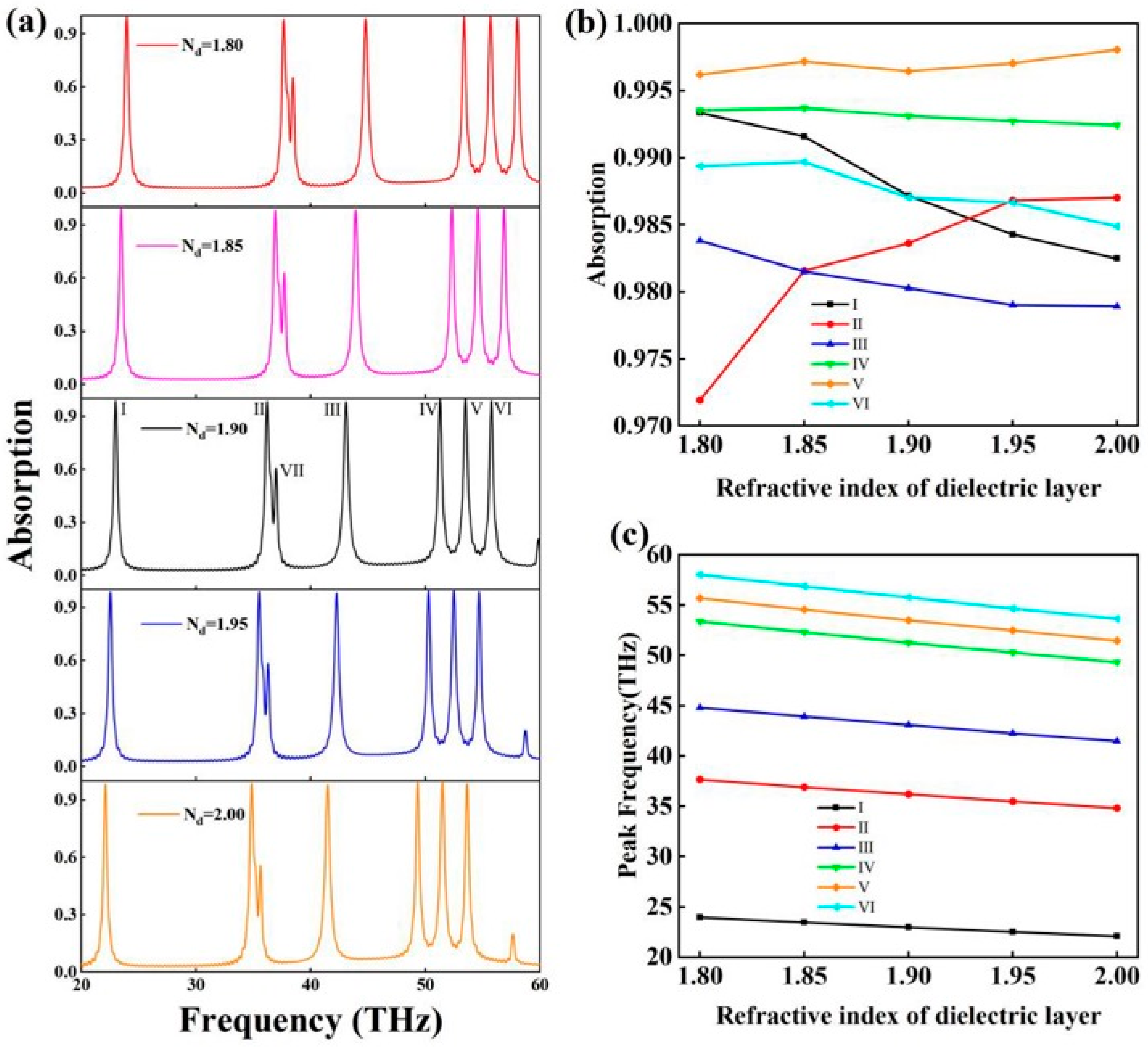
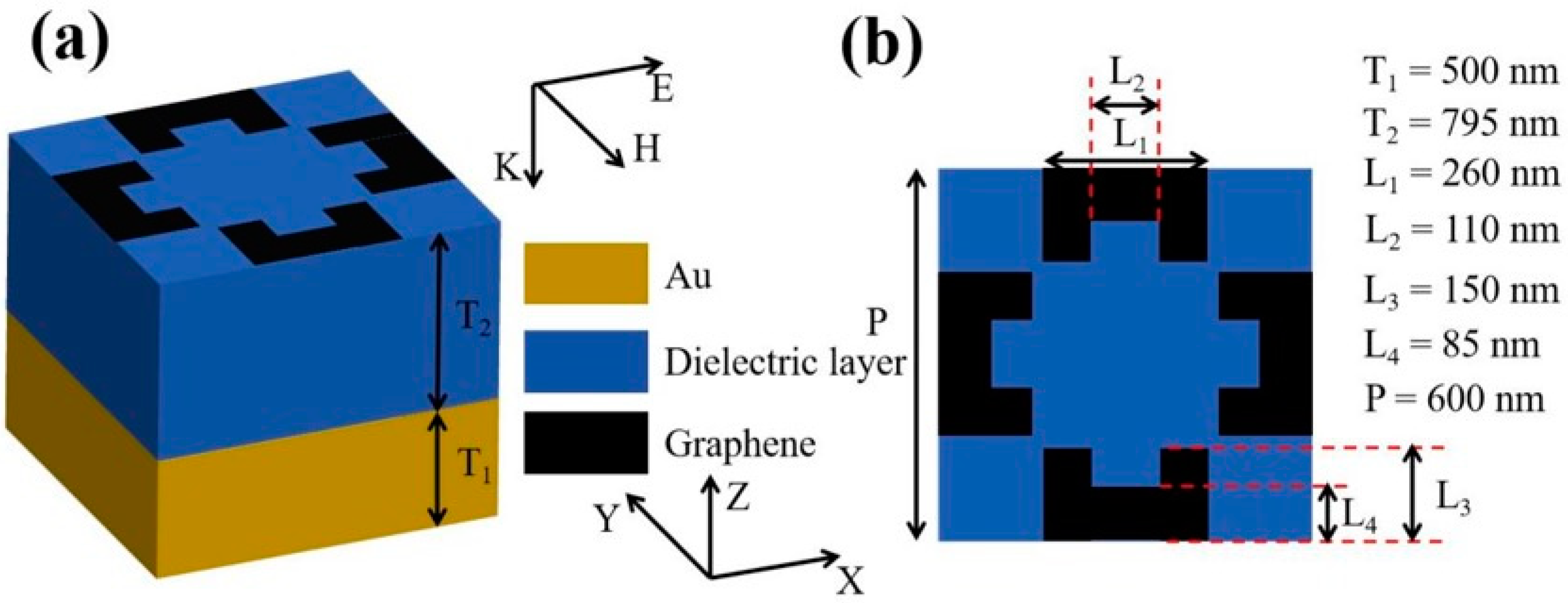
2. Results and Discussion
3. Theory and the Structural Models
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, Z.; Li, M.; Xing, Z.; Gao, H.; Liu, Z.; Pu, S.; Mao, H.; Cai, H.; Ma, Q.; Ren, W.; et al. Genetic algorithm assisted meta-atom design for high-performance metasurface optics. Opto-Electron. Sci. 2024, 3, 240016. [Google Scholar] [CrossRef]
- Berhe, A.M.; As’ham, K.; Al-Ani, I.; Hattori, H.T.; Miroshnichenko, A.E. Strong coupling and catenary field enhancement in the hybrid plasmonic metamaterial cavity and TMDC monolayers. Opto-Electron. Adv. 2024, 7, 230181. [Google Scholar] [CrossRef]
- Zhang, B.W.; Luo, Y.N. Dynamic optical tuning and sensing in L-shaped dirac semimetal-based terahertz metasurfaces. Phys. Lett. A 2025, 541, 130419. [Google Scholar] [CrossRef]
- Yang, C.; Luo, M.H.; Ju, X.W.; Hu, J.Y. Ultra-narrow dual-band perfect absorber based on double-slotted silicon nanodisk arrays. J. Phys. D Appl. Phys. 2024, 57, 345104. [Google Scholar] [CrossRef]
- Wang, Z.; Pan, W.; He, Y.; Zhu, Z.; Jin, X.; Liu, M.; Ma, S.; He, Q.; Sun, S.; Zhou, L. Efficient generation of vectorial terahertz beams using surface-wave excited metasurfaces. Opto-Electron. Sci. 2025, 4, 240024. [Google Scholar] [CrossRef]
- Zeng, L.L.; Li, B.X.; Wen, R.Q.; Zhang, X.J. Plasmonic Sensor Based on Multi Fano Resonance in Inverse T Shape Structure for Detection of CO2 Concentration. IEEE Photonics J. 2023, 15, 2201805. [Google Scholar] [CrossRef]
- Guillen, D.P.; Wharry, J.; Lu, Y.; Wu, M.; Sharapov, J.; Anderson, M. Microstructure of Neutron-Irradiated Al3Hf-Al Thermal Neutron Absorber Materials. Materials 2025, 18, 833. [Google Scholar] [CrossRef]
- Li, W.; Cheng, S.; Zhang, H.; Yi, Z.; Tang, B.; Ma, C.; Wu, P.; Zeng, Q.; Raza, R. Multi-functional metasurface: Ultra-wideband/multi-band absorption switching by adjusting guided mode resonance and local surface plasmon resonance effects. Commun. Theor. Phys. 2024, 76, 065701. [Google Scholar] [CrossRef]
- Liu, M.L.; Li, B.X.; Zeng, L.L.; Wei, Y.; Wen, R.Q.; Zhang, X.J.; Deng, C.S. Dynamic tunable narrow-band perfect absorber for fiber -optic communication band based on liquid crystal. J. Phys. D Appl. Phys. 2023, 56, 505102. [Google Scholar] [CrossRef]
- Xiang, T.; Sun, Z.; Wang, L.L.; Lin, Q.; Liu, G.D. Polarization independent perfect absorption of borophene metamaterials operating in the communication band. Phys. Scr. 2024, 99, 085519. [Google Scholar] [CrossRef]
- Hu, J.Y.; Bai, W.D.; Tan, C.X.; Li, Y.M.; Lin, Q.; Wang, L.L. Highly electric field enhancement induced by anapole modes coupling in the hybrid dielectric-metal nanoantenna. Opt. Commun. 2022, 511, 127987. [Google Scholar] [CrossRef]
- Ai, Z.; Liu, H.F.; Cheng, S.B.; Zhang, H.F.; Yi, Z.; Zeng, Q.D.; Wu, P.H.; Zhang, J.G.; Tang, C.J.; Hao, Z.Q. Four peak and high angle tilted insensitive surface plasmon resonance graphene absorber based on circular etching square window. J. Phys. D Appl. Phys. 2025, 58, 185305. [Google Scholar] [CrossRef]
- Wang, J.Q.; Sun, J.Y.; Sun, S.; Zhang, H.; Wang, Q.Q.; Yang, J.Y.; Mei, Y.W. Numerical simulation of electromagnetically induced transparency in composite metamaterial. Phys. Scr. 2025, 100, 025512. [Google Scholar] [CrossRef]
- Wang, Q.S.; Fang, Y.; Meng, Y.; Hao, H.; Li, X.; Pu, M.; Ma, X.; Luo, X. Vortex-field enhancement through high-threshold geometric metasurface. Opto-Electron. Adv. 2024, 7, 240112. [Google Scholar] [CrossRef]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect Metamaterial Absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 5696, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.Y.; Ma, R.; Liu, G.D.; Wang, L.L.; Lin, Q. Optical force conversion and conveyor belt effect with coupled graphene plasmon waveguide modes. Opt. Express 2023, 31, 32422. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.T.; Li, X.; Liu, G.D.; Wang, L.L.; Lin, Q. Analytical investigation of unidirectional reflectionless phenomenon near the exceptional points in graphene plasmonic system. Opt. Express 2023, 31, 30458. [Google Scholar] [CrossRef]
- Vafek, O. Thermo-Plasma Polariton within Scaling Theory of Single-Layer Graphene. Phys. Rev. Lett. 2006, 97, 266406. [Google Scholar] [CrossRef]
- Hanson, G.W. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. J. Appl. Phys. 2008, 103, 064302. [Google Scholar] [CrossRef]
- Chen, J.N.; Badioli, M.; Alonso-González, P.; Thongrattanasiri, S.; Huth, F.; Osmond, J.; Spasenović, M.; Centeno, A.; Pesquera, A.; Godignon, P.; et al. Optical nano-imaging of gate-tuneable graphene plasmons. Nature 2012, 487, 77–81. [Google Scholar] [CrossRef] [PubMed]
- Tang, C.; Zeng, Y.; Cai, P.; Deng, J.; Yan, Z.; Gu, P.; Huang, Z.; Ji, Y. Narrow-Band Absorption Enhancement and Modulation of Single Layer Graphene by Surface Plasmon Polaritons in Near-Infrared Region. Phys. B 2024, 695, 416521. [Google Scholar] [CrossRef]
- Li, Z.; Song, Q.J.; Jia, L.B.; Yi, Z.; Cheng, S.B.; Wang, J.Q.; Li, B.X. Actively tunable multi-frequency narrowband terahertz absorber using graphene metamaterials. Opt. Commun. 2025, 583, 131768. [Google Scholar] [CrossRef]
- Li, Y.M.; Tan, C.X.; Hu, J.Y.; Bai, W.D.; Zhang, R.L.; Lin, Q.; Zhang, Y.; Wang, L.L. Ultra-narrow band perfect absorbance induced by magnetic lattice resonances in dielectric dimer metamaterials. Results Phys. 2022, 39, 105730. [Google Scholar] [CrossRef]
- Li, Z.T.; Cheng, S.B.; Zhang, H.F.; Yang, W.X.; Yi, Z.; Yi, Y.G.; Wang, J.Q.; Ahmad, S.; Raza, R. Ultrathin broadband terahertz metamaterial based on single-layer nested patterned graphene. Phys. Lett. A 2025, 534, 130262. [Google Scholar] [CrossRef]
- Tang, C.J.; Nie, Q.M.; Cai, P.G.; Liu, F.X.; Gu, P.; Yan, Z.D.; Huang, Z.; Zhu, M.W. Ultra-broadband near-infrared absorption enhancement of monolayer graphene by multiple-resonator approach. Diam. Relat. Mater. 2024, 141, 110607. [Google Scholar] [CrossRef]
- Li, B.X.; Liu, M.L.; Wen, R.Q.; Wei, Y.; Zeng, L.L.; Deng, C.S. Dynamic control of Fano-like interference in the graphene periodic structure. J. Phys. D Appl. Phys. 2023, 56, 115104. [Google Scholar] [CrossRef]
- Lin, Z.; Yang, H.; Jin, G.; Zhu, Y.; Tang, B. Borophene-Based Anisotropic Metamaterial Perfect Absorber for Refractive Index Sensing. Nanomaterials 2025, 15, 509. [Google Scholar] [CrossRef]
- Hu, F.; Luan, Y.; Fei, Z.; Palubski, I.Z.; Goldflam, M.D.; Dai, S.; Wu, J.S.; Post, K.W.; Janssen, G.C.A.M.; Fogler, M.M.; et al. Imaging the Local-ized Plasmon Resonance Modes in Graphene Nanoribbons. Nano Lett. 2017, 17, 5423–5428. [Google Scholar] [CrossRef]
- Fei, Z.; Goldflam, M.D.; Wu, J.S.; Dai, S.; Wagner, M.; McLeod, A.S.; Liu, M.K.; Post, K.W.; Zhu, S.; Janssen, G.C.A.M.; et al. Edge and surface plasmons in graphene nanoribbons. Nano Lett. 2015, 15, 8271–8276. [Google Scholar] [CrossRef]
- Luo, M.H.; Hu, J.Y.; Li, Y.M.; Bai, W.D.; Zhang, R.L.; Lin, Q.; Wang, L.L. Anapole-assisted ultra-narrow-band lattice resonance in slotted silicon nanodisk arrays. J. Phys. D Appl. Phys. 2023, 56, 375102. [Google Scholar] [CrossRef]
- Zeng, Z.L.; Liu, H.F.; Zhang, H.F.; Cheng, S.B.; Yi, Y.G.; Yi, Z.; Wang, J.Q.; Zhang, J.G. Tunable ultra-sensitive four-band terahertz sensors based on Dirac semimetals. Photonics Nanostruct.-Fundam. Appl. 2025, 63, 101347. [Google Scholar] [CrossRef]
- Ghiat, A.; Pérez, J.R.; Torres, R.P.; Tribak, A.; Terhzaz, J. A Multiple-Input Multiple-Output Antenna with Metamaterial Enhancement for 5G Channel Sounding in the Upper 6 GHz Band. Electronics 2025, 14, 1339. [Google Scholar] [CrossRef]
- Li, W.; Yi, Y.; Yang, H.; Cheng, S.; Yang, W.X.; Zhang, H.; Yi, Z.; Yi, Y.; Li, H. Active Tunable Terahertz Band-width Absorber Based on single layer Graphene. Commun. Theor. Phys. 2023, 75, 045503. [Google Scholar] [CrossRef]
- Zeng, T.Y.; Liu, G.D.; Wang, L.L.; Lin, Q. Light-matter interactions enhanced by quasi-bound states in the continuum in a graphene-dielectric metasurface. Opt. Express 2021, 29, 40177–40186. [Google Scholar] [CrossRef]
- Abdulkarim, Y.I. Switchable and Tunable Terahertz Metamaterial Absorber with Ultra-Broadband and Multi-Band Response for Cancer Detection. Sensors 2025, 25, 1463. [Google Scholar] [CrossRef]
- Politano, G.G. Localized Effects in Graphene Oxide Systems: A Pathway to Hyperbolic Metamaterials. Photonics 2025, 12, 121. [Google Scholar] [CrossRef]
- Cheng, S.B.; Li, W.X.; Zhang, H.F.; Akhtar, M.N.; Yi, Z.; Zeng, Q.D.; Ma, C.; Sun, T.Y.; Wu, P.H.; Ahmad, S. High sensitivity five band tunable metamaterial absorption device based on block like Dirac semimetals. Opt. Commun. 2024, 569, 130816. [Google Scholar] [CrossRef]
- Li, B.X.; Zeng, L.L.; Wen, R.Q.; Zhang, X.J. Dynamic Regulation of Multiple Fano Resonances Based on Liquid Crystal. IEEE Photonics J. 2023, 15, 2200506. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Lin, Q.; Yan, X.Q.; Wang, L.L.; Liu, G.D. Flat-band Friedrich-Wintgen bound states in the continuum based on borophene metamaterials. Opt. Express 2024, 32, 10669–10678. [Google Scholar] [CrossRef]
- Karami, B.; Ghayesh, M.H. Forced Vibration Behaviour of Elastically Constrained Graphene Origami-Enabled Auxetic Metamaterial Beams. Math. Comput. Appl. 2025, 30, 5. [Google Scholar] [CrossRef]
- Wang, X.Y.; Lin, Q.; Wang, L.L.; Liu, G.D. Dynamic control of polarization conversion based on borophene nanostructures in optical communication bands. Phys. Scr. 2024, 99, 085531. [Google Scholar] [CrossRef]
- Wu, X.; Chen, J.; Wang, S.; Ren, Y.; Yang, Y.; He, Z. Sensing Based on Plasmon-Induced Transparency in H-Shaped Graphene-Based Metamaterials. Nanomaterials 2024, 14, 997. [Google Scholar] [CrossRef] [PubMed]
- Jo, Y.; Park, H.; Yoon, H.; Kim, I. Advanced biological imaging techniques based on metasurfaces. Opto-Electron. Adv. 2024, 7, 240122. [Google Scholar] [CrossRef]
- Ling, Z.X.; Zeng, Y.; Liu, G.D.; Wang, L.L.; Lin, Q. Unified model for plasmon-induced transparency with direct and indirect coupling in borophene-integrated metamaterials. Opt. Express 2022, 30, 21966. [Google Scholar] [CrossRef]
- Lu, W.Q.; Yi, Y.T.; Song, Q.J.; Zhou, Z.G.; Yi, Y.G.; Zeng, Q.D.; Yi, Z. Simulation of terahertz tunable seven-band perfect absorber based on high frequency detection function of Dirac semi-metallic nanowires. Acta Phys. Sin. 2025, 74, 034101. [Google Scholar] [CrossRef]
- Tan, C.Z.; Arndt, J. Temperature dependence of refractive index of glassy SiO2 in the infrared wavelength range. J. Phys. Chemis-Try Solids 2000, 61, 1315–1320. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, G.; Wei, J.; Miao, Y.; Zhang, W.; Wu, K.; Wang, Q. Ultrahigh-Q Polarization-Independent Terahertz Metamaterial Absorber Using Pattern-Free Graphene for Sensing Applications. Nanomaterials 2024, 14, 605. [Google Scholar] [CrossRef]
- Huang, Z.; Liu, G.D.; Wang, L. Active modulation of quasi-bound state in the continuum based on bulk Dirac semimetals metamaterial. Appl. Phys. Express 2022, 15, 032006. [Google Scholar] [CrossRef]
- Wang, J.; Qin, X.; Zhao, Q.; Duan, G.; Wang, B.X. Five-Band Tunable Terahertz Metamaterial Absorber Using Two Sets of Different-Sized Graphene-Based Copper-Coin-like Resonators. Photonics 2024, 11, 225. [Google Scholar] [CrossRef]
- Hu, J.Y.; Tan, C.X.; Bai, W.D.; Li, Y.M.; Lin, Q.; Wang, L.L. Dielectric nanocavity-coupled surface lattice resonances for high-efficiency plasmonic sensing. J. Phys. D Appl. Phys. 2022, 55, 075105. [Google Scholar] [CrossRef]
- Moon, I.; Kim, W.; Seo, Y.; Kahng, S. A Metamaterial Surface Avoiding Loss from the Radome for a Millimeter-Wave Signal-Sensing Array Antenna. Sensors 2024, 24, 1018. [Google Scholar] [CrossRef]
- Ma, R.; Zhang, L.; Liu, G.; Wang, L.; Lin, Q. The total optical force exerted on black phosphorus coated dielectric cylinder pairs enhanced by localized surface plasmon. J. Appl. Phys. 2021, 130, 113103. [Google Scholar] [CrossRef]
- Gu, X.; Liu, X.; Yan, X.F.; Du, W.J.; Lin, Q.; Wang, L.L.; Liu, G.D. Polaritonic coherent perfect absorption based on self-hybridization of a quasi-bound state in the continuum and exciton. Opt. Express 2023, 31, 4691–4700. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, W.Z.; Wu, Y.C.; Meng, D.; Cheng, Y.Y.; Chen, Y.S.; Liu, J.; Gu, Y. Multi-peak narrow-band metamaterial absorber for visible to near-infrared wavelengths. Results Phys. 2023, 47, 106374. [Google Scholar] [CrossRef]
- Wang, L.R.; Yi, Y.T.; Yi, Z.; Bian, L.; Zhang, J.G.; Yang, H.; Chen, J.; Wu, P.H.; Li, H.L.; Tang, C.J. A perfect absorber of multi-band, tunable monolayer patterned graphene based on surface plasmon resonance. Diam. Relat. Mater. 2022, 130, 109498. [Google Scholar] [CrossRef]
- Pan, M.; Tang, H.; Su, J.Z.; Zhou, B.M.; Fan, B.D.; Li, Q.F.; Huang, Z.G.; Wu, T.Y. Four-band tunable narrowband optical absorber built on surface plasmonically patterned square graphene. Phys. Lett. A 2025, 530, 130134. [Google Scholar] [CrossRef]
- Qi, Y.P.; Su, M.R.; Li, H.; Zhang, S.; Wu, Q.L.; Liu, F.F.; Wang, X.X. Graphene-Enhanced Refractive Index Sensing and Narrow-band Filtering with Crossed Bicircular Resonator Cavity Waveguides. Plasmonics 2024, 19, 1533–1544. [Google Scholar] [CrossRef]
- Xie, Y.D.; Liu, Z.M.; Zhou, F.Q.; Luo, X.; Cheng, Z.Q.; Yang, R.H.; Ji, C.; Yang, G.X. A multifrequency narrow-band perfect absorber based on graphene metamaterial. Diam. Relat. Mater. 2023, 137, 110100. [Google Scholar] [CrossRef]
- Yue, W.S.; Kravets, V.; Pu, M.B.; Wang, C.T.; Zhao, Z.Y.; Hu, Z.R. Multiple-resonant Pad-rod Nanoantennas for Surface-Enhanced Infrared Absorption Spectroscopy. Nanotechnology 2019, 30, 465206. [Google Scholar] [CrossRef]
- Chen, S.; Wu, X.H.; Fu, C.J. Active tuning of anisotropic phonon polaritons in natural van der Waals crystals with negative permittivity substrates and its application in energy transport. Opto-Electron. Sci. 2024, 3, 240002. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Cheng, S.B.; Zhang, H.F.; Yi, Z.; Tang, B.; Chen, J.; Zhang, J.G.; Tang, C.J. Ultra wideband absorption absorber based on Dirac semimetallic and graphene metamaterials. Phys. Lett. A 2024, 517, 129675. [Google Scholar] [CrossRef]
- Ma, R.; Zhang, L.G.; Zeng, Y.; Liu, G.D.; Wang, L.L.; Lin, Q. Extreme enhancement of optical force via the acoustic graphene plasmon mode. Opt. Express 2023, 31, 482723. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Yu, M.; Chen, Z.; Ai, S.; Kentsch, U.; Zhou, S.; Jia, Y.; Chen, F.; Liu, H. A novel approach towards robust construction of physical colors on lithium niobate crystal. Opto-Electron. Adv. 2025, 8, 240193. [Google Scholar] [CrossRef]
- Nan, T.; Zhao, H.; Guo, J.; Wang, X.; Tian, H.; Zhang, Y. Generation of structured light beams with polarization variation along arbitrary spatial trajectories using tri-layer metasurfaces. Opto-Electron. Sci. 2024, 3, 230052. [Google Scholar] [CrossRef]
- Wang, Y.J.; Liu, Z.M.; Zhou, F.Q.; Yi, Z.; Wang, J.Q. Perfect absorption properties of a near-infrared super-surface perfect absorber based on a multilayer subwavelength array structure. Phys. Lett. A 2025, 540, 130395. [Google Scholar] [CrossRef]
- Zeng, Y.; Ling, Z.X.; Liu, G.D.; Wang, L.L.; Lin, Q. Tunable plasmonically induced transparency with giant group delay in gain-assisted graphene metamaterials. Opt. Express 2022, 30, 455954. [Google Scholar] [CrossRef]
- Tan, Z.Q.; Lin, Q.; Du, W.J.; Wang, L.L.; Liu, G.D. Simultaneously enhance electric and magnetic Purcell factor by strong coupling between toroidal dipole quasi-BIC and electric dipole. J. Appl. Phys. 2025, 137, 033103. [Google Scholar] [CrossRef]
- Yan, D.Y.; Tang, C.J.; Yi, Z.; Wang, J.Q.; Li, B.X. A fully symmetric solar absorber for thermophotovoltaic power generation. Phys. Lett. A 2025, 542, 130461. [Google Scholar] [CrossRef]
- Yang, J.P.; Tang, A.; Lian, B.W.; Xiong, Z.J.; Ma, Z.B.; Gu, N.T. Optimal multi-spectrum polarization detection with full-Stokes in a single channel by using standard retarders. Measurement 2025, 242, 116052. [Google Scholar] [CrossRef]
- Fan, J.X.; Li, Z.L.; Xue, Z.Q.; Xing, H.Y.; Lu, D.; Xu, G.; Gu, J.; Han, J.; Cong, L. Hybrid bound states in the continuum in te-rahertz metasurfaces. Opto-Electron. Sci. 2023, 2, 230006. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, C.; Nong, H.; Weng, J.; Wang, D.; Yu, Y.; Zhang, J.; Zhang, C.; Yu, J.; Zhang, Z.; et al. Multi-photon neuron embedded bionic skin for high-precision complex texture and object reconstruction perception research. Opto-Electron. Adv. 2025, 8, 240152. [Google Scholar] [CrossRef]
- Li, W.X.; Cheng, S.B.; Yi, Z.; Zhang, H.F.; Song, Q.J.; Hao, Z.Q.; Sun, T.Y.; Wu, P.H.; Zeng, Q.D.; Raza, R. Advanced optical reinforcement materials based on three-dimensional four-way weaving structure and metasurface technology. Appl. Phys. Lett. 2025, 126, 033503. [Google Scholar] [CrossRef]


| Reference | Peak Number | Average Absorption (%) | Polarization Insensitive | Incident Angle (°) | Sensitivity (nm/RIU) | FOM (1/RIU) |
|---|---|---|---|---|---|---|
| [55] | 5 | 96.47 | Yes | 0–30 | 1208.5 | - |
| [56] | 3 | >99 | Yes | 0–30 | 942.6 | - |
| [57] | 4 | 96.78 | Yes | 0–50 | 1072.75 | 182.09 |
| [58] | 3 | 92.34 | No | - | 2000 | 188.54 |
| [59] | 4 | 97.99 | Yes | 0–65 | 455 | 111.23 |
| This work | 6 | 98.8 | Yes | 0–50 | 2785.22 | 30.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; He, X.; Yang, H.; Bao, X.; Tang, Y.; Wu, P.; Yi, Y. Graphene-Based Absorber: Tunable, Highly Sensitive, Six-Frequency. Molecules 2025, 30, 1688. https://doi.org/10.3390/molecules30081688
Wang X, He X, Yang H, Bao X, Tang Y, Wu P, Yi Y. Graphene-Based Absorber: Tunable, Highly Sensitive, Six-Frequency. Molecules. 2025; 30(8):1688. https://doi.org/10.3390/molecules30081688
Chicago/Turabian StyleWang, Xinmei, Xianding He, Hua Yang, Xu Bao, Yongjian Tang, Pinghui Wu, and Yougen Yi. 2025. "Graphene-Based Absorber: Tunable, Highly Sensitive, Six-Frequency" Molecules 30, no. 8: 1688. https://doi.org/10.3390/molecules30081688
APA StyleWang, X., He, X., Yang, H., Bao, X., Tang, Y., Wu, P., & Yi, Y. (2025). Graphene-Based Absorber: Tunable, Highly Sensitive, Six-Frequency. Molecules, 30(8), 1688. https://doi.org/10.3390/molecules30081688







