Process Simulation of High-Pressure Nanofiltration (HPNF) for Membrane Brine Concentration (MBC): A Pilot-Scale Case Study
Abstract
:1. Introduction
2. Model Development
2.1. Process Configuration
2.2. Membrane Transport Equations for HPNF
2.3. Mass Balance in HPNF
3. Materials and Methods
3.1. Pilot Plant and Operating Conditions
3.2. Feed Water Characteristics
3.3. Analytical Methods
4. Results and Discussion
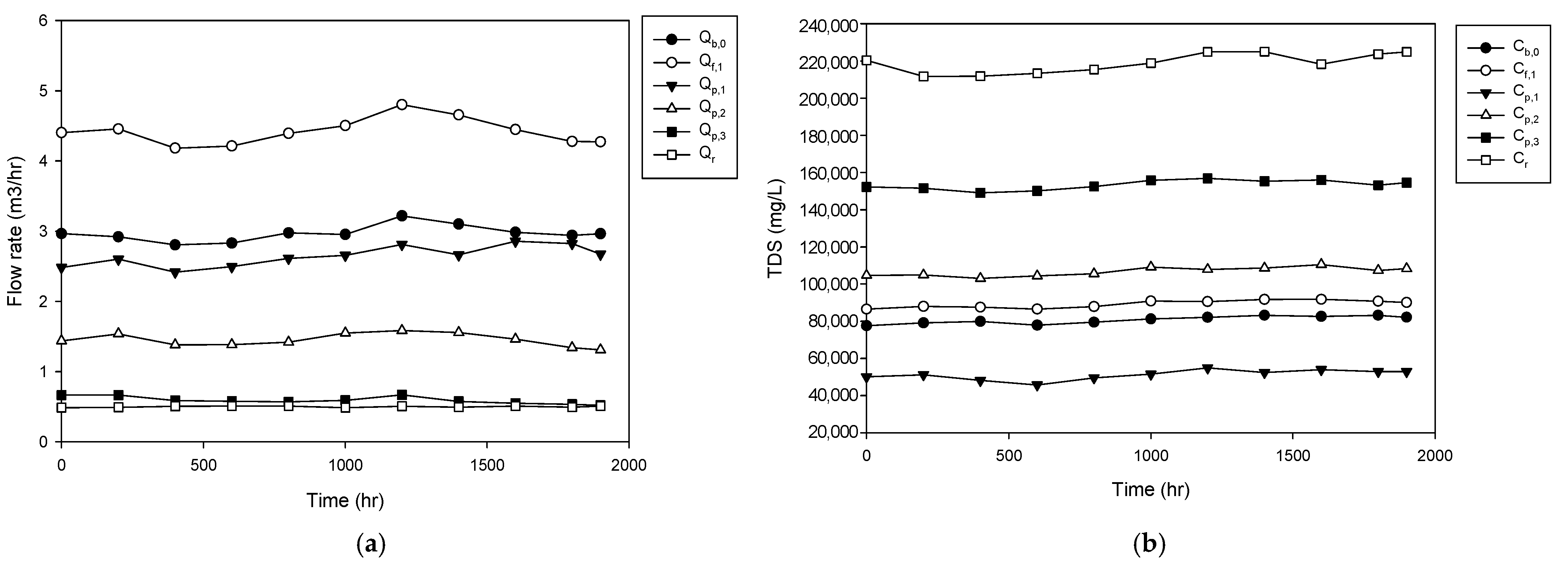
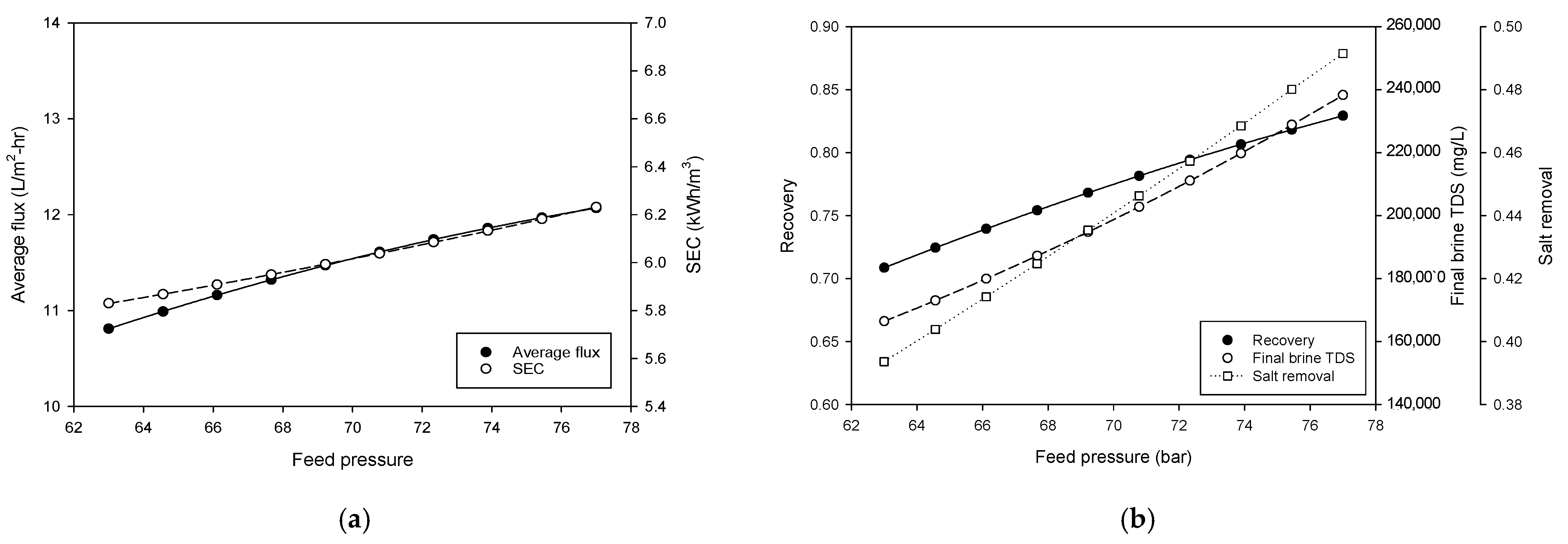
4.1. Operation of Pilot Plant
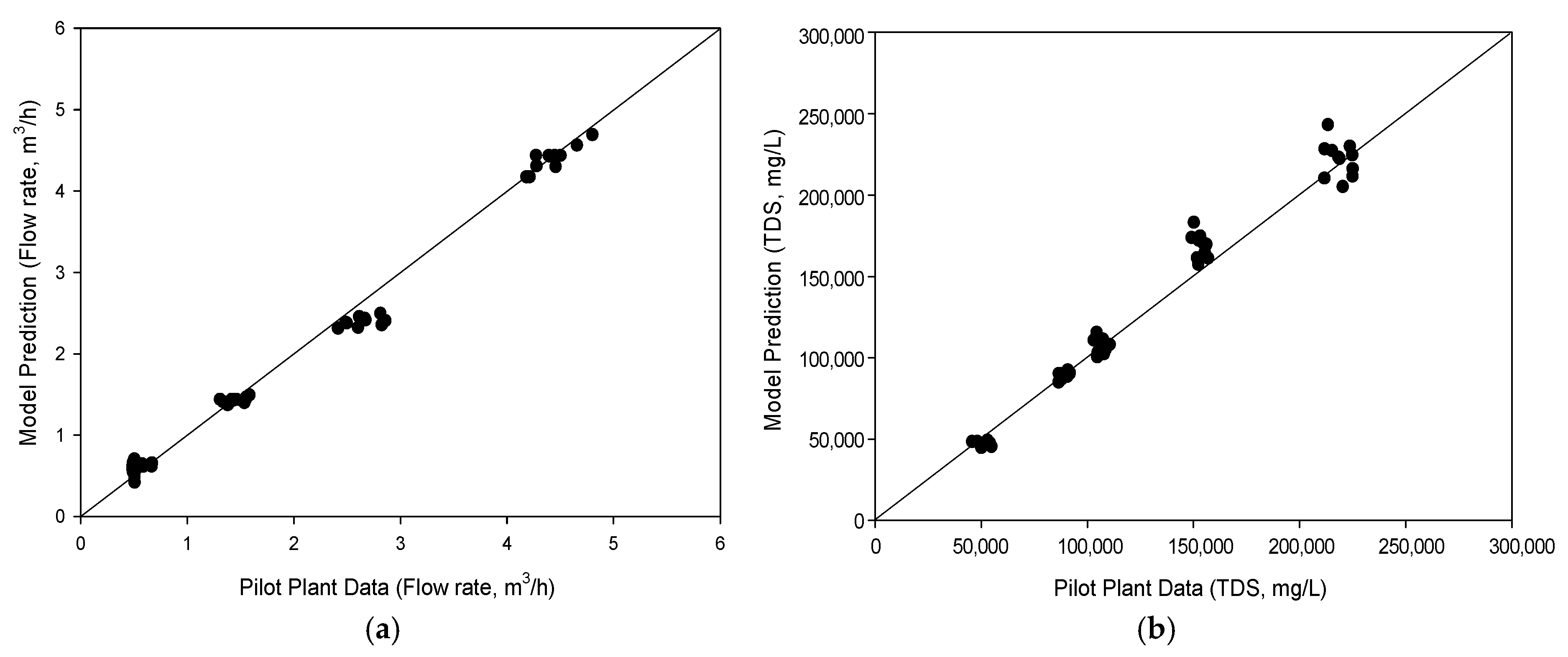
4.2. Comparison of Model Calculation with Pilot Plant Data
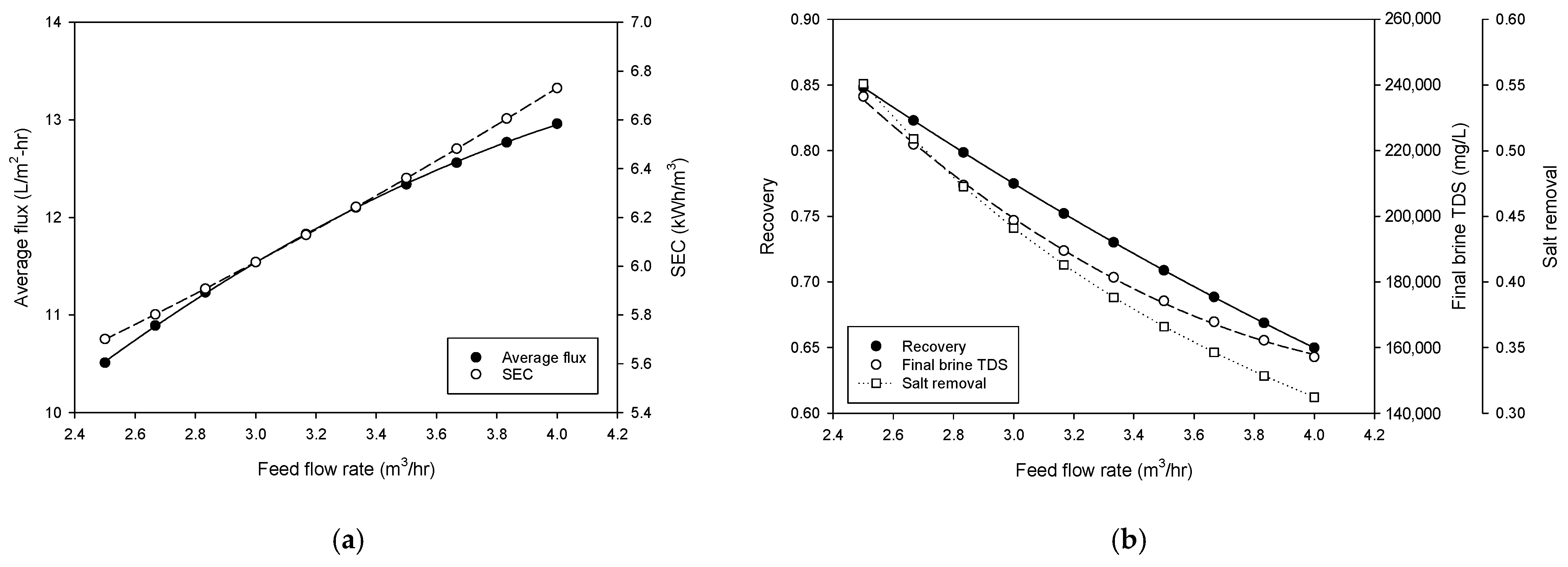
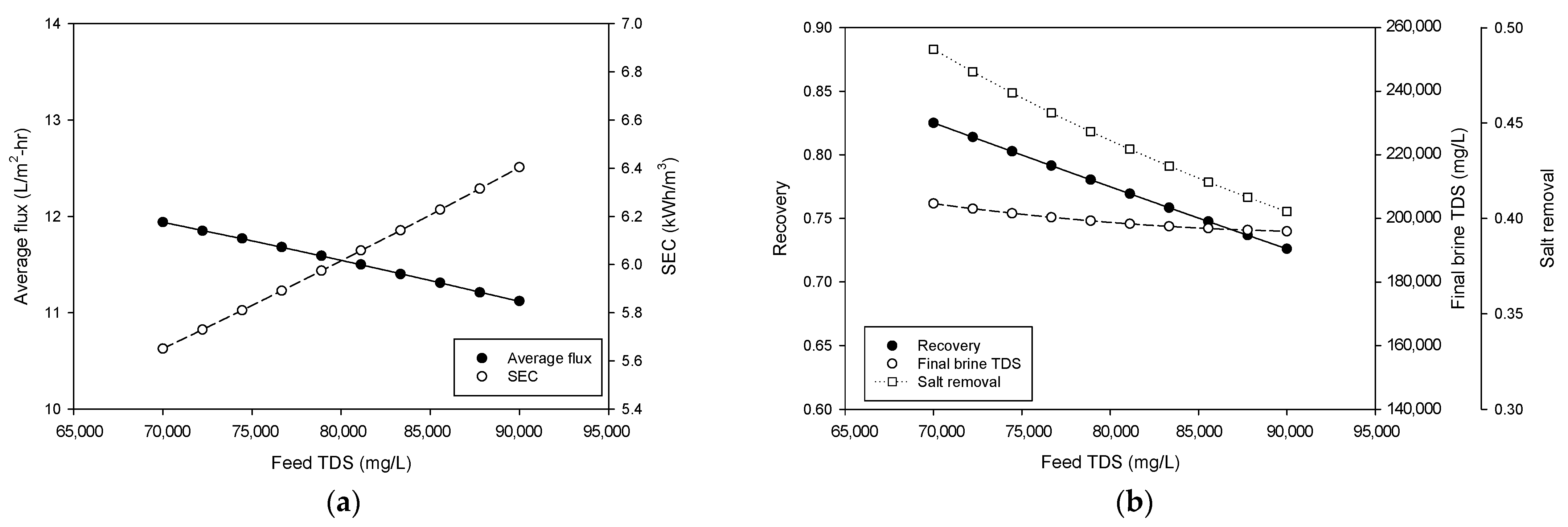
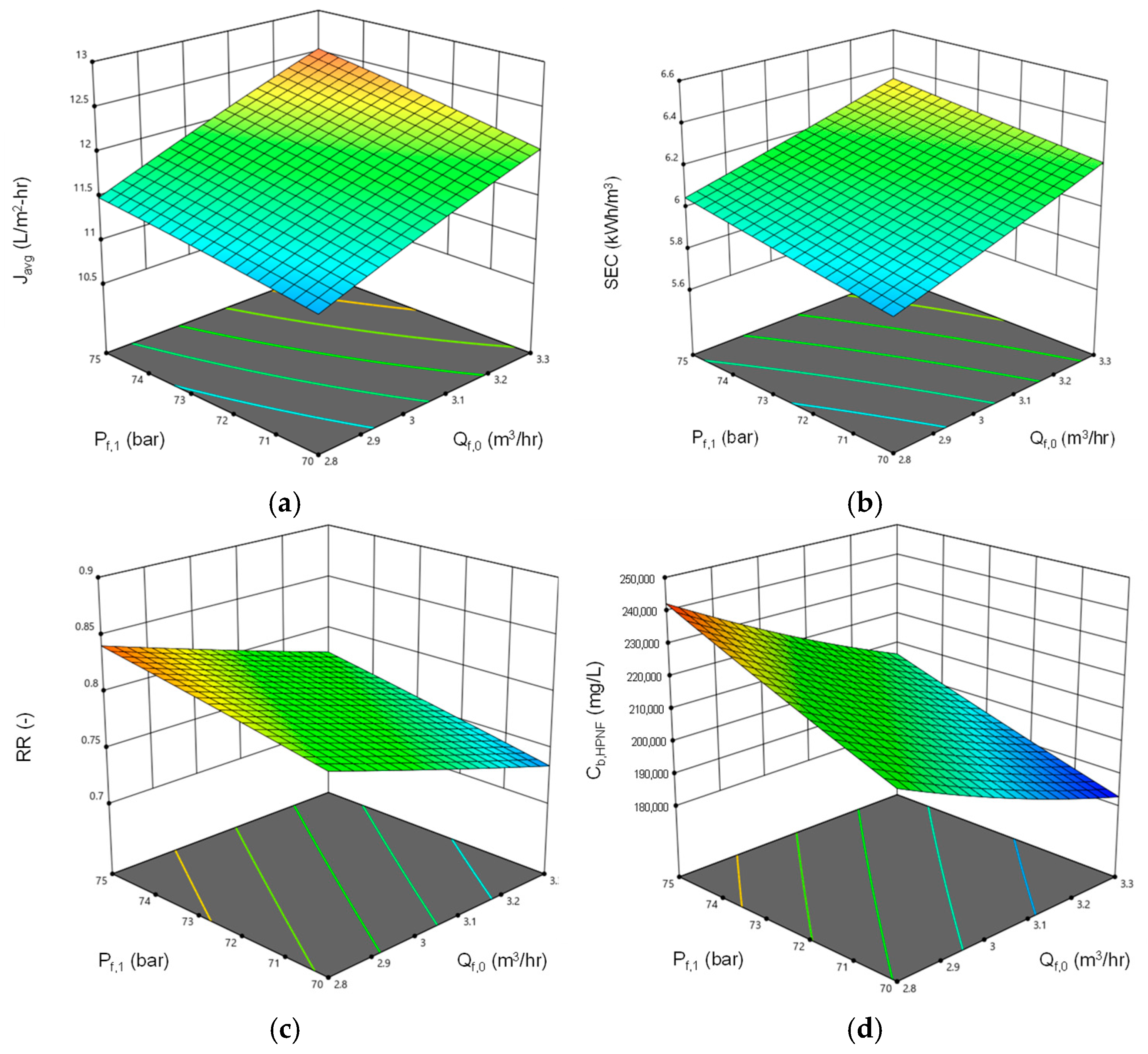
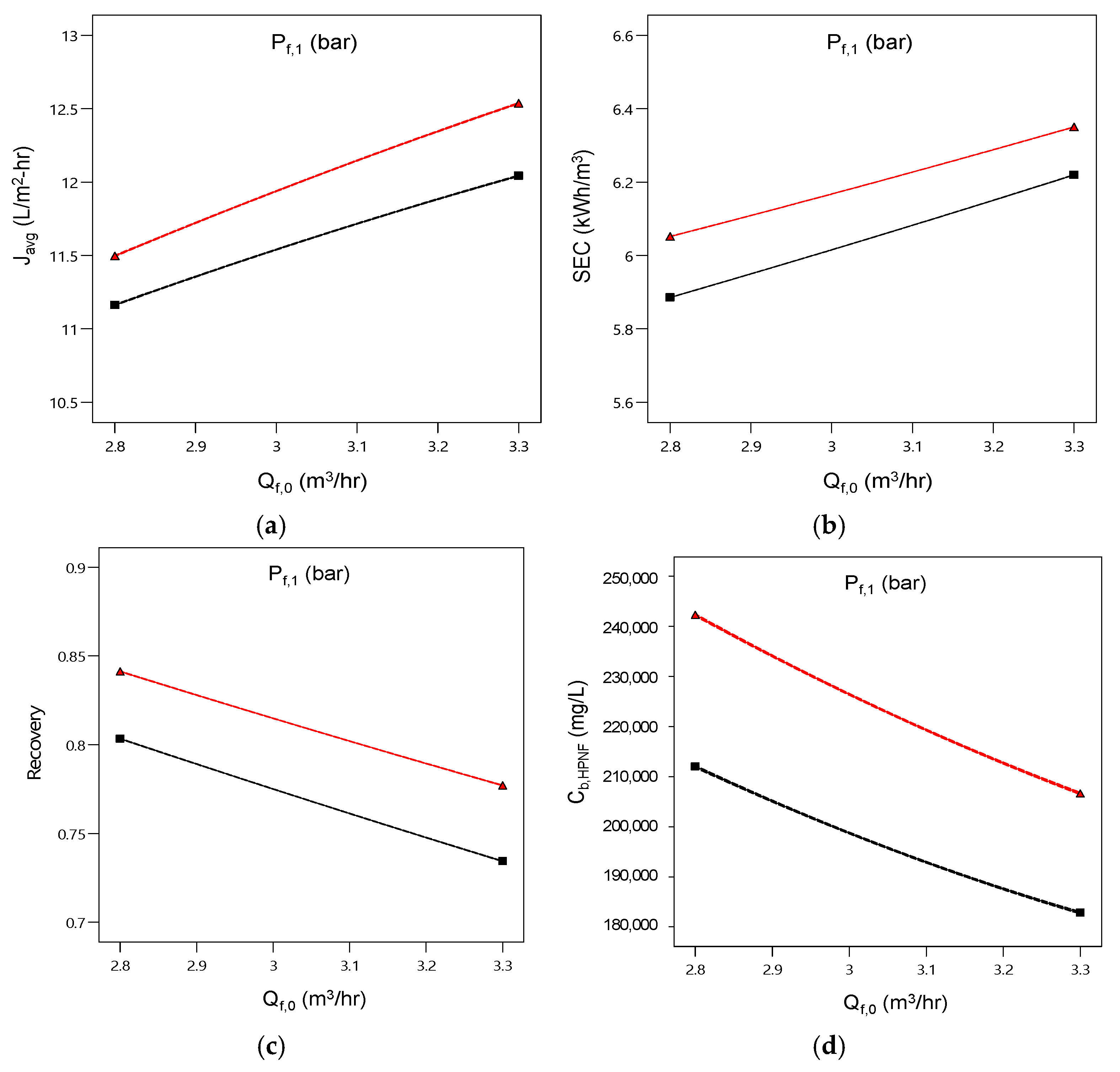
4.3. Simulation of Pilot Plant Performance
4.4. Application of Response Surface Methodology
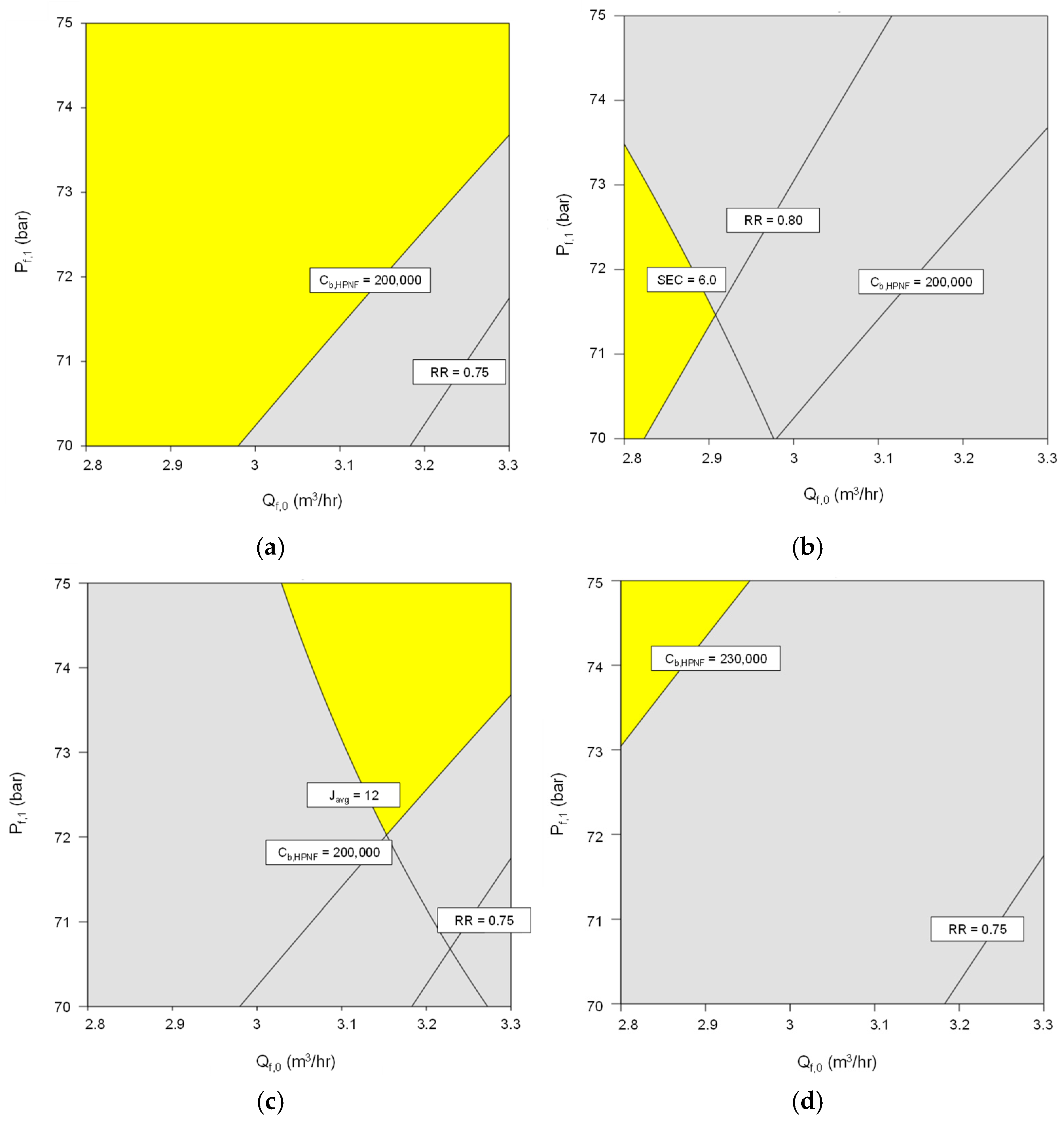
4.5. Multi-Criteria Improvement
5. Conclusions
- A mathematical model for HPNF was developed for MBC and compared with pilot plant data. Considering the limitations of the pilot plant data, the model showed reasonable accuracy in predicting flux and TDS, with R2 values above 0.99.
- Simulations showed that the lower feed flow rates and higher feed pressures favored recovery and brine concentration. Increasing flow rate and feed pressure improved flux at the expense of energy efficiency. An increase in feed TDS reduces flux, recovery, and final brine TDS and increases SEC.
- Response surface methodology (RSM) was used to optimize flux, SEC, recovery, and brine concentration. The F-values for all responses range from 81,057 to 341,700. The predicted R2 values for all responses are close to 1, and the adequate precision values are all well above the threshold value of 4. These results indicate that the developed models are statistically reliable.
- Using the RSM models, the optimum conditions were explored for four typical scenarios of MBC operation. Depending on the criteria in the scenarios, the optimal feed flow rate and pressures vary. For instance, the feed flow rate should be low, and pressure should be intermediate when high recovery (≥0.80) and low SEC (≤6.0 kWh/m3) are required (scenario 2). On the other hand, the feed flow rate and pressure should be high to achieve high flux (≥12 L/m2-h) (scenario 3). This suggests the importance of systematic process improvement for MBC.
- Instead of considering the recovery of the whole process, only the recovery of the HPNF was considered in this work. The first NF and SWRO stages were treated as boundary conditions. Accordingly, the current mode is not intended to optimize the entire NF-SWRO-HPNF system. Future work will explicitly integrate variable NF/RO performance into a holistic optimization framework.
- The SEC of the overall process was not included in the model. This study prioritizes the HPNF stage because the energy consumption of HPNF is much higher than that of SWRO and NF. Nevertheless, future work is needed to optimize the SEC of the whole system by a holistic approach.
- The purpose of this study was to develop a practical, industrially relevant tool for brine concentration, balancing computational efficiency with predictive utility. Future work will be needed to incorporate spatially resolved parameters and dynamic effects.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HPNF | High-pressure nanofiltration |
| MBC | Membrane brine concentration |
| NF | Nanofiltration |
| RO | Reverse osmosis |
| SEC | Specific electricity consumption |
| SWA | Saudi Water Authority (formerly known as SWCC, Saline Water Conversion Corporation) |
| SWRO | Seawater reverse osmosis |
| TDS | Total dissolved solids |
| WTIIRA | Water Technologies Innovation Institute and Research Advancement (formerly known as DTRI, Desalination Technologies Research Institute) |
References
- Sapkota, A. Water reuse, food production and public health: Adopting transdisciplinary, systems-based approaches to achieve water and food security in a changing climate. Environ. Res. 2019, 171, 576–580. [Google Scholar] [PubMed]
- McCarthy, M. Water sustainability: A looming global challenge. J. Am. Water Work. Assoc. 2008, 100, 46–47. [Google Scholar] [CrossRef]
- Panagopoulos, A.; Haralambous, K.; Loizidou, M. Desalination brine disposal and treatment—A review. Sci. Total Environ. 2019, 693, 133545. [Google Scholar] [CrossRef] [PubMed]
- Backer, S.; Bouaziz, I.; Kallayi, N.; Preethikumar, G.; Laoui, T. Review: Brine Solution: Current Status, Future Management and Technology Development. Sustainability 2022, 14, 6752. [Google Scholar] [CrossRef]
- Pistocchi, A.; Bleninger, T.; Breyer, C.; Caldera, U.; Dorati, C.; Ganora, D.; Millán, M.M.; Paton, C.; Poullis, D.; Herrero, F.S.; et al. Can seawater desalination be a win-win fix to our water cycle? Water Res. 2020, 182, 115906. [Google Scholar] [CrossRef] [PubMed]
- Sola, I.; Fernández-Torquemada, Y.; Forcada, A.; Valle, C.; Del Pilar-Ruso, Y.; González-Correa, J.; Sánchez-Lizaso, J. Long-term monitoring of brine discharge in marine environments. Mar. Pollut. Bull. 2020, 161, 111813. [Google Scholar] [CrossRef]
- Kelaher, B.; Clark, G.F.; Johnston, E.; Coleman, M. Effect of desalination discharge on reef fish diversity. Environ. Sci. Technol. 2019, 54, 735–744. [Google Scholar] [CrossRef]
- Abd-Elaty, I.; Shahawy, A.E.L.; Santoro, S.; Curcio, E.; Straface, S. Effects of groundwater abstraction and desalination brine deep injection on a coastal aquifer. Sci. Total Environ. 2021, 795, 148928. [Google Scholar]
- Einav, R.; Harussi, K.; Perry, D. The footprint of the desalination processes on the environment. Desalination 2003, 152, 141–154. [Google Scholar] [CrossRef]
- Jones, E.; Qadir, M.; van Vliet, M.V.; Smakhtin, V.; Kang, S. The state of desalination and brine production: A global outlook. Sci. Total Environ. 2019, 657, 1343–1356. [Google Scholar]
- Panagopoulos, A.; Haralambous, K. Environmental impacts of desalination and brine treatment. Mar. Pollut. Bull. 2020, 161, 111773. [Google Scholar] [CrossRef] [PubMed]
- Ariono, D.; Purwasasmita, M.; Wenten, I. Brine effluents: Characteristics, environmental impacts, and handling. J. Eng. Technol. Sci. 2016, 48, 367–387. [Google Scholar] [CrossRef]
- Mavukkandy, M.; Chabib, C.; Mustafa, I.; Al Ghaferi, A.; Almarzooqi, F. Brine management in the desalination industry: From waste to resource. Desalination 2019, 472, 114187. [Google Scholar] [CrossRef]
- Panagopoulos, A.; Giannika, V. A comprehensive assessment of the economic and technical viability of a zero liquid discharge (ZLD) hybrid desalination system for water and salt recovery. J. Environ. Manag. 2024, 359, 121057. [Google Scholar] [CrossRef] [PubMed]
- Elsaid, K.; Sayed, E.; Abdelkareem, M.; Baroutaji, A.; Olabi, A. Environmental impact of desalination processes: Mitigation and control strategies. Sci. Total Environ. 2020, 740, 140125. [Google Scholar] [CrossRef]
- Azadi Aghdam, M.; Zraick, F.; Simon, J.; Farrell, J.; Snyder, S.A. A novel brine precipitation process for higher water recovery. Desalination 2016, 385, 69–74. [Google Scholar] [CrossRef]
- Al-Absi, R.; Abu-Dieyeh, M.; Al-Ghouti, M. Brine management strategies and recovery using adsorption. Environ. Technol. Innov. 2021, 22, 101541. [Google Scholar] [CrossRef]
- Kress, N.; Gertner, Y.; Shoham-Frider, E. Seawater quality at the brine discharge site from two mega size seawater reverse osmosis desalination plants in Israel (Eastern Mediterranean). Water Res. 2019, 171, 115402. [Google Scholar] [CrossRef]
- Yizhi, S.; Minrui, W.; Bowen, H. Sustainability assessment and environmental impacts of water supply systems: A case study in Tampa Bay water supply system. E3S Web Conf. 2021, 308, 1010. [Google Scholar] [CrossRef]
- Pérez-González, A.; Urtiaga, A.; Ibáñez, R.; Ortiz, I. State of the art and review on the treatment technologies of water reverse osmosis concentrates. Water Res. 2012, 46, 267–283. [Google Scholar] [CrossRef]
- Al-Amoudi, A.S.; Ihm, S.; Farooque, A.M.; Al-Waznani, E.S.B.; Voutchkov, N. Dual brine concentration for the beneficial use of two concentrate streams from desalination plant—Concept proposal and pilot plant demonstration. Desalination 2023, 564, 116789. [Google Scholar] [CrossRef]
- Davenport, D.M.; Deshmukh, A.; Werber, J.R.; Elimelech, M. High-Pressure Reverse Osmosis for Energy-Efficient Hypersaline Brine Desalination: Current Status, Design Considerations, and Research Needs. Environ. Sci. Technol. Lett. 2018, 5, 467–475. [Google Scholar] [CrossRef]
- Sharkh, B.A.; Al-Amoudi, A.A.; Farooque, M.; Fellows, C.M.; Ihm, S.; Lee, S.; Li, S.; Voutchkov, N. Seawater desalination concentrate—A new frontier for sustainable mining of valuable minerals. npj Clean Water 2022, 5, 9. [Google Scholar]
- Abdalrhman, A.S.; Ihm, S.; Al-Waznani, E.S.; Fellows, C.; Li, S.; Lee, S.; Voutchkov, N. Novel Nf-Ro-Hpnf Membrane Brine Concentration (Mbc) System: A Pilot Study for Concentrating High Purity NaCl Brine from Seawater. Desalination 2025, 597, 118308. [Google Scholar]
- Wang, Z.; Deshmukh, A.; Du, Y.; Elimelech, M. Minimal and zero liquid discharge with reverse osmosis using low-salt-rejection membranes. Water Res. 2020, 170, 115317. [Google Scholar] [CrossRef]
- Atia, A.A.; Yip, N.Y.; Fthenakis, V. Pathways for minimal and zero liquid discharge with enhanced reverse osmosis technologies: Module-scale modeling and techno-economic assessment. Desalination 2021, 509, 115069. [Google Scholar] [CrossRef]
- Du, Y.; Wang, Z.; Cooper, N.J.; Gilron, J.; Elimelech, M. Module-scale analysis of low-salt-rejection reverse osmosis: Design guidelines and system performance. Water Res. 2022, 209, 117936. [Google Scholar] [CrossRef]
- Bargeman, G. Maximum allowable retention for low-salt-rejection reverse osmosis membranes and its effect on concentrating undersaturated NaCl solutions to saturation. Sep. Purif. Technol. 2023, 317, 123854. [Google Scholar] [CrossRef]
- Naderi Beni, A.; Alnajdi, S.M.; Garcia-Bravo, J.; Warsinger, D.M. Semi-batch and batch low-salt-rejection reverse osmosis for brine concentration. Desalination 2024, 583, 117670. [Google Scholar] [CrossRef]
- Heyrovská, R. Equations for Densities and Dissociation Constant of NaCl(aq) at 25 °C from “Zero to Saturation” Based on Partial Dissociation. J. Electrochem. Soc. 1997, 144, 2380. [Google Scholar] [CrossRef]
- Shahmansouri, A.; Min, J.; Jin, L.; Bellona, C. Feasibility of extracting valuable minerals from desalination concentrate: A comprehensive literature review. J. Clean. Prod. 2015, 100, 4–16. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, Z.; Chen, Y. A theoretical analysis on upgrading desalination plants with low-salt-rejection reverse osmosis. Desalination 2023, 565, 116827. [Google Scholar] [CrossRef]
- Atia, A.A.; Allen, J.; Young, E.; Knueven, B.; Bartholomew, T.V. Cost optimization of low-salt-rejection reverse osmosis. Desalination 2023, 551, 116407. [Google Scholar] [CrossRef]
- Beni, A.N.; Ghofrani, I.; Moosavi, A. On comparison of three multi-feed osmotic-mediation-based configurations for brine management: Techno-economic optimization and exergy analysis. Desalination 2022, 525, 115517. [Google Scholar] [CrossRef]
- Du, Y.; Wang, L.; Belgada, A.; Younssi, S.A.; Gilron, J.; Elimelech, M. A mechanistic model for salt and water transport in leaky membranes: Implications for low-salt-rejection reverse osmosis membranes. J. Membr. Sci. 2023, 678, 121642. [Google Scholar] [CrossRef]
- Peters, C.D.; Hankins, N.P. Osmotically assisted reverse osmosis (OARO): Five approaches to dewatering saline brines using pressure-driven membrane processes. Desalination 2019, 458, 1–13. [Google Scholar] [CrossRef]
- Kim, J.; Kim, D.I.; Hong, S. Analysis of an osmotically-enhanced dewatering process for the treatment of highly saline (waste)waters. J. Membr. Sci. 2018, 548, 685–693. [Google Scholar] [CrossRef]
- Schock, G.; Miquel, A. Mass transfer and pressure loss in spiral wound modules. Desalination 1987, 64, 339–352. [Google Scholar] [CrossRef]
- Oh, H.-J.; Hwang, T.-M.; Lee, S. A simplified simulation model of RO systems for seawater desalination. Desalination 2009, 238, 128–139. [Google Scholar] [CrossRef]
- Mo, Z.; Peters, C.D.; Long, C.; Hankins, N.P.; She, Q. How split-feed osmotically assisted reverse osmosis (SF-OARO) can outperform conventional reverse osmosis (CRO) processes under constant and varying electricity tariffs. Desalination 2022, 530, 115670. [Google Scholar] [CrossRef]
- Ju, J.; Lee, S.; Kim, Y.; Cho, H.; Lee, S. Theoretical and Experimental Analysis of Osmotically Assisted Reverse Osmosis for Minimum Liquid Discharge. Membranes 2023, 13, 814. [Google Scholar] [CrossRef] [PubMed]
- Nor, N.M.; Mohamed, M.S.; Loh, T.C.; Foo, H.L.; Rahim, R.A.; Tan, J.S.; Mohamad, R. Comparative analyses on medium optimization using one-factor-at-a-time, response surface methodology, and artificial neural network for lysine-methionine biosynthesis by Pediococcus pentosaceus RF-1. Biotechnol. Biotechnol. Equip. 2017, 31, 935–947. [Google Scholar] [CrossRef]
- Srivastava, A.; K, A.; Nair, A.; Ram, S.; Agarwal, S.; Ali, J.; Singh, R.; Garg, M.C. Response surface methodology and artificial neural network modelling for the performance evaluation of pilot-scale hybrid nanofiltration (NF) & reverse osmosis (RO) membrane system for the treatment of brackish ground water. J. Environ. Manag. 2021, 278, 111497. [Google Scholar] [CrossRef]

| Vendor | Model No. | Values |
|---|---|---|
| FTS H2O | HBR-TFC-4040 (4-inch) | Operating conditions: Maximum Operating Pressure: 1150 psi (80 bar) Maximum Temperature: 113 °F (45 °C) Feedwater pH Limits: 3.0–10.0 Test conditions: NaCl Feed Concentration: 90,000 ppm Applied Pressure: 1050 psi pH Range: 6.5 to 7.0, Temperature: 25 °C Permeate Salinity: 35,000 ppm, Reject Salinity: 96,000 ppm |
| Item (1) | Seawater | RO Brine (Feed to HPNF) |
|---|---|---|
| pH | 8.2 ± 0.15 | 6.62 ± 0.54 |
| Ca2+ | 0.45 ± 0.08 | 0.39 ± 0.07 |
| Mg2+ | 1.5 ± 0.15 | 0.41 ± 0.16 |
| Na+ | 14.2 ± 0.510 | 27.90 ± 0.30 |
| K+ | 0.42 ± 0.06 | 1.13 ± 0.04 |
| HCO3− | 0.13 ± 0.01 | 0.14 ± 0.16 |
| SO42− | 3.1 ± 0.38 | 0.28 ± 0.30 |
| Cl− | 25.00 ± 1.14 | 45.99 ± 0.29 |
| Br− | 0.07 ± 0.01 | 0.21 ± 0.00 |
| TDS | 45.00 ± 2.25 | 76.29 ± 2.03 |
| NaCl/TDS | 0.87 ± 0.01 | 0.97 ± 0.01 |
| Run No. | Factors | Responses | |||||
|---|---|---|---|---|---|---|---|
| Feed Flow Rate (m3/hr) | Feed TDS (mg/L) | Feed Pressure (bar) | Average Flux (L/m2-h) | SEC (kWh/m3) | Recovery | Final Brine TDS (mg/L) | |
| 1 | 3.05 | 80,500 | 72.5 | 11.83 | 6.14 | 0.7866 | 208,552 |
| 2 | 3.05 | 80,500 | 72.5 | 11.83 | 6.14 | 0.7866 | 208,552 |
| 3 | 3.3 | 77,000 | 70 | 12.19 | 6.097 | 0.7499 | 183,578 |
| 4 | 3.05 | 80,500 | 72.5 | 11.83 | 6.14 | 0.7866 | 208,552 |
| 5 | 2.8 | 77,000 | 75 | 11.58 | 5.952 | 0.8544 | 245,461 |
| 6 | 2.63 | 80,500 | 72.5 | 10.95 | 5.883 | 0.845 | 240,531 |
| 7 | 3.3 | 84,000 | 70 | 11.84 | 6.387 | 0.7141 | 182,343 |
| 8 | 3.3 | 84,000 | 75 | 12.36 | 6.51 | 0.7577 | 205,062 |
| 9 | 3.05 | 80,500 | 72.5 | 11.83 | 6.14 | 0.7866 | 208,552 |
| 10 | 2.8 | 84,000 | 75 | 11.38 | 6.188 | 0.8236 | 238,476 |
| jj | 2.8 | 77,000 | 70 | 11.27 | 5.781 | 0.8179 | 213,829 |
| 12 | 3.05 | 74,613.7 | 72.5 | 12.06 | 5.924 | 0.8152 | 212,293 |
| 13 | 3.05 | 80,500 | 76.7 | 12.15 | 6.269 | 0.8187 | 232,253 |
| 14 | 3.47 | 80,500 | 72.5 | 12.56 | 6.419 | 0.7325 | 185,983 |
| 15 | 3.05 | 80,500 | 72.5 | 11.83 | 6.14 | 0.7866 | 208,552 |
| 16 | 3.05 | 80,500 | 68.3 | 11.44 | 6.021 | 0.7503 | 187,422 |
| 17 | 3.05 | 80,500 | 72.5 | 11.83 | 6.14 | 0.7866 | 208,552 |
| 18 | 3.3 | 77,000 | 75 | 12.66 | 6.234 | 0.7917 | 208,439 |
| 19 | 2.8 | 84,000 | 70 | 11.02 | 6.028 | 0.7843 | 209,646 |
| 20 | 3.05 | 86,386.3 | 72.5 | 11.59 | 6.365 | 0.7583 | 205,973 |
| Responses | Model F-Value | Predicted R2 | Adequate Precision | Regression Equation |
|---|---|---|---|---|
| Flux | 38,824 | 0.9998 | 716.50 | 2.7354 + 2.1920 Qb,0 − 2.8×10−5 Cb,0 + 0.069494 Pf,1 − 2.9×10−5 Qb,0Cb,0 + 0.064 Qb,0Pf,1 + 1.43 × 10−6 Cb,0Pf,1 − 0.43048 Qb,02 − 1.76×10−10 Cb,02 − 0.00204 Pf,12 |
| SEC | 341,700 | 1.0000 | 2227.56 | −0.40953 + 0.33660 Qb,0 + 6.62 × 10−6 Cb,0 + 0.06117 Pf,1 + 0.000012 Qb,0Cb,0 − 0.0142 Qb,0Pf,1 -3.57 × 10−7 Cb,0Pf,1 + 0.06181 Qb,02 + 1.28×10−10 Cb,02 + 0.000279 Pf,12 |
| Recovery | 81,057 | 0.9999 | 1082.5 | 1.1394 − 0.28545 Qb,0 − 8.00×10−6 Cb,0 + 0.014026 Pf,1 −7.71 × 10−7 Qb,0Cb,0 + 0.0192 Qb,0Pf,1 + 6.57 × 10−8 Cb,0Pf,1 + 0.01226 Qb,02 + 4.83×10−12 Cb,02 − 0.00012 Pf,12 |
| Final brine TDS | 19,611.7 | 0.9996 | 477.78 | 39542 − 1.15 × 105 Qb,0 − 0.92961 Cb,0 + 8475.6 Pf,1 + 0.93657 Qb,0Cb,0 − 2576.4 Qb,0Pf,1 − 0.070628 Cb,0Pf,1 + 26,544 Qb,02 + 1.6404 × 10−5 Cb,02 + 72.005 Pf,12 |
| Scenario | Average Flux Javg (L/m2-h) | SEC (kWh/m3) | Recovery RR | Final Brine Concentration Cb, HPNF (mg/L) |
|---|---|---|---|---|
| 1 | ≥11 | ≤6.5 | ≥0.75 | ≥200,000 |
| 2 | ≥11 | ≤6.0 | ≥0.80 | ≥200,000 |
| 3 | ≥12 | ≤6.5 | ≥0.75 | ≥200,000 |
| 4 | ≥11 | ≤6.5 | ≥0.75 | ≥230,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdalrhman, A.S.; Lee, S.; Ihm, S.; Alwaznani, E.S.B.; Fellows, C.M.; Li, S. Process Simulation of High-Pressure Nanofiltration (HPNF) for Membrane Brine Concentration (MBC): A Pilot-Scale Case Study. Membranes 2025, 15, 113. https://doi.org/10.3390/membranes15040113
Abdalrhman AS, Lee S, Ihm S, Alwaznani ESB, Fellows CM, Li S. Process Simulation of High-Pressure Nanofiltration (HPNF) for Membrane Brine Concentration (MBC): A Pilot-Scale Case Study. Membranes. 2025; 15(4):113. https://doi.org/10.3390/membranes15040113
Chicago/Turabian StyleAbdalrhman, Abdallatif Satti, Sangho Lee, Seungwon Ihm, Eslam S. B. Alwaznani, Christopher M. Fellows, and Sheng Li. 2025. "Process Simulation of High-Pressure Nanofiltration (HPNF) for Membrane Brine Concentration (MBC): A Pilot-Scale Case Study" Membranes 15, no. 4: 113. https://doi.org/10.3390/membranes15040113
APA StyleAbdalrhman, A. S., Lee, S., Ihm, S., Alwaznani, E. S. B., Fellows, C. M., & Li, S. (2025). Process Simulation of High-Pressure Nanofiltration (HPNF) for Membrane Brine Concentration (MBC): A Pilot-Scale Case Study. Membranes, 15(4), 113. https://doi.org/10.3390/membranes15040113









