Model-Based Characterization of the Metabolism of Recombinant Adeno-Associated Virus (rAAV) Production via Human Embryonic Kidney (HEK293) Cells
Abstract
1. Introduction
2. Theoretical Background
2.1. Fitting Process
2.2. Global Sensitivity Analysis
3. Methodology
3.1. The Mathematical Model
3.2. Kinetic Model of the Bioprocesses
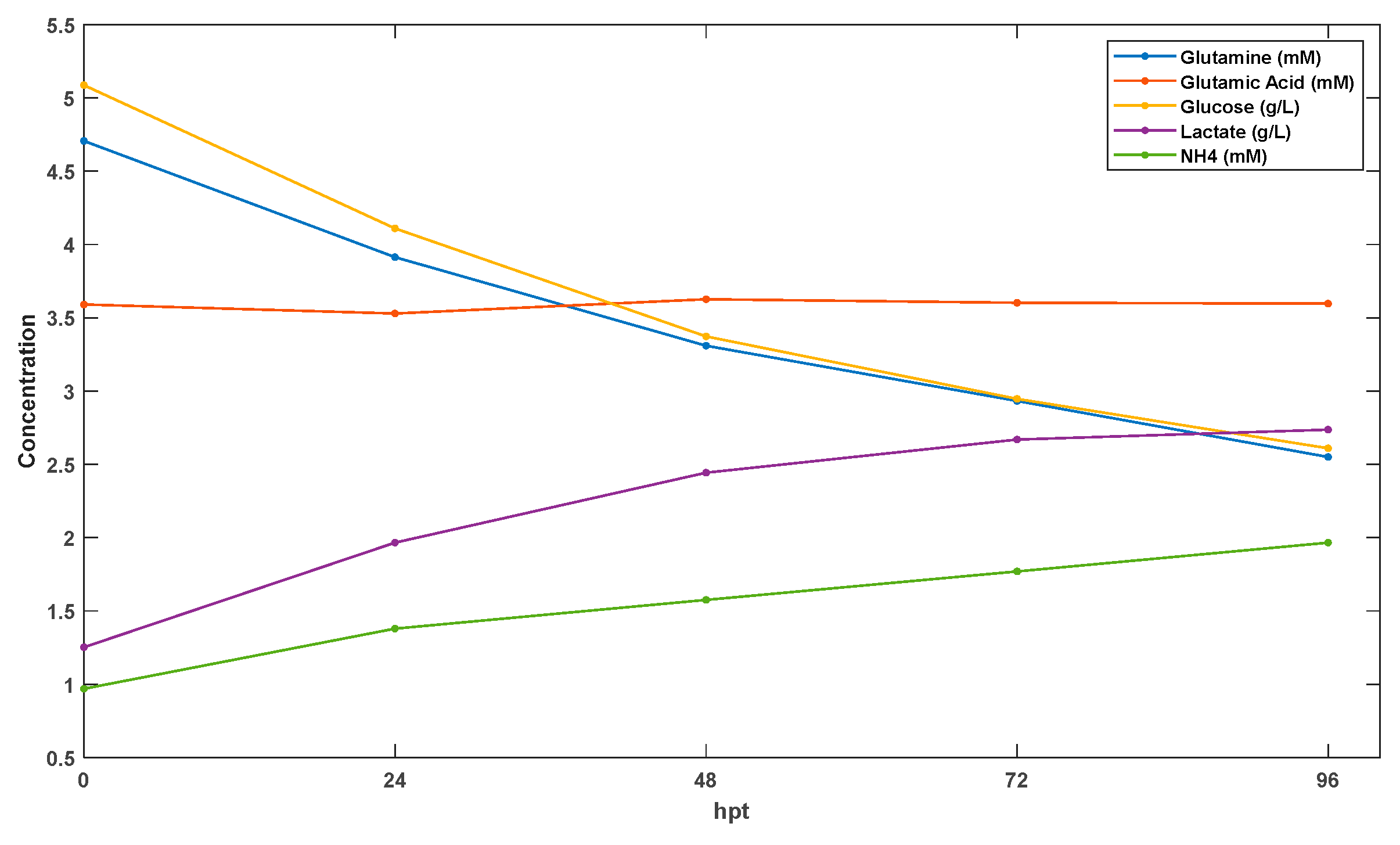
4. Experimental Data Sets
5. Results and Discussion
5.1. Model Optimization
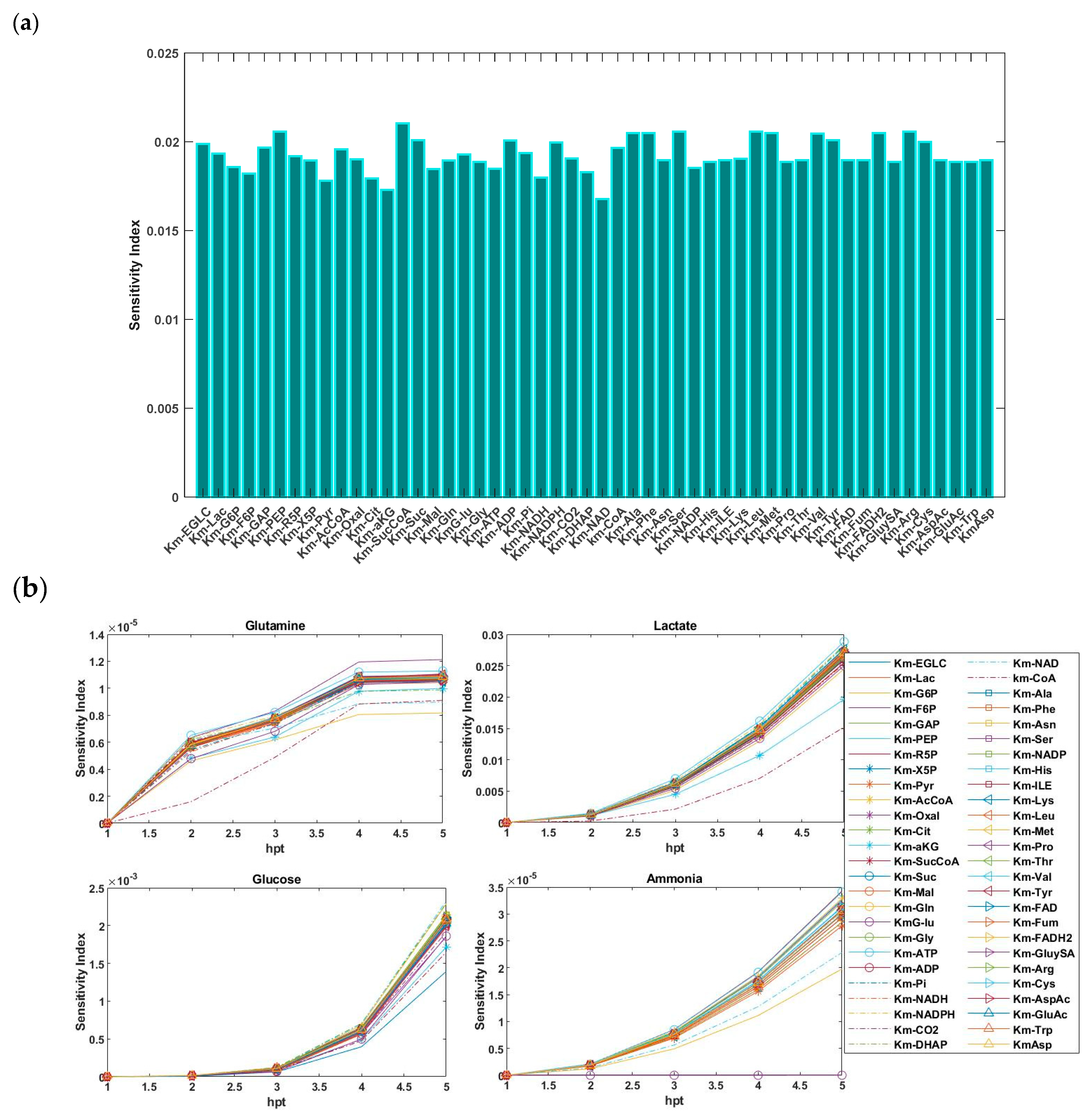
5.2. Sensitivity Analysis
6. Conclusions
7. Limitations and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Finer, M.; Glorioso, J. A brief account of viral vectors and their promise for gene therapy. Gene Ther. 2017, 24, 1–2. [Google Scholar] [CrossRef] [PubMed]
- Grabenhorst, E.; Schlenke, P.; Pohl, S.; Nimtz, M.; Conradt, H.S. Genetic engineering of recombinant glycoproteins and the glycosylation pathway in mammalian host cells. In Glycotechnology; Springer: Boston, MA, USA, 1999; pp. 1–17. [Google Scholar]
- Giorgetti, S.I.; Etcheverrigaray, M.; Terry, F.; Martin, W.; De Groot, A.S.; Ceaglio, N.; Oggero, M.; Mufarrege, E.F. Development of highly stable and de-immunized versions of recombinant alpha interferon: Promising candidates for the treatment of chronic and emerging viral diseases. Clin. Immunol. 2021, 233, 108888. [Google Scholar] [CrossRef] [PubMed]
- Clément, N.; Grieger, J.C. Manufacturing of recombinant adeno-associated viral vectors for clinical trials. Mol. Ther. Methods Clin. Dev. 2016, 3, 16002. [Google Scholar] [CrossRef] [PubMed]
- Sanchez-Martinez, Z.V.; Alpuche-Lazcano, S.P.; Stuible, M.; Durocher, Y. CHO cells for virus-like particle and subunit vaccine manufacturing. Vaccine 2024, 42, 2530–2542. [Google Scholar] [CrossRef] [PubMed]
- Abbate, T.; Dewasme, L.; Wouwer, A.V.; Bogaerts, P. Adaptive flux variability analysis of HEK cell cultures. Comput. Chem. Eng. 2020, 133, 106633. [Google Scholar] [CrossRef]
- Adamson-Small, L.; Potter, M.; Falk, D.J.; Cleaver, B.; Byrne, B.J.; Clément, N. A scalable method for the production of high-titer and high-quality adeno-associated type 9 vectors using the HSV platform. Mol. Ther. Methods Clin. Dev. 2016, 3, 16031. [Google Scholar] [CrossRef] [PubMed]
- Dash, S.; Sharon, D.M.; Mullick, A.; Kamen, A.A. Only a small fraction of cells produce assembled capsids during transfection-based manufacturing of adeno-associated virus vectors. Biotechnol. Bioeng. 2022, 119, 1685–1690. [Google Scholar] [CrossRef] [PubMed]
- Gagnon, P.; Goricar, B.; Mencin, N.; Zvanut, T.; Peljhan, S.; Leskovec, M.; Strancar, A. Multiple-monitor HPLC assays for rapid process development, in-process monitoring, and validation of AAV production and purification. Pharmaceutics 2021, 13, 113. [Google Scholar] [CrossRef] [PubMed]
- Rieser, R.; Koch, J.; Faccioli, G.; Richter, K.; Menzen, T.; Biel, M.; Winter, G.; Michalakis, S. Comparison of different liquid chromatography-based purification strategies for adeno-associated virus vectors. Pharmaceutics 2021, 13, 748. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.N.; Sha, S.; Hong, M.S.; Maloney, A.J.; Barone, P.W.; Neufeld, C.; Wolfrum, J.; Springs, S.L.; Sinskey, A.J.; Braatz, R.D. Mechanistic model for production of recombinant adeno-associated virus via triple transfection of HEK293 cells. Mol. Ther. Methods Clin. Dev. 2021, 21, 642–655. [Google Scholar] [CrossRef] [PubMed]
- Kyriakopoulos, S.; Ang, K.S.; Lakshmanan, M.; Huang, Z.; Yoon, S.; Gunawan, R.; Lee, D.Y. Kinetic modeling of mammalian cell culture bioprocessing: The quest to advance biomanufacturing. Biotechnol. J. 2018, 13, 1700229. [Google Scholar] [CrossRef] [PubMed]
- Rico, J.; Nantel, A.; Pham, P.L.; Voyer, R.; Durocher, Y.; Penny, S.; Surendra, A.; Pinto, D.; Sasseville, M.; Culf, E.; et al. Kinetic model of metabolism of monoclonal antibody producing CHO cells. Curr. Metabolomics 2018, 6, 207–217. [Google Scholar] [CrossRef]
- Ghorbaniaghdam, A.; Henry, O.; Jolicoeur, M. A kinetic-metabolic model based on cell energetic state: Study of CHO cell behavior under Na-butyrate stimulation. Bioprocess Biosyst. Eng. 2013, 36, 469–487. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Yan, X.; Dan, H. Review of sensitivity analysis. J. Beijing Norm. Univ. 2008, 1, 9–16. [Google Scholar]
- Maeder, M.; Neuhold, Y.-M. Practical Data Analysis in Chemistry; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Sobol’, I.M. On sensitivity estimation for nonlinear mathematical models. Mat. Model. 1990, 2, 112–118. [Google Scholar]
- Moço, P.D.; Xu, X.; Silva, C.A.T.; Kamen, A.A. Production of adeno-associated viral vector serotype 6 by triple transfection of suspension HEK293 cells at higher cell densities. Biotechnol. J. 2023, 18, 2300051. [Google Scholar] [CrossRef] [PubMed]
- Karimvand, S.K.; Maeder, M.; Abdollahi, H. A chemical equilibrium modelling strategy for tuning the apparent equilibrium constants of the chemical systems. Anal. Chim. Acta 2019, 1049, 29–37. [Google Scholar] [CrossRef] [PubMed]


| # | Metabolic Pathway | Metabolic Reaction Network |
|---|---|---|
| υ1 | Glycolysis | Glc + ATP → G6P + ADP |
| υ2 | G6P → F6P | |
| υ3 | F6P + ATP → DHAP + G3P + ADP | |
| υ4 | DHAP ↔ G3P | |
| υ5 | G3P + NAD+ + ADP ↔ PEP + NADH + ATP | |
| υ6 | PEP + ADP → Pyr + ATP | |
| υ7 | Tricarboxylic acid cycle | Pyr + NAD+ + CoA → AcCoA + CO2 + NADH |
| υ8 | AcCoA + Oxal + H2O → Cit + CoA | |
| υ9 | Cit + NADP+ → αKG + CO2 + NADPH | |
| υ10 | αKG + CoA + NAD+ → SucCoA + CO2 + NADH | |
| υ11 | SucCoA + ADP + Pi → Suc + ATP + CoA | |
| υ12 | Suc + FAD ↔ Fum + FADH2 | |
| υ13 | Fum ↔ Mal | |
| υ14 | Mal + NAD+ → Oxal + NADH | |
| υ15 | Pyruvate fates | G6P + 2NADP+ + H2O → R5P + 2NADPH + CO2 |
| υ16 | 2X5P + R5P → 2F6P + G3P | |
| υ17 | Anaplerotic reaction | Mal + NADP+ → Pyr + CO2 + NADPH |
| υ18 | Pyr + CO2 + ATP → Oxal | |
| υ19 | Amino acid metabolism | Glu + NAD+ → αKG + NH4 + NADH |
| υ20 | Oxal + Glu → Asp + αKG | |
| υ21 | Gln → Glu + NH4 | |
| υ22 | Ser → Pyr + NH4 | |
| υ23 | Asn → Asp + NH4 | |
| υ24 | Glu + ATP + 2NADPH + H+ → Pro- + ADP + 2NADP+ | |
| υ25 | GluySA → Pro- | |
| υ26 | His → Glu + NH4 | |
| υ27 | Nucleotides synthesis | 2Asp + Gly + 2Gln + 0.6R5P + CO2 → 2Mal + 2Glu |
| υ28 | Pentose phosphate pathway | G6P + 2NADP+ + H2O → R5P + 2NADPH + CO2 |
| υ29 | 2X5P + R5P → 2F6P + G3P | |
| υ30 | Biomass synthesis | 0.024*R5P + 0.029*G6P + 0.04*Gln + 0.013*Ala + 0.007*Arg + 0.026*Asp + 0.003*His + 0.0084*Ile + 0.013*Leu + 0.01*Lys + 0.099*Ser + 0.004*Tyr + 0.0096*Val + 0.016*Gly + 3.78*ATP → Biomass |
| υ31 | Protein folding | 0.05*Ala + 0.03*Cys + 0.06*AspAc + 0.07*GluAc + 0.03*Phe + 0.05*Gly + 0.02*His + 0.06*ILE + 0.08*Lys + 0.08*Leu + 0.02*Met + 0.04*Asn + 0.05*Pro + 0.05*Glu + 0.04*Arg + 0.07*Ser + 0.07*Thr + 0.06*Val + 0.03*Trp + 0.03*Tyr + ATP → Rep + ADP |
| υ32 | 0.07*Ala + 0.01*Cys + 0.06*AspAc + 0.05*GluAc + 0.05*Phe + 0.08*Gly + 0.02* His + 0.03* ILE + 0.05* Lys + 0.06* Leu + 0.01*Met + 0.09*Asn + 0.08*Pro + 0.05*Glu + 0.04*Arg + 0.07*Ser + 0.07*Thr + 0.05*Val + 0.02*Trp + 0.04*Tyr + ATP → Cap + ADP |
| Flux | Equations | Parameters |
|---|---|---|
| υHK | υmaxHK = 0.205 KmGlc = 5.100 KmATP = 0.594 | |
| υPGI | υmaxPGI = 2.283 KmG6P = 2.165 | |
| υPFK | υmaxPFK = 6.667 KmF6P = 0.016 | |
| υTPI | υmax-f-TPI = 1.296 KmDHAP = 0.043 υmax-r-TPI = 14.299 KmGAP = 4.6 × 10−6 | |
| υPGK | υmax-f-PGK = 3.841 υmax-r-PGK = 4.0 × 10−3 KmNAD = 2.4 × 10−5 KmADP = 4.3 × 10−7 KmPEP = 0.018 KmNADH = 0.017 | |
| υPK | υmaxPK = 2.520 | |
| υPDH | υmaxPDH = 0.571 KmPYr = 0.013 KmCoA = 6.4 × 10−4 | |
| υCS | υmaxCS = 0.125 KmAcCoA = 0.012 KmOxal = 0.004 | |
| υCITS | υmaxCITS = 1.634 KmCit = 0.082 KmNADP = 6.9 × 10−4 | |
| υAKGDH | υmaxAKGDH = 1.496 KmaKG = 1.9 × 10−5 | |
| υSCL | υmaxSCL = 1.300 KmSucCoA = 6 × 10−4 KmPi = 0.047 | |
| υSD | υmax-f-SD = 2.378 υmax-r-SD = 1.989 KmSuc = 0.034 KmFAD = 1.320 KmFUM = 0.041 KmFADH2 = 0.053 | |
| υFH | υmax-f-FH = 8.3 × 10−2 υmax-r-FH = 1.777 KmMal = 0.046 | |
| υMDH | υmaxMDH = 1.4 × 10−2 | |
| υLDH | υmax-f-LDH = 0.565 υmax-r-LDH = 0.275 KmLac = 3.119 | |
| υAlaTA | υmaxAlaTA = 3.1 × 10−2 KmGlu = 1.7 × 10−4 | |
| υG6PDH | υmaxG6PDH = 5 × 10−3 | |
| υTK | υmaxTK = 4 × 10−3 KmX5P = 7 × 10−3 KmR5P = 6.5 × 10−2 | |
| υME | υmaxME = 0.84 | |
| υPC | υmaxPC = 9.02 KmCO2 = 0.45 | |
| υGLDH | υmaxGLDH = 2.3 × 10−2 | |
| υASTA | υmaxASTA = 1.21 | |
| υGLNS | υmaxGLNS = 0.01 | |
| υSDHH | υmaxSDHH = 0.43 KmSer = 0.96 | |
| υASN | υmaxASN = 1 × 10−4 KmAsn = 1.7 × 10−3 | |
| υGlu | υmaxGlu = 0.98 KmNADPH = 8.06 × 10−5 | |
| υGluySA | υmaxGluySA = 8.5 × 10−2 KmGluySA = 2.15 × 10−3 | |
| υHis | υmaxHis = 6 × 10−4 KmHis = 1.89 × 10−2 | |
| υNS | υmaxNS = 0.79 KmAsp = 1.29 × 10−5 KmGly = 1.51 × 10−5 KmGln = 3 × 10−4 | |
| υGrowth | υGrowth = 1.8 × 10−2 KmAla = 2.8 × 10−2 KmArg = 1.2 × 10−2 KmIle = 1.7 × 10−2 KmLeu = 3.9 × 10−4 KmLys = 5.8 × 10−2 KmTyr = 8.1 × 10−3 KmVal = 0.60 | |
| υRep | υmaxRep = 2.5 × 10−3 KmCys = 4.94 × 10−2 KmAspAc = 4.95 × 10−2 KmGluAc = 5.03 × 10−2 KmPhe = 7.1 × 10−2 KmMet = 0.32 KmPro = 4.74 × 10−2 KmThr = 1.94 × 10−2 KmTrp = 4.99 × 10−2 | |
| υCep | υmaxCep = 2.9 × 10−2 |
| Metabolite | Name | Fitted Value | Metabolite | Name | Fitted Value |
|---|---|---|---|---|---|
| ATP | ATP | 19.95 mM | His | Histidine | 0.604 mM |
| ADP | ADP | 0.175 mM | Ile | Isoleucine | 0.777 mM |
| AcCoA | Acetyl-CoA | 0.016 mM | Lac 1 | Lactate | 13.91 mM |
| αKG | Alpha-ketoglutarate | 0.110 mM | Lys | Lysine | 0.017 mM |
| Ala | Alanine | 6.985 mM | Leu | Leucine | 0.517 mM |
| Asp | Aspartate | 3.065 mM | Mal | Malate | 4.262 mM |
| Asn | Asparagine | 0.495 mM | Met | Methionine | 1.150 mM |
| Arg | Arginine | 0.519 mM | NAD NADH | Nicotinamide adenine dinucleotide | 0.634 mM 0.029 mM |
| AspAc | Aspartic acid | 0.011 mM | NADP NADPH | Nicotinamide adenine dinucleotide phosphate | 0.009 mM 0.106 mM |
| CoA | Coenzyme A | 1.132 mM | NH4 1 | Ammonia | 0.97 mM |
| Cit | Citrate | 0.810 mM | Oxal | Oxaloacetate | 0.003 mM |
| CO2 | CO2 | 3.530 mM | Pep | 3-phosphoglycerate | 0.309 mM |
| Cys | Cysteine | 0.248 mM | Pyr | Pyruvate | 7.291 mM |
| DHAP | dihydroxyacetone phosphate | 3.072 mM | Pi | Orthophosphate or hydrogenphosphate | 0.498 mM |
| F6P | Fructose-6-phosphate | 0.685 mM | Pro | Proline | 1.520 mM |
| FAD | flavin adenine dinucleotide | 3.630 mM | Phe | Phenylalanine | 0.874 mM |
| Fum | Fumaric acid | 0.192 mM | R5P | Ribulose-5-phosphate | 1.169 mM |
| FADH2 | 0.753 mM | SucCoA | Succinate Coenzyme A | 0.007 mM | |
| GLC 1 | Glucose | 28.23 mM | Suc | Succinate | 0.997 mM |
| GAP | Glyceraldehyde 3-phosphate | 0.600 mM | Ser | Serine | 0.012 mM |
| G6P | Glucose-6-phosphate | 1.255 mM | Thr | Threonine | 0.205 mM |
| Glu | Glutamate | 2.82 × 10−5 mM | Trp | Tryptophan | 0.237 mM |
| Gln 1 | Glutamine | 4.7 mM | Tyr | Tyrosine | 0.255 mM |
| GluySA | Glutamateγ−semialdehyde | 0.034 mM | Val | Valine | 0.107 mM |
| GluAc 1 | Glutamic acid | 3.59 mM | X5P | Xylulose 5 − phosphate | 0.004 mM |
| Gly | Glycine | 1.155 mM |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khodadadi Karimvand, S.; Cuperlovic-Culf, M.; Kamen, A.A.; Bolic, M. Model-Based Characterization of the Metabolism of Recombinant Adeno-Associated Virus (rAAV) Production via Human Embryonic Kidney (HEK293) Cells. Bioengineering 2025, 12, 345. https://doi.org/10.3390/bioengineering12040345
Khodadadi Karimvand S, Cuperlovic-Culf M, Kamen AA, Bolic M. Model-Based Characterization of the Metabolism of Recombinant Adeno-Associated Virus (rAAV) Production via Human Embryonic Kidney (HEK293) Cells. Bioengineering. 2025; 12(4):345. https://doi.org/10.3390/bioengineering12040345
Chicago/Turabian StyleKhodadadi Karimvand, Somaiyeh, Miroslava Cuperlovic-Culf, Amine A. Kamen, and Miodrag Bolic. 2025. "Model-Based Characterization of the Metabolism of Recombinant Adeno-Associated Virus (rAAV) Production via Human Embryonic Kidney (HEK293) Cells" Bioengineering 12, no. 4: 345. https://doi.org/10.3390/bioengineering12040345
APA StyleKhodadadi Karimvand, S., Cuperlovic-Culf, M., Kamen, A. A., & Bolic, M. (2025). Model-Based Characterization of the Metabolism of Recombinant Adeno-Associated Virus (rAAV) Production via Human Embryonic Kidney (HEK293) Cells. Bioengineering, 12(4), 345. https://doi.org/10.3390/bioengineering12040345







