High-Fidelity Digital Twin Data Models by Randomized Dynamic Mode Decomposition and Deep Learning with Applications in Fluid Dynamics
Abstract
:1. Introduction
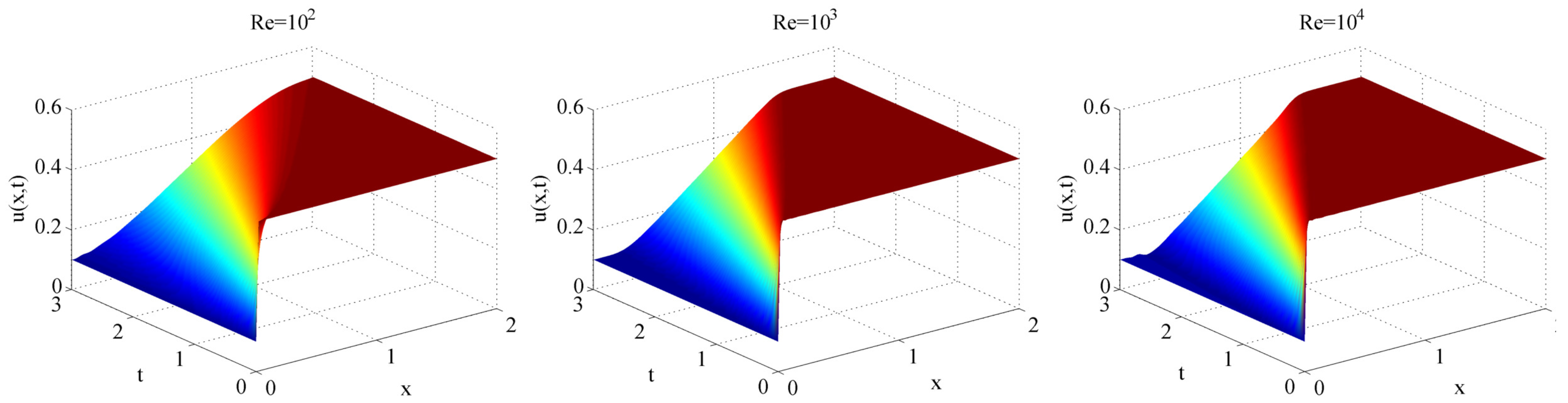
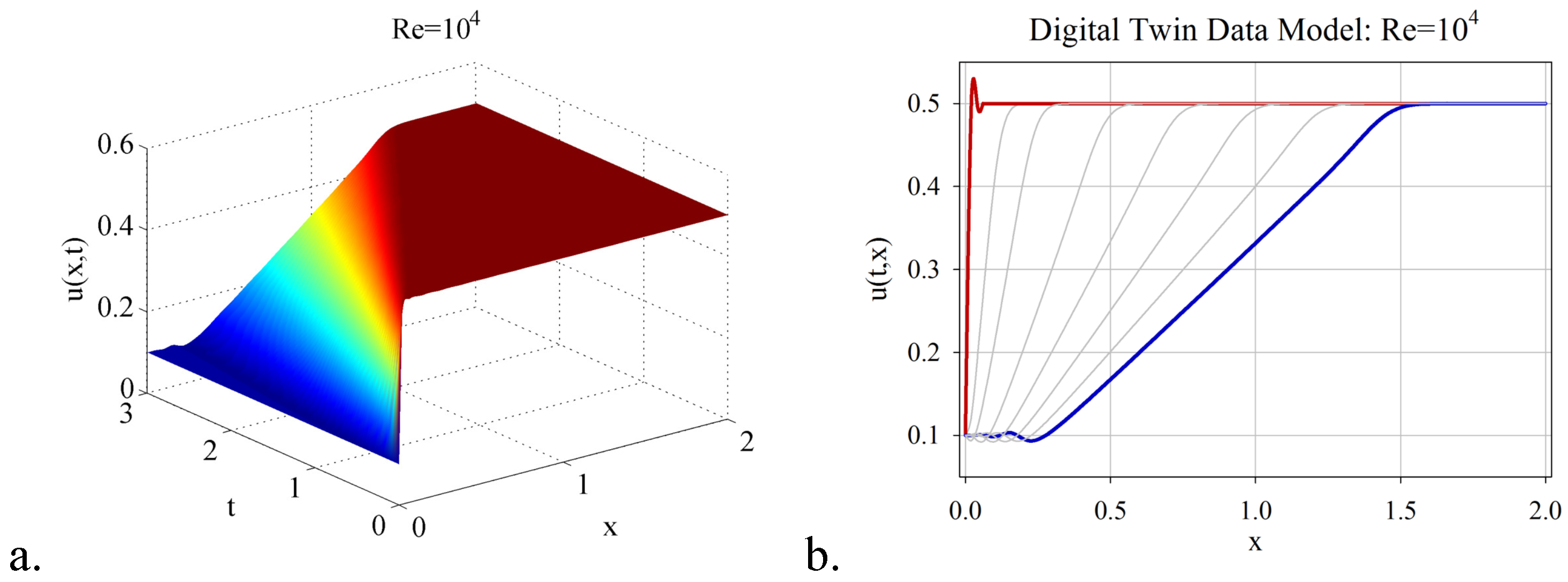
2. Shock Wave Phenomena: Full-Order Model of Nonlinear Viscous Burgers Equation
3. Reduced Order Modeling Based on Dynamic Mode Decomposition
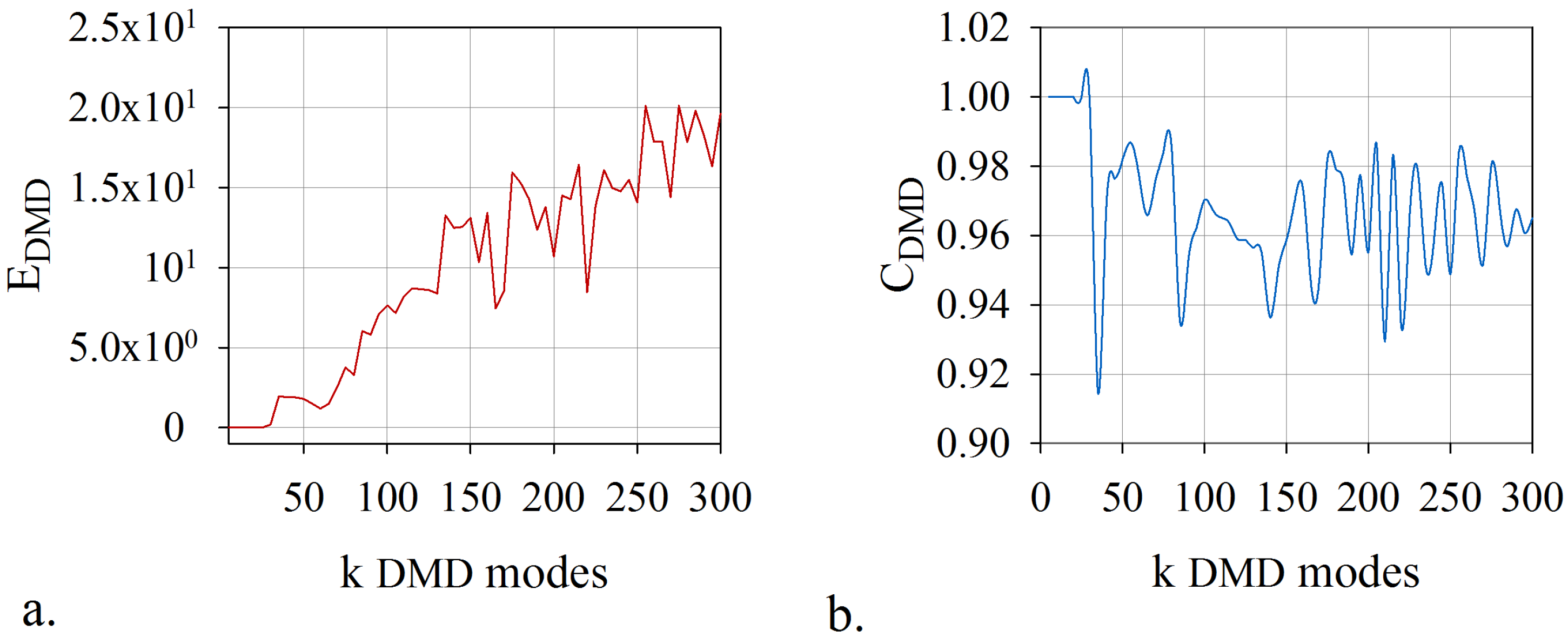
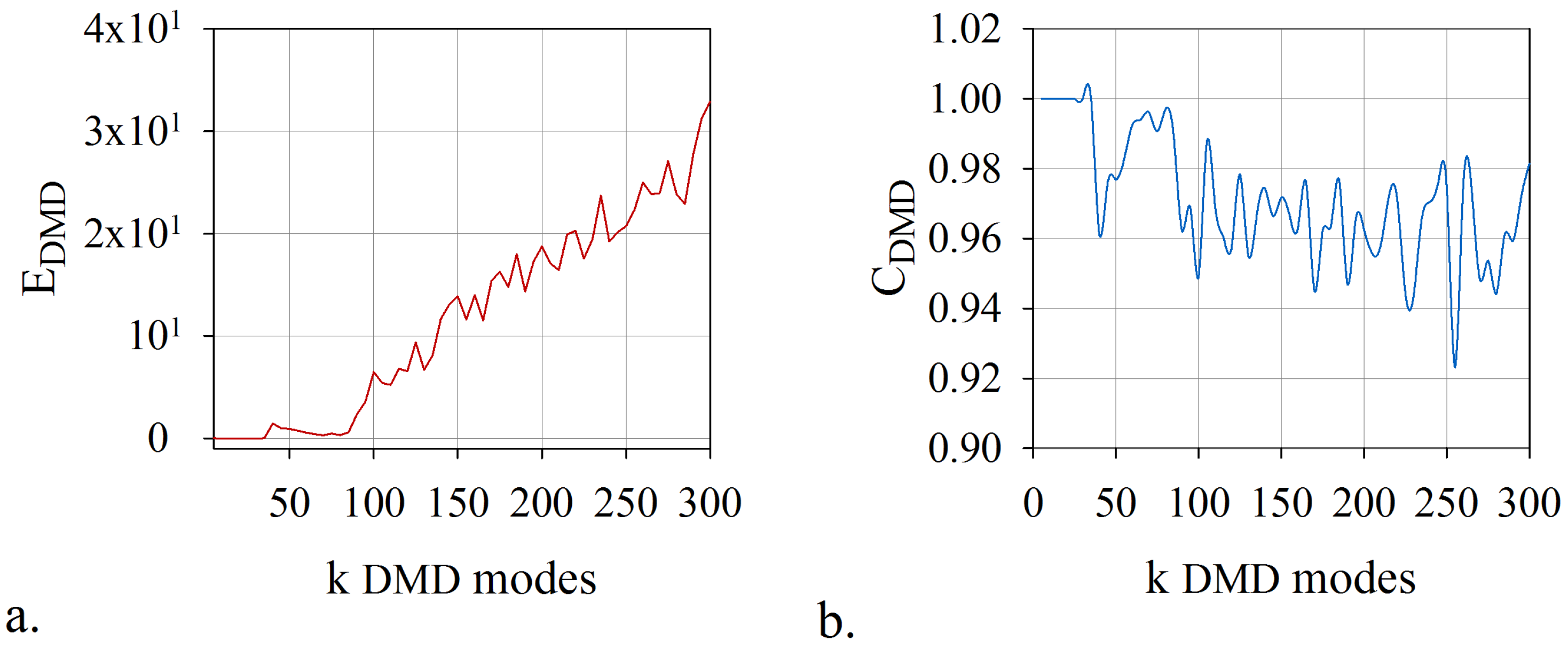
4. Offline Stage: Randomized Dynamic Mode Decomposition
| Algorithm 1: Randomized Dynamic Mode Decomposition |
Initial data:, , integer target rank and .
|
| Algorithm 2: Randomized Singular Value Decomposition of Rank k (k-RSVD) |
Initial data:, integer target rank and .
|
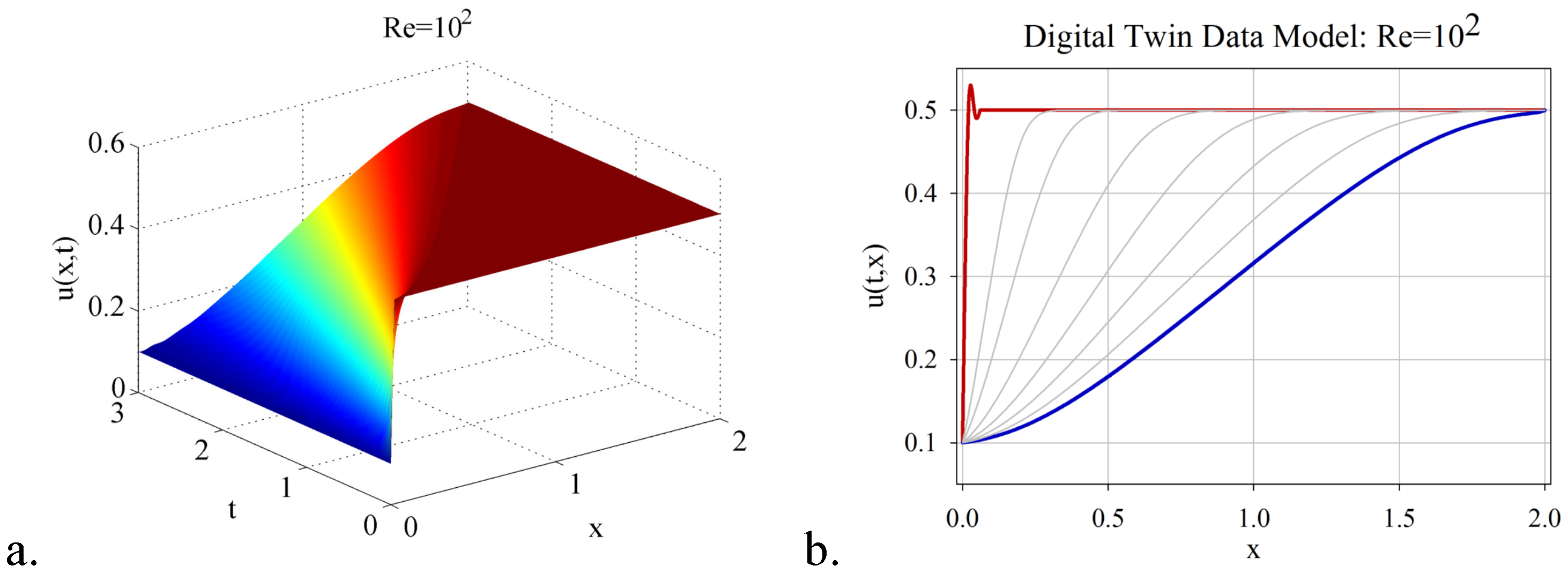
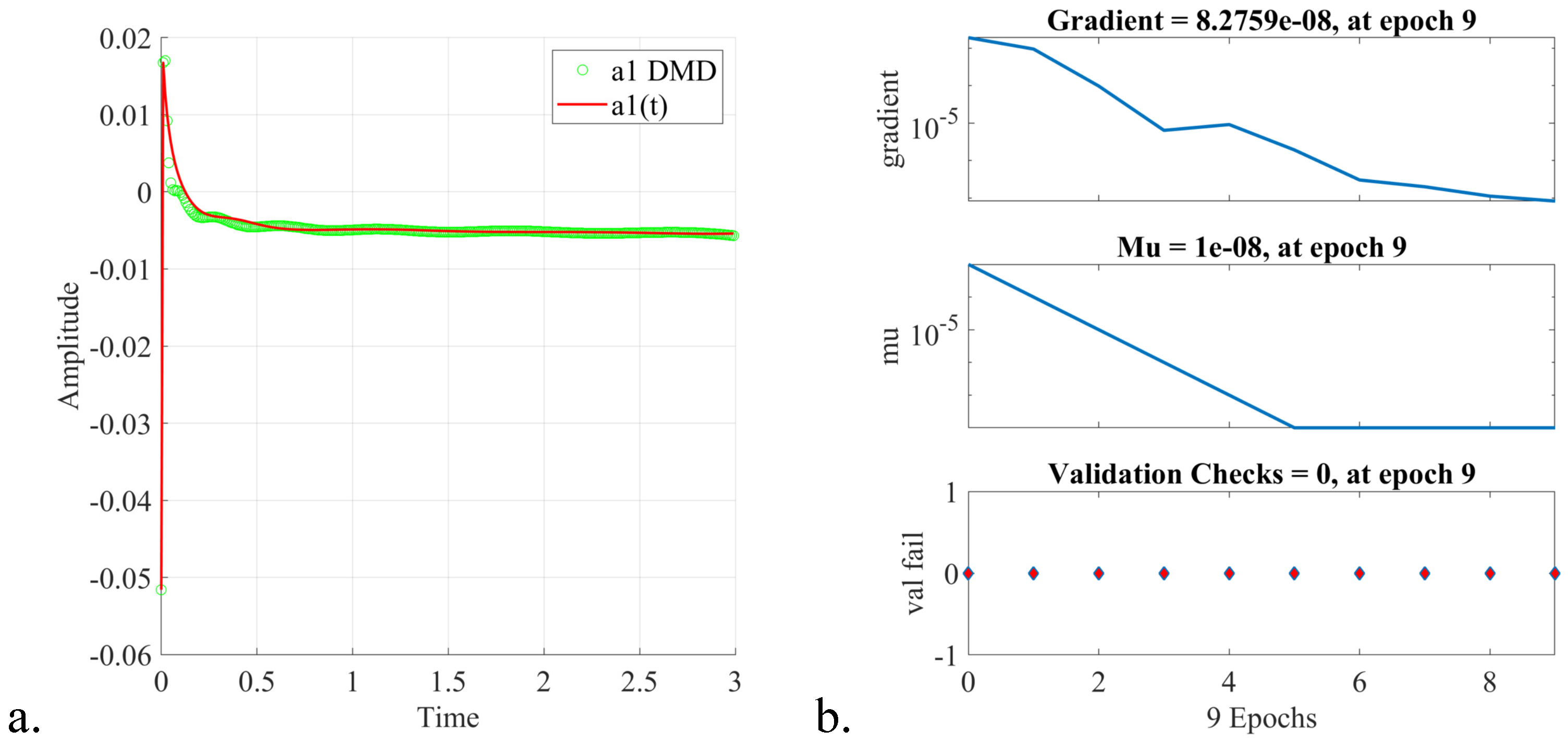
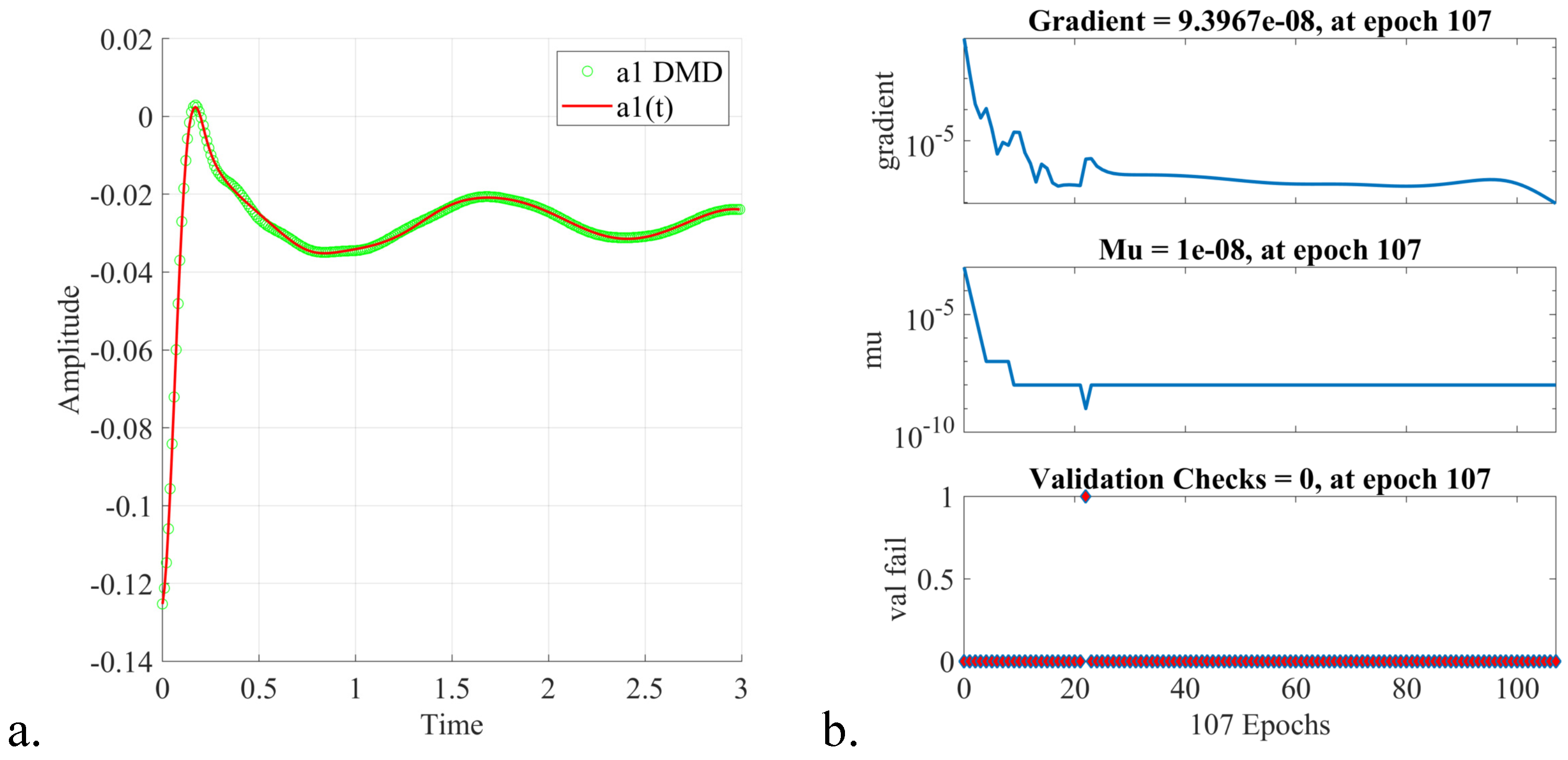
5. Online Stage: Fast Digital Twin Data Model Identification Using Deep Learning Nonlinear Autoregressive Estimators
6. Numerical Results: Computational Efficiency of the Algorithm
7. Conclusions
- This method overcomes the inconveniences of developing and implementing a mode selection criterion associated with dynamic mode decomposition. The proposed technique does not require an additional selection algorithm of the DMD modes. The rank of the model, the leading modes, and the temporal coefficients have been determined by coupling the randomized dynamic mode decomposition with an optimisation problem whose constraint consists in the smallest error of digital twin model. A fast and accurate algorithm was produced, which provided the lowest rank for the model and the leading modes with the most significant contribution.
- A significant reduction of the offline-online CPU time was achieved, which confirms the feasibility of the algorithm.
- Combining the randomized DMD with deep learning artificial intelligence, a digital twin data model for estimating the flow behaviour in the real-time window was derived. The DTM has been investigated in the numerical simulation of three shock wave phenomena with increasing complexity, with Reynolds number varying from to . It was demonstrated that the significant advantage of DTM is to map the dynamics with high accuracy and reduced costs in CPU time and hardware, even to settings difficult to explore because of the rapidly changing dynamics over time (e.g., high Reynolds numbers).
- The procedure of online estimation of the DTM temporal coefficients by employing deep learning nonlinear autoregressive estimators led to a fast and accurate identification of the digital twin data models. The computational efficiency of the proposed algorithm was thoroughly investigated, and a qualitative analysis of the DTM was provided in the three shock wave experiments.
Funding
Acknowledgments
Conflicts of Interest
References
- Kim, N.H.; Sankar, B.V.; Kumar, A.V. Introduction to Finite Element Analysis and Design; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Codina, R.; Badia, S.; Baiges, J.; Principe, J. Encyclopedia of Computational Mechanics; Chapter Variational Multiscale Methods in Computational Fluid Dynamics; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Xiao, D.; Heaney, C.E.; Fang, F.; Mottet, L.; Hu, R.; Bistrian, D.A.; Aristodemou, D.; Navon, I.M.; Pain, C.C. A domain decomposition non-intrusive reduced order model for turbulent flows. Comput. Fluids 2019, 182, 15–27. [Google Scholar] [CrossRef] [Green Version]
- Xiao, D.; Heaney, C.E.; Mottet, L.; Fang, F.; Lin, W.; Navon, I.M.; Guo, Y.; Matar, O.K.; Robins, A.G.; Pain, C.C. A reduced order model for turbulent flows in the urban environment using machine learning. Build. Environ. 2019, 148, 323–337. [Google Scholar] [CrossRef] [Green Version]
- Dimitriu, G.; Stefanescu, R.; Navon, I.M. POD-DEIM approach on dimension reduction of a multi-species host-parasitoid system. Ann. Acad. Rom. Sci. Ser. Math. Appl. 2015, 7, 173–188. [Google Scholar]
- Dumon, A.; Allery, C.; Ammar, A. Proper Generalized Decomposition method for incompressible Navier-Stokes equations with a spectral discretization. Appl. Math. Comput. 2013, 219, 8145–8162. [Google Scholar] [CrossRef] [Green Version]
- Stefanescu, R.; Navon, I.M. POD/DEIM nonlinear model order reduction of an ADI implicit shallow water equations model. J. Comput. Phys. 2013, 237, 95–114. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Akhtar, I.; Borggaard, J.; Iliescu, T. Proper orthogonal decomposition closure models for turbulent flows: A numerical comparison. Comput. Methods Appl. Mech. Eng. 2012, 10, 237–240. [Google Scholar] [CrossRef] [Green Version]
- Muralidhar, N.K.B.; Rauter, N.; Mikhaylenko, A.; Lammering, R.; Lorenz, D.A. Parametric model order reduction of guided ultrasonic wave propagation in fiber metal laminates with damage. Modelling 2021, 2, 591–608. [Google Scholar] [CrossRef]
- Mezic, I. Spectral properties of dynamical systems, model reduction and decompositions. Nonlinear Dyn. 2005, 41, 309–325. [Google Scholar] [CrossRef]
- Rowley, C.W.; Mezic, I.; Bagheri, S.; Schlatter, P.; Henningson, D.S. Reduced-order models for flow control: Balanced models and Koopman modes. In Proceedings of the Seventh IUTAM Symposium on Laminar-Turbulent Transition, IUTAM Bookseries. Stockholm, Sweden, 1 December 2009; Volume 18, pp. 43–50. [Google Scholar]
- Bagheri, S. Koopman-mode decomposition of the cylinder wake. J. Fluid Mech. 2013, 726, 596–623. [Google Scholar] [CrossRef]
- Schmid, P.J.; Violato, D.; Scarano, F. Decomposition of Time-Resolved Tomographic PIV; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Frederich, O.; Luchtenburg, D.M. Modal analysis of complex turbulent flow. In Proceedings of the The 7th International Symposium on Turbulence and Shear Flow Phenomena (TSFP-7), Ottawa, ON, Canada, 28–31 July 2011. [Google Scholar]
- Bistrian, D.A.; Navon, I.M. The method of dynamic mode decomposition in shallow water and a swirling flow problem. Int. J. Numer. Methods Fluids 2017, 83, 73–89. [Google Scholar] [CrossRef]
- Mezic, I. Koopman operator, geometry, and learning. arXiv 2020, arXiv:2010.05377. [Google Scholar]
- Chen, W.S. Use of recurrence plot and recurrence quantification analysis in Taiwan unemployment rate time series. Phys. A Stat. Mech. Its Appl. 2011, 390, 1332–1342. [Google Scholar] [CrossRef]
- Bistrian, D.A.; Navon, I.M. An improved algorithm for the shallow water equations model reduction: Dynamic Mode Decomposition vs POD. Int. J. Numer. Methods Fluids 2015, 78, 552–580. [Google Scholar] [CrossRef]
- Koopman, B. Hamiltonian systems and transformations in Hilbert space. Proc. Nat. Acad. Sci. USA 1931, 17, 315–318. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schmid, P.J.; Sesterhenn, J. Dynamic mode decomposition of numerical and experimental data. In Proceedings of the 61st Annual Meeting of the APS Division of Fluid Dynamics, San Antonio, TX, USA, 23–25 November 2008; Volume 53. [Google Scholar]
- Chen, K.K.; Tu, J.H.; Rowley, C.W. Variants of dynamic mode decomposition: Boundary condition, Koopman and Fourier analyses. Nonlinear Sci. 2012, 22, 887–915. [Google Scholar] [CrossRef]
- Tu, J.H.; Rowley, C.W.; Luchtenburg, D.M.; Brunton, S.L.; Kutz, J.N. On dynamic mode decomposition: Theory and applications. J. Comput. Dyn. 2014, 1, 391–421. [Google Scholar] [CrossRef] [Green Version]
- Jovanovic, M.R.; Schmid, P.J.; Nichols, J.W. Low-rank and sparse dynamic mode decomposition. Cent. Turbul. Res. Annu. Res. Briefs 2012, 2012, 139–152. [Google Scholar]
- Kutz, J.N.; Fu, X.; Brunton, S.L. Multiresolution dynamic mode decomposition. SIAM J. Appl. Dyn. Syst. 2016, 15, 713–735. [Google Scholar] [CrossRef] [Green Version]
- Kutz, J.; Sashidhar, D.; Sahba, S.; Brunton, S.; McDaniel, A.; Wilcox, C. Physics-informed machine-learning for modeling aero-optics. Int. Conf. Appl. Opt. Metrol. IV 2021, 11817, 70–77. [Google Scholar]
- Williams, M.O.; Kevrekidis, I.G.; Rowley, C.W. A data driven approximation of the Koopman operator: Extending Dynamic Mode Decomposition. Nonlinear Sci. 2015, 25, 1307–1346. [Google Scholar] [CrossRef] [Green Version]
- Noack, B.R.; Stankiewicz, W.; Morzynski, M.; Schmid, P. Recursive dynamic mode decomposition of transient and post-transient wake flows. J. Fluid Mech. 2016, 809, 843–872. [Google Scholar] [CrossRef] [Green Version]
- Proctor, J.L.; Brunton, S.L.; Kutz, J.N. Dynamic mode decomposition with control. SIAM J. Appl. Dyn. Syst. 2016, 15, 142–161. [Google Scholar] [CrossRef] [Green Version]
- Alla, A.; Kutz, J.N. Nonlinear model order reduction via dynamic mode decomposition. SIAM J. Sci. Comput. 2017, 39, B778–B796. [Google Scholar] [CrossRef]
- Erichson, N.B.; Donovan, C. Randomized low-rank Dynamic Mode Decomposition for motion detection. Comput. Vis. Image Underst. 2016, 146, 40–50. [Google Scholar] [CrossRef] [Green Version]
- Bistrian, D.A.; Navon, I.M. Randomized dynamic mode decomposition for nonintrusive reduced order modelling. Int. J. Numer. Methods Eng. 2017, 112, 3–25. [Google Scholar] [CrossRef] [Green Version]
- Bistrian, D.A.; Navon, I.M. Efficiency of randomised dynamic mode decomposition for reduced order modelling. Int. J. Comput. Fluid Dyn. 2018, 32, 88–103. [Google Scholar] [CrossRef]
- Le Clainche, S.; Vega, J.M. Higher Order Dynamic Mode Decomposition. SIAM J. Appl. Dyn. Syst. 2017, 16, 882–925. [Google Scholar] [CrossRef] [Green Version]
- Goldschmidt, A.; Kaiser, E.; Dubois, J.; Brunton, S.; Kutz, J. Bilinear dynamic mode decomposition for quantum control. New J. Phys. 2021, 23, 033035. [Google Scholar] [CrossRef]
- Ahmed, S.E.; Dabaghian, P.H.; San, O.; Bistrian, D.A.; Navon, I.M. Dynamic mode decomposition with core sketch. Phys. Fluids 2022, 34, 066603. [Google Scholar] [CrossRef]
- Mezic, I. On Numerical Approximations of the Koopman Operator. Mathematics 2022, 10, 1180. [Google Scholar] [CrossRef]
- Champion, K.P.; Brunton, S.L.; Kutz, J.N. Discovery of nonlinear multiscale systems: Sampling strategies and embeddings. SIAM J. Appl. Dyn. Syst. 2019, 18, 312–333. [Google Scholar] [CrossRef] [Green Version]
- Mauroy, A.; Sootla, A.; Mezic, I. The Koopman Operator in Systems and Control: Theory, Numerics, and Applications; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Ahmed, S.E.; San, O.; Bistrian, D.A.; Navon, I.M. Sampling and resolution characteristics in reduced order models of shallow water equations: Intrusive vs nonintrusive. Int. J. Numer. Methods Fluids 2020, 92, 992–1036. [Google Scholar] [CrossRef] [Green Version]
- Iliescu, T. ROM Closures and Stabilizations for Under-Resolved Turbulent Flows. In Proceedings of the 2022 Spring Central Sectional Meeting, West Lafayette, IN, USA, 26–27 March 2022. [Google Scholar]
- Cordier, L.; Majd, B.A.E.; Favier, J. Calibration of POD reduced-order models using Tikhonov regularization. Int. J. Numer. Methods Fluids 2010, 63, 269–296. [Google Scholar] [CrossRef] [Green Version]
- San, O.; Iliescu, T. A stabilized proper orthogonal decomposition reduced-order model for large scale quasigeostrophic ocean circulation. Adv. Comput. Math. 2015, 41, 1289–1319. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Navon, I.; Cheng, X.W.Y. 2d Burgers equations with large Reynolds number using POD/DEIM and calibration. Int. J. Numer. Methods Fluids 2016, 82, 909–931. [Google Scholar] [CrossRef]
- Burgers, J.M. A mathematical model illustrating the theory of turbulence. Adv. Appl. Mech. 1948, 1, 171–199. [Google Scholar]
- Cuesta, C.M.; Pop, I. Numerical schemes for a pseudo-parabolic Burgers equation: Discontinuous data and long-time behaviour. J. Comput. Appl. Math. 2009, 224, 269–283. [Google Scholar] [CrossRef] [Green Version]
- Kutz, J.N.; Proctor, J.L.; Brunton, S.L. Koopman theory for partial differential equations. arXiv 2016, arXiv:1607.07076. [Google Scholar]
- Golub, G.; van Loan, C.F. Matrix Computations, 3rd ed.; The Johns Hopkins University Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Schmid, P. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef] [Green Version]
- Chopra, A.K. Dynamics of Structures, 4th ed.; International Series in Civil Engineering and Engineering Mechanics; Prentice-Hall: Hoboken, NJ, USA, 2000. [Google Scholar]
- Noack, B.R.; Morzynski, M.; Tadmor, G. Reduced-Order Modelling for Flow Control; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Tissot, G.; Cordier, L.; Benard, N.; Noack, B.R. Model reduction using Dynamic Mode Decomposition. Comptes Rendus Mec. 2014, 342, 410–416. [Google Scholar] [CrossRef]
- Alekseev, A.K.; Bistrian, D.A.; Bondarev, A.E.; Navon, I.M. On linear and nonlinear aspects of dynamic mode decomposition. Int. J. Numer. Methods Fluids 2016, 82, 348–371. [Google Scholar] [CrossRef]
- Bistrian, D.A.; Dimitriu, G.; Navon, I.M. Processing epidemiological data using dynamic mode decomposition method. AIP Conf. Proc. 2019, 2164, 080002. [Google Scholar]
- Bistrian, D.A.; Dimitriu, G.; Navon, I.M. Modeling dynamic patterns from COVID-19 data using randomized dynamic mode decomposition in predictive mode and ARIMA. AIP Conf. Proc. 2020, 2302, 080002. [Google Scholar]
- Brunton, S.; Kutz, J. Data-Driven Science and Engineering: Machine Learning, Dynamical Systems and Control; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Kaptanoglu, A.; Callaham, J.; Hansen, C.; Brunton, S. Machine Learning to Discover Interpretable Models in Fluids and Plasmas. In Proceedings of the Bulletin of the American Physical Society APS March Meeting 2022, Chicago, IL, USA, 14–18 March 2022. [Google Scholar]
- Li, S.; Kaiser, E.; Laima, S.; Li, H.; Brunton, S.; Kutz, J. Discovering time-varying aerodynamics of a prototype bridge by sparse identification of nonlinear dynamical systems. Phys. Rev. E 2019, 100, 022220. [Google Scholar] [CrossRef]
- Nelles, O. Nonlinear System Identification: From Classical Approaches to Neural Networks and Fuzzy Models; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Pant, P.; Doshi, R.; Bahl, P.; Farimani, A.B. Deep learning for reduced order modelling and efficient temporal evolution of fluid simulations. Phys. Fluids 2021, 33, 107101. [Google Scholar] [CrossRef]
- Percic, M.; Zelenika, S.; Mezic, I. Artificial intelligence-based predictive model of nanoscale friction using experimental data. Friction 2021, 9, 1726–1748. [Google Scholar] [CrossRef]
- Peng, H.; Ozaki, T.; Haggan-Ozaki, V.; Toyoda, Y. Structured parameter optimization method for the radial basis function-based state-dependent autoregressive model. Int. J. Syst. Sci. 2002, 33, 1087–1098. [Google Scholar] [CrossRef]
- Wang, Z.; Xiao, D.; Fang, F.; Govindan, R.; Pain, C.; Guo, Y. Model identification of reduced order fluid dynamics systems using deep learning. Int. J. Numer. Methods Fluids 2018, 86, 255–268. [Google Scholar] [CrossRef] [Green Version]
- Sierra, C.; Metzler, H.; Muller, M.; Kaiser, E. Closed-loop and congestion control of the global carbon-climate system. Clim. Change 2021, 165, 1–24. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Yang, X.S. Engineering Optimization: An Introduction with Metaheuristic Applications; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]









| Test Case | Model Rank | Error | Correlation Coefficient |
|---|---|---|---|
| Index | Outputs, Inputs, Delay | DTM Error and Correlation Coefficient |
|---|---|---|
| 3–12, 14 | ||
| Index | Outputs, Inputs, Delay | DTM Error and Correlation Coefficient |
|---|---|---|
| 10–12 | ||
| j = 5–9 | ||
| j = 14–19 | ||
| Index | Outputs, Inputs, Delay | DTM Error and Correlation Coefficient |
|---|---|---|
| 16–20 | ||
| 9–15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bistrian, D.A. High-Fidelity Digital Twin Data Models by Randomized Dynamic Mode Decomposition and Deep Learning with Applications in Fluid Dynamics. Modelling 2022, 3, 314-332. https://doi.org/10.3390/modelling3030020
Bistrian DA. High-Fidelity Digital Twin Data Models by Randomized Dynamic Mode Decomposition and Deep Learning with Applications in Fluid Dynamics. Modelling. 2022; 3(3):314-332. https://doi.org/10.3390/modelling3030020
Chicago/Turabian StyleBistrian, Diana A. 2022. "High-Fidelity Digital Twin Data Models by Randomized Dynamic Mode Decomposition and Deep Learning with Applications in Fluid Dynamics" Modelling 3, no. 3: 314-332. https://doi.org/10.3390/modelling3030020
APA StyleBistrian, D. A. (2022). High-Fidelity Digital Twin Data Models by Randomized Dynamic Mode Decomposition and Deep Learning with Applications in Fluid Dynamics. Modelling, 3(3), 314-332. https://doi.org/10.3390/modelling3030020






