Molecular Dynamics-Based Two-Dimensional Simulation of Powder Bed Additive Manufacturing Process for Unimodal and Bimodal Systems
Abstract
:1. Introduction
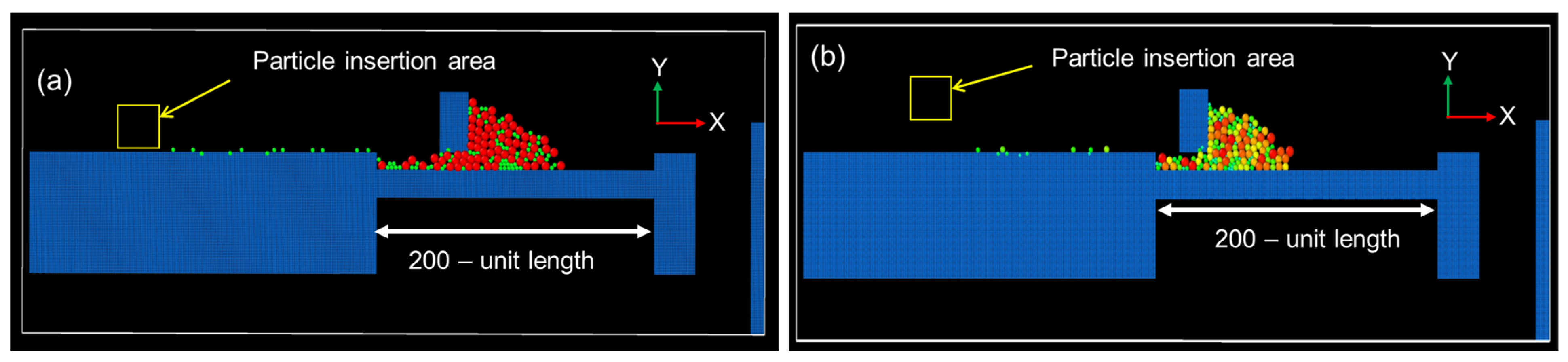
2. Methodology and Simulation Setup
- overlap distance between two particles;
- elastic constant for normal contact;
- elastic constant for tangential contact;
- radius of two different particles;
- viscoelastic damping constant for normal contact;
- viscoelastic damping constant for tangential contact;
- normal component of the relative velocity of two particles;
- tangential component of the relative velocity of two particles;
- tangential displacement vector between two particles;
- effective mass of two particles with and mass;
- unit vector that connects the centerline of two particles.
3. Simulation Results and Discussion
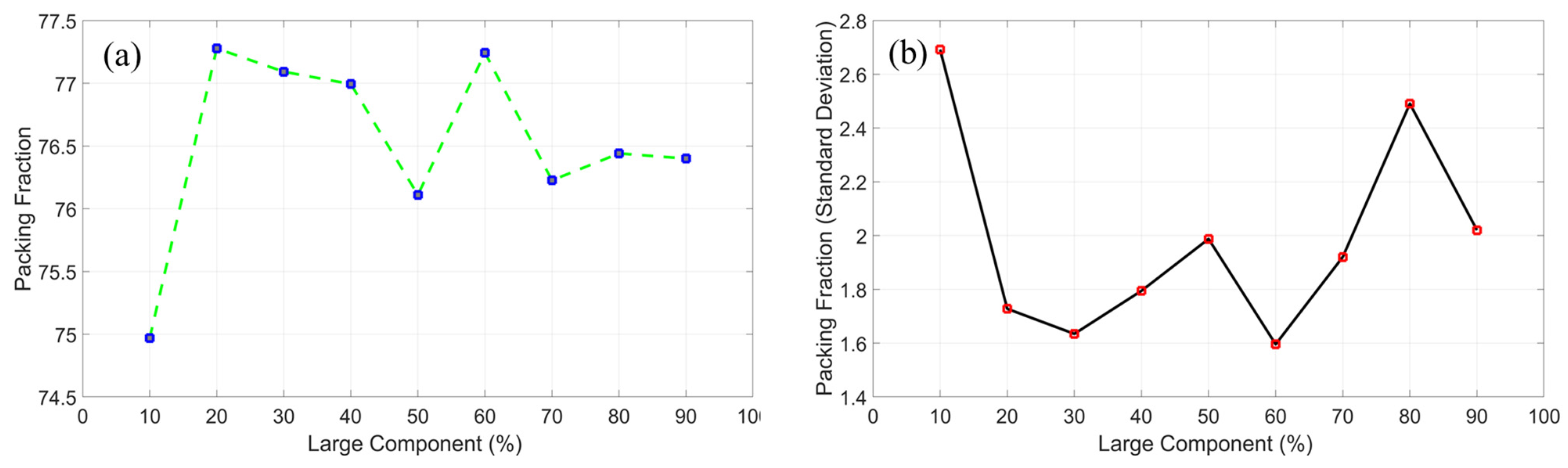
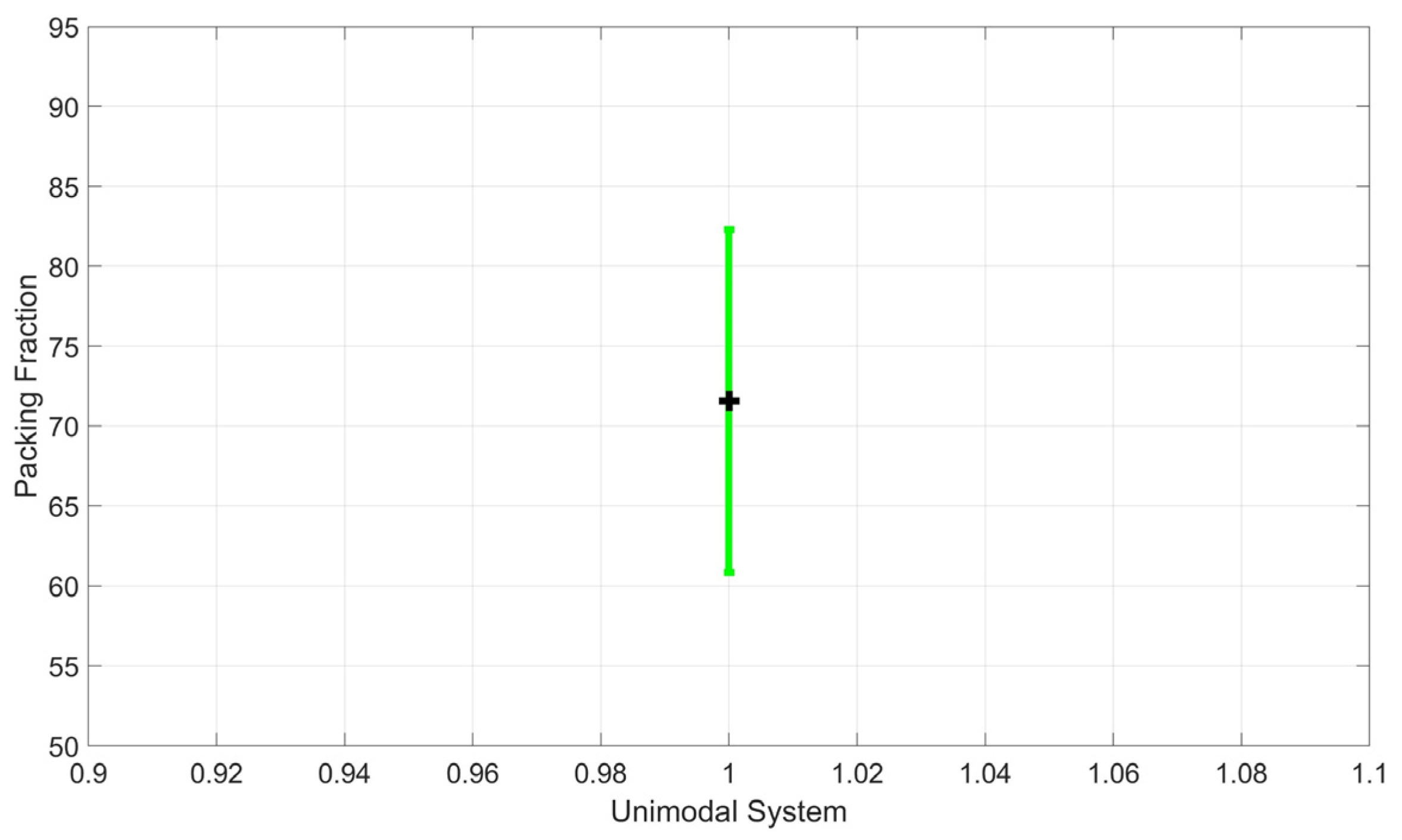
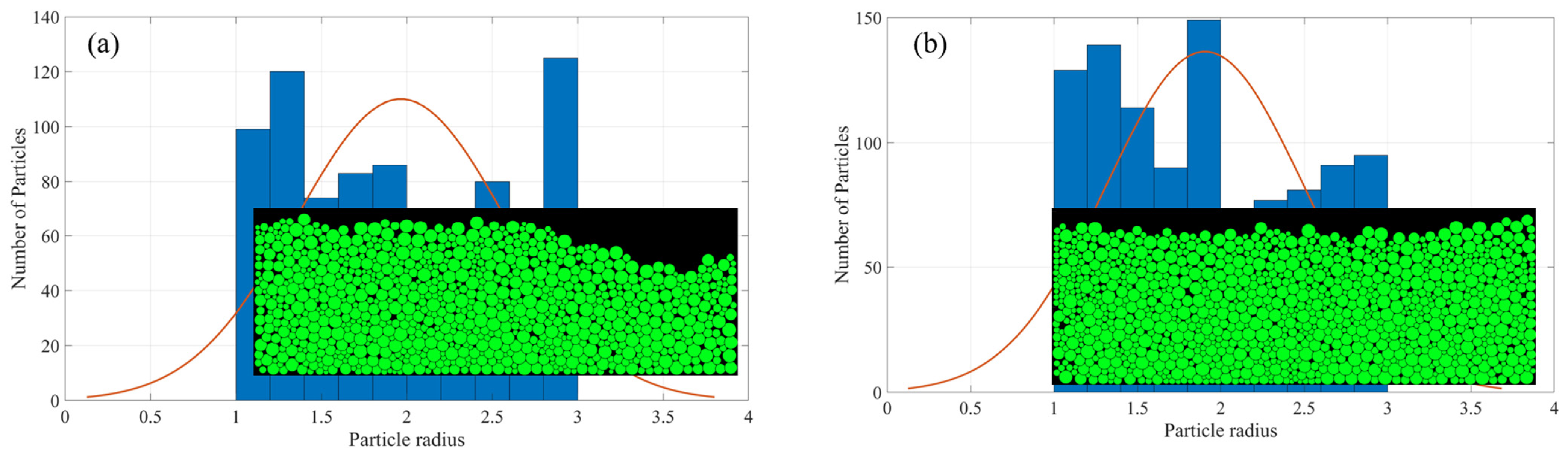
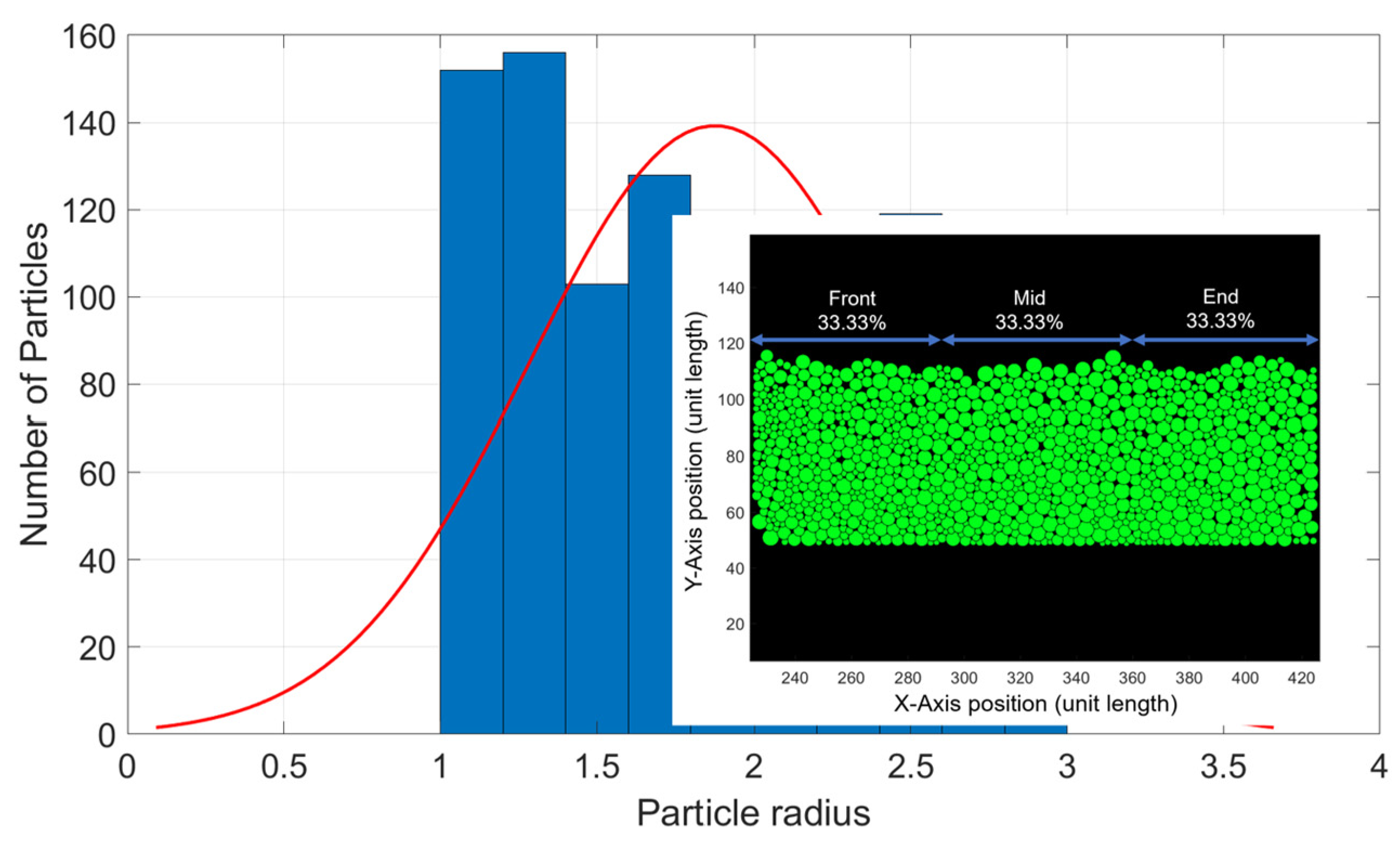
3.1. Packing Density
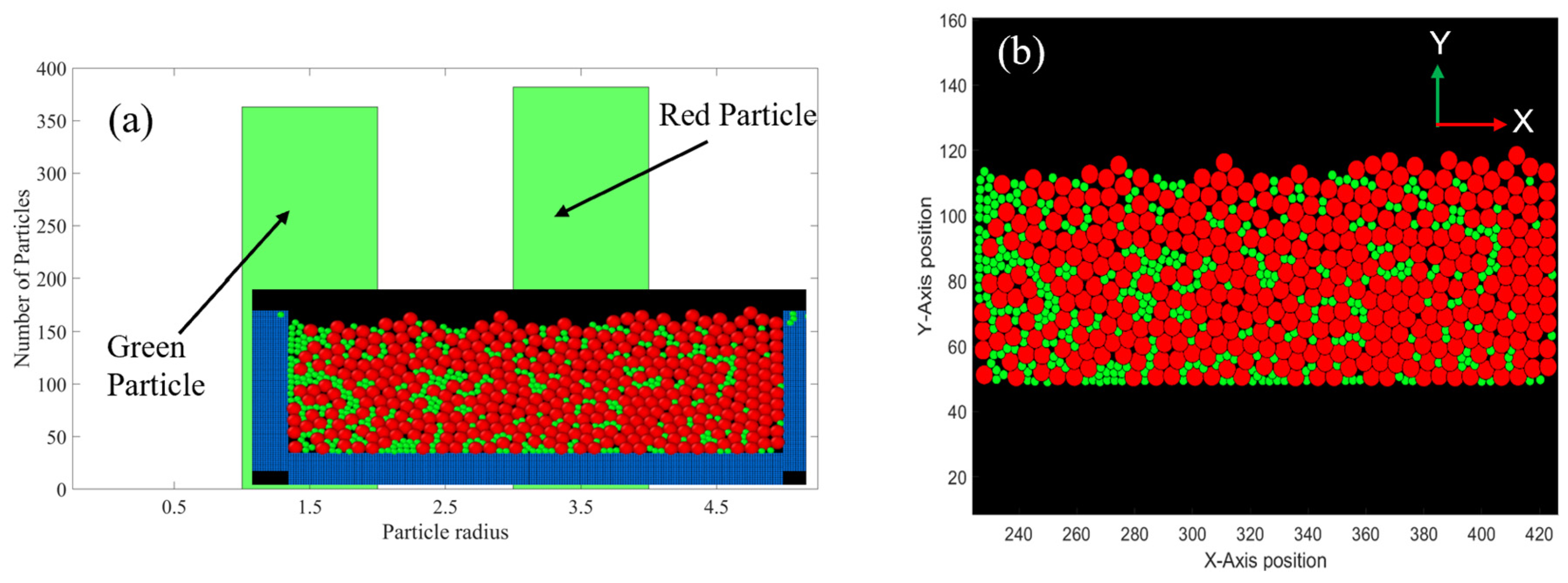
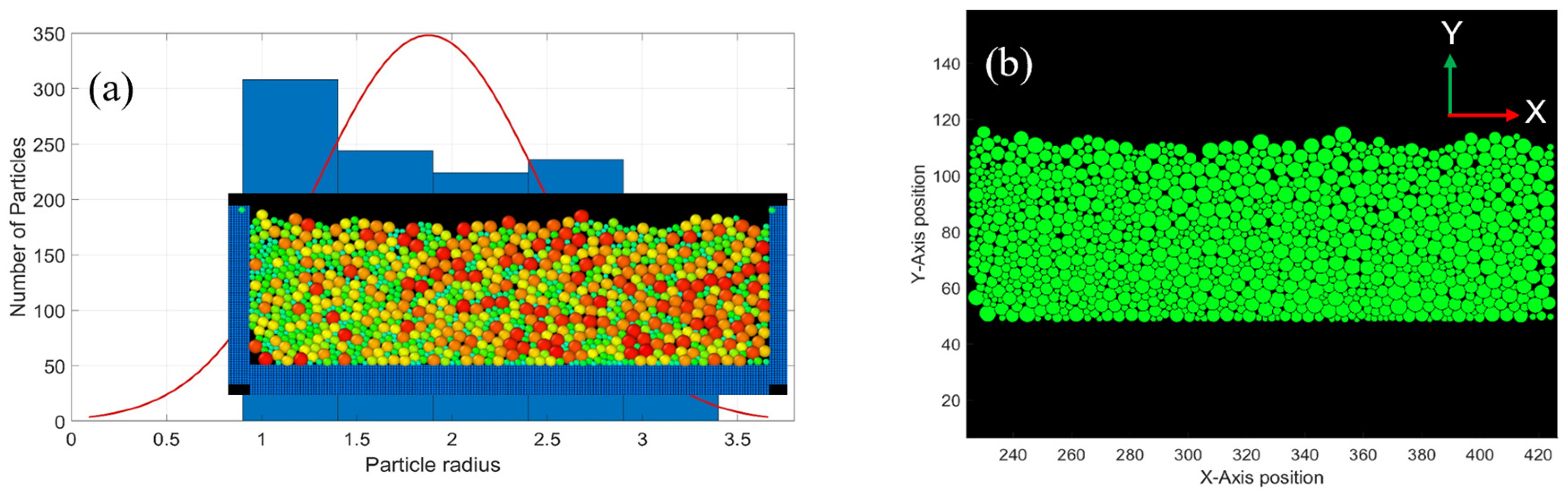
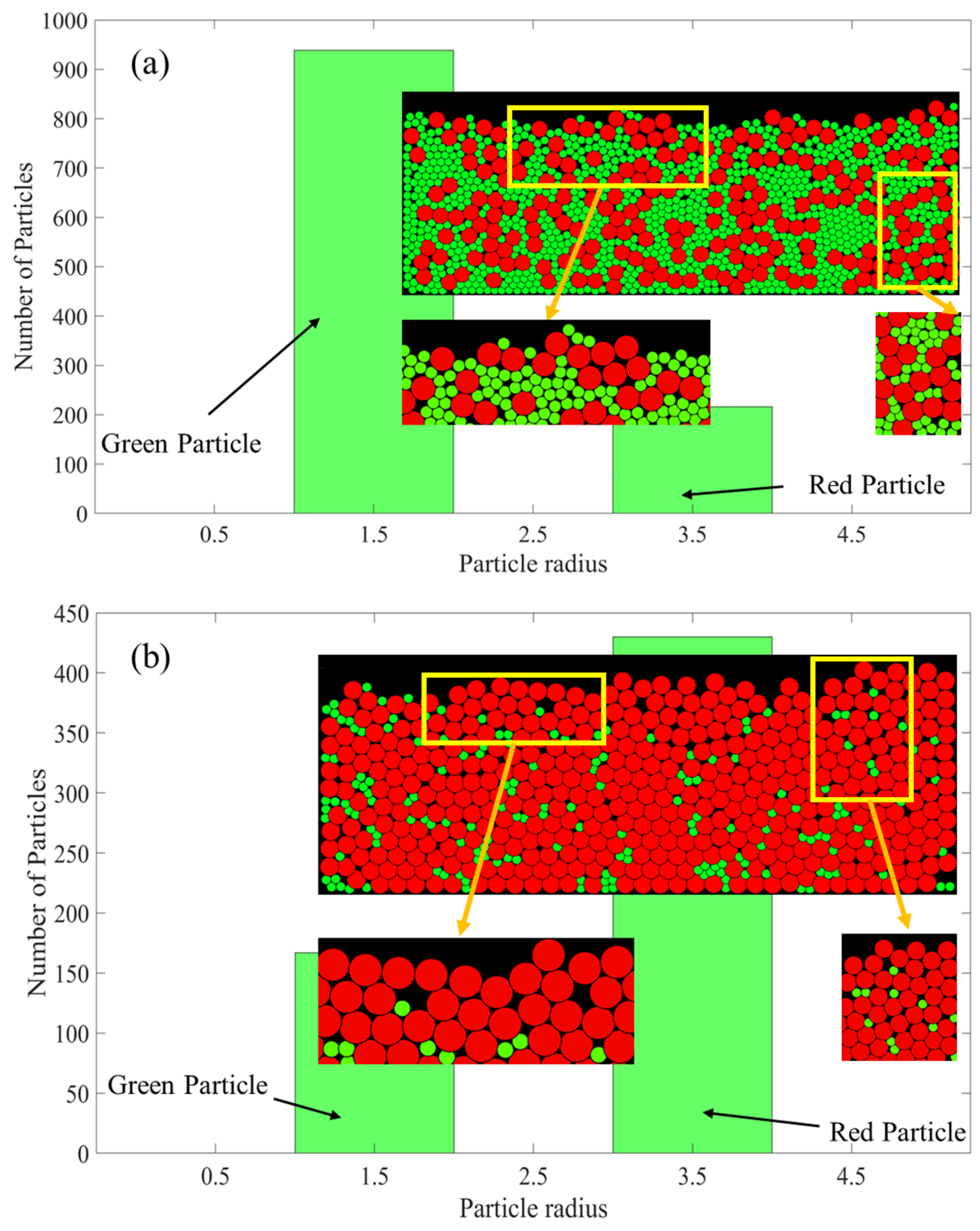
3.2. Powder Segregation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Buchbinder, D.; Schleifenbaum, H.; Heidrich, S.; Meiners, W.; Bültmann, J. High Power Selective Laser Melting (HP SLM) of Aluminum Parts. Phys. Procedia 2011, 12, 271–278. [Google Scholar] [CrossRef]
- Santos, E.C.; Shiomi, M.; Osakada, K.; Laoui, T. Rapid manufacturing of metal components by laser forming. Int. J. Mach. Tools Manuf. 2006, 46, 1459–1468. [Google Scholar] [CrossRef]
- Young, Z.; Qu, M.; Coday, M.M.; Guo, Q.; Hojjatzadeh, S.M.H.; Escano, L.I.; Fezzaa, K.; Chen, L. Effects of particle size distribution with efficient packing on powder flowability and selective laser melting process. Materials 2022, 15, 705. [Google Scholar] [CrossRef] [PubMed]
- Gibson, I.; Rosen, D.W.; Stucker, B.; Khorasani, M.; Rosen, D.; Stucker, B.; Khorasani, M. Additive Manufacturing Technologies; Springer: Cham, Switzerland, 2021; Volume 17. [Google Scholar]
- Gregorski, S.J. High Green Density Metal Parts by Vibrational Compaction of Dry Powder in the Three-Dimensional Printing Process. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2003. [Google Scholar]
- Gu, D.; Shen, Y. Balling phenomena in direct laser sintering of stainless steel powder: Metallurgical mechanisms and control methods. Mater. Des. 2009, 30, 2903–2910. [Google Scholar] [CrossRef]
- Qiu, Y.-D.; Wu, J.-M.; Chen, A.-N.; Chen, P.; Yang, Y.; Liu, R.-Z.; Chen, G.; Chen, S.; Shi, Y.-S.; Li, C.-H. Balling phenomenon and cracks in alumina ceramics prepared by direct selective laser melting assisted with pressure treatment. Ceram. Int. 2020, 46, 13854–13861. [Google Scholar] [CrossRef]
- Xiang, Z.; Yin, M.; Deng, Z.; Mei, X.; Yin, G. Simulation of forming process of powder bed for additive manufacturing. J. Manuf. Sci. Eng. 2016, 138, 081002. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, Y.; Chen, J.K. Numerical simulation of random packing of spherical particles for powder-based additive manufacturing. J. Manuf. Sci. Eng. 2009, 131, 031004. [Google Scholar] [CrossRef]
- Coe, H.G.; Pasebani, S. Use of bimodal particle size distribution in selective laser melting of 316L stainless steel. J. Manuf. Mater. Process. 2020, 4, 8. [Google Scholar] [CrossRef]
- Vermeer, P.A.; Diebels, S.; Ehlers, W.; Herrmann, H.J.; Luding, S.; Ramm, E. Continuous and Discontinuous Modelling of Cohesive-Frictional Materials; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001; Volume 568. [Google Scholar]
- Cheung, S.L.; Chua, C.K.; Zhou, K.; Wei, J. Effects of temperature on particle coalescence in the selective laser sintering process. In Proceedings of the 1st International Conference on Progress in Additive Manufacturing (Pro-AM 2014), Singapore, 26–28 May 2014. [Google Scholar]
- Herrmann, H.J. Molecular dynamics simulations of granular materials. Int. J. Mod. Phys. C 1993, 4, 309–316. [Google Scholar] [CrossRef]
- Li, S.; Yao, Q.; Chen, B.; Zhang, X.; Ding, Y. Molecular dynamics simulation and continuum modelling of granular surface flow in rotating drums. Chin. Sci. Bull. 2007, 52, 692–700. [Google Scholar] [CrossRef]
- Averardi, A.; Cola, C.; Zeltmann, S.E.; Gupta, N. Effect of particle size distribution on the packing of powder beds: A critical discussion relevant to additive manufacturing. Mater. Today Commun. 2020, 24, 100964. [Google Scholar] [CrossRef]
- Cao, L. Numerical simulation of the impact of laying powder on selective laser melting single-pass formation. Int. J. Heat Mass Transf. 2019, 141, 1036–1048. [Google Scholar] [CrossRef]
- Fouda, Y.M.; Bayly, A.E. A DEM study of powder spreading in additive layer manufacturing. Granul. Matter 2019, 22, 10. [Google Scholar] [CrossRef]
- Lee, Y.S.; Nandwana, P.; Zhang, W. Dynamic simulation of powder packing structure for powder bed additive manufacturing. Int. J. Adv. Manuf. Technol. 2018, 96, 1507–1520. [Google Scholar] [CrossRef]
- Ganeriwala, R.; Zohdi, T.I. A coupled discrete element-finite difference model of selective laser sintering. Granul. Matter 2016, 18, 21. [Google Scholar] [CrossRef]
- Markl, M.; Körner, C. Powder layer deposition algorithm for additive manufacturing simulations. Powder Technol. 2018, 330, 125–136. [Google Scholar] [CrossRef]
- Farzadfar, S.A.; Murtagh, M.J.; Venugopal, N. Impact of IN718 bimodal powder size distribution on the performance and productivity of laser powder bed fusion additive manufacturing process. Powder Technol. 2020, 375, 60–80. [Google Scholar] [CrossRef]
- Yang, W.; Cai, Z.; Duan, W.; Deng, X.; Lin, T.; Chen, Z.; Xie, F.; Liu, J.; Qu, Z.; Jin, F. Effect of feedstock bimodal powder design and cold isostatic pressing on the mechanical behavior of binder jetting additive manufactured Inconel 718 superalloy. J. Manuf. Process. 2025, 133, 607–622. [Google Scholar] [CrossRef]
- Clares, A.P.; Gao, Y.; Stebbins, R.; van Duin, A.C.; Manogharan, G. Increasing density and mechanical performance of binder jetting processing through bimodal particle size distribution. Mater. Sci. Addit. Manuf. 2022, 1, 20. [Google Scholar] [CrossRef]
- LAMMPS. Granular Pouring and Chute Flow. Available online: https://www.lammps.org/movies.html (accessed on 7 January 2024).
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D. LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Du, W.; Roa, J.; Hong, J.; Liu, Y.; Pei, Z.; Ma, C. Binder jetting additive manufacturing: Effect of particle size distribution on density. J. Manuf. Sci. Eng. 2021, 143, 091002. [Google Scholar] [CrossRef]
- Farr, R.S.; Groot, R.D. Close packing density of polydisperse hard spheres. J. Chem. Phys. 2009, 131, 244104. [Google Scholar] [CrossRef] [PubMed]
- Brilliantov, N.V.; Spahn, F.; Hertzsch, J.-M.; Pöschel, T. Model for collisions in granular gases. Phys. Rev. E 1996, 53, 5382. [Google Scholar] [CrossRef] [PubMed]
- Silbert, L.E.; Ertaş, D.; Grest, G.S.; Halsey, T.C.; Levine, D.; Plimpton, S.J. Granular flow down an inclined plane: Bagnold scaling and rheology. Phys. Rev. E 2001, 64, 051302. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.P.; Makse, H.A. Jamming transition in emulsions and granular materials. Phys. Rev. E 2005, 72, 011301. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Stovall, T.; De Larrard, F.; Buil, M. Linear packing density model of grain mixtures. Powder Technol. 1986, 48, 1–12. [Google Scholar] [CrossRef]
- Chu, F.; Zhang, K.; Shen, H.; Liu, M.; Huang, W.; Zhang, X.; Liang, E.; Zhou, Z.; Lei, L.; Hou, J. Influence of satellite and agglomeration of powder on the processability of AlSi10Mg powder in Laser Powder Bed Fusion. J. Mater. Res. Technol. 2021, 11, 2059–2073. [Google Scholar] [CrossRef]
- Liu, M.; Chiu, L.N.S.; Shen, H.; Fang, X.; Tao, Z.; Huang, A.; Davies, C.; Wu, X.; Yan, W. Effective thermal conductivities of metal powders for additive manufacturing. Powder Technol. 2022, 401, 117323. [Google Scholar] [CrossRef]
- Desmond, K.W.; Weeks, E.R. Random close packing of disks and spheres in confined geometries. Phys. Rev. E 2009, 80, 051305. [Google Scholar] [CrossRef]
- Tang, P.; Puri, V.M. Methods for minimizing segregation: A review. Part. Sci. Technol. 2004, 22, 321–337. [Google Scholar] [CrossRef]
- Nan, W.; Pasha, M.; Ghadiri, M. Numerical simulation of particle flow and segregation during roller spreading process in additive manufacturing. Powder Technol. 2020, 364, 811–821. [Google Scholar] [CrossRef]
- Arntz, M.; Beeftink, H.H.; den Otter, W.K.; Briels, W.J.; Boom, R.M. Segregation of granular particles by mass, radius, and density in a horizontal rotating drum. AIChE J. 2014, 60, 50–59. [Google Scholar] [CrossRef]
- Jha, A.K.; Puri, V.M. Percolation segregation of multi-size and multi-component particulate materials. Powder Technol. 2010, 197, 274–282. [Google Scholar] [CrossRef]
- Mindt, H.; Megahed, M.; Lavery, N.; Holmes, M.; Brown, S. Powder bed layer characteristics: The overseen first-order process input. Metall. Mater. Trans. A 2016, 47, 3811–3822. [Google Scholar] [CrossRef]
- Whiting, J.; Fox, J. Characterization of Feedstock in the Powder Bed Fusion Process: Sources of Variation in Particle Size Distribution and the Factors That Influence Them; The University of Texas at Austin: Austin, TX, USA, 2016. [Google Scholar]
- Tennakoon, S.; Kondic, L.; Behringer, R. Onset of flow in a horizontally vibrated granular bed: Convection by horizontal shearing. Europhys. Lett. 1999, 45, 470. [Google Scholar] [CrossRef]
- Haferkamp, L.; Liechti, S.; Spierings, A.; Wegener, K. Effect of bimodal powder blends on part density and melt pool fluctuation in laser powder bed fusion. Prog. Addit. Manuf. 2021, 6, 407–416. [Google Scholar] [CrossRef]
- Priyadarshi, A.; Shahrani, S.B.; Choma, T.; Zrodowski, L.; Qin, L.; Leung, C.L.A.; Clark, S.J.; Fezzaa, K.; Mi, J.; Lee, P.D. New insights into the mechanism of ultrasonic atomization for the production of metal powders in additive manufacturing. Addit. Manuf. 2024, 83, 104033. [Google Scholar] [CrossRef]



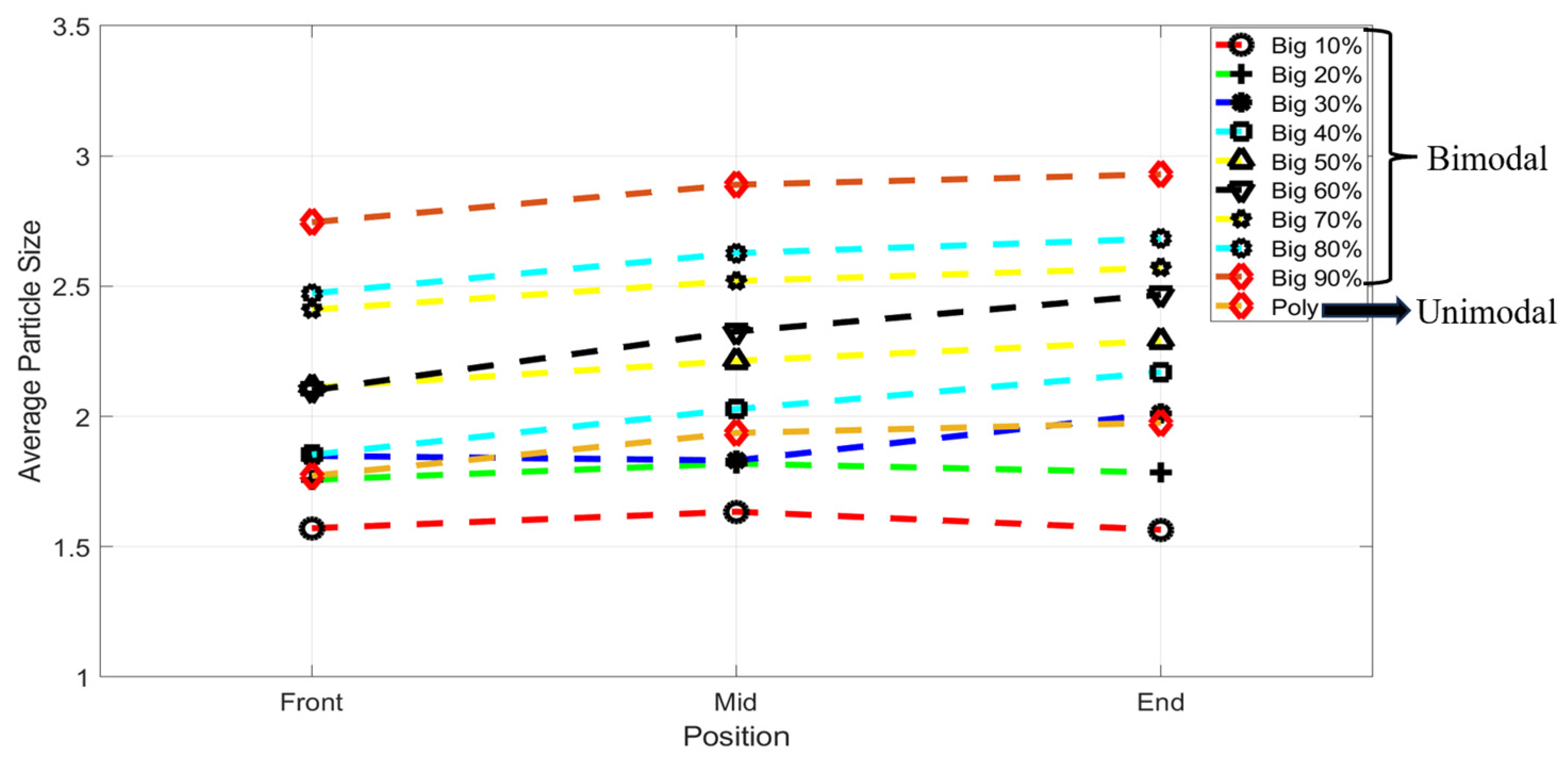
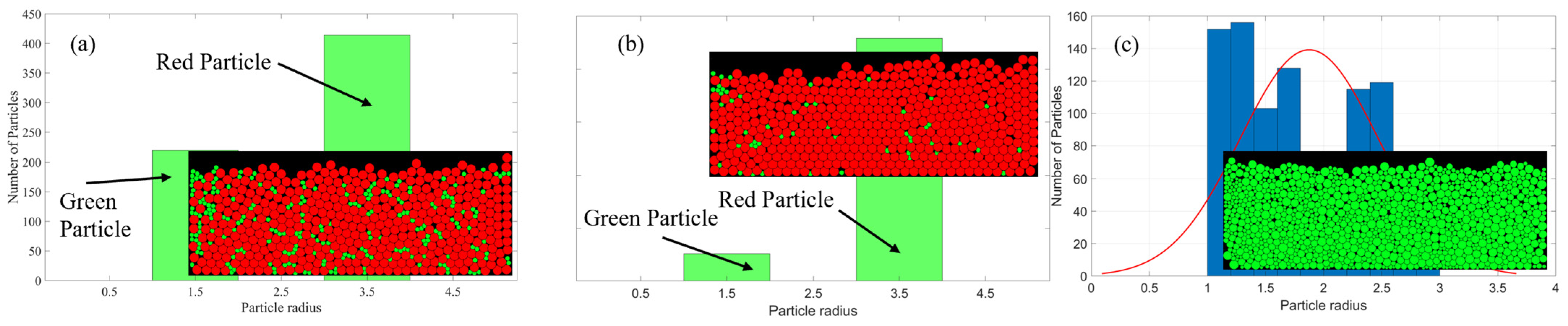
| Distribution | |||||
|---|---|---|---|---|---|
| Bimodal | |||||
| Unimodal |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akib, Y.M.; Marzbanrad, E.; Ahmed, F. Molecular Dynamics-Based Two-Dimensional Simulation of Powder Bed Additive Manufacturing Process for Unimodal and Bimodal Systems. J. Manuf. Mater. Process. 2025, 9, 9. https://doi.org/10.3390/jmmp9010009
Akib YM, Marzbanrad E, Ahmed F. Molecular Dynamics-Based Two-Dimensional Simulation of Powder Bed Additive Manufacturing Process for Unimodal and Bimodal Systems. Journal of Manufacturing and Materials Processing. 2025; 9(1):9. https://doi.org/10.3390/jmmp9010009
Chicago/Turabian StyleAkib, Yeasir Mohammad, Ehsan Marzbanrad, and Farid Ahmed. 2025. "Molecular Dynamics-Based Two-Dimensional Simulation of Powder Bed Additive Manufacturing Process for Unimodal and Bimodal Systems" Journal of Manufacturing and Materials Processing 9, no. 1: 9. https://doi.org/10.3390/jmmp9010009
APA StyleAkib, Y. M., Marzbanrad, E., & Ahmed, F. (2025). Molecular Dynamics-Based Two-Dimensional Simulation of Powder Bed Additive Manufacturing Process for Unimodal and Bimodal Systems. Journal of Manufacturing and Materials Processing, 9(1), 9. https://doi.org/10.3390/jmmp9010009







