Optimum Thickness of Thermal Insulation with Both Economic and Ecological Costs of Heating and Cooling
Abstract
1. Introduction
2. Literature Review
3. Optimum Insulation Thicknesses
3.1. Thermal Insulation Thickness, Optimum for Economic Reasons
- KOH—cost of heat generation for a given heat source (PLN/Wh);
- KOC—cost of producing coolness (PLN/Wh);
- c—24 (h/day);
- HDD—number of degree days of the heating period (K·day/year);
- CDD—number of degree days of the cooling period (K·day/year);
- d—thickness of the thermal insulation layer (m);
- Km—cost of 1 m3 of the thermal insulation material (PLN/m3);
- Kw—costs of performing thermal insulation of the 1 m2 building wall surface (PLN/m2);
- —cumulative discount factor;
- N—number of years of thermal insulation use;
- r—real annual interest rate;
- s—real annual growth (in percentage) of heating costs;
- λ—thermal conductivity of the thermal insulation material (W/mK);
- U0—heat transfer coefficient of the wall without the thermal insulation layer (W/m2K).
3.2. Optimum Thickness of Thermal Insulation for Ecological Reasons
- KEH—LCA analysis result of obtaining 1 Wh of useful thermal energy for a given heat source (Pt/Wh);
- KEC—LCA analysis result of obtaining 1 Wh of useful cooling energy (Pt/Wh);
- other—as defined earlier.
- Kl—LCA analysis result for 1 m3 of the thermal insulation material (Pt/m3);
- other—as defined earlier.
3.3. Optimum Thickness of Thermal Insulation Taking into Account Costs Both Economically and Ecologically
3.4. The Use of LCA for Ecological Assessment
4. Economic and Ecological Analysis for the Climatic Conditions in Poland
4.1. Description of Variants Accepted for Analysis
4.2. Optimum Thickness of Thermal Insulation for Economic Reasons
4.3. Optimum Thickness of Thermal Insulation for Ecological Reasons
4.4. Optimum Thickness of Thermal Insulation Taking into Account Costs Both Economically and Ecologically
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Energy Consumption in 2018, Primary and Final Energy Consumption Still 5% and 3% away from 2020 Targets. Available online: https://ec.europa.eu/eurostat/documents/2995521/10341545/8-04022020-BP-EN.pdf/39dcc365-bdaa-e6f6-046d-1b4d241392ad (accessed on 23 February 2021).
- Beretta, G.P. World energy consumption and resources: An outlook for the rest of the century. Int. J. Environ. Technol. Manag. 2007, 7, 99–112. [Google Scholar] [CrossRef]
- Good Practice in Energy Efficiency. For a Sustainable, Safer and More Competitive Europe. Available online: https://ec.europa.eu/energy/sites/ener/files/documents/good_practice_in_ee_-web.pdf (accessed on 23 February 2021).
- Directive 2006/32/EC of the European Parliament and of the Council of 5 April 2006 on Energy End-Use Efficiency and Energy Services and Repealing Council Directive 93/76/EEC. OJ L 114, 27.4.2006. pp. 64–85. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32006L0032&from=EN (accessed on 23 February 2021).
- Tsemekidi Tzeiranaki, S.; Bertoldi, P.; Diluiso, F.; Castellazzi, L.; Economidou, M.; Labanca, N.; Ribeiro Serrenho, T.; Zangheri, P. Analysis of the EU Residential Energy Consumption: Trends and Determinants. Energies 2019, 12, 1065. [Google Scholar] [CrossRef]
- Directive 2012/27/EU of the European Parliament and of the Council of 25 October 2012 on Energy Efficiency, Amending Directives 2009/125/EC and 2010/30/EU and Repealing Directives 2004/8/EC and 2006/32/EC Text with EEA Relevance. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?qid=1399375464230&uri=CELEX:32012L0027 (accessed on 23 February 2021).
- Directive (EU) 2018/2002 of the European Parliament and of the Council of 11 December 2018 Amending Directive 2012/27/EU on Energy Efficiency. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=uriserv%3AOJ.L_.2018.328.01.0210.01.ENG (accessed on 23 February 2021).
- Energy Statistics—An Overview. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php/Energy_statistics_-_an_overview#Final_energy_consumption (accessed on 23 February 2021).
- Directive 2002/91/EC of the European Parliament and of the Council of 16 December 2002 on the Energy Performance of Buildings. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32010L0031&from=PL (accessed on 3 March 2021).
- Fabbri, K.; Tronchin, L.; Tarabusi, V. Real Estate market, energy rating and cost. Reflections about an Italian case study. International Conference on Green Buildings and Sustainable Cities. Procedia Eng. 2011, 21, 303–310. [Google Scholar] [CrossRef]
- Tronchin, L.; Fabbri, K. Energy Performance Certificate of building and confidence interval in assessment: An Italian case study. Energy Policy 2012, 48, 176–184. [Google Scholar] [CrossRef]
- Directive 2010/31/EU of the European Parliament and of the Council of 19 May 2010 on the Energy Performance of Buildings. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=celex%3A32010L0031 (accessed on 3 March 2021).
- Dascalaki, E.G.; Balaras, C.A.; Gaglia, A.G.; Droutsa, K.G.; Kontoyiannidis, S. Energy performance of buildings—EPBD in Greece. Energy Policy 2012, 45, 469–477. [Google Scholar] [CrossRef]
- Gaitani, N.; Casesb, L.; Mastrapostolia, E.; Eliopoulou, E. Paving the way to nearly zero energy schools in Mediterranean region- ZEMedS project. 6th International Building Physics Conference. Energy Procedia 2015, 78, 3348–3353. [Google Scholar] [CrossRef]
- Directive (EU) 2018/844 of the European Parliament and of the Council of 30 May 2018 Amending Directive 2010/31/EU on the Energy Performance of Buildings and Directive 2012/27/EU on Energy Efficiency. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/HTML/?uri=CELEX:32018L0844&from=pl (accessed on 3 March 2021).
- Nematchoua, M.K.; Raminosoa, C.R.R.; Mamiharijaona, R.; René, T.; Orosa, J.A.; Elvis, W.; Meukam, P. Study of the economical and optimum thermal insulation thickness for buildings in a wet and hot tropical climate: Case of Cameroon. Renew. Sustain. Energy Rev. 2015, 50, 1192–1202. [Google Scholar] [CrossRef]
- Nematchouaa, M.K.; Ricciardia, P.; Reiterb, S.; Yvon, A. A comparative study on optimum insulation thickness of walls and energy savings in equatorial and tropical climate. Int. J. Sustain. Built Environ. 2017, 6, 170–182. [Google Scholar] [CrossRef]
- De’ Rossi, F.; Marigliano, M.; Marino, C.; Minichiello, F. A technical and economic analysis on optimal thermal insulation thickness for existing office building in Mediterranean climates. Int. J. Heat Technol. 2016, 34, S561–S568. [Google Scholar] [CrossRef]
- Sahu, D.K.; Sen, P.K.; Sahu, G.; Sharma, R.; Bohidar, S. A Review on Thermal Insulation and Its Optimum Thickness to Reduce Heat Loss. Int. J. Innov. Res. Sci. Technol. 2015, 2, 1–6. Available online: http://www.ijirst.org/articles/IJIRSTV2I6001.pdf (accessed on 23 February 2021).
- Aktemur, C.; Atikol, U. Optimum Insulation Thickness for the Exterior Walls of Buildings in Turkey Based on Different Materials, Energy Sources and Climate Regions. Int. J. Eng. Technol. 2017, 3, 72–82. [Google Scholar] [CrossRef][Green Version]
- Orzechowski, T.; Orzechowski, M. Optimal thickness of various insulation materials for different temperature conditions and heat sources in terms of economic aspect. J. Build. Phys. 2018, 41, 377–393. [Google Scholar] [CrossRef]
- Dylewski, R. Optimal Thermal Insulation Thicknesses of External Walls Based on Economic and Ecological Heating Cost. Energies 2019, 12, 3415. [Google Scholar] [CrossRef]
- Çetintaş, K.F.; Yilmaz, Z. Optimization of thermal insulation material and thickness for building energy efficiency in Mediterranean climates based on life cycle perspective. ITU A/Z 2017, 14, 99–112. [Google Scholar] [CrossRef]
- Yildiz, A.; Gürlek, G.; Erkek, M.; Özbalta, N. Economical and environmental analyses of thermal insulation thickness in buildings. J. Therm. Sci. Technol. 2008, 28, 25–34. [Google Scholar]
- Barrau, J.; Ibanez, M.; Badia, F. Impact of the insulation materials’ features on the determination of optimum insulation thickness. Int. J. Energy Environ. Eng. 2014, 5, 79. [Google Scholar] [CrossRef]
- Kon, O. Determination of optimum insulation thicknesses using economical analyse for exterior walls of buildings with different masses. Int. J. Optim. Control Theor. Appl. 2017, 7, 149–157. [Google Scholar] [CrossRef]
- Hernandez, P.; Kenny, P. From net energy to zero energy buildings: Defining life cycle zero energy buildings (LC-ZEB). Energy Build. 2010, 42, 815–821. [Google Scholar] [CrossRef]
- Hernandez, P.; Kenny, P. Development of a methodology for life cycle building energy ratings. Energy Policy 2011, 39, 3779–3788. [Google Scholar] [CrossRef]
- Dylewski, R.; Adamczyk, J. Impact of the Degree Days of the Heating Period on Economically and Ecologically Optimal Thermal Insulation Thickness. Energies 2021, 14, 97. [Google Scholar] [CrossRef]
- Brás, A.; Gomes, V. LCA implementation in the selection of thermal enhanced mortars for energetic rehabilitation of school buildings. Energy Build. 2015, 92, 1–9. [Google Scholar] [CrossRef]
- Dylewski, R.; Adamczyk, J. Life cycle assessment (LCA) of building thermal insulation materials. In Eco-Efficient Construction and Building Materials: LCA, Eco-Labelling and Case Studies; Pacheco-Torgal, F., Cabeza, L.F., Labrincha, J., de Magalhaes, A., Eds.; WoodHead Publishing Ltd.: Cambridge, UK, 2014; pp. 267–286. [Google Scholar]
- Dzikuć, M. Environmental management with the use of LCA in the Polish energy system. Management 2015, 19, 89–97. [Google Scholar] [CrossRef]
- Dzikuć, M.; Dzikuć, M. The analysis of opportunities to reduce low emissions in the Middle Odra using LCA techniques. In Społeczne i Ekologiczne Pogranicza: Monografia; Wawrzyniak, W., Zaborowski, T., Eds.; Instytut Badań i Ekspertyz Naukowych, Politechnika Poznańska: Poznań, Poland, 2018; pp. 150–162. [Google Scholar]
- ISO 14040 Environmental Management-Life Cycle Assessment-Principles and Framework; European Committee for Standardisation: Brussels, Belgium, 2006.
- ISO 14044 Environmental Management-Life Cycle Assessment-Requirements and Guidelines; European Committee for Standardisation: Brussels, Belgium, 2006.
- Dekker, E.; Zijp, M.C.; van de Kamp, M.E.; Temme, E.H.M.; van Zelm, R. A taste of the new ReCiPe for life cycle assessment: Consequences of the updated impact assessment method on food product LCAs. Int. J. Life Cycle Assess 2020, 25, 2315–2324. [Google Scholar] [CrossRef]
- Wolfova, M.; Estokova, A.; Ondova, M.; Monokova, A. Comparing of the external bearing wall using three cultural perspectives in the life cycle impact assessment. IOP Conf. Ser. Mater. Sci. Eng. 2018, 385, 012064. [Google Scholar] [CrossRef]
- Strefy Klimatyczne Polski. Available online: http://www.nieruchomosci.egospodarka.pl/art/galeria/55914,Kolektor-sloneczny-na-dachu-budynku,3,79,1.html (accessed on 3 March 2021).
- Eurostat. Available online: http://appsso.eurostat.ec.europa.eu/nui/show.do?dataset=nrg_chdd_a&lang=en (accessed on 15 March 2021).
- Rozporządzenie ministra transportu, budownictwa i gospodarki morskiej z dnia 5 lipca 2013 r. zmieniające rozporządzenie w sprawie warunków technicznych, jakim powinny odpowiadać budynki i ich usytuowanie, Dz. U. 2013, nr 0, poz. 926. Regulation of the minister of transport, construction and maritime economy of 5 July 2013 amending the regulation on the technical conditions to be met by buildings and their location. J. Laws 2013, 0, 926. Available online: http://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20130000926 (accessed on 3 March 2021). (In Polish).
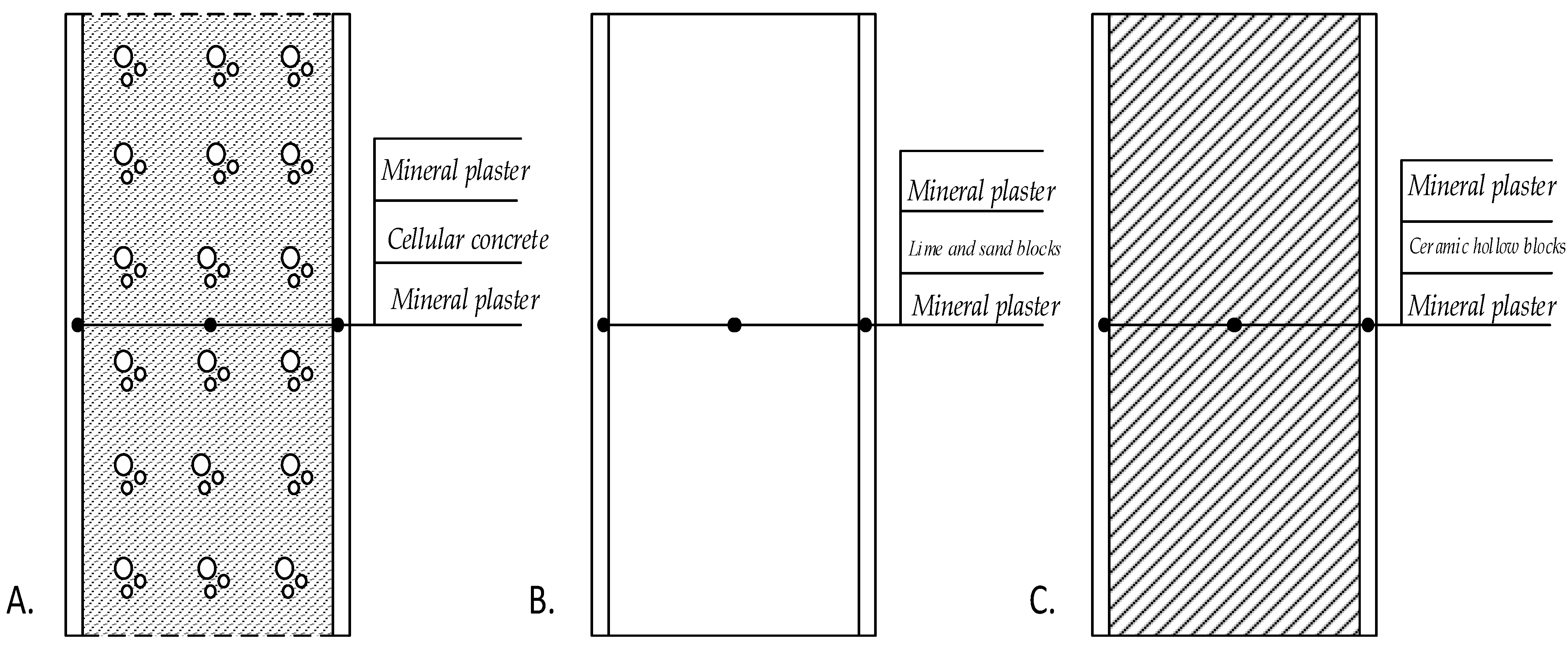

| HDD (K·Day/Year) | CDD (K·Day/Year) | |
|---|---|---|
| Poland | 3386.9 | 21.5 |
| Zachodniopomorskie (Zone I) | 3272.0 | 12.3 |
| Lubuskie (Zone II) | 3074.8 | 30.6 |
| Mazowieckie (Zone III) | 3448.0 | 23.4 |
| Podlaskie (Zone IV) | 3734.1 | 12.8 |
| Construction Material | Cellular Concrete 600 (C1) | Lime and Sand Blocks SILKA E (C2) | Ceramic Hollow Blocks Max (C3) |
|---|---|---|---|
| Thickness of walls (m) | 0.24 | 0.24 | 0.29 |
| Thermal conductivity λc (W/mK) | 0.16 | 0.55 | 0.29 |
| Heat transfer coefficient U0 (W/m2K) | 0.60 | 1.65 | 0.86 |
| Source of Heat | Coal Boiler (S1) | Condensing Gas Boiler (S2) | Electricity Boiler (S3) |
|---|---|---|---|
| Efficiency | 82% | 94% | 99% |
| KOH (PLN/Wh) | 0.162 × 10−3 | 0.245 × 10−3 | 0.707 × 10−3 |
| KEH (Pt/Wh) | 0.124 × 10−3 | 0.027 × 10−3 | 0.107 × 10−3 |
| Coolness Source | Air Conditioner (SC) |
|---|---|
| Seasonal energy efficiency ratio (SEER) | 5.30 |
| KOC (PLN/Wh) | 0.132 × 10−3 |
| KEC (Pt/Wh) | 0.020 × 10−3 |
| Thermal Insulation Mat. | Mineral Wool (I1) | Polystyrene EPS (I2) | Polystyrene XPS (I3) |
|---|---|---|---|
| Density ρ (kg/m3) | 90.0 | 12.5 | 40.0 |
| Thermal conductivity λ (W/mK) | 0.038 | 0.040 | 0.032 |
| Km (PLN/m3) | 233.00 | 205.00 | 420.00 |
| Kw (PLN/m2) | 45.00 | 40.00 | 40.00 |
| Kl (Pt/m3) | 19.10 | 6.77 | 31.90 |
| Constr. Mat. | Region | Heat Source and Thermal Insulation Mat. | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| S1-I1 | S1-I2 | S1-I3 | S2-I1 | S2-I2 | S2-I3 | S3-I1 | S3-I2 | S3-I3 | ||
| C1 | II | 0.122 | 0.136 | 0.074 | 0.165 | 0.183 | 0.102 | 0.323 | 0.356 | 0.211 |
| IV | 0.141 | 0.156 | 0.086 | 0.187 | 0.208 | 0.118 | 0.362 | 0.399 | 0.238 | |
| C2 | II | 0.163 | 0.179 | 0.107 | 0.205 | 0.225 | 0.136 | 0.364 | 0.399 | 0.245 |
| IV | 0.181 | 0.199 | 0.120 | 0.228 | 0.250 | 0.152 | 0.403 | 0.441 | 0.272 | |
| C3 | II | 0.141 | 0.157 | 0.090 | 0.184 | 0.203 | 0.119 | 0.342 | 0.376 | 0.227 |
| IV | 0.160 | 0.177 | 0.102 | 0.207 | 0.228 | 0.134 | 0.382 | 0.419 | 0.254 | |
| Constr. Mat. | Region | Heat Source and Thermal Insulation Mat. | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| S1-I1 | S1-I2 | S1-I3 | S2-I1 | S2-I2 | S2-I3 | S3-I1 | S3-I2 | S3-I3 | ||
| C1 | II | 0.205 | 0.197 | 0.252 | 0.167 | 0.160 | 0.205 | 0.098 | 0.095 | 0.121 |
| IV | 0.186 | 0.179 | 0.230 | 0.152 | 0.146 | 0.187 | 0.089 | 0.086 | 0.110 | |
| C2 | II | 0.205 | 0.197 | 0.252 | 0.167 | 0.160 | 0.205 | 0.098 | 0.095 | 0.121 |
| IV | 0.186 | 0.179 | 0.230 | 0.152 | 0.146 | 0.187 | 0.089 | 0.086 | 0.110 | |
| C3 | II | 0.205 | 0.197 | 0.252 | 0.167 | 0.160 | 0.205 | 0.098 | 0.095 | 0.121 |
| IV | 0.186 | 0.179 | 0.230 | 0.152 | 0.146 | 0.187 | 0.089 | 0.086 | 0.110 | |
| Constr. Mat. | Region | Heat Source and Thermal Insulation Mat. | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| S1-I1 | S1-I2 | S1-I3 | S2-I1 | S2-I2 | S2-I3 | S3-I1 | S3-I2 | S3-I3 | ||
| C1 | II | 0.612 | 1.097 | 0.426 | 0.253 | 0.478 | 0.171 | 0.564 | 1.014 | 0.392 |
| IV | 0.680 | 1.215 | 0.475 | 0.284 | 0.532 | 0.193 | 0.628 | 1.124 | 0.437 | |
| C2 | II | 0.652 | 1.139 | 0.460 | 0.293 | 0.520 | 0.205 | 0.604 | 1.057 | 0.426 |
| IV | 0.721 | 1.257 | 0.509 | 0.324 | 0.574 | 0.227 | 0.668 | 1.166 | 0.471 | |
| C3 | II | 0.631 | 1.117 | 0.442 | 0.272 | 0.498 | 0.187 | 0.583 | 1.034 | 0.408 |
| IV | 0.699 | 1.235 | 0.491 | 0.303 | 0.552 | 0.209 | 0.647 | 1.144 | 0.453 | |
| Constr. Mat. | Region | Heat Source and Thermal Insulation Mat. | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| S1-I1 | S1-I2 | S1-I3 | S2-I1 | S2-I2 | S2-I3 | S3-I1 | S3-I2 | S3-I3 | ||
| C1 | II | 0.056 | 0.034 | 0.067 | 0.120 | 0.073 | 0.143 | 0.061 | 0.037 | 0.072 |
| IV | 0.051 | 0.031 | 0.061 | 0.109 | 0.067 | 0.130 | 0.055 | 0.034 | 0.065 | |
| C2 | II | 0.056 | 0.034 | 0.067 | 0.120 | 0.073 | 0.143 | 0.061 | 0.037 | 0.072 |
| IV | 0.051 | 0.031 | 0.061 | 0.109 | 0.067 | 0.130 | 0.055 | 0.034 | 0.065 | |
| C3 | II | 0.056 | 0.034 | 0.067 | 0.120 | 0.073 | 0.143 | 0.061 | 0.037 | 0.072 |
| IV | 0.051 | 0.031 | 0.061 | 0.109 | 0.067 | 0.130 | 0.055 | 0.034 | 0.065 | |
| Constr. Mat. | Region | Heat Source and Thermal Insulation Mat. | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| S1-I1 | S1-I2 | S1-I3 | S2-I1 | S2-I2 | S2-I3 | S3-I1 | S3-I2 | S3-I3 | ||
| C1 | II | 0.130 | 0.151 | 0.075 | 0.184 | 0.219 | 0.115 | 0.389 | 0.460 | 0.257 |
| IV | 0.160 | 0.182 | 0.095 | 0.212 | 0.253 | 0.135 | 0.437 | 0.518 | 0.290 | |
| C2 | II | 0.212 | 0.237 | 0.140 | 0.235 | 0.286 | 0.159 | 0.438 | 0.522 | 0.298 |
| IV | 0.238 | 0.266 | 0.158 | 0.261 | 0.318 | 0.177 | 0.485 | 0.579 | 0.331 | |
| C3 | II | 0.171 | 0.193 | 0.107 | 0.209 | 0.252 | 0.137 | 0.412 | 0.490 | 0.277 |
| IV | 0.198 | 0.223 | 0.126 | 0.236 | 0.285 | 0.156 | 0.460 | 0.547 | 0.310 | |
| Constr. Mat. | Region | Heat Source and Thermal Insulation Mat. | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| S1-I1 | S1-I2 | S1-I3 | S2-I1 | S2-I2 | S2-I3 | S3-I1 | S3-I2 | S3-I3 | ||
| C1 | II | 0.196 | 0.184 | 0.249 | 0.154 | 0.140 | 0.190 | 0.084 | 0.076 | 0.103 |
| IV | 0.170 | 0.161 | 0.215 | 0.138 | 0.125 | 0.170 | 0.076 | 0.068 | 0.093 | |
| C2 | II | 0.162 | 0.153 | 0.201 | 0.147 | 0.129 | 0.180 | 0.082 | 0.073 | 0.101 |
| IV | 0.146 | 0.138 | 0.180 | 0.134 | 0.117 | 0.163 | 0.075 | 0.066 | 0.091 | |
| C3 | II | 0.177 | 0.167 | 0.221 | 0.150 | 0.134 | 0.184 | 0.083 | 0.075 | 0.102 |
| IV | 0.157 | 0.148 | 0.196 | 0.136 | 0.121 | 0.166 | 0.075 | 0.067 | 0.092 | |
| Variant | Insulation Mat. | dMKopt | UMKopt | NPV (dMKopt) | NPVE (dMKopt) | MK (dMKopt) |
|---|---|---|---|---|---|---|
| P1-S2-II | I1 | 0.184 | 0.154 | 54.34 | 18.88 | 98.7% |
| I2 | 0.220 | 0.140 | 61.60 | 21.62 | 95.8% | |
| I3 | 0.115 | 0.190 | 42.29 | 16.90 | 97.8% | |
| P1-S2-IV | I1 | 0.212 | 0.138 | 83.73 | 23.97 | 99.0% |
| I2 | 0.253 | 0.125 | 91.23 | 27.09 | 96.4% | |
| I3 | 0.135 | 0.170 | 69.13 | 21.78 | 98.3% |
| Variant | Insulation Mat. | dMKopt | UMKopt | NPV (dMKopt) | NPVE (dMKopt) | MK (dMKopt) |
|---|---|---|---|---|---|---|
| P3-S1-II | I1 | 0.171 | 0.177 | 59.52 | 153.32 | 93.8% |
| I2 | 0.193 | 0.167 | 66.82 | 157.48 | 92.5% | |
| I3 | 0.107 | 0.222 | 49.85 | 142.80 | 91.7% | |
| P3-S1-IV | I1 | 0.198 | 0.157 | 88.28 | 191.66 | 94.5% |
| I2 | 0.223 | 0.148 | 95.87 | 196.29 | 93.4% | |
| I3 | 0.126 | 0.196 | 76.50 | 180.53 | 92.8% |
| Variant | Insulation Mat. | dMKopt | UMKopt | NPV (dMKopt) | NPVE (dMKopt) | MK (dMKopt) |
|---|---|---|---|---|---|---|
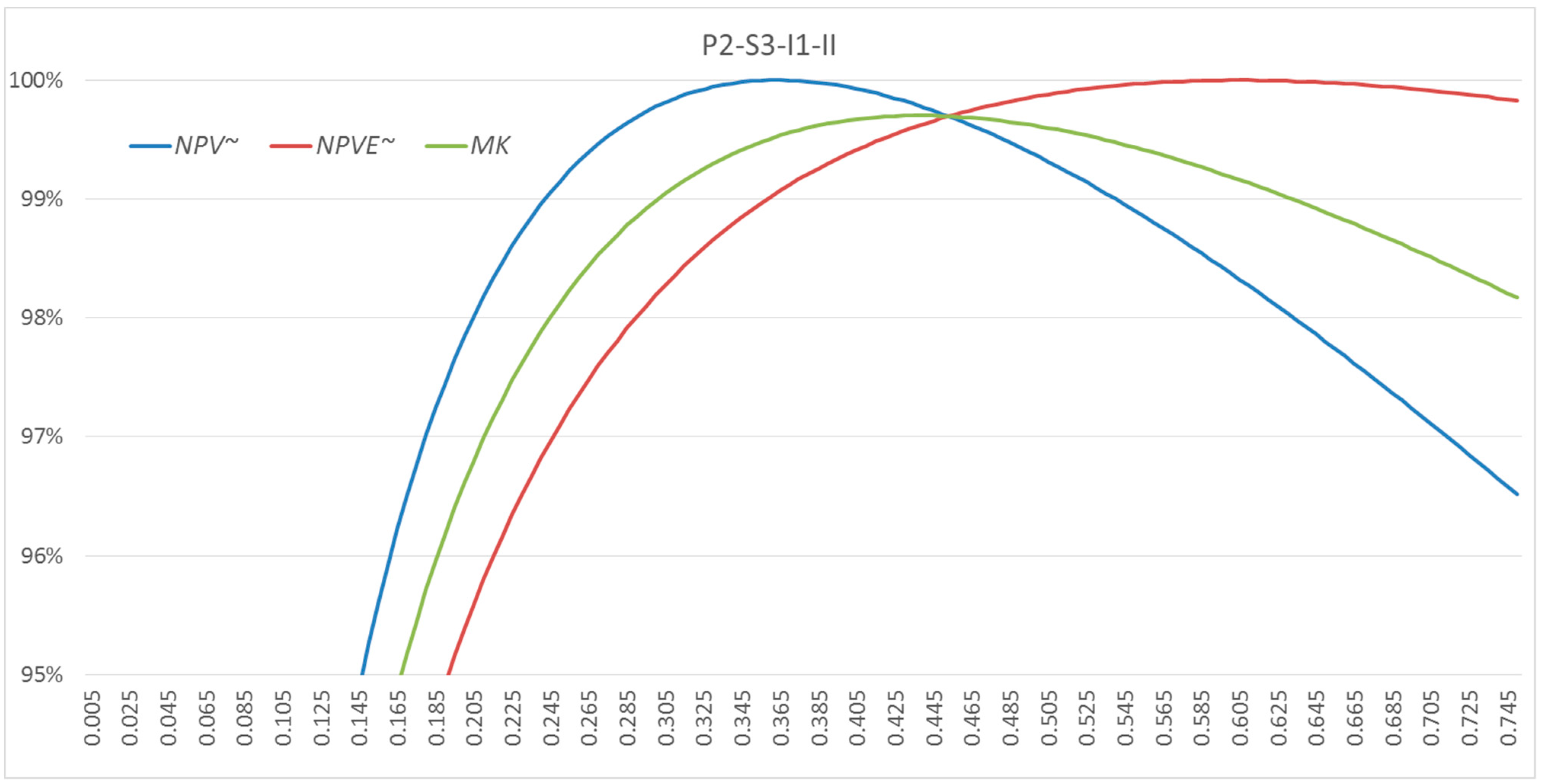
| P2-S3-II | I1 | 0.438 | 0.082 | 1289.13 | 301.65 | 99.7% |
| I2 | 0.522 | 0.073 | 1297.60 | 308.30 | 99.2% | |
| I3 | 0.298 | 0.101 | 1254.17 | 296.87 | 99.6% | |
| P2-S3-IV | I1 | 0.485 | 0.075 | 1592.48 | 368.60 | 99.7% |
| I2 | 0.579 | 0.066 | 1601.23 | 375.98 | 99.3% | |
| I3 | 0.331 | 0.091 | 1553.10 | 363.34 | 99.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dylewski, R.; Adamczyk, J. Optimum Thickness of Thermal Insulation with Both Economic and Ecological Costs of Heating and Cooling. Energies 2021, 14, 3835. https://doi.org/10.3390/en14133835
Dylewski R, Adamczyk J. Optimum Thickness of Thermal Insulation with Both Economic and Ecological Costs of Heating and Cooling. Energies. 2021; 14(13):3835. https://doi.org/10.3390/en14133835
Chicago/Turabian StyleDylewski, Robert, and Janusz Adamczyk. 2021. "Optimum Thickness of Thermal Insulation with Both Economic and Ecological Costs of Heating and Cooling" Energies 14, no. 13: 3835. https://doi.org/10.3390/en14133835
APA StyleDylewski, R., & Adamczyk, J. (2021). Optimum Thickness of Thermal Insulation with Both Economic and Ecological Costs of Heating and Cooling. Energies, 14(13), 3835. https://doi.org/10.3390/en14133835







