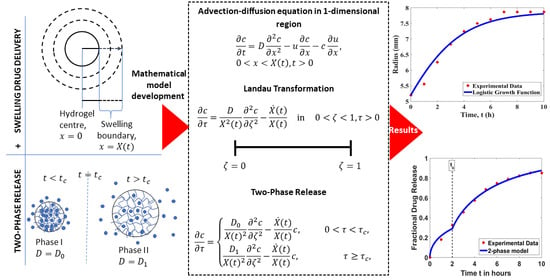
Mathematical Model for Estimating Parameters of Swelling Drug Delivery Devices in a Two-Phase Release
Abstract
:1. Introduction
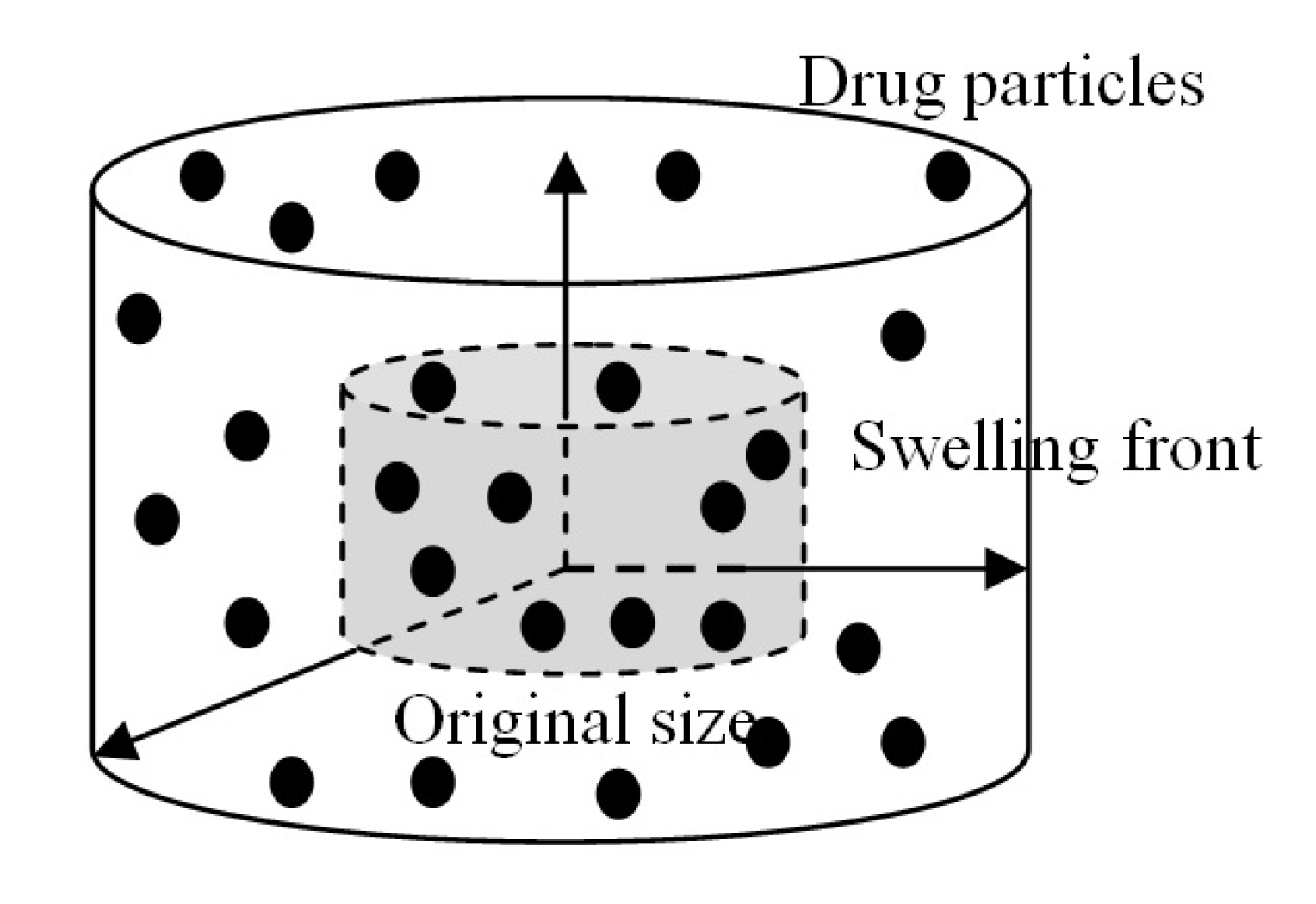
2. Mathematical Solution for Drug Release from a Swelling Device
2.1. One-Phase Model
2.2. Two-Phase Model
2.3. Algorithm for the Two-Phase Model
- Step 1
- Input the experimental data with discrete value .Time, : .Devices’ radius, : .Fractional drug release, : .
- Step 2
- Find the determined growth parameter, , such that it minimiseswhere function represents the devices’ radius at time and is the logistic function defined in Equation (12) using growth parameter g at time .
- Step 3
- Output the determined growth parameter, . Use for the next step.
- Step 4
- Find such that it minimiseswhere represents the fractional drug release data and iswhereandIf , then , and .
- Step 5
- Output the optimal parameters, , , and , and stop.
3. The Experiment
3.1. Drug Loading
3.2. Drug Release
4. Results and Discussion
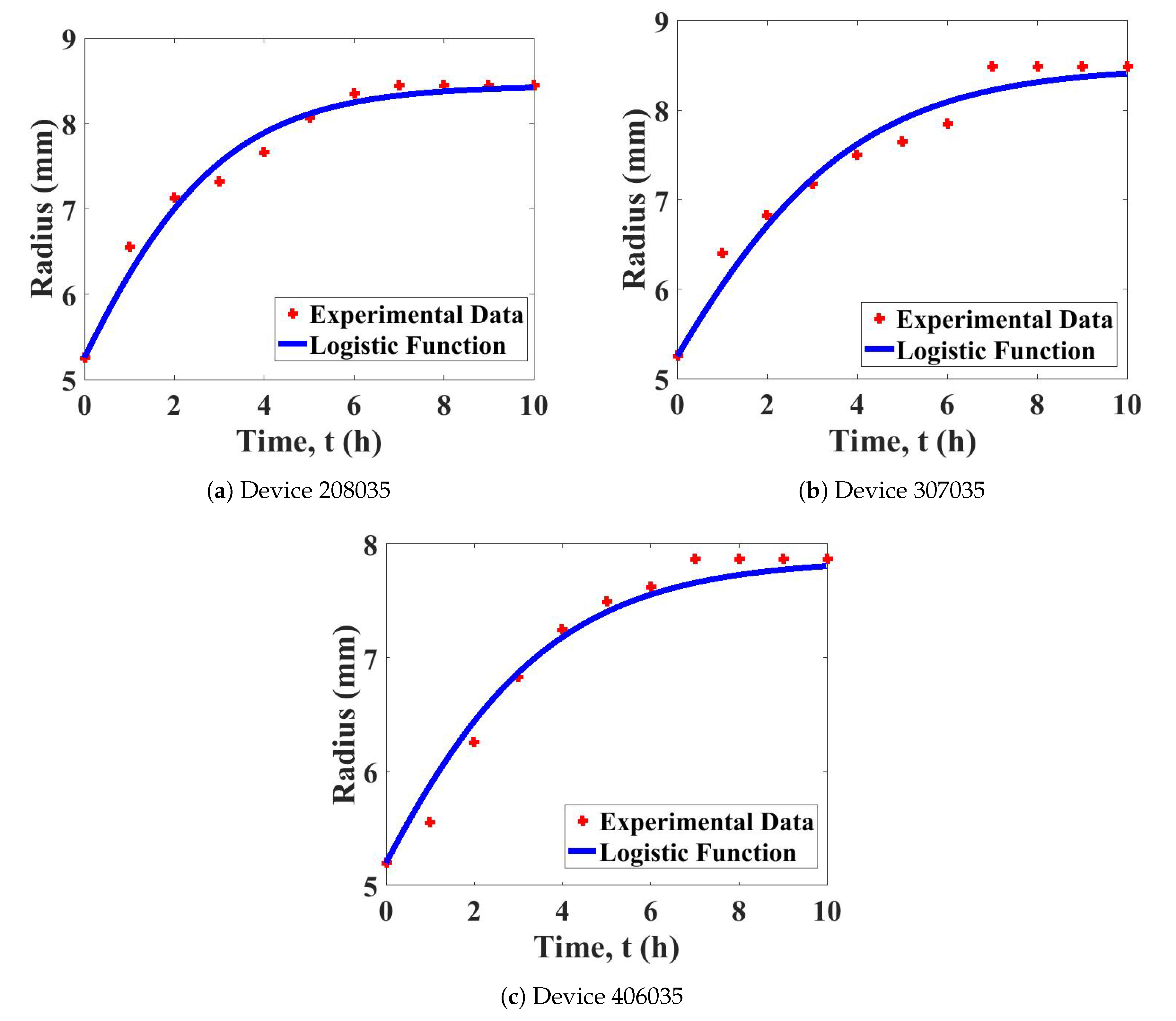
4.1. Model Test for Device Swelling
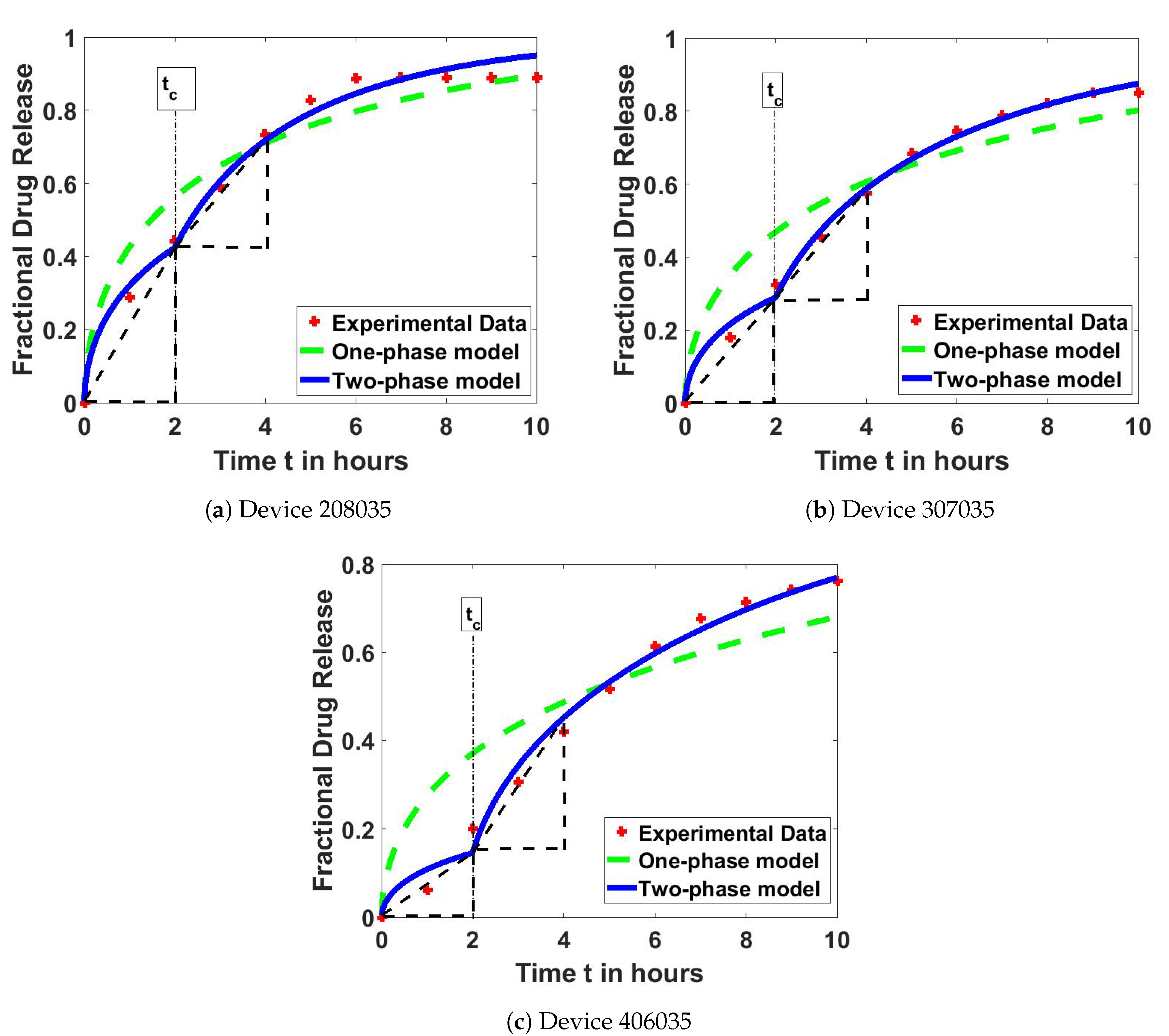
4.2. Model Test on Drug Release Profiles
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ulbrich, K.; Hola, K.; Subr, V.; Bakandritsos, A.; Tucek, J.; Zboril, R. Targeted drug delivery with polymers and magnetic nanoparticles: Covalent and noncovalent approaches, release control, and clinical studies. Chem. Rev. 2016, 116, 5338–5431. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Mooney, D.J. Designing hydrogels for controlled drug delivery. Nat. Rev. Mater. 2016, 1, 16071. [Google Scholar] [CrossRef] [PubMed]
- Pareek, A.; Maheshwari, S.; Cherlo, S.; Thavva, R.S.R.; Runakana, V. Modeling drug release through stimuli responsive polymer hydrogels. Int. J. Pharm. 2017, 532, 502–510. [Google Scholar] [CrossRef] [PubMed]
- Tibbitt, M.W.; Dahlman, J.E.; Langer, R. Emerging frontiers in drug delivery. J. Am. Chem. Soc. 2016, 138, 704–717. [Google Scholar] [CrossRef]
- Mura, S.; Nicolas, J.; Couvreur, P. Stimuli-responsive nanocarriers for drug delivery. Nat. Mater. 2013, 12, 991. [Google Scholar] [CrossRef]
- Karimi, M.; Ghasemi, A.; Zangabad, P.S.; Rahighi, R.; Basri, S.M.M.; Mirshekari, H.; Amiri, M.; Pishabad, Z.S.; Aslani, A.; Bozorgomid, M. Smart micro/nanoparticles in stimulus-responsive drug/gene delivery systems. Chem. Soc. Rev. 2016, 45, 1457–1501. [Google Scholar] [CrossRef] [Green Version]
- Koetting, M.C.; Peters, J.T.; Steichen, S.D.; Peppas, N.A. Stimulus-responsive hydrogels: Theory, modern advances, and applications. Mater. Sci. Eng. R. Rep. 2015, 93, 1–49. [Google Scholar] [CrossRef]
- Buwalda, S.J.; Boere, K.W.; Dijkstra, P.J.; Feijen, J.; Vermonden, T.; Hennink, W.E. Hydrogels in a historical perspective: From simple networks to smart materials. J. Control. Release 2014, 190, 254–273. [Google Scholar] [CrossRef]
- Ahmad, N.; Amin, M.C.I.M.; Mahali, S.M.; Ismail, I.; Chuang, V.T.G. Biocompatible and mucoadhesive bacterial cellulose-g-poly (acrylic acid) hydrogels for oral protein delivery. Mol. Pharm. 2014, 11, 4130–4142. [Google Scholar] [CrossRef]
- Bradley, D. Swell gel for natural drug delivery. Mater. Today 2016, 19, 6–7. [Google Scholar] [CrossRef]
- Lee, S.C.; Kwon, I.K.; Park, K. Hydrogels for delivery of bioactive agents: A historical perspective. Adv. Drug Deliv. Rev. 2013, 65, 17–20. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ahmad, N.; Mohd Amin, M.C.I.; Ismail, I.; Buang, F. Enhancement of oral insulin bioavailability: In vitro and in vivo assessment of nanoporous stimuli-responsive hydrogel microparticles. Expert Opin. Drug Deliv. 2016, 13, 621–632. [Google Scholar] [CrossRef] [PubMed]
- Peppas, N.A.; Narasimhan, B. Mathematical models in drug delivery: How modeling has shaped the way we design new drug delivery systems. J. Control. Release 2014, 190, 75–81. [Google Scholar] [CrossRef] [PubMed]
- Mathematical models of drug release. In Strategies to Modify the Drug Release from Pharmaceutical Systems; Woodhead Publishing Limited: Cambridge, UK, 2015; pp. 63–86.
- Fu, G.; Soboyejo, W. Investigation of swellable poly (N-isopropylacrylamide) based hydrogels for drug delivery. Mater. Sci. Eng. C 2011, 31, 1084–1090. [Google Scholar] [CrossRef]
- Maderuelo, C.; Zarzuelo, A.; Lanao, J.M. Critical factors in the release of drugs from sustained release hydrophilic matrices. J. Control. Release 2011, 154, 2–19. [Google Scholar] [CrossRef] [PubMed]
- Siepmann, J.; Siepmann, F. Modeling of diffusion controlled drug delivery. J. Control. Release 2012, 161, 351–362. [Google Scholar] [CrossRef] [PubMed]
- Mahali, S.M.; Saudi, M.H.; Amin, M.C.I.M.; Abdullah, I.; Ahmad, N. Mathematical Model for Estimating the Diffusion Coefficients of Protein Release from Bacterial Cellulose-based Hydrogel. Malays. J. Math. Sci. 2016, 10, 15–26. [Google Scholar]
- Mahali, S.M.; Setapa, A.; Zolkamal, N.N. Mathematical Model of Drug Release from a Logistically Swelling Hydrogel. AIP Conf. Proc. 2018, 1974, 020068. [Google Scholar]
- Bierbrauer, F. Hydrogel Drug Delivery: Diffusion Models; University of Wollongong: Wollongong, Australia, 2005. [Google Scholar]
- Saudi, M.H.; Mahali, S.M.; Harun, F.N. The analytical solution for drug delivery system with nonhomogeneous moving boundary condition. AIP Conf. Proc. 2017, 1870, 040069. [Google Scholar]
- Kalkhoran, A.H.Z.; Vahidi, O.; Naghib, S.M. A new mathematical approach to predict the actual drug release from hydrogels. Eur. J. Pharm. Sci. 2018, 111, 303–310. [Google Scholar] [CrossRef]
- Kohrs, N.J.; Liyanage, N.; Venkatesan, N.; Najarzadeh, A.; Puleo, D.A. Drug Delivery Systems and Controlled Release. In Encyclopedia of Biomedical Engineering; Elsevier: Amsterdam, The Netherlands, 2019; pp. 316–329. [Google Scholar]
- Fu, G.; Soboyejo, W.O. Swelling and diffusion characteristics of modified poly (N-isopropylacrylamide) hydrogels. Mater. Sci. Eng. C 2010, 30, 8–13. [Google Scholar] [CrossRef]
- Ray, N.; Rupp, A.; Schulz, R.; Knabner, P. Old and New Approaches Predicting the Diffusion in Porous Media. Transp. Porous Media 2018, 124, 803–824. [Google Scholar] [CrossRef]
- Blanco, A.; Gonzalez, G.; Cassanova, E.; Pirela, M.E.; Briceno, A. Mathematical Modeling of Hydrogels Swelling Based on the Finite Element Method. Appl. Math. 2013, 4, 161–170. [Google Scholar] [CrossRef]
- Wang, S.; Mahali, S.M.; McGuiness, A.; Lou, X. Mathematical models for estimating effective diffusion parameters of spherical drug delivery devices. Theor. Chem. Acc. 2010, 125, 659–669. [Google Scholar] [CrossRef] [Green Version]

| Device | Growth Parameter, | Least-Squares Error |
|---|---|---|
| 208035 | 1.49918 | 0.27483 |
| 307035 | 1.17298 | 0.44279 |
| 406035 | 1.16996 | 0.25559 |
| Devices | One-Phase Model | Two-Phase Model | ||
|---|---|---|---|---|
| (mm/s) | () | () | (s) | |
| 208035 | 1.30515 | 7.37805 | 2.22787 | 7200 |
| 307035 | 8.58865 | 3.25908 | 1.49489 | 7200 |
| 406035 | 5.10114 | 7.90305 | 9.35150 | 7200 |
| Device | ||
|---|---|---|
| () | () | |
| 208035 | 0.20984 | 0.14669 |
| 307035 | 0.14255 | 0.14895 |
| 406035 | 0.07102 | 0.15310 |
| Device | One-Phase Model | Two-Phase Model |
|---|---|---|
| 208035 | 0.06429 | 0.01237 |
| 307035 | 0.08800 | 0.00477 |
| 406035 | 0.13910 | 0.01015 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Setapa, A.; Ahmad, N.; Mohd Mahali, S.; Mohd Amin, M.C.I. Mathematical Model for Estimating Parameters of Swelling Drug Delivery Devices in a Two-Phase Release. Polymers 2020, 12, 2921. https://doi.org/10.3390/polym12122921
Setapa A, Ahmad N, Mohd Mahali S, Mohd Amin MCI. Mathematical Model for Estimating Parameters of Swelling Drug Delivery Devices in a Two-Phase Release. Polymers. 2020; 12(12):2921. https://doi.org/10.3390/polym12122921
Chicago/Turabian StyleSetapa, Amanina, Naveed Ahmad, Shalela Mohd Mahali, and Mohd Cairul Iqbal Mohd Amin. 2020. "Mathematical Model for Estimating Parameters of Swelling Drug Delivery Devices in a Two-Phase Release" Polymers 12, no. 12: 2921. https://doi.org/10.3390/polym12122921