An Improved Composite Multiscale Fuzzy Entropy for Feature Extraction of MI-EEG
Abstract
1. Introduction
2. Feature Extraction Based on WCMFE
2.1. Preprocessing of MI-EEG Times Series
2.2. Coarse-Graining for WCMFE
2.3. The Calculation of WCMFE
- (1)
- Given the embedding dimension m, the vectors are calculated, where and .
- (2)
- For and , the distance between and is described as
- (3)
- For a given boundary gradient n and boundary width r, is calculated from Equation (3).
- (4)
- Repeat the steps (1)–(3), can be obtained. Then, is defined as
2.4. Construction of Feature Vector
3. Experimental Research
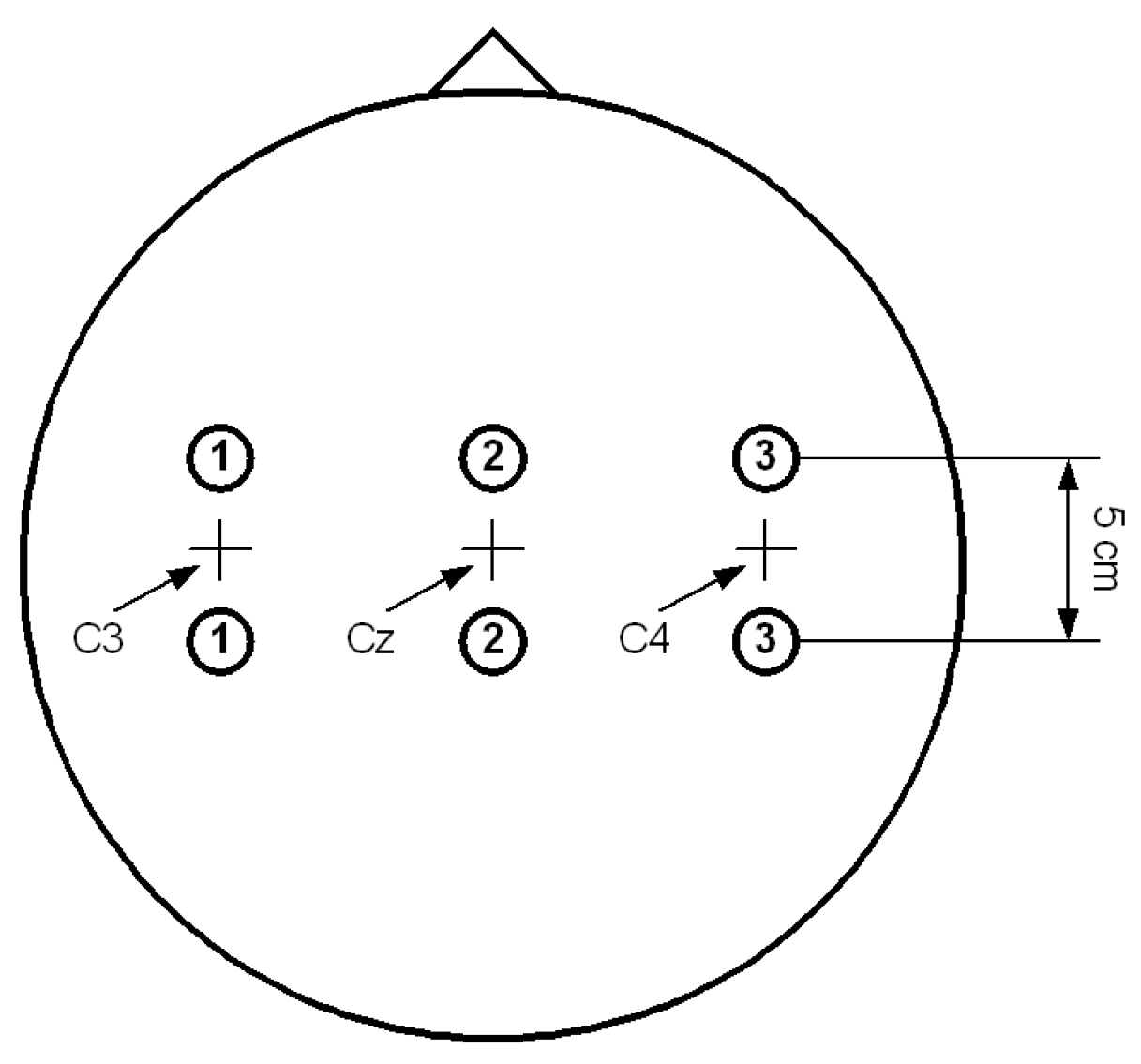
3.1. Data Source
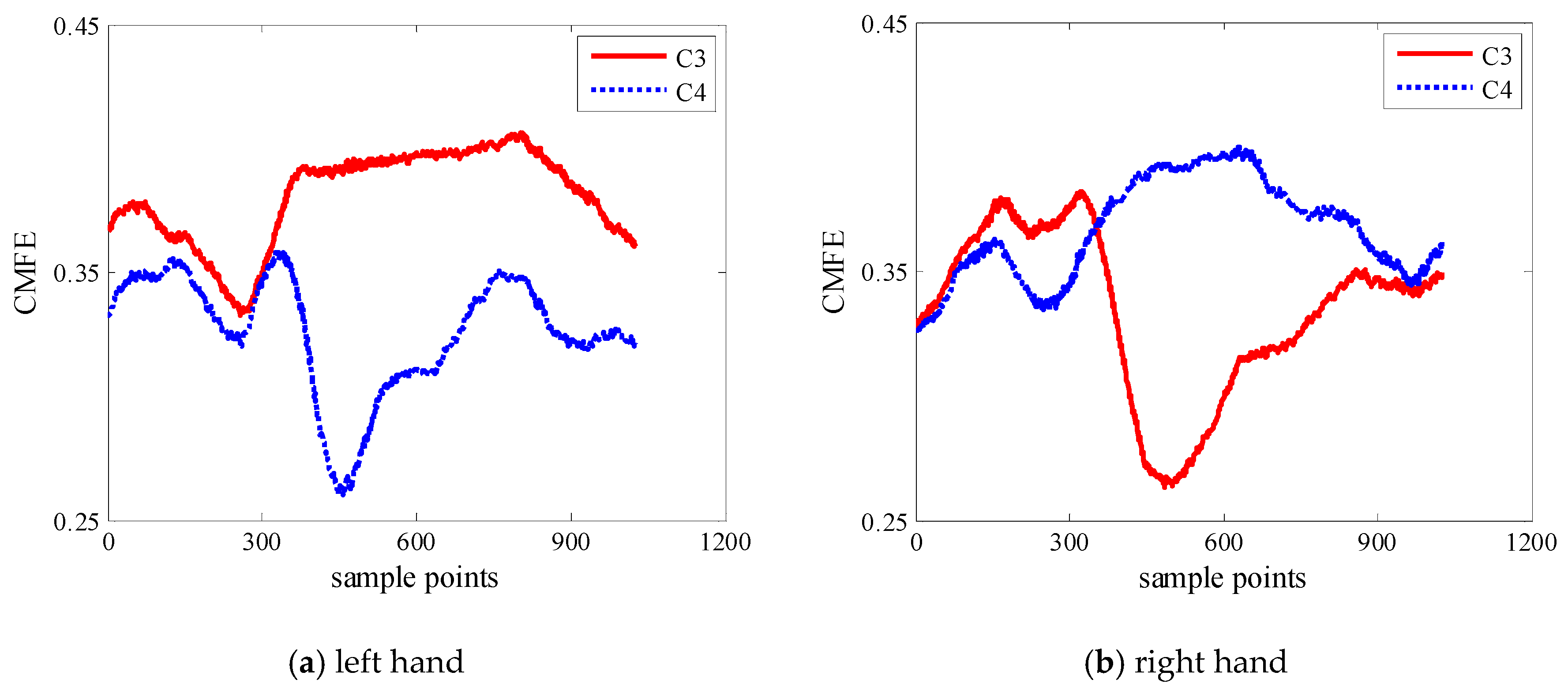
3.2. Interval Selection of MI-EEG
3.3. Comparative Study of WCMFE and CMFE
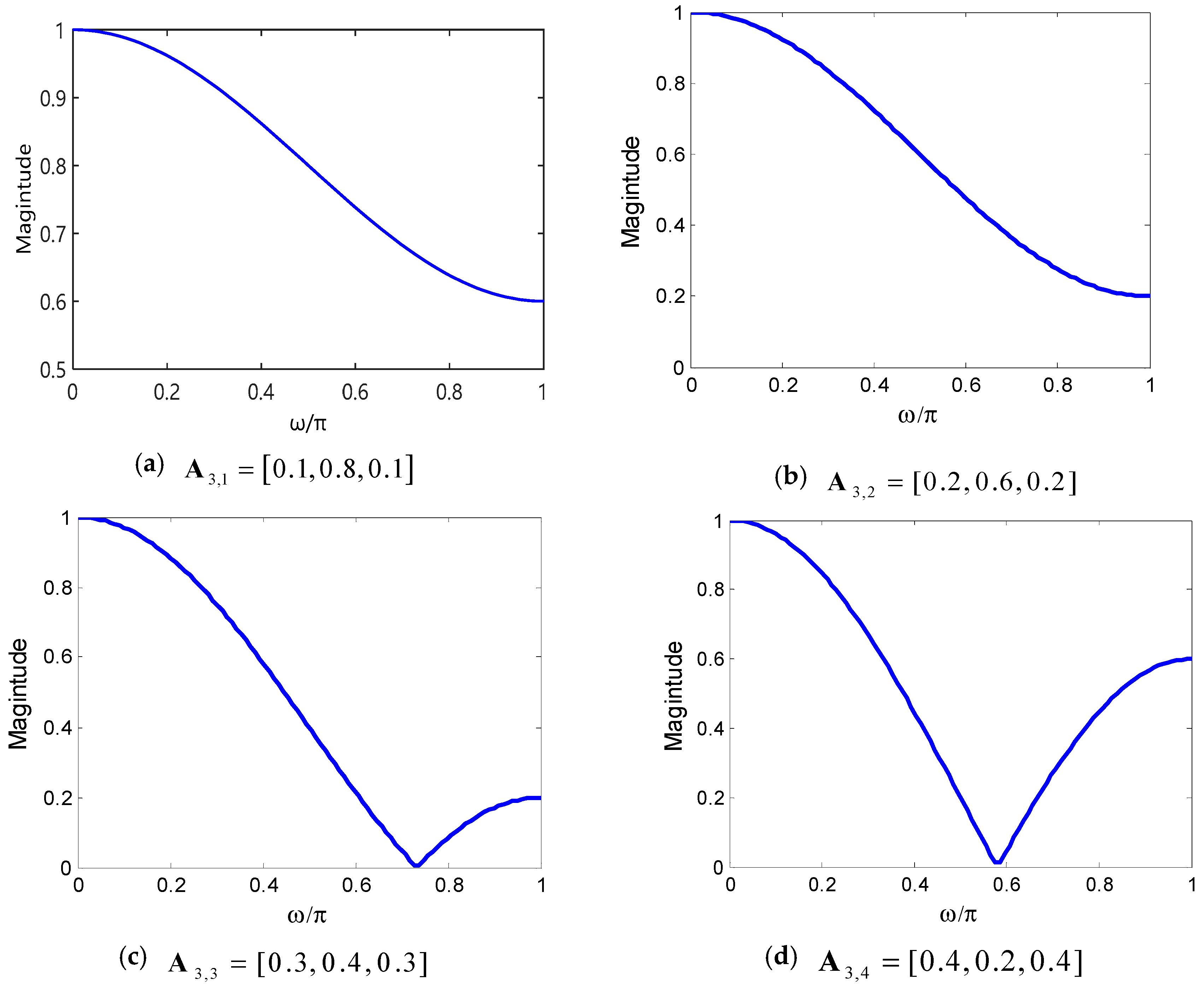
3.3.1. Selection of Weight Factors
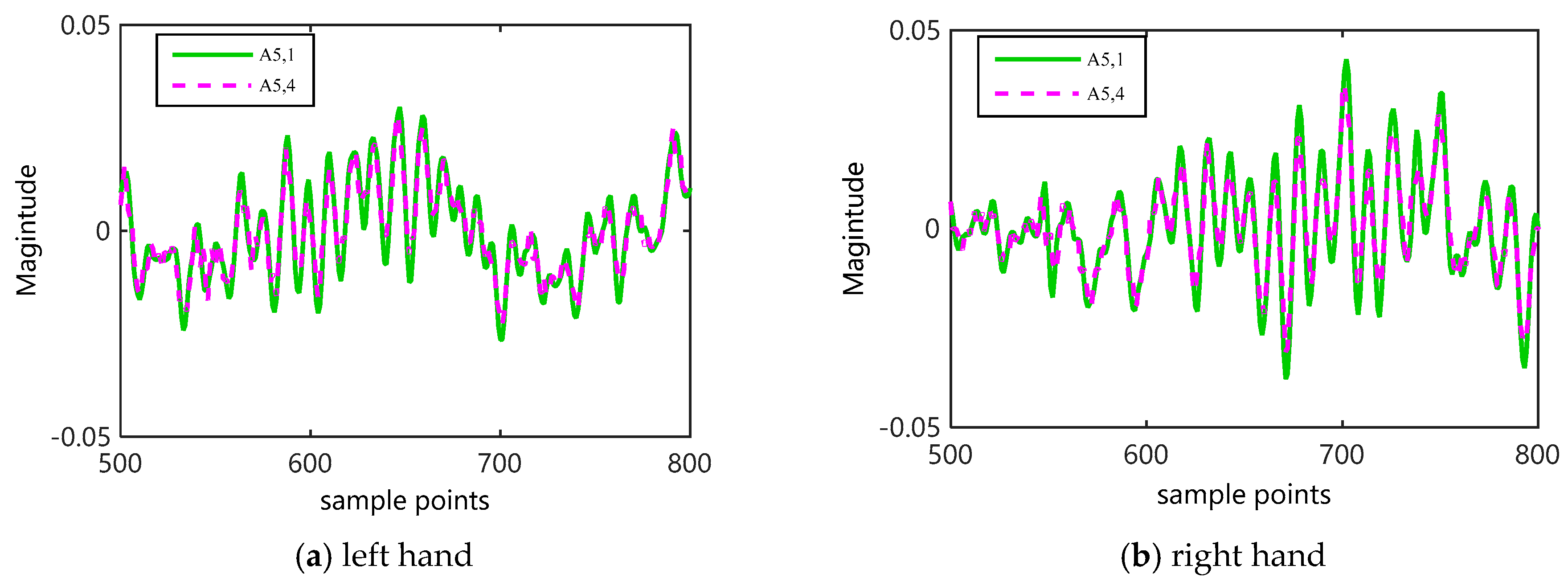
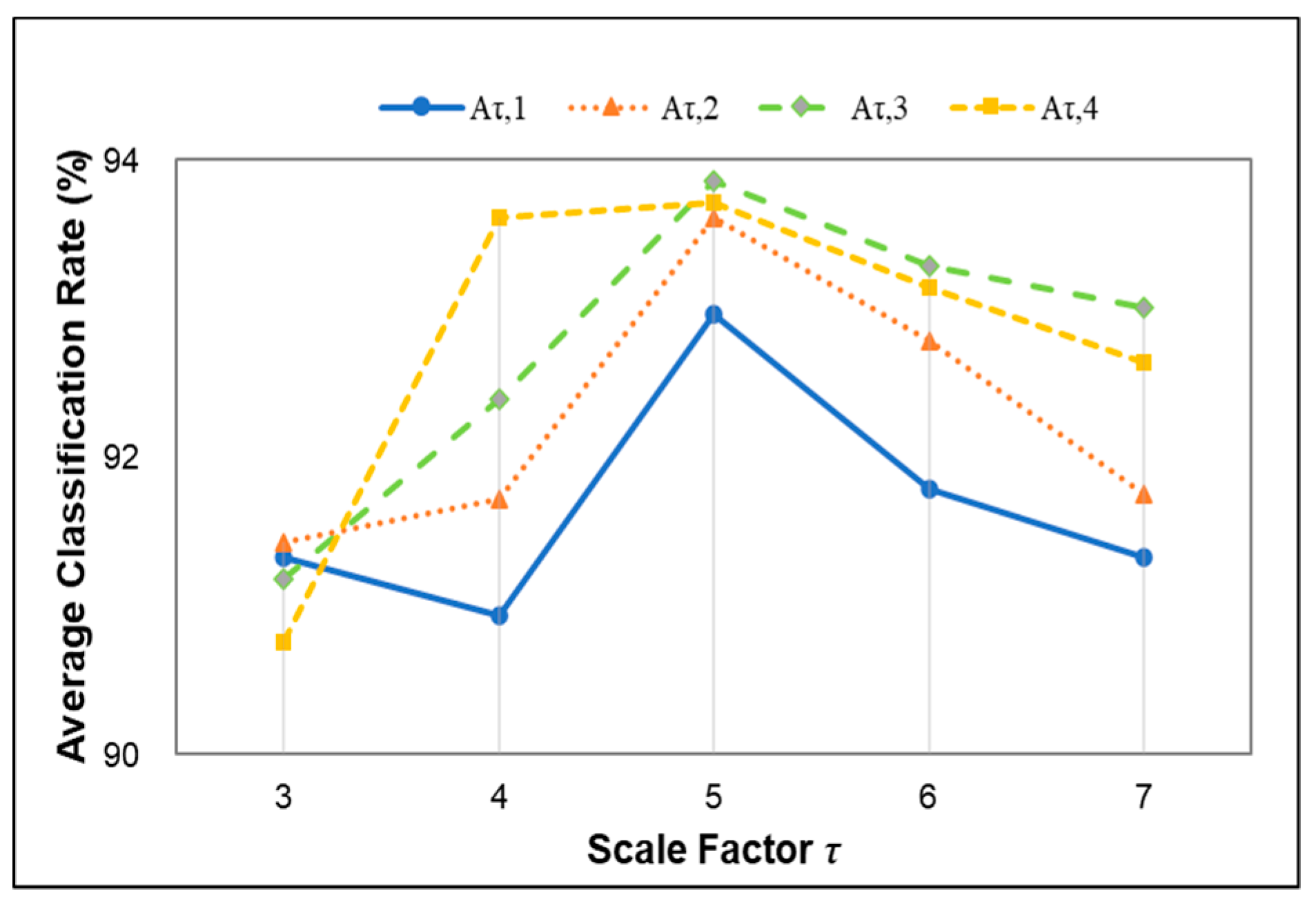
3.3.2. Selection of Scale Factor
3.3.3. Selection of Parameters in FE
3.3.4. Comparison of WCMFE and CMFE
3.3.5. Statistical Analysis
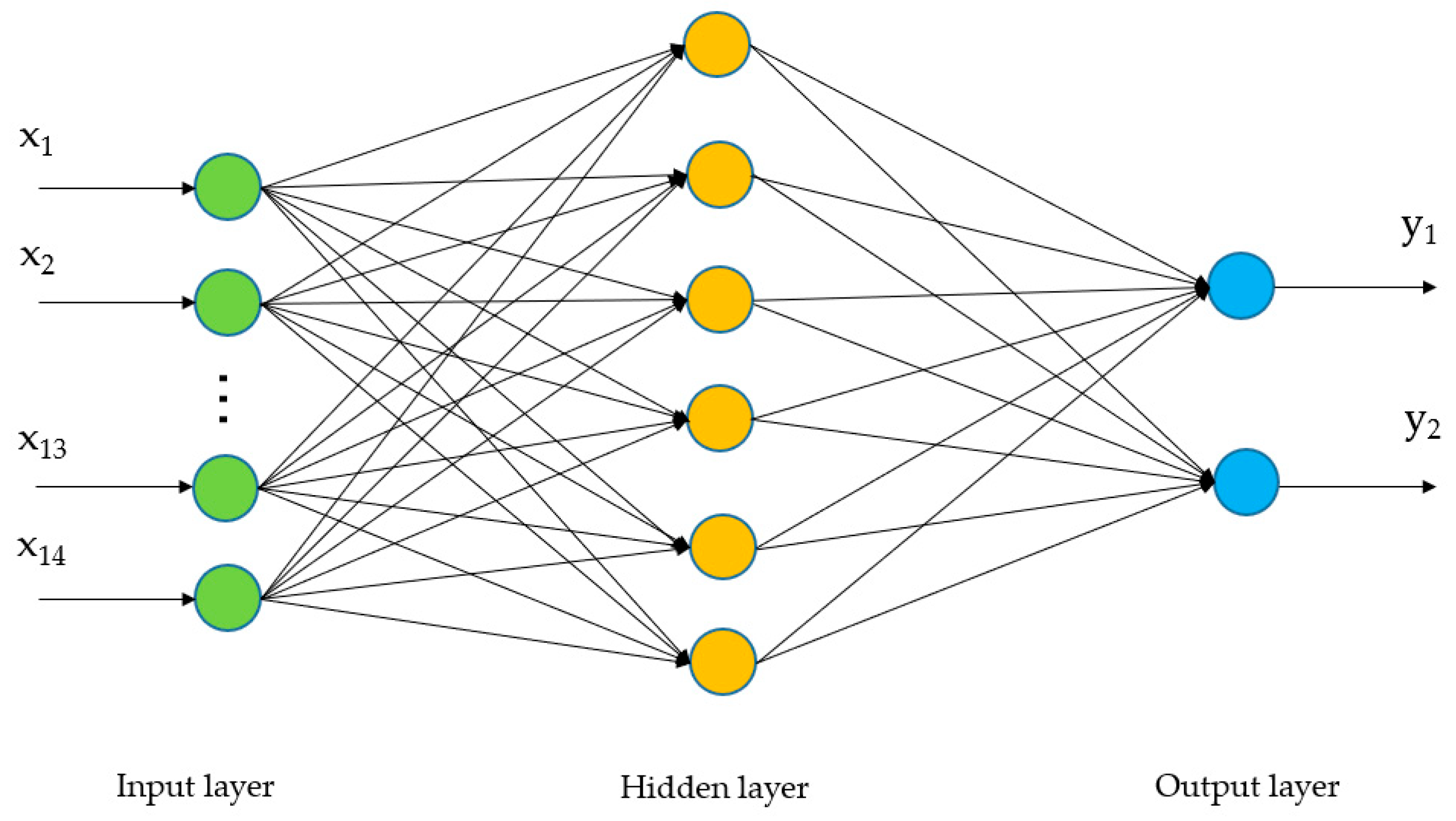
3.4. Comparison with Multiple Traditional Feature Extraction Methods Based on BP Neural Network
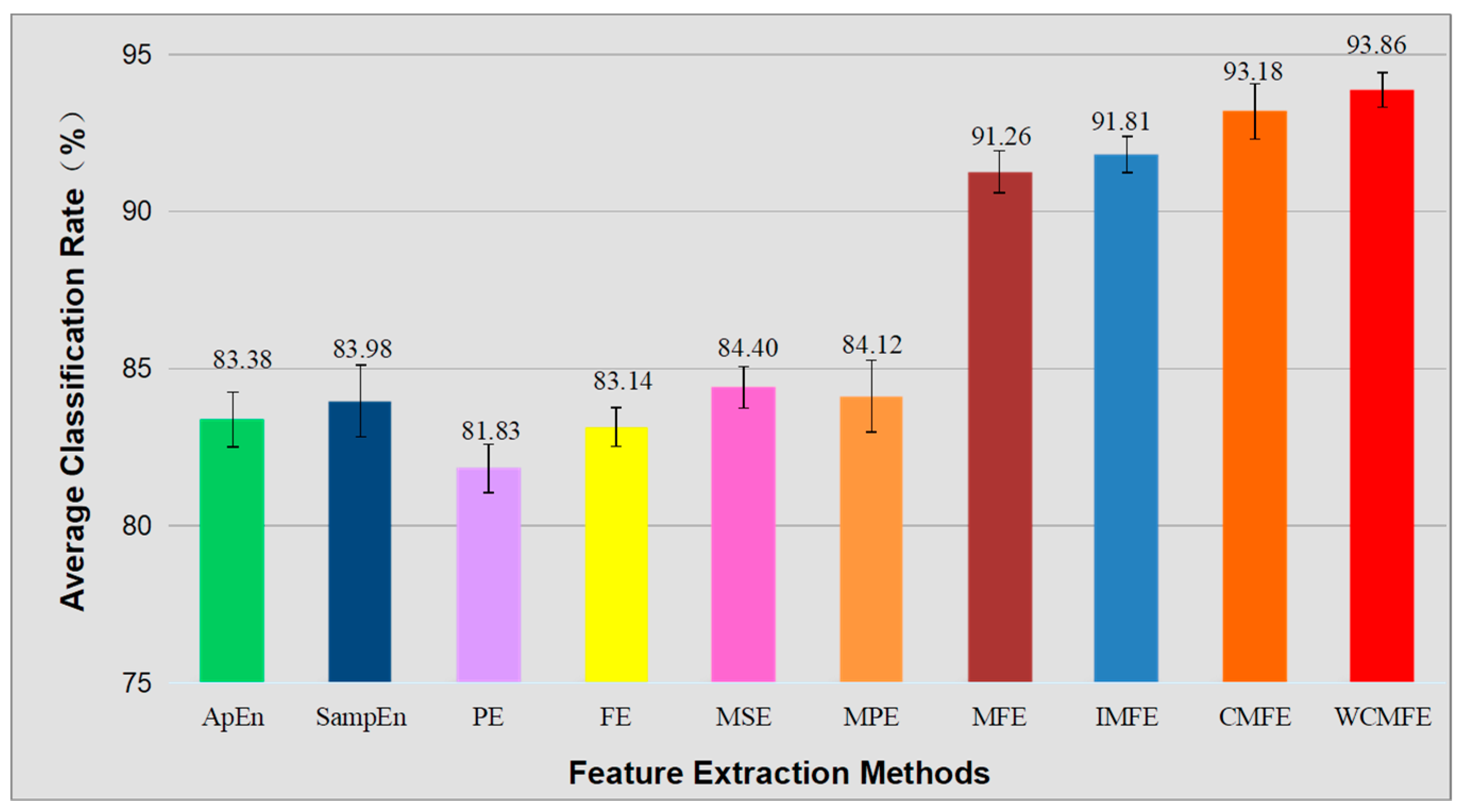
3.5. Comparison of Multiple Entropy-Based Feature Extraction Methods
3.6. Comparison with Multiple Traditional Recognition Methods
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yuan, L.; Yang, B.H.; Ma, S.W. Discrimination of movement imagery EEG based on HHT and SVM. Chin. J. Sci. Instrum. 2010, 31, 649–654. [Google Scholar]
- Ang, K.K.; Guan, C.; Chua, K.S.G.; Ang, B.T.; Kuah, C.; Wang, C.; Phua, K.S.; Chin, Z.Y.; Zhang, H. Clinical study of neurorehabilitation in stroke using EEG-based motor imagery brain-computer interface with robotic feedback. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August—4 September 2010. [Google Scholar]
- Zhang, Y.; Yang, L.; Li, M.; Luo, Y. Recognition of motor imagery EEG based on AR and SVM. J. Huazhong Univ. Sci. Technol. 2011, 39, 103–106. [Google Scholar]
- Lu, P.; Yuan, D.; Lou, Y.; Liu, C.; Huang, S. Single-Trial Identification of Motor Imagery EEG based on HHT and SVM. In Lecture Notes in Electrical Engineering; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2013; pp. 681–689. [Google Scholar]
- Jin, H.; Zhang, Z. Research of movement imagery EEG based on Hilbert-Huang transform and BP neural network. J. Biomed. Eng. 2013, 30, 249–253. [Google Scholar]
- Yu, W.; Han, Q.; Ma, J.J.; Xie, P. EEG Signal Processing Method Based on EMD and SVM. J. Kunming Univ. Sci. Technol. 2012, 37, 38–42. [Google Scholar]
- Salgado, B.M.; Muñoz, L.D. Fuzzy entropy relevance analysis in DWT and EMD for BCI motor imagery applications. Ingeniería 2015, 20, 9–19. [Google Scholar] [CrossRef]
- Bashar, S.K.; Bhuiyan, M.I.H. Classification of motor imagery movements using multivariate empirical mode decomposition and short time Fourier transform based hybrid method. Eng. Sci. Technol. Int. J. 2016, 19, 1457–1464. [Google Scholar] [CrossRef]
- Li, M.A.; Wang, R.; Hao, D.M. Feature extraction and classification of EEG for imagery left-right hands movement. Chin. J. Biomed. Eng. 2009, 28, 166–170. [Google Scholar]
- Xu, B.; Song, A. Pattern Recognition of Motor Imagery EEG using Wavelet Transform. J. Biomed. Sci. Eng. 2008, 1, 64–67. [Google Scholar] [CrossRef]
- Medina-Salgado, B.; Duque-Munoz, L.; Fandiño-Toro, H. Characterization of EEG signals using wavelet transform for motor imagination tasks in BCI systems. Symp. Signals Images Artif. Vis. 2013, 44, 1–4. [Google Scholar] [CrossRef]
- Ren, Y.L. Applying Wavelet Packet Entropy and BP neural networks in recognition of mental tasks. Comput. Appl. Softw. 2009, 26, 78–81. [Google Scholar]
- Kang, S.S.; Zhou, B.Y.; Lv, Z.; Wu, X.P. Automatic selection algorithm for multi-class motor imagery of EEG eigenvalues based on CSP. Beijing Biomed. Eng. 2016, 35, 339–346. [Google Scholar]
- Liu, C.; Zhao, H.B.; Li, C.S.; Wang, H. CSP/SVM-based EEG Classification of Imagined Hand Movements. J. Northeast. Univ. 2010, 31, 1098–1101. [Google Scholar]
- Wang, P.; Shen, J.Z.; Shi, J.H. Feature extraction of EEG for imagery left-right hands movement. Chin. J. Sens. Actuators 2010, 23, 1220–1225. [Google Scholar]
- Cao, R.; Li, L.; Chen, Y.J. Comparative study of approximate entropy and sample entropy in EEG data analysis. Biotechnol. Indian J. 2013, 7, 493–498. [Google Scholar]
- Kumar, Y.; Dewal, M.; Anand, R. Features extraction of EEG signals using approximate and sample entropy. In Proceedings of the 2012 IEEE Students’ Conference on Electrical, Electronics and Computer Science, Bhopal, India, 1–2 March 2012. [Google Scholar]
- Li, Y.; Chen, S.; Wang, L. Analysis and comparison of mental EEG signal based on approximate entropy and sample entropy. J. Chongqing Technol. Bus. Univ. 2013, 30, 44–47. [Google Scholar]
- Cao, Y.Z.; Cai, L.H.; Wang, J.; Wang, R.F.; Yu, H.T. Characterization of complexity in the electroencephalograph activity of Alzheimer’s disease based on fuzzy entropy. Chaos 2015, 25, 083116. [Google Scholar] [CrossRef]
- Chen, W.; Zhuang, J.; Yu, W.; Wang, Z. Measuring complexity using FuzzyEn, ApEn, and SampEn. Med. Eng. Phys. 2009, 31, 61–68. [Google Scholar] [CrossRef]
- Bruzzo, A.A.; Gesierich, B.; Santi, M.; Tassinari, C.A.; Birbaumer, N.; Rubboli, G. Permutation entropy to detect vigilance changes and preictal states from scalp EEG in epileptic patients. A preliminary study. Neurol. Sci. 2008, 29, 3–9. [Google Scholar] [CrossRef]
- Nicolaou, N.; Georgiou, J. The Use of Permutation Entropy to Characterize Sleep Electroencephalograms. Clin. EEG Neurosci. 2011, 42, 24–28. [Google Scholar] [CrossRef]
- Liu, Q.; Chen, Y.-F.; Fan, S.-Z.; Abbod, M.F.; Shieh, J.-S. EEG Signals Analysis Using Multiscale Entropy for Depth of Anesthesia Monitoring during Surgery through Artificial Neural Networks. Comput. Math. Methods Med. 2015, 2015, 1–16. [Google Scholar] [CrossRef]
- Zhang, L.; Xiong, G.; Liu, H.; Zou, H.; Guo, W. Bearing fault diagnosis using multi-scale entropy and adaptive neuro-fuzzy inference. Expert Syst. Appl. 2010, 37, 6077–6085. [Google Scholar] [CrossRef]
- Xi, M.; Zhu, G. Multi-scale Permutation Entropy and Its Applications in the Identification of Seizures. J. Biomed. Eng. 2015, 32, 751–756. [Google Scholar]
- Wu, Y.; Shang, P.; Li, Y. Modified generalized multiscale sample entropy and surrogate data analysis for financial time series. Nonlinear Dyn. 2018, 92, 1335–1350. [Google Scholar] [CrossRef]
- Yao, W.P.; Liu, T.B.; Dai, J.F.; Wang, J. Multiscale permutation entropy analysis of electroencephalogram. Acta Phys. Sin. 2013, 63, 427–433. [Google Scholar]
- Zheng, J.D.; Chen, M.J.; Cheng, J.S.; Yu, Y. Multiscale fuzzy entropy and its application in rolling bearing fault diagnosis. J. Vib. Eng. 2014, 27, 145–151. [Google Scholar]
- Li, Y.J.; Ma, L.Y.; Cui, X.H. Research on faulty diagnose for rotation machine based on multi-scale fuzzy entropy. Mod. Manuf. Eng. 2017, 10, 146–150. [Google Scholar]
- Zou, X.; Lei, M. Pattern recognition of surface electromyography signal based on multi-scale fuzzy entropy. J. Biomed. Eng. 2012, 29, 1184–1188. [Google Scholar]
- Li, M.; Liu, H.; Zhu, W.; Yang, J.-F. Applying Improved Multiscale Fuzzy Entropy for Feature Extraction of MI-EEG. Appl. Sci. 2017, 7, 92. [Google Scholar] [CrossRef]
- Li, Y.; Miao, B.; Zhang, W.; Chen, P.; Liu, J.; Jiang, X. Refined composite multiscale fuzzy entropy: Localized defect detection of rolling element bearing. J. Mech. Sci. Technol. 2019, 33, 109–120. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, H.; Cheng, J. Rolling bearing fault detection and diagnosis based on composite multiscale fuzzy entropy and ensemble support vector machines. Mech. Syst. Signal Process. 2017, 85, 746–759. [Google Scholar] [CrossRef]
- Zheng, J.D.; Pan, H.Y.; Cheng, J.S.; Zhang, J. Composite multi-scale fuzzy entropy based rolling bearing fault diagnosis method. J. Vib. Shock 2016, 35, 116–123. [Google Scholar]
- Li, J.; Yu, B.M. Data Collecting System in the Digital Filter Design. J. Anqing Teach. Coll. 2009, 15, 1284–1287. [Google Scholar]
- Zhao, Y. Arithmetic Mean Method and Weighting Mean Method of Digital Filter. Instrum. Technol. 2001, 4, 41–44. [Google Scholar]
- Ren, K.Q.; Liu, H. Algorithms of Digital Filter in the Microcomputer Control System. Mod. Electron. Tech. 2003, 3, 15–18. [Google Scholar]
- Schlögl, A.; Neuper, C.; Müller, G.; Graimann, B.; Pfurtscheller, G. BCI Competition. 2002. Available online: https://www.bbci.de/competition/ii/#datasets (accessed on 7 September 2018).
- Shao, P.; Wu, Z.J.; Zhou, X.Y. Particle swarm optimization algorithm based on opposite learning for linear phase low-pass FIR filter optimization. J. Jilin Univ. 2015, 45, 907–912. [Google Scholar]
- Zheng, J.; Cheng, J.; Yang, Y.; Luo, S. A rolling bearing fault diagnosis method based on multi-scale fuzzy entropy and variable predictive model-based class discrimination. Mech. Mach. Theory 2014, 78, 187–200. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nat. Cell Biol. 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Lemm, S.; Schäfer, C.; Curio, G. Probabilistic Modeling of Sensorimotor µ-Rhythms for Classification of Imaginary Hand Movements. Appl. Organomet. Chem. 2004, 18, 311–317. [Google Scholar]
- Jia, W.; Zhao, X.; Liu, H.; Gao, X.; Gao, S.; Yang, F. Classification of single trial EEG during motor imagery based on ERD. In Proceedings of the 2006 International Conference of the IEEE Engineering in Medicine and Biology Society, San Francisco, CA, USA, 1–5 September 2004. [Google Scholar]
- Blankertz, B.; Müller, K.R.; Curio, G.; Vaughan, T.M.; Schalk, G.; Wolpaw, J.R.; Schlögl, A.; Neuper, C.; Pfurtscheller, G.; Hinterberger, T.; et al. The BCI Competition 2003: Progress and perspectives in detection and discrimination of EEG single trials. IEEE Trans. Biomed. Eng. 2004, 51, 100–106. [Google Scholar] [CrossRef]




| Feature Extraction Method | Classification Method | Top Recognition Rate (%) | Average Recognition Rate with 10 × 10-fold CV (%) |
|---|---|---|---|
| CMFE | BP | 100.00 | 93.18 |
| WCMFE | BP | 100.00 | 93.86 |
| Type | Group | Count | Mean | h | p-Value |
|---|---|---|---|---|---|
| Normal distribution test | Population 1 | 100 | 93.86 | 0 | 0.50 |
| Population 2 | 100 | 93.18 | 0 | 0.27 | |
| Homogeneity test of variance | Pooled | 200 | 93.52 | - | 0.09 |
| Reference Number | Feature Extraction Method | Top Recognition Rate (%) | Average Recognition Rate with 10 × 10-fold CV (%) |
|---|---|---|---|
| [5] | HHT | 87.14 | - |
| [9] | DWT | 92.40 | - |
| [12] | WPE | 88.57 | - |
| [15] | WT+ICA | 95.30 | - |
| This paper | WCMFE | 100.00 | 93.86 |
| Reference Number | Feature Extraction Method | Classification Method | Top Classification Rate (%) | Average Classification Rate with 10 × 10-fold CV (%) |
|---|---|---|---|---|
| [5] | HHT | BP | 87.14 | - |
| [6] | EMD | POS+SVM | 87.60 | - |
| [7] | EMD | SVM | 99.48 | - |
| [7] | EMD+FE | KNN | 99.39 | - |
| [8] | MEMD+STFT | KNN | 90.71 | - |
| [10] | DWT+AR | LDA | 90.00 | - |
| [11] | DWT+FE | SVM | 98.44 | - |
| [12] | WPE | BP | 88.57 | - |
| [15] | CSP | SVM | 82.86 | - |
| [42] | WT | Bayes | 89.29 | - |
| [43] | ERD | LDA | 86.43 | - |
| [44] | AR | LDA | 84.29 | - |
| This paper | WCMFE | BP | 100.00 | 93.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Wang, R.; Xu, D. An Improved Composite Multiscale Fuzzy Entropy for Feature Extraction of MI-EEG. Entropy 2020, 22, 1356. https://doi.org/10.3390/e22121356
Li M, Wang R, Xu D. An Improved Composite Multiscale Fuzzy Entropy for Feature Extraction of MI-EEG. Entropy. 2020; 22(12):1356. https://doi.org/10.3390/e22121356
Chicago/Turabian StyleLi, Mingai, Ruotu Wang, and Dongqin Xu. 2020. "An Improved Composite Multiscale Fuzzy Entropy for Feature Extraction of MI-EEG" Entropy 22, no. 12: 1356. https://doi.org/10.3390/e22121356
APA StyleLi, M., Wang, R., & Xu, D. (2020). An Improved Composite Multiscale Fuzzy Entropy for Feature Extraction of MI-EEG. Entropy, 22(12), 1356. https://doi.org/10.3390/e22121356




