Black-Hole Models in Loop Quantum Gravity
Abstract
:1. Introduction
2. Proposals
2.1. Basic Premise of Bounce-Based Black Holes
- (i)
- It must be possible to obtain the effect as a specific solution of a consistent set of field equations.
- (ii)
- Together with the specific solution required by (i), there must be a set of solutions related to by gauge transformations that
- (a)
- Preserve the field equations and
- (b)
- Have corresponding coordinate transformations from to such that .
- (ii.b’)
- The gauge transformations are such that their classical limit has corresponding coordinate transformations from to with .
2.2. Modifications Suggested by Loop Quantum Cosmology
2.3. Violations of General Covariance
2.3.1. Slicing Dependence
2.3.2. Spherically Symmetric Models
3. Modified Space-Time Structure
3.1. Anomaly-Freedom
3.2. Signature Change
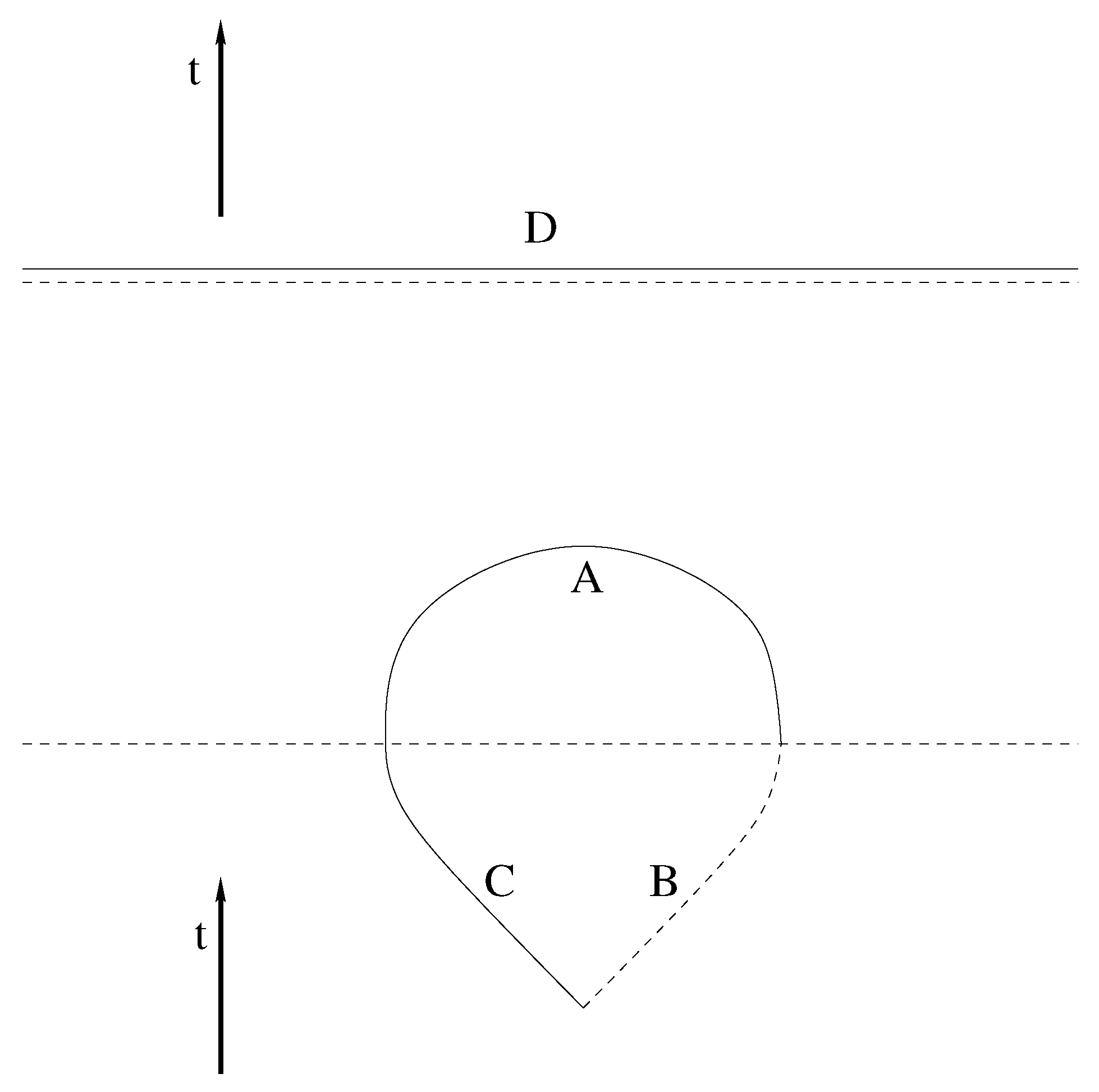
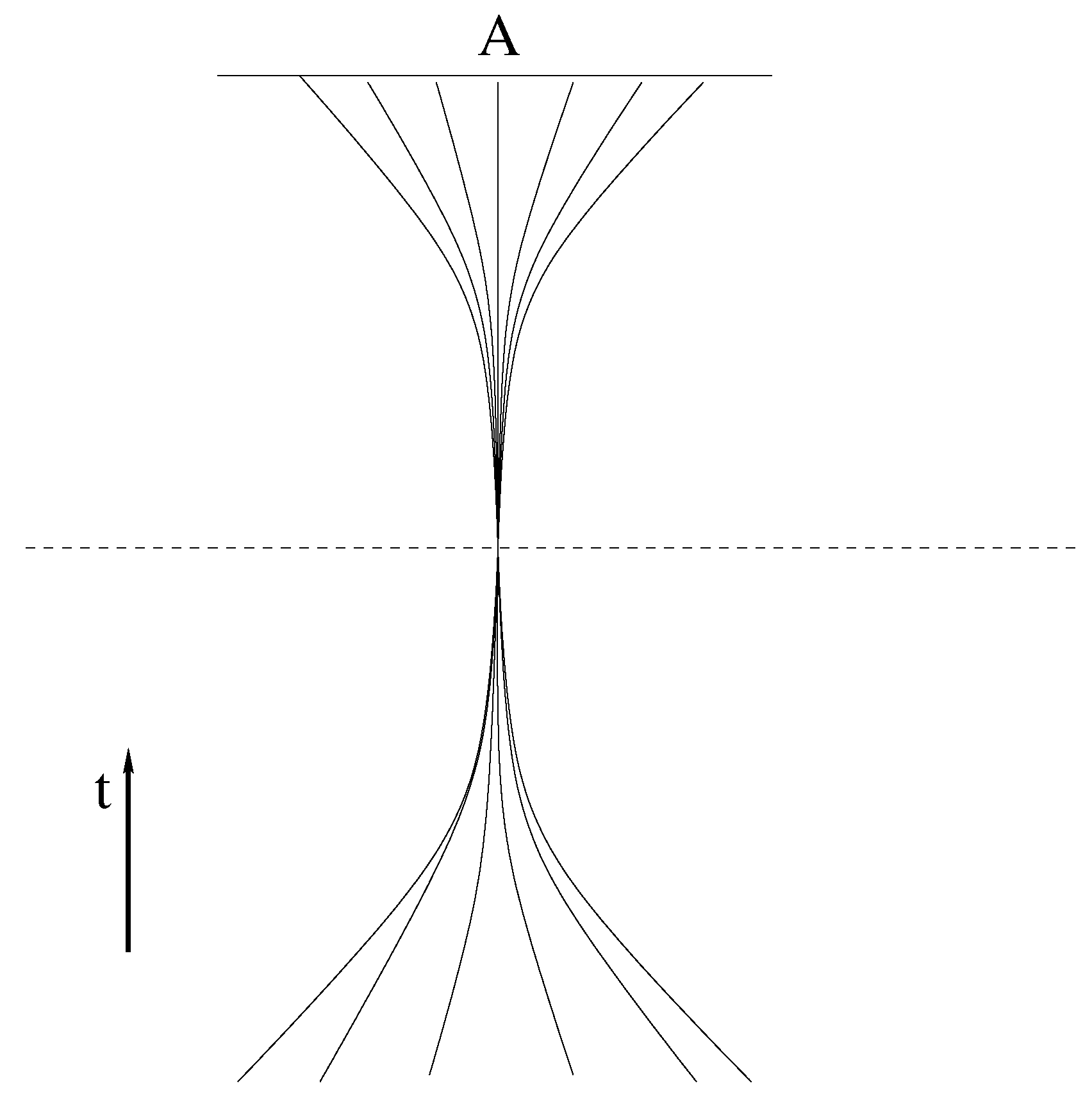
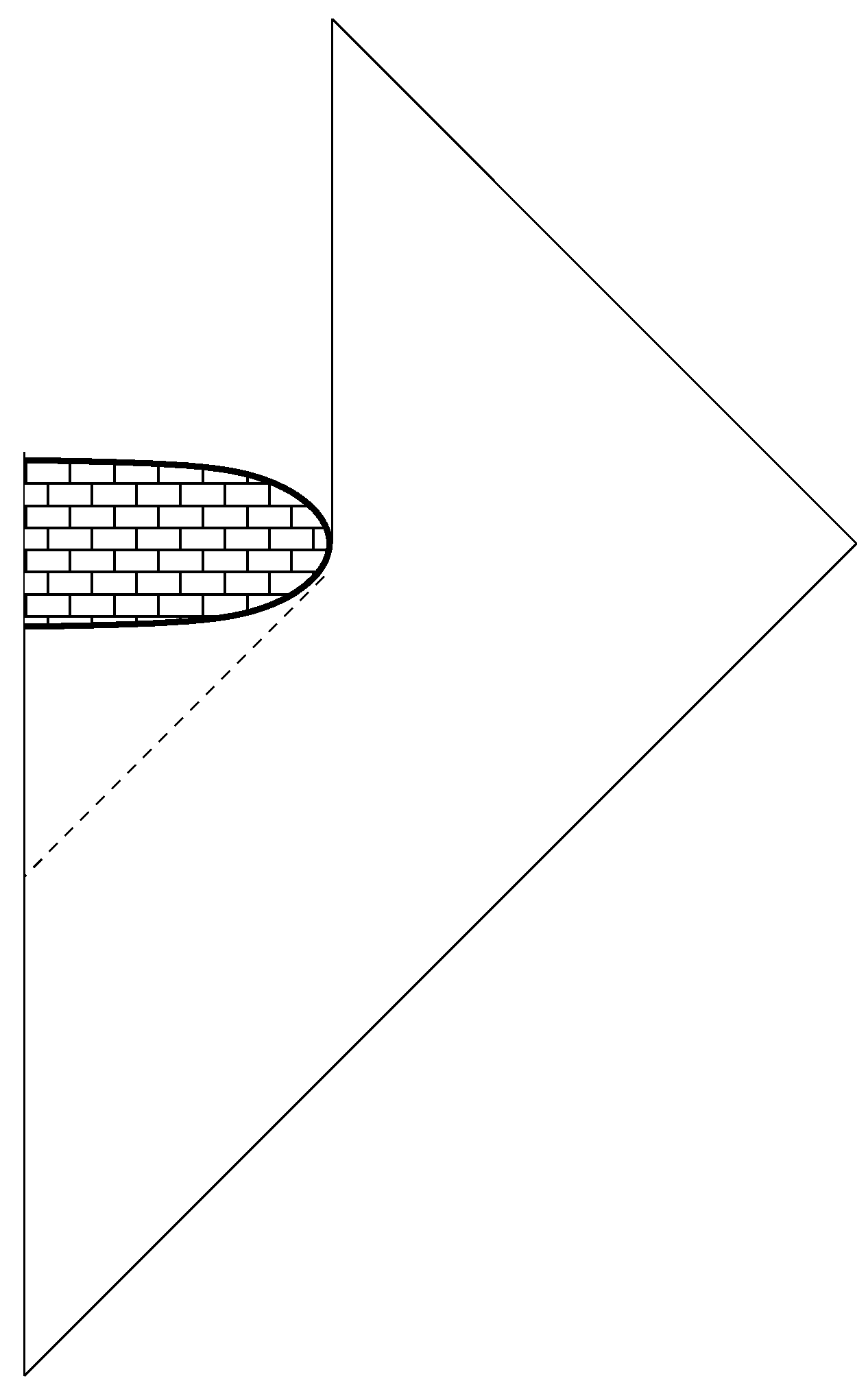
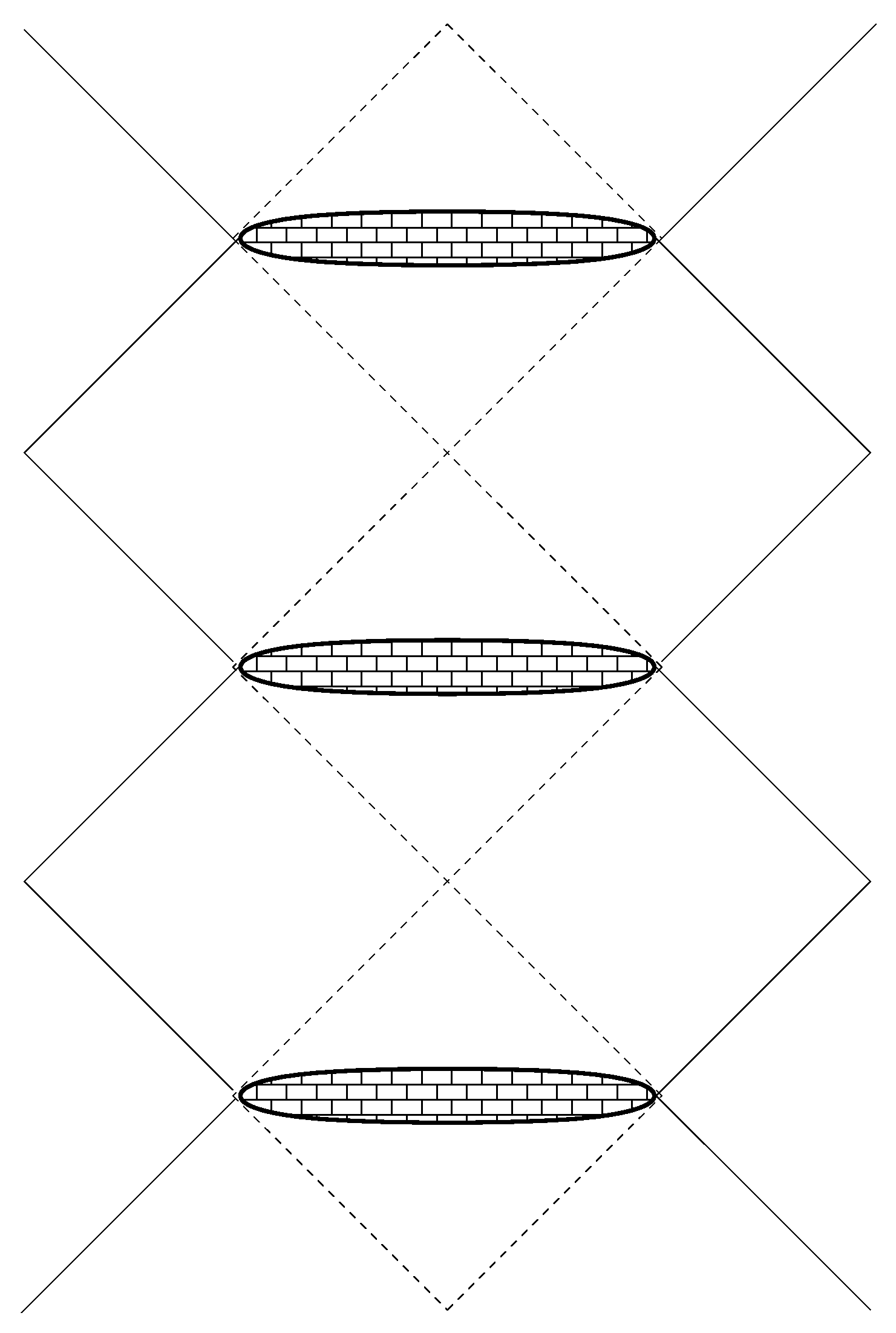
3.3. Signature Change and Non-Singular Space-Time
3.4. Evaporation Scenarios Ruled Out by Signature Change
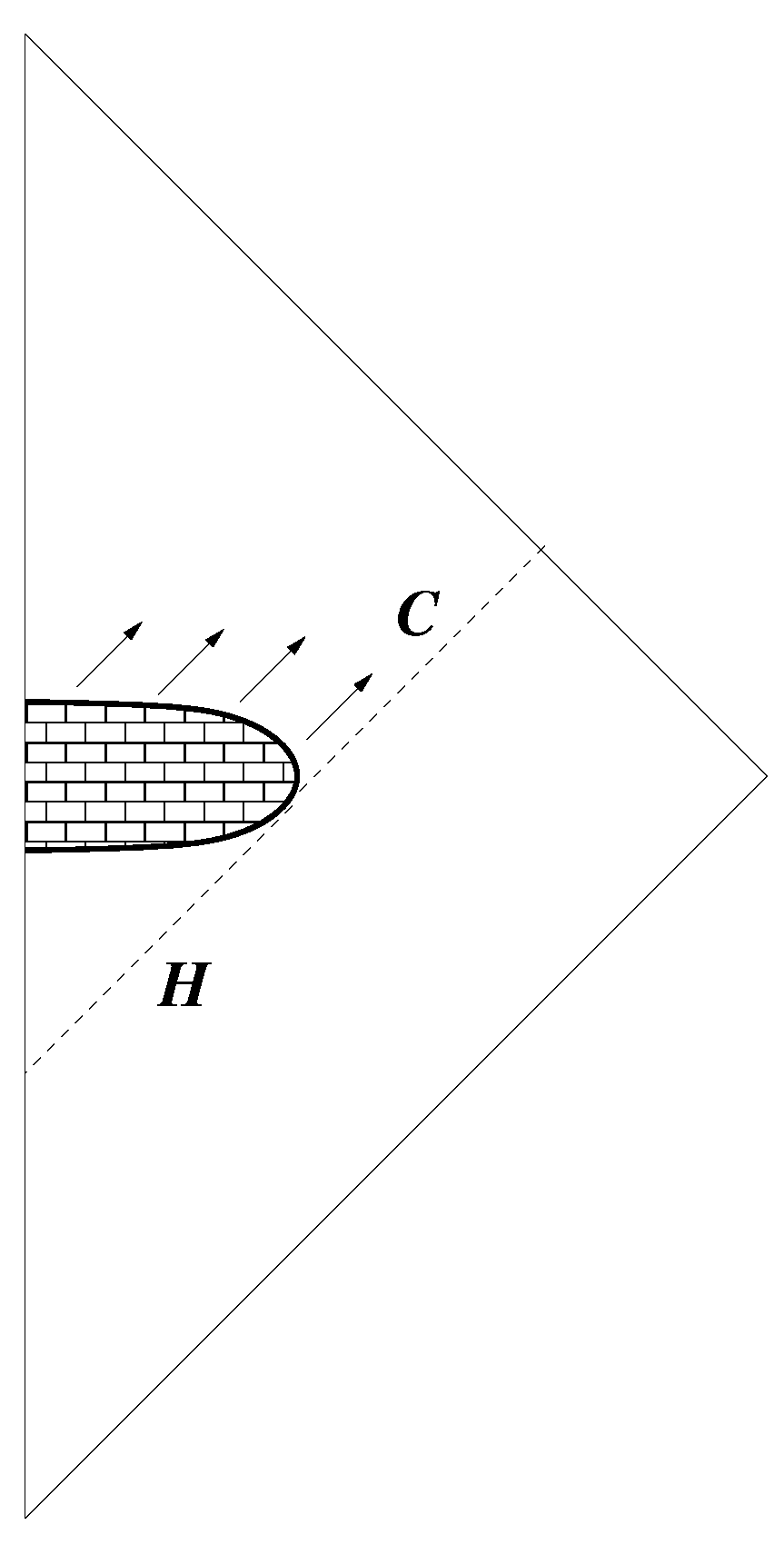
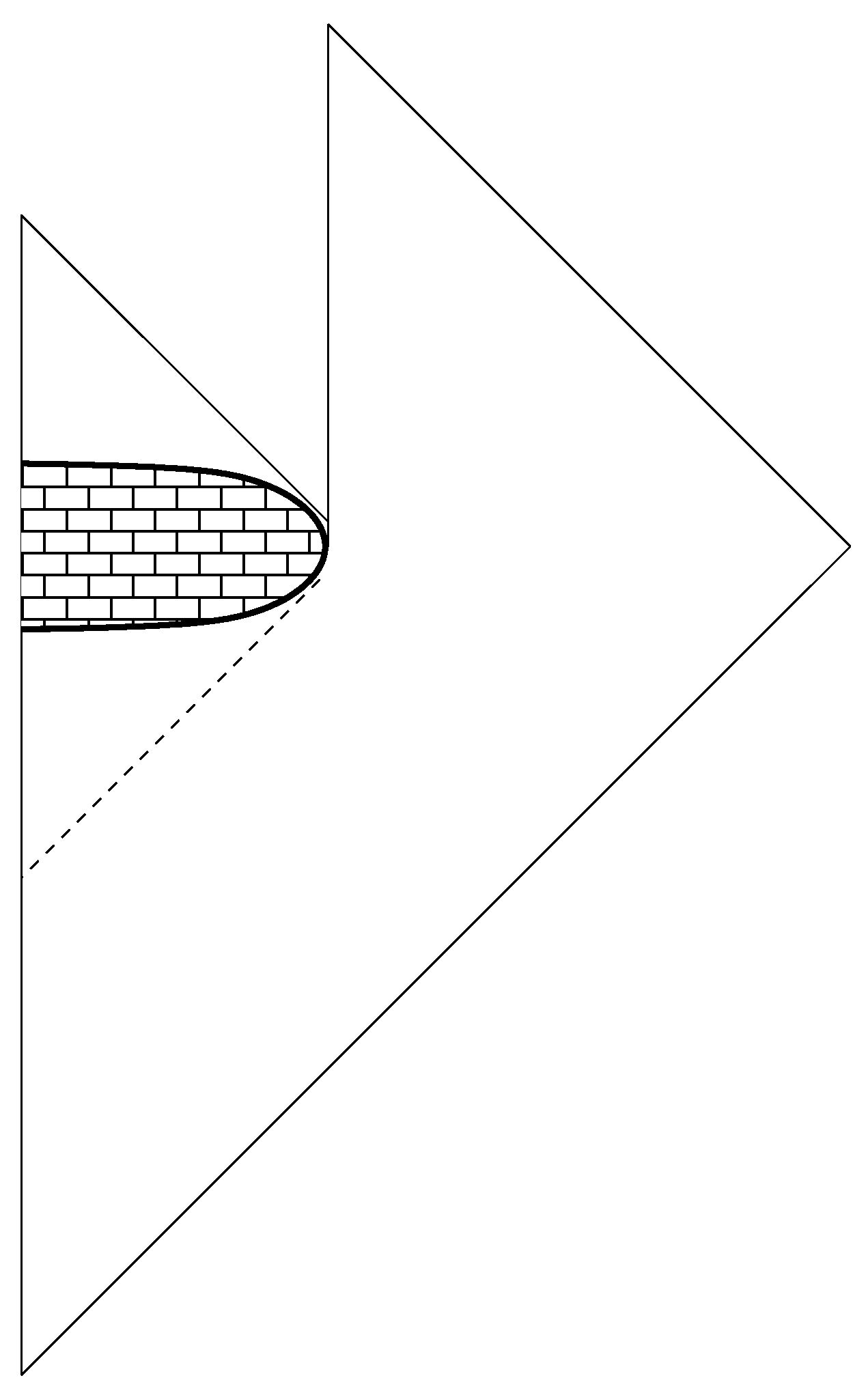
3.5. Evaporation Scenarios Consistent with Signature Change
3.6. Unexpected Relationships with Other Approaches
3.7. Avoiding Signature Change in Models of Loop Quantum Gravity
4. Conclusions
Funding
Conflicts of Interest
References
- Bojowald, M.; Brahma, S.; Reyes, J.D. Covariance in models of loop quantum gravity: Spherical symmetry. Phys. Rev. D 2015, 92, 045043. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M. Comment (2) on “Quantum Transfiguration of Kruskal Black Holes”. arXiv 2019, arXiv:1906.04650. [Google Scholar]
- Bojowald, M. Non-covariance of the dressed-metric approach in loop quantum cosmology. Phys. Rev. D 2020, 102, 023532. [Google Scholar] [CrossRef]
- Bojowald, M. No-go result for covariance in models of loop quantum gravity. Phys. Rev. D 2020, 102, 046006. [Google Scholar]
- Martín-Benito, M.; Garay, L.J.; Mena Marugán, G.A. Hybrid Quantum Gowdy Cosmology: Combining Loop and Fock Quantizations. Phys. Rev. D 2008, 78, 083516. [Google Scholar] [CrossRef] [Green Version]
- Agulló, I.; Ashtekar, A.; Nelson, W. An Extension of the Quantum Theory of Cosmological Perturbations to the Planck Era. Phys. Rev. D 2013, 87, 043507. [Google Scholar] [CrossRef] [Green Version]
- Gambini, R.; Pullin, J. Loop quantization of the Schwarzschild black hole. Phys. Rev. Lett. 2013, 110, 211301. [Google Scholar] [CrossRef] [Green Version]
- Ashtekar, A.; Olmedo, J.; Singh, P. Quantum Transfiguration of Kruskal Black Holes. Phys. Rev. Lett. 2018, 121, 241301. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M.; Hossain, G.; Kagan, M.; Shankaranarayanan, S. Anomaly freedom in perturbative loop quantum gravity. Phys. Rev. D 2008, 78, 063547. [Google Scholar] [CrossRef] [Green Version]
- Reyes, J.D. Spherically Symmetric Loop Quantum Gravity: Connections to 2-Dimensional Models and Applications to Gravitational Collapse. Ph.D. Thesis, The Pennsylvania State University, State College, PA, USA, 2009. [Google Scholar]
- Bojowald, M.; Reyes, J.D.; Tibrewala, R. Non-marginal LTB-like models with inverse triad corrections from loop quantum gravity. Phys. Rev. D 2009, 80, 084002. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M.; Paily, G.M.; Reyes, J.D. Discreteness corrections and higher spatial derivatives in effective canonical quantum gravity. Phys. Rev. D 2014, 90, 025025. [Google Scholar] [CrossRef] [Green Version]
- Brahma, S. Spherically symmetric canonical quantum gravity. Phys. Rev. D 2015, 91, 124003. [Google Scholar] [CrossRef] [Green Version]
- Cailleteau, T.; Mielczarek, J.; Barrau, A.; Grain, J. Anomaly-free scalar perturbations with holonomy corrections in loop quantum cosmology. Class. Quant. Grav. 2012, 29, 095010. [Google Scholar] [CrossRef]
- Cailleteau, T.; Linsefors, L.; Barrau, A. Anomaly-free perturbations with inverse-volume and holonomy corrections in Loop Quantum Cosmology. Class. Quantum Grav. 2014, 31, 125011. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M.; Paily, G.M. Deformed General Relativity and Effective Actions from Loop Quantum Gravity. Phys. Rev. D 2012, 86, 104018. [Google Scholar] [CrossRef] [Green Version]
- Barrau, A.; Bojowald, M.; Calcagni, G.; Grain, J.; Kagan, M. Anomaly-free cosmological perturbations in effective canonical quantum gravity. JCAP 2015, 2015, 051. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M.; Brahma, S.; Büyükçam, U.; Ronco, M. Extending general covariance: Moyal-type noncommutative manifolds. Phys. Rev. D 2018, 98, 026031. [Google Scholar] [CrossRef] [Green Version]
- Calcagni, G.; Ronco, M. Deformed symmetries in noncommutative and multifractional spacetimes. Phys. Rev. D 2017, 95, 045001. [Google Scholar] [CrossRef]
- Bojowald, M.; Paily, G.M. Deformed General Relativity. Phys. Rev. D 2013, 87, 044044. [Google Scholar] [CrossRef] [Green Version]
- Amelino-Camelia, G.; da Silva, M.M.; Ronco, M.; Cesarini, L.; Lecian, O.M. Spacetime-noncommutativity regime of Loop Quantum Gravity. Phys. Rev. D 2017, 95, 024028. [Google Scholar] [CrossRef] [Green Version]
- Perez, A. Black Holes in Loop Quantum Gravity. Rept. Prog. Phys. 2017, 80, 126901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rovelli, C.; Vidotto, F. Planck stars. Int. J. Mod. Phys. D 2014, 23, 1442026. [Google Scholar] [CrossRef]
- Bojowald, M. Critical Evaluation of Common Claims in Loop Quantum Cosmology. Universe 2020, 6, 36. [Google Scholar] [CrossRef] [Green Version]
- Hayward, S.A. Formation and evaporation of non-singular black holes. Phys. Rev. Lett. 2006, 96, 031103. [Google Scholar] [CrossRef] [Green Version]
- Haggard, H.M.; Rovelli, C. Black hole fireworks: Quantum-gravity effects outside the horizon spark black to white hole tunneling. Phys. Rev. D 2015, 92, 104020. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M.; Perez, A. Spin Foam Quantization and Anomalies. Gen. Rel. Grav. 2010, 42, 877. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M.; Skirzewski, A. Effective Equations of Motion for Quantum Systems. Rev. Math. Phys. 2006, 18, 713–745. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M.; Skirzewski, A. Quantum Gravity and Higher Curvature Actions. Int. J. Geom. Meth. Mod. Phys. 2007, 4, 25–52. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M.; Sandhöfer, B.; Skirzewski, A.; Tsobanjan, A. Effective constraints for quantum systems. Rev. Math. Phys. 2009, 21, 111–154. [Google Scholar] [CrossRef]
- Bojowald, M. Quantum cosmology: A review. Rep. Prog. Phys. 2015, 78, 023901. [Google Scholar] [CrossRef]
- Bojowald, M. Foundations of Quantum Cosmology; Institute of Physics: London, UK, 2020. [Google Scholar]
- Vandersloot, K. On the Hamiltonian Constraint of Loop Quantum Cosmology. Phys. Rev. D 2005, 71, 103506. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M. Isotropic Loop Quantum Cosmology. Class. Quantum Grav. 2002, 19, 2717–2741. [Google Scholar] [CrossRef] [Green Version]
- Rovelli, C.; Smolin, L. Loop Space Representation of Quantum General Relativity. Nucl. Phys. B 1990, 331, 80–152. [Google Scholar] [CrossRef]
- Ashtekar, A.; Lewandowski, J.; Marolf, D.; Mourão, J.; Thiemann, T. Quantization of Diffeomorphism Invariant Theories of Connections with Local Degrees of Freedom. J. Math. Phys. 1995, 36, 6456. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M. Large scale effective theory for cosmological bounces. Phys. Rev. D 2007, 75, 081301(R). [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M. How quantum is the big bang? Phys. Rev. Lett. 2008, 100, 221301. [Google Scholar] [CrossRef]
- Bojowald, M. The BKL scenario, infrared renormalization, and quantum cosmology. JCAP 2019, 2019, 026. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M. Effective field theory of loop quantum cosmology. Universe 2019, 5, 44. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M. Non-bouncing solutions in loop quantum cosmology. JCAP 2020, 2020, 029. [Google Scholar] [CrossRef]
- Thiemann, T. Quantum Spin Dynamics (QSD). Class. Quantum Grav. 1998, 15, 839–873. [Google Scholar] [CrossRef] [Green Version]
- Perez, A.; Pranzetti, D. On the regularization of the constraints algebra of Quantum Gravity in 2+1 dimensions with non-vanishing cosmological constant. Class. Quantum Grav. 2010, 27, 145009. [Google Scholar] [CrossRef] [Green Version]
- Tomlin, C.; Varadarajan, M. Towards an Anomaly-Free Quantum Dynamics for a Weak Coupling Limit of Euclidean Gravity. Phys. Rev. D 2013, 87, 044039. [Google Scholar] [CrossRef] [Green Version]
- Henderson, A.; Laddha, A.; Tomlin, C. Constraint algebra in LQG reloaded: Toy model of a U(1)3 Gauge Theory I. Phys. Rev. D 2013, 88, 044028. [Google Scholar] [CrossRef] [Green Version]
- Henderson, A.; Laddha, A.; Tomlin, C. Constraint algebra in LQG reloaded: Toy model of an Abelian gauge theory—II Spatial Diffeomorphisms. Phys. Rev. D 2013, 88, 044029. [Google Scholar] [CrossRef] [Green Version]
- Laddha, A. Hamiltonian constraint in Euclidean LQG revisited: First hints of off-shell Closure. arXiv 2014, arXiv:1401.0931. [Google Scholar]
- Varadarajan, M. The constraint algebra in Smolins’ G→0 limit of 4d Euclidean Gravity. Phys. Rev. D 2018, 97, 106007. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M. Homogeneous loop quantum cosmology. Class. Quantum Grav. 2003, 20, 2595–2615. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M.; Cartin, D.; Khanna, G. Lattice refining loop quantum cosmology, anisotropic models and stability. Phys. Rev. D 2007, 76, 064018. [Google Scholar] [CrossRef] [Green Version]
- Frolov, V.P.; Vilkovisky, G.A. Spherically symmetric collapse in quantum gravity. Phys. Lett. B 1981, 106, 307–313. [Google Scholar] [CrossRef]
- Roman, T.A.; Bergmann, P.G. Stellar collapse without singularities? Phys. Rev. D 1983, 28, 1265–1277. [Google Scholar] [CrossRef]
- Ashtekar, A.; Bojowald, M. Quantum Geometry and the Schwarzschild Singularity. Class. Quantum Grav. 2006, 23, 391–411. [Google Scholar] [CrossRef] [Green Version]
- Ashtekar, A.; Taveras, V.; Varadarajan, M. Information is Not Lost in the Evaporation of 2-dimensional Black Holes. Phys. Rev. Lett. 2008, 100, 211302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Modesto, L. The Kantowski-Sachs Space-Time in Loop Quantum Gravity. Int. J. Theor. Phys. 2006, 45, 2235–2246. [Google Scholar] [CrossRef] [Green Version]
- Modesto, L. Loop quantum black hole. Class. Quantum Grav. 2006, 23, 5587–5601. [Google Scholar] [CrossRef] [Green Version]
- Bodendorfer, N.; Mele, F.M.; Münch, J. A note on the Hamiltonian as a polymerisation parameter. Class. Quantum Grav. 2019, 36, 187001. [Google Scholar] [CrossRef] [Green Version]
- Bouhmadi-López, M.; Brahma, S.; Chen, C.Y.; Chen, P.; Yeom, D.H. Asymptotic non-flatness of an effective black hole model based on loop quantum gravity. Phys. Dark Univ. 2020, 30, 100701. [Google Scholar] [CrossRef]
- Bodendorfer, N.; Mele, F.M.; Münch, J. Effective Quantum Extended Spacetime of Polymer Schwarzschild Black Hole. Class. Quantum Grav. 2019, 36, 195015. [Google Scholar] [CrossRef] [Green Version]
- Bodendorfer, N.; Mele, F.M.; Münch, J. (b,v)-type variables for black to white hole transitions in effective loop quantum gravity. arXiv 2019, arXiv:1911.12646. [Google Scholar]
- Bodendorfer, N.; Mele, F.M.; Münch, J. Mass and Horizon Dirac Observables in Effective Models of Quantum Black-to-White Hole Transition. arXiv 2019, arXiv:1912.00774. [Google Scholar]
- Faraoni, V.; Giusti, A. Unsettling physics in the quantum-corrected Schwarzschild black hole. Symmetry 2020, 12, 1264. [Google Scholar] [CrossRef]
- Strobl, T. Gravity in Two Spacetime Dimensions. arXiv 2000, arXiv:hep-th/0011240. [Google Scholar]
- Bojowald, M.; Brahma, S. Signature change in 2-dimensional black-hole models of loop quantum gravity. Phys. Rev. D 2018, 98, 026012. [Google Scholar] [CrossRef] [Green Version]
- Kunstatter, G.; Maeda, H.; Taves, T. New 2D dilaton gravity for nonsingular black holes. Class. Quant. Grav. 2016, 33, 105005. [Google Scholar] [CrossRef]
- Takahashi, K.; Kobayashi, T. Generalized 2D dilaton gravity and KGB. Class. Quant. Grav. 2019, 36, 095003. [Google Scholar] [CrossRef] [Green Version]
- Horndeski, G.W. Second-order scalar-tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 1974, 10, 363–384. [Google Scholar] [CrossRef]
- Rovelli, C. Viewpoint: Black Hole Evolution Traced Out with Loop Quantum Gravity. arXiv 2019, arXiv:1901.04732. [Google Scholar]
- Benitez, F.; Gambini, R.; Lehner, L.; Liebling, S.; Pullin, J. Critical collapse of a scalar field in semiclassical loop quantum gravity. Phys. Rev. Lett. 2020, 124, 071301. [Google Scholar] [CrossRef] [Green Version]
- Kelly, J.G.; Santacruz, R.; Wilson-Ewing, E. Effective loop quantum gravity framework for vacuum spherically symmetric space-times. arXiv 2020, arXiv:2006.09302. [Google Scholar]
- Kelly, J.G.; Santacruz, R.; Wilson-Ewing, E. Black hole collapse and bounce in effective loop quantum gravity. arXiv 2020, arXiv:2006.09325. [Google Scholar]
- Dirac, P.A.M. The theory of gravitation in Hamiltonian form. Proc. Roy. Soc. A 1958, 246, 333–343. [Google Scholar]
- Arnowitt, R.; Deser, S.; Misner, C.W. The Dynamics of General Relativity. Gen. Rel. Grav. 2008, 40, 1997–2027. [Google Scholar] [CrossRef] [Green Version]
- Hojman, S.A.; Kuchař, K.; Teitelboim, C. Geometrodynamics Regained. Ann. Phys. (N. Y.) 1976, 96, 88–135. [Google Scholar] [CrossRef]
- Gambini, R.; Olmedo, J.; Pullin, J. Spherically symmetric loop quantum gravity: Analysis of improved dynamics. arXiv 2020, arXiv:2006.01513. [Google Scholar] [CrossRef]
- Tibrewala, R. Spherically symmetric Einstein-Maxwell theory and loop quantum gravity corrections. Class. Quantum Grav. 2012, 29, 235012. [Google Scholar] [CrossRef]
- Gambini, R.; Pullin, J. Hawking radiation from a spherical loop quantum gravity black hole. Class. Quant. Grav. 2014, 31, 115003. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M.; Brahma, S.; Ding, D.; Ronco, M. Deformed covariance in spherically symmetric vacuum models of loop quantum gravity: Consistency in Euclidean and self-dual gravity. Phys. Rev. D 2020, 101, 026001. [Google Scholar] [CrossRef] [Green Version]
- Deruelle, N.; Sasaki, M.; Sendouda, Y.; Yamauchi, D. Hamiltonian formulation of f(Riemann) theories of gravity. Prog. Theor. Phys. 2010, 123, 169–185. [Google Scholar] [CrossRef] [Green Version]
- Aruga, D.; Ben Achour, J.; Noui, K. Deformed General Relativity and Quantum Black Holes Interior. Universe 2020, 6, 39. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M.; Brahma, S.; Yeom, D.H. Effective line elements and black-hole models in canonical (loop) quantum gravity. Phys. Rev. D 2018, 98, 046015. [Google Scholar] [CrossRef] [Green Version]
- Salisbury, D.C.; Sundermeyer, K. The Realization in Phase Space of General Coordinate Transformations. Phys. Rev. D 1983, 27, 740. [Google Scholar] [CrossRef]
- Bojowald, M. Canonical Gravity and Applications: Cosmology, Black Holes, and Quantum Gravity; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Ben Achour, J.; Lamy, F.; Liu, H.; Noui, K. Polymer Schwarzschild black hole: An effective metric. Eur. Phys. Lett. 2018, 123, 20006. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M.; Mielczarek, J. Some implications of signature-change in cosmological models of loop quantum gravity. JCAP 2015, 2015, 052. [Google Scholar] [CrossRef] [Green Version]
- Tricomi, F.G. Repertorium der Theorie der Differentialgleichungen; Springer: Berlin/Heidelberg, Germany, 1968. [Google Scholar]
- Bolliet, B.; Barrau, A.; Grain, J.; Schander, S. Observational Exclusion of a Consistent Quantum Cosmology Scenario. Phys. Rev. D 2016, 93, 124011. [Google Scholar] [CrossRef] [Green Version]
- Barrau, A.; Grain, J. Cosmology without time: What to do with a possible signature change from quantum gravitational origin? arXiv 2016, arXiv:1607.07589. [Google Scholar]
- Ellis, G.F.R.; Sumeruk, A.; Coule, D.; Hellaby, C. Change of signature in classical relativity. Class. Quantum Grav. 1992, 9, 1535–1554. [Google Scholar] [CrossRef]
- Hayward, S.A. Junction Conditions for Signature Change. arXiv 1993, arXiv:gr-qc/9303034. [Google Scholar]
- Dray, T.; Manogue, C.A.; Tucker, R.W. Boundary conditions for the scalar field in the presence of signature change. Class. Quantum Grav. 1995, 12, 2767–2777. [Google Scholar] [CrossRef]
- Alty, L.J.; Fewster, C.J. Initial Value Problems and Signature Change. Class. Quant. Grav. 1996, 13, 1129–1148. [Google Scholar] [CrossRef]
- Dray, T.; Ellis, G.F.R.; Hellaby, C.; Manogue, C.A. Gravity and signature change. Gen. Rel. Grav. 1997, 29, 591–597. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M. Information loss, made worse by quantum gravity. Front. Phys. 2015, 3, 33. [Google Scholar] [CrossRef] [Green Version]
- Horowitz, G.T.; Maldacena, J.M. The Black hole final state. JHEP 2004, 2004, 008. [Google Scholar] [CrossRef] [Green Version]
- Bouhmadi-López, M.; Brahma, S.; Chen, C.Y.; Chen, P.; Yeom, D.H. Annihilation-to-nothing: A quantum gravitational boundary condition for the Schwarzschild black hole. arXiv 2019, arXiv:1911.02129. [Google Scholar]
- Engelhardt, N.; Horowitz, G.T. Holographic Consequences of a No Transmission Principle. Phys. Rev. D 2016, 93, 026005. [Google Scholar] [CrossRef] [Green Version]
- Ripley, J.L.; Pretorius, F. Gravitational Collapse in Einstein dilaton Gauss-Bonnet Gravity. Class. Quantum Grav. 2019, 36, 134001. [Google Scholar] [CrossRef] [Green Version]
- Ripley, J.L.; Pretorius, F. Dynamics of a Z2 symmetric EdGB gravity in spherical symmetry. Class. Quant. Grav. 2020, 37, 155003. [Google Scholar] [CrossRef]
- Papallo, G.; Reall, H.S. On the local well-posedness of Lovelock and Horndeski theories. Phys. Rev. D 2017, 96, 044019. [Google Scholar] [CrossRef] [Green Version]
- Papallo, G. On the hyperbolicity of the most general Horndeski theory. Phys. Rev. D 2017, 96, 124036. [Google Scholar] [CrossRef] [Green Version]
- Ripley, J.L.; Pretorius, F. Hyperbolicity in Spherical Gravitational Collapse in a Horndeski Theory. Phys. Rev. D 2019, 99, 084014. [Google Scholar] [CrossRef] [Green Version]
- Kovacs, A.D.; Reall, H.S. Well-posed formulation of Lovelock and Horndeski theories. Phys. Rev. D 2020, 101, 124003. [Google Scholar] [CrossRef]
- Martin, J. Hamiltonian quantization of general relativity with the change of signature. Phys. Rev. D 1994, 49, 5086–5095. [Google Scholar] [CrossRef] [Green Version]
- Perry, M.J.; Teo, E. Nonsingularity of the exact two-dimensional string black hole. Phys. Rev. Lett. 1993, 70, 2669–2672. [Google Scholar] [CrossRef] [Green Version]
- Chaney, A.; Lu, L.; Stern, A. Lorentzian fuzzy spheres. Phys. Rev. D 2015, 92, 064021. [Google Scholar] [CrossRef] [Green Version]
- Chaney, A.; Stern, A. Fuzzy CP2 Space-Times. Phys. Rev. D 2017, 95, 046001. [Google Scholar] [CrossRef] [Green Version]
- Steinacker, H. Cosmological space-times with resolved Big Bang in Yang-Mills matrix models. JHEP 2018, 2018, 033. [Google Scholar] [CrossRef] [Green Version]
- Stern, A.; Xu, C. Signature change in matrix model solutions. Phys. Rev. D 2018, 98, 086015. [Google Scholar] [CrossRef] [Green Version]
- Ambjørn, J.; Coumbe, D.N.; Gizbert-Studnicki, J.; Jurkiewicz, J. Signature Change of the Metric in CDT Quantum Gravity? JHEP 2015, 2015, 033. [Google Scholar] [CrossRef] [Green Version]
- Ben Achour, J.; Brahma, S.; Grain, J.; Marciano, A. A new look at scalar perturbations in loop quantum cosmology: (Un)Deformed algebra approach using self dual variables. arXiv 2016, arXiv:1610.07467. [Google Scholar]
- Ben Achour, J.; Brahma, S.; Marciano, A. Spherically symmetric sector of self dual Ashtekar gravity coupled to matter: Anomaly-free algebra of constraints with holonomy corrections. Phys. Rev. D 2017, 96, 026002. [Google Scholar] [CrossRef] [Green Version]
- Ben Achour, J.; Brahma, S. Covariance in self dual inhomogeneous models of effective quantum geometry: Spherical symmetry and Gowdy systems. Phys. Rev. D 2018, 97, 126003. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.P.; Bojowald, M.; Ma, Y. Anomaly freedom in perturbative models of Euclidean loop quantum gravity. Phys. Rev. D 2018, 98, 106009. [Google Scholar] [CrossRef] [Green Version]
- Brahma, S.; Ronco, M.; Amelino-Camelia, G.; Marciano, A. Linking loop quantum gravity quantization ambiguities with phenomenology. Phys. Rev. D 2017, 95, 044005. [Google Scholar] [CrossRef] [Green Version]
- Brahma, S.; Ronco, M. Constraining the loop quantum gravity parameter space from phenomenology. Phys. Lett. B 2018, 778, 184. [Google Scholar] [CrossRef]
- Bojowald, M. Absence of a Singularity in Loop Quantum Cosmology. Phys. Rev. Lett. 2001, 86, 5227–5230. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Donoghue, J.F. General relativity as an effective field theory: The leading quantum corrections. Phys. Rev. D 1994, 50, 3874–3888. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Burgess, C.P. Quantum Gravity in Everyday Life: General Relativity as an Effective Field Theory. Living Rev. Relativity 2004, 7, 5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bojowald, M.; Brahma, S.; Nelson, E. Higher time derivatives in effective equations of canonical quantum systems. Phys. Rev. D 2012, 86, 105004. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M.; Brahma, S. Effective constraint algebras with structure functions. J. Phys. A Math. Theor. 2016, 49, 125301. [Google Scholar] [CrossRef] [Green Version]

© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bojowald, M. Black-Hole Models in Loop Quantum Gravity. Universe 2020, 6, 125. https://doi.org/10.3390/universe6080125
Bojowald M. Black-Hole Models in Loop Quantum Gravity. Universe. 2020; 6(8):125. https://doi.org/10.3390/universe6080125
Chicago/Turabian StyleBojowald, Martin. 2020. "Black-Hole Models in Loop Quantum Gravity" Universe 6, no. 8: 125. https://doi.org/10.3390/universe6080125




