Noise Suppression Strategies in Computer Holography: Methods and Techniques
Abstract
1. Introduction
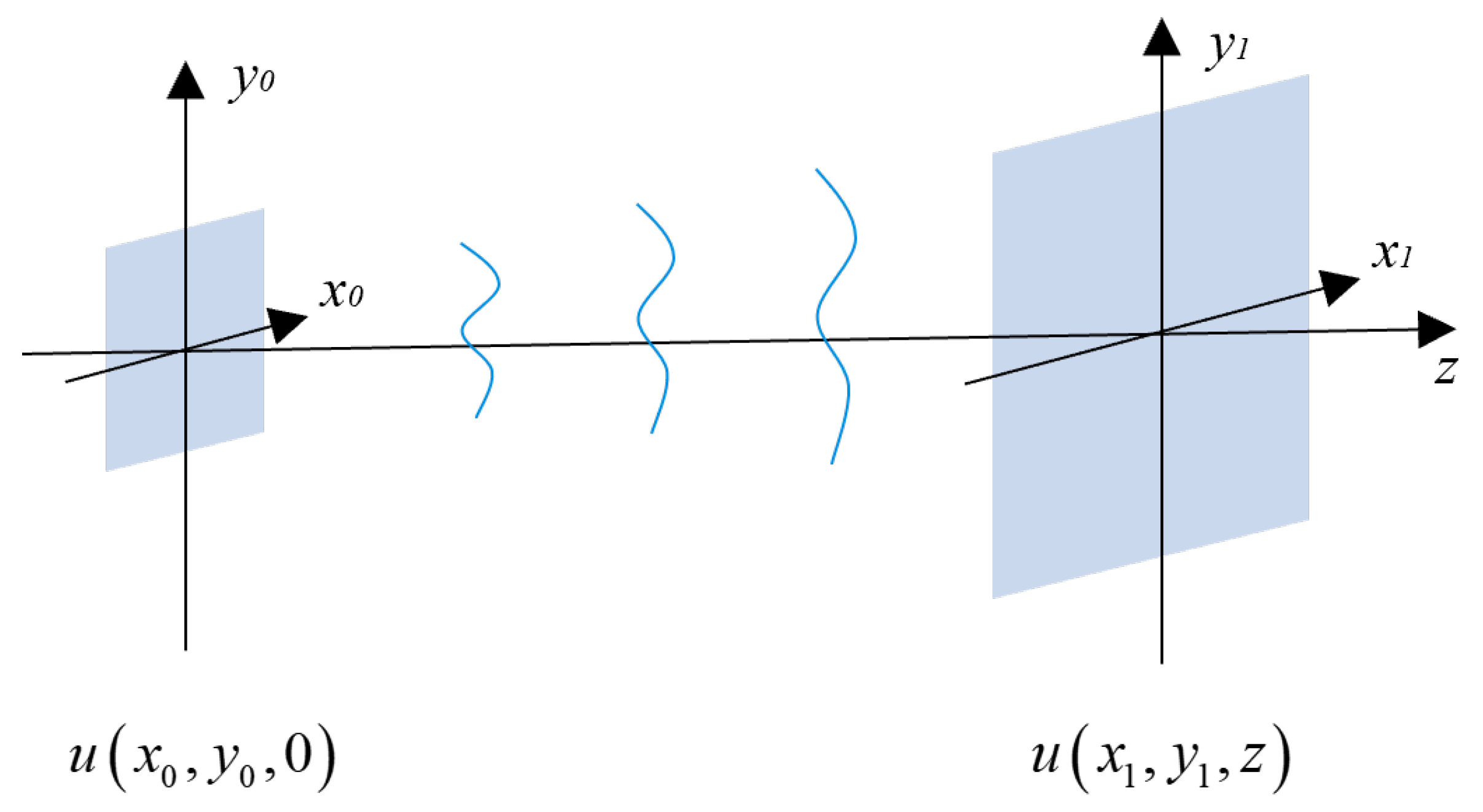
2. Diffraction Calculations
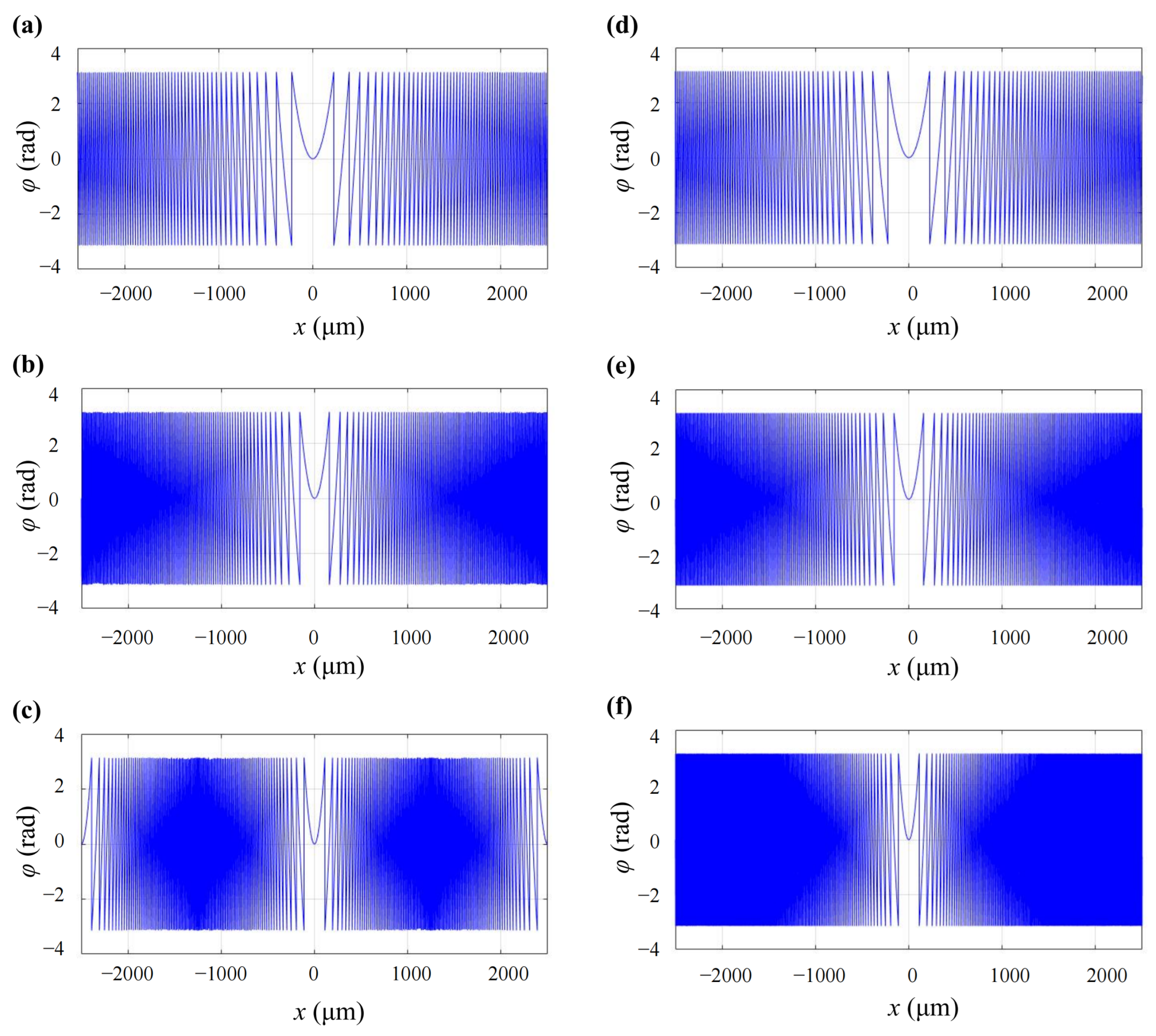
2.1. Sampling of Phase
2.2. Sampling of Intensity
2.3. Sampling of Amplitude
3. Encoding and Optimization Algorithms
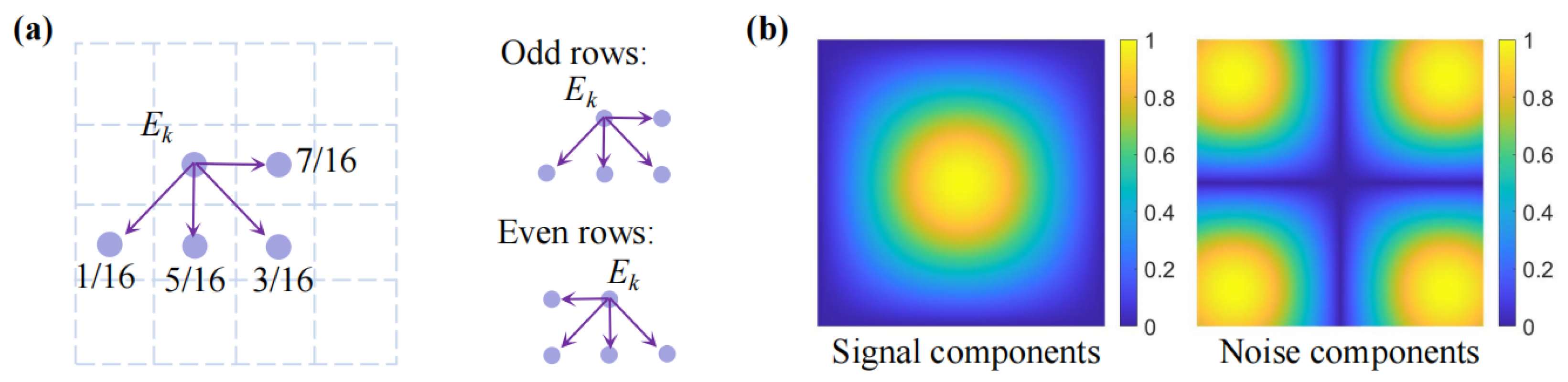
3.1. Encoding Method
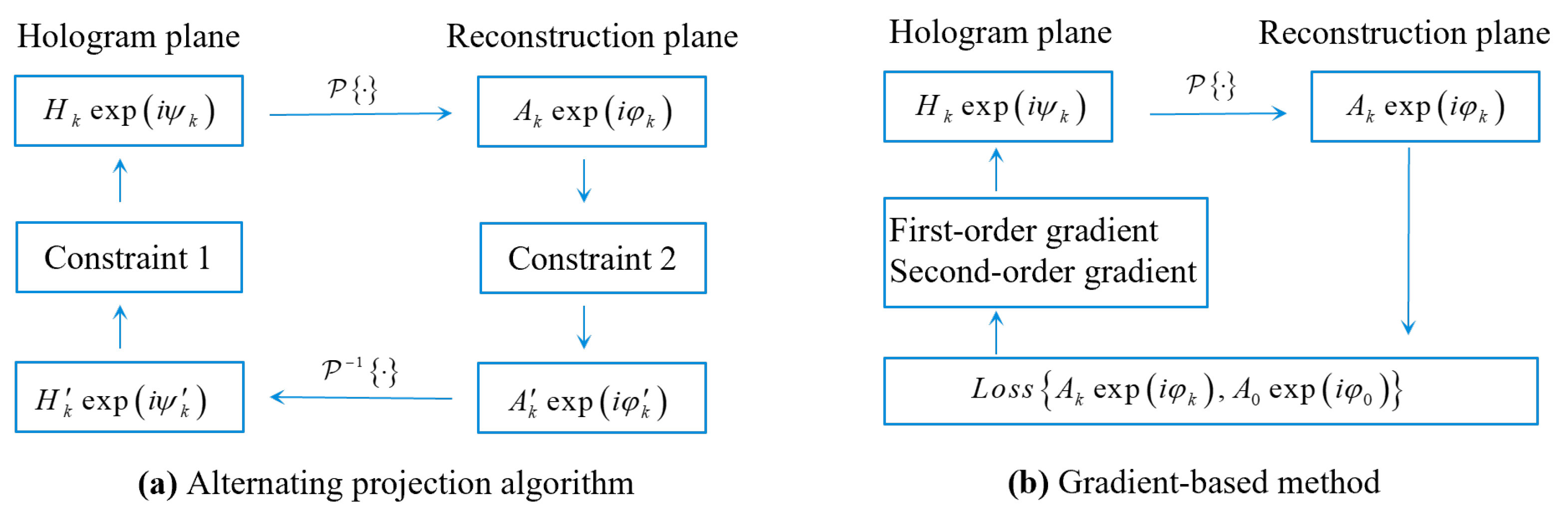
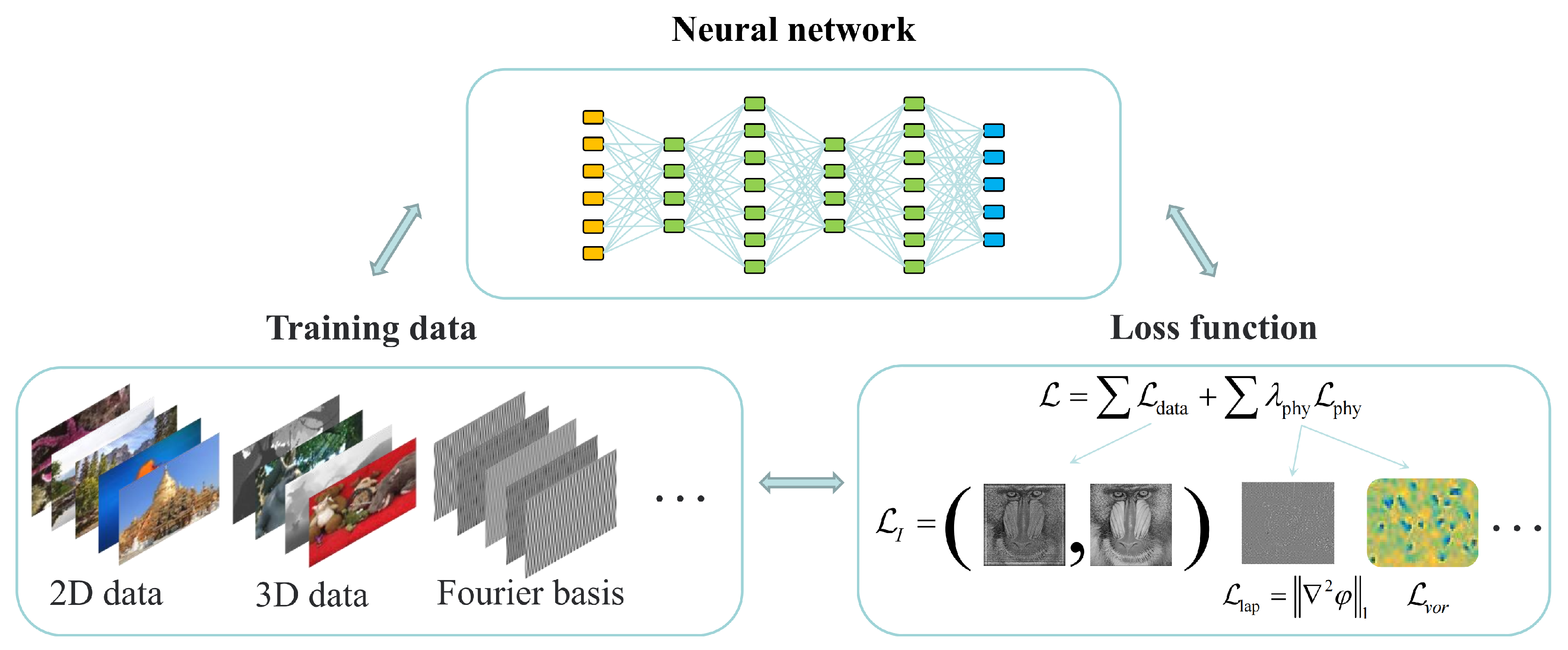
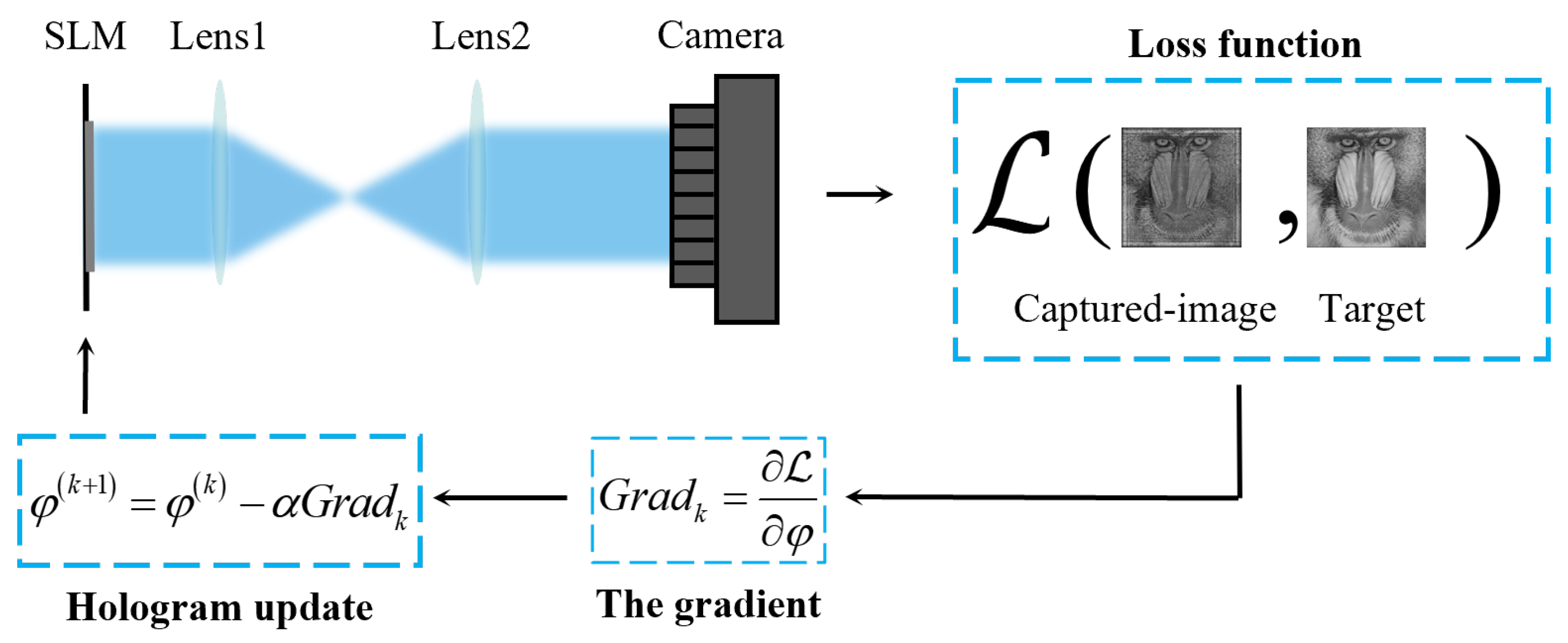
3.2. Optimization Algorithms
4. Modulation Device Noise
4.1. High Diffraction Order Noise
4.2. Quantization Noise
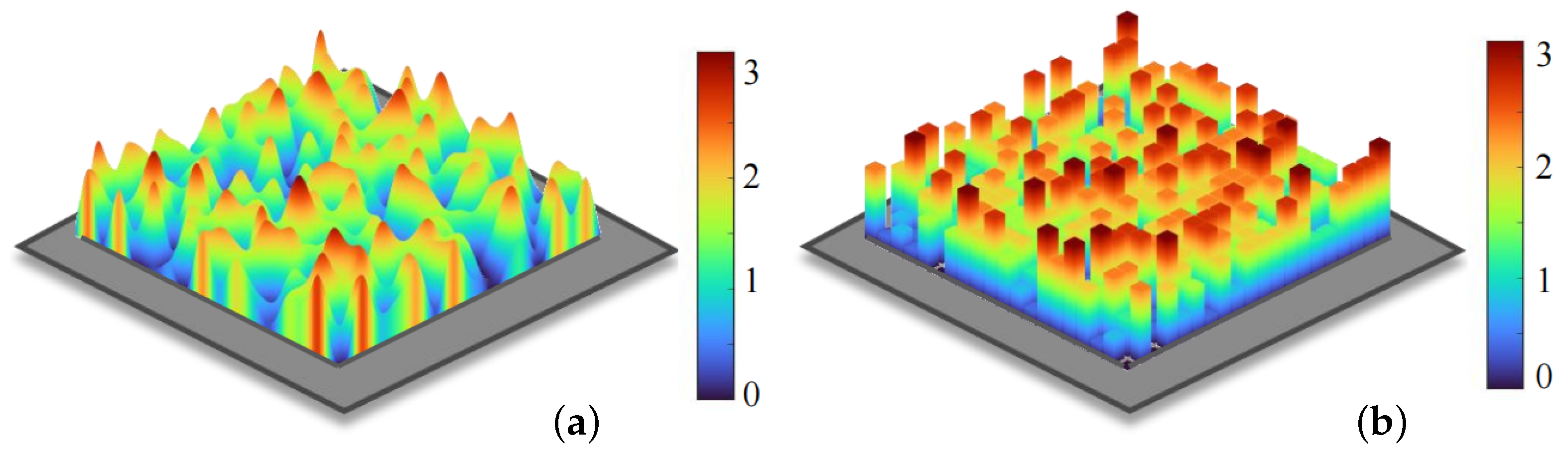
4.3. Zero-Order Noise
4.4. Modulation Errors
5. Coherent Noise
5.1. Speckle Noise
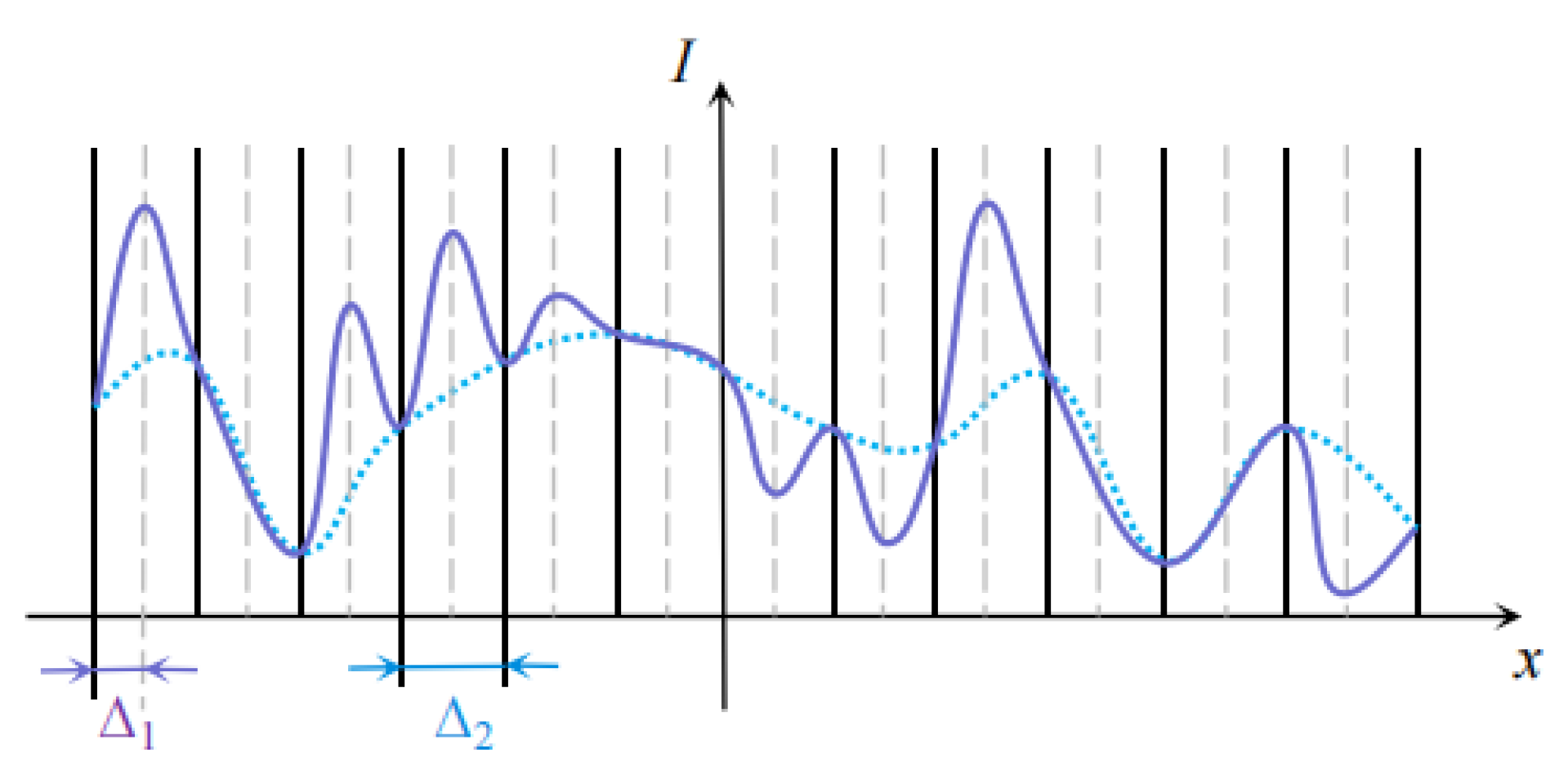
5.2. Gibbs Artifacts
6. Optical System Noise
7. Future Outlook
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gabor, D. A new microscopic principle. Nature 1948, 161, 777–778. [Google Scholar] [CrossRef]
- Leith, E.N.; Upatnieks, J. Reconstructed wavefronts and communication theory. J. Opt. Soc. Am. 1962, 52, 1123–1130. [Google Scholar] [CrossRef]
- Leith, E.N.; Upatnieks, J. Wavefront reconstruction with continuous-tone objects. J. Opt. Soc. Am. 1963, 53, 1377–1381. [Google Scholar] [CrossRef]
- Leith, E.N.; Upatnieks, J. Wavefront reconstruction with diffused illumination and three-dimensional objects. J. Opt. Soc. Am. 1964, 54, 1295–1301. [Google Scholar] [CrossRef]
- Javidi, B.; Carnicer, A.; Anand, A.; Barbastathis, G.; Chen, W.; Ferraro, P.; Goodman, J.W.; Horisaki, R.; Khare, K.; Kujawinska, M.; et al. Roadmap on digital holography. Opt. Express 2021, 29, 35078–35118. [Google Scholar] [CrossRef]
- Lohmann, A.W.; Weigelt, G.; Wirnitzer, B. Speckle masking in astronomy: Triple correlation theory and applications. Appl. Opt. 1983, 22, 4028–4037. [Google Scholar] [CrossRef] [PubMed]
- Bartelt, H.; Lohmann, A.W.; Wirnitzer, B. Phase and amplitude recovery from bispectra. Appl. Opt. 1984, 23, 3121–3129. [Google Scholar] [CrossRef] [PubMed]
- Lohmann, A.W.; Paris, D.P. Binary Fraunhofer holograms, generated by computer. Appl. Opt. 1967, 6, 1739–1748. [Google Scholar] [CrossRef]
- Brown, B.R.; Lohmann, A.W. Complex spatial filtering with binary masks. Appl. Opt. 1966, 5, 967–969. [Google Scholar] [CrossRef]
- Lesem, L.B.; Hirsch, P.M.; Jordan, J.A., Jr. Scientific applications: Computer synthesis of holograms for 3-D display. Commun. ACM 1968, 11, 661–674. [Google Scholar] [CrossRef]
- Lesem, L.B.; Hirsch, P.M.; Jordan, J.A. The kinoform: A new wavefront reconstruction device. IBM J. Res. Dev. 1969, 13, 150–155. [Google Scholar] [CrossRef]
- Maimone, A.; Georgiou, A.; Kollin, J.S. Holographic near-eye displays for virtual and augmented reality. ACM Trans. Graph. 2017, 36, 1–16. [Google Scholar] [CrossRef]
- Jang, C.; Bang, K.; Li, G.; Lee, B. Holographic near-eye display with expanded eye-box. ACM Trans. Graph. 2018, 37, 1–14. [Google Scholar] [CrossRef]
- Ren, H.; Briere, G.; Fang, X.; Ni, P.; Sawant, R.; Héron, S.; Chenot, S.; Vézian, S.; Damilano, B.; Brändli, V.; et al. Metasurface orbital angular momentum holography. Nat. Commun. 2019, 10, 2986. [Google Scholar] [CrossRef]
- Skirnewskaja, J.; Wilkinson, T.D. Automotive holographic head-up displays. Adv. Mater. 2022, 34, 2110463. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Ning, H.; Cao, H.; Luo, D.; Xu, Z.; Luo, C.; Su, G.; Liu, Y.; Yao, R.; Peng, J. Research progress of large viewing-area 3D holographic near-eye display. Laser Photonics Rev. 2024, 18, 2300641. [Google Scholar] [CrossRef]
- Zhao, N.; Xiao, J.; Weng, P.; Zhang, H. Tomographic waveguide-based augmented reality display. Opt. Express 2024, 32, 18692–18699. [Google Scholar] [CrossRef] [PubMed]
- Padgett, M.; Di Leonardo, R. Holographic optical tweezers and their relevance to lab on chip devices. Lab A Chip 2011, 11, 1196–1205. [Google Scholar] [CrossRef] [PubMed]
- Dolev, I.; Epstein, I.; Arie, A. Surface-plasmon holographic beam shaping. Phys. Rev. Lett. 2012, 109, 203903. [Google Scholar] [CrossRef]
- Otte, E.; Denz, C. Optical trapping gets structure: Structured light for advanced optical manipulation. Appl. Phys. Rev. 2020, 7, 041308. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, Y.; Du, W.; Wu, P.; Rao, S.; Cai, Z.; Lao, Z.; Xu, B.; Ni, J.; Li, J.; et al. Optimized holographic femtosecond laser patterning method towards rapid integration of high-quality functional devices in microchannels. Sci. Rep. 2016, 6, 33281. [Google Scholar] [CrossRef] [PubMed]
- Xue, G.; Zhai, Q.; Lu, H.; Zhou, Q.; Ni, K.; Lin, L.; Wang, X.; Li, X. Polarized holographic lithography system for high-uniformity microscale patterning with periodic tunability. Microsystems Nanoeng. 2021, 7, 31. [Google Scholar] [CrossRef] [PubMed]
- Wetzstein, G.; Ozcan, A.; Gigan, S.; Fan, S.; Englund, D.; Soljačić, M.; Denz, C.; Miller, D.A.B.; Psaltis, D. Inference in artificial intelligence with deep optics and photonics. Nature 2020, 588, 39–47. [Google Scholar] [CrossRef] [PubMed]
- Blanche, P.A.; Bablumian, A.; Voorakaranam, R.; Christenson, C.; Lin, W.; Gu, T.; Flores, D.; Wang, P.; Hsieh, W.Y.; Kathaperumal, M.; et al. Holographic three-dimensional telepresence using large-area photorefractive polymer. Nature 2010, 468, 80–83. [Google Scholar] [CrossRef]
- Forbes, A.; de Oliveira, M.; Dennis, M.R. Structured light. Nat. Photonics 2021, 15, 253–262. [Google Scholar] [CrossRef]
- Bryngdahl, O.; Lee, W.H. Laser beam scanning using computer-generated holograms. Appl. Opt. 1976, 15, 183–194. [Google Scholar] [CrossRef]
- Lohmann, A.W.; Thomas, J.A. Making an array illuminator based on the Talbot effect. Appl. Opt. 1990, 29, 4337–4340. [Google Scholar] [CrossRef]
- Lee, W.H. Method for converting a Gaussian laser beam into a uniform beam. Opt. Commun. 1981, 36, 469–471. [Google Scholar] [CrossRef]
- Makey, G.; Yavuz, Ö.; Kesim, D.K.; Turnalı, A.; Elahi, P.; Ilday, S.; Tokel, O.; Ilday, F.Ö. Breaking crosstalk limits to dynamic holography using orthogonality of high-dimensional random vectors. Nat. Photonics 2019, 13, 251–256. [Google Scholar] [CrossRef]
- Sommerfeld, A. Mathematische theorie der diffraction. Math. Ann. 1896, 47, 317–374. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Lohmann, A.W. Reconstruction of Vectorial Wavefronts. Appl. Opt. 1965, 4, 1667–1668. [Google Scholar] [CrossRef]
- Keller, J.B. Geometrical Theory of Diffraction. In Classical andModern Diffraction Theory; Klem-Musatov, K., Hoeber, H.C., Moser, T.J., Pelissier, M.A., Eds.; Society of Exploration Geophysicists: Houston, TX, USA, 2016. [Google Scholar] [CrossRef]
- Lee, W.H. Sampled Fourier Transform Hologram Generated by Computer. Appl. Opt. 1970, 9, 639–643. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier Optics; W. H. Freeman, Macmillan Learning: New York, NY, USA, 2017. [Google Scholar]
- Voelz, D.G. Computational fourier Optics: A MATLAB Tutorial; SPIE: Bellingham, WA, USA, 2011. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, H.; Jin, G. Frequency sampling strategy for numerical diffraction calculations. Opt. Express 2020, 28, 39916–39932. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Zhang, H.; Jin, G. Single-Fourier transform based full-bandwidth Fresnel diffraction. J. Opt. 2021, 23, 035604. [Google Scholar] [CrossRef]
- Gori, F. Fresnel transform and sampling theorem. Opt. Commun. 1981, 39, 293–297. [Google Scholar] [CrossRef]
- Voelz, D.G.; Roggemann, M.C. Digital simulation of scalar optical diffraction: Revisiting chirp function sampling criteria and consequences. Appl. Opt. 2009, 48, 6132–6142. [Google Scholar] [CrossRef] [PubMed]
- Kelly, D.P. Numerical calculation of the Fresnel transform. J. Opt. Soc. Am. A 2014, 31, 755–764. [Google Scholar] [CrossRef]
- Shen, F.; Wang, A. Fast-Fourier-transform based numerical integration method for the Rayleigh-Sommerfeld diffraction formula. Appl. Opt. 2006, 45, 1102–1110. [Google Scholar] [CrossRef]
- Xiao, Y.; Tang, X.; Qin, Y.; Peng, H.; Wang, W. Wide-window angular spectrum method for diffraction propagation in far and near field. Opt. Lett. 2012, 37, 4943–4945. [Google Scholar] [CrossRef]
- Matsushima, K.; Shimobaba, T. Band-limited angular spectrum method for numerical simulation of free-space propagation in far and near fields. Opt. Express 2009, 17, 19662–19673. [Google Scholar] [CrossRef]
- Shimobaba, T.; Kakue, T.; Okada, N.; Oikawa, M.; Yamaguchi, Y.; Ito, T. Aliasing-reduced Fresnel diffraction with scale and shift operations. J. Opt. 2013, 15, 075405. [Google Scholar] [CrossRef]
- Kim, Y.H.; Byun, C.W.; Oh, H.; Lee, J.; Pi, J.E.; Kim, G.H.; Lee, M.L.; Ryu, H.; Chu, H.Y.; Hwang, C.S. Non-uniform sampling and wide range angular spectrum method. J. Opt. 2014, 16, 125710. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, H.; Jin, G. Band-extended angular spectrum method for accurate diffraction calculation in a wide propagation range. Opt. Lett. 2020, 45, 1543–1546. [Google Scholar] [CrossRef] [PubMed]
- Xiao, J.; Zhang, W.; Zhang, H. Sampling analysis for Fresnel diffraction fields based on phase space representation. J. Opt. Soc. Am. A 2022, 39, A15–A28. [Google Scholar] [CrossRef]
- Wyrowski, F.; Bryngdahl, O. Iterative Fourier-transform algorithm applied to computer holography. J. Opt. Soc. Am. A 1988, 5, 1058–1065. [Google Scholar] [CrossRef]
- Wyrowski, F.; Bryngdahl, O. Speckle-free reconstruction in digital holography. J. Opt. Soc. Am. A 1989, 6, 1171–1174. [Google Scholar] [CrossRef]
- Bräuer, R.; Wyrowski, F.; Bryngdahl, O. Diffusers in digital holography. J. Opt. Soc. Am. A 1991, 8, 572–578. [Google Scholar] [CrossRef]
- Aagedal, H.; Schmid, M.; Beth, T.; Teiwes, S.; Wyrowski, F. Theory of speckles in diffractive optics and its application to beam shaping. J. Mod. Opt. 1996, 43, 1409–1421. [Google Scholar] [CrossRef]
- Qu, W.; Gu, H.; Tan, Q.; Jin, G. Precise design of two-dimensional diffractive optical elements for beam shaping. Appl. Opt. 2015, 54, 6521–6525. [Google Scholar] [CrossRef]
- Porfirev, A.P. Modification of the Gerchberg-Saxton algorithm for the generation of specle-reduced intensity distributions of micrometer and submicrometer dimensions. Optik 2019, 195, 163163. [Google Scholar] [CrossRef]
- Chen, L.; Tian, S.; Zhang, H.; Cao, L.; Jin, G. Phase hologram optimization with bandwidth constraint strategy for speckle-free optical reconstruction. Opt. Express 2021, 29, 11645–11663. [Google Scholar] [CrossRef] [PubMed]
- Wyrowski, F. Iterative quantization of digital amplitude holograms. Appl. Opt. 1989, 28, 3864–3870. [Google Scholar] [CrossRef] [PubMed]
- Cohen, L. Time-Frequency Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Burch, J.J. A computer algorithm for the synthesis of spatial frequency filters. Proc. IEEE 1967, 55, 599–601. [Google Scholar] [CrossRef]
- Lee, W.H. Binary synthetic holograms. Appl. Opt. 1974, 13, 1677–1682. [Google Scholar] [CrossRef]
- Lee, W.H. Binary computer-generated holograms. Appl. Opt. 1979, 18, 3661–3669. [Google Scholar] [CrossRef]
- Bryngdahl, O.; Lohmann, A. Single-sideband holography. J. Opt. Soc. Am. 1968, 58, 620–624. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, H.; Cao, L.; Jin, G. Generalized single-sideband three-dimensional computer-generated holography. Opt. Express 2019, 27, 2612–2620. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, T.; Shimobaba, T.; Kakue, T.; Ito, T. Time-division color holographic projection in large size using a digital micromirror device. Appl. Sci. 2021, 11, 6277. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, Y.; Li, Y.; Wang, D.; Wang, Q. Method of color holographic display with speckle noise suppression. Opt. Express 2022, 30, 25647–25660. [Google Scholar] [CrossRef]
- Yu, P.; Liu, Y.; Wang, Z.; Liang, J.; Liu, X.; Li, Y.; Qiu, C.; Gong, L. Ultrahigh-density 3D holographic projection by scattering-assisted dynamic holography. Optica 2023, 10, 481–490. [Google Scholar] [CrossRef]
- Blanche, P.A.; Ketchum, R.S. Texas instruments phase light modulator for holography. In Proceedings of the Digital Holography and Three-Dimensional Imaging, Washington, DC, USA, 19–23 July 2021; p. DW4B.3. [Google Scholar] [CrossRef]
- Barnard, E.; Vermeulen, P.; Casasent, D.P. Optical correlation CGHs with modulated error diffusion. Appl. Opt. 1989, 28, 5358–5362. [Google Scholar] [CrossRef]
- Buckley, E. Real-time error diffusion for signal-to-noise ratio improvement in a holographic projection system. J. Disp. Technol. 2011, 7, 70–76. [Google Scholar] [CrossRef]
- Tsang, P.W.M.; Poon, T.C. Novel method for converting digital Fresnel hologram to phase-only hologram based on bidirectional error diffusion. Opt. Express 2013, 21, 23680–23686. [Google Scholar] [CrossRef] [PubMed]
- Floyd, R.W. An adaptive algorithm for spatial gray-scale. In Proceedings of the Society of In-formation Display, New York, NY, USA, 7–10 June 1976; Volume 17, pp. 75–77. [Google Scholar]
- Chang, C.; Xia, J.; Lei, W. Speckle suppression in phase-only holographic display by optimizing phase distribution. In Proceedings of the Digital Holography and Three-Dimensional Imaging, Shanghai China, 24–28 May 2015; p. DW3A.5. [Google Scholar] [CrossRef]
- Yang, G.; Jiao, S.; Liu, J.P.; Lei, T.; Yuan, X. Error diffusion method with optimized weighting coefficients for binary hologram generation. Appl. Opt. 2019, 58, 5547–5555. [Google Scholar] [CrossRef] [PubMed]
- Jiao, S.; Zhang, D.; Zhang, C.; Gao, Y.; Lei, T.; Yuan, X. Complex-amplitude holographic projection with a digital micromirror device (DMD) and error diffusion algorithm. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1–8. [Google Scholar] [CrossRef]
- Liu, K.; He, Z.; Cao, L. Pattern-adaptive error diffusion algorithm for improved phase-only hologram generation. Chin. Opt. Lett. 2021, 19, 050501. [Google Scholar] [CrossRef]
- Omel, M.Y.; Gladys, M.V.; Jesús, L. Encoding complex fields by using a phase-only optical element. Opt. Lett. 2014, 39, 1740–1743. [Google Scholar] [CrossRef]
- Qi, Y.; Chang, C.; Xia, J. Speckleless holographic display by complex modulation based on double-phase method. Opt. Express 2016, 24, 30368–30378. [Google Scholar] [CrossRef]
- Chang, C.; Qi, Y.; Wu, J.; Xia, J.; Nie, S. Speckle reduced lensless holographic projection from phase-only computer-generated hologram. Opt. Express 2017, 25, 6568–6580. [Google Scholar] [CrossRef]
- Kim, Y.K.; Lee, J.S.; Won, Y.H. Low-noise high-efficiency double-phase hologram by multiplying a weight factor. Opt. Lett. 2019, 44, 3649–3652. [Google Scholar] [CrossRef]
- Sui, X.; He, Z.; Jin, G.; Chu, D.; Cao, L. Band-limited double-phase method for enhancing image sharpness in complex modulated computer-generated holograms. Opt. Express 2021, 29, 2597–2612. [Google Scholar] [CrossRef]
- Shimobaba, T.; Wang, F.; Starobrat, J.; Kowalczyk, A.; Suszek, J.; Ito, T. Comparison of double-phase hologram and binary amplitude encoding: Holographic projection and vortex beam generation. Appl. Opt. 2023, 62, 7471–7479. [Google Scholar] [CrossRef]
- Bättig, R.K.; Guest, C.C.; Schaefer, S.R.; Toms, D.J. Simulated annealing of binary holograms for the interconnection of single-mode structures. Appl. Opt. 1992, 31, 1059–1066. [Google Scholar] [CrossRef]
- Mahlab, U.; Shamir, J.; Caulfield, H.J. Genetic algorithm for optical pattern recognition. Opt. Lett. 1991, 16, 648–650. [Google Scholar] [CrossRef]
- Su, P.; Cai, C.; Song, Y.; Ma, J.; Tan, Q. A hybrid diffractive optical element design algorithm combining particle swarm optimization and a simulated annealing algorithm. Appl. Sci. 2020, 10, 5485. [Google Scholar] [CrossRef]
- Chhetri, B.B.; Yang, S.; Shimomura, T. Stochastic approach in the efficient design of the direct-binary-search algorithm for hologram synthesis. Appl. Opt. 2000, 39, 5956–5964. [Google Scholar] [CrossRef] [PubMed]
- Gerchberg, R.W.; Saxton, W.O. A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 1972, 35, 237–246. [Google Scholar]
- Fienup, J.R. Reconstruction of an object from modulus of its Fourier transform. Opt. Lett. 1978, 3, 27–29. [Google Scholar] [CrossRef] [PubMed]
- Fienup, J.R. Iterative method applied to image reconstruction and to computer-generated holograms. Opt. Eng. 1980, 19, 193297. [Google Scholar] [CrossRef]
- Fienup, J.R. Phase retrieval algorithms: A comparison. Appl. Opt. 1982, 21, 2758–2769. [Google Scholar] [CrossRef]
- Akahori, H. Spectrum leveling by an iterative algorithm with a dummy area for synthesizing the kinoform. Appl. Opt. 1986, 25, 802–811. [Google Scholar] [CrossRef]
- Kuzmenko, A.V. Weighting iterative Fourier transform algorithm of the kinoform synthesis. Opt. Lett. 2008, 33, 1147–1149. [Google Scholar] [CrossRef]
- Zhou, P.; Li, Y.; Liu, S.; Su, Y. Dynamic compensatory Gerchberg–Saxton algorithm for multiple-plane reconstruction in holographic displays. Opt. Express 2019, 27, 8958–8967. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, J.; Chen, C.; Liu, C.; Jin, F.; Chen, N. Adaptive weighted Gerchberg-Saxton algorithm for generation of phase-only hologram with artifacts suppression. Opt. Express 2021, 29, 1412–1427. [Google Scholar] [CrossRef]
- Georgiou, A.; Christmas, J.; Collings, N.; Moore, J.; Crossland, W.A. Aspects of hologram calculation for video frames. J. Opt. A Pure Appl. Opt. 2008, 10, 035302. [Google Scholar] [CrossRef]
- Hsu, W.F.; Lin, S.C. Iterative pixelwise approach applied to computer-generated holograms and diffractive optical elements. Appl. Opt. 2018, 57, A189–A196. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Chi, Y.; Fan, J.; Ma, C. Gradient descent with random initialization: Fast global convergence for nonconvex phase retrieval. Math. Program. 2019, 176, 5–37. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.; Wang, K.; Chi, Y.; Chen, Y. Implicit Regularization in Nonconvex Statistical Estimation: Gradient Descent Converges Linearly for Phase Retrieval and Matrix Completion. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; In Proceedings of Machine Learning Research. Dy, J., Krause, A., Eds.; PMLR: Stockholm, Sweden, 2018; Volume 80, pp. 3345–3354. [Google Scholar]
- Chakravarthula, P.; Peng, Y.; Kollin, J.; Fuchs, H.; Heide, F. Wirtinger holography for near-eye displays. ACM Trans. Graph. 2019, 38, 1–13. [Google Scholar] [CrossRef]
- Peng, Y.; Choi, S.; Padmanaban, N.; Wetzstein, G. Neural holography with camera-in-the-loop training. ACM Trans. Graph. 2020, 39, 1–14. [Google Scholar] [CrossRef]
- Wang, D.; Li, N.; Li, Y.; Zheng, Y.; Wang, Q. Curved hologram generation method for speckle noise suppression based on the stochastic gradient descent algorithm. Opt. Express 2021, 29, 42650–42662. [Google Scholar] [CrossRef]
- Chen, C.; Lee, B.; Li, N.; Chae, M.; Wang, D.; Wang, Q.; Lee, B. Multi-depth hologram generation using stochastic gradient descent algorithm with complex loss function. Opt. Express 2021, 29, 15089–15103. [Google Scholar] [CrossRef]
- Yang, F.; Kadis, A.; Mouthaan, R.; Wetherfield, B.; Kaczorowski, A.; Wilkinson, T.D. Perceptually motivated loss functions for computer generated holographic displays. Sci. Rep. 2022, 12, 7709. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Pégard, N.; Zhong, J.; Adesnik, H.; Waller, L. 3D computer-generated holography by non-convex optimization. Optica 2017, 4, 1306–1313. [Google Scholar] [CrossRef]
- Horisaki, R.; Takagi, R.; Tanida, J. Deep-learning-generated holography. Appl. Opt. 2018, 57, 3859–3863. [Google Scholar] [CrossRef]
- Barbastathis, G.; Ozcan, A.; Situ, G. On the use of deep learning for computational imaging. Optica 2019, 6, 921–943. [Google Scholar] [CrossRef]
- Rivenson, Y.; Wu, Y.; Ozcan, A. Deep learning in holography and coherent imaging. Light. Sci. Appl. 2019, 8, 85. [Google Scholar] [CrossRef]
- Cheremkhin, P.A.; Rymov, D.A.; Svistunov, A.S.; Zlokazov, E.Y.; Starikov, R.S. Neural-network-based methods in digital and computer-generated holography: A review. J. Opt. Technol. 2024, 91, 170–180. [Google Scholar] [CrossRef]
- Shi, L.; Li, B.; Kim, C.; Kellnhofer, P.; Matusik, W. Towards real-time photorealistic 3D holography with deep neural networks. Nature 2021, 591, 234–239. [Google Scholar] [CrossRef]
- Wu, J.; Liu, K.; Sui, X.; Cao, L. High-speed computer-generated holography using an autoencoder-based deep neural network. Opt. Lett. 2021, 46, 2908–2911. [Google Scholar] [CrossRef]
- Liu, K.; Wu, J.; He, Z.; Cao, L. 4K-DMDNet: Diffraction model-driven network for 4K computer-generated holography. Opto-Electron. Adv. 2023, 6, 220135. [Google Scholar] [CrossRef]
- Zhu, R.; Chen, L.; Zhang, H. Computer holography using deep neural network with Fourier basis. Opt. Lett. 2023, 48, 2333–2336. [Google Scholar] [CrossRef]
- Choi, S.; Gopakumar, M.; Peng, Y.; Kim, J.; Wetzstein, G. Neural 3D holography: Learning accurate wave propagation models for 3D holographic virtual and augmented reality displays. ACM Trans. Graph. 2021, 40, 1–12. [Google Scholar] [CrossRef]
- Zhu, R.; Chen, L.; Xiao, J.; Zhang, H. Three-dimensional computer holography with phase space tailoring. PhotoniX 2024, 5, 34. [Google Scholar] [CrossRef]
- Yang, Y.; Forbes, A.; Cao, L. A review of liquid crystal spatial light modulators:devices and applications. Opto-Electron. Sci. 2023, 2, 230026. [Google Scholar] [CrossRef]
- Ren, Y.; Lu, R.; Gong, L. Tailoring light with a digital micromirror device. Ann. Der Phys. 2015, 527, 447–470. [Google Scholar] [CrossRef]
- Huang, L.; Zhang, S.; Zentgraf, T. Metasurface holography: From fundamentals to applications. Nanophotonics 2018, 7, 1169–1190. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kazanskiy, N.L.; Skidanov, R.V.; Butt, M.A. Advancements and applications of diffractive optical elements in contemporary optics: A comprehensive overview. Adv. Mater. Technol. 2025, 10, 2401028. [Google Scholar] [CrossRef]
- Bang, K.; Jang, C.; Lee, B. Compact noise-filtering volume gratings for holographic displays. Opt. Lett. 2019, 44, 2133–2136. [Google Scholar] [CrossRef]
- Lee, K.; Park, Y. Exploiting the speckle-correlation scattering matrix for a compact reference-free holographic image sensor. Nat. Commun. 2016, 7, 13359. [Google Scholar] [CrossRef]
- Kim, Y.K.; Ryu, W.J.; Lee, J.S. Study of non-periodic pinhole array filter for decreasing high-order noise for compact holographic display. Appl. Sci. 2020, 10, 8671. [Google Scholar] [CrossRef]
- Li, G.; Jeong, J.; Lee, D.; Yeom, J.; Jang, C.; Lee, S.; Lee, B. Space bandwidth product enhancement of holographic display using high-order diffraction guided by holographic optical element. Opt. Express 2015, 23, 33170–33183. [Google Scholar] [CrossRef]
- Gopakumar, M.; Kim, J.; Choi, S.; Peng, Y.; Wetzstein, G. Unfiltered holography: Optimizing high diffraction orders without optical filtering for compact holographic displays. Opt. Lett. 2021, 46, 5822–5825. [Google Scholar] [CrossRef] [PubMed]
- Jo, Y.; Yoo, D.; Lee, D.; Kim, M.; Lee, B. Multi-illumination 3D holographic display using a binary mask. Opt. Lett. 2022, 47, 2482–2485. [Google Scholar] [CrossRef] [PubMed]
- Long, P.; Hsu, D. Quantization and sampling considerations of computer-generated hologram for optical interconnection. In Proceedings of the Practical Holography V, San Jose, CA, USA, 1 July 1991; In International Society for Optics and Photonics. Benton, S.A., Ed.; SPIE: Bellingham, WA, USA, 1991; Volume 1461, pp. 270–277. [Google Scholar] [CrossRef]
- Kober, V.; Yaroslavsky, L.P.; Campos, J.; Yzuel, M.J. Optimal filter approximation by means of a phase-only filter with quantization. Opt. Lett. 1994, 19, 978–980. [Google Scholar] [CrossRef][Green Version]
- Chaudhuri, R.; Papa, J.; Rolland, J.P. System design of a single-shot reconfigurable null test using a spatial light modulator for freeform metrology. Opt. Lett. 2019, 44, 2000–2003. [Google Scholar] [CrossRef]
- Engström, D.; Persson, M.; Bengtsson, J.; Goksör, M. Calibration of spatial light modulators suffering from spatially varying phase response. Opt. Express 2013, 21, 16086–16103. [Google Scholar] [CrossRef] [PubMed]
- Brown, B.R.; Lohmann, A.W. Computer-generated Binary Holograms. IBM J. Res. Dev. 1969, 13, 160–168. [Google Scholar] [CrossRef]
- Fetthauer, F.; Bryngdahl, O. Quantization noise and the error diffusion algorithm. J. Electron. Imaging 1994, 3, 37–44. [Google Scholar] [CrossRef]
- Fetthauer, F.; Weissbach, S.; Bryngdahl, O. Computer-generated Fresnel holograms: Quantization with the error diffusion algorithm. Opt. Commun. 1995, 114, 230–234. [Google Scholar] [CrossRef]
- Tsang, P.; Poon, T.C.; Cheung, W.K.; Liu, J.P. Computer generation of binary Fresnel holography. Appl. Opt. 2011, 50, B88–B95. [Google Scholar] [CrossRef][Green Version]
- Cao, W.; Ma, J.; Su, P.; Liang, X. Binary hologram generation based on discrete wavelet transform. Optik 2016, 127, 558–561. [Google Scholar] [CrossRef]
- Savchenkova, E.A.; Ovchinnikov, A.S.; Rodin, V.G.; Starikov, R.S.; Evtikhiev, N.N.; Cheremkhin, P.A. Adaptive non-iterative histogram-based hologram quantization. Optik 2024, 311, 171933. [Google Scholar] [CrossRef]
- Zhang, E.; Noehte, S.; Dietrich, C.H.; Männer, R. Gradual and random binarization of gray-scale holograms. Appl. Opt. 1995, 34, 5987–5995. [Google Scholar] [CrossRef]
- Dorsch, R.G.; Lohmann, A.W.; Sinzinger, S. Fresnel ping-pong algorithm for two-plane computer-generated hologram display. Appl. Opt. 1994, 33, 869–875. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Chen, G.; Zhang, Q. LCOS-SLM based intelligent hybrid algorithm for beam splitting. Electronics 2022, 11, 428. [Google Scholar] [CrossRef]
- Wyrowski, F. Diffractive optical elements: Iterative calculation of quantized, blazed phase structures. J. Opt. Soc. Am. A 1990, 7, 961–969. [Google Scholar] [CrossRef]
- Goi, H.; Komuro, K.; Nomura, T. Deep-learning-based binary hologram. Appl. Opt. 2020, 59, 7103–7108. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.; Kim, D.; Lee, S.; Chen, C.; Lee, B. High-contrast, speckle-free, true 3D holography via binary CGH Optimization. Sci. Rep. 2022, 12, 2811. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.; Gopakumar, M.; Peng, Y.; Kim, J.; O’Toole, M.; Wetzstein, G. Time-multiplexed neural holography: A flexible framework for holographic near-eye displays with fast heavily-quantized spatial light modulators. In Proceedings of the ACM SIGGRAPH 2022 Conference, SIGGRAPH ’22, Vancouver, BC, Canada, 7–11 August 2022; Association for Computing Machinery: New York, NY, USA, 2022; pp. 1–9. [Google Scholar] [CrossRef]
- Cuche, E.; Marquet, P.; Depeursinge, C. Spatial filtering for zero-order and twin-image elimination in digital off-axis holography. Appl. Opt. 2000, 39, 4070–4075. [Google Scholar] [CrossRef]
- Zhang, H.; Xie, J.; Liu, J.; Wang, Y. Elimination of a zero-order beam induced by a pixelated spatial light modulator for holographic projection. Appl. Opt. 2009, 48, 5834–5841. [Google Scholar] [CrossRef]
- Ronzitti, E.; Guillon, M.; de Sars, V.; Emiliani, V. LCoS nematic SLM characterization and modeling for diffraction efficiency optimization, zero and ghost orders suppression. Opt. Express 2012, 20, 17843–17855. [Google Scholar] [CrossRef]
- Milewski, G.; Engström, D.; Bengtsson, J. Diffractive optical elements designed for highly precise far-field generation in the presence of artifacts typical for pixelated spatial light modulators. Appl. Opt. 2007, 46, 95–105. [Google Scholar] [CrossRef] [PubMed]
- Palima, D.; Daria, V.R. Holographic projection of arbitrary light patterns with a suppressed zero-order beam. Appl. Opt. 2007, 46, 4197–4201. [Google Scholar] [CrossRef]
- Jesacher, A.; Booth, M.J. Parallel direct laser writing in three dimensions with spatially dependent aberration correction. Opt. Express 2010, 18, 21090–21099. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Wang, K.; Bai, J.; Zhao, W. Inhibiting zero-order light of a spatial light modulator with voltage optimization. Opt. Lett. 2023, 48, 5061–5064. [Google Scholar] [CrossRef]
- Sun, P.; Chang, S.; Liu, S.; Tao, X.; Wang, C.; Zheng, Z. Holographic near-eye display system based on double-convergence light Gerchberg-Saxton algorithm. Opt. Express 2018, 26, 10140–10151. [Google Scholar] [CrossRef] [PubMed]
- Chlipała, M.; Kozacki, T.; Yeom, H.J.; Martinez-Carranza, J.; Kukołowicz, R.; Kim, J.; Yang, J.H.; Choi, J.H.; Pi, J.E.; Hwang, C.S. Wide angle holographic video projection display. Opt. Lett. 2021, 46, 4956–4959. [Google Scholar] [CrossRef]
- Chen, C.; Kim, D.; Yoo, D.; Lee, B.; Lee, B. Off-axis camera-in-the-loop optimization with noise reduction strategy for high-quality hologram generation. Opt. Lett. 2022, 47, 790–793. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, H.; Matsushima, K.; Jin, G. Shifted band-extended angular spectrum method for off-axis diffraction calculation. Opt. Express 2021, 29, 10089–10103. [Google Scholar] [CrossRef]
- Chen, C.; Chang, K.; Liu, C.; Wang, J.; Wang, Q. Fast hologram generation using intermediate angular-spectrum method for high-quality compact on-axis holographic display. Opt. Express 2019, 27, 29401–29414. [Google Scholar] [CrossRef]
- Pi, D.; Liu, J.; Wang, Y. Optimized iterative algorithm to generate computer-generated holograms based on the intermediate angular-spectrum method. IEEE Photonics J. 2022, 14, 5228505. [Google Scholar] [CrossRef]
- Wang, J.; Lei, X.; Wu, Y.; Jin, F.; Chen, N. Holographic display with optical computational Fresnel convolution to broaden distance. Opt. Express 2022, 30, 4288–4301. [Google Scholar] [CrossRef]
- Cho, J.; Kim, S.; Park, S.; Lee, B.; Kim, H. DC-free on-axis holographic display using a phase-only spatial light modulator. Opt. Lett. 2018, 43, 3397–3400. [Google Scholar] [CrossRef]
- Tian, S.; Chen, L.; Zhang, H. Optimized Fresnel phase hologram for ringing artifacts removal in lensless holographic projection. Appl. Opt. 2022, 61, B17–B24. [Google Scholar] [CrossRef]
- Xiao, K.; Fu, C.; Karatzas, D.; Wuerger, S. Visual gamma correction for LCD displays. Displays 2011, 32, 17–23. [Google Scholar] [CrossRef]
- Yang, L.; Xia, J.; Chang, C.; Zhang, X.; Yang, Z.; Chen, J. Nonlinear dynamic phase response calibration by digital holographic microscopy. Appl. Opt. 2015, 54, 7799–7806. [Google Scholar] [CrossRef] [PubMed]
- Strauß, J.; Häfner, T.; Dobler, M.; Heberle, J.; Schmidt, M. Evaluation and calibration of LCoS SLM for direct laser structuring with tailored intensity distributions. Phys. Procedia 2016, 83, 1160–1169. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, H.; Li, J.; Qiao, Y.J.; Si, J.; Gao, W. Compensation of phase nonlinearity of liquid crystal spatial light modulator for high-resolution wavefront correction. J. Eur. Opt. Soc.-Rapid Publ. 2015, 10, 15036. [Google Scholar] [CrossRef]
- Zhang, H.; Lizana, A.; Iemmi, C.; Monroy-Ramírez, F.A.; Márquez, A.; Moreno, I.; Campos, J. LCoS display phase self-calibration method based on diffractive lens schemes. Opt. Lasers Eng. 2018, 106, 147–154. [Google Scholar] [CrossRef]
- Yang, H.; Robertson, B.; Chu, D.P. Transient crosstalk in LCOS based WSS and a method to suppress the crosstalk levels. In Proceedings of the Optical Fiber Communication Conference/National Fiber Optic Engineers Conference 2013, Anaheim, CA, USA, 17–21 March 2013; p. OW1C.3. [Google Scholar] [CrossRef]
- Yang, H.; Robertson, B.; Yu, D.; Zhang, Z.; Chu, D.P. Origin of transient crosstalk and its reduction in phase-only LCOS wavelength selective switches. J. Light. Technol. 2013, 31, 3822–3829. [Google Scholar] [CrossRef]
- Frisken, S.; Clarke, I.; Poole, S. Technology and applications of liquid crystal on silicon (LCoS) in Telecommunications. In Optical Fiber Telecommunications: Components and Subsystems: Sixth Edition; Kaminow, I.P., Li, T., Willner, A.E., Eds.; Academic Press: Cambridge, MA, USA, 2013; pp. 709–742. [Google Scholar] [CrossRef]
- Harriman, J.L.; Linnenberger, A.; Serati, S.A. Improving spatial light modulator performance through phase compensation. In Proceedings of the Advanced Wavefront Control: Methods, Devices, and Applications II, Denver, CO, USA, 2–6 August 2004; Volume 5553, p. 58. [Google Scholar] [CrossRef]
- Xu, J.; Qin, S.; Liu, C.; Fu, S.; Liu, D. Precise calibration of spatial phase response nonuniformity arising in liquid crystal on silicon. Opt. Lett. 2018, 43, 2993–2996. [Google Scholar] [CrossRef] [PubMed]
- Bianco, V.; Memmolo, P.; Leo, M.; Montresor, S.; Distante, C.; Paturzo, M.; Picart, P.; Javidi, B.; Ferraro, P. Strategies for reducing speckle noise in digital holography. Light. Sci. Appl. 2018, 7, 48. [Google Scholar] [CrossRef]
- Shimobaba, T.; Ito, T. Random phase-free computer-generated hologram. Opt. Express 2015, 23, 9549–9554. [Google Scholar] [CrossRef]
- Goodman, J.W. Speckle Phenomena in Optics: Theory and Applications; Roberts and Company Publishers: Greenwood Village, CO, USA, 2007. [Google Scholar]
- Park, J.H. Recent progress in computer-generated holography for three-dimensional scenes. J. Inf. Disp. 2016, 18, 1–12. [Google Scholar] [CrossRef]
- Amako, J.; Miura, H.; Sonehara, T. Speckle-noise reduction on kinoform reconstruction using a phase-only spatial light modulator. Appl. Opt. 1995, 34, 3165–3171. [Google Scholar] [CrossRef]
- Lee, B.; Yoo, D.; Jeong, J.; Lee, S.; Lee, D.; Lee, B. Wide-angle speckleless DMD holographic display using structured illumination with temporal multiplexing. Opt. Lett. 2020, 45, 2148–2151. [Google Scholar] [CrossRef]
- Makowski, M. Minimized speckle noise in lens-less holographic projection by pixel separation. Opt. Express 2013, 21, 29205–29216. [Google Scholar] [CrossRef] [PubMed]
- Mori, Y.; Fukuoka, T.; Nomura, T. Speckle reduction in holographic projection by random pixel separation with time multiplexing. Appl. Opt. 2014, 53, 8182–8188. [Google Scholar] [CrossRef]
- Wang, D.; Li, N.; Liu, C.; Wang, Q. Holographic display method to suppress speckle noise based on effective utilization of two spatial light modulators. Opt. Express 2019, 27, 11617–11625. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y.; Chu, D. Coherence properties of different light sources and their effect on the image sharpness and speckle of holographic displays. Sci. Rep. 2017, 7, 5893. [Google Scholar] [CrossRef]
- Kozacki, T.; Chlipala, M. Color holographic display with white light LED source and single phase only SLM. Opt. Express 2016, 24, 2189–2199. [Google Scholar] [CrossRef] [PubMed]
- Chlipala, M.; Kozacki, T. Color LED DMD holographic display with high resolution across large depth. Opt. Lett. 2019, 44, 4255–4258. [Google Scholar] [CrossRef] [PubMed]
- Lee, G.Y.; Yoon, G.; Lee, S.Y.; Yun, H.; Cho, J.; Lee, K.; Kim, H.; Rho, J.; Lee, B. Complete amplitude and phase control of light using broadband holographic metasurfaces. Nanoscale 2018, 10, 4237–4245. [Google Scholar] [CrossRef]
- Lee, S.; Kim, D.; Nam, S.W.; Lee, B.; Cho, J.; Lee, B. Light source optimization for partially coherent holographic displays with consideration of speckle contrast, resolution, and depth of field. Sci. Rep. 2020, 10, 18832. [Google Scholar] [CrossRef]
- Peng, Y.; Choi, S.; Kim, J.; Wetzstein, G. Speckle-free holography with partially coherent light sources and camera-in-the-loop calibration. Sci. Adv. 2021, 7, eabg5040. [Google Scholar] [CrossRef]
- Gilbert, J.A.; Dudderar, T.D.; Boehnlein, A.J. Ultra low frequency holographic interferometry using fiber optics. Opt. Lasers Eng. 1984, 5, 29–40. [Google Scholar] [CrossRef]
- Yurlov, V.; Lapchuk, A.; Yun, S.; Song, J.; Yang, H. Speckle suppression in scanning laser display. Appl. Opt. 2008, 47, 179–187. [Google Scholar] [CrossRef]
- Kuratomi, Y.; Sekiya, K.; Satoh, H.; Tomiyama, T.; Kawakami, T.; Katagiri, B.; Suzuki, Y.; Uchida, T. Speckle reduction mechanism in laser rear projection displays using a small moving diffuser. J. Opt. Soc. Am. A 2010, 27, 1812–1817. [Google Scholar] [CrossRef]
- Lee, D.; Jang, C.; Bang, K.; Moon, S.; Li, G.; Lee, B. Speckle reduction for holographic display using optical path difference and random phase generator. IEEE Trans. Ind. Inform. 2019, 15, 6170–6178. [Google Scholar] [CrossRef]
- Yao, P.H.; Chen, C.H.; Chen, C.H. Low speckle laser illuminated projection system with a vibrating diffractive beam shaper. Opt. Express 2012, 20, 16552–16566. [Google Scholar] [CrossRef]
- Mehta, D.S.; Naik, D.N.; Singh, R.K.; Takeda, M. Laser speckle reduction by multimode optical fiber bundle with combined temporal, spatial, and angular diversity. Appl. Opt. 2012, 51, 1894–1904. [Google Scholar] [CrossRef]
- Pang, H.; Wang, J.; Cao, A.; Deng, Q. High-accuracy method for holographic image projection with suppressed speckle noise. Opt. Express 2016, 24, 22766–22776. [Google Scholar] [CrossRef]
- Yang, F.; Zhu, L.; Wei, K.; Zhang, Y.; Cao, L. Speckle-reduced reconstruction of a single-shot hologram by multiple tip-tilt modulations. Appl. Opt. 2021, 60, 5220–5226. [Google Scholar] [CrossRef] [PubMed]
- Nagahama, Y.; Shimobaba, T.; Kakue, T.; Takaki, Y.; Ito, T. Image quality improvement of random phase-free holograms by addressing the cause of ringing artifacts. Appl. Opt. 2019, 58, 2146–2151. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.; Liu, J.; Duan, J.; Li, X.; Wang, Y. Image quality enhancement via gradient-limited random phase addition in holographic display. Opt. Commun. 2019, 442, 84–89. [Google Scholar] [CrossRef]
- He, Z.; Sui, X.; Zhang, H.; Jin, G.; Cao, L. Frequency-based optimized random phase for computer-generated holographic display. Appl. Opt. 2020, 60, A145–A154. [Google Scholar] [CrossRef]
- Gottlieb, D.; Shu, C.W. On the Gibbs Phenomenon and Its Resolution. SIAM Rev. 1997, 39, 644–668. [Google Scholar] [CrossRef]
- Jerri, A.J. The Gibbs Phenomenon in Fourier Analysis, Splines and Wavelet Approximations. In Mathematics and Its Applications, 1st ed.; Springer: New York, NY, USA, 1998; Volume 446. [Google Scholar] [CrossRef]
- Nagahama, Y.; Shimobaba, T.; Kawashima, T.; Kakue, T.; Ito, T. Holographic multi-projection using the random phase-free method. Appl. Opt. 2016, 55, 1118–1123. [Google Scholar] [CrossRef]
- Shimobaba, T.; Kakue, T.; Endo, Y.; Hirayama, R.; Hiyama, D.; Hasegawa, S.; Nagahama, Y.; Sano, M.; Oikawa, M.; Sugie, T.; et al. Improvement of the image quality of random phase-free holography using an iterative method. Opt. Commun. 2015, 355, 596–601. [Google Scholar] [CrossRef]
- Nagahama, Y.; Shimobaba, T.; Kakue, T.; Masuda, N.; Ito, T. Speeding up image quality improvement in random phase-free holograms using ringing artifact characteristics. Appl. Opt. 2017, 56, F61–F66. [Google Scholar] [CrossRef]
- Chen, C.; Wang, J.; Xiao, D.; Wang, Q. Fast method for ringing artifacts reduction in random phase-free kinoforms. Appl. Opt. 2019, 58, A13–A20. [Google Scholar] [CrossRef]
- Chakravarthula, P.; Tseng, E.; Srivastava, T.; Fuchs, H.; Heide, F. Learned hardware-in-the-loop phase retrieval for holographic near-eye displays. ACM Trans. Graph. 2020, 39, 1–18. [Google Scholar] [CrossRef]
- Choi, S.; Kim, J.; Peng, Y.; Wetzstein, G. Optimizing image quality for holographic near-eye displays with Michelson Holography. Optica 2021, 8, 143–146. [Google Scholar] [CrossRef]
- Chen, L.; Zhu, R.; Zhang, H. Speckle-free compact holographic near-eye display using camera-in-the-loop optimization with phase constraint. Opt. Express 2022, 30, 46649–46665. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Seo, D.W.; In, C.; Min, S.W. Phase-assisted camera-in-the-loop hologram optimization with Fourier aperture function constraint. Opt. Express 2025, 33, 21413–21424. [Google Scholar] [CrossRef] [PubMed]
- Yeom, H.J.; Hong, K.; Park, M. High-quality phase-only Fourier hologram generation with camera-in-the-loop. Opt. Express 2025, 33, 6615–6628. [Google Scholar] [CrossRef]

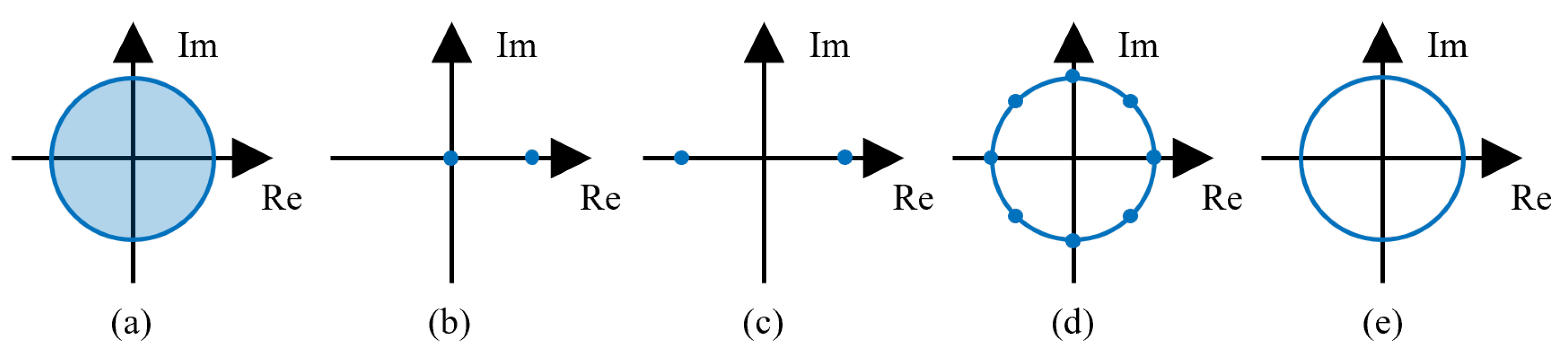
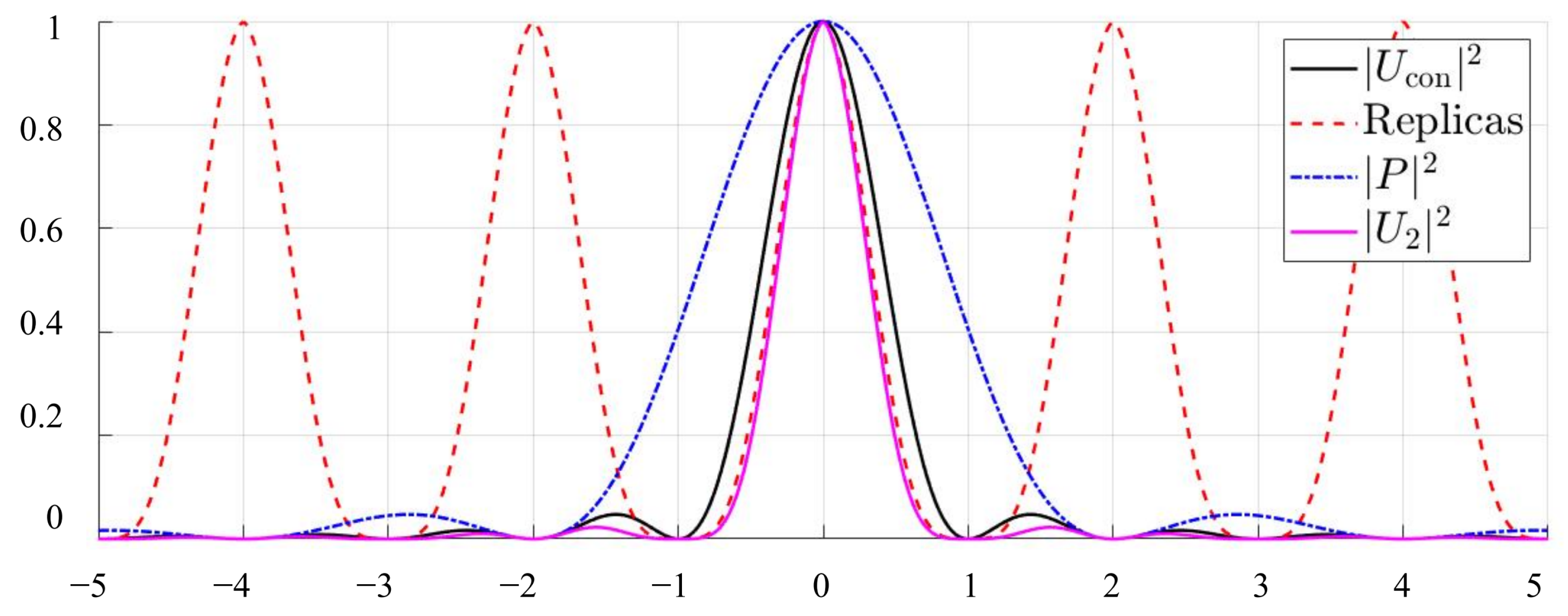



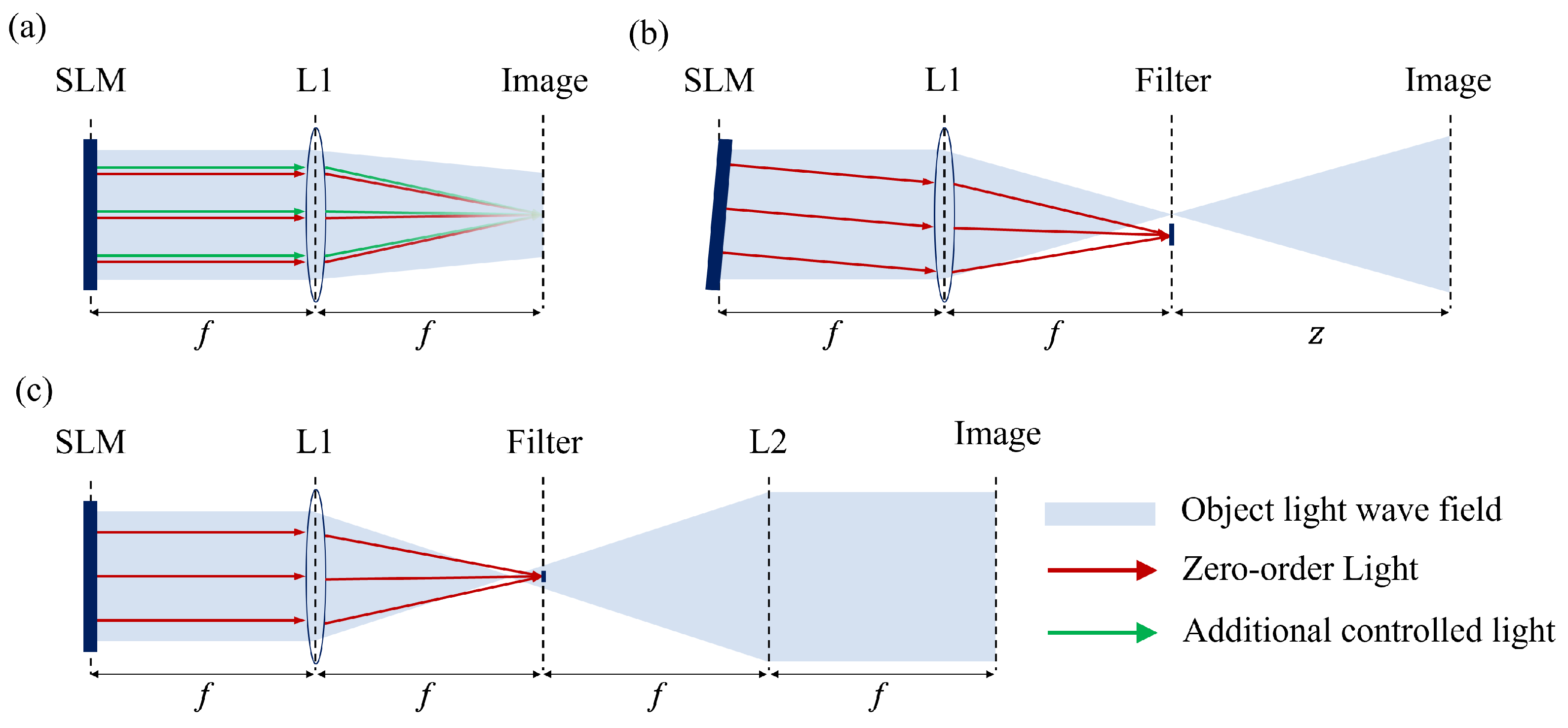
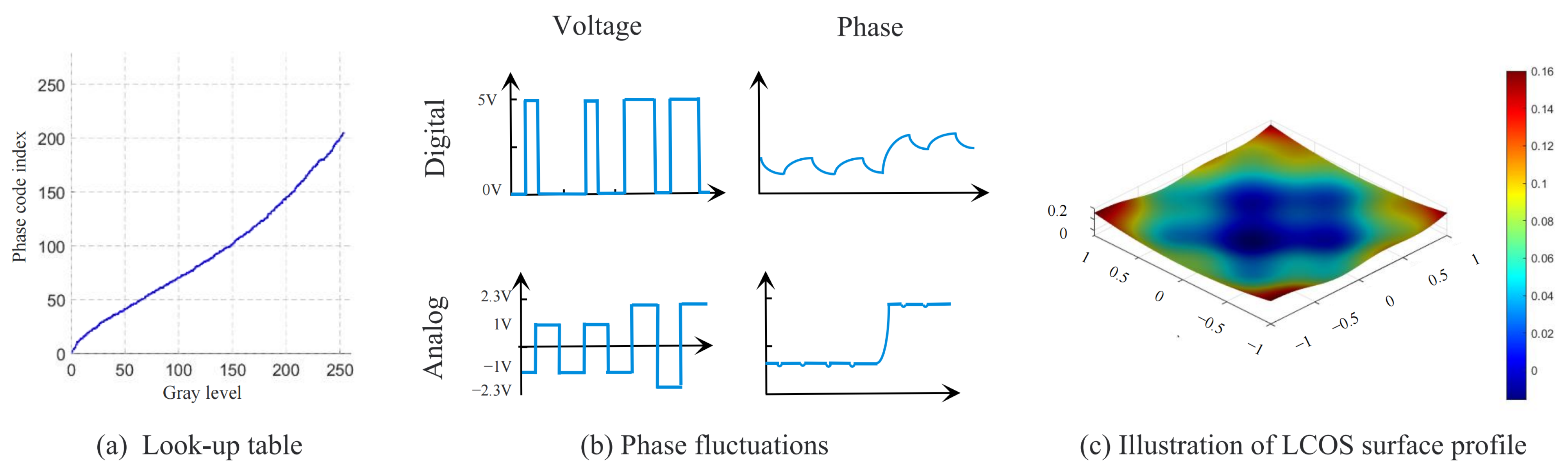

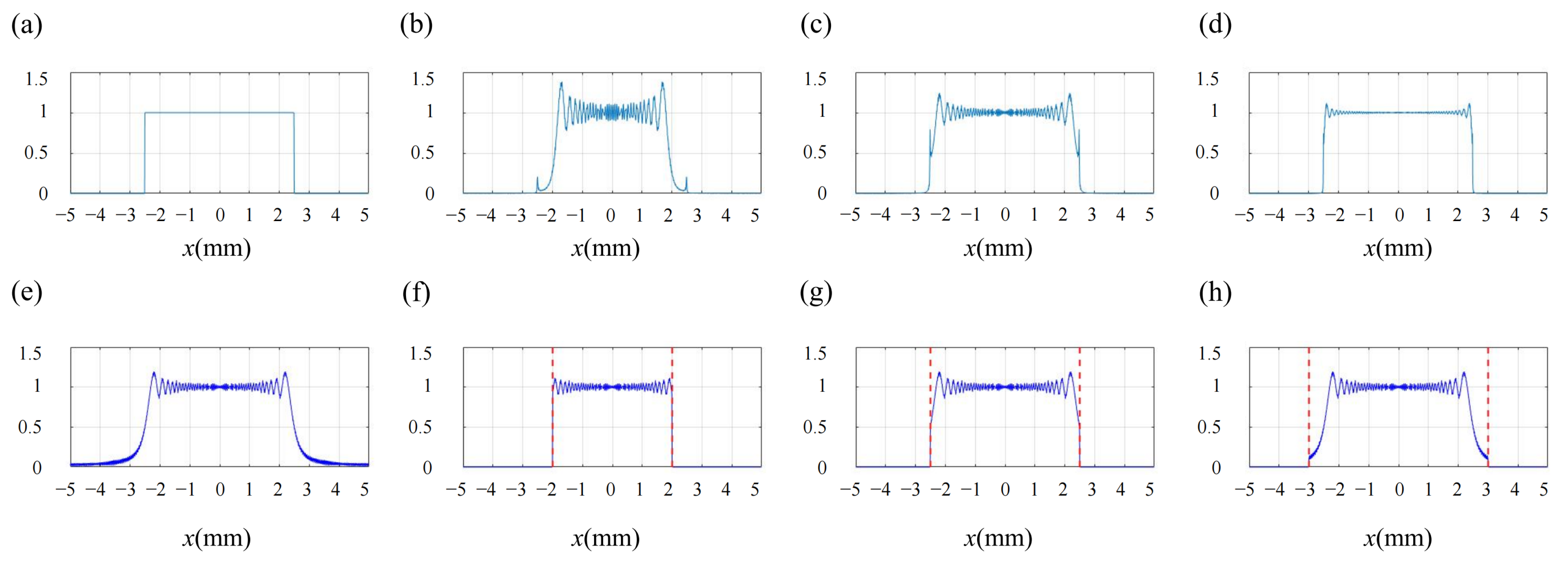
| Diffraction Algorithm | Phase Term | Sampling Condition | Non-Aliased Area |
|---|---|---|---|
| Fres-IR | |||
| Fres-TF | |||
| RSC | |||
| ASM |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, S.; Feng, Z.; Zhang, H.; Tan, Q.; Sun, L. Noise Suppression Strategies in Computer Holography: Methods and Techniques. Lights 2025, 1, 2. https://doi.org/10.3390/lights1010002
Tian S, Feng Z, Zhang H, Tan Q, Sun L. Noise Suppression Strategies in Computer Holography: Methods and Techniques. Lights. 2025; 1(1):2. https://doi.org/10.3390/lights1010002
Chicago/Turabian StyleTian, Songzhi, Zijia Feng, Hao Zhang, Qiaofeng Tan, and Liqun Sun. 2025. "Noise Suppression Strategies in Computer Holography: Methods and Techniques" Lights 1, no. 1: 2. https://doi.org/10.3390/lights1010002
APA StyleTian, S., Feng, Z., Zhang, H., Tan, Q., & Sun, L. (2025). Noise Suppression Strategies in Computer Holography: Methods and Techniques. Lights, 1(1), 2. https://doi.org/10.3390/lights1010002






