Abstract
Although various special materials have been studied for their potential for phosphorus removal in constructed wetlands, varying methodologies make direct comparisons of adsorption capacities observed in laboratory experiments difficult. This paper aims to establish a methodology for determining the optimal ratio of phosphate to material mass for different materials and for achieving the necessary contact time for adsorption isotherms. To minimise the number of experiments required, pretests over 24 h should be repeated to determine the phosphate-specific ratios until they show around 60% of the initial concentration. The tested materials included lava sand and expanded sand (ExS), which showed saturating kinetics curves after 24 to 48 h. However, aggregates containing calcium silicate hydrate (CSH) phases (autoclaved aerated concrete AAC, sand–lime brick SLB, and hydrothermal granules HTG) did not show saturating curves, complicating contact time determination. Consequently, adsorption velocity is proposed to identify the phase with the lowest adsorption rate, which is then used as the contact time in adsorption isotherm experiments. Using this method, adsorption times of 48 h were observed for HTG and SLB, while that for AAC was 24 h. This methodology is intended as an initial approach to establish a common basis for researchers investigating novel materials and make the results comparable.
1. Introduction
The protection of water bodies and further reducing the eutrophication potential of wastewater treatment plant (WWTP) effluent are still important topics. The new EU-UWWTD [1] targets middle-sized (>10.000 PE) and large (>150.000 PE) WWTP for stricter P-effluent values, especially in sensitive areas. In Germany in 2022, small WWTPs up to size class 3 (<10.000 PE) emitted around a quarter of the total phosphorus loads into rivers and streams; size class 4 alone is responsible for around 40% [2]. Of course, limitation values are also size-related, but more and more small WWTPs have to comply with lower total phosphorus (TP) threshold concentrations due to the sensitivity of the receiving water body [3]. While for larger WWTPs, technical systems for P elimination like precipitation and flocculation and/or filtration are viable options to reduce phosphate emissions [3], for smaller WWTPs, less technologically demanding solutions have to be considered.
Constructed wetlands (CW), which are a low-tech solution, could be used to treat the effluent of WWTPs further, to reduce phosphorus loads into rivers and streams. However, concerning phosphorus elimination, the standard CW filter materials like fluviatile sand exhibit highly variable elimination rates from less than 50% [4,5] up to 85% TP [6] and 90% phosphate-phosphorus (PO4-P) [7]. The performance strongly depends on the sand properties, which greatly influence phosphate removal efficiency [8]. The media composition is particularly critical: a high content of accessible aluminium (Al), iron (Fe), and calcium (Ca) compounds enhances phosphate elimination [8,9,10]. This improvement is achieved through adsorption onto the surface, as well as through precipitation processes involving Fe/Al minerals or the formation of Ca-phosphate minerals [11,12].
To improve phosphorus removal, filter materials with enhanced phosphate adsorption properties have been, therefore, a focus of research in the past years, for example, biochar activated carbon [13], volcanic sands [14] or construction and demolition waste containing calcium silicate hydrate (CSH) [15,16]. Recycling materials suitable for binding phosphate by CSH can include, for example, crushed concrete, autoclaved aerated concrete and sand–lime brick [11,17,18,19,20,21,22,23]. Some of these materials, such as concrete and aerated concrete, also contain calcium aluminate hydrate (CAH) or calcium aluminate silicate hydrate (CASH) phases, which further contribute to phosphorus binding [24,25,26].
To assess and compare the suitability for phosphorus elimination and the binding mechanisms behind it, the adsorption kinetics and the adsorption isotherm of phosphate on the filter material have to be determined. The adsorption kinetics show the loading of the target substance on a specific amount of solid over time. The time when equilibrium is achieved is called the equilibrium time. This time is also used as the contact time needed in the adsorption isotherm experiments [17] (p. 54).
For many materials, the equilibrium time and load capacity can be found in the literature, but usually the experimental conditions vary widely between kinetics studies. Therefore, the specified parameters in the literature can rarely be applied to one’s own research. The heterogeneity of kinetics studies is illustrated by Table 1, which compares experimental setups for gathering kinetics parameters of different materials for phosphorus removal. It shows that over the selected literature, the experiment setups are inconsistent concerning many parameters, e.g., tested grain sizes, the phosphate supply per gram of material, and the scale of the experiment. Due to the lack of a clear methodology, the results in the literature are heterogenous and difficult to compare. Also, a missing standardised method results in new researchers being unable to follow a protocol when testing new materials.

Table 1.
Comparison of experiment setups for kinetics experiments for phosphorus adsorption. Exp.: experiment; Ref.: reference.
In order to standardise the procedure for evaluation of unknown materials and to determine a sensible ratio of material to phosphate and test duration, this work developed an experiment scheme that can help to close this gap in methodology. The experiment scheme starts with an iteration of test experiments until the optimal experiment setup is found. Hereby, empirical values were used to find a threshold value, at which iteration was stopped. The kinetics experiments can then be conducted based on these obtained values.
The present methodology is intended as an initial approach to establish a common basis for researchers investigating novel materials, with a view to facilitating the comparison of results.
2. Materials and Methods
The materials used in this research are two kinds of volcanic sands from two different quarries in the “volcanic Eifel” region in Germany, LVI and LVII. Expanded sand (ExS), autoclaved aerated concrete (AAC), and sand–lime brick (SLB) were purchased from building material stores. Hydrothermal granules (HTG) were produced in-house from SiO2- and CaO-rich secondary raw materials, specifically masonry rubble and paper ash. The masonry rubble serves as the quartz component (SiO2). The paper ash supplies the lime component (CaO) and, additionally, contains hydraulic reactive calcium silicates and aluminates. After crushing and grinding, the masonry rubble was homogenised together with the paper ash. For shaping, the powder was then slightly moistened and granulated. The green granules were then hydrothermally treated in an autoclave at 180 °C in saturated water vapour atmosphere at approx. 12 bars. The strength and the microstructure of the hydrothermal granules develop through the formation of different CSH and CA(S)H phases. More information about CSH phases can be found in Supplementary Materials Additional Information S1. Further information about the properties of the HTG is given in [23,32].
The physical characteristics of the substrates are listed in Table 2. The BET surface area was determined using the N2 gas adsorption method. Sample preparation was performed by outgassing for at least 18 h in a vacuum at room temperature. The measurement itself was performed by measuring the whole ad- and desorption isotherm of N2 at 77.3 K.

Table 2.
Specifications of materials used in the experiments.
The moisture content was measured by the weight loss during sample preparation for the BET measurement, except for the moisture content of LVI. For LVI, the weight difference before and after heating to 40 °C for 3 days was used.
The materials LVI, LVII and ExS can be assigned into the group “sand and aggregates from thermal processes” and the others to the group “aggregates with CSH phases”.
An overview of the experiments carried out to obtain the experimental duration of adsorption isotherms is given in Figure 1. The determination of the adsorption isotherm itself (Figure 1, step 3) is not the subject of this work, but the way to obtain the equilibrium time. This time is extracted from kinetics experiments (Figure 1, step 2) and set as the experiment duration for the adsorption isotherm. The ratio of material mass (m), volume (V) and concentration (c) for the kinetics experiments needed to be determined in preliminary experiments (Figure 1, step 1).
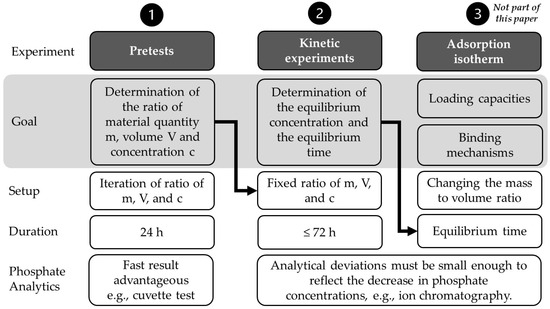
Figure 1.
Overview of the different experiments, including goals, differences in setup, duration, and phosphate analytics.
All experiments were conducted at room temperature with artificial phosphate solution to minimize the effect of other ions on adsorption. As a phosphate source, a stock solution was prepared with KH2PO4 and diluted to the required concentration with ultrapure water. The aim of this research is the treatment of effluent of WWTPs up to approx. 50,000 PE, which have already P elimination in the main treatment stage, reaching average effluent values of around 0.25–2 mg/L TP [33]. Based on the assumption that few solids are found in WWTP effluent and that the dissolved fraction consists mainly of orthophosphate, a concentration of 1 mg/L PO4-P was set. For AAC, the concentration of the phosphate solution had to be adapted to 2 mg/L, due to the small material mass used (see Supplementary Materials, Table S1). The pH of the solution was not adjusted to reduce the effect of interfering ions. As the solution of 1 mg/L PO4-P has an electrical conductivity of around 5 µS/cm, it is seen as a solution of low ionic strength. The measurement of pH is, therefore, problematic, with long stabilization times and incorrect measurements [34]. Therefore, the pH of the PO4-P solution was calculated based on [35] and [36] to be 5.81 for 1 mg/L and 5.65 for 2 mg/L. (For the calculation, see Supplementary Materials, Calculation S1.)
For the kinetics experiments, a separate sampling flask filled with weighed material was prepared for every sampling time to reduce the disturbance of the kinetics experiment [17] (p. 141). Depending on the experiment, different volumes were used. The volume of 0.05 L was measured with bulb pipettes; higher volumes were measured with volumetric flasks and then transferred to the sample flasks. For all experiments, an overhead shaker with twelve seats, in which bottles of different sizes can be clamped, was used. The speed was set to the maximum of 16 rpm. For samples of 0.05 L, Falcon tubes were used as experimental vessels. For higher volumes, wide-neck PE bottles of different sizes (0.1–1 L) were used.
The ground material was weighed on a precision balance and ranged between 0.15 and 1 g, depending on the experiment. Some of the materials used are produced in the laboratory and are, therefore, not available in large quantities. For this reason, for the first iteration of pretests, it was decided to use 0.5 g and 1 g of the material with 0.05 L of phosphate solution (at a concentration of 1 mg/L PO4-P) in a Falcon tube with shaking for 24 h in an overhead shaker. For the following experiments, the parameters V, m and, in one exception, c were iteratively adjusted until a threshold value was achieved. In the experiments, it was empirically determined that, for an experimental duration of 72 h, the target value for P elimination after 24 h should be around 60% (c24h/c0 = 40% removal). A detailed explanation of how this threshold was determined can be found in Section 3.1 Pretests.
To analyse the phosphate concentration, the supernatant of the samples of all experiments was filtered with a 0.45 µm syringe pre-filter and prepared for analysis. For the pretesting, phosphate concentrations were measured with LCK 349 Cuvette Tests (Hach Lange GmbH, Düsseldorf, Germany), as the results had to be quickly available to further proceed. In this stage, single determinations were conducted, as the values were then validated by the kinetics experiment. The test is valid for concentrations between 0.05 and 1.5 mg/L P. The limit of detection (LOD) is 0.007 mg/L. For graphical purposes, values below 0.05 mg/L are shown as 50% of 0.05 mg/L. Values below the LOD were assumed to be 0 mg/L. For the kinetics experiment, the samples were measured via ion chromatography for anions in double determination. For PO4-P, the LOQ in the ion chromatography was 0.03 mg/L PO4-P and the LOD was 0.013 mg/L PO4-P. For graphical purposes and to calculate adsorption, values below the LOQ were calculated to be 50% of the LOQ; if it was lower than the LOD, it was assumed to be 0. The calcium concentration was also measured with ion chromatography.
The equipment details can be found in Table S2.
The amount of P removed equals the amount of P adsorbed to the material and was calculated according to Equation (1):
c0: initial concentration of the solution in mg/L;
ct: concentration of solution after time t in mg/L;
V: volume of the solution in L;
m: mass of the adsorbent material in g.
As the moisture content of all the materials was below 3%, it was not considered in the specific loading.
When conducting kinetics adsorption experiments, the aim is to achieve a concentration that is low enough to minimise measurement inaccuracy, but high enough so that it does not reach zero. Otherwise, no statement can be made about the equilibrium concentration [17], and the experiment has to be repeated. To conduct the experiments, the ratio of phosphate provided to the quantity of material must be known. In this work, this ratio is called the “Specific Phosphate Provided” (SPP) and can be calculated via Equation (2):
It was assumed that the amount of P removed equals the loading of the material. The remaining PO4-P concentration after the 24 h test shows whether the ratio of material quantity to phosphate load needs to be adjusted.
After having determined the suitable ratio, kinetics experiments were conducted. Each kinetics experiment was conducted with at least one replicate; the kinetics experiment for LVI was conducted in triplicate. The samples were prepared with the material mass, volume and concentration determined in the step before. The sampling times were 30 min, 1 h, 2 h, 4 h, 8 h, 24 h, 48 h, and 72 h.
The time between samplings is defined as a sampling slot with a start and an end. The sampling time marks the end of the time slot (see Table 3).

Table 3.
Overview of the classification of sampling times.
With this information, the loading rate or velocity in between samplings can be calculated using Equation (3). To obtain a better understanding of the range of velocity, the relative loading rate in% is calculated using Equation (4). It relates the loading velocity at sample n to the maximum loading velocity of the overall experiment.
qn = loading at sampling n
qn−1 = loading at sampling (n − 1)
tn = time in minutes of sampling n
tn−1 = time in minutes of sampling n − 1
To determine the BET surface area of AAC during the experiments, the material of a sample after 24 h, 48 h, and 72 h was collected. To obtain a blank sample, the experiment was repeated with the same amount of material and volume of ultrapure water and stirred briefly. Then, the material was filtered on a paper filter with a diameter of 90 mm and a pore size of 4–7 µm, rinsed with ultrapure water and then dried in a drying cabinet at 40 °C for three days.
The experimental data were modelled with well-known kinetic adsorption models: the pseudo-first-order (PFO) model is based on Lagergren [37]. The adsorption rate is governed by the diffusion of the adsorbate across the adsorbent surface. The model predicts the equilibrium adsorption capacity qe, while the parameter k1 is often used to describe the velocity until the equilibrium is reached [38]. The PFO model is better suited to systems with high initial adsorbate concentrations. It provides a more accurate prediction of the initial adsorption stages and reflects conditions in which only a small number of adsorbate ions can interact with the available active sites [38].
PFO has the non-linear form presented in Equation (5):
qe = adsorption capacity at equilibrium (mg/g);
k1 = Pseudo-first-order rate constant (g/mg/h).
The pseudo-second-order (PSO) model [39] also predicts an equilibrium adsorption capacity qe and a rate constant k2 (see Equation (6)). The model performs best at low initial concentrations, provides a better fit for the final stages of the adsorption process, and works particularly well with materials that offer many active sites [38].
qe = adsorption capacity at equilibrium (mg/g);
k2 = Pseudo-second-order rate constant (g/mg/h).
The Weber–Morris intraparticle diffusion model (IPD) is an internal diffusion model [40] commonly applied to evaluate the contribution of intraparticle diffusion to the overall adsorption mechanism. The formula is displayed in Equation (7). It helps to distinguish whether intraparticle diffusion is the rate-limiting step or only one of several controlling processes. If C = 0, it can be assumed that intraparticle diffusion is the controlling process. If C > 0, other processes, like film diffusion or surface adsorption are also participating [38].
kdiff = intraparticle diffusion coefficient (mg/g/);
C = IPD Constant (mg/g).
The Elovich model [38,41] (Equation (8)) assumes that activation energy increases progressively with adsorption time, and that adsorption occurs on a heterogeneous surface [38]. The model is often connected with chemisorption processes [42], but the mechanisms are not always clear [38].
A = initial adsorption rate (mg/g/h);
B = desorption rate constant (mg/g/h).
The iteration algorithm used for modelling was Levenberg–Marquardt algorithm [43,44]. R2 and R2 adjusted (R2 adj.) are used as evaluation parameters and calculated when modelling with Origin® 2025.
3. Results and Discussion
3.1. Pretests
To determine a suitable SPP for the contact time experiments, the pretests were performed for each material iteratively. A graph comparing the removal after 24 h and the availability at start of the experiment helped to categorise the results and start the next iteration loop with a new SPP ratio, adjusting either the volume or material mass quantity (Figure 2). Only if the two parameters V and m could no longer be adjusted due to the conditions of the laboratory (e.g., if the amount of material was already 0.15 g), the concentration was raised, but only to a level within the same order of magnitude. The decision-making for each iteration step is also shown in Table S1 (Supplementary Materials).
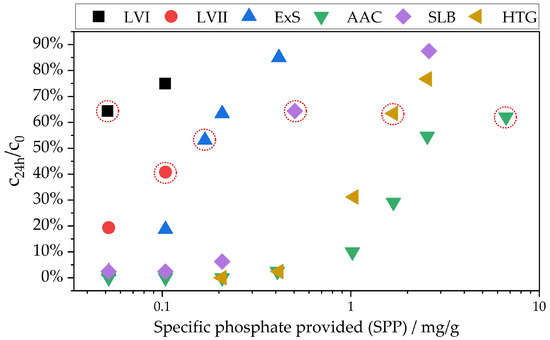
Figure 2.
Ratio of concentration after 24 h and start concentration applied against SPP. Red circles mark the ratio that was successfully used in the kinetics experiments. For cuvette tests, concentrations smaller than 0.05 mg/L are included in the calculation of the load with 0.025 mg/L. Values below the LOD were evaluated as 0 mg/L. LVI, LVII: lava sands; ExS: expanded sand; AAC: autoclaved aerated concrete; SLB: sand–lime brick; HTG: hydrothermal granules.
The iteration was stopped when the concentration after 24 h reached a target value. In the beginning, there was no information or experience regarding the range of the target value. Thus, some of the kinetics experiments had to be conducted several times because concentrations were either too small or changed too little over time, leading to unusable data. Whether the target value was chosen correctly could, therefore, only be determined in the kinetics studies. Empirically, it was determined that, for an experiment duration of 72 h, the target value after 24 h should be around 60% c24h/c0 (=40% phosphate elimination). As can be seen in Figure 2, the c24h/c0 ratios for successful kinetics experiments lie between 53% and 64%. An exception is LVII, where the kinetics experiment was conducted at 41% c24h/c0. This was only successful because lava sand shows a flattening curve, as will be discussed in Section 3.2. The target range can be set at 60 ± 7%. The parameters that led to usable kinetics experiments are displayed in Figure 2 with red circles, and in Table 4.

Table 4.
Experiment parameters for the kinetics studies determined after multiple iterations of pretests. LVI, LVII: lava sand; ExS: expanded sand; AAC: autoclaved aerated concrete; HTG: hydrothermal granules; SLB: sand–lime brick. c0: concentration at t = 0; SPP: specific phosphate provided.
3.2. Kinetics Curves
Figure 3 shows data from the kinetics experiments, including the fittings to the four well-known kinetics models. The R2 and adjusted R2 (R2 adj.) values are presented in Table 5. If comparing PFO and PSO models, all materials are better explained by PSO (see Table 5). In this study, low concentrations of adsorbent solution were used, which explains this observation [38]. PFO and PSO underestimate the real adsorption capacity seen in the data in all cases.
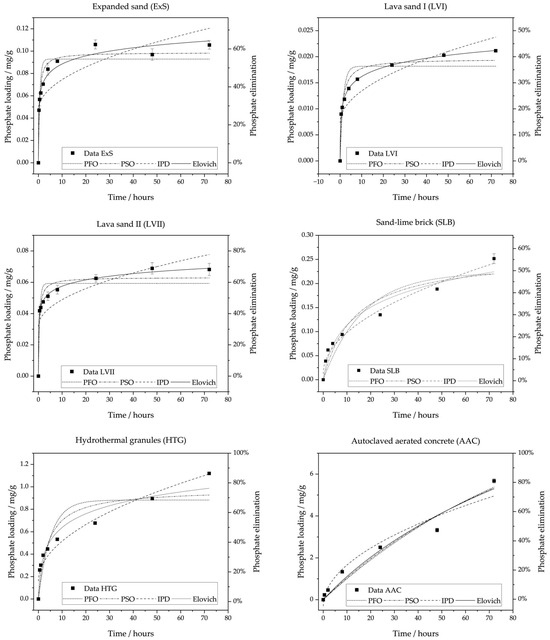
Figure 3.
Kinetics experiments and fitted pseudo-first-order (PFO), pseudo-second-order (PSO), Weber–Morris intraparticle diffusion (IPD), and Elovich models for the different materials: lava sand I (LVI), lava sand II (LVII), expanded sand (ExS), sand–lime brick (SLB), hydrothermal granules (HTG), and autoclaved aerated concrete (AAC). The experiments were conducted with the experimental design shown in Table 4.

Table 5.
R2 and R2 adjusted (R2 adj.) for the tested materials and the pseudo-first-order model, pseudo-second-order model, Weber–Morris intraparticle diffusion model, and Elovich model.
When comparing the six graphs, three different kinds of kinetics curves can be observed in the lab data presented in Figure 3.
ExS, LVI, and LVII show a quick rise in loading, followed by a plateau. These observations are supported by k2 being 23.63, 50.00, and 39.66 g/mg/h for the three materials, respectively. The PSO predicted equilibrium loading capacity is 0.099 mg/g, 0.018 mg/g, and 0.059 mg/g for ExS, LVI, and LVII, respectively. The standard errors are relatively low at 6%, 7%, and 6%. The material data of LVI, LVII, and ExS have the best fit with the Elovich model (R2: 99.94%, 99.67%, 97.82%), which indicates that the materials bind phosphate chemically on the surface. As lava sands have been known to bind phosphate with their aluminium and iron contents [45], this is plausible.
SLB and HTG show a flatter curve with no saturation. If comparing PSO parameters, the rate constant is substantially lower, than those of ExS, LVI, and LVII (k2 (SLB) = 0.29 g/mg/h, k2 (HTG) = 0.26 g/mg/h). The modelled equilibrium capacities are 0.98 mg/g and 0.26 mg/g, respectively, with standard errors of 10% and 13%. The equilibrium time of these materials is more difficult to determine graphically, as they exhibit neither a visible reduction in velocity nor the development of an equilibrium. As a similar curve was seen for red ceramic waste [11], it can be concluded that the slope of the HTG and SLB cannot reach an equilibrium.
For SLB, the fitting results are better with IPD. Even though CSLB is not zero, it is low at 0.012 mg/g, indicating a negligible effect of processes other than intraparticle diffusion.
HTG is equally well fitted by IPD (R2: 95.48%) and Elovich. CHTG is 0.16 mg/g, indicating that not only intraparticle diffusion, but also other processes take place.
On closer inspection, AAC differs from HTG and SLB as its adsorption curve shows a slowdown between 24 and 48 h, followed by a renewed acceleration after 48 h (Figure 3 and Figure 4). For AAC, the modelled PSO equilibrium capacity is the highest with 15.85 mg/g. The standard error is especially high for AAC, with 64%, indicating that, even though the R2 adj. of 95.5% is acceptable, the model’s predictions do not fit well. AAC has the best model fit with Elovich (R2: 96.44%).
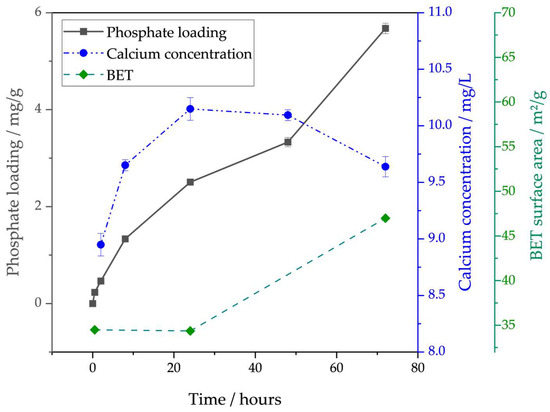
Figure 4.
Phosphate loading on AAC over time, corresponding calcium concentration in the supernatant at the same sampling times, and BET surface of AAC at experiment times t = 0 h, t = 24 h and t = 72 h, extracted from the liquid phase. AAC: aerated autoclaved concrete.
When excluding the last data point (Table 5: AAC adapted), the model fit improves strongly, to 99.89% R2 for Elovich. This might suggest chemisorption as the adsorption type, with another process taking over after 48 h, which cannot be predicted well by the Elovich model. Due to the material properties, chemisorption by calcium ions is most likely.
To better understand the unexpected curve for AAC, BET analyses of the material were performed at different time points (see Figure 4). The BET surface value of AAC after short contact with water falls from 48 g/m2 in the dry state to 34 m2/g as small particles are washed away. Then the value stays constant for 24 h until further increasing at 48 h to 47 m2/g. In parallel with this, the calcium concentration in the supernatant increases to a concentration of around 10 mg/L Ca at 24 h. Afterwards, the concentration starts decreasing (Figure 4).
These measurements can be explained with a crystallization process taking place:
- At contact with water, AAC starts dissolving calcium components that also contain CSH phases. At this point, phosphate precipitation only occurs in the solution and does not change the BET surface area of the material.
- The dissolution leads to an increase in pH, as well as an increase in Ca concentration. The alkaline environment promotes the precipitation of calcium phosphates. For precipitation products to crystallize, first the solution has to be supersaturated [46] (p. 237).
- Crystal seeds in the solution can act as catalysts, reducing the energy barrier for further crystallization [46]. The precipitation products in the solution can serve as precipitation seeds kickstarting the phosphorus uptake after 24 h. The crystallization now takes place on the surface of the material, making it rougher. The increase in roughness correlates with an increase in BET-value.
The influence of precipitation seeds with crystallized material was also shown by Song et al. [46]. In their study, they compared crystallization with and without calcite as crystallization nuclei. The experiment with calcite seeds showed faster phosphate removal compared to the experiment without calcite. After 24 h, the sample with calcite exhibited a clear increase in phosphate elimination compared to the one without. This study supports the assumption that, also in the tested AAC, crystallization nuclei cause a distinct rise in phosphorus retention, observed here after 48 h.
AAC appears to be the most effective adsorbent, with an adsorption capacity of up to 5.7 mg/g after 72 h. Next is HTG, with an adsorption capacity of 1.11 mg/g after 72 h. SLB has an adsorption capacity of 0.25 mg/g, while ExS has the next lowest capacity of 0.1 mg/g. LVII exhibits an adsorption capacity of 0.07 mg/g, while LVI demonstrates the lowest capacity of 0.02 mg/g after 72 h.
3.3. Determination of the Contact Time for the Different Kinetics
Since some of the kinetics experiments described in Section 3.2 do not show clear saturation, a method must be found to determine the contact time of all materials equally. For the S-shaped kinetics of AAC, it is particularly important to perform the adsorption isotherm at the point with the lowest adsorption rate, as even a slight delay in sample preparation can lead to different results. Other materials not showing saturation behaviour like HTG and SLB also do not have a “classic” equilibrium time.
Therefore, the loading velocity vn was used to determine the time slot with the lowest change in adsorption capacity (see Equation (3)). This time slot corresponds to the point at which equilibrium is reached, defined as the time when no further change in adsorption occurs. The relative loading capacity rvn (Equation (4)) helps to sort the velocities and find the lowest velocity immediately. The rvn value compares the vn of a given time interval with that of the remaining intervals, thereby indicating whether saturation is approaching (rvn → 0%), or whether the loading velocity remains relatively high compared to the maximum (rvn >> 0%).
Choosing the start time of the time slot with the lowest relative adsorption velocity is considered the best option so that the risk of distorted results due to a time lag is reduced as much as possible, even if it cannot be completely eliminated for materials with a minimal rvn >> 0%.
For all the materials discussed in this study, the loading velocities and relative loading velocities are shown in Table S3 (Supplementary Materials). The determined contact times for each material for the adsorption isotherms are summarized in Table 6.

Table 6.
Resulting contact times for the adsorption isotherm. LVI, LVII: lava sand; ExS: expanded sand; AAC: autoclaved aerated concrete; HTG: hydrothermal granules; SLB: sand–lime brick.
For LVI and LVII, the rv in the timeslot 24 h to 48 h is close to 0%, indicating an equilibrium state. In the time slot 48 to 72 h, the relative loading velocity reaches its minimum, resulting in 48 h as the equilibration time. For ExS, the rv of 24 h to 48 h is also close to 0%, and the equilibrium is, therefore, set at 24 h.
AAC has the lowest rv in the time slot of 24 to 48 h. After that, rv reaches over 7% of the maximum rvn seen in this experiment. As this is such a significant increase, it is essential to ensure that the sampling does not occur after the inflection point of the curve. For this reason, a contact time of 24 h has been selected.
For HTG, rvn remains stable at 2% between 8 and 72 h. As the increase was constant and relatively small, 48 h was chosen to maximize adsorption capacity. The same procedure was used for SLB (rv (24–72 h) = 3%), which also results in an equilibrium time of 48 h.
3.4. Discussion of the Overall Methodology
The complete methodology, which was developed based on the experiment results discussed, can be found in Figure 5. It explains graphically how to determine the ratio of material quantity and phosphorus load before starting the kinetics experiments. To ensure the reliability of the results, it is imperative that the test experiments are conducted for a minimum duration of 24 h. The materials used in this work cover a wide range of different structures and origins. For these materials, the target value of 60 ± 7% c/c0 after 24 h was a good benchmark over all materials.
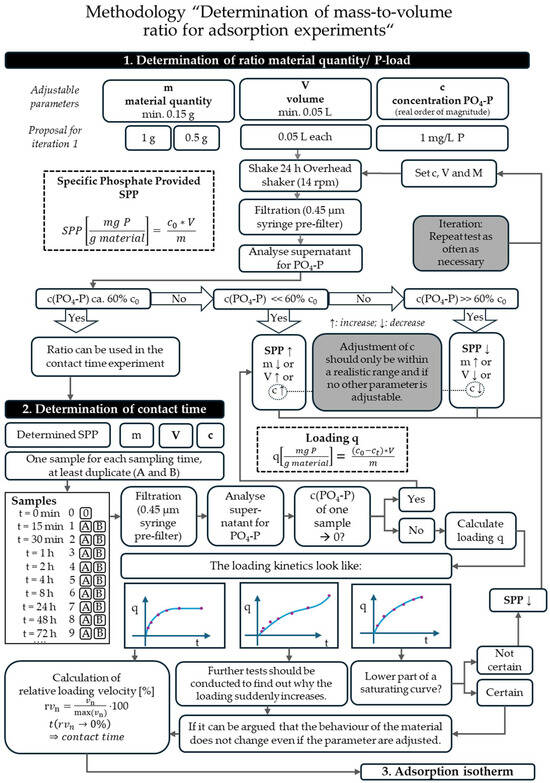
Figure 5.
Methodology for (1) determining the material-to-phosphorus ratio in kinetics adsorption experiments and (2) establishing the appropriate contact time for (3) adsorption isotherm experiments. Applicable across different materials, regardless of their distinct adsorption behaviors.
The methodology scheme specifies that the concentration should only be adjusted if the volume and material mass cannot be changed any further. This is because adsorption is greatly affected by concentration. In Özacar [30], the adsorption of phosphate on calcined alunite showed adsorption capacities of around 100 mg/g for a solution of 150 mg/L versus around 20 mg/g for a concentration of 25 mg/L. This was also confirmed by Li et al. [47] for phosphate removal in CSH phases. For increasing concentrations between 40 and 120 mg/L PO4 (approx. 13–39 mg/L PO4-P), the phosphate loading capacities increased from around 19 to around 50 mg/g. But in both cases, the equilibrium time was independent of the initial phosphate concentration [30,47]. It can be concluded that, when determining the contact time, the initial concentration is of minor importance. However, to accurately estimate the adsorption capacity in kinetics experiments, a concentration within the range expected in real applications is necessary. The pretests have to be repeated as long as SPP does not reach the aimed for concentrations.
Once SPP has been found, the trials can begin. This means that the determined amount of material is poured into individual sample vials that can hold the determined volume.
After the solution with the desired concentration has been added, the respective samples must be clamped in the overhead shaker. After that, the samples are removed, filtered and measured at the appropriate time. If one of the values is close to the determination limit, this means that the material removes phosphate better than expected. Since at least 40% elimination after 24 h is already proven beforehand, it can be guaranteed that the measurements will, in any case, produce a measurable difference, and SPP will not have to be corrected downwards, only upwards.
The three kinetics curves displayed in the methodology (Figure 5) were the ones that were produced in this work. Depending on the material, other curves might be possible, for example, if a material shows time-lagged dissolution properties and even desorbs phosphorus after some time. The curves should be examined to interpret their trends. For materials with a linear increase, such as SLB and HTG, the literature shows that saturation does not occur [11]. If the elimination does not approach a high level, this could also mean that the curve is simply in the lower part of a saturating curve and saturation has simply not yet taken place. This case should not actually occur with the 60% rule in the pretest.
If a researcher is unsure, the experiment should be conducted with a lower SPP to check whether the curve only flattens out when the concentration in the solution approaches zero. If the kinetics of the curves are clear, even for non-saturating materials with no visual equilibrium time, the contact time can be calculated via the formula presented. Using the relative loading velocity of the timesteps in between measurements, the smallest change in adsorption capacity over time can be determined. With this calculation, the most important parameter for determining adsorption isotherms, the experiment duration, can now be determined for materials behaving differently.
One notable aspect of the experimental conditions was that the pH was not adjusted, as the materials all reacted as a base, and already after few minutes, the pH was alkaline. But at least for the materials containing CSH, an acidic environment can lead to a decomposition of the material (e.g., [48,49]). In further studies, it should be investigated if and how a neutral pH would improve comparability of the materials. In this context, a buffer system with a neutral pH could also be established by utilising a mixture of potassium dihydrogen phosphate and dipotassium hydrogen phosphate [36].
The experiments were conducted with an artificial phosphate solution to minimise interactions with other ions. But when transferring the system to real operation requirements, the matrix of real treated wastewater could interact with the material and change the adsorption capacity. The buffer capacity of real wastewater also affects the pH, which is an important factor for adsorption. Depending on the objective of the study, real wastewater should, therefore, also be considered as a medium for the experiments. It must be considered that the composition of wastewater can vary greatly within short time periods; hence, the same batch of wastewater should be used throughout the experiments to ensure consistency.
To date, the processes of precipitation in the solution and adsorption of phosphate on the particles have not been analysed separately. Consequently, ions present in the solution capable of precipitating with phosphorus are also included in the adsorption capacity. In the case of solutions prepared with ultrapure water, this is minimal. Nevertheless, such ions might also be dissolved from the investigated materials and would subsequently precipitate as precipitation products in the solution. Although phosphate is not adsorbed on the particle surface, its elimination is added to the material’s adsorption capacity. It would be valuable to find a way to separate the two processes in the kinetics experiments to better understand what is happening at a particle level. In Cabral et al. [11] and in White et al. [29], they used potassium chloride to diminish the co-precipitation of calcium with phosphate. Future experiments should compare both options to also determine the effect of precipitation in some of the tested materials.
4. Conclusions
This study is a first attempt to find a common basis for adsorption experiments of materials for phosphate elimination in constructed wetlands. This is because inconsistent experimental designs for adsorption kinetics and isotherms make it very difficult to compare the adsorption capacities and performance of materials in different research projects and papers. This approach ensures that the contact time for kinetics experiments is scientifically proven and not just assumed. The presented methodology gives researchers a clear plan for carrying out kinetics experiments with completely unknown materials, so that the results are comparable not only between materials in the same paper, but also between different papers and working groups.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/purification1020007/s1. Additional Information S1. Additional Information on CSH. Table S1: Visualization of the iteration steps for the lava sands LVI, LVII, expanded sand (ExS), autoclaved aerated cement (AAC), sand–lime brick (SLB), hydrothermal granules (HTG). Calculation S1: Calculation of pH of a KH2PO4 solution with a low ionic strength and 1 mg/L and 2 mg/L PO4-P. Table S2: List of materials and brands used in the laboratory experiments and for analysis. Table S3: Overview of all loading velocities (vn) and relative loading velocities (rvn) for the materials ExS, LVI, LVII, AAV, HTG, and SLB. Refs. [50,51,52,53,54,55,56] are cited in Supplementary Materials File.
Author Contributions
Conceptualization, V.H. and H.S.; Investigation, V.H. and A.H.; Methodology, V.H.; Resources, K.R.; Supervision, H.S.; Visualization, V.H.; Writing—original draft, V.H.; Writing—review and editing, V.H., K.R., A.H. and H.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by DBU—Deutsche Bundesstiftung Umwelt, Project-ID 38489/01, “Further phosphorus elimination using resource-saving planted constructed wetlands as a downstream stage of small and medium-sized wastewater treatment plants”. Part of the laboratory equipment was funded by the research initiative NanoKat of the RPTU.
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Materials. Further inquiries can be directed to the corresponding author.
Acknowledgments
During the preparation of this manuscript, the authors used GPT-4o by Azure OpenAI Service and DeepL by DeepL SE for the purpose of improving readability and language. The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
Dr. Andreas Hahn was employed by the company ZetA Partikelanalytik GmbH. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| A | Initial Elovich adsorption rate, in mg/g/h |
| AAC | Autoclaved aerated concrete |
| Al | Aluminium |
| B | Elovich desorption rate constant, in mg/g/h |
| BET | Brunauer–Emmett–Teller model that determines the mass-related specific surface area of a solid. |
| C | IPD Constant, in mg/g |
| c | PO4-P-concentration, in mg/L |
| c0 | PO4-P-concentration at the beginning of the experiment, at t = 0 |
| c24h | PO4-P-concentration at t = 24 h |
| Ca | Calcium |
| CAH | Calcium aluminate hydrate phases |
| CASH | Mixed calcium aluminate silicate hydrate phases |
| CSH | Calcium silicate hydrate phases |
| CT | Cuvette test |
| CW | Constructed wetland(s) |
| EU-UWWTD | European urban wastewater treatment directive |
| ExS | Expanded sand |
| Fe | Iron |
| HTG | Hydrothermal granules |
| IC | Ion chromatography |
| IPD | Intraparticle diffusion (kinetic model) |
| k1 | Pseudo-first-order rate constant, in g/mg/h |
| k2 | Pseudo-second-order rate constant, in g/mg/h |
| kdiff | Intraparticle diffusion coefficient, in mg/g/ |
| LOD | Limit of detection |
| LOQ | Limit of quantification |
| LV | Lava sand |
| m | Material mass, in g |
| Mg | Magnesium |
| P | Phosphorus |
| PE | People equivalent |
| PFO | Pseudo-first-order (kinetic model) |
| PO4-P | Phosphate related to phosphorus |
| PFO | Pseudo-second-order (kinetic model) |
| q | Loading, in mg phosphate/(g material) |
| qe | adsorption capacity at equilibrium, in mg/g |
| Ref. | Reference |
| rvn | Relative loading velocity at time step n, in% |
| SLB | Sand–lime brick |
| SPP | Specific phosphate provided in mg PO4-P per g material |
| TP | Total phosphorus |
| V | Volume, in L |
| vn | Loading velocity at time step n, in mg/g/min |
| WWTP | Wastewater treatment plant |
References
- Urban Wastewater Treatment. European Parliament Legislative Resolution of 10 April 2024 on the Proposal for a Directive of the European Parliament and of the Council Concerning Urban Wastewater Treatment (Recast): P9_TC1-COD(2022)0345. 2024. Available online: https://eur-lex.europa.eu/eli/C/2025/1330/oj/eng (accessed on 28 August 2025).
- DWA. 35. Leistungsnachweis Kommunaler Kläranlagen: Fremdwasser. DWA-Leistungsnachweis 2022, Hennef. 2023. Available online: https://de.dwa.de/files/_media/content/06_SERVICE/ZahlenFaktenUmfragen/Leistungsnachweis/leistungsvergleich_2023_8seiter_A4_2024_Ansicht.pdf (accessed on 28 August 2025).
- Münch, K.; Angerbauer, F.; Jung, T. Auswertung der Pges-und AFS—Ablaufkonzentrationen von rheinland pfälzischen Belebungsanlagen an p1—Wasserkörpern. KA Korresp. Abwasser Abfall 2020, 67, 954–961. [Google Scholar]
- Priya, G.S.; Brighu, U. Comparison of Different Types of Media for Nutrient Removal Efficiency in Vertical Upflow Constructed Wetlands. Int. J. Environ. Eng. Manag. 2013, 4, 405–416. [Google Scholar]
- Arias, C.A.; Del Bubba, M.; Brix, H. Phosphorus removal by sands for use as media in subsurface flow constructed reed beds. Water Res. 2001, 35, 1159–1168. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Y.; Xu, W.; Wang, H.; Zhao, D.; Ding, H. Nitrogen and Phosphorus Removal Efficiency and Denitrification Kinetics of Different Substrates in Constructed Wetland. Water 2022, 14, 1757. [Google Scholar] [CrossRef]
- Thalla, A.K.; Devatha, C.P.; Anagh, K.; Sony, E. Performance evaluation of horizontal and vertical flow constructed wetlands as tertiary treatment option for secondary effluents. Appl. Water Sci. 2019, 9, 147. [Google Scholar] [CrossRef]
- Brix, H.; Arias, C.A.; Del Bubba, M. Media selection for sustainable phosphorus removal in subsurface flow constructed wetlands. Water Sci. Technol. 2001, 44, 47–54. [Google Scholar] [CrossRef] [PubMed]
- Stefanakis, A.; Akratos, C.S.; Tsihrintzis, V.A. (Eds.) Vertical Flow Constructed Wetlands: Eco-Engineering Systems for Wastewater and Sludge Treatment, 1st ed.; Elsevier: Amsterdam, The Netherlands; Boston, MA, USA; Heidelberg, Germany, 2014; ISBN 978-0-12-404612-2. [Google Scholar]
- Vohla, C.; Kõiv, M.; Bavor, H.J.; Chazarenc, F.; Mander, Ü. Filter materials for phosphorus removal from wastewater in treatment wetlands—A review. Ecol. Eng. 2011, 37, 70–89. [Google Scholar] [CrossRef]
- Cabral, L.L.; Pereira, I.C.; Perretto, F.; Nagalli, A.; Rizzo-Domingues, R.C.P.; Passig, F.H.; Carvalho, K.Q.d. Adsorption and desorption of phosphate onto chemically and thermochemically pre-activated red ceramic waste: Characteristics, batch studies, and mechanisms. J. Environ. Chem. Eng. 2021, 9, 106695. [Google Scholar] [CrossRef]
- Qin, Z.; Shober, A.L.; Scheckel, K.G.; Penn, C.J.; Turner, K.C. Mechanisms of Phosphorus Removal by Phosphorus Sorbing Materials. J. Environ. Qual. 2018, 47, 1232–1241. [Google Scholar] [CrossRef]
- Bolton, L.; Joseph, S.; Greenway, M.; Donne, S.; Munroe, P.; Marjo, C.E. Phosphorus adsorption onto an enriched biochar substrate in constructed wetlands treating wastewater. Ecol. Eng. 2019, 142, 100005. [Google Scholar] [CrossRef]
- Bruch, I.; Fritsche, J.; Bänninger, D.; Alewell, U.; Sendelov, M.; Hürlimann, H.; Hasselbach, R.; Alewell, C. Improving the treatment efficiency of constructed wetlands with zeolite-containing filter sands. Bioresour. Technol. 2011, 102, 937–941. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Y.; Wu, L.; Jin, Y.; Gong, Y.; Li, A.; Li, J.; Li, F. Recycled aggregates from construction and demolition waste as wetland substrates for pollutant removal. J. Clean. Prod. 2021, 311, 127766. [Google Scholar] [CrossRef]
- Patyal, V.; Jaspal, D.; Khare, K. Evaluation of composite matrix in constructed wetland for phosphorus removal. Bioresour. Technol. Rep. 2024, 26, 101870. [Google Scholar] [CrossRef]
- Worch, E. (Ed.) Adsorption Technology in Water Treatment; De Gruyter: Berlin, Germany, 2021; ISBN 9783110715507. [Google Scholar]
- Xu, D.; Xu, J.; Wu, J.; Muhammad, A. Studies on the phosphorus sorption capacity of substrates used in constructed wetland systems. Chemosphere 2006, 63, 344–352. [Google Scholar] [CrossRef]
- Li, W.; Zeng, L.; Kang, Y.; Zhang, Q.; Luo, J.; Guo, X. A solid waste, crashed autoclaved aerated concrete, as a crystalline nucleus for the removal of low concentration of phosphate. Desalination Water Treat. 2016, 57, 14169–14177. [Google Scholar] [CrossRef]
- Genetie Abetu, A.; Befekadu Kebede, A. Crushed Concrete as Adsorptive Material for Removal of Phosphate Ions from Aqueous Solutions. Water Conserv. Manag. 2020, 5, 58–64. [Google Scholar] [CrossRef]
- Deng, Y.; Wheatley, A. Mechanisms of Phosphorus Removal by Recycled Crushed Concrete. Int. J. Environ. Res. Public Health 2018, 15, 357. [Google Scholar] [CrossRef]
- Kuhn, D.C.; Cabral, L.L.; Pereira, I.C.; Gonçalves, A.J.; Maciel, G.M.; Haminiuk, C.W.I.; Nagalli, A.; Passig, F.H.; Carvalho, K.Q.d. Development of aerated concrete waste/white cement composite for phosphate adsorption from aqueous solutions: Characterization and modeling studies. Chem. Eng. Process. Process Intensif. 2023, 184, 109284. [Google Scholar] [CrossRef]
- Seher, J.; Rübner, K.; Schnell, A.; Hahn, A.; Bruch, I.; Alewell, U.; Vöge, M.; Shafiei, K.; Schumann, S. Hydrothermalgranulate—Verwertungsmöglichkeit für Mauerwerkbruch; Sitzungsberichte der Leibniz-Sozietät der Wissenschaften zu Berlin: Berlin, Germany, 2023; pp. 79–94. Available online: https://leibnizsozietaet.de/wp-content/uploads/2023/12/01_SB158-0.pdf (accessed on 28 August 2025).
- Zhang, J.; Fu, W. Sponge effect of aerated concrete on phosphorus adsorption-desorption from agricultural drainage water in rainfall. Soil Water Res. 2020, 15, 220–227. [Google Scholar] [CrossRef]
- Scott, I.S.P.C.; Penn, C.J.; Huang, C. Development of a Regeneration Technique for Aluminum-Rich and Iron-Rich Phosphorus Sorption Materials. Water 2020, 12, 1784. [Google Scholar] [CrossRef]
- Zha, Z.; Ren, Y.; Wang, S.; Qian, Z.; Yang, L.; Cheng, P.; Han, Y.; Wang, M. Phosphate adsorption onto thermally dehydrated aluminate cement granules. RSC Adv. 2018, 8, 19326–19334. [Google Scholar] [CrossRef] [PubMed]
- Oguz, E.; Gurses, A.; Yalcin, M. Removal of Phosphate from Waste Waters by Adsorption. Water Air Soil Pollut. 2003, 148, 279–287. [Google Scholar] [CrossRef]
- Cheng, G.; Li, Q.; Su, Z.; Sheng, S.; Fu, J. Preparation, optimization, and application of sustainable ceramsite substrate from coal fly ash/waterworks sludge/oyster shell for phosphorus immobilization in constructed wetlands. J. Clean. Prod. 2018, 175, 572–581. [Google Scholar] [CrossRef]
- White, S.A.; Taylor, M.D.; Albano, J.P.; Whitwell, T.; Klaine, S.J. Phosphorus retention in lab and field-scale subsurface-flow wetlands treating plant nursery runoff. Ecol. Eng. 2011, 37, 1968–1976. [Google Scholar] [CrossRef]
- Özacar, M. Contact time optimization of two-stage batch adsorber design using second-order kinetic model for the adsorption of phosphate onto alunite. J. Hazard. Mater. 2006, 137, 218–225. [Google Scholar] [CrossRef]
- Li, L.; Wang, W.; Jiang, Z.; Luo, A. Phosphate in Aqueous Solution Adsorbs on Limestone Surfaces and Promotes Dissolution. Water 2023, 15, 3230. [Google Scholar] [CrossRef]
- Rübner, K.; Prinz, C.; Adolphs, J.; Hempel, S.; Schnell, A. Microstructural characterisation of lightweight granules made from masonry rubble. Microporous Mesoporous Mater. 2015, 209, 113–121. [Google Scholar] [CrossRef]
- DWA. 36. Leistungsnachweis Kommunaler Kläranlagen: Auswirkung der Neuen EU-Kommunalabwasserrichtlinie (KARL) Auf Die Erforderliche Nährstoffelimination. 2024. Available online: https://de.dwa.de/files/_media/content/06_SERVICE/ZahlenFaktenUmfragen/Leistungsnachweis/leistungsnachweis-2024.pdf (accessed on 28 August 2025).
- Bier, A.W. pH Measurement in Low-ionic Strength (Pure) Samples. 2009. Available online: https://cdn.hach.com/7FYZVWYB/at/r6tzhzjkgh6pwjkgthjnvs4/LIT2073.pdf (accessed on 15 April 2025).
- Jüptner, G. 111 Rechenübungen zum Gebiet Chemische Technologie; Springer Spektrum: Berlin/Heidelberg, Germay, 2020; ISBN 9783662611173. [Google Scholar]
- Scholz, F.; Kahlert, H. Chemische Gleichgewichte in der Analytischen Chemie; Springer: Berlin/Heidelberg, Germany, 2020; ISBN 978-3-662-61106-7. [Google Scholar]
- Lagergren, S. About the Theory of So-Called Adsorption of Soluble Substances. K. Sven. Vetenskapsakademiens Handl. 1898, 24, 1–39. [Google Scholar]
- Wang, J.; Guo, X. Adsorption kinetic models: Physical meanings, applications, and solving methods. J. Hazard. Mater. 2020, 390, 122156. [Google Scholar] [CrossRef] [PubMed]
- Ho, Y.S.; Wase, D.; Forster, C.F. Removal of lead ions from aqueous solution using sphagnum moss peat as adsorbent. Water SA 1996, 22, 219–224. [Google Scholar]
- Weber, W.J.; Morris, J.H. Kinetics of adsorption on carbon from solution. J. Sanit. Eng. Div. 1963, 89, 31–59. [Google Scholar] [CrossRef]
- Elovich, S.Y.; Larionov, O.G. Theory of adsorption from nonelectrolyte solutions on solid adsorbents: 1. Simplified analysis of the equation of the adsorption isotherm from solutions. Russ. Chem. Bull. 1962, 11, 191–197. [Google Scholar] [CrossRef]
- Brandani, S. Kinetics of liquid phase batch adsorption experiments. Adsorption 2021, 27, 353–368. [Google Scholar] [CrossRef]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Quart. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Alewell, C.; Huang, J.-H.; McLaren, T.I.; Huber, L.; Bünemann, E.K. Phosphorus retention in constructed wetlands enhanced by zeolite- and clinopyroxene-dominated lava sand. Hydrol. Process. 2021, 35, 2. [Google Scholar] [CrossRef]
- Song, Y.; Weidler, P.G.; Berg, U.; Nüesch, R.; Donnert, D. Calcite-seeded crystallization of calcium phosphate for phosphorus recovery. Chemosphere 2006, 63, 236–243. [Google Scholar] [CrossRef]
- Li, C.; Yu, Y.; Li, Q.; Zhong, H.; Wang, S. Kinetics and equilibrium studies of phosphate removal from aqueous solution by calcium silicate hydrate synthesized from electrolytic manganese residue. Adsorpt. Sci. Technol. 2019, 37, 547–565. [Google Scholar] [CrossRef]
- Ernest, T.R. Sand-Lime Brick. Ph.D. Thesis, University of Illinois, Urbana, IL, USA, 1910. [Google Scholar]
- Wang, X.; Xu, K.; Li, Y.; Guo, S. Dissolution and leaching mechanisms of calcium ions in cement based materials. Constr. Build. Mater. 2018, 180, 103–108. [Google Scholar] [CrossRef]
- Okano, K.; Uemoto, M.; Kagami, J.; Miura, K.; Aketo, T.; Toda, M.; Honda, K.; Ohtake, H. Novel technique for phosphorus recovery from aqueous solutions using amorphous calcium silicate hydrates (A-CSHs). Water Res. 2013, 47, 2251–2259. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.-G.; Alvarez, P.J.J.; Kim, H.-G.; Jeong, S.; Lee, S.; Lee, K.B.; Lee, S.-H.; Choi, J.-W. Phosphorous recovery from sewage sludge using calcium silicate hydrates. Chemosphere 2018, 193, 1087–1093. [Google Scholar] [CrossRef] [PubMed]
- Berg, U.; Donnert, D.; Weidler, P.G.; Kaschka, E.; Knoll, G.; Nüesch, R. Phosphorus removal and recovery from wastewater by tobermorite-seeded crystallisation of calcium phosphate. Water Sci. Technol. 2006, 53, 131–138. [Google Scholar] [CrossRef] [PubMed]
- Ehbrecht, A.; Ritter, H.-J.; Schmidt, S.-O.; Schönauer, S.; Schuhmann, R.; Weber, N. Entwicklung Eines Kombinierten Kristallisationsverfahrens zur Gewinnung von Phosphatdünger aus dem Abwasserreinigungsprozess mit Vollständiger Verwertung der Restphasen in der Zementindustrie. Abschlussbericht AiF-Nr. 17899 N. 2016. Available online: https://fg-kalk-moertel.de/files/02_2016_Forschungsbericht_Phosphatrecycling.pdf (accessed on 5 September 2024).
- Zhang, Z.; Wang, X.; Zhao, J. Phosphate recovery from wastewater using calcium silicate hydrate (C-S-H): Sonochemical synthesis and properties. Environ. Sci. Water Res. Technol. 2019, 5, 131–139. [Google Scholar] [CrossRef]
- Hsu, P.H. Precipitation of phosphate from solution using aluminium salt. Water Res. 1975, 9, 1155–1161. [Google Scholar] [CrossRef]
- Morris, J.H.; Perkins, P.G.; Rose, A.E.A.; Smith, W.E. The Chemistry and Binding Properties of Aluminium Phosphates. Chem. Soc. Rev. 1977, 6, 173–194. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).