Nonlinear Regression Expansion Model for Fissured Highly Expansive Soils

Abstract

This study presents a nonlinear regression expansion model tailored to the characteristics of fissured highly expansive soils. Through in-depth investigations, fissure ratio (K_r), dry density (ρ_d), initial water content (w₀), and overburden stress (ln(1 + σ)) were identified as critical factors influencing expansion behavior. Experimental results revealed linear relationships between ultimate expansion (δ_ep) and w₀, ρ_d, and ln(1 + σ), and an exponential relationship with K_r. A multivariate nonlinear regression model was developed and validated, demonstrating high predictive accuracy. The model highlights the significant role of fissure infill materials, particularly gray-green clay, on soil expansiveness. It provides a reliable tool for predicting the expansion characteristics of fissured expansive soils under various conditions, offering theoretical and practical support for engineering applications in expansive soil regions. This study uses a single highly expansive clay from the Nanyang section. The soil is a transported Middle Pleistocene alluvial–proluvial clay (al-plQ2) in which fissures are predominantly filled by 2–5 mm gray-green clay. Accordingly, the proposed regression is most applicable to fissure systems that are largely infilled; extrapolation to open or partially infilled fissures should be made with caution.

1. Introduction

Highly expansive soils, as a type of special soil with significant expansiveness, exert substantial impacts and pose challenges to various engineering projects [1,2,3,4]. Based on on-site geological investigations conducted in the Nanyang section of the South-to-North Water Diversion Project’s middle route [5,6,7,8], over 100 expansive soil samples were collected and classified into expansion levels. The typical distribution areas of highly expansive soils were identified [8,9,10], including segments such as Nanyang Segment 2 and Nanyang Segment 3. These soils are primarily found at the excavation bases of channels, with some occurrences on channel slopes. Investigations reveal that highly expansive soils exhibit distinct macro-characteristics, notably the development of fissures filled with a significant amount of infill material. These fissured soils present considerable challenges to the design and construction of channels.

This study proposes a nonlinear regression expansion model tailored to the characteristics of fissured highly expansive soils. Through an in-depth analysis of the distribution characteristics of soil fissures, the model aims to elucidate the expansion mechanism of expansive soils and their relationship with fissure characteristics. By integrating field geological data and employing nonlinear regression methods, the model provides more accurate predictions of the expansive behavior of highly expansive soils under various construction conditions. This serves as theoretical and technical support for the design and construction of channels in regions with highly expansive soils.

In recent years, machine learning has emerged as an effective approach for analyzing the complex nonlinear behavior of expansive soils. Neural-network-based models have shown high accuracy in estimating swelling pressure and deformation parameters. Taherdangkoo et al. [11] developed an efficient neural network model for predicting the maximum swelling pressure of clayey soils, while Elakiya and Keerthana [12] confirmed the feasibility of applying artificial neural networks to represent soil–water interaction processes.

Subsequent studies have further extended these methods to more complex and small-sample problems. Mohammed et al. [13] demonstrated that data-driven regression approaches outperform traditional empirical formulas in predicting soil swelling. Li et al. [14] proposed a multi-algorithm ensemble framework to improve generalization in high-dimensional, small-sample datasets, and Yao et al. [15] incorporated fissure ratio, density, moisture, and loading effects into a nonlinear regression model, verifying that fissure development plays a dominant role in swelling behavior.

Meanwhile, time-dependent and stress-dependent responses have been investigated to capture long-term deformation characteristics. Li et al. [10] examined the in-situ creep behavior of expansive soils through pressuremeter tests, and Alnmr et al. [16] introduced a machine-learning-powered approach for optimizing unit weight and stress parameters to mitigate swelling.

These advances demonstrate that data-driven modeling provides a promising pathway for improving the accuracy of swelling prediction and control. However, few existing studies have explicitly coupled fissure ratio with key physical parameters in a unified nonlinear framework. To address this limitation, the present study develops a nonlinear regression expansion model that integrates fissure ratio, dry density, initial water content, and overburden stress. The proposed model enhances predictive reliability for fissured expansive soils and offers practical guidance for deformation control and risk management in dam and channel engineering.

2. Characteristics of Fissures and Quantitative Representation

Fissures in expansive soils are generally categorized into primary and secondary types according to their formation mechanisms. The primary fissures arise from differential shrinkage stresses within the soil mass and represent the original structural planes; they usually taper downward and are commonly filled with later-deposited clay. Secondary fissures are mainly tension- or shear-induced cracks produced by variations in external or internal stresses. They are more widespread, have relatively smooth surfaces, and are frequently filled with gray-green or grayish-white clay that is more expansive and exhibits poorer engineering performance than the parent material [17], as illustrated in Figure 1.

Field observations indicate that fissures in the Nanyang expansive clay are predominantly filled rather than open. Even at depths greater than 15 m, well-developed fissure traces can still be observed within the slope profile. Under high overburden stress, the fissures are typically filled with gray-green clay rich in hydrophilic minerals such as montmorillonite and illite. The infill, believed to result from long-term groundwater-mediated ion exchange and mineral deposition, usually ranges from 2 to 5 mm in thickness, occasionally reaching more than 10 mm. These fine-grained, high-moisture infills exhibit pronounced expansiveness and low strength (modified from [17]).

In the expansive soil slopes of Nanyang, where groundwater activity is frequent, most fissures are filled with gray-green clay, with a smaller proportion filled with calcareous or ferruginous material. Fissures without infill are rare. Studies indicate that weakly expansive soils have 64.3% to 83.9% of fissures filled with gray-green clay. In moderately expansive soil zones, this proportion exhibits vertical zonation, with approximately 80% of fissures within 6 m’ depth being filled. In contrast, in highly expansive soils, where the depth is greater, over 90% of fissures are filled with gray-green clay. In practice, Kr was prescribed at mixing by converting oven-dry masses of the gray-green infill and the matrix to volumes using their particle densities (V = m/ρ_s, measured by pycnometer); thus the reported Kr equals the target volumetric fraction at mixing.

Geological setting (Nanyang). The tested soil in this study comes from the Nanyang section and belongs to the lower part of the Middle Pleistocene alluvial–proluvial deposits (al-plQ2). Macroscopically, the strong expansive layer is light-yellow to light-brown with gray-green streaks; very large fissures are absent, large fissures occur, and small fissures are extremely dense. Fissure surfaces are smooth and slightly undulating and are predominantly filled by gray-green clay of 2–5 mm thickness; no groundwater was observed during excavation of the strong expansive layer.

Mineralogical composition (XRD, Nanyang). Representative bulk X-ray diffraction of the Nanyang strong expansive clay (al-plQ2) shows a smectite-dominated assemblage with the following average composition taken from the Nanyang entry of our XRD table: smectite 53.0%, chlorite 4.0%, illite 3.0%, kaolinite 3.0%, quartz 40.0%, feldspar 1.0%, calcite ~0%. The gray-green fissure infill was sampled from the same stratigraphic horizon; separate XRD was not performed, and no additional mineral phases were identified at the macroscopic investigation scale. Accordingly, the remolded specimens are treated as volumetric mixtures of matrix and infill within the same mineral suite.

Representativeness of remolded specimens. The specimens in this study were intentionally remolded as controlled volumetric mixtures of the matrix clay and the gray-green fissure infill, both sampled from the same stratigraphic horizon of the Nanyang section. This design prescribes the fissure ratio K_r through the mixture proportion and thereby isolates the compositional effect (mineral suite and fines content) together with the state variables (ρ_d, w_i, σ_v) on the ultimate expansion δ_ep under confinement. In the Nanyang field setting, fissures are predominantly infilled and the infill shares the same clay-mineral assemblage as the matrix; under one-dimensional inundation tests, the final expansion magnitude is therefore expected to be governed primarily by composition and state, rather than by the intact macro-fissure geometry. Consequently, the present regression model does not address behaviors controlled by open or partially infilled fissures or by intact macro-fabric anisotropy (which mainly affect wetting paths and early-time kinetics). Applications to such cases should be made with caution.

To quantify fissure development in highly expansive soils, the infill content is proposed as a determinant. Assuming that fissures in highly expansive soils are entirely filled with gray-green clay, the fissure ratio (K_r), defined as the ratio of fissure volume to the volume of the surrounding soil matrix, can be indirectly described using the ratio of gray-white clay to yellow-brown matrix clay content. This establishes a quantitative index for the fissure content in highly expansive soils.

Swell test procedure. One-dimensional swell tests were performed in an oedometer following ASTM D4546-14 [18] under a constant vertical stress (σ_v). Remolded specimens were prepared to the target dry density (ρ_d) and initial water content (w_i), placed in the ring, seated under σ_v, and then inundated at room temperature. Vertical deformation was recorded versus time on a logarithmic schedule until the deformation–time curve stabilized (plateau), at which point the ultimate expansion δ_ep (%) was read. Because swelling causes irreversible structural changes, one freshly prepared specimen per condition was tested under standardized preparation/compaction/moisture-conditioning.

Specimen preparation and test conditions. Cylindrical specimens were prepared in oedometer rings with an inner diameter of 61.8 mm and a height of 20 mm, consistent with the Specification of Soil Test Methods (SL 237-1999) [19]. The test procedure followed ASTM D4546-14 for one-dimensional swelling under vertical stresses of 0, 25, and 50 kPa. Specimens were compacted to target dry densities of 1.45, 1.50, and 1.55 g/cm³ with initial water contents of 20, 25, and 30%. Each condition was tested on three parallel specimens, and the average ultimate expansion (δ_ep) was reported. After seating under the applied stress, distilled water was added until the water level was 1–2 mm above the specimen surface. Vertical deformation was monitored at 20 ± 2 °C with a displacement transducer of 0.001 mm resolution. Swelling was considered complete when the deformation rate was less than 0.01 mm h⁻¹ for 24 h, and the ultimate expansion was calculated as the ratio of stabilized vertical deformation to the initial specimen height.

3. Analysis of Factors Influencing Hygroscopic Expansion in Fissured Expansive Soils

Using the quantified fissure ratio (K_r) as a key factor, the hygroscopic expansion deformation of expansive soils was incorporated into the model. Expansion rate experiments were conducted using fissure-filling gray-white clay collected from Nanyang Segment 2 and Segment 3. The matrix soil samples, consisting of yellow-brown expansive soil from channel slopes and bottoms, had their physical properties analyzed (see

Table 1. Physical Properties of Expansive Soil Samples.

Type	Water Content (%)	Density (g/cm3)	Grain (mm) Composition (%)			Liquid Limit (%)	Plastic Limit (%)	Free Expansion Rate (%)
			<0.05	<0.005	<0.002
Fissure Matrix	29.54	1.92	92	41	15	93.51	32.76	112
Soil Matrix	24.87	1.93	87	30	12	55.42	27.45	68

).

Gray-white clay content ratios of 35%, 50%, and 65% were used to prepare remolded expansive soil samples in the laboratory, simulating fissure ratios of 35%, 50%, and 65% for highly expansive soils. Hygroscopic expansion deformation was studied under different conditions, including dry densities (1.45, 1.50, 1.55 g/cm³), initial water contents (20%, 25%, 30%), and loads (0, 25, 50 kPa). Expansion experiments were conducted, and results are summarized in

Table 2. Expansion Experiment Results for Fissured Expansive Soils.

Fissure Ratio Kr (%)	Dry Density ρd (g/cm3)	Initial Water Content w0 (%)	Ultimate Expansion δep (%)
			0 kPa	25 kPa	50 kPa
35	1.45	20	13.1	3.2	0.8
		25	10.9	1.9	0.4
		30	5.4	1.2	0.2
	1.5	20	13.5	3.7	1.6
		25	11.4	2.2	0.9
		30	6.2	1.5	0.4
	1.55	20	13.9	4.0	3.0
		25	11.9	2.6	1.7
		30	7.3	1.8	0.8
50	1.45	20	14.2	4.3	2.0
		25	12.1	3.0	1.6
		30	6.6	2.3	1.0
	1.5	20	14.5	4.6	2.7
		25	12.4	3.4	2.0
		30	7.2	2.6	1.4
	1.55	20	15.0	5.2	4.1
		25	13.1	3.7	2.7
		30	8.5	3.0	1.9
65	1.45	20	16.4	6.3	4.0
		25	14.3	5.3	3.5
		30	8.7	4.4	3.2
	1.5	20	16.8	6.7	4.8
		25	14.6	5.8	4.1
		30	9.5	4.9	3.5
	1.55	20	17.2	7.5	6.3
		25	15.2	5.9	5.2
		30	10.8	5.2	4.3

Note: Expansion values (δ_ep, %) represent ultimate expansion under applied vertical stresses of 0, 25 and 50 kPa.

.

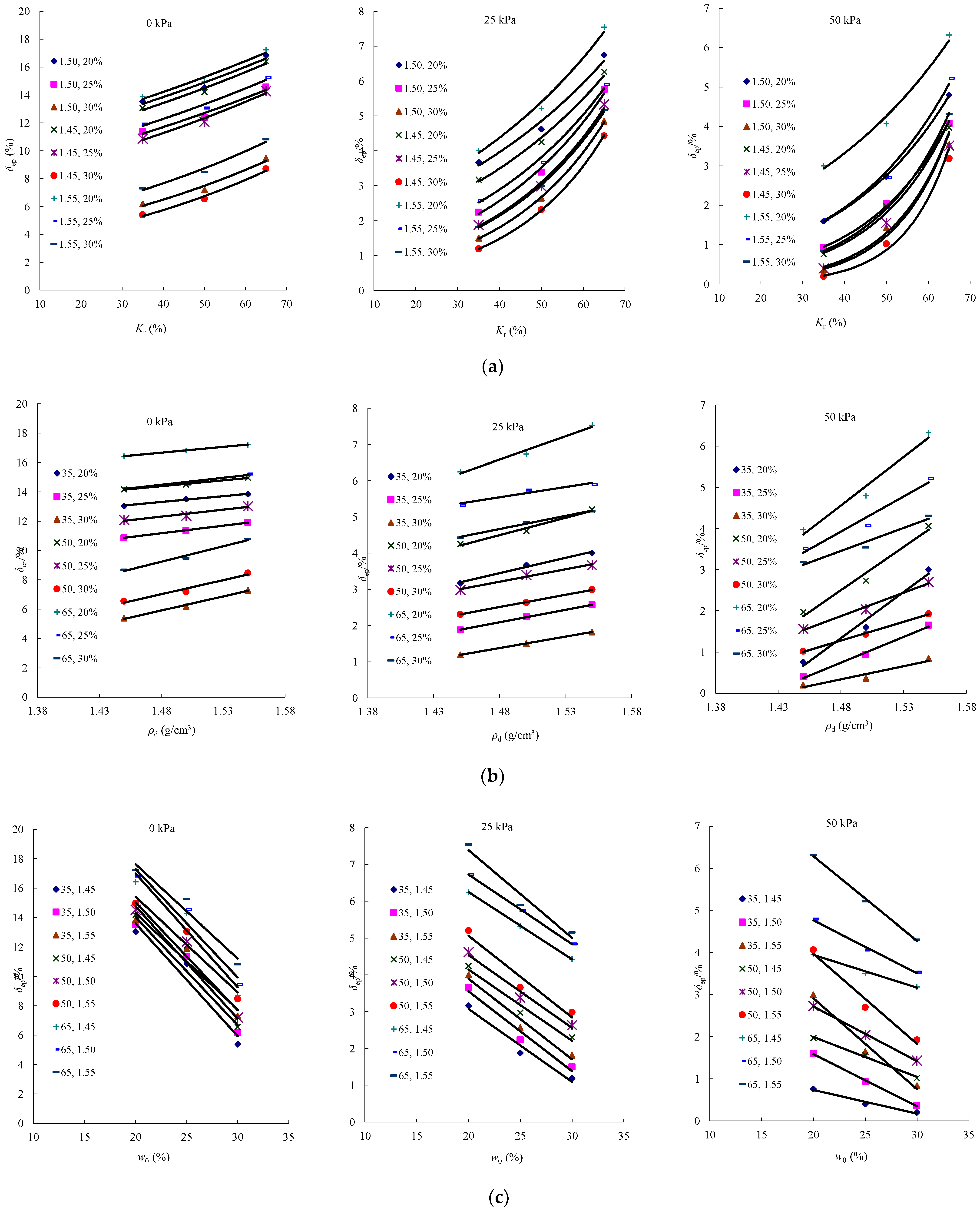
Subsequently, the correlations between the ultimate expansion (δ_ep) and fissure ratio (K_r), dry density (ρ_d), and initial water content (w₀) are illustrated in Figure 2 and analyzed as follows:

3.1. Correlation Between Ultimate Expansion (δ_ep) and Fissure Ratio (K_r)

The relationship between ultimate expansion (δ_ep) and fissure ratio (K_r) under varying conditions of overburden stress (σ), dry density (ρ_d), and initial water content (w₀) is illustrated in Figure 2a.

Analysis reveals that, under different initial water contents, dry densities, and overburden stress levels, the trend of ultimate expansion (δ_ep) with fissure ratio (K_r) remains consistent, following an exponential relationship. A higher fissure ratio corresponds to stronger fissure characteristics in expansive soils, greater infill material content, and a larger ultimate expansion. Additionally, soils with more infill-filled fissures exhibit greater variation in ultimate expansion.

Overall, fissure ratio primarily reflects the structural characteristics of the soil, while dry density represents the compaction state of the matrix. Their combined influence governs the overall swelling potential.

3.2. Correlation Between Ultimate Expansion (δ_ep) and Dry Density (ρ_d)

The relationship between ultimate expansion (δ_ep) and dry density (ρ_d) under varying conditions of overburden stress (σ), fissure ratio (K_r), and initial water content (w₀) is illustrated in Figure 2b.

It is observed that, for all given conditions, the ultimate expansion (δ_ep) exhibits a nearly linear relationship with dry density (ρ_d). In particular, when initial water content (w₀) and fissure ratio (K_r) are constant, increasing dry density leads to an increase in the ultimate expansion (δ_ep), indicating that dry density plays a significant role in determining the expansion behavior of fissured expansive soils.

In addition to fissure ratio and dry density, the initial water content also plays a critical role, as it directly controls the moisture absorption and subsequent expansion of the soil skeleton.

3.3. Correlation Between Ultimate Expansion (δ_ep) and Initial Water Content (w₀)

The relationship between ultimate expansion (δ_ep) and initial water content (w₀) under varying conditions of overburden stress (σ), fissure ratio (K_r), and dry density (ρ_d), is illustrated in Figure 2c.

Analysis shows that, across different dry densities, fissure ratios, and overburden stresses, the ultimate expansion (δ_ep) exhibits a negative linear relationship with initial water content (w₀). Specifically, under identical conditions, when the dry density is higher, the ultimate expansion is more significantly influenced by the initial water content, with a rapid decrease in the ultimate expansion as the initial water content increases.

4. Expansion Models and Sensitivity Analysis for Expansive Soils with Different Fissure Ratios

Based on the results of the expansion rate experiments, the ultimate expansion of expansive soils (δ_ep) is influenced by the combined effects of initial water content (w₀), dry density (ρ_d), overburden stress (σ), and fissure ratio (K_r). The ultimate expansion exhibits linear relationships with w₀, ρ_d, and ln(1 + σ), while showing an exponential relationship with K_r. To this end, statistical analysis software (SPSS 26.0) was employed to conduct regression analysis on the ultimate expansion of highly expansive soils. Sensitivity analysis indicators for the influencing factors were established, and multivariate linear and nonlinear regression expansion models were developed accordingly.

When the fissure ratio (K_r) is constant, the ultimate expansion (δ_ep) exhibits linear relationships with its influencing factors w₀, ρ_d, and ln(1 + σ). Therefore, multivariate linear regression models can be established under different fissure ratios (K_r). SPSS provides multiple methods for regression analysis, including enter method, stepwise elimination method, forward selection method, backward elimination method, and stepwise selection method. In this study, the ultimate expansion (δ_ep) was set as the dependent variable, while w₀, ρ_d, and ln(1 + σ) were set as independent variables. The relationships and significance of these variables with the dependent variable were analyzed theoretically. To ensure the completeness and comprehensiveness of the model, the enter method was adopted, which incorporates all selected independent variables into the regression model during analysis.

The significance of the multivariate regression equation and regression coefficients was evaluated using standard statistical procedures implemented in SPSS 26.0 (IBM Corp., Armonk, NY, USA). The analysis was conducted to examine whether the key physical parameters, namely initial water content (w₀), dry density (ρ_d), and overburden stress ln(1 + σ), had statistically significant effects on the ultimate expansion (δ_ep) under different fissure ratios (K_r).

The overall significance of the regression model was tested using the F-test. The null hypothesis assumes that none of the independent variables contribute to δ_ep:

$$H_0:{\beta }_1={\beta }_2=\dots ={\beta }_p=0$$

(1)

$$F={\displaystyle \frac{R^2}{1-R^2}}{\displaystyle \frac{n-p-1}{p}}~F(p,n-p-1)$$

(2)

where R² is the coefficient of determination, n is the sample size, and p is the number of independent variables included in the regression model. The obtained p-values (<0.05) confirmed that the regression equations were significant at the 95% confidence level, indicating that the three independent variables jointly affect the expansion behavior.

The contribution of each independent variable was further evaluated using the t-test:

$$H_0:{\beta }_j=0,\hspace{0.33em}\hspace{0.33em}j=1,2,\dots ,p$$

(3)

$$T_j={\displaystyle \frac{{\widehat{\beta }}_j/\sqrt{l_{jj}}}{\sqrt{{\displaystyle \sum _{t=1}^n{(Y_t-{\widehat{Y}}_t)}^2/(n-p-1)}}}}~t(p,\hspace{0.33em}n-p-1)$$

(4)

where ${\widehat{\beta }}_j$ denotes the estimated regression coefficient of the j-th independent variable, lⱼⱼ is the corresponding diagonal element of the covariance matrix, and Yᵢ and Ŷᵢ are the measured and predicted values of the dependent variable, respectively. The results showed that both w₀ and ρ_d exerted significant effects on δ_ep, while ln(1 + σ) had a comparatively weaker but still meaningful influence, consistent with the physical trends observed in Figure 2.

4.1. Fissure Ratios K_r = 35%

The summary of Regression Model and the Analysis of Variance (ANOVA) under fissure ratios K_r = 35% are listed in

Table 3. Summary of Regression Model (K_r = 35%).

Model	R	$\sqrt{{\mathit{R}}^2}$	$\sqrt{{\overline{\mathit{R}}}^2}$	Standard Error
Kr = 35%	0.984	0.967	0.963	1.24093

and

Table 4. Analysis of Variance (ANOVA) (K_r = 35%).

Model	Sum of Squares	Degrees of Freedom	Mean Square	F	Sig.
Regression	1096.268	3	365.423	237.303	0.000
Residual	36.958	24	1.540
Total	1133.225	27

.

The regression analysis results are as follows:

It can be observed that the square root of the defined model’s coefficient of determination R is 0.984, the determination coefficient $\sqrt{R^2}$ is 0.967, and the adjusted determination coefficient $\sqrt{{\overline{R}}^2}$ is 0.963, with a standard error of 1.24. These results indicate a high covariation ratio between the independent variables (w₀, ρ_d, and ln(1 + σ)) and the dependent variable, demonstrating a good fit between the model and data. The ANOVA table (Table 2) lists the sources of variation, degrees of freedom, mean squares, F-value, and the significance test for F. The significance level (Sig. < 0.05) confirms the validity and high significance of the regression equation.

The regression coefficients are summarized in

Table 5. Regression Coefficients (K_r = 35%).

Model	Unstandardized Coefficient		t	Sig.
	B	Standard Error
${\rho }_{\mathrm{d}}$	12.757	0.998	12.786	0.000
w0	−35.122	5.770	−6.087	0.000
ln(1 + σ)	−2.386	0.139	−17.164	0.000

.

Table 5 lists the values of the regression coefficients and their significance tests. The significance levels for w₀, ρ_d, and ln(1 + σ) are all Sig. = 0.000, indicating that these factors significantly influence the ultimate expansion (δ_ep). Thus, the regression equation for K_r = 35% is:

$${\delta }_{\mathrm{ep}}=12.757{\rho }_{\mathrm{d}}-35.122w_0-2.386\ln (1+\sigma )$$

(5)

The sensitivity coefficients for dry density (ρ_d), initial water content (w₀), and overburden stress (ln(1 + σ)) are 12.757, −35.122, and −2.386, respectively, indicating that initial water content has the greatest impact on ultimate expansion, followed by dry density, with overburden stress having the smallest influence.

4.2. Fissure Ratios K_r = 50%

Following the same regression procedure as in Section 4.1, the regression analysis results for K_r = 50% are summarized in

Table 6. Summary of Regression Model (K_r = 50%).

Model	R	$\sqrt{{\mathit{R}}^2}$	$\sqrt{{\overline{\mathit{R}}}^2}$	Standard Error
Kr = 50%	0.987	0.975	0.972	1.22341

,

Table 7. Analysis of Variance (ANOVA) (K_r = 50%).

Model	Sum of Squares	Degrees of Freedom	Mean Square	F	Sig.
Regression	1405.842	3	468.614	313.091	0.000
Residual	35.922	24	1.497
Total	1441.764	27

and

Table 8. Regression Coefficients (K_r = 50%).

Model	Unstandardized Coefficient		t	Sig.
	B	Standard Error
${\rho }_{\mathrm{d}}$	13.501	0.984	13.725	0.000
w0	−35.161	5.689	−6.181	0.000
ln(1 + σ)	−2.389	0.137	−17.433	0.000

.

As shown in the results, the square root of the determination coefficient (R) is 0.987, the determination coefficient ($\sqrt{R^2}$) is 0.975, and the adjusted determination coefficient ($\sqrt{{\overline{R}}^2}$) is 0.972, with a standard error of 1.22. The high R-value indicates a strong fit between the regression model and the data. The significance level of the regression equation (Sig. < 0.05) demonstrates that the model is statistically significant.

Additionally, the significance levels (Sig. = 0.000) for w₀, ρ_d, and ln(1 + σ) indicate that all independent variables have a significant impact on the dependent variable. Therefore, the regression equation for K_r = 35% is given as:

$${\delta }_{\mathrm{ep}}=13.501{\rho }_{\mathrm{d}}-35.161w_0-2.389\ln (1+\sigma )$$

(6)

The sensitivity coefficients for dry density (ρ_d), initial water content (w₀), and overburden stress (ln(1 + σ)) are 13.501, −35.161, and −2.389, respectively. This indicates that initial water content has the greatest influence on the ultimate expansion, followed by dry density, with overburden stress having the smallest influence.

4.3. Fissure Ratios K_r = 65%

Following the same regression procedure as in Section 4.1, the regression analysis results for K_r =65% are summarized in

Table 9. Summary of Regression Model (K_r = 65%).

Model	R	$\sqrt{{\mathit{R}}^2}$	$\sqrt{{\overline{\mathit{R}}}^2}$	Standard Error
Kr = 65%	0.992	0.984	0.982	1.23721

,

Table 10. Analysis of Variance (ANOVA) (K_r = 65%).

Model	Sum of Squares	Degrees of Freedom	Mean Square	F	Sig.
Regression	2225.203	3	741.734	484.575	0.000
Residual	36.737	24	1.531
Total	2261.940	27

and

Table 11. Regression Coefficients (K_r = 65%).

Model	Unstandardized Coefficient		t	Sig.
	B	Standard Error
${\rho }_{\mathrm{d}}$	14.934	0.995	15.013	0.000
w0	−34.811	5.753	−6.051	0.000
ln(1 + σ)	−2.404	0.139	−17.343	0.000

.

As with the cases for K_r = 35% and K_r = 50%, the regression model for K_r = 65% demonstrates a high R-value, indicating a strong fit to the data. The significance level of the regression equation (Sig. < 0.05) confirms the validity of the model, and the coefficients of the independent variables (w₀, ρ_d, and ln(1 + σ)) are also statistically significant (Sig. = 0.000).

For K_r = 65%, the sensitivity coefficients for dry density (ρ_d), initial water content (w₀), and overburden stress (ln(1 + σ)) are 14.934, −34.811, and −2.404, respectively. Thus, the regression equation is given as:

$${\delta }_{\mathrm{ep}}=14.934{\rho }_{\mathrm{d}}-34.811w_0-2.404\ln (1+\sigma )$$

(7)

4.4. Expansion Model Including Fissure Ratio

According to previous analysis from Section 4.1, Section 4.2, Section 4.3, the regression equation across different fissure ratios can be unified into a generalized form based on Equations (5)–(7):

$${\delta }_{\mathrm{ep}}=a{\rho }_{\mathrm{d}}-b{w}_0-c\ln (1+\sigma )$$

(8)

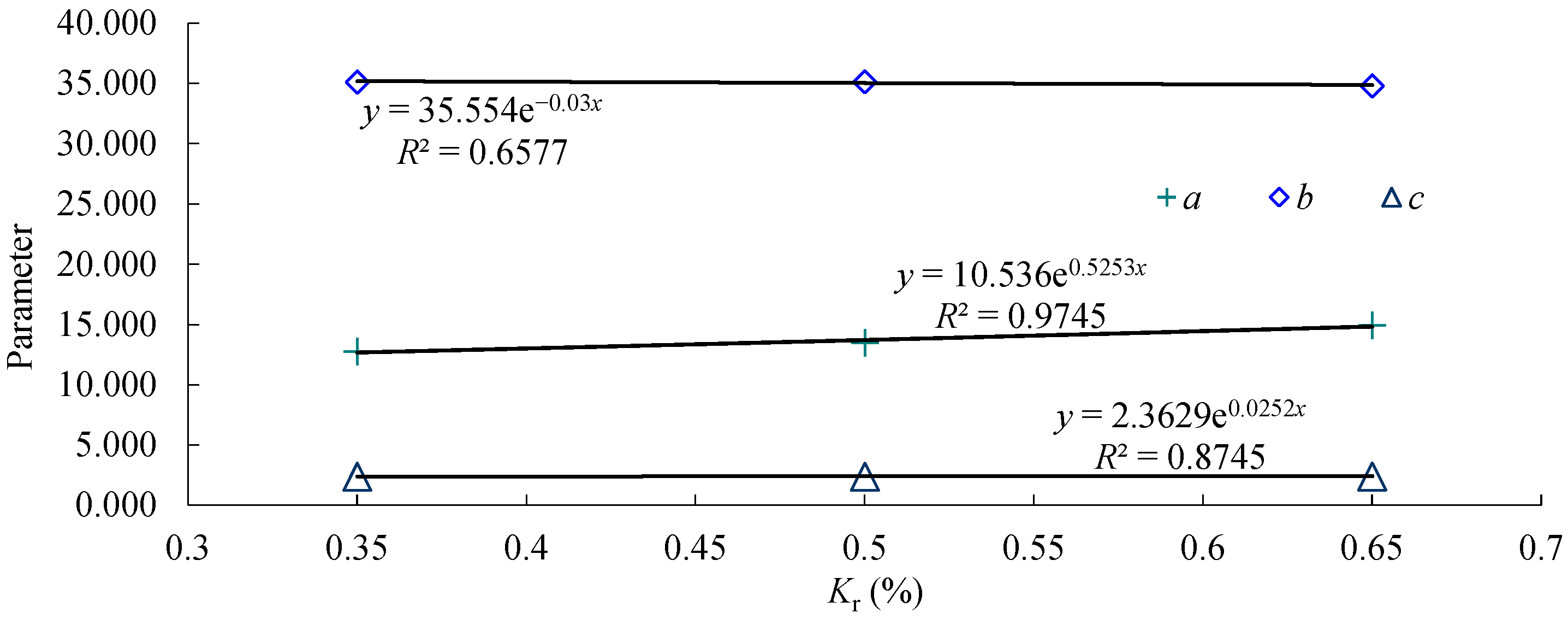
where a, b, and c are empirical parameters that vary with K_r. The values of a, b, and c for different fissure ratios are summarized in

Table 12. Values of parameters a, b, c under different K_r conditions.

Kr	a	b	c
0.35	12.757	35.122	2.386
0.50	13.501	35.161	2.389
0.65	14.934	34.811	2.404

. These values were fitted using exponential functions, and the resulting fitted curves are shown in Figure 3.

The relationships between fissure ratios K_r and the parameters a, b, and c are expressed as exponential functions:

a = 10.536e^0.5253Kr, b = 35.554e^−0.03Kr, c = 2.3629e^0.0252Kr

(9)

Although linear fitting gives a similar coefficient of determination within the tested K_r range, the exponential form was retained because it better represents the nonlinear and asymptotic influence of fissure ratio on the expansion parameters.

Using the above relationships, the expansion rate model including fissured expansive soils can be expressed as:

$${\delta }_{\mathrm{ep}}=10.536{\mathrm{e}}^{0.5253K\mathrm{r}}{\rho }_{\mathrm{d}}-35.554{\mathrm{e}}^{-0.03K\mathrm{r}}{w}_0-2.3629{\mathrm{e}}^{0.0252K\mathrm{r}}\ln (1+\sigma ), (0.35\le K_r\le 0.65)$$

(10)

5. Nonlinear Regression Expansion Model for Fissured Highly Expansive Soils

5.1. Influencing Factors and Model Coupling

Given that the ultimate expansion (δ_ep) of fissured highly expansive soils exhibits linear relationships with initial water content (w₀), dry density (ρ_d), and overburden stress (ln(1 + σ)), as well as an exponential relationship with fissure ratio (K_r), K_r was further directly incorporated into the model to perform a nonlinear regression analysis of δ_ep as a function of K_r, w₀, ρ_d, and ln(1 + σ). The regression equation adopted is as follows:

$${\delta }_{\mathrm{ep}}=m{\mathrm{e}}^{nK\mathrm{r}}+a{\rho }_{\mathrm{d}}+b{w}_0+c\ln (1+\sigma )$$

(11)

5.2. Regression Results

The parameter estimates from the regression analysis are summarized in

Table 13. Parameter Estimates.

Parameter	Estimate	Standard Error	95% Confidence Interval
			Lower Limit	Upper Limit
m	0.225	0.431	−0.634	1.084
n	4.580	2.520	−0.440	9.600
a	12.054	1.005	10.051	14.056
b	−35.311	3.221	−0.417	−0.289
c	−2.395	0.078	−2.549	−2.240

. These include the estimated values, standard errors, and 95% confidence intervals for each parameter. The analysis of variance (ANOVA) for the regression equation is presented in

Table 14. Analysis of Variance (ANOVA) for Regression Equation.

Source	Sum of Squares	Degrees of Freedom	Mean Square
Regression	4727.682	5	945.536
Residual	109.247	76	1.437
Uncorrected Total	4836.929	81
Corrected Total	1818.281	80

, which provides a breakdown of the sum of squares, degrees of freedom, and mean squares for the regression and residual components. The correlations between the parameters are summarized in

Table 15. Parameter Correlation Matrix.

	m	n	a	b	c
m	1.000	−0.999	−0.824	−0.043	−0.010
n	−0.999	1.000	0.817	0.042	0.010
a	−0.824	0.817	1.000	−0.496	−0.112
b	−0.043	0.042	−0.496	1.000	−0.006
c	−0.010	0.010	−0.112	−0.006	1.000

, revealing key interactions.

5.3. Model Analysis, Equation, and Visualization

The regression model’s residual sum of squares (RSS) (Table 14) is 109.198, and the total sum of squares (TSS) is 1818.281, yielding a coefficient of determination (R² = 1-RSS/TSS) of 0.9399. This high R² value indicates that the regression equation provides a strong fit to the data.

From the parameter correlations (Table 15):

• m, n, and a exhibit high mutual correlations, suggesting that changes in one of these parameters significantly influence the others.
• m, n, and b, c have weaker correlations, indicating limited interactions between these groups.
• m negatively correlates with all other parameters, indicating that as m increases, the values of the other parameters decrease. Conversely, n is positively correlated with the other parameters. Parameters a, b, and c are negatively correlated with all parameters except n.

From the parameter estimates (Table 13), the nonlinear regression equation for ultimate expansion (δ_ep) as a function of K_r, w₀, ρ_d, and ln(1 + σ) (i.e., the nonlinear expansion model for fissured expansive soils) is derived as follows:

$${\delta }_{\mathrm{ep}}=0.225{\mathrm{e}}^{4.580K\mathrm{r}}+12.054{\rho }_{\mathrm{d}}-35.311w_0-2.395\ln (1+\sigma )$$

(12)

The typical regression surfaces derived from the nonlinear expansion model for fissured expansive soils are shown in Figure 4.

5.4. Model Validation

By employing this model, the ultimate expansion (δ_ep) of fissured highly expansive soils was predicted based on the measured values of fissure ratio (K_r), initial water content (w₀), dry density (ρ_d), and overburden stress (ln(1 + σ)). The predicted values were compared with the observed values, and the results are presented in Figure 5.

It can be observed that the predicted values show a high degree of agreement with the observed values, with the regression line exhibiting a slope (k) close to 1. Therefore, this nonlinear regression model effectively describes the relationships between ultimate expansion and factors such as fissure ratio, initial water content, dry density, and overburden stress, making it a reliable predictive tool for characterizing the expansion properties of fissured highly expansive soils.

6. Conclusions

This study presents a nonlinear regression expansion model based on fissure ratio through an in-depth investigation of fissured highly expansive soils. The main conclusions are as follows:

(1)

Fissure characteristics and expansion behavior. Fissure ratio was found to be a dominant structural parameter governing volumetric change. The presence of filled fissures substantially amplifies expansion potential and increases variability in swelling response. Experimental results demonstrated an exponential relationship between ultimate expansion and K_r, confirming that fissure development enhances both the rate and magnitude of swelling deformation.

(2)

Influence of physical state variables. Among the four major factors, initial water content exerts the strongest negative influence on expansion, followed by dry density and overburden stress. The sensitivity analysis further indicates that the suppressive effect of overburden stress weakens under higher dry densities, revealing an interactive coupling between soil structure and stress state.

(3)

Role of infill composition. The gray-green clay infill, rich in smectitic minerals, plays a critical role in controlling the swelling mechanism. Since fissures are primarily filled rather than open, increasing K_r effectively raises the volumetric proportion of this highly expansive infill, which in turn enhances the total expansion magnitude. This finding underscores the importance of considering fissure-filling materials in predictive models of expansive soil behavior.

(4)

Model performance and applicability. The proposed nonlinear regression model accurately captures the combined effects of fissure ratio, moisture, density, and confining stress, with a coefficient of determination (R²) exceeding 0.93. The model demonstrates strong predictive reliability for remolded, fully filled fissured soils under one-dimensional swelling conditions, offering a practical tool for deformation assessment and design optimization in channel and dam engineering.

(5)

Engineering implications and future work. The results highlight that data-driven regression frameworks can serve as effective substitutes for purely empirical formulations in expansive soil analysis. In future research, the model will be extended to site-specific validation across different geological formations and to natural soils containing open or partially filled fissures, incorporating time-dependent swelling and stress–path coupling effects. These efforts will further enhance the model’s generalization and its value for long-term stability evaluation of expansive soil infrastructures.