A Laguerre-Type Action for the Solution of Geometric Constraint Problems

Abstract

A well-known idea is to identify spheres, points, and hyperplanes in Euclidean space ${\mathbb{R}}^n$ with points in real projective space. To address geometric constraints such as intersections, tangencies, and angle requirements, it is important to also encode the orientations of hyperplanes and spheres. The natural space for encoding such geometric objects is the real projective quadric with signature $(n+1,2)$. In this article, we first provide a general formula for calculating the angles formed by the geometric objects encoded by the points of the quadric. The main result is the determination of a very simple parametrization of a Laguerre-type subgroup that acts transitively on the quadric while preserving the geometric nature of its points. That is, points of the quadric representing oriented spheres, points, and oriented hyperplanes in ${\mathbb{R}}^n$ are mapped by the action to points of the same geometric type. We also provide simple parametrizations of the isotropies of the action. The action described in this article provides the foundation for an effective solution to geometric constraint problems.

1. Introduction

Lie’s [1] geometry of oriented spheres was published in his dissertation as a paper in Mathematische Annalen in 1872. Lie established a bijective correspondence between the set of all oriented hyperspheres, oriented hyperplanes, and points in ${\mathbb{R}}^n\cup \{\infty \}$ and the set of points on the real projective quadric ${\overline{Q}}_{n+1}$ in ${\mathbb{P}}^{n+2}$ given by the zero locus of an indefinite scalar product $\langle ·,·\rangle$ with signature $(n+1,2)$ on ${\mathbb{R}}^{n+3}$.

The quadric ${\overline{Q}}_{n+1}$ above contains projective lines but no projective linear subspaces of higher dimension. According to Lie [1], a Lie sphere transformation is a projective transformation of the projective space ${\mathbb{P}}^{n+2}$ which maps the quadric ${\overline{Q}}_{n+1}$ into itself. Lie [1] discussed the so-called “Fundamental Theorem of Lie sphere geometry” in the case $n=3$, and Pinkall [2] related this to arbitrary dimensions.

The theorem states that any line-preserving diffeomorphism of ${\overline{Q}}_{n+1}$ is the restriction to ${\overline{Q}}_{n+1}$ of a projective transformation of ${\mathbb{P}}^{n+2}$. One can show that a Lie sphere transformation is induced by an orthogonal transformation of ${\mathbb{R}}^{n+3}$ endowed with the scalar product $\langle ·,·\rangle$. This is the subgroup of Lorentz matrices with unitary determinant denoted usually as $O(n+1,2)$.

Thus, the projectivization of the group of Lie sphere transformations is isomorphic to the quotient group of $O(n+1,2)$ with ± the identity matrix. It is known from Lie [1] that a Lie sphere transformation maps oriented spheres into generalized oriented spheres. The term generalized here means that we include points in ${\mathbb{R}}^n$. The above statement is effective in the sense that it can occur that a Lie sphere transformation maps an oriented sphere into a point.

There is indeed a subgroup of Lie transformations that map points to points in ${\mathbb{R}}^n\cup \{\infty \}$. This subgroup is called the Möbius group, as it is induced by the Möbius conformal transformations of ${\mathbb{R}}^n\cup \{\infty \}$.

Therefore, in order to study geometric constraint problems, such as intersections, tangencies, and angle requirements between oriented spheres, points, and oriented hyperplanes, it is fundamental to identify a subgroup of the group of Lie sphere transformations that preserves the geometric nature of its points. That is, points on the quadric ${\overline{Q}}_{n+1}$ representing oriented spheres, points, and oriented hyperplanes in ${\mathbb{R}}^n$ are mapped by the action of this subgroup to points of the same geometric type. (In particular, the point ∞ is mapped to itself.)

But this is not sufficient for the study of geometric constraint problems! It is also essential that the subgroup mentioned above acts transitively on the projective quadric ${\overline{Q}}_{n+1}$. Moreover, in view of the algorithmic complexity of general constraint problems, the required subgroup must have the simplest possible parametrization.

In the present article, we discover for the first time this important subgroup. This is indeed the Laguerre subgroup ${Lag}_{n+3}^{0,+}$ in Theorem 1. We show there the existence of a parametrization of ${Lag}_{n+3}^{0,+}$ over the manifold ${\mathbb{R}}_{>0}\times O\left(n\right)\times {\mathbb{R}}^n$.

In the present article, we discover for the first time such an important subgroup. This is indeed the Laguerre subgroup ${Lag}_{n+3}^{0,+}$ in Theorem 1. We show the existence of a parametrization of ${Lag}_{n+3}^{0,+}$ over the manifold ${\mathbb{R}}_{>0}\times O\left(n\right)\times {\mathbb{R}}^n$.

It should be pointed out here that parametrizations of the orthogonal group $O\left(n\right)$ are by far simpler than parametrizations of the group $O(n+1,2)$, which has been used so far in solving geometric constraints problems. For this reason, it is much simpler and more effective to solve the constraints and apply ad hoc gradient flow techniques over the manifold ${\mathbb{R}}_{>0}\times O\left(n\right)\times {\mathbb{R}}^n$.

We wish to point out to the readers, mathematicians, that no prerequisites or background knowledge are needed to understand this article. All notations necessary for understanding the statement of Theorem 1 are included within it.

The present article is organized as follows. In Section 2, we recall some basic facts and introduce the first fundamental notations. In Section 3, we establish the general angle Formula (3) needed in the setup in consideration, in order to formulate geometric constraints problems, such as intersections, tangencies, and angle requirements between oriented spheres, points, and oriented hyperplanes. These constraints are given by a finite number of conditions expressed via the general angle Formula (3). In Section 4, we prove the part of the statement in Theorem 1 concerning the above-mentioned fundamental properties of the Laguerre subgroup ${Lag}_{n+3}^{0,+}$ as well as its parametrization over the manifold ${\mathbb{R}}_{>0}\times O\left(n\right)\times {\mathbb{R}}^n$.

In Section 5, we prove the part of the statement in Theorem 1 concerning the isotropies of the action. We recall that, by definition, an isotropy is a subgroup of the group acting on a manifold (in our case, the manifold is the projective quadric ${\overline{Q}}_{n+1}$) that fixes a given point of the manifold. The isotropies of the action of ${Lag}_{n+3}^{0,+}$ over ${\overline{Q}}_{n+1}$ differ in the cases of points, oriented spheres, and oriented hyperplanes. In the statement of Theorem 1, we provide a simple parametrization of the isotropies.

In future investigations, we will study gradient flow techniques over the manifold ${\mathbb{R}}_{>0}\times O\left(n\right)\times {\mathbb{R}}^n$ in order to solve geometric constraint problems.

2. Basic Facts and Notations

In this section, we present a few very well-known facts (the reader can also see [3,4]) and we fix some useful notations. We observe first that the equation of the sphere $S(p,r)\subset {\mathbb{R}}^n$, ${|x-p|}^2=r^2$, with $r⩾0$ rewrites as

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{2}}{\left|x\right|}^2-p·x+{\displaystyle \frac{1}{2}}{\left(\right|p|}^2-r^2)& =& 0,\hfill \end{array}$$

where $p·x$ indicates the standard scalar product in ${\mathbb{R}}^n$. We observe also that any quadratic form over ${\mathbb{R}}^n$ of the type

$$\begin{array}{ccc}\hfill q\left(x\right)& :=& {k\left|x\right|}^2-a·x+h,\hfill \end{array}$$

with $k\ne 0$ and ${\left|a\right|}^2-4kh⩾0$, represents the equation of a sphere of center $p:=a/2k$ and radius

$$\begin{array}{ccc}\hfill r^2& :=& {\displaystyle \frac{{\left|a\right|}^2-4kh}{4k^2}}\hfill \\ & =& {\left|p\right|}^2-{\displaystyle \frac{h}{k}}.\hfill \end{array}$$

We consider now the Lorentz product $(·,·)$ over ${\mathbb{R}}^{n+2}$ with signature $(n+1,1)$, given by

$$\begin{array}{ccc}\hfill (\xi ,\xi )& :=& {\xi }_1^2+\cdots +{\xi }_{n+1}^2-{\xi }_{n+2}^2.\hfill \end{array}$$

To any vector $\xi \in {\mathbb{R}}^{n+1}\setminus \left\{0\right\}$

$$\begin{array}{ccc}\hfill \xi & =& ({\xi }_1,\dots ,{\xi }_{n+2})\hfill \\ & \equiv & (a,k-h,k+h),\hfill \end{array}$$

we associate the quadratic form

$$\begin{array}{ccc}\hfill q_{\xi }\left(x\right)& :=& {\displaystyle \frac{1}{2}}({\xi }_{n+1}+{\xi }_{n+2})-a·x+{\displaystyle \frac{1}{2}}({\xi }_{n+2}-{\xi }_{n+1})\hfill \\ & =& {k\left|x\right|}^2-a·x+h,\hfill \end{array}$$

and we notice the equalities

$$\begin{array}{ccc}\hfill (\xi ,\xi )& =& {\left|a\right|}^2+{\xi }_{n+1}^2-{\xi }_{n+2}^2\hfill \\ & =& {\left|a\right|}^2+({\xi }_{n+1}+{\xi }_{n+2})({\xi }_{n+1}-{\xi }_{n+2})\hfill \\ & =& {\left|a\right|}^2-4kh.\hfill \end{array}$$

(1)

If we consider $\xi$ such that $(\xi ,\xi )⩾0$ and ${\xi }_{n+1}+{\xi }_{n+2}=1$, then $k=1/2$, $(\xi ,\xi )=r^2$ (with $r⩾0$ defined as before) and $a=p$. Thus, by the previous equalities

$$\begin{array}{ccc}\hfill r^2& =& {\left|p\right|}^2+{\xi }_{n+1}-{\xi }_{n+2},\hfill \end{array}$$

and so

$$\begin{array}{ccc}\hfill \xi & =& \left(p,{\displaystyle \frac{1-{\left|p\right|}^2+r^2}{2}},{\displaystyle \frac{1+{\left|p\right|}^2-r^2}{2}}\right),\hfill \end{array}$$

with $q_{\xi }=0$ representing the equation of the sphere $S(p,r)\subset {\mathbb{R}}^n$.

(2)

If we consider $\xi$ such that ${\xi }_{n+1}+{\xi }_{n+2}=0$, then $(\xi ,\xi )={\left|a\right|}^2$ and $\xi =(a,-h,h)$ with $q_{\xi }\left(x\right)=-a·x+h$. In particular, if $a\ne 0$, then $q_{\xi }=0$ is the equation of a hyperplane $H\subset {\mathbb{R}}^n$.

3. Oriented Angles

A good way of algebraically encoding the condition $(\xi ,\xi )⩾0$ is to consider the Lorentz product $\langle ·,·\rangle$ over ${\mathbb{R}}^{n+3}$ of signature $(n+1,2)$, and $\zeta =({\zeta }_0,\dots {\zeta }_{n+2})\equiv (\rho ,\xi )\ne 0$ such that

$$\begin{array}{ccc}\hfill \langle \zeta ,\zeta \rangle & =& -{\rho }^2+{\xi }_1^2+\cdots +{\xi }_{n+1}^2-{\xi }_{n+2}^2\hfill \\ & =& -{\rho }^2+{\xi }_1^2+\cdots +{\xi }_n^2+({\xi }_{n+1}+{\xi }_{n+2})({\xi }_{n+1}-{\xi }_{n+2})\hfill \\ & =& 0.\hfill \end{array}$$

Thus,

(a) if ${\zeta }_{n+1}+{\zeta }_{n+2}\ne 0$, then the vector

$${\displaystyle \frac{\zeta }{{\zeta }_{n+1}+{\zeta }_{n+2}}}$$

represents the sphere $S(p,r)\subset {\mathbb{R}}^n$ with

$$\begin{array}{ccc}\hfill p& :=& {\displaystyle \frac{({\zeta }_1,\dots ,{\zeta }_n)}{{\zeta }_{n+1}+{\zeta }_{n+2}}},\hfill \\ \hfill r^2& =& {\displaystyle \frac{{\zeta }_0^2}{{({\zeta }_{n+1}+{\zeta }_{n+2})}^2}},\hfill \end{array}$$

with the convention that $S(p,r)\subset {\mathbb{R}}^n$ is positive-oriented if

$$\begin{array}{ccc}\hfill r:={\displaystyle \frac{{\zeta }_0}{{\zeta }_{n+1}+{\zeta }_{n+2}}}& >& 0.\hfill \end{array}$$

We represent positive-oriented spheres by the inward unit normal vector field and negative-oriented spheres by the outward unit normal vector field. (This convention looks quite strange at first sight. It seem more natural to represent positive-oriented spheres by the outward unit normal vector field and negative-oriented spheres by the inward unit normal vector field. We will see below that the convention chosen is the right one.)

(b1) If ${\zeta }_{n+1}+{\zeta }_{n+2}=0$, and ${\zeta }_0=0$, then $\zeta =(0,\mathbf{0},-{\zeta }_{n+2},{\zeta }_{n+2})$.

(b2) If ${\zeta }_{n+1}+{\zeta }_{n+2}=0$, and ${\zeta }_0\ne 0$, then the vector $\zeta /{\zeta }_0$ represents the hyperplane $H\subset {\mathbb{R}}^n$ of equation $Nx={\zeta }_{n+2}/{\zeta }_0$ with

$$\begin{array}{ccc}\hfill N& :=& {\displaystyle \frac{({\zeta }_1,\dots ,{\zeta }_n)}{{\zeta }_0}},\hfill \end{array}$$

of unitary Euclidean norm, which selects the orientation of H. In other terms, $({\eta }_1,\dots ,{\eta }_{n-1})$ is a positive-oriented basis of H if $(N,{\eta }_1,\dots ,{\eta }_{n-1})$ is the canonical orientation of ${\mathbb{R}}^n$. On the negative side, we say that $({\eta }_1,\dots ,{\eta }_{n-1})$ is a negative-oriented basis of H if $(N,{\eta }_1,\dots ,{\eta }_{n-1})$ is the opposite of the canonical orientation of ${\mathbb{R}}^n$.

Orientation is important in order to determine exactly the angle of intersection of two hypersurfaces represented by two vectors $\zeta$, ${\zeta }^{\prime }$. Without orientation the angle is determined up to the additive constant $\pi$. We consider, for instance, the case where $\zeta \equiv (\rho ,\xi )$, ${\zeta }^{\prime }\equiv ({\rho }^{\prime },{\xi }^{\prime })$ represent two proper-oriented spheres $S(p,|r\left|\right)$ and $S(p^{\prime },|r^{\prime }\left|\right)$. In other terms, we can consider that up to multiplicative constants ${\xi }_{n+1}+{\xi }_{n+2}={\xi }_{n+1}^{\prime }+{\xi }_{n+2}^{\prime }=1$. Then, by the considerations concerning this case $\zeta \equiv (r,\xi )$, ${\zeta }^{\prime }\equiv (r^{\prime },{\xi }^{\prime })$, and

$$\begin{array}{ccc}\hfill (\xi ,{\xi }^{\prime })& =& p·p^{\prime }+(k-h)(k^{\prime }-h^{\prime })-(k+h)(k^{\prime }+h^{\prime }),\hfill \end{array}$$

with $k=k^{\prime }=1/2$ and $2h={\left|p\right|}^2-r^2$, $2h^{\prime }={\left|p^{\prime }\right|}^2{-r^{\prime }}^2$. Thus,

$$\begin{array}{ccc}\hfill 4(\xi ,{\xi }^{\prime })& =& 4p·p^{\prime }+(1-2h)(1-2h^{\prime })-(1+2h)(1+2h^{\prime }),\hfill \\ & =& 4p·p^{\prime }-4h-4h^{\prime }\hfill \\ & =& 4p·p^{\prime }-{2\left|p\right|}^2-2{\left|p^{\prime }\right|}^2+2r^2{+2r^{\prime }}^2\hfill \\ & =& -2|p-p^{\prime }{|}^2+2r^2{+2r^{\prime }}^2.\hfill \end{array}$$

We infer the equality

$$\begin{array}{ccc}\hfill {\displaystyle \frac{(\xi ,{\xi }^{\prime })}{r{r}^{\prime }}}& =& {\displaystyle \frac{r^2{+r^{\prime }}^2-{|p-p^{\prime }|}^2}{2r{r}^{\prime }}}.\hfill \end{array}$$

Using the polarization identity for the Euclidean product, we infer that in the case $r{r}^{\prime }>0$ the left-hand side equals the cousins of the angle of intersection of the two spheres determined by counterclockwise parametrization of the two circles obtained by the intersection of the two spheres with any plane passing through their origins (see Figures below).

By the law of cosines, this angle coincides with the angle between the unit normal fields (providing the orientation) at the points of intersection (see Figure below).

In the case $r{r}^{\prime }<0$, the left-hand side equal the cousins of the angle of intersection of the two spheres determined by counterclockwise parametrization of one of the above circles and clockwise parametrization of the other (see Figure below).

Once again, this angle coincides with the angle between the unit normal fields (providing the orientation) at the points of intersection.

In both cases, this angle is uniquely determined by the oriented spheres represented by the vectors $\zeta$, ${\zeta }^{\prime }$. We will denote it by $\alpha (\zeta ,{\zeta }^{\prime })$. Thus,

$$\begin{array}{ccc}\hfill cos\alpha (\zeta ,{\zeta }^{\prime })& =& {\displaystyle \frac{(\xi ,{\xi }^{\prime })}{r{r}^{\prime }}}.\hfill \end{array}$$

Using the trivial equality $\langle \zeta ,{\zeta }^{\prime }\rangle =(\xi ,{\xi }^{\prime })-r{r}^{\prime }$, we infer the general formula

$$cos\alpha (\zeta ,{\zeta }^{\prime })=1+{\displaystyle \frac{\langle \zeta ,{\zeta }^{\prime }\rangle }{{\zeta }_0{\zeta }_0^{\prime }}}.$$

(1)

This formula shows that in the case of two spheres $\langle \zeta ,{\zeta }^{\prime }\rangle =0$ if and only if $\alpha (\zeta ,{\zeta }^{\prime })=0$, which corresponds to the case where the vectors representing the orientation of the corresponding two circles have the same direction at the point of intersection of the two circles. In equivalent and simpler therms, the above condition is equivalent to say that the above unit normal vectors coincide at the point of intersection of the spheres. On the other hand, using the identity

$$\begin{array}{ccc}\hfill cos\alpha (\zeta ,{\zeta }^{\prime })& =& {\displaystyle \frac{r^2{+r^{\prime }}^2-{|p-p^{\prime }|}^2}{2r{r}^{\prime }}},\hfill \end{array}$$

we see that the previous condition is equivalent to the identity $|p-p^{\prime }|=|r-r^{\prime }|$. In general, the condition for a non-empty intersection of the two spheres is

$$\left\{\begin{array}{c}|r-r^{\prime }|⩽|p-p^{\prime }|⩽|r+r^{\prime }|,ifr{r}^{\prime }>0,\hfill \\ \\ |r+r^{\prime }|⩽|p-p^{\prime }|⩽|r-r^{\prime }|,ifr{r}^{\prime }<0,\hfill \end{array}\right.$$

which corresponds to the condition

$$-2⩽{\displaystyle \frac{\langle \zeta ,{\zeta }^{\prime }\rangle }{{\zeta }_0{\zeta }_0^{\prime }}}⩽0.$$

(2)

We notice finally that the above considerations are independent of the convention chosen on the orientation via the unit normals. However, the convention decided before is the right one in general. This will be clear from the case explained below.

We consider now the case when $\zeta =(r,\xi )\equiv (r,p,k-h,k+h)$, with $k=1/2$, $r>0$ represents a proper-oriented sphere $S(p,|r\left|\right)$, and ${\zeta }^{\prime }=(1,{\xi }^{\prime })\equiv (1,N,-h^{\prime },h^{\prime })$ represents the oriented hyperplane $H:=N^{\perp }+hN$. Then,

$$\begin{array}{ccc}\hfill (\xi ,{\xi }^{\prime })& =& p·N+\left({\displaystyle \frac{1}{2}}-h\right)(-h^{\prime })-\left({\displaystyle \frac{1}{2}}+h\right)h^{\prime }\hfill \\ & =& p·N-h^{\prime },\hfill \end{array}$$

represents the signed Euclidean distance from the center p of the sphere to the hyperplane H (see Figures below).

Then, (according to Figure above), the quantity

$$\begin{array}{ccc}\hfill {\displaystyle \frac{(\xi ,{\xi }^{\prime })}{r}}& =& {\displaystyle \frac{p·N-h^{\prime }}{r}},\hfill \end{array}$$

represents the cousins of the angle $\alpha (\zeta ,{\zeta }^{\prime })$ of the intersection of the oriented sphere $S(p,|r\left|\right)$ with the oriented hyperplane H corresponding to the angle between the unit normal vectors at the points of intersection representing the respective orientations.

As in the case of two spheres, we infer the Formula (1) and $\langle \zeta ,{\zeta }^{\prime }\rangle =0$ if and only if $\alpha (\zeta ,{\zeta }^{\prime })=0$, which corresponds to the case where the vectors representing the orientation have the same direction at the point of intersection. The previous condition is equivalent to the identity $p·N=r+h^{\prime }$. This shows, in particular, that the convention chosen on the orientation of the proper spheres via the unit normals is the right one in general.

We notice also that the condition for a non-empty intersection of a sphere with a hyperplane is

$$-\left|r\right|⩽p·N-h^{\prime }⩽\left|r\right|,$$

which corresponds to the condition (2). Formula (1) also holds in the case of two oriented hyperplanes. So in general, given a constraint angle of intersection $\alpha (\zeta ,{\zeta }^{\prime })\in [0,\pi ]$, the vectors $\zeta$ and ${\zeta }^{\prime }$ must satisfy the equation

$$\langle \zeta ,{\zeta }^{\prime }\rangle +\left[1-cos\alpha (\zeta ,{\zeta }^{\prime })\right]{\zeta }_0{\zeta }_0^{\prime }=0.$$

(3)

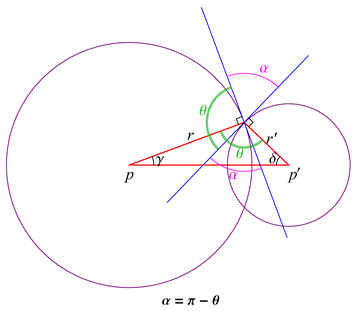
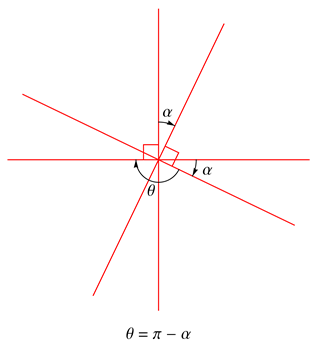
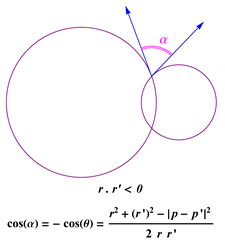
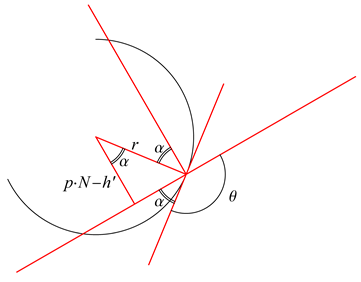
4. Automorphisms for Geometric Constraint Problems

We consider the set

$$\begin{array}{ccc}\hfill Q_{n+1}& :=& \left\{\zeta \in {\mathbb{R}}^{n+3}\setminus \left\{0\right\}\mid \langle \zeta ,\zeta \rangle =0\right\},\hfill \end{array}$$

and we notice that ${\zeta }_{\infty }=(0,\mathbf{0},-1,1)\in Q_{n+1}$. We set ${\overline{\zeta }}_{\infty }:={\mathbb{R}}^{*}{\zeta }_{\infty }$, ${\mathbb{R}}^{*}:=\mathbb{R}\setminus \left\{0\right\}$ and we consider its orthogonal space with respect to the Lorentz product $\langle ·,·\rangle$

$$\begin{array}{ccc}\hfill {\overline{\zeta }}_{\infty }^{\perp }& :=& \left\{\zeta \in {\mathbb{R}}^{n+3}\mid \langle \zeta ,{\zeta }_{\infty }\rangle =0\right\}\hfill \\ & =& \left\{\zeta \in {\mathbb{R}}^{n+3}\mid {\zeta }_{n+1}+{\zeta }_{n+2}=0\right\}.\hfill \end{array}$$

We notice that for any point $\zeta \in {\overline{\zeta }}_{\infty }^{\perp }$, $\zeta \notin {\overline{\zeta }}_{\infty }$ the line ${\mathbb{R}}^{*}\zeta$ represents an oriented hyperplane of ${\mathbb{R}}^n$.

Lemma 1.

Let $A=c{A}^{\prime }$ with $c\in {\mathbb{R}}^{*}$ and $A^{\prime }\in GL(n+3)$, $n⩾2$, preserving the Lorentz product $\langle ·,·\rangle$ such that $A{\overline{\zeta }}_{\infty }={\overline{\zeta }}_{\infty }$. Then, $A{\overline{\zeta }}_{\infty }^{\perp }={\overline{\zeta }}_{\infty }^{\perp }$ and

$$\begin{array}{c}\hfill A\left({\overline{\zeta }}_{\infty }^{\perp }\cap Q_{n+1}\right)={\overline{\zeta }}_{\infty }^{\perp }\cap Q_{n+1}.\end{array}$$

(4)

In particular, A sends lines representing oriented hyperplanes to lines of the same nature.

Proof. 

For any $\zeta \in {\overline{\zeta }}_{\infty }^{\perp }$, we have $0=c^2\langle \zeta ,{\zeta }_{\infty }\rangle =\langle A\zeta ,A{\zeta }_{\infty }\rangle =\langle A\zeta ,\lambda {\zeta }_{\infty }\rangle$ with $\lambda \ne 0$, which shows that $A\zeta \in {\overline{\zeta }}_{\infty }^{\perp }$. The fact that by definition $A{Q}_{n+1}=Q_{n+1}$ implies the equality (4). □

We infer also the equality

$$\begin{array}{ccc}\hfill A\left(Q_{n+1}\setminus {\overline{\zeta }}_{\infty }^{\perp }\right)& =& Q_{n+1}\setminus {\overline{\zeta }}_{\infty }^{\perp }\hfill \\ & =& \left\{\zeta \in Q_{n+1}\mid {\zeta }_{n+1}+{\zeta }_{n+2}\ne 0\right\},\hfill \end{array}$$

which tells us that A sends lines representing oriented spheres or points of ${\mathbb{R}}^n$ to lines of the same nature. We consider

$$\begin{array}{ccc}\hfill Q_{n+1}^{\prime }& :=& \left\{\zeta \in Q_{n+1}\mid {\zeta }_{n+1}+{\zeta }_{n+2}=1\right\},\hfill \end{array}$$

and we notice the isomorphism

$$\begin{array}{ccc}\hfill \mathsf{\Phi }:{\mathbb{R}}^{n+1}& ⟶& Q_{n+1}^{\prime }\hfill \\ \hfill Z& ⟼& \zeta :=(2Z,1-(Z,Z),1+(Z,Z\left)\right)/2,\hfill \end{array}$$

where $(·,·)$ denotes the Lorentz product over ${\mathbb{R}}^{n+1}$ with signature $(n,1)$ given by

$$\begin{array}{ccc}\hfill (Z,Z)& :=& -z_0^2+z_1^2+\cdots z_n^2,\hfill \end{array}$$

for any $Z=(z_0,\dots ,z_n)$. Let also

$$\begin{array}{ccc}\hfill H& :=& \left\{\zeta \in {\mathbb{R}}^{n+3}\mid {\zeta }_{n+1}+{\zeta }_{n+2}=1\right\}.\hfill \end{array}$$

Lemma 2.

Let $A^{\prime }\in GL(n+3)$, $n⩾2$, preserving the Lorentz product $\langle ·,·\rangle$ such that $A^{\prime }{\overline{\zeta }}_{\infty }={\overline{\zeta }}_{\infty }$. Then, there exists a unique $c\in {\mathbb{R}}^{*}$ such that $A:=c{A}^{\prime }$ satisfies $AH=H$.

Proof. 

By Lemma 1, we have $A^{\prime }{\overline{\zeta }}_{\infty }^{\perp }={\overline{\zeta }}_{\infty }^{\perp }$, which implies

$$\begin{array}{c}\hfill A^{\prime }\left({\mathbb{R}}^{n+3}\setminus {\overline{\zeta }}_{\infty }^{\perp }\right)={\mathbb{R}}^{n+3}\setminus {\overline{\zeta }}_{\infty }^{\perp }.\end{array}$$

The fact that $H\subset {\mathbb{R}}^{n+3}\setminus {\overline{\zeta }}_{\infty }^{\perp }$ implies $A^{\prime }H\cap {\overline{\zeta }}_{\infty }^{\perp }=\varnothing$, i.e., $A^{\prime }H$ is parallel to ${\overline{\zeta }}_{\infty }^{\perp }$. We infer

$$\begin{array}{ccc}\hfill A^{\prime }H& =& \left\{\zeta \in {\mathbb{R}}^{n+3}\mid {\zeta }_{n+1}+{\zeta }_{n+2}=c_1\right\},\hfill \end{array}$$

with $c_1\in {\mathbb{R}}^{*}$. Then, $c:=1/c_1$ satisfies the required property. □

We introduce the Laguerre subgroup

$$\begin{array}{ccc}\hfill {Lag}_{n+3}& :=& \left\{A\in GL(n+3)\mid \exists c\in {\mathbb{R}}^{*}:\langle Ax,Ax\rangle =c^2\langle x,x\rangle \forall x\in {\mathbb{R}}^{n+3},\right.\hfill \\ \\ & & A{\overline{\zeta }}_{\infty }=\left.{\overline{\zeta }}_{\infty },AH=H\right\}.\hfill \end{array}$$

Since $A{Q}_{n+1}^{\prime }=Q_{n+1}^{\prime }$ for any $A\in {Lag}_{n+3}$, the isomorphism $\mathsf{\Phi }$ induces an action of A on ${\mathbb{R}}^{n+1}$. Indeed, we explicitly show this in the following commutative diagram.

$$\begin{array}{c}{Q}_{n+1}^{\prime }\\ \mathsf{\Phi }\uparrow \\ {\mathbb{R}}^{n+1}\end{array}\begin{array}{c}\stackrel{A}{\to }\\ \\ \stackrel{T}{\to }\end{array}\begin{array}{c}{Q}_{n+1}^{\prime }\\ \mathsf{\Phi }\uparrow \\ {\mathbb{R}}^{n+1}\end{array},\begin{array}{c}x\\ \uparrow \\ X\end{array}\begin{array}{c}⟼\\ \\ ⟼\end{array}\begin{array}{c}y=Ax\\ \uparrow \\ Y=TX\end{array}.$$

We notice first that the condition $A{\zeta }_{\infty }=c{\zeta }_{\infty }$, with $c\in {\mathbb{R}}^{*}$ and with

$$A={\left(a_{j,k}\right)}_{j,k=0\dots n+2},$$

rewrites as

$$\left\{\begin{array}{c}{a}_{j,n+1}=a_{j,n+2},j=0,\dots ,n,\hfill \\ \\ a_{n+1,n+1}=a_{n+1,n+2}+c,\hfill \\ \\ a_{n+2,n+2}=a_{n+2,n+1}+c.\hfill \end{array}\right.$$

(5)

Thus, if we compute for $j=0,\dots ,n$,

$$\begin{array}{ccc}\hfill y_j& =& \sum _{k=0}^n{a}_{j,k}{x}_k+a_{j,n+1}{x}_{n+1}+a_{j,n+2}{x}_{n+2}\hfill \\ & =& \sum _{k=0}^n{a}_{j,k}{x}_k+a_{j,n+2}(x_{n+1}+x_{n+2})\hfill \\ & =& \sum _{k=0}^n{a}_{j,k}{x}_k+a_{j,n+2}.\hfill \end{array}$$

Thus, if we set $B:={\left(a_{j,k}\right)}_{j,k=0\dots n}$ and

$$\begin{array}{ccc}\hfill C& :=& \left(\begin{array}{c}{a}_{0,n+2}\\ ⋮\\ a_{n,n+2}\end{array}\right),\hfill \end{array}$$

then $Y=TX=BX+C$. Obviously, $B\in GL(n+1)$ and the matrix A writes under the form

$$A=\begin{array}{|ccc|}\hline B& C& C\\ L_1& a_{n+1,n+1}& a_{n+1,n+1}-c\\ L_2& a_{n+2,n+2}-c& a_{n+2,n+2}\\ \hline\end{array}.$$

(6)

We notice now that for any $x,y\in Q_{n+1}^{\prime }$

$$\begin{array}{ccc}\hfill \langle x,y\rangle & =& (X,Y)+x_{n+1}{y}_{n+1}-x_{n+2}{y}_{n+2}\hfill \\ & =& (X,Y)+{\displaystyle \frac{1}{4}}[1-(X,X)][1-(Y,Y)]-{\displaystyle \frac{1}{4}}[1+(X,X)][1+(Y,Y)]\hfill \\ & =& {\displaystyle \frac{1}{4}}[1-(X,X)-(Y,Y)+(X,X)(Y,Y)]\hfill \\ & -& {\displaystyle \frac{1}{4}}[1+(X,X)+(Y,Y)+(X,X)(Y,Y)]+(X,Y)\hfill \\ & =& -{\displaystyle \frac{1}{2}}[(X,X)-2(X,Y)+(Y,Y)]\hfill \\ & =& -{\displaystyle \frac{1}{2}}(X-Y,X-Y).\hfill \end{array}$$

Thus for any $x,y\in Q_{n+1}^{\prime }$ the condition $\langle x,y\rangle =0$ is equivalent to the condition $(X-Y,X-Y)=0$. On the other hand, if $A\in {Lag}_{n+3}$, then the condition $\langle x,y\rangle =0$ is equivalent to the condition $\langle Ax,Ay\rangle =0$. The later is equivalent to $(TX-TY,TX-TY)=0$, which rewrites as

$$\left(B\right(X-Y),B(X-Y\left)\right)=0.$$

(7)

We infer $B=\sqrt{\lambda }D$ with $\lambda \in {\mathbb{R}}_{>0}$ and $D\in GL(n+1)$ preserves the Lorentz product $(·,·)$. We write now

$$\begin{array}{ccc}\hfill y& =& Ax\hfill \\ & =& \left(2Y,1-(Y,Y),1+(Y,Y)\right)/2\hfill \\ & =& \left(2BX+2C,1-(BX+C,BX+C),1+(BX+C,BX+C)\right)/2\hfill \\ & =& \left(2BX+2C,1-\lambda (X,X)-2(BX,C)-(C,C)\right.,\hfill \\ & & \left.,1+\lambda (X,X)+2(BX,C)+(C,C)\right)/2.\hfill \end{array}$$

On the other hand,

$$\begin{array}{ccc}\hfill y& =& Ax\hfill \\ & =& \left(BX+C,L_1·X+a_{n+1,n+1}{x}_{n+1}+a_{n+1,n+2}{x}_{n+2},\right.\hfill \\ & & ,\left.L_{2}X+a_{n+2,n+1}{x}_{n+1}+a_{n+2,n+2}{x}_{n+2}\right)\hfill \\ & =& \left(BX+C,L_1·X+a_{n+1,n+1}{\displaystyle \frac{1-(X,X)}{2}}+a_{n+1,n+2}{\displaystyle \frac{1+(X,X)}{2}},\right.\hfill \\ & & \left.,L_2·X+a_{n+2,n+1}{\displaystyle \frac{1-(X,X)}{2}}+a_{n+2,n+2}{\displaystyle \frac{1+(X,X)}{2}}\right)\hfill \\ & =& \left(BX+C,L_1·X+{\displaystyle \frac{a_{n+1,n+2}-a_{n+1,n+1}}{2}}(X,X)+{\displaystyle \frac{a_{n+1,n+1}+a_{n+1,n+2}}{2}}\right.,\hfill \\ & & \left.,L_{2}X+{\displaystyle \frac{a_{n+2,n+2}-a_{n+2,n+1}}{2}}(X,X)+{\displaystyle \frac{a_{n+2,n+1}+a_{n+2,n+2}}{2}}\right).\hfill \end{array}$$

Comparing the two previous expressions, we infer

$$\left\{\begin{array}{c}{a}_{n+1,n+2}-a_{n+1,n+1}=-\lambda ,\hfill \\ \\ a_{n+2,n+2}-a_{n+2,n+1}=\lambda ,\hfill \\ \\ a_{n+1,n+1}+a_{n+1,n+2}=1-(C,C),\hfill \\ \\ a_{n+2,n+1}+a_{n+2,n+2}=1+(C,C),\hfill \\ \\ L_1=-L_2,\hfill \\ \\ L_2·X=(BX,C).\hfill \end{array}\right.$$

(8)

Thus, if we set ${\widehat{B}}_{j,k}:={(-1)}^{{\delta }_{0,j}}{B}_{j,k}$, then $L_2=C^t\widehat{B}$ and A writes under the form

$$A=\begin{array}{|ccc|}\hline B& C& C\\ -C^t\widehat{B}& {\displaystyle \frac{1}{2}}[1+\lambda -(C,C)]& {\displaystyle \frac{1}{2}}[1-\lambda -(C,C)]\\ C^t\widehat{B}& {\displaystyle \frac{1}{2}}[1-\lambda +(C,C)]& {\displaystyle \frac{1}{2}}[1+\lambda +(C,C)]\\ \hline\end{array},$$

(9)

where $C^t$ denotes the transposed matrix of C. We infer the final form

$$A=\begin{array}{|ccc|}\hline \sqrt{\lambda }D& C& C\\ -\sqrt{\lambda }{C}^t\widehat{D}& {\displaystyle \frac{1}{2}}[1+\lambda -(C,C)]& {\displaystyle \frac{1}{2}}[1-\lambda -(C,C)]\\ \sqrt{\lambda }{C}^t\widehat{D}& {\displaystyle \frac{1}{2}}[1-\lambda +(C,C)]& {\displaystyle \frac{1}{2}}[1+\lambda +(C,C)]\\ \hline\end{array}.$$

(10)

We notice that the first two equalities in (8) compared with the last two in (5) imply $c=\lambda$. We show now that the map

$$\begin{array}{ccc}\hfill {\mathbb{R}}_{>0}\times O(n,1)\times {\mathbb{R}}^{n+1}& ⟶& {Lag}_{n+3}\hfill \\ \hfill (\lambda ,D,C)& ⟼& A(\lambda ,D,C),\hfill \end{array}$$

with $A(\lambda ,D,C)$ given by (10) is well defined. Then, it follows from the previous considerations that the above map is a bijection. We notice first that by the previous computations $A\equiv A(\lambda ,D,C)$ satisfies $A{\overline{\zeta }}_{\infty }={\overline{\zeta }}_{\infty }$ and $A{Q}_{n+1}^{\prime }\subseteq Q_{n+1}^{\prime }$. Moreover, $A\in GL(n+3)$ since

$$det\begin{array}{|cc|}\hline [1+\lambda -(C,C\left)\right]/2& [1-\lambda -(C,C\left)\right]/2\\ [1-\lambda +(C,C\left)\right]/2& [1+\lambda +(C,C\left)\right]/2\\ \hline\end{array}=\hspace{1em}\lambda /2>0.$$

Therefore, $A{Q}_{n+1}^{\prime }=Q_{n+1}^{\prime }$ and so

$$A\left(Q_{n+1}\setminus {\overline{\zeta }}_{\infty }^{\perp }\right)=Q_{n+1}\setminus {\overline{\zeta }}_{\infty }^{\perp }.$$

Taking the closure in the previous equality, we infer $A{Q}_{n+1}=Q_{n+1}$. The fact that $D\in O(n,1)$ implies that for any $x,y\in Q_{n+1}^{\prime }$ the condition $\langle x,y\rangle =0$ is equivalent to the condition (7), which in its turn is equivalent to the condition $\langle Ax,Ay\rangle =0$ since $Ax,Ay\in Q_{n+1}^{\prime }$. We infer that A sends the line

$$\begin{array}{ccc}\hfill l_{x,y}& :=& \left\{\alpha x+\beta y\mid (\alpha ,\beta )\in {\mathbb{R}}^2\setminus \left\{0\right\}\right\}\subset Q_{n+1},\hfill \end{array}$$

to the line

$$\begin{array}{ccc}\hfill A{l}_{x,y}& =& \left\{\alpha Ax+\beta Ay\mid (\alpha ,\beta )\in {\mathbb{R}}^2\setminus \left\{0\right\}\right\}\subset Q_{n+1}.\hfill \end{array}$$

It is obvious that the previous property extends to any $x,y\in Q_{n+1}\setminus {\overline{\zeta }}_{\infty }^{\perp }$. In the cases $x\in {\overline{\zeta }}_{\infty }^{\perp }\cap Q_{n+1}$ or $y\in {\overline{\zeta }}_{\infty }^{\perp }\cap Q_{n+1}$ or $x,y\in {\overline{\zeta }}_{\infty }^{\perp }\cap Q_{n+1}$ we can choose two sequences ${\left(x_k\right)}_{k⩾1},{\left(y_k\right)}_{k⩾1}\subset Q_{n+1}$ such that $x_k\to x$ and $y_k\to y$. The fact that $A{l}_{x_k,y_k}\subset Q_{n+1}$ by the previous considerations implies $A{l}_{x,y}\subset Q_{n+1}$. The fundamental theorem of Lie sphere geometry (see [1,2,5]) asserts that any line preserving diffeomorphism of $Q_{n+1}$ is the restriction to $Q_{n+1}$ of a projective transformation of ${\mathbb{P}}^{n+2}$ induced by an element of $O(n+1,2)$. We infer that A satisfies the identity $\langle Ax,Ax\rangle =c^2\langle x,x\rangle$ for some $c\in {\mathbb{R}}^{*}$ and for all $x\in {\mathbb{R}}^{n+3}$. We observe finally the equality $AH=H$. Indeed, by the proof of Lemma 2 we have

$$\begin{array}{ccc}\hfill AH& =& \left\{\zeta \in {\mathbb{R}}^{n+3}\mid {\zeta }_{n+1}+{\zeta }_{n+2}=c_1\right\},\hfill \end{array}$$

with $c_1\in {\mathbb{R}}^{*}$. The equality $A{Q}_{n+1}^{\prime }=Q_{n+1}^{\prime }$ implies $c_1=1$.

We consider now $Q_{n+1}^0:=Q_{n+1}\cap \{{\zeta }_0=0\}$. We notice that ${\zeta }_{\infty }\in Q_{n+1}^0$. We define the subgroup

$$\begin{array}{ccc}\hfill {Lag}_{n+3}^0& :=& \left\{A\in {Lag}_{n+3}\mid A\left(Q_{n+1}^0\right)=Q_{n+1}^0\right\}.\hfill \end{array}$$

Each element of ${Lag}_{n+3}^0$ sends vectors in $Q_{n+1}$ representing points in ${\mathbb{R}}^n$ in vectors of the same nature. We deduce that each element of ${Lag}_{n+3}^0$ sends vectors in $Q_{n+1}$ representing proper spheres in ${\mathbb{R}}^n$ in vectors of the same nature.

We denote by ${Lag}_{n+3}^{0,+}$ the subgroup of orientation preserving elements in ${Lag}_{n+3}^0$ and we set

$$\begin{array}{ccc}\hfill {Lag}_{n+3}^{0,-}& :=& {Lag}_{n+3}^0\setminus {Lag}_{n+3}^{0,+}.\hfill \end{array}$$

We have the following lemma.

Lemma 3.

The map

$$\begin{array}{ccc}\hfill {\mathbb{R}}_{>0}\times O\left(n\right)\times {\mathbb{R}}^n& ⟶& {Lag}_{n+3}^{0,\pm }\hfill \\ \hfill (\lambda ,D,C)& ⟼& A^{\pm }(\lambda ,D,C),\hfill \end{array}$$

with $A^{\pm }(\lambda ,D,C)$ given by the matrix

$$\begin{array}{|cccc|}\hline \pm \lambda & \mathbf{0}& 0& 0\\ \mathbf{0}& \lambda D& C& C\\ 0& -\lambda C^{t}D& {\displaystyle \frac{1}{2}}(1+{\lambda }^2-{\left|C\right|}^2)& {\displaystyle \frac{1}{2}}(1-{\lambda }^2-{\left|C\right|}^2)\\ 0& \lambda C^{t}D& {\displaystyle \frac{1}{2}}(1-{\lambda }^2+{\left|C\right|}^2)& {\displaystyle \frac{1}{2}}(1+{\lambda }^2+{\left|C\right|}^2)\\ \hline\end{array},$$

(11)

is well defined and represents a bijection.

Proof. 

The matrix A corresponding to an element in ${Lag}_{n+3}^0$ must be written as

$$A=\begin{array}{|cc|}\hline c& 0\\ 0& A^{\prime }\\ \hline\end{array},$$

with $c\in {\mathbb{R}}^{*}$. This implies that the matrix $D\in O(n,1)$ in the expression (10) must be written as

$$D=\begin{array}{|cc|}\hline c^{\prime }& 0\\ 0& D^{\prime }\\ \hline\end{array},$$

with $c^{\prime }\in {\mathbb{R}}^{*}$. All the elements $D\in O(n,1)$ of this form must be written as

$$D=\begin{array}{|cc|}\hline \pm 1& 0\\ 0& D^{\prime }\\ \hline\end{array},$$

with $D^{\prime }\in O\left(n\right)$. The conclusion follows performing the adequate change in notations in the expression (10). □

In view of its remarkable properties of the action of the group ${Lag}_{n+3}^{0,+}$ on the projectivization ${\overline{Q}}_{n+1}\subset {\mathbb{P}}^{n+2}$ of $Q_{n+1}$, we see that ${Lag}_{n+3}^{0,+}$ is the right group for the study of the geometric constraint problems.

5. Transitivity and Isotropies of the Action

In this section, we establish the transitivity of the action of the group ${Lag}_{n+3}^{0,+}$ on ${\overline{Q}}_{n+1}$ and we compute its isotropy subgroups. We consider first the case of points. We take a vector ${\zeta }_p\in Q_{n+1}$ representing a point $p\in {\mathbb{R}}^n$ that is written as ${\zeta }_p={(0,2p,1-|p|}^2,1+{\left|p\right|}^2)$. Then, for any $A\in {Lag}_{n+3}^{0,+}$

$$\begin{array}{ccc}\hfill A{\zeta }_p& =& {(0,2q,1-|q|}^2,1+{\left|q\right|}^2)\equiv {\zeta }_q,\hfill \end{array}$$

for some $q\in {\mathbb{R}}^n$, thanks to the fact that A sends vectors in $Q_{n+1}$ representing points in ${\mathbb{R}}^n$ in vectors of the same nature and thanks to the fact that $AH=H$. If we write $A=A^{+}(\lambda ,D,C)$, then the point q satisfies $q=\lambda D·p+C$, thanks to the expression (11). Thus, for any two points $p,q\in {\mathbb{R}}^n$ we can find $(\lambda ,D,C)\in {\mathbb{R}}_{>0}\times O\left(n\right)\times {\mathbb{R}}^n$ as follows such that ${\zeta }_q=A^{+}(\lambda ,D,C){\zeta }_p$:

If $p=0$, then $C:=q$ and $(\lambda ,D)\in {\mathbb{R}}_{>0}\times O\left(n\right)$ can be taken arbitrarily. If $p\ne 0$, then the fact that D must be orthogonal implies $\lambda \left|p\right|=|q-C|$ and thus for all $C\in {\mathbb{R}}^n$ we set

$$\begin{array}{ccc}\hfill \lambda & :=& {\displaystyle \frac{|q-C|}{\left|p\right|}}.\hfill \end{array}$$

Then, the transitivity of the natural right action of $O\left(n\right)$ on $S^{n-1}(0,{\lambda }^{-1}|q-C|)$ implies the existence of $D\in O\left(n\right)$ such that $D·p={\lambda }^{-1}(q-C)$.

We compute now the isotropy subgroup $Iso\left({\zeta }_p\right)$. We notice first that for any $A\in {Lag}_{n+3}^{0,+}$ the condition $A{\overline{\zeta }}_p={\overline{\zeta }}_p$ is equivalent to the condition $A{\zeta }_p={\zeta }_p$, since $AH=H$. Then,

$$\begin{array}{ccc}\hfill Iso\left({\zeta }_p\right)& =& \left\{A^{+}(\lambda ,D,C)\mid (\lambda ,D,C)\in {\mathbb{R}}_{>0}\times O\left(n\right)\times {\mathbb{R}}^n:p=\lambda D·p+C\right\}.\hfill \end{array}$$

We consider first the case of the spheres. For this example, let

$$\begin{array}{ccc}\hfill {\zeta }_{p,r}& :=& \left(2r,2p,1-{\left|p\right|}^2+r^2,1+{\left|p\right|}^2-r^2\right)\in Q_{n+1}\hfill \end{array}$$

be a vector representing the sphere $S(p,r)\subset {\mathbb{R}}^n$. Then, for any $A\in {Lag}_{n+3}^{0,+}$ with $A=A^{+}(\lambda ,D,C)$, we can write

$$\begin{array}{ccc}\hfill A{\zeta }_{p,r}& =& \left(2\lambda r,2q,1-{\left|q\right|}^2+r^2,1+{\left|q\right|}^2-r^2\right)\equiv {\zeta }_{q,\lambda r},\hfill \end{array}$$

for some $q\in {\mathbb{R}}^n$ thanks to the fact that A sends vectors in $Q_{n+1}$ representing points in ${\mathbb{R}}^n$ in vectors of the same nature and thanks to the fact that $AH=H$. Moreover, the point q satisfies $q=\lambda D·p+C$, thanks to the expression (11). Thus for any two oriented spheres $S(p,r),S(q,\rho )\subset {\mathbb{R}}^n$ sharing the same orientation, we can find $(\lambda ,D,C)\in {\mathbb{R}}_{>0}\times O\left(n\right)\times {\mathbb{R}}^n$ such that ${\zeta }_{q,\rho }=A^{+}(\lambda ,D,C){\zeta }_{p,r}$, described as follows.

First, we set $\lambda :=\rho /r$, which is positive since the two spheres have same orientation. If $p=0$, then $C:=q$ and $D\in O\left(n\right)$ can be taken arbitrarily. If $p\ne 0$, then the fact that D must be orthogonal implies $\lambda \left|p\right|=|q-C|$ and thus we can take all $C\in {\mathbb{R}}^n$ such that $\lambda \left|p\right|=|q-C|$. Then, the transitivity of the natural right action of $O\left(n\right)$ on $S^{n-1}(0,{\lambda }^{-1}|q-C|)$ implies the existence of $D\in O\left(n\right)$ such that $D·p={\lambda }^{-1}(q-C)$.

We compute now the isotropy subgroup $Iso\left({\zeta }_{p,r}\right)$. We notice, as in the case of points, that for any $A\in {Lag}_{n+3}^{0,+}$ the condition $A{\overline{\zeta }}_p={\overline{\zeta }}_p$ is equivalent to the condition $A{\zeta }_p={\zeta }_p$, since $AH=H$. Then,

$$\begin{array}{ccc}\hfill Iso\left({\zeta }_{p,r}\right)& =& \left\{A^{+}(1,D,C)\mid (D,C)\in O\left(n\right)\times {\mathbb{R}}^n:p=D·p+C\right\}.\hfill \end{array}$$

We consider finally the case of oriented hyperplanes in ${\mathbb{R}}^n$. Let

$$\begin{array}{ccc}\hfill {\zeta }_{N,h}& :=& \left(1,N,-h,h\right)\in Q_{n+1}\hfill \end{array}$$

be a vector representing the hyperplane in ${\mathbb{R}}^n$ given by the equation $Nx=h$ and oriented by the unit normal vector N. Then, for any $A\in {Lag}_{n+3}^{0,+}$ with $A=A^{+}(\lambda ,D,C)$ we can write

$$A{\zeta }_{N,h}=\lambda {\zeta }_{N^{\prime },h^{\prime }},$$

(12)

for some $N^{\prime }\in {\mathbb{R}}^n$ of unitary Euclidean norm and some $h^{\prime }\in \mathbb{R}$ thanks to the fact that A sends vectors in $Q_{n+1}$ representing oriented hyperplanes in ${\mathbb{R}}^n$ in vectors of the same nature. Moreover, $N^{\prime }=D·N$ and $C·N^{\prime }+\lambda h=h^{\prime }$, thanks to the expression (11). Thus, for any two oriented hyperplanes represented by ${\zeta }_{N,h}$ and ${\zeta }_{N^{\prime },h^{\prime }}$ we can find $(D,C)\in O\left(n\right)\times {\mathbb{R}}^n$ such that (12) holds true. The existence of $D\in O\left(n\right)$ follows from the transitivity of the natural right action of $O\left(n\right)$ on $S^{n-1}(0,1)$ and C belongs to the hyperplane of equation $C·N^{\prime }=h^{\prime }-\lambda h$.

In order to compute the isotropy subgroup $Iso\left({\zeta }_{N,h}\right)$, we notice that the condition

$$\begin{array}{ccc}\hfill A^{+}(\lambda ,D,C){\overline{\zeta }}_{N,h}& =& {\overline{\zeta }}_{N,h}\hfill \end{array}$$

is equivalent to the condition $A^{+}(\lambda ,D,C){\zeta }_{N,h}=\lambda {\zeta }_{N,h}$, which rewrites as $D·N=N$ and $C·N=0$. We conclude the equality

$$\begin{array}{ccc}& & Iso\left({\zeta }_{N,h}\right)\hfill \\ \\ & =& \left\{A^{+}(\lambda ,D,C)\mid (\lambda ,D,C)\in {\mathbb{R}}_{>0}\times O\left(n\right)\times {\mathbb{R}}^n:D·N=N,C·N=0\right\}.\hfill \end{array}$$

6. Conclusions

We summarize the results obtained so far in the following theorem.

Theorem 1.

Let $\langle ·,·\rangle$ be the Lorentz product over ${\mathbb{R}}^{n+3}$ of signature $(n+1,2)$ given by

$$\begin{array}{ccc}\hfill \langle \zeta ,\zeta \rangle & :=& -{\zeta }_0^2+{\zeta }_1^2+\cdots +{\zeta }_{n+1}^2-{\zeta }_{n+2}^2,\hfill \end{array}$$

let ${\overline{Q}}_{n+1}\subset {\mathbb{P}}^{n+2}$ be the projectivization of the quadric

$$\begin{array}{ccc}\hfill Q_{n+1}& :=& \left\{\zeta \in {\mathbb{R}}^{n+3}\setminus \left\{0\right\}\mid \langle \zeta ,\zeta \rangle =0\right\},\hfill \end{array}$$

let

$$\begin{array}{ccc}\hfill H& :=& \left\{\zeta \in {\mathbb{R}}^{n+3}\mid {\zeta }_{n+1}+{\zeta }_{n+2}=1\right\}\hfill \end{array}$$

and consider the Laguerre group

$$\begin{array}{ccc}\hfill {Lag}_{n+3}& :=& \left\{A\in GL(n+3)\mid \exists c\in {\mathbb{R}}^{*}:\langle Ax,Ax\rangle =c^2\langle x,x\rangle \forall x\in {\mathbb{R}}^{n+3},\right.\hfill \\ \\ & & A{\overline{\zeta }}_{\infty }=\left.{\overline{\zeta }}_{\infty },AH=H\right\},\hfill \end{array}$$

with ${\overline{\zeta }}_{\infty }:={\mathbb{R}}^{*}{\zeta }_{\infty }$, ${\mathbb{R}}^{*}:=\mathbb{R}\setminus \left\{0\right\}$, ${\zeta }_{\infty }=(0,\mathbf{0},-1,1)\in Q_{n+1}$ as well as the subgroup

$$\begin{array}{ccc}\hfill {Lag}_{n+3}^0& :=& \left\{A\in {Lag}_{n+3}\mid A\left(Q_{n+1}^0\right)=Q_{n+1}^0\right\},\hfill \end{array}$$

with $Q_{n+1}^0:=Q_{n+1}\cap \{{\zeta }_0=0\}$. Then, the following statements hold true.

$\left(\mathbf{A}\right)$The action of the group ${Lag}_{n+3}^0$ on ${\overline{Q}}_{n+1}$ preserves the geometric nature of the points, i.e., points in ${\overline{Q}}_{n+1}$ representing, respectively spheres, points, and hyperplanes in ${\mathbb{R}}^n$ are sent by the action in points of the same geometric nature.

$\left(\mathbf{B}\right)$The subgroup ${Lag}_{n+3}^{0,+}$ of orientation preserving elements in ${Lag}_{n+3}^0$ is parameterized by the map

$$\begin{array}{ccc}\hfill {\mathbb{R}}_{>0}\times O\left(n\right)\times {\mathbb{R}}^n& ⟶& {Lag}_{n+3}^{0,+}\hfill \\ \hfill (\lambda ,D,C)& ⟼& A^{+}(\lambda ,D,C),\hfill \end{array}$$

with $A^{+}(\lambda ,D,C)$ given by the matrix

$$\begin{array}{|cccc|}\hline \lambda & \mathbf{0}& 0& 0\\ \mathbf{0}& \lambda D& C& C\\ 0& -\lambda C^{t}D& {\displaystyle \frac{1}{2}}(1+{\lambda }^2-{\left|C\right|}^2)& {\displaystyle \frac{1}{2}}(1-{\lambda }^2-{\left|C\right|}^2)\\ 0& \lambda C^{t}D& {\displaystyle \frac{1}{2}}(1-{\lambda }^2+{\left|C\right|}^2)& {\displaystyle \frac{1}{2}}(1+{\lambda }^2+{\left|C\right|}^2)\\ \hline\end{array},$$

where C^t denotes the transposed matrix of the vertical matrix C.

$\left(\mathbf{C}\right)$The action of the group ${Lag}_{n+3}^{0,+}$ on ${\overline{Q}}_{n+1}$ is transitive. The isotropy of any point ${\zeta }_p\in {\overline{Q}}_{n+1}$ representing a point $p\in {\mathbb{R}}^n$ is given by

$$\begin{array}{ccc}\hfill Iso\left({\zeta }_p\right)& =& \left\{A^{+}(\lambda ,D,C)\mid (\lambda ,D,C)\in {\mathbb{R}}_{>0}\times O\left(n\right)\times {\mathbb{R}}^n:p=\lambda D·p+C\right\}.\hfill \end{array}$$

The isotropy of any point ${\zeta }_{p,r}\in {\overline{Q}}_{n+1}$ representing the oriented sphere $S(p,r)\subset {\mathbb{R}}^n$ is given by

$$\begin{array}{ccc}\hfill Iso\left({\zeta }_{p,r}\right)& =& \left\{A^{+}(1,D,C)\mid (D,C)\in O\left(n\right)\times {\mathbb{R}}^n:p=D·p+C\right\}.\hfill \end{array}$$

The isotropy of any point ${\zeta }_{N,h}\in {\overline{Q}}_{n+1}$, representing the hyperplane in ${\mathbb{R}}^n$ given by the equation $Nx=h$ and oriented by the unit normal vector N is given by

$$\begin{array}{ccc}& & Iso\left({\zeta }_{N,h}\right)\hfill \\ \\ & =& \left\{A^{+}(\lambda ,D,C)\mid (\lambda ,D,C)\in {\mathbb{R}}_{>0}\times O\left(n\right)\times {\mathbb{R}}^n:D·N=N,C·N=0\right\}.\hfill \end{array}$$