How Null Vector Performs in a Rational Bézier Curve with Mass Points

Abstract

This article points out the kinematics in tracing a Bézier curve defined by control mass points. A mass point is a point with a non-positive weight, a non-negative weight or a vector with a null weight. For any Bézier curve, the speeds at endpoints can be modified at the same time for both endpoints. The use of a homographic parameter change allows us to choose any arc of the curve without changing the degree but not offer to change the speeds at both endpoints independently. The homographic parameter change performs weighted points with any non-null real number as weight and also vectors. The curve is thus called a rational Bézier curve with control mass points. In order to build independent stationary points at endpoints, a quadratic parameter change is required. Adding null vectors in the Bézier representation is also an answer. Null vectors are obtained when converting any power function in a rational Bézier curve and their inverse. The authors propose a new approach on placing null vectors in the representation of the rational Bézier curve. It allows us to break free from projective geometry where there is no null vector. The paper ends with some examples of known curves and some perspectives.

1. Introduction

In the CAD domain, polynomial Bézier curves [1,2,3] have evolved into rational curves, then into splines and B splines [4]; additionally, the CAM needs performant algorithms. Mainly, most of them are based on de Casteljau’s algorithm [5,6]. A Bézier curve is, naturally, the geometric locus of barycenters whose weights are either the Bernstein polynomials or these polynomials multiplied by a non-zero number.

Andréas Müller highlights Paul de Casteljau’s course, ideas, and realization [7], which built a system for the calculation of curves. The computing lays on barycenters of points. The weights are defined by Bernstein polynomials. Only a few points called control points are required to set the curve before machining.

To start this article, some recalls about barycenters are provided. The length of the vector $\overrightarrow{MN}$ is $MN=\parallel \overrightarrow{MN}\parallel$. Let $\omega$ and $\mu$ be two reals. If the condition

$$\omega +\mu \ne 0$$

(1)

is satisfied, then the barycenter of the weighted points $\left(M,\omega \right)$ and $\left(N,\mu \right)$ is the unique point G, defined by

$$\omega \overrightarrow{GM}+\mu \overrightarrow{GN}=\overrightarrow{0},$$

(2)

which is equivalent to

$${\displaystyle \overrightarrow{MG}=\frac{\mu }{\omega +\mu }\overrightarrow{MN}}$$

(3)

and the construction of this barycenter is given in Figure 1, where the vectors $\overrightarrow{M{M}_2}$ and $\overrightarrow{N{N}_2}$ are parallel but have opposite directions and

$$\left\{\begin{array}{ccc}\hfill N{N}_2& =& \left|\omega \right|M{M}_1\hfill \\ \hfill M{M}_2& =& \left|\mu \right|M{M}_1.\hfill \end{array}\right.$$

Based on the construction of Figure 1, the construction of the barycenter is possible if the weights have opposite signs, as shown in Figure 2. The barycenter of points M and N with respective weights $-1$ and 1 does not exist, and the lines $\left(MN\right)$ and $\left(M_1{N}_1\right)$ are strictly parallel.

A fundamental property of the concept of barycenter is associativity, or partial barycenter; one can replace a subset of some weighted points by their barycenter, weighted by the sum of the weights of the previous points.

The left-hand side of Formula (2) can result in a non-zero vector, meaning that the barycenter no longer exists; for example, when considering the distinct weighted points $\left(M,-1\right)$ and $\left(N,1\right)$,

$$-1\overrightarrow{GM}+1\overrightarrow{GN}=\overrightarrow{MG}+\overrightarrow{GN}=\overrightarrow{MN}\ne \overrightarrow{0},$$

(4)

and it is therefore natural to seek a concept that generalizes the notion of barycenter and takes this result into account. This generalization is supported by its use in chemistry through the concept of the dipole moment $\overrightarrow{u}$ of a molecule, which reflects its polarity. Let $G_{+}$ (resp., $G_{-}$) be the barycenter of the atoms with positive (resp., negative) charges of value $\delta$ (resp., $-\delta$). Then,

$$\overrightarrow{u}=\delta \overrightarrow{G_{-}{G}_{+}}$$

(5)

which can be defined, using any point O, by

$$\overrightarrow{u}=-\delta \overrightarrow{O{G}_{-}}+\delta \overrightarrow{O{G}_{+}}=\delta \overrightarrow{G_{-}O}+\delta \overrightarrow{O{G}_{+}}$$

(6)

and Figure 3a shows the dipole moment of a molecule of water $H_{2}O$. If $G_{-}=G_{+}$, then $\overrightarrow{u}=\overrightarrow{0}$ and the molecule is said to be nonpolar, as in the case of the methane molecule, Figure 3b.

Let us give an example about the associativity of barycenter. Let us define $A\left(0,0\right)$, $B\left(5,0\right)$ and $C\left(1,4\right)$ and the weighted point $\left(G,2\right)$ is the barycenter of $\left(A,2\right)$, $\left(B,1\right)$ and $\left(C,-1\right)$. Three constructions of $G_2$ are possible:

1.

First construction. Let us introduce the barycenter $\left(B_1,1\right)$ of the weighted points $\left(A,2\right)$ and $\left(C,-1\right)$, i.e., $B_1$ is the symmetric of C with respect to A (see $G_2$ in Figure 2). Then, $\left(G,2\right)$ is the barycenter of $\left(B_1,1\right)$, $\left(B,1\right)$, i.e., G is the midpoint of the segment $\left[B_{1}B\right]$, (Figure 4a).

2.

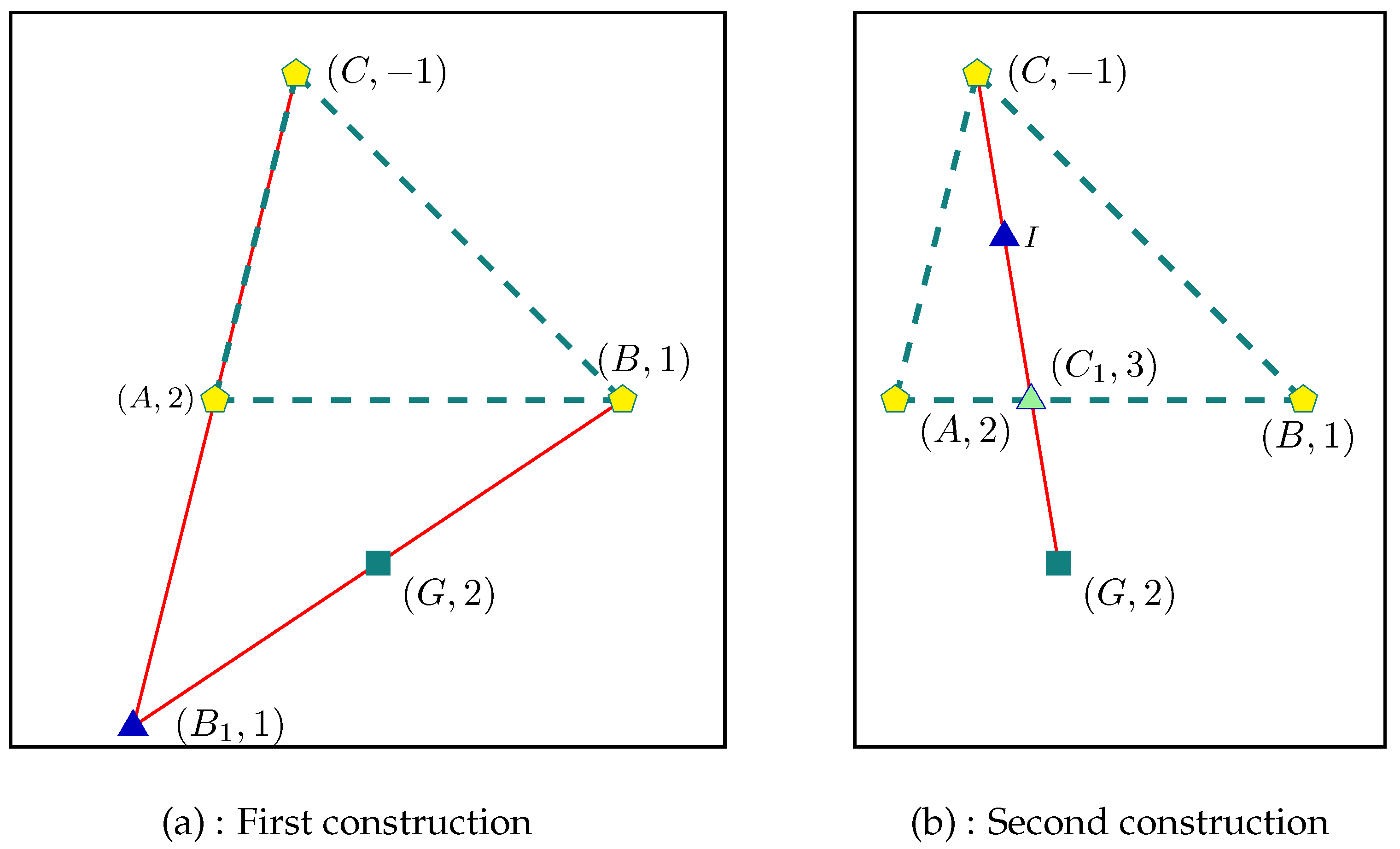
Second construction. Let us introduce the barycenter $\left(C_1,3\right)$ of the weighted points $\left(A,2\right)$ and $\left(B,1\right)$, i.e., $C_1$ is one-third of the way along the segment $\left[AB\right]$ starting from A (see G in Figure 1). Then, $\left(G,2\right)$ is the barycenter of $\left(C_1,3\right)$, $\left(C,-1\right)$, i.e., G is the symmetric of the midpoint I of the segment $\left[C_{1}C\right]$ with respect to the point $C_1$ (see $G_1$ in Figure 2) (Figure 4b).

3.

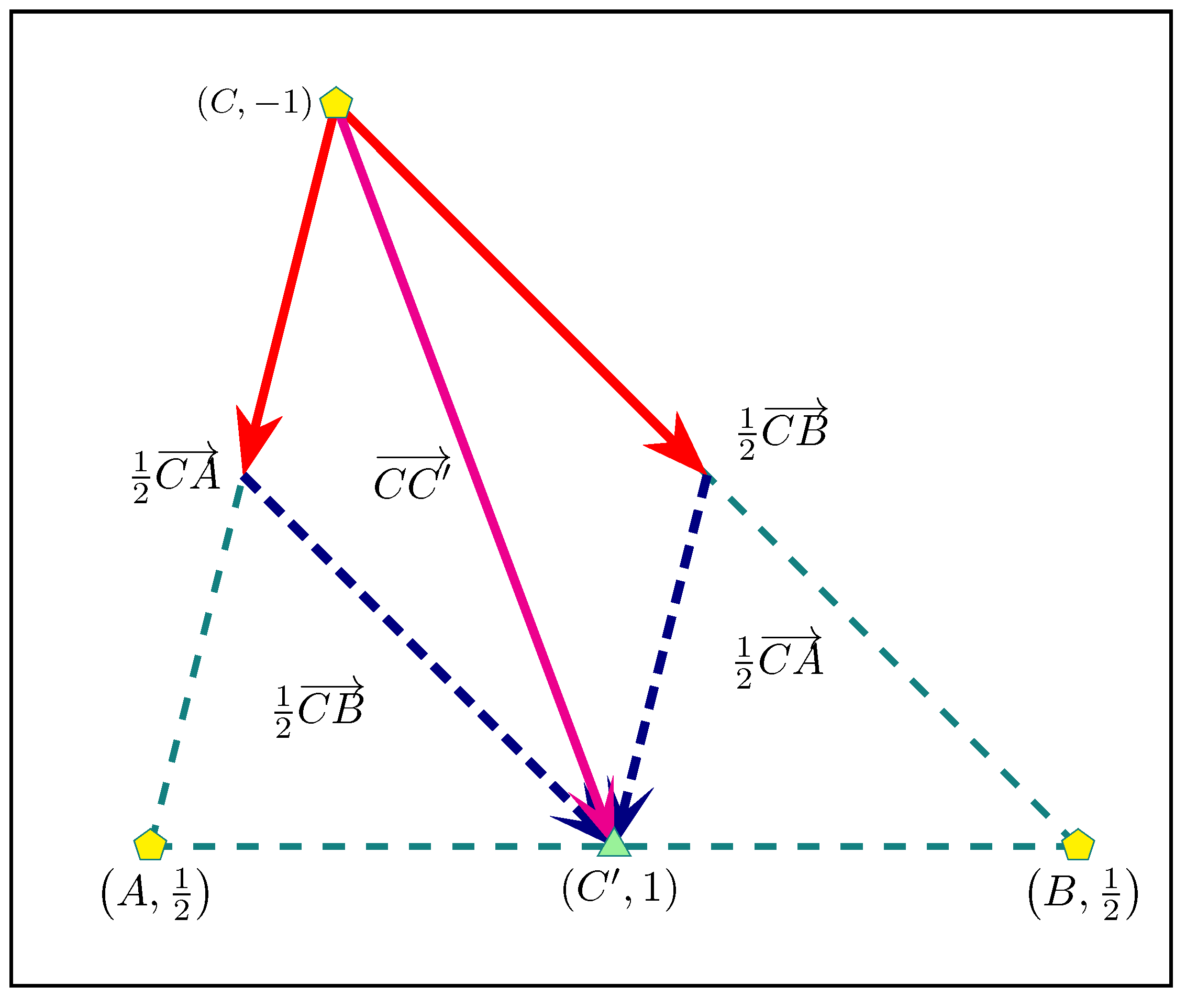
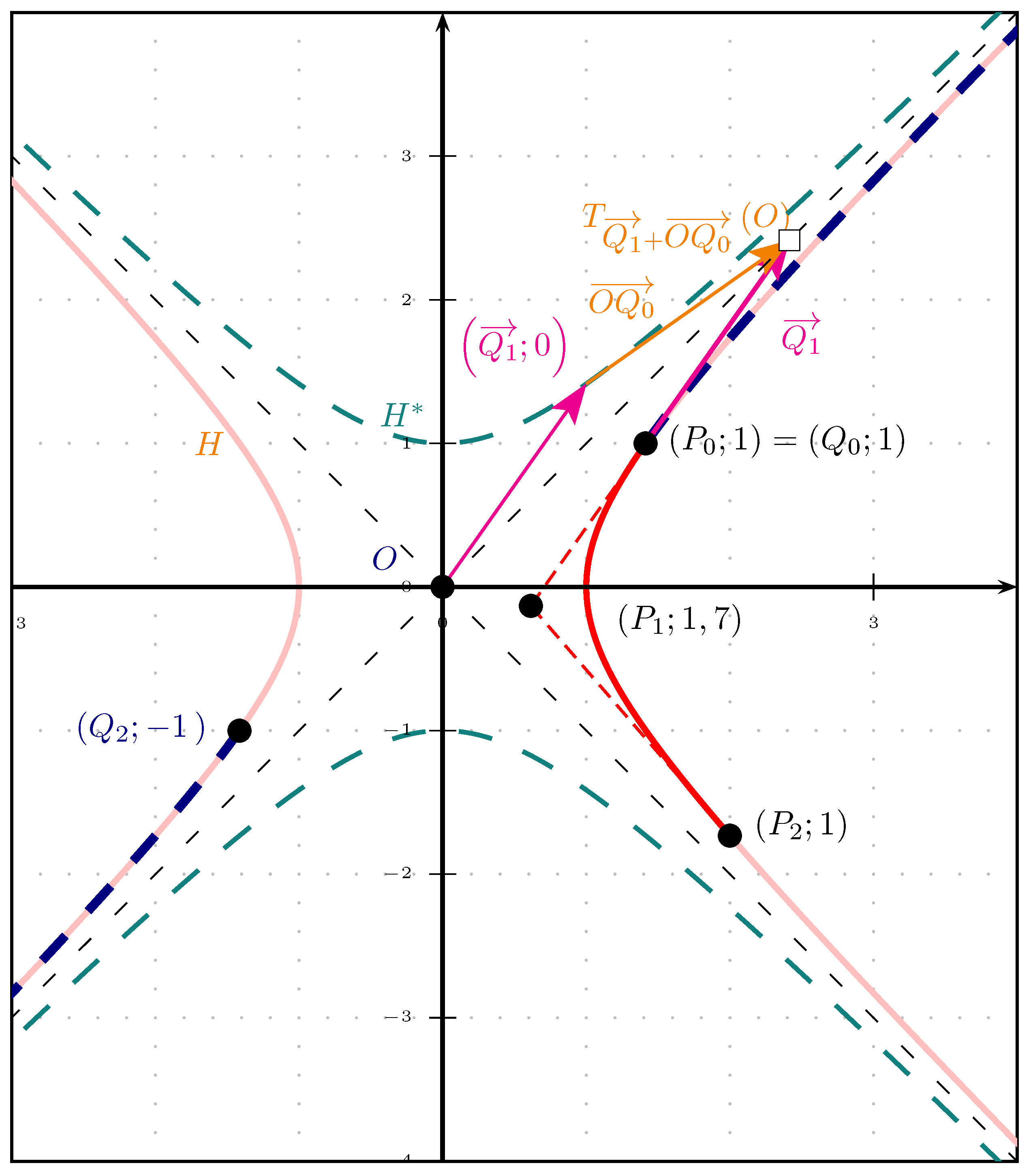
Third construction. The weighted points $\left(B,1\right)$ and $\left(C,-1\right)$ define the vector $\overrightarrow{CB}$ with a null mass. Then, there is the relationship between the points A and G and the vector $\overrightarrow{CB}$: G is the image of A under the translation by the vector ${\displaystyle \frac{1}{2}}\overrightarrow{CB}$ (Figure 5).

When the sum of the weights is null, we need to obtain a vector via a search of the barycenter of the points $\left(A,{\displaystyle \frac{1}{2}}\right)$, $\left(B,{\displaystyle \frac{1}{2}}\right)$, and $\left(C,-1\right)$, as shown below:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{2}\overrightarrow{GA}+\frac{1}{2}\overrightarrow{GB}-\overrightarrow{GC}}& =& {\displaystyle \frac{1}{2}\overrightarrow{GA}-\frac{1}{2}\overrightarrow{GC}+\frac{1}{2}\overrightarrow{GB}-\frac{1}{2}\overrightarrow{GC}}\hfill \\ \hfill & =& {\displaystyle \frac{1}{2}\overrightarrow{CA}+\frac{1}{2}\overrightarrow{CB}}\hfill \\ & =& \overrightarrow{C{C}^{\prime }}\hfill \end{array}$$

where $C^{\prime }$ is the midpoint of the segment $\left[AB\right]$ (Figure 6).

So, it is interesting to construct a set containing points with non-zero weights and vectors with zero weight, generalizing the notion of the barycenter. On this set, an addition operation is defined, then the barycenter of two points or the image of a weighted point under a translation is constructed, as well as a scalar multiplication to modify the weight of a weighted point or directly multiply a vector. This set will be the set of mass points, used by J. C. Fiorot and P. Jeannin [8,9] and Ron Goldman [10,11,12] (Section 2). The use of mass points as control points of a Bézier curve now makes it possible to model semi-ellipses, semi-hyperbolas, or hyperbola branches.

Bézier curves are the simplest control point curves, which were invented by Pierre Bézier [1] at Renault and Paul de Faget de Casteljau [5] at Citroën. Initially, these curves were the barycentric locus of a list of weighted points called control points. These points are weighted by Bernstein polynomials. The number of points equals the degree of these polynomials plus one. Thus, a curve of degree 2 with three control points $P_0$, $P_1$ and $P_2$ represents the parabolic arc of the endpoints $P_0$ and $P_2$ and has the lines $\left(P_0{P}_1\right)$ at $P_0$ and $\left(P_2{P}_1\right)$ at $P_2$ as tangent lines. This model has two disadvantages.

First, the same point $P_1$ defines the tangents at $P_0$ and $P_2$. One solution consists of increasing the degree and taking a 3-degree curve with four control points $P_0$, $P_1$, $P_2$ and $P_3$, which can represent cubic curve arcs with endpoints $P_0$ and $P_3$ and having the lines $\left(P_0{P}_1\right)$ at $P_0$ and $\left(P_3{P}_2\right)$ at $P_2$ as tangents.

Let us start with a polynomial Bézier curve $\gamma$ with control points $P_0$, $P_1$, and $P_2$, all with weight 1. The curve $\gamma$ is an arc of a parabola. In the equivalence class of $P_1$, let $P_{1a}$ (resp., $P_{1b}$) be of strictly greater weight than 1 (resp., between 0 and 1), and the curve ${\gamma }_a$ (resp., ${\gamma }_b$) with control points $P_0$ and $P_{1a}$ (resp., $P_{1b}$), and $P_2$ is an arc of a hyperbola (resp., an ellipse). The points $P_1$, $P_{1a}$, and $P_{1b}$ are equivalent, which means that the curves $\gamma$, ${\gamma }_a$, and ${\gamma }_b$ are equivalent: using projective geometry, a parabola, a hyperbola, and an ellipse are of the same type, that is, a conic section [13].

However, any arc of ellipse or hyperbola cannot be represented by this model. Taking account of weighted points is one answer. The points $P_0$, $P_1$, and $P_2$ are replaced by weighted points $\left(P_0;{\omega }_0\right)$, $\left(P_1;{\omega }_1\right)$, and $\left(P_2;{\omega }_2\right)$; see [3,6,14]. But using a rational Bézier curve representation, a new problem arises. In the case where the sum of the weights equals zero, the barycenter no longer exists [15,16,17]. The result of the calculation provides a vector. The solution that generalizes the notion of barycenter consists of using mass points [8,9].

In [18], L. Piegl defines a semicircle arc with an intermediate control vector and two weighted endpoints, specifying that apart from the intermediate control points which can be vector points, the endpoints must be weighted points. In fact, an endpoint being a vector allows for asymptotes or asymptotic directions [19], and the nature of the conic generated by the Bézier curve of weighted control points $\left(P_0;{\omega }_0\right)$, $\left(P_1;{\omega }_1\right)$, and $\left(P_2;{\omega }_2\right)$ depends on the sign of the reduced discriminant of the denominator [8]:

$${\Delta }^{\prime }={\omega }_1^2-{\omega }_2{\omega }_0$$

(7)

and then, the following are applied:

⋆

If ${\omega }_1^2-{\omega }_2{\omega }_0=0$, then the denominator vanishes exactly once and the conic is a parabola;

⋆

If ${\omega }_1^2-{\omega }_2{\omega }_0<0$, then the denominator does not vanish and the conic is an ellipse;

⋆

If ${\omega }_1^2-{\omega }_2{\omega }_0>0$, then the denominator vanishes twice and the conic is a hyperbola.

Table 1. Euclidean type of the conic based on the control vectors of the Bézier curve.

Point 1	Point 2	Point 3	Condition	Type
$\left(P_0;{\omega }_0\ne 0\right)$	${\left(\overrightarrow{P_1};{\omega }_1=0\right)}^{{\phantom{(}}^{\phantom{(}}}$	$\left(P_2;{\omega }_2\ne 0\right)$	${\omega }_0{\omega }_2>0$	Semi-ellipse
$\left(P_0;{\omega }_0\ne 0\right)$	${\left(\overrightarrow{P_1};{\omega }_1=0\right)}^{{\phantom{(}}^{\phantom{(}}}$	$\left(\overrightarrow{P_2};{\omega }_2=0\right)$		Parabola arc
$\left(\overrightarrow{P_0};{\omega }_0=0\right)$	${\left(\overrightarrow{P_1};{\omega }_1=0\right)}^{{\phantom{(}}^{\phantom{(}}}$	$\left(P_2;{\omega }_2\ne 0\right)$		Parabola arc
$\left(P_0;{\omega }_0\ne 0\right)$	${\left(\overrightarrow{P_1};{\omega }_1=0\right)}^{{\phantom{(}}^{\phantom{(}}}$	$\left(P_2;{\omega }_2\ne 0\right)$	${\omega }_0{\omega }_2<0$	Semi-hyperbola
${\left(\overrightarrow{P_0};{\omega }_0=0\right)}^{{\phantom{(}}^{\phantom{(}}}$	$\left(P_1;{\omega }_1\ne 0\right)$	$\left(\overrightarrow{P_2};{\omega }_2=0\right)$		Hyperbola branch

shows the link between the position of the vectors and the type of the generated conic arc [20,21].

Using this concept of mass points and the help of a homographic parameter change, the De Casteljau algorithm can be used to achieve regular subdivision [22], and also to determine any conic feature [20,21,23]. This is impossible by using the concept of projective geometry [24].

In [2], G. Farin defines Bézier curves of any degree with control vectors and zero weights, specifying that they can be eliminated by degree elevation. However, the vectors can be useful when modeling a Dupin cyclide with quadratic rational Bézier curves in the 5-dimensional affine Minkowski–Lorentz space ${\mathrm{L}}_{4,1}$, of origin $O_5$ with the attached vector space $\overrightarrow{{\mathrm{L}}_{4,1}}$, as follows: a weighted point $\sigma$ of ${\mathrm{L}}_{4,1}$, such that the vector $\overrightarrow{O_5\sigma }$ has a norm of 1, represents an oriented sphere $\mathtt{S}$ in ${\mathbb{R}}^3$; an isotropic vector $\overrightarrow{m}$ of $\overrightarrow{{\mathrm{L}}_{4,1}}$ represents a point M in ${\mathbb{R}}^3$, i.e., a singular point of a canal surface or the vector $\overrightarrow{e_{\infty }}$ of $\overrightarrow{{\mathrm{L}}_{4,1}}$, which represents the point at infinity of ${\mathbb{R}}^3$.

Table 2. Nature of control points in ${\mathrm{L}}_{41}$ or in $\overrightarrow{{\mathrm{L}}_{41}}$ and type of the generated Dupin cyclide.

Point 1	Point 2	Point 3	Kind of the Dupin Cyclide
$\left({\sigma }_0;{\omega }_0\ne 0\right)$	${\left(P_1;{\omega }_1\ne 0\right)}^{{\phantom{(}}^{\phantom{(}}}$	$\left(\overrightarrow{e_{\infty }};{\omega }_2=0\right)$	Circular cylinder
${\left(\overrightarrow{m};{\omega }_0=0\right)}^{{\phantom{(}}^{\phantom{(}}}$	$\left(P_1;{\omega }_1\ne 0\right)$	$\left(\overrightarrow{e_{\infty }};{\omega }_2=0\right)$	Semicircular cone with apex M
${\left(\overrightarrow{m};{\omega }_0=0\right)}^{{\phantom{(}}^{\phantom{(}}}$	$\left(P_1;{\omega }_1\ne 0\right)$	$\left(\overrightarrow{n};{\omega }_2=0\right)$	Patch of Dupin cyclide with endpoints M and N

shows the link between the position of the vectors and the type of the Dupin cyclide [25,26]:

• A cylinder of revolution has no singular point but contains the point at infinity;
• A cone of revolution has a singular point M, the apex, and the point at infinity;
• A spindle or horned Dupin cyclide has two singular points M and N;
• A one-singularity spindle or singly horned Dupin cyclide has only one singular point M.

Considering the point at infinity, the data of two spheres ${\mathtt{S}}_1$ and ${\mathtt{S}}_2$, with the respective algebraic radii ${\rho }_1$ and ${\rho }_2$ [25], define the following:

• A circular cylinder if ${\rho }_1={\rho }_2$.
• A circular cone if ${\rho }_1\ne {\rho }_2$. If ${\rho }_1{\rho }_2<0$, the apex is between the spheres ${\mathtt{S}}_1$ and ${\mathtt{S}}_2$, i.e., there is $t\in \left(0,1\right)$ such that a mass point of the Bézier curve representing this cone is a vector.

In the space of weighted points, we can define any pseudo-norm or restrict the Lorentz quadratic form to a 2-plane in the Minkowski–Lorentz space, and the hyperbola arc satisfies the conditions of a circle (orthogonality between a radius and the tangent at the point of contact) [25,26]. It is possible to use it in the Minkowski–Lorentz space [27,28,29,30,31] to represent canal surfaces [25,32]. It is also possible, through this model, to construct Dupin cyclides as subdivided surfaces [33,34] or to determine Dandelin spheres [35].

This article focuses on sketching, from a kinematic point of view, a segment or a Bézier curve arc, which allows us to design a polygon or curves with ${\mathrm{G}}^0$-${\mathcal{C}}^1$ joints. For example, in the case of the triangle $ABC$, the following steps are as follows:

• Trace the segment $\left[AB\right]$ starting from A with a zero velocity and arriving at B with a zero velocity;
• Trace the segment $\left[BC\right]$ starting from B with a zero velocity and arriving at C with a zero velocity;
• Trace the segment $\left[CA\right]$ starting from C with a zero velocity and arriving at A with a zero velocity.

Section 2 recalls some definitions on mass points, whose containing set is denoted as $\tilde{P}$ and Bézier curves with control mass points. Some examples of computations with mass points are given in Appendix A, which can refresh one’s mind on the properties of rational Bézier curves with mass control points at the endpoints, i.e., at 0 and 1. This space formally defines the tools for rational Bézier curves using mass points. The former idea was to build operators on a mix of weighted points and vectors called mass points. The operators generalize the barycentric notion that was illustrated at the start of this paper. Mass points can be considered as control points in a representation of rational curves. This type of representation describes half a circle by two points and a vector. An example can be found herein.

Section 3 shows the role of the null vector in creating stationary points during the sketch of a segment. Section 3 also deals with global central conics based on mass control points in a rational Bézier curve representation.

The conversion of any power function into a rational Bézier curve with mass points provides a list of mass points that contains weighted points and vectors, including the null vector. The formulae are derived from the calculation of the control points after a homographic parameter change from 2 degrees to 4. A quadratic parameter change function allows us to control independently the tangent vectors at the ends of the curve. It models the entire curve as well. The circle arc, Descartes Folium (cubic), and Bernoulli Lemniscate (quartic) are significant examples of curves of degrees 2, 3, and 4. After the conclusion, some perspectives are proposed to the reader.

2. Rational Bézier Curves in $\tilde{\mathcal{P}}$

In the following, $\left(O;\overrightarrow{\mathcal{ı}};\overrightarrow{\mathcal{j}}\right)$ designates a direct reference frame in the usual Euclidean affine plane $\mathcal{P}$, and $\overrightarrow{\mathcal{P}}$ is the set of vectors of the plane. The set of mass points is defined by

$$\tilde{\mathcal{P}}=\left(\mathcal{P}\times {\mathbb{R}}^{\ast }\right)\cup \left(\overrightarrow{\mathcal{P}}\times \left\{\overrightarrow{0}\right\}\right).$$

On the mass point space, the addition, denoted by ⊕, is defined as follows:

• $\omega \ne 0⟹\left(M;\omega \right)\oplus \left(N;-\omega \right)=\left(\omega \overrightarrow{NM};0\right)$;
• $\omega \mu \left(\omega +\mu \right)\ne 0⟹$$\left(M;\omega \right)\oplus \left(N;\mu \right)=\left(\mathtt{bar}\left\{\left(M;\omega \right);{\left(N;\mu \right)}_{{\phantom{(}}_{\phantom{(}\phantom{(}}}\right\};\omega +\mu \right)$, where the notation $\mathtt{bar}\left\{\left(M;\omega \right);{\left(N;\mu \right)}_{{\phantom{(}}_{\phantom{(}\phantom{(}}}\right\}$ denotes the barycenter of the weighted points $\left(M;\omega \right)$ and $\left(N;\mu \right)$;
• $\left(\overrightarrow{u};0\right)\oplus \left(\overrightarrow{v};0\right)=\left(\overrightarrow{u}+\overrightarrow{v};0\right)$;
• $\omega \ne 0⟹\left(M;\omega \right)\oplus \left(\overrightarrow{u};0\right)=\left(T_{{\displaystyle \frac{1}{\omega }}\overrightarrow{u}}\left(M\right);\omega \right)$, where $T_{\overrightarrow{W}}$ is the translation of $\mathcal{P}$ of vector $\overrightarrow{W}$.

In the same way, on the space $\tilde{\mathcal{P}}$, the multiplication by a scalar, denoted by ⊙, is defined as follows:

• $\omega \alpha \ne 0⟹\alpha \odot \left(M;\omega \right)=\left(M;\alpha \omega \right)$;
• $\omega \ne 0⟹0\odot \left(M;\omega \right)=\left(\overrightarrow{0};0\right)$;
• $\alpha \odot \left(\overrightarrow{u};0\right)=\left(\alpha \overrightarrow{u};0\right)$.

One can note that $\left(\tilde{\mathcal{P}},\oplus ,\odot \right)$ is a vector space [21]. So, a mass point is a weighted point $\left(M,\omega \right)$ with $\omega \ne 0$ or a vector $\left(\overrightarrow{u},0\right)$. The Bernstein polynomials of degree n are defined by

$$B_{i,n}\left(t\right)=\left(\begin{array}{c}n\\ i\end{array}\right){\left(1-t\right)}^{n-i}{t}^i$$

(8)

and

$$\sum _{i=0}^n{B}_{i,n}\left(t\right)={\left(\left(1-t\right)+t^{{\phantom{(}}^{{\phantom{(}}^{\phantom{(}}}}\right)}^n=1.$$

These Bernstein polynomials provide the definition of the rational Bézier curve (BR curve) in $\tilde{\mathcal{P}}$, as given below.

Definition 1.

Rational Bézier curve (BR curve) in $\tilde{\mathcal{P}}$

Let ${\left(P_i;{\omega }_i\right)}_{i\in \left[\right[0;n\left]\right]}$ be $n+1$ mass points in $\tilde{\mathcal{P}}$.

Define two sets:

$$\begin{array}{ccccccc}I& =& \left\{i|{\omega }_i\ne 0\right\}\hfill & \mathit{and}& J& =& \left\{i|{\omega }_i=0\right\}\hfill \end{array}$$

Define the function ${\omega }_f$ as follows:

$$\begin{array}{cccc}{\omega }_f:& \left[0;1\right]& ⟶& \mathbb{R}\\ & t& ⟼& {\displaystyle {\omega }_f\left(t\right)=\sum _{i\in I}{\omega }_i\times B_{i,n}\left(t\right)}\end{array}$$

(9)

A mass point $\left(M;\omega \right)$ or $\left(\overrightarrow{u};0\right)$ lays to the Rational Bézier curve that is defined by the three control mass points $\left(P_0;{\omega }_0\right)$, $\left(P_1;{\omega }_1\right)$, and $\left(P_2;{\omega }_2\right)$ if there is a real $t_0$ in $\left[0;1\right]$ such that

• If ${\omega }_f\left(t_0\right)\ne 0$, then
  $$\left\{{\displaystyle \begin{array}{c}\overrightarrow{OM}=\frac{1}{{\omega }_f\left(t_0\right)}\left({\displaystyle \sum _{i\in I}{\omega }_i{B}_{i,n}\left(t_0\right)\overrightarrow{O{P}_i}}\right)+\frac{1}{{\omega }_f\left(t_0\right)}\left(\sum _{i\in J}{B}_{i,n}\left(t_0\right)\overrightarrow{P_i}\right)\hfill \\ \hspace{1em}\hspace{1em}\omega ={\omega }_f\left(t_0\right).\hfill \end{array}}\right.$$

  (10)
• If ${\omega }_f\left(t_0\right)=0$, then

  $$\overrightarrow{u}=\sum _{i\in I}{\omega }_i{B}_{i,n}\left(t_0\right)\overrightarrow{O{P}_i}+\sum _{i\in J}{B}_{i,n}\left(t_0\right)\overrightarrow{P_i}.$$

  (11)

Such a curve is denoted $BR\left\{\left(P_0;{\omega }_0\right);\left(P_1;{\omega }_1\right);\left(P_2;{\omega }_2\right)\right\}.$

Using ⊕ and ⊙, the mass point $\left(M;\omega \right)$ is written as

$$\left(M;\omega \right)=\sum _{i\in I\cup J}^{\oplus }{B}_i\left(t\right)\odot \left(P_i;{\omega }_i\right)$$

where ${\displaystyle \sum _{i\in I\cup J}^{\oplus }}$ denotes a sum of ⊕. If $J=\varnothing$, this definition leads to the usual rational quadratic Bézier curve. This kind of curve can model a circular arc as detailed in the next result.

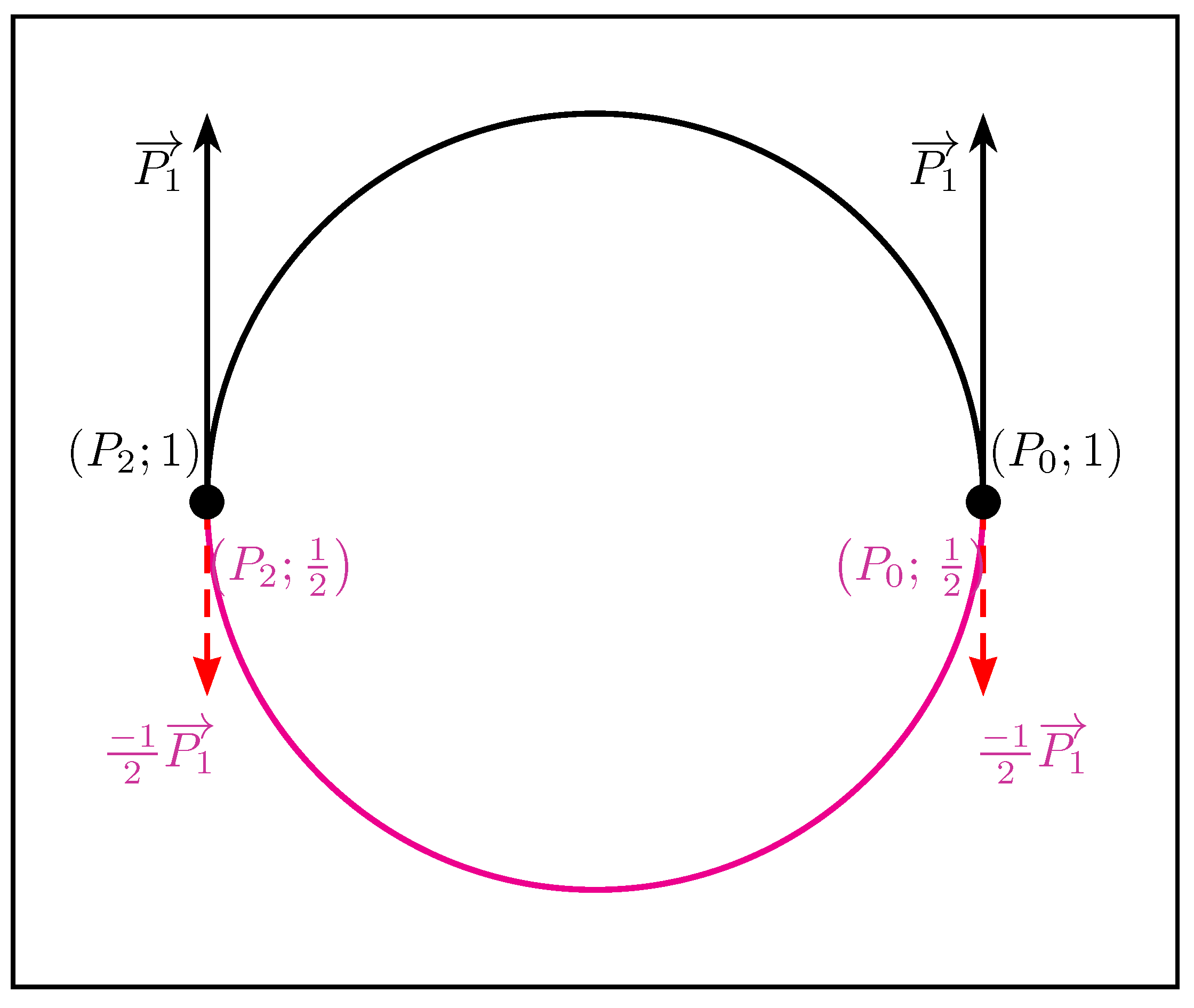
2.1. Modeling Euclidean Circular Arcs with Mass Points

Theorem 1.

Let $C$ be a circle of center $O_0$ and of radius R.

Let $P_0$ and $P_2$ be two points belonging to the circle $C$.

Let ${\omega }_0$ and ${\omega }_2$ be two non-negative reals.

• If $O_0$ is not the midpoint of the segment $\left[P_0{P}_2\right]$,
  let $I_1$ be the midpoint of the segment $\left[P_0{P}_2\right]$.
  The point $P_1$ is defined as

  $$\begin{array}{ccc}\overrightarrow{I_1{P}_1}=t_1\overrightarrow{O_0{I}_1}& \mathit{with}& {\displaystyle t_1=\frac{\overrightarrow{O_0{P}_0}•\overrightarrow{I_1{P}_0}}{\overrightarrow{O_0{P}_0}•\overrightarrow{O_0{I}_1}}}\end{array}$$

  (12)
  where • is the usual dot product.
  The $BR\left\{\left(P_0;{\omega }_0\right);\left(P_1;{\omega }_1\right);\left(P_2;{\omega }_2\right)\right\}$ is a circular arc iff

  $${\omega }_1^2={\omega }_0{\omega }_2{cos}^2\left(\widehat{\overrightarrow{P_0{P}_1};\overrightarrow{P_0{P}_2}}\right)$$

  (13)
• If $O_0$ is the midpoint of the segment $\left[P_0{P}_2\right]$, the $BR\left\{\left(P_0;{\omega }_0\right);\left(\overrightarrow{P_1};0\right);\left(P_2;{\omega }_2\right)\right\}$ is a semicircle of $C$ iff

  $$\left\{\begin{array}{ccc}\hfill \overrightarrow{P_1}•\overrightarrow{P_0{P}_2}& =& 0\hfill \\ \hfill {\omega }_0{\omega }_2{\overrightarrow{P_0{P}_2}}^2& =& 4{\overrightarrow{P_1}}^2\hfill \end{array}\right.$$

  (14)

Proof. 

See [36] for Formulae (12) and (13) and Proposition 5.4.2 of [8]. □

To obtain the black curve in Figure 7, the control mass points of the black curve are $\left(P_0;1\right)$, $\left(\overrightarrow{P_1};0\right)$, and $\left(P_2;1\right)$, i.e., the weights ${\omega }_0$ and ${\omega }_2$ are equal to one and it is always possible to obtain this case after a parameter change [21]. The control mass points of the magenta curve are $\left(P_0;{\displaystyle \frac{1}{2}}\right)$, $\left(-{\displaystyle \frac{1}{2}}\overrightarrow{P_1};0\right)$, and $\left(P_2;{\displaystyle \frac{1}{2}}\right)$.

2.2. Circles, Pseudo-Circles, Central Conics and Mass Points

In an orthogonal frame, the hyperbola of the equation

$${\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=1}$$

can be seen as a unit pseudo-circle, taking into account the quadratic form

$${\mathcal{Q}}_{\mathrm{H}}\left(\overrightarrow{u}\right)={\displaystyle \frac{x^2}{a^2}}-{\displaystyle \frac{y^2}{b^2}},$$

where $\overrightarrow{u}\left(x,y\right)$. The BR representation of the hyperbola can be chosen similarly to the representation seen in Theorem 1. This is pointed out by Theorem 2.

Theorem 2.

Let $\mathrm{H}=BR\{\left(P_0;1\right),\left(P_1;{\omega }_1\right),\left(P_2;1\right)\}$ with ${\omega }_1>1$. Let ε be in $\{-1;1\}$.

The following homographic parameter change

$$\begin{array}{cccc}\hfill h:& \overline{\mathbb{R}}& ⟶& \overline{\mathbb{R}}\hfill \\ \hfill & u& ⟼& {\displaystyle \frac{{\displaystyle \frac{\epsilon }{{\sqrt{{\omega }_1^{2^{\phantom{(}}}-1}}^{\phantom{(}}}u}}{{\displaystyle 1-u+\epsilon \frac{1-{\omega }_1^{\phantom{(}}}{{\sqrt{{\omega }_1^{2^{\phantom{(}}}-1}}^{\phantom{(}}}u}}}\hfill \end{array}$$

(15)

provides the new representation of $\mathrm{H}=BR\left\{\left(Q_0;1\right);\left(\overrightarrow{Q_1};0\right);\left(Q_2;-1\right)\right\}$, where

$$\left\{\begin{array}{ccc}\left(Q_0;1\right)& =& \left(P_0;1\right)\hfill \\ \left(\overrightarrow{Q_1};0\right)& =& \left({\displaystyle \frac{\epsilon {\omega }_1}{{\sqrt{{\omega }_1^{2^{\phantom{(}}}-1}}^{\phantom{(}}}\overrightarrow{P_0{P}_1};0}\right)\hfill \\ \left(Q_2;-1\right)& =& \mathtt{bar}\left\{\left({\displaystyle P_0;\frac{{\omega }_1^2}{{\omega }_1^2-1}}\right);\left({\displaystyle P_1;\frac{-2{\omega }_1^2}{{\omega }_1^2-1}}\right);\left({\displaystyle P_2;\frac{1}{{\omega }_1^2-1}}\right).\right\}\hfill \end{array}\right.$$

Proof. 

By the use of Theorem 1, see [21]. □

In Figure 8, the BR curve of control mass points $\left(Q_0;1\right)$, $\left(\overrightarrow{Q_1};0\right)$, and $\left(Q_2;-1\right)$ is a pseudo-semicircle of the unit pseudo-circle $\mathrm{H}$. Moreover,

$$\underset{t\to {\displaystyle \frac{1}{2}}}{lim}\left(Q_0;B_{0,n}\left(t\right)\right)\oplus \left(B_{1,n}\left(t\right)\overrightarrow{Q_1};0\right)\oplus \left(Q_2;-B_{2,n}\left(t\right)\right)=\left({\displaystyle \frac{1}{2}}\left(\overrightarrow{O{Q}_0}+\overrightarrow{Q_1}\right);0\right).$$

The vector ${\displaystyle \frac{1}{2}}\left(\overrightarrow{O{Q}_0}+\overrightarrow{Q_1}\right)$ gives one asymptotic direction of $\mathrm{H}$.

Formula (14) applied to ${\mathcal{Q}}_{\mathrm{H}}$ gives

$$1\times -1\times {\mathcal{Q}}_{\mathrm{H}}\left(\overrightarrow{Q_0{Q}_2}\right)=-4=4\times {\mathcal{Q}}_{\mathrm{H}}\left(\overrightarrow{Q_1}\right).$$

As the result is negative, the point $Q_1$ defined by $\overrightarrow{O{Q}_1}=\overrightarrow{Q_1}$ does not belong to the pseudo-circle $\mathrm{H}$.

Moreover, any tangent vector $\overrightarrow{{\displaystyle \frac{d\gamma }{dt}}}\left(t\right)$ to the BR curve $\gamma$ with control mass points $\left(Q_0;1\right)$, $\left(\overrightarrow{Q_1};0\right)$, and $\left(Q_2;-1\right)$ can define a point $M\left(t\right)$ such that

$$\overrightarrow{OM\left(t\right)}=\overrightarrow{{\displaystyle \frac{d\gamma }{dt}}}\left(t\right).$$

The point $M\left(t\right)$ lays to the pseudo-circle ${\mathrm{H}}^{\ast }$ of center O, and the square of its radius equals $-1$. Its equation is as follows:

$${\displaystyle \frac{x^2}{a^2}}-{\displaystyle \frac{y^2}{b^2}}=-1\mathrm{or}-{\displaystyle \frac{x^2}{a^2}}+{\displaystyle \frac{y^2}{b^2}}=1.$$

The last representation can be considered as a pseudo-semicircle of $\mathrm{H}$ when the parameter runs in $[0;1]$; see Figure 8. These results are setting the basics of the Minkowski–Lorentz space in order to work with spheres, canal surfaces, and Dupin cyclides [25,30,31,33,34,35,37].

3. The Null Vector in a Bézier Representation with Mass Points

This section deals with the null vectors. First, they perform in the definition of stationary points at the endpoints of a BR curve. And an adequate quadratic parameter change provides new results for these kinds of stationary points.

• Second, the section ends with a natural behavior of null vectors obtained in the expression of a power curve in a BR form.

The following result is concerned with stationary points.

3.1. Differential Properties of Bézier Curves at 0 and 1 and Stationary Points

Theorem 3.

Let n be an integer equal to or greater than 2. Let ${\omega }_0$ be a non-zero real number. Consider a Bézier curve with the following mass control points: $\left(P_0;{\omega }_0\right)$, $\left(P_1;{\omega }_1\right)$, ⋯,$\left(P_n;{\omega }_n\right)$. Two cases are distinguished:

• If ${\omega }_1=0$, the velocity vector of the curve at $P_0$ is given by

  $${\displaystyle \frac{d}{dt}\overrightarrow{OM\left(0\right)}=\frac{n}{{\omega }_0}\overrightarrow{P_1}.}$$

  (16)
• If ${\omega }_1\ne 0$, the velocity vector of the curve at $P_0$ is given by

  $${\displaystyle \frac{d}{dt}\overrightarrow{OM\left(0\right)}=n\frac{{\omega }_1}{{\omega }_0}\overrightarrow{P_0{P}_1}.}$$

  (17)

Proof. 

The proof is left to the reader. □

Applying the theorem provides the following.

Corollary 1

(Stationary point at 0). Let n be an integer equal to or greater than 2. Let ${\omega }_0$ be a non-zero real number. Consider a Bézier curve with the mass control points $\left(P_0;{\omega }_0\right)$, $\left(P_1;{\omega }_1\right)$, ⋯,$\left(P_n;{\omega }_n\right)$.

If $\overrightarrow{P_1}=\overrightarrow{0}$ (thus, ${\omega }_1=0$) or $P_1=P_0$, then $P_0$ is a stationary point.

Given the symmetry of Bézier curves, the following theorem is stated:

Theorem 4.

Let ${\omega }_n$ be a non-zero real number. Consider a Bézier curve of degree n with mass control points $\left(P_0;{\omega }_0\right)$, ⋯, $\left(P_{n-1};{\omega }_{n-1}\right)$, $\left(P_n;{\omega }_n\right)$.

Two cases are separated:

• If ${\omega }_{n-1}=0$, the velocity vector of the curve at $P_n$ is given by

  $${\displaystyle \frac{d}{dt}\overrightarrow{OM\left(1\right)}=-\frac{n}{{\omega }_n}\overrightarrow{P_{n-1}}.}$$

  (18)
• If ${\omega }_{n-1}\ne 0$, the velocity vector of the curve at $P_n$ is given by

  $${\displaystyle \frac{d}{dt}\overrightarrow{OM\left(1\right)}=-n\frac{{\omega }_{n-1}}{{\omega }_n}\overrightarrow{P_n{P}_{n-1}}.}$$

  (19)

Corollary 2

(Stationary points at 1). Let ${\omega }_n$ be non zero-real number. Consider a Bézier curve of degree n, with the mass control points $\left(P_0;{\omega }_0\right)$, ⋯, $\left(P_{n-1};{\omega }_{n-1}\right)$, $\left(P_n;{\omega }_n\right)$.

If $\overrightarrow{P_{n-1}}=\overrightarrow{0}$ (thus, ${\omega }_{n-1}=0$) or $P_n=P_{n-1}$, then $P_n$ is a stationary point.

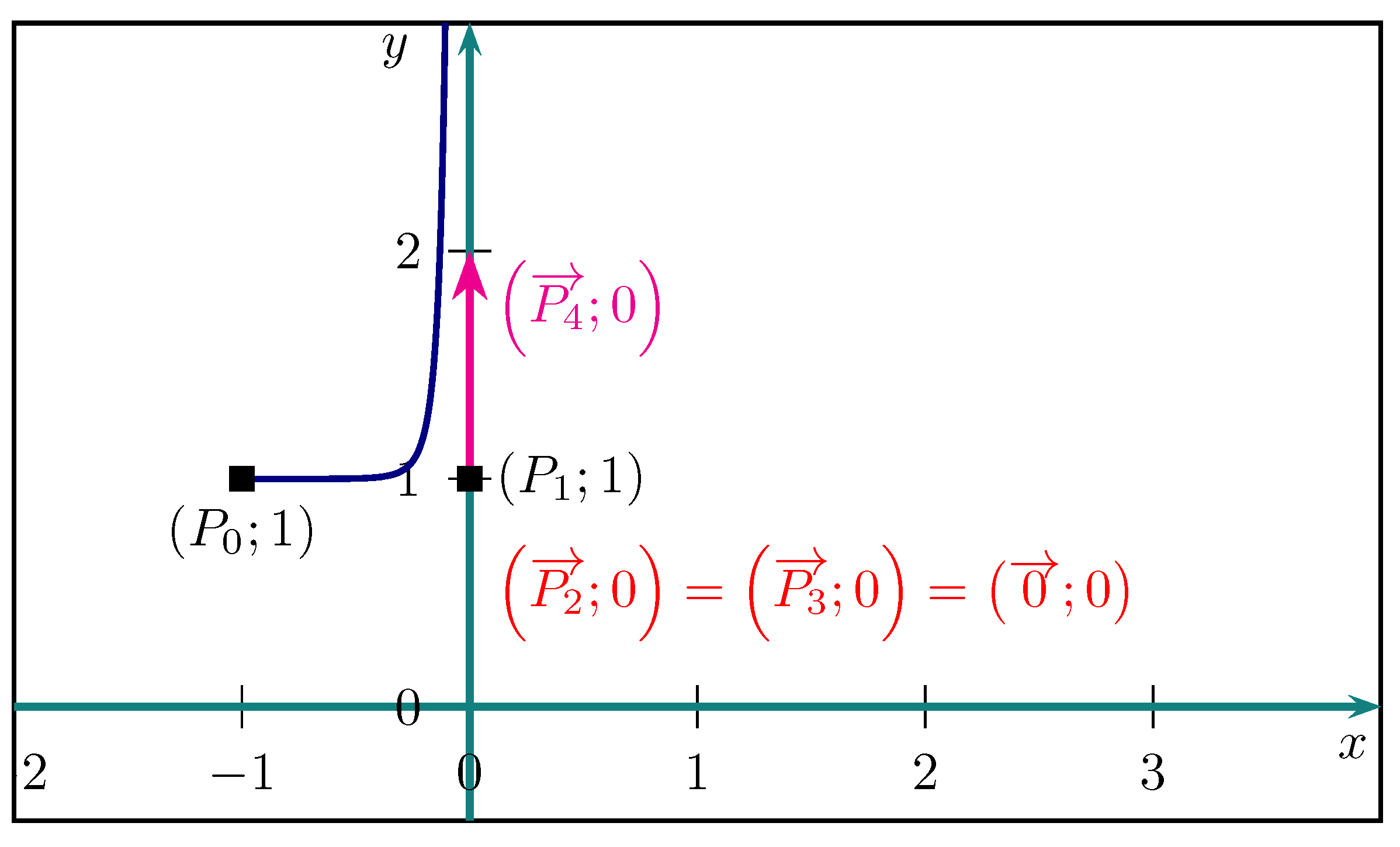
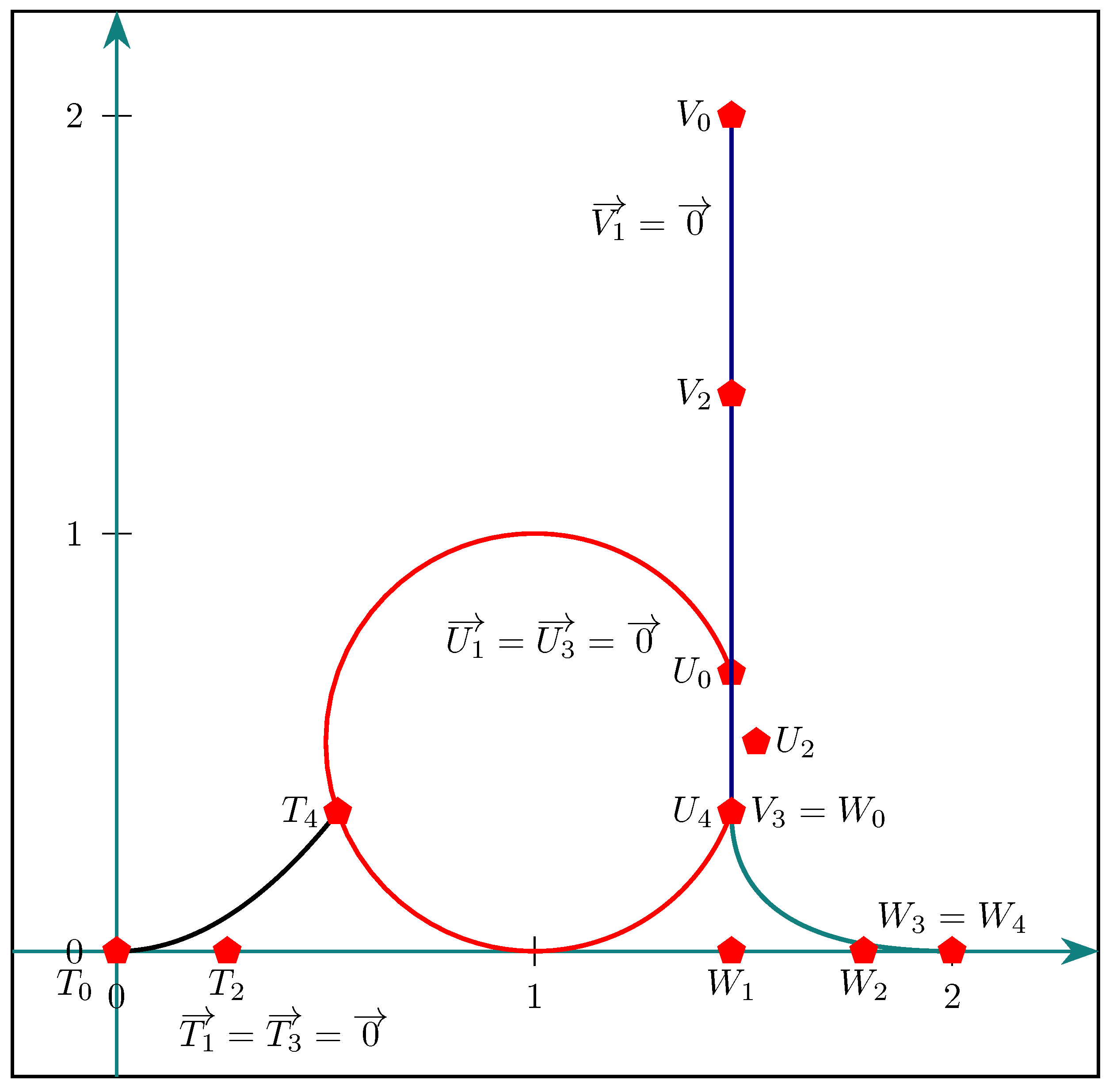
3.2. The Null Vector and Stationary Points at the Endpoints of a Segment

Let $\left[AB\right]$ be a segment, the points $M\left(t\right)$ of $\left[AB\right]$ are defined by

$$\overrightarrow{OM\left(t\right)}=\left(1-t\right)\overrightarrow{OA}+t\overrightarrow{OB},$$

(20)

where $t\in \left[0;1\right]$, and the point $M\left(t\right)$ does not depend on the point O. The velocity vector

$${\displaystyle \frac{d}{dt}\overrightarrow{OM\left(t\right)}=-\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{AB}}$$

(21)

is constant along the segment. While a human being is drawing a segment, the velocity vectors equal null vector $\overrightarrow{0}$ at both ends. To model this human behavior, a classic solution is to double the endpoints of the segment and use a cubic Bézier curve with control points A, A, B, and B. Another answer is based on an ellipse represented by three mass points $(A;1);\overrightarrow{X};(B,1)$. If $\overrightarrow{X}$ tends to $\overrightarrow{0}$, the ellipse arc is degenerated in the segment $[A,B]$ with null speed at $t=0$ and $t=1$.

Figure 9 shows five quadratic rational Bézier curves with mass points of control $\left(A,1\right)$, $\left(\overrightarrow{X};0\right)$, and $\left(B,1\right)$, where $\overrightarrow{X}$ is chosen as follows:

1.

$\overrightarrow{X}=\overrightarrow{P_1}$ with $AB=2∥\overrightarrow{P_1}∥$ for the semicircle in red.

2.

$\overrightarrow{X}=\overrightarrow{Q_1}={\displaystyle \frac{1}{2}}\overrightarrow{P_1}$ for the semi-ellipse in blue.

3.

$\overrightarrow{X}=\overrightarrow{R_1}={\displaystyle \frac{1}{4}}\overrightarrow{P_1}$ for the semi-ellipse in magenta.

4.

$\overrightarrow{X}=\overrightarrow{S_1}={\displaystyle \frac{1}{8}}\overrightarrow{P_1}$ for the semi-ellipse in green.

5.

$\overrightarrow{X}=\overrightarrow{0}$ for the segment $\left[AB\right]$. The bounds are stationary points.

In case of $\overrightarrow{X}=\overrightarrow{0}$, the points $M\left(t\right)$ of the segment are defined by

$$\begin{array}{cc}\hfill \overrightarrow{OM\left(t\right)}=& {\displaystyle \frac{1}{B_{0,2}\left(t\right)+B_{2,2}\left(t\right)}\left(B_{0,2}\left(t\right)\overrightarrow{OA}+B_{1,2}\left(t\right)\overrightarrow{0}+B_{2,2}\left(t\right)\overrightarrow{OB}\right)}\hfill \\ \hfill =& {\displaystyle \frac{1}{{\left(1-t\right)}^{2\phantom{(}}+t^2}\left({\left(1-t\right)}^2\overrightarrow{OA}+t^2\overrightarrow{OB}\right)}\hfill \end{array}$$

(22)

where $t\in \left[0,1\right]$.

Using Corollaries 1 and 2, it yields

$${\displaystyle \frac{d}{dt}\overrightarrow{OM\left(0\right)}=\frac{d}{dt}\overrightarrow{OM\left(1\right)}=\overrightarrow{0}}$$

In this case, it is not possible to independently change the speed at endpoints. One answer is based on a quadratic parameter change described below.

3.3. Quadratic Parameter Change for Kinematic

Let $h_2$ be a quadratic parameter change defined by

$${\displaystyle h_2\left(u\right)=\frac{a{\left(1-u\right)}^2+2bu\left(1-u\right)+c{u}^2}{d{\left(1-u\right)}^2+2eu\left(1-u\right)+f{u}^2}}$$

(23)

and the Bézier curve of mass control points ${\left(P_i;{\omega }_i\right)}_{i\in \left[\right[0;n\left]\right]}$ is transformed into the Bézier curve of new mass control points ${\left(Q_i;{\varpi }_i\right)}_{i\in \left[\right[0;2n\left]\right]}.$ The Appendix B, Appendix C and Appendix D give the formulae to compute the new control mass points for a quadratic, cubic, and quartic curve. Consider first the conditions of not changing the curve’s endpoints, that is

$$\left\{\begin{array}{ccc}\hfill h_2\left(0\right)& =& 0\hfill \\ \hfill h_2\left(1\right)& =& 1\hfill \end{array}\right.$$

and the function $h_2$ is chosen to be continuous and, increasing on $\left[0,1\right]$, is given by

$${\displaystyle h_2\left(u\right)=\frac{2bu\left(1-u\right)+c{u}^2}{d{\left(1-u\right)}^2+2eu\left(1-u\right)+c{u}^2}.}$$

(24)

Table 3. Quadratic change function keeping the endpoints invariant, expressions of $h_2\left(u\right)$, and differential conditions.

Conditions	Expression of ${\mathit{h}}_2$, Formula (24)
${\left\{\begin{array}{ccc}\hfill {\displaystyle {\frac{d{h}_2}{du}}_{{\phantom{(}}_{{\phantom{(}}_{\phantom{(}}}}^{{\phantom{(}}^{{\phantom{(}}^{\phantom{(}}}}\left(0\right)}& =& 0\hfill \\ \hfill {\displaystyle {\frac{d{h}_2}{du}}_{{\phantom{(}}_{{\phantom{(}}_{\phantom{(}}}}^{{\phantom{(}}^{{\phantom{(}}^{\phantom{(}}}}\left(1\right)}& =& 0\hfill \end{array}\right.}_{{\phantom{(}}_{{\phantom{(}}_{\phantom{(}}}}^{{\phantom{(}}^{{\phantom{(}}^{\phantom{(}}}}$	${\displaystyle \frac{c{u}^2}{d{\left(1-u\right)}^2+c{u}^2}}$
${\left\{\begin{array}{ccc}\hfill {\displaystyle {\frac{d{h}_2}{du}}_{{\phantom{(}}_{{\phantom{(}}_{\phantom{(}}}}^{{\phantom{(}}^{{\phantom{(}}^{\phantom{(}}}}\left(0\right)}& =& 0\hfill \\ \hfill {\displaystyle {\frac{d{h}_2}{du}}_{{\phantom{(}}_{{\phantom{(}}_{\phantom{(}}}}^{{\phantom{(}}^{{\phantom{(}}^{\phantom{(}}}}\left(1\right)}& =& {\lambda }_1>0\hfill \end{array}\right.}_{{\phantom{(}}_{{\phantom{(}}_{\phantom{(}}}}^{{\phantom{(}}^{{\phantom{(}}^{\phantom{(}}}}$	${\displaystyle 2\frac{e^{{\phantom{(}}^{{\phantom{(}}^{\phantom{(}}}}}{{\lambda }_1}\frac{u^2}{{\displaystyle d{\left(1-u\right)}^2+2eu\left(1-u\right)+2{\frac{e}{{\lambda }_1}}_{{\phantom{(}}_{{\phantom{(}}_{\phantom{(}}}}^{{\phantom{(}}^{\phantom{(}}}{u}^2}}}$
${\left\{\begin{array}{ccc}\hfill {\displaystyle {\frac{d{h}_2}{du}}_{{\phantom{(}}_{{\phantom{(}}_{\phantom{(}}}}^{{\phantom{(}}^{{\phantom{(}}^{\phantom{(}}}}\left(0\right)}& =& {\lambda }_0>0\hfill \\ \hfill {\displaystyle {\frac{d{h}_2}{du}}_{{\phantom{(}}_{{\phantom{(}}_{\phantom{(}}}}^{{\phantom{(}}^{{\phantom{(}}^{\phantom{(}}}}\left(1\right)}& =& 0\hfill \end{array}\right.}_{{\phantom{(}}_{{\phantom{(}}_{\phantom{(}}}}^{{\phantom{(}}^{{\phantom{(}}^{\phantom{(}}}}$	${\displaystyle \frac{2bu\left(1-u\right)+c{u}^2}{{\displaystyle {\frac{2b}{{\lambda }_0}}_{{\phantom{(}}_{{\phantom{(}}_{\phantom{(}}}}^{{\phantom{(}}^{\phantom{(}}}{\left(1-u\right)}^2+2bu\left(1-u\right)+c{u}^2}}}$
${\left\{\begin{array}{ccc}\hfill {\displaystyle {\frac{d{h}_2}{du}}_{{\phantom{(}}_{{\phantom{(}}_{\phantom{(}}}}^{{\phantom{(}}^{{\phantom{(}}^{\phantom{(}}}}\left(0\right)}& =& {\lambda }_0>0\hfill \\ \hfill {\displaystyle {\frac{d{h}_2}{du}}_{{\phantom{(}}_{{\phantom{(}}_{\phantom{(}}}}^{{\phantom{(}}^{{\phantom{(}}^{\phantom{(}}}}\left(1\right)}& =& {\lambda }_1>0\hfill \end{array}\right.}_{{\phantom{(}}_{{\phantom{(}}_{\phantom{(}}}}^{{\phantom{(}}^{{\phantom{(}}^{\phantom{(}}}}$	${\displaystyle \frac{{\displaystyle 2bu\left(1-u\right)+2{\frac{e-b}{{\lambda }_1}}_{{\phantom{(}}_{\phantom{(}}}^{{\phantom{(}}^{{\phantom{(}}^{\phantom{(}}}}{u}^2}}{{\displaystyle {\frac{2b}{{\lambda }_0}}^{{\phantom{(}}^{\phantom{(}}}{\left(1-u\right)}^2+2eu\left(1-u\right)+2{\frac{e-b}{{\lambda }_1}}_{{\phantom{(}}_{{\phantom{(}}_{\phantom{(}}}}{u}^2}}}$

sums up the four quadratic change functions that keep the endpoints invariant. This will be applied in order to change the velocity vector at the endpoints.

At the start of this work, the authors showed how the mass points are obtained naturally in the definition of a rational curve with weighted points of any weight.

The representation can also include vectors that lead to infinity branches, considered as tangent lines at the starting endpoints.

In the present case, the curve of any representation power function is converted into a classical representation with Bernstein polynomials. The curve is contained in the convex hull of the control polygon.

In order to obtain a parabolic branch of such a curve, a homographic parameter change sends the segment $\left[0,1\right]$ into the segment $\left[0,+\infty \right]$. The parameter change results in the weighted points, pure vectors, and null vectors obtained from the rational Bézier representation.

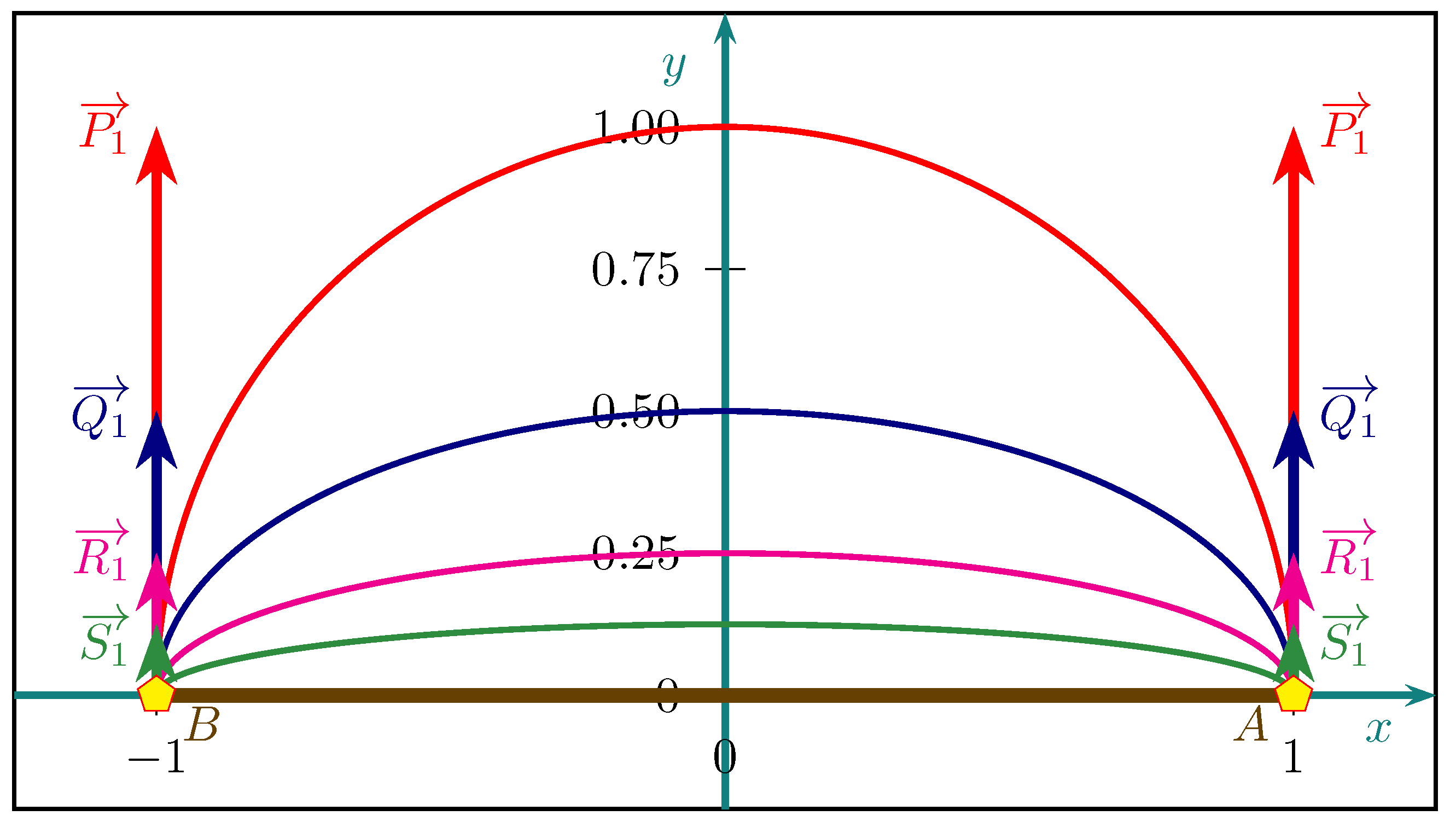
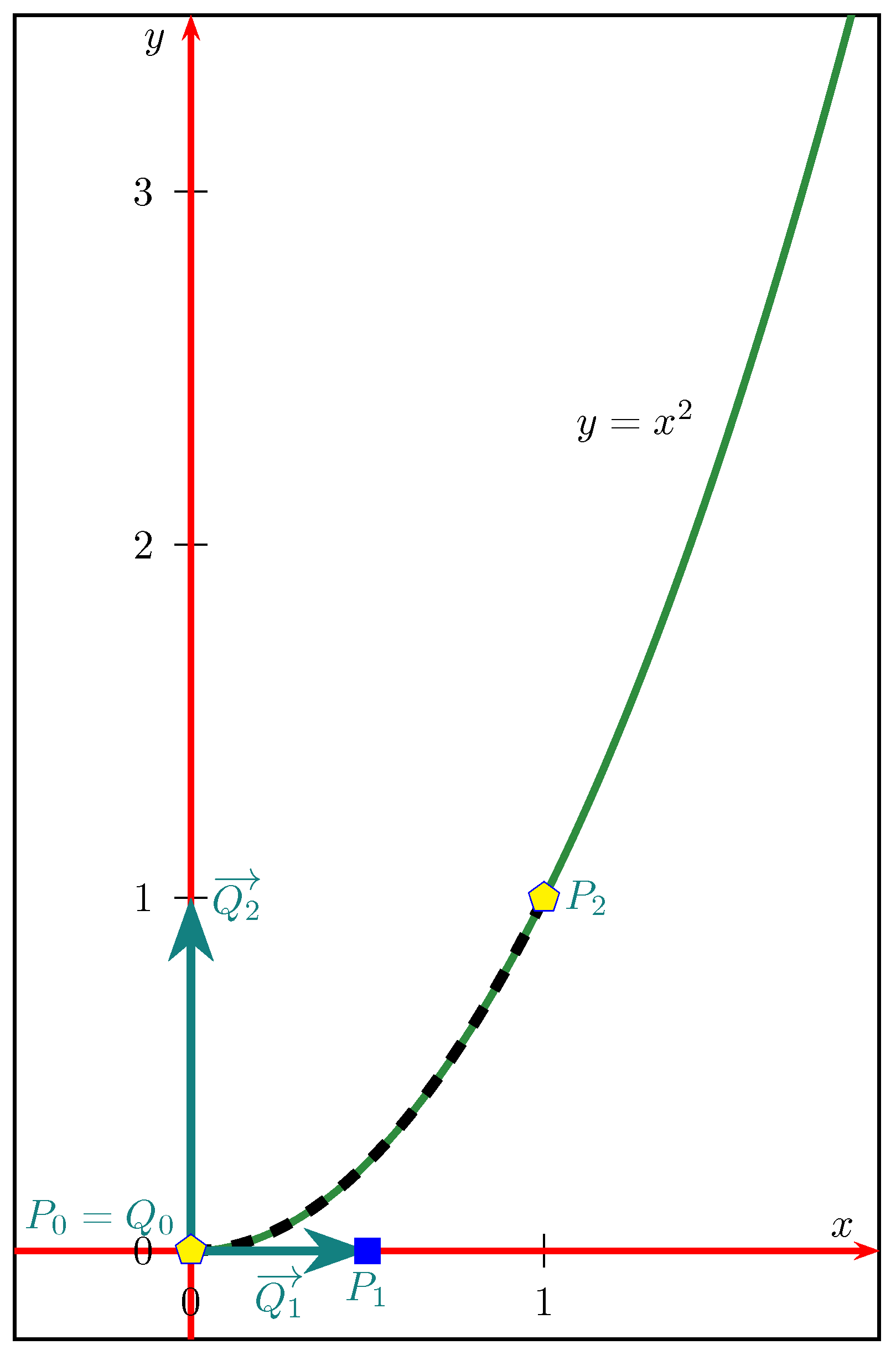
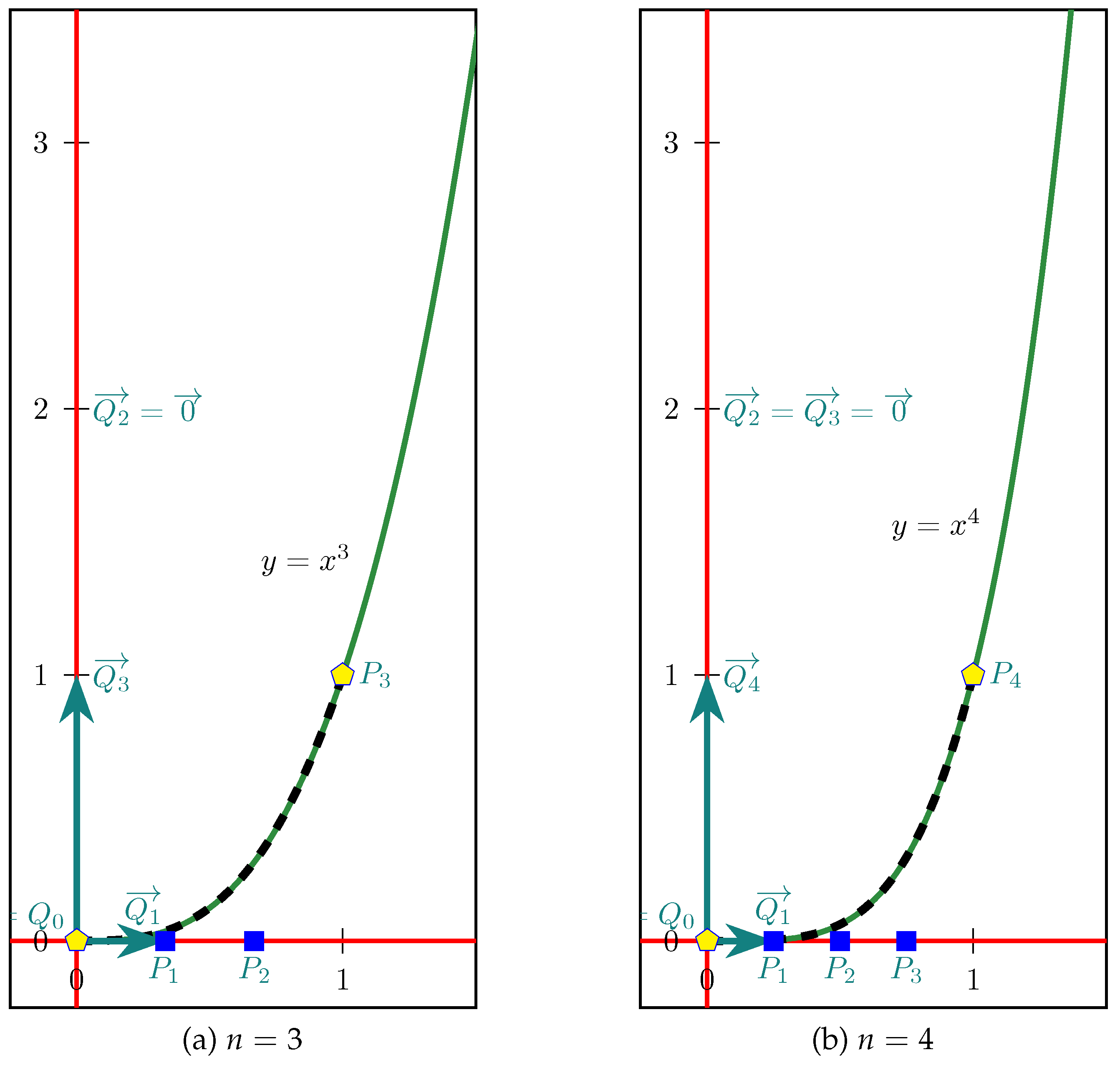
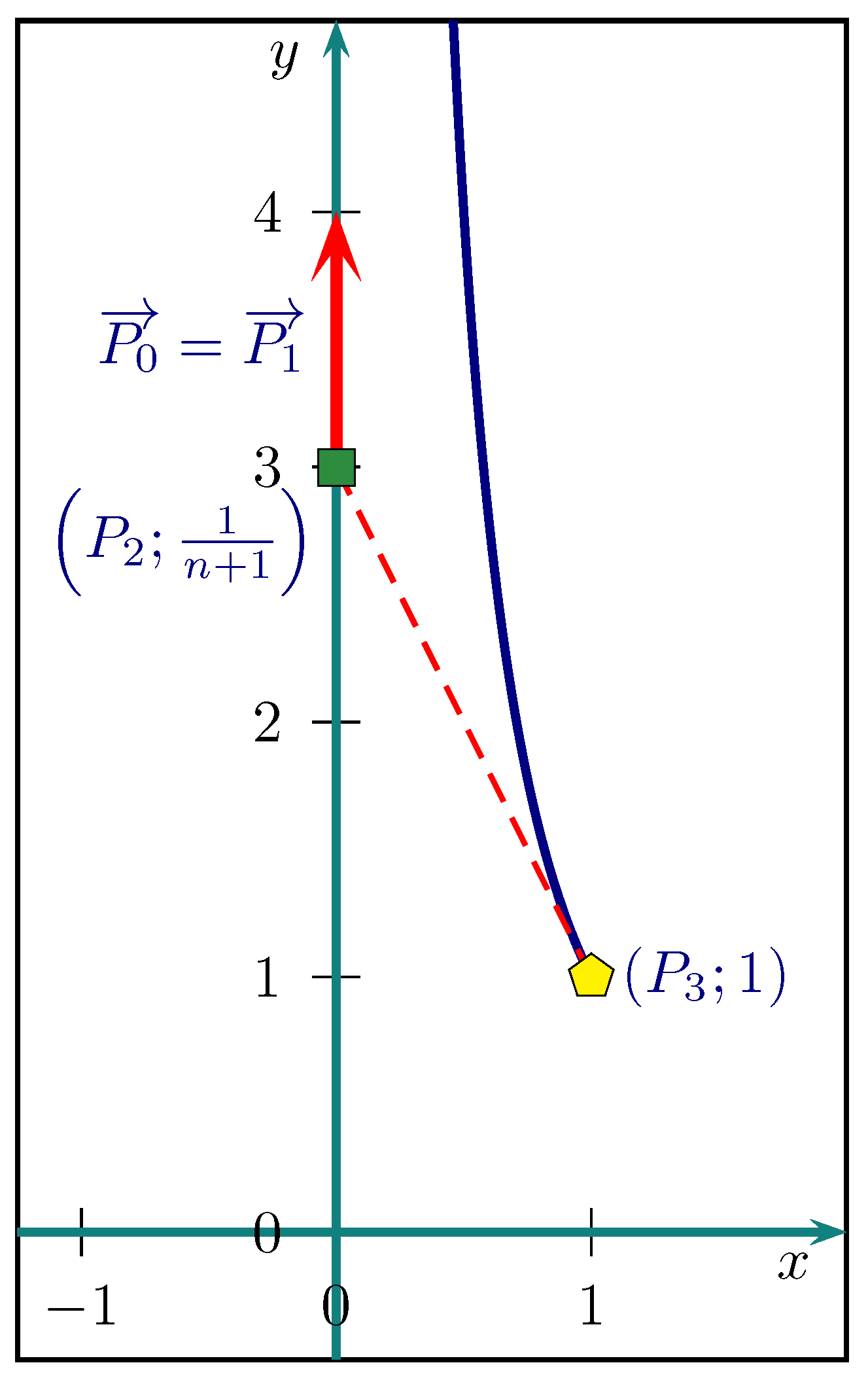
3.4. Multiple Vectors Performed in the Power Curve or the Inverse Power Curve

3.4.1. Multiple Null Vectors $\overrightarrow{0}$ Performed in the Power Curve

Let n be an integer greater than 2. Let f be the power function defined on ${\mathbb{R}}^{+}$ by

$$f\left(x\right)=x^n$$

(25)

Its parametric equation is given by

$$\left\{\begin{array}{ccccc}\hfill x\left(t\right)& =& t& =& {\displaystyle \sum _{k=0}^n{B}_{n,k}\left(t\right)\times \frac{k}{n}}\hfill \\ \hfill y\left(t\right)& =& t^n& =& B_{n,n}\left(t\right)\times 1\hfill \end{array}\right.,t\in \left[0;+\infty \right]$$

(26)

and then $P_0\left(0,0\right)$; $P_n\left(1,1\right)$; and for k in $\left[\right[1;n-1\left]\right]$, $P_k\left({\displaystyle \frac{k}{n}},0\right)$ (Figure 10 with $n=2$; Figure 11a with $n=3$; and Figure 11b with $n=4$).

As a Bézier curve is defined on $\left[0,1\right],$ the parameter change

$${\displaystyle t=\frac{u}{1-u}}$$

is applied and the parametric equation becomes

$$\left\{\begin{array}{ccccccc}\hfill x\left(u\right)& =& {\displaystyle \frac{u}{1-u}}& =& {\displaystyle \frac{u{\left(1-u\right)}^{n-1}}{{\left(1-u\right)}^n}}\hfill & =& {\displaystyle \frac{{\displaystyle \frac{1}{n}{B}_{1,n}\left(u\right)}}{B_{0,n}\left(u\right)}}\\ \hfill y\left(u\right)& =& {\displaystyle {\left(\frac{u}{1-u}\right)}^n}& =& {\displaystyle \frac{u^n}{{\left(1-u\right)}^n}}\hfill & =& {\displaystyle \frac{B_{n,n}\left(u\right)}{B_{0,n}\left(u\right)}}\end{array}\right.,$$

(27)

where ${\omega }_0=1$ and ${\omega }_1={\omega }_2=\cdots ={\omega }_n=0$ on one hand, and $Q_0\left(0;0\right)$, $\overrightarrow{Q_1}\left({\displaystyle \frac{1}{n}};0\right)$, and $\overrightarrow{Q_n}\left(0;1\right)$ on the other hand. If $n>2$, then

$$\overrightarrow{Q_2}=\cdots =\overrightarrow{Q_{n-1}}=\overrightarrow{0}$$

and $\overrightarrow{Q_1}$ is the tangent to the curve at $Q_0$, where the vector $\overrightarrow{Q_n}$ gives the direction of the parabolic branch. This is shown in Figure 10 with $n=2$; Figure 11a with $n=3$; $P_0$, $P_1$, $P_2$, and $P_3$ on one hand and $Q_0$, $\overrightarrow{Q_1},$$\overrightarrow{Q_2}=\overrightarrow{0}$, and $\overrightarrow{Q_3}$ on the other hand; and Figure 11b, with $n=4$, $P_0$, $P_1$, $P_2$, $P_3$, and $P_4$ on one hand and $Q_0$, $\overrightarrow{Q_1},$$\overrightarrow{Q_2}=\overrightarrow{Q_3}=\overrightarrow{0}$, and $\overrightarrow{Q_4}$ on the other hand.

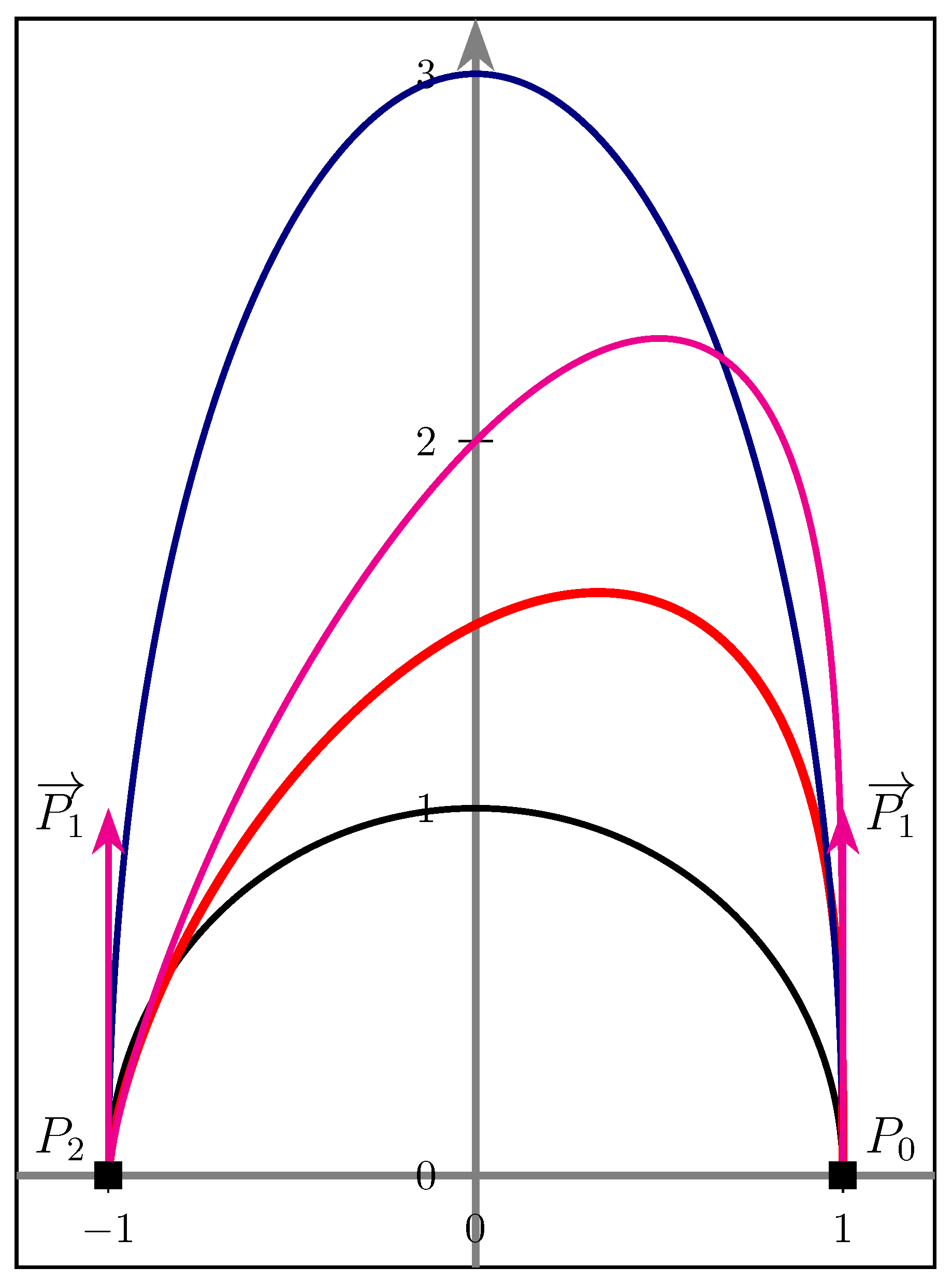
3.4.2. An Example of a Bounded Area

The following choices define a quartic rational Bézier curve (see Figure 12):

• weights ${\omega }_2={\omega }_3={\omega }_4=0$ and ${\omega }_0={\omega }_1=1$;
• vectors $\overrightarrow{P_2}\left(0;0\right)$, $\overrightarrow{P_3}\left(0;0\right)$, $\overrightarrow{P_4}\left(0;1\right)$;
• and points $P_0\left(-1;1\right)$ and $P_1\left(0;1\right)$.

And the parametric equation is given by

$$\left\{\begin{array}{ccc}\hfill x\left(t\right)& =& {\displaystyle \frac{t^4-4t^3+6t^2-4t+1}{3t^4-8t^3+6t^2-1}}\hfill \\ \hfill y\left(t\right)& =& {\displaystyle \frac{2t^4-8t^3+6t^2-1}{3t^4-8t^3+6t^2-1}}\hfill \end{array}\right.$$

(28)

with

$${\displaystyle x=\frac{t^4-4t^3+6t^2-4t+1}{3t^4-8t^3+6t^2-1}.}$$

The value t becomes

$${\displaystyle t=\frac{x+1}{-3x+1}}$$

which is derived from the following rational expression:

$${\displaystyle f\left(x\right)=\frac{-x^4+252x^3-6x^2-4x-1}{256x^3}.}$$

Without the two null vectors, the expression becomes

$${\displaystyle f\left(x\right)=\frac{-{\left(x-1\right)}^2}{4x}.}$$

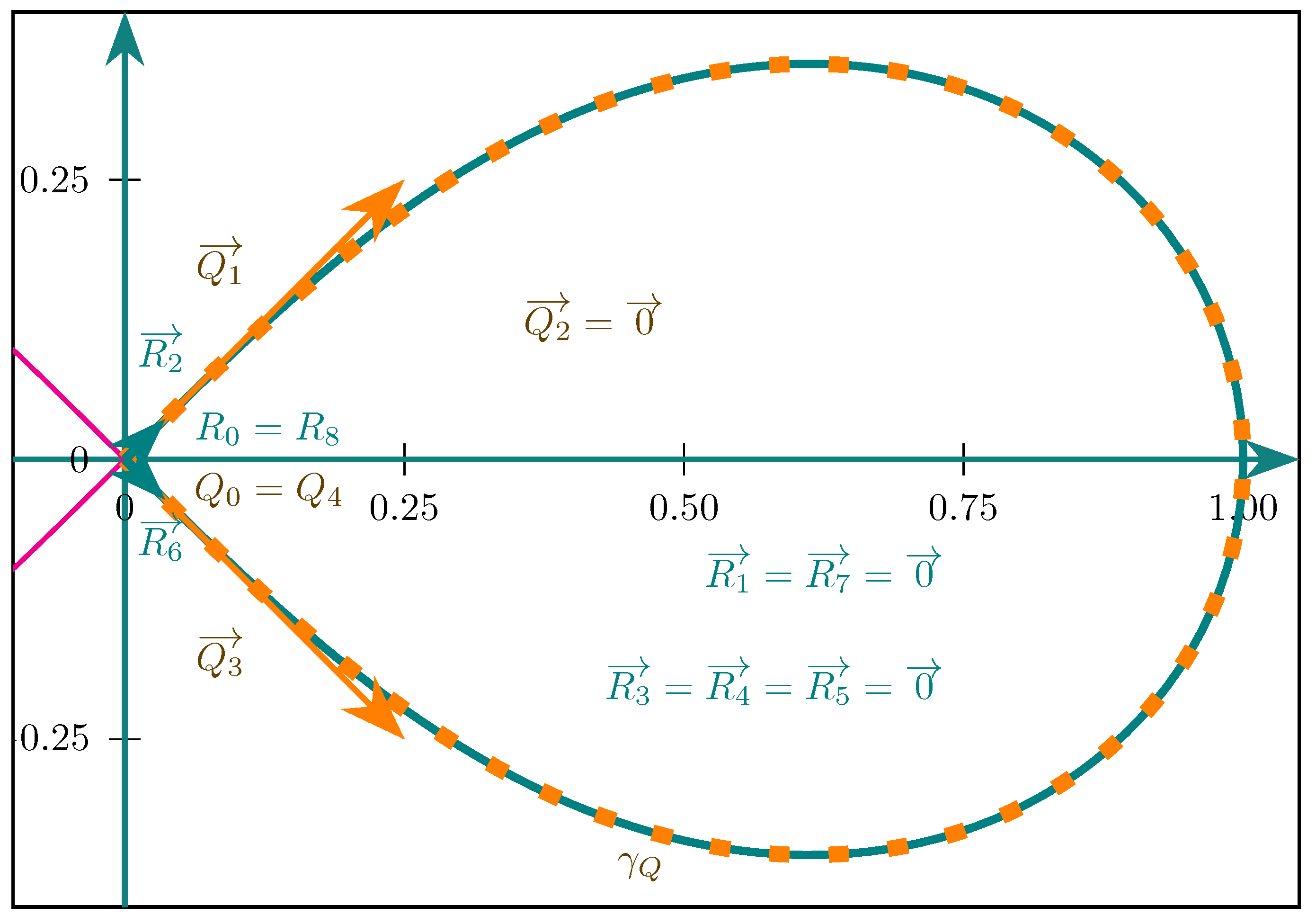
3.4.3. Multiple Vectors in the Inverse Power Curve

The inverse function defined by $x\mapsto {\displaystyle \frac{1}{x^n}}$ has the following parametric representation:

$$\left\{\begin{array}{ccccc}\hfill x\left(t\right)& =& t& =& {\displaystyle \frac{t^{n+1}}{t^n}}\hfill \\ \hfill y\left(t\right)& =& {\displaystyle \frac{1}{t^n}}& \end{array}\right.,t\in \left[0;1\right]$$

(29)

Thus, the point $M\left(t\right)$ of the rational Bézier representation is defined by

$$\overrightarrow{OM\left(t\right)}={\displaystyle \frac{1}{{\displaystyle \sum _{i=n}^{n+1}{\omega }_i{B}_{i,n+1}\left(t\right)}}}\left({\displaystyle \sum _{i=0}^{n-1}{B}_{i,n+1}\left(t\right)\overrightarrow{P_i}+\sum _{i=n}^{n+1}{\omega }_i{B}_{i,n+1}\left(t\right)\overrightarrow{O{P}_i}}\right)$$

where ${\omega }_i=0$ and $\overrightarrow{P_i}(0,1)$ for $i\in \left[\right[0;n-1\left]\right]$, ${\omega }_n={\displaystyle \frac{1}{n+1}}$, $P_n(0,n+1)$, ${\omega }_{n+1}=1$ and $P_{n+1}(1,1)$ (see Figure 13 with $n=2$).

3.5. Stationary Points and Null Vectors

This section deals with stationary points of a mass Bézier curve. Null mass points or collinear vectors are added to the BR representation of a mass curve. Increasing the degree of the curve does not change the control endpoints but can give them the status of stationary points. The example in Figure 14 illustrates this case.

Consider a black circular arc in the drawing defined by the quadratic rational Bézier curve of mass control points:

$$\left(P_0;1\right), \left(\overrightarrow{P_1};0\right), \mathrm{and} \left(P_2;1\right).$$

Adding a null vector defines a cubic rational Bézier curve, shown in red in the drawing. It has the following mass control points:

$$\left(P_0;1\right), \left(\overrightarrow{P_1};0\right), \left(\overrightarrow{0};0\right), \mathrm{and} \left(P_2;1\right).$$

The blue drawing shows a quartic rational Bézier curve with the following mass control points:

$$\left(P_0;1\right), \left(\overrightarrow{0};0\right), \left(\overrightarrow{P_1};0\right), \left(\overrightarrow{0};0\right) \mathrm{and} \left(P_2;1\right).$$

Finally, the magenta drawing shows another quartic rational Bézier curve with the following mass control points:

$$\left(P_0;1\right), \left(\overrightarrow{P_1};0\right), \left(\overrightarrow{0};0\right), \left(\overrightarrow{0};0\right), \mathrm{and} \left(P_2;1\right).$$

3.6. Segment and Kinematics

Let A and B be two distinct points. In Formula (20), to obtain stationary points at A and B, the change in variable from Table 3 with $c=1$ and $d=1$ gives

$${\displaystyle t=\frac{u^2}{{\left(1-u\right)}^{2^{{\phantom{(}}^{\phantom{(}}}}+u^2}}$$

for $t\in \left[0;1\right]$, the points $M\left(t\right)$ of $\left[AB\right]$ are defined by

$${\displaystyle \overrightarrow{OM\left(t\right)}=\frac{{\left(1-u\right)}^2}{{\left(1-u\right)}^{2^{{\phantom{(}}^{\phantom{(}}}}+u^2}\overrightarrow{OA}+\frac{u^{2^{{\phantom{(}}^{\phantom{(}}}}}{{\left(1-u\right)}^{2^{{\phantom{(}}^{\phantom{(}}}}+u^2}\overrightarrow{OB}}$$

(30)

and the segment $\left[AB\right]$ is modeled by the rational Bézier curve with mass control points $\left(A;1\right)$, $\left(\overrightarrow{0};0\right)$, and $\left(B;1\right)$.

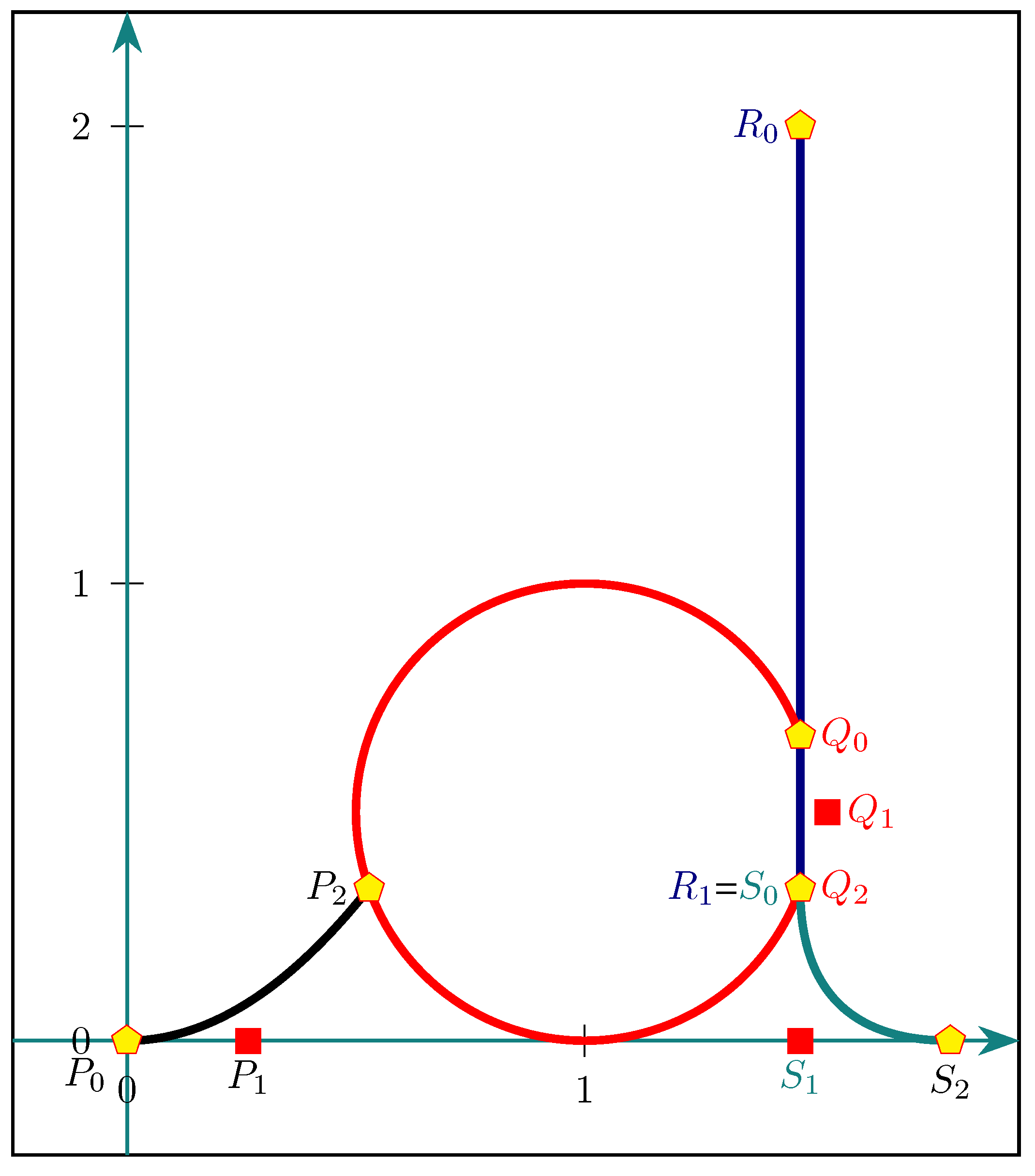
4. Examples of Two Stationary Endpoints

The choice of $a=0$, $f=c$, and the calculations are easier with $c=d=1$ and $b=e=0$. This gives $h_2\left(\left[0;1\right]\right)=\left[0;1\right]$ and the points for $t=0$ and $t=1$ become two stationary endpoints. From a Bézier curve with mass control points $\left(P_0,{\omega }_0\right)$, ⋯ and $\left(P_n,{\omega }_n\right)$, the new Bézier curve verifies

$$\left(Q_1,{\varpi }_1\right)=\left(Q_{2n-1},{\varpi }_{2n-1}\right)=\left(\overrightarrow{0},0\right).$$

Some examples of degrees 2 and 4 are as follows.

4.1. Case of Quadratic Curves

Let $\gamma$ be a quadratic Bézier curve of mass control points $\left(P_0;{\omega }_0\right)$, $\left(P_1;{\omega }_1\right)$, and $\left(P_2;{\omega }_2\right)$, with support from the conic C. Let $h_2$ be defined by Formula (23), then $\gamma \circ h_2$ is the quartic Bézier curve of control mass points $\left(Q_0;{\varpi }_0\right)$, $\left(Q_1;{\varpi }_1\right)$, $\left(Q_2;{\varpi }_2\right)$, $\left(Q_3;{\varpi }_3\right)$, and $\left(Q_4;{\varpi }_4\right)$ with support from the conic C, where

$$\left\{\begin{array}{ccc}\left(Q_0;{\varpi }_0\right)& =& \left(P_0;{\omega }_0\right)\\ \left(Q_1;{\varpi }_1\right)& =& \left(\overrightarrow{0};0\right)\\ \left(Q_2;{\varpi }_2\right)& =& {\displaystyle \frac{1}{3}\odot \left(P_1;{\omega }_1\right)}\\ \left(Q_3;{\varpi }_3\right)& =& \left(\overrightarrow{0};0\right)\\ \left(Q_4;{\varpi }_4\right)& =& \left(P_2;{\omega }_2\right)\end{array}\right..$$

(31)

All of these results are applied to a quarter circle and a semicircle.

4.1.1. Quarter Circle Case

Figure 15 illustrates the quarter circle of the following equation:

$$x^2+y^2=4$$

in the first quadrant. The control points of the quadratic Bézier curve are given by $\left(P_0;1\right)$, $\left(P_1;1\right)$ and $\left(P_2;2\right)$ with $P_0\left(2;0\right)$, $P_1\left(2;2\right)$ and $P_2\left(0;2\right)$. Applying expressions in Formula (31), the control points of the quartic Bézier curve are thus calculated as $\left(P_0;1\right)$, $\left(\overrightarrow{0};0\right)$, $\left(P_1;{\displaystyle \frac{1}{3}}\right)$, $\left(\overrightarrow{0};0\right)$, and $\left(P_2;2\right)$.

4.1.2. Half a Circle Case

In Figure 16, the control points of the quadratic Bézier curve are given by $\left(P_0;1\right)$, $\left(\overrightarrow{P_1};0\right)$ and $\left(P_2;1\right)$ with $P_0\left(2;0\right)$, $\overrightarrow{P_1}\left(0;2\right)$ and $P_2\left(-2;0\right)$. Via Formula (31), the control points of the quartic Bézier curve are given by $\left(Q_0;1\right)=\left(P_0;1\right)$, $\left(\overrightarrow{Q_1};0\right)=\left(\overrightarrow{0};0\right)$, $\left(\overrightarrow{Q_2};0\right)=\left({\displaystyle \frac{1}{3}}\overrightarrow{P_1};0\right)$, $\left(\overrightarrow{Q_3};0\right)=\left(\overrightarrow{0};0\right)$ and $\left(Q_4;1\right)=\left(P_2;0\right)$.

4.2. Case of a Quartic Curve

In the quartic case, starting from Theorem A3 and the function $h_2$ with $a=0$, $f=c$, $c=d=1$, and $b=e=0$, the following Corollary is given.

Corollary 3.

From a quadratic Bézier curve γ of control mass points $\left(P_0;{\omega }_0\right)$, $\left(P_1;{\omega }_1\right)$, $\left(P_2;{\omega }_2\right)$, $\left(P_3;{\omega }_3\right)$ and $\left(P_4;{\omega }_4\right)$, supporting the quartic $C$, the mass control points of the new 8th-degree Bézier curve are

$$\begin{array}{ccc}\left(Q_0;{\varpi }_0\right)& =& \left(P_0;{\omega }_0\right)\end{array}$$

(32)

$$\begin{array}{ccc}\left(Q_1;{\varpi }_1\right)& =& \left(\overrightarrow{0};0\right)\end{array}$$

(33)

$$\begin{array}{ccc}\left(Q_2;{\varpi }_2\right)& =& {\displaystyle \frac{1}{7}⊡\left(P_1;{\omega }_1\right)}\end{array}$$

(34)

$$\begin{array}{ccc}\left(Q_3;{\varpi }_3\right)& =& \left(\overrightarrow{0};0\right)\end{array}$$

(35)

$$\begin{array}{ccc}\left(Q_4;{\varpi }_4\right)& =& {\displaystyle \frac{3}{35}⊡\left(P_2;{\omega }_2\right)}\end{array}$$

(36)

$$\begin{array}{ccc}\left(Q_5;{\varpi }_5\right)& =& \left(\overrightarrow{0};0\right)\end{array}$$

(37)

$$\begin{array}{ccc}\left(Q_6;{\varpi }_6\right)& =& {\displaystyle \frac{1}{7}⊡\left(P_3;{\omega }_3\right)}\end{array}$$

(38)

$$\begin{array}{ccc}\left(Q_7;{\varpi }_7\right)& =& \left(\overrightarrow{0};0\right)\end{array}$$

(39)

$$\begin{array}{ccc}\left(Q_8;{\varpi }_8\right)& =& \left(P_4;{\omega }_4\right)\end{array}$$

(40)

4.3. Case of Canonical Bernouilli Lemniscate

The Bernouilli Lemniscate of parameter d has an equation given by

$$\left\{\begin{array}{ccc}\hfill x\left(t\right)& =& {\displaystyle d\sqrt{2}\frac{t+t^3}{1+t^4}}\hfill \\ \hfill y\left(t\right)& =& {\displaystyle d\sqrt{2}\frac{t-t^3}{1+t^4}}\hfill \end{array}\right.$$

(41)

and the point $O\left(0;0\right)$ is a triple point obtained by 0, $+\infty$, and $-\infty$. Using $d={\displaystyle \frac{\sqrt{2}}{2}}$, Equation (41) becomes

$$\left\{\begin{array}{ccc}\hfill x\left(t\right)& =& {\displaystyle \frac{{\displaystyle \frac{1}{4_{\phantom{(}}}{B}_1\left(t\right)+\frac{1}{2}{B}_2\left(t\right)+B_3\left(t\right)+2B_4\left(t\right)}}{B_0\left(t\right)+B_1\left(t\right)+B_2\left(t\right)+B_3\left(t\right)+2B_4\left(t\right)}}\hfill \\ \hfill y\left(t\right)& =& {\displaystyle \frac{{\displaystyle \frac{1}{4_{\phantom{(}}}{B}_1\left(t\right)+\frac{1}{2}{B}_2\left(t\right)+\frac{1}{2}{B}_3\left(t\right)}}{B_0\left(t\right)+B_1\left(t\right)+B_2\left(t\right)+B_3\left(t\right)+2B_4\left(t\right)}}\hfill \end{array}\right.$$

and its representation for $t\in \left[0;1\right]$ is the quartic Bézier curve ${\gamma }_P$ of control mass points $\left(P_0\left(0,0\right),1\right)$, $\left(P_1\left({\displaystyle \frac{1}{4}},{\displaystyle \frac{1}{4}}\right),1\right)$, $\left(P_2\left({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}}\right),1\right)$, $\left(P_3\left(1,{\displaystyle \frac{1}{2}}\right),1\right)$, and $\left(P_4\left(1,0\right)2\right)$. Figure 17 shows the Bernoulli Lemniscate and the Bézier curve ${\gamma }_P$.

To obtain the loop of the Bernoulli Lemniscate located in the positive abscissa half-plane, i.e., $t\in \left[0;+\infty \right]$ in Equation (41), we apply ${\gamma }_P$, the homographic parameter change, with parameters $a=d=0$ and $b=c=1$, to obtain the quartic rational Bézier curve rationnelle quartique ${\gamma }_Q$ of mass control points $\left(Q_0\left(0,0\right),1\right)$, $\left(\overrightarrow{Q_1}\left({\displaystyle \frac{1}{4}},{\displaystyle \frac{1}{4}}\right),0\right)$, $\left(\overrightarrow{0_2},0\right)$, $\left(\overrightarrow{Q_3}\left({\displaystyle \frac{1}{4}},-{\displaystyle \frac{1}{4}}\right),0\right)$, and $\left(Q_4\left(0,0\right),1\right)$. Figure 18 shows the arc of the Bernoulli Lemniscate for $t\in \left[0;1\right]$ by the quadratic rational Bézier curves ${\gamma }_P$ and ${\gamma }_Q$.

By applying Corollary 3 to the curve ${\gamma }_Q$, we obtain the degree 8 rational Bézier curve ${\gamma }_R$ the 8th degree of control points: $\left(R_0\left(0,0\right),1\right)$, $\left(\overrightarrow{R_1}=\overrightarrow{0_1};0\right)$, $\left(\overrightarrow{R_2}\left({\displaystyle \frac{1}{28}},{\displaystyle \frac{1}{28}}\right),0\right)$, $\left(\overrightarrow{R_3}=\overrightarrow{0_3},0\right)$, $\left(\overrightarrow{R_4}=\overrightarrow{0_4},0\right),$ $\left(\overrightarrow{R_5}=\overrightarrow{0_5},0\right)$, $\left(\overrightarrow{R_6}\left({\displaystyle \frac{1}{28}},-{\displaystyle \frac{1}{28}}\right),0\right)$, $\left(\overrightarrow{R_7}=\overrightarrow{0_7};0\right)$, and $\left(R_8\left(0,0\right);1\right)$. Figure 19 shows a loop of the Lemniscate by the degree 8 rational Bézier curve ${\gamma }_R$ with two stationary extreme points, of control points obtained from the quadratic rational Bézier curve $\left(R_0;1\right)$ $\left(\overrightarrow{R_1};0\right)=\left(\overrightarrow{0};0\right)$, $\left(\overrightarrow{R_2};0\right)$, $\left(\overrightarrow{R_3};0\right)=\left(\overrightarrow{0};0\right)$, $\left(\overrightarrow{R_4};0\right)=\left(\overrightarrow{0};0\right),$ $\left(\overrightarrow{R_5};0\right)=\left(\overrightarrow{0};0\right)$, $\left(\overrightarrow{R_6};0\right)$, $\left(\overrightarrow{R_7};0\right)=\left(\overrightarrow{0};0\right)$ and $\left(R_8;1\right)$ obtained from the quadratic rational Bézier curve ${\gamma }_Q$ of control points $\left(Q_0;1\right)$, $\left(\overrightarrow{Q_1};0\right)$, $\left(\overrightarrow{Q_2};0\right)=\left(\overrightarrow{0};0\right)$, $\left(\overrightarrow{Q_3};0\right)$ and $\left(Q_4;1\right)$ avec $\overrightarrow{Q_2}=\overrightarrow{0}$.

Construction of the Letter d

Figure 20 shows the letter d defined by four curves:

1.

${\gamma }_P$ is an arc of a parabola, and the control mass points of the quadratic Bézier curve are $\left(P_0\left(0;0\right),1\right)$, $\left(P_1\left(0.264;0\right),1\right)$ and $\left(P_2\left(0.529;0.333\right),1\right)$;

2.

${\gamma }_Q$ is an arc of a circle, and the three control mass points of the quadratic Bézier curve are $\left(Q_0\left(1.471;0.667\right),1\right)$, $\left(Q_1\left(1.530;0.5\right),-0.943\right)$ and $\left(Q_2\left(1.471;0.333\right),1\right)$;

3.

${\gamma }_R$ is the segment, and the control mass points of the Bézier curve of degree are $\left(R_0\left(1.471;2\right),1\right)$ and $\left(R_1\left(1.471;0.333\right),1\right)$;

4.

${\gamma }_S$ is an arc of a parabola, and the control mass points of the quadratic Bézier curve are $\left(S_0\left(1.471;0.333\right),1\right)$, $\left(S_1\left(1.471;0\right),1\right)$ and $\left(S_2\left(1.8;0\right),1\right)$.

From Figure 20, Figure 21 shows the modeling of the letter ’d’, taking into account the kinetics of the tracing:

1.

${\gamma }_T$ is an arc of a parabola and the control mass points of the quartic Bézier curve are $\left(T_0\left(0,0\right),1\right)$, $\left(\overrightarrow{T_1}\left(0,0\right),0\right)$, $\left(T_2\left(0.264,0\right),{\displaystyle \frac{1}{3}}\right)$, $\left(\overrightarrow{T_3}\left(0,0\right),0\right)$ and $\left(T_4\left(0.529,{\displaystyle \frac{1}{3}}\right),1\right)$;

2.

${\gamma }_U$ is an arc of a circle and the five control mass points of the quartic Bézier curve are $\left(U_0\left(1.471,{\displaystyle \frac{2}{3}}\right),1\right)$, $\left(\overrightarrow{U_1}\left(0,0\right),0\right)$, $\left(U_2\left(1.530,0.5\right),-0.314\right)$, $\left(\overrightarrow{U_3}\left(0,0\right),0\right)$ and $\left(U_4\left(1.471,{\displaystyle \frac{1}{3}}\right),1\right)$;

3.

The control mass points of the cubic Bézier curve ${\gamma }_V$ are $\left(V_0\left(1.471,2\right),1\right)$, $\left(\overrightarrow{V_1}\left(0;0\right),0\right)$, $\left(V_2\left(1.471,{\displaystyle \frac{4}{3}}\right),1\right)$ and $\left(V_3\left(1.471,{\displaystyle \frac{1}{3}}\right),3\right)$;

4.

${\gamma }_W$ is a parabola arc and the control mass points of the quartic Bézier curve are $\left(W_0\left(1.471,{\displaystyle \frac{1}{3}}\right),1.778\right)$, $\left(W_1\left(1.471,0\right),{\displaystyle \frac{4}{3}}\right)$, $\left(W_2\left(1.789,0\right),1.111\right)$, $\left(W_3\left(2,0\right),1\right)$ and $\left(W_4\left(2,0\right),1\right)$.

5. Conclusions and Perspectives

In this article, we focused on the influence of the null vector $\overrightarrow{0}$ as a control point of a Bézier curve. This vector allows us, without changing the curve and using a quadratic parameter change, to focus on the kinematics of the trace of a curve, and thus, to create ${\mathrm{G}}^0$ as well as ${\mathcal{C}}^1$ joints between two curves at a stationary point. The last point of the first curve is the first point of the second curve; the velocity vectors at these points are the null vectors; the tangents of the two curves at this junction point are not necessarily the same. Moreover, if the tangents are the same, the joint is ${\mathrm{G}}^1$. The influence of the null vector $\overrightarrow{0}$ is then studied on the convergence of the Bézier curve to an asymptote or in an asymptotic direction. In the near future, we plan to study the influence of the null vector at a finite point and on the creation of inflection points. We then plan to use this work in the kinematics of handwriting and introduce the use of complex mass points.