Curved Geometries in Persistent Homology: From Euclidean to AdS Metrics in Bow Echo Dynamics
Abstract
1. Introduction
- The Euclidean metric , commonly used in TDA but sensitive to scale and local noise.
- A bounded AdS-inspired metric:
2. Theoretical Framework
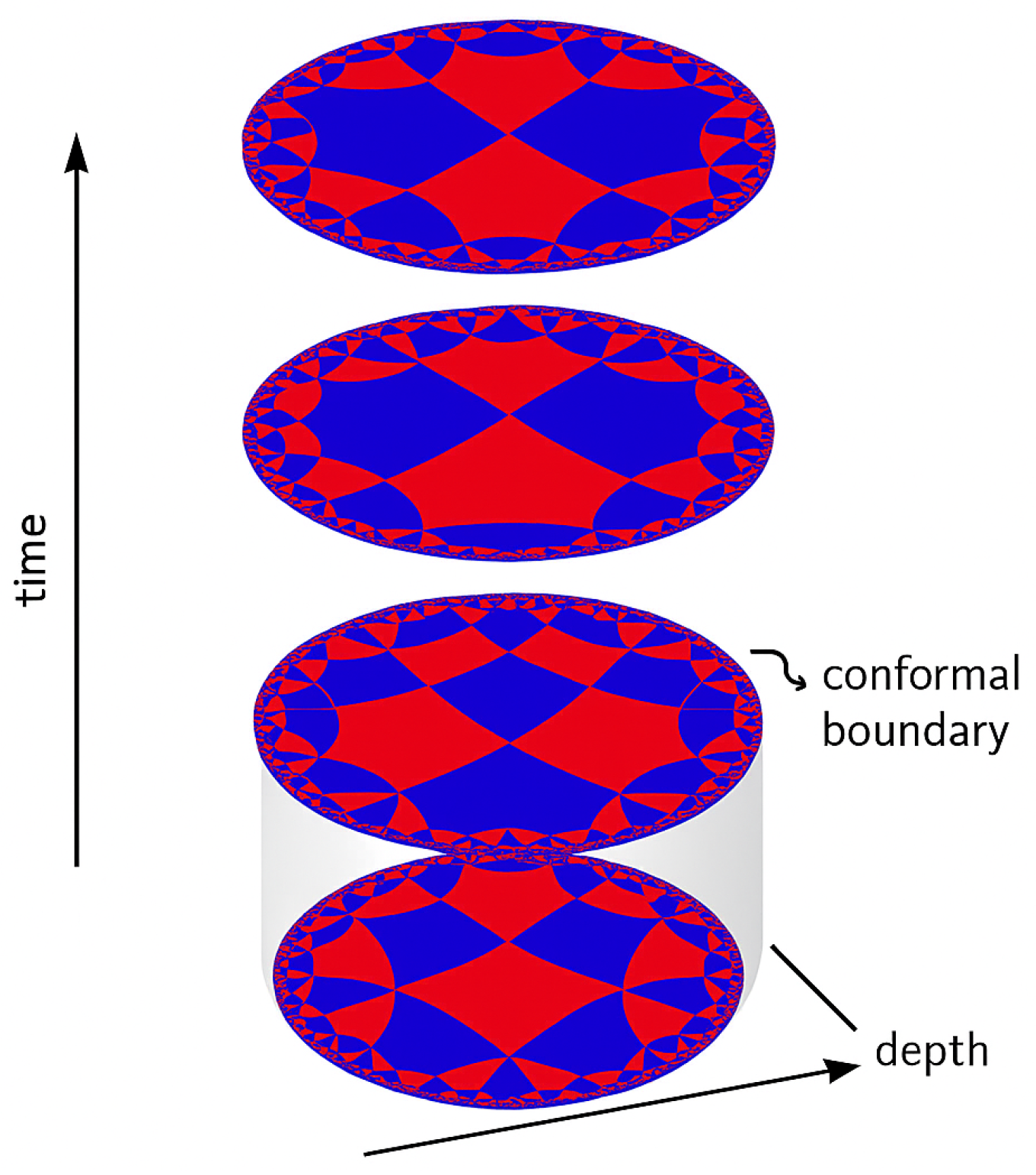
2.1. Physical Background: ADS-CFT Correspondance
2.1.1. Review of Anti-de Sitter Space: Geometry of AdSd+1
2.1.2. Examples of Holographic Phenomena
- Quark-gluon plasma: the holographic evaluation of the viscosity-to-entropy ratio remarkably matches RHIC measurements.
- Holographic superconductors: the Hartnoll–Herzog–Horowitz (2008) model produces a type II phase transition via the condensation of a charged scalar field in AdS4.
- Fluid/gravity duality: long-wavelength perturbations of the AdS5 metric map to relativistic hydrodynamics on the boundary.
- Entanglement entropy: the Ryu–Takayanagi formula () generalizes black hole thermodynamics to out-of-equilibrium quantum systems.
2.2. Mathematical Backgroud
Simplicial Homology
2.3. Topological Data Analysis
2.3.1. Nerve of a Cover and Simplicial Complex
2.3.2. Persistence Module
2.3.3. Vietoris–Rips Complex Construction
- Each data point in X is a vertex (0-simplex).
- A k-simplex is included for any points if every pair satisfies
2.3.4. Filtration and Persistent Homology
2.3.5. Persistence Diagrams
- : the scale at which the i-th k-dimensional feature appears (is born).
- : the scale at which it disappears (dies).

2.3.6. Stability and Comparison: Wasserstein Distances
2.4. Metrics
2.4.1. Euclidean Metric
2.4.2. Continuity of the AdS Metric
2.4.3. Topological Consequences of the AdS-Inspired Metric
2.4.4. Continuity and Lipschitz Behavior
- Continuous on , as the denominator is strictly positive;
- Strictly increasing, since ;
- Concave, since .
2.4.5. Stability of Persistence Diagrams Under the AdS Metric
Stability Theorem
Application to the AdS Metric
2.4.6. Scale Invariance and Topological Sensitivity
2.4.7. Compatibility with Vietoris–Rips Filtration
- Symmetry: ;
- Positivity: and ;
- Triangle inequality: ;
- Continuity (optional for stability, but not for definition).
2.4.8. Computational Methodology
3. Comparative Analysis of Euclidean and Ads Metrics for Arc and Cells
3.1. Pipeline Overview
- Contour extraction: From each radar frame, we obtain a binary contour of the target structure (arc or internal cells) using standard image processing steps (thresholding, edge detection).
- Point-cloud generation: The extracted contours are converted into 2D point clouds that represent the geometry of the meteorological object at a given time.
- Metric assignment: Each point cloud is endowed with a metric, either the classical Euclidean distance or the bounded AdS-inspired distance.
- Vietoris–Rips filtration: A Vietoris–Rips filtration is built on the resulting metric space, encoding the evolution of topology across scales.
- Persistent-homology computation: Persistence diagrams (and barcode lifetimes) are computed from the filtration, capturing connected components, loops, and cavities—features that often reflect spatial separation or internal organization.
- Time series construction: The lifetimes of persistent features are tracked across successive radar timestamps to form topological time series for both the arc and the internal cells.
- Topological interaction via cross-correlation: These time series are cross-correlated to quantify temporal alignment and asymmetry between arc and cell topologies, revealing potential causal influence or sequential activation.
- Differential indicator and alert triggering: A topological differential indicator is computed at each time step from the Wasserstein distance between the arc and cell persistence diagrams. When exceeds a learned threshold , a structural reconfiguration is detected and an early-warning alert is issued.
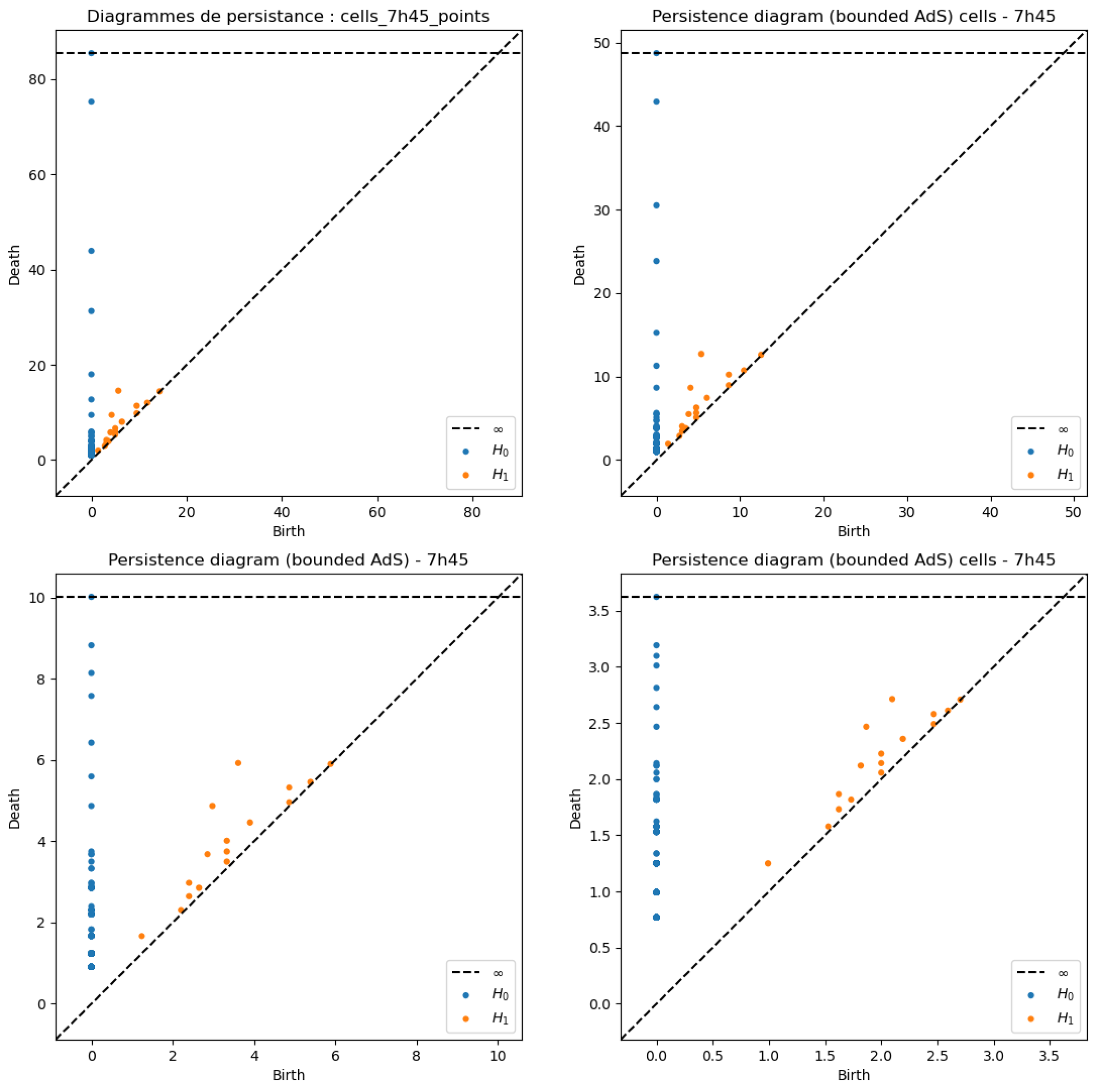
3.2. Persistence Diagrams
3.2.1. Comparative Analysis of Persistence Diagrams Across Metrics and Time
3.2.2. Temporal Analysis of Persistence Diagrams for the Arc (AdS, )
3.2.3. Temporal Analysis of Persistence Diagrams for the Cells (AdS, )
3.3. Metric Induced Scaling Effects in Persistence Diagrams
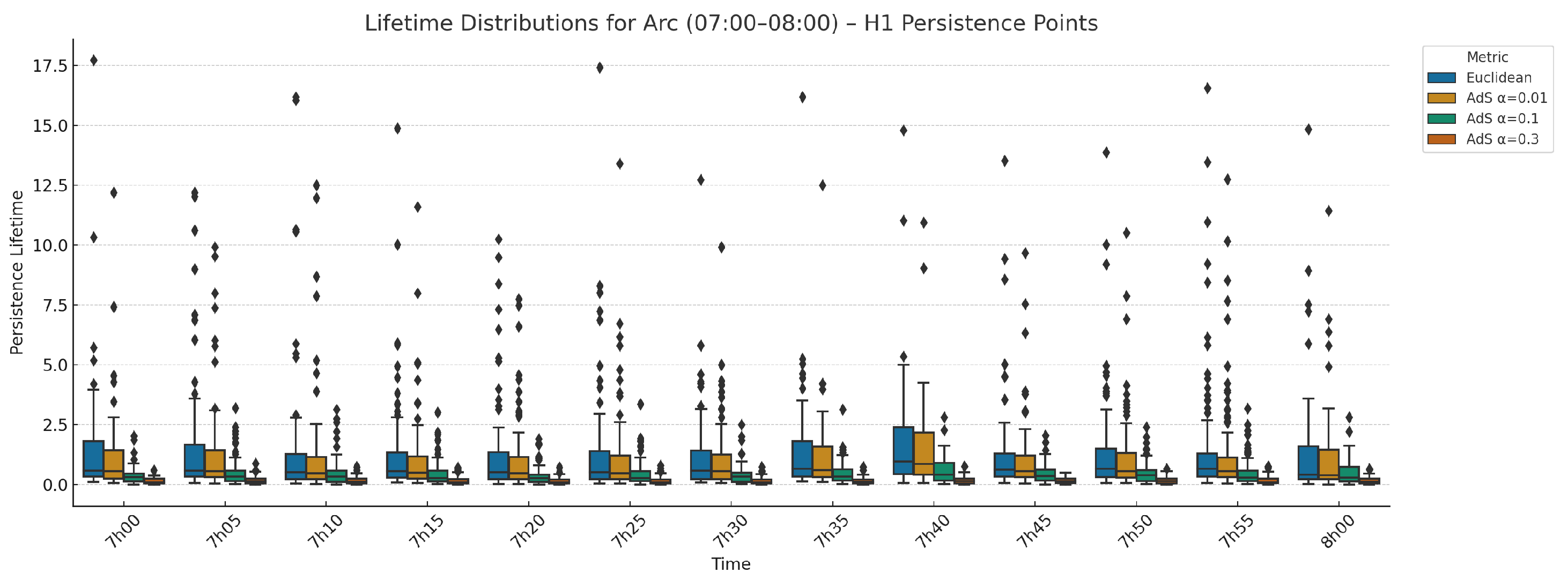
3.4. Lifetime Analysis
3.5. Temporal Evolution of Lifetimes for the Arc (AdS, )
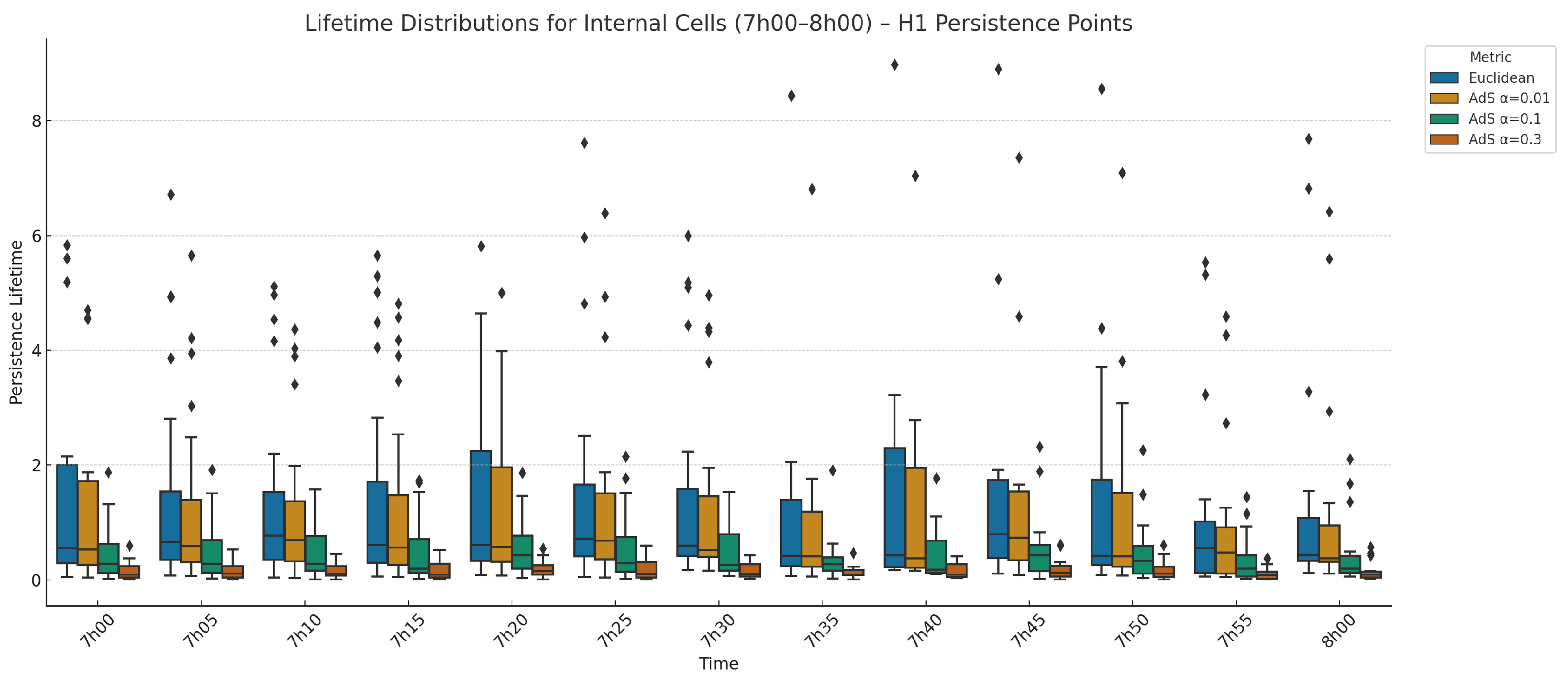
3.6. Temporal Evolution of Lifetimes for Internal Cells (AdS, )
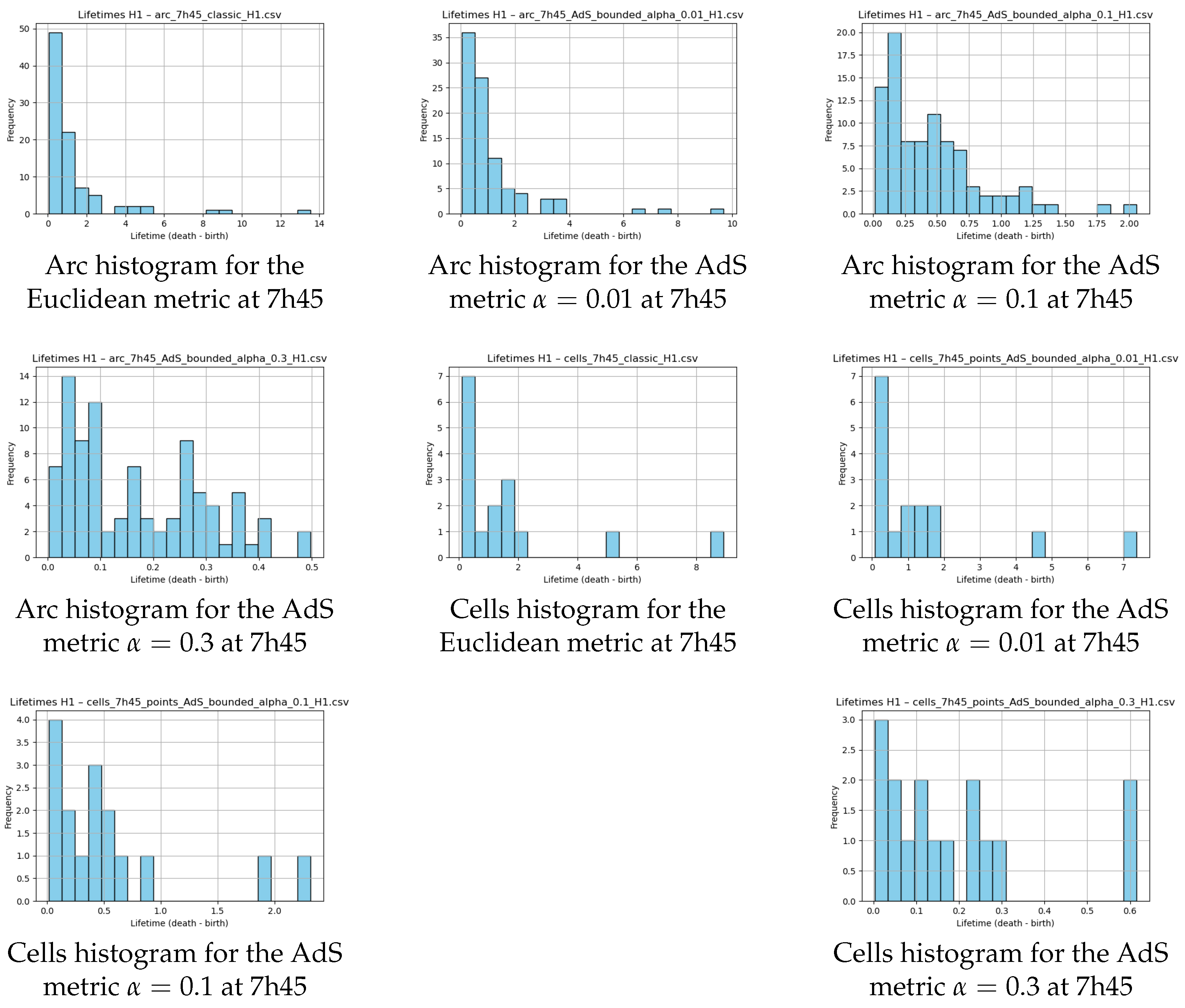
3.7. Analysis of Lifetime Distributions
3.7.1. Arc Topology
3.7.2. Internal Cell Topology
3.7.3. Comparative Analysis of Arc and Internal Cells (AdS )
3.8. Analysis of Wasserstein Distances Between Diagrams (Ads vs. Euclidean)
3.8.1. Arc
3.8.2. Internal Cells
3.9. Discussion
3.10. Perspectives
4. Arc/Cell of Bow Echo Topological Interaction and Alert Triggering
4.1. Cross-Correlation of Persistence Lifetimes
4.2. Topological Alert Indicator Based on Lifetimes for AdS
Definition of the Indicator
4.3. Results and Discussion
5. Conclusions and Perspectives
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Persistence Diagrams H1
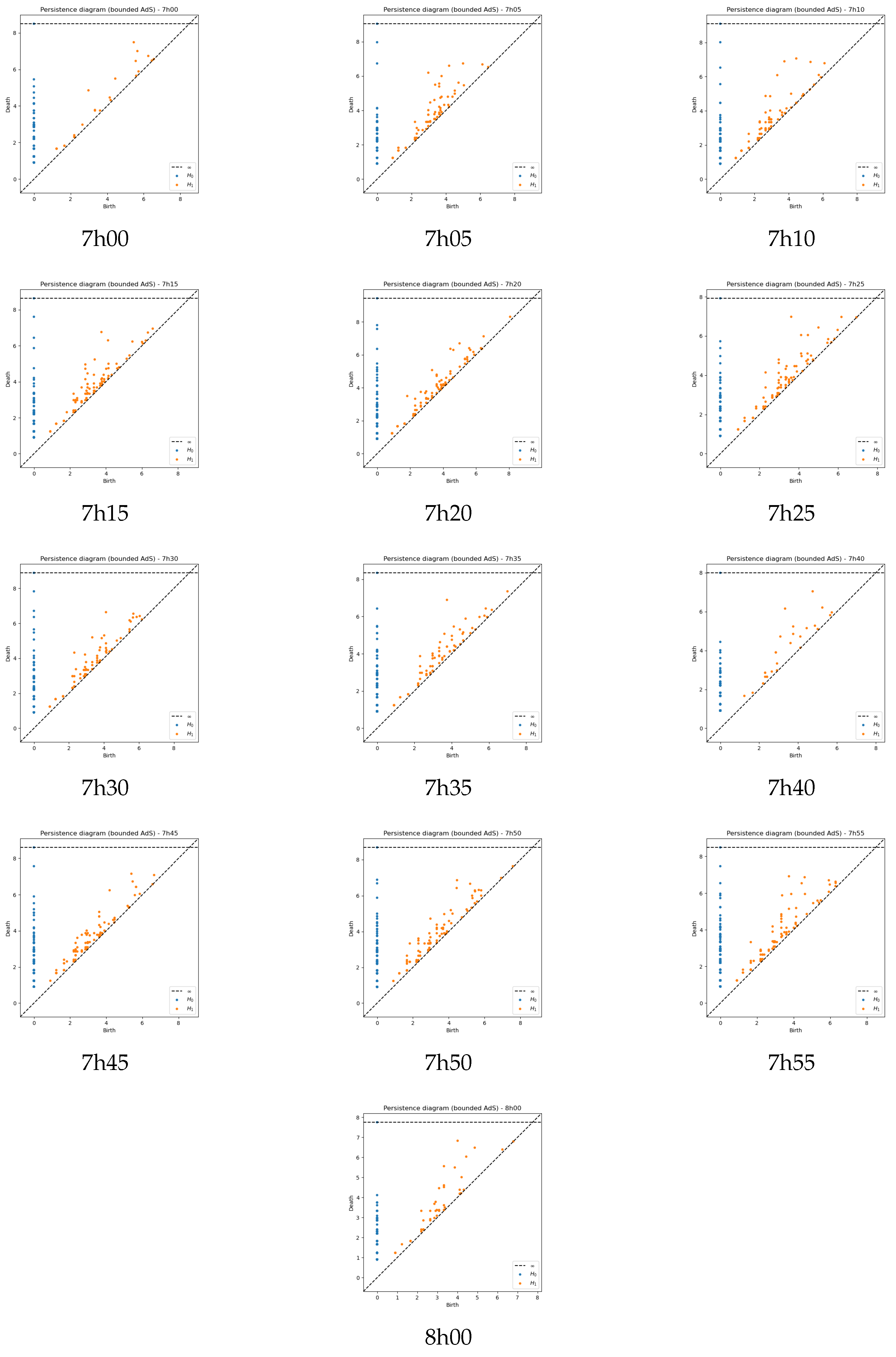
Appendix B. Persistence Diagrams for the Cells

Appendix C. Histograms of H1 Lifetimes for the Arc
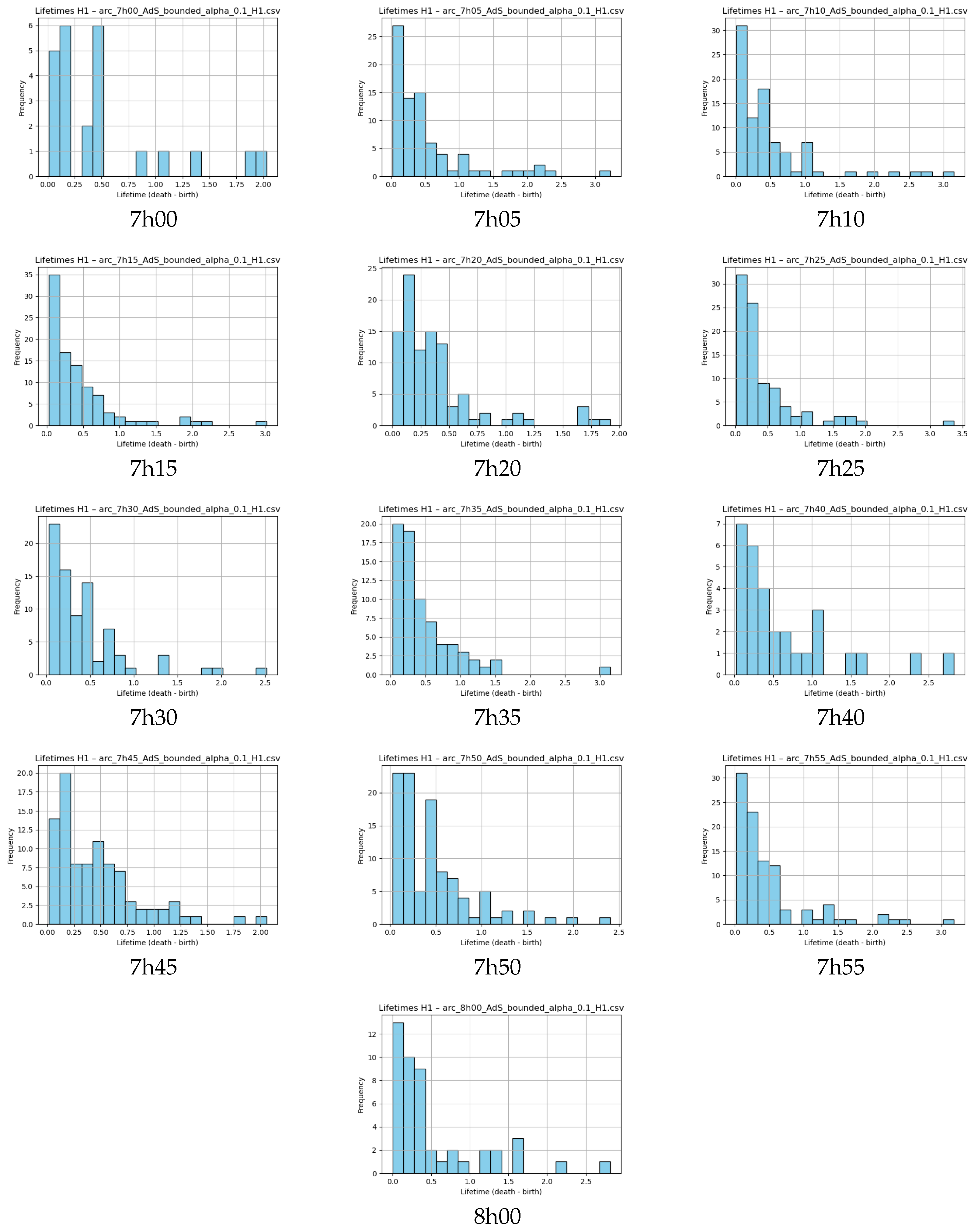
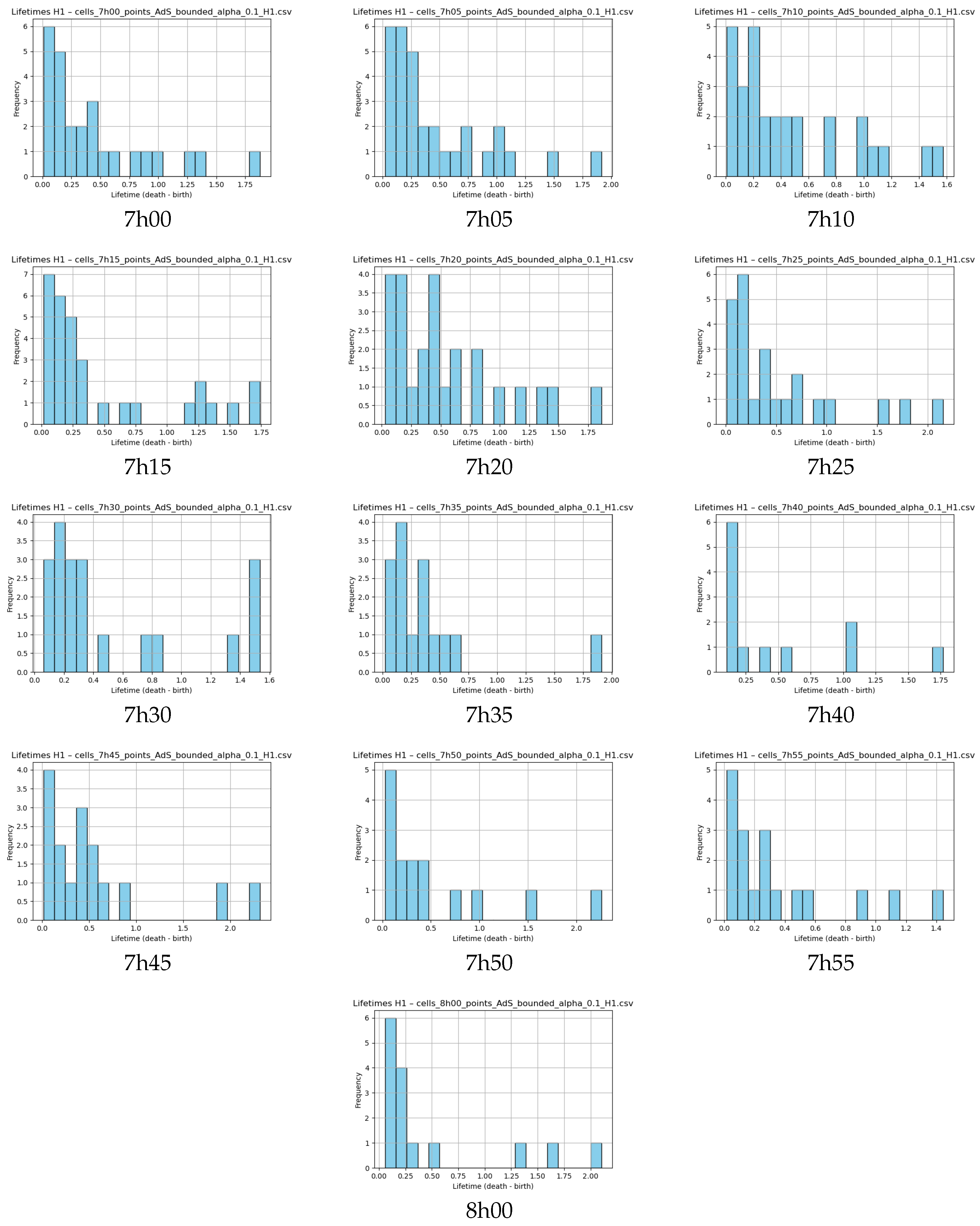
Appendix D. Histograms of H1 Lifetimes for the Cells
Appendix E. Temporal Evolution of Arcus Radar Images
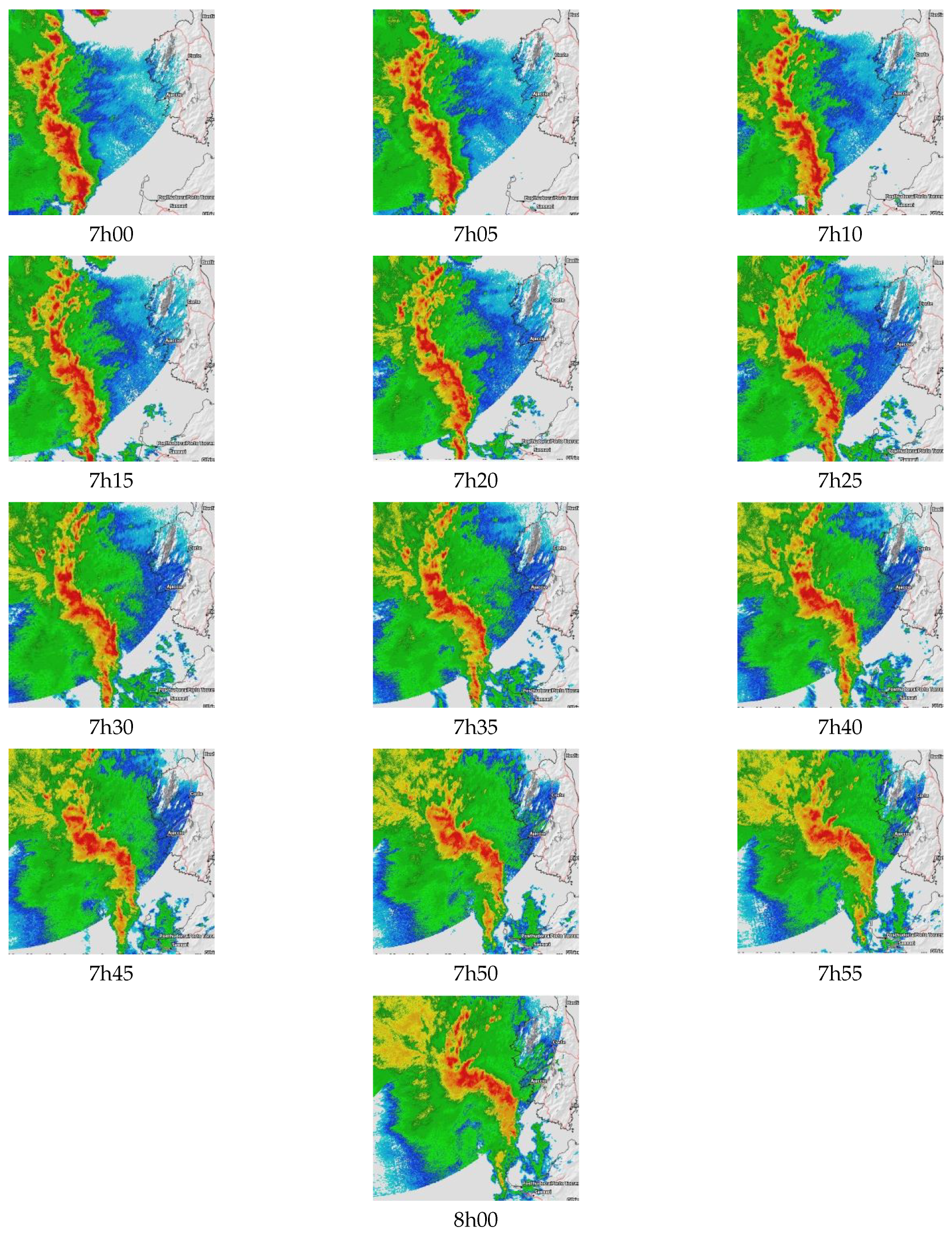
References
- Fujita, T.T. Manual of Downburst Identification for Project NIMROD; University of Chicago: Chicago, IL, USA, 1978. [Google Scholar]
- Coniglio, M.C.; Stensrud, D.J. Simulation of a progressive derecho using a high-resolution mesoscale model. Weather. Forecast. 2001, 16, 686–705. [Google Scholar]
- Przybylinski, R.W. The bow echo: Observations, numerical simulations, and severe weather detection methods. Weather Forecast. 1995, 10, 203–218. [Google Scholar] [CrossRef]
- Weisman, M.L. The Genesis of Mesoscale Convective Systems: Interaction of Large-Scale Forcing and Convective Instabilities. J. Atmos. Sci. 1993. [Google Scholar]
- Weisman, M.L.; Trapp, R.J. Low-level mesovortices within numerically simulated bow echoes. Mon. Weather. Rev. 2003. [Google Scholar]
- Evans, J.S.; Doswell, C.A., III. Examination of derecho environments using proximity soundings. Weather. Forecast. 2001, 16, 329–342. [Google Scholar] [CrossRef]
- Kamani, M.M.; Farhat, F.; Wistar, S.; Wang, J.Z. Skeleton Matching with Applications in Severe Weather Detection. Appl. Soft Comput. 2018, 70, 1154–1166. [Google Scholar] [CrossRef]
- Britt, K.C.; Potvin, C.K.; Roberts, B.; Skinner, P.S.; Heinselman, P.L.; Potvin, C.K.; Flora, M.L.; Matilla, B.; Knopfmeier, K.H.; Reinhart, A.E. Verification of Quasi-Linear Convective Systems Predicted by the NSSL Warn-on-Forecast System Using Object-Based Methods. Weather Forecast. 2024, 39, 155–176. [Google Scholar] [CrossRef]
- Potvin, C.K.; Gallo, B.T.; Reinhart, A.E.; Roberts, B.; Skinner, P.S.; Sobash, R.A.; Wilson, K.A.; Britt, K.C.; Broyles, C.; Flora, M.L.; et al. An Iterative Storm Segmentation and Classification Algorithm for Convection-Allowing Models and Gridded Radar Analyses. J. Atmos. Ocean. Technol. 2022, 39, 999–1013. [Google Scholar] [CrossRef]
- Jergensen, G.E.; McGovern, A.; Lagerquist, R.; Smith, T. Classifying Convective Storms Using Machine Learning. Weather Forecast. 2020, 35, 537–559. [Google Scholar] [CrossRef]
- Sobash, R.A.; Gagne, D.J.; Becker, C.L.; Ahijevych, D.; Gantos, G.N.; Schwartz, C.S. Diagnosing Storm Mode with Deep Learning in Convection-Allowing Models. Mon. Weather. Rev. 2023, 151, 2009–2027. [Google Scholar] [CrossRef]
- Mounier, A.; Raynaud, L.; Rottner, L.; Plu, M.; Arbogast, P.; Kreitz, M.; Mignan, L.; Touzé, B. Detection of Bow Echoes in Kilometer-Scale Forecasts Using a Convolutional Neural Network. Artif. Intell. Earth Syst. 2022, 1, e210010. [Google Scholar] [CrossRef]
- McGovern, A.; Chase, R.J.; Flora, M.; Gagne, D.J.; Lagerquist, R.; Potvin, C.K.; Snook, N.; Loken, E. A Review of Machine Learning for Convective Weather. Artif. Intell. Earth Syst. 2023, 2, e220077. [Google Scholar] [CrossRef]
- Nugroho, G.A.; Halimurrahman; Awaludin, A.; Fathrio, I.; Trilaksono, N.J.; Maryadi, E.; Sinatra, T.; Renggono, F.; Renggono, D.; Makmur, E.; et al. A 4-years of radar-based observation of bow echo over Bandung basin Indonesia. Geoenviron. Disasters 2024, 11, 19. [Google Scholar] [CrossRef]
- Meteo-France. Données radar—Orage du 18 août 2022, Corse. 2022. Available online: https://meteofrance.com (accessed on 15 July 2025).
- Edelsbrunner, H.; Harer, J. Computational Topology: An Introduction; American Mathematical Society: Providence, RI, USA, 2010. [Google Scholar]
- Chazal, F.; Cohen-Steiner, D.; Glisse, M.; Guibas, L.J.; Oudot, S.Y. Proximity of persistence modules and their diagrams. In Proceedings of the 25th Annual Symposium on Computational Geometry, Aarhus, Denmark, 8–10 June 2009. [Google Scholar]
- Munch, E. A user’s guide to topological data analysis. J. Learn. Anal. 2020, 4, 47–61. [Google Scholar] [CrossRef]
- Carlsson, G. Topology and Data. Bull. Am. Math. Soc. 2009, 46, 255–308. [Google Scholar] [CrossRef]
- Ghrist, R. Barcodes: The Persistent Topology of Data. Bull. Am. Math. Soc. 2008, 45, 61–75. [Google Scholar] [CrossRef]
- Oudot, S.Y. Persistence Theory: From Quiver Representations to Data Analysis: AMS Mathematical Surveys and Monographs; American Mathematical Society: Providence, RI, USA, 2016; Volume 209. [Google Scholar]
- Gidea, M.; Katz, Y. Topological Data Analysis of Financial Time Series: Landscapes of Crashes. Phys. A Stat. Mech. Its Appl. 2018, 491, 820–834. [Google Scholar] [CrossRef]
- Perea, J.A. Topological time series analysis. Not. Am. Math. Soc. 2019, 66, 686–694. [Google Scholar] [CrossRef]
- Khasawneh, F.A.; Munch, E. Chatter detection in turning using persistent homology. Mech. Syst. Signal Process. 2016, 70, 527–541. [Google Scholar] [CrossRef]
- Lum, P.Y.; Singh, G.; Lehman, A.; Ishkanov, T.; Vejdemo-Johansson, M.; Alagappan, M.; Carlsson, J.; Carlsson, G. Extracting insights from the shape of complex data using topology. Sci. Rep. 2013, 3, 1236. [Google Scholar] [CrossRef]
- Ver Hoef, L.; Adams, H.; King, E.J.; Ebert-Uphoff, I. A Primer on Topological Data Analysis to Support Image Analysis Tasks in Environmental Science. Artif. Intell. Earth Syst. 2023, 2, e220039. [Google Scholar] [CrossRef]
- Sena, C.Á.P.; da Paixão, J.A.R.; de Almeida França, J.R. A Topological Data Analysis approach for retrieving Local Climate Zones patterns in satellite data. Environ. Chall. 2021, 5, 100359. [Google Scholar] [CrossRef]
- Muszynski, G.; Kashinath, K.; Kurlin, V.; Wehner, M.; Prabhat. Topological data analysis and machine learning for recognizing atmospheric river patterns in large climate datasets. Geosci. Model Dev. 2019, 12, 613–628. [Google Scholar] [CrossRef]
- Strommen, K.; Chantry, M.; Dorrington, J.; Otter, N. A topological perspective on weather regimes. Clim. Dyn. 2023, 60, 1415–1445. [Google Scholar] [CrossRef]
- Ma, T.; Su, Y.; Abdel Wahab, M.M.; Khalil, A.A.E. ZPDSN: Spatio-temporal meteorological forecasting with topological data analysis. Appl. Intell. 2025, 55, 9. [Google Scholar] [CrossRef]
- Tymochko, S.; Munch, E.; Dunion, J.; Corbosiero, K.; Torn, R. Using persistent homology to quantify a diurnal cycle in hurricanes. Pattern Recognit. Lett. 2020, 133, 137–143. [Google Scholar] [CrossRef]
- Canot, H.; Durand, P.; Frénod, E. Bow Echo Alarm System using Topological Data Analysis. Appl. Math. Mod. Challenges 2025, 3, 44–63. [Google Scholar] [CrossRef]
- Grande, V.P.; Schaub, M.T. Non-isotropic persistent homology: Leveraging the metric dependency of PH. arXiv 2022, arXiv:2201.06480. [Google Scholar]
- Chazal, F.; Cohen-Steiner, D.; Mérigot, Q. Geometric inference for probability measures. Found. Comput. Math. 2011, 11, 733–751. [Google Scholar] [CrossRef]
- Coifman, R.R.; Lafon, S.; Lee, A.B.; Maggioni, M.; Nadler, B.; Warner, F.; Zucker, S.W. Geometric diffusions as a tool for harmonic analysis and structure definition. Proc. Natl. Acad. Sci. USA 2005, 102, 7426–7431. [Google Scholar] [CrossRef]
- Silva, V.; Tenenbaum, J. Global versus local methods in nonlinear dimensionality reduction. Adv. Neural Inf. Process. Syst. 2003, 15, 721–728. [Google Scholar]
- Carrière, M.; Chazal, F.; Ike, Y.; Lacombe, T.; Royer, M.; Umeda, Y. PersLay: A neural network layer for persistence diagrams and new graph topological signatures. In Proceedings of the Twenty Third International Conference on Artificial Intelligence and Statistics (AISTATS), Online, 26–28 August 2020. [Google Scholar]
- Maldacena, J. The Large N Limit of Superconformal Field Theories and Supergravity. Adv. Theor. Math. Phys. 1998, 2, 231–252. [Google Scholar] [CrossRef]
- Moschella, U. The de Sitter and anti-de Sitter Sightseeing Tour. Semin. Poincaré 2005, 1, 1–12. Available online: http://www.bourbaphy.fr/moschella.pdf (accessed on 15 July 2025).
- Hooft, G. Dimensional Reduction in Quantum Gravity. arXiv 1993, arXiv:gr-qc/9310026. [Google Scholar]
- Susskind, L. The World as a Hologram. J. Math. Phys. 1995, 36, 6377. [Google Scholar] [CrossRef]
- Villani, C. Optimal Transport: Old and New; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Chazal, F.; Cohen-Steiner, D.; Glisse, M.; Guibas, L.J.; Oudot, S.Y. The Wasserstein distance between persistence diagrams. In Proceedings of the 25th Annual Symposium on Computational Geometry (SoCG 2009), Aarhus, Denmark, 8–10 June 2009. [Google Scholar]
- Mileyko, Y.; Mukherjee, S.; Harer, J. Probability measures on the space of persistence diagrams. Inverse Probl. 2011, 27, 124007. [Google Scholar] [CrossRef]
- Bubenik, P. Statistical topological data analysis using persistence landscapes. J. Mach. Learn. Res. 2015, 16, 77–102. [Google Scholar]
- Cohen-Steiner, D.; Edelsbrunner, H.; Harer, J. Stability of persistence diagrams. Discret. Comput. Geom. 2007, 37, 103–120. [Google Scholar] [CrossRef]
- Bauer, U. Ripser: Efficient computation of Vietoris–Rips persistence barcodes. J. Appl. Comput. Topol. 2021, 5, 391–423. [Google Scholar] [CrossRef]











Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Canot, H.; Durand, P.; Frenod, E. Curved Geometries in Persistent Homology: From Euclidean to AdS Metrics in Bow Echo Dynamics. Int. J. Topol. 2025, 2, 19. https://doi.org/10.3390/ijt2040019
Canot H, Durand P, Frenod E. Curved Geometries in Persistent Homology: From Euclidean to AdS Metrics in Bow Echo Dynamics. International Journal of Topology. 2025; 2(4):19. https://doi.org/10.3390/ijt2040019
Chicago/Turabian StyleCanot, Hélène, Philippe Durand, and Emmanuel Frenod. 2025. "Curved Geometries in Persistent Homology: From Euclidean to AdS Metrics in Bow Echo Dynamics" International Journal of Topology 2, no. 4: 19. https://doi.org/10.3390/ijt2040019
APA StyleCanot, H., Durand, P., & Frenod, E. (2025). Curved Geometries in Persistent Homology: From Euclidean to AdS Metrics in Bow Echo Dynamics. International Journal of Topology, 2(4), 19. https://doi.org/10.3390/ijt2040019





