Topological Types of Convergence for Nets of Multifunctions

Abstract

This article proposes a unified concept of topological types of convergence for nets of multifunctions between topological spaces. Any kind of convergence is representable by a (2n + 2)-tuple, n = 0, 1, …, of two special functions u and l, such that their compositions $ul$ and $lu$ create the Choquet supremum and infimum operations, respectively, on the filters considered in terms of the upper Vietoris topology on the range hyperspace of the considered multifunctions. Convergence operators are defined by establishing the order of composition of the functions from such (2n + 2) tuples. An allocation of places for the two distinguished functions in a convergence operator reflects the structure of the used (2n + 2)-tuple. A monoid of special three-parameter functions called products describes the set of all possible structures. The monoid of products is the domain space of the convergence operators. The family of all convergence operators forms a finite monoid whose neutral element determines the pointwise convergence and possesses the structure determined by the neutral element of the monoid of products. We demonstrate the construction process of every convergence operator and show that the notions of the presented concept can characterize many well-known classical types of convergence. Of particular importance are the types of convergence derived from the concept of continuous convergence. We establish some general theorems about the necessary and sufficient conditions for the continuity of the limit multifunctions without any assumptions about the type of continuity of the members of the nets.

1. Introduction

We denote the closure (resp. interior) of a subset A of a topological space $(X,\tau )$ by $Cl\left(A\right)$ (resp. $Int\left(A\right)$). To simplify the lecture, throughout the paper, we will assume that $(X,\tau )$ is $T_1$.

For any nonempty set A, let $\mathcal{P}\left(A\right)$ denote the family of all nonempty subsets of A. Generally, we will use the notation ${\mathcal{P}}^{n+1}\left(A\right)=\mathcal{P}\left({\mathcal{P}}^n\left(A\right)\right)$ where $n\in \mathbb{N}$ and ${\mathcal{P}}^0\left(A\right)=A$. The hyperspace topologies which we are about to use were introduced by L. Vietoris in [1,2] (see also [3,4]). We recall that for a topological space $(X,\tau )$, the upper (resp. lower) Vietoris topology ${\tau }^u$ (resp. ${\tau }^l$) on $\mathcal{P}\left(X\right)$ is generated by the basis $\left\{\left\{A\subset X:A\subset U\right\}:U\in \tau \right\}$ (resp. subbasis $\left\{\left\{A\subset X:A\cap U\ne \varnothing \right\}:U\in \tau \right\}$). The upper Vietoris topology plays a crucial role in our investigation. The closure of a subset $\mathcal{A}\subset \mathcal{P}\left(X\right)$ with respect to ${\tau }^u$ will be denoted by $\overline{\mathcal{A}}$.

The following specific property of the upper Vietoris topology will be used later, without explicitly referring to it.

Remark 1.

For any family $\lambda \subset {\mathcal{P}}^2$(X) and U $\in \tau$ the following properties are equivalent:

• $\mathcal{P}\left(U\right)\cap {\bigcap }_{\mathcal{K}\in \lambda }\overline{\mathcal{K}}\ne \varnothing$;
• $\mathcal{P}\left(U\right)\cap \overline{\mathcal{K}}\ne \varnothing$ for all $\mathcal{K}\in \lambda$.

By a multifunction $F:(X,\tau )\to (Y,\sigma )$ from one topological space $(X,\tau )$ to another $(Y,\sigma )$ we mean a point-to-set correspondence and we always assume that $F\left(x\right)\ne \varnothing$ for all $x\in X$. Given a multifunction F, we denote its upper and lower inverse images of a subset B of Y by $F^{+}\left(B\right)$ and $F^{-}\left(B\right)$, respectively, i.e., $F^{+}\left(B\right)=\left\{x\in X:F\left(x\right)\subset B\right\}$ and $F^{-}\left(B\right)=\left\{x\in X:F\left(x\right)\cap B\ne \varnothing \right\}$ [5]. Of course, a single-valued function $f:X\to Y$ is naturally associated with the multifunction F given by $F\left(x\right)=\left\{f\left(x\right)\right\}$ for all $x\in X$. Obviously, in this case, $F^{+}\left(B\right)=F^{-}\left(B\right)=f^{-1}\left(B\right)$ and $F\left(A\right)=f\left(A\right)$ for all $A\subset X$ and $B\subset Y$. The inverse images of a multifunction F we formulate in the topological terms by using the following two functions from X to ${\mathcal{P}}^2\left(Y\right)$:

$x⟶\overline{\left\{F\left(x\right)\right\}}$ and $x⟶\overline{\mathcal{P}\left(F\right(x\left)\right)}$ for all $x\in X$.

The usefulness of these functions results from the following properties:

Remark 2.

For any multifunction $F:(X,\tau )⟶(Y,\sigma )$, $x\in X$ and $W\in \sigma$, the following equivalences hold:

• $x\in F^{+}\left(W\right)$ if and only if $\mathcal{P}\left(W\right)\cap \overline{\left\{F\left(x\right)\right\}}\ne \varnothing$;
• $x\in F^{-}\left(W\right)$ if and only if $\mathcal{P}\left(W\right)\cap \overline{\mathcal{P}\left(F\right(x\left)\right)}\ne \varnothing$.

It follows from the following obvious equivalences for any $B\subset Y$ and $W\in \sigma$:

• $B\subset W$ if and only if $\mathcal{P}\left(W\right)\cap \overline{\left\{B\right\}}\ne \varnothing$;
• $B\cap W\ne \varnothing$ if and only if $\mathcal{P}\left(W\right)\cap \overline{\mathcal{P}\left(B\right)}\ne \varnothing$.

In this paper, we will use the notion of filter as a tool for studying multifunctions. For the sake of fixing notation, we recall some classical notions that can be found, e.g., in [6,7]. A filter base $\mathcal{B}$ on a set Y is a nonempty collection of nonempty subsets of Y such that the intersection of any two members of $\mathcal{B}$ contains a member of $\mathcal{B}$. A filter $\mathcal{F}$ on a set Y is a nonempty collection of nonempty subsets of Y such that:

• If A $\in \mathcal{F}$ and $\mathrm{A}\subset \mathrm{B}$, then B $\in \mathcal{F}$;
• If A $\in \mathcal{F}$ and B $\in \mathcal{F}$, then A∩B $\in \mathcal{F}$ for all $A,B\subset Y$.

For a family $\mathcal{A}$ of subsets of Y, let [$\mathcal{A}$] denote the family that consists of all supersets of each $A\in \mathcal{A}$. Every filter base $\mathcal{B}$ on Y generates a unique smallest filter containing $\mathcal{B}$ as a subset, which consists of the subsets of Y containing a member of $\mathcal{B}$, i.e., it is equal to $\left[\mathcal{B}\right]$. Obviously, if $\mathcal{B}\subset \mathcal{A}\subset \left[\mathcal{B}\right]$, then $\left[\mathcal{A}\right]=\left[\mathcal{B}\right]$. A family of type $\left[\right\{B\left\}\right]$, where $B\subset Y$, is called the principal filter generated by B. In the case when $B=\left\{y\right\}$ for some $y\in Y$, the term principal filter generated by y is used.

G. Choquet [7] has used the concept of supremum (Sup) and the infimum (Inf) of filters on $\mathcal{P}\left(Y\right)$ as follows.

If $(Y,\sigma )$ is a topological space and $\lambda$ is a filter on $\mathcal{P}\left(Y\right)$, then

• The supremum of $\lambda$ is the set of all points $y\in Y$ such that for every open set W containing y and for each $\mathcal{K}\in \lambda$ there exists $K\in \mathcal{K}$ such that $W\cap$ K $\ne \varnothing$;
• The infimum of $\lambda$ is the set of all points $y\in Y$ such that for every open set W containing y, there exists $\mathcal{K}\in \lambda$ such that for each K $\in \mathcal{K}$, W ∩ K $\ne \varnothing$.

In this paper, we will use Choquet’s concept of limits in the case of filters $\xi \subset {\mathcal{P}}^3\left(Y\right)$ on ${\mathcal{P}}^2\left(Y\right)$, considered in terms of the upper Vietoris topology ${\sigma }^u$ on $\mathcal{P}\left(Y\right)$. To simplify the notation, we denote the infimum and supremum operations by $\mathcal{I}$ and $\mathcal{S}$, respectively. The following characterizations of the infimum and supremum operations will serve as useful tools in our investigations. They follow immediately from the definition and the equivalences from Remark 1.

Remark 3.

Let $(Y,\sigma )$ be a topological space and $\xi \subset {\mathcal{P}}^3\left(Y\right)$ be a filter on ${\mathcal{P}}^2\left(Y\right)$. Then,

• $\mathcal{I}\left(\xi \right)=\overline{{\bigcup }_{\lambda \in \xi }{\bigcap }_{\mathcal{K}\in \lambda }\overline{\mathcal{K}}}$;
• $\mathcal{S}\left(\xi \right)={\bigcap }_{\lambda \in \xi }\overline{{\bigcup }_{\mathcal{K}\in \lambda }\mathcal{K}}$.

2. The Monoid of Cluster Operators

In this section, we introduce the concepts of cluster functions and cluster operators, which are broad generalizations of the concept of cluster sets for multifunctions, as discussed in [8], and earlier concepts related to single-valued functions studied in [9].

For that purpose, we will use the supremum and infimum operations represented by the pair (l, u) of functions $u,l$:${\mathcal{P}}^3\left(Y\right)\to {\mathcal{P}}^2\left(Y\right)$ defined in terms of the upper Vietoris topology ${\sigma }^u$ on $\mathcal{P}\left(Y\right)$ as follows:

• $u\left(\lambda \right)={\bigcap }_{\mathcal{K}\in \lambda }\overline{\mathcal{K}}$;
• $l\left(\lambda \right)=\overline{{\bigcup }_{\mathcal{K}\in \lambda }\mathcal{K}}$ for any $\lambda \in {\mathcal{P}}^3\left(Y\right)$.

The functions u and l are highly related to each other, as we will show in the lemma below. First, let us consider the relation $\cong$ on ${\mathcal{P}}^2\left(Y\right)$ defined by the formula:

• $\mathcal{A}\cong \mathcal{B}$, if $\mathcal{A}\subset \bigcap \left\{\overline{\mathcal{P}\left(W\right)}:\mathcal{P}\left(W\right)\cap \mathcal{B}\ne \varnothing ,W\in \sigma \right\}$,

where $\mathcal{A},\mathcal{B}\in {\mathcal{P}}^2\left(Y\right)$.

It is easy to see that the relation $\cong$ is symmetric. Indeed, if $\mathcal{A}\cong \mathcal{B}$, $B\in \mathcal{B}$, $\mathcal{P}\left(V\right)\cap \mathcal{A}\ne \varnothing$ and $\mathcal{P}\left(W\right)\cap \mathcal{B}\ne \varnothing$, where $V,W\in \sigma$, then using the assumption that $\mathcal{A}\subset \overline{\mathcal{P}\left(W\right)}$ we obtain $\mathcal{P}\left(W\right)\cap \mathcal{P}\left(V\right)\ne \varnothing$ which proves that $\mathcal{B}\subset \overline{\mathcal{P}\left(V\right)}$ and consequently, that $\mathcal{B}\cong \mathcal{A}$.

For any set X, the relation $\cong$ induces a relation on ${\mathcal{P}}^2{\left(Y\right)}^X$, also denoted by ≅, which consists of all pairs $(\alpha ,\beta )\in {\mathcal{P}}^2{\left(Y\right)}^X\times {\mathcal{P}}^2{\left(Y\right)}^X$ that satisfy the following condition:

• $\alpha \left(x\right)\cong \beta \left(x\right)$ for all $x\in X$.

The following property will be used later to prove one of the two main results of this work about the continuity of limits of nets of multifunctions.

Lemma 1.

Let $(Y,\sigma )$ be a topological space and let X be a nonempty set. If α and β are functions from X into ${\mathcal{P}}^2\left(Y\right)$ such that $\alpha \cong \beta$, then $l\left(\alpha \right(A\left)\right)\cong u\left(\beta \right(A\left)\right)$ for any $A\subset X$.

Proof. 

Assuming that $\alpha \cong \beta$, we will show that $\overline{{\bigcup }_{x\in A}\alpha \left(x\right)}\cong {\bigcap }_{x\in A}\overline{\beta \left(x\right)}$. We, therefore, take two arbitrary sets $W,V\in \sigma$ such that $\mathcal{P}\left(W\right)\cap {\bigcap }_{x\in A}\overline{\beta \left(x\right)}\ne \varnothing$ and $\mathcal{P}\left(V\right)\cap \overline{{\bigcup }_{x\in A}\alpha \left(x\right)}\ne \varnothing$. Then, there exists $x\in A$ such that $\mathcal{P}\left(W\right)\cap \beta \left(x\right)\ne \varnothing$ and $\mathcal{P}\left(V\right)\cap \alpha \left(x\right)\ne \varnothing$. Using the assumption, we obtain $\alpha \left(x\right)\subset \overline{\mathcal{P}\left(W\right)}$ and consequently, $\mathcal{P}\left(V\right)\cap \mathcal{P}\left(W\right)\ne \varnothing$ which implies that $\overline{{\bigcup }_{x\in A}\alpha \left(x\right)}\subset \overline{\mathcal{P}\left(W\right)}$ and ends the proof. □

The following characterizations of the infimum and supremum operations will serve as useful tools in our investigations. They follow immediately from the definitions and Remark 3.

Lemma 2.

Let $(Y,\sigma )$ be a topological space and let $\xi \subset {\mathcal{P}}^3\left(Y\right)$ be a filter on ${\mathcal{P}}^2\left(Y\right)$. Then,

(i)

$\mathcal{I}\left(\xi \right)=\overline{{\bigcup }_{\lambda \in \xi }{\bigcap }_{\mathcal{K}\in \lambda }\overline{\mathcal{K}}}=l\circ u\left(\xi \right)$;

(ii)

$\mathcal{S}\left(\xi \right)={\bigcap }_{\lambda \in \xi }\overline{{\bigcup }_{\mathcal{K}\in \lambda }\mathcal{K}}=u\circ l\left(\xi \right)$.

2.1. Limits of Filters in Terms of the Upper Vietoris Topology

The following elementary property will be used in the proof of Theorem 1, which will be stated later.

Lemma 3.

Let $(Y,\sigma )$ be a topological space, $\mathcal{A}\in {\mathcal{P}}^2\left(Y\right)$, and let $\xi \subset {\mathcal{P}}^3\left(Y\right)$ be a filter on ${\mathcal{P}}^2\left(Y\right)$ such that $\mathcal{A}\in \bigcap \xi$; then, $\mathcal{I}\left(\xi \right)\subset \overline{\mathcal{A}}\subset \mathcal{S}\left(\xi \right)$.

Proof. 

Since $\overline{\mathcal{A}}\in \{\overline{\mathcal{K}}:\mathcal{K}\in \lambda \}$ for every $\lambda \in \xi$, we have ${\bigcap }_{\mathcal{K}\in \lambda }\overline{\mathcal{K}}\subset \overline{\mathcal{A}}\subset \overline{{\bigcup }_{\mathcal{K}\in \lambda }\mathcal{K}}$ for any $\lambda \in \xi$ and consequently, $\overline{{\bigcup }_{\lambda \in \xi }{\bigcap }_{\mathcal{K}\in \lambda }\overline{\mathcal{K}}}\subset \overline{\mathcal{A}}\subset {\bigcap }_{\lambda \in \xi }\overline{{\bigcup }_{\mathcal{K}\in \lambda }\mathcal{K}}$ which, according to the above lemma, finishes the proof. □

Any filter base ${\mathcal{B}}^{\xi }$ that generates a filter $\xi$ on ${\mathcal{P}}^2\left(Y\right)$ can be used to characterize the value of the operations $\mathcal{I}$ and $\mathcal{S}$ by the combinations $l\circ u$ and $u\circ l$, respectively. Namely,

$l\circ u\left(\xi \right)=l\circ u({\mathcal{B}}^{\xi }$) and $u\circ l\left(\xi \right)=u\circ l\left({\mathcal{B}}^{\xi }\right)$.

This property immediately follows from the following one.

Lemma 4.

Let $(Y,\sigma )$ be a topological space and ${\mathcal{B}}^{*}\subset {\mathcal{P}}^3\left(Y\right)$ a filter base on ${\mathcal{P}}^2\left(Y\right)$. Then, the following equalities hold for any family $\mathcal{B}$ such that ${\mathcal{B}}^{*}\subset \mathcal{B}\subset \left[{\mathcal{B}}^{*}\right]$:

(i)

$u\circ l\left({\mathcal{B}}^{*}\right)=u\circ l\left(\mathcal{B}\right)$;

(ii)

$l\circ u\left({\mathcal{B}}^{*}\right)=l\circ u\left(\mathcal{B}\right)$.

Proof. 

Since $\mathcal{B}\subset \left[{\mathcal{B}}^{*}\right]$, for every $\lambda \in \mathcal{B}$ there exists ${\lambda }^{\star }\in {\mathcal{B}}^{\star }$ such that ${\lambda }^{\star }\subset \lambda$, which gives $\overline{{\bigcup }_{\mathcal{K}\in {\lambda }^{\star }}\mathcal{K}}\subset \overline{{\bigcup }_{\mathcal{K}\in \lambda }\mathcal{K}}$ and ${\bigcap }_{\mathcal{K}\in {\lambda }^{\star }}\overline{\mathcal{K}}\supset {\bigcap }_{\mathcal{K}\in \lambda }\overline{\mathcal{K}}$, i.e., $l\left({\lambda }^{\star }\right)\subset l\left(\lambda \right)$ and $u\left({\lambda }^{\star }\right)\supset u\left(\lambda \right)$. So, in summary, we now know that, for every $l\left(\lambda \right)\in l\left(\mathcal{B}\right)$ (resp. $u\left(\lambda \right)\in u\left(\mathcal{B}\right)$), there exists $l\left({\lambda }^{\star }\right)\in l\left({\mathcal{B}}^{\star }\right)$ (resp. $u{\left(\lambda \right)}^{\star }\in u\left({\mathcal{B}}^{\star }\right)$) such that $l\left({\lambda }^{\star }\right)\subset l\left(\lambda \right)$ (resp. $u\left({\lambda }^{\star }\right)\supset u\left(\lambda \right)$). Consequently,

${\bigcap }_{{\lambda }^{*}\in {\mathcal{B}}^{*}}\overline{l\left({\lambda }^{*}\right)}\subset {\bigcap }_{\lambda \in \mathcal{B}}\overline{l\left(\lambda \right)}$ and $\overline{{\bigcup }_{{\lambda }^{*}\in {\mathcal{B}}^{*}}u\left({\lambda }^{*}\right)}\supset \overline{{\bigcup }_{\lambda \in \mathcal{B}}u\left(\lambda \right)}$, i.e.,

$u\circ l\left({\mathcal{B}}^{*}\right)\subset u\circ l\left(\mathcal{B}\right)$ and $l\circ u\left({\mathcal{B}}^{*}\right)\supset l\circ u\left(\mathcal{B}\right)$.$(\ast )$

Let us now note that the inclusion ${\mathcal{B}}^{*}\subset \mathcal{B}$ implies the inclusions

$\left\{l\left({\lambda }^{*}\right):{\lambda }^{*}\in {\mathcal{B}}^{*}\right\}\subset \left\{l\left(\lambda \right):\lambda \in \mathcal{B}\right\}$ and $\left\{u\left({\lambda }^{*}\right):{\lambda }^{*}\in {\mathcal{B}}^{*}\right\}\subset \left\{u\left(\lambda \right):\lambda \in \mathcal{B}\right\}$.

Hence, ${\bigcap }_{{\lambda }^{*}\in {\mathcal{B}}^{*}}\overline{l\left({\lambda }^{*}\right)}\supset {\bigcap }_{\lambda \in \mathcal{B}}\overline{l\left(\lambda \right)}$ and $\overline{{\bigcup }_{{\lambda }^{*}\in {\mathcal{B}}^{*}}u\left({\lambda }^{*}\right)}\subset \overline{{\bigcup }_{\lambda \in \mathcal{B}}u\left(\lambda \right)}$, i.e.,

$u\circ l\left({\mathcal{B}}^{*}\right)\supset u\circ l\left(\mathcal{B}\right)$ and $l\circ u\left({\mathcal{B}}^{*}\right)\subset l\circ u\left(\mathcal{B}\right)$.

Thus, according to $(\ast )$, the proof is completed. □

Remark 4.

Let us note that the following hold for any topological space $(Y,\sigma )$ and a filter ξ on ${\mathcal{P}}^2\left(Y\right)$:

$l\circ l\left(\xi \right)=\mathcal{P}\left(Y\right)$ and $u\circ u\left(\xi \right)=\left\{Y\right\}$.

However, it is easy to check that in the case of a filter base ξ on ${\mathcal{P}}^2\left(Y\right)$, the above equalities do not have to be true.

Indeed, if $B\in \mathcal{P}\left(Y\right)$ and $B\in \mathcal{P}\left(W\right)$, where $W\in \sigma$, then we can take $\lambda ={\mathcal{P}}^2\left(Y\right)$ that, of course, belongs to ξ and $\mathcal{P}\left(B\right)\in \lambda$. So, certainly, $\mathcal{P}\left(W\right)\cap \mathcal{P}\left(B\right)\ne \varnothing$, which proves that $B\in \overline{{\bigcup }_{\lambda \in \xi }{\bigcup }_{\mathcal{K}\in \lambda }\mathcal{K}}$ and consequently, $\mathcal{P}\left(Y\right)\subset l\circ l\left(\xi \right)$.

Now, suppose that $B\notin \left\{Y\right\}$, then $B\in \mathcal{P}\left(W\right)$, where $W=Y\setminus \left\{y\right\}\in \sigma$ for some $y\notin B$. If we take $\lambda ={\mathcal{P}}^2\left(Y\right)\in \xi$ and $\mathcal{K}=\left\{\right\{y\left\}\right\}\in \lambda$, then $P\left(W\right)\cap \mathcal{K}=\varnothing$. So, $B\notin {\bigcap }_{\lambda \in \xi }{\bigcap }_{\mathcal{K}\in \lambda }\overline{\mathcal{K}}$, i.e., $B\notin u\circ u\left(\xi \right)$. Therefore, we have proved that $u\circ u\left(\xi \right)=\left\{Y\right\}$. On the other hand, it is clear that $Y\in \overline{\mathcal{K}}$ for every $\mathcal{K}\in {\mathcal{P}}^2\left(Y\right)$, so $Y\in {\bigcap }_{\lambda \in \xi }{\bigcap }_{\mathcal{K}\in \lambda }\overline{\mathcal{K}}$, which means that $\left\{Y\right\}\subset u\circ u\left(\xi \right)$, and finishes the proof of the equalities.

Now, let us consider a function Ψ from X to ${\mathcal{P}}^2\left(Y\right)$, where X is a topological space with a topology τ. Then, for any $x_0\in X$, the family $\tau \left(x_0\right)=\left\{U\in \tau :x_0\in U\right\}$, is a filter base on X. So, the family ${\mathcal{B}}_{x_0}=\Psi \left(\tau \left(x_0\right)\right)=\{\{\Psi \left(x\right):x\in U\}:U\in \tau \left(x_0\right)\}$ is a filter base on ${\mathcal{P}}^2\left(Y\right)$ and then, as we will show, the following equalities are true:

$l\circ l\left({\mathcal{B}}_{x_0}\right)=\overline{{\bigcup }_{x\in X}\Psi \left(x\right)}$ and $u\circ u\left({\mathcal{B}}_{x_0}\right)={\bigcap }_{x\in X}\overline{\Psi \left(x\right)}$.

Indeed, by definition, we have

$l\circ l\left({\mathcal{B}}_{x_0}\right)=\overline{{\bigcup }_{U\in \tau \left(x_0\right)}{\bigcup }_{x\in U}\Psi \left(x\right)}$ and $u\circ u\left({\mathcal{B}}_{x_0}\right)={\bigcap }_{U\in \tau \left(x_0\right)}{\bigcap }_{x\in U}\overline{\Psi \left(x\right)}$.

Since $X\in \tau \left(x_0\right)$, we conclude that

$l\circ l\left({\mathcal{B}}_{x_0}\right)\supset \overline{{\bigcup }_{x\in X}\Psi \left(x\right)}$ and $u\circ u\left({\mathcal{B}}_{x_0}\right)\subset {\bigcap }_{x\in X}\overline{\Psi \left(x\right)}$.

The opposite inclusions are evident because $U\subset X$ for all $U\in \tau \left(x_0\right)$.

Remark 5.

It is easy to see that the formulas for the functions u and l permit the use of $\overline{\mathcal{K}}$ instead of $\mathcal{K}$ for each $\mathcal{K}\in \lambda$. So, the following equalities are true for any filter base ${\mathcal{B}}^{\xi }$ which generates a filter ξ:

$\mathcal{I}\left(\xi \right)=\mathcal{I}\left(\overline{\xi }\right)=\mathcal{I}\left(\overline{{\mathcal{B}}^{\xi }}\right)$ and $\mathcal{S}\left(\xi \right)=\mathcal{S}\left(\overline{\xi }\right)=\mathcal{S}\left(\overline{{\mathcal{B}}^{\xi }}\right)$,

• where $\overline{\zeta }=\{\{\overline{\mathcal{K}}:\mathcal{K}\in \lambda \}:\lambda \in \zeta \}$ for $\zeta \subset {\mathcal{P}}^3\left(Y\right)$.

We will follow the tradition by denoting the principal filter on ${\mathcal{P}}^2\left(Y\right)$ generated by ${\lambda }^{*}\subset {\mathcal{P}}^2\left(Y\right)$, as $\left[{\lambda }^{*}\right]$ instead of $\left[\left\{{\lambda }^{*}\right\}\right]$, and denoting the principal filter on ${\mathcal{P}}^2\left(Y\right)$ generated by $\mathcal{A}\in {\mathcal{P}}^2\left(Y\right)$, as $\left[\mathcal{A}\right]$ instead of $\left[\right\{\left\{\mathcal{A}\right\}\left\}\right]$.

Let us note some facts concerning the filters of type $\left[{\mathcal{P}}^2\left(A\right)\right]$, where $A\subset Y$, that will prove useful for the investigation of functions in terms of filters. Namely, using the lemma stated below and Remark 2, one can note the following fact:

Remark 6.

For a multifunction $F:(X,\tau )\to (Y,\sigma )$, $x\in X$ and $W\in \sigma$, the following equivalences are true:

• $\mathcal{P}\left(W\right)\cap l\circ u\left(\left[{\mathcal{P}}^2\left(F\left(x\right)\right)\right]\right)\ne \varnothing$ if and only if $x\in F^{+}\left(W\right)$;
• $\mathcal{P}\left(W\right)\cap u\circ l\left(\left[{\mathcal{P}}^2\left(F\left(x\right)\right)\right]\right)\ne \varnothing$ if and only if $x\in F^{-}\left(W\right)$.

Lemma 5.

For any topological space $(Y,\sigma )$, $A\subset Y$ and $\mathcal{A}\subset \mathcal{P}\left(Y\right)$, the following hold:

(i)

$l\circ u\left(\left[{\mathcal{P}}^2\left(A\right)\right]\right)=\overline{\left\{A\right\}}$ and $u\circ l\left(\left[{\mathcal{P}}^2\left(A\right)\right]\right)=\overline{\mathcal{P}\left(A\right)}$;

(ii)

$l\circ u\left(\left[\mathcal{A}\right]\right)=u\circ l\left(\left[\mathcal{A}\right]\right)=\overline{\mathcal{A}}$.

Proof. 

(i). According to Remark 4, we have

• $l\circ u\left(\left[\left\{{\mathcal{P}}^2\left(A\right)\right\}\right]\right)={\bigcap }_{\mathcal{K}\in {\mathcal{P}}^2\left(A\right)}\overline{\mathcal{K}}$;
• $u\circ l\left(\left[\left\{{\mathcal{P}}^2\left(A\right)\right\}\right]\right)=\overline{{\bigcup }_{\mathcal{K}\in {\mathcal{P}}^2\left(A\right)}\mathcal{K}}$.

So, if $B\in l\circ u\left(\left[{\mathcal{P}}^2\left(A\right)\right]\right)$ and B $\in \mathcal{P}\left(W\right)$, where $W\in \sigma$, then for $\mathcal{K}=\left\{A\right\}$ we obtain $\mathcal{P}\left(W\right)\cap \mathcal{K}\ne \varnothing$, i.e., $A\in \mathcal{P}\left(W\right)$ which proves that B $\in \overline{\left\{A\right\}}$. Conversely, if B $\in \overline{\left\{A\right\}}$, $\mathcal{K}\in {\mathcal{P}}^2\left(A\right)$ and B $\in \mathcal{P}\left(W\right)$, where $W\in \sigma$, then $\mathcal{P}\left(A\right)\subset \mathcal{P}\left(W\right)$ and, since $\mathcal{K}\subset \mathcal{P}\left(A\right)$, we have $\mathcal{P}\left(W\right)\cap \mathcal{K}\ne \varnothing$ which proves that B $\in {\bigcap }_{\mathcal{K}\in {\mathcal{P}}^2\left(A\right)}\overline{\mathcal{K}}$.

Now, suppose that $B\in u\circ l\left(\left[{\mathcal{P}}^2\left(A\right)\right]\right)$ and B $\in \mathcal{P}\left(W\right)$, where $W\in \sigma$, then there exists $\mathcal{K}\subset \mathcal{P}\left(A\right)$ such that $\mathcal{P}\left(W\right)\cap \mathcal{K}\ne \varnothing$. Consequently, for some $K\in \mathcal{K}$, $K\in \mathcal{P}\left(A\right)\cap \mathcal{P}\left(W\right)$, so $\mathcal{P}\left(W\right)\cap \mathcal{P}\left(A\right)\ne \varnothing$, which proves that B $\in \overline{\mathcal{P}\left(A\right)}$. Conversely, let $B\in \overline{\mathcal{P}\left(A\right)}$ and $B\in \mathcal{P}\left(W\right)$, where $W\in \sigma$, then there exist $K\subset Y$ such that $K\in \mathcal{P}\left(W\right)\cap \mathcal{P}\left(A\right)$; hence, we have $\mathcal{K}=\left\{K\right\}\in {\mathcal{P}}^2\left(A\right)$ such that $\mathcal{P}\left(W\right)\cap \mathcal{K}\ne \varnothing$ which proves that $B\in \overline{{\bigcup }_{\mathcal{K}\in {\mathcal{P}}^2\left(A\right)}\mathcal{K}}$.

Part (ii) follows immediately from Remark 5. □

Since each filter on a set Y belongs to the set ${\mathcal{P}}^2$(Y), it is convenient to denote by ${\mathcal{P}}_{\phi }^2\left(Y\right)$ the set of all such filters. If a set Y is itself a filter, we will use the following notation:

${\mathcal{P}}_{{\phi }^n}^{2n}\left(Y\right)={\mathcal{P}}_{\phi }^2\left({\mathcal{P}}_{{\phi }^{n-1}}^{2(n-1)}\left(Y\right)\right)$ for n = 1, 2, …,

• where ${\mathcal{P}}_{{\phi }^0}^0\left(Y\right)=Y$ and ${\mathcal{P}}_{{\phi }^1}^2\left(Y\right)={\mathcal{P}}_{\phi }^2\left(Y\right)$.

It is clear that, according to Lemma 2 and Remark 4, the operations $\mathcal{I}=l\circ u$ and $\mathcal{S}=u\circ l$, as well as the compositions $u\circ u$ and $l\circ l$, might be thought to be the functions from ${\mathcal{P}}_{\phi }^2\left({\mathcal{P}}^2\left(Y\right)\right)$ to ${\mathcal{P}}^2\left(Y\right)$.

Following Schwarz [10], for each function f:X →Y, we will also denote by f the induced function that assigns to each nonempty subset A of X its image f(A)$\in \mathcal{P}\left(Y\right)$. In general, for $\alpha \subset {\mathcal{P}}^n\left(X\right)$ and $n\in N$, we have $f\left(\alpha \right)$ = $\left\{f\left(\beta \right)\in {\mathcal{P}}^n\left(Y\right):\beta \in \alpha \right\}$. So, we will consider the following compositions:

${\mathcal{P}}_{{\phi }^n}^{2n}({\mathcal{P}}^2$(Y))$\stackrel{f_1}{⟶}{\mathcal{P}}_{{\phi }^{n-1}}^{2(n-1)}({\mathcal{P}}^2$(Y))$\stackrel{f_2}{⟶}$…$\stackrel{f_{n-1}}{⟶}{\mathcal{P}}_{\phi }^2({\mathcal{P}}^2$(Y))$\stackrel{f_n}{⟶}{\mathcal{P}}^2$(Y), i.e.,

$f_i:{\mathcal{P}}_{{\phi }^{n+1-i}}^{2(n+1-i)}({\mathcal{P}}^2$(Y))$⟶{\mathcal{P}}_{{\phi }^{n-i}}^{2(n-i)}({\mathcal{P}}^2$(Y)),

• where i = 1, 2, …, n, and $f_i\in \left\{l\circ u,u\circ l,u\circ u,l\circ l\right\}$.

Equivalently,

$h_{2n}\circ h_{2n-1}\circ \dots \circ h_2\circ h_1:{\mathcal{P}}_{{\phi }^n}^{2n}\left({\mathcal{P}}^2\left(Y\right)\right)⟶{\mathcal{P}}^2$(Y),

• where $h_{2i}\circ h_{2i-1}:{\mathcal{P}}_{{\phi }^{n+1-i}}^{2(n+1-i)}({\mathcal{P}}^2$(Y))$⟶{\mathcal{P}}_{{\phi }^{n-i}}^{2(n-i)}({\mathcal{P}}^2$(Y)), $i=1,2,\dots ,n$ and ($h_{2i},h_{2i-1}$) $\in \left\{(l,u),(u,l),(u,u),(l,l)\right\}$.

Bearing in mind the case described in Remark 4 and according to Lemma 4, one can use in the above compositions instead of filters, their filter bases, when ($h_{2i},h_{2i-1}$) $\in \left\{(l,u),(u,l)\right\}$.

2.2. Cluster Operators

Given a topological space $(X,\tau )$, we will use the notation $\tau$ also for the function $\tau :X⟶{\mathcal{P}}^2\left(X\right)$ defined by the formula

$\tau \left(x\right)$ = $\left\{U\in \tau :x\in U\right\}$ for all $x\in X$.

We denote by ${\tau }^2$ the function ${\tau }^2:X⟶{\mathcal{P}}^4\left(X\right)$ defined as

${\tau }^2\left(x\right)=\tau \left(\tau \left(x\right)\right)$ for all $x\in X$, i.e.,

${\tau }^2\left(x\right)=\left\{\left\{\tau \left(u\right):u\in U\right\}:U\in \tau \left(x\right)\right\}$ for all $x\in X$.

In general, for any $n\in N$, we consider the function ${\tau }^n:X⟶{\mathcal{P}}^{2n}\left(X\right)$ defined by the pattern

${\tau }^n\left(x\right)=\tau ({\tau }^{n-1}$(x)) for all $x\in X$,

• where ${\tau }^1=\tau$, and ${\tau }^0$ denotes the identity function on X.

It is easy to show inductively that ${\tau }^n\left({\tau }^k\left(x\right)\right)={\tau }^k\left({\tau }^n\left(x\right)\right)$ for all $n,k\in N$ and $x\in X$. Of course, because of the assumption that $(X,\tau )$ is a $T_1$ space, the function $\tau$ is injective.

Indeed, if $a,b\in X$ and $a\ne b$, then the subset $U=X\setminus \left\{a\right\}$ belongs to $\tau$ and $b\in U$, so $U\in \tau \left(b\right)$, but $U\notin \tau \left(a\right)$.

Remark 7.

From now on, we will use the following three alternative formulas for ${\tau }^n\left(x_0\right)$, where $x_0\in X$ and $n=1,2,\dots$.

Directly from definition:

• $\left\{\dots \left\{\left\{x_n:{\tau }^i\left(x_{n-i}\right)\in {\tau }^i\left(U_{n-i}\right)\right\}:{\tau }^i\left(U_{n-i}\right)\in {\tau }^{i+1}\left(x_{n-(i+1)}\right)\right\}:i=0,\dots ,n-1\right\}$

or, on the short form:

$\left\{\dots \left\{x_n:{\mathcal{B}}_{(i-1)mod2}^{(n,⌊{\displaystyle \frac{i-1}{2}}⌋)}\in {\mathcal{B}}_{imod2}^{(n,⌊{\displaystyle \frac{i}{2}}⌋)}\right\}:i=1,\dots ,2n\right\}$, where

${\mathcal{B}}_0^{(n,i)}$ = ${\tau }^i\left(x_{n-i}\right)$ for $i\in \left\{0,\dots ,n\right\}$ and,

${\mathcal{B}}_1^{(n,i)}$ = ${\tau }^i\left(U_{n-i}\right)$ for $i\in \left\{0,\dots ,n-1\right\}$.

So, any 2n-tuple of index sets of ${\tau }^n\left(x_0\right)$ is of the form

$({\mathcal{B}}_1^{(n,0)}$, ${\mathcal{B}}_0^{(n,1)}$, ${\mathcal{B}}_1^{(n,1)}$, ${\mathcal{B}}_0^{(n,2)}$, ${\mathcal{B}}_1^{(n,2)}$, …, ${\mathcal{B}}_1^{(n,n-1)}$, ${\mathcal{B}}_0^{(n,n)})\in$

${\mathcal{P}}^1\left(X\right)\times {\mathcal{P}}^2\left(X\right)\times \dots \times {\mathcal{P}}^{2n-1}\left(X\right)\times {\mathcal{P}}^{2n}\left(X\right)$,

i.e., ${\mathcal{B}}_{kmod2}^{(n,⌊{\displaystyle \frac{k}{2}}⌋)}\in {\mathcal{P}}^k\left(X\right)$, where $k\in \left\{1,2,\dots ,2n\right\}$.

The justification of the third formula comes from the lemma below.

$\left(iii\right)$$\left\{\dots \left\{\left\{x_n:z_{n-i}\in U_{n-i}\right\}:U_{n-i}\in \tau \left(x_{n-(i+1)}\right)\right\}:i=0,\dots ,n-1\right\}$.

For the same reasons, we have the following two equivalences:

$\left(iv\right)$ (1) ${\mathcal{B}}_0^{(n,i)}\in {\mathcal{B}}_1^{(n,i)}$ if and only if ${\mathcal{B}}_0^{(n-m,i-m)}\in {\mathcal{B}}_1^{(n-m,i-m)}$ and,

    (2) ${\mathcal{B}}_1^{(n,i)}\in {\mathcal{B}}_0^{(n,i+1)}$ if and only if ${\mathcal{B}}_1^{(n-m,i-m)}\in {\mathcal{B}}_0^{(n-m,i+1-m)}$

for $i\in \left\{0,\dots ,n-1\right\}$ and $m\in \left\{0,\dots ,i\right\}$.

Lemma 6.

Let $(X,\tau )$ be a topological space, $x\in X$ and $i=1,2,\dots$ Then, the following statements are equivalent for any $W\in \tau$:

(i)

$x\in$ W;

(ii)

${\tau }^i\left(x\right)\in {\tau }^i\left(W\right)$;

(iii)

${\tau }^i\left(W\right)\in {\tau }^{i+1}\left(x\right)$.

Proof. 

Let us first show that for any $n\in N$, the function ${\tau }^n$ is injective. If ${\tau }^2\left(a\right)={\tau }^2\left(b\right)$ for some $a,b\in X$, which means that $\left\{\tau \left(U\right):U\in \tau \left(a\right)\right\}=\left\{\tau \left(V\right):V\in \tau \left(b\right)\right\}$, then for every $U\in \tau \left(a\right)$ there exists $V\in \tau \left(b\right)$ such that $\tau \left(U\right)=\tau \left(V\right)$ which implies that $U=V$, because the function $\tau$ is injective. Consequently, $\tau \left(a\right)\subset \tau \left(b\right)$. Analogously, one can show that $\tau \left(b\right)\subset \tau \left(a\right)$. Since $\tau$ is injective, the equality $\tau \left(a\right)=\tau \left(b\right)$ implies that $a=b$ and proves that the function ${\tau }^2$ is injective. Now, assume that the function ${\tau }^k$ is injective for $k\in N$, and let ${\tau }^{k+1}\left(a\right)={\tau }^{k+1}\left(b\right)$ for $a,b\in X$. Then, we have ${\tau }^k\left(\tau \left(a\right)\right)={\tau }^k\left(\tau \left(b\right)\right)$, so $\left\{{\tau }^k\left(U\right):U\in \tau \left(a\right)\right\}=\left\{{\tau }^k\left(V\right):V\in \tau \left(b\right)\right\}$ and, using the assumption on ${\tau }^k$, analogously as in the case of ${\tau }^2$, we obtain that $a=b$.

The implication $\left(i\right)\Rightarrow \left(ii\right)$ is obvious, so assume that ${\tau }^i\left(x\right)\in {\tau }^i\left(W\right)$. Then, there exists a w $\in W$ such that ${\tau }^i\left(x\right)={\tau }^i\left(w\right)$ and, because of the injectivity property of ${\tau }^i$ we have $x=w$. So, $W\in \tau \left(x\right)$ and thus ${\tau }^i\left(W\right)\in {\tau }^{i+1}\left(x\right)$, i.e., $\left(iii\right)$. The assumption (iii) means that ${\tau }^i\left(W\right)\in {\tau }^i\left({\tau }^i\left(W\right)\right)=\left\{{\tau }^i\left(U\right):U\in \tau \left(x\right)\right\}$. Therefore, ${\tau }^i\left(W\right)={\tau }^i\left(U\right)$ for some $U\in \tau \left(z\right)$ and consequently $W=U$, so $x\in W$ which finishes the proof. □

It is evident that, for a given pair $\left(\right(X,\tau )$, $(Y,\sigma ))$ of topological spaces, for any function $\Psi :X⟶{\mathcal{P}}^2\left(Y\right)$ and $x\in X$, the set $\Psi \circ \tau \left(x\right)=\left\{\left\{\Psi \left(x_1\right):x_1\in U_1\right\}:U_1\in \tau \left(x\right)\right\}$ is a filter base on ${\mathcal{P}}^2\left(Y\right)$, so $[\Psi \circ \tau \left(x\right)]\in {\mathcal{P}}_{\phi }^2\left({\mathcal{P}}^2\left(Y\right)\right)$. For the same reason, in the case of a function $\mathcal{F}:X⟶{\mathcal{P}}_{\phi }^2\left({\mathcal{P}}^2\left(Y\right)\right)$ we have $[\mathcal{F}\circ \tau \left(x\right)]\in {\mathcal{P}}_{{\phi }^2}^4\left({\mathcal{P}}^2\left(Y\right)\right)$.

In general, given a function $\Psi :X⟶{\mathcal{P}}^2\left(Y\right)$ and $n\in \left\{1,2,3,\dots \right\}$, we define the function

$[\Psi \circ {\tau }^n]:X⟶{\mathcal{P}}_{{\phi }^n}^{2n}\left({\mathcal{P}}^2\left(Y\right)\right)$ by

$[\Psi \circ {\tau }^n]\left(x\right)$ = $\left[[\Psi \circ {\tau }^{n-1}]\left(\tau \left(x\right)\right)\right]$ for all $x\in X$,

• where $[\Psi \circ {\tau }^1]\left(x\right)=[\Psi \circ \tau \left(x\right)]$.

We also consider such a function corresponding to the number n = 0, defined by

$[\Psi \circ {\tau }^0]\left(x\right)$ = $[\Psi (x\left)\right]$ for all $x\in X$.

Of course, sets of the form $[\Psi \circ {\tau }^n]\left(x\right)$, $x\in X$, $n\in \left\{1,2,\dots \right\}$, are arguments of the compositions $h_{2n}\circ h_{2n-1}\circ \dots \circ h_2\circ h_1$, where $h_i\in \left\{u,l\right\}$ for i = 1, 2, …, 2n, so we can consider the following functions:

$h_{2n}\circ h_{2n-1}\circ \dots h_2\circ h_1\circ [\Psi \circ {\pi }^n]:X⟶{\mathcal{P}}^2\left(Y\right)$.

Because the number of the functions $h_i\in \left\{u,l\right\}$ for i = 1, 2, …, 2n, that is used in this expression is determined by ${\tau }^n$, we will use the following short notation to describe those compositions:

  (C.F) $〈h_{2n},h_{2n-1},\dots ,h_2,h_1,\Psi 〉:X\to {\mathcal{P}}^2\left(Y\right)$.

The function $[\Psi \circ {\pi }^0]$ plays a special role since, according to Lemma 5(ii), we have $l\circ u\circ [\Psi \circ {\tau }^0]\left(x\right)=u\circ l\circ [\Psi \circ {\tau }^0]\left(x\right)=\overline{\Psi \left(x\right)}$ for all $x\in X$. So, denoting the function $l\circ u\circ [\Psi \circ {\tau }^0]=u\circ l\circ [\Psi \circ {\pi }^0]$ by $\overline{\Psi }$, i.e.,

$\overline{\Psi }\left(x\right)=\overline{\Psi \left(x\right)}$ for all $x\in X$,

and bearing in mind Remark 5, we obtain the following equality:

$h_{2n}\circ h_{2n-1}\circ \dots h_2\circ h_1\circ [\Psi \circ {\tau }^n]=h_{2n}\circ h_{2n-1}\circ \dots h_2\circ h_1\circ [\overline{\Psi }\circ {\tau }^n]$

for all $n\in \left\{1,2,\dots \right\}$, where $h_i\in \left\{u,l\right\}$ for i = 1, 2, …, 2n.

Therefore, in the special case when n = 0, we mean that $\overline{\Psi \left(x\right)}$ is the value of the function denoted in accordance with the above convention (CL.F), by $〈\Psi 〉$, i.e.,

$〈\Psi 〉=\overline{\Psi }$.

So, according to the above findings, we have the following equality:

$〈h_{2n},h_{2n-1},\dots ,h_2,h_1,\Psi 〉=〈h_{2n},h_{2n-1},\dots ,h_2,h_1,〈\Psi 〉〉$

• for all $\Psi \in {\mathcal{P}}^2{\left(Y\right)}^X$.

Given $\mathcal{A}\in {\mathcal{P}}^2\left(Y\right)$, we denote by $〈\mathcal{A}〉$ the constant function taking the value $\overline{\mathcal{A}}$, i.e.,

$〈\mathcal{A}〉\left(x\right)=\overline{\mathcal{A}}$ for all $x\in X$.

For any composition $h_{2n}\circ h_{2n-1}\circ \dots \circ h_2\circ h_1$, where $h_i\in \left\{u,l\right\}$ for i = 1, 2, …, 2n, we will use the symbol $〈h_{2n},h_{2n-1},\dots ,h_2,h_1〉$ to denote the function

    (C.O) $〈h_{2n},h_{2n-1},\dots ,h_2,h_1〉:{\mathcal{P}}^2{\left(Y\right)}^X⟶{\mathcal{P}}^2{\left(Y\right)}^X$

• defined by

$〈h_{2n},h_{2n-1},\dots ,h_2,h_1〉(\Psi )=〈h_{2n},h_{2n-1},\dots ,h_2,h_1,\Psi 〉$

• for all $\Psi$:X $\to {\mathcal{P}}^2\left(Y\right)$.

For the case where $n=0$, $〈\Psi 〉$ is understood to be the value of the function of type (C.O) denoted by $〈\dots 〉$, for the argument $\Psi$, i.e.,

$〈\dots 〉(\Psi )=〈\Psi 〉$ for all $\Psi \in {\mathcal{P}}^2{\left(Y\right)}^X$.

For a convenient terminology, we establish the following definition.

Definition 1.

Let $(X,\tau )$ and $(Y,\sigma )$ be topological spaces and let Ψ be a function from X to ${\mathcal{P}}^2{\left(Y\right)}^X$.

(i)

Any function of the form

$〈h_{2n},h_{2n-1},\dots ,h_2,h_1,\Psi 〉:X\to {\mathcal{P}}^2\left(Y\right)$

defined in (C.F) will be called a cluster function.

(ii)

By a cluster operator, we mean any function of the form

$〈h_{2n},h_{2n-1},\dots ,h_2,h_1〉:{\mathcal{P}}^2{\left(Y\right)}^X⟶{\mathcal{P}}^2{\left(Y\right)}^X$

defined in (C.O).

The following simple properties will be used later, where $\mathcal{C}.\mathcal{O}(X,Y)$ denotes the collection of all cluster operators for a given pair $\left(\right(X,\tau ),(Y,\sigma \left)\right)$ of topological spaces.

Lemma 7.

For any functions Ψ, ${\Psi }^{*}\in {\mathcal{P}}^2{\left(Y\right)}^X$ and $\mathcal{A}\in {\mathcal{P}}^2\left(Y\right)$, the following conditions hold:

(i)

$〈h_{2n},h_{2n-1},\dots ,h_2,h_1,〈g_{2m},g_{2m-1},\dots ,g_2,g_1,\Psi 〉〉$=

$\hspace{1em}〈h_{2n},h_{2n-1},\dots ,h_2,h_1,g_{2m},g_{2m-1},\dots ,g_2,g_1,\Psi 〉$ for all

$\hspace{1em}〈h_{2n},h_{2n-1},\dots ,h_2,h_1〉$, $〈g_{2m},g_{2m-1},\dots ,g_2,g_1〉\in \mathcal{C}.\mathcal{O}(X,Y)$.

(ii)

For any $〈h_{2n},h_{2n-1},\dots ,h_2,h_1〉\in \mathcal{C}.\mathcal{O}(X,Y)$ we have:

(a)

$\hspace{1em}〈l,l,h_{2n},h_{2n-1},\dots ,h_2,h_1,\Psi 〉=〈l,l,\Psi 〉$;

(b)

$\hspace{1em}〈u,u,h_{2n},h_{2n-1},\dots ,h_2,h_1,\Psi 〉=〈u,u,\Psi 〉$;

(c)

$\hspace{1em}〈l,u,〈\mathcal{A}〉〉=〈u,l,〈\mathcal{A}〉〉=〈\mathcal{A}〉$.

(iii)

For any $\alpha \in \left\{l,u\right\}$ we have:

(a)

$\hspace{1em}〈u,l,u,\alpha 〉$ = $〈u,\alpha 〉$;

(b)

$\hspace{1em}〈l,u,l,\alpha 〉$ = $〈l,\alpha 〉$;

(c)

$\hspace{1em}〈\alpha ,u,l,u〉$ = $〈\alpha ,u〉$;

(d)

$\hspace{1em}〈\alpha ,l,u,l〉$ = $〈\alpha ,l〉$.

(iv)

If $\Psi \left(x\right)\subset {\Psi }^{*}\left(x\right)$ for all $x\in X$, then

$〈h_{2n},h_{2n-1},\dots ,h_2,h_1,\Psi 〉\left(x\right)\subset 〈h_{2n},h_{2n-1},\dots ,h_2,h_1,{\Psi }^{*}〉\left(x\right)$ for all

$〈h_{2n},h_{2n-1},\dots ,h_2,h_1〉\in \mathcal{C}.\mathcal{O}(X,Y)$ and $x\in X$.

Proof. 

To show (i), let us observe that

$g_{2m}\circ g_{2m-1}\circ \dots \circ g_2\circ g_1\circ [\Psi \circ {\tau }^{m+n}]=$

$[g_{2m}\circ g_{2m-1}\circ \dots \circ g_2\circ g_1\circ [\Psi \circ {\tau }^m]\circ {\tau }^n]=$

$[〈g_{2m},g_{2m-1},\dots ,g_2,g_1,\Psi 〉\circ {\tau }^n]$, thus

$〈h_{2n},h_{2n-1},\dots ,h_2,h_1,g_{2m},g_{2m-1},\dots ,g_2,g_1,\Psi 〉=$

$h_{2n}\circ h_{2n-1}\circ \dots \circ h_2\circ h_1\circ g_{2m}\circ g_{2m-1}\circ \dots \circ g_2\circ g_1\circ [\Psi \circ {\tau }^{m+n}]=$

$h_{2n}\circ h_{2n-1}\circ \dots \circ h_2\circ h_1\circ [〈g_{2m},g_{2m-1},\dots ,g_2,g_1,\Psi 〉\circ {\tau }^n]=$

$〈h_{2n},h_{2n-1},\dots ,h_2,h_1,〈g_{2m},g_{2m-1},\dots ,g_2,g_1,\Psi 〉〉$.

The properties (a) and (b) described in part (ii) follow immediately from Remark 4 after using (i). To check property (c), one needs only note that $[〈\mathcal{A}〉\circ {\pi }^1]\left(z\right)=\left[\overline{\mathcal{A}}\right]$ for any $z\in Z$, and then to use Lemma 5(ii) and Remark 5.

For the proof of (iii), we consider the two cases, $\alpha =u$ or $\alpha =l$, and then, using (ii), part (c) (resp. part (b)), we obtain $〈u,l,u,u〉$ = $〈u,u〉$ (resp. $〈u,u,l,u〉$ = $〈u,u〉$) or, using (ii), part (c) (resp. part (a)), we obtain $〈l,u,l,l〉$ = $〈l,l〉$ (resp. $〈l,l,u,l〉$ = $〈l,l〉$). So, it remains to show that $〈u,l,u,l〉$ = $〈u,l〉$ and $〈l,u,l,u〉$ = $〈l,u〉$.

For this purpose, let us take a function $\Psi :X\to {\mathcal{P}}^2\left(Y\right)$, $x\in X$, $U_1\in \tau \left(x\right)$ and let us apply Lemma 3. It is clear that, for all $x_1\in U_1$, we have $l(\Psi \left(U_1\right))\in \left\{l(\Psi \left(U_2\right)):U_2\in \tau \left(x_1\right)\right\}$ and $u(\Psi \left(U_1\right))\in \left\{u(\Psi \left(U_2\right)):U_2\in \tau \left(x_1\right)\right\}$, hence

${\bigcap }_{U_2\in \tau \left(x_1\right)}l(\Psi \left(U_2\right))\subset l(\Psi \left(U_1\right))$ and $u(\Psi \left(U_1\right))\subset \overline{{\bigcup }_{U_2\in \pi \left(x_1\right)}u(\Psi \left(U_2\right))}$.

Consequently,

$\overline{{\bigcup }_{x_1\in U_1}{\bigcap }_{U_2\in \tau \left(x_1\right)}l(\Psi \left(U_2\right))}\subset l(\Psi \left(U_1\right))$ and

$u(\Psi \left(U_1\right))\subset {\bigcap }_{x_1\in U_1}\overline{{\bigcup }_{U_2\in \tau \left(x_1\right)}u(\Psi \left(U_2\right))}$ for all $U_1\in \tau \left(x\right)$ which implies that

${\bigcap }_{U_1\in \tau \left(x\right)}\overline{{\bigcup }_{x_1\in U_1}{\bigcap }_{U_2\in \tau \left(x_1\right)}l(\Psi \left(U_2\right))}\subset {\bigcap }_{U_1\in \tau \left(x\right)}l(\Psi \left(U_1\right))$ and

$\overline{{\bigcup }_{U_1\in \tau \left(x\right)}u(\Psi \left(U_1\right))}\subset \overline{{\bigcup }_{U_1\in \tau \left(x\right)}{\bigcap }_{x_1\in U_1}\overline{{\bigcup }_{U_2\in \tau \left(x_1\right)}u(\Psi \left(U_2\right))}}$, and proves the following inclusions:

• $〈u,l,u,l,\Psi 〉\left(x\right)\subset 〈u,l,\Psi 〉\left(x\right)$ and $〈l,u,\Psi 〉\left(x\right)\subset 〈l,u,l,u,\Psi 〉\left(x\right)$, respectively, for all $\Psi :X\to {\mathcal{P}}^2\left(Y\right)$ and $x\in X.$

To prove the inverse inclusions, let us note that $〈u,l,\Psi 〉\left(x\right)\in 〈u,l,\Psi 〉\left(U_1\right)$ and $〈l,u,\Psi 〉\left(x\right)\in 〈l,u,\Psi 〉\left(U_1\right)$ for all $U_1\in \tau \left(x\right)$.

So, $〈u,l,\Psi 〉\left(x\right)\in {\bigcap }_{U_1\in \tau \left(x\right)}〈u,l,\Psi 〉\left(U_1\right)\subset \bigcap [〈u,l,\Psi 〉\circ \tau \left(x\right)]$ and

$〈l,u,\Psi 〉\left(x\right)\in {\bigcap }_{U_1\in \tau \left(x\right)}〈l,u,\Psi 〉\left(U_1\right)\subset \bigcap [〈l,u,\Psi 〉\circ \tau \left(x\right)]$ which implies, according to Lemma 3, that

$〈u,l,\Psi 〉\left(x\right)\subset u\circ l\circ [〈u,l,\Psi 〉\circ \tau \left(x\right)]=〈u,l,〈u,l,\Psi 〉〉\left(x\right)=〈u,l,u,l,\Psi 〉\left(x\right)$ and

$〈l,u,l,u,\Psi 〉\left(x\right)=〈l,u,〈l,u,\Psi 〉〉\left(x\right)=l\circ u\circ [〈l,u,\Psi 〉\circ \tau \left(x\right)]\subset 〈l,u,\Psi 〉\left(x\right)$ So, the following inclusions hold true:

••

$〈u,l,\Psi 〉\left(x\right)\subset 〈u,l,u,l,\Psi 〉\left(x\right)$ and $〈l,u,l,u,\Psi 〉\left(x\right)\subset 〈l,u,\Psi 〉\left(x\right)$, respectively.

Finally, using • and ••, we obtain $〈u,l,u,l〉$ = $〈u,l〉$ and $〈l,u,l,u〉$ = $〈l,u〉$ which finishes the proof of part (iii). The statement (iv) follows immediately from the definitions of functions u and l. □

Of course, the set ${\mathcal{P}}^2\left(Y\right)$ is partially ordered by the inclusion relation. Thus, there is a naturally induced partial order ⪯ on ${\mathcal{P}}^2{\left(Y\right)}^X$ in which one function dominates another if this is true pointwise, i.e., for ${\Psi }_1,{\Psi }_2\in {\mathcal{P}}^2{\left(Y\right)}^X$, ${\Psi }_1⪯{\Psi }_2$ means that ${\Psi }_1\left(x\right)\subset {\Psi }_2\left(x\right)$ for all $x\in X$.

Analogously, the partial order ⪯ on ${\mathcal{P}}^2{\left(Y\right)}^X$ induces a partial order on $\mathcal{C}.\mathcal{O}(X,Y)$, which we will also denote by ⪯, i.e.,

if $〈h_{2n},h_{2n-1},\dots ,h_2,h_1〉$ and $〈g_{2m},g_{2m-1},\dots ,g_2,g_1〉$ belong to $\mathcal{C}.\mathcal{O}(X,Y)$, then

$〈h_{2n},h_{2n-1},\dots ,h_2,h_1〉⪯〈g_{2m},g_{2m-1},\dots ,g_2,g_1〉$ just when

$〈h_{2n},h_{2n-1},\dots ,h_2,h_1,\Psi 〉⪯〈g_{2m},g_{2m-1},\dots ,g_2,g_1,\Psi 〉$

for all $\Psi \in {\mathcal{P}}^2{\left(Y\right)}^X$, i.e.,

for every $\Psi \in {\mathcal{P}}^2{\left(Y\right)}^X$ and $x\in X$, the following inclusion holds:

$〈h_{2n},h_{2n-1},\dots ,h_2,h_1,\Psi 〉\left(x\right)\subset 〈g_{2m},g_{2m-1},\dots ,g_2,g_1,\Psi 〉\left(x\right)$.

Now, let us recall some definitions. By a monoid, we mean a semigroup with a neutral element. A partially ordered monoid [11] is an ordered quadruple $(\mathcal{S},\odot ,e,⪯)$ such that

(i)

$(\mathcal{S},\odot ,e)$ is a monoid,

(ii)

$(\mathcal{S},⪯)$ is a partially ordered set and

(iii)

the order ⪯ is compatible with ⊙, in the sense that for all $a,b,c\in \mathcal{S}$, $a⪯b$ implies $a\odot c⪯b\odot c$ and $c\odot a⪯c\odot b$.

Lemma 8.

For any topological spaces $(X,\tau )$ and $(Y,\sigma )$, the set $\mathcal{C}.\mathcal{O}(X,Y)$ has the structure of a partially ordered monoid $(\mathcal{C}.\mathcal{O}(X,Y),\odot ,〈\dots 〉,⪯)$ under the binary operation ⊙ defined by

$〈h_{2n},h_{2n-1},\dots ,h_2,h_1〉\odot 〈g_{2m},g_{2m-1},\dots ,g_2,g_1〉(\Psi )$=

$〈h_{2n},h_{2n-1},\dots ,h_2,h_1,〈g_{2m},g_{2m-1},\dots ,g_2,g_1,\Psi 〉〉$

• for any $〈h_{2n},h_{2n-1},\dots ,h_2,h_1〉$, $〈g_{2m},g_{2m-1},\dots ,g_2,g_1〉\in \mathcal{C}.\mathcal{O}(X,Y)$ and a function $\Psi :X⟶{\mathcal{P}}^2\left(Y\right)$.

Proof. 

According to Lemma 7 (i), for any

$〈h_{2n},h_{2n-1},\dots ,h_1〉,〈g_{2m},g_{2m-1},\dots ,g_1〉$, $〈p_{2k},p_{2k-1},\dots ,p_2〉\in \mathcal{C}.\mathcal{O}(X,Y)$ we have

$(〈h_{2n},h_{2n-1},\dots ,h_2,h_1〉\odot 〈g_{2m},g_{2m-1},\dots ,g_2,g_1〉)\odot 〈p_{2k},p_{2k-1},\dots ,p_2,p_1〉=$

$〈h_{2n},h_{2n-1},\dots ,h_2,h_1,g_{2m},g_{2m-1},\dots ,g_2,g_1,p_{2k},p_{2k-1},\dots ,p_2,p_1〉=$

$〈h_{2n},h_{2n-1},\dots ,h_2,h_1〉\odot (〈g_{2m},g_{2m-1},\dots ,g_2,g_1〉\odot 〈p_{2k},p_{2k-1},\dots ,p_2,p_1〉)$. So, the operation ⊙ fulfills the associative law.

The function $〈\dots 〉:{\mathcal{P}}^2{\left(Y\right)}^X⟶{\mathcal{P}}^2{\left(Y\right)}^X$ defined by $〈\dots 〉(\Psi )=〈\Psi 〉$ for all $\Psi \in {\mathcal{P}}^2{\left(Y\right)}^X$, is the neutral element for the operation ⊙.

Indeed, applying Lemma 7 (i), we get

$〈h_{2n},h_{2n-1},\dots ,h_2,h_1〉\odot 〈\dots 〉(\Psi )$ = $〈h_{2n},h_{2n-1},\dots ,h_2,h_1,〈\Psi 〉〉=$

$〈h_{2n},h_{2n-1},\dots ,h_2,h_1〉(\Psi )$

for all $\Psi \in {\mathcal{P}}^2{\left(Y\right)}^X$ and $〈h_{2n},h_{2n-1},\dots ,h_2,h_1〉\in \mathcal{C}.\mathcal{O}(X,Y)$.

In the reverse order, we have

$〈\dots 〉\odot 〈h_{2n},h_{2n-1},\dots ,h_1〉(\Psi )=$

$〈〈h_{2n},h_{2n-1},\dots ,h_2,h_1,\Psi 〉〉=\overline{〈h_{2n},h_{2n-1},\dots ,h_2,h_1,\Psi 〉}=$

$〈h_{2n},h_{2n-1},\dots ,h_2,h_1,\Psi 〉=〈h_{2n},h_{2n-1},\dots ,h_2,h_1〉(\Psi )$ because, according to Lemma 2, the values of cluster functions are closed in the space ($\mathcal{P}\left(Y\right),{\sigma }^u)$.

We will now show that the relation ⪯ is compatible with ⊙. For this purpose, let us take two arbitrary cluster operators $〈h_{2n},h_{2n-1},\dots ,h_2,h_1〉$ and $〈g_{2m},g_{2m-1},\dots ,g_2,g_1〉$ such that $〈h_{2n},h_{2n-1},\dots ,h_2,h_1〉⪯〈g_{2m},g_{2m-1},\dots ,g_2,g_1〉$. So, according to the definition,

$〈h_{2n},h_{2n-1},\dots ,h_2,h_1〉(\Psi )⪯〈g_{2m},g_{2m-1},\dots ,g_2,g_1〉(\Psi )$ i.e.,

$〈h_{2n},h_{2n-1},\dots ,h_2,h_1,\Psi 〉⪯〈g_{2m},g_{2m-1},\dots ,g_2,g_1,\Psi 〉(\ast )$

• for every $\Psi \in {\mathcal{P}}^2{\left(Y\right)}^X$.

Of course, it holds for every function $\Psi$ such that $\Psi =〈s_{2k},s_{2k-1},\dots ,s_2,s_1,{\Psi }^{*}〉$, where ${\Psi }^{*}\in {\mathcal{P}}^2{\left(Y\right)}^X$ and $〈s_{2k},s_{2k-1},\dots ,s_2,s_1〉\in \mathcal{C}.\mathcal{O}(X,Y)$. Thus, for every $\Psi \in {\mathcal{P}}^2{\left(Y\right)}^X$ and $〈s_{2k},s_{2k-1},\dots ,s_2,s_1〉\in \mathcal{C}.\mathcal{O}(X,Y)$ we have

$〈h_{2n},h_{2n-1},\dots ,h_2,h_1,〈s_{2k},s_{2k-1},\dots ,s_2,s_1,\Psi 〉〉⪯$

$〈g_{2m},g_{2m-1},\dots ,g_2,g_1,〈s_{2k},s_{2k-1},\dots ,s_2,s_1,\Psi 〉〉$ which means that

$〈h_{2m},h_{2m-1},\dots ,h_2,h_1,s_{2k},s_{2k-1},\dots ,s_2,s_1〉(\Psi )⪯$

$〈g_{2m},g_{2m-1},\dots ,g_2,g_1,s_{2k},s_{2k-1},\dots ,s_2,s_1〉(\Psi )$ or equivalently,

$〈h_{2m},h_{2m-1},\dots ,h_2,h_1〉\odot 〈s_{2k},s_{2k-1},\dots ,s_2,s_1〉(\Psi )⪯$

$〈g_{2m},g_{2m-1},\dots ,g_2,g_1〉\odot 〈s_{2k},s_{2k-1},\dots ,s_2,s_1〉(\Psi )$. So,

$〈h_{2m},h_{2m-1},\dots ,h_2,h_1〉\odot 〈s_{2k},s_{2k-1},\dots ,s_2,s_1〉⪯$

$〈g_{2m},g_{2m-1},\dots ,g_2,g_1〉\odot 〈s_{2k},s_{2k-1},\dots ,s_2,s_1〉$. $(\ast \ast )$

Now, let us note that the assumption $(\ast )$ means that $〈h_{2n},h_{2n-1},\dots ,h_2,h_1,\Psi 〉\left(x\right)\subset 〈g_{2m},g_{2m-1},\dots ,g_2,g_1,\Psi 〉\left(x\right)$ for all $x\in X$. Consequently, according to Lemma 7 (iv), for every $\Psi \in {\mathcal{P}}^2{\left(Y\right)}^X$ and $x\in X$ we have

$〈s_{2k},s_{2k-1},\dots ,s_2,s_1,〈h_{2n},h_{2n-1},\dots ,h_2,h_1,\Psi 〉〉\left(x\right)\subset$

$〈s_{2k},s_{2k-1},\dots ,s_2,s_1,〈g_{2m},g_{2m-1},\dots ,g_2,g_1,\Psi 〉〉\left(x\right)$. So,

$〈s_{2k},s_{2k-1},\dots ,s_2,s_1,〈h_{2n},h_{2n-1},\dots ,h_2,h_1,\Psi 〉〉⪯$

$〈s_{2k},s_{2k-1},\dots ,s_2,s_1,〈g_{2m},g_{2m-1},\dots ,g_2,g_1,\Psi 〉〉$ for all $\Psi \in {\mathcal{P}}^2{\left(Y\right)}^X$, i.e.,

$〈s_{2k},s_{2k-1},\dots ,s_2,s_1〉\odot 〈h_{2n},h_{2n-1},\dots ,h_1〉⪯$

$〈s_{2k},s_{2k-1},\dots ,s_2,s_1〉\odot 〈g_{2m},g_{2m-1},\dots ,g_2,g_1〉$ which, according to $(\ast \ast )$, completes the proof of compatibility between ⪯ and ⊙. □

Theorem 1.

For any topological spaces $(X,\tau )$ and $(Y,\sigma )$, the monoid $\mathcal{C}.\mathcal{O}(X,Y)$ has at most nine elements related to each other, as shown in the diagram below, where the arrows are compatible with the relation ⪯.

Proof. 

When it comes to the diagram, let us first prove that

• $〈\mathcal{I}〉⪯〈\mathcal{I},\mathcal{S},\mathcal{I}〉$;
• $〈\mathcal{I},\mathcal{S},\mathcal{I}〉⪯〈\mathcal{S},\mathcal{I}〉$ and $〈\mathcal{I},\mathcal{S},\mathcal{I}〉⪯〈\mathcal{I},\mathcal{S}〉$;
• $〈\mathcal{S},\mathcal{I}〉⪯〈\mathcal{S},\mathcal{I},\mathcal{S}〉$ and $〈\mathcal{I},\mathcal{S}〉⪯〈\mathcal{S},\mathcal{I},\mathcal{S}〉$;
• $〈\mathcal{S},\mathcal{I},\mathcal{S}〉⪯〈\mathcal{S}〉$, i.e.,

for all $\Psi \in {\mathcal{P}}^2{\left(Y\right)}^X$ and $x\in X$, the following hold:

(a)

$〈\mathcal{I},\Psi 〉\left(x\right)\subset 〈\mathcal{I},\mathcal{S},\mathcal{I},\Psi 〉\left(x\right)\subset 〈\mathcal{S},\mathcal{I},\Psi 〉\left(x\right)\cap 〈\mathcal{I},\mathcal{S},\Psi 〉\left(x\right)$;

(b)

$〈\mathcal{S},\mathcal{I},\Psi 〉\left(x\right)\cup 〈\mathcal{I},\mathcal{S},\Psi 〉\left(x\right)\subset 〈\mathcal{S},\mathcal{I},\mathcal{S},\Psi 〉\left(x\right)\subset 〈\mathcal{S},\Psi 〉\left(x\right)$.

For that purpose, let us note that

-

$〈\mathcal{I},\Psi 〉\left(x\right)\in 〈\mathcal{I},\Psi 〉\left(U\right)\in 〈\mathcal{I},\Psi 〉\left(\tau \left(x\right)\right)$;

-

$〈\mathcal{S},\Psi 〉\left(x\right)\in 〈\mathcal{S},\Psi 〉\left(U\right)\in 〈\mathcal{S},\Psi 〉\left(\tau \left(x\right)\right)$

• for any $x\in X$ and $U\in \tau \left(x\right)$.

Therefore, using Lemma 3, we obtain

$〈\mathcal{I},\Psi 〉\left(x\right)\subset 〈\mathcal{S},\mathcal{I},\Psi 〉\left(x\right)$ and $〈\mathcal{I},\mathcal{S},\Psi 〉\left(x\right)\subset 〈\mathcal{S},\Psi 〉\left(x\right)$ for all $x\in X$, respectively. Hence, since according to Lemma 7 (iii) and (iv), we have $〈\mathcal{I},\mathcal{I}〉$ = $〈\mathcal{I}〉$ and $〈\mathcal{S},\mathcal{S}〉$ = $〈\mathcal{S}〉$ and therefore $〈\mathcal{I},\Psi 〉\left(x\right)\subset 〈\mathcal{I},\mathcal{S},\mathcal{I},\Psi 〉\left(x\right)$ and $〈\mathcal{S},\mathcal{I},\mathcal{S},\Psi 〉\left(x\right)\subset 〈\mathcal{S},\Psi 〉\left(x\right)$ for all $x\in X$, i.e., the first inclusion in (a) and the second inclusion in (b) are true.

Now, let us observe that, by Lemma 3, we have $〈\mathcal{I},\Psi 〉\left(x\right)\subset \overline{\Psi \left(x\right)}\subset 〈\mathcal{S},\Psi 〉\left(x\right)$ or equivalently, $〈\mathcal{I},\Psi 〉\left(x\right)\subset 〈\Psi 〉\left(x\right)\subset 〈\mathcal{S},\Psi 〉\left(x\right)$ for all $x\in X$ since $\Psi \left(x\right)\in \Psi \left(U\right)\in \Psi \left(\tau \right(x\left)\right)$ for all $x\in X$ and $U\in \tau \left(x\right)$. So, according to Lemma 7 (iv) and (i), we have

-

$〈\mathcal{S},\mathcal{I},\Psi 〉\left(x\right)\subset 〈\mathcal{S},\Psi 〉\left(x\right)$ and $〈\mathcal{I},\Psi 〉\left(x\right)\subset 〈\mathcal{I},\mathcal{S},\Psi 〉\left(x\right)$

• for all $x\in X$.

Consequently, again from Lemma 7 (iv), we obtain

-

$〈\mathcal{I},\mathcal{S},\mathcal{I},\Psi 〉\left(x\right)\subset 〈\mathcal{I},\mathcal{S},\Psi 〉\left(x\right)$ and $〈\mathcal{S},\mathcal{I},\Psi 〉\left(x\right)\subset 〈\mathcal{S},\mathcal{I},\mathcal{S},\Psi 〉\left(x\right)$

for all $x\in X$.

We will finish the proof of (a) and (b) by showing, in an entirely analogous way, that

-

$〈\mathcal{I},\mathcal{S},\mathcal{I},\Psi 〉\left(x\right)\subset 〈\mathcal{S},\mathcal{I},\Psi 〉\left(x\right)$ and $〈\mathcal{I},\mathcal{S},\Psi 〉\left(x\right)\subset 〈\mathcal{S},\mathcal{I},\mathcal{S},\Psi 〉\left(x\right)$ for all $x\in X$.

Indeed, since it is clear that

-

$〈\mathcal{S},\mathcal{I},\Psi 〉\left(x\right)\in 〈\mathcal{S},\mathcal{I},\Psi 〉\left(U\right)\in 〈\mathcal{S},\mathcal{I},\Psi 〉\left(\tau \left(x\right)\right)$;

-

$〈\mathcal{I},\mathcal{S},\Psi 〉\left(x\right)\in 〈\mathcal{I},\mathcal{S},\Psi 〉\left(U\right)\in 〈\mathcal{I},\mathcal{S},\Psi 〉\left(\tau \left(x\right)\right)$.

for all $x\in X$ and $U\in \tau \left(x\right)$, applying Lemma 2.3 we obtain

-

$〈\mathcal{I},\mathcal{S},\mathcal{I},\Psi 〉\left(x\right)\subset 〈\mathcal{S},\mathcal{I},\Psi 〉\left(x\right)$;

-

$〈\mathcal{I},\mathcal{S},\Psi 〉\left(x\right)\subset 〈\mathcal{S},\mathcal{I},\mathcal{S},\Psi 〉\left(x\right)$, respectively,

for all $x\in X$.

We now show that the set $\left\{〈\mathcal{I}〉,〈\mathcal{S},〉,〈\mathcal{S},\mathcal{I}〉,〈\mathcal{I},\mathcal{S}〉,〈\mathcal{S},\mathcal{I},\mathcal{S}〉,〈\mathcal{I},\mathcal{S},\mathcal{I}〉\right\}$ is closed under the operation ⊙ as presents the following table, where the factor that labels the row comes first.

⊙	$〈\mathcal{I}〉$	$〈\mathcal{I},\mathcal{S},\mathcal{I}〉$	$〈\mathcal{S},\mathcal{I}〉$	$〈\mathcal{I},\mathcal{S}〉$	$〈\mathcal{S},\mathcal{I},\mathcal{S}〉$	$〈\mathcal{S}〉$
$〈\mathcal{I}〉$	$〈\mathcal{I}〉$	$〈\mathcal{I},\mathcal{S},\mathcal{I}〉$	$〈\mathcal{I},\mathcal{S},\mathcal{I}〉$	$〈\mathcal{I},\mathcal{S}〉$	$〈\mathcal{I},\mathcal{S}〉$	$〈\mathcal{I},\mathcal{S}〉$
$〈\mathcal{I},\mathcal{S},\mathcal{I}〉$	$〈\mathcal{I},\mathcal{S},\mathcal{I}〉$	$〈\mathcal{I},\mathcal{S},\mathcal{I},〉$	$〈\mathcal{I},\mathcal{S},\mathcal{I}〉$	$〈\mathcal{I},\mathcal{S}〉$	$〈\mathcal{I},\mathcal{S}〉$	$〈\mathcal{I},\mathcal{S}〉$
$〈\mathcal{S},\mathcal{I}〉$	$〈\mathcal{S},\mathcal{I}〉$	$〈\mathcal{S},\mathcal{I}〉$	$〈\mathcal{S},\mathcal{I}〉$	$〈\mathcal{S},\mathcal{I},\mathcal{S}〉$	$〈\mathcal{S},\mathcal{I},\mathcal{S}〉$	$〈\mathcal{S},\mathcal{I},\mathcal{S}〉$
$〈\mathcal{I},\mathcal{S}〉$	$〈\mathcal{I},\mathcal{S},\mathcal{I}〉$	$〈\mathcal{I},\mathcal{S},\mathcal{I}〉$	$〈\mathcal{I},\mathcal{S},\mathcal{I}〉$	$〈\mathcal{I},\mathcal{S}〉$	$〈\mathcal{I},\mathcal{S}〉$	$〈\mathcal{I},\mathcal{S}〉$
$〈\mathcal{S},\mathcal{I},\mathcal{S}〉$	$〈\mathcal{S},\mathcal{I}〉$	$〈\mathcal{S},\mathcal{I}〉$	$〈\mathcal{S},\mathcal{I}〉$	$〈\mathcal{S},\mathcal{I},\mathcal{S}〉$	$〈\mathcal{S},\mathcal{I},\mathcal{S}〉$	$〈\mathcal{S},\mathcal{I},\mathcal{S}〉$
$〈\mathcal{S}〉$	$〈\mathcal{S},\mathcal{I}〉$	$〈\mathcal{S},\mathcal{I}〉$	$〈\mathcal{S},\mathcal{I}〉$	$〈\mathcal{S},\mathcal{I},\mathcal{S}〉$	$〈\mathcal{S},\mathcal{I},\mathcal{S}〉$	$〈\mathcal{S}〉$

It is enough to verify the following two pairs of equalities:

(c) $〈h_{2n},\dots ,h_1,\mathcal{I},\mathcal{I},g_{2m},\dots ,g_1〉$= $〈h_{2n},\dots ,h_1,\mathcal{I},g_{2m},\dots ,g_1〉$ and

$〈h_{2n},\dots ,h_1,\mathcal{S},\mathcal{S},g_{2m},\dots ,g_1〉$= $〈h_{2n},\dots ,h_1,\mathcal{S},g_{2m},\dots ,g_1〉$

for any $〈h_{2n},h_{2n-1},\dots ,h_1〉$, $〈g_{2m},g_{2m-1},\dots ,g_1〉\in \mathcal{C}.\mathcal{O}(X,Y)$ and,

(d) $〈\mathcal{I},\mathcal{S},\mathcal{I},\mathcal{S}〉=〈\mathcal{I},\mathcal{S}〉$ and $〈\mathcal{S},\mathcal{I},\mathcal{S},\mathcal{I}〉=〈\mathcal{S},\mathcal{I}〉$.

For the proof of (c), let us note that by applying Lemma 7 (iii), we have $〈\mathcal{S},\mathcal{S}〉$ = $〈\mathcal{S}〉$ and $〈\mathcal{I},\mathcal{I}〉$ = $〈\mathcal{I}〉$ and, according to part (i) of this lemma we get

$〈h_{2n},h_{2n-1},\dots ,h_1,\mathcal{I},\mathcal{I},g_{2m},g_{2m-1},\dots ,g_1〉(\Psi )=$

$〈h_{2n},h_{2n-1},\dots ,h_1,〈\mathcal{I},\mathcal{I},g_{2m},g_{2m-1},\dots ,g_1,\Psi 〉〉=$

$〈h_{2n},h_{2n-1},\dots ,h_1,〈\mathcal{I},\mathcal{I},〈g_{2m},g_{2m-1},\dots ,g_1,\Psi 〉〉〉=$

$〈h_{2n},h_{2n-1},\dots ,h_1,〈\mathcal{I},〈g_{2m},g_{2m-1},\dots ,g_1,\Psi 〉〉〉=$

$〈h_{2n},h_{2n-1},\dots ,h_1,\mathcal{I},〈g_{2m},g_{2m-1},\dots ,g_1,\Psi 〉〉=$

$〈h_{2n},h_{2n-1},\dots ,h_1,\mathcal{I},g_{2m},g_{2m-1},\dots ,g_1〉(\Psi )$ for any $\Psi \in {\mathcal{P}}^2{\left(Y\right)}^X$.

In the same way, one can check the second part of (c).

Now, since condition (b) implies that $〈\mathcal{I},\mathcal{S},\Psi 〉\left(x\right)\subset 〈\mathcal{S},\Psi 〉\left(x\right)$, by Lemma 7 (iv) we have $〈\mathcal{S},\mathcal{I},\mathcal{S},\Psi 〉\left(x\right)\subset 〈\mathcal{S},\mathcal{S},\Psi 〉\left(x\right)=〈\mathcal{S},\Psi 〉\left(x\right)$ and consequently,

-

$〈\mathcal{I},\mathcal{S},\mathcal{I},\mathcal{S},\Psi 〉\left(x\right)\subset 〈\mathcal{I},\mathcal{S},\Psi 〉\left(x\right)$ for all $\Psi \in {\mathcal{P}}^2{\left(Y\right)}^X$ and $x\in X$.

On the other hand, for the same reason as the above, we obtain $〈\mathcal{I},\mathcal{S},\Psi 〉\left(x\right)\subset 〈\mathcal{S},\mathcal{I},\mathcal{S},\Psi 〉\left(x\right)$ and consequently,

-

$〈\mathcal{I},\mathcal{S},\Psi 〉\left(x\right)\subset 〈\mathcal{I},\mathcal{S},\mathcal{I},\mathcal{S},\Psi 〉\left(x\right)$ for all $\Psi \in {\mathcal{P}}^2{\left(Y\right)}^X$ and $x\in X$.

This ends the proof of the first equality in (d).

The checking of the second equality proceeds analogously by using condition (a) instead of (b).

To finish the proof, it suffices to note that for all $〈h_{2n},h_{2n-1},\dots ,h_1〉\in \mathcal{C}.\mathcal{O}(X,Y)$, $\Psi \in {\mathcal{P}}^2{\left(Y\right)}^X$ and $x\in X$, the following two properties hold:

• $〈u,u,\Psi 〉\left(x\right)\subset 〈h_{2n},h_{2n-1},\dots ,h_1,\Psi 〉\left(x\right)\subset 〈l,l,\Psi 〉\left(x\right)$ and
• If $(h_{2i},h_{2i-1})\in \left\{(u,u),(l,l)\right\}$ for some $i\in \left\{1,2,\dots n\right\}$, then
  $〈h_{2n},h_{2n-1},\dots ,h_1,\Psi 〉\left(x\right)=〈u,u,\Psi 〉\left(x\right)$ or
  $〈h_{2n},h_{2n-1},\dots ,h_1,\Psi 〉\left(x\right)=〈l,l,\Psi 〉\left(x\right)$.

The first property is an obvious consequence of Remark 4 and Lemma 2. When it comes to the second property, according to Remark 4, applying Lemma 7 (i) and then (ii) parts (a) and (c), we obtain

$〈h_{2n},h_{2n-1},\dots ,h_{2i+1},u,u,h_{2i-2},\dots ,h_1,\Psi 〉=$

$〈h_{2n},h_{2n-1},\dots ,h_{2i+1},〈u,u,h_{2i-2},\dots ,h_1,\Psi 〉〉=$

$〈h_{2n},h_{2n-1},\dots ,h_{2i+1},〈u,u,\Psi 〉〉=〈u,u,\Psi 〉$.

The proof for the case $(h_{2i},h_{2i-1})=(l,l)$ follows exactly in the same manner. So, the proof of Theorem 1 is finished. □

2.3. Generalized Continuity in Terms of the Cluster Operators

The concept of cluster functions of the form $〈h_{2n},h_{2n-1},\dots ,h_2,h_1,\Psi 〉$ is closely related to the classical notion of cluster sets of a single-valued function $f:(X,\tau )\to (Y,\sigma )$ at a point $x\in X$ [9,12] defined by

$C_f\left(x\right)=\bigcap \left\{Cl\left(f\right(U\left)\right)\subset Y:U\in \tau \left(x\right)\right\}$.

In [8], this concept has naturally been extended to multifunctions $F:(X,\tau )\to (Y,\sigma )$ as

$C_F\left(x\right)=\bigcap \left\{Cl\left(F\right(U\left)\right)\subset Y:U\in \tau \left(x\right)\right\}$.

It is easy to check that

$C_F\left(x\right)=\left\{y\in Y:x\in {\bigcap }_{W\in \sigma \left(y\right)}Cl(F^{-}\left(W\right)\right\}$.

According to Remark 2, we use the functions defined as

$x⟶\overline{\left\{F\left(x\right)\right\}}$ and $x⟶\overline{\mathcal{P}\left(F\right(x\left)\right)}$ for all $x\in X$.

Using Lemma 5, we can see that these functions may be presented in the form of patterns through the operations $\mathcal{I}$ and $\mathcal{S}$ as

$\overline{\left\{F\right(x\left)\right\}}=\mathcal{I}\left(\left[{\mathcal{P}}^2\left(F\left(x\right)\right)\right]\right)$ and $\overline{\mathcal{P}\left(F\right(x\left)\right)}=\mathcal{S}\left(\left[{\mathcal{P}}^2\left(F\left(x\right)\right)\right]\right)$ for all $x\in X$.

We will use the shorter notation, namely $\mathcal{I}F$ and $\mathcal{S}F$, respectively, i.e.,

$\mathcal{I}F\left(x\right)=\overline{\left\{F\right(x\left)\right\}}$ and $\mathcal{S}F\left(x\right)=\overline{\mathcal{P}\left(F\right(x\left)\right)}$ for all $x\in X$.

Of course, $\mathcal{I}F,\mathcal{S}F\in {\mathcal{P}}^2{\left(Y\right)}^X$ so, one can consider the cluster functions of types $〈h_{2n},h_{2n-1},\dots ,h_2,h_1,\mathcal{I}F〉$ and $〈h_{2n},h_{2n-1},\dots ,h_2,h_1,\mathcal{S}F〉$.

Using the concept of cluster functions, we can characterize cluster sets as follows:

Remark 8.

For any multifunction $F:(X,\tau )\to (Y,\sigma )$ and $x\in X$, the following properties are equivalent:

(i)

$y\in C_F\left(x\right)$;

(ii)

$\left\{y\right\}\in 〈\mathcal{S},\mathcal{S}F〉\left(x\right)$.

Indeed, it is enough to use, according to the characterization of $\mathcal{S}$ given in Lemma 2, the equality $〈\mathcal{S},\mathcal{S}F〉\left(x\right)={\bigcap }_{U_1\in \tau \left(x\right)}\overline{{\bigcup }_{x_1\in U_1}\mathcal{P}\left(F\left(x_1\right)\right)}$. Next, according to Remark 1, the property (ii) means that for every open sets W and $U_1$ with $\left\{y\right\}\in \mathcal{P}\left(W\right)$ and $x\in U_1$, there exists $x_1\in U_1$ such that $\mathcal{P}\left(W\right)\cap \mathcal{P}\left(F\left(x_1\right)\right)\ne \varnothing$, i.e., $x_1\in F^{-}\left(W\right)$.

The analogous characterizations we have in the case of the other types of cluster sets listed below that are investigated in [13] as an extension of the concept studied in [14,15]. Those types of cluster sets describe many kinds of generalized continuity of multifunctions [13], and for many types of convergence of nets of multifunctions, there are strict relations between the cluster set of the limit multifunction and the appropriate cluster sets of the members of the nets of multifunctions [16].

• $u.\alpha C_F\left(x\right)=\left\{y\in Y:x\in {\bigcap }_{W\in \sigma \left(y\right)}Int\left(Cl\left(Int\left(F^{+}\left(W\right)\right)\right)\right)\right\}$;
• $l.\alpha C_F\left(x\right)=\left\{y\in Y:x\in {\bigcap }_{W\in \sigma \left(y\right)}Int\left(Cl\left(Int\left(F^{-}\left(W\right)\right)\right)\right)\right\}$;
• $u.q.C_F\left(x\right)=\left\{y\in Y:x\in {\bigcap }_{W\in \sigma \left(y\right)}Cl\left(Int\left(F^{+}\left(W\right)\right)\right)\right\}$;
• $l.q.C_F\left(x\right)=\left\{y\in Y:x\in {\bigcap }_{W\in \sigma \left(y\right)}Cl\left(Int\left(F^{-}\left(W\right)\right)\right)\right\}$;
• $u.p.C_F\left(x\right)=\left\{y\in Y:x\in {\bigcap }_{W\in \sigma \left(y\right)}Int\left(Cl\left(F^{+}\left(W\right)\right)\right)\right\}$;
• $l.p.C_F\left(x\right)=\left\{y\in Y:x\in {\bigcap }_{W\in \sigma \left(y\right)}Int\left(Cl\left(F^{-}\left(W\right)\right)\right)\right\}$;
• $u.\beta C_F\left(x\right)=\left\{y\in Y:x\in {\bigcap }_{W\in \sigma \left(y\right)}Cl\left(Int\left(Cl\left(F^{+}\left(W\right)\right)\right)\right)\right\}$;
• $l.\beta C_F\left(x\right)=\left\{y\in Y:x\in {\bigcap }_{W\in \sigma \left(y\right)}Cl\left(Int\left(Cl\left(F^{-}\left(W\right)\right)\right)\right)\right\}$.

In the case of single-valued functions $f:(X,\tau )⟶(Y,\sigma )$ that are interpreted as multifunctions F defined by $F\left(x\right)=\left\{f\left(x\right)\right\}$ for all $x\in X$, we have the following suitable definitions of cluster sets:

• $\alpha .C_f\left(x\right)=l.\alpha C_F\left(x\right)=l.\alpha C_F\left(x\right)$;
• $q.C_f\left(x\right)=l.q.C_F\left(x\right)=u.q.C_F\left(x\right)$;
• $p.C_f\left(x\right)=l.p.C_F\left(x\right)=u.p.C_F\left(x\right)$;
• $\beta .C_f\left(x\right)=l.\beta C_F\left(x\right)=u.\beta C_F\left(x\right)$.

The concept of cluster sets of type $q.C_f\left(x\right)$ was introduced in [14] and used later in [15,17]. Another type of cluster set [18], of multifunctions $F:(X,\tau )⟶(Y,\sigma )$ has been defined as follows:

If $\mathcal{B}$ is a non-empty family of non-empty subsets of X, then a point $y\in Y$ is called a $\mathcal{B}$-cluster point of F at $x\in X$, i.e., $y\in {\mathcal{B}}_F\left(x\right)$, if for any open sets U, V with $x\in U$ and $y\in V$, there exists $B\in \mathcal{B}$ such that $B\subset U$ and $B\subset F^{-}\left(W\right)$.

This concept is used in further investigations, e.g., [18,19,20,21,22,23,24,25], and it describes two of those listed above types. Namely, it is easy to show that, in the case when $\mathcal{B}$ is the family of all nonempty open subsets $B\subset X$, then ${\mathcal{B}}_F\left(x\right)=l.q.C_F\left(x\right)$ and the equality is also true if $\mathcal{B}$ is the family of all nonempty $\alpha$-open [26] (resp. semi-open [27]) subsets $A\subset X$ defined by the condition $A\subset Int\left(Cl\right(Int\left(A\right)\left)\right)$ (resp. $A\subset Cl\left(Int\right(A)$). Analogously, in the case when $\mathcal{B}$ is the family of all nonempty pre-open (locally dense) subsets $A\subset X$ [28,29] defined by the condition $A\subset Int\left(Cl\right(A\left)\right))$, we have ${\mathcal{B}}_F\left(x\right)=l.\beta .C_F\left(x\right)$ and the equality is also true if $\mathcal{B}$ is the family of all nonempty $\beta$-open [30] subsets $A\subset X$ defined by the condition $A\subset Cl\left(Int\right(Cl\left(A\right)\left)\right)$.

Cluster sets may be also considered as the values of multifunctions from $(X,\tau )$, to $(Y,\sigma )$. Such multifunctions have been used in [19,20,31].

Analogously to Remark 8, the following simple observation shows the connection between the concepts of cluster functions of the forms $〈h_{2n},h_{2n-1},\dots ,h_2,h_1,\mathcal{I}F〉$ and $〈h_{2n},h_{2n-1},\dots ,h_2,h_1,\mathcal{S}F〉$, and cluster sets.

Remark 9.

For any multifunction $F:(X,\tau )\to (Y,\sigma )$, $x\in X$ and $y\in Y$, the following equivalences hold:

(i)

$y\in l.\alpha .C_F\left(x\right)$ if and only if $\left\{y\right\}\in 〈\mathcal{I},\mathcal{S},\mathcal{I},\mathcal{S}F〉\left(x\right)$

(resp. $y\in u.\alpha .C_F\left(x\right))$ if and only if and $\left\{y\right\}\in 〈\mathcal{I},\mathcal{S},\mathcal{I},\mathcal{I}F〉\left(x\right))$;

(ii)

$y\in l.q.C_F\left(x\right)$ if and only if $\left\{y\right\}\in 〈\mathcal{S},\mathcal{I},\mathcal{S}F〉\left(x\right)$

(resp. $y\in u.q.C_F\left(x\right))$ if and only if and $\left\{y\right\}\in 〈\mathcal{S},\mathcal{I},\mathcal{I}F〉\left(x\right))$;

(iii)

$y\in l.p.C_F\left(x\right)$ if and only if $\left\{y\right\}\in 〈\mathcal{I},\mathcal{S},\mathcal{S}F〉\left(x\right)$

(resp. $y\in u.p.C_F\left(x\right))$ if and only if and $\left\{y\right\}\in 〈\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(x\right))$;

(iv)

$y\in l.\beta .C_F\left(x\right)$ if and only if $\left\{y\right\}\in 〈\mathcal{S},\mathcal{I},\mathcal{S},\mathcal{S}F〉\left(x\right)$

(resp. $y\in u.\beta .C_F\left(x\right))$ if and only if and $\left\{y\right\}\in 〈\mathcal{S},\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(x\right))$.

Proof. 

Let us note that, according to the characterizations of $\mathcal{I}$ and $\mathcal{S}$ given in Lemma 2, we have the following equalities:

(${\alpha }_l$) $〈\mathcal{I},\mathcal{S},\mathcal{I},\mathcal{S}F〉\left(x\right)$=

$\overline{{\bigcup }_{U_1\in \tau \left(x\right)}{\bigcap }_{x_1\in U_1}{\bigcap }_{U_2\in \tau \left(x_1\right)}\overline{{\bigcup }_{x_2\in U_2}{\bigcup }_{U_3\in \tau \left(x_2\right)}{\bigcap }_{x_3\in U_3}\overline{\mathcal{P}\left(F\left(x_3\right)\right)}}}$,

(${\alpha }_u$) $〈\mathcal{I},\mathcal{S},\mathcal{I},\mathcal{I}F〉\left(x\right)$=

$\overline{{\bigcup }_{U_1\in \tau \left(x\right)}{\bigcap }_{x_1\in U_1}{\bigcap }_{U_2\in \tau \left(x_1\right)}\overline{{\bigcup }_{x_2\in U_2}{\bigcup }_{U_3\in \tau \left(x_2\right)}{\bigcap }_{x_3\in U_3}\overline{\left\{F\left(x_3\right)\right\}}}}$,

($q_l$) $〈\mathcal{S},\mathcal{I},\mathcal{S}F〉\left(x\right)$= ${\bigcap }_{U_1\in \tau \left(x\right)}\overline{{\bigcup }_{x_1\in U_1}{\bigcup }_{U_2\in \tau \left(x_1\right)}{\bigcap }_{x_2\in U_2}\overline{\mathcal{P}\left(F\left(x_2\right)\right)}}$,

($q_u$) $〈\mathcal{S},\mathcal{I},\mathcal{I}F〉\left(x\right)$= ${\bigcap }_{U_1\in \tau \left(x\right)}\overline{{\bigcup }_{x_1\in U_1}{\bigcup }_{U_2\in \tau \left(x_1\right)}{\bigcap }_{x_2\in U_2}\overline{\left\{F\left(x_2\right)\right\}}}$,

($p_l$) $〈\mathcal{I},\mathcal{S},\mathcal{S}F〉\left(x\right)$=$\overline{{\bigcup }_{U_1\in \tau \left(x\right)}{\bigcap }_{x_1\in U_1}{\bigcap }_{U_2\in \tau \left(x_1\right)}\overline{{\bigcup }_{x_2\in U_2}\mathcal{P}\left(F\left(x_2\right)\right)}}$,

($p_u$) $〈\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(x\right)$= $\overline{{\bigcup }_{U_1\in \tau \left(x\right)}{\bigcap }_{x_1\in U_1}{\bigcap }_{U_2\in \tau \left(x_1\right)}\overline{{\bigcup }_{x_2\in U_2}\left\{F\left(x_2\right)\right\}}}$,

(${\beta }_l$) $〈\mathcal{S},\mathcal{I},\mathcal{S},\mathcal{S}F〉\left(x\right)$=

${\bigcap }_{U_1\in \tau \left(x\right)}\overline{{\bigcup }_{x_1\in U_1}{\bigcup }_{U_2\in \tau \left(x_1\right)}{\bigcap }_{x_2\in U_2}{\bigcap }_{U_3\in \tau \left(x_2\right)}\overline{{\bigcup }_{x_3\in U_3}\mathcal{P}\left(F\left(x_3\right)\right)}}$,

(${\beta }_l$) $〈\mathcal{S},\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(x\right)$=

${\bigcap }_{U_1\in \tau \left(x\right)}\overline{{\bigcup }_{x_1\in U_1}{\bigcup }_{U_2\in \tau \left(x_1\right)}{\bigcap }_{x_2\in U_2}{\bigcap }_{U_3\in \tau \left(x_2\right)}\overline{{\bigcup }_{x_3\in U_3}\left\{F\left(x_3\right)\right\}}}$.

Now, it is enough to use Remark 1 and then, we immediately obtain the following equivalences for each $W\in \sigma$:

• $\mathcal{P}\left(W\right)\cap 〈\mathcal{I},\mathcal{S},\mathcal{I},\mathcal{S}F〉\left(x\right)\ne \varnothing$ if and only if $x\in Int(Cl\left(Int\left(F^{-}\left(W\right)\right)\right)$;
• $\mathcal{P}\left(W\right)\cap 〈\mathcal{I},S,\mathcal{I},\mathcal{I}F〉\left(x\right)\ne \varnothing$ if and only if $x\in Int(Cl\left(Int\left(F^{+}\left(W\right)\right)\right)$;
• $\mathcal{P}\left(W\right)\cap 〈\mathcal{S},\mathcal{I},\mathcal{S}F〉\left(x\right)\ne \varnothing$ if and only if $x\in Cl(Int\left(F^{-}\left(W\right)\right)$;
• $\mathcal{P}\left(W\right)\cap 〈\mathcal{S},\mathcal{I},\mathcal{I}F〉\left(x\right)\ne \varnothing$ if and only if $x\in Cl(Int\left(F^{+}\left(W\right)\right)$;
• $\mathcal{P}\left(W\right)\cap 〈\mathcal{I},\mathcal{S},\mathcal{S}F〉\left(x\right)\ne \varnothing$ if and only if $x\in Int(Cl\left(F^{-}\left(W\right)\right)$;
• $\mathcal{P}\left(W\right)\cap 〈\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(x\right)\ne \varnothing$ if and only if $x\in Int(Cl\left(F^{+}\left(W\right)\right)$;
• $\mathcal{P}\left(W\right)\cap 〈\mathcal{S},\mathcal{I},\mathcal{S},\mathcal{S}F〉\left(x\right)\ne \varnothing$ if and only if $x\in Cl(Int\left(Cl\left(F^{-}\left(W\right)\right)\right)$;
• $\mathcal{P}\left(W\right)\cap 〈\mathcal{S},\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(x\right)\ne \varnothing$ if and only if $x\in Cl(Int\left(Cl\left(F^{+}\left(W\right)\right)\right)$.

□

The cluster functions of the form $〈h_{2n},h_{2n-1},\dots ,h_2,h_1,\Psi 〉:X\to {\mathcal{P}}^2\left(Y\right)$ are convenient tools to characterize the properties related to the continuity of multifunctions. By way of illustration, let us recall the classical types of continuity for multifunctions.

The continuity of a multifunction is defined by its upper and lower continuity [32]. A multifunction $F:(X,\tau )\to (Y,\sigma )$ is said to be upper semi continuous (briefly $u.s.c.$) (resp. lower semi continuous (briefly $l.s.c.$)) at a point $x\in X$ if whenever W is an open subset of Y such that $x\in F^{+}\left(W\right)$ (resp. $x\in F^{-}\left(W\right))$, then $x\in Int\left(F^{+}\left(W\right)\right)$ (resp. $x\in Int\left(F^{-}\left(W\right)\right))$. The set of all such points will be denoted by $C_u\left(F\right)$ (resp. $C_l\left(F\right)$). A multifunction F is called $u.s.c.$ (resp. $l.s.c.$) if $C_u\left(F\right)=X$ (resp. $C_l\left(F\right)=X$).

It is easy to see that a multifunction $F:(X,\tau )\to (Y,\sigma )$ is $u.s.c.$ (resp. $l.s.c.$) if and only if it is continuous when it is considered to be a single-valued function $F:(X,\tau )\to (\mathcal{P}\left(Y\right),{\sigma }^u)$ (resp. $F:(X,\tau )\to (\mathcal{P}\left(Y\right),{\sigma }^l)$) [3,33].

By using the concept of cluster functions of the forms $〈h_{2n},h_{2n-1},\dots ,h_2,h_1,\mathcal{I}F〉$ and $〈h_{2n},h_{2n-1},\dots ,h_2,h_1,\mathcal{S}F〉$, both these types of continuity can be characterized in terms of the upper Vietoris topology as follows:

Lemma 9.

A multifunction $F:(X,\tau )\to (Y,\sigma )$ is upper semi continuous (resp. lower semi continuous) at a point $x\in X$ if and only if

$〈\mathcal{I}F〉\left(x\right)\subset 〈\mathcal{I},\mathcal{I}F〉\left(x\right)$(resp. $〈\mathcal{S}F〉\left(x\right)\subset 〈\mathcal{I},\mathcal{S}F〉\left(x\right))$.

Proof. 

Since, according to Lemma 2, we have

($c_u$) $〈\mathcal{I},\mathcal{I}F〉\left(x\right)$=$\overline{{\bigcup }_{U_1\in \tau \left(x\right)}{\bigcap }_{x_1\in U_1}\overline{\left\{F\left(x_1\right)\right\}}}$ and

($c_l$) $〈\mathcal{I},\mathcal{S}F〉\left(x\right)$=$\overline{{\bigcup }_{U_1\in \tau \left(x\right)}{\bigcap }_{x_1\in U_1}\overline{\mathcal{P}\left(F\left(x_1\right)\right)}}$.

So, the following pairs of statements are equivalent for each $W\in \sigma$ and $x\in X$:

• $\mathcal{P}\left(W\right)\cap 〈\mathcal{I},\mathcal{I}F〉\left(x\right)\ne \varnothing$ and $x\in Int\left(F^{+}\left(W\right)\right)$;
• $\mathcal{P}\left(W\right)\cap 〈\mathcal{I},\mathcal{S}F〉\left(x\right)\ne \varnothing$ and $x\in Int\left(F^{-}\left(W\right)\right)$.

Of course, $\mathcal{P}\left(W\right)\cap 〈\mathcal{I}F〉\left(x\right)\ne \varnothing$ (resp. $\mathcal{P}\left(W\right)\cap 〈\mathcal{S}F〉\left(x\right)\ne \varnothing )$ means that $x\in F^{+}\left(W\right)$ (resp. $x\in F^{-}\left(W\right)$). Hence, the characterization is true. □

Remark 10.

One can also consider the other two possible relations, namely

$〈\mathcal{I}F〉\left(x\right)\subset 〈\mathcal{I},\mathcal{S}F〉\left(x\right)$ and

$〈\mathcal{S}F〉\left(x\right)\subset 〈\mathcal{I},\mathcal{I}F〉\left(x\right)$ for $x\in X$.

We denote those types of continuity as $u.l.s.c.$ and $l.u.s.c.$, respectively. The set of all such points will be denoted by $C_{ul}\left(F\right)$ and $C_{lu}\left(F\right)$), respectively. Of course, the first of these properties is equivalent to $x\in Int\left(F^{-}\left(W\right)\right)$ for any open subset W such that $x\in F^{+}\left(W\right)$, which defines the type of continuity introduced in [34].

The second property means that $x\in Int\left(F^{+}\left(W\right)\right)$ for any open subset W such that $x\in F^{-}\left(W\right)$ or equivalently, F is $u.s.c.$ at x and $F\left(x\right)$ is a singleton.

Analogous characterizations one can formulate for many types of generalized continuity. Let us first quote the definitions of some classical types of them.

Definition 2.

A multifunction $F:(X,\tau )\to (Y,\sigma )$ is called

• $u.\alpha .c.$ (resp. $l.\alpha .c.$) [35] at a point $x\in X$, i.e.,
  $x\in \alpha .C_u\left(F\right)$ (resp. $x\in \alpha .C_l\left(F\right)$), if $x\in F^{+}\left(W\right)$ (resp. $x\in F^{-}\left(W\right))$
  implies $x\in Int\left(Cl\left(Int\left(F^{+}\left(W\right)\right)\right)\right)$ (resp. $x\in Int\left(Cl\left(Int\left(F^{-}\left(W\right)\right)\right)\right))$
  for all $W\in \sigma$;
• $u.q.c.$ (resp. $l.q.c.$) [36] at a point $x\in X$, i.e.,
  $x\in q.C_u\left(F\right)$ (resp. $x\in q.C_l\left(F\right)$), if $x\in F^{+}\left(W\right)$ (resp. $x\in F^{-}\left(W\right))$
  implies $x\in Cl\left(Int\left(F^{+}\left(W\right)\right)\right)$ (resp. $x\in Cl\left(Int\left(F^{-}\left(W\right)\right)\right))$
  for all $W\in \sigma$;
• $u.p.c.$ (resp. $l.p.c.$) [37] at a point $x\in X$, i.e.,
  $x\in p.C_u\left(F\right)$ (resp. $x\in p.C_l\left(F\right)$), if $x\in F^{+}\left(W\right)$ (resp. $x\in F^{-}\left(W\right))$
  implies $x\in Int\left(Cl\left(F^{+}\left(W\right)\right)\right)$ (resp. $x\in Int\left(Cl\left(F^{-}\left(W\right)\right)\right))$
  for all $W\in \sigma$;
• $u.\beta .c.$ (resp. $l.\beta .c.$) [38]) at a point x ∈ X, i.e.,
  $x\in \beta .C_u\left(F\right)$ (resp. $x\in \beta .C_l\left(F\right)$), if $x\in F^{+}\left(W\right)$ (resp. $x\in F^{-}\left(W\right))$
  implies $x\in Cl\left(Int\left(Cl\left(F^{+}\left(W\right)\right)\right)\right)$ (resp. $x\in Cl\left(Int\left(Cl\left(F^{-}\left(W\right)\right)\right)\right))$
  for all $W\in \sigma$.

In [39] the property $l.\beta .c.$ is called the lower demicontinuity ($l.d.c.$).

Analogously to the case of $u.s.c$ and $l.s.c.$, a multifunction F is $u.\alpha .c.$ (or. $l.\alpha .c.$) (resp. $u.q.c.$ (or $l.q.c.$), $u.p.c.$ (or $l.p.c.$), $u.\beta .c.$ (or $l.\beta .c.$)) if and only if it is $\alpha$-continuous (resp. semi-continuous, pre-continuous, $\beta$-continuous) when it is considered to be a function $F:(X,\tau )\to (\mathcal{P}\left(Y\right),{\sigma }^u)$ (or $F:(X,\tau )\to (\mathcal{P}\left(Y\right),{\sigma }^l$)).

The requirements stated in the above forms of generalized continuity apply to upper inverse image $F^{+}\left(W\right)$—in the type u (resp. lower inverse image $F^{-}\left(W\right)$—in the type l) of open subsets W of Y. The use of mixed types of the inverse images leads to the following kinds of continuity.

Definition 3.

A multifunction $F:(X,\tau )\to (Y,\sigma )$ is said to be

• $u.l.\alpha .c.$ (resp. $l.u.\alpha .c.$) [40] at a point $x\in X$, i.e.,
  $x\in \alpha .C_{ul}\left(F\right)$ (resp. $x\in \alpha .C_{lu}\left(F\right)$), if $x\in F^{+}\left(W\right)$ (resp. $x\in F^{-}\left(W\right))$
  implies $x\in Int\left(Cl\left(Int\left(F^{-}\left(W\right)\right)\right)\right)$ (resp. $x\in Int\left(Cl\left(Int\left(F^{+}\left(W\right)\right)\right)\right))$
  for all $W\in \sigma$;
• $u.l.q.c.$ [40] (or $l.u.q.c.$, [39]), at a point $x\in X$, i.e.,
  $x\in q.C_{ul}\left(F\right)$ (resp. $x\in q.C_{lu}\left(F\right)$), if $x\in F^{+}\left(W\right)$ (resp. $x\in F^{-}\left(W\right))$
  implies $x\in Cl\left(Int\left(F^{-}\left(W\right)\right)\right)$ (resp. $x\in Cl\left(Int\left(F^{+}\left(W\right)\right)\right))$
  for all $W\in \sigma$;
• $u.l.p.c.$ (or $l.u.p.c.$,) [40], at a point $x\in X$, i.e.,
  $x\in p.C_{ul}\left(F\right)$ (resp. $x\in p.C_{lu}\left(F\right)$), if $x\in F^{+}\left(W\right)$ (resp. $x\in F^{-}\left(W\right))$
  implies $x\in Int\left(Cl\left(F^{-}\left(W\right)\right)\right)$ (resp. $x\in Int\left(Cl\left(F^{+}\left(W\right)\right)\right))$
  for all $W\in \sigma$;
• $u.l.\beta .c.$ (resp. $l.u.\beta .c.$) [40] at a point $x\in X$, i.e.,
  $x\in \beta .C_{ul}\left(F\right)$ (resp. $x\in \beta .C_{lu}\left(F\right)$), if $x\in F^{+}\left(W\right)$ (resp. $x\in F^{-}\left(W\right))$
  implies $x\in Cl\left(Int\left(Cl\left(F^{-}\left(W\right)\right)\right)\right)$ (resp. $x\in Cl\left(Int\left(Cl\left(F^{+}\left(W\right)\right)\right)\right))$
  for all $W\in \sigma$.

In [41,42], the $l.u.q.c.$ property was used under the name of minimality of $u.s.c.o.$ ($u.s.c.$ with compact values) multifunction. But in [39,43,44], this property has been used independently of the condition $u.s.c.o.$

Of course, if a single-valued function $f:(X,\tau )\to (Y,\sigma )$ is treated as a multifunction F given by $F\left(x\right)=\left\{f\left(x\right)\right\}$ for all $x\in X$, then we have the following equalities:

• $C_u\left(F\right)=C_l\left(F\right)=C_{ul}\left(F\right)=C_{lu}\left(F\right)=C\left(f\right)$;
• $\alpha .C_u\left(F\right)=\alpha .C_l\left(F\right)=\alpha .C_{ul}\left(F\right)=\alpha .C_{lu}\left(F\right)=\alpha .C\left(f\right)$;
• $q.C_u\left(F\right)=q.C_l\left(F\right)=q.C_{ul}\left(F\right)=q.C_{lu}\left(F\right)=q.C\left(f\right)$;
• $p.C_u\left(F\right)=p.C_l\left(F\right)=p.C_{ul}\left(F\right)=p.C_{lu}\left(F\right)=p.C\left(f\right)$;
• $\beta .C_u\left(F\right)=\beta .C_l\left(F\right)=\beta .C_{ul}\left(F\right)=\beta .C_{lu}\left(F\right)=\beta .C\left(f\right)$.

• where $C\left(f\right)$ (resp. $\alpha .C\left(f\right)$, $q.C\left(f\right)$, $p.C\left(f\right)$, $\beta .C\left(f\right)$) denotes the set of all continuity (resp. $\alpha$-continuity [45], semi-continuity [27,46], pre-continuity [28], $\beta$-continuity [30]) points of f.

The following characterizations are analogous to those in Lemma 9.

Lemma 10.

For any multifunction $F:(X,\tau )\to (Y,\sigma )$ and $x\in X$, the following equivalences hold:

(α)

•$x\in \alpha .C_u\left(F\right)$ if and only if $〈\mathcal{I}F〉\left(x\right)\subset 〈\mathcal{I},\mathcal{S},\mathcal{I},\mathcal{I}F〉\left(x\right)$;

•$x\in \alpha .C_l\left(F\right)$ if and only if $〈\mathcal{S}F〉\left(x\right)\subset 〈\mathcal{I},\mathcal{S},\mathcal{I},\mathcal{S}F〉\left(x\right)$;

•$x\in \alpha .C_{ul}\left(F\right)$ if and only if $〈\mathcal{I}F〉\left(x\right)\subset 〈\mathcal{I},\mathcal{S},\mathcal{I},\mathcal{S}F〉\left(x\right)$;

•$x\in \alpha .C_{lu}\left(F\right)$ if and only if $〈\mathcal{S}F〉\left(x\right)\subset 〈\mathcal{I},\mathcal{S},\mathcal{I},\mathcal{I}F〉\left(x\right)$;

(q)

•$x\in q.C_u\left(F\right)$ if and only if $〈\mathcal{I}F〉\left(x\right)\subset 〈\mathcal{S},\mathcal{I},\mathcal{I}F〉\left(x\right)$;

•$x\in q.C_l\left(F\right)$ if and only if $〈\mathcal{S}F〉\left(x\right)\subset 〈\mathcal{S},\mathcal{I},\mathcal{S}F〉\left(x\right)$;

•$x\in q.C_{ul}\left(F\right)$ if and only if $〈\mathcal{I}F〉\left(x\right)\subset 〈\mathcal{S},\mathcal{I},\mathcal{S}F〉\left(x\right)$;

•$x\in q.C_{lu}\left(F\right)$ if and only if $〈\mathcal{S}F〉\left(x\right)\subset 〈\mathcal{S},\mathcal{I},\mathcal{I}F〉\left(x\right)$;

(p)

•$x\in p.C_u\left(F\right)$ if and only if $〈\mathcal{I}F〉\left(x\right)\subset 〈\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(x\right)$;

•$x\in p.C_l\left(F\right)$ if and only if $〈\mathcal{S}F〉\left(x\right)\subset 〈\mathcal{I},\mathcal{S},\mathcal{S}F〉\left(x\right)$;

•$x\in p.C_{ul}\left(F\right)$ if and only if $〈\mathcal{I}F〉\left(x\right)\subset 〈\mathcal{I},\mathcal{S},\mathcal{S}F〉\left(x\right)$;

•$x\in p.C_{lu}\left(F\right)$ if and only if $〈\mathcal{S}F〉\left(x\right)\subset 〈\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(x\right)$;

(β)

•$x\in \beta .C_u\left(F\right)$ if and only if $〈\mathcal{I}F〉\left(x\right)\subset 〈\mathcal{S},\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(x\right)$;

•$x\in \beta .C_l\left(F\right)$ if and only if $〈\mathcal{S}F〉\left(x\right)\subset 〈\mathcal{S},\mathcal{I},\mathcal{S},\mathcal{S}F〉\left(x\right)$;

•$x\in \beta .C_{ul}\left(F\right)$ if and only if $〈\mathcal{I}F〉\left(x\right)\subset 〈\mathcal{S},\mathcal{I},\mathcal{S},\mathcal{S}F〉\left(x\right)$;

•$x\in \beta .C_{lu}\left(F\right)$ if and only if $〈\mathcal{S}F〉\left(x\right)\subset 〈\mathcal{S},\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(x\right)$.

Proof. 

It is enough to use the equivalences resulting from the characterizations (${\alpha }_l$), (${\alpha }_u$), ($q_l$), ($q_u$), ($p_l$), ($p_u$), (${\beta }_l$), and (${\beta }_u$) listed in Remark 9, and the equivalences listed in its proof. □

The following quite different types of generalized continuity can also be characterized using cluster operators.

Definition 4.

A multifunction $F:(X,\tau )\to (Y,\sigma )$ is said to be

• α-continuous [47,48] at a point $x\in X$, i.e., $x\in A.C\left(F\right)$, if
  $x\in Int\left(Cl\left(Int(F^{+}\left(W_1\right)\cap F^{-}\left(W_2\right))\right)\right)$ holds for all $W_1,W_2\in \sigma$
  such that $x\in F^{+}\left(W_1\right)\cap F^{-}\left(W_2\right)$;
• Quasicontinuous [49] at a point $x\in X$, i.e., $x\in Q.C\left(F\right)$, if
  $x\in Cl\left(Int(F^{+}\left(W_1\right)\cap F^{-}\left(W_2\right))\right)$ holds for all $W_1,W_2\in \sigma$
  such that $x\in F^{+}\left(W_1\right)\cap F^{-}\left(W_2\right)$;
• Pre-continuous [47,48] at a point $x\in X$, i.e., $x\in P.C\left(F\right)$, if
  $x\in Int\left(Cl(F^{+}\left(W_1\right)\cap F^{-}\left(W_2\right))\right)$ holds for all $W_1,W_2\in \sigma$
  such that $x\in F^{+}\left(W_1\right)\cap F^{-}\left(W_2\right)$;
• β-continuous [48] at a point $x\in X$, i.e., $x\in B.C\left(F\right)$, if
  $x\in Cl\left(Int\left(Cl(F^{+}\left(W_1\right)\cap F^{-}\left(W_2\right))\right)\right)$ holds for all $W_1,W_2\in \sigma$
  such that $x\in F^{+}\left(W_1\right)\cap F^{-}\left(W_2\right)$.

With any multifunction $F:(X,\tau )\to (Y,\sigma )$ we consider the function

$\mathcal{I}F$×$\mathcal{S}F:X\to \mathcal{P}\left(\mathcal{P}\right(Y)\times \mathcal{P}(Y\left)\right)$ defined by

$\mathcal{I}F$×$\mathcal{S}F\left(x\right)=\overline{\left\{F\left(x\right)\right\}}\times \overline{\mathcal{P}\left(F\right(x\left)\right)}$ for all $x\in X$,

• where $\mathcal{P}\left(Y\right)\times \mathcal{P}\left(Y\right)$ is equipped with the product topology derived from the upper Vietoris topology ${\sigma }^u$ on $\mathcal{P}\left(Y\right)$. So, it is clear that

$(\mathcal{P}\left(W_1\right)\times \mathcal{P}\left(W_2\right))\cap \mathcal{I}F$×$\mathcal{S}F\left(x\right)\ne \varnothing$ if and only if $x\in F^{+}\left(W_1\right)\cap F^{-}\left(W_2\right)$ for all $W_1,W_2\in \sigma$, and $x\in X$.

We will use the following functions:

(A)

$〈\mathcal{I},\mathcal{S},\mathcal{I},\mathcal{I}F\times \mathcal{S}F〉\left(x\right)$=

$\overline{{\bigcup }_{U_1\in \tau \left(x\right)}{\bigcap }_{x_1\in U_1}{\bigcap }_{U_2\in \tau \left(x_1\right)}\overline{{\bigcup }_{x_2\in U_2}{\bigcup }_{U_3\in \tau \left(x_2\right)}{\bigcap }_{x_3\in U_3}\overline{\left\{F\left(x_3\right)\right\}}\times \overline{\mathcal{P}\left(F\left(x_3\right)\right)}}}$,

(Q)

$〈\mathcal{S},\mathcal{I},\mathcal{I}F\times \mathcal{S}F〉\left(x\right)$= ${\bigcap }_{U_1\in \tau \left(x\right)}\overline{{\bigcup }_{x_1\in U_1}{\bigcup }_{U_2\in \tau \left(x_1\right)}{\bigcap }_{x_2\in U_2}\overline{\left\{F\left(x_2\right)\right\}}\times \overline{\mathcal{P}\left(F\left(x_2\right)\right)}}$,

(P)

$〈\mathcal{I},\mathcal{S},\mathcal{I}F\times \mathcal{S}F〉\left(x\right)$= $\overline{{\bigcup }_{U_1\in \tau \left(x\right)}{\bigcap }_{x_1\in U_1}{\bigcap }_{U_2\in \tau \left(x_1\right)}\overline{{\bigcup }_{x_2\in U_2}\left\{F\left(x_2\right)\right\}\times \mathcal{P}\left(F\left(x_2\right)\right)}}$,

(B)

$〈\mathcal{S},\mathcal{I},\mathcal{S},\mathcal{I}F\times \mathcal{S}F〉\left(x\right)$=

${\bigcap }_{U_1\in \tau \left(x\right)}\overline{{\bigcup }_{x_1\in U_1}{\bigcup }_{U_2\in \tau \left(x_1\right)}{\bigcap }_{x_2\in U_2}{\bigcap }_{U_3\in \tau \left(x_2\right)}\overline{{\bigcup }_{x_3\in U_3}\left\{F\left(x_3\right)\right\}\times \mathcal{P}\left(F\left(x_3\right)\right)}}$.

Thus, the following pairs of statements are equivalent for all $W_1,W_2\in \sigma$ and $x\in X$:

• $(\mathcal{P}\left(W_1\right)\times \mathcal{P}\left(W_2\right))\cap 〈\mathcal{I},\mathcal{S},\mathcal{I},\mathcal{I}F\times \mathcal{S}F〉\left(x\right)\ne \varnothing$ and
  $x\in Int\left(Cl\left(Int(F^{+}\left(W_1\right)\cap F^{-}\left(W_2\right))\right)\right)$;
• $(\mathcal{P}\left(W_1\right)\times \mathcal{P}\left(W_2\right))\cap 〈\mathcal{S},\mathcal{I},\mathcal{I}F\times \mathcal{S}F〉\left(x\right)\ne \varnothing$ and
  $x\in Cl\left(Int(F^{+}\left(W_1\right)\cap F^{-}\left(W_2\right))\right)$;
• $(\mathcal{P}\left(W_1\right)\times \mathcal{P}\left(W_2\right))\cap 〈\mathcal{I},\mathcal{S},\mathcal{I}F\times \mathcal{S}F〉\left(x\right)\ne \varnothing$ and
  $x\in Int\left(Cl(F^{+}\left(W_1\right)\cap F^{-}\left(W_2\right))\right)$;
• $(\mathcal{P}\left(W_1\right)\times \mathcal{P}\left(W_2\right))\cap 〈\mathcal{S},\mathcal{I},\mathcal{S},\mathcal{I}F\times \mathcal{S}F〉\left(x\right)\ne \varnothing$ and $x\in Cl\left(Int\left(Cl(F^{+}\left(W_1\right)\cap F^{-}\left(W_2\right))\right)\right)$.

Hence, we have the following characterizations:

Lemma 11.

For any multifunction $F:(X,\tau )\to (Y,\sigma )$ and $x\in X$, the following equivalences hold:

• $x\in A.C\left(F\right)$ if and only if $\mathcal{I}F\times \mathcal{S}F\left(x\right)\subset 〈\mathcal{I},\mathcal{S},\mathcal{I},\mathcal{I}F\times \mathcal{S}F〉\left(x\right)$;
• $x\in Q.C\left(F\right)$ if and only if $\mathcal{I}F\times \mathcal{S}F\left(x\right)\subset 〈\mathcal{S},\mathcal{I},\mathcal{I}F\times \mathcal{S}F〉\left(x\right)$;
• $x\in P.C\left(F\right)$ if and only if $\mathcal{I}F\times \mathcal{S}F\left(x\right)\subset 〈\mathcal{I},\mathcal{S},\mathcal{I}F\times \mathcal{S}F〉\left(x\right)$;
• $x\in B.C\left(F\right)$ if and only if $\mathcal{I}F\times \mathcal{S}F\left(x\right)\subset 〈\mathcal{S},\mathcal{I},\mathcal{S},\mathcal{I}F\times \mathcal{S}F〉\left(x\right)$.

At the end of this chapter, we will characterize some types of continuity, originating in some generalized continuity of functions with the values in metric spaces.

A function f from a topological space $(X,\tau )$ to a metric space $(Y,d)$ is said to be cliquish at a point $x\in X$ [50,51], if for any $\epsilon >0$ and any open subset $U\subset X$ containing x there exists an open nonempty subset $G\subset U$ such that $d(f\left(x_1\right),f\left(x_2\right))<ϵ$ for all $x_1,x_2\in G$. Or equivalently,

$x\in Cl(\bigcup \left\{Int\left(f^{-1}\left(V\right)\right):V\in {\mathcal{V}}_{•}\right\})$ for any $ϵ>0$,

where ${\mathcal{V}}_{•}=\left\{B(y,ϵ):y\in Y\right\}$ and $B(y,ϵ)$ denotes the ball with center y and radius $ϵ$.

The appropriate topological form of this condition called $T_1$−cliquishness [52] (equivalently ${\chi }^1$−cliquish [53], (Proposition 2.3 (iii)), applies to functions f from a topological space $(X,\tau )$ to a topological space $(Y,\sigma )$ and is given by the property

• $x\in Cl(\bigcup \left\{Int\left(f^{-1}\left(V\right)\right):V\in \mathcal{V}\right\})$

for any open covering $\mathcal{V}$ of $(Y,\sigma )$.

It is a simple generalization of the notion of $T_1$−continuity [53] defined by

$x\in \bigcup \left\{Int\left(f^{-1}\left(V\right)\right):V\in \mathcal{V}\right\}$

for any open covering $\mathcal{V}$ of $(Y,\sigma )$.

The other types of topological forms of cliquishness [54] called pre ${\chi }^1$−cliquishness (resp. ${\chi }^1-s$−cliquishness, pre ${\chi }^1-s$−cliquishness, ${\chi }^1-\alpha$−cliquishness, pre ${\chi }^1-\alpha$−cliquishness) at a point $x\in$ X, are defined by the following conditions:

• $x\in Cl(\bigcup \left\{Int\left(Cl\left(f^{-1}\left(V\right)\right)\right):V\in \mathcal{V}\right\})$; (resp.
• $x\in \bigcup \left\{Cl\left(Int\left(f^{-1}\left(V\right)\right)\right):V\in \mathcal{V}\right\}$;
• $x\in \bigcup \left\{Cl\left(Int\left(Cl\left(f^{-1}\left(V\right)\right)\right)\right):V\in \mathcal{V}\right\}$;
• $x\in \bigcup \left\{Int\left(Cl\left(Int\left(f^{-1}\left(V\right)\right)\right)\right):V\in \mathcal{V}\right\}$;
• $x\in \bigcup \left\{Int\left(Cl\left(f^{-1}\left(V\right)\right)\right):V\in \mathcal{V}\right\}$).

for any open covering $\mathcal{V}$ of $(Y,\sigma )$.

The extensions of those definitions to multifunctions have the following forms.

Definition 5.

A multifunction $F:(X,\tau )\to (Y,\sigma )$ is said to be

• u-t-α-cliquish (resp. l-t-α-cliquish) [13] at a point $x\in X$, i.e.,
  $x\in \alpha K_u\left(F\right)$ (resp. $x\in \alpha K_l\left(F\right)$), if $x\in \bigcup \left\{Int\left(Cl\left(Int\left(F^{+}\left(V\right)\right)\right)\right):V\in \mathcal{V}\right\}$
  (resp. $x\in \bigcup \left\{Int\left(Cl\left(Int\left(F^{-}\left(V\right)\right)\right)\right):V\in \mathcal{V}\right\})$ for any open cover $\mathcal{V}$ of Y;
• u-t-q-cliquish (resp. l-t-q-cliquish) [13] at a point $x\in X$, i.e.,
  $x\in q{K}_u\left(F\right)$ (resp. $x\in q{K}_l\left(F\right)$), if $x\in \bigcup \left\{Cl\left(Int\left(F^{+}\left(V\right)\right)\right):V\in \mathcal{V}\right\}$
  (resp. $x\in \bigcup \left\{Cl\left(Int\left(F^{-}\left(V\right)\right)\right):V\in \mathcal{V}\right\})$ for any open cover $\mathcal{V}$ of Y;
• u-t-p-cliquish (resp. l-t-p-cliquish) [13] at a point $x\in X$, i.e.,
  $x\in p{K}_u\left(F\right)$ (resp. $x\in p{K}_l\left(F\right)$), if $x\in \bigcup \left\{Int\left(Cl\left(F^{+}\left(V\right)\right)\right):V\in \mathcal{V}\right\}$
  (resp. $x\in \bigcup \left\{Int\left(Cl\left(F^{-}\left(V\right)\right)\right):V\in \mathcal{V}\right\})$ for any open cover $\mathcal{V}$ of Y;
• u-t-β-cliquish (resp. l-t-β-cliquish) [13] at a point $x\in X$, i.e.,
  $x\in \beta K_u\left(F\right)$ (resp. $x\in \beta K_l\left(F\right)$), if $x\in \bigcup \left\{Cl\left(Int\left(Cl\left(F^{+}\left(V\right)\right)\right)\right):V\in \mathcal{V}\right\}$
  (resp. $x\in \bigcup \left\{Cl\left(Int\left(Cl\left(F^{-}\left(V\right)\right)\right)\right):V\in \mathcal{V}\right\})$ for any open cover $\mathcal{V}$ of Y;
• u-t-cliquish (resp. l-t-cliquish) [31] at a point $x\in X$, i.e.,
  $x\in K_u\left(F\right)$ (resp. $x\in K_l\left(F\right)$), if $x\in Cl(\bigcup \left\{Int\left(F^{+}\left(V\right)\right):V\in \mathcal{V}\right\})$
  (resp. $x\in Cl(\bigcup \left\{Int\left(F^{-}\left(V\right)\right):V\in \mathcal{V}\right\})$ for any open cover $\mathcal{V}$ of Y;
• Pre- u-t-cliquish (resp. pre l-t-cliquish) at a point $x\in X$, i.e.,
  $x\in P{K}_u\left(F\right)$ (resp. $x\in P{K}_l\left(F\right)$), if $x\in Cl(\bigcup \left\{Int\left(Cl\left(F^{+}\left(V\right)\right)\right):V\in \mathcal{V}\right\})$
  (resp. $x\in Cl(\bigcup \left\{Int\left(Cl\left(F^{-}\left(V\right)\right)\right):V\in \mathcal{V}\right\}))$ for any open cover $\mathcal{V}$ of Y.

We have the following characterizations of those types of generalized continuity in terms of the cluster operators.

Lemma 12.

For any multifunction $F:(X,\tau )\to (Y,\sigma )$ and $x\in X$, the following equivalences hold:

(i)

$x\in \alpha .K_u\left(F\right)$(resp. $x\in \alpha .K_l\left(F\right))$ if and only if the family

$〈\mathcal{I},\mathcal{S},\mathcal{I},\mathcal{I}F〉\left(x\right)$(resp. $〈\mathcal{I},\mathcal{S},\mathcal{I},\mathcal{S}F〉\left(x\right))$ contains a singleton;

(ii)

$x\in q.K_u\left(F\right)$(resp. $x\in q.K_l\left(F\right))$ if and only is the family

$〈\mathcal{S},\mathcal{I},\mathcal{I}F〉\left(x\right)$(resp. $〈\mathcal{S},\mathcal{I},\mathcal{S}F〉\left(x\right))$ contains a singleton;

(iii)

$x\in p.K_u\left(F\right)$(resp. $x\in p.K_l\left(F\right))$ if and only if the family

$〈\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(x\right)$(resp. $〈\mathcal{I},\mathcal{S},\mathcal{S}F〉\left(x\right))$ contains a singleton;

(iv)

$x\in \beta .K_u\left(F\right)$(resp. $x\in \beta .K_l\left(F\right))$ if and only if the family

$〈\mathcal{S},\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(x\right)$(resp. $〈\mathcal{S},\mathcal{I},\mathcal{S},\mathcal{S}F〉\left(x\right))$ contains a singleton;

(v)

$x\in K_u\left(F\right)$(resp. $x\in K_l\left(F\right))$ if and only if for any $U\in \pi \left(x\right)$,

$l\left(〈\mathcal{I},\mathcal{I}F〉\left(U\right)\right)$(resp. $l\left(〈\mathcal{I},\mathcal{S}F〉\left(U\right)\right))$ contains a singleton;

(vi)

$x\in P{K}_u\left(F\right)$(resp. $x\in P{K}_l\left(F\right))$ if and only if for any $U\in \pi \left(x\right)$,

the family $l\left(〈\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(U\right)\right)$ (resp. $l\left(〈\mathcal{I},\mathcal{S},\mathcal{S}F〉\left(U\right)\right))$ contains

a singleton.

Proof. 

If $\mathcal{V}$ is an open covering of $(Y,\sigma )$ and $\left\{y\right\}\in 〈\mathcal{I},\mathcal{S},\mathcal{I},\mathcal{I}F〉\left(x\right)$ (resp. $\left\{y\right\}\in 〈\mathcal{S},\mathcal{I},\mathcal{I}F〉\left(x\right)$, $\left\{y\right\}\in 〈\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(x\right)$, $\left\{y\right\}\in 〈\mathcal{S},\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(x\right))$ for some $y\in Y$, then $\left\{y\right\}\in \mathcal{P}\left(V\right)$ for some $V\in \mathcal{V}$ and according to the equivalences listed in the proof of Remark 9, we obtain

• $x\in Int(Cl\left(Int\left(F^{+}\left(V\right)\right)\right)$ (resp. $x\in Cl(Int\left(F^{+}\left(V\right)\right),x\in Int\left(Cl\left(F^{+}\left(V\right)\right)\right),$
• $x\in Cl(Int\left(Cl\left(F^{+}\left(V\right)\right)\right)$. So, $x\in \alpha .K_u\left(F\right)$ (resp. $x\in q.K_u\left(F\right)$, $x\in p.K_u\left(F\right)$, $x\in \beta .K_u\left(F\right)$).

Now assume that $x\in \alpha .K_u\left(F\right)$ (resp. $x\in q.K_u\left(F\right)$, $x\in p.K_u\left(F\right)$, $x\in \beta .K_u\left(F\right)$) and $\left\{y\right\}\notin 〈\mathcal{I},\mathcal{S},\mathcal{I},\mathcal{I}F〉\left(x\right)$ (resp. $\left\{y\right\}\notin 〈\mathcal{S},\mathcal{I},\mathcal{I}F〉\left(x\right)$, $\left\{y\right\}\notin 〈\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(x\right)$, $\left\{y\right\}\notin 〈\mathcal{S},\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(x\right))$ for all points $y\in Y$. Then, since the values of cluster functions are closed with respect to the upper Vietoris topology, for every $y\in Y$ there exists an open $V_y\subset Y$ such that

• $\left\{y\right\}\in \mathcal{P}\left(V_y\right)$ and $\mathcal{P}\left(V_y\right)\cap 〈\mathcal{I},\mathcal{S},\mathcal{I},\mathcal{I}F〉\left(x\right)=\varnothing$
• (resp. $\mathcal{P}\left(V_y\right)\cap 〈\mathcal{S},\mathcal{I},\mathcal{I}F〉\left(x\right)=\varnothing$, $\mathcal{P}\left(V_y\right)\cap 〈\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(x\right)=\varnothing$,
• $\mathcal{P}\left(V_y\right)\cap 〈\mathcal{S},\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(x\right)=\varnothing )$. So, the family $\mathcal{V}=\left\{V_y:y\in Y\right\}$ forms an open covering of Y such that $x\notin \bigcup \left\{Int\left(Cl\left(Int\left(F^{+}\left(V\right)\right)\right)\right):V\in \mathcal{V}\right\}$
• (resp. $x\notin \bigcup \left\{Cl\left(Int\left(F^{+}\left(V\right)\right)\right):V\in \mathcal{V}\right\},x\notin \bigcup \left\{Int\left(Cl\left(F^{+}\left(V\right)\right)\right):V\in \mathcal{V}\right\},x\notin \bigcup \left\{Cl\left(Int\left(Cl\left(F^{+}\left(V\right)\right)\right)\right):V\in \mathcal{V}\right\})$ which gives a contradiction and finishes the proof of $\left(i\right)-\left(iv\right)$, the case “$u$”. The proof of the second case is analogous.

To prove $\left(v\right)$ and $\left(vi\right)$, let assume first that $x\in K_u\left(F\right)$

• (resp. $x\in P{K}_u\left(F\right)$) and there exists $U\in \pi \left(x\right)$ such that $\left\{y\right\}\notin l\left(〈\mathcal{I},\mathcal{I}F〉\left(U\right)\right)$ (resp. $\left\{y\right\}\notin l\left(〈\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(U\right)\right)$) for every $y\in Y$. Then, for every $y\in Y$ there exists an open $V_y\subset Y$ such that $\mathcal{P}\left(V_y\right)\cap \overline{\bigcup \left\{〈\mathcal{I},\mathcal{I}F〉\left(x\right):x\in U\right\}}=\varnothing$
• (resp. $\mathcal{P}\left(V_y\right)\cap \overline{\bigcup \left\{〈\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(x\right):x\in U\right\}}=\varnothing$) which is equivalent to
• $U\cap Int\left(F^{+}\left(V_y\right)\right)=\varnothing$ (resp. $U\cap Int(Cl\left(F^{+}\left(V_y\right)\right)=\varnothing$. As a result, we obtain an open covering $\mathcal{V}=\left\{V_y:y\in Y\right\}$ of Y such that
• $x\notin Cl(\bigcup \left\{Int\left(F^{+}\left(V\right)\right):V\in \mathcal{V}\right\})$ (resp. $x\notin Cl(\bigcup \left\{Int\left(Cl\left(F^{+}\left(V\right)\right)\right):V\in \mathcal{V}\right\}))$ which gives a contradiction.

Now, let us take an open covering $\mathcal{V}$ of $(Y,\sigma )$ and assume that for every $U\in \tau \left(x\right)$ there exists $y\in Y$ such that $\left\{y\right\}\in l\left(〈\mathcal{I},\mathcal{I}F〉\left(U\right)\right)$

• (resp. $\left\{y\right\}\in l\left(〈\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(U\right)\right)$). Then, there exists $V\in \mathcal{V}$ such that $y\in V$ and $\mathcal{P}\left(V\right)\cap \overline{\bigcup \left\{〈\mathcal{I},\mathcal{I}F〉\left(x\right):x\in U\right\}}\ne \varnothing$
• (resp. $\mathcal{P}\left(V\right)\cap \overline{\bigcup \left\{〈\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(x\right):x\in U\right\}}\ne \varnothing$) which means that
• $\mathcal{P}\left(V\right)\cap 〈\mathcal{I},\mathcal{I}F〉\left(x\right)\ne \varnothing$ (resp. $\mathcal{P}\left(V\right)\cap 〈\mathcal{I},\mathcal{S},\mathcal{I}F〉\left(x\right)\ne \varnothing$) for some $x\in U$.
• So, we have $U\cap Int\left(F^{+}\left(V\right)\right)\ne \varnothing$ (resp. $U\cap Int(Cl\left(F^{+}\left(V\right)\right)\ne \varnothing$.
• This shows that $U\cap \bigcup \left\{Int\left(F^{+}\left(V\right)\right):V\in \mathcal{V}\right\}\ne \varnothing$
• (resp. $U\cap \bigcup \left\{Int\left(Cl\left(F^{+}\left(V\right)\right)\right):V\in \mathcal{V}\right\}\ne \varnothing )$ for any open set U containing x, i.e., that $x\in Cl(\bigcup \left\{Int\left(F^{+}\left(V\right)\right):V\in \mathcal{V}\right\})$
• (resp. $x\in Cl(\bigcup \left\{Int\left(Cl\left(F^{+}\left(V\right)\right)\right):V\in \mathcal{V}\right\}))$ and finishes the proof of $\left(v\right)$ and $\left(vi\right)$, the case “$u$”. The proof of the second case is analogous. □

3. Convergence in Terms of Topologically Determined Operators

Given any net $H:\Sigma \to \mathcal{P}{\left(Y\right)}^X$ of multifunctions $H_{\alpha }:(X,\tau )\to (Y,\sigma )$, shortly ${\left(H_{\alpha }\right)}_{\alpha \in \Sigma }$, where $H\left(\alpha \right)=H_{\alpha }$, $\alpha \in \Sigma$ and $(\Sigma ,⪯)$ is a directed set, we will apply the function $\overline{H}:\Sigma \times X\to \mathcal{P}\left(Y\right)$ defined by

$\overline{H}(\alpha ,x)=H_{\alpha }\left(x\right)$ for all $(\alpha ,x)\in \Sigma \times X$,

i.e., H is the value $E\left(\overline{H}\right)$ of the exponential map:

$E:\mathcal{P}{\left(Y\right)}^{\Sigma \times X}\to {\left(\mathcal{P}{\left(Y\right)}^X\right)}^{\Sigma }$

given by the formula:

$E\left(f\right)\left(\alpha \right)\left(x\right)=f(\alpha ,x)$,

• where $f\in \mathcal{P}{\left(Y\right)}^{\Sigma \times X}$, $\alpha \in \Sigma$ and $x\in X$,

It defines one-to-one correspondence between $\mathcal{P}{\left(Y\right)}^{\Sigma \times X}$ and ${\left(\mathcal{P}{\left(Y\right)}^X\right)}^{\Sigma }$.

Analogously to the case of multifunctions $F:(X,\tau )\to (Y,\sigma )$, we will use the following two functions $\mathcal{I}\overline{H},\mathcal{S}\overline{H}:\Sigma \times X\to {\mathcal{P}}^2\left(Y\right)$ defined by

$\mathcal{I}\overline{H}(\alpha ,x)$ = $\overline{\left\{H_{\alpha }\left(x\right)\right\}}$ and $\mathcal{S}\overline{H}(\alpha ,x)$ = $\overline{\mathcal{P}(H_{\alpha }\left(x\right)})$ for all $(\alpha ,x)\in \Sigma \times X$.

Of course, the following equivalences are true:

• $H_{\alpha }\left(x\right)\subset W$ if and only if $\mathcal{P}\left(W\right)\cap \mathcal{I}\overline{H}(\alpha ,x)\ne \varnothing$;
• $H_{\alpha }\left(x\right)\cap W\ne \varnothing$ if and only if $\mathcal{P}\left(W\right)\cap \left\}\right\}S\overline{H}(\alpha ,x)\ne \varnothing$

for any open subset $W\subset Y$ and $(\alpha ,x)\in \Sigma \times X$.

In the chapter below, we introduce a class of functions called products, which play an analogous role to the functions of type ${\tau }^n\left(x\right)$ used in the definition of cluster operators. For this purpose, we shall need a special type of functions from ${\mathcal{P}}^n\left(X\right)$ to ${\mathcal{P}}^{2n+2}(\Sigma \times X)$. Here, we introduce the general form of such functions.

Namely, for a Cartesian product $Z\times X$ and a point $z\in Z$, using the same symbol to denote the function $z:X\to Z\times X$ defined by $z\left(x\right)=(z,x)$ for all $x\in X$, for any subset $A\subset Z$ and for any non-negative integer k, we define the function $A^{\left(k\right)}:{\mathcal{P}}^k\left(X\right)\to {\mathcal{P}}^{k+1}(Z\times X)$, by

$A^{\left(k\right)}\left(\beta \right)=\left\{a\left(\beta \right):a\in A\right\}$ for all $\beta \in {\mathcal{P}}^k\left(X\right)$.

The Cartesian product reference is visible in the following equality:

$\bigcup A^{\left(0\right)}\left(B\right)=A\times B$ for all $A\subset Z$ and $B\subset X$.

For each non-decreasing n-tuple ($k_1,k_2,\dots ,k_n$), $n\ge$2, of non-negative integers, and for each $\lambda \in {\mathcal{P}}^n$(Z), we define the function

${\lambda }^{(k_1,k_2,\dots ,k_n)}:{\mathcal{P}}^{k_n}\left(X\right)\to {\mathcal{P}}^{k_n+n}(Z\times X)$, by

${\lambda }^{(k_1,k_2,\dots ,k_n)}\left(\beta \right)=\left\{{\alpha }^{(k_1,k_2,\dots ,k_{n-1})}\left(\beta \right):\alpha \in \lambda \right\}$ for all $\beta \in {\mathcal{P}}^{k_n}\left(X\right)$.

3.1. The Monoid of Products

Let us consider a Cartesian product $\Sigma \times X$, of a directed set $(\Sigma ,⪯)$ and a topological space $(X,\tau )$. ${\mathcal{F}}_{\Sigma }$ denotes the filter base of sections of $(\Sigma ,⪯)$, more precisely, ${\mathcal{F}}_{\Sigma }$ = $\left\{K_{\gamma }:\gamma \in \Sigma \right\}$, where $K_{\gamma }$ = $\left\{\alpha \in \Sigma :\gamma ⪯\alpha \right\}$. To simplify, we will write $\alpha \in K\in \mathcal{F}$ instead of $\alpha \in K_{\gamma }\in {\mathcal{F}}_{\Sigma }$, where $\gamma \in \Sigma$. Of course, $\mathcal{F}\in {\mathcal{P}}^2(\Sigma )$ and hence we can contemplate the use of the functions

${\mathcal{F}}^{(p,q)}:{\mathcal{P}}^q\left(X\right)\to {\mathcal{P}}^{q+2}(\Sigma \times X)$, where $p\le q$.

Since ${\tau }^n\left(x\right)\in {\mathcal{P}}^{2n}\left(X\right)$ for any $x\in X$, one can then consider the following compositions

${\mathcal{F}}^{(p,q)}\circ {\tau }^n:X\to {\mathcal{P}}^{2n+2}(\Sigma \times X)$

• whenever $p\le q\le 2n$.

Definition 6.

Let $(\Sigma ,⪯)$ be a directed set and let $(X,\tau )$ be a topological space. Then, the functions of the form ${\mathcal{F}}^{(p,q)}\circ {\tau }^n$, where n, p, q are non-negative integers such that $p\le q\le 2n$, will be called the products of the pair $\left(\right(\Sigma ,⪯)$, $(X,\tau ))$ (or simply of $(\Sigma ,X)$).

By $\mathcal{P}\mathcal{R}(\Sigma ,X)$, we will denote the set of all products of $(\Sigma ,X)$.

Adequately to the formulas given in Remark 7, any product ${\mathcal{F}}^{(s,q)}\circ {\tau }^n$ of $(\Sigma ,X)$ is uniquely determined by the structure of the 2(n + 1)-tuple of the sets of indices as the lemma below shows, where, according to Remark 7 (ii), we will use the notations:

${\mathcal{B}}_0^{(n,i)}$ = ${\tau }^i\left(x_{n-i}\right)$ for $i\in \left\{0,1,\dots ,n\right\}$;

${\mathcal{B}}_1^{(n,i)}$ = ${\tau }^i\left(U_{n-i}\right)$ for $i\in \left\{0,1,\dots ,n-1\right\}$.

We will, in the lemma below, introduce a uniform denotation for these two types of index sets as follows:

${\mathcal{D}}^{(n,i)}={\mathcal{B}}_{imod2}^{(n,⌊{\displaystyle \frac{i}{2}}⌋)}$ for $i=0,1,\dots ,2n$.

Lemma 13.

Let n, s, q be non-negative integers such that $s\le q\le 2n$ and $x_0\in X$. Then, any 2(n + 1)-tuple of index sets of ${\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x_0\right)$ is of the form

$({\mathcal{D}}^{(n,1)},\dots ,{\mathcal{D}}^{(n,s)},K,\dots ,{\mathcal{D}}^{(n,q)},\mathcal{F},\dots ,{\mathcal{D}}^{(n,2n)})\in$

• ${\mathcal{P}}^1\left(X\right)\times \dots \times {\mathcal{P}}^s\left(X\right)\times {\mathcal{P}}^1(\Sigma )\times \dots \times {\mathcal{P}}^q\left(X\right)\times {\mathcal{P}}^2(\Sigma )\times \dots \times {\mathcal{P}}^{2n}\left(X\right)$, i.e.,

any product ${\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x_0\right)$ is of the form

• $\left\{\right\{\left\{\right\{\left\{\right\{\{\dots \{(\alpha ,x_n):{\mathcal{D}}^{(n,i-1)}\in {\mathcal{D}}^{(n,i)}\}:i=1,\dots ,s\}:\alpha \in K\}:$

${\mathcal{D}}^{(n,j-1)}\in {\mathcal{D}}^{(n,j)}\}:j=s+1,\dots ,q\}:K\in \mathcal{F}\}:$

${\mathcal{D}}^{(n,k-1)}\in {\mathcal{D}}^{(n,k)}\}:k=q+1,\dots ,2n\}$.

Proof. 

According to Remark 7, ${\mathcal{B}}_{qmod2}^{(n,⌊{\displaystyle \frac{q}{2}}⌋)}$ belongs to the domain of ${\mathcal{F}}^{(s,q)}$ and thus,

• ${\mathcal{F}}^{(s,q)}\left({\tau }^n\left(x_0\right)\right)$ =
• $\{\dots \{{\mathcal{F}}^{(s,q)}({\mathcal{B}}_{qmod2}^{(n,⌊{\displaystyle \frac{q}{2}}⌋)}):{\mathcal{B}}_{(q+i)mod2}^{(n,⌊{\displaystyle \frac{q+i}{2}}⌋)}\in {\mathcal{B}}_{(q+i+1)mod2}^{(n,⌊{\displaystyle \frac{q+i+1}{2}}⌋)}\}:i=0,1,\dots ,2n-q-1\}$.

By the definition, we have ${\mathcal{F}}^{(s,q)}({\mathcal{B}}_{qmod2}^{(n,⌊{\displaystyle \frac{q}{2}}⌋)})=\{K^{\left(s\right)}({\mathcal{B}}_{qmod2}^{(n,⌊{\displaystyle \frac{q}{2}}⌋)}):K\in \mathcal{F}\}$ and in this exposition of ${\mathcal{F}}^{(s,q)}\left({\tau }^n\left(x\right)\right)$, we have used the following sequence of sets of indices:

$\left(\mathcal{F},{\mathcal{B}}_{(q+1)mod2}^{(n,⌊{\displaystyle \frac{q+1}{2}}⌋)},{\mathcal{B}}_{(q+2)mod2}^{(n,⌊{\displaystyle \frac{q+2}{2}}⌋)},\dots ,{\mathcal{B}}_{2nmod2}^{(n,⌊{\displaystyle \frac{2n}{2}}⌋)}\right)\in$

${\mathcal{P}}^2(\Sigma )\times {\mathcal{P}}^{q+1}\left(X\right)\times {\mathcal{P}}^{q+2}\left(X\right)\times \dots \times {\mathcal{P}}^{2n}\left(X\right).$$(\ast )$

Analogously, $K^{\left(s\right)}({\mathcal{B}}_{qmod2}^{(n,⌊{\displaystyle \frac{q}{2}}⌋)})$ =

• $\{\dots \{K^{\left(s\right)}({\mathcal{B}}_{smod2}^{(n,⌊{\displaystyle \frac{s}{2}}⌋)}):{\mathcal{B}}_{(s+i)mod2}^{(n,⌊{\displaystyle \frac{s+i}{2}}⌋)}\in {\mathcal{B}}_{(s+i+1)mod2}^{(n,⌊{\displaystyle \frac{s+i+1}{2}}⌋)}\}:i=0,1,\dots ,q-s-1\}$
• and, by definition, $K^{\left(s\right)}({\mathcal{B}}_{smod2}^{(n,⌊{\displaystyle \frac{s}{2}}⌋)})=\{\alpha ({\mathcal{B}}_{smod2}^{(n,⌊{\displaystyle \frac{s}{2}}⌋)}):\alpha \in K\}.$ So, we have used the following sequence of sets of indices

$\left(K,{\mathcal{B}}_{(s+1)mod2}^{(n,⌊{\displaystyle \frac{s+1}{2}}⌋)},{\mathcal{B}}_{(s+2)mod2}^{(n,⌊{\displaystyle \frac{s+2}{2}}⌋)},\dots ,{\mathcal{B}}_{qmod2}^{(n,⌊{\displaystyle \frac{q}{2}}⌋)}\right)\in$

${\mathcal{P}}^1(\Sigma )\times {\mathcal{P}}^{s+1}\left(X\right)\times {\mathcal{P}}^{s+2}\left(X\right)\times \dots \times {\mathcal{P}}^q\left(X\right)$. $(\ast \ast )$

Finally, $\alpha \left({\mathcal{B}}_{smod2}^{⌊{\displaystyle \frac{s}{2}}⌋}\right)=$

$\{\dots \{\alpha ({\mathcal{B}}_{0mod2}^{(n,⌊{\displaystyle \frac{0}{2}}⌋)}):{\mathcal{B}}_{imod2}^{(n,⌊{\displaystyle \frac{i}{2}}⌋)}\in {\mathcal{B}}_{(i+1)mod2}^{(n,⌊{\displaystyle \frac{i+1}{2}}⌋)}\}:i=0,1,\dots ,s-1\}$ and, we have used the following sequence of sets of indices

$\left({\mathcal{B}}_{1mod2}^{(n,⌊{\displaystyle \frac{1}{2}}⌋)},{\mathcal{B}}_{2mod2}^{(n,⌊{\displaystyle \frac{2}{2}}⌋)},\dots ,{\mathcal{B}}_{smod2}^{(n,⌊{\displaystyle \frac{s}{2}}⌋)}\right)\in$${\mathcal{P}}^1\left(X\right)\times {\mathcal{P}}^2\left(X\right)\times \dots \times {\mathcal{P}}^s\left(X\right)$. $(\ast \ast \ast )$

So, $(\ast )$, $(\ast \ast )$ and $(\ast \ast \ast )$ taken together show that any 2(n + 1)-tuple of index sets of ${\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x\right)$ is of the form

$({\mathcal{D}}^{(n,1)},\dots ,{\mathcal{D}}^{(n,s)},K,\dots ,{\mathcal{D}}^{(n,q)},\mathcal{F},{\mathcal{D}}^{(n,q+1)},\dots ,{\mathcal{D}}^{(n,2n)})\in$

• ${\mathcal{P}}^1\left(X\right)\times \dots \times {\mathcal{P}}^s\left(X\right)\times {\mathcal{P}}^1(\Sigma )\times \dots \times {\mathcal{P}}^q\left(X\right)\times {\mathcal{P}}^2(\Sigma )\times {\mathcal{P}}^{q+1}\left(X\right)\times \dots \times {\mathcal{P}}^{2n}\left(X\right)$ which finishes the proof. □

Remark 11.

With the above lemma, we can see that the equivalences established in Remark 7 (iv) take the following form:

${\mathcal{D}}^{(n,i)}\in {\mathcal{D}}^{(n,i+1)}$ if and only if ${\mathcal{D}}^{(n-m,i-2m)}\in {\mathcal{D}}^{(n-m,i+1-2m)}$,

• where $i=0,1,\dots ,2n-1$ and $m=0,1,\dots ,⌊{\displaystyle \frac{i}{2}}⌋$.

Theorem 2.

Let $(X,\tau )$ be a topological space, and $(\Sigma ,\le )$ a directed set. Then, the set $\mathcal{P}\mathcal{R}(\Sigma ,X)$ of all products of $\left(\right(\Sigma ,⪯),(X,\tau \left)\right)$ forms an Abelian monoid under the operation ⊕ defined by

$({\mathcal{F}}^{(s,q)}\circ {\tau }^n)\oplus ({\mathcal{F}}^{(s^{*},q^{*})}\circ {\tau }^{n^{*}})={\mathcal{F}}^{(s+s^{*},q+q^{*})}\circ {\tau }^{n+n^{*}}$,

• with the neutral element $e={\mathcal{F}}^{(0,0)}\circ {\tau }^0$.

The monoid $\left(\mathcal{P}\mathcal{R}\right(\Sigma ,X),\oplus ,e)$ is generated by the subset $\mathcal{B}\mathcal{P}\mathcal{R}(\Sigma ,X)\subset \mathcal{P}\mathcal{R}(\Sigma ,X)$ of all six products of the form ${\mathcal{F}}^{(s,q)}\circ {\tau }^1$.

Proof. 

The axioms for commutative monoids are clearly fulfilled. We will show that $\left(\mathcal{P}\mathcal{R}\right(\Sigma ,X),\oplus ,e)$ is generated by the family

$\mathcal{B}\mathcal{P}\mathcal{R}(\Sigma ,X)=\{A^{(i,j)}:i,j\in N$ and $i\le j\le 2\}$, where $A^{(i,j)}={\mathcal{F}}^{(i,j)}\circ {\tau }^1$.

Let us consider the functions ${\tau }_{\otimes }^n:\Sigma \times X\to {\mathcal{P}}^{2n}(\Sigma \times X)$ defined by

${\tau }_{\otimes }^n(\alpha ,x)=\alpha \left({\tau }^n\left(x\right)\right)$ for all $(\alpha ,x)\in \Sigma \times X$ and $n\in N$.

Firstly, we will show that

${\tau }_{\otimes }^k\circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x\right)={\mathcal{F}}^{(s+2k,q+2k)}\circ {\tau }^{n+k}\left(x\right)$$(\ast )$

• for all $x\in X$ and k = 0, 1, …

Indeed, basing on the description $(\ast ),(\ast \ast )$ and $(\ast \ast \ast )$ given in the proof of Lemma 3, we have

${\tau }_{\otimes }^k\circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x\right))=$

• $\left\{\dots \left\{\left\{{\tau }_{\otimes }^k\left(K^{\left(s\right)}\left({\mathcal{D}}^{(n,q)}\right)\right):K\in \mathcal{F}\right\}:{\mathcal{D}}^{(n,q+i)}\in {\mathcal{D}}^{(n,q+i+1)}\right\}:i=0,1,\dots ,2n-q-1\right\}$,

${\tau }_{\otimes }^k\left(K^{\left(s\right)}\left({\mathcal{D}}^{(n,q)}\right)\right)=$

• $\left\{\dots \left\{\left\{{\tau }_{\otimes }^k\left(\alpha \left({\mathcal{D}}^{(n,s)}\right)\right):\alpha \in K\right\}:{\mathcal{D}}^{(n,s+i)}\in {\mathcal{D}}^{(n,s+i+1)}\right\}:i=0,1,\dots ,q-s-1\right\}$ and ${\tau }_{\otimes }^k\left(\alpha \left({\mathcal{D}}^{(n,s)}\right)\right)$ = $\left\{\dots \left\{{\tau }_{\otimes }^k\left(\alpha \left(x_n\right)\right):{\mathcal{D}}^{(n,i)}\in {\mathcal{D}}^{(n,i+1)}\right\}:i=0,1,\dots ,s-1\right\}$, where, according to the notation of Remark 7 and Lemma 3, we have ${\mathcal{D}}^{(n,j)}\in {\mathcal{P}}^j$(X) for j = 1, 2, … and ${\mathcal{D}}^{(n,0)}=x_n$. So, any 2(n + 1)-tuple of index sets of such description of ${\tau }_{\otimes }^k\circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x\right)$ belongs to
• ${\mathcal{P}}^1\left(X\right)\times \dots \times {\mathcal{P}}^s\left(X\right)\times {\mathcal{P}}^1(\Sigma )\times \dots \times {\mathcal{P}}^q\left(X\right)\times {\mathcal{P}}^2(\Sigma )\times \dots \times {\mathcal{P}}^{2n}\left(X\right)$.

It follows by definition, that ${\tau }_{\otimes }^k\left(\alpha \left(x_n\right)\right)={\tau }_{\otimes }^k(\alpha ,x_n)=\alpha \left({\tau }^k\left(x_n\right)\right)=$

$\alpha \left(\left\{\dots \left\{\left\{x_{n,k}:{\mathcal{B}}_0^{(n,i)}\in {\mathcal{B}}_1^{(n,i)}\right\}:{\mathcal{B}}_1^{(n,i)}\in {\mathcal{B}}_0^{(n,i+1)}\right\}:i=0,\dots ,k-1\right\}\right)$, where

• ${\mathcal{B}}_0^{(n,i)}$ = ${\tau }^i\left(x_{n,k-i}\right)$, ${\mathcal{B}}_1^{(n,i)}$ = ${\tau }^i\left(U_{n,k-i}\right)$, i $\in \left\{0,\dots ,k-1\right\}$ and $x_{n,0}=x_n$. So, any 2k-tuple of index sets of ${\tau }_{\otimes }^k\left(\alpha \left(x_n\right)\right)$ belongs to
• ${\mathcal{P}}^1\left(X\right)\times {\mathcal{P}}^2\left(X\right)\times \dots \times {\mathcal{P}}^{2k-1}\left(X\right)\times {\mathcal{P}}^{2k}\left(X\right)$ and consequently, the structure of ${\tau }_{\otimes }^k({\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x\right))$ is determined by
• ${\mathcal{P}}^1\left(X\right)\times \dots \times {\mathcal{P}}^{2k}\left(X\right)\times {\mathcal{P}}^{1+2k}\left(X\right)\times \dots \times {\mathcal{P}}^{s+2k}\left(X\right)\times {\mathcal{P}}^1(\Sigma )\times {\mathcal{P}}^{s+2k+1}\left(X\right)\times \dots \times {\mathcal{P}}^{q+2k}\left(X\right)\times {\mathcal{P}}^2(\Sigma )\times {\mathcal{P}}^{q+2k+1}\left(X\right)\times \dots \times {\mathcal{P}}^{2n+2k}\left(X\right)$ which corresponds to ${\mathcal{F}}^{(s+2k,q+2k)}\circ {\tau }^{n+k}\left(x\right)$. Thus, we have proved the equality $(\ast )$.

We now show that every product ${\mathcal{F}}^{(s,q)}\circ {\tau }^n$, where $n\ge 1$, can be presented in the following form:

${\mathcal{F}}^{(s,q)}\circ {\tau }^n$= ${\tau }_{\otimes }^k\circ {\mathcal{F}}^{(\alpha ,\beta )}\circ {\tau }^{\gamma }\circ {\tau }^m$, $(\ast \ast )$

• where $k,m,\gamma \in \left\{0,1,2,\dots \right\}$ and, ${\mathcal{F}}^{(\alpha ,\beta )}\circ {\tau }^{\gamma }$ belongs to the set ${\mathcal{B}}^0\mathcal{P}\mathcal{A}(\Sigma ,X)$ of all products of type

${\mathcal{F}}^{(0,\beta )}\circ {\tau }^{\beta -⌊{\displaystyle \frac{\beta }{2}}⌋}$, or

${\mathcal{F}}^{(1,\beta )}\circ {\tau }^{\beta -⌊{\displaystyle \frac{\beta }{2}}⌋}$, where $\beta =1,2,\dots$

For this purpose, let us first note that

${\mathcal{F}}^{(s,q)}\circ {\tau }^n$= ${\tau }_{\otimes }^{⌊{\displaystyle \frac{s}{2}}⌋}\circ {\mathcal{F}}^{(s-2⌊{\displaystyle \frac{s}{2}}⌋,q-2⌊{\displaystyle \frac{s}{2}}⌋)}\circ {\tau }^{n-⌊{\displaystyle \frac{s}{2}}⌋}$,

• which follows directly from $(\ast )$. Next, we note that ${\mathcal{F}}^{(s-2⌊{\displaystyle \frac{s}{2}}⌋,q-2⌊{\displaystyle \frac{s}{2}}⌋)}$ is of the form ${\mathcal{F}}^{(0,\beta )}$ or ${\mathcal{F}}^{(1,\beta )}$, where $\beta =q-2⌊{\displaystyle \frac{s}{2}}⌋$.

Now, it is enough to decompose ${\tau }^{n-⌊{\displaystyle \frac{s}{2}}⌋}$ as follows:

${\tau }^{n-⌊{\displaystyle \frac{s}{2}}⌋}={\tau }^{\beta -⌊{\displaystyle \frac{\beta }{2}}⌋}\circ {\tau }^{n-⌊{\displaystyle \frac{s}{2}}⌋-\beta +⌊{\displaystyle \frac{\beta }{2}}⌋}$.

So, we obtain

${\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x\right)$= ${\tau }_{\otimes }^{⌊{\displaystyle \frac{s}{2}}⌋}\circ {\mathcal{F}}^{(s-2⌊{\displaystyle \frac{s}{2}}⌋,\beta )}\circ {\tau }^{\beta -⌊{\displaystyle \frac{\beta }{2}}⌋}\circ {\tau }^{n-⌊{\displaystyle \frac{s}{2}}⌋-\beta +⌊{\displaystyle \frac{\beta }{2}}⌋}$,

• where ${\mathcal{F}}^{(s-2⌊{\displaystyle \frac{s}{2}}⌋,\beta )}\circ {\tau }^{\beta -⌊{\displaystyle \frac{\beta }{2}}⌋}\in {\mathcal{B}}^0\mathcal{P}\mathcal{A}(\Sigma ,X)$, which ends the proof of $(\ast \ast )$.

We will now show that ${\mathcal{B}}^0\mathcal{P}\mathcal{R}(\Sigma ,X)$ is generated by $\mathcal{B}\mathcal{P}\mathcal{R}(\Sigma ,X)$.

Let us take ${\mathcal{F}}^{(0,\beta )}\circ {\tau }^{\beta -⌊{\displaystyle \frac{\beta }{2}}⌋}$, where $\beta =1,2,\dots$ and suppose that $\beta =2i+1$, where i = 0, 1, … Then, we have ${\mathcal{F}}^{(0,\beta )}\circ {\tau }^{\beta -⌊{\displaystyle \frac{\beta }{2}}⌋}=$

${\mathcal{F}}^{(0,2i+1)}\circ {\tau }^{i+1}={\mathcal{F}}^{(0,1)}\circ {\tau }^1\oplus {\mathcal{F}}^{(0,2i)}\circ {\tau }^i={\mathcal{F}}^{(0,1)}\circ {\tau }^1\oplus i{\mathcal{F}}^{(0,2)}\circ {\tau }^1$ i.e.,

${\mathcal{F}}^{(0,\beta )}\circ {\tau }^{\beta -⌊{\displaystyle \frac{\beta }{2}}⌋}=A^{(0,1)}\oplus i{A}^{(0,2)}$. $(\ast \ast \ast )$

If we assume that $\beta =2i$, where i = 1, 2, … Then,

${\mathcal{F}}^{(0,\beta )}\circ {\tau }^{\beta -⌊{\displaystyle \frac{\beta }{2}}⌋}={\mathcal{F}}^{(0,2i)}\circ {\tau }^i=i{A}^{(0,2)}$. $(\ast \ast \ast \ast )$

Let us now check the products ${\mathcal{F}}^{(1,\beta )}\circ {\tau }^{\beta -⌊{\displaystyle \frac{\beta }{2}}⌋}$, where $\beta =1,2,\dots$ and first suppose that $\beta =2i+1$, where i = 0, 1, … Then, ${\mathcal{F}}^{(1,\beta )}\circ {\tau }^{\beta -⌊{\displaystyle \frac{\beta }{2}}⌋}=$

${\mathcal{F}}^{(1,2i+1)}\circ {\tau }^{i+1}={\mathcal{F}}^{(1,1)}\circ {\tau }^1\oplus {\mathcal{F}}^{(0,2i)}\circ {\tau }^1={\mathcal{F}}^{(1,1)}\circ {\tau }^1\oplus i{\mathcal{F}}^{(0,2)}\circ {\tau }^1$ i.e.,

${\mathcal{F}}^{(1,\beta )}\circ {\tau }^{\beta -⌊{\displaystyle \frac{\beta }{2}}⌋}=A^{(1,1)}\oplus i{A}^{(0,2)}$. $(\ast \ast \ast \ast \ast )$

If $\beta =2i$, where i = 1, 2, … Then, ${\mathcal{F}}^{(1,\beta )}\circ {\tau }^{\beta -⌊{\displaystyle \frac{\beta }{2}}⌋}=$

${\mathcal{F}}^{(1,2i)}\circ {\tau }^i={\mathcal{F}}^{(1,2)}\circ {\tau }^1\oplus {\mathcal{F}}^{(0,2i-2)}\circ {\tau }^{i-1}={\mathcal{F}}^{(1,2)}\circ {\tau }^1\oplus (i-1){\mathcal{F}}^{(0,2)}\circ {\tau }^1$ i.e.,

${\mathcal{F}}^{(1,\beta )}\circ {\tau }^{\beta -⌊{\displaystyle \frac{\beta }{2}}⌋}=A^{(1,2)}\oplus (i-1)A^{(0,2)}$. $(\ast \ast \ast \ast \ast \ast )$

So, $(\ast \ast \ast ),(\ast \ast \ast \ast ),(\ast \ast \ast \ast \ast )$ and $(\ast \ast \ast \ast \ast \ast )$ together prove that the part ${\mathcal{F}}^{(\alpha ,\beta )}\circ {\tau }^{\gamma }$ of the presentation $(\ast \ast )$ can be built from the members of the set $\mathcal{B}\mathcal{P}\mathcal{A}(\Sigma ,X)$.

Finally, let us note that for every product ${\mathcal{F}}^{(\alpha ,\beta )}\circ {\tau }^{\gamma }\left(x\right)$, hold

${\mathcal{F}}^{(\alpha ,\beta )}\circ {\tau }^{\gamma }\circ {\tau }^m={\mathcal{F}}^{(\alpha ,\beta )}\circ {\tau }^{\gamma }\oplus m{A}^{(0,0)}$ and, according to $(\ast )$,

${\tau }_{\otimes }^k\circ {\mathcal{F}}^{(\alpha ,\beta )}\circ {\tau }^{\gamma }={\mathcal{F}}^{(\alpha ,\beta )}\circ {\tau }^{\gamma }\oplus k{A}^{(2,2)}$.

Indeed, ${\mathcal{F}}^{(\alpha ,\beta )}\circ {\tau }^{\gamma }\circ {\tau }^m={\mathcal{F}}^{(\alpha ,\beta )}\circ {\tau }^{\gamma +m}={\mathcal{F}}^{(\alpha ,\beta )}\circ {\tau }^{\gamma }\oplus {\mathcal{F}}^{(0,0)}\circ {\tau }^m=$

${\mathcal{F}}^{(\alpha ,\beta )}\circ {\tau }^{\gamma }\oplus m{\mathcal{F}}^{(0,0)}\circ {\tau }^1={\mathcal{F}}^{(\alpha ,\beta )}\circ {\tau }^{\gamma }\oplus m{A}^{(0,0)}$.

Similarly, we have

${\tau }_{\otimes }^k\circ {\mathcal{F}}^{(\alpha ,\beta )}\circ {\tau }^{\gamma }={\mathcal{F}}^{(\alpha +2k,\beta +2k)}\circ {\tau }^{\gamma +k}={\mathcal{F}}^{(\alpha ,\beta )}\circ {\tau }^{\gamma }\oplus {\mathcal{F}}^{(2k,2k)}\circ {\tau }^k=$

${\mathcal{F}}^{(\alpha ,\beta )}\circ {\tau }^{\gamma }\oplus k{\mathcal{F}}^{(2,2)}\circ {\tau }^1={\mathcal{F}}^{(\alpha ,\beta )}\circ {\tau }^{\gamma }\oplus k{A}^{(2,2)}$.

Therefore, the presentation $(\ast \ast )$ has the form $k{A}^{(2,2)}\oplus {\mathcal{F}}^{(\alpha ,\beta )}\circ {\tau }^{\gamma }\oplus m{A}^{(0,0)}$, i.e., one of the following forms:

(i)

$k{A}^{(2,2)}\oplus A^{(0,1)}\oplus i{A}^{(0,2)}\oplus m{A}^{(0,0)}$, i = 0, 1, …,

(ii)

$k{A}^{(2,2)}\oplus i{A}^{(0,2)}\oplus m{A}^{(0,0)}$, i = 1, 2, …,

(iii)

$k{A}^{(2,2)}\oplus A^{(1,1)}\oplus i{A}^{(0,2)}\oplus m{A}^{(0,0)}$, i = 0, 1, …, or

(iv)

$k{A}^{(2,2)}\oplus A^{(1,2)}\oplus (i-1)A^{(0,2)}\oplus m{A}^{(0,0)}$, i = 1, 2, ….

This finishes the proof. □

3.2. Convergence Operators

Let $\Theta$ be a function from $(\Sigma \times X)$ to ${\mathcal{P}}^2\left(Y\right)$ and let let us take a product ${\mathcal{F}}^{(s,q)}\circ {\tau }^n:X\to {\mathcal{P}}^{2n+2}(\Sigma \times X)$$(\Sigma ,X)$. It is evident that $\Theta \circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x\right)$ belongs to ${\mathcal{P}}^{2n+4}\left(Y\right)$ for all $x\in X$, so these sets belong to the domain of every composition of 2n + 2 functions taken from the set $\left\{u,l\right\}$. One can therefore consider the following functions:

$h_{2n+2}\circ h_{2n+1}\circ \dots \circ h_2\circ h_1\circ \Theta \circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n:X\to {\mathcal{P}}^2\left(Y\right)$,

• where $h_i\in \left\{u,l\right\}$ for i = 1, 2, …, 2n + 2.

Of course, the number of the functions $h_i$, $i=1,2,\dots ,2n+2$, in the above composition is determined by the function ${\mathcal{F}}^{(s,q)}\circ {\tau }^n$, so one can use the following shorter notation for such compositions:

$\langle h_{2n+2},h_{2n+1},\dots ,h_2,h_1,\Theta \rangle$.

As shown above, in Lemma 3, the structure of any product ${\mathcal{F}}^{(s,q)}\circ {\tau }^n$ is unequivocally represented by a sequence of index sets

$({\mathcal{D}}^{(n,1)},{\mathcal{D}}^{(n,2)},\dots ,{\mathcal{D}}^{(n,s)},K,{\mathcal{D}}^{(n,s+1)},\dots ,{\mathcal{D}}^{(n,q)},\mathcal{F},{\mathcal{D}}^{(n,q+1)},\dots ,{\mathcal{D}}^{(n,2n)})\in$

$({\mathcal{P}}^1\left(X\right),\dots ,{\mathcal{P}}^s\left(X\right),{\mathcal{P}}^1(\Sigma ),{\mathcal{P}}^{s+1}\left(X\right),\dots ,{\mathcal{P}}^q\left(X\right),{\mathcal{P}}^2(\Sigma ),{\mathcal{P}}^{q+1}\left(X\right),\dots ,{\mathcal{P}}^{2n}\left(X\right))$.

So, in accordance with the structure of ${\mathcal{F}}^{(s,q)}\circ {\tau }^n$ we will use the following more precise notation for the above compositions:

$\langle h_{2n},\dots ,h_{q+1},{\widehat{h}}_2,h_q,\dots ,h_{s+1},{\widehat{h}}_1,h_s,\dots ,h_1,\Theta \rangle$,

where ${\widehat{h}}_2$ and ${\widehat{h}}_1$ correspond to ${\mathcal{P}}^2(\Sigma )$ and ${\mathcal{P}}^1(\Sigma )$, respectively.

In fact, one might consider two kinds of functions:

• $(\mathbf{Conv}.\mathbf{F})$$\langle h_{2n},\dots ,h_{q+1},{\widehat{h}}_2,h_q,\dots ,h_{s+1},{\widehat{h}}_1,h_s,\dots ,h_1,\Theta \rangle :X\to {\mathcal{P}}^2\left(Y\right)$,
• $(\mathbf{Conv}.\mathbf{O})$$\langle h_{2n},\dots ,h_{q+1},{\widehat{h}}_2,h_q,\dots ,h_{s+1},{\widehat{h}}_1,h_s,\dots ,h_1\rangle :{\mathcal{P}}^2{\left(Y\right)}^{\Sigma \times X}⟶{\mathcal{P}}^2{\left(Y\right)}^X$
• which assigns to every function $\Theta :\Sigma \times X\to {\mathcal{P}}^2\left(Y\right)$, the function

$\langle h_{2n},\dots ,h_{q+1},{\widehat{h}}_2,h_q,\dots ,h_{s+1},{\widehat{h}}_1,h_s,\dots ,h_1\rangle (\Theta )$ =

$\langle h_{2n},\dots ,h_{q+1},{\widehat{h}}_2,h_q,\dots ,h_{s+1},{\widehat{h}}_1,h_s,\dots ,h_1,\Theta \rangle$.

Definition 7.

Let $(X,\tau )$ and $(Y,\sigma )$ be two topological spaces, $(\Sigma ,⪯)$ be a directed set, and let $\Theta \in {\mathcal{P}}^2{\left(Y\right)}^{\Sigma \times X}$.

(i)

Any function of the form

$\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1,\Theta \rangle$,

will be called a convergence function.

(ii)

Any function of the form

$\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1\rangle$,

will be called a convergence operator.

Let us denote by $\mathcal{CON}.\mathcal{O}(\Sigma ,X,Y)$ the set of all convergence operators for given ($\Sigma ,\le$), $(X,\tau )$, and $(Y,\sigma )$.

The function obtained from a convergence function $\langle \Delta ,\Theta \rangle$ (resp. operator $\Delta$) by exchanging u and l will be denoted by ${\langle \Delta ,\Theta \rangle }^{-1}$ (resp. ${\Delta }^{-1}$), where $\Theta \in \left\{\mathcal{I}\overline{H},\mathcal{S}\overline{H}\right\}$.

In connection with the characterization of $\overline{\left\{H_{\alpha }\left(x\right)\right\}}$ and $\overline{\mathcal{P}(H_{\alpha }\left(x\right)})$ by the operations $\mathcal{I}$ and $\mathcal{S}$ as $\mathcal{I}\overline{H}$ and $\mathcal{S}\overline{H}$, respectively, where $(\alpha ,x)\in \Sigma \times X$, according to Lemma 5, we have the following equalities:

${\Delta }^{-1}\left(\mathcal{S}\overline{H}\right)=\langle {\Delta }^{-1},\mathcal{S}\overline{H}\rangle ={\langle \Delta ,\mathcal{I}\overline{H}\rangle }^{-1}$ and

${\Delta }^{-1}\left(\mathcal{I}\overline{H}\right)=\langle {\Delta }^{-1},\mathcal{I}\overline{H}\rangle ={\langle \Delta ,\mathcal{S}\overline{H}\rangle }^{-1}$.

Of course,

${\langle \mathcal{I}F\rangle }^{-1}\left(x\right)=\langle \mathcal{S}F\rangle \left(x\right)=\mathcal{S}F\left(x\right)$ and

${\langle \mathcal{S}F\rangle }^{-1}\left(x\right)=\langle \mathcal{I}F\rangle \left(x\right)=\mathcal{I}F\left(x\right)$, $x\in X$.

We will use the notion of convergence operator to define many types of convergence of nets of multifunctions. A type of convergence of a net ${\left(H_{\alpha }\right)}_{\alpha \in \Sigma }$ to a multifunction F at a point $x\in X$ is determined by

• A convergence function $\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1,\Theta \rangle$,
  where $\Theta \in \left\{\mathcal{I}\overline{H},\mathcal{S}\overline{H}\right\}$;
• A function $\Psi \in \left\{\langle \mathcal{I}F\rangle ,\langle \mathcal{S}F\rangle \right\}$;
• Some relationship between $\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1,\Theta \rangle \left(x\right)$
  and $\Psi$.

So, by a type of convergence determined by a convergence operator $\Delta$, we mean a pair of the form $(\Psi ,\langle \Delta ,\Theta \rangle )$, where $\Psi \in \left\{\langle \mathcal{I}F\rangle ,\langle \mathcal{S}F\rangle \right\}$ and $\Theta \in \left\{\mathcal{I}\overline{H},\mathcal{S}\overline{H}\right\}$.

Definition 8.

We say that a net of multifunctions $H_{\alpha }:(X,\tau )\to (Y,\sigma )$, $\alpha \in \Sigma$, is $(\Psi ,\langle \Delta ,\Theta \rangle )$-convergent to a multifunction $F:(X,\tau )\to (Y,\sigma )$ at a point $x\in X$, if $\Psi \left(x\right)\subset \langle \Delta ,\Theta \rangle \left(x\right)$, where Δ is a convergence operator, $\Theta \in \left\{\mathcal{I}\overline{H},\mathcal{S}\overline{H}\right\}$ and $\Psi \in \left\{\langle \mathcal{I}F\rangle ,\langle \mathcal{S}F\rangle \right\}$.

3.3. Classical Types of Convergence in Terms of the Convergence Operators

We will show that the convergence operators characterize the classical types of convergence of nets of multifunctions. In this connection, we need to recall some definitions.

For a net, $\left\{A_{\alpha }:\alpha \in \Sigma \right\}$ of subsets $A_{\alpha }$ of a topological space X, a point $x\in X$ is called a limit point (resp. cluster point) of $\left\{A_{\alpha }:\alpha \in \Sigma \right\}$ shortly, $x\in Li$$A_{\alpha }$ (resp. $x\in Ls$$A_{\alpha }$) [32,55], if for every open subset $U\subset X$ such that $x\in U$, there is $\gamma \in \Sigma$ such that U meets $A_{\alpha }$ for each $\alpha \ge \gamma$ (resp. for every $\gamma \in \Sigma$ there is $\alpha \ge \gamma$ such that U meets $A_{\alpha })$.

We say that a net $\left\{A_{\alpha }:\alpha \in \Sigma \right\}$ topologically converges to a subset A, denoted by $Lt$$A_{\alpha }=A$, if $A=Li$$A_{\alpha }=Ls$$A_{\alpha }$.

By $lim$  $inf$  $A_{\alpha }$ and $lim$  $sup$  $A_{\alpha }$ we denote the upper and lower limits in the sense of the set-theory, i.e., the set $\bigcup \left\{\bigcap \left\{A_{\alpha }:\alpha \ge \gamma \right\}:\gamma \in \Sigma \right\}$ and $\bigcap \left\{\bigcup \left\{A_{\alpha }:\alpha \ge \gamma \right\}:\gamma \in \Sigma \right\}$, respectively.

The concepts of convergence of nets of subsets and convergence of nets of multi-functions are closely related. Generally, one could consider the following properties for a given multifunction $F:(X,\tau )\to (Y,\sigma )$, a net ${\left(H_{\alpha }\right)}_{\alpha \in \Sigma }$ of multifunctions $H_{\alpha }:(X,\tau )\to (Y,\sigma )$ and a point $x\in X$:

(PC1)  $F\left(x\right)=Lt$$H_{\alpha }\left(x\right)$;

(PC2)  $F\left(x\right)=Ls$$H_{\alpha }\left(x\right)$;

(PC3)  $F\left(x\right)=Li$$H_{\alpha }\left(x\right)$;

(PC4)  $F\left(x\right)\subset Li$$H_{\alpha }\left(x\right)$;

(PC5)  $F\left(x\right)\supset Li$$H_{\alpha }\left(x\right)$;

(PC6)  $F\left(x\right)\subset Ls$$H_{\alpha }\left(x\right)$;

(PC7)  $F\left(x\right)\supset Ls$$H_{\alpha }\left(x\right)$.

For the graphs of multifunctions, one can formulate conditions analogous to the above.

(GC1)  $Gr\left(F\right)=Lt$$Gr\left(H_{\alpha }\right)$;

(GC2)  $Gr\left(F\right)=Ls$$Gr\left(H_{\alpha }\right)$;

(GC3)  $Gr\left(F\right)=Li$$Gr\left(H_{\alpha }\right)$;

(GC4)  $Gr\left(F\right)\subset Li$$Gr\left(H_{\alpha }\right)$;

(GC5)  $Gr\left(F\right)\supset Li$$Gr\left(H_{\alpha }\right)$;

(GC6)  $Gr\left(F\right)\subset Ls$$Gr\left(H_{\alpha }\right)$;

(GC7)  $Gr\left(F\right)\supset Ls$$Gr\left(H_{\alpha }\right)$.

The theorem below shows that the types of convergences listed above can be characterized in terms of convergence operators.

Let us first recall some definitions. A subset B of a topological space is $\alpha$-paracompact [56], if every open cover of B has a locally finite open covering refinement.

We will use the following two properties of $\alpha$-paracompact subsets:

• For every $\alpha$−paracompact subset B of a regular topological space and for every open subset W with $B\subset W$ there exists an open subset V such that $B\subset V\subset Cl\left(V\right)\subset W$;
• For every $\alpha$−paracompact subset B of a $T_2$ topological space and for every point $x\notin B$ there exist disjoint open subsets V and W such that $x\in V$ and $B\subset W$.

Theorem 3.

The following conditions hold for an arbitrary net ${\left(H_{\alpha }\right)}_{\alpha \in \Sigma }$ of multifunctions $H_{\alpha }:(X,\tau )\to (Y,\sigma )$, a multifunction $F:(X,\tau )\to (Y,\sigma )$ and a point $x_0\in X:$

(i)

$F\left(x_0\right)\subset Li$$H_{\alpha }\left(x_0\right)$ if and only if $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle \left(x_0\right)$;

(ii)

$Gr\left(F\right)\subset Li$$Gr\left(H_{\alpha }\right)$ if and only if $\langle \mathcal{S}F\rangle ⪯\langle u,\widehat{l},\widehat{u},l,\mathcal{S}\overline{H}\rangle$;

(iii)

$F\left(x_0\right)\subset Ls$$H_{\alpha }\left(x_0\right)$ if and only if $\langle \mathcal{S}F\rangle \left(x_0\right)\subset {\langle \widehat{l},\widehat{u},\mathcal{I}\overline{H}\rangle }^{-1}\left(x_0\right)$;

(iv)

$Gr\left(F\right)\subset Ls$$Gr\left(H_{\alpha }\right)$ if and only if $\langle \mathcal{S}F\rangle ⪯{\langle l,\widehat{l},\widehat{u},u,\mathcal{I}\overline{H}\rangle }^{-1}$;

(v)

if $(Y,\sigma )$ is $T_2$ and the values of F are α-paracompact, then

(a)

$F\left(x_0\right)\supset Li$$H_{\alpha }\left(x_0\right)$ whenever $\langle \mathcal{I}F\rangle \left(x_0\right)\subset {\langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle }^{-1}\left(x_0\right)$;

(b)

$Gr\left(F\right)\supset Li$$Gr\left(H_{\alpha }\right)$ whenever $\langle \mathcal{I}F\rangle ⪯{\langle u,\widehat{l},\widehat{u},l,\mathcal{S}\overline{H}\rangle }^{-1}$;

(c)

$F\left(x_0\right)\supset$$Ls$$H_{\alpha }\left(x_0\right)$ whenever $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle \widehat{l},\widehat{u},\mathcal{I}\overline{H}\rangle \left(x_0\right)$;

(d)

$Gr\left(F\right)\supset Ls$$Gr\left(H_{\alpha }\right)$ whenever $\langle \mathcal{I}F\rangle ⪯\langle l,\widehat{l},\widehat{u},u,\mathcal{I}\overline{H}\rangle$.

Proof. 

(i): According to the definition,

$\langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle \left(x_0\right)=$

$l\circ u\circ \mathcal{S}\overline{H}\circ {\mathcal{F}}^{(0,0)}\circ {\tau }^0\left(x_0\right)=$

$l\circ u\circ \mathcal{S}\overline{H}\left(\{\{(\alpha ,x_0):\alpha \in K\}:K\in \mathcal{F}\}\right)=$

$l\circ u\left(\{\{\overline{\mathcal{P}\left(H_{\alpha }\left(x_0\right)\right)}:\alpha \in K\}:K\in \mathcal{F}\}\right)=$

$\overline{{\bigcup }_{K\in \mathcal{F}}{\bigcap }_{\alpha \in K}\overline{\mathcal{P}\left(H_{\alpha }\left(x_0\right)\right)}}$. $\left(1\right)$

The assumption $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle \left(x_0\right)$, implies that, for every $y\in F\left(x_0\right)$, we have $\left\{y\right\}\in \langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle \left(x_0\right)$ because $\mathcal{P}\left(F\left(x_0\right)\right)\subset \langle \mathcal{S}F\rangle \left(x_0\right)$. Consequently, according to $\left(I\right)$, for every open set W containing y, there exists $K\in \mathcal{F}$ such that for every $\alpha \in K$, $\mathcal{P}\left(W\right)\cap \mathcal{P}\left(H_{\alpha }\left(x_0\right)\right)\ne \varnothing$, i.e., $W\cap H_{\alpha }\left(x_0\right)\ne \varnothing$, which proves that $F\left(x_0\right)\subset Li$$H_{\alpha }\left(x_0\right)$.

Now, conversely, assume that $F\left(x_0\right)\subset Li$$H_{\alpha }\left(x_0\right)$. Since $\langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle \left(x_0\right)$ is a closed subset in the space $(\mathcal{P}\left(Y\right),{\sigma }^u)$, it is enough to show that for every $W\in \sigma$, the property $\mathcal{P}\left(W\right)\cap \langle \mathcal{S}F\rangle \left(x_0\right)\ne \varnothing$ implies that $\mathcal{P}\left(W\right)\cap \langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle \left(x_0\right)\ne \varnothing$. So, let us take $W\in \sigma$ such that $\mathcal{P}\left(W\right)\cap \langle \mathcal{S}F\rangle \left(x_0\right)\ne \varnothing$, i.e., $W\cap F\left(x_0\right)\ne \varnothing$; then, $W\cap Li$$H_{\alpha }\left(x_0\right)\ne \varnothing$ and consequently, there exists $K\in \mathcal{F}$ such that for every $\alpha \in K$, $W\cap H_{\alpha }\left(x_0\right))\ne \varnothing$ or equivalently, $\mathcal{P}\left(W\right)\cap \mathcal{P}\left(H_{\alpha }\left(x_0\right)\right)\ne \varnothing$. Thus, using Remark 1, we get $\mathcal{P}\left(W\right)\cap {\bigcap }_{\alpha \in K}\overline{\mathcal{P}\left(H_{\alpha }\left(x_0\right)\right)}\ne \varnothing$ for some $K\in \mathcal{F}$ and, according to (1) we have $\mathcal{P}\left(W\right)\cap \langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle \left(x_0\right)\ne \varnothing$.

Proof of $\left(ii\right)$. It is clear that

$\langle u,\widehat{l},\widehat{u},l,\mathcal{S}\overline{H}\rangle \left(x\right)=$

$u\circ l\circ u\circ l\circ \mathcal{S}\overline{H}\circ {\mathcal{F}}^{(1,1)}\circ {\tau }^1\left(x\right)=$

$u\circ l\circ u\circ l\circ \left(\{\{\{\{\overline{\mathcal{P}\left(H_{\alpha }\left(x_1\right)\right)}:x_1\in U_1\}:\alpha \in K\}:K\in \mathcal{F}\}:U_1\in \tau \left(x\right)\}\right)=$

${\bigcap }_{U_1\in \tau \left(x\right)}\overline{{\bigcup }_{K\in \mathcal{F}}{\bigcap }_{\alpha \in K}\overline{{\bigcup }_{x_1\in U_1}\mathcal{P}\left(H_{\alpha }\left(x_1\right)\right)}}.$$\left(2\right)$

The assumption that $\langle \mathcal{S}F\rangle \left(x\right)\subset \langle u,\widehat{l},\widehat{u},l,\mathcal{S}\overline{H}\rangle \left(x\right)$ for all $x\in X$, $(a,b)\in Gr\left(F\right)$ and $(a,b)\in U\times W$ for some $U\in \tau$ and $W\in \sigma$, implies $W\cap F\left(a\right)\ne \varnothing$, i.e., $\mathcal{P}\left(W\right)\cap \mathcal{P}\left(F\right(a\left)\right)\ne \varnothing$ and consequently we obtain $\mathcal{P}\left(W\right)\cap \langle u,\widehat{l},\widehat{u},l,\mathcal{S}\overline{H}\rangle \left(a\right)\ne \varnothing$. According to $\left(2\right)$, we get

      $\mathcal{P}\left(W\right)\cap {\bigcup }_{K\in \mathcal{F}}{\bigcap }_{\alpha \in K}\overline{{\bigcup }_{x_1\in U}\mathcal{P}\left(H_{\alpha }\left(x_1\right)\right)}\ne \varnothing$ i.e.,

      there exists $K\in \mathcal{F}$ such that for every $\alpha \in K$

      we have $\mathcal{P}\left(W\right)\cap \mathcal{P}\left(H_{\alpha }\left(x_1\right)\right)\ne \varnothing$ for some $x_1\in U$. $\left(3\right)$

The condition $\mathcal{P}\left(W\right)\cap \mathcal{P}\left(H_{\alpha }\left(x_1\right)\right)\ne \varnothing$ is equivalent to $W\cap H_{\alpha }\left(x_1\right)\ne \varnothing$, i.e., $(x_1,y)\in Gr\left(H_{\alpha }\right)$ for some $y\in W$, so $(U\times W)\cap Gr\left(H_{\alpha }\right)\ne \varnothing$ and, according to $\left(3\right)$, this ends the proof that $(a,b)\in Li$$Gr\left(H_{\alpha }\right)$.

For the converse implication, suppose that $\mathcal{P}\left(W\right)\cap \langle \mathcal{S}F\rangle \left(x\right)\ne \varnothing$, i.e., $W\cap F\left(x\right)\ne \varnothing$, where $W\in \sigma$ and $x\in X$. Then, for every $U_1\in \tau \left(x\right)$ we have $(x,y)\in (U_1\times W)\cap Gr\left(F\right)$ for some $y\in W\cap F\left(x\right)$ and according to the assumption, $(x,y)\in (U_1\times W)\cap Li$$Gr\left(H_{\sigma }\right)$. So, there exists $K\in \mathcal{F}$ such that for every $\alpha \in K$ we have $(U_1\times W)\cap Gr\left(H_{\alpha }\right)\ne \varnothing$.

The condition $(U_1\times W)\cap Gr\left(H_{\alpha }\right)\ne \varnothing$ is equivalent to the existence of $(x_1,y_1)\in U_1\times W$ such that $y_1\in H_{\alpha }\left(x_1\right)$, so $W\cap H_{\alpha }\left(x_1\right)\ne \varnothing$ or equivalently, $\mathcal{P}\left(W\right)\cap \mathcal{P}\left(H_{\alpha }\left(x_1\right)\right)\ne \varnothing$ and consequently, $\mathcal{P}\left(W\right)\cap {\bigcup }_{x_1\in U_1}\mathcal{P}\left(H_{\alpha }\left(x_1\right)\right)\ne \varnothing$ for all $\alpha \in K$. Finally, in accordance with Remark 1, we obtain $\mathcal{P}\left(W\right)\cap {\bigcup }_{K\in \mathcal{F}}{\bigcap }_{\alpha \in K}\overline{{\bigcup }_{x_1\in U_1}\mathcal{P}\left(H_{\alpha }\left(x_1\right)\right)}\ne \varnothing$ for all $U_1\in \pi \left(x\right)$ and again Remark 1 yields $\mathcal{P}\left(W\right)\cap {\bigcap }_{U_1\in \tau \left(x\right)}\overline{{\bigcup }_{K\in \mathcal{F}}{\bigcap }_{\alpha \in K}\overline{{\bigcup }_{x_1\in U_1}\mathcal{P}\left(H_{\alpha }\left(x_1\right)\right)}}\ne \varnothing$ which means, according to (2), that $\mathcal{P}\left(W\right)\cap \langle u,\widehat{l},\widehat{u},l,\mathcal{S}\overline{H}\rangle \left(x\right)\ne \varnothing$ and finishes the proof.

Proof of $\left(iii\right)$: In an entirely analogous way to the above, we have

${\langle \widehat{l},\widehat{u},\mathcal{I}\overline{H}\rangle }^{-1}\left(x_0\right)=\langle \widehat{u},\widehat{l},\mathcal{S}\overline{H}\rangle \left(x_0\right)={\bigcap }_{K\in \mathcal{F}}\overline{{\bigcup }_{\alpha \in K}\mathcal{P}\left(H_{\alpha }\left(x_0\right)\right)}$. $\left(4\right)$

If $\langle \mathcal{S}F\rangle \left(x_0\right)\subset {\langle \widehat{l},\widehat{u},\mathcal{I}\overline{H}\rangle }^{-1}\left(x_0\right)$, $y\in F\left(x_0\right)$ and $y\in W$, where $W\in \sigma$, then $\mathcal{P}\left(W\right)\cap \langle \mathcal{S}F\rangle \left(x_0\right)\ne \varnothing$ and consequently, according to (4), for every $K\in \mathcal{F}$ there exists $\alpha \in K$ such that $\mathcal{P}\left(W\right)\cap \mathcal{P}\left(H_{\alpha }\left(x_0\right)\right)\ne \varnothing$, i.e., $W\cap H_{\alpha }\left(x_0\right)\ne \varnothing$. So, $y\in Ls$$H_{\alpha }\left(x_0\right)$.

Now, assume that $F\left(x_0\right)\subset Ls$$H_{\alpha }\left(x_0\right)$ and let $\mathcal{P}\left(W\right)\cap \langle \mathcal{S}F\rangle \left(x_0\right)\ne \varnothing$, where $W\in \sigma$. It is enough to show that $\mathcal{P}\left(W\right)\cap {\langle \widehat{l},\widehat{u},\mathcal{I}\overline{H}\rangle }^{-1}\left(x_0\right)\ne \varnothing$. It is clear that $W\cap F\left(x_0\right)\ne \varnothing$ and therefore by the assumption, for every $K\in \mathcal{F}$, there exists $\alpha \in K$ such that $W\cap H_{\alpha }\left(x_0\right)\ne \varnothing$, i.e., $\mathcal{P}\left(W\right)\cap \mathcal{P}\left(H_{\alpha }\left(x_0\right)\right)$. So, $\mathcal{P}\left(W\right)\cap {\bigcup }_{\alpha \in K}\mathcal{P}\left(H_{\alpha }\left(x_0\right)\right)\ne \varnothing$ for all $K\in \mathcal{F}$ and using Remark 1 we get $\mathcal{P}\left(W\right)\cap {\bigcap }_{K\in \mathcal{F}}\overline{{\bigcup }_{\alpha \in K}\mathcal{P}\left(H_{\alpha }\left(x_0\right)\right)}\ne \varnothing$ which, according to (4), finishes the proof.

Proof of $\left(iv\right)$. Similarly to the previous cases, we note that

${\langle l,\widehat{l},\widehat{u},u,\mathcal{I}\overline{H}\rangle }^{-1}\left(x\right)=$$\langle u,\widehat{u},\widehat{l},l,\mathcal{S}\overline{H}\rangle \left(x\right)=$

${\bigcap }_{U_1\in \tau \left(x\right)}{\bigcap }_{K\in \mathcal{F}}\overline{{\bigcup }_{\alpha \in K}{\bigcup }_{x_1\in U_1}\mathcal{P}\left(H_{\alpha }\left(x_1\right)\right)}.$$\left(5\right)$

If $\langle \mathcal{S}F\rangle \left(x\right)\subset {\langle l,\widehat{l},\widehat{u},u,\mathcal{I}\overline{H}\rangle }^{-1}\left(x\right)$ for all $x\in X$, and $(a,b)\in U\times W$ for some $U\in \tau$, $W\in \sigma$ and $(a,b)\in Gr\left(F\right)$, then $W\cap F\left(a\right)\ne \varnothing$, equivalently, $\mathcal{P}\left(W\right)\cap \langle \mathcal{S}F\rangle \left(a\right)\ne \varnothing$ and therefore, according to (5), we have $\mathcal{P}\left(W\right)\cap {\bigcap }_{U_1\in \tau \left(a\right)}{\bigcap }_{K\in \mathcal{F}}\overline{{\bigcup }_{\alpha \in K}{\bigcup }_{x_1\in U_1}\mathcal{P}\left(H_{\alpha }\left(x_1\right)\right)}\ne \varnothing .$ Consequently, $\mathcal{P}\left(W\right)\cap {\bigcap }_{K\in \mathcal{F}}\overline{{\bigcup }_{\alpha \in K}{\bigcup }_{x_1\in U}\mathcal{P}\left(H_{\alpha }\left(x_1\right)\right)}\ne \varnothing$ i.e., for every $K\in \mathcal{F}$ there exist $\alpha \in K$ and $x_1\in U$ such that $\mathcal{P}\left(W\right)\cap \mathcal{P}\left(H_{\alpha }\left(x_1\right)\right)\ne \varnothing$, i.e., $W\cap H_{\alpha }\left(x_1\right)\ne \varnothing$. Thus, for some $y\in W\cap H_{\alpha }\left(x_1\right)$ we have $(x_1,y)\in (U\times W)\cap Gr\left(H_{\alpha }\right)$ thus $(U\times W)\cap Gr\left(H_{\alpha }\right)\ne \varnothing$ and the proof that $(a,b)\in Ls$$Gr\left(H_{\sigma }\right)$ is finished.

Conversely, assume now that $Gr\left(F\right)\subset Ls$$Gr\left(H_{\sigma }\right)$, $x\in X$ and $\mathcal{P}\left(W\right)\cap \langle \mathcal{S}F\rangle \left(x\right)\ne \varnothing$. It is enough to prove that $\mathcal{P}\left(W\right)\cap {\langle l,\widehat{l},\widehat{u},u,\mathcal{I}\overline{H}\rangle }^{-1}\left(x\right)\ne \varnothing$, i.e., considering (V), that $\mathcal{P}\left(W\right)\cap {\bigcap }_{U_1\in \tau \left(x\right)}{\bigcap }_{K\in \mathcal{F}}\overline{{\bigcup }_{\alpha \in K}{\bigcup }_{x_1\in U_1}\mathcal{P}\left(H_{\alpha }\left(x_1\right)\right)}\ne \varnothing$. It is clear that $W\cap F\left(x\right)\ne \varnothing$, so $(x,y)\in Gr\left(F\right)$ for some $y\in W$ and therefore, according to that assumption, for every $U_1\in \tau \left(x\right)$, we have $(U\times W)\cap Ls$$Gr\left(H_{\sigma }\right)\ne \varnothing$. Hence, for every $K\in \mathcal{F}$ there exists $\alpha \in K$ such that $(U\times W)\cap Gr\left(H_{\sigma }\right)\ne \varnothing$, i.e, there exist $x_1\in U_1$ and $y_1\in W$ such that $y_1\in W\cap H_{\alpha }\left(x_1\right)$. So, $W\cap H_{\alpha }\left(x_1\right)\ne \varnothing$ or equivalently, $\mathcal{P}\left(W\right)\cap \mathcal{P}\left(H_{\alpha }\left(x_1\right)\right)\ne \varnothing$ and, we have shown that $\mathcal{P}\left(W\right)\cap {\bigcup }_{\alpha \in K}{\bigcup }_{x_1\in U_1}\mathcal{P}\left(H_{\alpha }\left(x_1\right)\right)\ne \varnothing$ for all $K\in \mathcal{F}$. Now, using Remark 1, we get $\mathcal{P}\left(W\right)\cap {\bigcap }_{K\in \mathcal{F}}\overline{{\bigcup }_{\alpha \in K}{\bigcup }_{x_1\in U_1}\mathcal{P}\left(H_{\alpha }\left(x_1\right)\right)}\ne \varnothing$ for all $U_1\in \tau \left(x\right)$, and reusing Remark 1 finished the proof.

Proof of $\left(a\right)$ of $\left(v\right)$. Suppose on the contrary that $F\left(x_0\right)\not\supset Li$$H_{\alpha }\left(x_0\right)$, i.e., $y_0\notin F\left(x_0\right)$ for some $y_0\in Li$$H_{\alpha }\left(x_0\right)$. Because of the $T_2$ property of $(Y,\tau )$ and $\alpha$−paracompactness of $F\left(x_0\right)$ there exist two disjoint open subsets W and V of Y such that $F\left(x_0\right)\subset W$ and $y_0\in V$. Consequently, since $\mathcal{P}\left(W\right)\cap \langle \mathcal{I}F\rangle \left(x_0\right)\ne \varnothing$, we have $\mathcal{P}\left(W\right)\cap {\langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle }^{-1}\left(x_0\right)\ne \varnothing$, and since $V\cap Li$$H_{\alpha }\left(x_0\right)\ne \varnothing$, there exists $K\in \mathcal{F}$ such that $V\cap H_{\alpha }\left(x_0\right)\ne \varnothing$, i.e., $\mathcal{P}\left(V\right)\cap \mathcal{P}\left(H_{\alpha }\left(x_0\right)\right)\ne \varnothing$ holds for every $\alpha \in K$. This, according to Remark 1, means that $\mathcal{P}\left(V\right)\cap \overline{{\bigcup }_{K\in \mathcal{F}}{\bigcap }_{\alpha \in K}\overline{\mathcal{P}\left(H_{\alpha }\left(x_0\right)\right)}}\ne \varnothing$, i.e., by (I), $\mathcal{P}\left(V\right)\cap \langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle \left(x_0\right)\ne \varnothing$. Since, according to Lemma 1, $\langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle \left(x_0\right)\cong {\langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle }^{-1}\left(x_0\right)$, we obtain $W\cap V\ne \varnothing$ which gives a contradiction.

Proof of $\left(b\right)$. Let us assume on the contrary that $Gr\left(F\right)\not\supset Li$$Gr\left(H_{\alpha }\right)$, i.e., that there exists $(x_0,y_0)\in Li$$Gr\left(H_{\alpha }\right)$ such that $y_0\notin F\left(x_0\right)$. Then, the $T_2$ property of the space $(Y,\tau )$ and the $\alpha -$ paracompactness of $F\left(x_0\right)$ imply the existence of two disjoint open subsets W and V of Y such that $F\left(x_0\right)\subset W$ and $y_0\in V$. Therefore, since $\mathcal{P}\left(W\right)\cap \langle \mathcal{I}F\rangle \ne \varnothing$, we have $\mathcal{P}\left(W\right)\cap {\langle u,\widehat{l},\widehat{u},l,\mathcal{S}\mathcal{H}\rangle }^{-1}\left(x_0\right)\ne \varnothing$. But, analogously to (2), ${\langle u,\widehat{l},\widehat{u},l,\mathcal{S}\mathcal{H}\rangle }^{-1}\left(x_0\right)=\langle l,\widehat{u},\widehat{l},u,\mathcal{I}\mathcal{H}\rangle \left(x_0\right)=\overline{{\bigcup }_{U_1\in \tau \left(x_0\right)}{\bigcap }_{K\in \mathcal{F}}\overline{{\bigcup }_{\alpha \in K}{\bigcap }_{x_1\in U_1}\overline{\left\{H_{\alpha }\left(x_1\right)\right\}}}}$. So, the following holds for some $U_1\in \tau \left(x_0\right)$:

      for every $K\in \mathcal{F}$ there exists $\alpha \in K$ such that

      $H_{\alpha }\left(x_1\right)\subset W$ for all $x_1\in U_1$. $\left(6\right)$

Of course, $(x_0,y_0)\in (U_1\times V)\cap Li$$Gr\left(H_{\alpha }\right)\ne \varnothing$, hence there exists $K\in \mathcal{F}$ such that for all $\alpha \in K$ we have $(U_1\times V)\cap Gr\left(H_{\alpha }\right)\ne \varnothing$, i.e., $V\cap H_{\alpha }\left(x_1\right)\ne \varnothing$ for some $x_1\in U_1$, which contradicts $\left(6\right)$ because $V\cap W=\varnothing$.

The proof of $\left(c\right)$ goes analogously to (a). The assumption that $F\left(x_0\right)\not\supset Ls$$H_{\alpha }\left(x_0\right)$ implies the existence of two disjoint open subsets W and V of Y that satisfy the following conditions: $\mathcal{P}\left(W\right)\cap \langle \widehat{l},\widehat{u},\mathcal{I}\overline{H}\rangle \left(x_0\right)\ne \varnothing$ and $\mathcal{P}\left(V\right)\cap {\bigcap }_{K\in \mathcal{F}}\overline{{\bigcup }_{\alpha \in K}\mathcal{P}\left(H_{\alpha }\left(x_0\right)\right)}\ne \varnothing$. So, $\mathcal{P}\left(V\right)\cap \langle \widehat{u},\widehat{l},\mathcal{S}\overline{H}\rangle \left(x_0\right)\ne \varnothing$ or equivalently, $\mathcal{P}\left(V\right)\cap {\langle \widehat{l},\widehat{u},\mathcal{I}\overline{H}\rangle }^{-1}\left(x_0\right)\ne \varnothing$ which implies $W\cap V\ne \varnothing$ and gives a contradiction.

The proof of $\left(d\right)$. Analogously to the proof of $\left(b\right)$, let us assume that there exist $(x_0,y_0)\in Ls$$Gr\left(H_{\alpha }\right)$ such that $y_0\notin F\left(x_0\right)$, and disjoint open subsets W and V of Y such that $F\left(x_0\right)\subset W$ and $y_0\in V$. Consequently, we have $\mathcal{P}\left(W\right)\cap \langle l,\widehat{l},\widehat{u},u,\mathcal{I}\mathcal{H}\rangle \left(x_0\right)\ne \varnothing$ or equivalently, $\mathcal{P}\left(W\right)\cap \overline{{\bigcup }_{U_1\in \tau \left(x_0\right)}{\bigcup }_{K\in \mathcal{F}}{\bigcap }_{\alpha \in K}{\bigcap }_{x_1\in U_1}\overline{\left\{H_{\alpha }\left(x_1\right)\right\}}}\ne \varnothing$ which means that, for some $U_1\in \tau \left(x_0\right)$, the following holds:

      there exists $K\in \mathcal{F}$ such that for every $\alpha \in K$ we have

      $H_{\alpha }\left(x_1\right)\subset W$ for all $x_1\in U_1$.$\left(7\right)$

Since $(x_0,y_0)\in (U_1\times V)\cap Ls$$Gr\left(H_{\alpha }\right)\ne \varnothing$, for every $K\in \mathcal{F}$ there exists $\alpha \in K$ such that $(U_1\times V)\cap Gr\left(H_{\alpha }\right)\ne \varnothing$, i.e., $V\cap H_{\alpha }\left(x_1\right)\ne \varnothing$ for some $x_1\in U_1$. This gives, in accordance with $\left(VII\right)$, $V\cap W\ne \varnothing$, i.e., we have a contradiction. □

Let us quote some direct conclusions of the above theorem.

Corollary 1.

Let ${\left(H_{\alpha }\right)}_{\alpha \in \Sigma }$ be a net of multifunctions from a topological space $(X,\tau )$ to a $T_2$ topological space $(Y,\sigma )$, $F:(X,\tau )\to (Y,\sigma )$ a multifunction whose values are α-paracompact and let $x_0\in X$. Then, the following statements hold:

(i)

If $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle \left(x_0\right)$ and ${\langle \mathcal{S}F\rangle }^{-1}\left(x_0\right)\subset {\langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle }^{-1}\left(x_0\right)$,

then $F\left(x_0\right)=Li$$H_{\alpha }\left(x_0\right)$;

(ii)

If $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle \widehat{l},\widehat{u},\mathcal{I}\overline{H}\rangle \left(x_0\right)$ and ${\langle \mathcal{I}F\rangle }^{-1}\left(x_0\right)\subset {\langle \widehat{l},\widehat{u},\mathcal{I}\overline{H}\rangle }^{-1}\left(x_0\right)$,

then $F\left(x_0\right)=Ls$$H_{\alpha }\left(x_0\right)$;

(iii)

If $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle \left(x_0\right)$ and $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle \widehat{l},\widehat{u},\mathcal{I}\overline{H}\rangle \left(x_0\right)$,

then $F\left(x_0\right)=Lt$$H_{\alpha }\left(x_0\right)$;

(iv)

If $\langle \mathcal{S}F\rangle ⪯\langle u,\widehat{l},\widehat{u},l,\mathcal{S}\overline{H}\rangle$ and ${\langle \mathcal{S}F\rangle }^{-1}⪯{\langle u,\widehat{l},\widehat{u},l,\mathcal{S}\overline{H}\rangle }^{-1}$,

then $Gr\left(F\right)=Li$$Gr\left(H_{\alpha }\right)$;

(v)

If $\langle \mathcal{I}F\rangle ⪯\langle l,\widehat{l},\widehat{u},u,\mathcal{I}\overline{H}\rangle$ and ${\langle \mathcal{I}F\rangle }^{-1}⪯{\langle l,\widehat{l},\widehat{u},u,\mathcal{I}\overline{H}\rangle }^{-1}$,

then $Gr\left(F\right)=Ls$$Gr\left(H_{\alpha }\right)$;

(vi)

If $\langle \mathcal{S}F\rangle ⪯\langle u,\widehat{l},\widehat{u},l,\mathcal{S}\overline{H}\rangle$ and $\langle \mathcal{I}F\rangle ⪯\langle l,\widehat{l},\widehat{u},u,\mathcal{I}\overline{H}\rangle$,

then $Gr\left(F\right)=Lt$$Gr\left(H_{\alpha }\right)$.

The property $F\left(x_0\right)=Lt$$H_{\alpha }\left(x_0\right)$ is called topologically convergence in point [57], topologically convergence [58], or pointwise topologically convergence [59].

The property $Gr\left(F\right)=Lt$$Gr\left(H_{\alpha }\right)$ is called topological convergence in graphs [57], graph convergence [58], topological convergence [60,61], Hausdorff topological convergence of graphs [62], or topologically graph convergence [59].

The set $Ls$$Gr\left(H_{\alpha }\right)$ (resp. $Ls$$H_{\alpha }\left(x\right)$) is called the topological upper Kuratowski limit of $\left(H_{\alpha }\right)$ (resp. the pointwise upper Kuratowski limit of $\left(H_{\alpha }\right)$ at x) in [23,24,63].

It is easy to check [64], (Lemmas 1.4 and 1.5), that the property $F\left(x\right)\subset Li$$H_{\alpha }\left(x\right)$ is equivalent to the lower pointwise convergence defined in [65] as follows:

Definition 9.

A net ${\left(H_{\alpha }\right)}_{\alpha \in \Sigma }$ of multifunctions $H_{\alpha }:(X,\tau )\to (Y,\sigma )$ is said to be lower (resp. upper) pointwise convergent to $F:(X,\tau )\to (Y,\sigma )$ at $x\in X$ if for each open subset $W\subset Y$ such that $F\left(x\right)\cap W\ne \varnothing$) (resp. $F\left(x\right)\subset W$), there exists $\gamma \in \Sigma$ such that $H_{\alpha }\left(x\right)\cap W\ne \varnothing$ (resp. $H_{\alpha }\left(x\right)\subset W$) for all $\alpha \ge \gamma$. Equivalently,

$x\in$ lim inf $H_{\alpha }^{-}\left(W\right)$ (resp. $x\in$ lim inf $H_{\alpha }^{+}\left(W\right)$) for every open subset $W\subset Y$ such that $x\in F^{-}\left(W\right)$ (resp. $x\in F^{+}\left(W\right))$.

Remark 12.

As we can see (Theorem 3 (i)), the lower pointwise convergence can be characterized by the following three equivalent sentences:

(i)

$x_0\in F^{-}\left(W\right)$ implies $x_0\in$ lim inf $H_{\alpha }^{-}\left(W\right)$ for every open $W\subset Y$;

(ii)

$F\left(x_0\right)\subset Li$$H_{\alpha }\left(x_0\right)$;

(iii)

$\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle \left(x_0\right)$.

In the case of the upper pointwise convergence, analogously as in the proof of Theorem 3 (i), one can prove that this property is characterized by the following two equivalent sentences:

(iv)

$x_0\in F^{+}\left(W\right)$ implies $x_0\in$ lim inf $H_{\alpha }^{+}\left(W\right)$ for every open $W\subset Y$;

(v)

$\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle \widehat{l},\widehat{u},\mathcal{I}\overline{H}\rangle \left(x_0\right)$.

Remark 13.

The reasoning analogous to the above remark leads to the following two types of equivalent sentences:

Type lower:

(i)

$x_0\in F^{-}\left(W\right)$ implies $x_0\in$ lim sup $H_{\alpha }^{-}\left(W\right)$ for every open $W\subset Y$;

(ii)

$F\left(x_0\right)\subset Ls$$H_{\alpha }\left(x_0\right)$;

(iii)

$\langle \mathcal{S}F\rangle \left(x_0\right)\subset {\langle \widehat{l},\widehat{u},\mathcal{I}\overline{H}\rangle }^{-1}\left(x_0\right)$.

Type upper:

(iv)

$x_0\in F^{+}\left(W\right)$ implies $x_0\in$ lim sup $H_{\alpha }^{+}\left(W\right)$ for every open $W\subset Y$;

(v)

$\langle \mathcal{I}F\rangle \left(x_0\right)\subset {\langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle }^{-1}\left(x_0\right)$.

Those types of convergence are called the lower pointwise sub convergence and upper pointwise sub convergence [66], respectively.

Analogously to Remark 12, below we present the characterizations of the global version of the point types of graph convergences defined as follows:

Definition 10.

A net ${\left(H_{\alpha }\right)}_{\alpha \in \Sigma }$ of multifunctions $H_{\alpha }:(X,\tau )\to (Y,\sigma )$ is said to be lower (resp. upper) graph-convergent to $F:(X,\tau )\to (Y,\sigma )$ at $x\in X$ [65], if $x\in$$Li$$H_{\alpha }^{-}\left(W\right)$ (resp. $x\in Li$$H_{\alpha }^{+}\left(W\right)$) for every open subset $W\subset Y$ such that $x\in F^{-}\left(W\right)$ (resp. $x\in F^{+}\left(W\right))$.

Remark 14.

The following two lists of sentences present equivalent characterizations, respectively, for the lower and upper graph-convergence at all points $x\in X:$

Type lower:

(i)

$x\in F^{-}\left(W\right)$ implies $x\in Li$$H_{\alpha }^{-}\left(W\right)$ for every open subset $W\subset Y$

and all $x\in X$;

(ii)

$Gr\left(F\right)\subset Li$$Gr\left(H_{\alpha }\right)$;

(iii)

$\langle \mathcal{S}F\rangle ⪯\langle u,\widehat{l},\widehat{u},l,\mathcal{S}\overline{H}\rangle$.

Type upper:

(iv)

$x\in F^{+}\left(W\right)$ implies $x\in$ Li $H_{\alpha }^{+}\left(W\right)$ for every open subset $W\subset Y$

and all $x\in X$;

(v)

$\langle \mathcal{I}F\rangle ⪯\langle u,\widehat{l},\widehat{u},l,\mathcal{I}\overline{H}\rangle$.

The equivalence of (ii) and (iii) is proved in Theorem 3 (ii). We will show that (i) and (ii) are equivalent, as well as the sentences (iv) and (v).

Proof. 

If $Gr\left(F\right)\subset Li$$Gr{H}_{\alpha }$, $x\in X$ and W is an open subset of Y such that $x\in F^{-}\left(W\right)$, i.e., $F\left(x\right)\cap W\ne \varnothing$, then there exists $y\in F\left(x\right)\cap W$ such that for every open subset U of X containing x we have $(x,y)\in (U\times W)\cap Gr\left(F\right)\subset (U\times W)\cap Li$$Gr{H}_{\alpha }$. Consequently, there exists $\gamma \in \Sigma$ such that $(U\times W)\cap Gr\left(H_{\alpha }\right)\ne \varnothing$ for all $\alpha \ge \gamma$. The property $(U\times W)\cap Gr\left(H_{\alpha }\right)\ne \varnothing$ means that, for some $(a,b)\in U\times W$ we have $b\in H_{\alpha }\left(a\right)$ and hence $U\cap H_{\alpha }^{-}\left(W\right)\ne \varnothing$ which ends the proof that $x\in Li$$H_{\alpha }^{-}\left(W\right)$.

Conversely, if $(x,y)\in Gr\left(F\right)$ and $(x,y)\in U\times W$ for some open subsets $U\subset X$ and $W\subset Y$, then $y\in W\cap F\left(x\right)$ and therefore, $x\in U\cap F^{-}\left(W\right)$. According to (i), we have $x\in U\cap Li$$H_{\alpha }^{-}\left(W\right)$ and consequently, there exists $\gamma \in \Sigma$ such that $U\cap H_{\alpha }^{-}\left(W\right)\ne \varnothing$ for all $\alpha \ge \gamma$. The property $U\cap H_{\alpha }^{-}\left(W\right)\ne \varnothing$ means that $H_{\alpha }\left(p\right)\cap W\ne \varnothing$ for some $p\in U$ which implies the existence of $z\in H_{\alpha }\left(p\right)\cap W$ such that $(p,z)\in (U\times W)\cap Gr\left(H_{\alpha }\right)\ne \varnothing$. This proves that $(x,y)\in Li$$Gr{H}_{\alpha }$.

To prove the equivalence of (iv) and (v) let us assume that $\langle \mathcal{I}F\rangle ⪯\langle u,\widehat{l},\widehat{u},l,\mathcal{I}\overline{H}\rangle$ and let $x\in F^{+}\left(W\right)$, i.e., $F\left(x\right)\subset W$, for some open subset $W\subset Y$, which means that $\mathcal{P}\left(W\right)\cap \langle \mathcal{I}F\rangle \left(x\right)\ne \varnothing$. Therefore, $\mathcal{P}\left(W\right)\cap \langle u,\widehat{l},\widehat{u},l,\mathcal{I}\overline{H}\rangle \left(x\right)\ne \varnothing$, i.e., $\mathcal{P}\left(W\right)\cap {\bigcap }_{U\in \tau \left(x\right)}\overline{{\bigcup }_{K\in \mathcal{F}}{\bigcap }_{\alpha \in K}\overline{{\bigcup }_{x_1\in U}\left\{H_{\alpha }\left(x_1\right)\right\}}}\ne \varnothing$. Consequently, for every open set U containing x there exists $K\in \mathcal{F}$ such that, for all $\alpha \in K$, $\mathcal{P}\left(W\right)\cap {\bigcup }_{x_1\in U}\left\{H_{\alpha }\left(x_1\right)\right\}\ne \varnothing$, i.e., $H_{\alpha }\left(x_1\right)\subset W$ for some $x_1\in U$ or equivalently, $U\cap H_{\alpha }^{+}\left(W\right)\ne \varnothing$. So, $x\in Li$$H_{\alpha }^{+}\left(W\right)$.

Conversely, assume that (iv) holds and let $\mathcal{P}\left(W\right)\cap \langle \mathcal{I}F\rangle \left(x\right)\ne \varnothing$, where $x\in X$. Then, $F\left(x\right)\subset W$, i.e., $x\in F^{+}\left(W\right)$ and, according to the assumption, $x\in$ Li $H_{\alpha }^{+}\left(W\right)$. So, for every open set U containing x there exists $K\in \mathcal{F}$ such that for all $\alpha \in K$, $U\cap H_{\alpha }^{+}\left(W\right)\ne \varnothing$, i.e., $\mathcal{P}\left(W\right)\cap \left\{H_{\alpha }\left(x_1\right)\right\}\ne \varnothing$ for some $x_1\in U$. It means that $\mathcal{P}\left(W\right)\cap {\bigcup }_{x_1\in U}\left\{H_{\alpha }\left(x_1\right)\right\}\ne \varnothing$ for all $\alpha \in K$ which, according to Remark 1, gives $\mathcal{P}\left(W\right)\cap {\bigcap }_{\alpha \in K}\overline{{\bigcup }_{x_1\in U}\left\{H_{\alpha }\left(x_1\right)\right\}}\ne \varnothing$. In the same way, one can show that $\mathcal{P}\left(W\right)\cap {\bigcap }_{U\in \tau \left(x\right)}\overline{{\bigcup }_{K\in \mathcal{F}}{\bigcap }_{\alpha \in K}\overline{{\bigcup }_{x_1\in U}\left\{H_{\alpha }\left(x_1\right)\right\}}}\ne \varnothing$ which is equivalent to $\mathcal{P}\left(W\right)\cap \langle u,\widehat{l},\widehat{u},l,\mathcal{I}\overline{H}\rangle \left(x\right)\ne \varnothing$ and finishes the proof. □

The replacement of the $Li$ operation by the $Ls$ in Definition 10 gives the type of convergence called the lower (resp. upper) graph-subconvergence at the points [66]. Analogously to the remark above, we obtain the following characterizations.

Remark 15.

The following two lists of sentences give equivalent characterizations, respectively, for the lower and upper graph-subconvergence at all points $x\in X:$

Type lower:

(i)

$x\in F^{-}\left(W\right)$ implies $x\in Ls$$H_{\alpha }^{-}\left(W\right)$ for every open subset $W\subset Y$

and all $x\in X$;

(ii)

$Gr\left(F\right)\subset Ls$$Gr\left(H_{\alpha }\right)$;

(iii)

$\langle \mathcal{S}F\rangle ⪯{\langle l,\widehat{l},\widehat{u},u,\mathcal{I}\overline{H}\rangle }^{-1}$.

Type upper:

(iv)

$x\in F^{+}\left(W\right)$ implies $x\in$ Ls $H_{\alpha }^{+}\left(W\right)$ for every open subset $W\subset Y$

and all $x\in X$;

(v)

$\langle \mathcal{I}F\rangle ⪯{\langle l,\widehat{l},\widehat{u},u,\mathcal{S}\overline{H}\rangle }^{-1}$.

The equivalence of (ii) and (iii) is proved in Theorem 3 (iv). The proof that (i) and (ii) are equivalent is quite analogous to that in Remark 14. We will show the equivalence of (iv) and (v).

Proof. 

If $\langle \mathcal{I}F\rangle ⪯{\langle l,\widehat{l},\widehat{u},u,\mathcal{S}\overline{H}\rangle }^{-1}$ i.e., $\langle \mathcal{I}F\rangle ⪯\langle u,\widehat{u},\widehat{l},l,\mathcal{I}\overline{H}\rangle$ and $x\in F^{+}\left(W\right)$, then $\mathcal{P}\left(W\right)\cap \langle u,\widehat{u},\widehat{l},l,\mathcal{I}\overline{H}\rangle \ne \varnothing$, i.e., $\mathcal{P}\left(W\right)\cap {\bigcap }_{U\in \tau \left(x\right)}{\bigcap }_{K\in \mathcal{F}}\overline{{\bigcup }_{\alpha \in K}{\bigcup }_{x_1\in U}\left\{H_{\alpha }\left(x_1\right)\right\}}\ne \varnothing$. So, for every open set U containing x and $K\in \mathcal{F}$ there exist $\alpha \in K$ and $x_1\in U$ such that $H_{\alpha }\left(x_1\right)\subset W$, i.e., $U\cap H_{\alpha }^{+}\left(W\right)\ne \varnothing$ which proves that $x\in$ Ls $H_{\alpha }^{+}\left(W\right)$.

Conversely, assume that (iv) holds and let $\mathcal{P}\left(W\right)\cap \langle \mathcal{I}F\rangle \left(x\right)\ne \varnothing$, where $x\in X$. Then, $x\in F^{+}\left(W\right)$ and, according to the assumption, $x\in$ Ls $H_{\alpha }^{+}\left(W\right)$. So, for every open set U containing x and $K\in \mathcal{F}$ there exists $\alpha \in K$ such that $U\cap H_{\alpha }^{+}\left(W\right)\ne \varnothing$, i.e., $H_{\alpha }\left(x_1\right)\subset W$ for some $x_1\in U$, or equivalently, $\mathcal{P}\left(W\right)\cap {\bigcup }_{\alpha \in K}{\bigcup }_{x_1\in U}\left\{H_{\alpha }\left(x_1\right)\right\}\ne \varnothing$ for every $U\in \tau \left(x\right)$ and $K\in \mathcal{F}$. Hence, in accordance with Remark 1.1 we get $\mathcal{P}\left(W\right)\cap {\bigcap }_{U\in \tau \left(x\right)}{\bigcap }_{K\in \mathcal{F}}\overline{{\bigcup }_{\alpha \in K}{\bigcup }_{x_1\in U}\left\{H_{\alpha }\left(x_1\right)\right\}}\ne \varnothing$, i.e., $\mathcal{P}\left(W\right)\cap \langle u,\widehat{u},\widehat{l},l,\mathcal{I}\overline{H}\rangle \ne \varnothing$ or equivalently, $\mathcal{P}\left(W\right)\cap {\langle l,\widehat{l},\widehat{u},u,\mathcal{S}\overline{H}\rangle }^{-1}\ne \varnothing$, which finishes the proof. □

In the present work, we are particularly interested in the concept of convergence defined by O. Frink in [67]:

Definition 11.

A net ${\left(h_{\alpha }\right)}_{\alpha \in \Sigma }$ of functions $h_{\alpha }:(X,\tau )\to (Y,\sigma$) is said to be:

(i)

Continuously convergent to $f:(X,\tau )\to (Y,\sigma$) at $x\in X$ if, for each open subset $W\subset Y$ such that $f\left(x\right)\in W$ there exists an open subset U containing x and $\gamma \in \Sigma$ such that $h_{\alpha }\left(u\right)\in W$ for all $\alpha \ge \gamma$ and $u\in U$;

(ii)

Quasi-continuously convergent to $f:(X,\tau )\to (Y,\sigma$) at $x\in X$ if, for each open subset $W\subset Y$ such that $f\left(x\right)\in W$ there exists an open subset U containing x such that for every $u\in U$ there exists $\gamma \in \Sigma$ such that $h_{\alpha }\left(u\right)\in W$ for all $\alpha \ge \gamma$.

The basic result concerning those types of convergence is the following:

Theorem 4

([67]). Let ${\left(h_{\alpha }\right)}_{\alpha \in \Sigma }$ be a net of functions from a $T_1$ topological space X to a $T_1$ regular topological space Y convergent pointwise to a function $f:X\to Y$. Then, f is continuous if and only if the convergence is quasi-continuous.

This leads to the following conclusion:

Corollary 2

([67]). The limit f of a continuously convergent net ${\left(h_{\alpha }\right)}_{\alpha \in \Sigma }$ of functions from a $T_1$ topological space X to a $T_1$ regular topological space Y is continuous.

The continuous convergence was extended to the case of multifunctions in [57] as follows.

Definition 12.

A net ${\left(H_{\alpha }\right)}_{\alpha \in \Sigma }$ of multifunctions $H_{\sigma }:(X,\tau )\to (Y,\sigma$) is said to be lower (resp. upper) continuously convergent to F at x, if for each open subset $W\subset Y$ such that $F\left(x\right)\cap W\ne \varnothing$ (resp. $F\left(x\right)\subset W$), there exists an open subset U containing x and $\gamma \in \Sigma$ such that $H_{\alpha }\left(u\right)\cap W\ne \varnothing$ (resp. $H_{\alpha }\left(u\right)\subset W$) for all $\alpha \ge \gamma$ and $u\in U$.

Remark 16.

It follows directly from the definition that a net ${\left(H_{\alpha }\right)}_{\alpha \in \Sigma }$ of multifunctions $H_{\sigma }:(X,\tau )\to (Y,\sigma$) is lower (resp. upper) continuously convergent to F at x if and only if for every open subset $W\subset Y$,

• $x\in F^{-}\left(W\right)$ implies $x\in {\bigcup }_{\gamma \in \Sigma }Int{\bigcap }_{\alpha \ge \gamma }{H}_{\alpha }^{-}\left(W\right)$
  (resp. $x\in F^{+}\left(W\right)$ implies $x\in {\bigcup }_{\gamma \in \Sigma }Int{\bigcap }_{\alpha \ge \gamma }{H}_{\alpha }^{+}\left(W\right))$.

These types of convergence have the following characterization in terms of convergence operators.

Lemma 14.

A net ${\left(H_{\alpha }\right)}_{\alpha \in \Sigma }$ of multifunctions $H_{\alpha }:(X,\tau )\to (Y,\sigma )$ is lower (resp. upper) continuously convergent to $F:(X,\tau )\to (Y,\sigma )$ at a point $x_0\in X$ if and only if $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle l,\widehat{l},\widehat{u},u,\mathcal{S}\overline{H}\rangle \left(x_0\right)$ (resp. $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle l,\widehat{l},\widehat{u},u,\mathcal{I}\overline{H}\rangle \left(x_0\right)$).

Proof. 

According to the definition,

• $\langle l,\widehat{l},\widehat{u},u,\mathcal{S}\overline{H}\rangle \left(x_0\right)=$
• $l\circ l\circ u\circ u\circ \mathcal{S}\overline{H}\circ {\mathcal{F}}^{(1,1)}\circ {\tau }^1\left(x_0\right)=$
• $l\circ l\circ u\circ u\circ \left(\{\{\{\{\overline{\mathcal{P}\left(H_{\alpha }\left(x_1\right)\right)}:x_1\in U_1\}:\alpha \in K\}:K\in \mathcal{F}\}:U_1\in \tau \left(x_0\right)\}\right)=$
• $\overline{{\bigcup }_{U_1\in \tau \left(x_0\right)}{\bigcup }_{K\in \mathcal{F}}{\bigcap }_{\alpha \in K}{\bigcap }_{x_1\in U_1}\overline{\mathcal{P}\left(H_{\alpha }\left(x_1\right)\right)}}.$ Analogously,

$\langle l,\widehat{l},\widehat{u},u,\mathcal{I}\mathcal{H}\rangle \left(x_0\right)=\overline{{\bigcup }_{U_1\in \tau \left(x_0\right)}{\bigcup }_{K\in \mathcal{F}}{\bigcap }_{\alpha \in K}{\bigcap }_{x_1\in U_1}\overline{\left\{H_{\alpha }\left(x_1\right)\right\}}}.$

So, $\mathcal{P}\left(W\right)\cap \langle l,\widehat{l},\widehat{u},u,\mathcal{S}\mathcal{H}\rangle \left(x_0\right)\ne \varnothing$ (resp. $\mathcal{P}\left(W\right)\cap \langle l,\widehat{l},\widehat{u},u,\mathcal{I}\mathcal{H}\rangle \left(x_0\right)\ne \varnothing$) is equivalent to the existence of an open subset $U\subset X$ containing $x_0$ and $\gamma \in \Sigma$ such that for all $\alpha \ge \gamma$ and $u\in U$, $H_{\alpha }\left(u\right)\cap W\ne \varnothing$ (resp. $H_{\alpha }\left(u\right)\subset W$). Moreover, of course, the condition $\mathcal{P}\left(W\right)\cap \langle \mathcal{S}F\rangle \left(x_0\right)$ (resp. $\mathcal{P}\left(W\right)\cap \langle \mathcal{I}F\rangle \left(x_0\right)$) means that $F\left(x_0\right)\cap W\ne \varnothing$ (resp. $F\left(x_0\right)\subset W$) and the proof is finished. □

Remark 17.

A simple analysis of the above proof shows that

$\langle l,\widehat{l},\widehat{u},u\rangle =\langle \widehat{l},l,u,\widehat{u}\rangle$.

Using Theorem 3 (v), (d), we immediately get the following fact:

Corollary 3

([56], Theorem 3.2 (2)). If $(Y,\sigma )$ is a $T_2$ topological space and the values of $F:(X,\tau )\to (Y,\sigma )$ are α-paracompact, then the upper continuous convergence of ${\left(H_{\sigma }\right)}_{\alpha \in \Sigma }$ to F at any point $x\in X$ implies that $Gr\left(F\right)\supset LsGr\left(H_{\sigma }\right)$.

Proceeding analogously as in the case of continuous convergence, one can define quasi-continuous convergence for multifunctions as a generalization of Frink’s notion of quasi-continuous convergence for single-valued functions as follows.

Definition 13.

A net ${\left(H_{\alpha }\right)}_{\alpha \in \Sigma }$ of multifunctions $H_{\alpha }:(X,\tau )\to (Y,\sigma$) is said to be lower (resp. upper) quasi-continuously convergent to $F:(X,\tau )\to (Y,\sigma$) at $x_0\in X$ if, for each open subset $W\subset Y$ such that $F\left(x_0\right)\cap W\ne \varnothing$ (resp. $F\left(x_0\right)\subset W$), there exists an open subset U containing $x_0$ such that for every $u\in U$ there exists $\gamma \in \Sigma$ such that $H_{\alpha }\left(u\right)\cap W\ne \varnothing$ (resp. $H_{\alpha }\left(u\right)\subset W$) for all $\alpha \ge \gamma$.

Remark 18.

Analogously to Remark 16, we can say that a net ${\left(H_{\alpha }\right)}_{\alpha \in \Sigma }$ of multifunctions $H_{\sigma }:(X,\tau )\to (Y,\sigma$) is lower (resp. upper) quasi-continuously convergent to F at x if and only if for every open subset $W\subset Y$,

• $x\in F^{-}\left(W\right)$ implies $x\in Int{\bigcup }_{\gamma \in \Sigma }{\bigcap }_{\alpha \ge \gamma }{H}_{\alpha }^{-}\left(W\right)$
  (resp. $x\in F^{+}\left(W\right)$ implies $x\in Int{\bigcup }_{\gamma \in \Sigma }{\bigcap }_{\alpha \ge \gamma }{H}_{\alpha }^{+}\left(W\right))$.

The characterization of these types of convergence in terms of the convergence operators may be proven in an entirely analogous manner to such characterization for the continuous convergence given in the previous lemma.

Lemma 15.

A net ${\left(H_{\alpha }\right)}_{\alpha \in \Sigma }$ of multifunctions $H_{\alpha }:(X,\tau )\to (Y,\sigma )$ is lower (resp. upper) quasi-continuously convergent to $F:(X,\tau )\to (Y,\sigma )$ at a point $x_0\in X$ if and only if $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle l,u,\widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle \left(x_0\right)$(resp. $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle l,u,\widehat{l},\widehat{u},\mathcal{I}\overline{H}\rangle \left(x_0\right)$).

Proof. 

It is enough to observe that, by definition, for any point $x_0\in X$, we have

• $\langle l,u,\widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle \left(x_0\right)=$
• $l\circ u\circ l\circ u\circ \mathcal{S}\overline{H}\circ {\mathcal{F}}^{(0,0)}\circ {\tau }^1\left(x\right)=$
• $l\circ u\circ l\circ u\circ \left(\{\{\{\{\overline{\mathcal{P}\left(H_{\alpha }\left(x_1\right)\right)}:\alpha \in K\}:K\in \mathcal{F}\}:x_1\in U_1\}:U_1\in \tau \left(x_0\right)\}\right)=$
• $\overline{{\bigcup }_{U_1\in \tau \left(x_0\right)}{\bigcap }_{x_1\in U_1}\overline{{\bigcup }_{K\in \mathcal{F}}{\bigcap }_{\alpha \in K}\overline{\mathcal{P}\left(H_{\alpha }\left(x_1\right)\right)}}}$ and analogously,

$\langle l,u,\widehat{l},\widehat{u},\mathcal{I}\overline{H}\rangle \left(x_0\right)=\overline{{\bigcup }_{U_1\in \tau \left(x_0\right)}{\bigcap }_{x_1\in U_1}\overline{{\bigcup }_{K\in \mathcal{F}}{\bigcap }_{\alpha \in K}\overline{\{H_{\alpha }\left(x_1\right)\}}}}$. □

A direct generalization and extension of Frink’s result take the form of the following pair of theorems. We omit the proof because those theorems immediately follow from a general theorem about the continuity of the limit multifunctions, which we will state in the next chapter.

Theorem 5.

If ${\left(H_{\sigma }\right)}_{\sigma \in \Sigma }$ is a net of multifunctions from $(X,\tau )$ to a regular topological space $(Y,\sigma )$, then for every multifunction $F:(X,\tau )\to (Y,\sigma )$ the following hold:

(i)

Under the assumption that ${\langle \mathcal{S}F\rangle }^{-1}⪯{\langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle }^{-1}$,

the lower quasi-continuous convergence at $x_0$ implies that $x_0\in C_l\left(F\right)$.

(ii)

If $F\left(x_0\right)$ is α-paracompact, then under the assumption that

${\langle \mathcal{I}F\rangle }^{-1}⪯{\langle \widehat{l},\widehat{u},\mathcal{I}\overline{H}\rangle }^{-1}$, the upper quasi-continuous convergence at $x_0$

implies that $x_0\in C_u\left(F\right)$.

Theorem 6.

If ${\left(H_{\alpha }\right)}_{\alpha \in \Sigma }$ is a net of multifunctions from $(X,\tau )$ to $(Y,\sigma )$, then for every multifunction $F:(X,\tau )\to (Y,\sigma )$ the following hold:

(i)

Under the assumption that $\langle \mathcal{S}F\rangle ⪯\langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle$,

$x_0\in C_l\left(F\right)$ implies the lower quasi-continuous convergence at $x_0$.

(ii)

Under the assumption that $\langle \mathcal{I}F\rangle ⪯\langle \widehat{l},\widehat{u},\mathcal{I}\overline{H}\rangle$,

$x_0\in C_u\left(F\right)$ implies the upper quasi-continuous convergence at $x_0$.

Remark 19.

In the case of single-valued functions, the assumption $\langle \mathcal{S}F\rangle ⪯\langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle$ means the pointwise convergence, so Theorem 5 is an extension of Frink’s result to multifunctions. What is more, in the case of single-valued functions, the assumption ${\langle \mathcal{S}F\rangle }^{-1}⪯{\langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle }^{-1}$ is weaker than the pointwise convergence. Thus, Theorem 5 improves Frink’s result in the part concerning the sufficient condition for the continuity of the limit functions.

Indeed, if the single-valued functions $f,h_{\alpha }:(X,\tau )⟶(Y,\sigma )$, $\alpha \in \Sigma$ are interpreted as multifunctions F and $H_{\alpha }$ given by $F\left(x\right)=\left\{f\left(x\right)\right\}$ and $H_{\alpha }\left(x\right)=\left\{h_{\alpha }\left(x\right)\right\}$, respectively, for all $(\alpha ,x)\in \Sigma \times X$, then we have $\langle \mathcal{I}F\rangle \left(x\right)=\langle \mathcal{S}F\rangle \left(x\right)=\overline{\left\{\right\{f\left(x\right)\left\}\right\}}$, or equivalently, ${\langle \mathcal{S}F\rangle }^{-1}\left(x\right)=\langle \mathcal{S}F\rangle \left(x\right)={\langle \mathcal{I}F\rangle }^{-1}\left(x\right)=\langle \mathcal{I}F\rangle \left(x\right)=\overline{\left\{\right\{f\left(x\right)\left\}\right\}}$ and of course, $C_l\left(F\right)=C_{lu}\left(F\right)=C_{ul}\left(F\right)=C_u\left(F\right)=C\left(f\right)$.

Analogously, $\mathcal{I}\overline{H}(\alpha ,x)=\mathcal{S}\overline{H}(\alpha ,x)=\overline{\left\{\left\{h_{\alpha }\left(x\right)\right\}\right\}}$ and, because we are using the function $\Theta$ given by $\Theta (\alpha ,x)=\overline{\left\{\left\{h_{\alpha }\left(x\right)\right\}\right\}}$ for $(\alpha ,x)\in \Sigma \times X$, the following four conditions are equivalent for any open subset $W\subset Y$ and $(\alpha ,x)\in \Sigma \times X$:

• $\mathcal{P}\left(W\right)\cap \Theta (\alpha ,x)\ne \varnothing$;
• $\mathcal{P}\left(W\right)\cap \mathcal{I}\overline{H}(\alpha ,x)\ne \varnothing$;
• $\mathcal{P}\left(W\right)\cap \mathcal{S}\overline{H}(\alpha ,x)\ne \varnothing$;
• $h_{\alpha }\left(x\right)\in W$.

Of course, for the same reasons, for any open subset $W\subset Y$ and $x\in X$, the following three conditions are equivalent:

• $\mathcal{P}\left(W\right)\cap \langle \mathcal{I}F\rangle \left(x\right)\ne \varnothing$;
• $\mathcal{P}\left(W\right)\cap \langle \mathcal{S}F\rangle \left(x\right)\ne \varnothing$;
• $f\left(x\right)\in W$.

So, the pointwise convergence of a net ${\left(h_{\alpha }\right)}_{\alpha \in \Sigma }$ to a function f can be phrased in one of the following two equivalent ways:

• $\langle \mathcal{I}F\rangle ⪯\langle \widehat{l},\widehat{u},\Theta \rangle$;
• $\langle \mathcal{S}F\rangle ⪯\langle \widehat{l},\widehat{u},\Theta \rangle$.

Analogously, according to Lemmas 14 and 15, the continuous convergence (resp. quasi-continuous convergence) at a point $x_0$ in the sense of Frink means that

• $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle l,\widehat{l},\widehat{u},u,\Theta \rangle \left(x_0\right)$ (resp. $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle l,u,\widehat{l},\widehat{u},\Theta \rangle \left(x_0\right)$) or equivalently,
• $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle l,\widehat{l},\widehat{u},u,\Theta \rangle \left(x_0\right)$ (resp. $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle l,u,\widehat{l},\widehat{u},\Theta \rangle \left(x_0\right)$).

Finalle, let us note that the condition ${\langle \mathcal{S}F\rangle }^{-1}⪯{\langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle }^{-1}$ considered in the case of single-valued functions, means

• $\langle \mathcal{I}F\rangle ⪯\langle \widehat{u},\widehat{l},\Theta \rangle$ or equivalently,
• $\langle \mathcal{S}F\rangle ⪯\langle \widehat{u},\widehat{l},\Theta \rangle$.

And, this condition turns out to be weaker than the pointwise convergence because it means that $f^{-1}\left(W\right)$⊂$lim$  $sup$  $h_{\alpha }^{-1}\left(W\right)$ for all open subset $W\subset Y$, whereas the pointwise convergence means that $f^{-1}\left(W\right)$⊂$lim$  $inf$  $h_{\alpha }^{-1}\left(W\right)$ for all open subset $W\subset Y$.

3.4. Types of Convergence Guaranteeing the Continuity of the Limit

We are interested in finding all types of convergence of nets of multifunctions that guarantee the required types of continuity or some generalized form of continuity of the limit multifunction. We will present general theorems that constitute a complete concept of the relationship between the type of convergence of the nets of multifunctions and the type of continuity of the limit multifunction without any assumptions on the type of continuity of the members of the nets. The following result refers to Theorem 5. The results of Theorem 5 are obtained by taking $\langle \Delta ,\Theta \rangle =\langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle$ (resp. $\langle \Delta ,\Theta \rangle =\langle \widehat{l},\widehat{u},\mathcal{I}\overline{H}\rangle$) in part (i) (resp. part (ii)) of the below theorem.

Theorem 7.

Let ${\left(H_{\alpha }\right)}_{\alpha \in \Sigma }$ be a net of multifunctions from a topological space $(X,\tau )$ to a regular topological space $(Y,\sigma )$, $\Theta \in \left\{\mathcal{I}\overline{H},\mathcal{S}\overline{H}\right\}$ and let Δ be a convergence operator. Then, for any $x_0\in X$ and every multifunction $F:(X,\tau )\to (Y,\sigma )$ satisfying the condition ${\langle \mathcal{S}F\rangle }^{-1}⪯{\langle \Delta ,\Theta \rangle }^{-1}$ (resp. ${\langle \mathcal{I}F\rangle }^{-1}⪯{\langle \Delta ,\Theta \rangle }^{-1}$), the following hold:

(i)

$\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle l,u,\Delta ,\Theta \rangle \left(x_0\right)$ implies that $x_0\in C_l\left(F\right)$

(resp. $x_0\in C_{lu}\left(F\right)$).

(ii)

If additionally, $F\left(x_0\right)$ is α-paracompact, then

$\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle l,u,\Delta ,\Theta \rangle \left(x_0\right)$ implies that $x_0\in C_{ul}\left(F\right)$

(resp. $x_0\in C_u\left(F\right)$).

Proof. 

(i). Let $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle l,u,\Delta ,\Theta \rangle \left(x_0\right)$ and let us assume to the contrary that $x_0\notin C_l\left(F\right)$(resp. $x_o\notin C_{lu}\left(F\right))$. Then, according to Lemma 9 (resp. Remark 10), $\langle \mathcal{S}F\rangle \left(x_o\right)\not\subset 〈l,u,\mathcal{S}F〉\left(x_o\right)$ (resp. $\langle \mathcal{S}F\rangle \left(x_o\right)\not\subset 〈l,u,\mathcal{I}F〉\left(x_o\right)$). Thus, there exists an open subset $W\subset Y$ such that $\mathcal{P}\left(W\right)\cap P\left(F\left(x_o\right)\right)\ne \varnothing$ and $\mathcal{P}\left(W\right)\cap \overline{{\bigcup }_{U_1\in \tau \left(x_o\right)}{\bigcap }_{x_1\in U_1}\overline{\mathcal{P}\left(F\left(x_1\right)\right)}}=\varnothing$ (resp. $\mathcal{P}\left(W\right)\cap \overline{{\bigcup }_{U_1\in \tau \left(x_o\right)}{\bigcap }_{x_1\in U_1}\overline{\left\{F\left(x_1\right)\right\}}}=\varnothing$), i.e.,

for every $U_1\in \tau \left(x_o\right)$ there exists $x_1\in U_1$ such that

$\mathcal{P}\left(W\right)\cap \mathcal{P}\left(F\left(x_1\right)\right)=\varnothing$ (resp. $\mathcal{P}\left(W\right)\cap \left\{F\left(x_1\right)\right\}=\varnothing$) so,

$F\left(x_1\right)\subset Y\setminus W$ (resp. $F\left(x_1\right)\cap (Y\setminus W)\ne \varnothing$) or equivalently,

$\mathcal{P}(Y\setminus W)\cap \left\{F\left(x_1\right)\right\}\ne \varnothing$ (resp. $\mathcal{P}(Y\setminus W)\cap \mathcal{P}\left(F\left(x_1\right)\right)\ne \varnothing$). $(\ast )$

The regularity of $(Y,\tau )$ implies the existence of an open subset $V\subset Y$ such that $\mathcal{P}\left(V\right)\cap \mathcal{P}\left(F\left(x_o\right)\right)\ne \varnothing$ and $Cl\left(V\right)\subset W$, so

$\mathcal{P}(Y\setminus Cl\left(V\right))\cap \left\{F\left(x_1\right)\right\}\ne \varnothing$ (resp. $\mathcal{P}(Y\setminus Cl\left(V\right))\cap \mathcal{P}\left(F\left(x_1\right)\right)\ne \varnothing$) and therefore by $(\ast )$ and Remark 1, we obtain

$\mathcal{P}(Y\setminus Cl\left(V\right))\cap {\bigcap }_{U_1\in \tau \left(x_o\right)}\overline{{\bigcup }_{x_1\in U_1}\left\{F\left(x_1\right)\right\}}\ne \varnothing$;

(resp. $\mathcal{P}(Y\setminus Cl\left(V\right))\cap {\bigcap }_{U_1\in \tau \left(x_o\right)}\overline{{\bigcup }_{x_1\in U_1}\mathcal{P}\left(F\left(x_1\right)\right)}\ne \varnothing$), i.e.,

$\mathcal{P}(Y\setminus Cl\left(V\right))\cap 〈u,l,\mathcal{I}F〉\left(x_o\right)\ne \varnothing$

(resp. $\mathcal{P}(Y\setminus Cl\left(V\right))\cap 〈u,l,\mathcal{S}F〉\left(x_o\right)\ne \varnothing$). $(\ast \ast )$

By the assumption, $\mathcal{I}F\left(x\right)\subset {\langle \Delta ,\Theta \rangle }^{-1}\left(x\right)$

(resp. $\mathcal{S}F\left(x\right)\subset {\langle \Delta ,\Theta ,\rangle }^{-1}\left(x\right)$) for all $x\in X$. So, according to Lemma 7 (iv), we have $〈u,l,\mathcal{I}F〉\left(x_o\right)\subset 〈u,l,{\langle \Delta ,\Theta \rangle }^{-1}〉\left(x_o\right)$

(resp. $〈u,l,\mathcal{S}F〉\left(x_o\right)\subset 〈u,l,{\langle \Delta ,\Theta \rangle }^{-1}〉\left(x_o\right)$) and consequently,

$\mathcal{P}(Y\setminus Cl\left(V\right))\cap 〈u,l,{\langle \Delta ,\Theta \rangle }^{-1}〉\left(x_o\right)\ne \varnothing$ or equivalently,

$\mathcal{P}(Y\setminus Cl\left(V\right))\cap {〈l,u,\Delta ,\Theta 〉}^{-1}\left(x_o\right)\ne \varnothing$$(\ast \ast \ast )$.

Since $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle l,u,\Delta ,\Theta \rangle \left(x_0\right)$, and $\mathcal{P}\left(V\right)\cap \mathcal{P}\left(F\left(x_o\right)\right)\ne \varnothing$, we get $\mathcal{P}\left(V\right)\cap \langle l,u,\Delta ,\Theta \rangle \left(x_0\right)\ne \varnothing$, and since, by Lemma 2, $\langle l,u,\Delta ,\Theta \rangle \approx {\langle l,u,\Delta ,\Theta \rangle }^{-1}$, according to $(\ast \ast \ast )$, we obtain $\mathcal{P}\left(V\right)\cap \mathcal{P}(Y\setminus Cl(V\left)\right)\ne \varnothing$, which gives a contradiction and finishes the proof of (i).

(ii). Let $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle l,u,\Delta ,\Theta \rangle \left(x_0\right)$ and let $x_0\notin C_{ul}\left(F\right)$ (resp. $x_0\notin C_u\left(F\right)$); then, using Remark 10 (resp. Lemma 9), we have $\langle \mathcal{I}F\rangle \left(x_o\right)\not\subset 〈l,u,\mathcal{S}F〉\left(x_0\right)$ (resp. $\langle \mathcal{I}F\rangle \left(x_o\right)\not\subset 〈l,u,\mathcal{I}F〉\left(x_0\right)$). So, there exists an open subset $W\subset Y$ such that $F\left(x_0\right)\subset W$ and the condition $(\ast )$ is fulfilled. Since $F\left(x_0\right)$ is $\alpha$-paracompact, there exists an open subset $V\subset Y$ such that $F\left(x_0\right)\subset V$, and $Cl\left(V\right)\subset W$ and hence, analogously as above, we have $\mathcal{P}(Y\setminus Cl\left(V\right))\cap 〈u,l,\mathcal{I}F〉\left(x_0\right)\ne \varnothing$ (resp. $\mathcal{P}(Y\setminus Cl\left(V\right))\cap 〈u,l,\mathcal{S}F〉\left(x_0\right)\ne \varnothing$), i.e., the property $(\ast \ast )$. Now following the same procedure as above, we get a contradiction that finishes the proof of (ii). □

Remark 20.

The relation between types of convergence and types of continuity of the limits proved in the above theorem illustrates the following simplified table.

	${\langle \mathcal{S}F\rangle }^{-1}⪯{\langle \Delta ,\Theta \rangle }^{-1}$	${\langle \mathcal{I}F\rangle }^{-1}⪯{\langle \Delta ,\Theta \rangle }^{-1}$
$\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle l,u,\Delta ,\Theta \rangle \left(x_0\right)\Rightarrow$	$x_0\in C_l\left(F\right)$	$x_0\in C_{lu}\left(F\right)$
$\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle l,u,\Delta ,\Theta \rangle \left(x_0\right)\Rightarrow$	$x_0\in C_{ul}\left(F\right)$	$x_0\in C_u\left(F\right)$

The next theorem concerning the reverse implications states a generalized version of Theorem 6. By simplified table, it may be illustrated as follows.

	$\langle \mathcal{S}F\rangle ⪯\langle \Delta ,\Theta \rangle$	$\langle \mathcal{I}F\rangle ⪯\langle \Delta ,\Theta \rangle$
$\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle l,u,\Delta ,\Theta \rangle \left(x_0\right)\Leftarrow$	$x_0\in C_l\left(F\right)$	$x_0\in C_{lu}\left(F\right)$
$\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle l,u,\Delta ,\Theta \rangle \left(x_0\right)\Leftarrow$	$x_0\in C_{ul}\left(F\right)$	$x_0\in C_u\left(F\right)$

The equivalences stated in Corollary 4 of Theorems 7 and 8 have the following simple illustration.

	${\langle \mathcal{S}F\rangle }^{-1}⪯{\langle \Delta ,\Theta \rangle }^{-1}$	${\langle \mathcal{I}F\rangle }^{-1}⪯{\langle \Delta ,\Theta \rangle }^{-1}$
	$and$$\langle \mathcal{S}F\rangle ⪯\langle \Delta ,\Theta \rangle$	$and$$\langle \mathcal{I}F\rangle ⪯\langle \Delta ,\Theta \rangle$
$\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle l,u,\Delta ,\Theta \rangle \left(x_0\right)\iff$	$x_0\in C_l\left(F\right)$	$x_0\in C_{lu}\left(F\right)$
$\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle l,u,\Delta ,\Theta \rangle \left(x_0\right)\iff$	$x_0\in C_{ul}\left(F\right)$	$x_0\in C_u\left(F\right)$

Theorem 8.

Let ${\left(H_{\alpha }\right)}_{\alpha \in \Sigma }$ be a net of multifunctions $H_{\alpha }:(X,\tau )\to (Y,\sigma )$, $\Theta \in \left\{\mathcal{I}\overline{H},\mathcal{S}\overline{H}\right\}$ and let Δ be a convergence operator. Then, for any $x_0\in X$ and every multifunction $F:(X,\tau )\to (Y,\sigma )$ the following hold:

(i)

If $\langle \mathcal{S}F\rangle ⪯\langle \Delta ,\Theta \rangle$ then

(a)

$x_0\in C_l\left(F\right)$ implies that $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle l,u,\Delta ,\Theta \rangle \left(x_0\right)$ and

(b)

$x_0\in C_{ul}\left(F\right)$ implies that $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle l,u,\Delta ,\Theta \rangle \left(x_0\right)$.

(ii)

If $\langle \mathcal{I}F\rangle ⪯\langle \Delta ,\Theta \rangle$ then

(a′)

$x_0\in C_{lu}\left(F\right)$ implies that $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle l,u,\Delta ,\Theta \rangle \left(x_0\right)$ and

(b′)

$x_0\in C_u\left(F\right)$ implies that $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle l,u,\Delta ,\Theta \rangle \left(x_0\right)$.

Proof. 

(i). If $x_0\in C_{ul}\left(F\right)$ (resp. $x_0\in C_l\left(F\right)$) then, according to Remark 10 (resp. Lemma 9), $\langle \mathcal{I}F\rangle \left(x_0\right)\subset 〈l,u,\mathcal{S}F〉\left(x_0\right)$ (resp. $\langle \mathcal{S}F\rangle \left(x_0\right)\subset 〈l,u,\mathcal{S}F〉(x_0$). So, since by the assumption we have $\mathcal{P}\left(F\left(x\right)\right)\subset 〈\Delta ,\Theta 〉\left(x\right)$ for all $x\in X$, using Lemma 7 (iv), we obtain $\langle \mathcal{I}F\rangle \left(x_0\right)\subset 〈l,u,\mathcal{S}F〉\left(x_0\right)\subset 〈l,u,\Delta ,\Theta 〉\left(x_0\right)$ (resp. $\langle \mathcal{S}F\rangle \left(x_0\right)\subset 〈l,u,\mathcal{S}F〉\left(x_0\right)\subset 〈l,u,\Delta ,\Theta 〉\left(x_0\right)$ and the proof of (i) is finished. The proof of the second part proceeds in an analogous manner. □

Remark 21.

The results (i) and (ii) of Theorem 6 follow from the above theorem by taking $\langle \Delta ,\Theta \rangle =\langle \widehat{l},\widehat{u},\mathcal{S}\overline{H}\rangle$ (resp. $\langle \Delta ,\Theta \rangle =\langle \widehat{l},\widehat{u},\mathcal{I}\overline{H}\rangle$) in part (i) (resp. part (ii)).

As a corollary from Theorems 7 and 8, we obtain the following equivalences between the types of convergence of the nets of multifunctions and the types of continuity of the limit multifunctions.

Corollary 4.

Let ${\left(H_{\alpha }\right)}_{\alpha \in \Sigma }$ be a net of multifunctions from a topological space $(X,\tau )$ to a regular topological space $(Y,\sigma )$, $\Theta \in \left\{\mathcal{I}\overline{H},\mathcal{S}\overline{H}\right\}$ and let Δ be a convergence operator. Then, for any $x_0\in X$ and every multifunction $F:(X,\tau )\to (Y,\sigma )$ satisfying the conditions ${\langle \mathcal{S}F\rangle }^{-1}⪯{\langle \Delta ,\Theta \rangle }^{-1}$ and $\langle \mathcal{S}F\rangle ⪯\langle \Delta ,\Theta \rangle$(resp. ${\langle \mathcal{I}F\rangle }^{-1}⪯{\langle \Delta ,\Theta \rangle }^{-1}$ and $\langle \mathcal{I}F\rangle ⪯\langle \Delta ,\Theta \rangle$)), the following hold:

(i)

$\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle l,u,\Delta ,\Theta \rangle \left(x_0\right)$ is equivalent to $x_0\in C_l\left(F\right)$

(resp. $x_0\in C_{lu}\left(F\right)$).

(ii)

If additionally, $F\left(x_0\right)$ is α-paracompact, then

$\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle l,u,\Delta ,\Theta \rangle \left(x_0\right)$ is equivalent to $x_0\in C_{ul}\left(F\right)$

(resp. $x_0\in C_u\left(F\right)$).

In Theorems 9 and 10 below, we state the corresponding version of Theorems 7 and 8 for generalized types of continuity characterized in Lemma 10 where, as one can see, we have used the compositions $l\circ u\circ u\circ l\circ l\circ u$, $u\circ l\circ l\circ u$, $l\circ u\circ u\circ l$ or $u\circ l\circ l\circ u\circ u\circ l$ in these characterizations, whereas in the case of standard continuity (Lemma 9 and Remark 10), the composition $l\circ u$. We omit the proof of these theorems because it is analogous to that of Theorems 7 and 8, it is enough to use the compositions $l\circ u\circ u\circ l\circ l\circ u$, $u\circ l\circ l\circ u$, $l\circ u\circ u\circ l$ or $u\circ l\circ l\circ u\circ u\circ l$ instead of $l\circ u$.

Theorem 9.

Let ${\left(H_{\alpha }\right)}_{\alpha \in \Sigma }$ be a net of multifunctions from a topological space $(X,\tau )$ to a regular topological space $(Y,\sigma )$, $\Theta \in \left\{\mathcal{I}\overline{H},\mathcal{S}\overline{H}\right\}$ and let Δ be a convergence operator. Then, for any $x_0\in X$ and every multifunction $F:(X,\tau )\to (Y,\sigma )$ satisfying the condition ${\langle \mathcal{S}F\rangle }^{-1}⪯{\langle \Delta ,\Theta \rangle }^{-1}$ (resp. ${\langle \mathcal{I}F\rangle }^{-1}⪯{\langle \Delta ,\Theta \rangle }^{-1}$), the following hold:

(α)

(i) $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle l,u,u,l,l,u,\Delta ,\Theta \rangle \left(x_0\right)$ implies $x_0$$\in \alpha C_l\left(F\right)$

  (resp. $x_0\in \alpha C_{lu}\left(F\right)$).

(ii)  If additionally, $F\left(x_0\right)$ is α-paracompact, then

    $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle l,u,u,l,l,u,\Delta ,\Theta \rangle \left(x_0\right)$ implies $x_0\in \alpha C_{ul}\left(F\right)$

    (resp. $x_0\in \alpha C_u\left(F\right)$).

(q)

(i) $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle u,l,l,u,\Delta ,\Theta \rangle \left(x_0\right)$ implies $x_0\in q{C}_l\left(F\right)$

  (resp. $x_0\in q{C}_{lu}\left(F\right)$).

(ii)  If additionally, $F\left(x_0\right)$ is α-paracompact, then

    $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle u,l,l,u,\Delta ,\Theta \rangle \left(x_0\right)$ implies $x_0\in q{C}_{ul}\left(F\right)$

    (resp. $x_0\in q{C}_u\left(F\right)$).

(p)

(i) $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle l,u,u,l,\Delta ,\Theta \rangle \left(x_0\right)$ implies $x_0\in p{C}_l\left(F\right)$

  (resp. $x_0\in p{C}_{lu}\left(F\right)$).

(ii)  If additionally, $F\left(x_0\right)$ is α-paracompact, then

    $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle l,u,u,l,\Delta ,\Theta \rangle \left(x_0\right)$ implies $x_0\in p{C}_{ul}\left(F\right)$

    (resp. $x_0\in p{C}_u\left(F\right)$).

(β)

(i) $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle u,l,l,u,u,l,\Delta ,\Theta \rangle \left(x_0\right)$ implies $x_0\in \beta C_l\left(F\right)$

  (resp. $x_0\in \beta C_{lu}\left(F\right)$).

(ii)  If additionally, $F\left(x_0\right)$ is α-paracompact, then

    $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle u,l,l,u,u,l,\Delta ,\Theta \rangle \left(x_0\right)$ implies $x_0\in \beta C_{ul}\left(F\right)$

    (resp. $x_0\in \beta C_u\left(F\right)$).

Theorem 10.

Let ${\left(H_{\alpha }\right)}_{\alpha \in \Sigma }$ be a net of multifunctions $H_{\alpha }:(X,\tau )\to (Y,\sigma )$, $\Theta \in \left\{\mathcal{I}\overline{H},\mathcal{S}\overline{H}\right\}$ and let Δ be a convergence operator. Then, for any $x_0\in X$ and every multifunction $F:(X,\tau )\to (Y,\sigma )$ the following hold:

(α)

(i) If $\langle \mathcal{S}F\rangle ⪯\langle \Delta ,\Theta \rangle$ then

  – $x_0\in \alpha C_l\left(F\right)$ implies that $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle l,u,u,l,l,u,\Delta ,\Theta \rangle \left(x_0\right)$ and

  – $x_0\in \alpha C_{ul}\left(F\right)$ implies that $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle l,u,u,l,l,u,\Delta ,\Theta \rangle \left(x_0\right)$.

(ii) If $\langle \mathcal{I}F\rangle ⪯\langle \Delta ,\Theta \rangle$ then

  – $x_0\in \alpha C_u\left(F\right)$ implies that $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle l,u,u,l,l,u,\Delta ,\Theta \rangle \left(x_0\right)$ and

  – $x_0\in \alpha C_{lu}\left(F\right)$ implies that $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle l,u,u,l,l,u,\Delta ,\Theta \rangle \left(x_0\right)$.

(q)

(i) If $\langle \mathcal{S}F\rangle ⪯\langle \Delta ,\Theta \rangle$ then

  – $x_0\in q{C}_l\left(F\right)$ implies that $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle u,l,l,u,\Delta ,\Theta \rangle \left(x_0\right)$ and

  – $x_0\in q{C}_{ul}\left(F\right)$ implies that $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle u,l,l,u,\Delta ,\Theta \rangle \left(x_0\right)$.

(ii) If $\langle \mathcal{I}F\rangle ⪯\langle \Delta ,\Theta \rangle$ then

  – $x_0\in q{C}_u\left(F\right)$ implies that $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle u,l,l,u,\Delta ,\Theta \rangle \left(x_0\right)$ and

  – $x_0\in q{C}_{lu}\left(F\right)$ implies that $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle u,l,l,u,\Delta ,\Theta \rangle \left(x_0\right)$.

(p)

(i) If $\langle \mathcal{S}F\rangle ⪯\langle \Delta ,\Theta \rangle$ then

  – $x_0\in p{C}_l\left(F\right)$ implies that $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle l,u,u,l,\Delta ,\Theta \rangle \left(x_0\right)$ and

  – $x_0\in p{C}_{ul}\left(F\right)$ implies that $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle l,u,u,l,\Delta ,\Theta \rangle \left(x_0\right)$.

(ii) If $\langle \mathcal{I}F\rangle ⪯\langle \Delta ,\Theta \rangle$ then

  – $x_0\in p{C}_u\left(F\right)$ implies that $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle l,u,u,l,\Delta ,\Theta \rangle \left(x_0\right)$ and

  – $x_0\in p{C}_{lu}\left(F\right)$ implies that $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle l,u,u,l,\Delta ,\Theta \rangle \left(x_0\right)$.

(β)

(i) If $\langle \mathcal{S}F\rangle ⪯\langle \Delta ,\Theta \rangle$ then

  – $x_0\in \beta C_l\left(F\right)$ implies that $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle u,l,l,u,u,l,\Delta ,\Theta \rangle \left(x_0\right)$ and

  – $x_0\in \beta C_{ul}\left(F\right)$ implies that $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle u,l,l,u,u,l,\Delta ,\Theta \rangle \left(x_0\right)$.

(ii) If $\langle \mathcal{I}F\rangle ⪯\langle \Delta ,\Theta \rangle$ then

  – $x_0\in \beta C_u\left(F\right)$ implies that $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle u,l,l,u,u,l,\Delta ,\Theta \rangle \left(x_0\right)$ and

  – $x_0\in \beta C_{lu}\left(F\right)$ implies that $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle u,l,l,u,u,l,\Delta ,\Theta \rangle \left(x_0\right)$.

Analogous to Corollary 4, we immediately obtain the following equivalences:

Corollary 5.

Let ${\left(H_{\alpha }\right)}_{\alpha \in \Sigma }$ be a net of multifunctions from a topological space $(X,\tau )$ to a regular topological space $(Y,\sigma )$, $\Theta \in \left\{\mathcal{I}\overline{H},\mathcal{S}\overline{H}\right\}$ and let Δ be a convergence operator. Then, for any $x_0\in X$ and every multifunction $F:(X,\tau )\to (Y,\sigma )$ satisfying the condition ${\langle \mathcal{S}F\rangle }^{-1}⪯{\langle \Delta ,\Theta \rangle }^{-1}$ and $\langle \mathcal{S}F\rangle ⪯\langle \Delta ,\Theta \rangle$ (resp. ${\langle \mathcal{I}F\rangle }^{-1}⪯{\langle \Delta ,\Theta \rangle }^{-1}$ and $\langle \mathcal{I}F\rangle ⪯\langle \Delta ,\Theta \rangle$)), the following hold:

(α)

(i) $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle l,u,u,l,l,u,\Delta ,\Theta \rangle \left(x_0\right)$ is equivalent to

  $x_0\in \alpha C_l\left(F\right)$ (resp. $x_0\in \alpha C_{lu}\left(F\right)$).

(ii) If additionally, $F\left(x_0\right)$ is α-paracompact, then

  $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle l,u,u,l,l,u,\Delta ,\Theta \rangle \left(x_0\right)$ is equivalent to

  $x_0\in \alpha C_{ul}\left(F\right)$ (resp. $x_0\in \alpha C_u\left(F\right)$).

(q)

(i) $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle u,l,l,u,\Delta ,\Theta \rangle \left(x_0\right)$ is equivalent to

  $x_0\in q{C}_l\left(F\right)$ (resp. $x_0\in q{C}_{lu}\left(F\right)$).

(ii) If additionally, $F\left(x_0\right)$ is α-paracompact, then

  $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle u,l,l,u,\Delta ,\Theta \rangle \left(x_0\right)$ is equivalent to

  $x_0\in q{C}_{ul}\left(F\right)$ (resp. $x_0\in q{C}_u\left(F\right)$).

(p)

(i) $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle l,u,u,l,\Delta ,\Theta \rangle \left(x_0\right)$ is equivalent to

  $x_0\in p{C}_l\left(F\right)$ (resp. $x_0\in p{C}_{lu}\left(F\right)$).

(ii) If additionally, $F\left(x_0\right)$ is α-paracompact, then

  $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle l,u,u,l,\Delta ,\Theta \rangle \left(x_0\right)$ is equivalent to

  $x_0\in p{C}_{ul}\left(F\right)$ (resp. $x_0\in p{C}_u\left(F\right)$).

(β)

(i) $\langle \mathcal{S}F\rangle \left(x_0\right)\subset \langle u,l,l,u,u,l,\Delta ,\Theta \rangle \left(x_0\right)$ is equivalent to

  $x_0\in \beta C_l\left(F\right)$ (resp. $x_0\in \beta C_{lu}\left(F\right)$).

(ii) If additionally, $F\left(x_0\right)$ is α-paracompact, then

  $\langle \mathcal{I}F\rangle \left(x_0\right)\subset \langle u,l,l,u,u,l,\Delta ,\Theta \rangle \left(x_0\right)$ is equivalent to

  $x_0\in \beta C_{ul}\left(F\right)$ (resp. $x_0\in \beta C_u\left(F\right)$).

Remark 22.

The use of $\langle l,u,u,l,l,u\Delta ,\Theta \rangle$, $\langle u,l,l,u,\Delta ,\Theta \rangle$, $\langle l,u,u,l,\Delta ,\Theta \rangle$ or $\langle u,l,l,u,u,\Delta ,\Theta \rangle$, instead of $\langle l,u,\Delta ,\Theta \rangle$ in the tablets in Remark 20, gives the analogous simplified illustrations of Theorems 9 and 10, and of Corollary 5 concerning the α-continuity, quasi-continuity, pre-continuity, or β-continuity, respectively.

3.5. The Monoid of Convergence Operators

The basic idea in this chapter is to consider the binary operation

$\odot :\mathcal{CON}.\mathcal{O}(\Sigma ,X,Y)\times \mathcal{CON}.\mathcal{O}(\Sigma ,X,Y)⟶\mathcal{CON}.\mathcal{O}(\Sigma ,X,Y)$

• defined by

$\langle h_{2n},\dots ,h_{q+1},\widehat{l},\dots ,h_{s+1},\widehat{u},\dots ,h_1\rangle \star \langle f_{2n^{*}},\dots ,f_{q^{*}+1},\widehat{l},\dots ,f_{s^{*}+1},\widehat{u},\dots ,f_1\rangle =$$\langle h_{2n},\dots ,h_{q+1},f_{2n^{*}},\dots ,f_{q^{*}+1},\widehat{l},h_q,\dots ,h_{s+1},f_{q^{*}},\dots ,f_{s^{*}+1},\widehat{u},h_s,\dots ,h_1,f_{s^{*}},\dots ,f_1\rangle$,

• where $\mathcal{CON}.\mathcal{O}(\Sigma ,X,Y)$ denotes the set of all convergence operators for given ($\Sigma ,\le$), $(X,\tau )$ and $(Y,\sigma )$.

It is easy to see that the operator $\langle \widehat{l},\widehat{u}\rangle$ is the neutral element for this operation. We will denote this operator by $\left(O_0\right)$ adequately to the notations used in Theorem 2.

The associativity of the operation ⊙ can be shown in the same manner as in the proof of Lemma 8. So, the set $\mathcal{CON}.\mathcal{O}(\Sigma ,X,Y)$ forms a monoid.

In this chapter, we will consider the question of how many convergence operators are there. An application of the lemma below significantly narrows down the search area.

Lemma 16.

Any convergence operator can be presented in the following form

$\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1\rangle$,

where $s=q$ or, both s and q are even numbers.

Proof. 

Assume that there exists a convergence function

$\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1,\Psi \rangle$ such that s≠q and s is an odd number.

We will show that

$\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1,\Psi \rangle$=

$\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s^{*}+1},\widehat{u},h_{s^{*}},\dots ,h_1,\Psi \rangle$

for some even number $s^{*}$.

Let us consider the segment $\dots ,h_{s+1},\widehat{u},h_s,\dots$ of our convergence function. It is clear that this segment has one of the following forms:

(i)

$\dots ,h_{s+1},\widehat{u},h_s,\dots =\dots ,u,\widehat{u},l,\dots ,$;

(ii)

$\dots ,h_{s+1},\widehat{u},h_s,\dots =\dots ,l,\widehat{u},u,\dots ,$;

(iii)

$\dots ,h_{s+1},\widehat{u},h_s,\dots =\dots ,u,\widehat{u},u,\dots ,$;

(iv)

$\dots ,h_{s+1},\widehat{u},h_s,\dots =\dots ,l,\widehat{u},l,\dots$.

The following equalities for the cases (i), (ii) and (iii) follow directly from the definition of the functions u and l:

• $\dots ,u,\widehat{u},l,\dots =\dots ,\widehat{u},u,l,\dots =\dots ,\widehat{u},h_{s+1},h_s,\dots$ (i.e., $s^{*}=s+1$);
• $\dots ,l,\widehat{u},u,\dots =\dots ,l,u,\widehat{u},\dots =\dots ,h_{s+1},h_s,\widehat{u},\dots$ (i.e., $s^{*}=s-1$);
• $\dots ,u,\widehat{u},u,\dots =\dots ,u,u,\widehat{u},\dots =\dots ,h_{s+1},h_s,\widehat{u},\dots$ (i.e., $s^{*}=s-1$).

We will prove that the following equality, corresponding to the case (iv), is also true:

• $\dots ,l,\widehat{u},l,\dots =\dots ,\widehat{u},l,l,\dots =\dots ,\widehat{u},h_{s+1},h_s,\dots$.

According to the definition of convergence function and Lemma 13 we have

$\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1,\Theta \rangle \left(x_0\right)=$

$h_{2n}\circ \dots \circ h_{q+1}\circ \widehat{l}\circ h_q\circ \dots \circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1\circ \Theta \circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x_0\right)$ and

$h_{s-1}\circ \dots \circ h_1\circ \Theta \circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x_0\right)=$

$\left\{\right\{\left\{\right\{\left\{\right\{\dots \{h_{s-1}\circ \dots \circ h_1\circ \Theta \left(\sigma \left({\mathcal{D}}^{(n,s-1)}\right)\right):$

${\mathcal{D}}^{(n,s-1)}\in {\mathcal{D}}^{(n,s)}\}:\alpha \in K\}:$

${\mathcal{D}}^{(n,i-1)}\in {\mathcal{D}}^{(n,i)}\}:i=s+1,\dots ,q\}:K\in \mathcal{F}\}:$

${\mathcal{D}}^{(n,i-1)}\in {\mathcal{D}}^{(n,i)}\}:i=q+1,\dots ,2n\}$.

Of course, the number $s-1$ is even, so ${\mathcal{D}}^{(n,s-1)}={\mathcal{B}}_0^{(n,{\displaystyle \frac{s-1}{2}})}={\tau }^{{\displaystyle \frac{s-1}{2}}}(x_{n-{\displaystyle \frac{s-1}{2}}})$ and this means that $h_{s-1}\circ \dots \circ h_1\circ \Theta \left(\alpha \left({\mathcal{D}}^{(n,s-1)}\right)\right)$ depends on $(\alpha ,x_{n-{\displaystyle \frac{s-1}{2}}})$. Therefore, denoting by ${\Theta }_{\Sigma }^{s-1}$ the function defined on the product $\Sigma \times X$ by

${\Theta }_{\Sigma }^{s-1}(\alpha ,x)=h_{s-1}\circ \dots \circ h_1(\Theta (\alpha ({\pi }^{{\displaystyle \frac{s-1}{2}}}\left(x\right))))$ for all $(\alpha ,x)\in \Sigma \times X$, we obtain

$h_{s-1}\circ \dots \circ h_1\circ \Theta \circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x_0\right)=$

$\left\{\right\{\left\{\right\{\left\{\right\{\dots \{{\Theta }_{\Sigma }^{s-1}(\alpha ,x_{n-{\displaystyle \frac{s-1}{2}}}):$

${\mathcal{D}}^{(n,s-1)}\in {\mathcal{D}}^{(n,s)}\}:\alpha \in K\}:$

${\mathcal{D}}^{(n,i-1)}\in {\mathcal{D}}^{(n,i)}\}:i=s+1,\dots ,q\}:K\in \mathcal{F}\}:$

${\mathcal{D}}^{(n,i-1)}\in {\mathcal{D}}^{(n,i)}\}:i=q+1,\dots ,2n\}$.

Now, using Remark 11 for the case that $m={\displaystyle \frac{s-1}{2}}$, since $j-1-2m=j-s$ and of course $j-2m=j-s+1$, we have

$h_{s-1}\circ \dots \circ h_1\circ \Theta \circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x_0\right)=$

$\left\{\right\{\left\{\right\{\left\{\right\{\dots \{{\Theta }_{\Sigma }^{s-1}(\alpha ,x_{n-m}):$

${\mathcal{D}}^{(n-m,0)}\in {\mathcal{D}}^{(n-m,1)}\}:\alpha \in K\}:$

${\mathcal{D}}^{(n-m,i-s)}\in {\mathcal{D}}^{(n-m,i-s+1)}\}:i=s+1,\dots ,q\}:K\in \mathcal{F}\}:$

${\mathcal{D}}^{(n-m,i-s)}\in {\mathcal{D}}^{(n-m,i-s+1)}\}:i=q+1,\dots ,2n\}$.

So, the structure of $h_{s-1}\circ \dots \circ h_1\circ \Theta \circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x_0\right)$ is represented by the sequence

$({\mathcal{D}}^{(n-m,1)},K,{\mathcal{D}}^{(n-m,2)},\dots ,{\mathcal{D}}^{(n-m,q-2m)},\mathcal{F},{\mathcal{D}}^{(m-n,q-2m+1)},\dots ,{\mathcal{D}}^{(n-m,2(n-m\left)\right)})$, i.e., the structure of ${\mathcal{F}}^{(1,q-2m)}\circ {\tau }^{n-m}\left(x_0\right)$. Therefore,

• $h_{2n}\circ \dots \circ h_{q+1}\circ \widehat{l}\circ h_q\circ \dots \circ h_{s+2}\circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1\circ \Theta \circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x_0\right)$ =
• $h_{2n}\circ \dots \circ h_{q+1}\circ \widehat{l}\circ h_q\circ \dots \circ h_{s+2}\circ h_{s+1}\circ \widehat{u}\circ h_s\circ {\Theta }_{\Sigma }^{s-1}\circ {\mathcal{F}}^{(1,q-2m)}\circ {\tau }^{n-m}\left(x_0\right)$.

We will show that

$h_{2n}\circ \dots \circ h_{q+1}\circ \widehat{l}\circ h_q\circ \dots \circ h_{s+2}\circ l\circ \widehat{u}\circ l\circ {\Theta }_{\Sigma }^{s-1}\circ {\mathcal{F}}^{(1,q-2m)}\circ {\tau }^{n-m}\left(x_0\right)$=

$h_{2n}\circ \dots \circ h_{q+1}\circ \widehat{l}\circ h_q\circ \dots \circ h_{s+2}\circ \widehat{u}\circ l\circ l\circ {\Theta }_{\Sigma }^{s-1}\circ {\mathcal{F}}^{(2,q-2m)}\circ {\tau }^{n-m}\left(x_0\right)$.

So, it is enough to prove that

• $l\circ \widehat{u}\circ l(\{\{\{{\Theta }_{\Sigma }^{s-1}(\alpha ,x_{n-m}):x_{n-m}\in U_{n-m}\}:\alpha \in K\}:U_{n-m}\in \tau \left(x_{m-n-1}\right)\}$
• = $\widehat{u}\circ l\circ l(\{\{\{{\Theta }_{\Sigma }^{s-1}(\alpha ,x_{n-m}):x_{n-m}\in U_{n-m}\}:U_{n-m}\in \tau \left(x_{m-n-1}\right)\}:\alpha \in K\}$, i.e., the family

${\mathcal{L}}^{*}=\overline{{\bigcup }_{U_{n-m}\in \tau \left(x_{n-m-1}\right)}{\bigcap }_{\alpha \in K}\overline{{\bigcup }_{x_{n-m}\in U_{n-m}}{\Theta }_{\Sigma }^{s-1}(\alpha ,x_{n-m})}}$

is equal to the family

${\mathcal{R}}^{*}={\bigcap }_{\alpha \in K}\overline{{\bigcup }_{U_{n-m}\in \tau \left(x_{n-m-1}\right)}{\bigcup }_{x_{n-m}\in U_{n-m}}{\Theta }_{\Sigma }^{s-1}(\alpha ,x_{n-m})}$.

For this purpose, let us note that ${\mathcal{R}}^{*}={\bigcap }_{\alpha \in K}\overline{{\bigcup }_{x\in X}{\Theta }_{\Sigma }^{s-1}(\alpha ,x)}$. So,

${\bigcap }_{\alpha \in K}\overline{{\bigcup }_{x_{n-m}\in U_{n-m}}{\Theta }_{\Sigma }^{s-1}(\alpha ,x_{n-m})}\subset {\mathcal{R}}^{*}$ for all $U_{n-m}\in \tau \left(x_{n-m-1}\right)$.

Therefore, ${\bigcup }_{U_{n-m}\in \tau \left(x_{n-m-1}\right)}{\bigcap }_{\alpha \in K}\overline{{\bigcup }_{x_{n-m}\in U_{n-m}}{\Theta }_{\Sigma }^{s-1}(\alpha ,x_{n-m})}\subset {\mathcal{R}}^{*}$ and thus, ${\mathcal{L}}^{*}\subset {\mathcal{R}}^{*}$ because the set ${\mathcal{R}}^{*}$ is closed in the space $(\mathcal{P}\left(Y\right),{\alpha }^u)$.

Now let us observe that ${\bigcap }_{\alpha \in K}\overline{{\bigcup }_{x\in X}{\Theta }_{\Sigma }^{s-1}(\alpha ,x)}\in \{{\bigcap }_{\alpha \in K}\overline{{\bigcup }_{x_{n-m}\in U_{n-m}}{\Theta }_{\Sigma }^{s-1}(\alpha ,x_{n-m})}:U_{n-m}\in \tau \left(x_{n-m-1}\right)\}$ because $X\in \tau \left(x_{n-m-1}\right)$, so

${\bigcap }_{\alpha \in K}\overline{{\bigcup }_{x\in X}{\Theta }_{\Sigma }^{s-1}(\alpha ,x)}\subset \overline{{\bigcup }_{U_{n-m}\in \tau \left(x_{n-m-1}\right)}{\bigcap }_{\alpha \in K}\overline{{\bigcup }_{x_{n-m}\in U_{n-m}}{\Theta }_{\Sigma }^{s-1}(\alpha ,x_{n-m})}}$ which means that ${\mathcal{R}}^{*}\subset {\mathcal{L}}^{*}$ and ends the proof of the equality ${\mathcal{R}}^{*}={\mathcal{L}}^{*}$.

Now, let us consider a convergence function

$\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1,\Theta \rangle$ such that s ≠ q and q is an odd number. We will show that

$\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1,\Theta \rangle$=

$\langle h_{2n},\dots ,h_{q^{*}+1},\widehat{l},h_{q^{*}},\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1,\Theta \rangle$

for some even number $q^{*}$.

Analogously to the previous case (with the number s), let us consider the segment $\dots ,h_{q+1},\widehat{l},h_q,\dots$ of our convergence function, in one of the following forms:

(v) $\dots ,h_{q+1},\widehat{l},h_q,\dots =\dots ,u,\widehat{l},l,\dots ,$;

(vi)$\dots ,h_{q+1},\widehat{l},h_q,\dots =\dots ,l,\widehat{l},u,\dots ,$;

(vii) $\dots ,h_{q+1},\widehat{l},h_q,\dots =\dots ,l,\widehat{l},l,\dots ,$;

(viii) $\dots ,h_{q+1},\widehat{l},h_q,\dots =\dots ,u,\widehat{l},u,\dots$.

Of course,

• $\dots ,u,\widehat{l},l,\dots =\dots ,u,l,\widehat{l},\dots =\dots ,h_{q+1},h_q,\widehat{l},\dots$ (i.e., $q^{*}=q-1$);
• $\dots ,l,\widehat{l},u,\dots =\dots ,\widehat{l},l,u,\dots =\dots ,\widehat{l},h_{q+1},h_q,\dots$ (i.e., $q^{*}=q+1$);
• $\dots ,l,\widehat{l},l,\dots =\dots ,\widehat{l},l,l,\dots =\dots ,\widehat{l},h_{q+1},h_q,\dots$ (i.e., $q^{*}=q+1$).

For the case (viii) we will prove the following equality which will finish the proof of the lemma:

• $\dots ,u,\widehat{l},u,\dots =\dots ,\widehat{l},u,u,\dots =\dots ,\widehat{l},h_{q+1},h_q,\dots$.

Analogously to the first part of this proof, we have

$\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1,\Theta \rangle \left(x_0\right)=$

$h_{2n}\circ \dots \circ h_{q+1}\circ \widehat{l}\circ h_q\circ \dots \circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1\circ \Theta \circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x_0\right)$ and

$h_{q-1}\circ \dots \circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1\circ \Theta \circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x_0\right)=$

$\left\{\right\{\{\dots \{h_{q-1}\circ \dots \circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1\circ \Theta \left(K^{\left(s\right)}\left({\mathcal{D}}^{(n,q-1)}\right)\right):$

${\mathcal{D}}^{(n,q-1)}\in {\mathcal{D}}^{(n,q)}\}:K\in \mathcal{F}\}:$

${\mathcal{D}}^{(n,i-1)}\in {\mathcal{D}}^{(n,i)}\}:i=q+1,\dots ,2n\}$.

Since $q-1$ is an even number, we have ${\mathcal{D}}^{(n,q-1)}={\mathcal{B}}_0^{(n,{\displaystyle \frac{q-1}{2}})}={\tau }^{{\displaystyle \frac{q-1}{2}}}(x_{n-{\displaystyle \frac{q-1}{2}}})$. So, $h_{q-1}\circ \dots \circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1\circ \Theta \left(K^{\left(s\right)}\left({\mathcal{D}}^{(n,q-1)}\right)\right)$ depends on $(K,x_{n-{\displaystyle \frac{q-1}{2}}})$ and denoting by ${\Theta }_{\mathcal{F}}^{(s,q-1)}$ the function given by

${\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x)=h_{q-1}\circ \dots \circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1\circ \Theta (K^{\left(s\right)}({\tau }^{{\displaystyle \frac{q-1}{2}}}\left(x\right)))$ for all $(K,x)\in \mathcal{F}\times X$, we get

$h_{q-1}\circ \dots \circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1\circ \Theta \circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x_0\right)=$

$\left\{\right\{\{\dots \{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x_{n-{\displaystyle \frac{q-1}{2}}}):$

${\mathcal{D}}^{(n,q-1)}\in {\mathcal{D}}^{(n,q)}\}:K\in \mathcal{F}\}:$

${\mathcal{D}}^{(n,i-1)}\in {\mathcal{D}}^{(n,i)}\}:i=q+1,\dots ,2n\}$.

Using Remark 11 for $m={\displaystyle \frac{q-1}{2}}$, we have

$h_{q-1}\circ \dots \circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1\circ \Theta \circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x_0\right)=$

$\left\{\right\{\{\dots \{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x_{n-m}):$

${\mathcal{D}}^{(n-m,0)}\in {\mathcal{D}}^{(n-m,1)}\}:K\in \mathcal{F}\}:$

${\mathcal{D}}^{(n-m,i-q)}\in {\mathcal{D}}^{(n-m,i-q+1)}\}:i=q+1,\dots ,2n\}$.

Therefore, $h_{2n}\circ \dots \circ h_{q+1}\circ \widehat{l}\circ h_q\circ \dots \circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1\circ \Theta \circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x_0\right)=$

$h_{2n}\circ \dots \circ h_{q+1}\circ \widehat{l}\circ h_q\left(\right\{\left\{\right\{\dots \{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x_{n-m}):$

${\mathcal{D}}^{(n-m,0)}\in {\mathcal{D}}^{(n-m,1)}\}:K\in \mathcal{F}\}:$

${\mathcal{D}}^{(n-m,i-q)}\in {\mathcal{D}}^{(n-m,i-q+1)}\}:i=q+1,\dots ,2n\})$.

We will show that the family

$h_{2n}\circ \dots \circ h_{q+2}\circ u\circ \widehat{l}\circ u\left(\right\{\left\{\right\{\dots \{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x_{n-m}):$

${\mathcal{D}}^{(n-m,0)}\in {\mathcal{D}}^{(n-m,1)}\}:K\in \mathcal{F}\}:$

${\mathcal{D}}^{(n-m,i-q)}\in {\mathcal{D}}^{(n-m,i-q+1)}\}:i=q+1,\dots ,2n\})$

is equal to the family

$h_{2n}\circ \dots \circ h_{q+2}\circ \widehat{l}\circ u\circ u\left(\right\{\left\{\right\{\dots \{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x_{n-m}):$

${\mathcal{D}}^{(n-m,0)}\in {\mathcal{D}}^{(n-m,1)}\}:{\mathcal{D}}^{(n-m,1)}\in {\mathcal{D}}^{(n-m,2)}\}:K\in \mathcal{F}\}:$

${\mathcal{D}}^{(n-m,i-q)}\in {\mathcal{D}}^{(n-m,i-q+1)}\}:i=q+2,\dots ,2n\})$.

We claim that

$u\circ \widehat{l}\circ u\left(\right\{\left\{\right\{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x_{n-m}):$$x_{n-m}\in U_{n-m}\}:$

$K\in \mathcal{F}\}:U_{n-m}\in \tau \left(x_{n-m-1}\right)\left\}\right)=$

$\widehat{l}\circ u\circ u\left(\right\{\left\{\right\{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x_{n-m}):$$x_{n-m}\in U_{n-m}\}:$

$U_{n-m}\in \tau \left(x_{n-m-1}\right)\}:K\in \mathcal{F}\})$, i.e.,

the family

${\mathcal{L}}^{**}={\bigcap }_{U_{n-m}\in \tau \left(x_{n-m-1}\right)}\overline{{\bigcup }_{K\in \mathcal{F}}{\bigcap }_{x_{n-m}\in U_{n-m}}\overline{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x_{n-m})}}$

is equal to the family

${\mathcal{R}}^{**}=\overline{{\bigcup }_{K\in \mathcal{F}}{\bigcap }_{U_{n-m}\in \tau \left(x_{n-m-1}\right)}{\bigcap }_{x_{n-m}\in U_{n-m}}\overline{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x_{n-m})}}$.

Indeed, for any $U_{n-m}\in \tau \left(x_{n-m-1}\right)$ and $K\in \mathcal{F}$ the inclusion

${\bigcap }_{x_{n-m}\in U_{n-m}}\overline{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x_{n-m})}\subset \overline{{\bigcup }_{K\in \mathcal{F}}{\bigcap }_{x_{n-m}\in U_{n-m}}\overline{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x_{n-m})}}$ holds.

So, ${\bigcap }_{U_{n-m}\in \tau \left(x_{n-m-1}\right)}{\bigcap }_{x_{n-m}\in U_{n-m}}\overline{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x_{n-m})}\subset$

${\bigcap }_{U_{n-m}\in \tau \left(x_{n-m-1}\right)}\overline{{\bigcup }_{K\in \mathcal{F}}{\bigcap }_{x_{n-m}\in U_{n-m}}\overline{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x_{n-m})}}$ for any $K\in \mathcal{F}$ and

hence, ${\bigcup }_{K\in \mathcal{F}}{\bigcap }_{U_{n-m}\in \tau \left(x_{n-m-1}\right)}{\bigcap }_{x_{n-m}\in U_{n-m}}\overline{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x_{n-m})}\subset$

${\bigcap }_{U_{n-m}\in \tau \left(x_{n-m-1}\right)}\overline{{\bigcup }_{K\in \mathcal{F}}{\bigcap }_{x_{n-m}\in U_{n-m}}\overline{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x_{n-m})}}$ which gives

${\mathcal{R}}^{**}\subset {\mathcal{L}}^{**}$.

Now let us note that the family $\overline{{\bigcup }_{K\in \mathcal{F}}{\bigcap }_{x\in X}\overline{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x)}}$ belongs to

$\{\overline{{\bigcup }_{K\in \mathcal{F}}{\bigcap }_{x_{n-m}\in U_{n-m}}\overline{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x_{n-m})}}:U_{n-m}\in \tau \left(x_{n-m-1}\right)\}$ because of

$X\in \tau \left(x_{n-m-1}\right)$ and consequently, ${\mathcal{L}}^{**}\subset \overline{{\bigcup }_{K\in \mathcal{F}}{\bigcap }_{x\in X}\overline{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x)}}$.

But $\overline{{\bigcup }_{K\in \mathcal{F}}{\bigcap }_{x\in X}\overline{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x)}}\subset {\mathcal{R}}^{**}$ since

${\bigcap }_{x\in X}\overline{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x)}\subset {\bigcap }_{x_{n-m}\in U_{n-m}}\overline{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x_{n-m})}$ for all $K\in \mathcal{F}$ and any $U_{n-m}\in \tau \left(x_{n-m-1}\right)$, and consequently, for all $K\in \mathcal{F}$ we have

${\bigcap }_{x\in X}\overline{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x)}\subset {\bigcap }_{U_{n-m}\in \tau \left(x_{n-m-1}\right)}{\bigcap }_{x_{n-m}\in U_{n-m}}\overline{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x_{n-m})}$. So, $\overline{{\bigcup }_{K\in \mathcal{F}}{\bigcap }_{x\in X}\overline{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x)}}\subset \overline{{\bigcup }_{K\in \mathcal{F}}{\bigcap }_{U_{n-m}\in \tau \left(x_{n-m-1}\right)}{\bigcap }_{x_{n-m}\in U_{n-m}}\overline{{\Theta }_{\mathcal{F}}^{(s,q-1)}(K,x_{n-m})}}$.

This proves the inclusion ${\mathcal{L}}^{**}\subset {\mathcal{R}}^{**}$ and finishes the proof of the lemma. □

As the above lemma shows, a combination $h_{2n}\circ \dots \circ h_{q+1}\circ \widehat{l}\circ h_q\circ \dots \circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1$ can be an ambiguous description of the operator $\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1\rangle$ in the sense of order. The following lemma shows that the descriptions of convergence operators can reduce.

Lemma 17.

The following segments of a convergence operator

$\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1\rangle$ are equal:

(a)

${\Delta }_1^{\widehat{l}}=u\circ l\circ \widehat{l}\circ l\circ u\circ u\circ l\circ l\circ u$ (resp. ${\Delta }_1^{\widehat{u}}=l\circ u\circ u\circ l\circ l\circ u\circ \widehat{u}\circ u\circ l$);

(b)

${\Delta }_2^{\widehat{l}}=u\circ l\circ \widehat{l}\circ l\circ u$ (resp. ${\Delta }_2^{\widehat{u}}=l\circ u\circ \widehat{u}\circ u\circ l$);

(c)

${\Delta }_3^{\widehat{l}}=u\circ l\circ l\circ u\circ u\circ l\circ \widehat{l}\circ l\circ u$ (resp. ${\Delta }_3^{\widehat{u}}=l\circ u\circ \widehat{u}\circ u\circ l\circ l\circ u\circ u\circ l$);

(d)

${\Delta }_4^{\widehat{l}}=u\circ l\circ l\circ u\circ \widehat{l}\circ u\circ l\circ l\circ u$ (resp. ${\Delta }_4^{\widehat{u}}=l\circ u\circ u\circ l\circ \widehat{u}\circ l\circ u\circ u\circ l$).

Proof. 

We will start by showing that for any convergence function

$\langle \Delta ,\Theta \rangle$= $h_{2n}\circ \dots \circ h_{q+1}\circ \widehat{l}\circ h_q\circ \dots \circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1\circ \Theta \circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n$,

where s and q are even numbers, the segments of the following types one may regard as cluster operators in the sense of Definition 1:

(i)

$h_{s^{*}}\circ h_{s^{*}-1}\circ \dots \circ h_1$ for some even number $s^{*}$ such that $s\ge s^{*}\ge 1$;

(ii)

$h_{k^{*}}\circ h_{k^{*}-1}\circ \dots \circ h_k$ for some even number $k^{*}$ and an odd number k such that

$q\ge k^{*}>k\ge s+1$;

(iii)

$h_{p^{*}}\circ h_{p^{*}-1}\circ \dots \circ h_p$ for some even number $p^{*}$ and an odd number p such that

$2n\ge p^{*}>p\ge q+1$.

This will allow us to use Lemma 7 and Theorem 1.

Of course, the appropriate 2(n + 1)-tuple of index sets of ${\mathcal{F}}^{(s,q)}\circ {\tau }^n$ has the form

$({\mathcal{D}}^{(n,1)},{\mathcal{D}}^{(n,2)},\dots ,{\mathcal{D}}^{(n,s)},K,{\mathcal{D}}^{(n,s+1)},\dots ,{\mathcal{D}}^{(n,q)},\mathcal{F},{\mathcal{D}}^{(n,q+1)},\dots ,{\mathcal{D}}^{(n,2n)})$.

So, consider a segment $h_{s^{*}}\circ h_{s^{*}-1}\circ \dots \circ h_1$ of $\Delta$ for some even number $s^{*}\le s$. Then,

$h_{s^{*}}\circ h_{s^{*}-1}\circ \dots \circ h_1(\Theta \circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n)\left(x_0\right)=$

$\left\{\right\{\left\{\right\{\left\{\right\{\dots \{h_{s^{*}}\circ h_{s^{*}-1}\circ \dots \circ h_1(\Theta \left(\alpha \left({\mathcal{D}}^{(n,s^{*})}\right)\right)):$

${\mathcal{D}}^{(n,i)}\in {\mathcal{D}}^{(n,i+1)}\}:i=s^{*},\dots ,s-1\}:\alpha \in K\}:$

${\mathcal{D}}^{(n,i-1)}\in {\mathcal{D}}^{(n,i)}\}:i=s+1,\dots ,q\}:K\in \mathcal{F}\}:$

${\mathcal{D}}^{(n,i-1)}\in {\mathcal{D}}^{(n,i)}\}:i=q+1,\dots ,2n\}$.

Of course, ${\mathcal{D}}^{(n,s^{*})}={\tau }^{{\displaystyle \frac{s^{*}}{2}}}(x_{n-{\displaystyle \frac{s^{*}}{2}}})$ and $\Psi$ = $\Theta \circ \alpha$ is a function from X to ${\mathcal{P}}^2\left(Y\right)$. Hence,

$h_{s^{*}}\circ h_{s^{*}-1}\circ \dots \circ h_1(\Theta \left(\alpha \left({\mathcal{D}}^{(n,s^{*})}\right)\right))=h_{s^{*}}\circ h_{s^{*}-1}\circ \dots \circ h_1(\Psi ({\tau }^{{\displaystyle \frac{s^{*}}{2}}}(x_{n-{\displaystyle \frac{s^{*}}{2}}}))$ and therefore we can regard the composition $h_{s^{*}}\circ h_{s^{*}-1}\circ \dots \circ h_1$ as a cluster operator in the sense of Definition 1.

Let us now consider a segment $h_{k^{*}}\circ h_{k^{*}-1}\circ \dots \circ h_k$ of $\Delta$ for some even number $k^{*}$ and an odd number k such that $q\ge k^{*}>k\ge s+1$.

It is clear that

$h_{k-1}\circ \dots \circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1\circ \Theta \circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x_0\right)=$

$\left\{\right\{\{\dots \{h_{k-1}\circ \dots \circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1\circ \Theta \left(K^{\left(s\right)}\left({\mathcal{D}}^{(n,k-1)}\right)\right):$

${\mathcal{D}}^{(n,i-1)}\in {\mathcal{D}}^{(n,i)}\}:i=k,\dots ,q\}:K\in \mathcal{F}\}:$

${\mathcal{D}}^{(n,i-1)}\in {\mathcal{D}}^{(n,i)}\}:i=q+1,\dots ,2n\}=$

$\left\{\right\{\{\dots \{h_{k-1}\circ \dots \circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1\circ \Theta \left(K^{\left(s\right)}\left({\alpha }^m\left(x_{n-m}\right)\right)\right):$

${\mathcal{D}}^{(n-m,i-1-2m)}\in {\mathcal{D}}^{(n-m,i-2m)}\}:i=k,\dots ,q\}:K\in \mathcal{F}\}:$

${\mathcal{D}}^{(n-m,i-1-2m)}\in {\mathcal{D}}^{(n-m,i-2m)}\}:i=q+1,\dots ,2n\}=$

$\left\{\right\{\{\dots \{\Psi \left(x_{n-m}\right):$${\mathcal{D}}^{(n-m,i-1-2m)}\in {\mathcal{D}}^{(n-m,i-2m)}\}:i=k,\dots ,q\}:K\in \mathcal{F}\}:$

${\mathcal{D}}^{(n-m,i-1-2m)}\in {\mathcal{D}}^{(n-m,i-2m)}\}:i=q+1,\dots ,2n\}$,

where $m={\displaystyle \frac{k-1}{2}}$ and $\Psi$ is defined by

$h_{k-1}\circ \dots \circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1\circ \Theta \left(K^{\left(s\right)}\left({\alpha }^m\left(x\right)\right)\right))$ for all $x\in X$.

For this reason, one can write the function

$h_{k^{*}}\circ \dots \circ h_k\circ h_{k-1}\circ \dots \circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1\circ \Theta \circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x_0\right)$ as follows

$h_{k^{*}}\circ h_{k^{*}-1}\circ \dots \circ h_k(h_{k-1}\circ \dots \circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1\circ \Theta \circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x_0\right))=$

$\left\{\right\{\{\dots \{h_{k^{*}}\circ h_{k^{*}-1}\circ \dots \circ h_k\left(\right\{\Psi \left(x_{n-m}\right):$

${\mathcal{D}}^{(n-m,i-1-2m)}\in {\mathcal{D}}^{(n-m,i-2m)}\}:i=k,\dots ,k^{*}\left\}\right):$

${\mathcal{D}}^{(n-m,i-1-2m)}\in {\mathcal{D}}^{(n-m,i-2m)}\}:i=k^{*}+1,\dots ,q\}:K\in \mathcal{F}\}:$

${\mathcal{D}}^{(n-m,i-1-2m)}\in {\mathcal{D}}^{(n-m,i-2m)}\}:i=q+1,\dots ,2n\}=$

$\left\{\right\{\{\dots \{h_{k^{*}}\circ h_{k^{*}-1}\circ \dots \circ h_k(\Psi ({\tau }^{{\displaystyle \frac{k^{*}-2m}{2}}}(x_{n-m-{\displaystyle \frac{k^{*}-2m}{2}}})):$

${\mathcal{D}}^{(n-m,i-1-2m)}\in {\mathcal{D}}^{(n-m,i-2m)}\}:i=k^{*}+1,\dots ,q\}:K\in \mathcal{F}\}:$

${\mathcal{D}}^{(n-m,i-1-2m)}\in {\mathcal{D}}^{(n-m,i-2m)}\}:i=q+1,\dots ,2n\}$ since

${\tau }^{{\displaystyle \frac{k^{*}-2m}{2}}}(x_{n-m-{\displaystyle \frac{k^{*}-2m}{2}}})={\mathcal{D}}^{(n-m,k^{*}-2m)}$.

So, we can regard the family $h_{k^{*}}\circ h_{k^{*}-1}\circ \dots \circ h_k(\Psi ({\tau }^{{\displaystyle \frac{k^{*}-2m}{2}}}(x_{n-m-{\displaystyle \frac{k^{*}-2m}{2}}})))$ as a value of the cluster function $\langle h_{k^{*}},h_{k^{*}-1},\dots h_k,\Psi \rangle$.

Finally, let us consider a segment $h_{p^{*}}\circ h_{p^{*}-1}\circ \dots \circ h_p$ of $\Delta$ for some even number $p^{*}$ and an odd number p such that $p^{*}>p\ge q+1$. Then,

$h_{p-1}\circ \dots \circ h_{q+1}\circ \widehat{l}\circ h_q\circ \dots \circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1\circ \Theta \circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x_0\right)=$

$\{\dots \{h_{p-1}\circ \dots \circ h_{q+1}\circ \widehat{l}\circ h_q\circ \dots \circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1\circ \Theta \circ {\mathcal{F}}^{(s,q)}\left({\mathcal{D}}^{(n,p-1)}\right):$

${\mathcal{D}}^{(n,i-1)}\in {\mathcal{D}}^{(n,i)}\}:i=p,\dots ,2n\}=$

$\{\dots \{\Psi (x_{n-{\displaystyle \frac{p-1}{2}}}):$${\mathcal{D}}^{(n-m,i-1-2m)}\in {\mathcal{D}}^{(n-m,i-2m)}\}:i=p,\dots ,2n\}$, where $m={\displaystyle \frac{p-1}{2}}$ and $\Psi$ is defined by $h_{p-1}\circ \dots \circ h_{q+1}\circ \widehat{l}\circ h_q\circ \dots \circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1\circ \Theta \circ {\mathcal{F}}^{(s,q)}\circ {\tau }^{{\displaystyle \frac{p-1}{2}}}$.

Therefore,

$h_{p^{*}}\circ \dots \circ h_p\circ h_{p-1}\circ \dots \circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1\circ \Theta \circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x_0\right)=$

$h_{p^{*}}\circ h_{p^{*}-1}\circ \dots \circ h_p\left(\right\{\dots \{\Psi (x_{n-{\displaystyle \frac{p-1}{2}}}):$

${\mathcal{D}}^{(n-m,i-1-2m)}\in {\mathcal{D}}^{(n-m,i-2m)}\}:i=p,\dots ,2n\}=$

$\left\{\right\{\{\dots \{h_{p^{*}}\circ h_{p^{*}-1}\circ \dots \circ h_p(\Psi ({\tau }^{{\displaystyle \frac{p^{*}-2m}{2}}}(x_{n-m-{\displaystyle \frac{p^{*}-2m}{2}}})):$

${\mathcal{D}}^{(n-m,i-1-2m)}\in {\mathcal{D}}^{(n-m,i-2m)}\}:i=p^{*}+1,\dots ,2n\}$.

Thus, the family $h_{p^{*}}\circ h_{p^{*}-1}\circ \dots \circ h_p(\Psi ({\tau }^{{\displaystyle \frac{p^{*}-2m}{2}}}(x_{n-m-{\displaystyle \frac{p^{*}-2m}{2}}})))$ is a value of the cluster function $\langle h_{p^{*}},h_{p^{*}-1},\dots h_p,\Psi \rangle$.

We are now ready to prove that ${\Delta }_1^{\widehat{l}}={\Delta }_2^{\widehat{l}}={\Delta }_3^{\widehat{l}}={\Delta }_4^{\widehat{l}}$ and

${\Delta }_1^{\widehat{u}}={\Delta }_2^{\widehat{u}}={\Delta }_3^{\widehat{u}}={\Delta }_4^{\widehat{u}}$.

Applying Lemma 7 (iii)(b) and (a), and the equalities (d) stated in the proof of Theorem 1, we get

${\Delta }_1^{\widehat{l}}=u\circ l\circ \widehat{l}\circ l\circ u\circ u\circ l\circ l\circ u$

$=u\circ \widehat{l}\circ l\circ l\circ u\circ u\circ l\circ l\circ u$

$=u\circ \widehat{l}\circ l\circ u\circ l\circ l\circ u\circ u\circ l\circ l\circ u$

$=u\circ \widehat{l}\circ l\circ u\circ l\circ l\circ u$

$=u\circ \widehat{l}\circ l\circ l\circ u$

$=u\circ l\circ \widehat{l}\circ l\circ u={\Delta }_2^{\widehat{l}}$. And,

${\Delta }_1^{\widehat{u}}=l\circ u\circ u\circ l\circ l\circ u\circ \widehat{u}\circ u\circ l$

$=l\circ u\circ u\circ l\circ l\circ u\circ u\circ \widehat{u}\circ l$

$=l\circ u\circ u\circ l\circ l\circ u\circ u\circ l\circ u\circ \widehat{u}\circ l$

$=l\circ u\circ u\circ l\circ u\circ \widehat{u}\circ l$

$=l\circ u\circ u\circ \widehat{u}\circ l$

$=l\circ u\circ \widehat{u}\circ u\circ l={\Delta }_2^{\widehat{u}}$.

Analogously,

${\Delta }_3^{\widehat{l}}=u\circ l\circ l\circ u\circ u\circ l\circ \widehat{l}\circ l\circ u$

$=u\circ l\circ l\circ u\circ u\circ l\circ l\circ \widehat{l}\circ u$

$=u\circ l\circ l\circ u\circ u\circ l\circ l\circ u\circ l\circ \widehat{l}\circ u$

$=u\circ l\circ l\circ u\circ l\circ \widehat{l}\circ u$

$=u\circ l\circ l\circ \widehat{l}\circ u$

$=u\circ l\circ \widehat{l}\circ l\circ u={\Delta }_2^{\widehat{l}}$.

And,

${\Delta }_3^{\widehat{u}}=l\circ u\circ \widehat{u}\circ u\circ l\circ l\circ u\circ u\circ l$

$=l\circ \widehat{u}\circ u\circ u\circ l\circ l\circ u\circ u\circ l$

$=l\circ \widehat{u}\circ u\circ l\circ u\circ u\circ l\circ l\circ u\circ u\circ l$

$=l\circ \widehat{u}\circ u\circ l\circ u\circ u\circ l$

$=l\circ \widehat{u}\circ u\circ u\circ l$

$=l\circ u\circ \widehat{u}\circ u\circ l={\Delta }_2^{\widehat{u}}$.

Finally,

${\Delta }_4^{\widehat{l}}=u\circ l\circ l\circ u\circ \widehat{l}\circ u\circ l\circ l\circ u$

$⪯u\circ l\circ l\circ u\circ u\circ l\circ \widehat{l}\circ u\circ l\circ l\circ u$

$=u\circ l\circ l\circ u\circ u\circ \widehat{l}\circ l\circ u\circ l\circ l\circ u$

$=u\circ l\circ l\circ u\circ u\circ \widehat{l}\circ l\circ l\circ u$

$=u\circ l\circ l\circ u\circ u\circ l\circ \widehat{l}\circ l\circ u={\Delta }_3^{\widehat{l}}$

$⪯u\circ l\circ l\circ u\circ u\circ l\circ \widehat{l}\circ l\circ u\circ u\circ l\circ l\circ u$

$⪯u\circ l\circ \widehat{l}\circ l\circ u\circ u\circ l\circ l\circ u$

$=u\circ l\circ l\circ \widehat{l}\circ u\circ u\circ l\circ l\circ u$

$=u\circ l\circ l\circ u\circ l\circ \widehat{l}\circ u\circ u\circ l\circ l\circ u$

$=u\circ l\circ l\circ u\circ \widehat{l}\circ l\circ u\circ u\circ l\circ l\circ u$

$⪯u\circ l\circ l\circ u\circ \widehat{l}\circ u\circ l\circ l\circ u={\Delta }_4^{\widehat{l}}$.

So, ${\Delta }_4^{\widehat{l}}={\Delta }_3^{\widehat{l}}$.

Analogously one can prove that ${\Delta }_4^{\widehat{u}}={\Delta }_3^{\widehat{u}}$ and finish the proof of the lemma. □

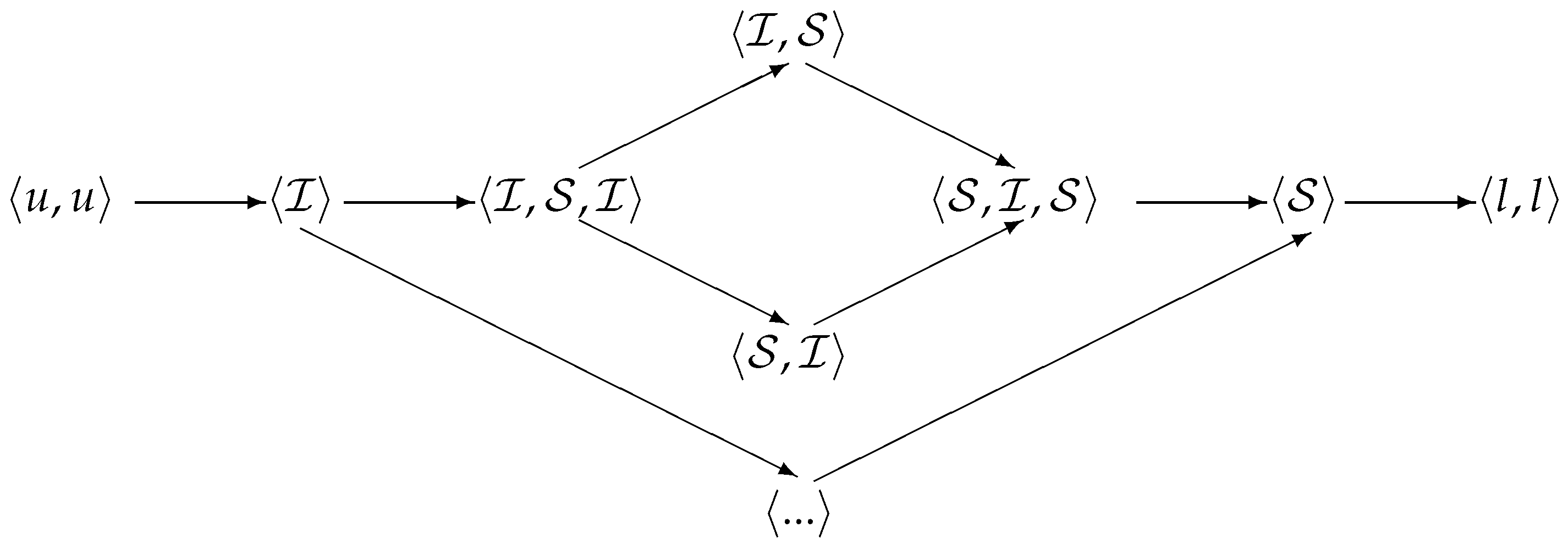
Theorem 2 shows that the set of all six products of the form ${\mathcal{F}}^{(s,q)}\circ {\tau }^1$, i.e., $\{{\mathcal{F}}^{(0,0)}\circ {\tau }^1,{\mathcal{F}}^{(0,1)}\circ {\tau }^1,{\mathcal{F}}^{(1,1)}\circ {\tau }^1,{\mathcal{F}}^{(0,2)}\circ {\tau }^1,{\mathcal{F}}^{(1,2)}\circ {\tau }^1,{\mathcal{F}}^{(2,2)}\circ {\tau }^1\}$, generates the monoid $\mathcal{P}\mathcal{R}(\Sigma ,X)$ of all products of $\left(\right(\Sigma ,⪯),(X,\tau \left)\right)$. It is easy to check that these products designate at most the following seven operators:

$\mathcal{B}=\{\langle \widehat{l},\widehat{u},l,u\rangle ,\langle \widehat{l},\widehat{u},u,l,\rangle ,\langle l,u,\widehat{l},\widehat{u}\rangle ,\langle u,l,\widehat{l},\widehat{u}\rangle ,\langle \widehat{l},l,u,\widehat{u}\rangle ,\langle \widehat{l},u,l,\widehat{u}\rangle ,\langle u,\widehat{l},\widehat{u},l\rangle \}.$

For simplicity purposes, we will use the following shorter denotes:

$\langle A\rangle =\langle \widehat{l},\widehat{u},l,u\rangle ,\langle B\rangle =\langle \widehat{l},\widehat{u},u,l,\rangle ,\langle C\rangle =\langle l,u,\widehat{l},\widehat{u}\rangle ,\langle D\rangle =\langle u,l,\widehat{l},\widehat{u}\rangle$,

$\langle E\rangle =\langle \widehat{l},l,u,\widehat{u}\rangle ,\langle F\rangle =\langle \widehat{l},u,l,\widehat{u}\rangle$ and $\langle G\rangle =\langle u,\widehat{l},\widehat{u},l\rangle$.

Below, we will indicate all possible convergence operators and present them in the form of multiplications of members of the collection $\mathcal{B}$.

Theorem 11.

For given ($\Sigma ,\le$), $(X,\tau )$, and $(Y,\sigma )$, the set $\mathcal{CON}.\mathcal{O}(\Sigma ,X,Y)$ of all convergence operators contains at most the following non-neutral elements:

(i)

Specified by ${\mathcal{F}}^{(0,2n)}\circ {\tau }^n$,n = 1, 2, …:

$\left(O_1\right)$ $\langle \widehat{l},l,u,\widehat{u}\rangle =\langle E\rangle$,

$\left(O_2\right)$ $\langle \widehat{l},u,l,\widehat{u}\rangle =\langle F\rangle$,

$\left(O_3\right)$ $\langle \widehat{l},l,u,u,l,l,u,\widehat{u}\rangle =\langle E\rangle \odot \langle F\rangle \odot \langle E\rangle$,

$\left(O_4\right)$ $\langle \widehat{l},u,l,l,u,\widehat{u}\rangle =\langle F\rangle \odot \langle E\rangle$,

$\left(O_5\right)$ $\langle \widehat{l},l,u,u,l,\widehat{u}\rangle =\langle E\rangle \odot \langle F\rangle$,

$\left(O_6\right)$ $\langle \widehat{l},u,l,l,u,u,l,\widehat{u}\rangle =\langle F\rangle \odot \langle E\rangle \odot \langle F\rangle$.

(ii)

Specified by ${\mathcal{F}}^{(s,s)}\circ {\tau }^n$ for an even natural number s:

$\left(O_7\right)$ $\langle \widehat{l},\widehat{u},l,u\rangle =\langle A\rangle$,

$\left(O_8\right)$ $\langle \widehat{l},\widehat{u},u,l,\rangle =\langle B\rangle$,

$\left(O_9\right)$ $\langle l,u,\widehat{l},\widehat{u}\rangle =\langle C\rangle$,

$\left(O_{10}\right)$ $\langle u,l,\widehat{l},\widehat{u}\rangle =\langle D\rangle$,

$\left(O_{11}\right)$ $\langle \widehat{l},\widehat{u},l,u,u,l,l,u\rangle =\langle A\rangle \odot \langle B\rangle \odot \langle A\rangle$,

$\left(O_{12}\right)$ $\langle \widehat{l},\widehat{u},u,l,l,u\rangle =\langle B\rangle \odot \langle A\rangle$,

$\left(O_{13}\right)$ $\langle \widehat{l},\widehat{u},l,u,u,l\rangle =\langle A\rangle \odot \langle B\rangle$,

$\left(O_{14}\right)$ $\langle \widehat{l},\widehat{u},u,l,l,u,u,l\rangle =\langle B\rangle \odot \langle A\rangle \odot \langle B\rangle$,

$\left(O_{15}\right)$ $\langle l,u,u,l,l,u,\widehat{l},\widehat{u}\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle C\rangle$,

$\left(O_{16}\right)$ $\langle u,l,l,u,\widehat{l},\widehat{u}\rangle =\langle D\rangle \odot \langle C\rangle$,

$\left(O_{17}\right)$ $\langle l,u,u,l,\widehat{l},\widehat{u}\rangle =\langle C\rangle \odot \langle D\rangle$,

$\left(O_{18}\right)$ $\langle u,l,l,u,u,l,\widehat{l},\widehat{u}\rangle =\langle D\rangle \odot \langle C\rangle \odot \langle D\rangle$,

$\left(O_{19}\right)$ $\langle l,u,\widehat{l},\widehat{u},l,u\rangle =\langle C\rangle \odot \langle A\rangle$,

$\left(O_{20}\right)$ $\langle l,u,u,l,l,u,\widehat{l},\widehat{u},l,u\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle C\rangle \odot \langle A\rangle$,

$\left(O_{21}\right)$ $\langle u,l,l,u,\widehat{l},\widehat{u},l,u\rangle =\langle D\rangle \odot \langle C\rangle \odot \langle A\rangle$,

$\left(O_{22}\right)$ $\langle l,u,u,l,\widehat{l},\widehat{u},l,u\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle A\rangle$,

$\left(O_{23}\right)$ $\langle u,l,l,u,u,l,\widehat{l},\widehat{u},l,u\rangle =\langle D\rangle \odot \langle C\rangle \odot \langle D\rangle \odot \langle A\rangle$,

$\left(O_{24}\right)$ $\langle u,l,\widehat{l},\widehat{u},l,u\rangle =\langle D\rangle \odot \langle A\rangle$,

$\left(O_{25}\right)$ $\langle l,u,\widehat{l},\widehat{u},l,u,u,l,l,u\rangle =\langle C\rangle \odot \langle A\rangle \odot \langle B\rangle \odot \langle A\rangle$,

$\left(O_{26}\right)$ $\langle l,u,u,l,l,u,\widehat{l},\widehat{u},l,u,u,l,l,u\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle C\rangle \odot \langle A\rangle \odot \langle B\rangle \odot \langle A\rangle$,

$\left(O_{27}\right)$ $\langle u,l,l,u,\widehat{l},\widehat{u},l,u,u,l,l,u\rangle =\langle D\rangle \odot \langle C\rangle \odot \langle A\rangle \odot \langle B\rangle \odot \langle A\rangle$,

$\left(O_{28}\right)$ $\langle l,u,u,l,\widehat{l},\widehat{u},l,u,u,l,l,u\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle A\rangle \odot \langle B\rangle \odot \langle A\rangle$,

$\left(O_{29}\right)$ $\langle u,l,l,u,u,l,\widehat{l},\widehat{u},l,u,u,l,l,u\rangle =\langle D\rangle \odot \langle C\rangle \odot \langle D\rangle \odot \langle A\rangle \odot \langle B\rangle \odot \langle A\rangle$,

$\left(O_{30}\right)$ $\langle u,l,\widehat{l},\widehat{u},l,u,u,l,l,u\rangle =\langle D\rangle \odot \langle A\rangle \odot \langle B\rangle \odot \langle A\rangle$,

$\left(O_{31}\right)$ $\langle l,u,\widehat{l},\widehat{u},u,l,l,u\rangle =\langle C\rangle \odot \langle B\rangle \odot \langle A\rangle$,

$\left(O_{32}\right)$ $\langle l,u,u,l,l,u,\widehat{l},\widehat{u},u,l,l,u\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle C\rangle \odot \langle B\rangle \odot \langle A\rangle$,

$\left(O_{33}\right)$ $\langle u,l,l,u,\widehat{l},\widehat{u},u,l,l,u\rangle =\langle D\rangle \odot \langle C\rangle \odot \langle B\rangle \odot \langle A\rangle$,

$\left(O_{34}\right)$ $\langle l,u,u,l,\widehat{l},\widehat{u},u,l,l,u\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle B\rangle \odot \langle A\rangle$,

$\left(O_{35}\right)$ $\langle u,l,l,u,u,l,\widehat{l},\widehat{u},u,l,l,u\rangle =\langle D\rangle \odot \langle C\rangle \odot \langle D\rangle \odot \langle B\rangle \odot \langle A\rangle$,

$\left(O_{36}\right)$ $\langle u,l,\widehat{l},\widehat{u},u,l,l,u\rangle =\langle D\rangle \odot \langle B\rangle \odot \langle A\rangle$,

$\left(O_{37}\right)$ $\langle l,u,\widehat{l},\widehat{u},l,u,u,l\rangle =\langle C\rangle \odot \langle A\rangle \odot \langle B\rangle$,

$\left(O_{38}\right)$ $\langle l,u,u,l,l,u,\widehat{l},\widehat{u},l,u,u,l\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle C\rangle \odot \langle A\rangle \odot \langle B\rangle$,

$\left(O_{39}\right)$ $\langle u,l,l,u,\widehat{l},\widehat{u},l,u,u,l\rangle =\langle D\rangle \odot \langle C\rangle \odot \langle A\rangle \odot \langle B\rangle$,

$\left(O_{40}\right)$ $\langle l,u,u,l,\widehat{l},\widehat{u},l,u,u,l\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle A\rangle \odot \langle B\rangle$,

$\left(O_{41}\right)$ $\langle u,l,l,u,u,l,\widehat{l},\widehat{u},l,u,u,l\rangle =\langle D\rangle \odot \langle C\rangle \odot \langle D\rangle \odot \langle A\rangle \odot \langle B\rangle$,

$\left(O_{42}\right)$ $\langle u,l,\widehat{l},\widehat{u},l,u,u,l\rangle =\langle D\rangle \odot \langle A\rangle \odot \langle B\rangle$,

$\left(O_{43}\right)$ $\langle l,u,\widehat{l},\widehat{u},u,l,l,u,u,l\rangle =\langle C\rangle \odot \langle B\rangle \odot \langle A\rangle \odot \langle B\rangle$,

$\left(O_{44}\right)$ $\langle l,u,u,l,l,u,\widehat{l},\widehat{u},u,l,l,u,u,l\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle C\rangle \odot \langle B\rangle \odot \langle A\rangle \odot \langle B\rangle$,

$\left(O_{45}\right)$ $\langle u,l,l,u,\widehat{l},\widehat{u},u,l,l,u,u,l\rangle =\langle D\rangle \odot \langle C\rangle \odot \langle B\rangle \odot \langle A\rangle \odot \langle B\rangle$,

$\left(O_{46}\right)$ $\langle l,u,u,l,\widehat{l},\widehat{u},u,l,l,u,u,l\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle B\rangle \odot \langle A\rangle \odot \langle B\rangle$,

$\left(O_{47}\right)$ $\langle u,l,l,u,u,l,\widehat{l},\widehat{u},u,l,l,u,u,l\rangle =\langle D\rangle \odot \langle C\rangle \odot \langle D\rangle \odot \langle B\rangle \odot \langle A\rangle \odot \langle B\rangle$,

$\left(O_{48}\right)$ $\langle u,l,\widehat{l},\widehat{u},u,l,l,u,u,l\rangle =\langle D\rangle \odot \langle B\rangle \odot \langle A\rangle \odot \langle B\rangle$,

$\left(O_{49}\right)$ $\langle l,u,\widehat{l},\widehat{u},u,l\rangle =\langle C\rangle \odot \langle B\rangle$,

$\left(O_{50}\right)$ $\langle l,u,u,l,l,u,\widehat{l},\widehat{u},u,l\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle C\rangle \odot \langle B\rangle$,

$\left(O_{51}\right)$ $\langle u,l,l,u,\widehat{l},\widehat{u},u,l\rangle =\langle D\rangle \odot \langle C\rangle \odot \langle B\rangle$,

$\left(O_{52}\right)$ $\langle l,u,u,l,\widehat{l},\widehat{u},u,l\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle B\rangle$,

$\left(O_{53}\right)$ $\langle u,l,l,u,u,l,\widehat{l},\widehat{u},u,l\rangle =\langle D\rangle \odot \langle C\rangle \odot \langle D\rangle \odot \langle B\rangle$,

$\left(O_{54}\right)$ $\langle u,l,\widehat{l},\widehat{u},u,l\rangle =\langle D\rangle \odot \langle B\rangle$.

(iii)

Specified by ${\mathcal{F}}^{(s,s+2)}\circ {\tau }^n$, for an even natural number s:

$\left(O_{55}\right)$ $\langle \widehat{l},l,u,\widehat{u},u,l,l,u\rangle =\langle E\rangle \odot \langle B\rangle \odot \langle A\rangle$,

$\left(O_{56}\right)$ $\langle \widehat{l},l,u,\widehat{u},u,l\rangle =\langle E\rangle \odot \langle B\rangle$,

$\left(O_{57}\right)$ $\langle l,u,u,l,\widehat{l},l,u,\widehat{u}\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle E\rangle$,

$\left(O_{58}\right)$ $\langle u,l,\widehat{l},l,u,\widehat{u}\rangle =\langle D\rangle \odot \langle E\rangle$,

$\left(O_{59}\right)$ $\langle l,u,u,l,\widehat{l},l,u,\widehat{u},u,l,l,u\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle E\rangle \odot \langle B\rangle \odot \langle A\rangle$,

$\left(O_{60}\right)$ $\langle u,l,\widehat{l},l,u,\widehat{u},u,l,l,u\rangle =\langle D\rangle \odot \langle E\rangle \odot \langle B\rangle \odot \langle A\rangle$,

$\left(O_{61}\right)$ $\langle l,u,u,l,\widehat{l},l,u,\widehat{u},u,l\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle E\rangle \odot \langle B\rangle$,

$\left(O_{62}\right)$ $\langle u,l,\widehat{l},l,u,\widehat{u},u,l\rangle =\langle D\rangle \odot \langle E\rangle \odot \langle B\rangle$,

$\left(O_{63}\right)$ $\langle \widehat{l},u,l,\widehat{u},l,u\rangle =\langle F\rangle \odot \langle A\rangle$,

$\left(O_{64}\right)$ $\langle \widehat{l},u,l,\widehat{u},l,u,u,l,l,u\rangle =\langle F\rangle \odot \langle A\rangle \odot \langle B\rangle \odot \langle A\rangle$,

$\left(O_{65}\right)$ $\langle \widehat{l},u,l,\widehat{u},l,u,u,l\rangle =\langle F\rangle \odot \langle A\rangle \odot \langle B\rangle$,

$\left(O_{66}\right)$ $\langle l,u,\widehat{l},u,l,\widehat{u}\rangle =\langle C\rangle \odot \langle F\rangle$,

$\left(O_{67}\right)$ $\langle l,u,u,l,l,u,\widehat{l},u,l,\widehat{u}\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle C\rangle \odot \langle F\rangle$,

$\left(O_{68}\right)$ $\langle u,l,l,u,\widehat{l},u,l,\widehat{u}\rangle =\langle D\rangle \odot \langle C\rangle \odot \langle F\rangle$,

$\left(O_{69}\right)$ $\langle l,u,\widehat{l},u,l,\widehat{u},l,u\rangle =\langle C\rangle \odot \langle F\rangle \odot \langle A\rangle$,

$\left(O_{70}\right)$ $\langle l,u,u,l,l,u,\widehat{l},u,l,\widehat{u},l,u\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle C\rangle \odot \langle F\rangle \odot \langle A\rangle$,

$\left(O_{71}\right)$ $\langle u,l,l,u,\widehat{l},u,l,\widehat{u},l,u\rangle =\langle D\rangle \odot \langle C\rangle \odot \langle F\rangle \odot \langle A\rangle$,

$\left(O_{72}\right)$ $\langle l,u,\widehat{l},u,l,\widehat{u},l,u,u,l,l,u\rangle =\langle C\rangle \odot \langle F\rangle \odot \langle A\rangle \odot \langle B\rangle \odot \langle A\rangle$,

$\left(O_{73}\right)$ $\langle l,u,u,l,l,u,\widehat{l},u,l,\widehat{u},l,u,u,l,l,u\rangle =$

$\langle C\rangle \odot \langle D\rangle \odot \langle C\rangle \odot \langle F\rangle \odot \langle A\rangle \odot \langle B\rangle \odot \langle A\rangle$,

$\left(O_{74}\right)$ $\langle u,l,l,u,\widehat{l},u,l,\widehat{u},l,u,u,l,l,u\rangle =\langle D\rangle \odot \langle C\rangle \odot \langle F\rangle \odot \langle A\rangle \odot \langle B\rangle \odot \langle A\rangle$,

$\left(O_{75}\right)$ $\langle l,u,\widehat{l},u,l,\widehat{u},l,u,u,l\rangle =\langle C\rangle \odot \langle F\rangle \odot \langle A\rangle \odot \langle B\rangle$,

$\left(O_{76}\right)$ $\langle l,u,u,l,l,u,\widehat{l},u,l,\widehat{u},l,u,u,l\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle C\rangle \odot \langle F\rangle \odot \langle A\rangle \odot \langle B\rangle$,

$\left(O_{77}\right)$ $\langle u,l,l,u,\widehat{l},u,l,\widehat{u},l,u,u,l\rangle =\langle D\rangle \odot \langle C\rangle \odot \langle F\rangle \odot \langle A\rangle \odot \langle B\rangle$.

(iv)

Specified by ${\mathcal{F}}^{(s,s+4)}\circ {\tau }^n$, for an even natural number s:

$\left(O_{78}\right)$ $\langle \widehat{l},l,u,u,l,\widehat{u},l,u\rangle =\langle E\rangle \odot \langle F\rangle \odot \langle A\rangle$,

$\left(O_{79}\right)$ $\langle l,u,u,l,\widehat{l},l,u,u,l,\widehat{u}\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle E\rangle \odot \langle F\rangle$,

$\left(O_{80}\right)$ $\langle u,l,\widehat{l},l,u,u,l,\widehat{u}\rangle =\langle D\rangle \odot \langle E\rangle \odot \langle F\rangle$,

$\left(O_{81}\right)$ $\langle l,u,u,l,\widehat{l},l,u,u,l,\widehat{u},l,u\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle E\rangle \odot \langle F\rangle \odot \langle A\rangle$,

$\left(O_{82}\right)$ $\langle u,l,\widehat{l},l,u,u,l,\widehat{u},l,u\rangle =\langle D\rangle \odot \langle E\rangle \odot \langle F\rangle \odot \langle A\rangle$,

$\left(O_{83}\right)$ $\langle \widehat{l},u,l,l,u,\widehat{u},u,l,l,u\rangle =\langle F\rangle \odot \langle E\rangle \odot \langle B\rangle \odot \langle A\rangle$,

$\left(O_{84}\right)$ $\langle \widehat{l},u,l,l,u,\widehat{u},u,l\rangle =\langle F\rangle \odot \langle E\rangle \odot \langle B\rangle$,

$\left(O_{85}\right)$ $\langle l,u,\widehat{l},u,l,l,u,\widehat{u}\rangle =\langle C\rangle \odot \langle F\rangle \odot \langle E\rangle$,

$\left(O_{86}\right)$ $\langle l,u,\widehat{l},u,l,l,u,\widehat{u},u,l,l,u\rangle =\langle C\rangle \odot \langle F\rangle \odot \langle E\rangle \odot \langle B\rangle \odot \langle A\rangle$,

$\left(O_{87}\right)$ $\langle l,u,\widehat{l},u,l,l,u,\widehat{u},u,l\rangle =\langle C\rangle \odot \langle F\rangle \odot \langle E\rangle \odot \langle B\rangle$,

(v)

Specified by ${\mathcal{F}}^{(s,s+6)}\circ {\tau }^n$, for an even natural number s:

$\left(O_{88}\right)$ $\langle \widehat{l},u,l,l,u,u,l,\widehat{u},l,u\rangle =\langle F\rangle \odot \langle E\rangle \odot \langle F\rangle \odot \langle A\rangle$,

$\left(O_{89}\right)$ $\langle l,u,\widehat{l},u,l,l,u,u,l,\widehat{u}\rangle =\langle C\rangle \odot \langle F\rangle \odot \langle E\rangle \odot \langle F\rangle$,

$\left(O_{90}\right)$ $\langle l,u,\widehat{l},u,l,l,u,u,l,\widehat{u},l,u\rangle =\langle C\rangle \odot \langle F\rangle \odot \langle E\rangle \odot \langle F\rangle \odot \langle A\rangle$,

(vi)

Specified by ${\mathcal{F}}^{(s,s)}\circ {\tau }^n$ for an odd natural number q:

$\left(O_{91}\right)$ $\langle u,\widehat{l},\widehat{u},l\rangle =\langle G\rangle$,

$\left(O_{92}\right)$ $\langle u,\widehat{l},\widehat{u},l,l,u,\rangle =\langle G\rangle \odot \langle A\rangle$,

$\left(O_{93}\right)$ $\langle u,\widehat{l},\widehat{u},l,l,u,u,l\rangle =\langle G\rangle \odot \langle A\rangle \odot \langle B\rangle$,

$\left(O_{94}\right)$ $\langle l,u,u,\widehat{l},\widehat{u},l\rangle =\langle C\rangle \odot \langle G\rangle$,

$\left(O_{95}\right)$ $\langle u,l,l,u,u,\widehat{l},\widehat{u},l\rangle =\langle D\rangle \odot \langle C\rangle \odot \langle G\rangle$,

$\left(O_{96}\right)$ $\langle l,u,u,\widehat{l},\widehat{u},l,l,u\rangle =\langle C\rangle \odot \langle G\rangle \odot \langle A\rangle$,

$\left(O_{97}\right)$ $\langle u,l,l,u,u,\widehat{l},\widehat{u},l,l,u\rangle =\langle D\rangle \odot \langle C\rangle \odot \langle G\rangle \odot \langle A\rangle$,

$\left(O_{98}\right)$ $\langle l,u,u,\widehat{l},\widehat{u},l,l,u,u,l\rangle =\langle C\rangle \odot \langle G\rangle \odot \langle A\rangle \odot \langle B\rangle$,

$\left(O_{99}\right)$ $\langle u,l,l,u,u,\widehat{l},\widehat{u},l,l,u,u,l\rangle =\langle D\rangle \odot \langle C\rangle \odot \langle G\rangle \odot \langle A\rangle \odot \langle B\rangle$.

Proof. 

For a given function $\Theta :\Sigma \times X\to {\mathcal{P}}^2\left(Y\right)$ and $\alpha \in \Sigma$, the composition $\Theta \circ \alpha$ is a function from X to ${\mathcal{P}}^2\left(Y\right)$. So, we can consider the cluster functions in the sense of Definition 1, of type $\langle f_{2k},f_{2k-1},\dots ,f_1,\Theta \circ \alpha \rangle$. Thus, any cluster operator $\langle f_{2k},f_{2k-1},\dots ,f_1\rangle$ designates the function

${\Theta }^{\langle f_{2k},\dots ,f_1\rangle }:\Sigma \times X\to {\mathcal{P}}^2\left(Y\right)$ defined by

${\Theta }^{\langle f_{2k},f_{2k-1},\dots ,f_1\rangle }(\alpha ,x)=\langle f_{2k},f_{2k-1},\dots ,f_1,\Theta \circ \alpha \rangle \left(x\right)$ for all $(\alpha ,x)\in \Sigma \times X$.

In the first step, we will prove that for any convergence operator

$\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1\rangle$, the following equality holds true:

$\left(R\right)$$\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1,{\Theta }^{\langle f_{2k},\dots ,f_1\rangle }\rangle$=

$\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1,f_{2k},\dots ,f_1,\Theta \rangle$.

Indeed, by definition, for any $x_0\in X$, we have

$(\ast )$$\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1,{\Theta }^{\langle f_{2k},\dots ,f_1\rangle }\rangle \left(x_0\right)$=$h_{2n}\circ \dots \circ h_{q+1}\circ \widehat{l}\circ h_q\circ \dots \circ h_{s+1}\circ \widehat{u}\circ h_s\circ \dots \circ h_1\circ {\Theta }^{\langle f_{2k},\dots ,f_1\rangle }\circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x_0\right)$.

According to Lemma 13 we have ${\Theta }^{\langle f_{2k},\dots ,f_1\rangle }\circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x_0\right)=$

{…$\{{\Theta }^{\langle f_{2k},\dots ,f_1\rangle }(\alpha ,{\mathcal{D}}^{(n,0)})$:

${\mathcal{D}}^{(n,0)}\in {\mathcal{D}}^{(n,1)}\}$:…}:${\mathcal{D}}^{(n,s-1)}\in {\mathcal{D}}^{(n,s)}\}$:$\alpha \in K\}$:

${\mathcal{D}}^{(n,s)}\in {\mathcal{D}}^{(n,s+1)}\}$: …}: ${\mathcal{D}}^{(n,q-1)}\in {\mathcal{D}}^{(n,q)}\}$:$K\in \mathcal{F}\}$:

${\mathcal{D}}^{(n,q)}\in {\mathcal{D}}^{(n,q+1)}\}$:…}:${\mathcal{D}}^{(n,2n-1)}\in {\mathcal{D}}^{(n,2n)}\}=$

{…$\{f_{2k}\circ \dots \circ f_1\circ \Theta \circ \alpha \circ {\tau }^k\left({\mathcal{D}}^{(n,0)}\right)$:

${\mathcal{D}}^{(n,0)}\in {\mathcal{D}}^{(n,1)}\}$:…}:${\mathcal{D}}^{(n,s-1)}\in {\mathcal{D}}^{(n,s)}\}$:$\alpha \in K\}$:

${\mathcal{D}}^{(n,s)}\in {\mathcal{D}}^{(n,s+1)}\}$:…}: ${\mathcal{D}}^{(n,q-1)}\in {\mathcal{D}}^{(n,q)}\}$:$K\in \mathcal{F}\}$:

${\mathcal{D}}^{(n,q)}\in {\mathcal{D}}^{(n,q+1)}\}$:…}:${\mathcal{D}}^{(n,2n-1)}\in {\mathcal{D}}^{(n,2n)}\}=$

$f_{2k}\circ \dots \circ f_1\left(\right\{\dots \{\Theta \circ \alpha \circ {\tau }^k\left({\mathcal{D}}^{(n,0)}\right)$:

${\mathcal{D}}^{(n,0)}\in {\mathcal{D}}^{(n,1)}\}$:…}:${\mathcal{D}}^{(n,s-1)}\in {\mathcal{D}}^{(n,s)}\}$:$\alpha \in K\}$:

${\mathcal{D}}^{(n,s)}\in {\mathcal{D}}^{(n,s+1)}\}$:…}: ${\mathcal{D}}^{(n,q-1)}\in {\mathcal{D}}^{(n,q)}\}$:$K\in \mathcal{F}\}$:

${\mathcal{D}}^{(n,q)}\in {\mathcal{D}}^{(n,q+1)}\}$:…}:${\mathcal{D}}^{(n,2n-1)}\in {\mathcal{D}}^{(n,2n)}\left\}\right)=$

$f_{2k}\circ \dots \circ f_1\left(\right\{\dots \{\Theta (\alpha ,{\mathcal{D}}^{(n+k,0)})$:${\mathcal{D}}^{(n+k,0)}\in {\mathcal{D}}^{(n+k,1)}\}$:…}:

${\mathcal{D}}^{(n+k,2k-1)}\in {\mathcal{D}}^{(n+k,2k)}\}$:

${\mathcal{D}}^{(n,0)}\in {\mathcal{D}}^{(n,1)}\}$:…}:${\mathcal{D}}^{(n,s-1)}\in {\mathcal{D}}^{(n,s)}\}$:$\alpha \in K\}$:

${\mathcal{D}}^{(n,s)}\in {\mathcal{D}}^{(n,s+1)}\}$:…}: ${\mathcal{D}}^{(n,q-1)}\in {\mathcal{D}}^{(n,q)}\}$:$K\in \mathcal{F}\}$:

${\mathcal{D}}^{(n,q)}\in {\mathcal{D}}^{(n,q+1)}\}$:…}:${\mathcal{D}}^{(n,2n-1)}\in {\mathcal{D}}^{(n,2n)}\left\}\right)=$

$f_{2k}\circ \dots \circ f_1\left(\right\{\dots \{\Theta (\alpha ,{\mathcal{D}}^{(n+k,0)})$:${\mathcal{D}}^{(n+k,0)}\in {\mathcal{D}}^{(n+k,1)}\}$:…}:

${\mathcal{D}}^{(n+k,2k-1)}\in {\mathcal{D}}^{(n+k,2k)}\}$:

${\mathcal{D}}^{(n+k,2k)}\in {\mathcal{D}}^{(n+k,2k+1)}\}$:…}:

${\mathcal{D}}^{(n+k,2k+s-1)}\in {\mathcal{D}}^{(n+k,2k+s)}\}$:$\alpha \in K\}$:

${\mathcal{D}}^{(n+k,2k+s)}\in {\mathcal{D}}^{(n+k,2k+s+1)}\}$:…}:

${\mathcal{D}}^{(n+k,2k+q-1)}\in {\mathcal{D}}^{(n+k,2k+q)}\}$:$K\in \mathcal{F}\}$:

${\mathcal{D}}^{(n+k,2k+q)}\in {\mathcal{D}}^{(n+k,2k+q+1)}\}$:…}:

${\mathcal{D}}^{(n+k,2k+2n-1)}\in {\mathcal{D}}^{(n+k,2k+2n)}\left\}\right)$, where in the last two equations, we have used the property noted in Remark 11 and the fact that ${\tau }^k\left({\mathcal{D}}^{(n,0)}\right)={\mathcal{D}}^{(n+k,2k)}$.

So, ${\Theta }^{\langle f_{2k},\dots ,f_1\rangle }\circ {\mathcal{F}}^{(s,q)}\circ {\tau }^n\left(x_0\right)=f_{2k}\circ \dots \circ f_1\circ \Theta \circ {\mathcal{F}}^{(s+2k,q+2k)}\circ {\tau }^{n+k}\left(x_0\right)$ and consequently, the value described in $(\ast )$ is equal to

$h_{2n}\circ \dots \circ h_{q+1}\circ {\widehat{h}}_2\circ h_q\circ \dots \circ h_{s+1}\circ {\widehat{h}}_1\circ h_s\circ \dots \circ h_1\circ f_{2k}\circ \dots \circ f_1\circ \Theta \circ {\mathcal{F}}^{(s+2k,q+2k)}\circ {\tau }^{n+k}\left(x_0\right)$ which proves the equality $\left(R\right)$.

According to Theorem 1, one can use at most the following six non-neutral cluster operators $\langle f_{2k},\dots ,f_1\rangle$ in the formula ${\Theta }^{\langle f_{2k},\dots ,f_1\rangle }$:

$\langle l,u\rangle$, $\langle l,u,u,l,l,u\rangle$, $\langle u,l,l,u\rangle$, $\langle l,u,u,l\rangle$, $\langle u,l,l,u,u,l\rangle$ and $\langle u,l\rangle$.

So, as a consequence of $\left(R\right)$, for any convergence operator

$\Delta =\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1\rangle$, where $s\ge 2$,

there exist at most the following six convergence operators of the type

$\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1,f_{2k},\dots ,f_1\rangle$, namely:

$\left(r_1\right)$$R_{\langle l,u\rangle }(\Delta )=\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1,l,u\rangle$;

$\left(r_2\right)$$R_{\langle l,u,u,l,l,u\rangle }(\Delta )=\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1,l,u,u,l,l,u\rangle$;

$\left(r_3\right)$$R_{\langle u,l,l,u\rangle }(\Delta )=\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1,u,l,l,u,\rangle$;

$\left(r_4\right)$$R_{\langle l,u,u,l\rangle }(\Delta )=\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1,l,u,u,l\rangle$;

$\left(r_5\right)$$R_{\langle u,l,l,u,u,l\rangle }(\Delta )=\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1,u,l,l,u,u,l\rangle$;

$\left(r_6\right)$$R_{\langle u,l\rangle }(\Delta )=\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1,u,l\rangle$.

Now, let us observe that any convergence function

$\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1,\Theta \rangle$

is a function from X to ${\mathcal{P}}^2\left(Y\right)$. So, any convergence function of the type

$\langle f_{2k},\dots ,f_1,h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1,\Theta \rangle$

• is a cluster function in the sense of Definition 1, and consequently, according to Theorem 1, for any convergence operator

$\langle h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1\rangle$, where $k\ge 2$, we can obtain at most the following convergence operators of the type

$\langle f_{2k},\dots ,f_1,h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1\rangle$:

$\left(l_1\right)$$L_{\langle l,u\rangle }(\Delta )=\langle l,u,h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1\rangle$;

$\left(l_2\right)$$L_{\langle l,u,u,l,l,u\rangle }(\Delta )=\langle l,u,u,l,l,u,h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1\rangle$;

$\left(l_3\right)$$L_{\langle u,l,l,u\rangle }(\Delta )=\langle u,l,l,u,h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1\rangle$;

$\left(l_4\right)$$L_{\langle l,u,u,l\rangle }(\Delta )=\langle l,u,u,l,h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1\rangle$;

$\left(l_5\right)$$L_{\langle u,l,l,u,u,l\rangle }(\Delta )=\langle u,l,l,u,u,l,h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1\rangle$;

$\left(l_6\right)$$L_{\langle u,l\rangle }(\Delta )=\langle u,l,h_{2n},\dots ,h_{q+1},\widehat{l},h_q,\dots ,h_{s+1},\widehat{u},h_s,\dots ,h_1\rangle$.

Now, considering the convergence operators of the type $\langle \widehat{l},f_{2n},\dots ,f_1,\widehat{u}\rangle$, for a given function $\Theta :\Sigma \times X\to {\mathcal{P}}^2\left(Y\right)$ and $K\in \mathcal{F}$, we define the function ${\Psi }_{\langle u\rangle }^K:X\to {\mathcal{P}}^2\left(Y\right)$ by

${\Psi }_{\langle u\rangle }^K\left(x\right)=u\circ \Theta \circ K^{\left(0\right)}\left(x\right)$, for all $x\in X$.

Then, for each point $x_0\in X$ we have

$\langle \widehat{l},f_{2n},\dots ,f_1,\widehat{u},\Theta \rangle \left(x_0\right)=$

$\widehat{l}\circ f_{2n}\circ \dots \circ f_1\circ \widehat{u}\circ \Theta \circ {\mathcal{F}}^{(0,2n)}\circ {\alpha }^n\left(x_0\right)=$

$\widehat{l}\circ f_{2n}\circ \dots \circ f_1\circ \widehat{u}\circ \Theta \left(\left\{K^{\left(0\right)}\circ {\alpha }^n\left(x_0\right):K\in \mathcal{F}\right\}\right)=$

$\widehat{l}\left(\left\{f_{2n}\circ \dots \circ f_1\circ \widehat{u}\circ \Theta \circ K^{\left(0\right)}\circ {\alpha }^n\left(x_0\right):K\in \mathcal{F}\right\}\right)=$

$\widehat{l}\left(\left\{f_{2n}\circ \dots \circ f_1\circ {\Psi }_{\langle u\rangle }^K\circ {\alpha }^n\left(x_0\right):K\in \mathcal{F}\right\}\right)=$

$\widehat{l}\left(\left\{\langle f_{2n},\dots ,f_1,{\Psi }_{\langle u\rangle }^K\rangle \left(x_0\right):K\in \mathcal{F}\right\}\right)$.

But, because of Theorem 1, we know that $\langle f_{2n},\dots ,f_1\rangle$ must be equal to $\langle l,u\rangle$, $\langle u,l\rangle$, $\langle l,u,u,l\rangle$, $\langle u,l,l,u\rangle$, $\langle l,u,u,l,l,u\rangle$, $\langle u,l,l,u,u,l\rangle$ or $\langle \dots \rangle$.

So, all possible non-neutral operators of the type $\langle \widehat{l},f_{2k},\dots ,f_1,\widehat{u}\rangle$ are listed in part (i) of the theorem as $\left(O_1\right)$, $\left(O_2\right)$, $\left(O_3\right)$, $\left(O_4\right)$, $\left(O_5\right)$ and $\left(O_6\right)$, respectively.

For this reason, we can obtain the following seven types of operators of the form

$\langle h_{2n},\dots ,h_{s+2k+1},\widehat{l},f_{2k},\dots ,f_1,\widehat{u},h_s,\dots ,h_1\rangle$:

 (C1) $\langle h_{2n},\dots ,h_{s+3},\widehat{l},l,u,\widehat{u},h_s,\dots ,h_1\rangle$;

 (C2) $\langle h_{2n},\dots ,h_{s+3},\widehat{l},u,l,\widehat{u},h_s,\dots ,h_1\rangle$;

 (C3) $\langle h_{2n},\dots ,h_{s+5},\widehat{l},l,u,u,l,\widehat{u},h_s,\dots ,h_1\rangle$,

 (C4) $\langle h_{2n},\dots ,h_{s+5},\widehat{l},u,l,l,u,\widehat{u},h_s,\dots ,h_1\rangle$;

 (C5) $\langle h_{2n},\dots ,h_{s+7},\widehat{l},l,u,u,l,l,u,\widehat{u},h_s,\dots ,h_1\rangle$;

 (C6) $\langle h_{2n},\dots ,h_{s+7},\widehat{l},u,l,l,u,u,l\widehat{u},h_s,\dots ,h_1\rangle$;

 (C7) $\langle h_{2n},\dots ,h_{s+3},\widehat{l},\widehat{u},h_s,\dots ,h_1\rangle$.

The alternating application of the operations $\left(r_1\right),\dots ,\left(r_6\right)$ and $\left(l_1\right),\dots ,\left(l_6\right)$ on the operator $\langle \widehat{l},\widehat{u}\rangle$, allows for the determination of all convergence operators of the type (C7), i.e., specified by ${\mathcal{F}}^{(s,s)}\circ {\pi }^n$ for an even natural number s, listed in part (ii) of the theorem.

Below, in the same way, using the operators listed in part (i) instead of $\langle \widehat{l},\widehat{u}\rangle$, we will determine all operators of the type (C1), …,(C6), i.e., specified by ${\mathcal{F}}^{(s,s+2)}\circ {\tau }^n$, ${\mathcal{F}}^{(s,s+4)}\circ {\tau }^n$ or ${\mathcal{F}}^{(s,s+6)}\circ {\tau }^n$, for an even natural number s. We will consider all possible cases. Next, by applying Lemma 7, and the equalities (d) stated in the proof of Theorem 1 without reference to them and using Lemma 17, we will show that some of the descriptions designate the same operator. As a result, we will indicate all possible operators of this type mentioned in parts (iii), (iv), and (v) of the theorem.

In the case (C1).

• Type $\langle \widehat{l},l,u,\widehat{u},h_s,\dots ,h_1\rangle =R_{\langle h_s,\dots ,h_1\rangle }\left(\langle \widehat{l},l,u,\widehat{u}\rangle \right)=R_{\langle h_s,\dots ,h_1\rangle }\left(O_1\right)$:

  -

  $R_{\langle l,u\rangle }\left(O_1\right)=\langle \widehat{l},l,u,\widehat{u},l,u\rangle =\langle \widehat{l},l,\widehat{u},u,l,u\rangle =\langle \widehat{l},l,\widehat{u},u\rangle$

  $=\langle \widehat{l},l,u,\widehat{u}\rangle =\langle E\rangle$, i.e., $\left(O_1\right)$;

  -

  $R_{\langle l,u,u,l,l,u\rangle }(\left(O_1\right)=\langle \widehat{l},l,u,\widehat{u},l,u,u,l,l,u\rangle =\langle \widehat{l},l,\widehat{u},u,l,u,u,l,l,u\rangle$

  $=\langle \widehat{l},l,\widehat{u},u,u,l,l,u\rangle =\langle \widehat{l},l,u,\widehat{u},u,l,l,u\rangle$

  $=R_{\langle u,l,l,u\rangle }\left(O_1\right)=\langle E\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{55}\right)$;

  -

  $R_{\langle l,u,u,l\rangle }\left(O_1\right)=\langle \widehat{l},l,u,\widehat{u},l,u,u,l\rangle$ = $\langle \widehat{l},l,\widehat{u},u,l,u,u,l\rangle$ = $\langle \widehat{l},l,\widehat{u},u,u,l\rangle$

  $=\langle \widehat{l},l,u,\widehat{u},u,l\rangle$$=R_{\langle u,l\rangle }\left(O_1\right)=\langle E\rangle \odot \langle B\rangle$, i.e., $\left(O_{56}\right)$;

  -

  $R_{\langle u,l,l,u,u,l\rangle }\left(O_1\right)=\langle \widehat{l},l,u,\widehat{u},u,l,l,u,u,l\rangle$ = $\langle \widehat{l},l,u,\widehat{u},u,l\rangle$

  $=R_{\langle u,l\rangle }\left(O_1\right)$, i.e., $\left(O_{56}\right)$.

• Type $\langle h_{2n},\dots ,h_3,\widehat{l},l,u,\widehat{u}\rangle =L_{\langle h_{2n},\dots ,h_3\rangle }\left(\langle \widehat{l},l,u,\widehat{u}\rangle \right)=L_{\langle h_{2n},\dots ,h_3\rangle }\left(O_1\right)$:

  -

  $L_{\langle l,u\rangle }\left(O_1\right)=\langle l,u,\widehat{l},l,u,\widehat{u}\rangle$ = $\langle l,u,l,\widehat{l},u,\widehat{u}\rangle$ = $\langle l,\widehat{l},u,\widehat{u}\rangle$

  $=\langle \widehat{l},l,u,\widehat{u}\rangle$ =$\langle E\rangle$, i.e., $\left(O_1\right)$;

  -

  $L_{\langle l,u,u,l,l,u\rangle }\left(O_1\right)=\langle l,u,u,l,l,u,\widehat{l},l,u,\widehat{u}\rangle$ = $\langle l,u,u,l,l,u,l,\widehat{l},u,\widehat{u}\rangle$

  $=\langle l,u,u,l,l,\widehat{l},u,\widehat{u}\rangle$$=\langle l,u,u,l,\widehat{l},l,u,\widehat{u}\rangle$

  $=L_{\langle l,u,u,l\rangle }\left(O_1\right)=\langle C\rangle \odot \langle D\rangle \odot \langle E\rangle$, i.e., $\left(O_{57}\right)$;

  -

  $L_{\langle u,l,l,u\rangle }\left(O_1\right)=\langle u,l,l,u,\widehat{l},l,u,\widehat{u}\rangle$ = $\langle u,l,l,u,l,\widehat{l},u,\widehat{u}\rangle$ = $\langle u,l,l,\widehat{l},u,\widehat{u}\rangle$

  $=\langle u,l,\widehat{l},l,u,\widehat{u}\rangle =L_{\langle u,l\rangle }\left(O_1\right)=\langle D\rangle \odot \langle E\rangle$, i.e., $\left(O_{58}\right)$;

  -

  $L_{\langle u,l,l,u,u,l\rangle }\left(O_1\right)=\langle u,l,l,u,u,l,\widehat{l},l,u,\widehat{u}\rangle$ = $\langle u,l,\widehat{l},l,u,\widehat{u}\rangle$

  $=L_{\langle u,l\rangle }\left(\langle E\rangle \right)$, i.e., $\left(O_{58}\right)$.

• Type $\langle h_{2n},\dots ,h_7,\widehat{l},l,u,\widehat{u},u,l,l,u\rangle =L_{\langle h_{2n},\dots ,h_7\rangle }\left(O_{55}\right)$:

  -

  $L_{\langle l,u\rangle }\left(O_{55}\right)=\langle l,u,\widehat{l},l,u,\widehat{u},u,l,l,u\rangle$ = $\langle l,u,l,\widehat{l},u,\widehat{u},u,l,l,u\rangle$

  $=\langle l,\widehat{l},u,\widehat{u},u,l,l,u\rangle$$=\langle \widehat{l},l,u,\widehat{u},u,l,l,u\rangle$

  =$\langle E\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{55}\right)$;

  -

  $L_{\langle l,u,u,l,l,u\rangle }\left(O_{55}\right)=\langle l,u,u,l,l,u,\widehat{l},l,u,\widehat{u},u,l,l,u\rangle$

  $=\langle l,u,u,l,l,u,l,\widehat{l},u,\widehat{u},u,l,l,u\rangle$

  $=\langle l,u,u,l,l,\widehat{l},u,\widehat{u},u,l,l,u\rangle$

  $=\langle l,u,u,l,\widehat{l},l,u,\widehat{u},u,l,l,u\rangle$

  $=L_{\langle l,u,u,l\rangle }\left(O_{55}\right)$

  $=\langle C\rangle \odot \langle D\rangle \odot \langle E\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{59}\right)$;

  -

  $L_{\langle u,l,l,u\rangle }\left(O_{55}\right)=\langle u,l,l,u,\widehat{l},l,u,\widehat{u},u,l,l,u\rangle$ = $\langle u,l,l,u,l,\widehat{l},u,\widehat{u},u,l,l,u\rangle$

  $=\langle u,l,l,\widehat{l},u,\widehat{u},u,l,l,u\rangle$$=\langle u,l,\widehat{l},l,u,\widehat{u},u,l,l,u\rangle$

  $=L_{\langle u,l\rangle }\left(O_{55}\right)$

  $=\langle D\rangle \odot \langle E\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{60}\right)$;

  -

  $L_{\langle u,l,l,u,u,l\rangle }\left(O_{55}\right)=\langle u,l,l,u,u,l,\widehat{l},l,u,\widehat{u},u,l,l,u\rangle$

  $=\langle u,l,\widehat{l},l,u,\widehat{u},u,l,l,u\rangle$

  $=L_{\langle u,l\rangle }\left(O_{55}\right)$, i.e., $\left(O_{60}\right)$.

• Type $\langle h_{2n},\dots ,h_5,\widehat{l},l,u,\widehat{u},u,l\rangle =L_{\langle h_{2n},\dots ,h_5\rangle }\left(O_{56}\right)$:

  -

  $L_{\langle l,u\rangle }\left(O_{56}\right)=\langle l,u,\widehat{l},l,u,\widehat{u},u,l\rangle$ = $\langle l,u,l,\widehat{l},u,\widehat{u},u,l\rangle$ = $\langle l,\widehat{l},u,\widehat{u},u,l\rangle$

  $=\langle \widehat{l},l,u,\widehat{u},u,l\rangle$ =$\langle E\rangle \odot \langle B\rangle$, i.e., $\left(O_{56}\right)$;

  -

  $L_{\langle l,u,u,l,l,u\rangle }\left(O_{56}\right)=\langle l,u,u,l,l,u,\widehat{l},l,u,\widehat{u},u,l\rangle$ = $\langle l,u,u,l,l,u,l,\widehat{l},u,\widehat{u},u,l\rangle$

  $=\langle l,u,u,l,l,\widehat{l},u,\widehat{u},u,l\rangle$$=\langle l,u,u,l,\widehat{l},l,u,\widehat{u},u,l\rangle$

  $=L_{\langle l,u,u,l\rangle }\left(O_{56}\right)$$=\langle C\rangle \odot \langle D\rangle \odot \langle E\rangle \odot \langle B\rangle$, i.e., $\left(O_{61}\right)$;

  -

  $L_{\langle u,l,l,u\rangle }\left(O_{56}\right)=\langle u,l,l,u,\widehat{l},l,u,\widehat{u},u,l\rangle$ = $\langle u,l,l,u,l,\widehat{l},u,\widehat{u},u,l\rangle$

  $=\langle u,l,l,\widehat{l},u,\widehat{u},u,l\rangle =$$\langle u,l,\widehat{l},l,u,\widehat{u},u,l\rangle$

  $=L_{\langle u,l\rangle }\left(O_{56}\right)=\langle D\rangle \odot \langle E\rangle \odot \langle B\rangle$, i.e., $\left(O_{62}\right)$;

  -

  $L_{\langle u,l,l,u,u,l\rangle }\left(O_{56}\right)=\langle u,l,l,u,u,l,\widehat{l},l,u,\widehat{u},u,l\rangle =$$\langle u,l,\widehat{l},l,u,\widehat{u},u,l\rangle$

  $=L_{\langle u,l\rangle }\left(\right)$, i.e., $\left(O_{62}\right)$.

In the case (C2).

• Type $\langle \widehat{l},u,l,\widehat{u},h_s,\dots ,h_1\rangle =R_{\langle h_s,\dots ,h_1\rangle }\left(\langle \widehat{l},u,l,\widehat{u}\rangle \right)=R_{\langle h_s,\dots ,h_1\rangle }\left(O_2\right)$:

  -

  $R_{\langle l,u\rangle }\left(O_2\right)=\langle \widehat{l},u,l,\widehat{u},l,u\rangle =\langle F\rangle \odot \langle A\rangle$, i.e., $\left(O_{63}\right)$;

  -

  $R_{\langle l,u,u,l,l,u\rangle }\left(O_2\right)=\langle \widehat{l},u,l,\widehat{u},l,u,u,l,l,u\rangle$

  $=\langle F\rangle \odot \langle A\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{64}\right)$;

  -

  $R_{\langle u,l,l,u\rangle }\left(O_2\right)=\langle \widehat{l},u,l,\widehat{u},u,l,l,u\rangle$ = $\langle \widehat{l},u,l,u,\widehat{u},l,l,u\rangle$ = $\langle \widehat{l},u,\widehat{u},l,l,u\rangle$

  $=\langle \widehat{l},\widehat{u},u,l,l,u,\rangle =\langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{12}\right)$;

  -

  $R_{\langle l,u,u,l\rangle }\left(O_2\right)=\langle \widehat{l},u,l,\widehat{u},l,u,u,l\rangle =\langle F\rangle \odot \langle A\rangle \odot \langle B\rangle$, i.e., $\left(O_{65}\right)$;

  -

  $R_{\langle u,l,l,u,u,l\rangle }\left(O_2\right)=\langle \widehat{l},u,l,\widehat{u},u,l,l,u,u,l\rangle$ = $\langle \widehat{l},u,l,u,\widehat{u},l,l,u,u,l\rangle$

  $=\langle \widehat{l},u,\widehat{u},l,l,u,u,l\rangle$$=\langle \widehat{l},\widehat{u},u,l,l,u,u,l\rangle$

  $=\langle B\rangle \odot \langle A\rangle \odot \langle B\rangle$, i.e., $\left(O_{14}\right)$;

  -

  $R_{\langle u,l\rangle }\left(O_2\right)=\langle \widehat{l},u,l,\widehat{u},u,l\rangle$ = $\langle \widehat{l},u,l,u,\widehat{u},l\rangle$ = $\langle \widehat{l},u,\widehat{u},l\rangle$

  $=\langle \widehat{l},\widehat{u},u,l\rangle =\langle A\rangle$, i.e., $\left(O_8\right)$.

• Type $\langle h_{2n},\dots ,h_3,\widehat{l},u,l,\widehat{u}\rangle =L_{\langle h_{2n},\dots ,h_3\rangle }\left(\langle \widehat{l},u,l,\widehat{u}\rangle \right)=L_{\langle h_{2n},\dots ,h_3\rangle }\left(O_2\right):$:

  -

  $L_{\langle l,u\rangle }\left(O_2\right)=\langle l,u,\widehat{l},u,l,\widehat{u}\rangle =\langle C\rangle \odot \langle F\rangle$, i.e., $\left(O_{66}\right)$;

  -

  $L_{\langle l,u,u,l,l,u\rangle }\left(O_2\right)=\langle l,u,u,l,l,u,\widehat{l},u,l,\widehat{u}\rangle$

  $=\langle C\rangle \odot \langle D\rangle \odot \langle C\rangle \odot \langle F\rangle$, i.e., $\left(O_{67}\right)$;

  -

  $L_{\langle u,l,l,u\rangle }\left(O_2\right)=\langle u,l,l,u,\widehat{l},u,l,\widehat{u}\rangle =\langle D\rangle \odot \langle C\rangle \odot \langle F\rangle$, i.e., $\left(O_{68}\right)$;

  -

  $L_{\langle l,u,u,l\rangle }\left(O_2\right)=\langle l,u,u,l,\widehat{l},u,l,\widehat{u}\rangle =$$\langle l,u,u,\widehat{l},l,u,l,\widehat{u}\rangle =$$\langle l,u,u,\widehat{l},l,\widehat{u}\rangle$

  $=\langle l,u,u,l,\widehat{l},\widehat{u}\rangle =\langle C\rangle \odot \langle D\rangle$, i.e., $\left(O_{17}\right)$;

  -

  $L_{\langle u,l,l,u,u,l\rangle }\left(O_2\right)=\langle u,l,l,u,u,l,\widehat{l},u,l,\widehat{u}\rangle =$$\langle u,l,l,u,u,\widehat{l},l,u,l,\widehat{u}\rangle$

  $=\langle u,l,l,u,u,\widehat{l},l,\widehat{u}\rangle$$=\langle u,l,l,u,u,l,\widehat{l},\widehat{u}\rangle$

  $=\langle D\rangle \odot \langle C\rangle \odot \langle D\rangle$, i.e., $\left(O_{18}\right)$;

  -

  $L_{\langle u,l\rangle }\left(O_2\right)=\langle u,l,\widehat{l},u,l,\widehat{u}\rangle$$\langle u,\widehat{l},l,u,l,\widehat{u}\rangle =$$\langle u,\widehat{l},l,\widehat{u}\rangle =$$\langle u,l,\widehat{l},\widehat{u}\rangle$

  $=\langle D\rangle$, i.e., $\left(O_{10}\right)$.

• Type $\langle h_{2n},\dots ,h_5,\widehat{l},u,l,\widehat{u},l,u\rangle =L_{\langle h_{2n},\dots ,h_5\rangle }\left(\langle \widehat{l},u,l,\widehat{u},l,u\rangle \right)$
  $=L_{\langle h_{2n},\dots ,h_5\rangle }\left(O_{63}\right):$:

  -

  $L_{\langle l,u\rangle }\left(O_{63}\right)=\langle l,u,\widehat{l},u,l,\widehat{u},l,u\rangle =\langle C\rangle \odot \langle F\rangle \odot \langle A\rangle$, i.e., $\left(O_{69}\right)$;

  -

  $L_{\langle l,u,u,l,l,u\rangle }\left(O_{63}\right)=\langle l,u,u,l,l,u,\widehat{l},u,l,\widehat{u},l,u\rangle$

  $=\langle C\rangle \odot \langle D\rangle \odot \langle C\rangle \odot \langle F\rangle \odot \langle A\rangle$, i.e., $\left(O_{70}\right)$;

  -

  $L_{\langle u,l,l,u\rangle }\left(O_{63}\right)=\langle u,l,l,u,\widehat{l},u,l,\widehat{u},l,u\rangle$

  $=\langle D\rangle \odot \langle C\rangle \odot \langle F\rangle \odot \langle A\rangle$, i.e., $\left(O_{71}\right)$;

  -

  $L_{\langle l,u,u,l\rangle }\left(O_{63}\right)=\langle l,u,u,l,\widehat{l},u,l,\widehat{u},l,u\rangle =$$\langle l,u,u,\widehat{l},l,u,l,\widehat{u},l,u\rangle$

  $=\langle l,u,u,\widehat{l},l,\widehat{u},l,u\rangle =$$\langle l,u,u,l,\widehat{l},\widehat{u},l,u\rangle =$,

  $=\langle C\rangle \odot \langle D\rangle \odot \langle A\rangle$, i.e., $\left(O_{22}\right)$;

  -

  $L_{\langle u,l,l,u,u,l\rangle }(\langle F\rangle \odot \langle A\rangle )=\langle u,l,l,u,u,l,\widehat{l},u,l,\widehat{u},l,u\rangle =$$\langle u,l,l,u,u,\widehat{l},l,u,l,\widehat{u},l,u\rangle$

  $=\langle u,l,l,u,u,\widehat{l},l,\widehat{u},l,u\rangle$$=\langle u,l,l,u,u,l,\widehat{l},\widehat{u},l,u\rangle =$

  $=\langle D\rangle \odot \langle C\rangle \odot \langle D\rangle \odot \langle A\rangle$, i.e., $\left(O_{23}\right)$;

  -

  $L_{\langle u,l\rangle }\left(O_{63}\right)=\langle u,l,\widehat{l},u,l,\widehat{u},l,u\rangle =$$\langle u,\widehat{l},l,u,l,\widehat{u},l,u\rangle =$$\langle u,\widehat{l},l,\widehat{u},l,u\rangle$

  $=\langle u,l,\widehat{l},\widehat{u},l,u\rangle$$=\langle D\rangle \odot \langle A\rangle$, i.e., $\left(O_{24}\right)$.

• Type $\langle h_{2n},\dots ,h_9,\widehat{l},u,l,\widehat{u},l,u,u,l,l,u\rangle =L_{\langle h_{2n},\dots ,h_9\rangle }\left(\langle \widehat{l},u,l,\widehat{u},l,u,u,l,l,u\rangle \right)$
  $=L_{\langle h_{2n},\dots ,h_9\rangle }\left(O_{64}\right):$:

  -

  $L_{\langle l,u\rangle }\left(O_{64}\right)=\langle l,u,\widehat{l},u,l,\widehat{u},l,u,u,l,l,u\rangle$

  $=\langle C\rangle \odot \langle F\rangle \odot \langle A\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{72}\right)$;

  -

  $L_{\langle l,u,u,l,l,u\rangle }\left(O_{64}\right)$$=\langle l,u,u,l,l,u,\widehat{l},u,l,\widehat{u},l,u,u,l,l,u\rangle$

  $=\langle C\rangle \odot \langle D\rangle \odot \langle C\rangle \odot \langle F\rangle \odot \langle A\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{73}\right)$;

  -

  $L_{\langle u,l,l,u\rangle }\left(O_{64}\right)=\langle u,l,l,u,\widehat{l},u,l,\widehat{u},l,u,u,l,l,u\rangle$

  $=\langle D\rangle \odot \langle C\rangle \odot \langle F\rangle \odot \langle A\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{74}\right)$;

  -

  $L_{\langle l,u,u,l\rangle }\left(O_{64}\right)=\langle l,u,u,l,\widehat{l},u,l,\widehat{u},l,u,u,l,l,u\rangle$

  $=\langle l,u,u,\widehat{l},l,u,l,\widehat{u},l,u,u,l,l,u\rangle$

  $=\langle l,u,u,\widehat{l},l,\widehat{u},l,u,u,l,l,u\rangle$

  $=\langle l,u,u,l,\widehat{l},\widehat{u},l,u,u,l,l,u\rangle$

  $=\langle C\rangle \odot \langle D\rangle \odot \langle A\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{28}\right)$;

  -

  $L_{\langle u,l,l,u,u,l\rangle }\left(O_{64}\right)=\langle u,l,l,u,u,l,\widehat{l},u,l,\widehat{u},l,u,u,l,l,u\rangle$

  $=\langle u,l,l,u,u,\widehat{l},l,u,l,\widehat{u},l,u,u,l,l,u\rangle$

  $=\langle u,l,l,u,u,\widehat{l},l,\widehat{u},l,u,u,l,l,u\rangle$

  $=\langle u,l,l,u,u,l,\widehat{l},\widehat{u},l,u,u,l,l,u\rangle$

  $=\langle D\rangle \odot \langle C\rangle \odot \langle D\rangle \odot \langle A\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{29}\right)$;

  -

  $L_{\langle u,l\rangle }\left(O_{64}\right)=\langle u,l,\widehat{l},u,l,\widehat{u},l,u,u,l,l,u\rangle$

  $=\langle u,\widehat{l},l,u,l,\widehat{u},l,u,u,l,l,u\rangle$

  $=\langle u,\widehat{l},l,\widehat{u},l,u,u,l,l,u\rangle$$=\langle u,l,\widehat{l},\widehat{u},l,u,u,l,l,u\rangle$

  $=\langle D\rangle \odot \langle A\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{30}\right)$.

• Type $\langle h_{2n},\dots ,h_7,\widehat{l},u,l,\widehat{u},l,u,u,l\rangle =L_{\langle h_{2n},\dots ,h_7\rangle }\left(\langle \widehat{l},u,l,\widehat{u},l,u,u,l\rangle \right)$
  $=L_{\langle h_{2n},\dots ,h_7\rangle }\left(O_{65}\right)$:

  -

  $L_{\langle l,u\rangle }\left(O_{65}\right)=\langle l,u,\widehat{l},u,l,\widehat{u},l,u,u,l\rangle$

  $=\langle C\rangle \odot \langle F\rangle \odot \langle A\rangle \odot \langle B\rangle$, i.e., $\left(O_{75}\right)$;

  -

  $L_{\langle l,u,u,l,l,u\rangle }\left(O_{65}\right)=\langle l,u,u,l,l,u,\widehat{l},u,l,\widehat{u},l,u,u,l\rangle$

  $=\langle C\rangle \odot \langle D\rangle \odot \langle C\rangle \odot \langle F\rangle \odot \langle A\rangle \odot \langle B\rangle$, i.e., $\left(O_{76}\right)$;

  -

  $L_{\langle u,l,l,u\rangle }\left(O_{65}\right)=\langle u,l,l,u,\widehat{l},u,l,\widehat{u},l,u,u,l\rangle$

  $=\langle D\rangle \odot \langle C\rangle \odot \langle F\rangle \odot \langle A\rangle \odot \langle B\rangle$, i.e., $\left(O_{77}\right)$;

  -

  $L_{\langle l,u,u,l\rangle }\left(O_{65}\right)=\langle l,u,u,l,\widehat{l},u,l,\widehat{u},l,u,u,l\rangle$

  $=\langle l,u,u,\widehat{l},l,u,l,\widehat{u},l,u,u,l\rangle$

  $=\langle l,u,u,\widehat{l},l,\widehat{u},l,u,u,l\rangle$$=\langle l,u,u,l,\widehat{l},\widehat{u},l,u,u,l\rangle$

  $=\langle C\rangle \odot \langle D\rangle \odot \langle A\rangle \odot \langle B\rangle$, i.e., $\left(O_{40}\right)$;

  -

  $L_{\langle u,l,l,u,u,l\rangle }\left(O_{65}\right)=\langle u,l,l,u,u,l,\widehat{l},u,l,\widehat{u},l,u,u,l\rangle$

  $=\langle u,l,l,u,u,\widehat{l},l,u,l,\widehat{u},l,u,u,l\rangle$

  $=\langle u,l,l,u,u,\widehat{l},l,\widehat{u},l,u,u,l\rangle$

  $=\langle u,l,l,u,u,l,\widehat{l},\widehat{u},l,u,u,l\rangle$

  $=\langle D\rangle \odot \langle C\rangle \odot \langle D\rangle \odot \langle A\rangle \odot \langle B\rangle$, i.e., $\left(O_{41}\right)$;

  -

  $L_{\langle u,l\rangle }\left(O_{65}\right)=\langle u,l,\widehat{l},u,l,\widehat{u},l,u,u,l\rangle =$$\langle u,\widehat{l},l,u,l,\widehat{u},l,u,u,l\rangle$

  $=\langle u,\widehat{l},l,\widehat{u},l,u,u,l\rangle$$=\langle u,l,\widehat{l},\widehat{u},l,u,u,l\rangle$

  $=\langle D\rangle \odot \langle A\rangle \odot \langle B\rangle$, i.e., $\left(O_{42}\right)$.

In the case (C3).

• Type $\langle \widehat{l},l,u,u,l,\widehat{u},h_s,\dots ,h_1\rangle =R_{\langle h_s,\dots ,h_1\rangle }\left(\langle \widehat{l},l,u,u,l,\widehat{u}\rangle \right)=R_{\langle h_s,\dots ,h_1\rangle }\left(O_5\right)$:

  -

  $R_{\langle l,u\rangle }\left(O_5\right)=\langle \widehat{l},l,u,u,l,\widehat{u},l,u\rangle =\langle E\rangle \odot \langle F\rangle \odot \langle A\rangle$, i.e., $\left(O_{78}\right)$;

  -

  $R_{\langle l,u,u,l,l,u\rangle }\left(O_5\right)=\langle \widehat{l},l,u,u,l,\widehat{u},l,u,u,l,l,u\rangle =$$\langle \widehat{l},l,u,\widehat{u},u,l,l,u\rangle$

  $=\langle F\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{55}\right)$;

  -

  $R_{\langle u,l,l,u\rangle }\left(O_5\right)=\langle \widehat{l},l,u,u,l,\widehat{u},u,l,l,u\rangle =$$\langle \widehat{l},l,u,u,l,u,\widehat{u},l,l,u\rangle$

  $=\langle \widehat{l},l,u,u,\widehat{u},l,l,u\rangle$$=\langle \widehat{l},l,u,\widehat{u},u,l,l,u\rangle$

  $=\langle F\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{55}\right)$;

  -

  $R_{\langle l,u,u,l\rangle }\left(O_5\right)=\langle \widehat{l},l,u,u,l,\widehat{u},l,u,u,l\rangle =$$\langle \widehat{l},l,u,\widehat{u},u,l\rangle$

  $=\langle E\rangle \odot \langle B\rangle$, i.e., $\left(O_{56}\right)$;

  -

  $R_{\langle u,l,l,u,u,l\rangle }\left(O_5\right)=\langle \widehat{l},l,u,u,l,\widehat{u},u,l,l,u,u,l\rangle =$$\langle \widehat{l},l,u,u,l,u,\widehat{u},l,l,u,u,l\rangle$

  $=\langle \widehat{l},l,u,u,\widehat{u},l,l,u,u,l\rangle$$=\langle \widehat{l},l,u,\widehat{u},u,l,l,u,u,l\rangle$

  $=\langle \widehat{l},l,u,\widehat{u},u,l\rangle =\langle E\rangle \odot \langle B\rangle$, i.e., $\left(O_{56}\right)$;

  -

  $R_{\langle u,l\rangle }\left(O_5\right)=\langle \widehat{l},l,u,u,l,\widehat{u},u,l\rangle =$$\langle \widehat{l},l,u,u,l,u,\widehat{u},l\rangle =$$\langle \widehat{l},l,u,u,\widehat{u},l\rangle$

  $=\langle \widehat{l},l,u,\widehat{u},u,l\rangle =\langle E\rangle \odot \langle B\rangle$, i.e., $\left(O_{56}\right)$.

• Type $\langle h_{2n},\dots ,h_5,\widehat{l},l,u,u,l,\widehat{u}\rangle =L_{\langle h_{2n},\dots ,h_5\rangle }\left(\langle \widehat{l},l,u,u,l,\widehat{u}\rangle \right)$
  $=L_{\langle h_{2n},\dots ,h_5\rangle }\left(O_5\right)$:

  -

  $L_{\langle l,u\rangle }\left(O_5\right)=\langle l,u,\widehat{l},l,u,u,l,\widehat{u}\rangle =\langle l,u,l,\widehat{l},u,u,l,\widehat{u}\rangle =\langle l,\widehat{l},u,u,l,\widehat{u}\rangle$

  $=\langle E\rangle \odot \langle F\rangle$, i.e., $\left(O_5\right)$;

  -

  $L_{\langle l,u,u,l,l,u\rangle }\left(O_5\right)=\langle l,u,u,l,l,u,\widehat{l},l,u,u,l,\widehat{u}\rangle =$$\langle l,u,u,l,l,u,l,\widehat{l},u,u,l,\widehat{u}\rangle$

  $=\langle l,u,u,l,l,\widehat{l},u,u,l,\widehat{u}\rangle =$$\langle l,u,u,l,\widehat{l},l,u,u,l,\widehat{u}\rangle$

  $=L_{\langle l,u,u,l\rangle }\left(O_5\right)=\langle C\rangle \odot \langle D\rangle \odot \langle E\rangle \odot \langle F\rangle$, i.e., $\left(O_{79}\right)$;

  -

  $L_{\langle u,l,l,u\rangle }\left(O_5\right)=\langle u,l,l,u,\widehat{l},l,u,u,l,\widehat{u}\rangle =$$\langle u,l,l,u,l,\widehat{l},u,u,l,\widehat{u}\rangle$

  $=\langle u,l,l,\widehat{l},u,u,l,\widehat{u}\rangle =$$\langle u,l,\widehat{l},l,u,u,l,\widehat{u}\rangle$

  $=L_{\langle u,l\rangle }\left(O_5\right)=\langle D\rangle \odot \langle E\rangle \odot \langle F\rangle$, i.e., $\left(O_{80}\right)$;

  -

  $L_{\langle u,l,l,u,u,l\rangle }\left(O_5\right)=\langle u,l,l,u,u,l,\widehat{l},l,u,u,l,\widehat{u}\rangle =$$\langle u,l,\widehat{l},l,u,u,l,\widehat{u}\rangle$

  $=L_{\langle u,l\rangle }\left(O_5\right)=\langle D\rangle \odot \langle E\rangle \odot \langle F\rangle$, i.e., $\left(O_{80}\right)$.

• Type $\langle h_{2n},\dots ,h_7,\widehat{l},l,u,u,l,\widehat{u},l,u\rangle =L_{\langle h_{2n},\dots ,h_7\rangle }\left(\langle \widehat{l},l,u,u,l,\widehat{u},l,u\rangle \right)$
  $=L_{\langle h_{2n},\dots ,h_7\rangle }\left(O_{78}\right)$:

  -

  $L_{\langle l,u\rangle }\left(O_{78}\right)=\langle l,u,\widehat{l},l,u,u,l,\widehat{u},l,u\rangle =$$\langle l,u,l,\widehat{l},u,u,l,\widehat{u},l,u\rangle$

  $=\langle l,\widehat{l},u,u,l,\widehat{u},l,u\rangle$$=\langle \widehat{l},l,u,u,l,\widehat{u},l,u\rangle$

  $=\langle E\rangle \odot \langle F\rangle \odot \langle A\rangle$, i.e., $\left(O_{78}\right)$;

  -

  $L_{\langle l,u,u,l,l,u\rangle }\left(O_{78}\right)=\langle l,u,u,l,l,u,\widehat{l},l,u,u,l,\widehat{u},l,u\rangle$

  $=\langle l,u,u,l,l,u,l,\widehat{l},u,u,l,\widehat{u},l,u\rangle$

  $=\langle l,u,u,l,l,\widehat{l},u,u,l,\widehat{u},l,u\rangle$

  $=\langle l,u,u,l,\widehat{l},l,u,u,l,\widehat{u},l,u\rangle$

  $=L_{\langle l,u,u,l\rangle }\left(O_{78}\right)$

  $=\langle C\rangle \odot \langle D\rangle \odot \langle E\rangle \odot \langle F\rangle \odot \langle A\rangle$, i.e., $\left(O_{81}\right)$;

  -

  $L_{\langle u,l,l,u\rangle }\left(O_{78}\right)=\langle u,l,l,u,\widehat{l},l,u,u,l,\widehat{u},l,u\rangle =$$\langle u,l,l,u,l,\widehat{l},u,u,l,\widehat{u},l,u\rangle$

  $=\langle u,l,l,\widehat{l},u,u,l,\widehat{u},l,u\rangle =$$\langle u,l,\widehat{l},l,u,u,l,\widehat{u},l,u\rangle$

  $=L_{\langle u,l\rangle }\left(O_{78}\right)$

  $=\langle D\rangle \odot \langle E\rangle \odot \langle F\rangle \odot \langle A\rangle$, i.e., $\left(O_{82}\right)$;

  -

  $L_{\langle u,l,l,u,u,l\rangle }\left(O_{78}\right)=\langle u,l,l,u,u,l,\widehat{l},l,u,u,l,\widehat{u},l,u\rangle$

  $=\langle u,l,\widehat{l},l,u,u,l,\widehat{u},l,u\rangle$

  $=\langle D\rangle \odot \langle E\rangle \odot \langle F\rangle \odot \langle A\rangle$, i.e., $\left(O_{82}\right)$.

In the case (C4).

• Type $\langle \widehat{l},u,l,l,u,\widehat{u},h_s,\dots ,h_1\rangle =R_{\langle h_s,\dots ,h_1\rangle }\left(\langle \widehat{l},u,l,l,u,\widehat{u}\rangle \right)=R_{\langle h_s,\dots ,h_1\rangle }\left(O_4\right)$:

  -

  $R_{\langle l,u\rangle }\left(O_4\right)=\langle \widehat{l},u,l,l,u,\widehat{u},l,u\rangle =$$\langle \widehat{l},u,l,l,\widehat{u},u,l,u\rangle =$$\langle \widehat{l},u,l,l,\widehat{u},u\rangle$

  $=\langle \widehat{l},u,l,l,u,\widehat{u}\rangle =\langle E\rangle \odot \langle F\rangle$, i.e., $\left(O_4\right)$;

  -

  $R_{\langle l,u,u,l,l,u\rangle }\left(O_4\right)=\langle \widehat{l},u,l,l,u,\widehat{u},l,u,u,l,l,u\rangle =$$\langle \widehat{l},u,l,l,\widehat{u},u,l,u,u,l,l,u\rangle$

  $=\langle \widehat{l},u,l,l,\widehat{u},u,u,l,l,u\rangle$$=\langle \widehat{l},u,l,l,u,\widehat{u},u,l,l,u\rangle$

  $=R_{\langle u,l,l,u,\rangle }\left(O_4\right)=\langle F\rangle \odot \langle E\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{83}\right)$;

  -

  $R_{\langle l,u,u,l\rangle }\left(O_4\right)=\langle \widehat{l},u,l,l,u,\widehat{u},l,u,u,l\rangle =$$\langle \widehat{l},u,l,l,\widehat{u},u,l,u,u,l\rangle$

  $=\langle \widehat{l},u,l,l,\widehat{u},u,u,l\rangle$$=\langle \widehat{l},u,l,l,u,\widehat{u},u,l\rangle$$=R_{\langle u,l\rangle }\left(O_4\right)$

  $=\langle F\rangle \odot \langle E\rangle \odot \langle B\rangle$, i.e., $\left(O_{84}\right)$;

  -

  $R_{\langle u,l,l,u,u,l\rangle }\left(O_4\right)=\langle \widehat{l},u,l,l,u,\widehat{u},u,l,l,u,u,l\rangle =$$\langle \widehat{l},u,l,l,u,\widehat{u},u,l\rangle R_{\langle u,l\rangle }\left(O_4\right)$

  $=R_{\langle u,l\rangle }\left(O_4\right)=\langle F\rangle \odot \langle E\rangle \odot \langle B\rangle$, i.e., $\left(O_{84}\right)$.

• Type $\langle h_{2n},\dots ,h_5,\widehat{l},u,l,l,u,\widehat{u}\rangle =L_{\langle h_{2n},\dots ,h_5\rangle }\left(\langle \widehat{l},u,l,l,u,\widehat{u}\rangle \right)=L_{\langle h_{2n},\dots ,h_5\rangle }\left(O_4\right)$:

  -

  $L_{\langle l,u\rangle }\left(O_4\right)=\langle l,u,\widehat{l},u,l,l,u,\widehat{u}\rangle =\langle C\rangle \odot \langle F\rangle \odot \langle E\rangle$, i.e., $\left(O_{85}\right)$;

  -

  $L_{\langle l,u,u,l,l,u\rangle }\left(O_4\right)=\langle l,u,u,l,l,u,\widehat{l},u,l,l,u,\widehat{u}\rangle =$$\langle l,u,u,l,\widehat{l},l,u,\widehat{u}\rangle$

  $=\langle C\rangle \odot \langle D\rangle \odot \langle E\rangle$, i.e., $\left(O_{57}\right)$;

  -

  $L_{\langle u,l,l,u\rangle }\left(O_4\right)=\langle u,l,l,u,\widehat{l},u,l,l,u,\widehat{u}\rangle =$$\langle u,l,\widehat{l},l,u,\widehat{u}\rangle$

  $=\langle D\rangle \odot \langle E\rangle$, i.e., $\left(O_{58}\right)$;

  -

  $L_{\langle l,u,u,l\rangle }\left(O_4\right)=\langle l,u,u,l,\widehat{l},u,l,l,u,\widehat{u}\rangle =$$\langle l,u,u,\widehat{l},l,u,l,l,u,\widehat{u}\rangle =\langle l,u,u,\widehat{l},l,l,u,\widehat{u}\rangle$

  $=\langle l,u,u,l,\widehat{l},l,u,\widehat{u}\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle E\rangle$, i.e., $\left(O_{57}\right)$;

  -

  $L_{\langle u,l,l,u,u,l\rangle }\left(O_4\right)=\langle u,l,l,u,u,l,\widehat{l},u,l,l,u,\widehat{u}\rangle =$$\langle u,l,l,u,u,\widehat{l},l,u,l,l,u,\widehat{u}\rangle$

  $=\langle u,l,l,u,u,\widehat{l},l,l,u,\widehat{u}\rangle =$$\langle u,l,l,u,u,l,\widehat{l},l,u,\widehat{u}\rangle$

  $=\langle u,l,\widehat{l},l,u,\widehat{u}\rangle =\langle D\rangle \odot \langle E\rangle$, i.e., $\left(O_{58}\right)$;

  -

  $L_{\langle u,l\rangle }\left(O_4\right)=\langle u,l,\widehat{l},u,l,l,u,\widehat{u}\rangle =$$\langle u,\widehat{l},l,u,l,l,u,\widehat{u}\rangle$$=\langle u,\widehat{l},l,l,u,\widehat{u}\rangle$

  $=\langle u,l,\widehat{l},l,u,\widehat{u}\rangle =\langle D\rangle \odot \langle E\rangle$, i.e., $\left(O_{58}\right)$.

• Type $\langle h_{2n},\dots ,h_9,\widehat{l},u,l,l,u,\widehat{u},u,l,l,u\rangle =L_{\langle h_{2n},\dots ,h_9\rangle }\left(\langle \widehat{l},u,l,l,u,\widehat{u},u,l,l,u\rangle \right)$
  $=L_{\langle h_{2n},\dots ,h_9\rangle }\left(O_{83}\right)$:

  -

  $L_{\langle l,u\rangle }\left(O_{83}\right)=\langle l,u,\widehat{l},u,l,l,u,\widehat{u},u,l,l,u\rangle$

  $=\langle C\rangle \odot \langle F\rangle \odot \langle E\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{86}\right)$;

  -

  $L_{\langle l,u,u,l,l,u\rangle }\left(O_{83}\right)=\langle l,u,u,l,l,u,\widehat{l},u,l,l,u,\widehat{u},u,l,l,u\rangle$$=\langle l,u,u,l,\widehat{l},l,u,\widehat{u},u,l,l,u\rangle$

  $=\langle C\rangle \odot \langle D\rangle \odot \langle E\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{59}\right)$;

  -

  $L_{\langle u,l,l,u\rangle }\left(O_{83}\right)=\langle u,l,l,u,\widehat{l},u,l,l,u,\widehat{u},u,l,l,u\rangle =$$\langle u,l,\widehat{l},l,u,\widehat{u},u,l,l,u\rangle$

  $=\langle D\rangle \odot \langle E\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{60}\right)$;

  -

  $L_{\langle l,u,u,l\rangle }\left(\langle 70\rangle \right)=\langle l,u,u,l,\widehat{l},u,l,l,u,\widehat{u},u,l,l,u\rangle =$$\langle l,u,u,\widehat{l},l,u,l,l,u,\widehat{u},u,l,l,u\rangle$

  $=\langle l,u,u,\widehat{l},l,l,u,\widehat{u},u,l,l,u\rangle$$=\langle l,u,u,l,\widehat{l},l,u,\widehat{u},u,l,l,u\rangle$

  $=\langle C\rangle \odot \langle D\rangle \odot \langle E\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{59}\right)$;

  -

  $L_{\langle u,l,l,u,u,l\rangle }\left(O_{83}\right)=\langle u,l,l,u,u,l,\widehat{l},u,l,l,u,\widehat{u},u,l,l,u\rangle$

  $=\langle u,l,l,u,u,\widehat{l},l,u,l,l,u,\widehat{u},u,l,l,u\rangle$

  $=\langle u,l,l,u,u,\widehat{l},l,l,u,\widehat{u},u,l,l,u\rangle$$=\langle u,l,l,u,u,l,\widehat{l},l,u,\widehat{u},u,l,l,u\rangle$

  $=\langle u,l,\widehat{l},l,u,\widehat{u},u,l,l,u\rangle$

  $=\langle D\rangle \odot \langle E\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{60}\right)$;

  -

  $L_{\langle u,l\rangle }\left(O_{83}\right)=\langle u,l,\widehat{l},u,l,l,u,\widehat{u},u,l,l,u\rangle =$$\langle u,\widehat{l},l,u,l,l,u,\widehat{u},u,l,l,u\rangle$

  $=\langle u,\widehat{l},l,l,u,\widehat{u},u,l,l,u\rangle$$=\langle u,l,\widehat{l},l,u,\widehat{u},u,l,l,u\rangle$

  $=\langle D\rangle \odot \langle E\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{60}\right)$.

• Type $\langle h_{2n},\dots ,h_7,\widehat{l},u,l,l,u,\widehat{u},u,l\rangle =L_{\langle h_{2n},\dots ,h_7\rangle }\left(\langle \widehat{l},u,l,l,u,\widehat{u},u,l\rangle \right)$
  $=L_{\langle h_{2n},\dots ,h_7\rangle }\left(O_{84}\right)$:

  -

  $L_{\langle l,u\rangle }\left(O_{84}\right)=\langle l,u,\widehat{l},u,l,l,u,\widehat{u},u,l\rangle$

  $=\langle C\rangle \odot \langle F\rangle \odot \langle E\rangle \odot \langle B\rangle$, i.e., $\left(O_{87}\right)$;

  -

  $L_{\langle l,u,u,l,l,u\rangle }\left(O_{84}\right)=\langle l,u,u,l,l,u,\widehat{l},u,l,l,u,\widehat{u},u,l\rangle =$$\langle l,u,u,l,\widehat{l},l,u,\widehat{u},u,l\rangle$

  $=\langle C\rangle \odot \langle D\rangle \odot \langle E\rangle \odot \langle B\rangle$, i.e., $\left(O_{61}\right)$;

  -

  $L_{\langle u,l,l,u\rangle }\left(O_{84}\right)=\langle u,l,l,u,\widehat{l},u,l,l,u,\widehat{u},u,l\rangle =$$\langle u,l,\widehat{l},l,u,\widehat{u},u,l\rangle$

  $=\langle D\rangle \odot \langle E\rangle \odot \langle B\rangle$, i.e., $\left(O_{62}\right)$;

  -

  $L_{\langle l,u,u,l\rangle }\left(O_{84}\right)=\langle l,u,u,l,\widehat{l},u,l,l,u,\widehat{u},u,l\rangle =$$\langle l,u,u,\widehat{l},l,u,l,l,u,\widehat{u},u,l\rangle$

  $=\langle l,u,u,\widehat{l},l,l,u,\widehat{u},u,l\rangle$$=\langle l,u,u,l,\widehat{l},l,u,\widehat{u},u,l\rangle$

  $=\langle C\rangle \odot \langle D\rangle \odot \langle E\rangle \odot \langle B\rangle$, i.e., $\left(O_{61}\right)$;

  -

  $L_{\langle u,l,l,u,u,l\rangle }\left(O_{84}\right)=\langle u,l,l,u,u,l,\widehat{l},u,l,l,u,\widehat{u},u,l\rangle$

  $=\langle u,l,l,u,u,\widehat{l},l,u,l,l,u,\widehat{u},u,l\rangle$$=\langle u,l,l,u,u,\widehat{l},l,l,u,\widehat{u},u,l\rangle$

  $=\langle u,l,l,u,u,l,\widehat{l},l,u,\widehat{u},u,l\rangle$$=\langle u,l,\widehat{l},l,u,\widehat{u},u,l\rangle$

  $=\langle D\rangle \odot \langle E\rangle \odot \langle B\rangle$, i.e., $\left(O_{62}\right)$;

  -

  $L_{\langle u,l,\rangle }\left(O_{84}\right)=\langle u,l,\widehat{l},u,l,l,u,\widehat{u},u,l\rangle =$$\langle u,\widehat{l},l,u,l,l,u,\widehat{u},u,l\rangle$

  $=\langle u,\widehat{l},l,l,u,\widehat{u},u,l\rangle$$=\langle u,l,\widehat{l},l,u,\widehat{u},u,l\rangle$

  $=\langle D\rangle \odot \langle E\rangle \odot \langle B\rangle$, i.e., $\left(O_{62}\right)$.

In the case (C5).

• Type $\langle \widehat{l},l,u,u,l,l,u,\widehat{u},h_s,\dots ,h_1\rangle =R_{\langle h_s,\dots ,h_1\rangle }\left(\langle \widehat{l},l,u,u,l,l,u,\widehat{u}\rangle \right)$ $=R_{\langle h_s,\dots ,h_1\rangle }\left(O_3\right)$:

  -

  $R_{\langle l,u\rangle }\left(O_3\right)=\langle \widehat{l},l,u,u,l,l,u,\widehat{u},l,u\rangle =$$\langle \widehat{l},l,u,u,l,l,\widehat{u},u,l,u\rangle$$=\langle \widehat{l},l,u,u,l,l,\widehat{u},u\rangle$

  $=\langle \widehat{l},l,u,u,l,l,u,\widehat{u}\rangle =\langle E\rangle \odot \langle F\rangle \odot \langle E\rangle$, i.e., $\left(O_3\right)$;

  -

  $R_{\langle l,u,u,l,l,u\rangle }\left(O_3\right)=\langle \widehat{l},l,u,u,l,l,u,\widehat{u},l,u,u,l,l,u\rangle$$=\langle \widehat{l},l,u,u,l,l,\widehat{u},u,l,u,u,l,l,u\rangle$

  $=\langle \widehat{l},l,u,u,l,l,\widehat{u},u,u,l,l,u\rangle$$=\langle \widehat{l},l,u,u,l,l,u,\widehat{u},u,l,l,u\rangle$

  $=\langle \widehat{l},l,u,\widehat{u},u,l,l,u\rangle =\langle E\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{55}\right)$;

  -

  $R_{\langle u,l,l,u\rangle }\left(O_3\right)=\langle \widehat{l},l,u,u,l,l,u,\widehat{u},u,l,l,u\rangle =$$\langle \widehat{l},l,u,\widehat{u},u,l,l,u\rangle =$

  $=\langle E\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{55}\right)$;

  -

  $R_{\langle l,u,u,l\rangle }\left(O_3\right)=\langle \widehat{l},l,u,u,l,l,u,\widehat{u},l,u,u,l\rangle =$$\langle \widehat{l},l,u,u,l,l,\widehat{u},u,l,u,u,l\rangle$

  $=\langle \widehat{l},l,u,u,l,l,\widehat{u},u,u,l\rangle$$=\langle \widehat{l},l,u,u,l,l,u,\widehat{u},u,l\rangle =\langle \widehat{l},l,u,\widehat{u},u,l\rangle =$

  $=\langle E\rangle \odot \langle B\rangle$, i.e., $\left(O_{56}\right)$;

  -

  $R_{\langle u,l,l,u,u,l\rangle }\left(O_3\right)=\langle \widehat{l},l,u,u,l,l,u,\widehat{u},u,l,l,u,u,l\rangle =$$\langle \widehat{l},l,u,\widehat{u},u,l,l,u,u,l\rangle$

  $=\langle \widehat{l},l,u,\widehat{u},u,l\rangle =\langle E\rangle \odot \langle B\rangle$, i.e., $\left(O_{56}\right)$;

  -

  $R_{\langle u,l\rangle }\left(O_3\right)=\langle \widehat{l},l,u,u,l,l,u,\widehat{u},u,l\rangle =\langle \widehat{l},l,u,\widehat{u},u,l\rangle$

  $=\langle E\rangle \odot \langle B\rangle$, i.e., $\left(O_{56}\right)$.

• Type $\langle h_{2n},\dots ,h_7,\widehat{l},l,u,u,l,l,u,\widehat{u}\rangle =L_{\langle h_{2n},\dots ,h_7\rangle }\left(\langle \widehat{l},l,u,u,l,l,u,\widehat{u}\rangle \right)=$
  $=L_{\langle h_{2n},\dots ,h_7\rangle }\left(O_3\right)$:

  -

  $L_{\langle l,u\rangle }\left(O_3\right)=\langle l,u,\widehat{l},l,u,u,l,l,u,\widehat{u}\rangle =$$\langle l,u,l,\widehat{l},u,u,l,l,u,\widehat{u}\rangle =\langle l,\widehat{l},u,u,l,l,u,\widehat{u}\rangle$

  $=\langle \widehat{l},l,u,u,l,l,u,\widehat{u}\rangle =\langle E\rangle \odot \langle F\rangle \odot \langle E\rangle$, i.e., $\left(O_3\right)$;

  -

  $L_{\langle l,u,u,l,l,u\rangle }\left(O_3\right)=\langle l,u,u,l,l,u,\widehat{l},l,u,u,l,l,u,\widehat{u}\rangle$

  $=\langle l,u,u,l,l,u,l,\widehat{l},u,u,l,l,\widehat{u}\rangle$$=\langle l,u,u,l,l,\widehat{l},u,u,l,l,u,\widehat{u}\rangle$

  $=\langle l,u,u,l,\widehat{l},l,u,u,l,l,u,\widehat{u}\rangle$$=\langle l,u,u,l,\widehat{l},l,u,l,u,\widehat{u}\rangle$

  $=\langle l,u,u,l,\widehat{l},l,u,\widehat{u}\rangle =\langle C\rangle \odot \langle D\rangle \odot \langle E\rangle$, i.e., $\left(O_{57}\right)$;

  -

  $L_{\langle u,l,l,u\rangle }\left(O_3\right)=\langle u,l,l,u,\widehat{l},l,u,u,l,l,u,\widehat{u}\rangle =$$\langle u,l,l,u,l,\widehat{l},u,u,l,l,u,\widehat{u}\rangle$

  $=\langle u,l,l,\widehat{l},u,u,l,l,u,\widehat{u}\rangle$$=\langle u,l,\widehat{l},l,u,u,l,l,u,\widehat{u}\rangle =\langle u,l,\widehat{l},l,u,\widehat{u}\rangle$

  $=\langle D\rangle \odot \langle E\rangle$, i.e., $\left(O_{58}\right)$;

  -

  $L_{\langle l,u,u,l\rangle }\left(O_3\right)=\langle l,u,u,l,\widehat{l},l,u,u,l,l,u,\widehat{u}\rangle =$$\langle l,u,u,l,\widehat{l},l,u,\widehat{u}\rangle$

  $=\langle C\rangle \odot \langle D\rangle \odot \langle E\rangle$, i.e., $\left(O_{57}\right)$;

  -

  $L_{\langle u,l,l,u,u,l\rangle }\left(O_3\right)=\langle u,l,l,u,u,l,\widehat{l},l,u,u,l,l,u,\widehat{u}\rangle =$$\langle u,l,\widehat{l},l,u,u,l,l,u,\widehat{u}\rangle$

  $=\langle u,l,\widehat{l},l,u,\widehat{u}\rangle =\langle D\rangle \odot \langle E\rangle$, i.e., $\left(O_{58}\right)$;

  -

  $L_{\langle u,l\rangle }\left(O_3\right)=\langle u,l,\widehat{l},l,u,u,l,l,u,\widehat{u}\rangle =$$\langle u,l,\widehat{l},l,u,\widehat{u}\rangle$

  $=\langle D\rangle \odot \langle E\rangle$, i.e., $\left(O_{58}\right)$.

In the case (C6).

• Type $\langle \widehat{l},u,l,l,u,u,l,\widehat{u},h_s,\dots ,h_1\rangle =R_{\langle h_s,\dots ,h_1\rangle }\left(\langle \widehat{l},u,l,l,u,u,l,\widehat{u}\rangle \right)$
  $=R_{\langle h_s,\dots ,h_1\rangle }\left(O_6\right)$:

  -

  $R_{\langle l,u\rangle }\left(O_6\right)=\langle \widehat{l},u,l,l,u,u,l,\widehat{u},l,u\rangle =\langle F\rangle \odot \langle E\rangle \odot \langle F\rangle \odot \langle A\rangle$, i.e., $\left(O_{88}\right)$;

  -

  $R_{\langle l,u,u,l,l,u\rangle }\left(O_6\right)=\langle \widehat{l},u,l,l,u,u,l,\widehat{u},l,u,u,l,l,u\rangle =$$\langle \widehat{l},u,l,l,u,\widehat{u},u,l,l,u\rangle =$

  $=\langle F\rangle \odot \langle E\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{83}\right)$;

  -

  $R_{\langle u,l,l,u\rangle }\left(O_6\right)=\langle \widehat{l},u,l,l,u,u,l,\widehat{u},u,l,l,u\rangle =$$\langle \widehat{l},u,l,l,u,u,l,u,\widehat{u},l,l,u\rangle$

  $=\langle \widehat{l},u,l,l,u,u,\widehat{u},l,l,u\rangle$$=\langle \widehat{l},u,l,l,u,\widehat{u},u,l,l,u\rangle$

  $=\langle F\rangle \odot \langle E\rangle \odot \langle B\rangle \odot \langle A\rangle$, i.e., $\left(O_{83}\right)$;

  -

  $R_{\langle l,u,u,l\rangle }\left(O_6\right)=\langle \widehat{l},u,l,l,u,u,l,\widehat{u},l,u,u,l\rangle =$$\langle \widehat{l},u,l,l,u,\widehat{u},u,l\rangle$

  $=\langle F\rangle \odot \langle E\rangle \odot \langle B\rangle$, i.e., $\left(O_{84}\right)$;

  -

  $R_{\langle u,l,l,u,u,l\rangle }\left(O_6\right)=\langle \widehat{l},u,l,l,u,u,l,\widehat{u},u,l,l,u,u,l\rangle$$=\langle \widehat{l},u,l,l,u,u,l,u,\widehat{u},l,l,u,u,l\rangle$

  $=\langle \widehat{l},u,l,l,u,u,\widehat{u},l,l,u,u,l\rangle$$=\langle \widehat{l},u,l,l,u,\widehat{u},u,l,l,u,u,l\rangle$

  $=\langle \widehat{l},u,l,l,u,\widehat{u},u,l\rangle$$=\langle F\rangle \odot \langle E\rangle \odot \langle B\rangle$, i.e., $\left(O_{84}\right)$;

  -

  $R_{\langle u,l\rangle }\left(O_6\right)=\langle \widehat{l},u,l,l,u,u,l,\widehat{u},u,l\rangle =$$\langle \widehat{l},u,l,l,u,u,l,u,\widehat{u},l\rangle$$=\langle \widehat{l},u,l,l,u,u,\widehat{u},l\rangle$

  $=\langle \widehat{l},u,l,l,u,\widehat{u},u,l\rangle =\langle F\rangle \odot \langle E\rangle \odot \langle B\rangle$, i.e., $\left(O_{84}\right)$.

• Type $\langle h_{2n},\dots ,h_7,\widehat{l},u,l,l,u,u,l,\widehat{u},\rangle =L_{\langle h_{2n},\dots ,h_7\rangle }\left(\langle \widehat{l},u,l,l,u,u,l,\widehat{u}\rangle \right)$
  $=L_{\langle h_{2n},\dots ,h_7\rangle }\left(O_6\right)$:

  -

  $L_{\langle l,u\rangle }\left(O_6\right)=\langle l,u,\widehat{l},u,l,l,u,u,l,\widehat{u}\rangle =\langle C\rangle \odot \langle F\rangle \odot \langle E\rangle \odot \langle F\rangle$, i.e., $\left(O_{89}\right)$;

  -

  $L_{\langle l,u,u,l,l,u\rangle }\left(O_6\right)=\langle l,u,u,l,l,u,\widehat{l},u,l,l,u,u,l,\widehat{u}\rangle =$$\langle l,u,u,l,\widehat{l},l,u,u,l,\widehat{u}\rangle$

  $=\langle C\rangle \odot \langle D\rangle \odot \langle E\rangle \odot \langle F\rangle$, i.e., $\left(O_{79}\right)$;

  -

  $L_{\langle u,l,l,u\rangle }\left(O_6\right)=\langle u,l,l,u,\widehat{l},u,l,l,u,u,l,\widehat{u}\rangle =$$\langle u,l,\widehat{l},l,u,u,l,\widehat{u}\rangle$

  $=\langle D\rangle \odot \langle E\rangle \odot \langle F\rangle$, i.e., $\left(O_{80}\right)$;

  -

  $L_{\langle l,u,u,l\rangle }\left(O_6\right)=\langle l,u,u,l,\widehat{l},u,l,l,u,u,l,\widehat{u}\rangle =$$\langle l,u,u,\widehat{l},l,u,l,l,u,u,l,\widehat{u}\rangle$

  $=\langle l,u,u,\widehat{l},l,l,u,u,l,\widehat{u}\rangle =$$\langle l,u,u,l,\widehat{l},l,u,u,l,\widehat{u}\rangle$

  $=\langle C\rangle \odot \langle D\rangle \odot \langle E\rangle \odot \langle F\rangle$, i.e., $\left(O_{79}\right)$;

  -

  $L_{\langle u,l,l,u,u,l\rangle }\left(O_6\right)=\langle u,l,l,u,u,l,\widehat{l},u,l,l,u,u,l,\widehat{u}\rangle$$=\langle u,l,l,u,u,\widehat{l},l,u,l,l,u,u,l,\widehat{u}\rangle$

  $=\langle u,l,l,u,u,\widehat{l},l,l,u,u,l,\widehat{u}\rangle$$=\langle u,l,l,u,u,l,\widehat{l},l,u,u,l,\widehat{u}\rangle$

  $=\langle u,l,\widehat{l},l,u,u,l,\widehat{u}\rangle =\langle D\rangle \odot \langle E\rangle \odot \langle F\rangle$, i.e., $\left(O_{80}\right)$;

  -

  $L_{\langle u,l\rangle }\left(O_6\right)=\langle u,l,\widehat{l},u,l,l,u,u,l,\widehat{u}\rangle =$$\langle u,\widehat{l},l,u,l,l,u,u,l,\widehat{u}\rangle$$=\langle u,\widehat{l},l,l,u,u,l,\widehat{u}\rangle$

  $=\langle u,l,\widehat{l},l,u,u,l,\widehat{u}\rangle =\langle D\rangle \odot \langle E\rangle \odot \langle F\rangle$, i.e., $\left(O_{80}\right)$.

• Type $\langle h_{2n},\dots ,h_9,\widehat{l},u,l,l,u,u,l,\widehat{u},l,u\rangle =L_{\langle h_{2n},\dots ,h_9\rangle }\left(\langle \widehat{l},u,l,l,u,u,l,\widehat{u},l,u\rangle \right)=$
  $=L_{\langle h_{2n},\dots ,h_9\rangle }\left(O_{88}\right)$:

  -

  $L_{\langle l,u\rangle }\left(O_{88}\right)=\langle l,u,\widehat{l},u,l,l,u,u,l,\widehat{u},l,u\rangle$

  $=\langle C\rangle \odot \langle F\rangle \odot \langle E\rangle \odot \langle F\rangle \odot \langle A\rangle$, i.e., $\left(O_{90}\right)$;

  -

  $L_{\langle l,u,u,l,l,u\rangle }\left(O_{88}\right)=\langle l,u,u,l,l,u,\widehat{l},u,l,l,u,u,l,\widehat{u},l,u\rangle$$=\langle l,u,u,l,\widehat{l},l,u,u,l,\widehat{u},l,u\rangle$

  $=\langle C\rangle \odot \langle D\rangle \odot \langle E\rangle \odot \langle F\rangle \odot \langle A\rangle$, i.e., $\left(O_{81}\right)$;

  -

  $L_{\langle u,l,l,u\rangle }\left(O_{88}\right)=\langle u,l,l,u,\widehat{l},u,l,l,u,u,l,\widehat{u},l,u\rangle =$$\langle u,l,\widehat{l},l,u,u,l,\widehat{u},l,u\rangle$

  $=\langle D\rangle \odot \langle E\rangle \odot \langle F\rangle \odot \langle A\rangle$, i.e., $\left(O_{82}\right)$;

  -

  $L_{\langle l,u,u,l\rangle }\left(O_{88}\right)=\langle l,u,u,l,\widehat{l},u,l,l,u,u,l,\widehat{u},l,u\rangle =$$\langle l,u,u,\widehat{l},l,u,l,l,u,u,l,\widehat{u},l,u\rangle$

  $=\langle l,u,u,\widehat{l},l,l,u,u,l,\widehat{u},l,u\rangle =$$\langle l,u,u,l,\widehat{l},l,u,u,l,\widehat{u},l,u\rangle$

  $=\langle C\rangle \odot \langle D\rangle \odot \langle E\rangle \odot \langle F\rangle \odot \langle A\rangle$, i.e., $\left(O_{81}\right)$;

  -

  $L_{\langle u,l,l,u,u,l\rangle }\left(O_{88}\right)=\langle u,l,l,u,u,l,\widehat{l},u,l,l,u,u,l,\widehat{u},l,u\rangle$

  $=\langle u,l,l,u,u,\widehat{l},l,u,l,l,u,u,l,\widehat{u},l,u\rangle$

  $=\langle u,l,l,u,u,\widehat{l},l,l,u,u,l,\widehat{u},l,u\rangle$

  $=\langle u,l,l,u,u,l,\widehat{l},l,u,u,l,\widehat{u},l,u\rangle$$=\langle u,l,\widehat{l},l,u,u,l,\widehat{u},l,u\rangle$

  $=\langle D\rangle \odot \langle E\rangle \odot \langle F\rangle \odot \langle A\rangle$, i.e., $\left(O_{82}\right)$;

  -

  $L_{\langle u,l\rangle }\left(O_{88}\right)=\langle u,l,\widehat{l},u,l,l,u,u,l,\widehat{u},l,u\rangle =$$\langle u,\widehat{l},l,u,l,l,u,u,l,\widehat{u},l,u\rangle$

  $=\langle u,\widehat{l},l,l,u,u,l,\widehat{u},l,u\rangle$$=\langle u,l,\widehat{l},l,u,u,l,\widehat{u},l,u\rangle =L_{\langle u,l\rangle }\left(\langle 40\rangle \right)$

  $=\langle D\rangle \odot \langle E\rangle \odot \langle F\rangle \odot \langle A\rangle$, i.e., $\left(O_{82}\right)$.

Finally, we will prove that the alternating application of the operations $\left(r_1\right),\dots ,\left(r_6\right)$ and $\left(l_1\right),\dots ,\left(l_6\right)$ on the operator $\langle u,\widehat{l},\widehat{u},l\rangle$ leads to the determination of all convergence operators specified by ${\mathcal{F}}^{(s,s)}\circ {\pi }^n$ for an odd natural number s, listed in part (vi) of the theorem.

• Type $\langle u,\widehat{l},\widehat{u},l,h_s,\dots ,h_1\rangle =R_{\langle h_s,\dots ,h_1\rangle }\left(\langle u,\widehat{l},\widehat{u},l\rangle \right)$ $=R_{\langle h_s,\dots ,h_1\rangle }\left(O_{91}\right)$:

  -

  $R_{\langle l,u\rangle }\left(O_{91}\right)=\langle u,\widehat{l},\widehat{u},l,l,u,\rangle =\langle G\rangle \odot \langle A\rangle$, i.e., $\left(O_{92}\right)$;

  -

  $R_{\langle l,u,u,l,l,u\rangle }\left(O_{91}\right)=\langle u,\widehat{l},\widehat{u},l,u,l,l,u,u,l,l,u\rangle =\langle u,\widehat{l},\widehat{u},l,u,l,l,u\rangle$

  $=\langle u,\widehat{l},\widehat{u},l,l,u\rangle =\langle G\rangle \odot \langle A\rangle$, i.e., $\left(O_{92}\right)$;

  -

  $R_{\langle u,l,l,u\rangle }\left(O_{91}\right)=\langle u,\widehat{l},\widehat{u},l,u,l,l,u\rangle$$=\langle u,\widehat{l},\widehat{u},l,l,u\rangle$

  $=\langle G\rangle \odot \langle A\rangle$, i.e., $\left(O_{92}\right)$;

  -

  $R_{\langle l,u,u,l\rangle }\left(O_{91}\right)=\langle u,\widehat{l},\widehat{u},l,l,u,u,l\rangle =\langle G\rangle \odot \langle A\rangle \odot \langle B\rangle$, i.e., $\left(O_{93}\right)$;

  -

  $R_{\langle u,l,l,u,u,l\rangle }\left(O_{91}\right)=\langle u,\widehat{l},\widehat{u},l,u,l,l,u,u,l\rangle$$=\langle u,\widehat{l},\widehat{u},l,l,u,u,l\rangle =R_{\langle l,u,u,l\rangle }\left(O_{91}\right)$

  $=\langle G\rangle \odot \langle A\rangle \odot \langle B\rangle$, i.e., $\left(O_{93}\right)$;

  -

  $R_{\langle u,l\rangle }\left(O_{91}\right)=\langle u,\widehat{l},\widehat{u},l,u,l\rangle =\langle u,\widehat{l},\widehat{u},l\rangle =\langle G\rangle$, i.e., $\left(O_{91}\right)$.

• Type $\langle h_{2n},\dots ,h_3,u,\widehat{l},\widehat{u},l\rangle =L_{\langle h_{2n},\dots ,h_3\rangle }\left(\langle u,\widehat{l},\widehat{u},l\rangle \right)$ $=L_{\langle h_{2n},\dots ,h_3\rangle }\left(O_{91}\right)$:

  -

  $L_{\langle l,u\rangle }\left(O_{91}\right)=\langle l,u,u,\widehat{l},\widehat{u},l\rangle =\langle C\rangle \odot \langle G\rangle$, i.e., $\left(O_{94}\right)$;

  -

  $L_{\langle l,u,u,l,l,u\rangle }\left(O_{91}\right)=\langle l,u,u,l,l,u,u,\widehat{l},\widehat{u},l\rangle =\langle l,u,u,l,l,u,u,l,u,\widehat{l},\widehat{u},l\rangle$

  $=\langle l,u,u,l,u,\widehat{l},\widehat{u},l\rangle =\langle l,u,u,\widehat{l},\widehat{u},l\rangle$

  $=\langle C\rangle \odot \langle G\rangle$, i.e., $\left(O_{94}\right)$;

  -

  $L_{\langle u,l,l,u\rangle }\left(O_{91}\right)=\langle u,l,l,u,u,\widehat{l},\widehat{u},l\rangle =\langle D\rangle \odot \langle C\rangle \odot \langle G\rangle$, i.e., $\left(O_{95}\right)$;

  -

  $L_{\langle l,u,u,l\rangle }\left(O_{91}\right)=\langle l,u,u,l,u,\widehat{l},\widehat{u},l\rangle =\langle l,u,u,\widehat{l},\widehat{u},l\rangle$

  $=\langle C\rangle \odot \langle G\rangle$, i.e., $\left(O_{94}\right)$;

  -

  $L_{\langle u,l,l,u,u,l\rangle }\left(O_{91}\right)=\langle u,l,l,u,u,l,u,\widehat{l},\widehat{u},l\rangle =\langle u,l,l,u,u,\widehat{l},\widehat{u},l\rangle$

  $=\langle D\rangle \odot \langle C\rangle \odot \langle G\rangle$, i.e., $\left(O_{95}\right)$;

  -

  $L_{\langle u,l\rangle }\left(O_{91}\right)=\langle u,l,u,\widehat{l},\widehat{u},l\rangle =$$\langle u,\widehat{l},\widehat{u},l\rangle =\langle G\rangle$, i.e., $\left(O_{91}\right)$.

• Type $\langle h_{2n},\dots ,h_5,u,\widehat{l},\widehat{u},l,l,u\rangle =L_{\langle h_{2n},\dots ,h_5\rangle }\left(\langle u,\widehat{l},\widehat{u},l,l,u\rangle \right)$ $=L_{\langle h_{2n},\dots ,h_5\rangle }\left(O_{92}\right)$:

  -

  $L_{\langle l,u\rangle }\left(O_{92}\right)=\langle l,u,u,\widehat{l},\widehat{u},l,l,u\rangle =\langle C\rangle \odot \langle G\rangle \odot \langle A\rangle$, i.e., $\left(O_{96}\right)$;

  -

  $L_{\langle l,u,u,l,l,u\rangle }\left(O_{92}\right)=\langle l,u,u,l,l,u,u,\widehat{l},\widehat{u},l,l,u\rangle =\langle l,u,u,l,l,u,u,l,u,\widehat{l},\widehat{u},l,l,u\rangle$

  $=\langle l,u,u,l,u,\widehat{l},\widehat{u},l,l,u\rangle =\langle l,u,u,\widehat{l},\widehat{u},l,l,u\rangle$,

  $=\langle C\rangle \odot \langle G\rangle \odot \langle A\rangle$, i.e., $\left(O_{96}\right)$;

  -

  $L_{\langle u,l,l,u\rangle }\left(O_{92}\right)=\langle u,l,l,u,u,\widehat{l},\widehat{u},l,l,u\rangle$

  $=\langle D\rangle \odot \langle C\rangle \odot \langle G\rangle \odot \langle A\rangle$, i.e., $\left(O_{97}\right)$;

  -

  $L_{\langle l,u,u,l\rangle }\left(O_{92}\right)=\langle l,u,u,l,u,\widehat{l},\widehat{u},l,l,u\rangle =\langle l,u,u,\widehat{l},\widehat{u},l,l,u\rangle$

  $=\langle C\rangle \odot \langle G\rangle \odot \langle A\rangle$, i.e., $\left(O_{96}\right)$;

  -

  $L_{\langle u,l,l,u,u,l\rangle }\left(O_{92}\right)=\langle u,l,l,u,u,l,u,\widehat{l},\widehat{u},l,l,u\rangle =\langle u,l,l,u,u,\widehat{l},\widehat{u},l,l,u\rangle$

  $=\langle D\rangle \odot \langle C\rangle \odot \langle G\rangle \odot \langle A\rangle$, i.e., $\left(O_{97}\right)$;

  -

  $L_{\langle u,l\rangle }\left(O_{92}\right)=\langle u,l,u,\widehat{l},\widehat{u},l,l,u\rangle =$$\langle u,\widehat{l},\widehat{u},l,l,u\rangle$

  $=\langle G\rangle \odot \langle A\rangle$, i.e., $\left(O_{92}\right)$.

• Type $\langle h_{2n},\dots ,h_7,u,\widehat{l},\widehat{u},l,l,u,u,l\rangle =L_{\langle h_{2n},\dots ,h_7\rangle }\left(\langle u,\widehat{l},\widehat{u},l,l,u,u,l\rangle \right)$
  $=L_{\langle h_{2n},\dots ,h_7\rangle }\left(O_{93}\right)$:

  -

  $L_{\langle l,u\rangle }\left(O_{93}\right)=\langle l,u,u,\widehat{l},\widehat{u},l,l,u,u,l\rangle$

  $=\langle C\rangle \odot \langle G\rangle \odot \langle A\rangle \odot \langle B\rangle$, i.e., $\left(O_{98}\right)$;

  -

  $L_{\langle l,u,u,l,l,u\rangle }\left(O_{93}\right)=\langle l,u,u,l,l,u,u,\widehat{l},\widehat{u},l,l,u,u,l\rangle$

  $=\langle l,u,u,l,l,u,u,l,u,\widehat{l},\widehat{u},l,l,u,u,l\rangle$$=\langle l,u,u,l,u,\widehat{l},\widehat{u},l,l,u,u,l\rangle$

  $=\langle l,u,u,\widehat{l},\widehat{u},l,l,u,u,l\rangle$

  $=\langle C\rangle \odot \langle G\rangle \odot \langle A\rangle \odot \langle B\rangle$, i.e., $\left(O_{98}\right)$;

  -

  $L_{\langle u,l,l,u\rangle }\left(O_{93}\right)=\langle u,l,l,u,u,\widehat{l},\widehat{u},l,l,u,u,l\rangle$

  $=\langle D\rangle \odot \langle C\rangle \odot \langle G\rangle \odot \langle A\rangle \odot \langle B\rangle$, i.e., $\left(O_{99}\right)$;

  -

  $L_{\langle l,u,u,l\rangle }\left(O_{93}\right)=\langle l,u,u,l,u,\widehat{l},\widehat{u},l,l,u,u,l\rangle =\langle l,u,u,\widehat{l},\widehat{u},l,l,u,u,l\rangle$

  $=\langle C\rangle \odot \langle G\rangle \odot \langle A\rangle \odot \langle B\rangle$, i.e., $\left(O_{98}\right)$;

  -

  $L_{\langle u,l,l,u,u,l\rangle }\left(O_{93}\right)=\langle u,l,l,u,u,l,u,\widehat{l},\widehat{u},l,l,u,u,l\rangle =\langle u,l,l,u,u,\widehat{l},\widehat{u},l,l,u,u,l\rangle$

  $=\langle D\rangle \odot \langle C\rangle \odot \langle G\rangle \odot \langle A\rangle \odot \langle B\rangle$, i.e., $\left(O_{99}\right)$;

  -

  $L_{\langle u,l\rangle }\left(O_{93}\right)=\langle u,l,u,\widehat{l},\widehat{u},l,l,u,u,l\rangle =\langle u,\widehat{l},\widehat{u},l,l,u,u,l\rangle$

  $=\langle G\rangle \odot \langle A\rangle \odot \langle B\rangle$, i.e., $\left(O_{93}\right)$.

The proof is finished. □

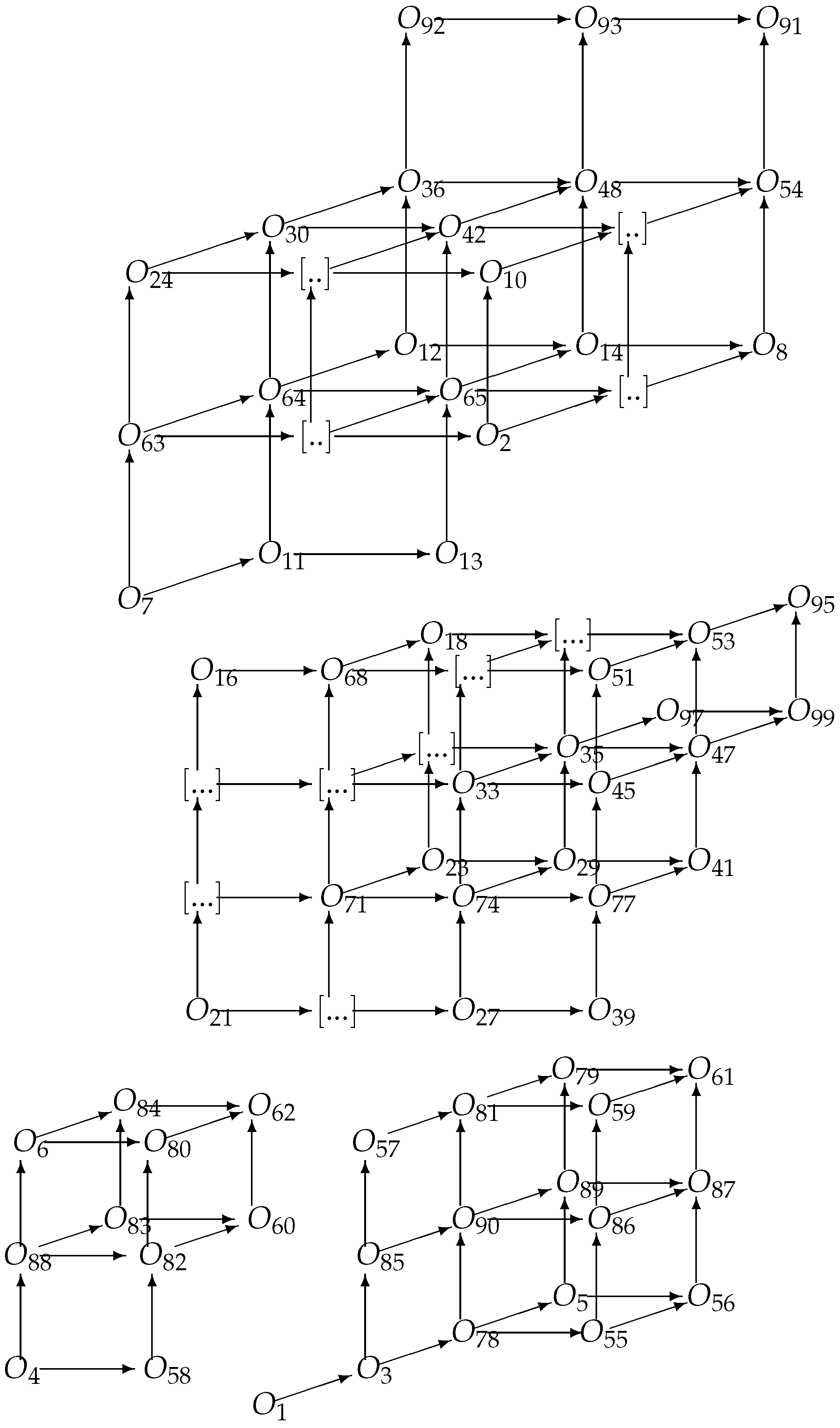
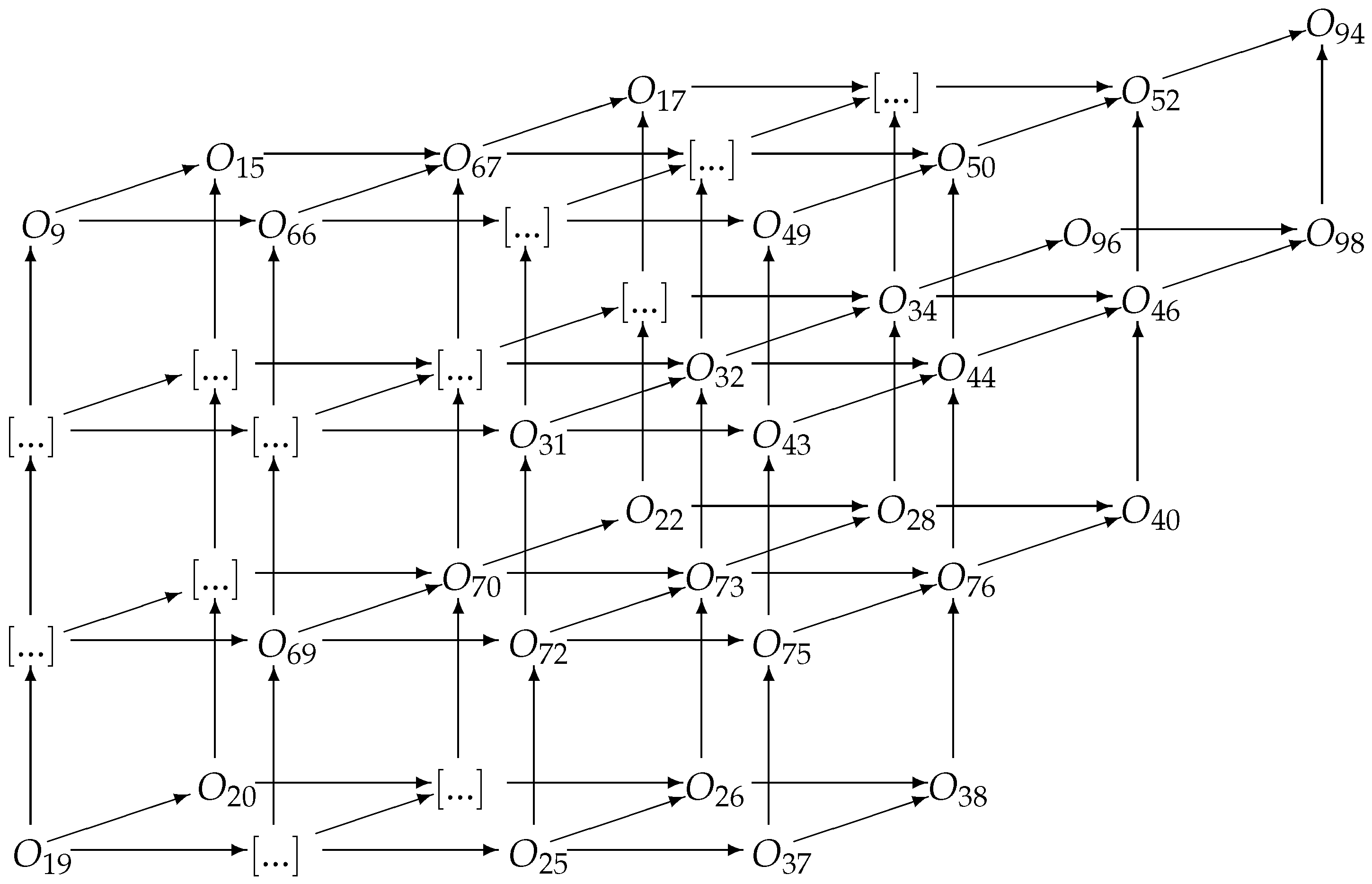
Finally, in the diagrams below, we present the relationships between the studied here operators, where we will use only the numbers used in the denotations of the operators listed in the last theorem.

Diagrams.

4. Conclusions

Various types of continuity of multifunctions and types of convergences of nets of multifunctions examined in the literature on the subject are characterized uniformly, based on the terminology proposed here. The proposed concept is fundamentally algebraic, yet it is grounded in topological foundations. Namely, two special functions, u and l, have a topological character. Any kind of convergence is representable by a (2n + 2)-tuple, n = 1, 2, … of the functions u and l with special conditions on their compositions. A monoid of special three-parameter functions called products describes the set of all possible structures and forms the domain space of the convergence operators. So, the presented concept is essentially an algorithm designed for constructing convergence operators. Additionally, we establish some general theorems about the necessary and sufficient conditions for the continuity of the limit multifunctions without any assumptions about the type of continuity of the members of the nets. The algebraic nature of the proposed concept suggests its potential application in computer science theory.