Topological Transformations in Hand Posture: A Biomechanical Strategy for Mitigating Raynaud’s Phenomenon Symptoms
Abstract
1. Introduction
2. Materials and Methods
- Initializing the thermal field using empirical temperature data;
- Solving the heat diffusion equation iteratively using explicit time-stepping;
- Updating the blood viscosity and flow properties based on local temperature changes;
- Tracking the resultant changes in vascular perfusion.
Summary of Key Parameters Used in Heat Transfer and Blood Flow Simulations
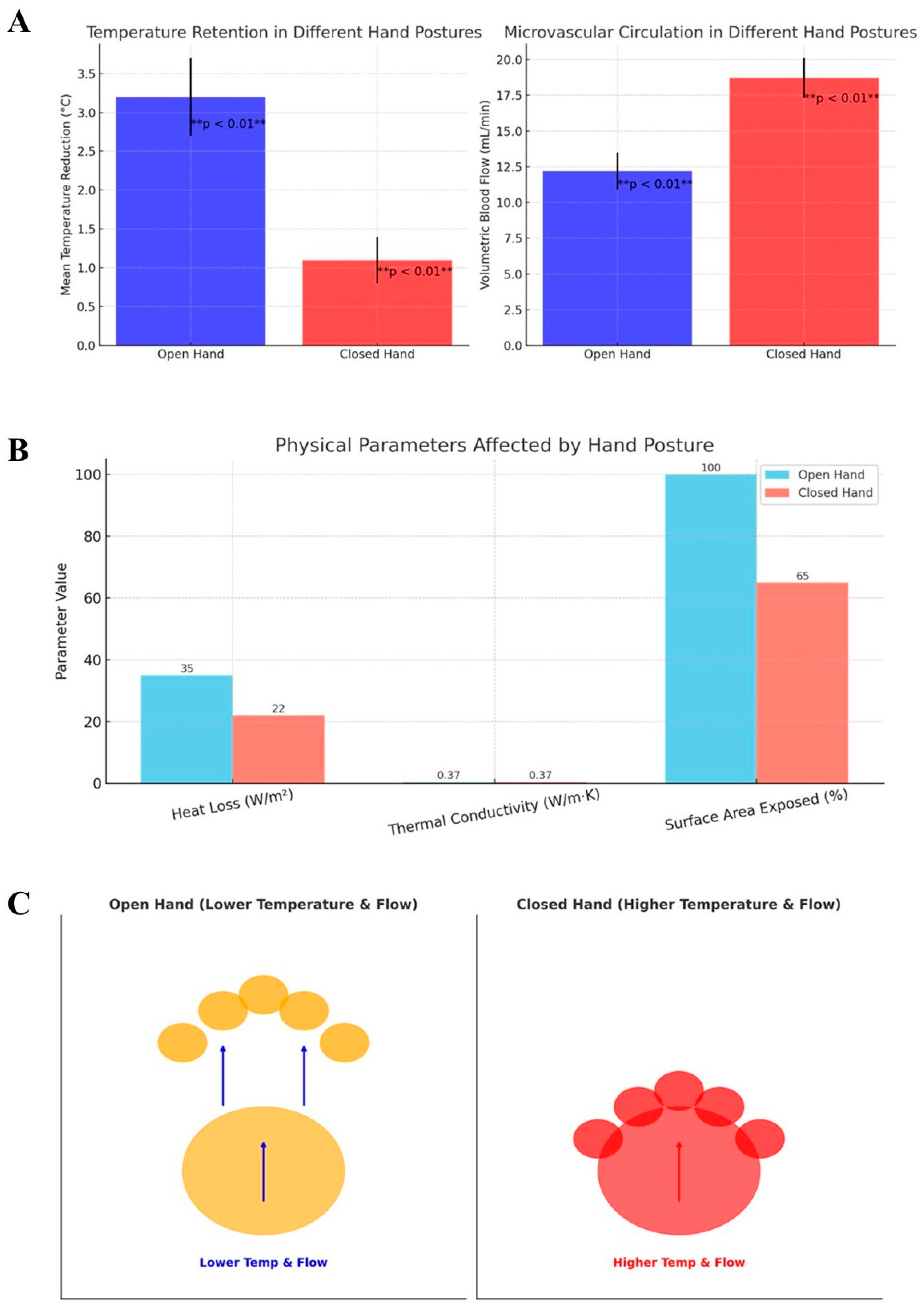
3. Results
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Haque, A.; Hughes, M. Raynaud’s phenomenon. Clin. Med. 2020, 20, 580–587. [Google Scholar] [CrossRef] [PubMed]
- Teaw, S.; Gupta, A.; Williams, A.; Wilson, F.P.; Sumpio, B.J.; Sumpio, B.E.; Hinchcliff, M. Hyperspectral imaging in systemic sclerosis-associated Raynaud phenomenon. Arthritis Res. Ther. 2023, 25, 10. [Google Scholar] [CrossRef] [PubMed]
- Brunner-Ziegler, S.; Dassler, E.; Müller, M.; Pratscher, M.; Forstner, N.F.-F.M.; Koppensteiner, R.; Schlager, O.; Jilma, B. Capillaroscopic differences between primary Raynaud phenomenon and healthy controls indicate potential microangiopathic involvement in benign vasospasms. Vasc. Med. 2024, 29, 200–207. [Google Scholar] [CrossRef] [PubMed]
- Su, K.Y.; Sharma, M.; Kim, H.J.; Kaganov, E.; Hughes, I.; Abdeen, M.H.; Ng, J.H.K. Vasodilators for primary Raynaud’s phenomenon. Cochrane Database Syst. Rev. 2021, 2021, CD006687. [Google Scholar] [CrossRef]
- Ture, H.Y.; Lee, N.Y.; Kim, N.R.; Nam, E.J. Raynaud’s Phenomenon: A Current Update on Pathogenesis, Diagnostic Workup, and Treatment. Vasc. Spec. Int. 2024, 40, 26. [Google Scholar] [CrossRef]
- Busuioc, S.; Kusumaatmaja, H.; Ambruş, V.E. Axisymmetric flows on the torus geometry. J. Fluid Mech. 2020, 901, A9. [Google Scholar] [CrossRef]
- Wang, Y.-P.; Cheng, R.-H.; He, Y.; Mu, L.-Z. Thermal Analysis of Blood Flow Alterations in Human Hand and Foot Based on Vascular-Porous Media Model. Front. Bioeng. Biotechnol. 2022, 9, 786615. [Google Scholar] [CrossRef]
- Brand Paul, W.; Hollister, A.M. Clinical Mechanics of the Hand, Mosby-Year Book, 3rd ed.; Mosby: St. Louis, MO, USA, 1999; ISBN 13:978-0815127864. [Google Scholar]
- Duncan, S.F.; Saracevic, C.E.; Kakinoki, R. Biomechanics of the Hand. Hand Clin. 2013, 29, 483–492. [Google Scholar] [CrossRef]
- Schreuders, T.A.R.; Brandsma, J.W.; Stam, H.J. Functional Anatomy and Biomechanics of the Hand. In Hand Function; Duruöz, M., Ed.; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Chen, Y.-P.; Yeh, C.-I.; Lee, T.-C.; Huang, J.-J.; Pei, Y.-C. Relative posture between head and finger determines perceived tactile direction of motion. Sci. Rep. 2020, 10, 5494. [Google Scholar] [CrossRef]
- Hartmann, F.; Maiello, G.; Rothkopf, C.A.; Fleming, R.W. Estimation of Contact Regions Between Hands and Objects During Human Multi-Digit Grasping. J. Vis. Exp. 2023, 194, e64877. [Google Scholar] [CrossRef]
- Schlesinger, G. Der mechanische Aufbau der künstlichen Glieder. In Ersatzglieder und Arbeitshilfen; Borchardt, M., Hartmann, K., Leymann, R.R., Schlesinger, S., Eds.; Springer: Berlin/Heidelberg, Germany, 1919. [Google Scholar] [CrossRef]
- Hertling, D.; Kessler, R.; Shimandle, S.A. Management of common musculoskeletal disorders, physical therapy principles and methods. Dimens. Crit. Care Nurs. 1990, 9, 279. [Google Scholar] [CrossRef]
- Li, Z.-M.; Yue, G.H. Dependence of finger flexion force on the posture of the nonperforming fingers during key pressing tasks. J. Mot. Behav. 2002, 34, 329–338. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.-S.; Mo, S.-M.; Hwang, J.-J.; Wang, H.; Jung, M.-C. Relaxed hand postures. Jpn. J. Ergon. 2008, 44, 436–439. [Google Scholar] [CrossRef]
- Lee, K.-S.; Jung, M.-C. Flexion and Extension Angles of Resting Fingers and Wrist. Int. J. Occup. Saf. Ergon. 2014, 20, 91–101. [Google Scholar] [CrossRef]
- Romano, D.; Tamè, L.; Amoruso, E.; Azañón, E.; Maravita, A.; Longo, M.R. The standard posture of the hand. J. Exp. Psychol. Hum. Percept. Perform. 2019, 45, 1164–1173. [Google Scholar] [CrossRef]
- Jaworski, Ł.; Karpiński, R. Biomechanics of the Human Hand. J. Technol. Exploit. Mech. Eng. 2017, 3, 28–33. [Google Scholar] [CrossRef]
- Tanrıkulu, S.; Bekmez, Ş.; Üzümcügil, A.; Leblebicioğlu, G. Anatomy and Biomechanics of the Wrist and Hand. In Sports Injuries; Doral, M.N., Karlsson, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Wang, T.; Dai, Z.; Potier-Ferry, M.; Xu, F. Curvature-Regulated Multiphase Patterns in Tori. Phys. Rev. Lett. 2023, 130, 048201. [Google Scholar] [CrossRef]
- Wang, G.; Fei, L.; Luo, K.H. Unified Lattice Boltzmann Method with Improved Schemes for Multiphase Flow Simulation: Application to Droplet Dynamics under Realistic Conditions. Phys. Rev. E 2022, 105, 045314. [Google Scholar] [CrossRef]
- Jantzen, R.T. Geodesics on the Torus and other Surfaces of Revolution Clarified Using Undergraduate Physics Tricks with Bonus: Nonrelativistic and Relativistic Kepler Problems. arXiv 2012, arXiv:1212.6206. [Google Scholar]
- Celano, K.; Coll, V.E.; Dodd, J. Why Curves Curve: The Geodesics on the Torus. Math. Mag. 2022, 95, 230–239. [Google Scholar] [CrossRef]
- Levick, J.R.; Michel, C.C. The effects of position and skin temperature on the capillary pressures in the fingers and toes. J. Physiol. 1978, 274, 97–109. [Google Scholar] [CrossRef] [PubMed]
- Ye, Y.; Griffin, M.J. Effects of temperature on reductions in finger blood flow induced by vibration. Int. Arch. Occup. Environ. Health 2011, 84, 315–323. [Google Scholar] [CrossRef] [PubMed]
- Landim, S.F.; Bertolo, M.B.; de Abreu, M.F.M.; Del Rio, A.P.; Mazon, C.C.; Marques-Neto, J.F.; Poole, J.L.; Magalhães, E.d.P. The evaluation of a home-based program for hands in patients with systemic sclerosis. J. Hand Ther. 2019, 32, 313–321. [Google Scholar] [CrossRef] [PubMed]
- Tapia-Haro, R.M.; García-Ríos, M.C.; Castro-Sánchez, A.M.; Toledano-Moreno, S.; Casas-Barragán, A.; Aguilar-Ferrándiz, M.E. Analysis of Hand Function, Upper Limb Disability, and Its Relationship with Peripheral Vascular Alterations in Raynaud’s Phenomenon. Diagnostics 2024, 14, 93. [Google Scholar] [CrossRef]
- Malakoutikhah, H.; Latt, L.D. Disease-Specific Finite Element Analysis of the Foot and Ankle. Foot Ankle Clin. 2023, 28, 155–172. [Google Scholar] [CrossRef]
- Hirata, K. Heat loss from the upper extremities and clothing thermal comfort. J. Text. Eng. Fash. Technol. 2017, 3, 616–619. [Google Scholar] [CrossRef]
- Klabunde, R.E.; Johnson, P.C. Effects of reduced temperature on capillary flow and reactive hyperemia in red and white skeletal muscle. Microvasc. Res. 1980, 19, 99–107. [Google Scholar] [CrossRef]
- Hales, J.R.S.; Fawcett, A.A.; Bennett, J.W.; Needham, A.D. Thermal control of blood flow through capillaries and arteriovenous anastomoses in skin of sheep. Pflug. Arch. Eur. J. Physiol. 1978, 378, 55–63. [Google Scholar] [CrossRef]
- Mayer, D.B.; Franosch, T.; Mast, C.; Braun, D. Thermophoresis beyond Local Thermodynamic Equilibrium. Phys. Rev. Lett. 2023, 130, 168202. [Google Scholar] [CrossRef]
- Brorsson, S.; Nilsdotter, A.; Pedersen, E.; Bremander, A.; Thorstensson, C. Relationship between finger flexion and extension force in healthy women and women with rheumatoid arthritis. J. Rehabil. Med. 2012, 44, 605–608. [Google Scholar] [CrossRef]
- Biswas, D.; Kartha, S.A. Conceptual modeling of temperature effects on capillary pressure in dead-end pores. Sadhana 2019, 44, 117. [Google Scholar] [CrossRef]
- Dodds, R.; Kuh, D.; Sayer, A.A.; Cooper, R. Physical activity levels across adult life and grip strength in early old age: Updating findings from a British birth cohort. Age Ageing 2013, 42, 794–798. [Google Scholar] [CrossRef] [PubMed]
- Abe, Y.; Nishizawa, M. Electrical aspects of skin as a pathway to engineering skin devices. APL Bioeng. 2021, 5, 041509. [Google Scholar] [CrossRef] [PubMed]
- Kolimechkov, S.; Seijo, M.; Swaine, I.; Thirkell, J.; Colado, J.C.; Naclerio, F. Physiological effects of microcurrent and its application for maximising acute responses and chronic adaptations to exercise. Eur. J. Appl. Physiol. 2023, 123, 451–465. [Google Scholar] [CrossRef]
- Shutova, M.S.; Boehncke, W.-H. Mechanotransduction in Skin Inflammation. Cells 2022, 11, 2026. [Google Scholar] [CrossRef]
- Bogert, N.V.; Werner, I.; Kornberger, A.; Meybohm, P.; Moritz, A.; Keller, T.; Stock, U.A.; Beiras-Fernandez, A. Influence of hypothermia and subsequent rewarming upon leukocyte-endothelial interactions and expression of Junctional-Adhesion-Molecules A and B. Sci. Rep. 2016, 6, 21996. [Google Scholar] [CrossRef]
- Peake, J.; Peiffer, J.J.; Abbiss, C.R.; Nosaka, K.; Okutsu, M.; Laursen, P.B.; Suzuki, K. Body temperature and its effect on leukocyte mobilization, cytokines and markers of neutrophil activation during and after exercise. Eur. J. Appl. Physiol. 2008, 102, 391–401. [Google Scholar] [CrossRef]
- Jämsä, J.; Huotari, V.; Savolainen, E.; Syrjälä, H.; Ala-Kokko, T. Analysis of the temperature affects on leukocyte surface antigen expression. J. Clin. Lab. Anal. 2011, 25, 118–125. [Google Scholar] [CrossRef]
- Köllner, B.; Kotterba, G. Temperature dependent activation of leucocyte populations of rainbow trout, Oncorhynchus mykiss, after intraperitoneal immunisation with Aeromonas salmonicida. Fish Shellfish. Immunol. 2002, 12, 35–48. [Google Scholar] [CrossRef]
- Fang, R.; Zhu, H.; Li, Z.; Zhu, X.; Zhang, X.; Huang, Z.; Li, K.; Yan, W.; Huang, Y.; Maisotsenko, V.S.; et al. Temperature Effect on Capillary Flow Dynamics in 1D Array of Open Nanotextured Microchannels Produced by Femtosecond Laser on Silicon. Nanomaterials 2020, 10, 796. [Google Scholar] [CrossRef]
- Grant, S.A.; Bachmann, J. Effect of Temperature on Capillary Pressure; Raats, P.A.C., Smiles, D., Warrick, A.W., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002. [Google Scholar] [CrossRef]
- Szilágyi, T.; Csernyánszky, H.; Csákó, G.; Benkö, K. The influence of hypothermia on arthus-phenomenon and leucotaxis. Spec.-Haemotologica Immunol. 1971, 27, 1469–1470. [Google Scholar] [CrossRef]
| Parameter | Value | Unit | Description |
|---|---|---|---|
| Thermal conductivity (tissue) | 0.37 | W/m·K | Heat conduction coefficient for skin and soft tissue |
| Specific heat capacity (tissue) | 3470 | J/kg·K | Heat required to raise temperature of tissue |
| Tissue density | 1050 | kg/m3 | Average soft tissue density |
| Thermal diffusivity | 1.4 × 10−7 | m2/s | Derived from α = k/(ρcp) \alpha = k/(\rho c_p) α = k/(ρcp) |
| Blood viscosity | 3.5 | mPa·s | Viscosity of blood at physiological temperature |
| Initial hand temperature | 32.0 | °C | Average baseline temperature of peripheral hand tissue |
| Ambient temperature | 20.0 | °C | External environment temperature |
| Time step duration | 0.5 | seconds | Duration of each simulation step |
| Total simulation time | 60 | seconds | Total duration for thermal and flow evolution |
| Grid resolution (mesh) | 100 × 100 | nodes | Discretized simulation grid |
| Boundary conditions | Convective & radiative | — | Applied at exposed surfaces to simulate heat exchange |
| Convective heat transfer coefficient | 10 | W/m2·K | Assumed for natural air convection around the hand |
| Blood flow model | Darcy-Weisbach | — | Used to estimate pressure–flow relationship |
| Heat transfer model | Heat diffusion equation | — | Solves temporal-spatial temperature distribution |
| Solver scheme | Explicit finite-difference | — | Numerical scheme used in simulation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tozzi, A. Topological Transformations in Hand Posture: A Biomechanical Strategy for Mitigating Raynaud’s Phenomenon Symptoms. Int. J. Topol. 2025, 2, 6. https://doi.org/10.3390/ijt2020006
Tozzi A. Topological Transformations in Hand Posture: A Biomechanical Strategy for Mitigating Raynaud’s Phenomenon Symptoms. International Journal of Topology. 2025; 2(2):6. https://doi.org/10.3390/ijt2020006
Chicago/Turabian StyleTozzi, Arturo. 2025. "Topological Transformations in Hand Posture: A Biomechanical Strategy for Mitigating Raynaud’s Phenomenon Symptoms" International Journal of Topology 2, no. 2: 6. https://doi.org/10.3390/ijt2020006
APA StyleTozzi, A. (2025). Topological Transformations in Hand Posture: A Biomechanical Strategy for Mitigating Raynaud’s Phenomenon Symptoms. International Journal of Topology, 2(2), 6. https://doi.org/10.3390/ijt2020006






