When the Anomalistic, Draconitic and Sidereal Orbital Periods Do Not Coincide: The Impact of Post-Keplerian Perturbing Accelerations
Abstract
1. Introduction
2. The pK Accelerations
2.1. The 1 pN Gravitoelectric Acceleration
2.2. The 1 pN Gravitomagnetic Lense–Thirring Acceleration
2.3. The Newtonian Quadrupolar Acceleration
3. The Apsidal Period
3.1. General Calculational Scheme
3.2. The 1pN Gravitoelectric Correction
3.3. The 1pN Gravitomagnetic Lense–Thirring Correction
3.4. The Newtonian Quadrupolar Correction
4. The Draconitic Period
4.1. General Calculational Scheme
4.2. The 1pN Gravitoelectric Correction
4.3. The 1 pN Gravitomagnetic Lense–Thirring Correction
4.4. The Newtonian Quadrupolar Correction
5. The Sidereal Period
5.1. General Calculational Scheme
5.2. The 1 pN Gravitoelectric Correction
5.3. The 1 pN Gravitomagnetic Lense–Thirring Correction
5.4. The Newtonian Quadrupolar Correction
6. Some Numerical Evaluations
7. Summary and Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mashhoon, B. Gravitoelectromagnetism. In Reference Frames and Gravitomagnetism; Pascual-Sánchez, J.F., Floría, L., San Miguel, A., Vicente, F., Eds.; World Scientific: Singapore, 2001. [Google Scholar]
- Mashhoon, B. Gravitoelectromagnetism: A Brief Review. In The Measurement of Gravitomagnetism: A Challenging Enterprise; Iorio, L., Ed.; Nova Science: Hauppauge, NY, USA, 2007; pp. 29–39. [Google Scholar]
- Capderou, M. Satellites: Orbits and Missions; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Iorio, L. Post–Keplerian corrections to the orbital periods of a two–body system and their measurability. Mon. Not. Roy. Astron. Soc. 2016, 460, 2445–2452. [Google Scholar] [CrossRef]
- Deeg, H.J.; Belmonte, J.A. Handbook of Exoplanets; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Kitchin, C. Exoplanets. Finding, Exploring, and Understanding Alien Worlds; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Mason, J.W. Exoplanets. Detection, Formation, Properties, Habitability; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Perryman, M. The Exoplanet Handbook, 2nd ed.; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Seager, S. Exoplanets; University of Arizona Press: Tucson, AZ, USA, 2011. [Google Scholar]
- Adams, F.C.; Laughlin, G. Effects of Secular Interactions in Extrasolar Planetary Systems. Astrophys. J. 2006, 649, 992–1003. [Google Scholar] [CrossRef]
- Adams, F.C.; Laughlin, G. Long-Term Evolution of Close Planets Including the Effects of Secular Interactions. Astrophys. J. 2006, 649, 1004–1009. [Google Scholar] [CrossRef]
- Adams, F.C.; Laughlin, G. Relativistic Effects in Extrasolar Planetary Systems. Int. J. Mod. Phys. D 2006, 15, 2133–2140. [Google Scholar] [CrossRef]
- Blanchet, L.; Hébrard, G.; Larrouturou, F. Detecting the general relativistic orbital precession of the exoplanet HD 80606b. Astron. Astrophys. 2019, 628, A80. [Google Scholar] [CrossRef]
- Antoniciello, G.; Borsato, L.; Lacedelli, G.; Nascimbeni, V.; Barragán, O.; Claudi, R. Detecting general relativistic orbital precession in transiting hot Jupiters. Mon. Not. R. Astron. Soc. 2021, 505, 1567–1574. [Google Scholar] [CrossRef]
- Damiani, C.; Lanza, A.F. Prospecting transit duration variations in extrasolar planetary systems. Astron. Astrophys. 2011, 535, A116. [Google Scholar] [CrossRef]
- Eibe, M.T.; Cuesta, L.; Ullán, A.; Pérez-Verde, A.; Navas, J. Analysis of variations in transit time and transit duration in WASP–3. Evidence of secular perturbations reconsidered. Mon. Not. R. Astron. Soc. 2012, 423, 1381–1389. [Google Scholar] [CrossRef]
- Fukui, A.; Narita, N.; Tristram, P.J.; Sumi, T.; Abe, F.; Itow, Y.; Sullivan, D.J.; Bond, I.A.; Hirano, T.; Tamura, M.; et al. Measurements of Transit Timing Variations for WASP–5b. Publ. Astron. Soc. Pac. 2011, 63, 287–300. [Google Scholar] [CrossRef]
- Gou, X.; Pan, X.; Wang, L. General Relativity Testing in Exoplanetary Systems. IOP Conf. Ser. Earth Environ. Sci. 2021, 658, 012051. [Google Scholar] [CrossRef]
- Iorio, L. Are we far from testing general relativity with the transitting extrasolar planet HD 209458b “Osiris”? New Astron. 2006, 11, 490–494. [Google Scholar] [CrossRef]
- Iorio, L. Classical and relativistic node precessional effects in WASP–33b and perspectives for detecting them. Astrophys. Space Sci. 2011, 331, 485–496. [Google Scholar] [CrossRef]
- Iorio, L. Classical and relativistic long–term time variations of some observables for transiting exoplanets. Mon. Not. R. Astron. Soc. 2011, 411, 167–183. [Google Scholar] [CrossRef]
- Jordán, A.; Bakos, G.Á. Observability of the General Relativistic Precession of Periastra in Exoplanets. Astrophys. J. 2008, 685, 543–552. [Google Scholar] [CrossRef]
- Jordán, A.; Bakos, G.Á. Observability of the General Relativistic Precession of Periastra in Exoplanets. In Transiting Planets. Proceedings IAU Symposium No. 253; Pont, F., Sasselov, D., Holman, M., Eds.; Cambridge University Press: Cambridge, UK, 2009; Volume 253, pp. 492–495. [Google Scholar] [CrossRef]
- Kane, S.R.; Horner, J.; Braun, K. Cyclic Transit Probabilities of Long–period Eccentric Planets due to Periastron Precession. Astrophys. J. 2012, 757, 105. [Google Scholar] [CrossRef]
- Kozak, A.; Wojnar, A. Metric—Affine gravity effects on terrestrial exoplanet profiles. Phys. Rev. D 2021, 104, 084097. [Google Scholar] [CrossRef]
- Iorio, L.; Ruggiero, M.L. Constraining the Kehagias–Sfetsos Solution of the Hořava—Lifshitz Modified Gravity with Extrasolar Planets. Open Astron. J. 2010, 3, 167–171. [Google Scholar] [CrossRef]
- Li, L.-S. Parameterized post–Newtonian orbital effects in extrasolar planets. Astrophys. Space Sci. 2012, 341, 323–330. [Google Scholar] [CrossRef]
- Marzari, F.; Nagasawa, M. Influence of general-relativity effects, dynamical tides, and collisions on planet—Planet scattering close to the star. Astron. Astrophys. 2019, 625, A121. [Google Scholar] [CrossRef]
- Pál, A.; Kocsis, B. Periastron precession measurements in transiting extrasolar planetary systems at the level of general relativity. Mon. Not. Roy. Astron. Soc. 2008, 389, 191–198. [Google Scholar] [CrossRef]
- Ragozzine, D.; Wolf, A.S. Probing the Interiors of very Hot Jupiters Using Transit Light Curves. Astrophys. J. 2009, 698, 1778–1794. [Google Scholar] [CrossRef]
- Ruggiero, M.L.; Iorio, L. Probing a r−n modification of the Newtonian potential with exoplanets. J. Cosmol. Astropart. Phys. 2020, 2020, 042. [Google Scholar] [CrossRef]
- Santos, M.V.D.; Mota, D.F. Extrasolar planets as a probe of modified gravity. Phys. Lett. B 2017, 769, 485–490. [Google Scholar] [CrossRef]
- Xie, Y.; Deng, X.-M. On the (im)possibility of testing new physics in exoplanets using transit timing variations: Deviation from inverse–square law of gravity. Mon. Not. Roy. Astron. Soc. 2014, 438, 1832–1838. [Google Scholar] [CrossRef]
- Zhao, S.-S.; Xie, Y. Parametrized post–Newtonian secular transit timing variations for exoplanets. Res. Astron. Astrophys. 2013, 13, 1231–1239. [Google Scholar] [CrossRef]
- Will, C.M. The Confrontation between General Relativity and Experiment. Living Rev. Relativ. 2014, 17, 4. [Google Scholar] [CrossRef] [PubMed]
- Will, C.M. Theory and Experiment in Gravitational Physics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar] [CrossRef]
- Will, C.M.; Yunes, N. Is Einstein still Right? Oxford Universiy Press: Oxford, UK, 2020. [Google Scholar]
- Bertotti, B.; Farinella, P.; Vokrouhlický, D. Physics of the Solar System; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- Brouwer, D.; Clemence, G.M. Methods of Celestial Mechanics; Academic Press: Cambridge, MA, USA, 1961. [Google Scholar]
- Brumberg, V.A. Essential Relativistic Celestial Mechanics; Adam Hilger: London, UK, 1991. [Google Scholar]
- Kopeikin, S.M.; Efroimsky, M.; Kaplan, G. Relativistic Celestial Mechanics of the Solar System; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Poisson, E.; Will, C.M. Gravity. Newtonian, Post—Newtonian, Relativistic; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Roy, A.E. Orbital Motion, 4th ed.; IOP Publishing: Bristol, UK, 2005. [Google Scholar]
- Soffel, M.H. Relativity in Astrometry, Celestial Mechanics and Geodesy; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar] [CrossRef]
- Soffel, M.H.; Han, W.-B. Applied General Relativity; Astronomy and Astrophysics Library; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Damour, T.; Deruelle, N. General relativistic celestial mechanics of binary systems. I. The post–Newtonian motion. Ann. Inst. Henri Poincaré Phys. Théor. 1985, 43, 107–132. [Google Scholar]
- Damour, T.; Soffel, M.; Xu, C. General–relativistic celestial mechanics. IV. Theory of satellite motion. Phys. Rev. D 1994, 49, 618–635. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Ries, J.C.; Tapley, B.D.; Watkins, M.M. Relativistic effects for near—Earth satellite orbit determination. Celest. Mech. Dyn. Astr. 1990, 48, 167–185. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. (Eds.) IERS Conventions (2010); IERS Technical Note; Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010; Volume 36. [Google Scholar]
- Kidder, L.E. Coalescing binary systems of compact objects to (post)5/2–Newtonian order. V. Spin effects. Phys. Rev. D 1995, 52, 821–847. [Google Scholar] [CrossRef]
- Barker, B.M.; O’Connell, R.F. Gravitational two–body problem with arbitrary masses, spins, and quadrupole moments. Phys. Rev. D 1975, 12, 329–335. [Google Scholar] [CrossRef]
- Mioc, V.; Radu, E. Perturbations in the anomalistic period of artificial satellites caused by the direct solar radiation pressure. Astron. Nachr. 1979, 300, 313–315. [Google Scholar] [CrossRef]
- Zhongolovich, I.D. Certain Formulas Related to the Motion of a Material Point Within the Gravitational Field of an Ellipsoid of Revolution. Byul. Inst. Teor. Astron. 1960, 7, 521–536. [Google Scholar]
- Egorov, V.A. Definition of the True Anomaly in Perturbed Motion. Sov. Astron. 1958, 2, 147–149. [Google Scholar]
- Taratynova, G.P. Über die Bewegung von künstlichen Satelliten im nicht-zentralen Schwerefeld der Erde unter Berücksichtigung des Luftwiderstandes. Fortschritte Phys. 1959, 7, 55–64. [Google Scholar] [CrossRef]
- Iorio, L. Post–Keplerian perturbations of the orbital time shift in binary pulsars: An analytical formulation with applications to the galactic center. Eur. Phys. J. C 2017, 77, 439. [Google Scholar] [CrossRef]
- Mioc, V.; Radu, E. The influence of direct solar radiation pressure on the nodal period of artificial earth satellites. Astron. Nachr. 1977, 298, 107–110. [Google Scholar] [CrossRef]
- Ochocimskij, D.E.; Eneev, T.M.; Taratynova, G.P. Bestimmung der Lebensdauer eines künstlichen Erdsatelliten und Untersuchung der säkularen Störungen seiner Bahn. Fortschritte Phys. 1959, 7, 34–54. [Google Scholar] [CrossRef]
- Taff, L. Celestial Mechanics: A Computational Guide for the Practitioner; Wiley: Hoboken, NJ, USA, 1985. [Google Scholar]
- Goldstein, H. Classical Mechanics, 2nd ed.; Addison Wesley: Boston, MA, USA, 1980. [Google Scholar]
- Lorimer, D.; Kramer, M. Handbook of Pulsar Astronomy; Cambridge Observing Handbooks for Research Astronomers; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Montenbruck, O.; Kirschner, M.; D’Amico, S.; Bettadpur, S. E/I–vector separation for safe switching of the GRACE formation. E/I–Vektor Trennung für den sicheren Wechsel der GRACE Formation. Aerosp. Sci. Technol. 2006, 10, 628–635. [Google Scholar] [CrossRef]
- Amelin, V.M. Determination of the Quasi–Nodal Period of the Satellite 1960 ε 3 from Simultaneous Visual Tracking Data. In Trajectories of Artificial Celestial Bodies as Determined from Observations/Trajectoires des Corps Celestes Artificiels Déterminées D’après les Observations; Kovalevsky, J., Ed.; Springer: Berlin/Heidelberg, Germany, 1966; pp. 15–18. [Google Scholar]
- Kassimenko, T.V. Evaluation of the Satellite Period on the Base of Simultaneous Visual Tracking from Two Given Stations. In Trajectories of Artificial Celestial Bodies as Determined from Observations/Trajectoires des Corps Celestes Artificiels Déterminées D’après les Observations; Kovalevsky, J., Ed.; Springer: Berlin/Heidelberg, Germany, 1966; pp. 19–22. [Google Scholar] [CrossRef]
- Zhongolovich, I.D. On the Use of the Results Obtained from Synchronous Observations of the Artificial Satellites of the Earth from the INTEROBS Programme for Scientific Purposes. In Trajectories of Artificial Celestial Bodies as Determined from Observations/Trajectoires des Corps Celestes Artificiels Déterminées D’après les Observations; Kovalevsky, J., Ed.; Springer: Berlin/Heidelberg, Germany, 1966; pp. 1–5. [Google Scholar] [CrossRef]
- Murray, C.D.; Dermott, S.F. Solar System Dynamics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar] [CrossRef]
- Shevchenko, I.I. The Lidov-Kozai Effect-Applications in Exoplanet Research and Dynamical Astronomy; volume 441 of Astrophysics and Space Science Library; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Broucke, R.A.; Cefola, P.J. On the Equinoctial Orbit Elements. Celest. Mech. Dyn. Astr. 1972, 5, 303–310. [Google Scholar] [CrossRef]
- Haswell, C.A. Transiting Exoplanets; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar] [CrossRef]
- Casewell, S.L.; Belardi, C.; Parsons, S.G.; Littlefair, S.P.; Braker, I.P.; Hermes, J.J.; Debes, J.; Vanderbosch, Z.; Burleigh, M.R.; Gänsicke, B.T.; et al. WD1032 + 011, an inflated brown dwarf in an old eclipsing binary with a white dwarf. Mon. Not. R. Astron. Soc. 2020, 497, 3571–3580. [Google Scholar] [CrossRef]
- Lyne, A.G.; Burgay, M.; Kramer, M.; Possenti, A.; Manchester, R.N.; Camilo, F.; Mclaughlin, M.A.; Lorimer, D.R.; D’Amico, N.; Joshi, B.C.; et al. A Double–Pulsar System: A Rare Laboratory for Relativistic Gravity and Plasma Physics. Science 2004, 303, 1153–1157. [Google Scholar] [CrossRef] [PubMed]
- Burgay, M.; D’Amico, N.; Possenti, A.; Manchester, R.N.; Lyne, A.G.; Joshi, B.C.; McLaughlin, M.A.; Kramer, M.; Sarkissian, J.M.; Camilo, F.; et al. An increased estimate of the merger rate of double neutron stars from observations of a highly relativistic system. Nature 2003, 426, 531–533. [Google Scholar] [CrossRef]
- Kramer, M.; Stairs, I.H.; Manchester, R.N.; Mclaughlin, M.A.; Lyne, A.G.; Ferdman, R.D.; Burgay, M.; Lorimer, D.R.; Possenti, A.; D’Amico, N.; et al. Tests of General Relativity from Timing the Double Pulsar. Science 2006, 314, 97–102. [Google Scholar] [CrossRef] [PubMed]
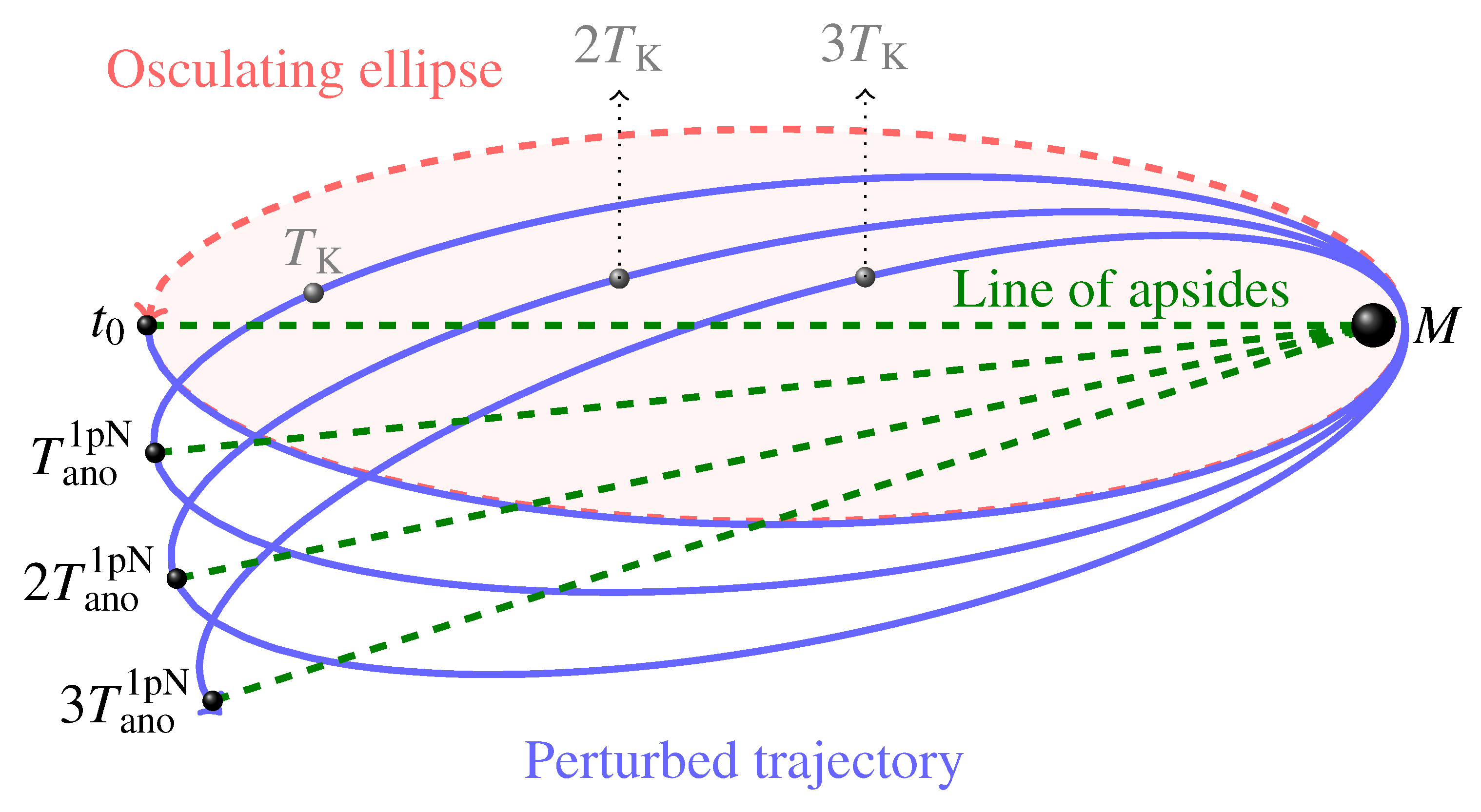
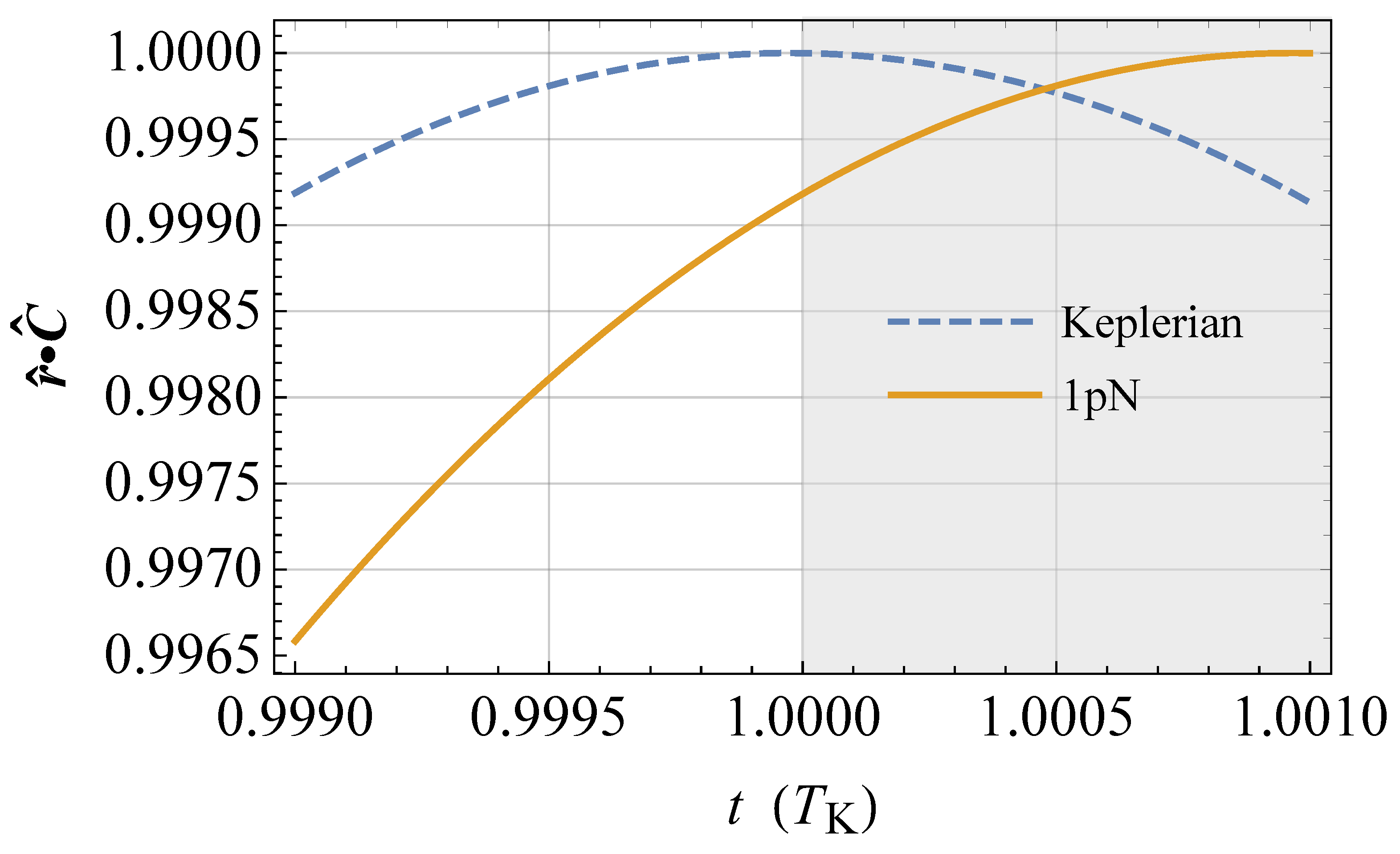
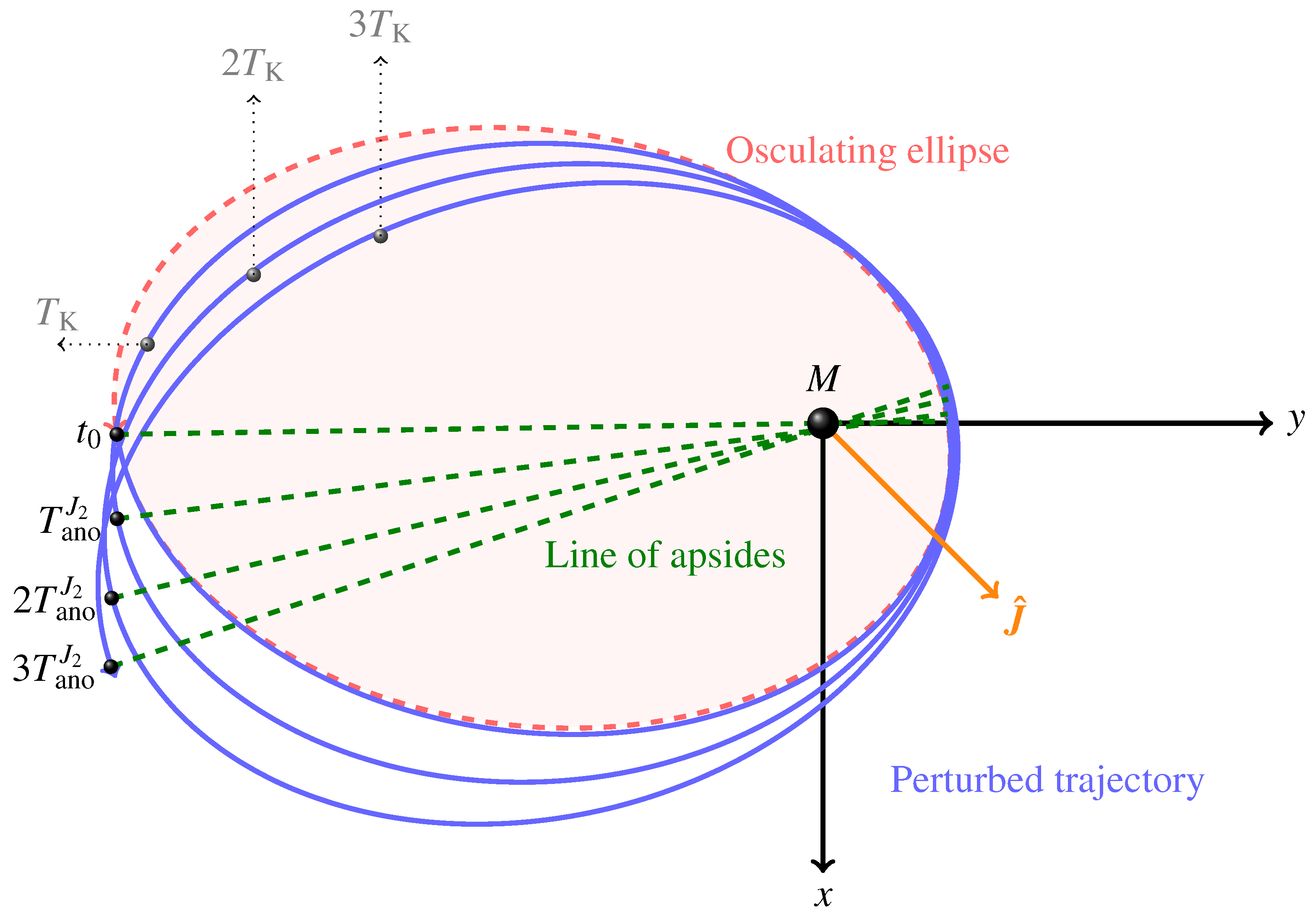

 ()), i.e., ; the semimajor axis is . The physical parameters of the Earth are adopted. The 1 pN acceleration is suitably rescaled in such a way that . The time needed to come back to the initial position on the (fixed) line of nodes so that again is longer than in the Keplerian case by an amount equal to , as shown by the shaded area, in agreement with Equation (79).
()), i.e., ; the semimajor axis is . The physical parameters of the Earth are adopted. The 1 pN acceleration is suitably rescaled in such a way that . The time needed to come back to the initial position on the (fixed) line of nodes so that again is longer than in the Keplerian case by an amount equal to , as shown by the shaded area, in agreement with Equation (79).
 ()), i.e., ; the semimajor axis is . The physical parameters of the Earth are adopted. The 1 pN acceleration is suitably rescaled in such a way that . The time needed to come back to the initial position on the (fixed) line of nodes so that again is longer than in the Keplerian case by an amount equal to , as shown by the shaded area, in agreement with Equation (79).
()), i.e., ; the semimajor axis is . The physical parameters of the Earth are adopted. The 1 pN acceleration is suitably rescaled in such a way that . The time needed to come back to the initial position on the (fixed) line of nodes so that again is longer than in the Keplerian case by an amount equal to , as shown by the shaded area, in agreement with Equation (79).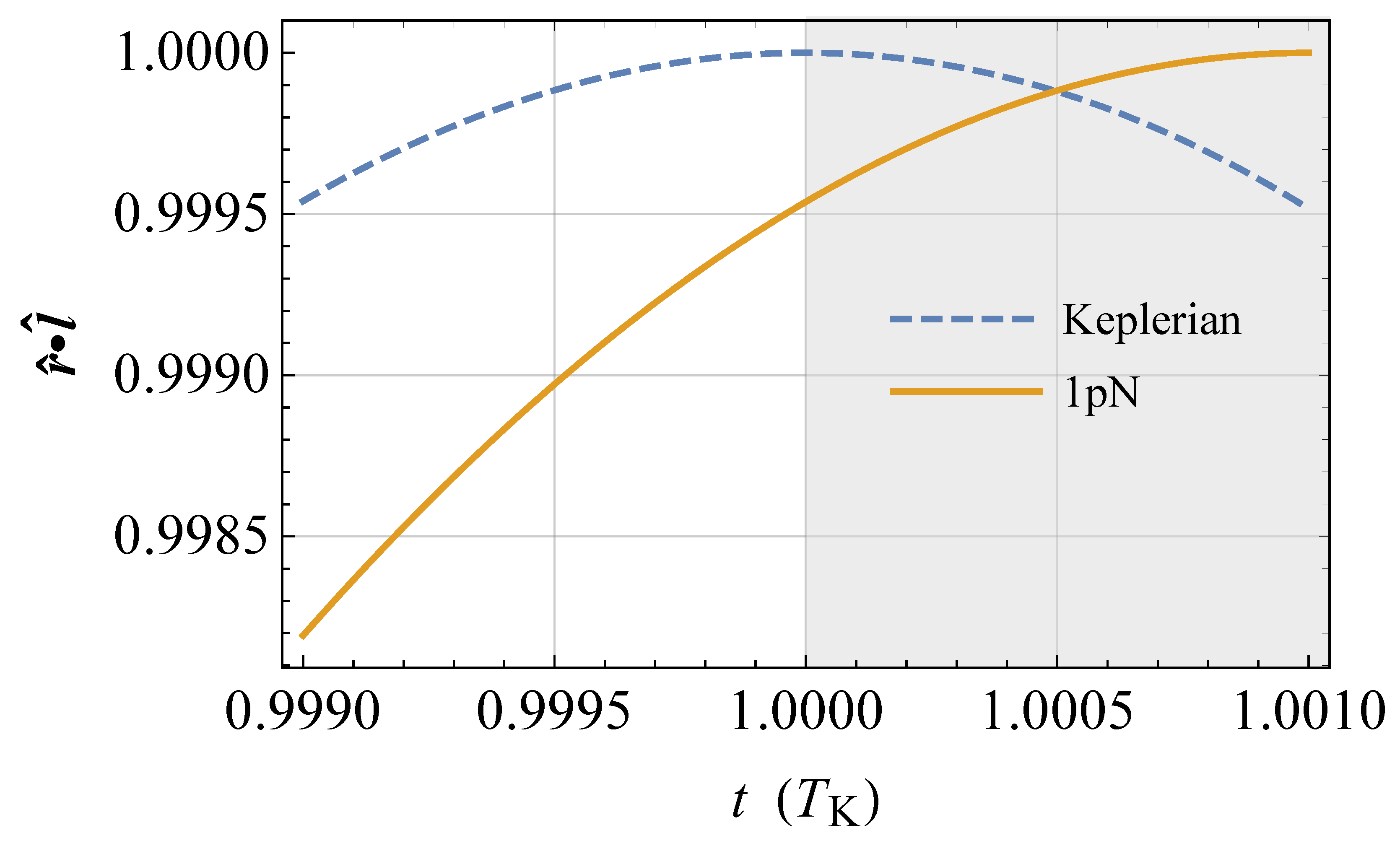

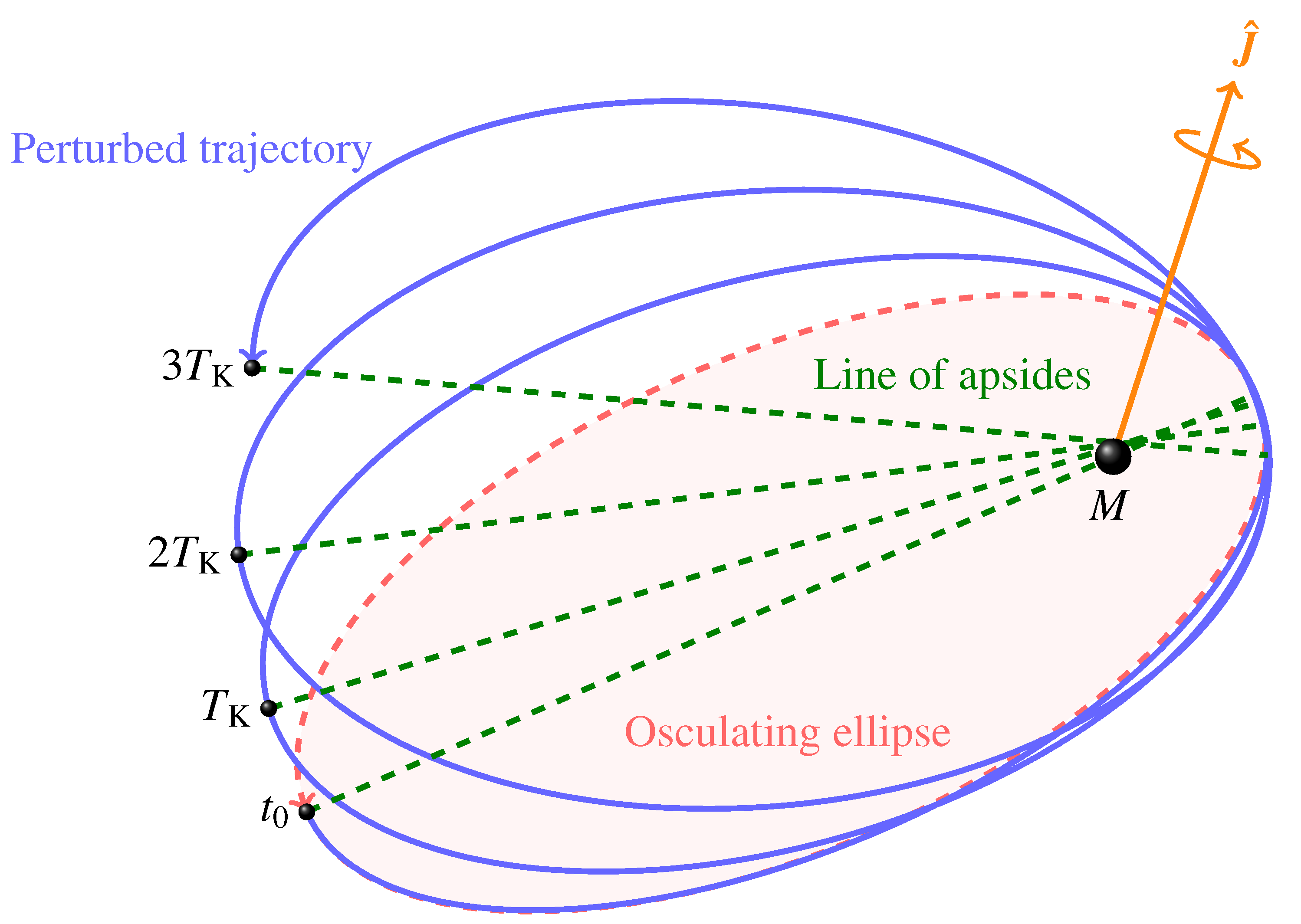
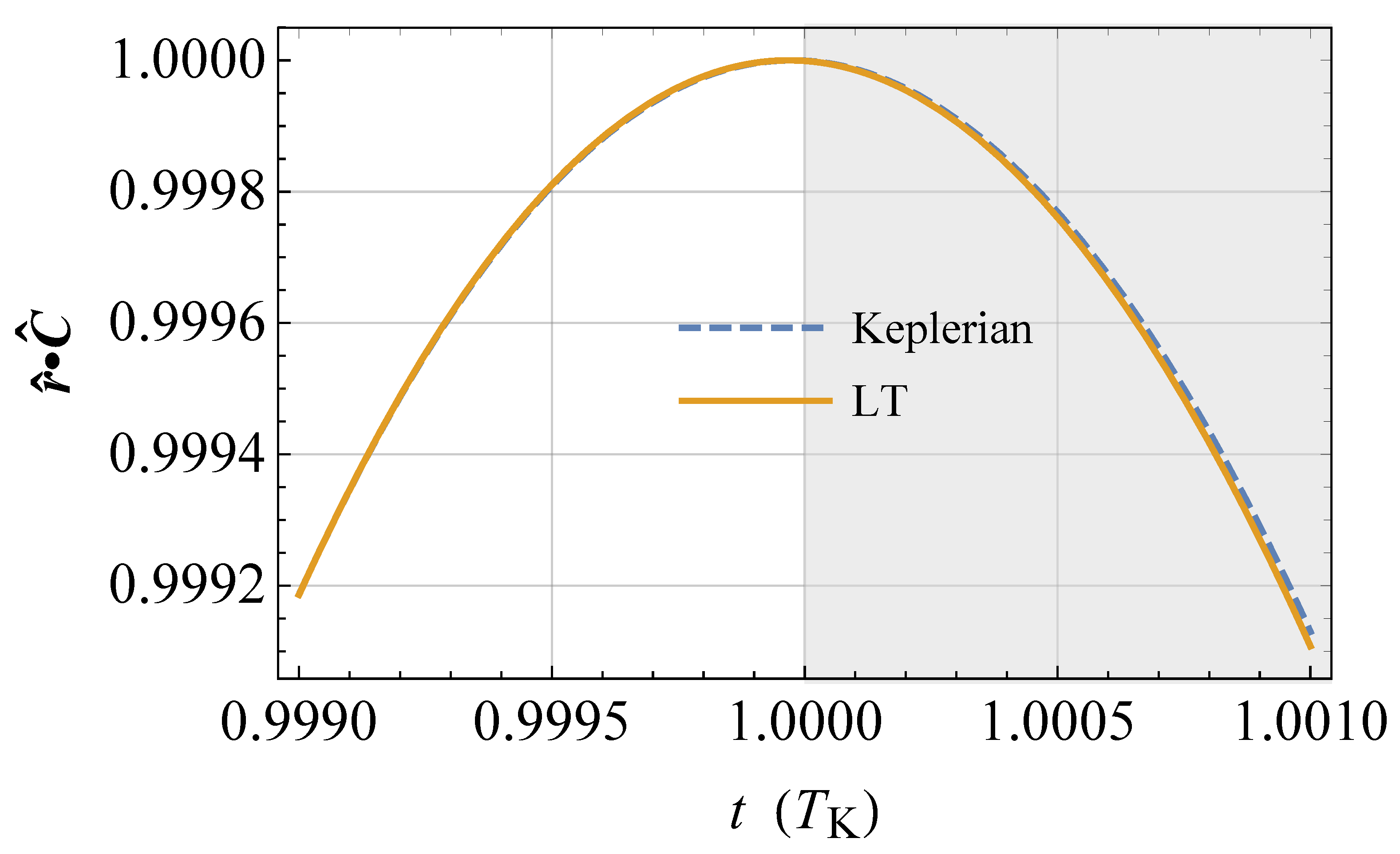
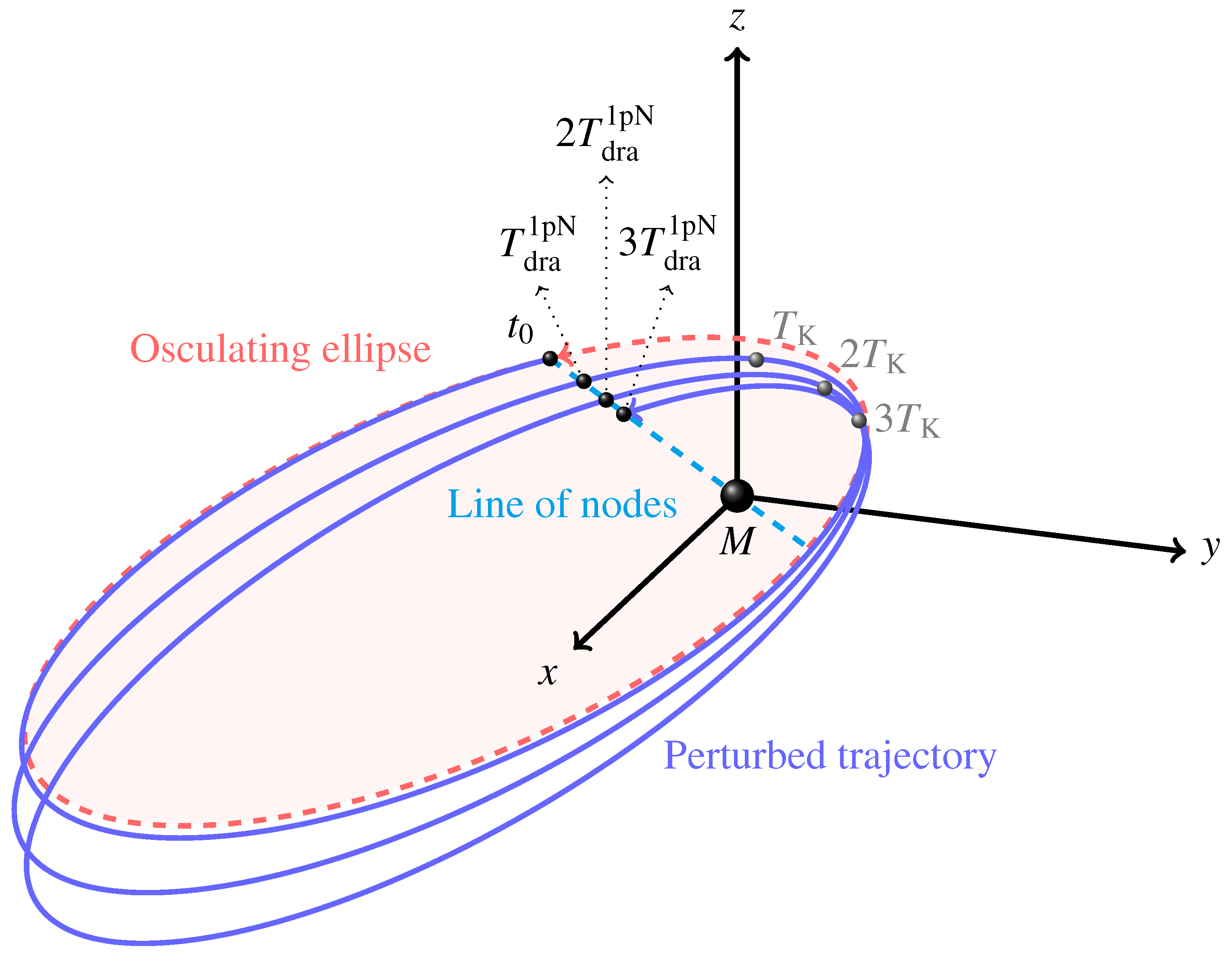
 (), i.e., ; the semimajor axis is . The physical parameters of the Earth are adopted, apart from the spin axis position set by . The LT acceleration is suitably rescaled in such a way that . The time needed to come back to the initial position on the (moving) line of nodes so that again is longer than in the Keplerian case by an amount equal to , as shown by the shaded area, in agreement with Equation (81).
(), i.e., ; the semimajor axis is . The physical parameters of the Earth are adopted, apart from the spin axis position set by . The LT acceleration is suitably rescaled in such a way that . The time needed to come back to the initial position on the (moving) line of nodes so that again is longer than in the Keplerian case by an amount equal to , as shown by the shaded area, in agreement with Equation (81).
 (), i.e., ; the semimajor axis is . The physical parameters of the Earth are adopted, apart from the spin axis position set by . The LT acceleration is suitably rescaled in such a way that . The time needed to come back to the initial position on the (moving) line of nodes so that again is longer than in the Keplerian case by an amount equal to , as shown by the shaded area, in agreement with Equation (81).
(), i.e., ; the semimajor axis is . The physical parameters of the Earth are adopted, apart from the spin axis position set by . The LT acceleration is suitably rescaled in such a way that . The time needed to come back to the initial position on the (moving) line of nodes so that again is longer than in the Keplerian case by an amount equal to , as shown by the shaded area, in agreement with Equation (81).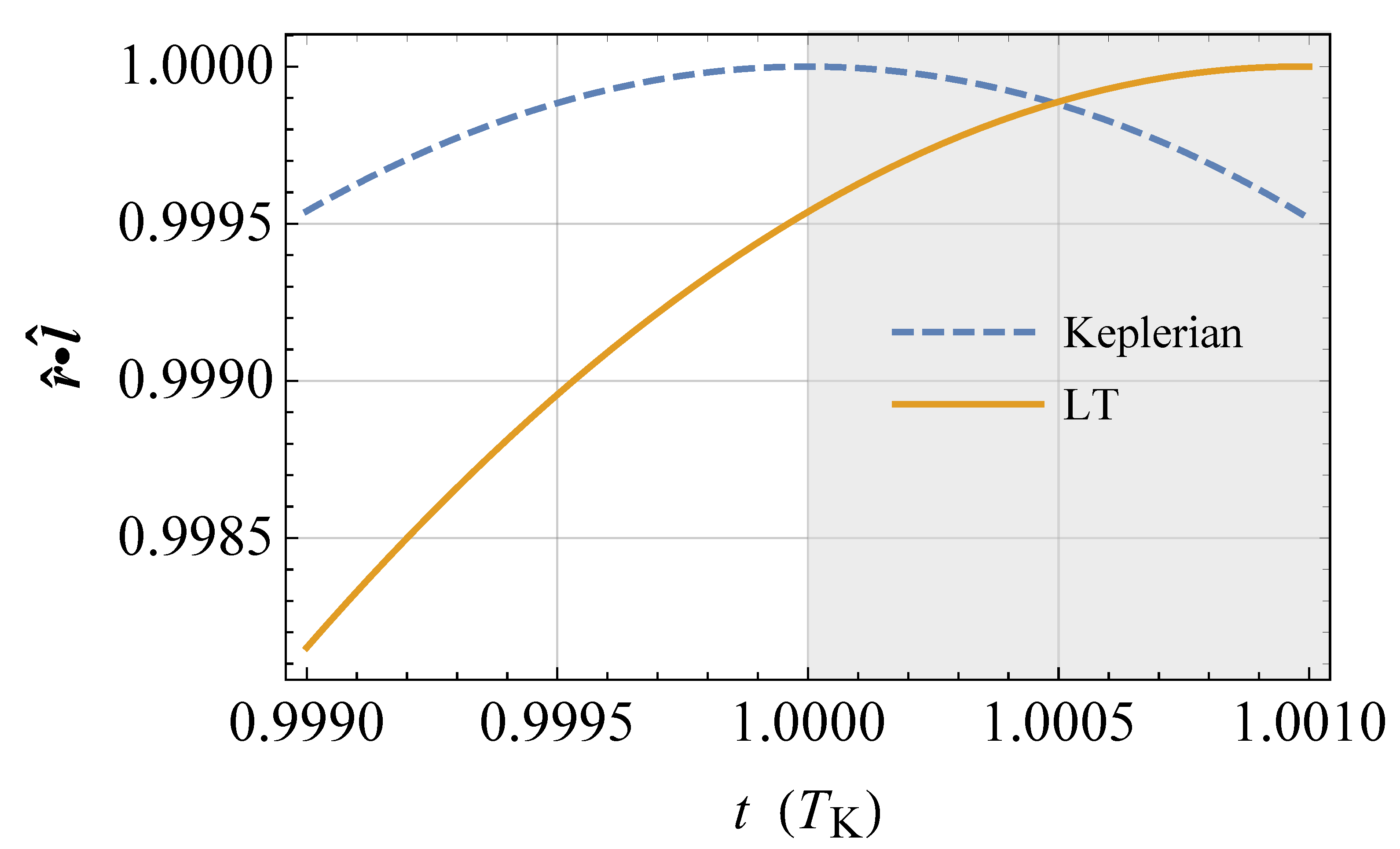

 (), i.e., ; the semimajor axis is . The physical parameters of the Earth are adopted, apart from the spin axis position set by . The acceleration is suitably rescaled in such a way that . The time needed to come back to the initial position on the (moving) line of nodes so that again is longer than in the Keplerian case by an amount equal to , as shown by the shaded area, in agreement with Equation (86).
(), i.e., ; the semimajor axis is . The physical parameters of the Earth are adopted, apart from the spin axis position set by . The acceleration is suitably rescaled in such a way that . The time needed to come back to the initial position on the (moving) line of nodes so that again is longer than in the Keplerian case by an amount equal to , as shown by the shaded area, in agreement with Equation (86).
 (), i.e., ; the semimajor axis is . The physical parameters of the Earth are adopted, apart from the spin axis position set by . The acceleration is suitably rescaled in such a way that . The time needed to come back to the initial position on the (moving) line of nodes so that again is longer than in the Keplerian case by an amount equal to , as shown by the shaded area, in agreement with Equation (86).
(), i.e., ; the semimajor axis is . The physical parameters of the Earth are adopted, apart from the spin axis position set by . The acceleration is suitably rescaled in such a way that . The time needed to come back to the initial position on the (moving) line of nodes so that again is longer than in the Keplerian case by an amount equal to , as shown by the shaded area, in agreement with Equation (86).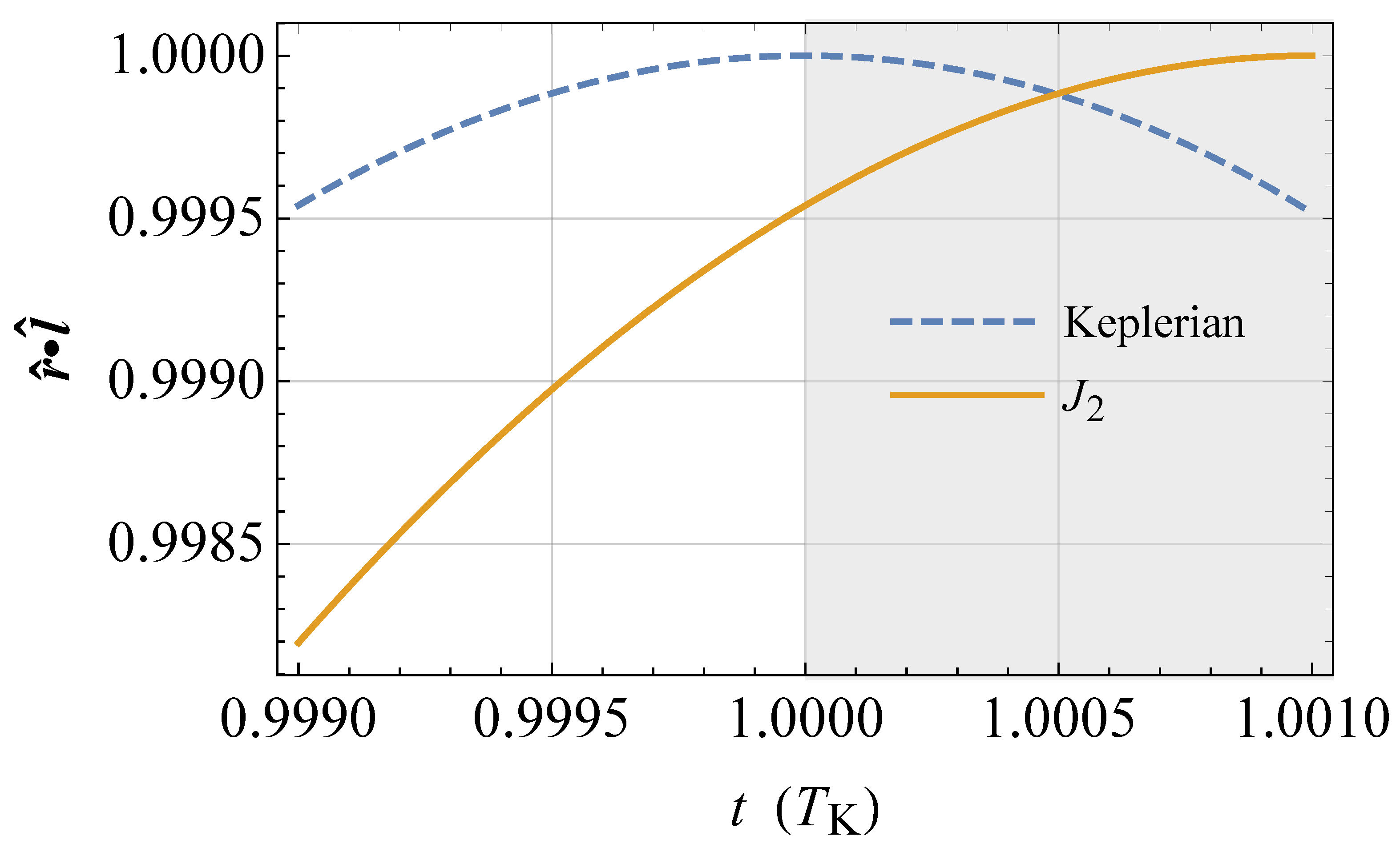
 (); the semimajor axis is . The physical parameters of the Earth are adopted. The 1 pN acceleration is suitably rescaled in such a way that . The time needed for to assume its initial value of again is longer than in the Keplerian case by an amount equal to , as shown by the shaded area, in agreement with the sum of Equation (79).
(); the semimajor axis is . The physical parameters of the Earth are adopted. The 1 pN acceleration is suitably rescaled in such a way that . The time needed for to assume its initial value of again is longer than in the Keplerian case by an amount equal to , as shown by the shaded area, in agreement with the sum of Equation (79).
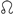 (); the semimajor axis is . The physical parameters of the Earth are adopted. The 1 pN acceleration is suitably rescaled in such a way that . The time needed for to assume its initial value of again is longer than in the Keplerian case by an amount equal to , as shown by the shaded area, in agreement with the sum of Equation (79).
(); the semimajor axis is . The physical parameters of the Earth are adopted. The 1 pN acceleration is suitably rescaled in such a way that . The time needed for to assume its initial value of again is longer than in the Keplerian case by an amount equal to , as shown by the shaded area, in agreement with the sum of Equation (79).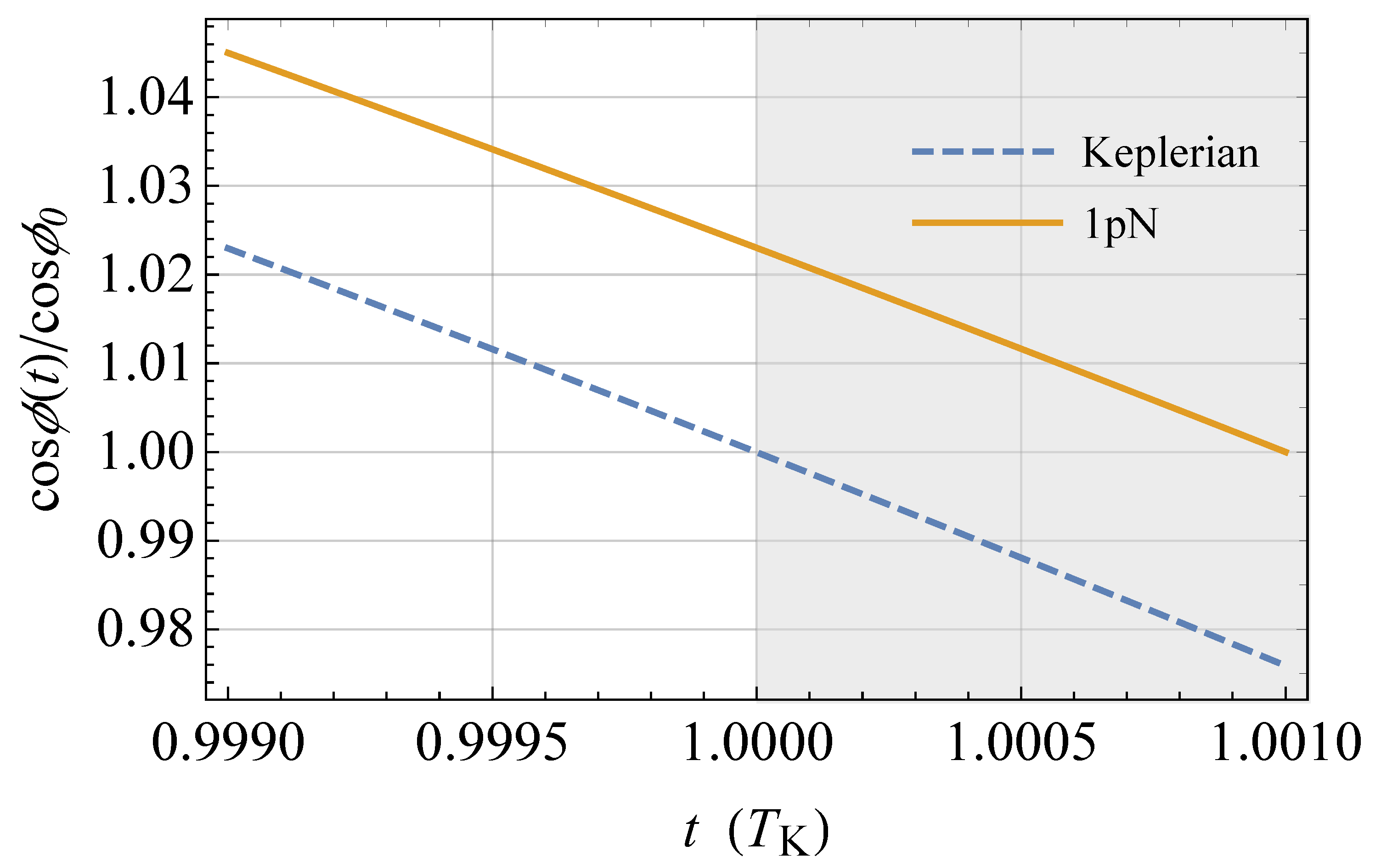

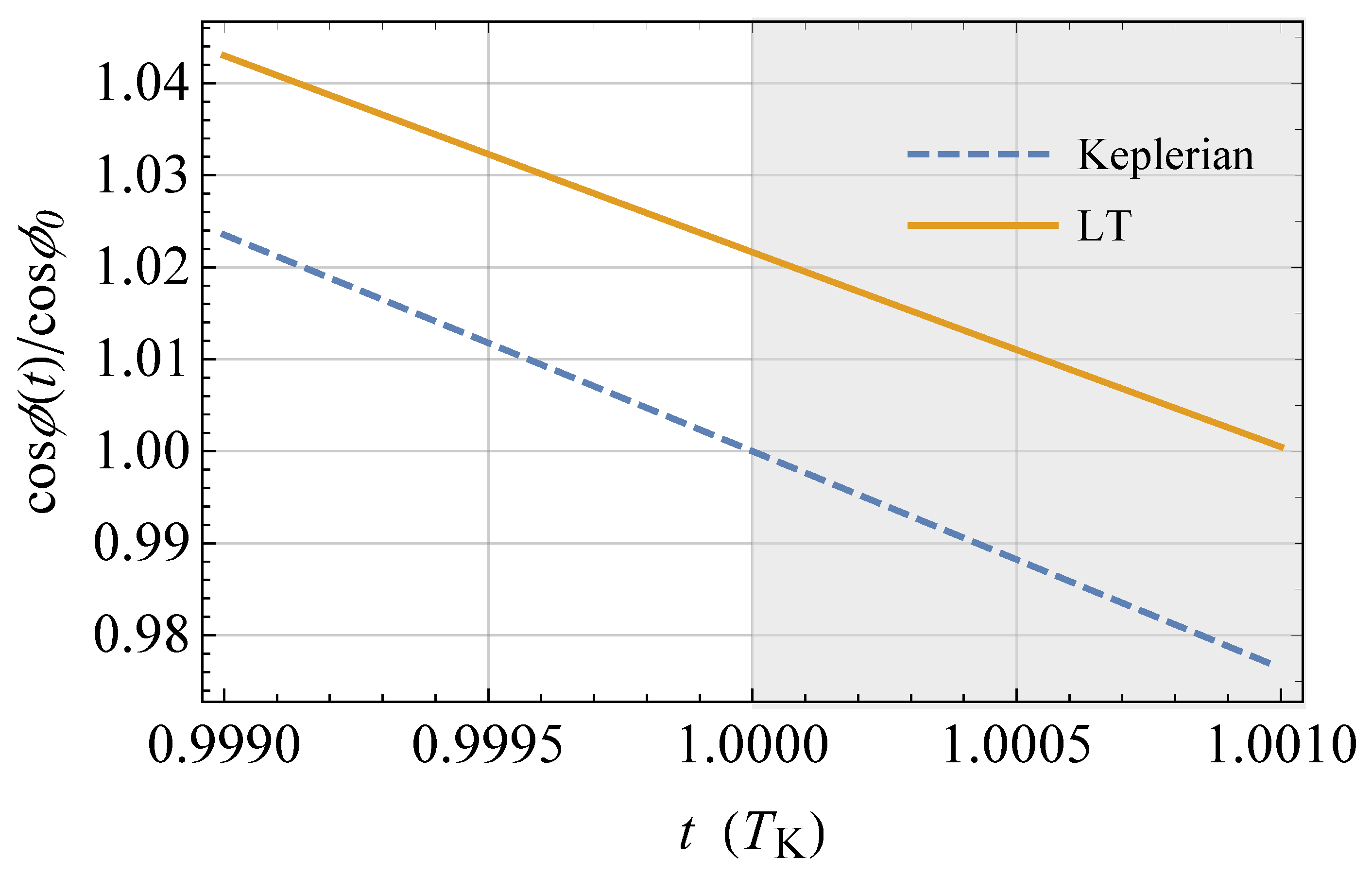
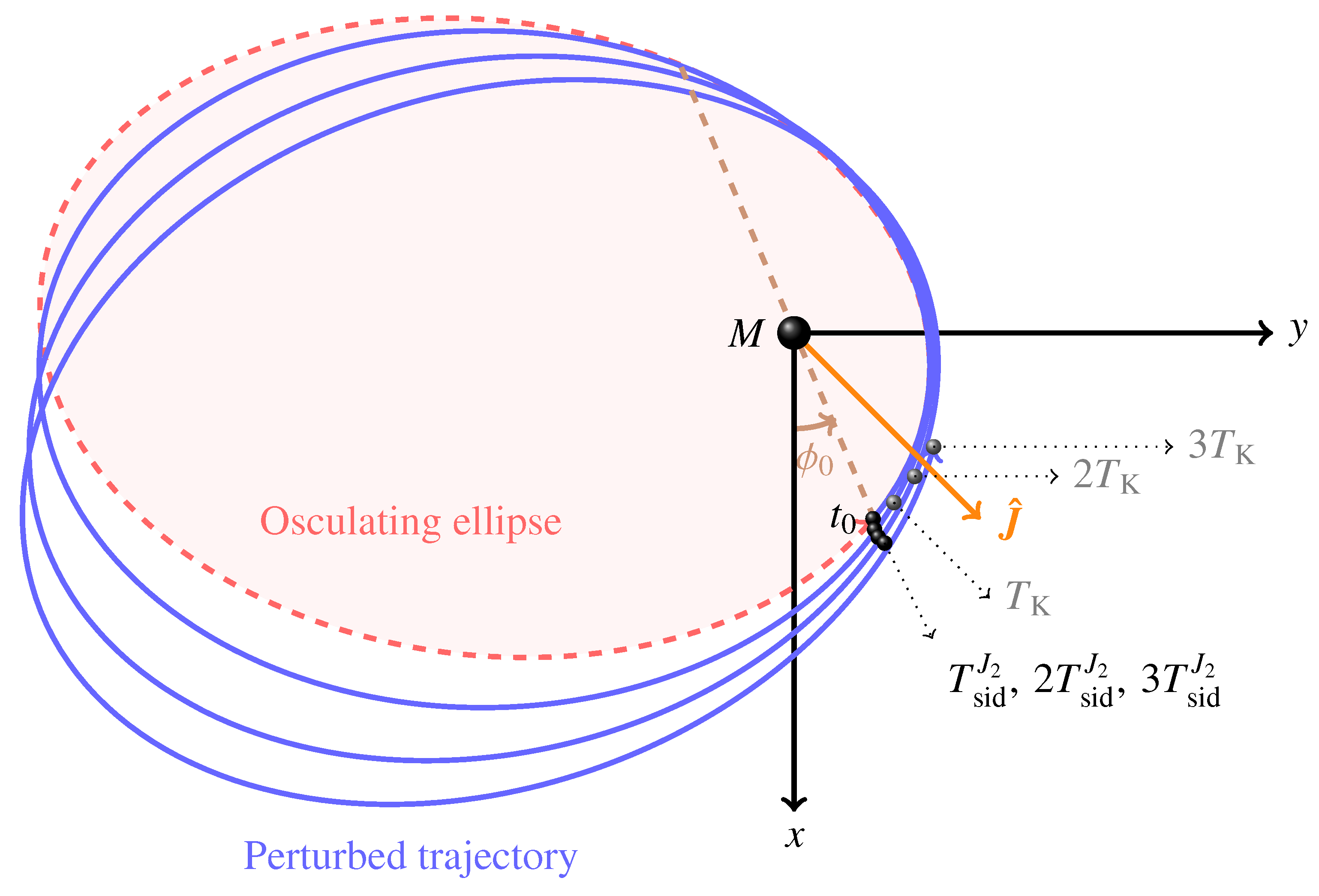
 ) (); the semimajor axis is . The physical parameters of the Earth are adopted, apart from the spin axis position set by . The acceleration is suitably rescaled in such a way that . The time needed for to assume its initial value () again is longer than in the Keplerian case by an amount equal to , as shown by the shaded area, in agreement with the sum of Equations (86) and (113).
) (); the semimajor axis is . The physical parameters of the Earth are adopted, apart from the spin axis position set by . The acceleration is suitably rescaled in such a way that . The time needed for to assume its initial value () again is longer than in the Keplerian case by an amount equal to , as shown by the shaded area, in agreement with the sum of Equations (86) and (113).
 ) (); the semimajor axis is . The physical parameters of the Earth are adopted, apart from the spin axis position set by . The acceleration is suitably rescaled in such a way that . The time needed for to assume its initial value () again is longer than in the Keplerian case by an amount equal to , as shown by the shaded area, in agreement with the sum of Equations (86) and (113).
) (); the semimajor axis is . The physical parameters of the Earth are adopted, apart from the spin axis position set by . The acceleration is suitably rescaled in such a way that . The time needed for to assume its initial value () again is longer than in the Keplerian case by an amount equal to , as shown by the shaded area, in agreement with the sum of Equations (86) and (113).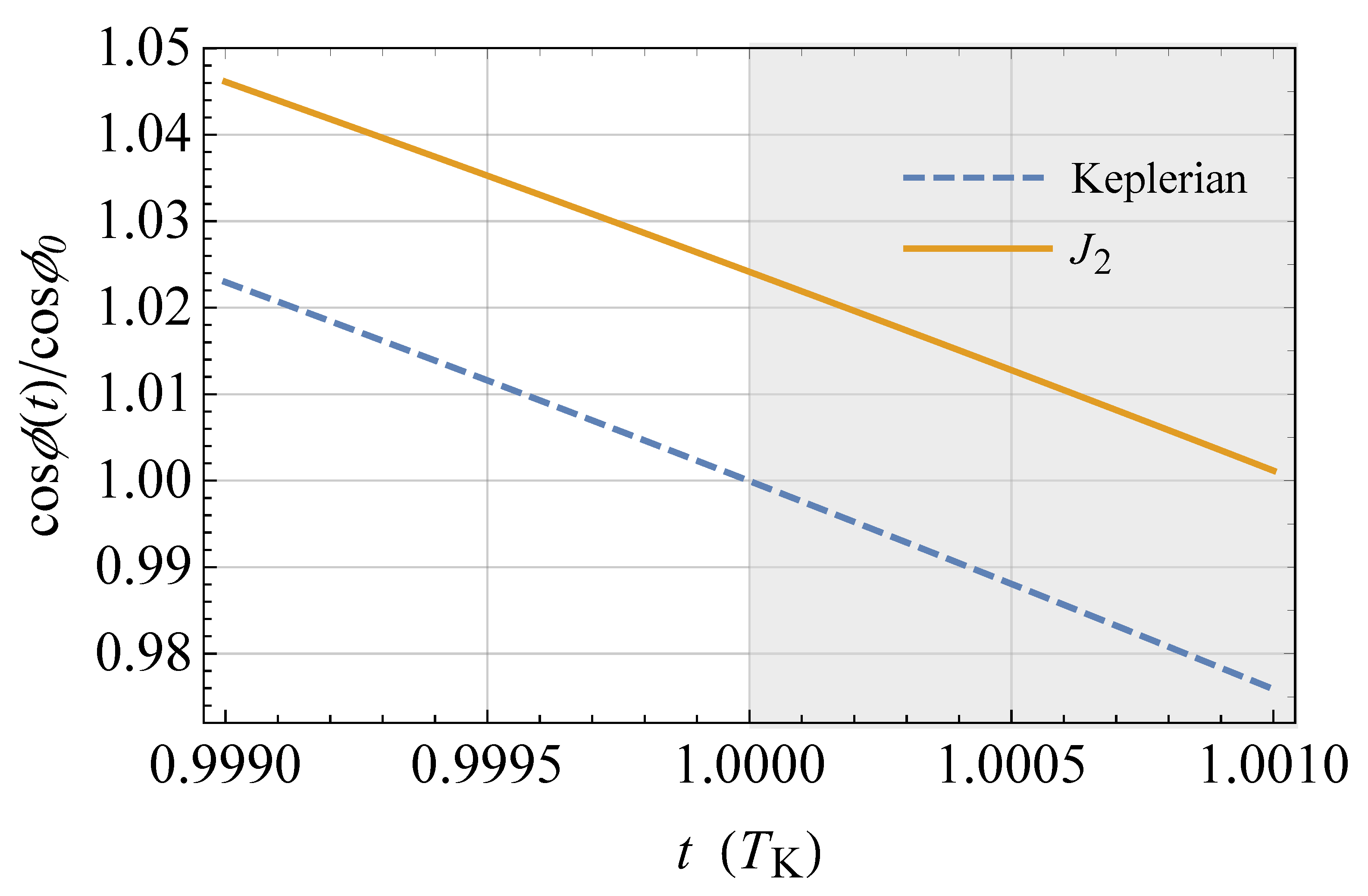
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iorio, L. When the Anomalistic, Draconitic and Sidereal Orbital Periods Do Not Coincide: The Impact of Post-Keplerian Perturbing Accelerations. Time Space 2025, 1, 2. https://doi.org/10.3390/timespace1010002
Iorio L. When the Anomalistic, Draconitic and Sidereal Orbital Periods Do Not Coincide: The Impact of Post-Keplerian Perturbing Accelerations. Time and Space. 2025; 1(1):2. https://doi.org/10.3390/timespace1010002
Chicago/Turabian StyleIorio, Lorenzo. 2025. "When the Anomalistic, Draconitic and Sidereal Orbital Periods Do Not Coincide: The Impact of Post-Keplerian Perturbing Accelerations" Time and Space 1, no. 1: 2. https://doi.org/10.3390/timespace1010002
APA StyleIorio, L. (2025). When the Anomalistic, Draconitic and Sidereal Orbital Periods Do Not Coincide: The Impact of Post-Keplerian Perturbing Accelerations. Time and Space, 1(1), 2. https://doi.org/10.3390/timespace1010002





