Modeling Power Consumption: A Novel Correlation for Stirred Media Mills with Variable Bead Filling Ratios
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection (from Experimental Work)
2.1.1. Data for Model Development
2.1.2. Data for Model Validation
2.2. Theoretical
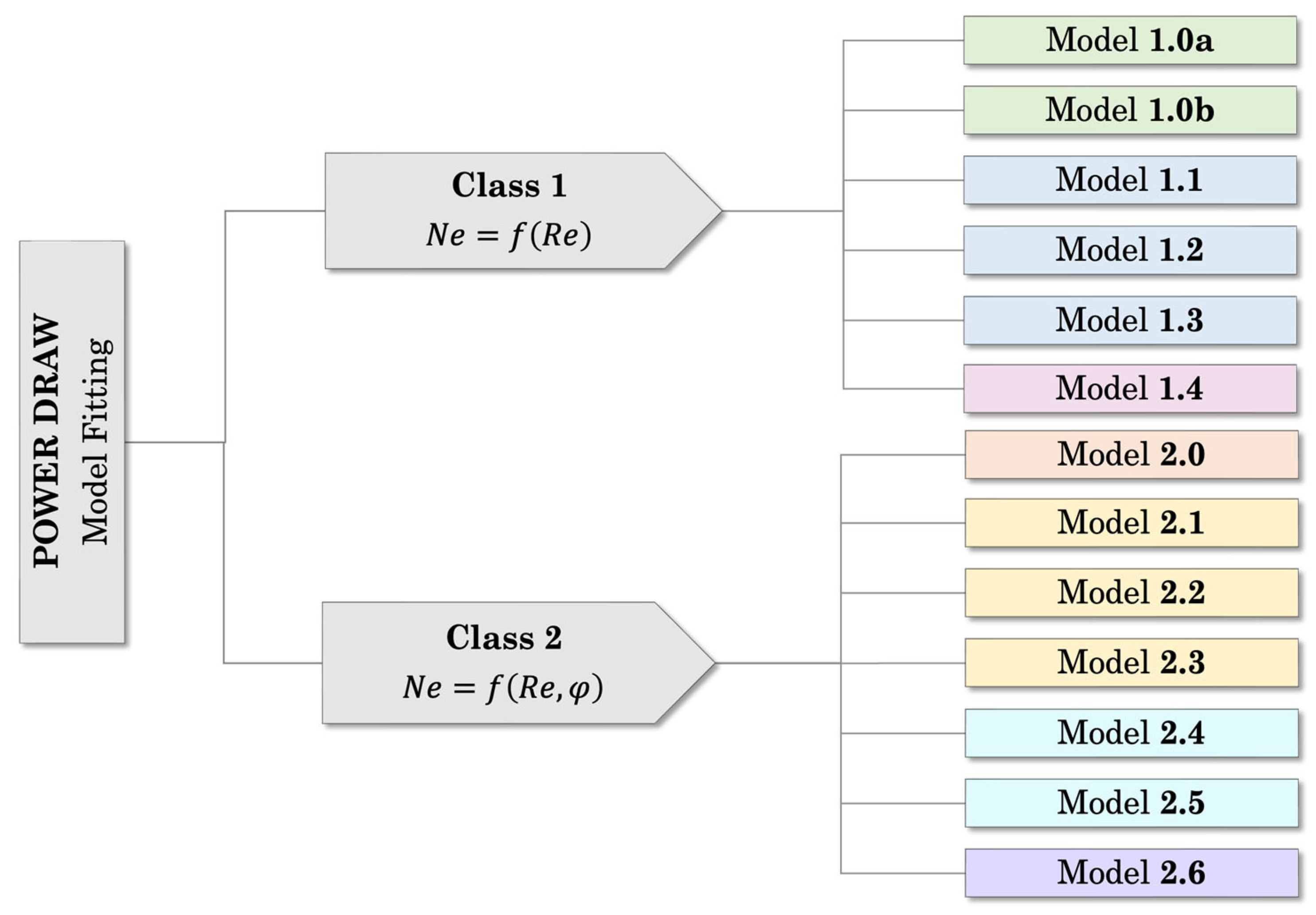
2.2.1. Mathematical Models
2.2.2. Statistical Analysis
3. Results and Discussion
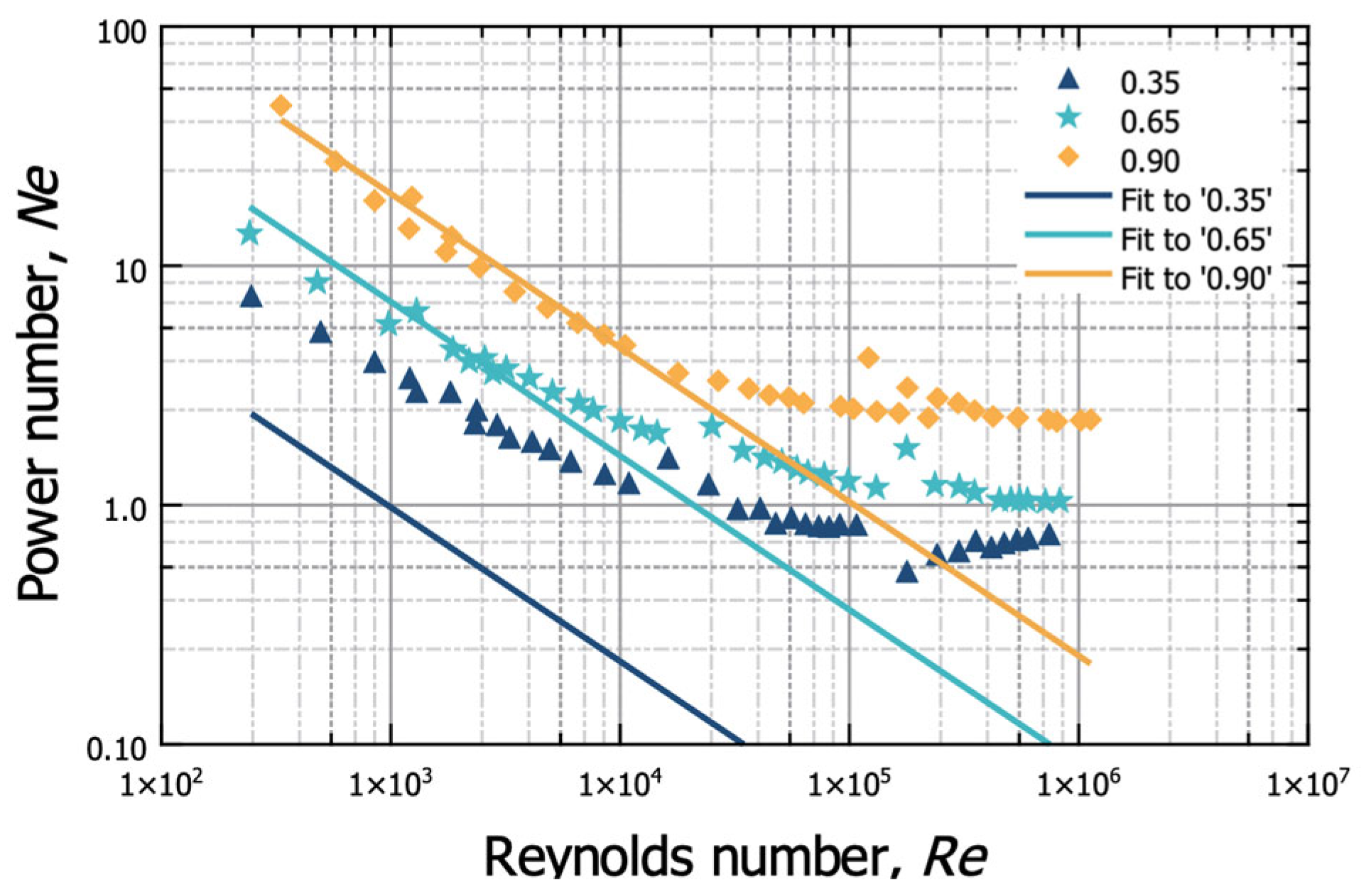
3.1. Class 1 Models for Ne–Re Correlations
3.2. Class 2 Models for Ne–Re–φ Correlations
3.3. Overview of Class 1 and Class 2 Models
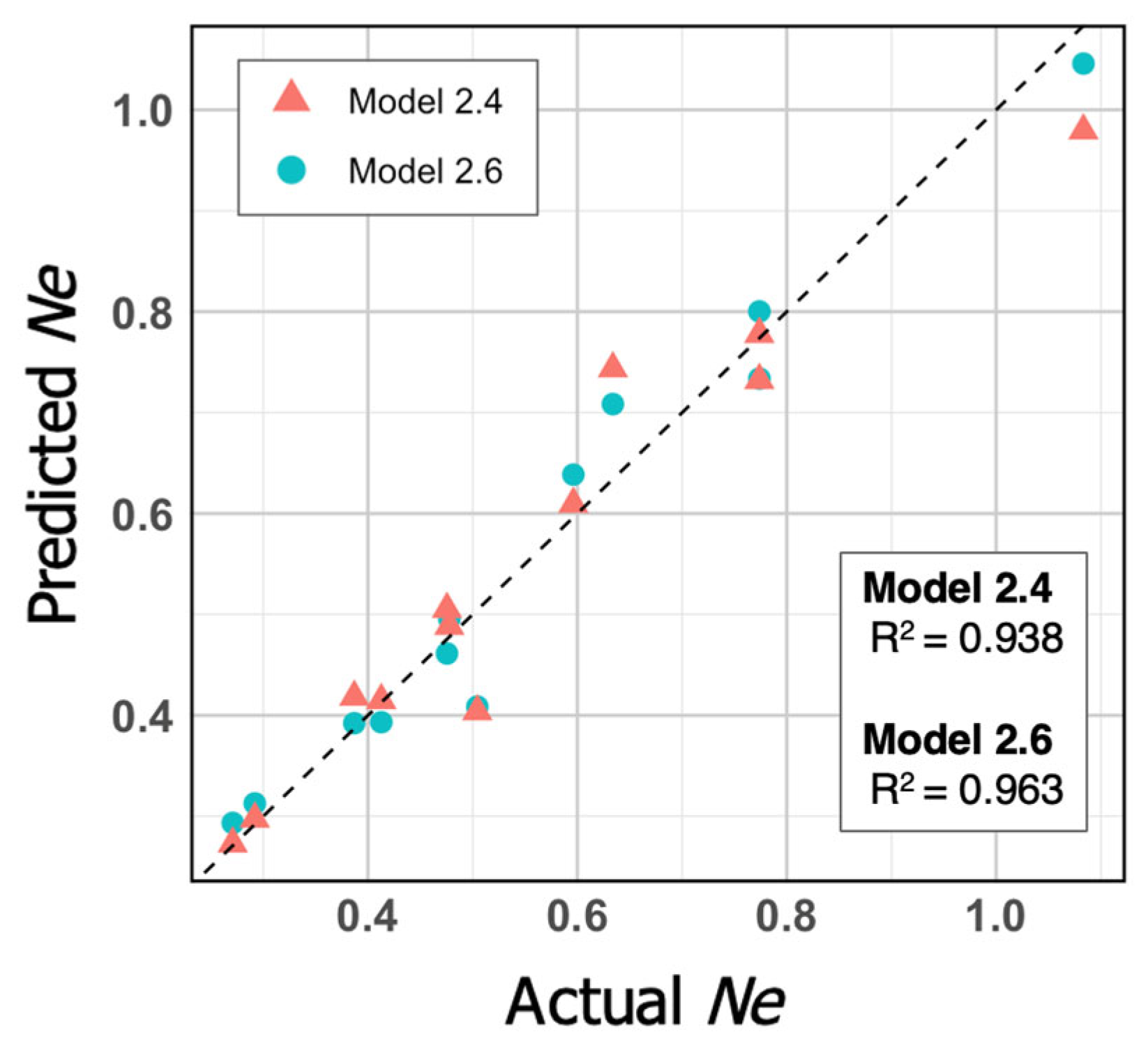
3.4. Model Validation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Cd | Drag coefficient, − |
| D | Internal diameter of the pipe, m |
| Db | Bead diameter, m |
| Dr | Stirrer (rotor) diameter, m |
| f | Friction factor, − |
| Ne | Power number (Newton number), − |
| P | Power applied by the mill stirrer (rotor), W |
| Re | Reynolds number, − |
| RMSE | Root mean squared error |
| RPM | Revolutions per minute |
| R2 | Coefficient of determination |
| SE | Standard error |
| SSR | Sum of squared residuals |
| SM | Supplementary Materials |
| YSZ | Yttrium-stabilized zirconia |
| Greek letters | |
| ε | Absolute roughness of the pipe, m |
| φ | Bead filling ratio in the milling chamber, − |
| ρs | Density, kg/m3 |
| μs | Apparent shear viscosity of the suspension, Pa·s |
| ω | Stirrer (rotational) speed, rpm |
| Subscripts | |
| b | Bead |
| d | Drag |
| r | Rotor (stirrer) |
| s | Suspension |
| Superscripts | |
| i | Bead filling ratios (0.35, 0.65, and 0.90) |
References
- Jankovic, A. Variables affecting the fine grinding of minerals using stirred mills. Miner. Eng. 2003, 16, 337–345. [Google Scholar] [CrossRef]
- Taylor, L.; Skuse, D.; Blackburn, S.; Greenwood, R. Stirred media mills in the mining industry: Material grindability, energy-size relationships, and operating conditions. Powder Technol. 2020, 369, 1–16. [Google Scholar] [CrossRef]
- Larsson, S.; Pålsson, B.I.; Parian, M.; Jonsén, P. A novel approach for modelling of physical interactions between slurry, grinding media and mill structure in wet stirred media mills. Miner. Eng. 2020, 148, 106180. [Google Scholar] [CrossRef]
- Toziopoulou, F.; Malamatari, M.; Nikolakakis, I.; Kachrimanis, K. Production of aprepitant nanocrystals by wet media milling and subsequent solidification. Int. J. Pharm. 2017, 533, 324–334. [Google Scholar] [CrossRef] [PubMed]
- Nakach, M.; Authelin, J.-R.; Agut, C. New approach and practical modelling of bead milling process for the manufacturing of nanocrystalline suspensions. J. Pharm. Sci. 2017, 106, 1889–1904. [Google Scholar] [CrossRef]
- Breitung-Faes, S.; Kwade, A. Mill, material, and process parameters—A mechanistic model for the set-up of wet-stirred media milling processes. Adv. Powder Technol. 2019, 30, 1425–1433. [Google Scholar] [CrossRef]
- Eskin, D.; Zhupanska, O.; Hamey, R.; Moudgil, B.; Scarlett, B. Microhydrodynamics of stirred media milling. Powder Technol. 2005, 156, 95–102. [Google Scholar] [CrossRef]
- Mende, S.; Stenger, F.; Peukert, W.; Schwedes, J. Mechanical production and stabilization of submicron particles in stirred media mills. Powder Technol. 2003, 132, 64–73. [Google Scholar] [CrossRef]
- Jankovic, A. Developments in iron ore comminution and classification technologies. In Iron Ore; Lu, L., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 251–282. [Google Scholar] [CrossRef]
- Kumar, A.; Sahu, R.; Tripathy, S.K. Energy-efficient advanced ultrafine grinding of particles using stirred mills—A review. Energies 2023, 16, 5277. [Google Scholar] [CrossRef]
- Kawatra, S.K. Advances in Comminution; SME Inc.: Littleton, CO, USA, 2006. [Google Scholar]
- Guner, G.; Yilmaz, D.; Yao, H.F.; Clancy, D.J.; Bilgili, E. Predicting the temperature evolution during nanomilling of drug suspensions via a semi-theoretical lumped-parameter model. Pharmaceutics 2022, 14, 2840. [Google Scholar] [CrossRef]
- Guner, G.; Mehaj, M.; Seetharaman, N.; Elashri, S.; Yao, H.F.; Clancy, D.J.; Bilgili, E. Do mixtures of beads with different sizes improve wet stirred media milling of drug suspensions? Pharmaceutics 2023, 15, 2213. [Google Scholar] [CrossRef] [PubMed]
- Guner, G.; Heidari, H.; Lehman, K.; Desai, P.M.; Clancy, D.; Bilgili, E.; Chattoraj, S. Comparative analysis of polystyrene versus zirconia beads on breakage kinetics, heat generation, and amorphous formation during wet bead milling. J. Pharm. Sci. 2025, 114, 1175–1185. [Google Scholar] [CrossRef]
- Guner, G.; Seetharaman, N.; Elashri, S.; Mehaj, M.; Bilgili, E. Analysis of heat generation during the production of drug nanosuspensions in a wet stirred media mill. Int. J. Pharm. 2022, 624, 122020. [Google Scholar] [CrossRef]
- Li, M.; Alvarez, P.; Bilgili, E. A microhydrodynamic rationale for selection of bead size in preparation of drug nanosuspensions via wet stirred media milling. Int. J. Pharm. 2017, 524, 178–192. [Google Scholar] [CrossRef]
- De Bakker, J. Energy use of fine grinding in mineral processing. Metall. Mater. Trans. E 2014, 1, 8–19. [Google Scholar] [CrossRef]
- Li, M.; Yaragudi, N.; Afolabi, A.; Dave, R.; Bilgili, E. Sub-100 nm drug particle suspensions prepared via wet milling with low bead contamination through novel process intensification. Chem. Eng. Sci. 2015, 130, 207–220. [Google Scholar] [CrossRef]
- Gao, M.-W.; Forssberg, K.; Weller, K. Power predictions for a pilot scale stirred ball mill. Int. J. Miner. Process. 1996, 44, 641–652. [Google Scholar] [CrossRef]
- Li, M.; Azad, M.; Davé, R.; Bilgili, E. Nanomilling of drugs for bioavailability enhancement: A holistic formulation-process perspective. Pharmaceutics 2016, 8, 17. [Google Scholar] [CrossRef]
- Jenczewski, T.J. The grinding of organic dyestuffs. Can. J. Chem. Eng. 1972, 50, 59–65. [Google Scholar] [CrossRef]
- Kwade, A.; Schwedes, J. Wet grinding in stirred media mills. Handb. Powder Technol. 2007, 12, 251–382. [Google Scholar]
- Tuzun, M.A. A Study of Comminution in a Vertical Stirred Ball Mill. Ph.D. Thesis, University of Natal, Durban, South Africa, 1993. [Google Scholar]
- Mannheim, V.; Siménfalvi, Z. Determination of Power Consumption for Suspension Mixing in Stirring Equipments and Stirred Ball Mills. J. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2012, 2, 572–578. [Google Scholar]
- Radziszewski, P.; Allen, J. Towards a better understanding of stirred milling technologies—Estimating power consumption and energy use. In Proceedings of the 46th Annual Canadian Mineral Processors Operators Conference, Ottawa, ON, Canada, 21–23 January 2014; pp. 55–66. [Google Scholar]
- Guner, G.; Elashri, S.; Mehaj, M.; Seetharaman, N.; Yao, H.F.; Clancy, D.J.; Bilgili, E. An enthalpy-balance model for timewise evolution of temperature during wet stirred media milling of drug suspensions. Pharm. Res. 2022, 39, 2065–2082. [Google Scholar] [CrossRef] [PubMed]
- Mannheim, V.; Siménfalvi, Z. Determination of Power Consumption for Suspension Mixing and Wet Grinding with Dimensional Analysis in Stirred Mills. Available online: https://www.researchgate.net/profile/Viktoria-Mannheim/publication/329948710_Determination_of_power_consumption_for_suspension_mixing_and_wet_grinding_with_dimensional_analysis_in_stirred_mills/links/5c250782299bf12be39d3d39/Determination-of-power-consumption-for-suspension-mixing-and-wet-grinding-with-dimensional-analysis-in-stirred-mills.pdf (accessed on 30 August 2025).
- Mannheim, V. Empirical and scale-up modeling in stirred ball mills. Chem. Eng. Res. Des. 2011, 89, 405–409. [Google Scholar] [CrossRef]
- Heath, A.; Keikkala, V.; Paz, A.; Lehto, H. A power model for fine grinding HIGmills with castellated rotors. Miner. Eng. 2017, 103, 25–32. [Google Scholar] [CrossRef]
- Heidari, H.; Vargas, A.; Macris, A.; Muller, F.; Pikhard, O.; Guner, G.; Clancy, D.J.; Bilgili, E. Control of temperature rise during wet stirred media milling. Adv. Powder Technol. 2025, 36, 104981. [Google Scholar] [CrossRef]
- Weit, H.; Schwedes, J. Scale-up of power consumption in agitated ball mills. Chem. Eng. Technol. 1987, 10, 398–404. [Google Scholar] [CrossRef]
- Schönstedt, B.; Jacob, H.-J.; Schilde, C.; Kwade, A. Scale-up of the power draw of inline-rotor–stator mixers with high throughput. Chem. Eng. Res. Des. 2015, 93, 12–20. [Google Scholar] [CrossRef]
- Zheng, J.; Harris, C.; Somasundaran, P. Power consumption of stirred media mills. Min. Metall. Explor. 1995, 12, 34–40. [Google Scholar] [CrossRef]
- Radziszewski, P. Shear based stirred mill power model—An adimensional analysis. Miner. Eng. 2015, 73, 16–20. [Google Scholar] [CrossRef]
- Kwade, A. Specific energy consumption, stress energy, and power draw of stirred media mills and their effect on the production rate. In Proceedings of the SME Annual Conference—Advances in Comminution, Littleton, CO, USA, 28 February–2 March 2006; pp. 99–114. [Google Scholar]
- Zheng, J.; Harris, C.C.; Somasundaran, P. A study on grinding and energy input in stirred media mills. Powder Technol. 1996, 86, 171–178. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Posit Team. RStudio: Integrated Development Environment for R; Posit Software; PBC: Boston, MA, USA, 2023. [Google Scholar]
- Johnson, S.G. The NLopt Nonlinear-Optimization Package, Version 2.7.1. Available online: http://github.com/stevengj/nlopt (accessed on 30 August 2025).
- Goossens, W.R. Review of the empirical correlations for the drag coefficient of rigid spheres. Powder Technol. 2019, 352, 350–359. [Google Scholar] [CrossRef]
- Khan, A.; Richardson, J. The resistance to motion of a solid sphere in a fluid. Chem. Eng. Commun. 1987, 62, 135–150. [Google Scholar] [CrossRef]
- Fang, X.; Xu, Y.; Zhou, Z. New correlations of single-phase friction factor for turbulent pipe flow and evaluation of existing single-phase friction factor correlations. Nucl. Eng. Des. 2011, 241, 897–902. [Google Scholar] [CrossRef]
- Turgut, O.E.; Asker, M.; Coban, M.T. A review of non iterative friction factor correlations for the calculation of pressure drop in pipes. Bitlis Eren Univ. J. Sci. Technol. 2014, 4, 1–8. [Google Scholar] [CrossRef]
- Altun, O.; Benzer, H.; Enderle, U. Effects of operating parameters on the efficiency of dry stirred milling. Miner. Eng. 2013, 43, 58–66. [Google Scholar] [CrossRef]
- Parker, N.; Rahman, M.; Bilgili, E. Impact of media material and process parameters on breakage kinetics–energy consumption during wet media milling of drugs. Eur. J. Pharm. Biopharm. 2020, 153, 52–67. [Google Scholar] [CrossRef]


| Model | Equation | Parameters |
|---|---|---|
| Model 1.0a | Lower transition region a: Upper transition region b: model extension Lower turbulent region c: constant value Upper turbulent region d: constant value | |
| Model 1.0b | Lower + upper transition region: Lower turbulent region c: constant value Upper turbulent region d: constant value | |
| Model 1.1 | Lower transition region a:
Upper transition region b: Lower turbulent region c: Upper turbulent region d: | |
| Model 1.2 | Lower transition region a:
Upper transition region b: Lower turbulent region c: Upper turbulent region d: | |
| Model 1.3 | Lower transition region a:
Upper transition region b: Lower turbulent region c: Upper turbulent region d: | |
| Model 1.4 |
| Model | Equation | Parameters |
|---|---|---|
| Model 2.0 | ||
| Model 2.1 | Lower transition region a:
Upper transition region b: Lower turbulent region c: Upper turbulent region d: | |
| Model 2.2 | Lower transition region a:
Upper transition region b: Lower turbulent region c: Upper turbulent region d: | |
| Model 2.3 | Lower transition region a:
Upper transition region b: Lower turbulent region c: Upper turbulent region d: | |
| Model 2.4 | ||
| Model 2.5 | ||
| Model 2.6 |
| SSR a | RMSE b | R2 |
|---|---|---|
| 36.71 | 0.591 | 0.990 |
| Parameter | Estimate | SE c |
| 1.27 × 100 | 1.46 × 10−2 | |
| 1.15 × 10−1 | 2.91 × 10−3 | |
| 2.85 × 10−1 | 8.40 × 10−3 | |
| 2.67 × 100 | 2.79 × 10−1 |
| SSR a | RMSE b | R2 |
|---|---|---|
| 0.0221 | 0.0429 | 0.963 |
| Parameter | Estimate | SE c |
| 3.47 × 105 | 16.63 | |
| 1.96 × 100 | 0.011 | |
| 2.79 × 10−1 | 0.010 | |
| 1.46 × 100 | 0.174 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ozsoysal, S.; Heidari, H.; Guner, G.; Clancy, D.J.; Bilgili, E. Modeling Power Consumption: A Novel Correlation for Stirred Media Mills with Variable Bead Filling Ratios. J. Pharm. BioTech Ind. 2025, 2, 14. https://doi.org/10.3390/jpbi2030014
Ozsoysal S, Heidari H, Guner G, Clancy DJ, Bilgili E. Modeling Power Consumption: A Novel Correlation for Stirred Media Mills with Variable Bead Filling Ratios. Journal of Pharmaceutical and BioTech Industry. 2025; 2(3):14. https://doi.org/10.3390/jpbi2030014
Chicago/Turabian StyleOzsoysal, Simay, Hamidreza Heidari, Gulenay Guner, Donald J. Clancy, and Ecevit Bilgili. 2025. "Modeling Power Consumption: A Novel Correlation for Stirred Media Mills with Variable Bead Filling Ratios" Journal of Pharmaceutical and BioTech Industry 2, no. 3: 14. https://doi.org/10.3390/jpbi2030014
APA StyleOzsoysal, S., Heidari, H., Guner, G., Clancy, D. J., & Bilgili, E. (2025). Modeling Power Consumption: A Novel Correlation for Stirred Media Mills with Variable Bead Filling Ratios. Journal of Pharmaceutical and BioTech Industry, 2(3), 14. https://doi.org/10.3390/jpbi2030014








