Forecasting the Housing Market Sales in Italy: An MLP Neural Network Model

Abstract

Using panel data on 99 Italian provinces in the period between 2005 and 2020, the research investigates the effects of fundamental economic factors on the home sales at the provincial level, in order to build a forecasting model using a non-linear artificial intelligence approach (MLP-Multiple Linear Perceptron neural network). There are multiple objectives to this: (a) to test the hypothesis that national, regional and local fundamentals such as interest rates, income, inflation rate, unemployment and demography affect the activity’s degree of the housing market; (b) to verify the effectiveness of a neural network in describing the dynamics of the real estate market; (c) to build a simulation model capable of predicting the effect of changes in fundamentals, also due to economic policy measures, on the market. Empirical results show that neural networks offer better capabilities than linear models in representing the complex relationships between the economic situation and the real estate market. The study provides useful information for regulators to improve the effectiveness of monetary policy to stabilize real estate markets as well as for stakeholders to draw up scenarios of market development.

1. Introduction

Study of the real estate market has developed considerably in recent years. A search carried out in January 2025 on Scopus using the keywords that characterize the housing market revealed over 4000 works, 90% of which were published since 2000 and 70% since 2015. This interest seems to be due to various factors. The first is the role of the construction sector in GDP, particularly residential construction: in 2023, the aggregate of the construction and real estate services sector contributed almost 19% to the added Italian value. Secondly, about 50% of household wealth is made up of the value of the owned property, and the home (utilities, maintenance, furniture) comprises about 40% of average household expenditure. Thirdly, there is the purchase of housing, which is an important investment of savings and the largest source of household debt, and the role of the real estate sector in the national and global financial system, which absorbs a significant share of bank loans. Finally, great interest was aroused by the subprime mortgage crisis triggered by the illiquidity of bonds issued by the Federal National Mortgage Association (Fannie Mae) and the Federal Home Loan Mortgage Corporation (Freddie Mac) to finance the granting of mortgages for home purchase in the United States. The crisis has resulted in a collapse in confidence among financial institutions, with a collapse of liquidity, credit restriction, insolvency of indebted households for the purchase of houses, forced real estate sales, price contraction and collapse of transactions with heavy repercussions on the entire world economy [1,2].

Trends in the real estate market is therefore a reliable indicator of the health of the economic system [3,4] and can be briefly described by the dynamics of purchase and sale prices and the number of transactions that present an evident synchronism with the economic cycle.

Most of the scientific articles analyzing the real estate market have focused on prices and the factors that influence them. However, there are few studies that have delved into the dynamics of transactions. Nevertheless, if we look at the trend in purchase prices and the number of transactions over time, we notice that the latter varies more than the former, especially during the aforementioned crisis between 2008 and 2013.

Calculating the variation coefficient of the average prices of residential homes from 2005 to 2020, a value of 7.9% is obtained, while that of transactions is equal to 24.5%. Furthermore, the number of transactions is closely correlated with the turnover of the residential real estate market. Pearson’s correlation index between turnover and real estate market intensity index (IMI) is 0.98 and 0.99 with number of transactions (NTN) (development by the authors on the data published at the Real Estate Market Observatory of the Revenue Agency) [5]. NTN, which was extracted from the Database of Real Estate Advertising Offices, is the number of transactions carried out in a year normalized with respect to the share of property bought and sold and was. The IMI, which was extracted from the Land Registry Database, is the percentage share of the stock of real estate units subject to sale; the stock is the number of real estate units in a municipality distinguished by building type [6].

The evidence that the economic situation has a heavier impact on the number of transactions than on prices implies that the volume of sales has very important implications on the construction sector, the services related to transactions (intermediation and legal services), tax collection, the location of savings, the volume of credit and much more [7].

The paper illustrates research aimed at developing a neural network for forecasting the activity degree of the housing market at the provincial level in Italy. The database consists of a time period from 2005 to 2020, IMI and NTN by province and the main factors that the extensive scientific literature has identified as being significantly connected with the real estate market trend.

The analysis was conducted by combining a preliminary econometric analysis with a neural network of the MLP (Multiple Linear Perceptron) type in order to verify its ability to interpret the complex relationships that exist among the socioeconomic structure of the territories, the dynamics of the “fundamentals” of the economic situation and the level of activity of the residential real estate market. The MLP neural network offered a very good compromise between the need to use a more flexible model over econometric ones and, nevertheless, was usable with a small database consisting of the time series on transactions from 2005 to 2020 in 99 Italian provinces. The paper is structured in five sections. After the introduction, the second section reports the literature review. The third illustrates the main characteristics of the MLP neural network. The fourth describes the variables used and presents a synthetic statistical analysis aimed at identifying the factors to be used in the neural network. The fifth illustrates the results and presents an analysis of the sensitivity of IMI to the most influential “fundamentals” on transactions. Finally, some summary considerations are formulated.

2. The State of the Art

As mentioned above, there is a vast body of literature that has deepened the relationships between real estate prices and macroeconomic fundamentals with various tools, the review of which is beyond the scope of this contribution. However, some recent reviews are useful for tracing the general picture of scientific production in recent years. The first, edited by Vergara-Perucich [2], concerns the use of hedonic models in real estate valuations and examines a sample of 2276 documents, finding that there has been a considerable production of articles on the real estate market since the 2007 bubble, with a particular emphasis on the price definition process. The second, edited by Khoshnoud et al. [8], provides a review of the literature on econometric models published from 2005 to 2021 for a total of 252 studies mostly appearing in the three main specialist journals: Journal of Real Estate Finance and Economics, Journal of Real Estate Research and Real Estate Economics. This review shows that although research on real estate markets is global, most studies have focused on the U.S. market and have been performed by U.S. researchers.

As mentioned above, in the face of the very prolific literature on the trend of house values and estimates, there are few contributions that have specifically deepened the study and forecasting of the degree of market activity.

Table 1. Summary of the literature on residential property transactions.

#	Authors	Year	Scope	Method	Ambit	Factors	Findings
1	Dua P., Smyth D. J.	1995	Sales forecast	Bayesian Vector Autoregressive Model	USA	Households’ buying attitudes, price of homes, mortgage rate, real personal disposable income, unemployment rate	Including consumers’ attitude does not improves Sales forecast
2	Dua P., Miller S. M.	1996	Sales forecast	Bayesian Vector Autoregressive Model	Connecticut (USA)	Composite indices of economic conditions	Indices perform better than single fundamentals
3	Dua P., Miller S. M., Smyth D. J.	1999	Sales forecast	Bayesian Vector Autoregressive Model	USA	Composite indices, Home price, Mortgage rate, Income, Unemployment rate, Building permit	Building permit outperform other indices
4	Leamer E.E.	2007	Residential investments and business cycle	Multivariate Analysis, OLS	USA	Various investment, GDP, FED funds,	It’s a volume cycle not a price cycle. Home investments has an high impact on GDP
5	Hamilton J.D.	2008	FED policy actions and home sales	Vector Autoregressive Model	USA	Mortgage rates and home sales	There is a structural lag between mortgage rate change and home sales
6	Gupta R., Tpoy C. K., Das S.	2010	Sales forecast	Random Walk, Bayesian and Error Vector Autoregressive Model	USA Four Census Region	Home price, Mortgage rate, Income, Unemployment rate, Building permit	Bayesian model has good performances in predicting home sales and the various models have different performances in different census regions
7	Miller N. G., Peng L., Sklartz M.A.	2010	Economic impact of anticipated home sale	Vector Error Correction Model	USA Metropolitan Statistical Areas	Home sales, Home prices, Gross Metropolitan Production, Population, Unemployment Ratio, Income	Home sales highly impact GMP
8	Chen H.L.	2010	Forecast sales	Time series regression	37 large construction firms in Taiwan	Financial, macroeconomic and firm specific variables	Financial and macroeconomic variables are significant predictors of firm sales
9	Shan H.	2011	Gains taxation and home sales	Linear probability model	Boston metropolitan areas	Gains taxation, Price, Lot size, Location	Tax reduction increases sales in low price homes
10	Baghestani H., Kaya I., Kherfy S.	2013	Consumer attitude and home sales	Contingency analysis	USA	Consumers attitude, Mortgage rates, Housing cost, Home sales	Change in consumers’ attitude affects three months later sales
11	Baghestani H., Kaya I.	2016	Financial indicators and home sales	Contingency analysis, Random walk regression	USA	Mortgages rate, Federal funds rate, Spread	Financial indicators have different predictability in different time periods on home sales
12	Moro M.F., Compagnoni dos Reis C.C., De Almeida Flores S., Weise A.D., Vincenzi S.L.	2016	Financial indicators and home sales	OLS Regression	Sao Paulo (Brazil)	Official discount rate, Inflation, Construction cost, dollar exchange rate, Taxation, Wage, Credit.	Home sales from depend from official discount rate and bank credits
13	Hassani S., Ghodsi Z., Gupta R., Segnon M.	2017	Forecasting home sale	Singular spectrum analysis	USA	Home sales	Univariate vector single spectrum analysis perform better than other model in forecasting overall US home sales
14	Han S., Ko Y., Kim S.,Shin D.H.	2017	Forecasting home sale index	Cluster analysis, Principal component analysis, Regression	South Korea	Big data, Web search queries, Home sales index	Principal component and cluster analysis improve regression approach in sales index prediction
15	Han S., Ko Y., Kim S.,Shin D.H.	2018	Forecasting home sale index	Multiple regression analysis, Varimax rotation, Genetic algorithm	South Korea	Big data, Web search queries, Home sales index	Varimax rotation and Genetic algorithm improve classical approaches in home sales index prediction
16	Temur A. S., Akgun M., Temur G.	2019	Predicting housing sale	ARIMA, LSTM network, Hybrid model	Turkey	Home sales time series	Hybrid model perform better than ARIMA and LSTM network
17	Gupta R., Lau C.K.M., Plakandaras V., Wong W.	2019	Home sales forecast	Classical and bayesian vector autoregressive model	USA	House buying sentiment index, home sale, mortgage rate, Income, Unemployment, Building permits	House buying sentiment index improves the accuracy of home sales forecast
18	Strobel J., Thamh B.N., Lee G.S.	2020	Impact of uncertainty on home sales and prices	Fixed effects regression	USA	Macro, Policy, State uncertainty indexes, Labour demand shock	Uncertainties negatively impact no home prices but not on sales
19	Moro M.F., Weise A.D., Bornia A.C.	2020	Home sales forecast	Exponential softening, Box-Jenkins, Artificial neural network	Sao Paulo (Brazil)	Home sales time series	The combination of time series modelling increases the forecast performances
20	Cepni O., Gupta R., Wohar M.E.	2020	Role of uncertainty on home sales distribution	Quantile bayesian model averaging	USA	House prices, home sale, mortgage rate, Income, Unemployment, Building permits	Real estate uncertainty reduce house sale growth
21	Lee C., Park K.K.	2022	Home sales forecast in local housing market	ARIMA, Recurrent neural network	Seoul, Incheon, Gyeonggi, Gangwon (South Korea)	Home sales time series	ARIMA and RNN have similar performances in forecasting home sale at local level
22	Tochaiwat K., Seniwong P., Rinchunphu D.	2023	Home sales rate forecast	Neural network	Thailand	Prices, Location, House characteristics	Neural networks have good performances in predicting sale rate

summarizes the main results of the 22 articles examined. The review does not claim to be exhaustive but aims to identify the methodologies adopted and the main results obtained from the most well-known literature.

To the authors’ knowledge, the first analyses of transactions’ volume and their forecast date back to the end of the last century with contributions from Dua and Smyth [9], Dua and Miller [10] and Dua et al. [11]. These works aimed to create predictive models with Bayesian Vector Autoregressive Models (BVARs). The models used various sets of independent variables among which the classic fundamentals (house prices, mortgage rates for home purchase, disposable income per capita, unemployment rates, etc.) were distinguished, as well as more specific variables such as the number of building permits and the “sentiment” of households on the purchase of a home. The results of these first works can be summarized in the fact that (a) complex indices explain the trend of transactions better than the single “fundamentals”; (b) including the number of building permits in the models improves the models compared to the use of complex indices alone; and (c) including household sentiment in models does not improve the forecasting performance of the models.

In 2007, Leamer [3] published a report for the National Bureau of Economic Research (NEBR) where he explored in detail the relationship between the business cycle and the real estate cycle using multivariate and regression analysis. First, he shows that the real estate cycle is essentially determined by sales volumes and not so much by house prices. It also highlights the high impact of the sales trend on the economic cycle. Hamilton [12] focuses on monetary policy measures to stabilize the housing market and transaction patterns by deepening interest rate actions and identifying a systematic lag in the volume of sales compared to changes in interest rates. Subsequently, Gupta et al. [13] focus on the use of Vector and Bayesian Autoregressive Model to make forecasts on sales in the U.S. census regions and show that Bayesian approaches perform well but differently in the various U.S. census regions. Miller et al. [14] return to the problem addressed by Leamer and confirm, through a Vector Error Correction Model, that home sales have a high impact on GDP.

Chen [15] explores the large construction companies in Korea through time series analysis, using both cyclical and specific variables of the various companies. The analysis of time series shows that the so-called “fundamentals” also have a high impact on the sales of individual companies. Shan [16] investigates the effect of the level of taxation on profits on the sales volume and, using a linear model, shows that a sudden change in taxation affects the volume of house sales at a lower price (<500,000 dollars). Baghestani et al. [17] return to the effect of household sentiment on house sales and, contrary to Dua and Smyth [9], identify a positive delayed effect on the change in sentiment. Furthermore, Baghestani and Kaya [18] and Moro et al. [18] study the impact of financial variables (interest rates, government bond yields, spreads) on sales and show that rates have a different impact in different periods. In particular, Moro et al. [19] find a significant link between the official discount rate, the credit provided by banks and sales.

Subsequent works on sales forecasting focused on evaluating the effectiveness of various approaches. Hassani et al. [20] find that Single Spectrum Analysis outperforms other approaches in predicting sales at the aggregate level in the United States. Han et al. [21] proposes the integrated use of Cluster and Principal Components Analysis while Han et al. [22] successfully experiment with the use of genetic algorithms and the use of big data obtained from Web searches for homes to buy.

In the last five years there has been an evolution in the procedures used for forecasting models. Alongside the classical econometric approaches [23,24,25], neural networks are beginning to be used, and it is highlighted that they have similar performance to classical econometric models [26], but that, integrated with the latter, they produce better results [27,28,29].

Some significant points emerge from the review carried out: (1) most of the work concerns the U.S. real estate market and few are applied to other countries (Brazil, South Korea, Thailand); (2) most of the research has used auto-regressive models of various kinds; (3) all works identify an effect, sometimes delayed in time, of variations in the economic parameters on the volume of sales; and (4) recently, applications of neural networks have appeared which demonstrate their potential.

The literature review highlights interesting opportunities for extending and deepening the study of real estate market dynamics from the perspective of sales volume. First, expand existing studies to the European context in general, and Italy in particular, as the literature review highlighted a lack of specific insights. Then, begin applying neural approaches already widely tested in the study of price dynamics to market volumes; indeed, real estate markets, in terms of volumes and prices, exhibit complex relationships with local economic and social dynamics, often too complex to be modeled with traditional econometric approaches. Lastly, but not least, begin exploring the possibility of simulating the impact of economic variables on real estate market size, a matter of considerable economic and social importance.

3. The Multi-Layer Perceptron (MLP) Artificial Neural Network

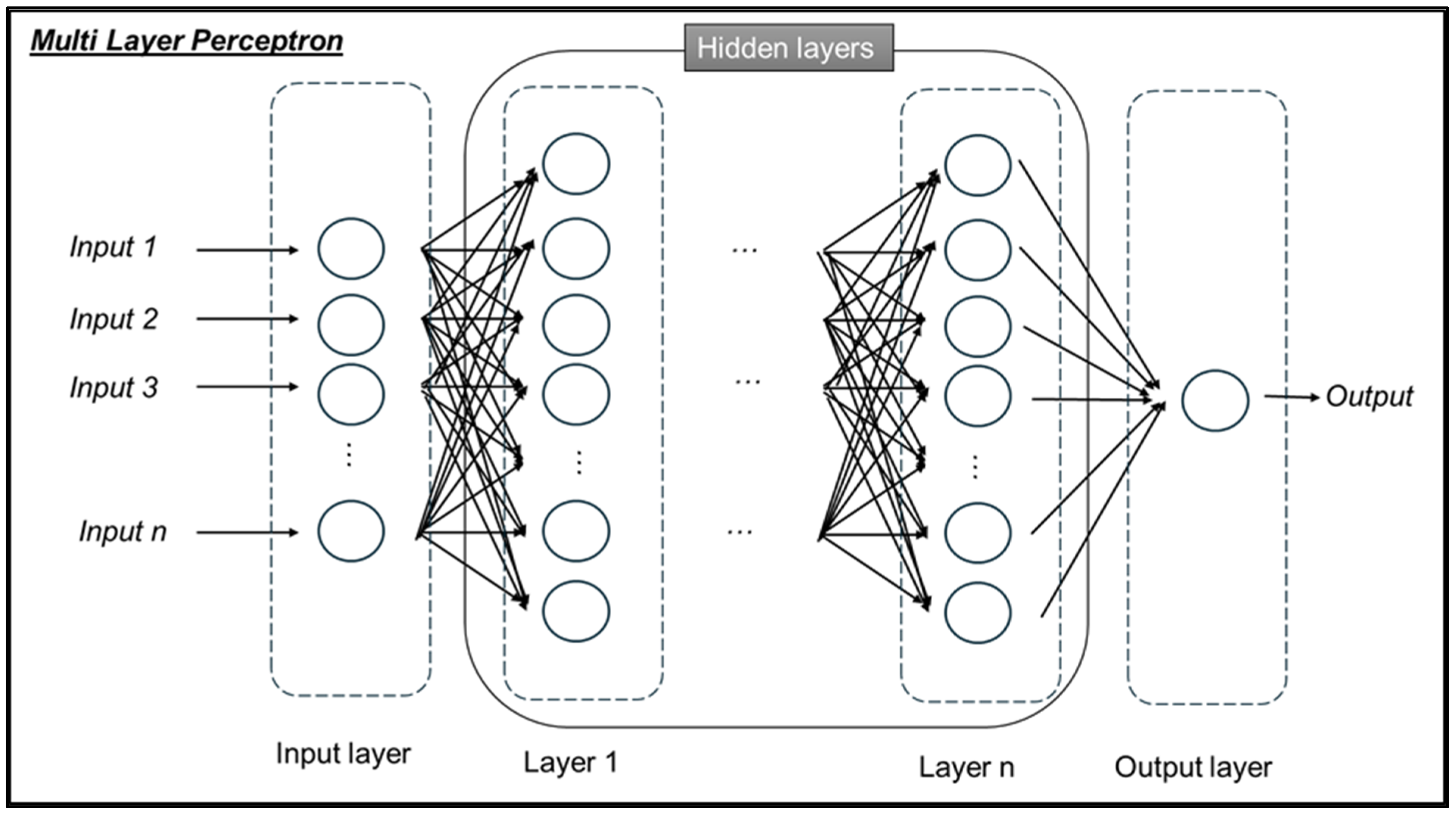
Neural networks are inferential models that are inspired by the way biological neurons learn and process information [30]. Neural networks are organized into basic processing units (artificial neurons) functionally connected with other artificial neurons, distributed in various layers and characterized by different functions: (1) the input layer; (2) the hidden layers; and (3) the output layer. In traditional networks, such as Multi-Layer Perceptron (MLP) neural networks, all neurons in a certain layer are connected with all neurons in adjacent layers. These connections are known as synapses.

The network feeds on the data introduced into the nodes of the input layer and processes them in the neurons of the hidden layers using the signals that come from synaptic interconnections. The processed inputs thus reach the output layer, which then provides the response. In this way, a neural network is able to represent relationships between independent and dependent variables which are much more complex than normal econometric models.

From the original insight of McCulloch and Pitts [31] to present, there have been hundreds of thousands of scientific articles on the application of artificial neural networks in a wide variety of fields. In recent years, the basic principle of the neural network has been declined, operationally, in numerous variants [32]. In this research we present the results of the application of a Multi-Layer Perceptron (MLP) network which leads to a good modeling of the phenomenon considered. Other types of networks have also been tested (such as recursive networks of the Long Short-Term Memory type [33]), but the results observed were not equally satisfactory, probably due to the small size of the database which generated overfitting in the training phase.

The MLP network is well known and applied in numerous areas. It is a quick and simple network to train and is made up of a series of nodes (neurons) fully interconnected with neurons of the next level. The network has an input layer, at least one hidden layer and an output layer, which returns the expected value (Figure 1). Inside each neuron, there is a function (named “Activation Function”) that processes the input data and returns a value. The definition of the optimal values within the network, which maximizes the probability of obtaining estimates close to the values observed, takes place through a training process. The process is obtained by presenting the model with the observed input–output pairs and delegating the task of adjusting the parameters to a special algorithm. The adjustment is made in order to improve the estimate when each new observation occurs. This type of training is known as “supervised” because, as mentioned, it is carried out by showing the input–output pairs to the model example. These pairs are extracted from the available dataset and form the so called “training set”. Data that is not included in the training set is used to verify the network’s ability to predict new data and forms the “test set”. Usually, the selection of data between training sets and test sets is random, in order to minimize the probability of incurring the so-called overfitting phenomenon, i.e., the network “learns by heart” what is shown to it with the training data but, not having grasped the real links underlying the phenomenon to be studied, is unable to perform adequately with the data in the test set. In other words, it does not have sufficient generalization capacity. The problem of the optimal selection of training and test sets of the real estate market has been explored by Galante et al. [34].

4. The Case Study

The MLP neural network described above has been applied to a database consisting of IMI, NTN, quotations and “fundamentals” in the Italian provinces from 2005 to 2020. A total of 99 provinces were taken into consideration and thus, 1584 observations were obtained. The territories excluded from the analysis were those where the Tavolare land registry (formerly Austrian) existed (Provinces of Bolzano, Gorizia, Trento and Trieste). Recently established provinces such as Monza and Brianza in Lombardy, Fermo in the Marche, Barletta, Andria and Trani in Puglia, and Carbonia-Iglesias, Medio Campidano, Ogliastra and Olbia-Tempio in Sardinia were not considered separately since their municipalities were included in the original provinces.

The variables used in the analysis (

Table 2. The variables used in the analysis.

Variable	Description	Source
ABIT	Number of dwelling	ISTAT
DENS	Population density	ISTAT
DISOCC	Unemployment rate	ISTAT
IMI	Real estate market intensity	OMI-Tax Agency, ISTAT
INFLA	Inflation rate	ISTAT
NTN	Number of normalized transactions	OMI-Tax Agency
POP	Resident population of the province	ISTAT
Q_MEDIA	Average municipal quotations, civil housing in normal conditions	OMI-Tax Agency
RED_PC	Disposable income per capita	ISTAT
SALDO_DEMO	Percentage change in resident population	ISTAT
TASSI	Average interest rate on home loans	Bank of Italy

) have been selected on the basis of the scientific literature, which identifies house stock, incomes, population, employment, inflation and interest rates as the most influential factors on the real estate market [35].

Overall, the analyzed territory amounts to 276,957 km², equal to 92% of the national territory. The resident population in 2020 was 56.2 million (94.6% of the national population). In the provinces under analysis in 2020 there were almost 558 thousand transactions, equal to almost all of those detected by the OMI of the Tax Agency [5].

The IMI has a wide variability both at the provincial level and over the years. The highest values occurred in the period 2005–2009 and in the northern provinces. The lowest values, on the other hand, occurred in the following decade in the southern and island provinces.

Table 3. Main variables’ characteristics.

Variable	Min	Max	Average	Dev. Std.	V. C.
ABIT (numb.)	52,128	2,210,601	302,979	287,768	0.95
DENS (inhabit./km2)	36.36	2,611.28	246.74	326.91	1.32
DISOCC (%)	2.24	31.80	10.22	5.69	0.56
IMI (%)	0.58	7.00	1.88	0.86	0.46
INFLA (%)	−0.14	3.35	1.35	1.07	0.79
NTN (numb.)	399.81	74,401.87	5946.14	7967.05	1.34
POP (numb. Residents)	83.099	4263.542	567.621	610.504	1.08
Q_MEDIA (€)	324.71	2650.9	968.18	388.29	0.40
RED_PC (0.000 €)	11.70	23.20	17.88	3.50	0.20
TASSI (%)	1.25	5.92	3.19	1.23	0.39

shows some descriptive statistics of the variables used in the neural networks.

The OMI database reports very detailed quotations for residential properties at municipal level, distinguished by location, type of building and state of conservation. With the necessity of referring to an “ordinary” value, the average price of civil properties in “normal” conditions and located in urban centers (Zone B) was used. The values calculated (Q_MEDIA) at the provincial level vary between 300 EUR/sqm in the inland provinces of the south and over 2500 EUR/sqm in the metropolitan provinces of Rome and Milan. It should be remembered that the real estate values used in this work, being averaged at the provincial level, hide a much wider variability at the intra-provincial level. However, the trend in the average price calculated at national level is almost overlapping with the IPAB index processed by Istat (Corr. Pearson 0.871).

The number of normalized transactions (NTN) varies greatly depending on the population of the province (POP) and the number of dwellings present (ABIT). The population density (DENS) depends on the settlement aspect: it is very low in the inland Alpine provinces, the Apennines and the islands, and it is very high in the metropolitan area of Milan, Naples and Rome.

The unemployment rate (DISOCC) is rather different across provinces and time. It ranges from 3 to 4% in the northern provinces in 2005–2010 to 20–25% in the southern and island provinces in the years 2015 to 2020.

The average disposable income per capita (RED_PC at current values) shows a distribution that is consistent, with some exceptions, with the unemployment rate. The highest incomes are in the provinces of Lombardy, Emilia, Piedmont and Liguria, while the lowest are in the southern and island provinces (Sicily).

Average mortgage rates (TASSI) have very little variability at the territorial level and modest volatility over time. The highest rates were recorded around 2007–2008 following the aforementioned financial crisis. The lowest rates are around 2018–2020. The inflation rate is, on average, quite low.

The following

Table 4. The correlation matrix between the variables.

	DENS	DISOCC	IMI	INFLA	NTN	POP	Q_MEDIA	RED_PC	TASSI
ABIT	0.663 **	0.074 **	0.127 **	−0.04	0.891 **	0.986 **	0.359 **	−0.076 **	−0.045
DENS		0.047	0.183 **	−0.004	0.629 **	0.734 **	0.355 **	−0.009	−0.001
DISOCC			−0.570 **	−0.219 **	−0.155 **	0.054 *	−0.237 **	0.210 **	−0.244 **
IMI				0.318 **	0.415 **	0.166 **	0.227 **	−0.054 *	0.391 **
INFLA					0.066 **	−0.004	−0.034	−0.052 *	0.701 **
NTN						0.888 **	0.373 **	−0.122 **	0.079 **
POP							0.370 **	−0.094 **	0.001
Q_MEDIA								−0.037	0.031
RED_PC									−0.096 **

**: Significant correlation at 0.01 (2-tailed); *: Significant correlation at 0.05 (2-tailed).

and

Table 5. The regression analysis stepwise and panel on IMI.

	Stepwise		Panel (16 Years; 1584 Obs.)		Panel Lag 1 (15 Years; 1485 Obs.)
	Coeff.	t	Coeff.	t	Coeff.	t
(Constant)	1.20 × 10−2	11.79	1.22 × 10−2	5.71	1.28 × 10−2	6.31
DENS	3.45 × 10−6	4.94	3.45 × 10−6	1.39	3.28 × 10−6	1.34
DISOCC	−7.40 × 10−2	−25.41	−7.41 × 10−2	−9.57	−6.82 × 10−2	−9.22
INFLA	1.00 × 10−3	3.28	6.75 × 10−4	7.62	−3.54 × 10−4	−3.65
POP	1.44 × 10−9	3.82	1.44 × 10−9	1.95	1.43 × 10−9	1.99
RED_PC	1.00 × 10−10	4.60	2.11 × 10−4	1.80	1.78 × 10−4	1.59
STA_OCC	4.00 × 10−3	11.75	3.82 × 10−3	16.49	4.52 × 10−3	19.00
TASSI	1.86 × 10−1	10.41	1.86 × 10−1	16.50	1.73 × 10−1	16.80
Model Summary	Adj. R Sq.	Std. Err.	Adj. R Sq.	Std. Err.	Adj. R Sq.	Std. Err.
	0.490	0.006	0.490	0.006	0.453	0.006

report an initial statistical and econometric analysis of the variables. Table 4 illustrates the main correlations, while Table 5 shows the result of some regressions carried out to identify the variables which, overall, best contribute to explaining the variability observed in the IMI, taken as a proxy for the “liveliness” of the housing market.

The correlation analysis highlights some obvious facts, such as the high correlations between population, housing stock, population density and the number of transactions. The prices show a limited but significant positive correlation with the variables that characterize the settlement structure mentioned above and the degree of activity (IMI) of the real estate market. The IMI is negatively correlated with the unemployment rate and positively correlated with interest rates. The interest rate on mortgages is positively correlated with inflation and market activity and negatively correlated with unemployment.

The regressions were carried out by means of a “stepwise” and “panel” procedure, with 16- and 15-year time series repeated for the 99 provinces.

The stepwise procedure selects a set of seven significant independent variables with an Adj. R sq. of 0.49. The most important and negative factor appears to be the unemployment rate, while all other variables have a positive effect. In order of significance, they are employment stability (the variable STA_OCC is dichotomous with a value of 1 if the unemployment rate has not decreased in the last two years and 0 otherwise), interest rates, population density, per capita income, resident population and inflation.

The panel model considers all variables potentially influencing IMI, initially without introducing time delays. All panel models have been estimated with the “robust error” procedure of Arellano [36] given the presence of autocorrelation in the residues.

The results of the “panel” regression substantially confirm the results of the stepwise regression. Population density and per capita income lose their significance, while the significance of interest rates and the stability of per capita disposable income increases. The Adj. R sq. and standard error of the model are almost unchanged compared to stepwise regression.

Table 5 also reports the results of a “panel” regression with delayed independent variables. For example, the forecast of the trend of the IMI variable for the year 2010 for a specific province included all variables but only the independent variables observed in the year 2009 for the same province. Therefore, the first dependent variables of 2006 are used, since those of 2005 would have required the observations of 2004 which were not available. A total of 1485 useful observations were finally available.

The introduction of the one-year (LAG_1) delay in the independent variables slightly reduces the R sq index, while the standard error of the model remains constant. The results substantially confirm what emerged from the panel model without time lag, except for the effect of inflation, which remains significant but changes sign.

Overall, the analyses carried out seem to show that the degree of activity of the real estate market at the provincial level and in the period from 2005 to 2020 is mainly influenced by the availability and stability of labor. This, among other things, strongly affects access to credit, which is fundamental in shaping the demand for housing.

The other variables seem to play a significant but ancillary role. Per capita income positively influences IMI in the stepwise model but loses significance in panel models. The evanescence of the effect could be due to the fact that there are properties on the market at low prices that make them accessible even to modest incomes as long as they are stable. In the light of the regressions, the IMI appears substantially consistent with the a priori on cyclical and local “fundamentals” with only a few exceptions. The exceptions are the effect of interest rates, which always appears positive, and that of inflation, which is contradictory. The effect of rates may be related to the fact that rates are slightly higher in northern regions where the market is historically more active. The effect of inflation, on the other hand, is more elusive, also due to the fact that in the time interval considered, it was very, if not excessively, low.

5. Results

The data available for the simulations relate to the period 2005 to 2020 and refer to a total of 99 provinces. In total, 1584 annual observations were therefore recovered.

Based on the regression results and the literature [12,17], the decision was made to adopt a one-year delay for the independent variables.

All variables were normalized using the following formula:

$$z={\displaystyle \frac{x-\mu }{\delta }}$$

(1)

where x represents the original value of the observation, μ represents the average values (calculated on the training set), σ represents the standard deviation (calculated on the training set) and z represents the transformed (standardized) value. Data normalization has several advantages in the use of neural networks, one of which being faster training. This is because of the better convergence of the optimizer and more robust networks, since no input value of independent variables is predominant due to an excessive scale factor compared to the others.

5.1. The Performance of the MLP Network

As mentioned above, MLPs are usually trained with a non-sequential dataset, randomly selected from all available data. In this work, 75% of the available observations (1113 records) were randomly chosen as the training set. The remaining 25% (372 records) were used for the test set.

The MLP model has been designed with an input layer of eight neurons, equal to the independent variables that emerged from the statistical analysis already described. The second level has 15 neurons with “tanh” activation function, and the third level is formed by 12 neurons with a “Rectified Linear Unit (ReLu)” activation function. An output layer composed of a single neuron with linear activation function is finally used to obtain the estimated value. Training has been performed by minimizing the mean squared error (MSE) loss function.

In summary, the network had to estimate 340 parameters, and the 1113 records available for training seem to be sufficient to ensure the required flexibility in the fitting of the model. During the analyses, it emerged that it was very difficult to use an LSTM network, which initially seemed more suitable for dealing with time series, since these models are very expensive in terms of parameters estimated [37]. The data available were not enough to estimate such a number of parameters and consequently, the performances observed were much worse than the ones obtained by MLP as the model was clearly in overfitting.

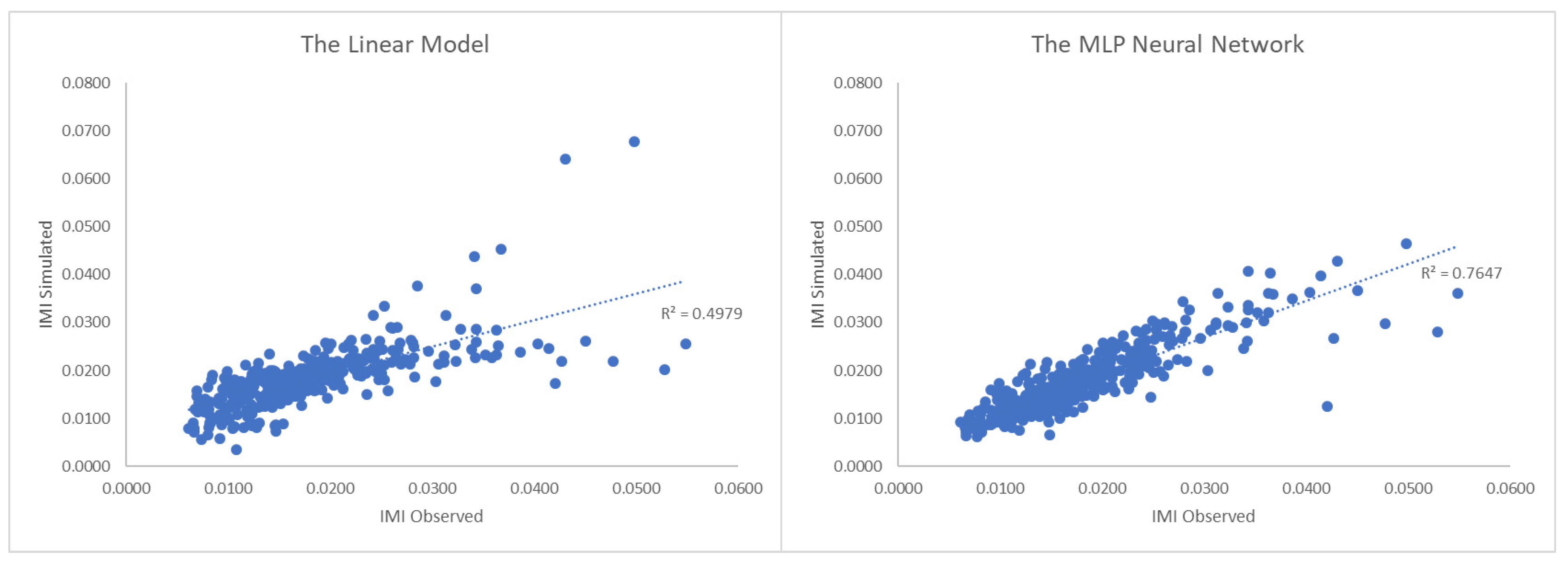
In order to evaluate its performance, the MLP model was compared with a linear model (Ordinary Least Squares Estimator).

The predictions in the test set obtained by the two models are illustrated in Figure 2 and detailed in

Table 6. The performances of the two models.

Model	Indicator
	MAE	MSE	RMSE	R2	MAPE
Linear OLS	0.4990	0.5240	0.7239	0.4901	181.44
MLP Neural Network	0.3244	0.2429	0.4929	0.7636	1180.81

MAE: Mean Absolute Error; MSE: Mean Square Error; RMSE; Root Mean Square Error; MAPE: Mean Absolute Percentage Error.

,

Table 7. The distribution of model errors.

Model	Percentile
	5%	25%	Median	75%	95%
Linear OLS	0.019%	0.121%	0.300%	0.543%	1.050%
MLP Neural Network	0.013%	0.089%	0.180%	0.353%	0.657%

and

Table 8. Model errors in the geographical areas of Italy.

Area	Linear Model OLS				MLP Neural Network
	Min	Average	Max	Std. Dev.	Min	Average	Max	Std. Dev.
Center	0.00%	0.38%	1.89%	0.36%	0.00%	0.26%	0.93%	0.22%
Islands	0.01%	0.45%	3.27%	0.60%	0.00%	0.33%	2.49%	0.46%
North East	0.01%	0.40%	2.08%	0.41%	0.00%	0.29%	1.60%	0.24%
North West	0.01%	0.46%	2.93%	0.46%	0.00%	0.26%	1.87%	0.24%
South	0.01%	0.34%	2.49%	0.32%	0.00%	0.22%	2.96%	0.33%

.

The graphs highlight the best performance of the MLP model with a lower dispersion of the simulated data compared to the observed one. Both models work quite well for medium and low IMI values, while for the (few) provinces with higher observed IMI, the error increases significantly.

Taking into consideration the ten largest errors in the two models, it can be observed that, apart from some errors in the linear model for the province of Milan, the higher errors are the same in the two models and concern provinces with small demographic dimensions (Sassari, Lodi, Livorno, Isernia, Forlì).

Table 6 provides a summary of some well-known statistical indicators of performance. These metrics evidence that the MLP network can reach better estimations than those of the linear model, with the sole exception of MAPE, which is influenced by the estimation error on small provinces mentioned above.

Table 7 shows the distribution of the percentage errors of the two models. Again, the superiority of the MLP network with the lowest values in all thresholds is proven. In particular, the median value of the MLP network is 66% lower than that of the linear model and that of the 95th percentile is 60% lower.

Finally, Table 8 shows the performance of the two models in the different geographical areas of the Italian peninsula. The average error of the MLP network is lower than that of the linear model in all geographical areas, while the minimum error is always lower or at most, the same in cases where it is zero. The maximum error is also smaller, except in southern Italy where the maximum error of MLP network is higher in the small province of Isernia, located in the Molise region.

5.2. The Robustness of MLP Network Performances

As previously anticipated, the MLP network was trained by randomly selecting data from the original database. Consequently, by repeating the random selection, both the training set and the test set are composed of a different set of examples on which to train and then trial the network. The results would certainly be different for both the MLP network and the OLS linear model. It is therefore interesting to verify the variability of performance as the data on which the two models are calibrated vary. If they were stable, it would mean that the selected model lends itself well to analyzing the investigated phenomenon. If, on the other hand, the performance was very variable, it would not be possible to adopt that particular model to formulate predictions, since their reliability would be uncertain.

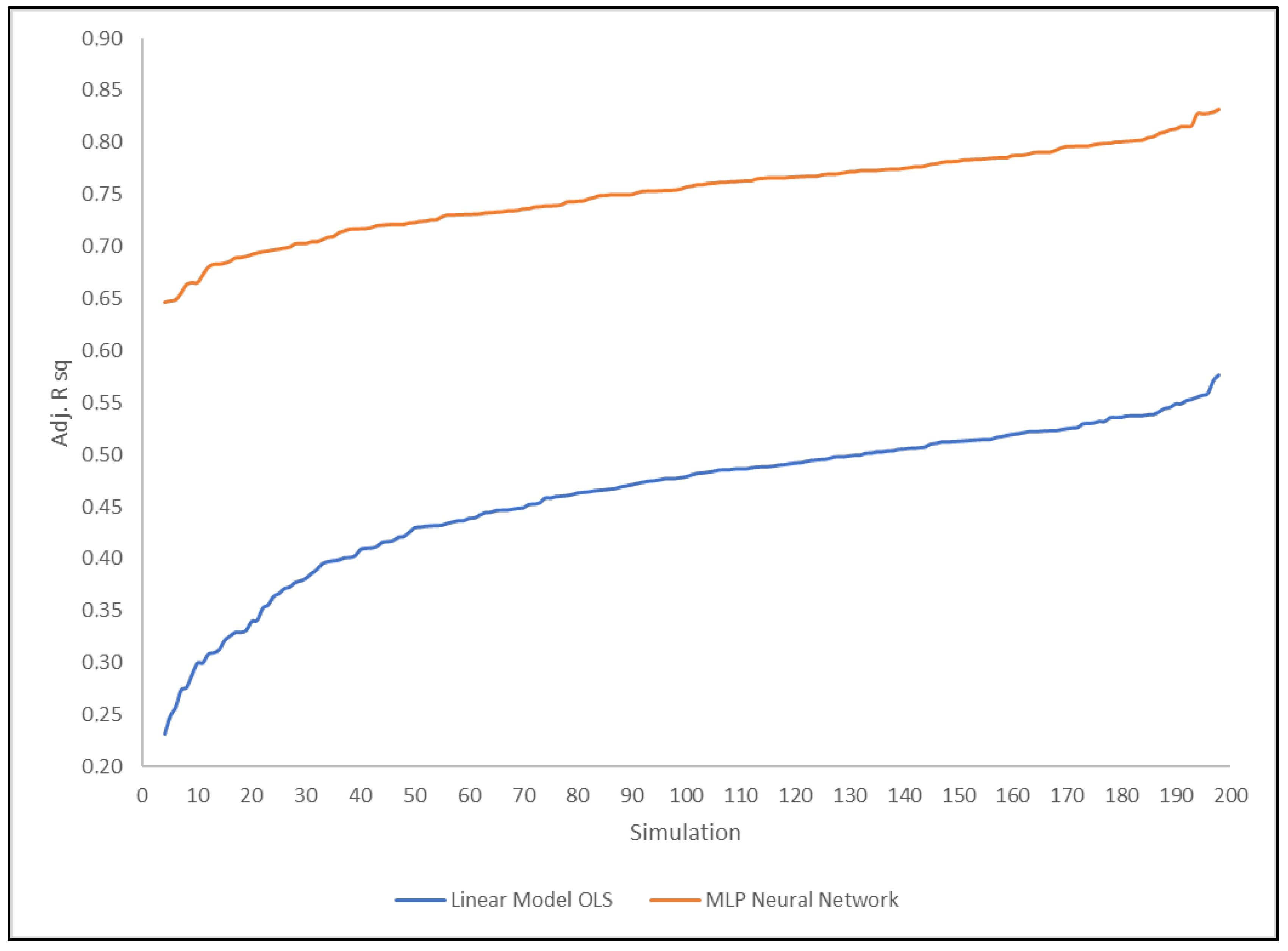
In order to verify the robustness of the models, 200 resampling and consequent training of the networks were carried out. Subsequently, all MLP networks and the corresponding linear models were tested in their respective 200 test sets and Adj. R² were calculated.

The results, ordered by increasing R² for both models, are shown in Figure 3 were the R² of the first quintile have been excluded because the OLS linear model because of some negative values.

While excluding the Adj. R² simulations in the first quintile from the analysis, Figure 3 unequivocally highlights the greater robustness of the MLP network compared to the OLS linear model. The Adj. R² index of the network is higher than that of the linear model in all 200 simulations and is more stable, since the variation coefficient of the MLP network is really lower than the OLS linear model’s one (

Table 9. MLP network performances in 200 training stimulations.

Model	Adj. R2
	Min	Average	Max	Std Dev.	V.C.
Linear OLS	0.231	0.462	0.577	0.070	15.2%
MLP Neural Network	0.604	0.751	0.832	0.043	5.7%

).

5.3. The Sensitivity of the MLP Network to the Variation in Some “Fundamentals”

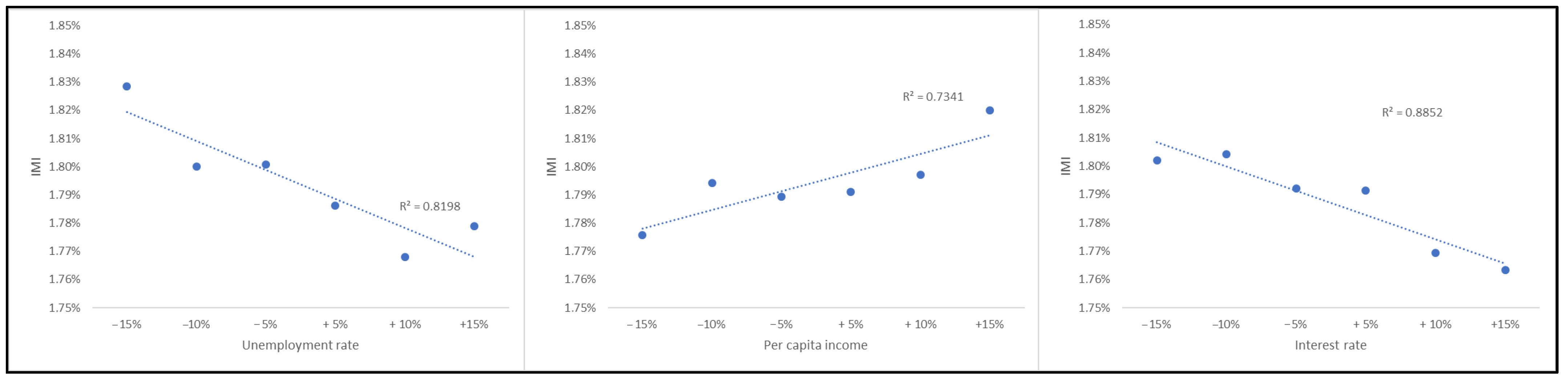
The analyses concluded with some simulations on the effect of changes in some “fundamentals” (unemployment, per capita disposable income, mortgages rates) on the degree of activity of the housing market. The goal is to verify the predicted trends in the IMI obtained in the test set using network input modified values instead of data observed in the test sample. Changes in a single variable at a time were simulated by multiplying the observed value by a factor (1 + k), where k is a variable parameter in the range [−15%, +15%].

The results of this sensitivity analysis, for the main variables, are shown in

Table 10. IMI and changes (%) in fundamentals.

Variable	Variation
	−15%	−10%	−5%	+5%	+10%	+15%
Unemployment rate	1.829%	1.800%	1.801%	1.786%	1.768%	1.779%
Per capita income	1.776%	1.794%	1.789%	1.791%	1.797%	1.820%
Mortgages rate	1.802%	1.804%	1.791%	1.791%	1.769%	1.763%

and Figure 4.

The trend of the IMI and changes in the “fundamentals” taken into consideration is consistent with expectations, as well as with the economic a priori: when mortgages rates and unemployment increase, the IMI decreases, while when the per capita disposable income increases, the IMI increases. It should be noted, however, that the effect produced by changes in individual economic parameters has not a monotonic trend. These are aspects that deserve further study, both to formulate complex and “consistent” scenarios where the various parameters are varied in accordance with the characteristics of the scenario and to test the stability of the simulation results as the sets selected from time to time vary.

6. Conclusions

The research in this article is motivated by the observation that the close relationship between the economic situation and the real estate market manifests more in the dynamics of the number of transactions than in that of prices. In addition, the number of transactions has a greater impact than prices on a variety of aspects, such as the turnover of the construction sector (new buildings and renovations), services related to transactions (brokerage and legal services), tax revenue, lending and much more. However, transaction dynamics have received less attention than price dynamics in the scientific literature.

The research used a panel of data on 99 Italian provinces in the period 2005–2020 to build a forecasting model of the degree of activity of the housing market using a non-linear model. Various neural networks were tested, and the final choice fell on the classic MLP neural network. The time interval was chosen on the basis of the available data, which includes the well-known crisis of 2007–08 and the subsequent phase of adjustment and recovery.

The network training was preceded by a statistical analysis that showed that the degree of activity of the real estate market is mainly influenced by the availability and stability of labor, which, among other things, strongly affect access to credit, fundamental in shaping the demand for housing. Other variables seem to play a significant but ancillary role, at least in the considered time horizon. In particular, this seems to explain the greater fragility of the real estate market in regions with high unemployment rates (Southern Italy), which, in times of crisis, seems to contract more than in other regions.

The statistical analysis confirmed that IMI is broadly consistent with a priori on cyclical and local “fundamentals”.

The network training and testing showed that the MLP network is more capable than linear models of representing the complex relationships between the economic situation and the degree of activity of the real estate market, while offering smaller errors and less dispersion of the estimated data than those observed.

Finally, the MLP network responds consistently to changes in “fundamentals”, increasing IMI when mortgages rates and unemployment fall and when per capita disposable income increases. The MLP network, unlike econometric analysis, responds coherently to changes in the interest rate in accordance with economic a priori assumptions. However, the limitations of the model should not be overlooked, since despite being partly known due to the premise of the study, others emerged during the analyses and simulations.

In particular, (a) the restricted time interval that limits the validity of the model to the phenomena observed in the period; (b) having used aggregate data at the provincial level which underestimates the variability of the phenomenon at the local level; and (c) having used the regional data for some variables and not the provincial one. These limits can only be solved with a more in-depth collection of basic information or by examining more homogeneous territorial units, for example, by taking into consideration municipal observation or only the provincial capitals.

The limits of the neural network model just described also affect its use in evaluating real estate policies. In this regard, it is useful to remember that the model was calibrated with reference to observations from 2005 to 2020 and, therefore, cannot interpret relationships that occur over longer time horizons, such as demographic dynamics. Furthermore, it is unable to capture phenomena occurring at a lower spatial scale than the provincial level, such as local housing policies. However, it appears to have a good ability to simulate the effects of more general policies, such as those affecting access to and the cost of real estate credit and employment. These are aspects that deserve further study, both to formulate complex and “consistent” scenarios, where the various parameters vary in accordance with the characteristics of the scenario itself, and to test the stability of the simulation results as the selected sets vary.

However, in the authors’ opinion, the proposed approach constitutes a starting point for developing useful models to simulate the structure of the real estate market and, therefore, for supporting regulatory authorities in calibrating policies for the real estate market, as well as for economic actors to trace market development scenarios in light of the evolution of the economic situation.