Abstract
We examine the use of a Geometric Distribution for pre-calculating the publication deadlines of blocks in a simulation of proof-of-work Blockchain. Specifically, we focus on Discrete-Event Simulation, where the simulator identifies events to be simulated, calculates their deadlines, places them in an Event Queue ordered by deadline, and processes them sequentially. In Blockchain, these events include the publication and reception of a block by each Miner. While a Geometric Distribution allows the calculation of block publication deadlines in the absence of Difficulty updates, in the case of evolving Difficulty, it must be extended to a non-homogeneous Geometric Distribution. To address this issue, we introduce the Geometric Distribution with a Variable Probability, a non-homogeneous Geometric Distribution that enables the calculation of block publication deadlines in the presence of Difficulty Regulation—a distinctive feature of proof-of-work Blockchain. We then present the architecture and operating principles of a Discrete-Event Simulator based on this distribution, along with simulation results that validate our approach.
1. Introduction
In this paper, we focus on the pre-calculation of Valid Block (VB) publication deadlines in a proof-of-work (PoW) Blockchain (hereafter referred to as Blockchain), a fundamental aspect of Blockchain Discrete-Event Simulation [1].
In Blockchain, a set of independent nodes called Miners publish VBs autonomously, with no coordination [2,3,4,5]. Each Miner, continuously engaged in a computationally intensive block validation process of random duration called Mining, occasionally succeeds in obtaining a VB and publishes it. While the lack of coordination may lead to conflicts among Miners, resulting in overlapping VB publications, Blockchain’s distinctive mechanism resolves such conflicts and ensures that a single VB sequence eventually prevails.
Since VB publication in Blockchain is a result of the occurrence of multiple independent events, each corresponding to a VB publication by a Miner, it can be modeled using a Poisson distribution [6]. Following this approach, Blockchain simulators [7,8,9,10,11,12,13] typically generate VBs at exponentially distributed intervals, as dictated by Poisson statistics, and focus on Blockchain operation, often concentrating on existing Blockchain-based systems, e.g., typically Bitcoin and Ethereum.
In contrast with these approaches, this study focuses on VB generation and specifically on VB generation by Miners. For each Miner, the simulator calculates the deadline for the publication of the next VB and schedules the corresponding event accordingly. The deadline is determined as the product of a random component, representing the number of hash operations required for block validation, and a deterministic component, representing the hash calculation time, i.e., the inverse of the Miner’s hashpower. Considering Miners independently enables the analysis of sets of Miners with varying computational power.
In each Miner, VB publication follows Geometric Distribution (GD) [14] as a Miner publishes a VB when drawing a binary random variable that results in Success, with probability p (typically very low), after several drawings of the same variable resulting in Failure, with probability . The drawing of a binary random variable corresponds to a hash operation that produces a result H uniformly distributed over the considered range [15], followed by a comparison with a given threshold ( is Success). Consequently, , where R is the hash range.
However, the straightforward application of GD to determine Miners’ VB publication deadlines is insufficient, as it must be adapted to scenarios in which the probability of each event, i.e., a successful hash, varies over time. This is necessary because Miners periodically adjust threshold T to maintain a constant average time between consecutive VBs despite fluctuations in global computing power over time. This process is known as Difficulty Regulation, as threshold T is defined as the inverse of parameter D, which is associated with the Difficulty of the cryptographic problem [16,17,18,19]. When D, and consequently T and , vary over time, GD must evolve from homogeneous to non-homogeneous [20].
This is the motivation behind the work presented in this paper. In summary, GD allows us to compute the number of iterations a Miner needs before publishing the next VB based on a fixed success probability per iteration. Since this probability evolves over time in Blockchain, depending on Difficulty, the number of iterations a Miner needs before publishing the next VB must be updated at each Difficulty adjustment. To address this, we introduce a non-homogeneous variant of a Geometric Distribution, termed the Geometric Distribution with a Variable Probability (GD-VP), which assumes the existence of time intervals during which the success probability remains constant, which are separated by discrete updates to the probability. We show that in a Blockchain simulation, Difficulty Regulation can be implemented by rescheduling VB publication deadlines at Difficulty updates using GD-VP and that GD-VP can be structured recursively, thus significantly reducing the overhead associated with rescheduling. To accomplish this, we describe the architecture and operation of a Blockchain Execution Environment (BEE), which is the foundation of a Blockchain simulator that leverages GD-VP in Discrete-Event Blockchain simulation.
Our contribution is relevant as, to the best of our knowledge, no existing scientific studies have formally characterized GD-VP or investigated its application within the context of Blockchain systems.
The remaining sections of this document are organized as follows. Section 2 describes the context in which this study is situated. Section 3 and Section 4 recall VB publication deadline calculation through GD and Difficulty Regulation, respectively, Section 5 introduces GD-VP, Section 6 describes the BEE, Section 7 presents a series of numerical experiments that validate GD-VP in a Blockchain simulation, and Section 8 provides a summary and a conclusion.
2. Background and Contextualization
We remind readers that a Permissionless Blockchain based on Proof of Work consists of a set of Miners characterized by hash-power and connected through a broadcast service. This setup enables each Miner to publish a to all others. The broadcast service is characterized by a latency matrix {L}, where denotes the average transmission time between Miner and Miner .
We also remind readers that block validation is computationally intensive, as it requires finding a VB, i.e., a block whose hash falls below a given threshold, and the only way to achieve this is by repeatedly hashing the block, varying a special field called the nonce to differentiate each attempt.
We finally remind readers that since the number and the computational power of Miners are unknown and vary over time in Permissionless Blockchain, it is not possible to configure the parameters in such a way as to achieve a target Blockchain Progress Rate (BPR). On the contrary, a mechanism is needed to regulate BPR at run time. Such a mechanism is based on a parameter called Difficulty, which is periodically increased or decreased in response to increases or decreases in the BPR to maintain its constant value.
We now turn to simulation. Blockchain simulation clearly cannot rely on executing the vast number of hash operations performed by Miners. Instead, a mechanism is needed to pre-calculate the publication times of VBs, which are the events that trigger all subsequent actions of the simulator.
This mechanism can be either global or local. The global mechanism refers to the entire Blockchain. In this case, the independence of Miners implies that VB publication follows Poisson distribution, and that the time between the publication of two consecutive VBs is exponentially distributed, with a rate corresponding to the target global Blockchain rate (e.g., one VB every ten minutes in Bitcoin).
On the contrary, the local mechanism, which is considered in this article, refers to each individual Miner. Each Miner publishes a VB only after obtaining a positive outcome from a binary random variable implemented through a hash operation followed by a comparison with a threshold. Since the positive outcome occurs with very low probability after many negative outcomes, each with high probability, the number of trials required to obtain a positive result naturally follows GD. Consequently, the expected VB publication rate of each individual Miner is given by the product of the expected value of GD and the Miner’s average hash time. The local mechanism enables a fine-grained configuration of infrastructural parameters, in particular, the computing power of each Miner and the latency between pairs of Miners.
However, due to Difficulty regulation, the probability of a positive outcome of the binary random variable varies over time. When a Miner detects a Difficulty change, the Miner must update the deadline of its next publication. Unfortunately, GD assumes a constant success probability and is therefore unable to model VB publication deadlines when the success probability evolves over time. GD must then be extended to Geometric Distribution with a Variable Probability (GD-VP), which is precisely the contribution proposed in this article.
We introduce GD-VP as a natural extension of GD to cases with varying probability. Its application to Blockchain simulation demonstrates its effectiveness in updating deadlines in response to Difficulty adjustments.
In short, each Miner generates its next publication deadline by drawing a geometrically distributed random variable. Subsequently, whenever Difficulty changes, the Miner updates this deadline using GD-VP. This is described in detail later in the article.
3. Miner Operating Model
In Blockchain, a set of Miners independently create and publish VBs to be linked to a data structure called the Block Tree, which is replicated across all Miners. Due to communication latency, VB spreading is not instantaneous. As a result, multiple Miners may make inconsistent decisions, resulting in Block Tree forks. Over time, Blockchain resolves these inconsistencies by ensuring that only one branch of the Block Tree survives.
To publish a VB, a Miner executes a loop in which at each iteration, it creates a new block, hashes it, checks to see if the hash result is smaller than a given threshold T, and, if so, declares the new block valid (i.e., a VB), and publishes it. Pseudo-Code 1 summarizes this process.
| Miner Loop | |||
| 1 | while (forever) { | ||
| 2 | Select Parent Valid Block; | ||
| 3 | Assemble New Block, by including: | ||
| |||
| 4 | Hash New Block; | ||
| 5 | if (Hash of New Block < ) { | ||
| 6 | Declare New Block Valid (i.e., a VB) and publish it | ||
| 7 | } | ||
| 8 | } | ||
| Pseudo-Code 1—Miner Loop. | |||
The nonce field guarantees block differentiation at each iteration even in the absence of changes from the previous iteration. The while (forever) clause indicates that Miners are constantly busy trying to create new VBs. Being that block hashing is by far the most time-consuming operation to be executed to create a VB, Miners can be considered permanently engaged in hashing blocks. Continuous hashing is what is typically referred to as Mining.
Considering that the hash operation produces a result that is uniformly distributed over the hash range, the Miner loop can be abstracted as shown in Pseudo-Code 2.
| Miner Loop Abstraction | |||
| 1 | while (forever) { | ||
| 2 | Draw Binary Random Value with P(True) = R/T; | ||
| 3 | if (Drawn Binary Random Variable == True) { | ||
| 4 | Publish a VB; | ||
| 5 | } | ||
| 6 | } | ||
| Pseudo-Code 2—Miner Loop Abstraction. | |||
Based on this abstraction, we can analyze mining statistically by observing that each Miner publishes a VB at the trial after failed trials, i.e., hashes that did not meet the acceptance condition, followed by a successful trial, i.e., a hash that met the acceptance condition. This behavior is a clear instance of GD. If and respectively denote the probability of success and the probability of failure of each trial, then the probability that the hash is successful after failures can be described by the GD Probability Density Function (PDF), , and Cumulative Distribution Function (CDF), .
Considering that and introducing the Difficulty parameter , we obtain , which captures the fact that the probability of success for each hash is inversely proportional to Difficulty. Of course, .
Consequently, the VB publication deadline of each Miner can be pre-calculated by drawing a geometrically distributed random variable, representing the number of hash operations required before a successful hash, dividing this value by the Miner’s hash rate, and adding this value to the current time.
In the BEE, we draw geometrically distributed random variables using the Inverse Transform Method [21]. This allows mapping the value of a random number uniformly distributed in the [0, 1] range (a function typically made available by operating systems and/or programming libraries, e.g., the rand(3) function in Linux [22]) on the value of a random number distributed according to any by rescaling through the inverse of the of , i.e., .
In the case of GD, is the number of hash operations after which a Miner will generate a VB. This result, divided by the Miner’s hashpower, i.e., the number of hash operations per second that the Miner can execute, and added to current time results in the next Miner publication deadline.
4. Difficulty Regulation
As introduced in Section 2, the only way to maintain a constant average Blockchain Progress Rate (), which can be expressed as the inverse of the Inter Block Time (), is by compensating for the variability of the Global Hash Rate (), i.e., the collective hash rate of all Miners through Difficulty Regulation, as shown in Figure 1.
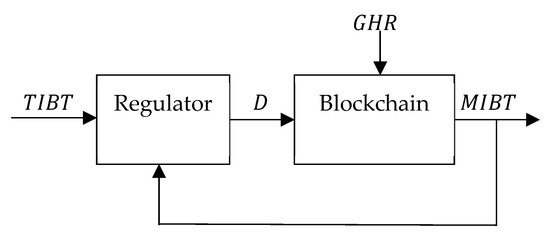
Figure 1.
Difficulty Regulation.
As in any regulation problem, we have a target value of a variable, i.e., Target Inter Block Time ( (which in Bitcoin is 10 min), a measured value of the same variable, i.e., Measured Inter Block Time , an external variable that unpredictably influences the process, i.e., the Global Hash Rate (), and a control variable, i.e., Difficulty , calculated by the Regulator as a function of and , to compensate for the effect of the external variable. It should be noted that the scheme in Figure 1 is conceptual, as the Regulator does not exist as a separate entity but is instead implemented inside each Miner.
Since MIBT is influenced by statistical noise, it is first averaged over a sequence of values—yielding — and then used by the Regulator. For example, Bitcoin averages MIBT over 2016 blocks, corresponding to a period of two weeks.
At the beginning of each sequence, Miners recalculate Difficulty ( by rescaling the one used in the previous sequence (i.e., ). In contrast, Difficulty remains constant during each sequence.
It is worth noting that regardless of the Difficulty Regulation mechanism adopted, Blockchain progresses as a succession of VB sequences operating at constant Difficulty, which is separated by Difficulty updates. Since different Difficulty levels correspond to different probabilities of success, the deadline calculation based on standard GD is not applicable when a deadline falls in future VB sequences with respect to the one in which it is generated. In the following section, we present GD-VP, an extension of GD that considers evolving Difficulty and, consequently, evolving probabilities of success.
5. Geometric Distribution with a Variable Probability
We consider a sequence of trials, each yielding a binary outcome. More specifically we examine a case organized as a set of subsequences , with each being associated with a constant probability of success () and consisting of events, as shown in Figure 2.
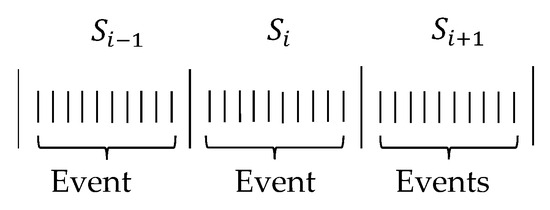
Figure 2.
A sequence of Events organized as a set of subsequences.
We focus on the probability distribution of the number of failed events preceding a successful event occurring in subsequence . The PDF and CDF of such a number, which we call , follow GD-VP and can be computed as follows (see Appendix A for the theoretical analysis):
In Appendix A, we also show how to draw a random variable following GD-VP by applying the Inverse Transform Method. The formula, adapted for use in Blockchain, where the events are the successful hash operations and consequently , is as follows:
In summary, is the number of hash operations that a Miner must perform before a successful hash, i.e., before being allowed to publish a VB. A key property of this formula is that it can be computed recursively by defining two accumulators, namely, and , and updating them at each Difficulty change with O(1) complexity.
6. Miner Deadline Calculation Through the Geometric Distribution with a Variable Probability
We now describe how GD-VP can be incorporated in a Blockchain simulation and, more specifically, how we incorporated it in the BEE.
6.1. Design Objectives
The goal of the BEE project is to provide a Discrete-Event Simulation environment for Proof of Work–based Blockchains leveraging the original features of GD-VP, specifically its ability to update the publication deadlines of VBs upon Difficulty adjustments. We first present the data structure that forms the foundation of the BEE, i.e., the , then we provide an overview of the BEE’s organization, and finally, we outline the BEE’s configuration capabilities.
6.2. Event Queue Structure
According to Discrete-Event Simulation, the BEE leverages a data structure called , organized as a Calendar Queue [23], each element of which is a quadruple (, , , ), where
- is the Id of the Miner supposed to handle the ;
- is the time when the is scheduled to take place;
- is either
- ○
- Reception Deadline: The time at which a Miner is supposed to receive a ;
- ○
- Publication Deadline: The time at which a Miner is supposed to publish a ;
- is the content of the .
Below, we focus on , Deadline, and Type while omitting , as it pertains to higher layers of processing that fall outside the scope of this paper.
6.3. Program Organization
The BEE is implemented through a set of Miner Execution Engines (MEEs) operating autonomously following Blockchain’s modus operandi and through an Event Processing Engine (EPE). The EPE is a program organized as an endless loop that dequeues from the and activates their processing. The loop operates over Virtual Time, a variable that is set to the deadline of the next in the at each iteration. More specifically, at each iteration, the BEE dequeues an , advances the Virtual Time to the deadline, and activates the simulation of the associated to the (i.e., the MEE), as visualized in Pseudo-Code 3.
| Blockchain Execution Environment | |||||
| // Initialization | |||||
| 1 | for each Miner { | ||||
| 2 | Generate first Miner Publication Deadline; | ||||
| 3 | Insert first Miner Publication Deadline in Event Queue; | ||||
| 4 | } | ||||
| // EPE Loop | |||||
| 5 | while (forever) { | ||||
| 6 | Extract Event; | ||||
| 7 | Extract the Miner Id from the Event (say ); | ||||
| 8 | if (Event Type == VB Reception) { | ||||
| 9 | Append VB to the Local Block Tree of ; | ||||
| 10 | Find Longest Branch in the Local Block Tree of ; | ||||
| 11 | if (Difficulty change) { | ||||
| 12 | Reschedule the Publication Deadline of ; | ||||
| 13 | } | ||||
| 14 | } | ||||
| 15 | if (Event Type == VB Publication) { | ||||
| Create VB; | |||||
| 16 | for each Miner { | ||||
| 17 | Set Reception Deadline of =Current Time+; | ||||
| 18 | Insert Reception Event into Event Queue at such a Deadline\; | ||||
| 19 | } | ||||
| 20 | Generate next Publication Deadline of ; | ||||
| 21 | Insert next Publication Deadline of in Event Queue; | ||||
| 22 | } | ||||
| 23 | } | ||||
| 24 | } | ||||
| Pseudo-Code 3—Blockchain Execution Environment. | |||||
With reference to the EPE loop, processing operates as follows:
- On Reception, the MEE associated to the appends the just received to its copy of the Block Tree, recalculates the Longest Branch, and checks whether the new causes a variation in Difficulty. If so, it reschedules the Miner Publication Deadline. To implement rescheduling, the Miner determines the number of hash operations performed since the previous scheduling and adds this value to accumulators and , corresponding to the two summations in Equation (3). After updating the two accumulators, the Miner reschedules its Publication Deadline leveraging the recursive implementation of Equation (3).
Pseudo-Code 4 shows such a procedure:
| Publication Deadline Rescheduling | |||
| : Number of hash operations performed since previous scheduling | |||
| 1 | ; | ||
| 2 | +=; | ||
| 3 | +=; | ||
| 4 | Reschedule Publication Deadline at: | ||
| (()) | |||
| Pseudo-Code 4—Publication Deadline Rescheduling. | |||
- On Publication, the MEE associated to the creates a and publishes it. Publication is implemented through the insertion of a Reception for each Miner at the appropriate deadlines, i.e., at a random latency normally distributed around the values provided in the BEE configuration (see next paragraph). After publishing the , the Miner generates its next Publication Deadline using and places it in the . Pseudo-Code 5 shows the procedure to generate the next Publication Deadline.
| Publication Deadline Generation | |||
| 1 | ; | ||
| 2 | ; | ||
| 3 | ; | ||
| 4 | ; | ||
| 5 | Set new VB Publication Deadline at | ||
| Pseudo-Code 5—Publication Deadline Generation. | |||
It should be noted that most Miners’ actions take place at Reception, while at Publication, the Miners simply publish the s by posting Reception deadlines for all Miners and then recalculate their next Publication deadlines using a regular .
6.4. Program Configuration
We propose the BEE as a tool to investigate Blockchain as a consensus mechanism for distributed systems rather than as a simulator for existing Blockchains. Hence, the BEE focuses on the abstract Blockchain model based on computation-intensive mining and broadcast-based VB publication. Thus, it should be regarded as a configurable framework that allows users to test new Blockchain solutions, analyze their behavior, and evaluate their performance.
Specifically, the BEE allows configuration of the following:
- Algorithms
- ○
- to identify the Best Branch, implemented by default as the Longest Branch;
- ○
- to adjust Difficulty, implemented by default through Difficulty rescaling every 2016 VBs.
- Infrastructure
- ○
- Miner Number ();
- ○
- Miner Hash Rates, through array , each element of which () denotes the hash rate of ;
- ○
- Network Latency, through matrix Latency , each element of which () denotes the mean value of a normal distribution modeling communication latency from to .
Finally, the BEE supports hot configuration updates, that is, the modification of , , and during execution. This capability enables the simulation of Miner entries and exits, changes in computing power, and evolving network performance resulting from path activations/deactivations and traffic fluctuations.
7. Validation
In this section, we present the results of the experiments through which we validated the approach introduced in the previous sections. The experiments were conducted using a custom-built simulator that we developed from scratch in the C programming language. As expected, testing the simulator revealed the need for both high precision—to distinguish publication deadlines that are very close in time—and a wide numerical range—to accommodate deadlines set far in the future. We addressed these challenges by leveraging the long double type, which proved sufficient to meet both the precision and range requirements of our simulation.
In the rest of this section, we first illustrate how VB publication deadlines are computed using the standard GD under constant Difficulty. Next, we demonstrate how GD-VP updates these deadlines in response to Difficulty adjustments. Finally, we highlight a particularly noteworthy phenomenon that emerged from the simulation—the benefit of rapid publication deadline updates, made possible by the efficiency of update computation, which in turn stems from the recursive nature of the proposed algorithm.
7.1. Publication Deadline Computation Under Constant Difficulty
Here, we show the pre-calculation of Blockchain publication deadlines based on GD.
Figure 3 and Figure 4 show the inter VB times at constant difficulty. Specifically, Figure 3 shows the actual times, which vary around an average time of approximately ten minutes (using the Bitcoin progress rate as a reference), while Figure 4 shows their histogram. The two figures illustrate the high variability of inter VB times, as highlighted by the simulation that uses standard GD to compute publication deadlines.
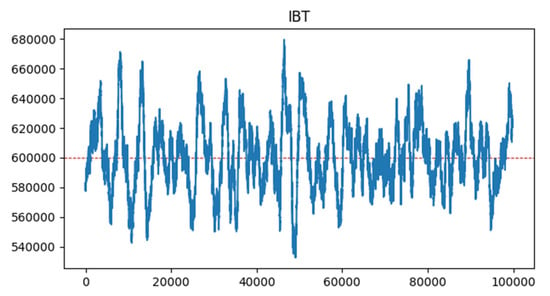
Figure 3.
Inter block times.
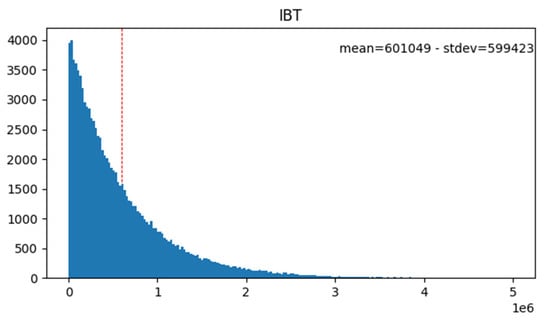
Figure 4.
Histogram of the inter block times.
7.2. Publication Deadline Computation Under Variable Difficulty
Here, we validate the update of Blockchain publication deadlines based on GD-VP.
Figure 5 shows how Difficulty Regulation impacts Blockchain evolution for an increasing number of Miners and consequently of . More specifically, it shows the evolution of Difficulty, driven by Regulation, due to the evolution of the number of Miners, which the BEE receives as an input using the hot reconfiguration capability. The chart shows that the growth of Difficulty, driven by regulation, proceeds in steps, where each step represents a sequence of 2016 VBs at constant Difficulty (again using Bitcoin as a reference). It is therefore at every Difficulty adjustment that GD-VP comes into play. When detecting a Difficulty change, a Miner updates its next publication deadline.
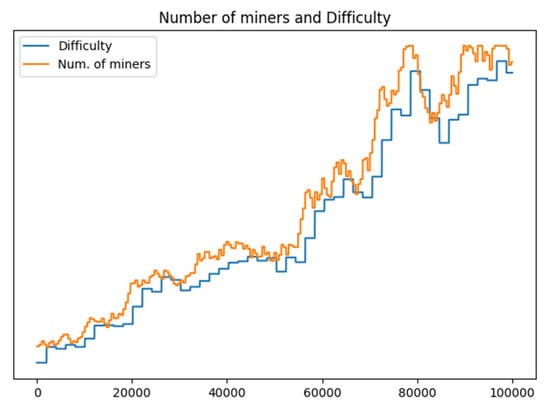
Figure 5.
Regulation based on variable Miner power.
Finally, Figure 6 zooms in on the border between consecutive sequences at increasing , where Difficulty Regulation occurs. The chart shows that immediately before Regulation, the average inter time is lower than its nominal value (600 s) because Regulation has not yet raised Difficulty. After Regulation, the average inter VB time immediately returns to its nominal value due to the rescheduling of VB deadlines.
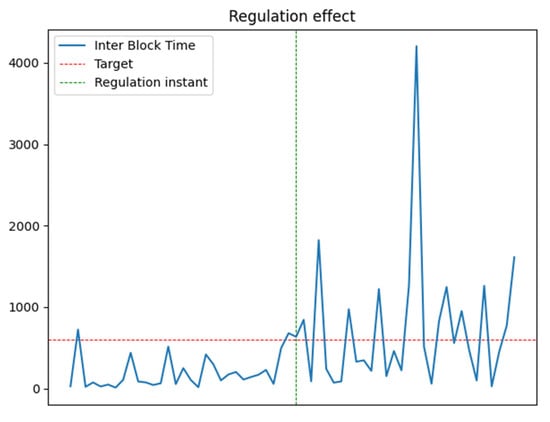
Figure 6.
Effect of Difficulty Regulation around the sequence border.
These results validate GD-VP, which is shown to adapt the deadlines to the evolving immediately. In particular, the average rate is shown to be constant in the presence of evolving , which is compensated for by Difficulty Regulation, and the histogram is shown to maintain an exponential distribution, as expected.
7.3. Rapid Publication Deadline Updates Enabled by Recursive Calculation
A particular aspect of Difficulty Regulation, highlighted by the BEE, deserves attention. We first consider the ideal case in which the Blockchain proceeds linearly, without forks at the border between consecutive sequences, as shown in Figure 7. In this case, Difficulty Regulation simply updates Difficulty at the border between the two sequences.
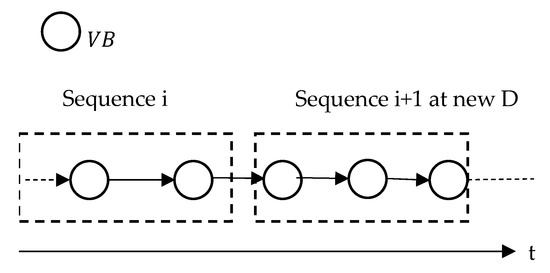
Figure 7.
Difficulty update without forks.
In contrast, when a fork occurs at the border between two consecutive VB sequences, as shown in Figure 8, the value of Difficulty differs across Block Tree branches, and consequently, different branches correspond to different VB publication deadlines. In this case, switching from one branch to another requires VB Publication Deadline recalculation. GD-VP addresses this issue by enabling rapid VB Publication deadline updating through recursive deadline calculation.
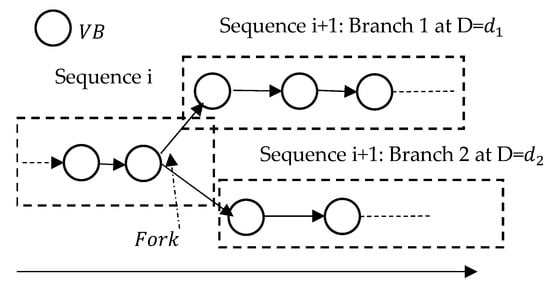
Figure 8.
Branch-dependent Difficulty.
8. Summary and Concluding Remarks
In this paper, we focused on a Discrete-Event simulation of a PoW Blockchain and have introduced the pre-calculation of publication deadlines through GD. We have noted that the operating principle of a PoW Blockchain, which involves Difficulty Regulation, requires GD to adapt to a variable probability of success of hash operations; in response, we have introduced GD-VP. We have then described the structure of a Blockchain Execution Environment (BEE) based on such a distribution and have presented simulation results that validate our proposition, visualizing the evolution of the VB publication rate following Difficulty Regulation.
In summary, the BEE exhibits the following distinctive characteristics:
- General Approach to Blockchain: The BEE addresses a PoW Blockchain as a consensus mechanism rather than focusing on specific Blockchain implementations (e.g., Bitcoin). The aim of the BEE is to serve as a tool to investigate PoW Blockchain as a paradigm and to explore its behavior across different application environments.
- Introduction of GD-VP: The BEE leverages GD-VP, i.e., a non-homogeneous GD, to update Miner deadlines during Difficulty adjustments and Blockchain branch switches.
- Miner-centric Simulation: The BEE simulates Blockchain through the joint action of Miners and simulates Miners individually through an MEE. The MEE leverages GD-VP to replace the PoW and pre-calculate VB deadlines.
- High Scalability: By employing GD-VP and recursive deadline updates, the BEE achieves the highest scalability. Since the is organized as a Calendar Queue, dequeuing an has a computational complexity of , while the adoption of a self-balancing binary tree (e.g., AVL [24]) to post achieves logarithmic complexity for insertion.
- Dynamic Reconfigurability: The BEE supports hot configuration updates.
These characteristics collectively make the BEE a powerful tool for investigating Blockchain consensus and for analyzing Blockchain behavior under diverse scenarios and constraints. In this context, it is worth recalling that the motivation behind the project was to implement a simulator to be used for teaching Proof-of-Work-based Blockchain systems to Master’s students [25].
In addition, GD-VP is an autonomous scientific result as it introduces a new probability distribution suitable for a variety of contexts in which probability evolves over time.
Author Contributions
Conceptualization, M.M.; Formal Analysis: M.M.; Software: M.M. and L.A.; Writing-original draft preparation, M.M.; Writing-review and editing, M.M., L.A. and P.B.; Project Administration: P.B.; Funding Acquisition: P.B. All authors have read and agreed to the published version of the manuscript.
Funding
Funded by the European Union—NextGenerationEU and by the Ministry of University and Research (MUR), National Recovery and Resilience Plan (NRRP), Mission 4, Component 2, Investment 1.5, project “RAISE—Robotics and AI for Socio-economic Empowerment” (ECS00000035).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Here, we calculate the PDF and CDF of , a random variable representing the number of iterations required to obtain a successful binary variable drawing after unsuccessful attempts, in the case where the drawings are organized into a sequence of sequences m − 1, with the probability of success varying across sequences but remaining constant within each one. The result is obtained using induction.
We start with in sequence . The following formulas express the probability of success of drawings at times and the cumulative probability up to time as a function of :
With no loss of generality, we now assume that at time , the Miner updates the probability from to and thus enters sequence . The following formulas express the probability of success at times and the cumulative probability up to time as a function of starting at and up to :
Finally, again with no loss of generality, we assume that at time , the Miner updates the probability from to and thus enters sequence . The following formulas express the probability of success at times and the cumulative probability up to time as a function of starting at , from to and from to :
In general, by induction, we obtain the following formulas:
Considering the sequences of hash operations at constant probability, we can write the PDF and the CDF of random variable , geometrically distributed with variable probability, respectively, as follows:
We now show how to generate a random variable following GD-VP using its Cumulative Distribution Function (CDF) as a basis for the Inverse Transform Method. More specifically, we map the value of a random variable , uniformly distributed in [0, 1], onto the value of a random variable distributed according to , i.e., .
To calculate , we invert and obtain the following formula:
References
- Banks, J.; Carson, J.S.; Nelson, B.L.; Nicol, D.M. Discrete-Event System Simulation, 4th ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 2005. [Google Scholar]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Cryptography Mailing List. Available online: https://metzdowd.com (accessed on 16 August 2021).
- Belotti, M.; Bozi, N.; Pujolle, G.; Secci, S. A vademecum on’ Blockchain technologies: When, which, and how. IEEE Commun. Surv. Tutor. 2019, 21, 3796–3838. [Google Scholar] [CrossRef]
- Zohar, A. Bitcoin: Under the hood. Commun. ACM 2015, 58, 104–113. [Google Scholar] [CrossRef]
- Sultan, K.; Umar, R.; Lakhani, R. Conceptualizing Blockchains: Characteristics & applications. arXiv 2018, arXiv:1806.03693. [Google Scholar]
- Bowden, R.; Keeler, H.P.; Krzesinski, A.E.; Taylor, P.G. Block Arrivals in the Bitcoin Blockchain. arXiv 2018, arXiv:1801.07447. [Google Scholar] [CrossRef]
- Paulavičius, R.; Grigaitis, S.; Filatovas, E. A Systematic Review and Empirical Analysis of Blockchain Simulators. IEEE Access 2021, 9, 38010–38028. [Google Scholar] [CrossRef]
- Gouda, D.K.; Jolly, S.; Kapoor, K. Design and Validation of BlockEval, A Blockchain Simulator. In Proceedings of the International Conference on COMmunication Systems & NETworkS (COMSNETS), Bangalore, India, 5–9 January 2021; pp. 281–289. [Google Scholar]
- Yajam, H.; Ebadi, E.; Akhaee, M.A. JABS: A Blockchain Simulator for Researching Consensus Algorithms. IEEE Trans. Netw. Sci. Eng. 2024, 11, 3–13. [Google Scholar] [CrossRef]
- Faria, C.; Correia, M. BlockSim: Blockchain Simulator. In Proceedings of the 2019 IEEE International Conference on Blockchain (Blockchain), Atlanta, GA, USA, 14–17 July 2019; pp. 439–446. [Google Scholar]
- Alharby, M.; Van Moorsel, A. BlockSim: A Simulation Framework for Blockchain Systems. Sigmetrics Perform. Eval. Rev. 2018, 46, 135–138. [Google Scholar] [CrossRef]
- Aoki, Y.; Otsuki, K.; Kaneko, T.; Banno, R.; Shudo, K. SimBlock: A Blockchain Network Simulator. In Proceedings of the IEEE INFOCOM 2019—IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Paris, France, 29 April–2 May 2019; pp. 325–329. [Google Scholar]
- Cui, B.; Hu, Y. BSELA: A Blockchain Simulator with Event-Layered Architecture. Future Gener. Comput. Syst. C 2024, 151, 182–195. [Google Scholar] [CrossRef]
- Ross, S.M. Introduction to Probability Models, 11th ed.; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Knuth, D.E. The Art of Computer Programming, 3rd ed.; Addison Wesley: Boston, MA, USA, 1997. [Google Scholar]
- Kraft, D. Difficulty control for Blockchain-based consensus systems. Peer Peer Netw. Appl. 2016, 9, 397–413. [Google Scholar] [CrossRef]
- Fullmer, D.; Morse, A.S. Analysis of Difficulty Control in Bitcoin and Proof-of-Work Blockchains. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami, FL, USA, 17–19 December 2018; pp. 5988–5992. [Google Scholar] [CrossRef]
- Zhang, X.; Qin, R.; Yuan, Y.; Wang, F.-Y. An Analysis of Blockchain-based Bitcoin Mining Difficulty: Techniques and Principles. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018; pp. 1184–1189. [Google Scholar] [CrossRef]
- Ilie, D.I.; Werner, S.M.; Stewart, I.D.; Knottenbelt, W.J. Unstable Throughput: When the Difficulty Algorithm Breaks. In Proceedings of the 2021 IEEE International Conference on Blockchain and Cryptocurrency (ICBC), Sydney, Australia, 3–6 May 2021; pp. 1–5. [Google Scholar]
- Mandelbaum, M.; Hlynka, M.; Brill, P.H. Nonhomogeneous geometric distributions with relations to birth and death processes. TOP 2007, 15, 281–296. [Google Scholar] [CrossRef]
- Law, A.M.; Kelton, W.D. Simulation Modeling and Analysis, 3rd ed.; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Rand(3) Linux Manual Page. Available online: https://man7.org/linux/man-pages/man3/rand.3.html (accessed on 16 August 2021).
- Brown, R. Calendar queues: A fast 0(1) priority queue implementation for the simulation event set problem. Commun. ACM 1988, 31, 1220–1227. [Google Scholar] [CrossRef]
- Adelson-Velsky, G.M.; Landis, E.M. An algorithm for the organization of information. Proc. USSR Acad. Sci. 1962, 146, 263–266. [Google Scholar]
- Maresca, M.; Andreoli, L. Modelling Valid Block Publication in PoW Simulation. In Technical Report: CIPI; University of Genoa: Genoa, Italy, 2025. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).