Addressing Non-Uniqueness in Guided Wave Tomography for Limited-View Corrosion Mapping

Abstract

Guided wave tomography has proven to be an effective method for detecting pipeline corrosion, providing both location and quantitive estimates of wall thickness loss. However, the limited view geometry of source–receiver pairs on pipes leads to a significantly ill-posed problem. In practical terms, this means that the wall thickness measurements become unreliable, as small errors or noise in the data can result in large inaccuracies in the reconstructed thickness profile. To address the non-uniqueness inherent in Full Waveform Inversion (FWI) for guided wave tomography, we explore a joint inversion framework that combines multiple guided wave modes: specifically $A_0$, $S_0$, and $S{H}_1$. These modes have different sensitivities to wall thickness variations in pipelines, and by jointly inverting them, we aim to enhance the overall information content available to the inversion process. By deriving statistical measures of solution precision and accuracy through sampling-based analysis, we quantify the reliability of inversion outcomes under different mode-frequency configurations. These measures offer practical guidance for selecting suitable combinations in future experiments, helping to mitigate non-uniqueness without altering the sensor layout. This insight supports more informed system design choices for corrosion monitoring applications.

1. Introduction

Pipeline corrosion is a major concern in the petrochemical industry, as it reduces wall thickness and increases the risk of leaks or ruptures. Accurate assessment of the minimum remaining wall thickness is therefore essential for ensuring safety and preventing failures. Guided wave testing has proven to be an effective non-destructive testing (NDT) method for detecting such defects, offering the ability to inspect large areas from limited access points—unlike conventional ultrasonic thickness measurements that require direct access [1,2,3]. A defining characteristic of guided waves is their dispersive nature, where the wave speed varies with frequency and material thickness. While this complicates signal interpretation, it also provides valuable diagnostic information [4]. This property is exploited in Guided Wave Tomography (GWT), which uses model-based inversion to reconstruct quantitative wall thickness maps by iteratively refining a forward model to match measured data.

Early algorithms for defect imaging in GWT relied primarily on ray theory-based velocity inversion methods [5,6]. Although these approaches offered computational efficiency, they inherently neglected wave diffraction effects, which limited the achievable resolution. To overcome this limitation, diffraction tomography techniques were introduced [7], followed by hybrid methods that integrate ray-based and diffraction-based models to enhance reconstruction accuracy [8,9,10,11]. These methods have demonstrated improved resolution, particularly in full-view configurations where the defect is insonified from all directions. As a result, GWT is typically applied to plate-like structures using circular sensor arrays that provide comprehensive angular coverage. However, such full-view configurations are not feasible in practical pipeline inspections. In these cases, the geometry of the pipe and the placement of transducers—typically in rings around the circumference—restrict the available range of insonification angles, leading to a fundamentally limited-view problem [12,13]. This restricted angular coverage makes the inverse problem significantly more ill-posed and introduces non-uniqueness, where multiple thickness distributions can produce similar wavefield responses [14,15]. Moreover, when reconstructing multiple parameters, trade-offs may occur whereby different parameter combinations produce similar data fits [16,17]. While regularisation techniques are commonly used to stabilise such ill-posed problems, another strategy for improving inversion robustness is to enrich the dataset. This can be achieved by incorporating more diverse wave paths, such as helical configurations for higher-angle illumination [13], or by fully exploiting the waveform content through Full Waveform Inversion (FWI), a technique widely adopted in exploration seismology [18,19,20]. Recent advances in machine learning and deep learning have introduced powerful alternatives for GWT, offering rapid inversion and enhanced resolution. Notable examples include a physics embedded inversion neural network [21] and deep convolutional descent full waveform inversion [22]. However, in this study, we focus on a classical FWI approach to maintain a high degree of physical interpretability and to leverage established methods for exploring solution space and uncertainty.

FWI offers advantages over conventional tomographic methods by incorporating both waveform arrival times and amplitudes. In the context of guided wave testing, inverse algorithms have been developed to reconstruct corrosion damage by transforming the inherently 3D guided wave thickness inversion into a more computationally efficient 2D acoustic velocity inversion. This transformation is based on the dispersive relationship between wall thickness and wave velocity [23,24]. While this simplification improves computational performance, it neglects mode conversion effects intrinsic to guided wave behaviour. In practice, guided wave scattering is strongly influenced by defect geometry, leading to multimodal interactions and complex scattering patterns due to thickness variations. In this study, real-world defects, such as corrosion areas with localised pitting, are assumed to be relatively smooth, exhibiting gradual thickness variations. This characteristic limits mode conversion and reflection, making these defects suitable for acoustic imaging [25]. In contrast, reflection-based guided wave testing approaches are commonly used for the detection and localisation of cracks [26,27,28], but this lies outside the scope of the present work. Nonetheless, a well-recognised limitation is the reduction in resolution when acoustic algorithms are applied to elastic data. For instance, the HARBUT algorithm [9,29] achieves a resolution of approximately $\lambda /2$ with acoustic data, but this degrades to around $1.5$–$2\lambda$ when using elastic data. This discrepancy arises from differences in the scattered fields, with the acoustic model only accurately approximating elastic behaviour at low scattering angles, particularly near forward scattering [9,29]. However, in the limited-view setup, scattering is inherently restricted to lower angles, typically below 50 degrees, where acoustic and elastic models tend to align more closely. The effectiveness of this configuration, particularly when combined with recursive wavefield extrapolation, has been demonstrated by the prior validation study of Hassefras et al. [25].

FWI has recently been applied to GWT in both full aperture [30,31] and limited-view configurations [12,32]. While limited-view FWI enables practical deployment in constrained access scenarios, it remains vulnerable to non-uniqueness in the inversion results. To address this, strong regularisation is often required. Although such smoothing is generally effective for recovering simple defects with Gaussian-like profiles, it tends to oversmooth more complex corrosion morphologies, potentially obscuring critical morphological details. To maintain fidelity in thickness reconstructions without distorting features, we deliberately avoid applying regularisation. While this increases sensitivity to noise and inversion artefacts, it also ensures that complex defect morphologies are not artificially smoothed.

Alongside the choice of imaging technique, the selection of guided wave modes plays a significant role in determining the achievable resolution and image quality. High-resolution imaging of wall thickness and corrosion has been effectively demonstrated using the fundamental Lamb wave modes, A₀ and S₀, in a range of metallic plate configurations, with and without liquid loading conditions [33]. However, because of their relatively low frequencies and longer wavelengths, these lower-order modes face limitations when resolving shallow- or fine-scale corrosion features. In contrast, shear horizontal (SH) modes, particularly SH₁, offer significant advantages, especially in environments that involve liquid loading. SH modes are inherently less sensitive to the presence of liquid, and the SH₁ mode, in particular, benefits from higher frequencies, shorter wavelengths, and distinct phase velocity dispersion characteristics. These properties enable SH₁-based imaging to achieve superior spatial resolution under conditions that challenge traditional Lamb wave modes. Recent studies by Zimmermann et al. [11] and Wen et al. [34] have demonstrated that SH₁-guided wave imaging consistently provides more detailed thickness maps, outperforming Lamb modes in defect characterisation. While modes A₀, S₀, and SH₁ have traditionally been used in plate structures, recent studies have extended their application to pipe inspections [13,23,35]. To address the non-uniqueness in limited-view guided wave tomography, we implement a joint inversion framework that combines these modes, leveraging their distinct sensitivities to wall thickness variations. We further constrain the inversion by incorporating higher-order helical paths [13,21,36]. Although we use discrete single frequencies, we investigate whether inverting them jointly enhances sensitivity and improves the inversion outcome. While the effectiveness of this multimodal strategy has yet to be fully established, it will be explored in this study as a potentially valuable approach to improving the robustness of the reconstruction. It is important to note that robustness in this context does not necessarily imply higher accuracy, but may instead reflect improved consistency or precision in the inversion results.

The Full Waveform Inversion approach employed in this study iteratively minimises a waveform misfit objective function, typically a $L_2$ norm, between modelled and measured data. To guide this minimisation and gain insight into the model space, the method involves explicitly computing the Frechét derivative, which provides access to the Gauss–Newton approximation of the Hessian matrix. This information is critical for evaluating resolution, diagnosing parameter trade-offs, and understanding the local curvature of the misfit landscape, all of which are essential for interpreting and improving inversion performance. Posterior covariance estimates, derived as the inverse of the Hessian, are widely used for this purpose [37]. While many studies rely on approximations such as adjoint-state methods or L-BFGS to estimate Hessian vector products [38,39,40], this implementation directly evaluates the Frechét derivatives, providing more explicit and detailed information about the model space. This level of insight becomes particularly valuable when dealing with sparse or incomplete data, where the inversion problem is inherently underdetermined, and multiple models may fit the observations equally well. In such contexts, uncertainty quantification is not only beneficial but necessary for assessing the reliability of inversion results and for guiding experimental design. To better capture non-uniqueness, methods such as null-space shuttling [41,42,43] explore parameter perturbations that leave the data misfit unchanged. These techniques aim to characterise the effective null space: the set of models that fit the data within a prescribed tolerance [43,44]. The first eigenpair of the posterior covariance matrix, which forms the basis for null-space shuttling perturbations [42,45], can provide insight into individual parameter trade-offs and how these relate to experimental design, particularly in the selection of guided wave mode and frequency combinations. In addition to exploring parameter trade-offs, this study focusses on quantifying the variability introduced by noise and its impact on the reconstructed thickness map. A practical approach based on repeated inversions is adopted using different noise realisations at a fixed noise level. This enables the evaluation of the sensitivity of the inversion to noise and supports the derivation of statistical measures of solution stability and ambiguity. The implementation benefits from a computationally efficient forward modelling scheme and a reduced parameter space defined by a subgrid of thickness parameters, allowing for the exploration of mode and frequency combinations. This targeted uncertainty analysis informs the experimental design and provides a clearer understanding of the robustness of the inversion results.

This study presents the following contributions:

• Statistical measures to guide system configuration, helping to mitigate non-uniqueness.
• Joint multimode inversion of guided waves $A_0$, $S_0$, and $S{H}_1$, improving the precision of the inversion and reducing the sensitivity to noise.
• A mode filtering technique based on the non-uniform discrete Fourier transform.

2. Background

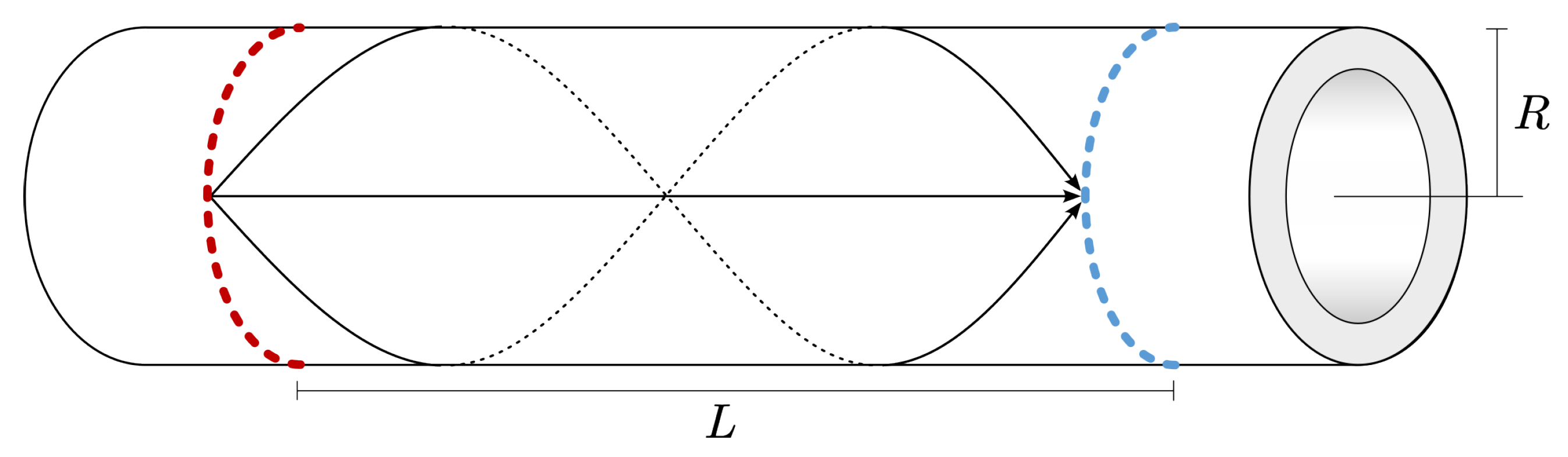
2.1. Guided Wave Tomography

Tomographic techniques typically employ rings of ultrasonic transducers arranged around the circumference of the pipe, as illustrated in Figure 1 [35,36,46,47]. Exciting non-axisymmetric modes by cycling through every source position and capturing at every receiver. This full matrix measurement configurations enable the capture of guided wave signals from multiple angles. For cylindrical structures such as pipes, where the thickness of the wall is significantly less than the radius of the pipe, straight sections can reasonably be approximated as an unwrapped plate [48,49,50,51]. As these waves propagate through the pipe wall, they follow helical paths, resulting in multiple arrivals of the same wave mode at the receiver, as depicted in Figure 2.

The dispersive nature of guided wave modes, where wave propagation is governed by the product of frequency and thickness, forms the basis for thickness mapping. When the excitation frequency is kept constant, the phase velocities of these modes become sensitive to local thickness variations, making them effective indicators for tomographic imaging. Figure 3 illustrates the dispersion behaviour of guided waves in a steel plate.

Selecting an appropriate wave mode and operating point on the frequency-thickness axis is important in the design of guided wave tomography systems, as different modes exhibit varying sensitivity to thickness variations and respond differently to experimental uncertainties such as attenuation and noise. The presence of multiple dispersive wave modes complicates signal interpretation due to modal interference at the receiver. To mitigate such effects, tomography systems often operate at lower frequencies and utilise fundamental Lamb modes -specifically the symmetric ($S_0$) and asymmetric ($A_0$) modes - due to their relatively simple and well-characterised dispersion behaviour [4,30,52]. More recently, shear-horizontal (SH) guided waves have gained attention, particularly the first-order mode ($S{H}_1$), which has demonstrated superior spatial resolution in imaging applications compared to the fundamental Lamb modes [11]. However, the $S{H}_1$ mode exists only above a certain cut-off frequency. Operating above this threshold introduces a practical trade-off: while resolution improves, higher-order modes also emerge. These modes are typically more complex, exhibit increased dispersion, and are more challenging to excite, especially when omnidirectional transducers are used. This study focusses on the $S_0$, $A_0$, and $S{H}_1$ modes, each offering distinct advantages and limitations in guided wave tomography. Their selection is based on previous studies that have evaluated their performance in terms of resolution, robustness, and ease of excitation [4,11]. However, rather than limiting the analysis to a single mode, this study also explores combinations of these modes to investigate their complementary strengths, aiming to improve both the robustness of the tomographic reconstructions.

2.2. Full Waveform Inversion

Full Waveform Inversion is a well-established technique in seismic imaging and is increasingly being adopted in ultrasonic guided wave tomography (GWT) [12,17,30,34]. FWI reconstructs wall thickness by minimising the mismatch between measured wavefields ${\mathbf{d}}_{\mathrm{obs}}$ and simulated wavefields $\mathbf{u}$, by minimising an objective function $\chi$. The complete workflow applied in this study is illustrated in Figure 4. A distinctive feature of this implementation is the preprocessing of the (synthetic) dataset using a Non-Uniform Discrete Fourier Transform (NUDFT). This step serves two purposes: first, it enables accurate characterisation of dispersion directly from the receiver array data, which forms the basis for constructing the velocity model used in the acoustic wave extrapolation; second, it provides a means to filter out unwanted modes present in the data. To reduce computational cost, the wall thickness parameters are updated on a coarser subgrid [23,32,53]. The sensitivity kernel is computed using the adjoint state method [38], not to calculate the gradient, but to identify the regions where parameter updates are necessary. Instead of relying on the adjoint-derived gradient, the Fréchet derivative (Jacobian) is approximated using central finite differences by perturbing the active nodes and recalculating the misfit. The inversion is carried out using a Gauss–Newton optimisation scheme. After each iteration, the updated parameters at the coarse grid nodes are interpolated back to the full-resolution forward model mesh using cubic interpolation. The misfit is then re-evaluated with the updated model, and this iterative process continues until a predefined step-size tolerance criterion is met.

Applying FWI to GWT presents several challenges. Low-frequency data is often unavailable, and initial models are typically limited to nominal wall thickness, increasing the risk of convergence to incorrect solutions. While enforcing positive wall thickness is feasible [12], smoothness regularisation is less effective due to sharp boundaries from corrosion. To address convergence issues, seismic research has introduced alternative misfit functions—such as envelope, instantaneous phase, and cross-correlation metrics—to mitigate cycle skipping [19,54,55,56,57]. Careful design of misfit functions is, therefore, essential and forms a central focus of this study.

2.2.1. Misfit Functions

The misfit function, denoted as $\chi \left(\mathbf{m}\right)$, quantifies the discrepancy between observed data ${\mathbf{d}}_{\mathrm{obs}}$ and synthetic data $\mathbf{u}\left(\mathbf{m}\right)$ generated from a model $\mathbf{m}$. In the context of corrosion mapping, $\mathbf{m}$ represents the spatial distribution of phase velocity, which is subsequently related to wall thickness. The traditional $L_2$ norm misfit function for complex-valued wavefield data is expressed as

$$\chi \left(\mathbf{m}\right)={\displaystyle \frac{1}{2}}\delta {\mathbf{d}}^T\delta {\mathbf{d}}^{*}$$

(1)

where $\delta \mathbf{d}=\mathbf{u}\left(\mathbf{m}\right)-{\mathbf{d}}_{\mathrm{obs}}$ is the data residual, and $\delta {\mathbf{d}}^{*}$ is its complex conjugate. This formulation captures both amplitude and phase differences between the synthetic and observed wavefields. In FWI, this misfit function is typically combined with the adjoint state method, where the residual $\delta \mathbf{d}$ is backpropagated and cross-correlated with the forward wavefield to compute the gradient [7,56,58]. However, in this work, we explicitly compute the Fréchet derivative (Jacobian matrix), which allows for the decoupling of amplitude and phase information in the misfit. Following the approach of Bozdağ et al. [19], we define misfit functions that treat phase and amplitude information separately. The phase-only misfit isolates phase differences in the frequency domain. The phase residual at receiver r and frequency $\omega$ is defined as

$$\Delta {\varphi }_r\left(\omega \right)=arg\left({\mathbf{d}}_{\mathrm{obs},r}\left(\omega \right)·{\mathbf{u}}_r^{*}\left(\omega \right)\right)$$

(2)

where $arg(·)$ denotes the phase angle of the complex product. The corresponding phase-misfit function is

$${\chi }_{\varphi }\left(\mathbf{m}\right)={\displaystyle \frac{1}{2}}\sum _{r=1}^N\sum _{\omega }{\left|\Delta {\varphi }_r\left(\omega \right)\right|}^2$$

(3)

In addition, an amplitude-only misfit is defined using the logarithmic ratio of observed to synthetic amplitudes:

$${\chi }_A\left(\mathbf{m}\right)={\displaystyle \frac{1}{2}}\sum _{r=1}^N\sum _{\omega }{\left|ln\left({\displaystyle \frac{|{\mathbf{d}}_{\mathrm{obs},r}\left(\omega \right)|}{|{\mathbf{u}}_r\left(\omega \right)|}}\right)\right|}^2$$

(4)

where $|·|$ denotes the magnitude of the complex signal. This formulation allows amplitude differences to be treated independently of phase. This study explores both phase inversion and full-waveform inversion. The latter involves minimising both ${\chi }_{\varphi }$ and ${\chi }_A$ during inversion. In our implementation, the amplitudes are normalised relative to the phase, and equal normalisation is applied across all modes and frequencies before optimisation.

2.2.2. Defect Localisation and Parameterisation

Corrosion defects, which often exhibit irregular, pitted surfaces and relatively sharp edges, are inherently challenging to analyse. In the absence of prior information about the geometry of the defect, we adopt a regular parameterisation of the pipe, assuming a maximum parameter spacing of 1.25$\lambda$ [9,29] in both the axial and circumferential directions. To reduce the number of parameters required for inversion, an initial localisation of the defect is performed based on the measured data. This is achieved using the adjoint method to compute summed sensitivity kernels across all sources and helical paths. As is common in FWI, the sensitivity kernel is obtained by backpropagating the data residuals and correlating them with the forward propagated wavefield [38,59]. Although typically used to calculate the inversion gradient, the kernel is used here solely to identify the region of interest, as illustrated in Figure 5a. The figure shows a corrosion defect surrounded by active parameter points, selected by thresholding the sensitivity kernel. Due to the limited view, the kernel appears elongated in the propagation direction; however, a circular threshold is applied to ensure conservative coverage. The activated nodes remain fixed in both the axial and circumferential directions throughout the inversion process. While regular gridding provides a systematic approach to parameterisation, it often struggles to capture the complex and irregular geometry of corrosion defects—particularly when cubic interpolation is used to map the defect onto the model mesh. This regular sampling can fundamentally limit the ability to accurately describe defect shapes, regardless of the inversion method used. As a result, the true accuracy of reconstructions obtained under different mode-frequency configurations may be obscured by artefacts that arise not merely from interpolation errors but also from inadequate spatial representation. Moreover, different guided wave modes operate at different frequencies and therefore exhibit different wavelengths. This constraint becomes problematic in joint inversion scenarios, where multiple wave modes with varying wavelengths are used simultaneously, leading to conflicting grid resolution requirements. To mitigate these issues and better isolate the influence of the data misfit on reconstruction performance, we aim to eliminate parameterisation and interpolation errors from the uncertainty analysis.

This is achieved by optimally positioning a fixed number of active parameter points in the x–z plane to better conform to the actual defect geometry. Here, we adopt the seismic convention for 2D in-plane coordinates, where z denotes the propagation direction and x the circumferential direction; the y-axis corresponds to the out-of-plane direction. Importantly, we maintain the same number of nodes in all wave modes, as illustrated in Figure 5b, thus ensuring a consistent basis for comparison. To determine the optimal node locations, we make use of a priori knowledge of the true defect shape. While such information is not available in practical applications, this controlled setup allows us to decouple the effects of parameter placement from those of the inversion algorithm. It enables a more accurate assessment of how different wave modes and frequencies influence the quality of reconstruction. Ideally, the inversion would jointly estimate the node positions and the wall loss values. However, the primary objective of this study is to address the issue of non-uniqueness by improving the determinacy of the objective function. Therefore, we restrict our current investigation to pre-optimised node locations, leaving adaptive meshing strategies for future work.

2.3. Uncertainty Quantification

The importance of uncertainty quantification and resolution analysis is increasingly recognised in seismic FWI [15,16,37,42,43,60,61], yet these aspects remain underexplored in Guided Wave Tomography (GWT). Such analyses are essential for interpreting inversion results, particularly in underdetermined settings where multiple models may explain the data equally well. A common approach to quantifying uncertainty is to examine the local curvature of the misfit function $\chi \left(\mathbf{m}\right)$ near its minimum, which is captured by the Hessian matrix [37,40],

$$\mathbf{H}\left(\tilde{\mathbf{m}}\right)={\nabla }^2\chi \left(\mathbf{m}\right){|}_{\mathbf{m}=\tilde{\mathbf{m}}}$$

(5)

where $\tilde{\mathbf{m}}$ is the model that minimises the misfit function $\chi \left(\mathbf{m}\right)$ and ${\nabla }^2$ is the Laplace operator. The gradient of the misfit function is given by

$$\nabla \chi \left(\mathbf{m}\right)={\displaystyle \frac{\mathsf{\partial }\chi \left(\mathbf{m}\right)}{\mathsf{\partial }\mathbf{m}}}=\Re \left({\mathbf{J}}^T\delta {\mathbf{d}}^{*}\right),$$

(6)

where $\mathbf{J}$ is the Jacobian (or Frechét derivative) of the forward model with respect to $\mathbf{m}$ and ℜ the real part. Consequently, the Hessian becomes

$$\mathbf{H}={\nabla }^2\chi \left(\mathbf{m}\right)={\mathbf{J}}^T\mathbf{J}+{\left({\displaystyle \frac{\mathsf{\partial }\mathbf{J}}{\mathsf{\partial }\mathbf{m}}}\right)}^T\delta \mathbf{d},$$

(7)

The first term, ${\mathbf{J}}^T\mathbf{J}$, is the Gauss–Newton approximation and typically dominates near the minimum of the misfit function. The second term accounts for the variation of the Jacobian with respect to the model parameters and reflects higher-order scattering effects in the wave propagation [62,63]. These effects become significant when the model is far from the true solution or when strong nonlinearities are present. However, near convergence, where $\delta \mathbf{d}$ is small and the forward model behaves approximately linearly, this term contributes little to the overall curvature and is often neglected. Using a second-order Taylor expansion, the misfit function near $\tilde{\mathbf{m}}$ can be approximated as

$$\chi \left(\mathbf{m}\right)\approx \chi \left(\tilde{\mathbf{m}}\right)+{\displaystyle \frac{1}{2}}{(\mathbf{m}-\tilde{\mathbf{m}})}^T\mathbf{H}\left(\tilde{\mathbf{m}}\right)(\mathbf{m}-\tilde{\mathbf{m}}).$$

(8)

Assuming Gaussian-distributed data noise and local linearity of the forward model, the inverse Hessian approximates the posterior covariance matrix [37]:

$${\mathbf{C}}_{\mathbf{m}}\approx {\mathbf{H}}^{-1},$$

(9)

where ${\mathbf{C}}_{\mathbf{m}}$ is the posterior covariance of the model parameters. This implies that the posterior distribution is centred at $\tilde{\mathbf{m}}$ and has ellipsoidal uncertainty contours aligned with the eigenvectors of ${\mathbf{H}}^{-1}$. To explore model non-uniqueness, we examine the eigendecomposition of the inverse Hessian:

$${\mathbf{H}}^{-1}=\mathbf{V}\mathbf{\Lambda }{\mathbf{V}}^T,$$

(10)

where $\mathbf{V}$ contains the eigenvectors and $\mathbf{\Lambda }$ is a diagonal matrix of the corresponding eigenvalues. The eigenvectors define the directions in the model space, and the eigenvalues quantify the uncertainty along those directions. In this study, we focus on the dominant eigenpair $({\lambda }_1,{\mathbf{v}}_1)$, where ${\lambda }_1$ is the largest eigenvalue and ${\mathbf{v}}_1$ the corresponding eigenvector. This pair defines the principal axis of the effective null space and highlights the direction in model space where the data misfit is flattest and the model is least constrained. This interpretation is supported by the fact that, in our problem, there is a steep drop from ${\lambda }_1$ to ${\lambda }_2$, and the subsequent eigenvalues decay rapidly, indicating a strongly dominant direction in the model space. The first eigenpair forms the basis for null-space shuttling perturbations [42,45], and provides insight into individual parameter trade-offs and their relationship to experimental design, particularly in the selection of guided wave mode and frequency combinations. In addition to exploring parameter trade-offs, this study quantifies the variability introduced by measurement noise and its impact on the reconstructed thickness map. A practical noise-sampling approach is adopted: for each wave mode and frequency combination, 500 independent inversions are performed using different realisations of Gaussian noise at a fixed signal-to-noise ratio. This ensemble enables a statistical evaluation of the inversion sensitivity.

2D Misfit Landscapes

To illustrate the relationship between the misfit landscape and model non-uniqueness, we conduct a synthetic 2D experiment. The setup involves a Gaussian-shaped defect embedded in a steel plate of nominal thickness 10 mm. The defect is fully described by two parameters: depth and width. The true defect has a depth of 2 mm and a width of 20 cm, as shown in Figure 6. To simulate more realistic measurement conditions, white noise is added to the time-domain signals, resulting in a signal-to-noise ratio (SNR) of 35 dB.We evaluate the misfit between synthetic data and the true data for varying defect depths and widths, using different guided wave modes: S₀ at 130, 160, and 190 kHz; A₀ at 60, 85, and 110 kHz; and their combinations. This allows us to visualise the full misfit landscape and assess how different mode and frequency combinations influence the inversion outcome. The inversion is then performed starting from the nominal plate thickness, resulting in the reconstructed defect shown in Figure 6.

First, we apply phase-only inversion (based on Equation (3)) using the A₀ mode. The resulting misfit landscapes for single-frequency (60 kHz) and multifrequency inversion are shown in Figure 7. In the single-frequency case, the misfit landscape exhibits a characteristic “banana-shaped valley,” indicating that multiple depth–width combinations can produce similar misfit values. This reflects a trade-off between depth and width, where the inversion is ill-posed. The steepness of this valley, that is, the gradient of the misfit function, is influenced by the slope of the dispersion curve, which governs the sensitivity of the phase to thickness variations. For the A₀ mode, lower frequencies correspond to steeper dispersion curves, resulting in sharper misfit gradients and thus higher sensitivity to changes in defect geometry.

In the multi-frequency case, the misfit valley becomes significantly steeper and more confined. This suggests that combining multiple frequencies helps to better pose the inversion problem and reduces nonuniqueness. When comparing the results for S₀, A₀, and their combination (Figure 8), we observe that the A₀ mode is generally more sensitive than S₀. However, the combination of both modes further increases the steepness of the misfit landscape, indicating improved resolution and reduced ambiguity.

The results displayed in Figure 9 are derived from full waveform inversion (FWI), which uses both phase and amplitude data as detailed in Equations (3) and (4). In this case, the convexity of the misfit function increases substantially. The improvement in the misfit landscape is primarily attributed to the amplitude term. To ensure a balanced and effective inversion, the contributions of the phase and amplitude misfits must be weighted relative to each other. For the S₀ mode, the ambiguity remains mainly in the depth direction, while for the A₀ mode, it is more pronounced in the width direction. When both modes are combined in a weighted fashion, these ambiguities tend to cancel out, resulting in a more isotropic and well-defined misfit basin. This effect is further highlighted in Figure 10, which shows cross sections of the misfit landscape.

This simplified experiment illustrates how the selection of guided wave mode and frequency influences both the steepness of the misfit landscape and the degree of non-uniqueness. While such analysis is intuitive in two dimensions, it becomes impractical in higher-dimensional settings, where uncertainty quantification must instead rely on posterior covariance analysis and sampling-based methods.

3. Modelling

To support the inversion and uncertainty quantification framework introduced earlier, we employ two complementary modelling approaches. A high-fidelity 3D finite-difference time-domain (FDTD) model is used to generate synthetic full matrix datasets to evaluate inversion performance under controlled conditions. In parallel, a computationally efficient recursive wavefield extrapolation (FX) method is used both as a forward model within the inversion scheme and as a data generator for uncertainty sampling. In the latter case, noise is added to the FX-simulated data to reflect realistic measurement variability and to ensure that the inversion is tested under non-ideal conditions. All models considered in this study have a length L of 1 m between the source and receiver array and a centre-line circumference of 0.5 m, corresponding to an outer diameter of 0.159 m. Each model includes 10 sources and 30 receivers.

3.1. 3D Elastic Model

We adopt a finite difference scheme based on a 3D rotated staggered grid (RSG) to simulate guided wave propagation in complex and heterogeneous media [64]. This method mitigates the numerical instabilities common in traditional staggered grid approaches by colocating all components of the stiffness tensor within the elementary cell. The RSG scheme enables stable and accurate modelling in the presence of strong elastic contrasts, such as corrosion-induced wall thinning and air-filled voids. Free boundaries and complex geometries are handled by assigning vacuum-like properties, such as zero stiffness and near zero density, to the corresponding grid cells, eliminating the need for specialised boundary conditions. This makes the method particularly well suited for simulating wave scattering and mode conversion at arbitrary defect geometries.

The RSG model is used to generate synthetic datasets for individual guided wave modes ($A_0$, $S_0$, and $S{H}_1$) using single-mode excitation strategies, following the approach outlined in earlier work [25]. While generally effective, the excitation of a pure $S_0$ mode often results in residual mode content with limited temporal separation. To resolve this issue, we apply a non-uniform discrete Fourier transform (NUDFT) filter to improve mode separation, as detailed in the Appendix A. This filtering step also allows for accurate extraction of dispersion curves directly from the receiver array signals, correcting for any numerical dispersion introduced by the RSG scheme. The resulting data sets provide realistic yet controlled input for evaluating the performance of the inversion algorithm.

3.2. Recursive Wavefield Extrapolation

To enable efficient inversion and uncertainty sampling, we use a recursive wavefield extrapolation method based on the 2D frequency-domain acoustic wave equation, also known as the Helmholtz equation.

$${\displaystyle \frac{{\mathsf{\partial }}^{2}P(x,z,\omega )}{\mathsf{\partial }{x}^2}}+{\displaystyle \frac{{\mathsf{\partial }}^{2}P(x,z,\omega )}{\mathsf{\partial }{z}^2}}+{\displaystyle \frac{{\omega }^2}{c^2}}P(x,z,\omega )=S(x,z,\omega )$$

(11)

where $P(x,z,\omega )$ represents the pressure field at position $(x,z)$ and angular frequency $\omega$, $S(x,z,\omega )$ is the source term representing external sources in the frequency domain and c is the sound speed in the medium.

Wave propagation along the z-direction to a new position $z+\Delta z$ is described by the extrapolation operator $\tilde{W}(z+\Delta z,k_x,\omega )$ in the $\omega$-$k_x$ domain. The wavefield at $z+\Delta z$ is then given by

$$\tilde{P}(z+\Delta z,k_x,\omega )=\tilde{P}(z,k_x,\omega )·\tilde{W}(z+\Delta z,k_x,\omega )$$

(12)

The extrapolation operator is defined as

$$\tilde{W}(z+\Delta z,k_x,\omega )=e^{i{k}_z\Delta z}$$

(13)

where $k_z$ is the vertical wavenumber (in the z-direction), and it depends on the angular frequency $\omega$ and the horizontal wavenumber $k_x$. Specifically, it is given by

$$k_z=\left\{\begin{array}{cc}\sqrt{{\displaystyle \frac{{\omega }^2}{c^2}}-k_x^2}\hfill & \mathrm{if}{k}_x^2\le {\displaystyle \frac{{\omega }^2}{c^2}}\left(\mathrm{propagating}\right)\hfill \\ i\sqrt{k_x^2-{\displaystyle \frac{{\omega }^2}{c^2}}}\hfill & \mathrm{if}{k}_x^2>{\displaystyle \frac{{\omega }^2}{c^2}}\left(\mathrm{evanescent}\right)\hfill \end{array}\right.$$

(14)

In the case of velocity heterogeneity, the extrapolation operator in the spatial domain becomes a local convolution operator $W(z+\Delta z,x,\omega )$. This operator is the inverse Fourier transform of the extrapolation operator $\tilde{W}(z+\Delta z,k_x,\omega )$. Therefore, the wavefield at $z+\Delta z$ is computed by

$$P(z+\Delta z,x,\omega )=P(z,x,\omega )\ast W(z+\Delta z,x,\omega )$$

(15)

This method is used as the forward model in the inversion scheme because of its computational efficiency and suitability for iterative evaluations. For a detailed validation of this acoustic model against experimental data, the reader is referred to [25]. This previous study demonstrates that the recursive wavefield extrapolation approach achieves a timing error on the order of one-tenth of a microsecond. For context, this corresponds to a phase discrepancy approximately one-tenth of the maximum phase misfit observed for the smallest defect case analysed in this study.

Noise

To better reflect practical conditions, additive white Gaussian noise (AWGN) is applied to the synthetic waveforms within the uncertainty quantification framework. Although generated under controlled conditions, the inclusion of noise introduces variability that enables a more realistic assessment of the inversion algorithm’s robustness. A time-domain signal-to-noise ratio (SNR) of 35 dB is applied, affecting both amplitude and phase. As the inversion is performed in the frequency domain, the impact of noise varies with frequency due to dispersion. For instance, at 130 kHz, the $S_0$ mode exhibits limited dispersion and lower phase sensitivity, resulting in an effective phase SNR of approximately 23 dB. In contrast, at 180 kHz, stronger dispersion improves the phase SNR to around 32 dB.

3.3. Defect

The tomography framework is applied to two distinct corrosion defects embedded in a 10 mm thick steel plate, as shown in Figure 11. Both defects are asymmetric in shape, but differ in size, depth, and complexity. The first defect is wider and deeper, and its maximum depth is located in the centre. It represents a more pronounced corrosion scenario with a broad affected area. The second defect is smaller and shallower, featuring a pit that is offset from the centre of an otherwise relatively flat plateau.

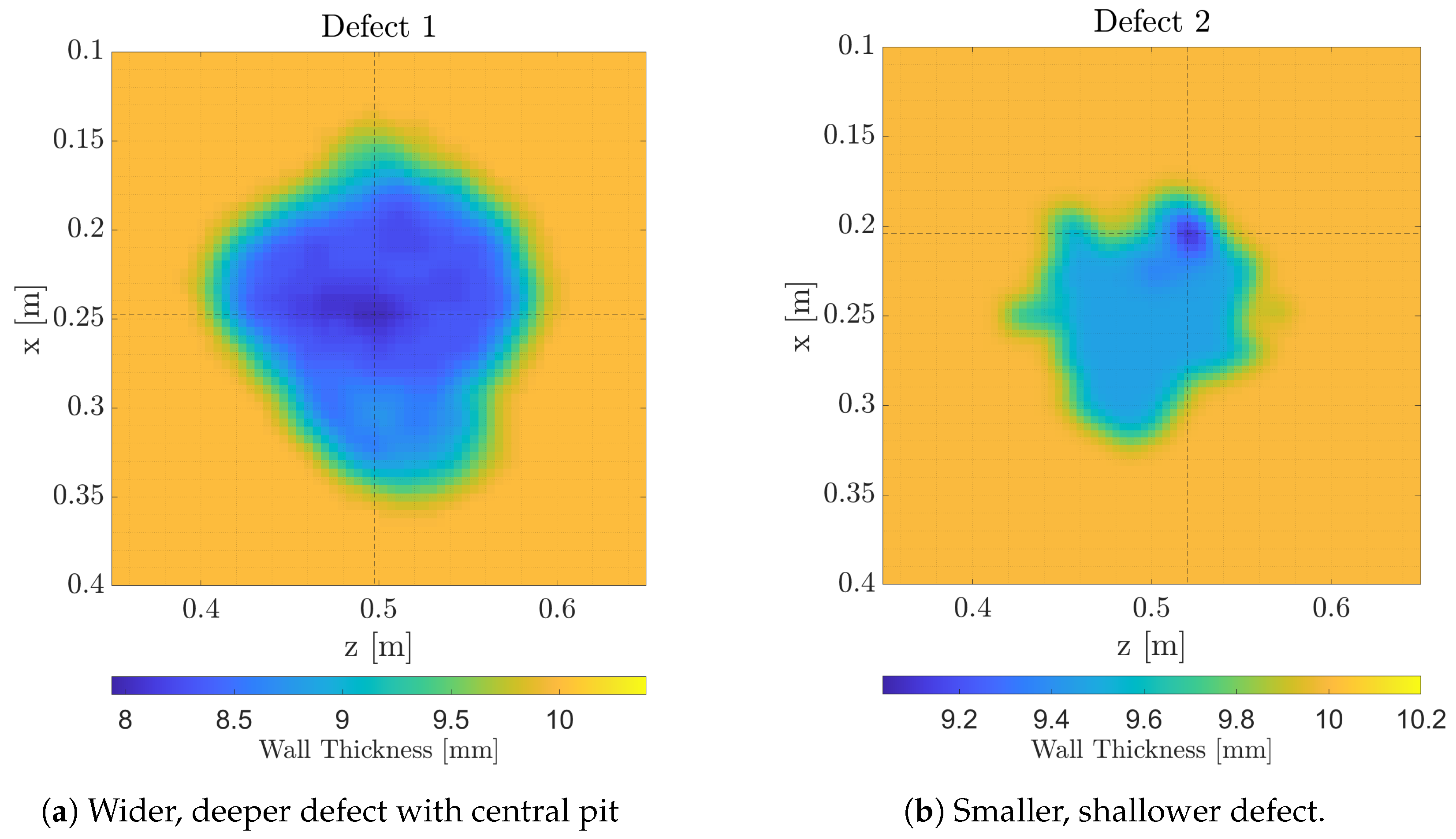
Image reconstruction is performed for both defects to evaluate the general performance of the inversion algorithm. However, the uncertainty quantification analysis specifically focusses on the second defect.

3.4. Error Analysis

To evaluate the accuracy of the reconstructed images for the two corrosion defects shown in Figure 11, we define two complementary error metrics: the depth error ${\epsilon }_{\mathrm{depth}}$ and the shape error ${\epsilon }_{\mathrm{shape}}$. These metrics quantify how well the inversion algorithm captures both the maximum depth and the overall geometry of the defects. The depth error ${\epsilon }_{\mathrm{depth}}$ measures the deviation in the maximum depth of the estimated defect and is defined as

$${\epsilon }_{\mathrm{depth}}={\displaystyle \frac{|D_m-D_m^{*}|}{D_0}}$$

(16)

Here, $D_m$ and $D_m^{*}$ denote the minimum thickness values (that is, the deepest points) in the true and reconstructed models, respectively, and $D_0=10\mathrm{mm}$ is the nominal plate thickness.The shape error ${\epsilon }_{\mathrm{shape}}$ captures the overall geometric discrepancy between the true and reconstructed thickness maps:

$${\epsilon }_{\mathrm{shape}}=\sqrt{{\displaystyle \frac{\int \int {[D(x,z)-D^{*}(x,z)]}^{2}dxdz}{D_0^2\int \int dxdz}}}$$

(17)

In this expression, $D(x,z)$ and $D^{*}(x,z)$ represent the true and reconstructed thickness distributions, respectively, with lower values of ${\epsilon }_{\mathrm{shape}}$ indicating better geometric agreement. Unlike previous studies [11,29], no circular windowing is applied to spatially weight the error—an approach that typically emphasises the defect centre. While such weighting would align the metric with prior work, it compresses the error range and can obscure improvements introduced by algorithmic changes. Instead, the error is computed as a discrete sum over all pixels without spatial weighting, enhancing sensitivity to inversion strategy changes, particularly in misfit function tuning. Note that, even with optimised parameterisation, the shape error typically plateaus around 5%, corresponding to absolute deviations of less than one-tenth of a millimetre across the defect profile. This reflects the practical resolution limit imposed by the current parameterisation.

4. Results

The results are structured into three main components: reconstructions performed on a regular grid using synthetic 3D elastic wave data; analysis of the effective nullspace for a reconstruction on an optimised parameter grid; and uncertainty quantification based on 500 acoustic tomography realisations with added noise.

4.1. Tomography on a Regular Grid

Initially, we analyse the inversion results for Defect 1 utilising the $A_0$ and $S_0$ modes to a grid of regular nodes of parameters. Figure 12 provides an overview: subfigures (a–d) depict the reconstructed wall thickness profiles, and subfigures (e–h) offer circumferential cross-sections at $z=0.5\mathrm{m}$ for detailed comparison of the defect’s recovered geometry.

The results clearly show that the $A_0$ mode at 110 kHz significantly outperforms the $S_0$ mode at 180 kHz. In the case of the $S_0$ mode, the deepest point of the defect at $x=0.25\mathrm{m}$, $z=0.5\mathrm{m}$ is completely missed, as is clearly visible in the cross-section shown in Figure 12e, and is also reflected in the highest minimum error. Figure 12c,g further shows that when amplitude information and multiple frequencies (60, 85, and 110 kHz) are added to the $A_0$ mode, both the shape error and the minimum error are substantially reduced. In contrast, when the $S_0$ mode (130, 155, and 180 kHz) is added, as shown in Figure 12d,h, the shape error increases—most likely due to the coarser node sampling used for the $S_0$ mode, which limits the ability to accurately describe the defect geometry. This coarser sampling in the mode combinations was chosen to avoid oscillatory thickness updates caused by oversampling. While the minimum thickness estimate improves in this case, the axial structure of the defect becomes more smeared along vertical bands, resulting in a higher shape error.

For Defect 2, we now include all working frequencies: 60, 85, and 110 kHz for the $A_0$ mode; 130, 155, and 180 kHz for the $S_0$ mode; and 240, 260, and 280 kHz for the ${\mathit{SH}}_1$ mode. However, in the combined mode configurations, only the highest frequency is used for the mode with the largest wavelength, while all three frequencies are retained for the mode with the smallest wavelength. This approach ensures that the parameterisation, which is dictated by the largest wavelength, remains sufficiently refined. Figure 13 presents the corresponding results for Defect 2. Subfigures (a–c, g–i) show the reconstructions for individual and combined wave modes, while subfigures (d–f, j–l) display the associated circumferential cross-sections.

An immediate observation from Figure 13a,b,d,e is that both the $S_0$ and $A_0$ modes have difficulty accurately reconstructing the defect, although the general outline is still discernible. The combination of $S_0$ and $A_0$ performs slightly better in terms of minimum error, but worse in shape error, as shown in Figure 13g,j. In this case, vertical bands of thickness smearing are also clearly visible. The ${\mathit{SH}}_1$ mode, shown in Figure 13c,f, yields a lower shape and minimum errors, although it tends to slightly overestimate the depth of the defect. The combinations of ${\mathit{SH}}_1$ with either $A_0$ or $S_0$, shown in Figure 13h,i,k,l, result in improved performance across both error metrics compared to the individual $S{H}_1$ mode.

For both defects, and across all multi-frequency results, the shape and minimum errors are combined into a single plot. Figure 14 displays the shape error versus the minimum error for all individual wave modes and mode combinations used in the multi-frequency FWI reconstructions. As shown in Figure 14a, the addition of amplitude information consistently improves the reconstructions for Defect 1 across all mode combinations. However, when combining the $S_0$ and $A_0$ modes in a multi-mode inversion, the benefit is less apparent. Although a modest reduction in the minimum error is observed, this improvement is not clearly reflected in the shape error.

For the smaller Defect 2, shown in Figure 14b, a similar trend is observed. Amplitude information contributes to improved performance in the multi-mode cases, with both shape and minimum errors generally reduced. In contrast, the single-mode, multi-frequency cases show no consistent trend. This inconsistency may be due to the less reliable amplitude content in the data. In such cases, the inclusion of an additional mode appears to help compensate for the discrepancy between the measured and modelled amplitudes. Overall, the $S_0$-${\mathit{SH}}_1$ and $A_0$-${\mathit{SH}}_1$ combinations yield the lowest shape and minimum errors among the tested configurations. However, significant shape errors persist, which can be attributed to the sparse parameter grid. This spacing is insufficient to accurately represent the defect geometry. Further reduction of the shape error requires grid optimisation, as refining the grid beyond one point per wavelength does not improve accuracy and will only increase the nonuniqueness of the solution.

4.2. Tomography on an Optimized Grid: Null-Space Perturbation

As previously observed, the individual parameterisations and the relative data quality of the phase and amplitude contributions have a significant impact on the reconstruction quality. To enable precise non-uniqueness evaluation, we analyse synthetic data from wavefield extrapolation and a consistent parameter grid across misfit scenarios, optimised for defect representation via cubic interpolation. This optimisation allocates more nodes in regions with strong gradients and fewer in relatively flat areas, as illustrated in Figure 5b. The Hessian is computed for each thickness update iteration using the Gauss–Newton approximation defined in Equation (7). Figure 15 presents the Hessian and covariance matrices of the misfit function at the final iteration for different inversion configurations. Figure 15a,b show the Hessian and covariance matrices for the $A_0$ mode using phase-only data. Figure 15c,d show the corresponding matrices for the combined $A_0+{\mathit{SH}}_1$ mode using FWI with multiple frequencies.

The covariance matrix in the mode combination case exhibits significantly lower maximum values, approximately two orders of magnitude smaller, compared to the single-mode case. A notable feature of the Hessians is that parameter points 33 and 41 exhibit relatively high values in both mode configurations, indicating that the curvature of the misfit function at these locations is significantly higher than at other parameter points. This can be attributed to the fact that these points lie in relatively flat regions of the defect, where the spacing to the neighbouring defect parameters is comparatively large. In other words, it is more difficult to exchange thickness with these points during the inversion process. Another clear observation is the overall magnitude: for the joint inversion, the Hessian values are approximately two orders of magnitude larger, indicating a steeper descent in the misfit landscape. Turning to the covariance matrices, we observe a prominent positive diagonal band with several interruptions, and adjacent off-diagonal bands that are predominantly negative. This suggests a tendency for negative correlation between neighbouring parameters, that is, a slight increase in wall thickness at one point can be compensated by a slight decrease at an adjacent point to achieve a similar data fit. This banded structure repeats periodically, which in terms of parameter indexing corresponds to new slices in the circumference, indicating that adjacent points along the pipe axis also exhibit a negative correlation.

Figure 16a–d present the initial eigenpair of the covariance matrix, corresponding to the $A_0$ phase-only single frequency, $A_0$ phase-only multifrequency, $A_0+{\mathit{SH}}_1$ phase-only multifrequency, and $A_0+{\mathit{SH}}_1$ FWI multifrequency, in that order. The eigenvectors are visualised using a sign-preserving logarithmic scale. Due to the large dynamic range, maximum values are clipped to emphasise the spatial structure of the eigenpairs. Across all cases, a characteristic “zebra” pattern is visible: due to the limited-view geometry, thickness exchange occurs predominantly between neighbouring axial parameters. This arises because restricted source–receiver angles make the inversion underdetermined—different thickness distributions can produce similar wavefield responses. However, as more information is incorporated into the misfit function, through additional frequencies, wave modes, or amplitude data, the influence of nonuniqueness becomes less pronounced.

4.3. Tomography on an Optimised Grid: Uncertainty Quantification

To assess the impact of measurement noise on the inversion results, we repeat the experiment on the same optimised parameter grid, now adding 35 dB random white noise to the time-domain signal and performing 500 independent realisations. This enables quantification of the variability introduced by noise and its effect on the reconstructed thickness maps. Figure 17 shows the reconstruction of Defect 2 corresponding to the sample whose shape error is closest to the mean shape error across the 500 realisations, for each wave mode case. These reconstructions are obtained using multi-frequency FWI on an optimised parameter grid and serve as representative examples of typical reconstruction quality. Subfigures (a–c, g–i) show the mean reconstructed profiles, while subfigures (d–f, j–l) display circumferential cross-sections through the deepest point of the defect. Each cross section includes the minimum, mean (solid line), and maximum shape error realisations. Figure 17 further illustrates that the $A_0$ mode performs better than the $S_0$ mode, while the ${\mathit{SH}}_1$ mode clearly outperforms both. Visually, the vertical band structure, an indicator of axial thickness smearing, is prominent in reconstructions using $S_0$ and $A_0$, but is nearly absent in the results. ${\mathit{SH}}_1$.

This zebra pattern becomes more apparent when plotting the difference between the mean reconstructed profile and the true defect geometry, as shown in Figure 18. Subfigure (a) displays the thickness difference for the $A_0$ mode, while subfigures (b,c) show axial cross-sections for the $A_0$ and $A_0+{\mathit{SH}}_1$ mode combinations. These cross sections demonstrate that the use of multiple modes can reduce the likelihood of thickness overshoots and undershoots.

Moreover, Figure 17 illustrates that on the optimised grid, unlike the regular grid results, the combination of $S_0$ and $A_0$ does outperform the single-mode variants in both shape and minimum error. The circumferential cross sections further demonstrate that the spread of error realisations, minimum, mean, and maximum, is narrower for the $S_0+A_0$ combination, indicating increased precision in the tomographic reconstruction. For the ${\mathit{SH}}_1$ mode and the $S_0+{\mathit{SH}}_1$ combination, the results are closely aligned, while the $A_0+{\mathit{SH}}_1$ combination exhibits slightly higher error values and greater variability. Although the minimum remaining wall thickness and its associated error are often considered the most critical parameters in defect assessment, the results presented here again emphasise the importance of shape error in evaluating the robustness of the inversion. When the complete distribution of shape errors is plotted, we obtain the results shown in Figure 19. Figure 19 presents histograms of the shape error distributions for different combinations of wave modes under multifrequency FWI. Subfigures (a–c) correspond to individual wave modes, while subfigures (d–f) show the results for combined mode configurations.

These distributions, shown in Figure 19, provide insight into the variability and consistency of the inversion outcomes, offering a statistical perspective on the influence of wave mode selection on reconstruction precision. Examining the standard deviations across the different scenarios, we observe the expected trend: mode combinations and the ${\mathit{SH}}_1$ mode consistently produce lower reconstruction variance. Interestingly, the ${\mathit{SH}}_1$ mode alone performs comparably well in terms of precision, raising the question of why it is so effective in this regard. However, one might intuitively expect that adding more information to the misfit function would always improve precision. To explore this further, we plot the mean shape error against the standard deviation of the shape error to examine the general trend. Figure 20 shows scatter plots of the mean shape error versus its standard deviation for different types of defects, evaluated at a signal-to-noise ratio (SNR) of 35 dB and a higher SNR of 50 dB.

The results again reveal a clear trend: reconstruction precision improves as more information is incorporated into the misfit function. In phase-only inversions, for instance, multi-frequency cases consistently outperform single-frequency ones—except for the $S_0$ mode. This exception is attributed to the flattening of the dispersion curve at lower frequencies (particularly around 130 kHz), which reduces the phase sensitivity to thickness variations. Although 35 dB white noise is added to the time-domain signal, this SNR applies to the central carrier frequency. At the flatter end of the dispersion curve, the effective SNR for a single frequency component is significantly lower. As a result, the inversion is effectively fitting to noise at these frequencies, degrading reconstruction quality. This explains why, in the multi-frequency multi-mode configuration for the $S_0$ mode, only the highest frequency (180 kHz) is retained. As shown in Figure 20b, incorporating amplitude information further improves the precision of the tomographic reconstruction in the multi-frequency cases.

Finally, regarding the effect of mode combinations, the results for the $S{H}_1$ mode and the $S_0+S{H}_1$ combination are nearly identical, as already observed in the tomograms. To understand this, we again consider the role of dispersion and noise. The key idea is that as the SNR increases across all wave modes, the influence of noise in the less sensitive modes becomes less dominant. To illustrate this, additional inversions were performed at a higher noise level of 50 dB. As shown in Figure 20c, the overall reconstruction precision improves, with a clear reduction in standard deviation across all cases. The mean shape error also approaches the maximum achievable accuracy of 5%, which reflects the resolution limit imposed by the optimised parameter grid. This explains why the trend line does not pass through the origin. Now, a slight improvement is observed in the $S_0+S{H}_1$ combination compared to $S{H}_1$ alone. Specifically, the mean shape error for the combined case is 5.9% with a standard deviation of 0.19%, compared to 6.7% and 0.22% for $S{H}_1$ alone. This suggests that including a lower-sensitivity mode such as $S_0$ can be beneficial—provided the SNR at its operating frequency is sufficiently high. In this study, the frequency for the $S_0$ mode is limited to 180 kHz. Although not discussed in much detail earlier, this choice is informed by the expected increase in attenuation at higher frequencies due to liquid loading. Ideally, higher frequencies would be preferable, as they offer greater dispersion and improved sensitivity for the $S_0$ mode. However, attenuation imposes a practical upper limit on the usable frequency range. Consequently, achieving a high SNR at 180 kHz becomes critical. In practical terms, this implies that additional signal averaging may be required in experimental settings to sufficiently enhance the SNR of the $S_0$ mode before it can be effectively included in a joint inversion with the more sensitive $S{H}_1$ mode.

5. Discussion

5.1. Accuracy Versus Precision

A central theme in this study is the distinction between accuracy and precision in guided wave tomography. Although often used interchangeably, these terms describe fundamentally different aspects of reconstruction quality. Precision refers to the consistency or repeatability of the results under similar conditions, and is reflected in the standard deviation of the shape error across multiple realisations. Accuracy, by contrast, describes how closely the reconstructed wall thickness matches the true defect geometry, and is captured by the mean shape error. Our results show that enriching the misfit function with additional information—such as amplitude data, multiple frequencies, and multiple wave modes—generally improves the precision of the inversion. This is evidenced by a reduction in the standard deviation of the shape error, indicating more stable and repeatable reconstructions in the presence of noise. However, this increased precision does not necessarily imply improved accuracy, as the mean shape error may remain unchanged. These findings highlight the importance of carefully balancing parameterisation, wave mode selection, and frequency content. Over-parameterisation, particularly at low frequencies, can lead to instability and oscillatory updates. Conversely, under-parameterisation at higher frequencies may fail to capture the complexity of defect geometries. The quality of wall thickness reconstructions therefore depends on both precision and accuracy. While shaping the misfit function helps reduce uncertainty, thereby improving precision, achieving high accuracy requires a parameterisation strategy that is well matched to the underlying defect shape.

5.2. Frequency Selection and Weighting

The selection of operating frequencies and the weighting strategy between phase and amplitude terms are critical factors influencing the stability and accuracy of multimodal guided-wave tomography. In this study, the choice of discrete frequencies was guided by prior research [4,11,23,65]. Frequencies were selected at points along the dispersion curve where the slope differs for each mode, ensuring that each frequency contributes complementary and non-redundant information to the inversion process. Attenuation and mode separation, further informed the selection, for example, avoiding higher frequencies for the $S_0$ mode to minimise attenuation in liquid-loaded environments. While these choices are grounded in theoretical analysis and literature on isotropic steel plates and pipes, we acknowledge that experimental validation across different materials remains an area for future work. Signal-to-noise ratio (SNR) considerations were incorporated through selective inclusion of reliable data, following the lessons learned from the multi-frequency $S_0$ inversion results. Frequencies with insufficient SNR were excluded from the multi-mode inversion process, as detailed in Section 4.3. Static weights were applied across modes and frequencies, calculated from the maximum observed phase and amplitude differences along the receiver line for each mode–frequency combination. A fixed normalisation factor scales magnitudes prior to optimisation, ensuring equality between terms. Dynamic weighting strategies were explored but ultimately rejected due to their destabilising effect on convergence, particularly under noisy conditions. Assigning dominant weights to a single mode prior to optimisation was also avoided, as this effectively reduces the inversion to a single-mode case and negates the benefits of multimodal inversion.

5.3. Practical Inspection Conditions: Transition from Synthetic to Experimental Data

The present study employs synthetic data to systematically investigate non-uniqueness and uncertainty in guided wave tomography under controlled and reproducible conditions. This approach enables isolation of the effects of the inversion methodology without introducing confounding factors; however, it also introduces limitations that must be acknowledged when considering practical applications. First, the forward model used is acoustic rather than fully elastic, which inherently neglects mode-conversion effects. As discussed earlier, the acoustic approximation is valid primarily for low scattering angles and gradual wall-thickness variations. While this assumption reduces the impact of mode conversion, it remains a limitation of the technique. To mitigate residual effects, NUDFT-based filtering was applied to isolate the desired wave modes and suppress unwanted conversions, as detailed in the Appendix A.The use of synthetic data also simplifies noise modelling. Gaussian white noise was adopted to simulate random measurement noise, providing a well-controlled environment for comparison. In practice, however, systematic errors—such as inaccurate dispersion curves or misalignment of source–receiver arrays can severely affect convergence. To address this, our approach employs the NUDFT technique to extract velocity models and dispersion curves directly from observed data rather than relying solely on theoretical curves, thereby improving robustness against environmental variations. Nevertheless, without proper calibration and control of systematic effects, results can become unreliable, regardless of the sophistication of the inversion algorithm. Calibration procedures, such as using the non-dispersive SH₀ mode to correct transducer positioning, are therefore essential for reliable field implementation. Finally, the scope of this study is restricted to relatively smooth corrosion defects. Crack-like defects or sharp discontinuities would require fundamentally different modelling strategies. Expanding the defect library, assessing liquid-loading effects, and incorporating additional physical factors such as thermal and mechanical stresses represent important directions for future research.

6. Conclusions

Guided wave tomography for pipe wall thickness reconstruction is challenged by non-uniqueness, especially in limited-view configurations. This often leads to negative correlations between neighbouring parameters, where wall loss in one region is compensated by gain in another. Full waveform inversion reduces non-uniqueness by leveraging both phase and amplitude information, and further improvements are achieved by incorporating multiple frequencies and wave modes. These additions enhance the convexity of the misfit function and improve the stability and reliability of the inversion process. In two parameter problems, the convexity of the misfit function can be visualised directly. However, in higher-dimensional or multi-parameter settings, tools such as the eigenvectors of the posterior covariance matrix provide a more appropriate means of analysis.

Incorporating multiple frequencies and wave modes reduces variance and enhances precision under noisy conditions. The $S{H}_1$ mode consistently delivers high precision and accuracy, resulting from its short wavelength and high sensitivity, although its applicability is limited by the cut-off frequency. Beyond improving the misfit landscape, incorporating multiple wave modes can help mitigate the impact of degraded data quality. When the amplitude or phase of one mode is affected—due to attenuation, sensor coupling variability, or environmental noise—another mode may still provide useful information. The $S_0+S{H}_1$ combination offers a promising trade-off for corrosion tomography, as both modes are relatively robust under liquid loading in pipelines.

However, precision does not guarantee accuracy, which depends on whether the parameter grid can represent the true geometry of the defect. While denser parameter grids can increase spatial resolution, they may also introduce parameter crosstalk. Conversely, lower frequencies risk overparameterisation due to their limited spatial sensitivity. Specifically, modes with longer wavelengths (e.g., $S_0$) require coarser parameterisation to avoid instability, which can limit the ability to resolve complex defect shapes. Our analysis demonstrates that reconstruction quality is governed by the interplay between frequency content, wave mode selection, and parameter grid design.

Reconstructions were first performed on a regular grid, followed by a pre-optimised parameter grid, in order to isolate the effect of grid placement from the analysis of non-uniqueness. This approach ensures that the observed findings regarding non-uniqueness and robustness are not artefacts of the parameterisation strategy. Optimised parameterisation strategies outperform uniform grids by better dealing with sharp edges; however, this requires a priori knowledge of the defect shape. Consequently, adaptive parameterisation will be required. In this approach, node positions are treated as inversion parameters and updated within bounded limits during reconstruction. This ensures that the parameter grid can respond dynamically to the data. This will be an important step towards improving both the accuracy and precision of tomographic reconstructions in future work.