Abstract
Hybrid simulation integrates numerical and experimental techniques to analyze structural responses under static and dynamic loads. It physically tests components that are not fully characterized while modeling the rest of the structure numerically. Over the past two decades, hybrid testing platforms have become increasingly modular and versatile. This paper presents the development of a robust hybrid testing software framework at the National Laboratory for Civil Engineering (LNEC), Portugal, and evaluates the efficiency of its algorithms. The framework features a LabVIEW-based control and interface application that exchanges data with OpenSees via the OpenFresco middleware using a TCP/IP protocol. Designed for slow to real-time hybrid testing, it employs a predictor–corrector algorithm for motion control, enhanced by an adaptive time series (ATS)-based error tracking and delay compensation algorithm. Its modular design facilitates the integration of new simulation tools. The framework was first assessed through simulated hybrid tests, followed by validation via a hybrid test on a two-bay, one-story steel moment-resisting frame, where one exterior column was physically tested. The results emphasized the importance of the accurate system identification of the physical substructure and the precise calibration of the actuator control and delay compensation algorithms.
1. Introduction
To mitigate the severe damage of structures due to natural hazards, mainly earthquakes, a better understanding of the structural response to such actions is of paramount importance. A shaking table test is a reliable tool for simulating the dynamic response of structures subjected to earthquakes. Nevertheless, full-scale shaking table tests are often impractical to carry out, if not impossible, due to the limited size and capacity of shaking tables, as well as the cost of conducting such tests. Additionally, such tests are mainly required when severe damage is to be imposed to the test structure or when it should be tested until collapse. Hence, the search for less destructive techniques is valuable; a numerical simulation is the least expensive method for assessing the response of structures. However, numerical methods such as finite element analysis may fail to capture some complex mechanisms of damage, local and/or global. Furthermore, geometric and/or material nonlinearities of structures may not be fully represented. Hence, an alternative method that blends numerical and experimental approaches, i.e., hybrid simulation, is compelling. The prime goal is therefore to establish a practical and cost-effective solution to accurately determine the response of structures subjected to dynamic loads.
Hybrid simulation, also termed substructuring or pseudo-dynamic testing (PSD), was conceived to bridge the drawbacks of the two abovementioned simulation methodologies [1,2,3,4]. In this technique, the response simulation of a structure is conducted by experimentally testing the critical component (physical substructure) while numerically modeling the rest of the structure. The restoring forces of the physical substructure, which are measured in the laboratory, are then returned to the numerical program at each time-step of the analysis. In hybrid simulation, the loading history of the actuators is not known a priori, unlike a shaking table test. Instead, it is calculated during the experiment. Intuitively, the speed of execution of a hybrid simulation is therefore dependent on the rate of data communication between the physical and numerical substructures. The advancement in the speed of execution of an actuator command and the speed of communication between the physical and numerical substructures gave birth to real-time hybrid simulation (RTHS). In the past two decades, a considerable amount of research has been conducted in hybrid testing, thus improving its reliability for dynamic testing of structures. Among its widespread applications, it enabled researchers to experimentally simulate the effectiveness of energy dissipation devices without the need to experimentally test the complete structure [5,6]. Furthermore, the philosophy of hybrid simulation has not been limited to structural and earthquake engineering, but it was extended to other areas of study such as thermo-mechanical testing, industrial piping systems, and multi-hazard testing [7,8,9].
Nevertheless, hybrid simulation has never been without challenges. The propagation of experimental errors in the numerical substructure is a prime challenge. State-of-the-art hardware and efficient control algorithms are thus pivotal for successful hybrid testing. The technique has evolved rapidly in terms of its fidelity, robustness, and the spectrum of applications [10,11,12]. Given their importance, studies focused on the propagation of random and systematic errors were conducted in its early development [10]. In addition, the robustness of an integration scheme during a hybrid test also plays a vital role in the accuracy of hybrid simulation. Thus, considerable research was carried out on integration algorithms, aiming to improve error propagation and stability characteristics needed for hybrid testing. Shing et al. [11] investigated Newmark integration families resulting in a stable explicit algorithm suitable for PSD. Dermitzakis and Mahin [12] also proposed a mixed implicit–explicit algorithm to account for large nonlinearities during response simulation. In the latter, several PSD tests comprising multi-degree-of-freedom structures were performed to substantiate the reliability of the technique. In the search for an improved testing of stiff specimens, a mixed force and displacement actuator control was explored in the late 1980s, which gave birth to Effective Force Testing (EFT) [13].
The first implementation of RTHS comprised dynamic actuators, a digital servo-controller, and a staggered integration method to improve its computational efficiency [14]. Together with the development of nonlinear finite element software, such as DRAIN 2DX, a finite element method (FEM) approach for hybrid simulation emerged [15]. Thewalt and Roman [16] proposed the BFGS (Broyden–Fletcher–Goldfarb–Shanno) algorithm to estimate the tangent stiffness of an experimental element while other studies addressed the accuracy of the operator splitting (OS) algorithm [17,18]. Significant developments in pseudo-dynamic testing were also carried out at the European Laboratory for Structural Assessment (ELSA) [19,20]. To reduce actuator errors during RTHS, researchers proposed a compensation method via predicting displacements through extrapolation [21,22]. The control system approach for conducting a RTHS test thus surfaced [23]. Research at ELSA also contributed to the accuracy of continuous PSD by limiting the force relaxation phenomena inherent to the ramp-and-hold method [24]. On the forefront of the search for a reliable test framework, Takahashi and Fenves [25] developed an object-oriented software framework, named Open-Source Framework for Experimental Setup and Control (OpenFresco), comprising interlaced software classes that allowed the computational driver to talk to laboratory hardware in a modular and standardized manner. The framework was designed to handle both local and distributed tests. Further, its collapse simulation capabilities were improved by Schellenberg et al. [26]. The development of a MATLAB-based computational driver and a LabVIEW-based experimental controller in OpenFresco has played an important role in the versatility of the software framework. Efforts made in extending local hybrid testing to geographically distributed testing also gave satisfactory results. Mosqueda et al. [27] developed a three-loop architecture framework to enable a continuous geographically distributed hybrid testing accounting for force relaxation phenomena in actuators. To mitigate the challenge posed in testing stiff specimens, Reinhorn et al. [28] proposed force control for actuators, applicable to both EFT and RTHS. The control approach modified the mechanically stiff nature of actuators (suitable for position control) to become a low-impedance (compliant) system compatible with force control. The proof-of-concept experiment comprised of a spring element as a compliant system while controlling the inner loop using displacement commands [28].
The broad-spectrum applications of hybrid simulation have fascinated many researchers. Consequently, hybrid simulation was applied to various applications, e.g., magnetorheological dampers [6,29,30,31,32], base isolation systems [33], and so on. As a result, OpenFresco was extended to support mixed and switch control approaches [34,35] and online optimization techniques [36]. To meet the stringent requirements of real-time hybrid testing, control strategies such as loop-shaping and Model Reference Adaptive Control (MRAC) were developed [37]. Among others, researchers identified the importance of assessing the accuracy measure for hybrid testing. Criteria for measuring the performance of hybrid simulation were thus developed through error tracking methods [38]. As a result, tracking indicators (TI) and phase and amplitude error indices (PAEI) have surfaced [39]. The latter was developed to decouple the phase and amplitude errors. The PAEI algorithm, however, solves large eigenvalue problems at each time-step of analysis, thus limiting its application for online tracking. The authors of [39] also proposed a computationally lighter frequency-based error indicator to enable online tracking during a hybrid test. Schellenberg et al. [40], on the other hand, developed a model-based compensation for OpenFresco, augmenting its extrapolation scheme. Many other studies have examined the adequacy of model-based and adaptive techniques for actuator compensation ([41]—feedforward–feedback compensator, [42]—PLC compensator, [43]—Inverse and Adaptive Inverse compensation, etc.), while Chae et al. [44] proposed a novel compensation technique, referred to as an adaptive time series (ATS) compensator. The latter is based on Taylor series expansion and least-square (LS) optimization. Due to its moderate computational cost for online applications, the importance of reducing the size of the gradient matrix can be appreciable.
To date, numerous time-stepping algorithms suitable for RTHS have been developed and many of them are implemented in the OpenFresco middleware. Among others, the Newmark implicit algorithm with fixed number of iterations (also with an increment reduction factor), the Implicit Generalized Alpha (IG-α) method with constant iterations, and the OS algorithm, based on tangent or mixed experimental stiffnesses, are powerful [10]. Both explicit and unconditionally stable algorithms are particularly attractive for RTHS. Kolay and Ricles [45] modified the two-parameter IG-α method into an explicit single parameter integration method, named KR-α. In addition to its adjustable algorithmic damping, the period dispersion properties of the algorithm can be optimized to reduce distortion from contributing modes.
While hybrid simulation (HS) has traditionally been problem-specific, software frameworks like OpenFresco [10] and UI-SimCor [46] have demonstrated versatility. A robust HS framework should support various time-stepping algorithms, numerical simulation programs, testing configurations (e.g., actuator alone, shaking table alone, coupled actuator and shaking table), actuator control (MATLAB/Simulink, LabVIEW, etc.), different data acquisition systems, and communication protocols. This paper presents the development and validation of a robust and integrated software framework for hybrid simulation. The framework follows a three-loop architecture—servo-control, simulation coordinator, and integration loops—implemented using LabVIEW and National Instruments (NI) hardware. This paper is divided into four sections. Section 2 details the framework’s development, while Section 3 discusses its validation and hybrid test results. Section 4 summarizes the key findings.
2. Development of a Software Framework
2.1. Architecture
Hybrid simulation software frameworks can be developed using two main approaches: the structural analysis approach and the control system approach. The first approach treats hybrid simulation as a finite element analysis, embedding the experimental substructure within the reference structure. In contrast, the control system approach models hybrid simulation as a feedback system, where the physical substructure functions as a plant controlled by a computational driver. An example of the structural analysis approach is OpenFresco, which serves as middleware between a finite element software (commonly OpenSees) and a control software [27]. Its Object-Oriented Analysis (OOA) module ensures the framework meets key requirements, including modeling physical substructures, generating command signals, converting measured signals, communicating with control packages, and acquiring data. This module also manages communication speed in local and distributed hybrid testing. The Object-Oriented Model (OOM) module abstracts real-world objects into software classes, maintaining data encapsulation. OpenFresco features four abstract classes: experimental element, experimental site, experimental setup, and experimental control.
Developed at the University of California, Berkeley, within the Network for Earthquake Engineering and Simulation (NEES), a three-tier software framework provides modularity and flexibility. Its top client tier interfaces with various computational drivers, while the third-tier handles laboratory control and data acquisition, driving the test specimen and collecting data. The middle tier acts as the middleware loop. OpenSees can function in the outermost integration loop alongside OpenFresco, which facilitates communication between OpenSees and the control software. The top and middle tiers can operate on a single computer or separate machines connected via a TCP/IP socket. OpenFresco supports two configurations for local deployment. In the first, a generic client element is embedded in finite element software using user-defined elements, allowing data exchange through this embedded element. Data exchange between the finite element software and OpenFresco takes place through the embedded element. Input parameters of the generic client element include node number, the degrees of freedom of the control node, and a port to communicate its input parameters [10]. In the second configuration, an experimental element is added into the finite element software instead. This eliminates the need for the experimental element abstract class in the middleware. The first approach relies on existing OpenFresco elements, while the second provides greater flexibility by allowing users to define experimental elements within the finite element software. Another open-source framework, the University of Illinois Simulation Coordinator (UI-SimCor), is MATLAB-based and designed for multi-site and multi-platform hybrid testing [46]. It consists of two modules: MDL_RF (restoring force module) and MDL_AUX (auxiliary module). Originally developed for distributed testing, UI-SimCor has also been successfully applied to local hybrid simulations [47].
This research developed two hybrid simulation schemes at LNEC and integrated them into a single software package, LNEC-HS, for improved accessibility. The software framework, designed as a Stateflow machine using Virtual Instruments (VIs) in LabVIEW, ensures modularity and flexibility, enabling slow, fast, and real-time hybrid testing. The first scheme of this software framework can be perceived as a three-loop architecture (Figure 1a) comprising a control loop (innermost), a simulation coordinator (intermediate), and an integration loop (outermost). The control loop manages the servo-hydraulic actuator, while the simulation coordinator communicates with OpenFresco via TCP/IP, continuously generating command displacements and compensating for time delays using a dedicated algorithm. The integration loop connects OpenSees to OpenFresco through TCP/IP, receiving measured restoring forces from the experimental substructure and advancing the hybrid test by solving the equilibrium equation.
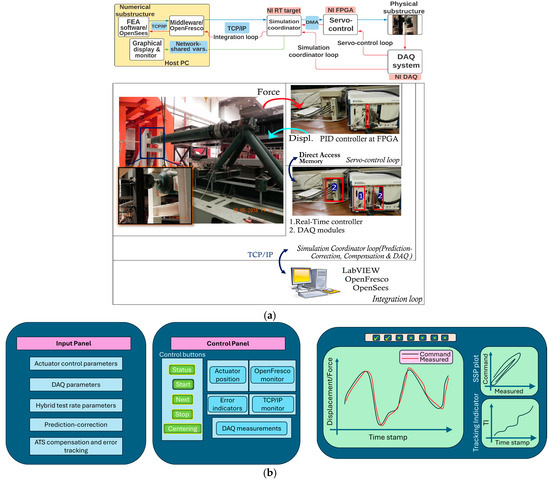
Figure 1.
(a) Three-loop architecture framework for hybrid simulation; (b) GUI of LNEC-HS.
The hardware of the LNEC-HS software framework comprises an NI embedded real-time (RT) controller and an NI Field-Programmable Gate Array (FPGA). The simulation coordinator was programmed in the RT controller and the FPGA module performs the control task. Additionally, the data acquisition board records displacement, acceleration, and force measurements during a hybrid test. The above-mentioned NI modules are inserted into a chassis and communicate with each other through Direct Memory Access (DMA). The DMA FIFO feature in LabVIEW can provide high throughput data transfer between the RT controller and FPGA. However, faster transfer of small-sized data is desired for a hybrid test. Thus, direct communication, using control and indicator variables, was adopted to improve the computational efficiency of the software framework. The building blocks of this software framework include the following: a real-time VI (referred to hereinafter as simulation coordinator VI), Host PC VI, and FPGA VI. The Stateflow machine is fully contained in the simulation coordinator VI. This VI calls the FPGA VI at each time-step of a hybrid test. On the other hand, the Host PC VI, shown in Figure 1b, provides a real-time display window for monitoring structural responses during a hybrid test. Furthermore, it serves as a user interface to initiate, manage, and end a hybrid test. The plots for subspace synchronization and error tracking can also be monitored from the display window.
Similarly to the first scheme, the second scheme of LNEC-HS follows a three-loop architecture but eliminates the need for an external numerical simulation program. Instead, a simple numerical model, integrated directly into the simulation coordinator, was developed in LabVIEW. This removes the dependency on OpenFresco and allows direct data exchange between the computational driver and the simulation coordinator, eliminating the need for TCP/IP communication. This numerical model is designed specifically for 2D elastic shear buildings, making the scheme ideal for structures with soft-story mechanisms where the upper numerical substructure remains primarily elastic. It is also applicable to soil–structure interaction (SSI) problems in structures with minimal nonlinearity in the numerically simulated upper stories. Additionally, this scheme enables significantly faster test execution, supporting hard real-time hybrid simulation.
Unlike the first scheme, it can simultaneously control an actuator and a shaking table, a key requirement for SSI hybrid testing. Due to their structural similarities, this paper focuses on developing and validating the middleware-based first scheme of LNEC-HS. The second scheme inherits its Stateflow machine architecture, and for convenience, “LNEC-HS” in subsequent discussions refers exclusively to the first scheme.
2.2. Integration Loop
The integration loop of LNEC-HS software framework incorporates finite element software such as OpenSees, an open-source, object-oriented platform for simulating the seismic response of structural and geotechnical systems. Its transparent and modular design enables users to develop and modify specialized modules with minimal interaction with the broader framework. This allows developers to focus on specific tasks without needing to understand the entire software implementation [48].
The OpenFresco middleware has an object-oriented architecture with two abstractions: the loading system (typically servo-hydraulic actuators) and the control and data acquisition (DAQ) system. The loading system imposes boundary conditions, such as displacement, velocity, acceleration, and force, while the control system ensures the accurate application of the target displacements that are received from the numerical program. The DAQ system records measured responses from transducers. OpenFresco consists of four abstract classes. The experimental setup class transforms response quantities between the degrees of freedom (DOFs) of the experimental element and the actuator, using geometry and kinematics of the loading system. Transformations can be as simple as linear transformation (compatible with small displacements) or nonlinear algebraic transformations. Communication with the LabVIEW-based control program is achieved through control points that separately send target displacements and receive measured forces. The experimental control class defines control points, loading directions, and actuator configurations. This study adopts the one-actuator subclass of the experimental control, which supports a two-point control scheme in the simulation coordinator. The experimental site class facilitates the deployment of OpenFresco for geographically distributed hybrid tests.
OpenFresco can interact with any finite element software as long as the software provides a means for modeling the experimental element [10]. In this study, OpenSees is primarily used as computational software due to its comprehensive library of materials and elements. To enable communication between OpenSees and OpenFresco software, the experimental element was added as a new abstract class into the existing element class of OpenSees [49]. This abstract class inherits the properties of the element class which has a member function that assigns trial displacements at element degrees of freedom and returns restoring forces. During hybrid testing, the experimental element class returns the initial stiffness, as determining tangent stiffness from limited measurements is challenging. However, techniques for estimating tangent stiffness are available in the literature. For example, Kim [34] modified OpenFresco’s Experimental Signal Filter class to estimate tangent stiffness and simulate experimental errors while developing a force-based hybrid simulation technique.
2.3. Simulation Coordinator VI
The operation of the LNEC-HS software framework (Figure 2a) begins in the Initialization (Init) state, where all input parameters to a hybrid test are set. Once the main pressure that drives the actuator, or a shaking table, reaches a working pressure (70 bar) and the hydraulic service manifold (HSM) is activated, the system prompts the Start-up state. This state holds the physical (experimental) substructure in its current position, facilitating test pauses and resumptions. At this stage, the FGPA-based control loop is activated via the Start-control-loop button (Figure 1b).
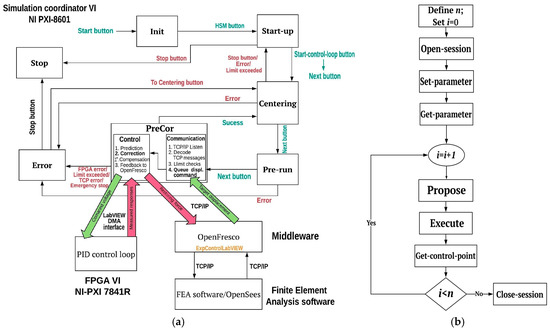
Figure 2.
(a) Schematic diagram of LNEC-HS software framework; (b) LNTCP dataflow.
Before a hybrid test, the actuator may require repositioning to properly connect with the test structure, or an initial displacement may be applied. The latter may be applied, for instance, in the case of a hybrid test for post-earthquake damage assessment based on a residual drift. The Centering state handles this initial positioning of the actuator, applying command displacements at 0.5 mm/s. After completing or interrupting a test, the software returns to this state, allowing the user to restart or terminate the experiment. The Next button initiates another test while the Stop button halts the actuator and gradually reduces hydraulic pressure to zero. When conducting consecutive tests without interruption, the TCP/IP port number must be updated because the TCP-listen VI reserves the active TCP/IP port for an extended amount of time after being closed. During this state, the proper functioning of the FPGA module, DAQ system, and actuator position are verified against predefined limits, with measurements being displayed in the interface (Figure 1b).
The Pre-run state supports the middleware-based scheme by establishing a TCP/IP listener to connect with OpenFresco and initializing data queues for the prediction–correction process in the subsequent PreCor state. The TCP/IP listener remains active for 3 s before timing out. If OpenFresco fails to establish connection within this period or the port is already reserved by the TCP/IP listener VI, the system transitions to the Error state. In the latter, the exceedance limit can be checked to help make changes before restarting the test.
The prediction–correction (PreCor) state executes the hybrid test and consists of three core modules: communication (interface) block, control & feedback block, and data acquisition block. The communication block receives TCP/IP messages from OpenFresco and verifies stroke limit compliance. Additionally, the received command displacements are queued for subsequent use in the prediction–correction process of the control block. The control and feedback block predicts actuator commands based on the last three time-steps, until the target displacement of the current time-step is available. The current algorithm predicts displacements for the first 60% of the time-step and corrects towards the target displacement during the remaining time. The DAQ block, running in parallel, records and displays measured responses and performs other auxiliary tasks. The data are buffered for a duration of 0.1 s before transferring it to the Host PC for saving via network-shared variables.
The Error state holds the actuator at its current position while the user decides to repeat or terminate a test. The software’s Stateflow machine architecture allows for immediate transition from the PreCor state to the Error state if stroke limits are exceeded, control or communication errors occur, or the Emergency stop button is triggered. Users can either stop the test or return to the Centering state, where test parameters can be modified before re-initializing all indicators in preparation for a new test.
2.4. TCP/IP Interface
The communication block of the PreCor state dialogs with OpenFresco via the TCP/IP network protocol using a LabVIEW program termed LNTCP. This collection of LabVIEW VIs facilitates bidirectional data exchange between the simulation coordinator VI and the middleware software, enabling the RT target to receive displacement commands and send feedback responses to the FEA software. The LabVIEW-based experimental control class of OpenFresco sends TCP/IP data packets to LNTCP and receives feedback forces. The communication starts at the TCP listen VI of the Pre-run state. Once the TCP/IP connection is established, the TCP read VI receives a command displacement, and a TCP write VI sends intermediate replies and a feedback force. The data packet, which has a variable-length tab-delimited ASCII format, is typically stored on a single line. In this data packet, a newline serves as a message delimiter. During a hybrid test, a transaction identifier is included in every message so that the client-side can be asynchronous and multithreaded. The schematic diagram of the program shown in Figure 2b presents the sequence of operations performed in LNTCP.
The Open-session message is received when the TCP/IP connection is established. It can be used to initialize hardware or do any other system-specific work. LNTCP duly ignores it by sending an ‘OK’ string. The next two steps, Set-parameter and Get-parameter, allow users to define and obtain parameters, respectively, that are necessary for the subsequent communications of LNTCP. These steps are optional, and they can be skipped by sending the ‘OK’ string back to the OpenFresco middleware. In each iteration of the integration loop, three mandatory steps, namely Propose, Execute, and Get-control-point, are executed. The message syntax of each step is important in decoding received data packets as well as in sending feedback messages. The Propose command can handle up to 12 control parameters depending on the number of control points supported by the application. In this study, a two-point control was developed, which has displacement as its only control parameter. Immediately after receiving this command, a separate loop in LNTCP matches the command with the actuator metadata stored in the RT target. In the receive-syntax, the axis of loading of the actuator is defined together with the control parameter—displacement, force, rotation, or moment, and its magnitude. No message is returned in response to the Propose command.
Furthermore, the Get-control-point command can support up to 12 control parameters. It mirrors the Propose command and returns measured responses to OpenFresco. In the current implementation, LNTCP can handle two feedback parameters, i.e., displacement and restoring force measurements. The Execute command message simply executes a previously accepted proposal. In the feedback phase, LNTCP uses a semaphore VI which only allows the execution of one command while blocking the remaining TCP threads to OpenFresco. Therefore, the TCP read VI that is responsible for this operation is set to run at a higher level of priority. The Close-session command, which mirrors the Open-session command, is executed at the end of the hybrid test, and performs no task.
The implementation of LNTCP includes a command-reader loop, a limit-checking loop, and a replier loop. The replier loop, as its name indicates, displays data packets that are received from and/or returned to OpenFresco. The command-reader loop reads the data packets received from OpenFresco byte by byte, since the data are an anonymous sequence of bytes [50,51]. Thus, data are collected byte by byte until the EOL (end of line) character, which marks the end of a message, is encountered. This ASCII message is then parsed and, eventually, enqueued into a Command queue. The data enqueued into the Command queue are then retrieved and a response is returned to OpenFresco. When the system prompts to execute the current time-step, the value of the control parameter is enqueued into a Position queue. The Command queue, at this stage, is emptied (dequeued), and it is ready to receive the next control parameter. The PreCor queue then receives the target displacement of the current time-step, from the Position queue, and drives the correction phase of the prediction–correction process.
2.5. Prediction–Correction Methods for Actuator Control
The measured forces during a hybrid test are returned to the numerical program at intervals of time depending on the speed of the test, the latency of the network layer, and the complexity of the numerical substructure. The numerical solution to the equation of motion can also be time-consuming considering nonlinear dynamic analysis. Data transfer is typically a potential source of time delay, meaning that the TCP/IP protocol that is integrated into the OpenFresco middleware has a notable latency. The rate of data transfer is not even constant, albeit small compared to geographically distributed testing. Consequently, the integration loop, which includes the time-stepping algorithm, must be synchronized with the clock speed of the controller. In this paradigm, the actuator is forced to move in a ramp-and-hold manner, thus causing force relaxing effects. This effect could potentially be strong in fast hybrid tests that include strain-dependent physical substructures. To circumvent this challenge, the command displacement to the actuator needs to be applied in a deterministic manner at short intervals of time. This objective can be performed using a predictor–corrector algorithm that ensures parallel execution of the two tasks. In this technique, command signals are predicted in a deterministic way (at the clock speed of the control system) while the computational driver solves the response of the structure at the current time-step. The prediction time can be constant or variable. Once the target response is available in the control system, the algorithm starts correcting towards it. This continuous movement of actuators can significantly reduce force relaxation effects. In this study, the prediction–correction task is performed using third-order Lagrange polynomials based on committed displacements. This conventional method (PreCor-D) has good accuracy for small values of , say for [22]. Considering nth-order polynomial, the predicted displacements are calculated as follows:
where is the last kth time-step displacement received by the numerical program; is the nth-order predictor polynomial; and is the fraction of the integration time-step. In the above equation, the Lagrange polynomial, , can be derived from the following:
The prediction is carried out until , where is the maximum duration of the prediction phase with respect to the simulation time, . The duration of the prediction phase varies depending on the complexity of the numerical substructure, which is dictated by time elapsed in solving the numerical substructure, and the latency of the TCP/IP network protocol. For relatively simple structures, = 60% is adequate. If a long prediction period is adopted, the actuator can overshoot deviating from its true trajectory. Also, prediction using a lower-order polynomial (first or second order), at large time-steps of integration in particular, can distort the true trajectory of the displacement response. The accuracy of predictors can be studied assuming the earthquake response of a structure is a sinusoidal vibration [22]. Large integration time-steps typically result in less accurate prediction; hence, the integration time-step must be adequately small. Corrector displacements are calculated once the target displacement at the current time-step is available. Like the prediction phase, corrector displacements are calculated using third-order polynomials:
where is the nth-order corrector polynomial. The accuracy analysis of the corrector algorithm is identical to that of the predictor except for the Lagrange polynomials. In general, the accuracy of the corrector algorithm is superior to that of the predictor because the current time-step displacement is included during the correction step. In this paper, the same polynomial order is used for the predictor and corrector steps.
In prediction–correction algorithms, the switching interval between the two phases is important. The difference between the last predicted displacement and the first corrector displacement, divided by the time-interval of controller δt, can be taken as the velocity, , at the switching interval. When is negative, it can lead to undesired loading and unloading during the nonlinear response simulation of a test structure [22]. Comparing the velocity at the switching interval to the true sinusoidal velocity, Nakashima and Masaoka [22] showed that first- and second-order polynomials give rise to switching velocities with large magnitudes of amplification and phase lead that can distort the true response. When a structure is loaded towards its peak displacement, this phase lead can cause unloading of the test structure. However, adopting third- or fourth-order polynomials, a more accurate switching velocity can be obtained with a certain phase lag. At larger frequencies, the magnitude amplification of the fourth-order polynomial is typically larger than the third-order polynomial, which explains why the latter has been a favorable choice in many applications [10,22]. The phase lag introduced by higher-order polynomials can also cause undesired reloading when the switching interval occurs during the initiation of the unloading cycle. This effect is not detrimental since most structures remain elastic during the initiation of the unloading cycle.
The conventional predictor–corrector algorithm explained above does not meet the requirements for C0-continuity, due to the discontinuous displacement at the switching interval and the accuracy of its velocity. The need for C1-continuity (continuity of the derivative at the switching interval) is less important as it may lead to unstable simulation. This instability is the result of the reduction in the accuracy of the corrector algorithm while improving the continuity at the switching interval. In practice, the step-like jump at the switching interval causes an actuator to oscillate because of a high-velocity demand. Although the step-like jump can be alleviated by employing higher-order polynomials, it does not provide a definitive solution. The algorithm based on the last predicted displacement (PreCor-LPD) [10] essentially uses the last prediction, replacing the current time-step displacement during the correction phase, thereby making the predictor C0-continuous. The corrector displacement is thus modified as follows:
where is the last predicted displacement and is the nth-order corrector Lagrange polynomial at . The accuracy characteristics of this corrector algorithm can again be studied considering a sinusoidal response of a structure. This corrector algorithm is less accurate compared to the conventional method since the corrector step includes the last predicted displacement which already has the prediction error. The trade-off between the accuracy and smoothness of this algorithm is therefore evident. The accuracy of this algorithm may be improved by limiting the prediction error while considering a small prediction time (small ). For practical purposes, the less accurate corrector algorithm is preferred against the disruptive property of the conventional algorithm. This is particularly true since actuator oscillations can be problematic when the algorithm is used with a responsive servo-hydraulic controller. Yet, is not only a user choice, but it is governed by the clock speed of the controller and the simulation time-step. The latter depends both on the complexity of the numerical substructure and the network delay. To address the challenges of the prediction–correction algorithms discussed above, methods based on trial velocities (PreCor-V) and accelerations were also studied [10]. From the simulation studies of these algorithms in MATLAB, Figure 3, which correspond to a hybrid test from Section 3.4, it is evident that the algorithms can perform well with reasonable deviations from the true trajectory as shown in Figure 3 (left), provided error accumulation is mitigated. In Figure 3 (right), a closer look at this trajectory shows that these errors tend to diminish for a relatively smaller prediction time and for algorithms which employ last-predicted displacement or velocity. Prediction–correction algorithms which employ displacement commands from the numerical program show overshot error if prediction time reaches 80% of the time-step, while 60% prediction time resulted in an undershot error. Even with the introduction of last-predicted displacements, which improved the overall trajectory, 60% of prediction time was found to be optimal.
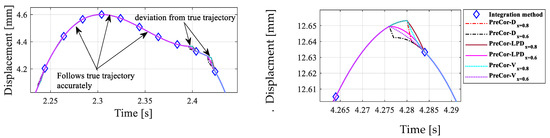
Figure 3.
Accuracy of prediction–correction algorithms for actuator control.
The prediction–correction method which uses the last predicted displacement has C0-continuity, but the accuracy of its velocity needs further improvement; hence, an algorithm based on velocities was also considered in this study. Several numerical integration methods, such as Runge–Kutta integration and KR-α are explicit for velocities and displacements. These trial velocities may therefore be used to improve the accuracy of velocity of the prediction–correction algorithms. Nonetheless, trial velocities can be inaccurate in many integration methods. In this research, velocities are derived through differentiation using Lagrange polynomials and the above-mentioned algorithms, excluding the method which include accelerations, were implemented in LNEC-HS.
2.6. Control Algorithm
The performance of a servo-hydraulic controller is essential for the accuracy of a hybrid test. In the current software framework, a proportional–integral–derivative (PID) controller was programmed into the NI PXI-7841R FPGA to achieve determinism and a high rate of execution. The PID algorithm works with a single-precision floating number necessary for accurate position control of the actuator. It uses the integral anti-windup technique to avoid the accumulation of errors of the integral term when a large change occurs in the setpoint or during a saturation phenomenon. The algorithm also features a bump-less controller output for changes in the PID gains.
Two PID loops, shown in Figure 4a, control the external/auxiliary actuator and shaking table actuator in parallel within the FPGA VI. One loop drives the auxiliary actuator, and the other drives the shaking table actuator. The control loop has an execution speed of 5 kHz (2 × 10−4 s). To reduce measurement noise, the measured displacement is filtered by a low-pass second-order Butterworth filter with a 200 Hz cut-off frequency. When operating under the middleware-based scheme, the PID loop for the shaking table is deactivated by disconnecting the drive signal. The servo-controller setpoints are checked against the actuator stroke limits in the RT target and a Boolean indicator, LimitExceeded, determines whether the PID loop executes. If the limit is exceeded, the actuators hold their position, and the RT target switches to the Error state. Additionally, data acquisition of acceleration (ENDEVCO) is handled within the FPGA VI to maximize resource efficiency.
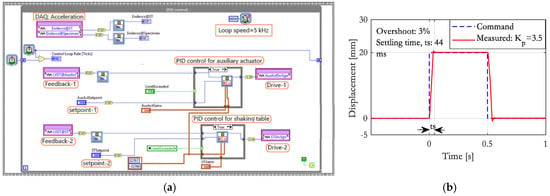
Figure 4.
(a) PID control loop; (b) PID tuning.
The PID gains are tuned to ensure a unit amplitude output–input relationship in the frequency range of interest. For the characterization of the controller, a square wave with a 10 mm amplitude and 1 Hz frequency, shown in Figure 4b, was applied to the uniaxial shaking table (ST1D) rigidly attached to a 600 kg mass. The proportional gain, kp, was set to keep the overshoot error below 5% and the settling time under 50 ms. The integral gain, ki, was kept small for stability. The derivative term, in theory, facilitates convergence, i.e., reduces settling time. However, it can also result in excessive volatility—spikes in the output of the controller (derivative kick). Thus, the derivative gain, kd, is set to zero.
To assess the load transfer system’s performance, the Frequency Response Function (FRF) of ST1D was determined by applying a band-limited white noise (0–20 Hz, RMS amplitude 1 mm, 10% cosine taper). The FRF amplitude, shown in Figure 5, is close to 0 dB (unit amplitude) in the 0–6 Hz range, which is the range of interest for the subsequent hybrid test. However, it drops to −5 dB (more than half of the original amplitude) around 12 Hz, indicating that the controller performance needs improvement for stiffer physical substructures. Since the FRF may change due to control–structure interaction (CSI), adaptive compensation is indispensable.

Figure 5.
Characterization of LNEC’s uniaxial shaking table.
2.7. Dataflow in LNEC-HS
The LNEC-HS software framework operation starts by applying the extrapolated displacements to the actuator while the finite element software computes the current time-step displacement. Once the target displacement is available at the simulation coordinator, the algorithm interpolates toward it. The schematic diagram shown in Figure 6 gives a complete picture of the dataflow and the interaction of the prediction–correction algorithm with the rest of the framework software. The default duration for the prediction phase, Δtpred, is 60% of the time-step and the remaining 40% of the time-step is assigned to the correction phase, Δtcor. This setting is adequate for moderate-sized frames. The prediction duration can be adjusted via the control panel, particularly for structures with many degrees of freedom (DOFs) or strong nonlinearity, which require longer extrapolation. However, the additional time needed remains negligible compared to the TCP/IP latency.
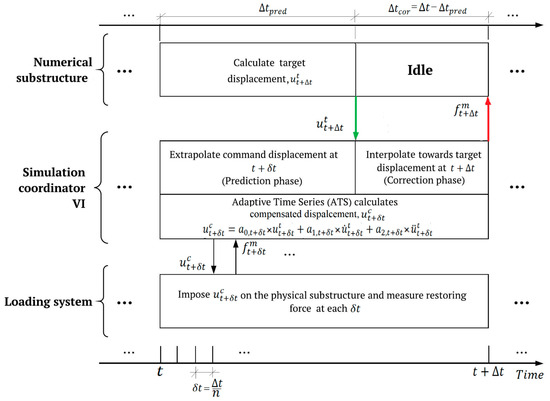
Figure 6.
Schematic representation of dataflow in the LNEC-HS software framework.
The conventional extrapolation method relies on the last four committed displacements (i.e., [,,,]). Meanwhile, an improved corrector algorithm incorporates the last predicted displacement, using [, , , ], where is the displacement predicted at of the time-step. For velocity-based prediction–correction, numerical differentiation using second-order Lagrange polynomials calculates velocities, while third-order Hermite polynomials refine the velocity-based prediction–correction process.
2.8. Error Tracking and Compensation
Error tracking is an integral part of a hybrid test where the magnitude and nature of errors are evaluated. Apart from its importance in assessing the accuracy of a hybrid test, it can be used for an early shutdown when stability problems prevail. It can also be essential for calibrating compensation algorithms. The tracking indicator (TI), widely used for monitoring experimental errors, relies on the area enclosed in the plot between command displacement and the measured displacement, termed the subspace synchronization plot (SSP) [52]. In the LNEC-HS software framework, TI can be monitored online from the GUI of the software with a refresh rate of 0.1 s. A positive rate of change in TI indicates that the measured displacement lagging the command displacement, adding energy to the test, while a negative rate of change corresponds to the measured displacement leading the command displacement. To decouple the phase (time delay) and amplitude errors of a load transfer system, SSP can be used in conjunction with TI to quantify control errors. If the fitting line of the SSP approaches 45° and the magnitude of TI remains large, phase error is dominant. The direction of the winding of SSP enables the further characterization of control errors. Essentially, the clockwise direction of winding indicates a phase lead whereas anti-clockwise winding indicates a phase lag. In addition, a plot inclination below 45° is interpreted as an undershoot error while an inclination above 45° is an overshoot error. Hessabi and Mercan [53] proposed a phase and amplitude error indicator (PAEI) to decouple the two errors using a least-squares solution for the ellipse equation of the SSP. This method is not implemented here due to its high computational cost.
Phase and amplitude errors of a command displacement evolve during a hybrid test due to the nonlinear characteristics of the test structure and load transfer system. Offline compensation approaches often fail to account for the overall system nonlinearity. In contrast, adaptive techniques rely on dynamically changing parameters, which is the core idea behind the adaptive time series (ATS) technique. The compensation coefficients of this technique are directly correlated to the phase and amplitude errors unlike many other compensation schemes [44]. The LNEC-HS software framework employs a modified ATS algorithm, replacing the Backward Difference (ATS-BD) approach for computing target velocities and accelerations with third-order Lagrange polynomials (ATS-LG). Initial compensator coefficients (, , and ) were estimated from characterization tests that employ band-limited white noise (BLWN) input. The compensator activates 1.024 s after the test commences, generating a compensation matrix of 1024 samples, assuming the clock speed of the command generation is 1 kHz. Low signal-to-noise (SNR) ratio, at the start and at the end of a test, can make the compensation matrix ill-conditioned, resulting in abrupt changes in the compensation coefficients which can destabilize the hybrid test. To mitigate this, the updating process halts if the peak measured displacement within a 1 s window falls below a threshold displacement [44]. Following Dong [54], this study uses the RMS value of the measured displacement, defaulting to 1 mm, against the threshold value. This threshold value can be adjusted based on the level of noise in transducers and the performance of a loading system, i.e., a very small threshold value may be adequate for state-of-the-art hardware.
To achieve a stable compensation, the compensation coefficients must be constrained within defined intervals. The interval for can be derived from the maximum expected amplitude error within a ±30% margin from its initial value [44]. The range for depends on the maximum time delay of the actuator. The maximum actuator time delay, , can be computed directly from (assuming no gain error). The interval for can be assumed to have ±100% margins from the initial value while ensuring non-negative values. The upper bound for of is set as , within the interval [0, Additionally, the rate of change in the coefficients must be restricted depending on the practical values suitable for servo-hydraulic actuators, as suggested in [44]. Excessive and values can amplify the high-frequency component of a structural response while overly restrictive upper limits degrade compensation accuracy. Fine-tuning these limits is essential for optimal performance.
The accuracy of the ATS-LG, relative to the ATS-BD, is another important aspect worth exploring. The BD method for calculating derivatives has a first-order error to the exact solution. Taking 1 kHz as the clock speed of the controller, Δt, the target velocity, and the acceleration are calculated as follows:
where N and Δt are the number of sub-steps in a time-step and the integration time-step, respectively. Replacing the above formula in the second-order Taylor series and transforming the entire equation into the Z-transform, the discrete time transfer function, from the target displacement, , to the compensated displacement, becomes
On the other hand, considering third-order Lagrange polynomials for calculating the first two derivatives of the target displacement, the discrete time transfer function, from the target displacement, , to the compensated output displacement, , can be obtained:
The target displacement is typically less noisy; thus, any technique for differentiation is expected to have a small influence on higher frequency effects. Thus, the choice in computing the derivatives of the target displacement can be assumed to be solely dependent on accuracy criteria. Therefore, the accuracy of the above two formulations can be compared, meaning versus . To cover a wider spectrum of actuator performance, several values of amplitude error and time delay are considered in this comparison. With regard to this, the and coefficients corresponding to the time delay in the interval [20,40] ms are taken assuming a constant time delay of an actuator. This assumption is adequate to compare the two approaches provided that appropriate grid-spacing for the time delay is considered. The comparison was made for 10 ms, 20 ms, and 40 ms time delays, as shown in Figure 7. Also, cases without gain error and with ±10% gain error are considered, and they are superimposed with the time delay of the actuator.
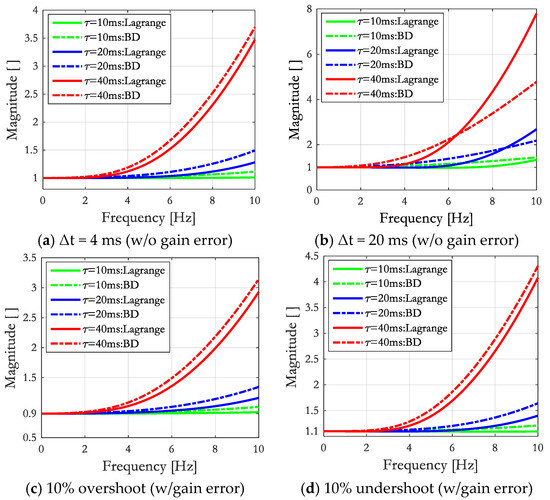
Figure 7.
Magnitude of GATS.
The magnitude of is close to one for time delay of an actuator in the order of 10 ms, provided that the time-step size is small. However, the compensator overshoots at relatively large frequencies when the time delay is greater than 20 ms. For instance, when the time delay is 40 ms, the target displacements of a test structure vibrating at 10 Hz can be amplified by a factor as large as 3.5. Nonetheless, the ATS-LG has shown superior performance compared to the BD method, as shown in Figure 7a, particularly when the time-step of the simulation is small. For frequencies greater than 6 Hz, the performance of the ATS-BD has improved relative to the ATS-LG considering time-step equal to 20 ms. Additionally, the performance of the ATS-LG appears to deteriorate as the time delay increases. In Figure 7, the characteristics of the compensator in the presence of undershoot errors explain the detrimental behavior of having both undershoot error and time delay. In this study, the theoretical relationship, , was adopted in defining the compensation coefficients when computing . However, the coefficients of the compensator are actually estimated by minimizing the square error between the compensated and measured displacements, i.e., the true compensation coefficients may not be necessarily related according to the theoretical relationship. For instance, considering <, the simulation results show a reduction in the overshoot error of the compensator. The latter increases in significance with increasing time delay of the actuator. To this end, the coefficients of the ATS compensator must be carefully monitored during a hybrid test.
2.9. Data Acquisition
The data acquisition block of the software framework records data from Linear Variable Displacement Transducers (LVDTs), accelerometers, and a load cell. The 68-pin shielded connector block, SCB-68, connects the FPGA module to the signal conditioners. The RDP600 signal conditioner rack uses the RDP 611 module for conditioning the analog signals from the LVDTs and the load cell. Likewise, the acceleration measurements from the ENDEVCO accelerometers were treated using a separate analog conditioner. The calibration of the 500 kN capacity INSTRON load cell was performed using a compression machine, whereas the RDP-type LVDTs were calibrated with a digital meter. The NI data acquisition (NI-DAQ) block of the simulation coordinator VI buffers 100 samples per transducer and transfers the data to the Host PC through the network-published variables of LabVIEW, thereby reducing the computational load during hybrid testing. In the current implementation, the DAQ loop operates at a rate of 1 kHz.
3. Validation of LNEC-HS Software Framework
3.1. Case Study
The LNEC-HS software framework was validated by conducting hybrid tests of a two-dimensional steel moment-resisting frame (MRF) structure, shown in Figure 8a. The steel structure comprises two-bays, each 3.6 m wide, with a one-story steel frame with rigid beams. One of the outer columns (labeled as “Exp”) represents the experimental substructure while the remaining parts of the structure were numerically modeled using OpenSees version 2.7. The columns, 1.8 m in height, are fixed at the base and hinged at the top. The one-actuator experimental setup of OpenFresco can therefore be used to control the horizontal DOF of the experimental column.
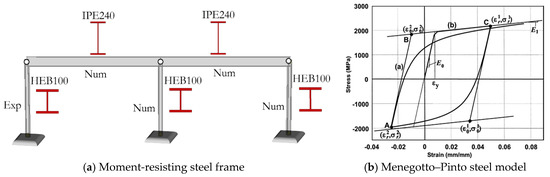
Figure 8.
Case study structure and modeling.
All columns of the steel MRF structure are made from HEB100 steel profiles characterized by S355 steel grade. The same grade of steel was also considered for the IPE240 beam elements. The fiber modeling approach was adopted while modeling the column elements using the Menegotto–Pinto (Steel02) constitutive model shown in Figure 8b. The beam elements, on the other hand, were assumed to remain elastic during the hybrid test. The force-based model for distributed plasticity, considering five integration points, was used during the response simulation.
3.2. Test Setup and Calibration of Test Parameters
The hybrid test of the steel frame was conducted using LNEC’s uniaxial shaking table (ST1D). The experimental column is welded to a steel base, and it is connected to a steel strut at the top, as shown in Figure 9. The INSTRON load cell is connected to the rear end of the loading strut and measures the restoring force of the test specimen. In this test setup, the displacement of the platen is transferred to the strut through a rigid space truss. The base frame of the shaking table and the steel base of the test specimen were both attached to the strong floor through a bolt and nut system.
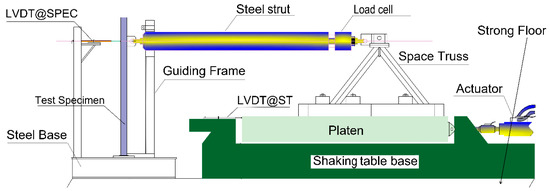
Figure 9.
Schematic representation of test setup for hybrid simulation.
To restrict the out-of-plane displacements of the test specimen, a guiding frame was provided at the end of the steel strut, as shown in Figure 9. Two Polytetrafluoroethylene (PTFE) boards were attached to the guiding frame, at the interface with the steel strut, to reduce friction. The command displacement generated from the predictor–corrector algorithm, after being converted to an equivalent voltage output, is applied to the servo-valve of the actuator that drives the shaking table. The shaking table in turn drives the experimental column through the assembly of the space truss and the steel strut. To achieve good command tracking of the actuator, i.e., the command displacement is equal to the displacement measured by the LDVT@SPEC (see Figure 9), the latter was used as the feedback displacement in the control loop.
In Figure 10a, the displacement measured by the LDVT@SPEC has a plateau after the peak response. This indicates the presence of small gaps in the connections of the test setup. The hysteresis plot in Figure 10b shows the presence of a 0.1 mm gap. To reduce the size of the gap, all connections were therefore tightened after careful inspection.
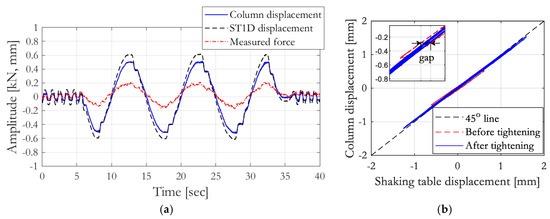
Figure 10.
(a) Measured responses; (b) identification of gaps in the test setup.
The OpenFresco middleware does not return the tangent stiffness of an experimental element. Thus, the accurate estimation of the initial stiffness of the experimental substructure can improve the fidelity of the hybrid test. In this work, a hammer test was applied for estimating the modal frequencies of the experimental column. These estimates can be then readily used for calculating the initial stiffness of the steel column. During the hammer test, the steel column was divided into six equal sections, M1–M6, spaced by 30 cm, which were distributed along the useful height of the column. Six sensitive PCB accelerometers, of 0.5 g capacity, were attached to one of the flanges of the steel profile as shown in Figure 11a. The hammer impacts were then performed on the opposite flange of the profile in a roving manner at the height of the accelerometers, thus resulting in six hammer tests, H1-H6. The hammer has a rigid head, which is connected to a PCB accelerometer of 50 g capacity. Each hammer test had six impacts that were spaced by a 10 s idle time to ensure that the column’s oscillations from neighboring impacts did not overlap. The frequency response functions (FRFs) of all the impact tests were computed after filtering the acceleration measurements using a low-pass Butterworth filter with a 50 Hz cut-off frequency. More importantly, the enhanced frequency domain decomposition (EFDD) and canonical variate analysis (CVA) methods, i.e., operational modal analysis (OMA), were adopted to estimate the modal frequencies and the modal damping coefficients. In general, system identification through experimental modal analysis (EMA), considering input–output measurements, is more pragmatic, since the external force applied to the column is not an ambient load. The EMA estimates were therefore computed by superimposing the FRFs.
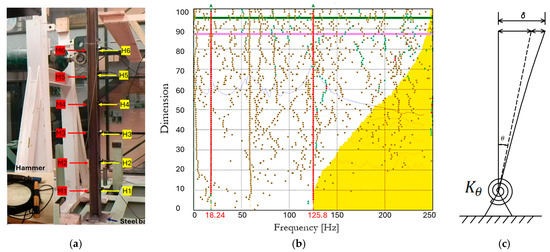
Figure 11.
(a) Test setup for hammer test; (b) modal identification using canonical variate analysis; (c) modeling a semi-rigid connection using a rotational spring.
In Figure 11b, red dots and green dots indicate stable and unstable modes, respectively, while brown dots represent measurement noise. The fundamental frequency estimates of the experimental substructure, 18.24 Hz (see the first vertical line made by red dots in Figure 11b), estimated using the OMA and EMA techniques, are approximately identical. We can therefore conclude that the connection between the steel base and the strong floor is only partially rigid since the theoretical fundamental frequency of the column is 25.08 Hz. Consequently, the fixed-base model of the experimental column is now modified as a pin-ended connection including a moment capacity that is defined by a rotational spring, . During the estimation of the rotational spring, , the first and second modal frequencies of the semi-rigid model of the experimental column, shown in Figure 11c, were matched to the corresponding experimentally estimated frequencies using a trial-and-error method, which resulted in = 1942 kNm/rad. The stiffness matrix, , of the steel column can therefore be derived, and it can be used to define the stiffness matrix of the experimental beamColumn element class of OpenFresco.
The benchmark for the subsequent hybrid tests was built creating a fully numerical model in OpenSees, whereby the rotational spring of the experimental column is represented using a zero-length element. The rotational restraint of the base node of the force-based inelastic beamColumn element is released along the major axes and the Steel02 constitutive model is adopted for columns. The strain hardening ratio of the constitutive model was obtained from the principles of the continuous strength method (CSM) [55]. This method, which is a strain-based approach, can accurately predict the section capacity of steel structures. It uses a quad-linear curve, shown in Figure 12, to define the stress–strain backbone of steel; the strain hardening ratio, b, can be estimated from the following equation:
where is the steel modulus, 210 GPa and and are the yield stress and the ultimate stress of steel, respectively. In Equation (8), the ultimate strain, , and the strain-hardening strain, , are used to compute two material coefficients, and , from predictive equations.
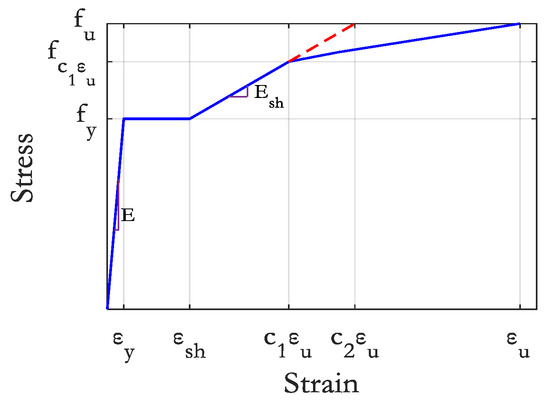
Figure 12.
Quad-linear stress–strain curve of hot-rolled steel ([55]).
In addition to accurately estimating the initial stiffness of the experimental column, a reliable estimation of the initial coefficients of the ATS compensator is essential for the accuracy of LNEC-HS software framework. As shown in Figure 13a,b, this was accomplished by applying an input displacement to the shaking table which is prepared by superimposing a 10 mm white Gaussian Noise (WGN) in the 0–1 Hz interval and a 2 mm WGN in the 0–20 Hz interval. The input signal, sampled at 0.02 s, was applied to the shaking table under no payload conditions. During this characterization work, the PID gains were set to = 3.5 and = 0.001. The ATS coefficients on the other hand were estimated by synthesizing the velocity response from displacement and acceleration measurements using a 4 Hz crossover frequency. Furthermore, both ends of the measured displacement were cropped to prevent the ill-conditioning of the estimation matrix and both the command and measured displacements were filtered, using a 20 Hz low-pass Fourier filter, for a reliable estimation. The estimated coefficients, = 0.9066, = 0.0015 s, and = 9.95 × 10−5 s2, are equivalent to having a time delay of 1.65 ms and an overshooting error of 10.3%.
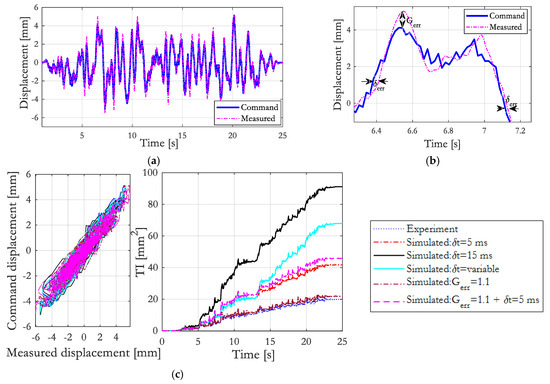
Figure 13.
(a) Command and measured displacements for estimating the initial ATS coefficients; (b) close view on the time delay and gain error; (c) SSP and TI plots in the presence of experimental errors.
Furthermore, the tracking indicator (TI) of ST1D is examined from the results of the above experiment. Additionally, an artificial delay is added to the measured displacement to investigate the capability of the TI in identifying the time delay and gain error of ST1D. As shown in Figure 13c, a gain factor (Gerr) as large as 1.1 (10% amplitude error) does not introduce a notable difference on the TI plot. On the other hand, the presence of time delay is apparent, and its magnitude is reflected on the amplitude of the TI plot. Also, a change in the gradient of the TI plot translates into a change in the amplitude of the time delay. In Figure 13c, the time delay in the first half of the simulation is 5 ms, but it changes to 15 ms in the second half of the simulation. It is therefore evident that TI is useful in detecting the time delay of an actuator, but less sensitive to a gain error. Likewise, in the SSP, the impact of the simulated experimental errors is evident, in that the scenario with a larger TI corresponds to larger hysteretic area.
3.3. Rehearsal Test
The first step in any hybrid test is to ensure the proper functioning of the software framework. Software bugs need to be detected and resolved at this stage, otherwise, the potential for premature damage of the test specimen is high. A rehearsal hybrid test, also termed simulated or open-loop hybrid test, is typically conducted by returning the simulated restoring forces into the finite element software. In rehearsal experiments, the loading system can be deactivated by disconnecting the drive signal to the actuator or a fraction of the drive signal can be applied to the test specimen. In the former, software bugs and communication issues can be identified while, in the latter, the performance of control and/or compensation algorithms can be examined by comparing the target and measured displacements, as shown in Figure 14b. The experimental element assumes a linear elastic relationship during the rehearsal test since the simulated restoring forces are proportional to the target displacements.
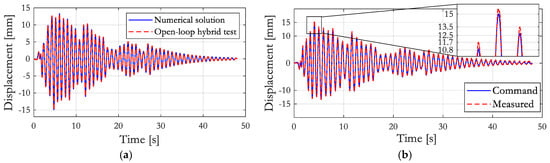
Figure 14.
(a) Lateral displacements of the case study structure; (b) experimental errors.
The El Centro (1994) earthquake, scaled to 0.03 g PGA, was adopted during the open-loop hybrid test of the steel frame. The lateral displacement of the steel frame, shown in Figure 14a, is in good agreement with the numerical results, thus validating the proper functioning of the software framework.
3.4. Hybrid Test
The closed-loop hybrid test, another name for an actual hybrid test, is conducted by returning the measured restoring forces to the computational driver. In addition to the rehearsal test, performing a closed-loop test at a low excitation level can help to detect errors in the feedback force. The experimental column again must remain strictly linear elastic. In this study, the measured restoring force has a small signal-to-noise ratio (SNR), which is inevitable as long as the level of excitation is low. Nonetheless, the level of noise can be useful in deciding the level of filtering needed for the force measurements. For brevity, the results of this rehearsal test are not discussed in this paper.
The numerical modeling considers the mass-proportional damping by taking ξ = 2% to represent the viscous damping of the case structure whose fundamental frequency is 1.08 Hz. This choice of damping model prevents the over-estimation of damping forces due to changes in the stiffness matrix. The α-OS algorithm, considering α = 0.9, is adopted for integrating the equation of motion of the numerical substructure. The steel frame was subjected to the El Centro input motion at an integration time-step equal to 4 ms (Δt), and a second-order low-pass Butterworth filter, 4 Hz cut-off frequency, was used in filtering the measured restoring forces. The ATS compensator was activated during this test and the prediction–correction process, taking Δtpred/Δt = 60%, was carried out through the algorithm which uses the last predicted displacement. The actual timescale of this hybrid test (Δtsim/Δt) is calculated as 27.8. In general, the time-scales smaller than 50 are regarded as fast hybrid tests; thus, the closed-loop hybrid test conducted here can be categorized as a fast hybrid test.
As shown in Figure 15a, the actuator displacements exceed the target displacements due to errors in the measured restoring force (Figure 15b). This discrepancy primarily stems from the damping component, where actuator delay induces negative damping. However, no significant error propagation occurred during the response simulation, as indicated by the small experimental errors at the test’s conclusion, suggesting that they remain within an acceptable range.
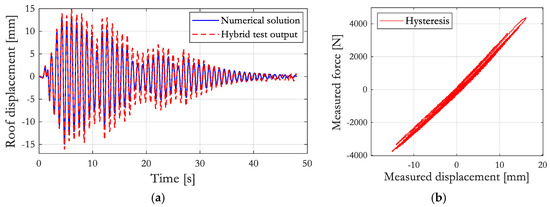
Figure 15.
(a) Lateral displacement response of the case study structure; (b) hysteresis loop.
To further explore the overshot error, the Fourier amplitude of the displacement response was examined. Figure 16 reveals that the second and third modes of the structure (f2 and f3)—previously identified in the numerical model—were excited during the hybrid test. This unintended excitation likely contributed to the observed displacement overshoot, highlighting the need for additional numerical damping. Improved damping can be achieved through numerical integration or the delay compensation algorithm, such as the ATS compensator. Despite this challenge, the hybrid test achieved its primary objective with reasonable accuracy.
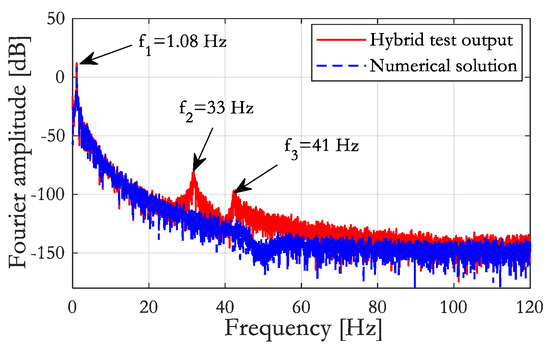
Figure 16.
Fourier amplitude of lateral displacement response.
4. Conclusions
This paper presented the development and validation of a novel integrated software framework for hybrid simulation, exploring its opportunities and challenges. The study demonstrated the importance of seamless integration and data transfer within the three-loop architecture framework using a Stateflow machine design in LabVIEW software. The flexibility and modularity qualities required by the software framework were also highlighted along with their implication for future extension. The relative speed of hybrid testing is important for the accuracy of response simulation. Hence, it is essential to equip a testing platform with an actuator motion controller by systematically incorporating an algorithm that works in synchronization with an internal PID controller. To address this, LNEC-HS integrates a predictor–corrector code based on Lagrangian polynomials, mitigating force-relaxation issues common in hybrid testing. Additionally, the framework supports both middleware-based and direct hybrid simulation, enhancing its versatility.
Actuator delay compensation plays a crucial role in simulation accuracy. The error tracking in LNEC-HS provides an estimate of the experimental errors to the ATS compensator. This study also addressed errors originating from the numerical program, ensuring the accurate representation of the experimental substructure’s initial stiffness using system identification techniques. Moreover, rehearsal hybrid testing proved effective in identifying and mitigating early technical issues before actual testing.
In summary, this paper demonstrated the capability of the developed software framework and its simulation tools for hybrid testing. Future works will focus on optimizing data transfer protocols to maximize the speed of the current TCP/IP communication block and expanding the platform’s capabilities to multi-actuator control.
Author Contributions
Conceptualization, G.G.T. and A.A.C.; methodology, G.G.T. and A.A.C.; software, G.G.T.; validation, G.G.T. and A.A.C.; formal analysis, G.G.T.; investigation, G.G.T.; resources, G.G.T. and A.A.C.; data curation, G.G.T.; writing—original draft preparation, G.G.T.; writing—review and editing, G.G.T. and A.A.C.; visualization, G.G.T.; supervision, A.A.C. and A.G.C.; project administration, G.G.T. and A.A.C.; funding acquisition, G.G.T., A.A.C. and A.G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by FCT, Portugal’s National Funding Agency for Science, Research, and Technology, through the fellowships PD/BI/113722/2015 and PD/BD/128305/2017, as well as in the framework of project PTDC/ECI-EST/6534/2020 (HybridNET – Hybrid Simulation Integrated Facility for Real-Time, Multi-Hazard and Geographically-Distributed Testing).
Data Availability Statement
Data may become available upon substantiated request.
Acknowledgments
The authors are grateful for the technical and material support from LNEC in setting up and conducting the hybrid testing.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hakuno, M.; Shidawara, M.; Hara, T. Dynamic Destructive Test of a Cantilever Beam Controlled by an Analog-Computer. Proc. Jpn. Soc. Civ. Eng. 1969, 171, 1–9. (In Japanese) [Google Scholar] [CrossRef]
- Mahin, S.A.; Shing, P.B. Pseudodynamic method for seismic testing. J. Struct. Eng. 1985, 111, 1482–1503. [Google Scholar] [CrossRef]
- Takanashi, K.; Nakashima, M. Japanese Activities on On-Line Testing. J. Eng. Mech. 1987, 113, 1014–1031. [Google Scholar] [CrossRef]
- Igarashi, A.; Iemura, H.; Suwa, T. Development of Substructured Shaking Table Test Method. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000. [Google Scholar]
- Dyke, S.J.; Bursi, O.S.; Stojadinovic, B. New Frontiers and Innovative Methods for Hybrid Simulation. Exp. Tech. 2020, 44, 667–668. [Google Scholar] [CrossRef]
- Carrion, J.E.; Spencer, B.F.; Phillips, B.M. Real-Time Hybrid Simulation for Structural Control Performance Assessment. Earthq. Eng. Eng. Vib. 2009, 8, 481–492. [Google Scholar] [CrossRef]
- Memari, M.; Wang, X.; Mahmoud, H.; Kwon, O. Hybrid Simulation of Small-Scale Steel Braced Frame Subjected to Fire and Fire Following Earthquake. J. Struct. Eng. 2020, 146, 04019182. [Google Scholar] [CrossRef]
- Chen, C.; Ricles, J.M.; Hodgson, I.C.; Sause, R. Real-Time Multi-Directional Hybrid Simulation of Building Piping Systems. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Strepelias, E.; Stathas, N.; Palios, X.; Bousias, S. Hybrid Simulation Framework for Multi-Hazard Testing. Am. J. Civ. Eng. 2020, 8, 10–19. [Google Scholar] [CrossRef]
- Schellenberg, A.; Mahin, S.A.; Fenves, G.L. Advanced Implementation of Hybrid Simulation. In PEER Report 2009/104; University of California: Berkeley, CA, USA, 2009. [Google Scholar]
- Shing, P.B.; Mahin, S.A. Elimination of Spurious Higher-mode Response in Pseudo-Dynamic Tests. Earthq. Eng. Struct. Dyn. 1987, 15, 425–445. [Google Scholar] [CrossRef]
- Dermitzakis, S.N.; Mahin, S.A. Development of Substructuring Techniques for On-Line Computer Controlled Seismic Performance Testing. In UCB/EERC-85/04 Report to NSF; University of California: Berkeley, CA, USA, 1985. [Google Scholar]
- Thewalt, C.R.; Mahin, S.A. Hybrid Solution Techniques for Generalized Pseudodynamic Testing. In UCB/EERC-87/09 Report to NSF; University of California: Berkeley, CA, USA, 1987. [Google Scholar]
- Nakashima, M.; Kato, H.; Takaoka, E. Development of Real-Time Pseudo-Dynamic Testing. Earthq. Eng. Struct. Dyn. 1992, 21, 79–92. [Google Scholar] [CrossRef]
- Schneider, S.P.; Roeder, C.W. An Inelastic Substructure Technique for the Pseudo-Dynamic Test Method. Earthq. Eng. Struct. Dyn. 1994, 23, 761–775. [Google Scholar] [CrossRef]
- Thewalt, C.; Roman, M. Pseudo-Dynamic Tests. J. Struct. Eng. 1994, 120, 2768–2781. [Google Scholar] [CrossRef]
- Combescure, D.; Pegon, P. α-Operator Splitting Time Integration Technique for Pseudodynamic Testing: Error Propagation Analysis. Soil Dyn. Earthq. Eng. 1997, 16, 427–443. [Google Scholar] [CrossRef]
- Nakashima, M.; Akazawa, T.; Sakaguchi, O. Integration Method Capable to Controlling Experimental Error Growth in Substructure Pseudo Dynamic Test. J. Struct. Constr. Eng. AIJ 1993, 454, 61–71. (In Japanese) [Google Scholar]
- Magonette, G.E.; Negro, P. Verification of the Pseudodynamic Test method. Eur. Earthq. Eng. 1998, XII, 40–50. [Google Scholar]
- Saouma, V.; Sivaselvan, M.V. Hybrid Simulation: Theory, Implementation and Applications; Taylor & Francis: New York, NY, USA, 2008. [Google Scholar]
- Horiuchi, T.; Inoue, M.; Konno, T.; Namita, Y. Real-Time Hybrid Experimental System with Actuator Delay Compensation and Its Application to a Piping System with Energy Absorber. Earthq. Eng. Struct. Dyn. 1999, 28, 1121–1141. [Google Scholar] [CrossRef]
- Nakashima, M.; Masaoka, N. Real-Time on-Line Test for MDOF Systems. Earthq. Eng. Struct. Dyn. 1999, 28, 393–420. [Google Scholar] [CrossRef]
- Darby, A.P.; Blakeborough, A.; Williams, M.S. Improved Control Algorithm for Real-Time Substructure Testing. Earthq. Eng. Struct. Dyn. 2001, 30, 431–448. [Google Scholar] [CrossRef]
- Magonette, G. Development and Application of Large-Scale Continuous Pseudo-Dynamic Testing Techniques. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2001, 359, 1771–1799. [Google Scholar] [CrossRef]
- Takahashi, Y.; Fenves, G.L. Software Framework for Distributed Experimental–Computational Simulation of Structural Systems. Earthq. Eng. Struct. Dyn. 2006, 35, 267–291. [Google Scholar] [CrossRef]
- Schellenberg, A.; Kim, H.; Mahin, S.A.; Fenves, G.L. Environment Independent Implementation of a Software Framework for Fast Local and Geographically Distributed Hybrid Simulations. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Stojadinovic, B.; Mosqueda, G.; Mahin, S.A. Event-driven control system for geographically distributed hybrid simulation. J. Struct. Eng. 2006, 132, 68–77. [Google Scholar] [CrossRef]
- Reinhorn, A.M.; Sivaselvan, M.V.; Weinreber, S.; Shao, X. A Novel Approach to Dynamic Force Control. In Proceedings of the 3rd European Conference on Structural Control, 3ECSC, Vienna, Austria, 12–15 July 2004. [Google Scholar]
- Lin, Y.Z. Real-Time Hybrid Testing of an MR Damper for Response Reduction. Ph.D. Thesis, The University of Connecticut, Storrs, CT, USA, 2009. [Google Scholar]
- Kim, S.J.; Christenson, R.; Phillips, B.; Spencer, B.F. Geographically Distributed Real-Time Hybrid Simulation of MR Dampers for Seismic Seismic Hazard Mitigation. In Proceedings of the 20th Analysis & Computation Specialty Conference, Chicago, IL, USA, 29–31 March 2012; pp. 382–393. [Google Scholar]
- Phillips, B.M.; Spencer, B.F. Model-Based Feedforward-Feedback Actuator Control for Real-Time Hybrid Simulation. J. Struct. Eng. 2012, 139, 1205–1214. [Google Scholar] [CrossRef]
- Friedman, A.; Dyke, S.J.; Phillips, B.; Ahn, R.; Dong, B.; Chae, Y.; Castaneda, N.; Jiang, Z.; Cha, Y.; Ozdagli, A.I.; et al. Large-Scale Real-Time Hybrid Simulation for Evaluation of Advanced Damping System Performance. J. Struct. Eng. 2015, 141, 04014150. [Google Scholar] [CrossRef]
- Lanese, I. Development and Implementation of an Integrated Architecture for Real-Time Dynamic Hybrid Testing in the Simulation of Seismic Isolated Structures. Ph.D. Thesis, University of Pavia, Pavia, Italy, 2012. [Google Scholar]
- Kim, H.K. Development and Implementation of Advanced Control Methods for Hybrid Simulation. Ph.D. Thesis, University of California, Berkeley, CA, USA, 2011. [Google Scholar]
- Kim, S.J.; Holub, C.J.; Elnashai, A.S. Experimental Investigation of the Behavior of RC Bridge Piers Subjected to Horizontal and Vertical Earthquake Motion. Eng. Struct. 2011, 33, 2221–2235. [Google Scholar] [CrossRef]
- Yang, Y.; Tsai, K.; Elnashai, A.S.; Hsieh, T. An Online Optimization Method for Bridge Dynamic Hybrid Simulations. Simul. Model. Pract. Theory 2012, 28, 42–54. [Google Scholar] [CrossRef]
- Gao, X.; Castaneda, N.; Dyke, S. Real-Time Hybrid Simulation: From Dynamic System, Motion Control to Experimental Error. Earthq. Eng. Struct. Dyn. 2013, 42, 815–832. [Google Scholar] [CrossRef]
- Ahmadizadeh, M.; Mosqueda, G. Online Energy-Based Error Indicator for the Assessment of Numerical and Experimental Errors in a Hybrid Simulation. Eng. Struct. 2009, 31, 1987–1996. [Google Scholar] [CrossRef]
- Hessabi, R.M.; Mercan, O. Assessment Measures for Hybrid Simulation: A Discussion of Recent Developments. 2015. Available online: https://scholar.google.ca/citations?view_op=view_citation&hl=en&user=_qFhUdcAAAAJ&citation_for_view=_qFhUdcAAAAJ:bEWYMUwI8FkC (accessed on 25 May 2015).
- Carrion, J.E.; Spencer, B.F. Model-Based Strategies for Real-Time Hybrid Testing. In NSEL Report Series, Report No. NSEL-006; Department of Civil and Environmental Engineering, University of Illinois at Urbana-Champaign: Champaign, IL, USA, 2007. [Google Scholar]
- Phillips, B.M.; Takada, S.; Spencer, B.F.; Fujino, Y. Feedforward Actuator Controller Development Using the Backward-Difference Method for Real-Time Hybrid Simulation. Smart Struct. Syst. 2014, 14, 1081–1103. [Google Scholar] [CrossRef]
- Zhao, J.; French, C.; Shield, C.; Posbergh, T. Comparison of Tests of a Nonlinear Structure Using a Shake Table and the EFT Method. J. Struct. Eng. 2006, 132, 1473–1481. [Google Scholar] [CrossRef]
- Chen, C.; Ricles, J.M. Tracking Error-Based Servohydraulic Actuator Adaptive Compensation for Real-Time Hybrid Simulation. J. Struct. Eng. 2010, 136, 432–440. [Google Scholar] [CrossRef]
- Chae, Y.; Kazemibidokhti, K.; Ricles, J.M. Adaptive Time Series Compensator for Delay Compensation of Servo-Hydraulic Actuator Systems for Real-Time Hybrid Simulation. Earthq. Eng. Struct. Dyn. 2013, 42, 1697–1715. [Google Scholar] [CrossRef]
- Kolay, C.; Ricles, J.M. Development of a Family of Unconditionally Stable Explicit Direct Integration Algorithms with Controllable Numerical Energy Dissipation. Earthq. Eng. Struct. Dyn. 2014, 43, 1361–1380. [Google Scholar] [CrossRef]
- Kwon, O.S.; Nakata, N.; Park, K.S.; Elnashai, A.; Spencer, B. User Manual and Examples for UI-SIMCOR v2.6 (Multi-Site Substructure Pseudo-Dynamic Simulation Coordinator) and NEES-SAM v2.0 (Static Analysis Module for NEESgrid); University of Illinois at Urbana-Champaign: Champaign, IL, USA, 2007; Available online: https://www.ut-sim.ca (accessed on 3 March 2025).
- Kwon, O.; Nakata, N.; Elnashai, A.S.; Spencer, B.F. A Framework for Multi-Site Distributed Simulation. J. Earthq. Eng. 2005, 9, 741–753. [Google Scholar] [CrossRef]
- Fenves, G.L.; Mckenna, F.; Scott, M.; Takahashi, Y. An Object-Oriented Software Environment for Collaborative Network Simulation. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–4 August 2004. [Google Scholar]
- Schellenberg, A.; Mahin, S.A. Integration of Hybrid Simulation within the General-Purpose Computational Framework OpenSees. In Proceedings of the 8th National Conference on Earthquake Engineering, San Francisco, CA, USA, 18–22 April 2006. [Google Scholar]
- Iniewski, K.; McCrosky, C.; Minoli, D. TCP/IP Protocol Suite. In Network Infrastructure and Architecture; John Wiley: Hoboken, NJ, USA, 2008; Chapter 5. [Google Scholar]
- Forouzan, B. TCP/IP Protocol Suite, 4th ed.; McGraw-Hill: Lisbon, Portugal, 2010. [Google Scholar]
- Mercan, O.; Ricles, J.M. Experimental Studies on Real-Time Testing of Structures with Elastomeric Dampers. J. Struct. Eng. 2009, 135, 1124–1133. [Google Scholar] [CrossRef]
- Hessabi, R.M.; Mercan, O. Phase and Amplitude Error Indices for Error Quantification in Pseudo-Dynamic Testing. Earthq. Eng. Struct. Dyn. 2011, 41, 1347–1364. [Google Scholar] [CrossRef]
- Dong, B. Large-Scale Experimental, Numerical, and Design Studies of Steel MRF Structures with Nonlinear Viscous Dampers under Seismic Loading. Ph.D. Thesis, Lehigh University, Bethlehem, PA, USA, 2015. [Google Scholar]
- Yun, X.; Gardner, L. Stress-Strain Curves for Hot-Rolled Steels. J. Constr. Steel Res. 2017, 133, 36–46. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).