Abstract
New methods for real-time materials phase identification based upon focal construct tomography (FCT) have been examined. Such quantitative assessment has significant potential in sectors where in-line analysis is required, including screening within aviation security. As a recent component of work programs developing FCT, its capability for accurate, quantitative analysis has been assessed for the first time. Diffraction signatures from mixed-phase materials were acquired from an energy-dispersive FCT system running under normal operational conditions. A calibration curve was constructed from the spectra and subsequently employed to assess the composition of ‘blind’ samples. The results demonstrated that this approach was able to precisely predict the polymorphic phase composition of samples to ±5 wt%. Conclusions: The potential impact of these findings is significant and will enable applications of FCT beyond those requiring a phase identification to those necessitating quantification, such as counterfeit medicines, pharmaceutical quality assurance, aging of explosives, and cement production.
1. Introduction
X-ray diffraction (XRD) is a foundational materials analysis technique that has found utility throughout many sectors. It can quantitatively determine crystallographic phase, even when data are confounded by preferred orientation and the presence of amorphous materials [1]. For the pharmaceutical industry, polymorph discrimination is essential [2], and for electronics industries, lattice location of dopants is critical [3]. XRD has become routinely capable of providing these types of material intelligence. A further challenge that other sectors face is that of acquiring useful diffraction signatures at relatively high speeds (e.g., <5 s). For example, materials discrimination associated with aviation security requires rapid phase identification of objects within suitcases to eliminate terrorist threats [4]. Of course, the speed of data acquisition may be decreased by increasing the number of incident photons, but this usually requires high-power X-ray sources (e.g., synchrotrons), and these are prohibitively costly and impractical for in-line deployment.
Focal construct tomography (FCT) is an elegant and simple approach that enhances data collection rate using a novel incident beam geometry [5]. This mitigates against the use of high-power X-ray sources and large-area detectors by exploiting the pseudo-focusing effect that occurs naturally when a diverging, conical incident beam intersects a polycrystalline sample [6]. The method has found use in high-temperature/pressure material studies [7,8] and has also been developed commercially for stream-of-commerce aviation screening [9,10]. Traditional powder X-ray diffraction (PXRD) is performed at relatively low, monochromatic photon energies (e.g., 8 keV) with scanning detectors and data collection times of the order of minutes. The low energies result in low penetration into most materials (10 s of microns), and thus diffraction is performed in reflection modes. However, many operational requirements are not consistent with these limitations and, in contrast, require high penetration and sub-second data collection times. For example, identification of contraband within suitcases at airports demands materials identification in situ of objects within complex and random local environments at stream-of-commerce speeds (belt speeds are ~0.2 ms−1). Thus, conventional PXRD is not appropriate. FCT was developed to generate diffraction signatures using broadband photon energies typically generated at >100 kV, thus enabling penetration through suitcase-sized objects and where target substances are obscured by other materials. The principal geometric differences between conventional X-ray diffraction and FCT are illustrated within the left-hand panel of Figure 1. The use of multi-energy and unique FCT geometry results in sub-second data acquisition times. Further, FCT’s inherent multi-perspective probe provides an intrinsic tomographic capability. However, the ensuing d-spacing resolution is compromised by the geometric elements and detector energy resolution. Thus, machine learning is frequently employed to provide accurate phase analysis from the diffraction signatures. This has the additional advantage that system performance is more robust for low S/N circumstances.
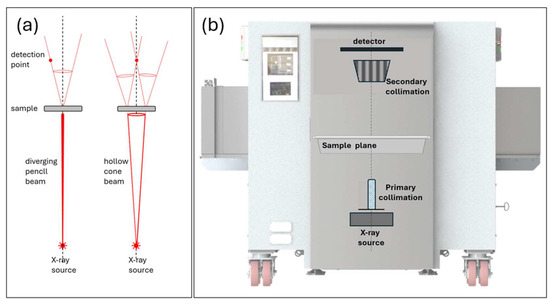
Figure 1.
Panel (a) illustrates a comparison of conventional transmission X-ray diffraction (left) and that of FCT (right) for a single set of diffraction planes. Panel (b) is the commercial HXT264 system employed for this study, with the principal system components illustrated schematically.
Within aviation security, current commercial systems based upon FCT are stand-alone assemblies but are added to primary screening devices (e.g., CT) as threat resolvers that significantly decrease the rate of false-positive alarms.
In contrast to conventional PXRD, multiple distinct diffraction maxima are not often characteristic of FCT data. Thus, FCT applications have focused upon qualitative phase determination, as quantification of mixed phases is challenging; conventional methods of quantification such as Rietveld refinement, reference intensity ratios, and external standards require well-defined, lattice-attributed diffraction maxima, frequently absent from operational FCT data. Further, other approaches such as internal standards and the addition method are inappropriate in circumstances such as those within aviation screening. The machine learning used for our FCT data analysis has, thus far, not been extended to challenge the quantitative capability of FCT.
Thus, we present initial results from a quantitative analysis study that indicate, for the first time, the precision with which FCT may quantify phase mixes. The work exploits a polymorphic biphasic system and uses conventional diffraction data from the same sample set for validation.
2. Materials and Methods
The materials used to initially assess the FCT quantification process were from the silica mineral family, as these have numerous industrial uses and it is frequently critical to assess the relative proportions of each phase. The polymorphs α-cristobalite (tetragonal, ρ = 2.65 gcm−3) and α-quartz (hexagonal, ρ = 2.3 gcm−3) were mixed in a systematic series of compositions, increasing the amount of α-quartz in 20% by weight (wt%) steps. A further pair of test samples (A and B) was also produced from admixtures of the polymorphs and unknown compositions (‘analyst-blind’). All samples were formed by compressing ~90 g of the powder mixtures into standard petri dishes (90 mm diameter, 15 mm depth).
To assess the FCT quantification capability, a commercial HXT264 system was used to collect diffraction data from all the samples. A critical comparison between conventional transmission X-ray diffraction and that of FCT for a single set of diffraction planes is illustrated in Figure 1a. Conventionally, a pencil beam illuminates a sample, and a detector is positioned to intersect a small component of the diffracted Debye cones. For FCT, the sample is illuminated with a hollow cone beam, and high-intensity diffraction maxima are formed along the principal axis.
The HXT264 system (illustrated in Figure 1b), designed for aviation screening, exploits FCT and a conveyor system for sample scanning. The incident radiation was polychromatic (200 kV), with a tube current of 2.5 mA. Data were collected in an energy-dispersive mode for 28 s.
A calibration curve was generated using a non-conventional approach that exploited the full energy range of the diffraction data; a partial least squares regression (PLSR, a multivariate regression technique to model the relationship between observed data and underlying structural variables by maximizing the covariance between them) was performed to determine the relationship between spectra and α-quartz concentration. This initially identified the minimum number of components to characterize the variance between the calibration set of spectra and enabled identification of the variance source. The components were then employed within a regression model for the α-quartz concentration.
To validate the FCT results, diffraction data from ~0.5 g of samples A and B were also collected using conventional methods (θ/θ mode), employing a Panalytical X’pert Pro diffractometer and CuKα incident radiation. Whole-pattern fitting [11] was used for quantification of the mixtures.
3. Results
Diffraction data from the FCT system have a form factor that is significantly distinct from that of a conventional diffractometer. The distinction arises from the energy-dispersive nature of data acquisition and the fundamentally different incident beam topography of the FCT system. Regardless, it was apparent by inspection that the raw FCT data were highly sensitive to discrimination between quartz and cristobalite (see Figure 2).
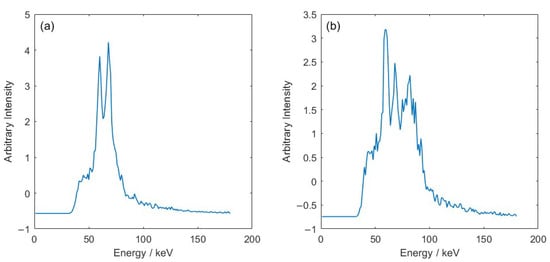
Figure 2.
Diffraction data from the FCT system: (a) 100% α-cristobalite, and (b) 100% α-quartz. Spectra have been normalised using z-score normalisation, with data centred to have a mean of 0 and scaled to have a standard deviation of 1.
As a first step in quantification, the minimum number of components to describe spectral variance was determined to be 3; the first component coefficient (shown in Figure 3) described almost 97% of the variance.
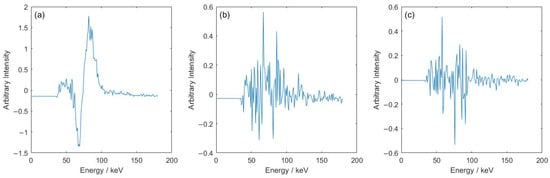
Figure 3.
The three PLSR coefficients used to provide quantitative discrimination. The first coefficient (a) describes almost 97% of the variance, while the other two components (b,c) describe the last 3%.
These coefficients reduce the dimensionality of the 180-component spectra to highlight the differences evident from the FCT diffraction data of pure quartz and pure cristobalite shown in Figure 2. The key differences are the ratios of the characteristic peak intensities (kα at 59 keV and kβ at 68 keV) and the presence of an extra peak at ~82 keV, visible in the quartz spectrum. As the amount of quartz is increased, there is an increase in the intensity of the peak at 82 keV and a decrease in the intensity of the kβ peak.
A PLSR model was then fitted using three components to produce a calibration curve. This is shown in Figure 4. The dashed line indicates ‘ideal’, linear performance, where the fitted response is equal to the observed response. The experimental data derived from the calibration series of samples are also presented, and the agreement is excellent. Further, the linear relationship was anticipated, as the polymorph densities differ by only ~13%.
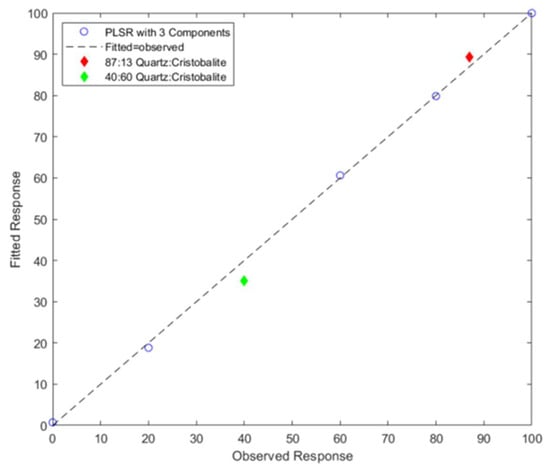
Figure 4.
Fitted vs. observed response for PLSR (points as circles). The black dashed line indicates the ideal performance, where the fitted response is equal to the observed. Red and green diamonds indicate the blinded samples.
Spectra from the analyst-blind test samples (A and B) were subsequently entered into the regression model, and the α-quartz wt% was determined. In summary, the amount of α-quartz for samples A and B was 89 wt% and 35 wt%, respectively. This compares well with the values determined by the conventional whole pattern fitting method of 87 wt% and 40 wt%.
While PLSR is a robust statistical method designed for use with high-dimensionality data, there are some potential error sources that could lead to the difference between the %wt predicted by PLSR compared to the true wt% of the blind sample. This could be due to data quality issues, including the noisiness of the spectra (evident in coefficient 2 and 3) and errors in sample preparation, such as mass measurements (measured to within +/−1 g).
4. Discussion
The work has demonstrated, for the first time, the prospect of FCT data acquisition to extend from qualitative phase identification to quantitative material composition, even in the case of polymorphs. We believe that this method is the only viable approach currently available for such analysis, especially given the potential of employing this approach for materials in obscura.
Of the many sectors that increasingly demand non-destructive, quantitative, high-speed materials evaluation for screening and quality assurance, FCT has matured mostly within aviation security, where, it may be argued, conventional methods of explosives detection (absorption X-ray imaging) have reached their discrimination limit. This sector requires data acquisition rates that are consistent with the throughput of passengers and also demands high materials specificity (not provided by X-ray absorption approaches) for the detection of threats that continue to evolve. FCT is able to meet these challenges without the requirement for divestment; when a threat object occurs within a noisy or cluttered environment, the tomographic capability of FCT enables segmentation of the object from its surroundings. It is currently employed to minimize false positive rates (FPR) of primary screening methods, such as computer tomography, with a typical FPR of ~20% [12].
More recently, development work has assessed the adoption of FCT within postal systems for the detection of opioids. The World Health Organisation reports >75,000 overdose deaths in 2022, primarily from fentanyls, in the US. Fentanyl and its analogues are potent synthetic narcotics, relatively simple to manufacture or import directly. A significant proportion of fentanyl powder and its precursors transits into the US via postal systems, and thus, technologies that are able to rapidly detect these drugs are in demand. In 2018, the “Opioid Challenge” [13], a worldwide call for technologies to detect fentanyls within postal systems, was launched. An FCT system was selected as one of the eight finalists due to its speed and materials discrimination. However, challenges remain focused upon addressing data acquisition from the high throughput of postal systems.
The worldwide problems of counterfeit medicines are well known to health organizations both in first and third world countries. The World Health Organisation estimates that >10% of medical products in low- and middle-income countries are substandard or falsified. These may contain no active pharmaceutical ingredient (API), the wrong API, the wrong amount of the correct API, or inappropriate excipients. Impacts can be significant; for example, the eradication of malaria has been significantly retarded due to falsified quinine-based pharmaceuticals. Currently, there are several techniques employed for counterfeit detection, including spectroscopy, chromatography, and mass spectrometry. However, most require sampling (thus not suitable for rapid screening), and although in-field Raman can interrogate tablets within some packaging, the approach is highly surface sensitive and is compromised by packaging and/or fluorescence from the API and/or excipient. In contrast, FCT methods would not be confounded by packaging, enabling simultaneous examination of large quantities of tablets, where, for example, the ratio of excipients (including polymorphs) within many medicines could indicate the authenticity of the medicine and may also be a key forensic marker of provenance [14]. This also includes non-crystalline components such as cellulose and starch, which produce broad scattering maxima.
Thus, overall, XRD detection systems based on FCT have high potential to fulfill the requirements of the next generation of material-specific screening across a number of sectors. Future developments will be sector- or operationally-specific; for example, requirements for smaller platforms, even greater photon energies, or improved resolution for smaller masses.
5. Conclusions
The study has shown that FCT possesses the ability to accurately quantify polycrystalline material combinations, including mixtures of polymorphs. Potential industrial applications of such a capability include explosives detection in aviation security, drug detection in postal systems, and counterfeit drug provenancing.
Author Contributions
Conceptualization, A.D., V.S. and K.R.; methodology, A.D. and L.F.; formal analysis, V.S. and D.S.; resources, S.G.; data curation, A.D.; writing—original draft preparation, K.R.; writing—review and editing, S.G., V.S. and A.D.; visualization, A.D.; project administration, S.G.; funding acquisition, S.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partly funded by the Higher Education Innovation Funding (HEIF).
Institutional Review Board Statement
The Cranfield University Ethics Review Board reviewed and approved the work herein (approval number: CURES/24133/2025) and provided authority to proceed with the program. No human or animal ethical issues were applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
We wish to acknowledge William Peck (WP) for his contribution to data collection.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analysis, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| FCT | Focal construct tomography |
| XRD | X-ray diffraction |
| PLSR | Partial least squares regression |
References
- Madsen, I.C.; Scarlett, N.V.; Kleeberg, R.; Knorr, K. Quantitative phase analysis. In International Tables for Crystallography, Volume H, Powder Diffraction, 2nd ed.; Gilmore, C.J., Kaduk, J.A., Schenk, H., Eds.; International Union of Crystallography: Chester, UK, 2019; Volume H, pp. 344–373. [Google Scholar]
- Chambi, J.T.; Fandaruff, C.; Cuffini, S.L. Identification and quantification techniques of polymorphic forms—A review. J. Pharm. Biomed. Anal. 2024, 242, 116038. [Google Scholar]
- Dolabella, S.; Borzì, A.; Dommann, A.; Neels, A. Lattice Strain and Defects Analysis in Nanostructured Semiconductor Materials and Devices by High-Resolution X-Ray Diffraction: Theoretical and Practical Aspects. Small Methods 2021, 6, e2100932. [Google Scholar] [CrossRef] [PubMed]
- Price, J.; Forrest, J. Practical Aviation Security: Predicting and Preventing Future Threats; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar]
- Rogers, K.; Evans, P.; Rogers, J.; Chan, J.; Dicken, A. Focal construct geometry—A novel approach to the acquisition of diffraction data. J. Appl. Cryst. 2010, 43, 264–268. [Google Scholar] [CrossRef]
- Evans, P.; Rogers, K.; Chan, J.; Rogers, J.; Dicken, A. High intensity x-ray diffraction in transmission mode employing an analog of Poisson’s spot. Appl. Phys. Lett. 2010, 97, 204101. [Google Scholar] [CrossRef]
- Li, F.; Liu, Z.; Sun, T. Annular beam high-intensity X-ray diffraction based on an ellipsoidal single-bounce monocapillary. J. Appl. Cryst. 2016, 49, 627–631. [Google Scholar] [CrossRef]
- Li, F.; Liu, Z.; Sun, T.; Jiang, B.; Zhu, Y. Focal construct geometry for high intensity energy dispersive x-ray diffraction based on x-ray capillary optics. J. Chem. Phys. 2016, 144, 104201. [Google Scholar] [CrossRef] [PubMed]
- Dicken, A.; Evans, J.P.; Rogers, K.D.; Prokopiou, D.; Godber, S.X.; Elarnaut, F.; Shevchuk, A.; Downes, D.; Wilson, M. Confocal energy-dispersive X-ray diffraction tomography employing a conical shell beam. Opt. Express 2019, 27, 19834–19841. [Google Scholar] [CrossRef] [PubMed]
- Spence, D.; Dicken, A.; Downes, D.; Rogers, K.; Evans, P. Conical shell illumination incorporating a moving aperture for depth-resolved high-energy X-ray diffraction. Analyst 2023, 148, 1123–1129. [Google Scholar] [CrossRef] [PubMed]
- Bish, B.L.; Post, J.E. Quantitative mineralogical analysis using the Rietveld full-pattern fitting method. Am. Mineral. 1993, 78, 932–940. [Google Scholar]
- Richmond, T.; Pike, D.; Franco, E.; Dudley, C.; Moody, R.; Lawe, A.; Peters, C.; Coccarelli, D.; Greenberg, J.A. Improved reconstruction and classification performance in a hybrid CT+XRD explosives detection system. In Anomaly Detection and Imaging with X-Rays (ADIX) IX; Proceedings of SPIE Volume 13043; SPIE: Bellingham, WA, USA, 2024. [Google Scholar] [CrossRef]
- Department of Homeland Security. [Opioid Detection Challenge]. DHS Medialibrary, 2023. Available online: https://www.dhs.gov/medialibrary/assets/videos/23098 (accessed on 20 May 2025).
- Budzianowski, A.; Pioruńska-Sędłak, K.; Popławska, M.; Maurin, J.K.; Błażewicz, A. Semiquantitative X-ray Powder Diffraction Analysis in Counterfeit Medicines Investigation—The Viagra Example. Crystals 2023, 13, 1485. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).